Точки экстремума функции. Как найти точки экстремума. Сумма точек экстремума
Важным понятием в математике является функция. С её помощью можно наглядно представить многие процессы, происходящие в природе, отразить с использованием формул, таблиц и изображений на графике взаимосвязь между определёнными величинами. Примером может служить зависимость давления слоя жидкости на тело от глубины погружения, ускорения — от действия на объект определённой силы, увеличения температуры — от передаваемой энергии и многие другие процессы. Исследование функции предполагает построение графика, выяснение её свойств, области определения и значений, промежутков возрастания и убывания. Важным моментом в данном процессе является нахождение точек экстремума. О том, как правильно это делать, и пойдёт разговор далее.

О самом понятии на конкретном примере
В медицине построение графика функции может рассказать о ходе развития болезни в организме пациента, наглядно отражая его состояние. Предположим, по оси ОХ откладывается время в сутках, а по оси ОУ — температура тела человека. На рисунке хорошо видно, как этот показатель резко поднимается, а потом падает. Нетрудно заметить также особые точки, отражающие моменты, когда функция, ранее возрастая, начинает убывать, и наоборот. Это точки экстремума, то есть критические значения (максимальные и минимальные) в данном случае температуры больного, после которых наступают изменения в его состоянии.
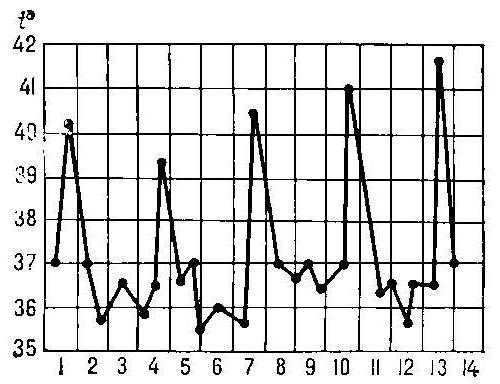
Угол наклона
Легко можно определить по рисунку, как изменяется производная функции. Если прямые линии графика с течением времени идут вверх, то она положительна. И чем они круче, тем большее значение принимает производная, так как растет угол наклона. В периоды убывания эта величина принимает отрицательные значения, в точках экстремума обращаясь в ноль, а график производной в последнем случае рисуется параллельно оси ОХ.
Любой другой процесс следует рассматривать аналогичным образом. Но лучше всего об этом понятии может рассказать перемещение различных тел, наглядно показанное на графиках.
Движение
Предположим, некоторый объект движется по прямой, равномерно набирая скорость. В этот период изменение координаты тела графически представляет собой некую кривую, которую математик назвал бы ветвью параболы. При этом функция постоянно возрастает, так как показатели координаты с каждой секундой изменяются всё быстрей. График скорости демонстрирует поведение производной, значение которой также увеличивается. А значит, движение не имеет критических точек.
Так бы и продолжалось бесконечно долго. Но если тело вдруг решит затормозить, остановиться и начать двигаться в другом направлении? В данном случае показатели координаты начнут уменьшаться. А функция перейдёт критическое значение и из возрастающей превратится в убывающую.
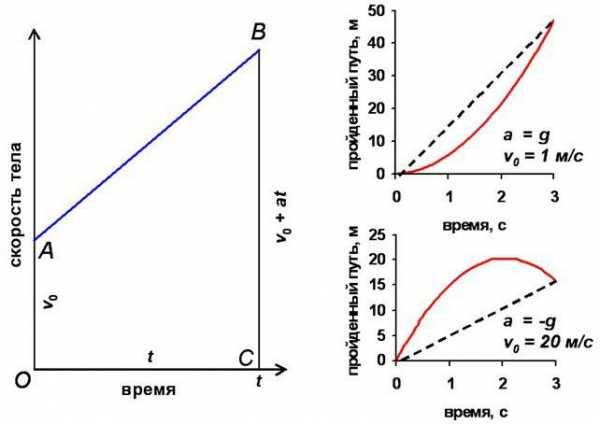
На этом примере снова можно понять, что точки экстремума на графике функции появляются в моменты, когда она перестаёт быть монотонной.
Физический смысл производной
Описанное ранее наглядно показало, что производная по сути является скоростью изменения функции. В данном уточнении и заключён её физический смысл. Точки экстремума – это критические области на графике. Их возможно выяснить и обнаружить, вычислив значение производной, которая оказывается равной нулю.
Существует и другой признак, который является достаточным условием экстремума. Производная в таких местах перегиба меняет свой знак: с «+» на «-» в области максимума и с «-» на «+» в районе минимума.

Движение под влиянием силы притяжения
Представим ещё одну ситуацию. Дети, играя в мяч, бросили его таким образом, что он начал двигаться под углом к горизонту. В начальный момент скорость данного объекта являлась самой большой, но под действием силы тяжести начала уменьшаться, причём с каждой секундой на одну и ту же величину, равную приблизительно 9,8 м/с2. Это значение ускорения, возникающего под влиянием земной гравитации при свободном падении. На Луне оно бы было примерно в шесть раз меньше.
Графиком, описывающим перемещение тела, является парабола с ветвями, направленными вниз. Как найти точки экстремума? В данном случае это вершина функции, где скорость тела (мяча) принимает нулевое значение. Производная функции становится равной нулю. При этом направление, а следовательно, и значение скорости, меняется на противоположное. Тело летит вниз с каждой секундой всё быстрее, причём ускоряется на ту же величину — 9,8 м/с2.
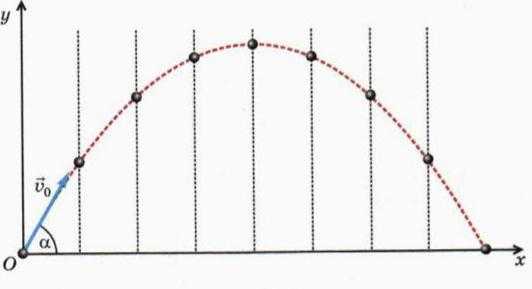
Вторая производная
В предыдущем случае график модуля скорости рисуется как прямая. Данная линия оказывается сначала направлена вниз, так как значение этой величины постоянно убывает. Достигнув нуля в один из моментов времени, далее показатели этой величины начинают возрастать, а направление графического изображения модуля скорости кардинально меняется. Теперь линия направлена вверх.
Скорость, являясь производной от координаты по времени, тоже имеет критическую точку. В этой области функция, вначале убывая, начинает возрастать. Это место точки экстремума производной функции. В данном случае угол наклона касательной становится равным нулю. А ускорение, являясь второй производной от координаты по времени, меняет знак с «-» на «+». И движение из равнозамедленного становится равноускоренным.
График ускорения
Теперь рассмотрим четыре рисунка. На каждом из них отображён график изменения с течением времени такой физической величины, как ускорение. В случае «А» значение его остаётся положительным и постоянным. Это означает, что скорость тела, как и его координата, постоянно увеличивается. Если представить, что объект будет двигаться таким образом бесконечно долго, функция, отражающая зависимость координаты от времени, окажется постоянно возрастающей. Из этого следует, что она не имеет критических областей. Точки экстремума на графике производной, то есть линейно изменяющейся скорости, также отсутствуют.
То же касается и случая «Б» с положительным и постоянно увеличивающимся ускорением. Правда, графики для координаты и скорости здесь будут несколько сложнее.
Когда ускорение стремится к нулю
Рассматривая рисунок «В», можно наблюдать совсем другую картину, характеризующую движение тела. Скорость его графически будет изображаться параболой с ветвями, направленными вниз. Если продолжить линию, описывающую изменение ускорения до пересечения её с осью ОХ, и дальше, то можно представить, что до этого критического значения, где ускорение окажется равным нулю, скорость объекта будет увеличиваться всё медленнее. Точка экстремума производной от функции координаты окажется как раз в вершине параболы, после чего тело кардинально поменяет характер движения и начнёт двигаться в другом направлении.
В последнем случае, «Г», характер движения точно определить невозможно. Здесь известно только, что ускорение за некоторый рассматриваемый период отсутствует. Значит, объект может оставаться на месте или движение происходит с постоянной скоростью.
Задача на сложение координат
Перейдём к заданиям, которые часто встречаются при изучении алгебры в школе и предлагаются для подготовки к ЕГЭ. На рисунке, который представлен ниже, изображён график функции. Требуется вычислить сумму точек экстремума.
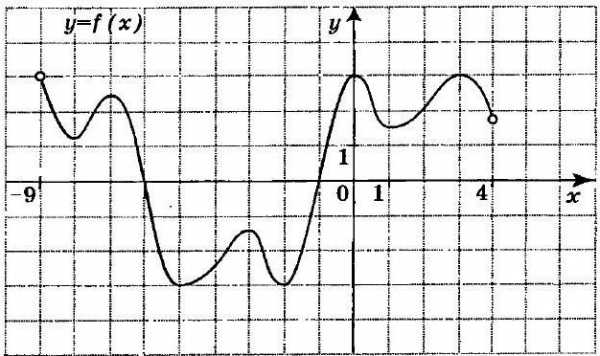
Сделаем это для оси ординат, определив координаты критических областей, где наблюдается изменение характеристик функции. Проще говоря, найдём значения по оси ОХ для точек перегиба, а затем перейдём к сложению полученных членов. По графику очевидно, что они принимают следующие значения: -8; -7 ; -5; -3; -2; 1; 3. В сумме это составляет -21, что и является ответом.
Оптимальное решение
Не стоит объяснять, насколько может оказаться важным в выполнении практических заданий выбор оптимального решения. Ведь путей достижения цели бывает много, а наилучший выход, как правило, — всего один. Это бывает крайне необходимо, к примеру, при конструировании судов, космических кораблей и самолётов, архитектурных сооружений для нахождения оптимальной формы данных рукотворных объектов.
Быстроходность средств передвижения во многом зависит от грамотного сведения к минимуму сопротивления, которое они испытывают при перемещении по воде и воздуху, от перегрузок, возникающих под действием гравитационных сил и многих других показателей. Кораблю на море необходимы такие качества, как устойчивость во время шторма, для речного судна важна минимальная осадка. При расчётах оптимальной конструкции точки экстремума на графике наглядно могут дать представление о наилучшем решении сложной проблемы. Задачи такого плана часто решаются в экономике, в хозяйственных областях, во множестве других жизненных ситуаций.
Из античной истории
Задачи на экстремум занимали даже древних мудрецов. Греческие учёные с успехом разгадали тайну площадей и объёмов путём математических вычислений. Это они первыми поняли, что на плоскости из разнообразных фигур, обладающих одним и тем же периметром, наибольшую площадь всегда имеет круг. Аналогичным образом шар наделён максимальным объёмом среди остальных предметов в пространстве с одинаковой величиной поверхности. Решению подобных задач посвятили себя такие известнейшие личности, как Архимед, Евклид, Аристотель, Аполлоний. Найти точки экстремума прекрасно удавалось Герону, который, прибегнув к расчётам, сооружал хитроумные устройства. К ним относились автоматы, перемещающиеся посредством пара, работающие по тому же принципу насосы и турбины.

Строительство Карфагена
Существует легенда, сюжет которой построен на решении одной из экстремальных задач. Результатом делового подхода, который продемонстрировала финикийская царевна, обратившаяся за помощью к мудрецам, стало строительство Карфагена. Земельный участок для этого древнего и прославленного города подарил Дидоне (так звали правительницу) вождь одного из африканских племён. Площадь надела не показалась ему вначале очень большой, так как по договору должна была покрываться воловьей шкурой. Но царевна повелела своим воинам разрезать её на тонкие полосы и составить из них ремень. Он получился настолько длинным, что охватил участок, где уместился целый город.
Истоки математического анализа
А теперь перенесёмся из античных времён в более позднюю эпоху. Интересно, что к осознанию основ математического анализа подтолкнула Кеплера в XVII веке встреча с продавцом вина. Торговец был настолько сведущ в своей профессии, что легко мог определить объём находящегося в бочке напитка, просто опуская туда железный жгут. Размышляя над подобным курьёзом, знаменитый учёный сумел решить для себя эту дилемму. Оказывается, искусные бочары тех времён наловчились изготавливать сосуды таким образом, чтобы при определённой высоте и радиусе окружности скрепляющих колец они имели максимальную вместимость.
Это стало для Кеплера поводом для дальнейших размышлений. Бочары пришли к оптимальному решению методом долгого поиска, ошибок и новых попыток, передавая свой опыт из поколения в поколение. Но Кеплер хотел ускорить процесс и научиться делать то же самое в короткий срок путём математических вычислений. Все его наработки, подхваченные коллегами, превратились в известные ныне теоремы Ферма и Ньютона — Лейбница.
Задача на нахождение максимальной площади
Представим, что мы имеем проволоку, длина которой равна 50 см. Как составить из неё прямоугольник, обладающий наибольшей площадью?
Начиная решение, следует исходить из простых и известных любому истин. Понятно, что периметр нашей фигуры будет составлять 50 см. Он же складывается из удвоенных длин обеих сторон. Это значит, что, обозначив за «Х» одну из них, другую возможно выразить как (25 – Х).
Отсюда получаем площадь, равную Х(25 – Х). Данное выражение можно представить как функцию, принимающую множество значений. Решение задачи требует найти максимальное из них, а значит, следует узнать точки экстремума.
Для этого находим первую производную и приравниваем её нулю. В результате получается простое уравнение: 25 – 2Х = 0.
Из него мы узнаём, что одна из сторон Х = 12,5.
Следовательно, другая: 25 – 12,5 = 12,5.
Получается, что решением задачи будет квадрат со стороной 12,5 см.
Как найти максимальную скорость
Рассмотрим ещё один пример. Представим, что существует тело, прямолинейное движение которого описывается уравнением S = — t3 + 9t2 – 24t – 8, где пройденное расстояние выражается в метрах, а время в секундах. Требуется найти максимальную скорость. Как это сделать? Скачала находим скорость, то есть первую производную.
Получаем уравнение: V = — 3t2 + 18t – 24. Теперь для решения задачи снова нужно найти точки экстремума. Сделать это необходимо тем же способом, что и в предыдущей задаче. Находим первую производную от скорости и приравниваем её к нулю.
Получаем: — 6t + 18 = 0. Отсюда t = 3 с. Это время, когда скорость тела принимает критическое значение. Подставляем полученное данное в уравнение скорости и получаем: V = 3 м/с.
Но как понять, что это именно максимальная скорость, ведь критическими точками функции могут быть наибольшие или наименьшие её значения? Для проверки необходимо найти вторую производную от скорости. Она выражается числом 6 со знаком минус. Это значит, что найденная точка является максимумом. А в случае положительного значения второй производной был бы минимум. Значит, найденное решение оказалось правильным.
Приведённые в качестве примера задачи являются лишь частью из тех, которые возможно решить, умея находить точки экстремума функции. На самом деле их гораздо больше. А подобные знания открывают перед человеческой цивилизацией неограниченные возможности.
fb.ru
Найти по графику сумму точек экстремума функции
Площадь круга равна 12. Найдите площадь сектора этого круга,если центральный угол сектора равен 150 градусов.Пожалуйста,помогите,дорогие**. Попроси больше объяснений; Следить ? Отметить нарушение ? Пуська98 21.04.2014. Войти чтобы добавить комментарий. Реклама.
Точки экстремума функции. Как найти точки экстремума. Сумма точек экстремума
Важным понятием в математике является функция. С её помощью можно наглядно представить многие процессы, происходящие в природе, отразить с использованием формул, таблиц и изображений на графике взаимосвязь между определёнными величинами. Примером может служить зависимость давления слоя жидкости на тело от глубины погружения, ускорения — от действия на объект определённой силы, увеличения температуры — от передаваемой энергии и многие другие процессы. Исследование функции предполагает построение графика, выяснение её свойств, области определения и значений, промежутков возрастания и убывания. Важным моментом в данном процессе является нахождение точек экстремума. О том, как правильно это делать, и пойдёт разговор далее.
О самом понятии на конкретном примере
В медицине построение графика функции может рассказать о ходе развития болезни в организме пациента, наглядно отражая его состояние. Предположим, по оси ОХ откладывается время в сутках, а по оси ОУ — температура тела человека. На рисунке хорошо видно, как этот показатель резко поднимается, а потом падает. Нетрудно заметить также особые точки, отражающие моменты, когда функция, ранее возрастая, начинает убывать, и наоборот. Это точки экстремума, то есть критические значения (максимальные и минимальные) в данном случае температуры больного, после которых наступают изменения в его состоянии.
Угол наклона
Легко можно определить по рисунку, как изменяется производная функции. Если прямые линии графика с течением времени идут вверх, то она положительна. И чем они круче, тем большее значение принимает производная, так как растет угол наклона. В периоды убывания эта величина принимает отрицательные значения, в точках экстремума обращаясь в ноль, а график производной в последнем случае рисуется параллельно оси ОХ.
Любой другой процесс следует рассматривать аналогичным образом. Но лучше всего об этом понятии может рассказать перемещение различных тел, наглядно показанное на графиках.
Предположим, некоторый объект движется по прямой, равномерно набирая скорость. В этот период изменение координаты тела графически представляет собой некую кривую, которую математик назвал бы ветвью параболы. При этом функция постоянно возрастает, так как показатели координаты с каждой секундой изменяются всё быстрей. График скорости демонстрирует поведение производной, значение которой также увеличивается. А значит, движение не имеет критических точек.
Так бы и продолжалось бесконечно долго. Но если тело вдруг решит затормозить, остановиться и начать двигаться в другом направлении? В данном случае показатели координаты начнут уменьшаться. А функция перейдёт критическое значение и из возрастающей превратится в убывающую.
На этом примере снова можно понять, что точки экстремума на графике функции появляются в моменты, когда она перестаёт быть монотонной.
Физический смысл производной
Описанное ранее наглядно показало, что производная по сути является скоростью изменения функции. В данном уточнении и заключён её физический смысл. Точки экстремума – это критические области на графике. Их возможно выяснить и обнаружить, вычислив значение производной, которая оказывается равной нулю.
Существует и другой признак, который является достаточным условием экстремума. Производная в таких местах перегиба меняет свой знак: с «+» на «-» в области максимума и с «-» на «+» в районе минимума.
Движение под влиянием силы притяжения
Представим ещё одну ситуацию. Дети, играя в мяч, бросили его таким образом, что он начал двигаться под углом к горизонту. В начальный момент скорость данного объекта являлась самой большой, но под действием силы тяжести начала уменьшаться, причём с каждой секундой на одну и ту же величину, равную приблизительно 9,8 м/с 2 . Это значение ускорения, возникающего под влиянием земной гравитации при свободном падении. На Луне оно бы было примерно в шесть раз меньше.
Графиком, описывающим перемещение тела, является парабола с ветвями, направленными вниз. Как найти точки экстремума? В данном случае это вершина функции, где скорость тела (мяча) принимает нулевое значение. Производная функции становится равной нулю. При этом направление, а следовательно, и значение скорости, меняется на противоположное. Тело летит вниз с каждой секундой всё быстрее, причём ускоряется на ту же величину — 9,8 м/с 2 .
Вторая производная
В предыдущем случае график модуля скорости рисуется как прямая. Данная линия оказывается сначала направлена вниз, так как значе
poiskvstavropole.ru
найти сумму точек экстремума функции по графику
точки экстремума на графике функции
В разделе Домашние задания на вопрос как находить на графике точку минимума и максимума,как найти экстремум и сумму точек экстремума? заранее спасибо заданный автором лучший ответ это на графике точка минимума эта та точка, ниже которой график не опускается. например у параболы (если она расположена ветвями вверх) точкка минимума — это её вершина. экстремумы находят через производную от функции. производную приравнивают к нулю и находят корни. потом эти корни наносятна числовую прямую и методом интервалов проверяют знак функции в интервале между двумя соседними точками. на положительном интервале функция возрастает, на отрицательном убывает.
Привет! Вот подборка тем с ответами на Ваш вопрос: как находить на графике точку минимума и максимума,как найти экстремум и сумму точек экстремума? заранее спасибо
Ответ от Европейский[гуру]
Точка минимума — точка, где график переходит из отрицательных значений вертикальной оси в положительные.
Все это находится по графику производной.
Ответ от Просвистать[гуру]
точки экстремума- это точки мин и максимума, то есть х
экстремум- это значения функции в точках мин и максимума, то есть f(x)=y
Ответ от Андрей Захаров[активный]
Такого типа задачи требуют от ученика умение читать график или аналитически, используя теорию найти тот или иной элемент графика функции, тут вы спросили про экстремумы, а именно о точках максимума и минимума. Если искать их на графике, то нужно придерживаться следующего правила (где функия возрастает потом резко убывает-точка, являющаяся границей этих двух изменений функции, будет точка максимума), ну и если убывает потом возрастает-минимум функции. Или с + на — макс, с-на+ мин. Эти точки называются точками экстремума. Ну а сумма этих точек-сумма всех точек максимума и минимума функции.
Ответ от 2 ответа[гуру]
Привет! Вот еще темы с нужными ответами:
Ответить на вопрос:
22oa.ru
Задачи В9. Применение производной к исследованию функции
Часть 3.
Здесь смотрите части 1, 2, 4
Продолжаем разбор Задач №8 ЕГЭ по математике.
Сегодня нам понадобится при решении задач следующая таблица, показывающая связь знака производной с характером монотонности функции.
Пожалуйста, будьте предельно внимательны в следующем. Смотрите, график ЧЕГО вам дан! Функции или ее производной
Если дан график производной, то интересовать нас будут только знаки функции и нули. Никакие «холмики» и «впадины» не интересуют нас в принципе!
Задача 1.
На рисунке изображен график функции , определенной на интервале . Определите количество целых точек, в которых производная функции отрицательна.
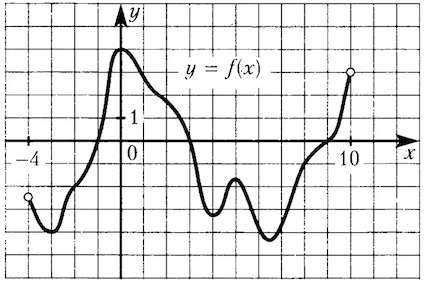
Решение: + показать
Задача 2.
На рисунке изображен график функции , определенной на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней.
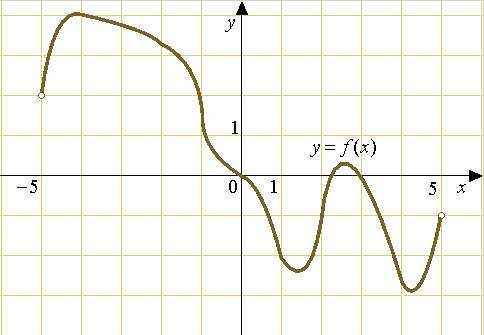
Решение:+ показать
Задача 3.
На рисунке изображен график производной функции , определенной на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней.
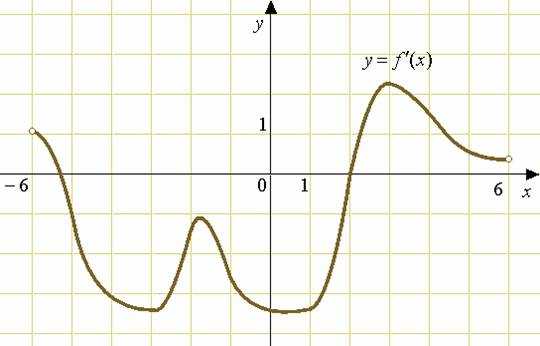
Решение: + показать
Задача 4.
На рисунке изображен график функции , определенной на интервале . Найдите количество точек, в которых производная функции равна 0.
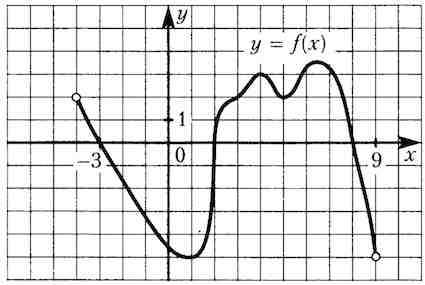
Решение: + показать
Производная равна нулю в точках экстремума. У нас их 4:
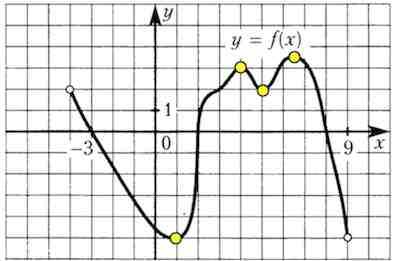
Ответ: 4.
Задача 5.
На рисунке изображён график функции и одиннадцать точек на оси абсцисс:. В скольких из этих точек производная функции отрицательна?
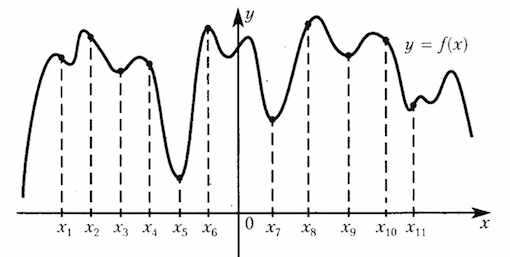
Решение: + показать
На промежутках убывания функции её производная принимает отрицательные значения. А убывает функция в точках. Таких точек 4.
Ответ: 4.
Задача 6.
На рисунке изображен график функции , определенной на интервале . Найдите сумму точек экстремума функции .
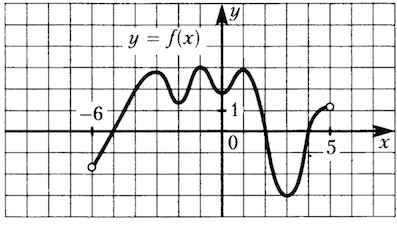
Решение: + показать
Точки экстремума – это точки максимума (-3, -1, 1) и точки минимума (-2, 0, 3).
Сумма точек экстремума: -3-1+1-2+0+3=-2.
Ответ: -2.
Задача 7.
На рисунке изображен график производной функции , определенной на интервале . Найдите промежутки возрастания функции . В ответе укажите сумму целых точек, входящих в эти промежутки.

Решение: + показать
Задача 8.
На рисунке изображен график производной функции , определенной на интервале . Найдите промежутки возрастания функции . В ответе укажите длину наибольшего из них.
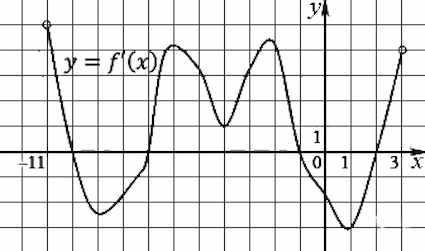
Решение: + показать
На рисунке выделены цветом все промежутки, на которых производная положительна, а значит сама функция возрастает на этих промежутках.
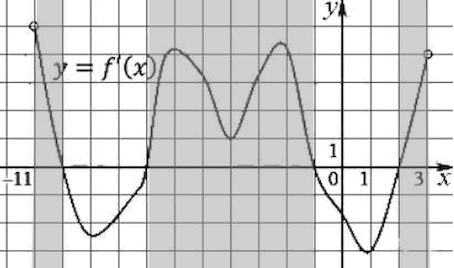
Длина наибольшего из них – 6.
Ответ: 6.
Задача 9.
На рисунке изображен график производной функции , определенной на интервале . В какой точке отрезка принимает наибольшее значение.
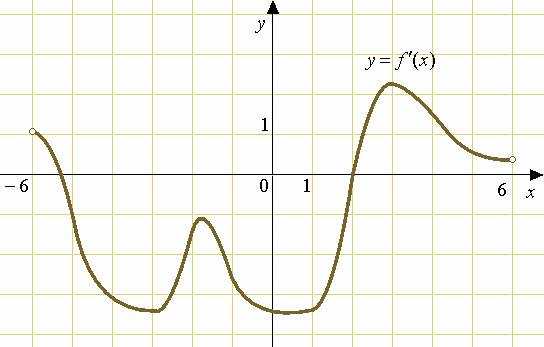
Решение: + показать
Задача 10.
На рисунке изображен график — производной функции , определенной на интервале . Найдите количество точек максимума функции , принадлежащих отрезку .
Решение: + показать
На рисунке изображен график производной, значит нас на этом рисунке будут интересовать только знаки и нули производной.
Мы видим на рисунке на указанном отрезке () три нуля у . Причем, производная мняет знак при переходе через них. Это точки экстремума функции (точки максимума и минимума).
При этом производная меняет знак с «+» на «-» в точке 8, помеченной красным цветом, и с «-» на «+» в двух точках (3 и 12), помеченных синим цветом.
Так вот при переходе через точку максимума функция меняет возрастание на убывание, а значит производная меняет знак с «+» на «-».
Итак, точка максимума одна (помечена красным цветом).
Ответ: 1.
Задача 11.
На рисунке изображен график функции и отмечены точки -3, 1, 6, 8. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
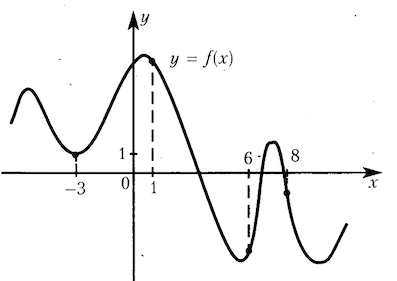
Решение: + показать
Значение производной в точке касания равно угловому коэффициенту касательной. В свою очередь, угловой коэффициент касательной равен тангенсу угла наклона данной касательной к оси .
В точке -3 (точка минимума) производная равна нулю.
В точке 6 производная положительна, так как точки лежат на промежутке возрастания функции.
А вот в точках 1 и 8 производная отрицательна.
При этом в точке 8 угол наклона касательной явно меньше, чем в точке 1.
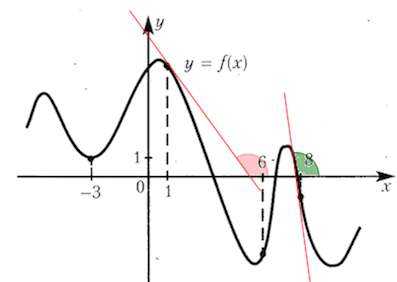
Поэтому в точке 8 тангенс угла наклона будет наименьшим, а значит и значение производной, будет наименьшее.
Ответ: 8.
🙂 Самое время немного отдохнуть. Неправда ли? –>+ показать
Вам было нелегко?..
Этим ребятам, наверное, тоже не сладко… Не сдавайтесь!

Вы можете пройти тест «Применение производной к исследованию функции»
egemaximum.ru
как находить на графике точку минимума и максимума,как найти экстремум и сумму точек экстремума? заранее спасибо
на графике точка минимума эта та точка, ниже которой график не опускается. например у параболы (если она расположена ветвями вверх) точкка минимума — это её вершина. экстремумы находят через производную от функции. производную приравнивают к нулю и находят корни. потом эти корни наносятна числовую прямую и методом интервалов проверяют знак функции в интервале между двумя соседними точками. на положительном интервале функция возрастает, на отрицательном убывает.
Точка минимума — точка, где график переходит из отрицательных значений вертикальной оси в положительные. Точка максимума — наоборот. Все это находится по графику производной.
точки экстремума- это точки мин и максимума, то есть х экстремум- это значения функции в точках мин и максимума, то есть f(x)=y
Такого типа задачи требуют от ученика умение читать график или аналитически, используя теорию найти тот или иной элемент графика функции, тут вы спросили про экстремумы, а именно о точках максимума и минимума. Если искать их на графике, то нужно придерживаться следующего правила (где функия возрастает потом резко убывает-точка, являющаяся границей этих двух изменений функции, будет точка максимума), ну и если убывает потом возрастает-минимум функции. Или с + на — макс, с-на+ мин. Эти точки называются точками экстремума. Ну а сумма этих точек-сумма всех точек максимума и минимума функции.
touch.otvet.mail.ru
сумма ординат точек экстремума
Записи с меткой «сумма ординат точек экстремума»
По вашим просьбам!
4. Найти наибольшее целое решение неравенства:
Умножим обе части неравенства на 15 — наименьший общий знаменатель данных дробей. Получаем равносильное неравенство:
3·(x-2)-5·(2x+3)>15. Раскрываем скобки: 3x-6-10x-15>15 и упрощаем:
3x-10x>15+6+15. Получаем -7x>36. Делим обе части неравенство на отрицательный коэффициент при х, поэтому знак неравенства меняем на противоположный:
x<-36/7. Выделим целую часть и покажем решения неравенства на числовой прямой.
Наибольшее целое число из заштрихованного промежутка — это число -6.
5. Определите верное решение неравенства: log2(x-4)≤3.
Представим число 3 в виде логарифма с основанием 2.
log2(x-4)≤ log223 ; отсюда log2(x-4)≤log28. Так как логарифмическая функция по основанию 2 является возрастающей на множестве всех положительных чисел, то последнее неравенство будет выполняться при условии, что х-4≤8, но в то же время: х-4>0. Из первого условия следует: х≤12, а из второго, что х>4. Общим будет значение х∈(4; 12].
7. Укажите функцию, график которой изображен на рисунке.
На рисунке мы видим параболу, которую можно задать уравнением вида: y=a(x-m)2+n, где (m; n) — координаты вершины параболы. На рисунке вершина параболы — точка (2; 1). Следовательно, m=2; n=1. А что по поводу значения коэффициента а? Смотрим на ответы: везде коэффициент перед скобкой равен единице. Ну и прекрасно — меньше забот! Получили формулу: y=(x-2)2+1.
11. Длина прямоугольного участка 120 м, а ширина составляет 75% длины. Вспахано 35% этого участка, тогда не вспахано:
По условию ширина составляет 75% от 120 метров — длины участка. Это 3/4 от длины, т.е. 120:4·3=90 метров. Площадь прямоугольного участка равна произведению длины участка на его ширину, значит, составляет 120 м·90 м= 10800 м2. Вспахано 35%, следовательно не вспахано 100%-35%=65%. Нам осталось найти 65% от 10800. Обращаем проценты в десятичную дробь: 65%=0,65 и умножаем эту дробь на 10800.
0,65·10800=7020. Отвечаем на вопрос задачи: не вспахано 7020 м2.
12. Решите уравнение:
К правой части равенства применим основное логарифмическое тождество:
Мы получили равные степени по основанию 2, следовательно, и показатели этих степеней будут равны. Получается квадратное уравнение: x2+x=2 или x2+x-2=0. По теореме Виета подбираем корни: x1=-2; x2=1.
14. Решите уравнение: sin2x-cos2x=cos(x/2).
По формуле косинуса двойного угла: cos2α=cos2α-sin2α, тогда данное равенство преобразуется к виду:
-cos2х=cos(x/2) ⇒ -cos2х-cos(x/2)=0 ⇒ cos2х+cos(x/2)=0. Сумму косинусов преобразуем в произведение, используя формулу:
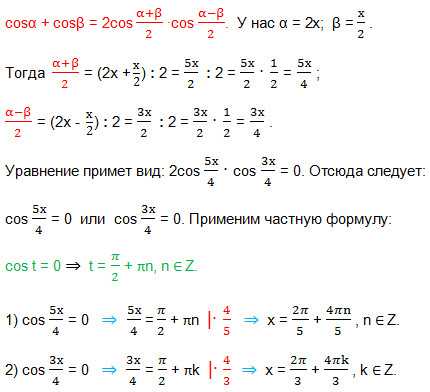
17. Найдите сумму ординат точек экстремума функции f(x)=x3/(x2-3).
Вы, конечно, знаете, что экстремумы — это минимумы и максимумы функции, возможные только в критических точках. Классическое решение этого задания: 1) найти производную данной функции; 2) найти критические точки и отметить их на числовой прямой; 3) определить знаки производной на промежутках, определенных критическими точками; 4) выяснить, какие из критических точек являются точками минимума и какие точками максимума; 5) найти значения самой функции в этих точках минимума и максимума — это и будут ординаты точек экстремума; 6) сложить эти значения ординат. Но в этом конкретном задании все гораздо проще! Функция нам дана нечетная, т.е. для всех возможных значений х выполняется равенство: f(-x)=f(x). График нечетной функции симметричен относительно начала координат. Что это значит, и чем это нам поможет? Рассуждаем: если эта функция имеет максимум в точке с абсциссой а, то в симметричной ей точке с абсциссой (-а) она будет иметь минимум. Опять же значения функции в этих точках а и -а также будут являться противоположными числами. А чему равна сумма противоположных чисел? Правильно: нулю. Вывод: если вам нужно найти сумму ординат точек экстремума нечетной функции, то ответ: 0.
21. Найдите сумму корней уравнения: x-2-16x-1-80=0.
Сделаем замену: x-1=y. Получим уравнение: y2-16y-80=0. Находим корни: y1=-4 и y2=20.
Тогда x-1=-4 или x-1=20.
22. Решить систему неравенств:
В одной системе координат построим графики функций y=sinx, y=cosx и y= 1/6. Определим промежуток значений х, при которых график синуса лежит выше, а график косинуса ниже прямой y= 1/6.
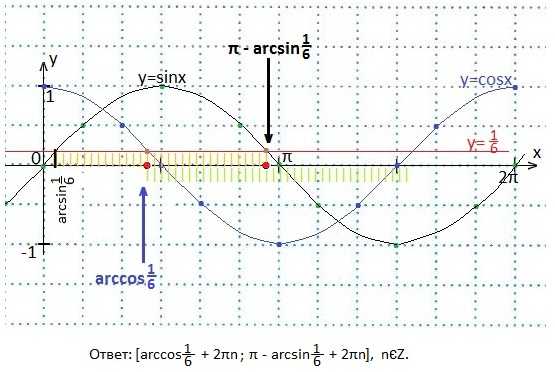
24. Найдите площадь параллелограмма ABCD, если А(5; 4), В(0; 3), С(4; 7), D(9; 8).
Площадь параллелограмма найдем по формуле: S=absinA, где a=АD и b=AB — стороны параллелограмма, А — угол между этими сторонами. Используем векторы: найдем координаты и модули векторов, выражающих стороны АD и AB параллелограмма, косинус угла между этими векторами. Затем найдем синус этого угла, и в формулу площади параллелограмма подставим все нужные значения.

25. Электронные часы показывают время в часах и минутах (от 00:00 до 23:59). Сколько раз за сутки можно увидеть на табло 4 цифры 2, 0, 1, 9 (в любом порядке). Так как нет, например 91 минуты или 29 часов, то комбинаторика нам не поможет. Просто будем перечислять все возможные в реальности показания времени.
1) 01:29; 2) 02:19; 3) 09:12; 4) 09:21; 5) 10:29; 6) 12:09; 7) 19:02; 8) 19:20; 9) 20:19; 10) 21:09. Других значений из этих 4-х цифр быть не может.
Друзья, повторяйте формулы. Желаю успехов!
test-training.ru
Точки экстремума функции. Как найти точки экстремума. Сумма точек экстремума
Образование 26 сентября 2017Важным понятием в математике является функция. С её помощью можно наглядно представить многие процессы, происходящие в природе, отразить с использованием формул, таблиц и изображений на графике взаимосвязь между определёнными величинами. Примером может служить зависимость давления слоя жидкости на тело от глубины погружения, ускорения — от действия на объект определённой силы, увеличения температуры — от передаваемой энергии и многие другие процессы. Исследование функции предполагает построение графика, выяснение её свойств, области определения и значений, промежутков возрастания и убывания. Важным моментом в данном процессе является нахождение точек экстремума. О том, как правильно это делать, и пойдёт разговор далее.

О самом понятии на конкретном примере
В медицине построение графика функции может рассказать о ходе развития болезни в организме пациента, наглядно отражая его состояние. Предположим, по оси ОХ откладывается время в сутках, а по оси ОУ — температура тела человека. На рисунке хорошо видно, как этот показатель резко поднимается, а потом падает. Нетрудно заметить также особые точки, отражающие моменты, когда функция, ранее возрастая, начинает убывать, и наоборот. Это точки экстремума, то есть критические значения (максимальные и минимальные) в данном случае температуры больного, после которых наступают изменения в его состоянии.
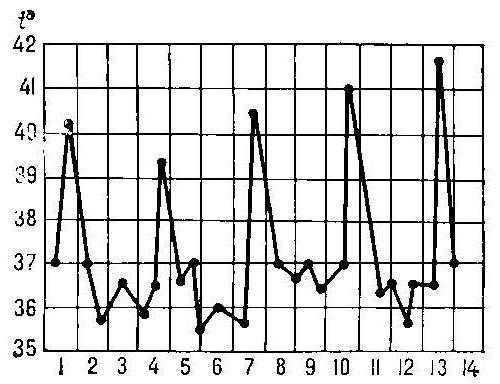
Угол наклона
Легко можно определить по рисунку, как изменяется производная функции. Если прямые линии графика с течением времени идут вверх, то она положительна. И чем они круче, тем большее значение принимает производная, так как растет угол наклона. В периоды убывания эта величина принимает отрицательные значения, в точках экстремума обращаясь в ноль, а график производной в последнем случае рисуется параллельно оси ОХ.
Любой другой процесс следует рассматривать аналогичным образом. Но лучше всего об этом понятии может рассказать перемещение различных тел, наглядно показанное на графиках.
Видео по теме
Движение
Предположим, некоторый объект движется по прямой, равномерно набирая скорость. В этот период изменение координаты тела графически представляет собой некую кривую, которую математик назвал бы ветвью параболы. При этом функция постоянно возрастает, так как показатели координаты с каждой секундой изменяются всё быстрей. График скорости демонстрирует поведение производной, значение которой также увеличивается. А значит, движение не имеет критических точек.
Так бы и продолжалось бесконечно долго. Но если тело вдруг решит затормозить, остановиться и начать двигаться в другом направлении? В данном случае показатели координаты начнут уменьшаться. А функция перейдёт критическое значение и из возрастающей превратится в убывающую.
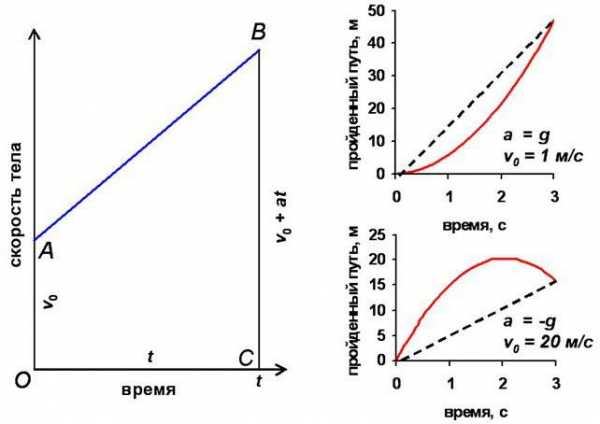
На этом примере снова можно понять, что точки экстремума на графике функции появляются в моменты, когда она перестаёт быть монотонной.
Физический смысл производной
Описанное ранее наглядно показало, что производная по сути является скоростью изменения функции. В данном уточнении и заключён её физический смысл. Точки экстремума – это критические области на графике. Их возможно выяснить и обнаружить, вычислив значение производной, которая оказывается равной нулю.
Существует и другой признак, который является достаточным условием экстремума. Производная в таких местах перегиба меняет свой знак: с «+» на «-» в области максимума и с «-» на «+» в районе минимума.

Движение под влиянием силы притяжения
Представим ещё одну ситуацию. Дети, играя в мяч, бросили его таким образом, что он начал двигаться под углом к горизонту. В начальный момент скорость данного объекта являлась самой большой, но под действием силы тяжести начала уменьшаться, причём с каждой секундой на одну и ту же величину, равную приблизительно 9,8 м/с2. Это значение ускорения, возникающего под влиянием земной гравитации при свободном падении. На Луне оно бы было примерно в шесть раз меньше.
Графиком, описывающим перемещение тела, является парабола с ветвями, направленными вниз. Как найти точки экстремума? В данном случае это вершина функции, где скорость тела (мяча) принимает нулевое значение. Производная функции становится равной нулю. При этом направление, а следовательно, и значение скорости, меняется на противоположное. Тело летит вниз с каждой секундой всё быстрее, причём ускоряется на ту же величину — 9,8 м/с2.
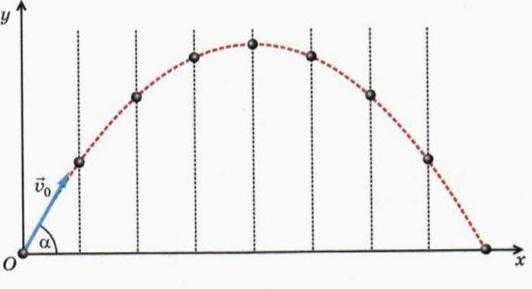
Вторая производная
В предыдущем случае график модуля скорости рисуется как прямая. Данная линия оказывается сначала направлена вниз, так как значение этой величины постоянно убывает. Достигнув нуля в один из моментов времени, далее показатели этой величины начинают возрастать, а направление графического изображения модуля скорости кардинально меняется. Теперь линия направлена вверх.
Скорость, являясь производной от координаты по времени, тоже имеет критическую точку. В этой области функция, вначале убывая, начинает возрастать. Это место точки экстремума производной функции. В данном случае угол наклона касательной становится равным нулю. А ускорение, являясь второй производной от координаты по времени, меняет знак с «-» на «+». И движение из равнозамедленного становится равноускоренным.
График ускорения
Теперь рассмотрим четыре рисунка. На каждом из них отображён график изменения с течением времени такой физической величины, как ускорение. В случае «А» значение его остаётся положительным и постоянным. Это означает, что скорость тела, как и его координата, постоянно увеличивается. Если представить, что объект будет двигаться таким образом бесконечно долго, функция, отражающая зависимость координаты от времени, окажется постоянно возрастающей. Из этого следует, что она не имеет критических областей. Точки экстремума на графике производной, то есть линейно изменяющейся скорости, также отсутствуют.
То же касается и случая «Б» с положительным и постоянно увеличивающимся ускорением. Правда, графики для координаты и скорости здесь будут несколько сложнее.
Когда ускорение стремится к нулю
Рассматривая рисунок «В», можно наблюдать совсем другую картину, характеризующую движение тела. Скорость его графически будет изображаться параболой с ветвями, направленными вниз. Если продолжить линию, описывающую изменение ускорения до пересечения её с осью ОХ, и дальше, то можно представить, что до этого критического значения, где ускорение окажется равным нулю, скорость объекта будет увеличиваться всё медленнее. Точка экстремума производной от функции координаты окажется как раз в вершине параболы, после чего тело кардинально поменяет характер движения и начнёт двигаться в другом направлении.
В последнем случае, «Г», характер движения точно определить невозможно. Здесь известно только, что ускорение за некоторый рассматриваемый период отсутствует. Значит, объект может оставаться на месте или движение происходит с постоянной скоростью.
Задача на сложение координат
Перейдём к заданиям, которые часто встречаются при изучении алгебры в школе и предлагаются для подготовки к ЕГЭ. На рисунке, который представлен ниже, изображён график функции. Требуется вычислить сумму точек экстремума.
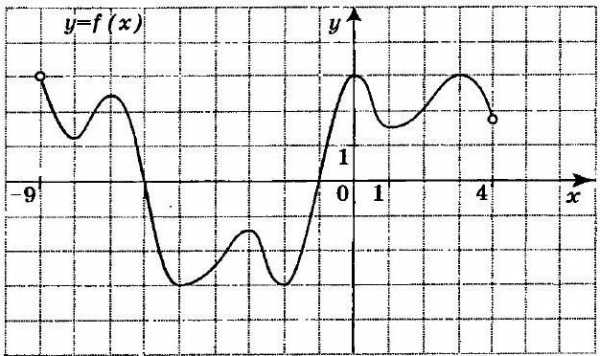
Сделаем это для оси ординат, определив координаты критических областей, где наблюдается изменение характеристик функции. Проще говоря, найдём значения по оси ОХ для точек перегиба, а затем перейдём к сложению полученных членов. По графику очевидно, что они принимают следующие значения: -8; -7 ; -5; -3; -2; 1; 3. В сумме это составляет -21, что и является ответом.
Оптимальное решение
Не стоит объяснять, насколько может оказаться важным в выполнении практических заданий выбор оптимального решения. Ведь путей достижения цели бывает много, а наилучший выход, как правило, — всего один. Это бывает крайне необходимо, к примеру, при конструировании судов, космических кораблей и самолётов, архитектурных сооружений для нахождения оптимальной формы данных рукотворных объектов.
Быстроходность средств передвижения во многом зависит от грамотного сведения к минимуму сопротивления, которое они испытывают при перемещении по воде и воздуху, от перегрузок, возникающих под действием гравитационных сил и многих других показателей. Кораблю на море необходимы такие качества, как устойчивость во время шторма, для речного судна важна минимальная осадка. При расчётах оптимальной конструкции точки экстремума на графике наглядно могут дать представление о наилучшем решении сложной проблемы. Задачи такого плана часто решаются в экономике, в хозяйственных областях, во множестве других жизненных ситуаций.
Из античной истории
Задачи на экстремум занимали даже древних мудрецов. Греческие учёные с успехом разгадали тайну площадей и объёмов путём математических вычислений. Это они первыми поняли, что на плоскости из разнообразных фигур, обладающих одним и тем же периметром, наибольшую площадь всегда имеет круг. Аналогичным образом шар наделён максимальным объёмом среди остальных предметов в пространстве с одинаковой величиной поверхности. Решению подобных задач посвятили себя такие известнейшие личности, как Архимед, Евклид, Аристотель, Аполлоний. Найти точки экстремума прекрасно удавалось Герону, который, прибегнув к расчётам, сооружал хитроумные устройства. К ним относились автоматы, перемещающиеся посредством пара, работающие по тому же принципу насосы и турбины.

Строительство Карфагена
Существует легенда, сюжет которой построен на решении одной из экстремальных задач. Результатом делового подхода, который продемонстрировала финикийская царевна, обратившаяся за помощью к мудрецам, стало строительство Карфагена. Земельный участок для этого древнего и прославленного города подарил Дидоне (так звали правительницу) вождь одного из африканских племён. Площадь надела не показалась ему вначале очень большой, так как по договору должна была покрываться воловьей шкурой. Но царевна повелела своим воинам разрезать её на тонкие полосы и составить из них ремень. Он получился настолько длинным, что охватил участок, где уместился целый город.
Истоки математического анализа
А теперь перенесёмся из античных времён в более позднюю эпоху. Интересно, что к осознанию основ математического анализа подтолкнула Кеплера в XVII веке встреча с продавцом вина. Торговец был настолько сведущ в своей профессии, что легко мог определить объём находящегося в бочке напитка, просто опуская туда железный жгут. Размышляя над подобным курьёзом, знаменитый учёный сумел решить для себя эту дилемму. Оказывается, искусные бочары тех времён наловчились изготавливать сосуды таким образом, чтобы при определённой высоте и радиусе окружности скрепляющих колец они имели максимальную вместимость.
Это стало для Кеплера поводом для дальнейших размышлений. Бочары пришли к оптимальному решению методом долгого поиска, ошибок и новых попыток, передавая свой опыт из поколения в поколение. Но Кеплер хотел ускорить процесс и научиться делать то же самое в короткий срок путём математических вычислений. Все его наработки, подхваченные коллегами, превратились в известные ныне теоремы Ферма и Ньютона — Лейбница.
Задача на нахождение максимальной площади
Представим, что мы имеем проволоку, длина которой равна 50 см. Как составить из неё прямоугольник, обладающий наибольшей площадью?
Начиная решение, следует исходить из простых и известных любому истин. Понятно, что периметр нашей фигуры будет составлять 50 см. Он же складывается из удвоенных длин обеих сторон. Это значит, что, обозначив за «Х» одну из них, другую возможно выразить как (25 – Х).
Отсюда получаем площадь, равную Х(25 – Х). Данное выражение можно представить как функцию, принимающую множество значений. Решение задачи требует найти максимальное из них, а значит, следует узнать точки экстремума.
Для этого находим первую производную и приравниваем её нулю. В результате получается простое уравнение: 25 – 2Х = 0.
Из него мы узнаём, что одна из сторон Х = 12,5.
Следовательно, другая: 25 – 12,5 = 12,5.
Получается, что решением задачи будет квадрат со стороной 12,5 см.
Как найти максимальную скорость
Рассмотрим ещё один пример. Представим, что существует тело, прямолинейное движение которого описывается уравнением S = — t3 + 9t2 – 24t – 8, где пройденное расстояние выражается в метрах, а время в секундах. Требуется найти максимальную скорость. Как это сделать? Скачала находим скорость, то есть первую производную.
Получаем уравнение: V = — 3t2 + 18t – 24. Теперь для решения задачи снова нужно найти точки экстремума. Сделать это необходимо тем же способом, что и в предыдущей задаче. Находим первую производную от скорости и приравниваем её к нулю.
Получаем: — 6t + 18 = 0. Отсюда t = 3 с. Это время, когда скорость тела принимает критическое значение. Подставляем полученное данное в уравнение скорости и получаем: V = 3 м/с.
Но как понять, что это именно максимальная скорость, ведь критическими точками функции могут быть наибольшие или наименьшие её значения? Для проверки необходимо найти вторую производную от скорости. Она выражается числом 6 со знаком минус. Это значит, что найденная точка является максимумом. А в случае положительного значения второй производной был бы минимум. Значит, найденное решение оказалось правильным.
Приведённые в качестве примера задачи являются лишь частью из тех, которые возможно решить, умея находить точки экстремума функции. На самом деле их гораздо больше. А подобные знания открывают перед человеческой цивилизацией неограниченные возможности.
Источник: fb.rumonateka.com

Leave A Comment