Куб. Формулы, признаки и свойства

Навигация по странице: Определение куба Грань куба Ребро куба Вершина куба Центр грани куба Центр куба Ось куба Диагональ куба Диагональ грани куба Объём куба Площадь поверхности куба Периметр куба Сфера вписана в куб Сфера описана вокруг куба Свойства куба Координати вершин куба Единичный куб Пересечение единичного куба плоскостью

Определение.

Куб (гексаедр) — это трехмерная фигура, которая состоит из шести динаковых квадратов так, что каждый квадрат полностью соприкасается своими четырьмя сторонами к сторонам остальных четырех квадратов под прямым углом. Куб является правильным многогранником, у которого грани образованы из квадратов. Также кубом можно назвать прямоугольный параллелепипед, у которого все ребра равны.


Определение. Грань куба — это часть плоскости, ограниченная сторонами квадрата.

— куб имеет шесть граней;

— каждая грань куба пересекается с четырьмя другими гранями под прямым углом и параллельная шестой грани;

— грани имеют одинаковую площадь, которую можно найти, используя формулы для вычисления площади квадрата.

Определение. Ребро куба — это отрезок, образованный пересечением двух граней куба.

— куб имеет двенадцать ребер;

— каждый конец ребра соединен с двумя соседними ребрами под прямым углом;

— ребра куба имеют одинаковую длину.

Определение. Вершина куба — это самая отдаленная от центра куба точка, которая лежит на пересечения трех граней куба.

— куб имеет восемь вершин;

— каждая вершина образована только тремя гранями и тремя ребрами.

Определение. Центр грани куба (O1) — это равноудалена точка от всех ребер грани куба.

Определение. Центр куба (O) — это равноудалена точка от всех граней куба.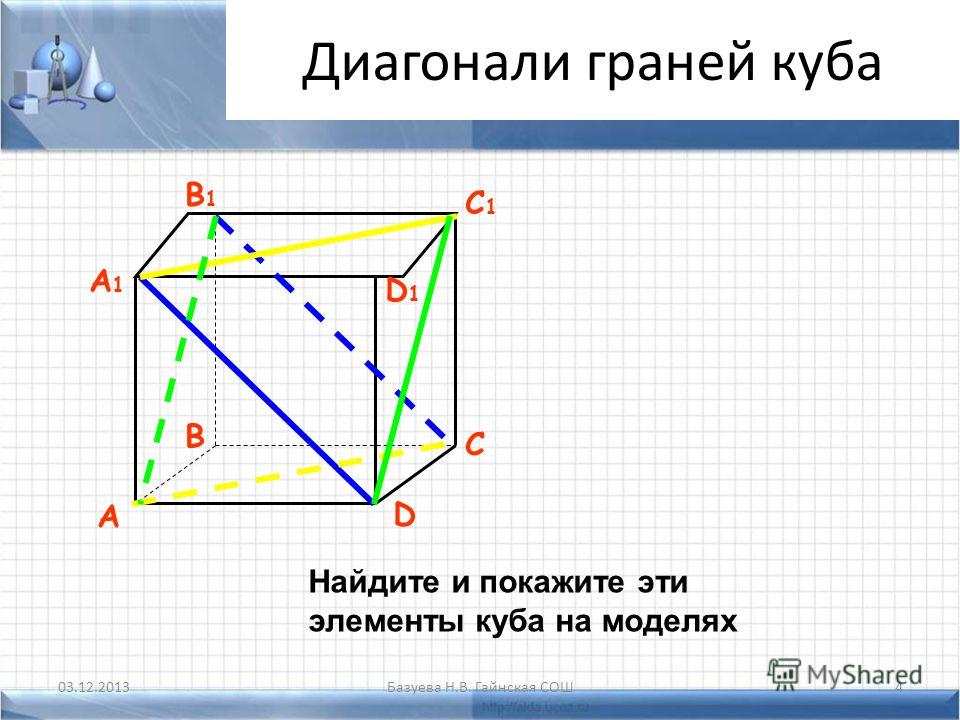

Определение. Ось куба (i) — это прямая, проходящая через центр куба и центры двух параллельных граней куба.

— куб имеет три оси;

— оси куба взаимно перпендикулярны.

Определение.

Диагональ куба (d1) — отрезок, который соединяет противоположные вершины куба и проходит через центр куба.

— куб имеет четыре диагонали;

— диагонали куба пересекаются и делятся пополам в центре куба;

— диагонали куба имеют одинаковую длину.

Формула. Диагональ куба d1 через длину ребра a:

d1 = a√3

Определение. Диагональ грани куба (d2) -отрезок, который соединяет противоположные углы грани куба и проходит через центр грани куба.

Формула. Диагональ грани d2 через длину ребра a:

d2 = a√2

Определение. Объём куба — это совокупность всех точек в пространстве, ограниченные гранями куба.

Формула. Объём куба через длину ребра a:

V = a3

Формула. Объём куба через длину диагонали куба d1:

V = d13
3√3

Определение. Площадь поверхности куба — это совокупность плоскостей всех граней.

Формула. Площадь поверхности куба через длину ребра a:

S = 6a2

Определение. Периметр куба — это совокупность длин всех ребер куба.

Формула. Периметр куба P через длину ребра a:

P = 12a

Определение. Сферой вписанной в куб называется сфера, центр которой совпадает с центром куба и которая касается центров граней куба.

— все шесть граней куба являются касательными плоскостями к вписанной сферы;

— радиус вписанной сферы равен половине длины ребра a.

Формула. Радиус вписанной сферы r через длину ребра a:

r = a
2

Формула. Объема вписанной сферы V через длину ребра a:

V = π a3
6

Определение. Сферой описанной вокруг куба называется сфера, центр которой совпадает с центром куба и которая соприкасается с восьмью вершинами куба.

— радиус описанной сферы равен половине длины диагонали (d1) куба.

Формула. Радиус описанной сферы R через длину ребра a:

R = 		a√3
2

Формула. Объема сферы описанной вокруг куба V через длину ребра a:

V = π a3√3
2

Свойства куба

1.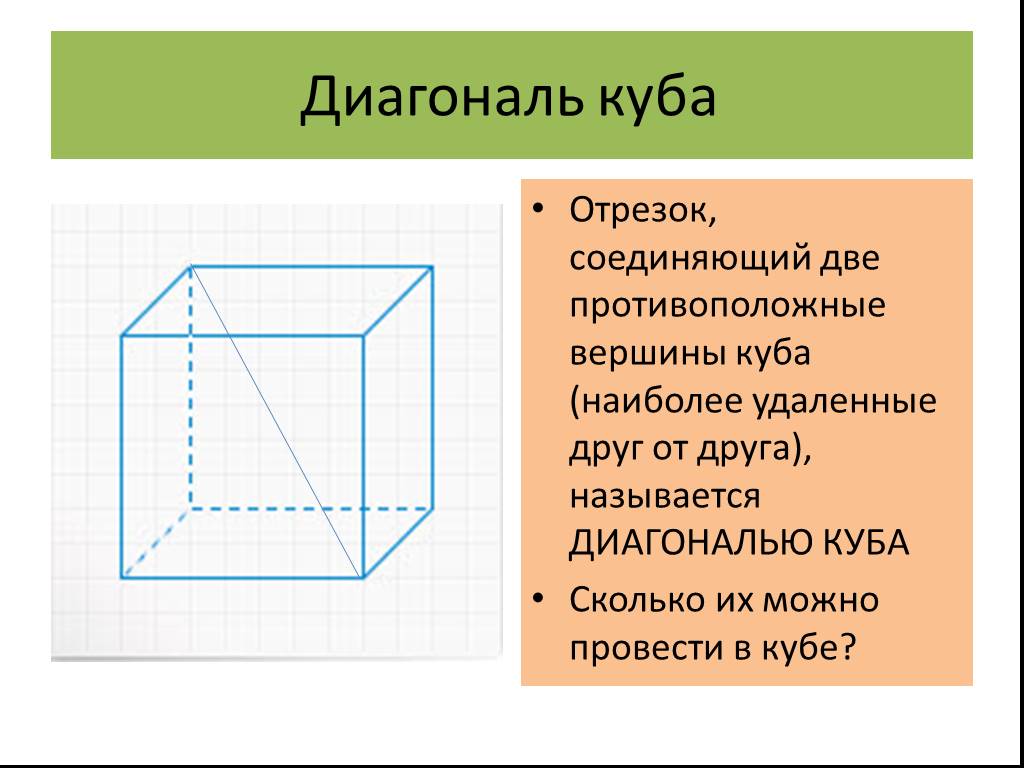 В куб можно вписать тетраэдр так, чтобы все четыре вершины тетраэдра лежали на четырех вершинах куба, а все шесть ребер тетраэдра будут лежать на шести гранях куба и ребра будут равны диагонали грани куба.

2. В куб можно вписать правильный шестиугольник так, что все шесть вершин лежат в центрах граней куба.

Координаты вершин куба

1. Координаты вершин куба со стороной a и вершиной D в начале декартовой системы координат так, что ребра этой вершины лежат на осях координат:

A(a, 0, 0), B(a, a, 0), C(0, a, 0), D(0, 0, 0),
E(a, 0, a), F(a, a, a), G(0, a, a), H(0, 0, a).

2. Координаты вершин куба с длиной стороны 2a, у которого центр куба находится в начале декартовой системы координат так, что ребра куба параллельны осям координат:

A(a, -a, -a), B(a, a, -a), C(-a, a, -a), D(-a, -a, -a),
E(a, -a, a), F(a, a, a), G(-a, a, a), H(-a, -a, a).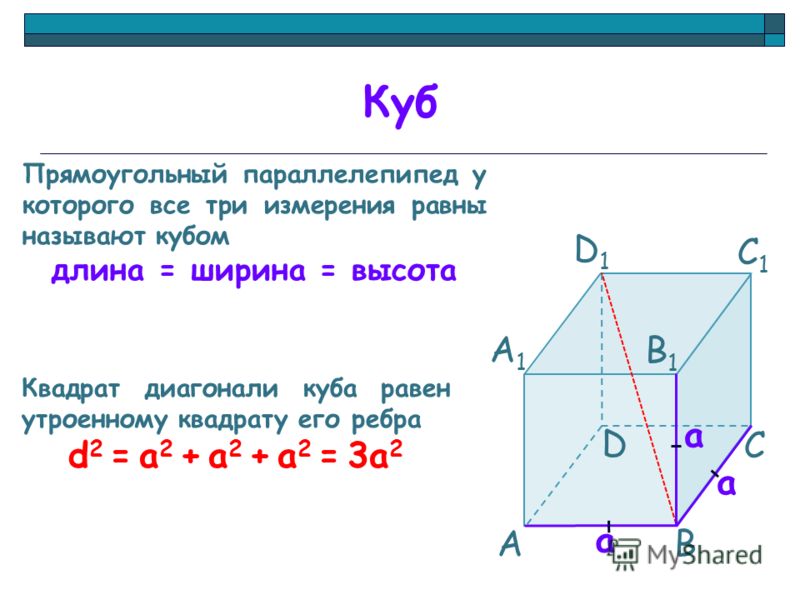

Определение. Единичный куб — это куб, у которого длина ребер равна единице.

Пересечение куба плоскостью

1. Если пересечь куб плоскостью, проходящей через центр куба и центры двух противоположных граней, то в сечении будет квадрат, длина стороны которого будет равна длине ребра куба. Эта плоскость делит куб два равных прямоугольных параллелепипеда.

2. Если пересечь куб с ребром a плоскостью, проходящей через центр куба и два параллельных ребра, то в сечении будет прямоугольник со сторонами a и a√2, площадью сечения a

2√2. Эта плоскость делит куб две равные призмы.

3. Если пересечь куб плоскостью, проходящей через центр и середины шести граней, то в сечении будет правильный шестиугольник со стороной a√2/2, площадью сечения a2(3√3)/4. У куба одна из диагоналей (FC) каждой грани, что пересекаются, перпендикулярна стороне шестиугольника.

4. Если пересечь куб плоскостью, проходящей через три вершины куба, то в сечении будет правильный треугольник со стороной a√2, площадью сечения a

2√3/2 и объемом большей части — 5a3/6 и меньшей — a3/6. Одна из диагоналей куба (EC) перпендикулярна к плоскости сечения и проходит через центр треугольника (M) и делится плоскостью в отношении MC:EМ = 2:1.


Все таблицы и формулы

Что такое диагональ куба, и как ее найти

Что такое куб, и какие диагонали он имеет

Куб (правильный многогранник или гексаэдр) представляет собой объемную фигуру, каждая грань – это квадрат, у которого, как нам известно, все стороны равны. Диагональю куба является отрезок, который проходит через центр фигуры и соединяет симметричные вершины. В правильном гексаэдре имеется 4 диагонали, и все они будут равны. Очень важно не путать диагональ самой фигуры с диагональю ее грани или квадрата, который лежит на его основании. Диагональ грани куба проходит через центр грани и соединяет противоположные вершины квадрата.

Формула, по которой можно найти диагональ куба

Диагональ правильного многогранника можно найти по очень простой формуле, которую необходимо запомнить. D=a√3, где D обозначаем диагональ куба, а – это ребро. Приведем пример задачи, где необходимо найти диагональ, если известно, что длина его ребра равна 2 см. Здесь все просто D = 2√3, даже считать ничего не надо. Во втором примере, пусть ребро куба будет равно √3 см, то тогда получаем D = √3√3=√9=3. Ответ: D равен 3 см.

Формула, по которой можно найти диагональ грани куба

Диаго

наль грани можно также найти по формуле. Диагоналей, которые лежат на гранях, всего 12 штук, и они все равны между собой. Теперь запоминаем d=a√2, где d – это диагональ квадрата, а – это также ребро куба или сторона квадрата. Понять откуда взялась эта формула, очень просто. Ведь две стороны квадрата и диагональ образуют прямоугольный треугольник. В этом трио диагональ играет роль гипотенузы, а стороны квадрата — это катеты, которые имеют одинаковую длину. Вспомним теорему Пифагора, и все тут же встанет на свои места. Теперь задача: ребро гексаэдра равняется √8 см, необходимо найти диагональ его грани. Вставляем в формулу, и у нас получается d=√8 √2=√16=4. Ответ: диагональ грани куба равняется 4 см.

Если известна диагональ грани куба

По условию задачи, нам дана только диагональ грани правильного многогранника, которая равна, предположим, √2 см, а нам необходимо найти диагональ куба. Формула решения этой задачи немного сложнее предыдущей. Если нам известно d, то мы можем найти ребро куба, исходя из нашей второй формулы d=a√2. Получаем а= d/√2= √2/√2=1см (это наше ребро). А если известна эта величина, то найти диагональ куба не составит труда: D = 1√3= √3. Вот так мы решили нашу задачку.

Если известна площадь поверхности

Следующий алгоритм решения строится на нахождении диагонали по площади поверхности куба.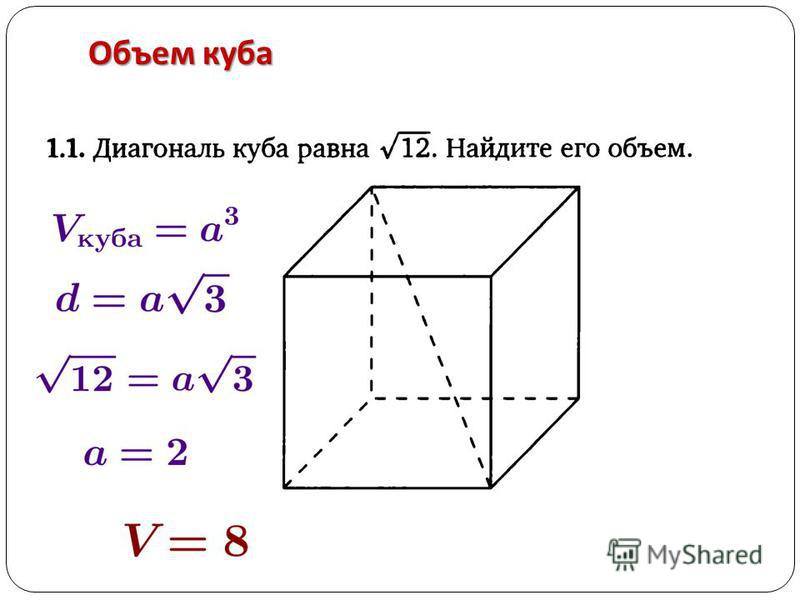 Предположим, что она равна 72 см2. Для начала найдем площадь одной грани, а всего их 6. Значит, 72 необходимо поделить на 6, получаем 12 см2. Это площадь одной грани. Чтобы найти ребро правильного многогранника, необходимо вспомнить формулу S=a2, значит a=√S. Подставляем и получаем a=√12 (ребро куба). А если мы знаем это значение, то и диагональ найти не сложно D= a√3= √12 √3 = √36 = 6. Ответ: диагональ куба равна 6 см2.

Если известна длина ребер куба

Бывают такие случаи, когда в задаче дана только длина всех ребер куба. Тогда необходимо это значение разделить на 12. Именно столько сторон в правильном многограннике. Например, если сумма всех ребер равна 40, то одна сторона будет равна 40/12=3,333. Вставляем в нашу первую формулу и получаем ответ!

Диагональ куба Формула

Диагональ формулы куба помогает в вычислении длин различных диагоналей куба — диагоналей грани и диагоналей тела. Куб — это трехмерная объемная фигура, также известная как квадратное тело, все грани которой имеют одинаковую меру. Это означает, что длина, ширина и высота куба равновелики, а каждая его грань — квадрат. Давайте узнаем больше о диагонали куба и диагонали куба формулы для измерения длин диагоналей лица и диагоналей тела на примерах.

Что такое диагональ куба?

Диагональ куба — это отрезок, соединяющий любые две несмежные вершины куба. Куб — одна из важных геометрических фигур, потому что эта трехмерная форма имеет все 12 равных граней, и это одна из наиболее часто встречающихся фигур вокруг нас. Некоторыми из реальных примеров куба являются кубики льда, кубики сахара, кубики Рубика, игральные кости и т. д. В кубе есть два вида диагоналей, потому что это трехмерная фигура.

Диагональ грани куба

Куб имеет 6 квадратных граней. На каждой грани есть две диагонали, соединяющие несмежные вершины. Следовательно, у куба 12 диагоналей граней.

Диагональ тела куба

Диагонали тела соединяют противоположные вершины куба, проходящие через тело куба. Следовательно, в кубе есть 4 диагонали тела, которые проходят через куб, соединяющий противоположные углы.

Формула диагонали куба

Длину диагоналей куба можно рассчитать по заданным параметрам и требованиям.

Длина диагонали грани куба

Формула, используемая для расчета длины диагонали грани куба, выражается следующим образом:

Длина каждой диагонали грани куба = √2a , где a = длина каждой стороны куба.

Пример: Найдите длину диагонали грани куба, если длина его стороны равна 6 см.

Решение:

Дано, длина стороны куба (а) = 6 см, Диагональ грани = ?

Длина каждой диагонали грани куба = √2a

Итак, подставим данное значение в формулу.

Длина каждой диагонали грани куба = √2a

⇒ √2a ⇒√2 × 6 = 8,48 см

Следовательно, длина диагонали грани равна 8,48 см

Длина диагонали тела куба формула, которая используется для расчета длины диагонали пространства или тела куба, задается как

Длина каждой диагонали тела куба = √3a , где a = длина каждой стороны куба.

Пример: Найдите длину диагонали тела куба, если длина его стороны 7 дюймов.

Решение:

Дана длина стороны куба (а) = 7 дюймов, диагональ тела = ?

Длина каждой диагонали тела куба = √3a

Итак, подставим данное значение в формулу.

Длина каждой диагонали тела куба = √3a

⇒ √3a ⇒√3 × 7 = 12,12 дюйма.

Следовательно, длина диагонали тела равна 12,12 дюйма.

Вывод формулы диагонали куба

Диагональ формулы куба обычно относится к диагонали тела куба. Эту формулу можно вывести, используя теорему Пифагора.

Обозначим сторону куба как ‘a’, диагональ грани как r и диагональ тела как d. Как только мы соединим диагональ лица и диагональ тела, мы увидим, что образуется прямоугольный треугольник со сторонами a, r и d. Диагональ тела становится гипотенузой образующегося прямоугольного треугольника.

Используя теорему Пифагора, мы имеем 2 + r 2 = d 2 (давайте сохраним это как уравнение 1)

Мы уже знаем, что диагональ грани равна √2a, поэтому ‘ r’ можно заменить на √2a, это означает, что ‘r’ = √2a

Подставляя значение r в уравнение 1, мы получаем

a 2 + (√2a) 2 = d 2

а 2 + 2а 2 = д 2

3а 2 = d 2

d = √(3a 2 )

d = √3a

Следовательно, формула диагонали куба = √3a

9003 разбивает простые визуальные концепции.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.

Запишитесь на бесплатный пробный урок

Примеры с использованием формулы вычисления диагонали куба

Пример 1. Вычислите длину диагонали куба, каждая сторона которого равна 5 единицам.

Решение:

Дана длина каждой стороны куба (а) = 5 единиц; диагональ тела = ?

Итак, подставим данные значения в формулу

Длина диагонали тела куба = √3a

= √3 × 5 = 8,66 единиц

Следовательно, длина диагонали тела данного куба = 8,66 ед.

Пример 2: Длина диагонали куба равна 8√3 единиц. Найдите длину каждой стороны куба.

Решение:

Дано, диагональ тела = 8√3 единиц; длина каждой стороны куба (а) = ?

Мы знаем, что формула диагонали тела куба выражается как

Длина диагонали тела куба = √3a

Итак, давайте подставим данные значения в формулу, чтобы получить неизвестное значение,

Длина диагонали тела куба = √3a

⇒ 8√3 = √3a

⇒ a = 8

Следовательно, длина каждой стороны данного куба = 8 единиц

Пример 3.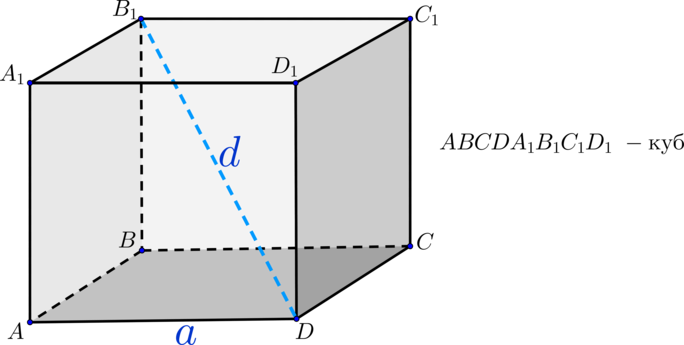 Найдите длину диагонали грани куба, если сторона куба равна 6 единицам. Используйте формулу диагонали грани куба.

Решение:

Дана длина каждой стороны куба (а) = 6 единиц, диагональ грани = ? Используя формулу диагонали грани куба,

Длина каждой диагонали грани куба = √2a

⇒ √2 × 6 = 8,49 единицы

Следовательно, длина диагонали грани куба составляет 8,49 единицы.

Часто задаваемые вопросы о формуле диагонали куба

Что такое диагональ куба?

Диагональ куба — это отрезок, соединяющий любые две его несмежные вершины. Поскольку куб представляет собой трехмерную форму (3D-форму), он имеет два вида диагоналей — диагонали грани и диагонали тела. Диагональ грани — это диагональ, образованная 6 гранями куба. А так как на каждой грани можно образовать две диагонали, значит в кубе 12 диагоналей граней. Если говорить о диагоналях тела, то мы знаем, что оно пересекает центр куба, а значит, в кубе можно составить 4 диагонали тела.

Что такое Диагональ формулы куба?

Диагональ куба Формула помогает в измерении диагоналей куба. Так как куб имеет два вида диагоналей, есть 2 разные формулы для вычисления их значения.

  • Диагональ грани куба формула = √2a; где а = длина каждой стороны куба.
  • Диагональ тела формулы куба = √3a; где а = длина каждой стороны куба.

По какой формуле найти диагональ грани куба?

Формула для расчета длины диагонали грани куба выражается следующим образом: Длина каждой диагонали грани куба = √2a, где a = длина каждой стороны куба

Какая формула для вычисления диагонали куба куб?

Формула для расчета длины диагонали тела или главной диагонали куба задается следующим образом: Длина диагонали тела куба = √3a, где a = длина каждой стороны куба

Используя диагональ Формула куба, Найдите длину диагонали со стороной, равной 8 единицам.

Длину диагонали тела куба можно рассчитать по формуле диагональ тела куба = √3a. Здесь «а» = 8. Итак, после подстановки значения «а» = 8 в формулу мы получаем, Диагональ тела = √3 × 8 = 13,86 единиц. Следовательно, длина диагонали данного куба = 13,86 ед.

Какова диагональ тела куба?

Поскольку куб является трехмерной фигурой, в кубе 4 диагонали тела. Диагональ тела также известна как «диагональ пространства» или «диагональ тела» куба. Диагонали тела соединяют противоположные вершины куба, проходящие через тело куба. Следовательно, в кубе есть 4 диагонали тела, которые проходят через куб, соединяющий противоположные углы.

Как найти диагональ куба

  • Войти
  • Биографии репетитора
  • Подготовка к тесту
    СРЕДНЯЯ ШКОЛА
    • ACT Репетиторство
    • SAT Репетиторство
    • Репетиторство PSAT
    • ASPIRE Репетиторство
    • ШСАТ Репетиторство
    • Репетиторство STAAR
    ВЫСШАЯ ШКОЛА
    • Репетиторство MCAT
    • Репетиторство GRE
    • Репетиторство по LSAT
    • Репетиторство по GMAT
    К-8
    • Репетиторство AIMS
    • Репетиторство по HSPT
    • Репетиторство ISEE
    • Репетиторство по ИСАТ
    • Репетиторство по SSAT
    • Репетиторство STAAR
    Поиск 50+ тестов
  • Академическое обучение
    репетиторство по математике
    • Алгебра
    • Исчисление
    • Элементарная математика
    • Геометрия
    • Предварительное исчисление
    • Статистика
    • Тригонометрия
    репетиторство по естественным наукам
    • Анатомия
    • Биология
    • Химия
    • Физика
    • Физиология
    иностранные языки
    • французский
    • немецкий
    • Латинский
    • Китайский мандарин
    • Испанский
    начальное обучение
    • Чтение
    • Акустика
    • Элементарная математика
    прочие
    • Бухгалтерский учет
    • Информатика
    • Экономика
    • Английский
    • Финансы
    • История
    • Письмо
    • Лето
    Поиск по 350+ темам
  • О
    • Обзор видео
    • Процесс выбора наставника
    • Онлайн-репетиторство
    • Мобильное обучение
    • Мгновенное обучение
    • Как мы работаем
    • Наша гарантия
    • Влияние репетиторства
    • Обзоры и отзывы
    • Освещение в СМИ
    • О преподавателях университета

Мы открыты в субботу и воскресенье!

Звоните прямо сейчас, чтобы записаться на обучение:

(888) 888-0446

Все математические ресурсы ACT

14 диагностических тестов 767 практических тестов Вопрос дня Карточки Learn by Concept

ACT Math Help » Геометрия » Твердая геометрия » Кубики » Как найти диагональ куба

Найдите длину диагонали куба со стороной .

Возможные ответы:

Правильный ответ:

Объяснение:

Начнем с рисунка, отметив, что диагональ, обозначенная как , представляет собой длину куба от одной вершины до противоположной вершины.

                               

Однако хитрость в решении задачи заключается в том, чтобы также нарисовать диагональ нижней грани куба, которую мы обозначили .

                                                          

Обратите внимание, что это создает два прямоугольных треугольника. Хотя наша конечная цель – найти , мы можем начать с поиска прямоугольного треугольника на нижней грани . Используя либо теорему Пифагора, либо тот факт, что у нас есть прямой треугольник 45-45-90, мы можем вычислить гипотенузу.

Теперь, когда мы знаем значение , мы можем обратиться к нашему второму прямоугольному треугольнику, чтобы найти его, используя теорему Пифагора.

Получение квадратного корня из обеих сторон и упрощение дает ответ.

Сообщить об ошибке

Какова длина диагонали куба объемом  ? Округлить до сотых.

Возможные ответы:

Правильный ответ:

 

Объяснение:

Напомним, что объем куба вычисляется с помощью уравнения

, где  это длина одной стороны куба.

Итак, для наших данных мы знаем:

С помощью калькулятора извлеките кубический корень из обеих сторон. Вы всегда можете сделать это, возведя число в степень, если на вашем калькуляторе нет кнопки с переменным корнем.

Если получилось , значение действительно нужно округлить до . Это из-за оценок калькулятора. Итак, если стороны равны  , вы можете найти диагональ, используя вариацию теоремы Пифагора для трех измерений:

Это . Округлите до .

Сообщить об ошибке

Какова длина диагонали куба объемом ?

Возможные ответы:

Правильный ответ:

Пояснение:

Вспомните, что диагональ куба легче всего найти, если известны его размеры. Для объема куба соответствующее уравнение:

, где  представляет собой длину одной стороны куба. Для наших данных это дает нам:

Теперь вы можете разложить это вручную или воспользоваться калькулятором. Вы увидите, что это так.

Теперь найдем диагональ, используя трехмерную версию теоремы Пифагора / формулы расстояния:

 или

Вы можете переписать это:

Сообщить об ошибке

Знак
Сертифицированный преподаватель

Главный кампус Университета Сент-Луиса, бакалавр искусств, преподаватель начальной школы. Вебстерский университет, магистр преподавания искусств.