Прямоугольный параллелепипед. Задания В9 и В11
Содержание ▲
- В прямоугольном параллелепипеде…
- Содержание Аналогичные задания прототипа…
- 1.1 Прототип задания B9 (№ 245359) Найдите…
- Теоретические сведения Прямоугольным…
- 1.2 Задание B9 (№ 270577) Прототип (№…
- 1.3 Задание B9 (№ 271063) Найдите квадрат…
- 2.1 Прототип задания B9 (№ 245360) Найдите…
- 2.2 Задание B9 (№ 271073) Найдите расстояние…
- 2.3 Задание B11 (№ 271567) Найдите расстояние…
- 3.1 Прототип задания B11 (№ 245361) Найдите…
- Теоретические сведения Прямая ɑ, проведенная в…
- 3.2 Задание B9 (№ 271575) Найдите угол АС1В1…
- 3.3 Задание B9 (№ 271811) Найдите угол B1DD1…
- 4.1 Прототип задания B9 (№ 245362) Найдите…
- 4.2 Задание B9 (№ 271813) Найдите угол CBD…
- 4.3 Задание B9 (№ 271817) Найдите угол DC1D1…
- 5.

- 5.2 Задание B9 (№ 272313) Найдите угол BD1B1…
- 5.3 Задание B9 (№ 272319) Найдите угол АС1В…
- Работа учителя математики Зениной Алевтины…
- Скоро ЕГЭ! Еще есть время подготовиться! …
- Скачать
- Похожие презентации
Вы можете ознакомиться и скачать презентацию на тему Прямоугольный параллелепипед. Задания В9 и В11. Доклад-сообщение содержит 21 слайдов. Презентации для любого класса можно скачать бесплатно. Если материал и наш сайт презентаций Mypresentation Вам понравились – поделитесь им с друзьями с помощью социальных кнопок и добавьте в закладки в своем браузере.
Слайд 1
Описание слайда:
В прямоугольном параллелепипеде Прототип задания B9 (№ 245359) — B9 (№ 245363)
Слайд 2
Содержание
Аналогичные задания прототипа задания B11(№ 245359)
Задание В9 1. 1 1.2 1.3
Аналогичные задания прототипа задания B9 (№ 245360)
Задание В9 2.1 2.2 2.3
Аналогичные задания прототипа задания B9 (№ 245361)
Задание В9 3.1 3.2 3.3
Аналогичные задания прототипа задания B9 (№ 245362)
Задание В9 4.1 4.2 4.3
Аналогичные задания прототипа задания B9 (№ 245363)
Задание В9 5.1 5.2 5.3
1 1.2 1.3
Аналогичные задания прототипа задания B9 (№ 245360)
Задание В9 2.1 2.2 2.3
Аналогичные задания прототипа задания B9 (№ 245361)
Задание В9 3.1 3.2 3.3
Аналогичные задания прототипа задания B9 (№ 245362)
Задание В9 4.1 4.2 4.3
Аналогичные задания прототипа задания B9 (№ 245363)
Задание В9 5.1 5.2 5.3
Слайд 3
Описание слайда:
1.1 Прототип задания B9 (№ 245359)
Найдите квадрат расстояния между вершинами С и А1 прямоугольного параллелепипеда, для которого АВ=5, АD = 4, AA1 = 3.
Слайд 4
Описание слайда:
Теоретические сведения Прямоугольным параллелепипедом называется прямой параллелепипед, основания которого –прямоугольники. Прямой параллелепипед- это параллелепипед, боковые ребра которого перпендикулярны к плоскостям основания
Слайд 5
Описание слайда:
1.2 Задание B9 (№ 270577) Прототип (№ 245359) Найдите квадрат расстояния между вершинами В и D1 прямоугольного параллелепипеда, для которого AB=5, AD=3, AA1=6 .
Слайд 6
Описание слайда:
1.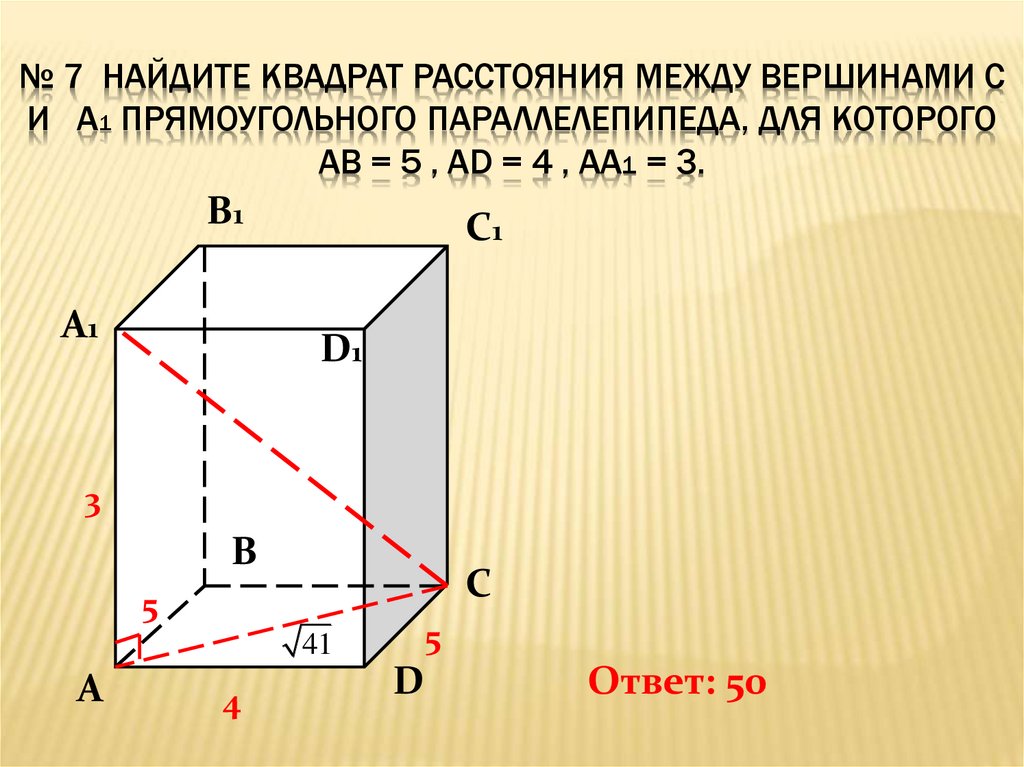 3 Задание B9 (№ 271063)
Найдите квадрат расстояния между вершинами A и C1 прямоугольного параллелепипеда, для которого AB=3, AD=5, AA1=5 .
3 Задание B9 (№ 271063)
Найдите квадрат расстояния между вершинами A и C1 прямоугольного параллелепипеда, для которого AB=3, AD=5, AA1=5 .
Слайд 7
Описание слайда:
2.1 Прототип задания B9 (№ 245360) Найдите расстояние между вершинами A и D1 прямоугольного параллелепипеда, для которого AB=5, AD=4, AA1=3 .
Слайд 8
Описание слайда:
2.2 Задание B9 (№ 271073) Найдите расстояние между вершинами В и С1 прямоугольного параллелепипеда, для которого АВ = 6, AD = 6, AA1 = 8.
Слайд 9
Описание слайда:
2. 3 Задание B11 (№ 271567)
Найдите расстояние между вершинами B и A1 прямоугольного параллелепипеда, для которого AB =9,
AD = 4, AA1 = 12 .
3 Задание B11 (№ 271567)
Найдите расстояние между вершинами B и A1 прямоугольного параллелепипеда, для которого AB =9,
AD = 4, AA1 = 12 .
Слайд 10
Описание слайда:
3.1 Прототип задания B11 (№ 245361) Найдите угол АBD1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 3 . Ответ дайте в градусах.
Слайд 11
Описание слайда:
Теоретические сведения Прямая ɑ, проведенная в плоскости β через точку М
Слайд 12
Описание слайда:
3.
Слайд 13
Описание слайда:
3.3 Задание B9 (№ 271811) Найдите угол B1DD1 прямоугольного параллелепипеда, для которого AB=12, AD=9, AA1=15 Ответ дайте в градусах.
Слайд 14
Описание слайда:
4.1 Прототип задания B9 (№ 245362) Найдите угол С1ВС прямоугольного параллелепипеда, для которого АВ=5, АD=4, AA1=4. Ответ дайте в градусах.
Слайд 15
Описание слайда:
4. 2 Задание B9 (№ 271813)
Найдите угол CBD прямоугольного параллелепипеда, для которого AB = 4, AD = 4, AA1 = 6. Ответ дайте в градусах.
2 Задание B9 (№ 271813)
Найдите угол CBD прямоугольного параллелепипеда, для которого AB = 4, AD = 4, AA1 = 6. Ответ дайте в градусах.
Слайд 16
Описание слайда:
4.3 Задание B9 (№ 271817) Найдите угол DC1D1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 5 . Ответ дайте в градусах.
Слайд 17
Описание слайда:
5.1 Прототип задания B9 (№ 245363) Найдите угол DBD1 прямоугольного параллелепипеда, для которого AB = 4, AD = 3, AA1 = 5. Ответ дайте в градусах.
Слайд 18
Описание слайда:
5. 2 Задание B9 (№ 272313)
Найдите угол BD1B1 прямоугольного параллелепипеда, для которого AB = 12, AD = 9, AA1 =15. Ответ дайте в градусах.
2 Задание B9 (№ 272313)
Найдите угол BD1B1 прямоугольного параллелепипеда, для которого AB = 12, AD = 9, AA1 =15. Ответ дайте в градусах.
Слайд 19
Описание слайда:
5.3 Задание B9 (№ 272319) Найдите угол АС1В прямоугольного параллелепипеда, для которого АВ =13, АD = 12, АА1 = 5. Ответ дайте в градусах.
Слайд 20
Описание слайда:
Работа учителя математики Зениной Алевтины Дмитриевны 2011год
Слайд 21
Описание слайда:
Скоро ЕГЭ! Еще есть время подготовиться!
ЕГЭ Профиль №2.
 Куб, прямоугольный параллелепипед — math200.ru Skip to content
Куб, прямоугольный параллелепипед — math200.ru Skip to contentЕГЭ Профиль №2. Куб, прямоугольный параллелепипедadmin2022-09-06T20:04:15+03:00
Скачать файл в формате pdf.
ЕГЭ Профиль №2. Куб, прямоугольный параллелепипед
| Задача 1. Площадь поверхности куба равна 18. Найдите его диагональ. Ответ ОТВЕТ: 3. |
| Задача 2. Объем куба равен 8. Найдите площадь его поверхности. Ответ ОТВЕТ: 24. |
| Задача 3. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба. Ответ ОТВЕТ: 4. |
| Задача 4. Во сколько раз увеличится объем куба, если его ребра увеличить в три раза? Ответ ОТВЕТ: 27. |
Задача 5. Диагональ куба равна \(\sqrt {12} \). Найдите его объем. Ответ ОТВЕТ: 8. |
| Задача 6. Объем куба равен \(24\sqrt 3 \). Найдите его диагональ. Ответ ОТВЕТ: 6. |
| Задача 7. Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба. Ответ ОТВЕТ: 2. |
| Задача 8. Диагональ куба равна 1. Найдите площадь его поверхности. Ответ ОТВЕТ: 2. |
| Задача 9. Площадь поверхности куба равна 24. Найдите его объем. Ответ ОТВЕТ: 8. |
| Задача 10. Объем одного куба в 8 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба? Ответ ОТВЕТ: 4. |
Задача 11. В кубе ABCDA1B1C1D1 точка K — середина ребра AA1, точка L — середина ребра A1B1, точка M — середина ребра A1D1. Найдите угол MLK. Ответ дайте в градусах. Найдите угол MLK. Ответ дайте в градусах.Ответ ОТВЕТ: 60. |
| Задача 12. В кубе ABCDA1B1C1D1 найдите угол между прямыми AD1 и B1D1. Ответ дайте в градусах. Ответ ОТВЕТ: 60. |
| Задача 13. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины. Ответ ОТВЕТ: 5. |
| Задача 14. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ. Ответ ОТВЕТ: 3. |
Задача 15. Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.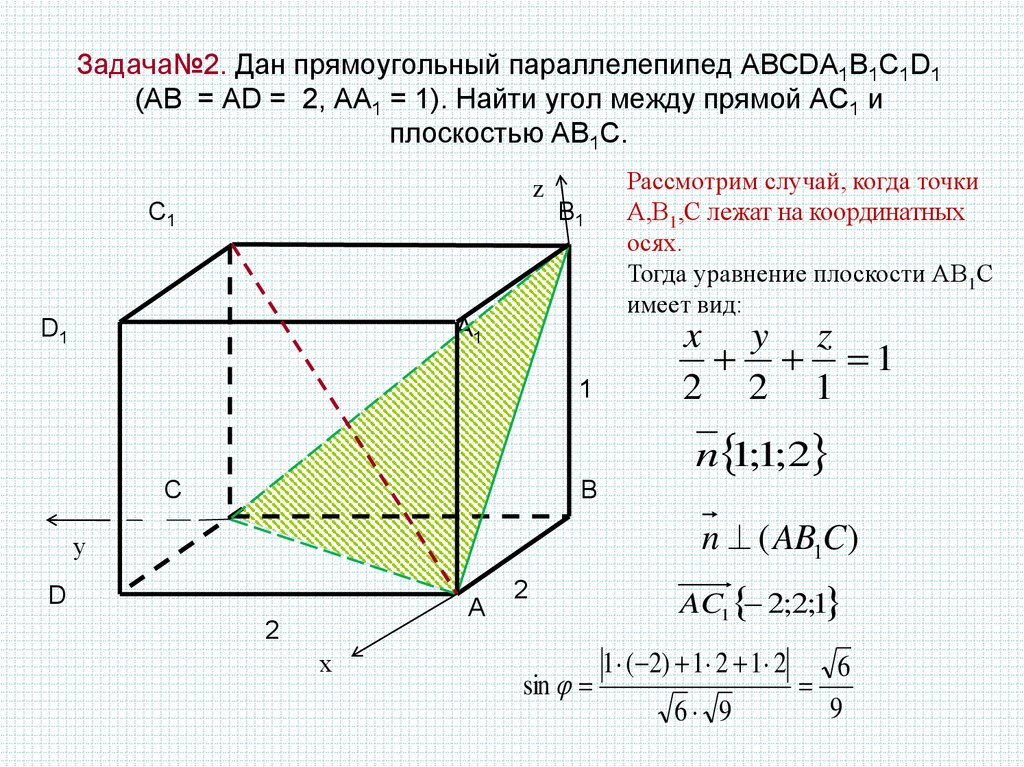 Ответ ОТВЕТ: 24. |
| Задача 16. Площадь грани прямоугольного параллелепипеда равна 12. Ребро, перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда. Ответ ОТВЕТ: 48. |
| Задача 17. Объем прямоугольного параллелепипеда равен 24. Одно из его ребер равно 3. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру. Ответ ОТВЕТ: 8. |
| Задача 18. Объем прямоугольного параллелепипеда равен 60. Площадь одной его грани равна 12. Найдите ребро параллелепипеда, перпендикулярное этой грани. Ответ ОТВЕТ: 5. |
| Задача 19. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины. Ответ ОТВЕТ: 4. |
Задача 20. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему куба. Найдите ребро равновеликого ему куба.Ответ ОТВЕТ: 6. |
| Задача 21. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда. Ответ ОТВЕТ: 32. |
| Задача 22. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 3. Объем параллелепипеда равен 36. Найдите его диагональ. Ответ ОТВЕТ: 7. |
| Задача 23. Одна из граней прямоугольного параллелепипеда – квадрат. Диагональ параллелепипеда равна \(\sqrt 8 \) и образует с плоскостью этой грани угол 45o. Найдите объем параллелепипеда. Ответ ОТВЕТ: 4. |
Задача 24. Диагональ прямоугольного параллелепипеда равна \(\sqrt 8 \) и образует углы 30o, 30o и 45o с плоскостями граней параллелепипеда.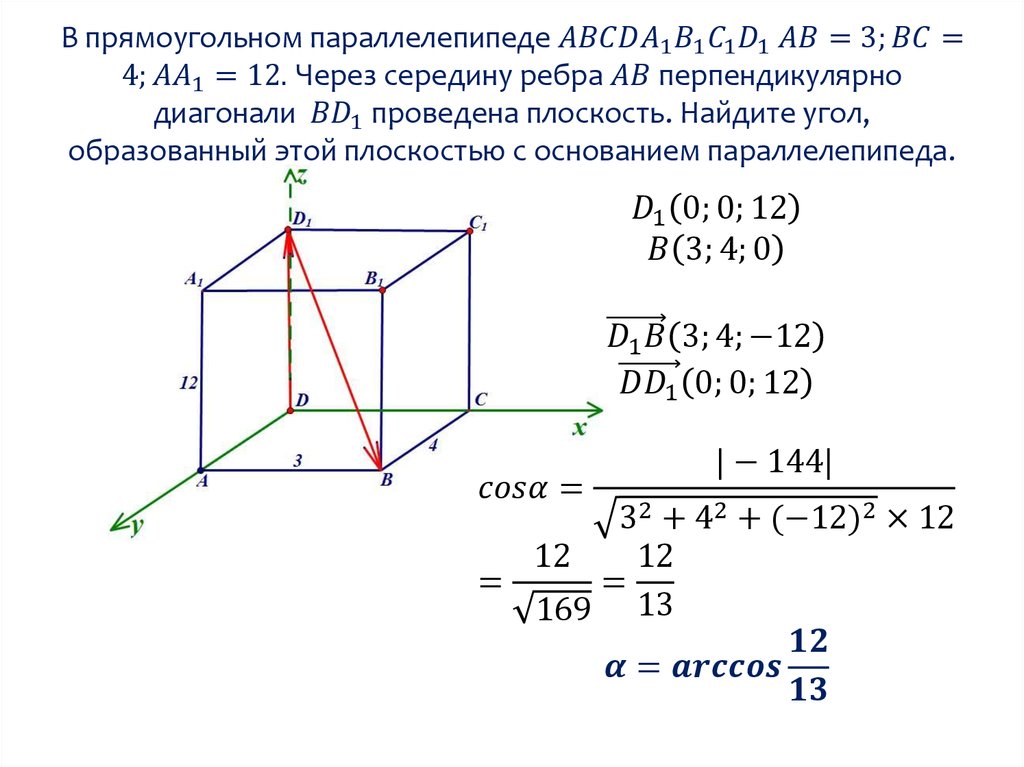 Найдите объем параллелепипеда. Найдите объем параллелепипеда.Ответ ОТВЕТ: 4. |
| Задача 25. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите площадь поверхности параллелепипеда. Ответ ОТВЕТ: 64. |
| Задача 26. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Объем параллелепипеда равен 6. Найдите площадь его поверхности. Ответ ОТВЕТ: 22. |
| Задача 27. Объем параллелепипеда ABCDA1B1C1D1 равен 4,5. Найдите объем треугольной пирамиды AD1CB1. Ответ ОТВЕТ: 1,5. |
Задача 28. Найдите объем многогранника, вершинами которого являются точки A, D, A1, B, C, B1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB = 3, AD = 4, AA1 = 5.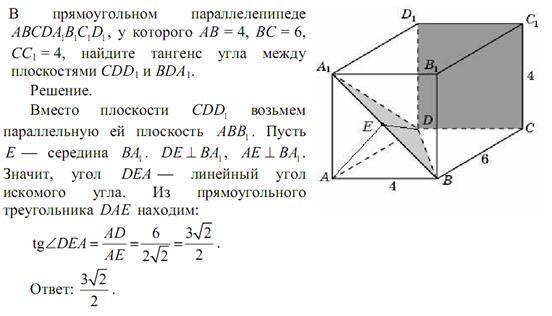 Ответ ОТВЕТ: 30. |
| Задача 29. Найдите объем многогранника, вершинами которого являются точки A, B, C, D1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB = 4, AD = 3, AA1 = 4. Ответ ОТВЕТ: 8. |
| Задача 30. Найдите объем многогранника, вершинами которого являются точки A1, B, C, C1, B1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB = 4, AD = 3, AA1 = 4. Ответ ОТВЕТ: 16. |
Задача 31. Найдите объем многогранника, вершинами которого являются точки A, B, C, B1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB = 3, AD = 3, AA1 = 4. Ответ ОТВЕТ: 6. |
| Задача 32. Найдите объем многогранника, вершинами которого являются точки A, B, B1, C1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB = 5, AD = 3, AA1 = 4. Ответ ОТВЕТ: 10. |
| Задача 33. Найдите угол ABD1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 3. Ответ дайте в градусах. Ответ ОТВЕТ: 45. |
| Задача 34. Найдите угол C1BC прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 4. Ответ дайте в градусах. Ответ ОТВЕТ: 45. |
Задача 35. Найдите угол DBD1 прямоугольного параллелепипеда, для которого AB = 4, AD = 3, AA1 = 5. Ответ дайте в градусах. Ответ дайте в градусах.Ответ ОТВЕТ: 45. |
| Задача 36. В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что AC1 = 13, C1D1 = 3, B1C1 = 12. Найдите длину ребра AA1. Ответ ОТВЕТ: 4. |
| Задача 37. В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BB1 = 11, C1D1 = 16, B1C1 = 8. Найдите длину диагонали DB1. Ответ ОТВЕТ: 21. |
Задача 38. В прямоугольном параллелепипеде ABCDA1B1C1D1 ребро \(AB = 2\), ребро \(AD = \sqrt 5 \), ребро \(A{A_1} = 2\). Точка K — середина ребра BB1. Найдите площадь сечения, проходящего через точки A1, D1 и K. Точка K — середина ребра BB1. Найдите площадь сечения, проходящего через точки A1, D1 и K.Ответ ОТВЕТ: 5. |
| Задача 39. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны ребра AB = 24, AD = 10, AA1 = 22. Найдите площадь сечения, проходящего через точки A, A1 и С. Ответ ОТВЕТ: 572. |
| Задача 40. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны ребра AB = 8, AD = 6, AA1 = 21. Найдите синус угла между прямыми CD и A1C1. Ответ ОТВЕТ: 0,6. |
Задача 41. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны ребра \(AB = 3,\;\;AD = 5,\;\;A{A_1} = 12\).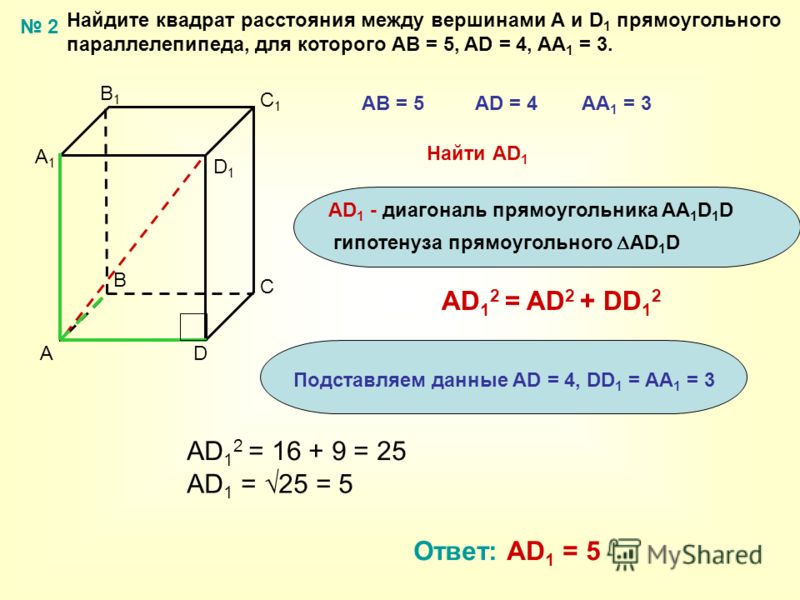 Найдите площадь сечения параллелепипеда, проходящего через точки A, B и С1. Найдите площадь сечения параллелепипеда, проходящего через точки A, B и С1.Ответ ОТВЕТ: 39. |
Реклама
Мы Вконтакте
Поддержать нас
Математическая задача: Угол двух прямых
Существует правильная четырехугольная пирамида ABCDV; | АБ | = 4 см; высота v = 6 см. Определить углы прямых AD и BV.
Правильный ответ:
α = 72,4516 °Пошаговое объяснение:
a=4 см v=6 см s=v2+(a/2)2
=62+(4/2) 2
=2 10
см ≐ 6,3246 см тангенс α = с/(а/2) α1= арктан(2⋅ с/а)=арктан(2⋅ 6,3246/4) ≐ 1,2645 рад α=α1 → °=α1⋅ π180 °=1,2645⋅ π180 °=72,452 °=72,4516∘=72°27′6″
Нашли ошибку или неточность? Не стесняйтесь
пишите нам . Спасибо!
Спасибо!
Советы по использованию связанных онлайн-калькуляторов
См. также наш калькулятор прямоугольного треугольника.
См. также наш калькулятор тригонометрического треугольника.
Чтобы решить эту математическую задачу, вам необходимо знать следующие знания:
- геометрия
- линия
- объемная геометрия пирамида0033 planimetrics
- right triangle
- triangle
- square
- quadrilateral
- goniometry and trigonometry
- tangent
- arctangent
Units of physical quantities:
- angle
Grade of the word problem :
- практика для 14-летних
- средняя школа
Мы рекомендуем вам посмотреть этот обучающий видеоролик по этой математической задаче: видео1
- Вычислить 8354
В правильной пирамиде, у которой ребро основания | АБ | = 4см; высота = 6 см, рассчитайте угол линий AV и CV, V = вершина.
- Расстояние точек
Дана правильная четырехугольная пирамида ABCDV, у которой ребро AB = a = 4 см, а высота v = 8 см. Пусть S будет центром CV. Найдите расстояние между точками A и S. - Высота пирамиды
Длина ребер пирамиды ABCDV: AB = 4, AV = 7. Какова ее высота? - Высота стены
Рассчитайте площадь и объем правильной четырехугольной пирамиды, если сторона a = 6 см, а высота стены v = 0,8 дм. - Четырехугольник 40551
Найдите объем и площадь поверхности правильного четырехугольника пирамиды ABCDV, если ее передняя грань имеет длину а = 10 см и высоту тела h = 12 см. - Четырехугольная пирамида
Дана правильная четырехугольная пирамида с квадратным основанием. Высота тела 30 см, объем V = 1000 см³. Вычислите его сторону и площадь поверхности. - Треугольная 46641
Правильная треугольная пирамида ABCDV имеет длину ребра основания a = 8 см и высоту 7 см. Вычислить площадь поверхности и объем пирамиды - Есть
Есть треугольник ABC: A(-2,3), B(4,-1), C(2,5). Определить общие уравнения прямых, на которых лежат: а) сторона АВ, б) высота к стороне с, в) ось стороны АВ, г) медиана стороны а
Определить общие уравнения прямых, на которых лежат: а) сторона АВ, б) высота к стороне с, в) ось стороны АВ, г) медиана стороны а - Расстояние прямых
Найти расстояние прямых AE, CG в прямоугольном параллелепипеде ABCDEFGH, если задано | АБ | = 3см, | ОБЪЯВЛЕНИЕ | = 2 см, | АЕ | = 4см - Правильная четырехугольная пирамида
Высота правильной четырехугольной пирамиды 6 см, длина основания 4 см. Чему равен угол между плоскостями ABV и BCV? - Пять окружностей
На отрезке CD = 6 через равные промежутки расположены пять окружностей одного радиуса. Найдите длины прямых AD, AF, AG, BD и CE. - Четырехсторонняя пирамида
Вычислите объем и поверхность правильной четырехугольной пирамиды, если длина ребра основания 4 см, а высота пирамиды 7 см. - Четырехугольник 80729
Четырехугольник ABCD имеет длины сторон AB=13см, CD=3см, AD=4см. Углы ACB и ADC прямые. Вычислите периметр четырехугольника ABCD. - Отклонение прямых
Найти отклонение прямых AG, BH в параллелепипеде ABCDEFGH, если задано | АБ | = 3см, | ОБЪЯВЛЕНИЕ | = 2см, | АЕ | = 4см - Четырехугольная пирамида
Рассчитайте площадь поверхности и объем правильной четырехугольной пирамиды: стороны оснований (низ, верх): а1 = 18 см, а2 = 6см угол α = 60° (Угол α угол между боковыми стенками и базовая плоскость. ) S =? , В =?
) S =? , В =? - Пирамида — угол
Рассчитайте поверхность правильной четырехугольной пирамиды, длина ребра основания которой равна 6 см, а отклонение от плоскости боковой стенки основания составляет 50 градусов. - Четырехугольная пирамида
Правильная четырехугольная пирамида имеет длину основания 6 см и длину бокового ребра 9 сантиметров. Вычислите его объем и площадь поверхности.
Вопросы в стиле IB SL Paper 2
Вопрос Все длины в этом вопросе указаны в сантиметрах. 9{0}\), найдите AB.
Объем пирамиды 57,2 см 3 , с точностью до трех значащих цифр.
(в) Найдите высоту пирамиды VX.
Второе украшение имеет форму прямоугольного параллелепипеда с прямоугольным основанием длиной 2x см, шириной x см и высотой y см. Кубоид имеет тот же объем, что и пирамида.
(d) Прямоугольный параллелепипед имеет минимальную площадь поверхности S см 2 . Найдите значение S.
Ответ:
(a) попытайтесь использовать формулу расстояния, чтобы найти AV 9{2}= 0\) ИЛИ x = 2,77849….
ЗАТЕМ
92,6401…
минимальная площадь поверхности = 92,6(см 2 )
Вопрос: Фермер устанавливает в земле столбы в точках A, B и C, чтобы обозначить границы треугольного участка земли на своем участке.
Из точки А он проходит 230 метров строго на запад до точки В.
Из точки В он проходит 175 метров по азимуту 063° до точки С.
Это показано на следующей диаграмме.
(а) Найдите расстояние от точки А до точки С.
(б) Найдите площадь этого участка земли.
(c) Найдите CAB.
Фермер хочет разделить участок земли на две части. Он поставит столб в точке D, которая находится между A и C. Он хочет, чтобы граница BD разделяла участок земли так, чтобы участки имели одинаковую площадь. Это показано на следующей диаграмме.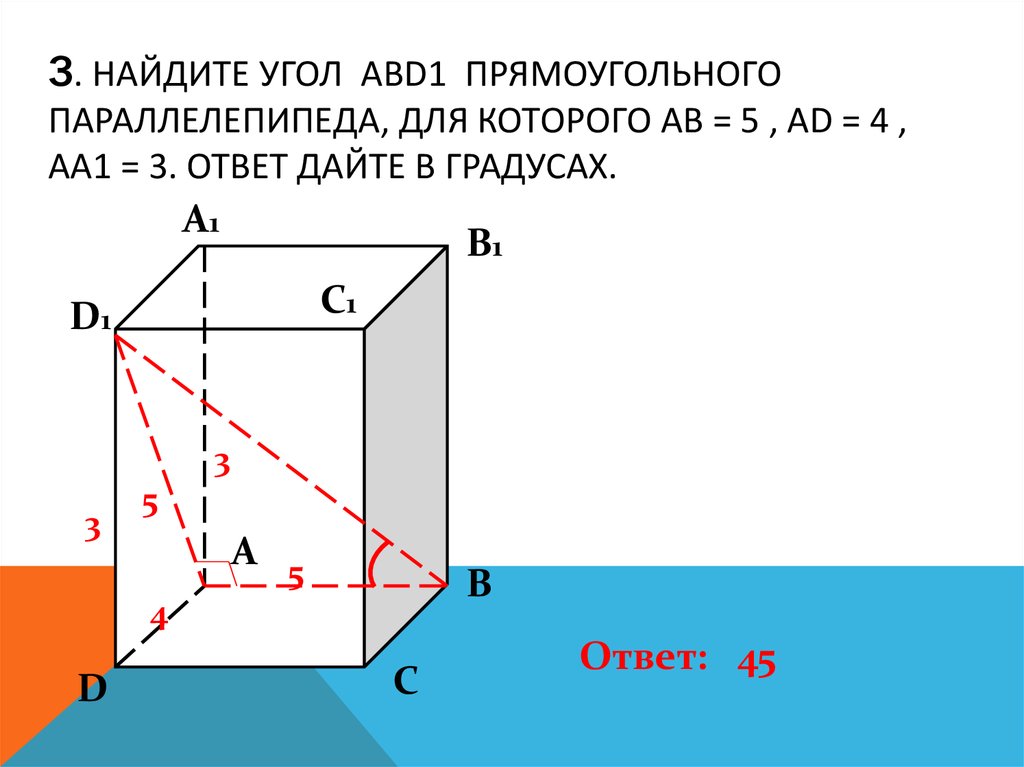
(d) Найдите расстояние от точки B до точки D.
Ответ/Пояснение 9{0}\)9136,55…
площадь = 9140 (м 2 )
(c) попытка подстановки по правилу синусов или по правилу косинусов
(d) МЕТОД 1 90 равно, AD=DC
\(AD = \frac{1}{2}AC = 54,3115…\)
попытка подстановки в теорему косинусов, чтобы найти BD
правильная подстановка в теорему косинусов
BD 2 = 230 2 + 54,3115 2 – 2(230) (54,3115) cos 47,0049 0
BD = 197.009….
BD = 197 (м)
МЕТОД 2
правильные выражения для площадей треугольников BDA и треугольников BCD с использованием BD
На следующем рисунке показана окружность с центром O и радиусом 5 метров.
Точки A и B лежат на окружности и \(A\hat{O}B\) 1,9 = радианы.
а) Найдите длину хорды [AB].
(b) Найдите площадь заштрихованного сектора.
Ans:
(a) EITHER
uses the cosine rule
AB 2 = 5 2 + 5 2 -2 × 5 × 5 × cos1.9
OR
uses прямоугольная тригонометрия
\(\frac{\frac{AB}{2}}{5}= sin 0,95\)
ИЛИ
использует правило синусов
\(\alpha = \frac{1} {2}\влево ( \pi -1,9 \вправо )\влево ( =0,6207… \вправо )\)
\(\frac{AB}{sin 1,9}=\frac{5}{sin 0,6207…}\)
ЗАТЕМ 9\circ \) A1 N2
[3 балла]
а.
\(P = 180 – 75 – R\)
\(P = 62,5\) (A1)
подстановка в любую правильную формулу A1 9.01415 9.0144 \({\text{площадь}}\Delta {\text{PQR}} = \frac{1}{2} \times 7 \times 10 \times \sin ({\text{их}}P)\)
\(= 31,0\) (см 2 ) A1 N2
[3 балла]
б.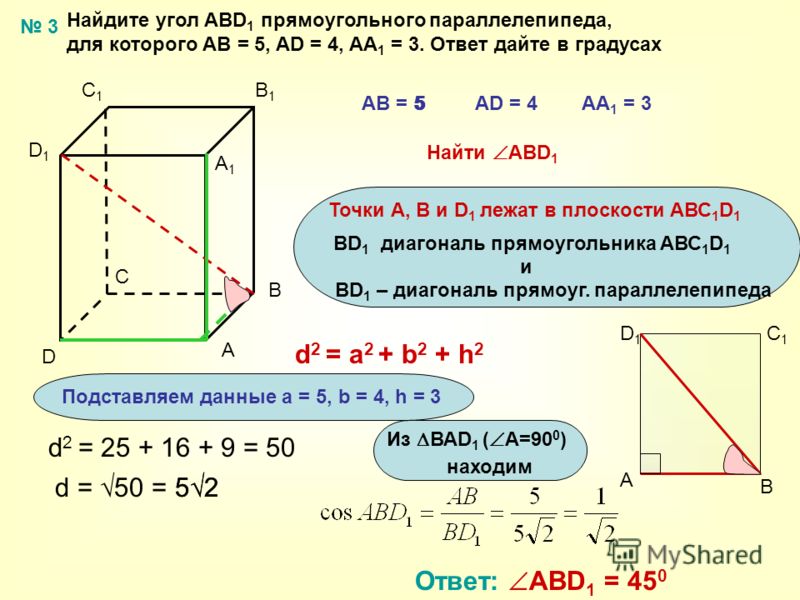
Вопрос
На приведенном ниже рисунке показан треугольник ABD с AB = 13 см и AD = 6,5 см.
Пусть C — точка на прямой BD такая, что BC = AC = 7 см.
Найдите величину угла ACB.
[3]
а.
Найдите размер угла CAD.
[5]
б.
Ответ/ПояснениеОтвет/Пояснение 9\circ )\) A1 N2
[3 балла]
а.
МЕТОД 1
\({\rm{A}}\widehat {\rm{C}} {\rm{D}} = \pi – 2,381\) \((180–136,4)\) (A1)
свидетельство выбора правила синусов в треугольнике ACD (M1)
правильная замена A1
\(\ frac{{6.5}}{{\sin 0,760 \ldots}} = \frac{7}{{\sin {\rm{A}}\widehat {\rm{D}} {\rm{C} }}}\) 9\circ )\) A1 N3МЕТОД 2
\({\rm{A}}\widehat {\rm{B}}{\rm{C}} = \frac{1} {2}(\pi – 2,381)\) \(\left( {\frac{1}{2}(180–136,4)} \right)\) (A1)
свидетельство выбора синуса правило в треугольнике ABD (M1)
правильная замена A1
напр. \(\ frac{{6.5}}{{\sin 0,380 \ldots}} = \frac{{13}}{{\sin {\rm{A}}\widehat {\rm{D}}{\rm{ С}}}}\) 9\цирк }\) .
\(\ frac{{6.5}}{{\sin 0,380 \ldots}} = \frac{{13}}{{\sin {\rm{A}}\widehat {\rm{D}}{\rm{ С}}}}\) 9\цирк }\) .
Используйте правило косинуса, чтобы показать, что \({\rm{AC}} = \sqrt {41 – 40\cos x} \) .
[1]
а.
Используйте правило синусов в треугольнике ABC, чтобы найти другое выражение для AC.
[2]
б.
(i) Следовательно, найдите x , давая ответ с точностью до двух знаков после запятой.
(ii) Найти AC .
[6]
в.
(i) Найти y .
(ii) Отсюда или иначе найдите площадь треугольника ACD. 92} – 2 \times 4 \times 5\cos x\)
\({\rm{AC}} = \sqrt {41 – 40\cos x} \) AG
[1 марка]
а.
правильная замена A1
напр. \(\frac{{{\rm{AC}}}}{{\sin x}} = \frac{4}{{\sin 30}}\) , \(\frac{1}{2}{\ rm{AC}} = 4\sin x\)
\({\rm{AC}} = 8\sin x\) (принять \(\frac{{4\sin x}}{{\sin 30} }\)) A1 N1
[2 балла]
б.



 Определить общие уравнения прямых, на которых лежат: а) сторона АВ, б) высота к стороне с, в) ось стороны АВ, г) медиана стороны а
Определить общие уравнения прямых, на которых лежат: а) сторона АВ, б) высота к стороне с, в) ось стороны АВ, г) медиана стороны а ) S =? , В =?
) S =? , В =?
Leave A Comment