8.1.3. Свойство углов и сторон параллелограмма

Задача 1. Один из углов параллелограмма равен 65°. Найти остальные углы параллелограмма.

Решение.

∠C =∠A = 65° как противоположные углы параллелограмма.

∠А +∠В = 180° как углы, прилежащие к одной стороне параллелограмма.

∠В = 180° — ∠А = 180° — 65° = 115°.

∠D =∠B = 115° как противолежащие углы параллелограмма.

Ответ: ∠А =∠С = 65°; ∠В =∠D = 115°.

Задача 2. Сумма двух углов параллелограмма равна 220°. Найти углы параллелограмма.

 Решение.

Так как у параллелограмма имеется  2 равных острых угла и 2 равных тупых угла, то нам дана сумма двух тупых углов, т.е. ∠В +∠D = 220°. Тогда ∠В =∠D = 220°: 2 = 110°.

∠А +∠В = 180° как углы, прилежащие к одной стороне параллелограмма, поэтому ∠А = 180° — ∠В = 180° — 110° = 70°. Тогда  ∠C =∠A = 70°.

Ответ: ∠А =∠С = 70°; ∠В =∠D = 110°.

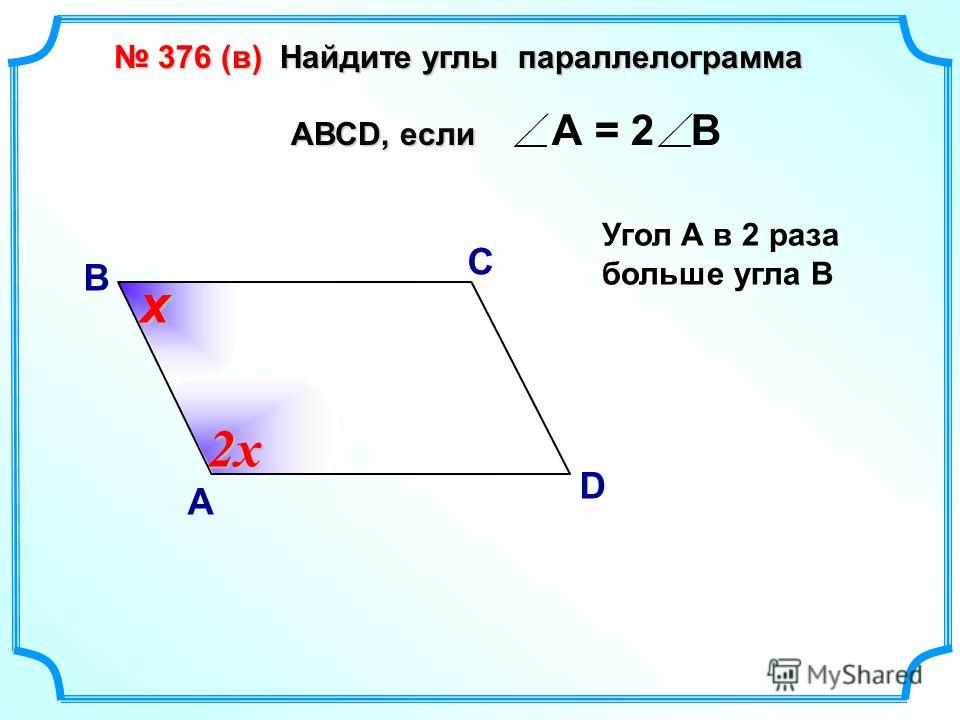
Задача 3. Один из углов параллелограмма в 3 раза больше другого. Найти углы параллелограмма.

Решение.

Пусть ∠А =х. Тогда ∠В = 3х. Зная, что сумма углов параллелограмма, прилежащих к одной его стороне равна 180°, составим уравнение.

х + 3х = 180;

4х = 180;

х = 180 : 4;

х = 45.

Получаем: ∠А =х = 45°, а ∠В = 3х = 3 ∙ 45° = 135°.

Противолежащие углы параллелограмма равны, следовательно,

∠А =∠С = 45°; ∠В =∠D = 135°.

Ответ: ∠А =∠С = 45°; ∠В =∠D = 135°.

Задача 4. Докажите, что если у четырехугольника две стороны параллельны и равны, то этот четырехугольник – параллелограмм.

 Доказательство.

Проведем диагональ BD  и рассмотрим  Δ ADB и Δ CBD.

AD = BC по условию. Сторона BD – общая.  ∠1 = ∠2 как внутренние накрест лежащие при параллельных (по условию) прямых AD и BC и секущей BD. Следовательно, Δ ADB = Δ CBD по двум сторонам и углу между ними (1-й признак равенства треугольников).  В равных треугольниках соответственные углы равны, значит, ∠3 =∠4. А эти углы являются внутренними накрест лежащими при прямых AB и CD и секущей BD. Отсюда следует параллельность прямых AB и CD. Таким образом, в данном четырехугольнике ABCD противолежащие стороны попарно параллельны, следовательно, по определению ABCD – параллелограмм, что и требовалось доказать.

Задача 5. Две стороны параллелограмма относятся как 2 : 5, а периметр равен 3,5 м. Найти стороны параллелограмма.

Решение.

Периметр параллелограмма PABCD= 2 ∙ (AB + AD).

Обозначим одну часть через х. тогда AB = 2x, AD = 5x метров. Зная, что периметр параллелограмма равен 3,5 м, составим уравнение:

2 ∙ (2x + 5x) = 3,5;

2 ∙ 7x = 3,5;

14x = 3,5;

x = 3,5 : 14;

x = 0,25.

Одна часть составляет 0,25 м. Тогда AB = 2 ∙ 0,25 = 0,5 м; AD = 5 ∙ 0,25 = 1,25 м.

Проверка.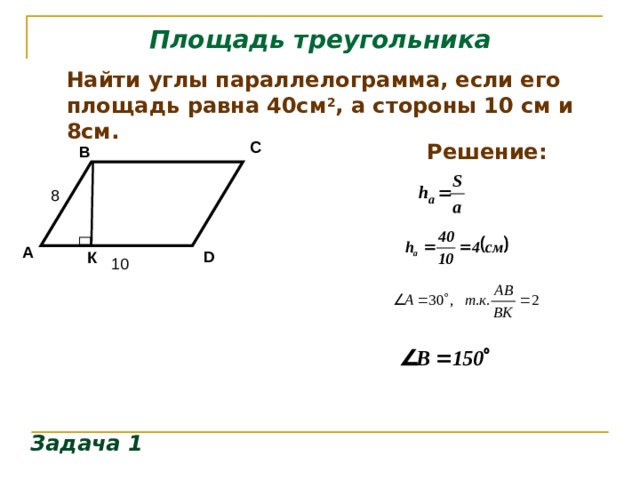

Периметр параллелограмма PABCD= 2 ∙ (AB + AD) = 2 ∙ (0,25 + 1,25) = 2 ∙ 1,75 = 3,5 (м).

Так как противоположные стороны параллелограмма равны, то CD = AB = 0,25 м; BC = AD = 1,25 м.

Ответ: CD = AB = 0,25 м; BC = AD = 1,25 м.

 

ABCD-параллелограмм. Угол А=40 градусов,угол С=35 градусов. Найти углы параллелограмма ABCD — Знания.site

Последние вопросы

  • Геометрия

    27 минут назад

    Знайдіть скалярний добуток векторів c ( 5; -2) і d ( -3; 1)

  • Геометрия

    42 минут назад

    Помогите пожалуйста с тестом по геометрии

  • Геометрия

    47 минут назад

    Помогите пожалуйста с геометрией :((:(:(:(

  • Геометрия

    57 минут назад

    Дз по геометрии

  • Геометрия

    1 час назад

    Кто придумав кубик рубик?

  • Геометрия

    1 час назад

    Напевно, мріяти любить кожен з нас. Про подорожі в незнайомі далекі країни, про красиві сучасні телефони, які постійно з’являються на ринку, вражаючи нас своїми технологіями. Хтось мріє покататися на великій швидкості на шикарному автомобілі з відкритим верхом, а хтось навіть полетіти в космос, щоб побачити нашу планету з боку галактики. Мрії у кожного свої, потаємні і різні. Комусь немає найбільшого щастя, ніж побродити по нових, ще незнайомих містах, захоплюючись їх архітектурними витворами і історичними пам’ятниками. А хтось інший мріє пірнути в глибини моря і насолоджуватися підводним плаванням. Я довго думав, яка ж моя потаємна мрія? Чого б мені хотілося найбільше і що б мені принесло найбільше щастя? Поїздки, телефони, море і автомобілі – все це, звичайно, непогано і це завжди приносить радість і ейфорію. Але ця радість не вічна і є речі набагато важливіші за все це. Я мрію знайти своє місце в житті. Вибрати саме ту професію, в якій я міг би реалізувати себе і не сказати після закінчення інституту, що це не моє. Я мрію, щоб мої батьки жили довго і були щасливі, адже коли у них все добре, щасливі і ми – їхні діти.
    Я мрію стати хорошим фахівцем у своїй справі. Можливо я стану, лікарем, вчителем, інженером, але я буду працювати так, щоб було видно результат моєї роботи і робота не була обтяжливою. Я думаю, головне просто мріяти. Ставити цілі і йти до них. І неважливо про що мрії, головне, щоб вони були і ми намагалися їх здійснювати. Адже йти до мети і прийти до неї – це величезне щастя. А якщо людина щаслива, вона буде намагатися зробити щасливим і оточуючих її людей. Буду мріяти про різне: про все прекрасне, що приносить радість і задоволення. Думати про море, і про гори, і про далекі закордонні країни і, звичайно ж, про своїх близьких та рідних, щоб вони завжди були поруч і завжди були здоровими та щасливими. Адже якщо сильно чогось хочеш, воно завжди здійсниться.

  • Геометрия

    1 час назад

    СРОЧНО ПОМОГИТЕ С ЗАДАНИЕМ!!!ДАЮ 20 БАЛЛОВ

  • Геометрия

    1 час назад

    геометрия ПРОШУ ПОМОЧЬ ​

  • Геометрия

    1 час назад

    СРОЧНО ПОМОГИТЕ С ЗАДАНИЕМ!!!Помогите пожалуйста с заданием!!! ДАЮ 20 БАЛЛОВ

  • Геометрия

    1 час назад

    помагить пожалуйста ​

  • Геометрия

    1 час назад

    ДАЮ 100 БАЛОВ СРОЧНО ОДНА ЗАДАЧА! Гострий кут паралелограма дорівнює 45°.
    Знайдіть висоту паралелограма, якщо його периметр дорівнює 80 , а діагональ ділить його тупий кут у відношенні 1: 2.

  • Геометрия

    1 час назад

    ДАЮ 100 БАЛОВ СРОЧНО ОДНА ЗАДАЧА! Гострий кут паралелограма дорівнює 45°. Знайдіть висоту паралелограма, якщо його периметр дорівнює 80 , а діагональ ділить його тупий кут у відношенні 1: 2.

  • Геометрия

    2 часа назад

    Объясните пожалуйста выполнение задач 1,2,3,4,5 задачу пж помогите!!!!!

  • Геометрия

    2 часа назад

    допоможіть будь ласка даю 50балів​

  • Геометрия

    2 часа назад

    Помогите пожалуйста, срочно У просторі задано точки М(1;5;-2), N(2;3;-1), К(3;4;-1). Знайдить площу трикутника MNK.

Все предметы

Выберите язык и регион

English

United States

Polski

Polska

Português

Brasil

English

India

Türkçe

Türkiye

English

Philippines

Español

España

Bahasa Indonesia

Indonesia

Русский

Россия

How much to ban the user?

1 hour 1 day 100 years

Как найти угол в параллелограмме

Все математические ресурсы ACT

14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 Следующая →

ACT Math Help » Геометрия » Плоская геометрия » Четырехугольники » Параллелограммы » Как найти угол в параллелограмме

В параллелограмме ,  и высота равна .

Что ?

Возможные ответы:

Правильный ответ:

Объяснение:

Мы можем начать эту задачу, нарисовав высоту и пометив длины заданными значениями.

Когда мы это делаем, мы видим, что мы нарисовали треугольник внутри паралеллограммы, включая . Поскольку мы знаем длины двух сторон этого треугольника, мы можем использовать тригонометрию, чтобы найти .

Что касается , мы знаем значения противоположной стороны и гипотенузы треугольника. Таким образом, мы можем использовать функцию синуса для решения .

Сообщить об ошибке

В параллелограмме ,  и . Находить .

Возможные ответы:

Правильный ответ:

Пояснение:

В параллелограмме последовательные углы являются дополнительными. Таким образом,

Сообщить об ошибке

 является параллелограммом. Находить .

Возможные ответы:

Правильный ответ:

Объяснение:

В параллелограмме последовательные углы являются дополнительными (т. е. складываются), а противоположные углы конгруэнтны (т. е. равны). Используя эти свойства, мы можем написать систему уравнений.

1. 

2. 

 

Начиная с уравнения 1.,

 0005

 

Наконец, поскольку противоположные углы равны, мы это знаем.

Сообщить об ошибке

 является параллелограммом. Находить .

Возможные ответы:

Правильный ответ:

Пояснение:

В параллелограмме смежные углы смежные, а противоположные углы равны. Используя эти свойства, мы можем написать систему уравнений.

1. 

2. 

3. 

 

Starting with equation 1.,

 

Substituting into equation 2.,

 

Используя уравнение 3.,

Сообщить об ошибке

Параллелограмм , . Что ?

Возможные ответы:

Правильный ответ:

Объяснение:

В пареллелограмме последовательные углы являются дополнительными.

Сообщить об ошибке

Параллелограмм , . Что ?

Возможные ответы:

Правильный ответ:

Пояснение:

В параллелограмме противоположные углы равны.

Сообщить об ошибке

 является параллелограммом. Находить .

Возможные ответы:

Правильный ответ:

Объяснение:

В параллелограмме смежные углы являются дополнительными, а противоположные углы равны.

 

5

0 Сообщить об ошибке0004 В параллелограмме ,  . Что такое 

Возможные ответы:

Правильный ответ:

Объяснение:

В приведенном выше параллелограмме и  являются последовательными углами (т. е. рядом друг с другом). В параллелограмме последовательные углы являются дополнительными, то есть они складываются.

Сообщить об ошибке

Параллелограмм , . Что ?

Возможные ответы:

Правильный ответ:

Объяснение:

В параллелограмме ,  и  противоположные углы. В параллелограмме противоположные углы равны. Это означает, что эти два угла равны.

Сообщить об ошибке

Чему равна сумма параллелограмма  и ?

Возможные ответы:

Правильный ответ:

Пояснение:

В параллелограмме последовательные углы являются дополнительными. и  последовательны, поэтому их сумма равна .

Сообщить об ошибке

← Предыдущая 1 2 Следующая →

Уведомление об авторских правах

Все ресурсы ACT Math

14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Learn by Concept

Углы параллелограмма — теоремы, доказательства, свойства

В параллелограмме четыре внутренних угла, а сумма внутренних углов параллелограмма всегда равна 360°. Противолежащие углы параллелограмма равны, а смежные углы параллелограмма попарно смежны. Познакомимся подробнее со свойствами углов параллелограмма.

1. Свойства углов параллелограмма
2. Теоремы, относящиеся к углам параллелограмма
3. Часто задаваемые вопросы об углах параллелограмма

Свойства углов параллелограмма

Параллелограмм – это четырехугольник с равными и параллельными противоположными сторонами. Есть некоторые особые свойства параллелограмма, которые отличают его от других четырехугольников. Обратите внимание на следующий параллелограмм, чтобы соотнести его свойства, указанные ниже:

  • Противоположные углы параллелограмма конгруэнтны (равны). Здесь ∠А = ∠С; ∠Д = ∠В.
  • Сумма всех углов параллелограмма равна 360°. Здесь ∠A + ∠B + ∠C + ∠D = 360°.
  • Все соответствующие последовательные углы являются дополнительными. Здесь ∠A + ∠B = 180°; ∠В + ∠С = 180°; ∠С + ∠D = 180°; ∠D + ∠А = 180°

Теоремы, относящиеся к углам параллелограмма

Теоремы, относящиеся к углам параллелограмма, помогают решать задачи, связанные с параллелограммом. Две важные теоремы приведены ниже:

  • Противоположные углы параллелограмма равны.
  • Смежные углы параллелограмма являются дополнительными.

Давайте узнаем об этих двух специальных теоремах параллелограмма подробно.

Противоположные углы параллелограмма равны

Теорема: В параллелограмме противоположные углы равны.

Дано: ABCD — параллелограмм с четырьмя углами ∠A, ∠B, ∠C, ∠D соответственно.

К Докажите: ∠A =∠C и ∠B=∠D

Доказательство: В параллелограмме ABCD диагональ AC делит параллелограмм на два треугольника.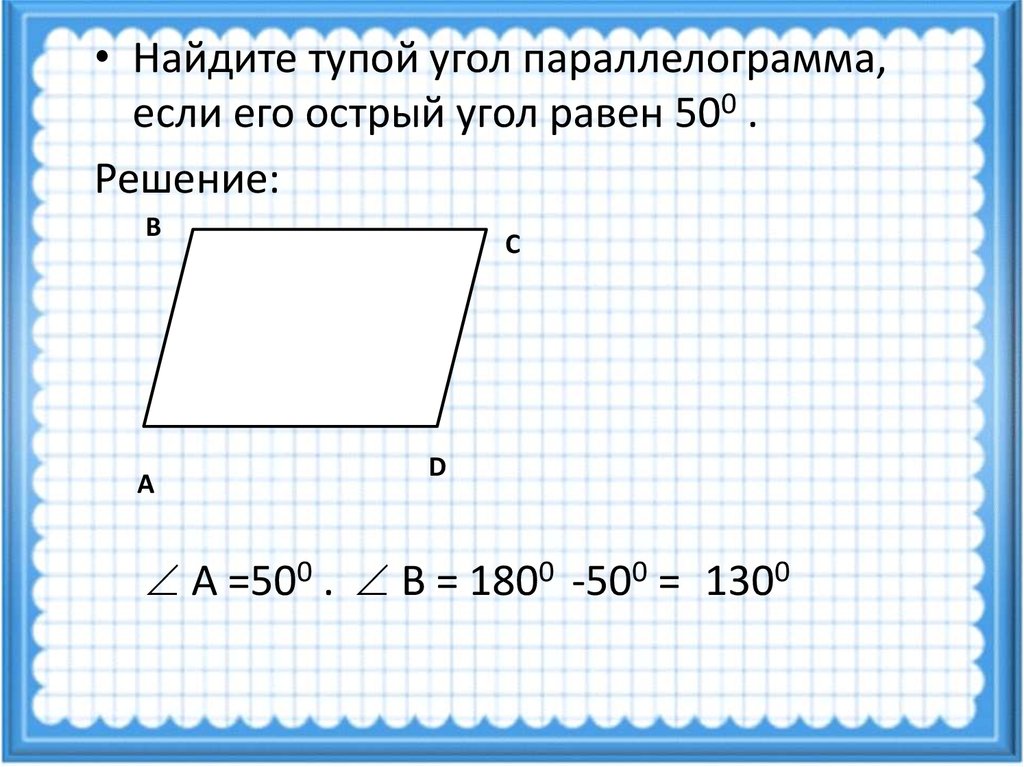 О сравнении треугольников ABC и ADC. Здесь у нас есть:
AC = AC (общие стороны)
∠1 = ∠4 (чередующиеся внутренние углы)
∠2 = ∠3 (чередующиеся внутренние углы)
Таким образом, два треугольника конгруэнтны, △ABC ≅ △ADC
. Это дает ∠B = ∠D по CPCT (соответствующие части конгруэнтных треугольников).
Точно так же мы можем показать, что ∠A = ∠C.
Отсюда доказано, что противоположные углы в любом параллелограмме равны.

Обратная теорема гласит, что если противоположные углы четырехугольника равны, то это параллелограмм. Докажем то же самое.

Дано: ∠A =∠C и ∠B=∠D в четырехугольнике ABCD.
Доказать: ABCD — параллелограмм.
Доказательство:
Сумма всех четырех углов этого четырехугольника равна 360°.
= [∠A + ∠B + ∠C + ∠D = 360º]
= 2(∠A + ∠B) = 360º (Мы можем заменить ∠C на ∠A и ∠D на ∠B, так как известно, что ∠A =∠C и ∠B =∠D)
= ∠А + ∠В = 180º. Это показывает, что соседние углы являются дополнительными. Следовательно, это означает, что AD || ДО Н.Э. Аналогично можно показать, что AB || CD.
Следовательно, АД || до н.э. и АВ || CD.
Следовательно, ABCD — параллелограмм.

Смежные углы параллелограмма являются дополнительными

Смежные углы параллелограмма являются дополнительными. Докажем это свойство, учитывая следующий факт и используя тот же рисунок.

Дано: ABCD — параллелограмм с четырьмя углами ∠A, ∠B, ∠C, ∠D соответственно.
Чтобы доказать: ∠A + ∠B = 180°, ∠C + ∠D = 180°.
Доказательство: Если AD считается секущей и AB || CD.
По свойству секущей мы знаем, что внутренние углы, лежащие по одну сторону от секущей, являются дополнительными.
Следовательно, ∠A + ∠D = 180°.
Точно так же
∠В + ∠С = 180°
∠С + ∠D = 180°
∠А + ∠В = 180°
Следовательно, сумма соответствующих двух смежных углов параллелограмма равна 180°.
Таким образом, доказано, что смежные углы параллелограмма являются дополнительными.

Похожие статьи об углах параллелограмма

Ознакомьтесь с приведенными ниже интересными статьями, посвященными углам параллелограмма.

  • Периметр параллелограмма
  • Параллелограмм Рабочие листы
  • Формула параллелограмма
  • Свойства параллелограммов

 

Решенные примеры на углы параллелограмма

  1. Пример 1: Один угол параллелограмма равен 75°. Найдите величину прилежащего к нему угла и меры всех остальных углов параллелограмма.

    Решение:

    Учитывая, что один угол параллелограмма = 75°
    Пусть прилежащий угол равен х
    Мы знаем, что последовательные (прилежащие) углы параллелограмма являются дополнительными.
    Следовательно, 75° + x° = 180°
    х = 180 ° — 75 ° = 105°
    Чтобы найти величину всех четырех углов параллелограмма, мы знаем, что противоположные углы параллелограмма равны.
    Отсюда ∠1 = 75°, ∠2 = 105°, ∠3 = 75°, ∠4 = 105°

  2. Пример 2: Значения противоположных углов параллелограмма даны следующим образом: ∠1 = 75°, ∠3 = (x + 30)°, найти значение x.
    Дано: ∠1 и ∠3 — противоположные углы параллелограмма.

    Решение:

    Дано: ∠1 = 75° и ∠3 = (x + 30)°
    Мы знаем, что противоположные углы параллелограмма равны.
    Следовательно,
    (х + 30)° = 75°
    х = 75° — 30°
    х = 45°
    Следовательно, значение x равно 45°.

перейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы по углам параллелограмма

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы об углах параллелограмма

Сумма углов параллелограмма равна 360°?

Да, все внутренние углы параллелограмма в сумме составляют 360°. Например, в параллелограмме ABCD ∠A + ∠B + ∠C + ∠D = 360°. Согласно свойству суммы углов многоугольников, сумма внутренних углов в многоугольнике может быть рассчитана с помощью количества треугольников, которые могут быть образованы внутри него. В данном случае параллелограмм состоит из 2-х треугольников, значит, сумма внутренних углов равна 360°. Это также можно рассчитать по формуле S = (n — 2) × 180 °, где «n» представляет количество сторон в многоугольнике. Здесь «n» = 4. Следовательно, сумма внутренних углов параллелограмма = S = (4 — 2) × 180 ° = (4 — 2) × 180 ° = 2 × 180 ° = 360 °.

Какая связь между смежными углами параллелограмма?

Смежные углы параллелограмма также известны как последовательные углы, и они всегда являются дополнительными (180°).

Как связаны противоположные углы параллелограмма?

Противоположные углы параллелограмма всегда равны, тогда как смежные углы параллелограмма всегда являются дополнительными.

Как найти недостающие углы параллелограмма?

Мы можем легко найти недостающие углы параллелограмма с помощью трех специальных свойств:

  • Противоположные углы параллелограмма конгруэнтны.
  • Последовательные углы параллелограмма являются дополнительными.
  • Сумма всех углов параллелограмма равна 360°.

Что такое внутренние углы параллелограмма?

Углы, образуемые внутри параллелограмма и образуемые каждой парой смежных сторон, являются его внутренними углами. Сумма внутренних углов параллелограмма равна 360°, а любые два соседних (последовательных) угла параллелограмма являются дополнительными.

Все ли углы параллелограмма равны?

Нет, у параллелограмма не все углы равны. Существуют две основные теоремы, касающиеся углов параллелограмма, которые утверждают, что противоположные углы параллелограмма равны, а последовательные (смежные) углы являются дополнительными.

Чему равна сумма внутренних углов параллелограмма?

Сумма внутренних углов параллелограмма всегда равна 360°. Согласно свойству суммы углов многоугольников, сумма внутренних углов многоугольника может быть найдена по формуле S = (n — 2) × 180 °, где «n» показывает количество сторон в многоугольнике.