Окружность — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Окружность
2. Надо знать:
• Вписанный угол равен половинедуги, на которую он опирается;
• Если вписанный угол опирается
на диаметр, то он прямой;
• В описанном четырехугольнике
суммы противоположных сторон
равны.
3. Следствие из теоремы синусов
4. Найдите радиус окружности, описанной около прямоугольника, две стороны которого равны 3 и 4.
 5
54
3
Ответ: 2,5
5. Гипотенуза прямоугольного треугольника равна 12. Найдите радиус описанной окружности этого треугольника.
6Ответ:6
6. Найдите диагональ прямоугольника, вписанного в окружность, радиус которой равен 5.
55
Ответ : 10
7. Найдите радиус окружности, описанной около прямоугольного треугольника ABC, если стороны квадратных клеток равны 1.
ОТВЕТ: 2,58. Найдите радиус окружности, вписанной в треугольник ABC, считая стороны квадратных клеток равными 1.
S = p·r5
4
р=6
S=½·3·4=6
Ответ:1
9. В треугольнике ABC ВС=6, угол C равен 90 градусов. Радиус описанной окружности этого треугольника равен 5. Найдите AC.
108
6
Ответ: 8
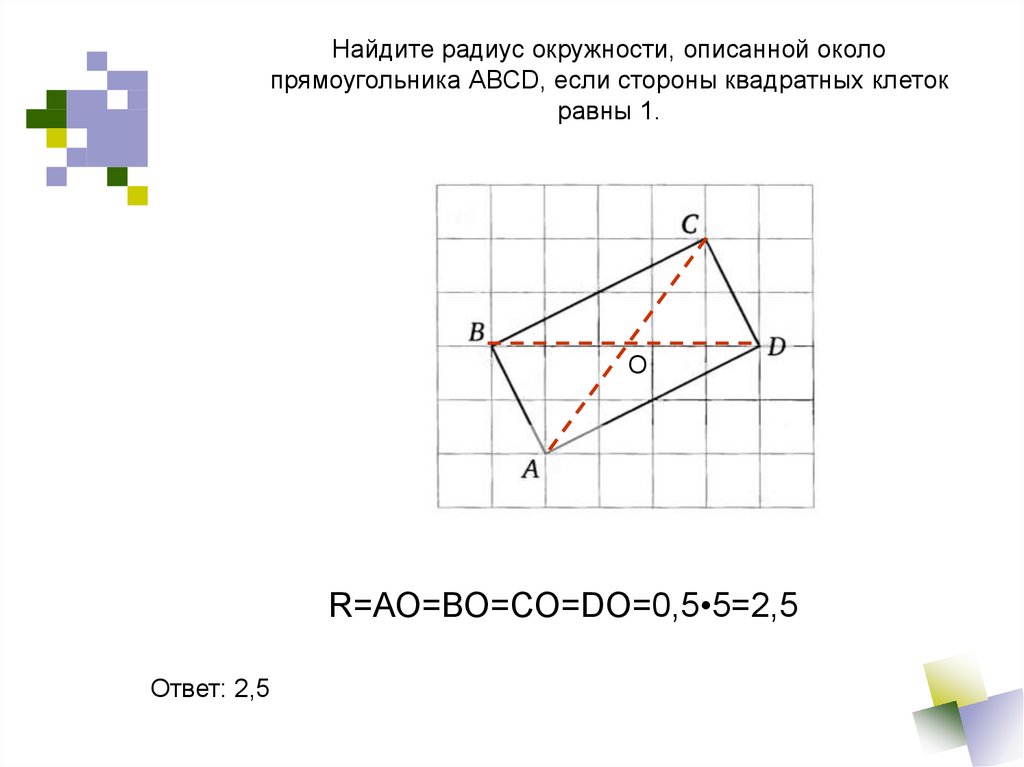
10. Найдите радиус окружности, описанной около прямоугольника ABCD, если стороны квадратных клеток равны 1.
Ответ: 2,511. Угол C треугольника ABC, вписанного в окружность радиуса 3, равен 30 градусов . Найдите сторону AB этого треугольника.
 30
30АВ=6·½=3
Ответ:3
3
12. Одна сторона треугольника равна радиусу описанной окружности. Найдите угол треугольника, противолежащий этой стороне. Ответ дайте в граду
Одна сторона треугольникаравна радиусу описанной
окружности. Найдите угол
треугольника, противолежащий
этой стороне. Ответ дайте в
градусах.
1
sin
2
R
Ответ:30
13. Найдите хорду, на которую опирается угол в 30 градусов, вписанный в окружность радиуса 3.
330
а=6·½=3
Ответ:3
14. В четырехугольник ABCD вписана окружность,АВ=10 , CD=16 . Найдите периметр четырехугольника.
В четырехугольник ABCDвписана окружность,АВ=10 ,
CD=16 . Найдите периметр
четырехугольника.
16
10
В описанном
четырехугольнике суммы
противоположных
сторон равны
Ответ:52
15. В четырехугольник ABCD вписана окружность,АВ=10,ВС=11 и СD=15. Найдите четвертую сторону четырехугольника.
Суммыпротивоположных
сторон равны
15
11
10
Ответ:14
16.
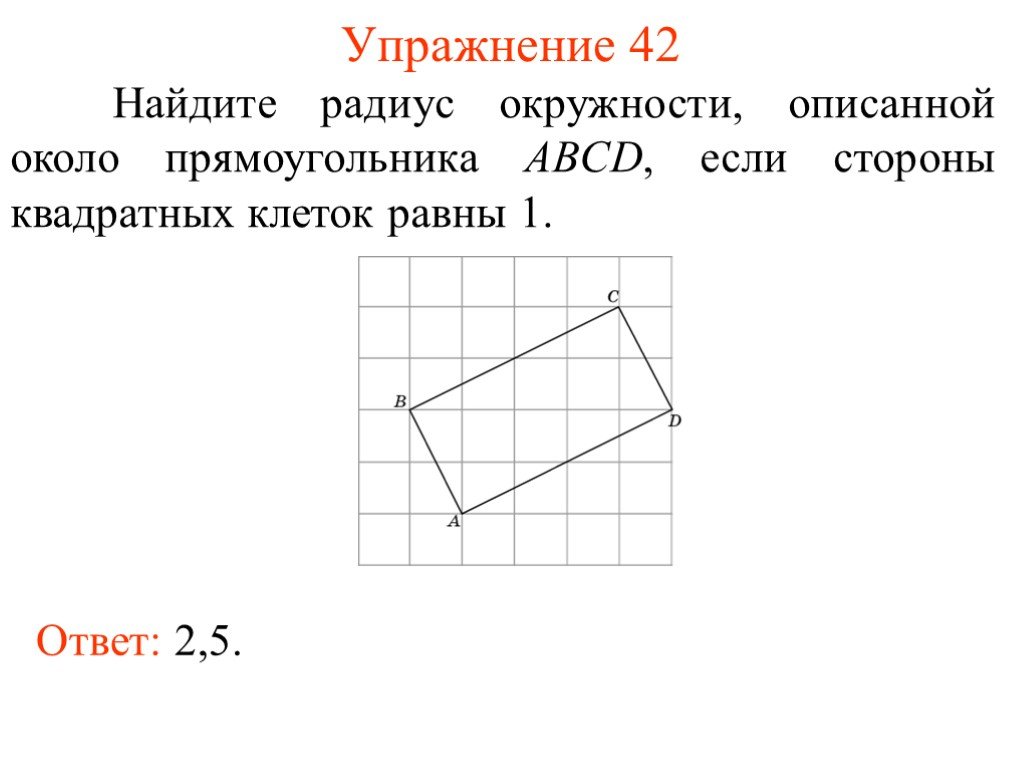 Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.Суммы
Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.Суммыпротивоположных
сторон равны
Ответ:10
17. Точки A, B, C, расположенные на окружности, делят ее на три дуги, градусные величины которых относятся как 1:3:5 . Найдите больший угол треугольн
Точки A, B, C, расположенные наокружности, делят ее на три дуги,
градусные величины которых
относятся как 1:3:5 . Найдите
больший угол треугольника ABC.
Ответ дайте в градусах.
3х
1х
1х+3х+5х=360
x=40
5х
200
Ответ:100
18. Острый угол ромба равен 30 градусов. Радиус вписанной в этот ромб окружности равен 2. Найдите сторону ромба.
S = p·r30
S=½a2
P=2a
19. Интернет ресурсы:
Открытый банк заданий по математикеhttp://mathege.ru:8080/or/ege/Main.acti
on
Картинка:
koms3.edurm.ru/images/42080-eg.jpg
English Русский Правила
Прямоугольник задачи
Прямоугольник. Задачи. Продолжаем рассматривать задания ЕГЭ. В этой заметке рассмотрим примеры с прямоугольниками и квадратами. Решения просты, вопросы связаны нахождением сторон, периметра, диагонали, углов. Необходимо знать свойства этих фигур, также в ходе решения может использоваться квадратное уравнение. Рассмотрим задачи:
Задачи. Продолжаем рассматривать задания ЕГЭ. В этой заметке рассмотрим примеры с прямоугольниками и квадратами. Решения просты, вопросы связаны нахождением сторон, периметра, диагонали, углов. Необходимо знать свойства этих фигур, также в ходе решения может использоваться квадратное уравнение. Рассмотрим задачи:
27601. Площадь прямоугольника равна 18. Найдите его большую сторону, если она на 3 больше меньшей стороны.
Площадь прямоугольника равна произведению его соседних сторон. Обозначим AD как х, тогда DC будет равно х+3. Можем записать:
Решив квадратное уравнение получим кони 3 и –6.
*Так как в условии числа небольшие, то можно обойтись без вычислений и решить её просто методом перебора: стороны могут быть равны 1 и 4, 2 и 5, 3 и 6. Сразу видно, что условию отвечает пара 3 и 6. То есть задачка решается за 10 секунд.
Ответ: 6
27603. Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1 : 2.
Соседние стороны соотносятся как 1 к 2, введём коэффициент пропорциональности х и выразим площадь, получим:
Значит дна сторона равна 3, другая в два раза больше, то есть 6. Периметр будет равен 3+6+3+6=18.
Ответ: 18
27606. Периметр прямоугольника равен 34, а площадь равна 60. Найдите диагональ этого прямоугольника.
Обозначим AD=x, AB=y. Периметр равен:
Площадь равна:
Имеем два уравнения, можем составить систему:
Выразим x во втором уравнении и подставим в первое:
Решая квадратное уравнение:
Значит
Получили, что то стороны равны 5 и 12. По теореме Пифагора вычислим диагональ:
Второй способ:
Обратите внимание! Диагональ у нас равна:
Имеем
Преобразуем первое:
Следовательно:
Ответ: 13
27810.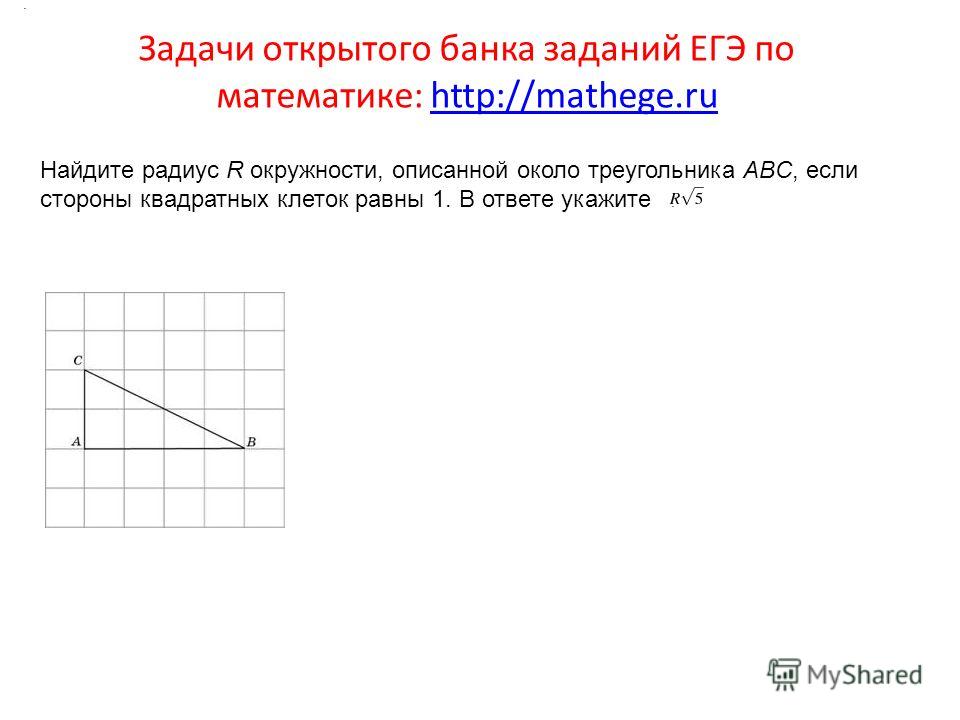 Меньшая сторона прямоугольника равна 6, диагонали пересекаются под углом 600. Найдите диагонали прямоугольника.
Меньшая сторона прямоугольника равна 6, диагонали пересекаются под углом 600. Найдите диагонали прямоугольника.
Вычисляется устно. Так как диагонали пересекаются по углом 600, то треугольники ADO и COB будут являться равносторонними, кроме этого они равны. Значит AD=DO=OB=3, следовательно диагональ равна 6.
Ответ: 6
27811. Найдите диагональ прямоугольника, две стороны которого равны 6 и 8.
По теореме Пифагора:
Ответ: 10
27812. Диагональ прямоугольника вдвое больше одной из его сторон. Найдите больший из углов, которые образует диагональ со сторонами прямоугольника? Ответ выразите в градусах.
Рассмотрим прямоугольный треугольник ACB. Известно, что катет лежащий против угла 30 градусов равен половине гипотенузы. У нас по условию AD равно половине AB, следовательно угол DCB равен 300.
Таким образом, искомый угол равен 600.
Ответ: 60
27813. В прямоугольнике диагональ делит угол в отношении 1:2, меньшая его сторона равна 6. Найдите диагональ данного прямоугольника.
Найдите диагональ данного прямоугольника.
Так как диагональ делит угол в отношении 1 к 2, то можем сделать вывод о том, что углы эти будут равны 300 и 600 (один в два раза больше другого).
Рассмотрим прямоугольный треугольник ADC. Известно, что катет лежащий против угла 300 равен половине гипотенузы. Катет этот равен, то есть AD=6. Следовательно АС=12.
Ответ: 12
27814. Найдите сторону квадрата, диагональ которого равна √8.
Пусть сторона квадрата равна а. По теореме Пифагора:
Ответ: 2
27815. В квадрате расстояние от точки пересечения диагоналей до одной из его сторон равно 7. Найдите периметр этого квадрата.
Расстояние от точки пересечения диагоналей до стороны равно половине стороны, значит сторона будет равна 14. Таким образом периметр равен 14∙4=56.
Ответ: 56
27830. Найдите диагональ прямоугольника, если его периметр равен 28, а периметр одного из треугольников, на которые диагональ разделила прямоугольник, равен 24.
Пусть одна сторона равна а, другая b. Выразим периметр прямоугольника:
Выразим периметр треугольника:
Выразим в первом уравнении:
Подставим во второе, получим:
Это и есть диагональ. То есть нам совсем необязательно вычислять сами стороны.
Ответ: 10
27831. Середины последовательных сторон прямоугольника, диагональ которого равна 5, соединены отрезками. Найдите периметр образовавшегося четырехугольника.
*Понятно, что образовавшийся является ромбом.
Рассмотрим треугольник ADC. В нём HG является средней линией, так как H и G это середины сторон. Известно, что средняя линия треугольника равна половине параллельного ему основания, то есть HG=2,5.
Значит периметр будет равен 4∙2,5=10.
Ответ: 10
27832. В прямоугольнике расстояние от точки пересечения диагоналей до меньшей стороны на 1 больше, чем расстояние от нее до большей стороны. Периметр прямоугольника равен 28.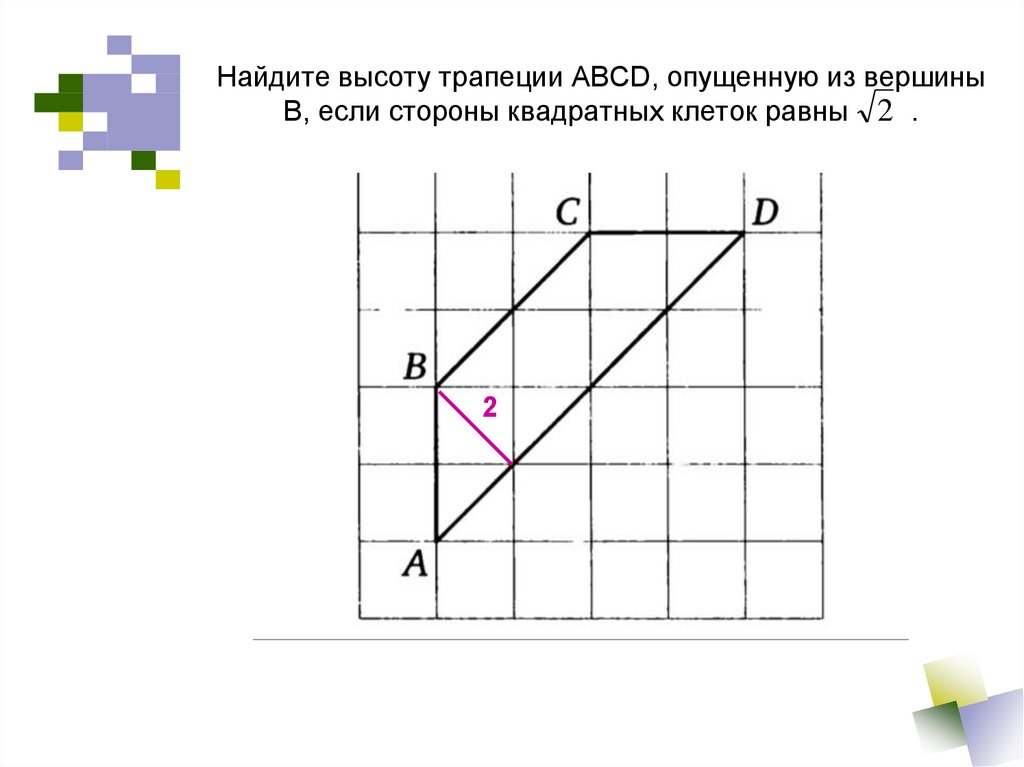 Найдите меньшую сторону прямоугольника.
Найдите меньшую сторону прямоугольника.
Пусть OG=х, тогда OH=х+1. Тогда
Таким образом
Ответ: 6
27947. Найдите радиус окружности, описанной около прямоугольника ABCD, если стороны квадратных клеток равны 1.
Центр описанной окружности лежит на середине диагоналей прямоугольника. По клеткам видно, что диагональ равна пяти. Следовательно радиус равен 2,5.
Ответ: 2,5
27948. Найдите радиус окружности, вписанной в квадрат ABCD, считая стороны квадратных клеток равными √2.
Центр вписанной в квадрат окружности лежит на точке пересечения диагоналей. По рисунку видно, что радиус указанной окружности равен диагонали клетки. Сторона клетки равна корню из двух. По теореме Пифагора:
Ответ: 2
Решить самостоятельно:
27583. Найдите диагональ квадрата, если его площадь равна 2.
Посмотреть решение
27584. Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 4 и 9.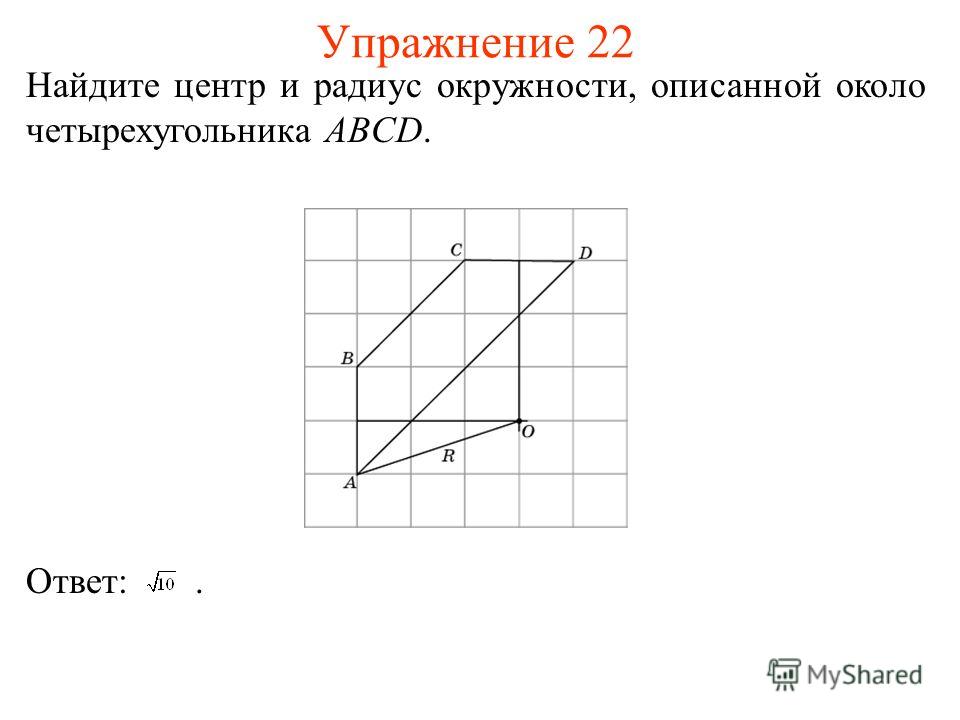
Посмотреть решение
27600. Найдите площадь прямоугольника, если его периметр равен 18, и одна сторона на 3 больше другой.
Посмотреть решение
27602. Найдите площадь прямоугольника, если его периметр равен 18, а отношение соседних сторон равно 1 : 2.
Посмотреть решение
27604. Периметр прямоугольника равен 42, а площадь 98. Найдите большую сторону прямоугольника.
Посмотреть решение
27605. Периметр прямоугольника равен 28, а диагональ равна 10. Найдите площадь этого прямоугольника.
Посмотреть решение
27607. Сторона прямоугольника относится к его диагонали, как 4:5, а другая сторона равна 6. Найдите площадь прямоугольника.
Посмотреть решение
27608. Даны два квадрата, диагонали которых равны 10 и 6. Найдите диагональ квадрата, площадь которого равна разности площадей данных квадратов.
Посмотреть решение
27609. Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в эту окружность?
Посмотреть решение
27610. 2} $, и удовлетворять точкам прямоугольника, так как он также должен лежать на окружности. Используя диаметр и вышеуказанную концепцию, выньте радиус и центр круга. Тогда можно было бы вычесть длину диагонали. Используйте Пифагора, чтобы узнать длину и ширину и, следовательно, площадь. 92} + 10g = 0$
2} $, и удовлетворять точкам прямоугольника, так как он также должен лежать на окружности. Используя диаметр и вышеуказанную концепцию, выньте радиус и центр круга. Тогда можно было бы вычесть длину диагонали. Используйте Пифагора, чтобы узнать длину и ширину и, следовательно, площадь. 92} + 10g = 0$
$ \Rightarrow 16g = 16$
$ \Rightarrow g = 1$
Теперь известно, что один из диаметров окружности равен $4y = x + 7$.
Итак, он проходит через центр окружности и удовлетворяет точке (g, f)
$ \Rightarrow 4f = g + 7$
Теперь подставим значение g в приведенное выше уравнение,
$ \Rightarrow 4f = 1 + 7 = 8$
$ \Rightarrow f = \dfrac{8}{4} = 2$
Итак, центр окружности равен (1, 2). 92} = 80 — 64 = 16$
$ \Rightarrow AD = \sqrt {16} = 4$
Теперь, когда мы знаем, что площадь (A) прямоугольника равна длине (AB), умноженной на ширину (AD) .
$ \Rightarrow A = 8 \times 4 = 32$ Квадратная единица.
Следовательно, вариант (б) правильный.
Примечание. Всякий раз, когда мы сталкиваемся с такого рода вопросами, ключевой концепцией здесь является хорошее понимание общего уравнения окружности. Схематическое представление предоставленной информации помогает лучше понять задействованную геометрию, чтобы помочь найти правильный путь для достижения решения.
Математическая задача: Вписать описанную окружность в квадрат
Найти длину окружности, описанной около квадрата со стороной 10 см. Сравните его с периметром этого квадрата.
Правильный ответ:
d = 0 смПошаговое объяснение:
a=10 o1=4⋅ a=4⋅ 10=40 D=2
⋅ a=2
⋅ 10 = 10 2
≐ 14,1421 r = D/2 = 14,1421/2 = 5 2
≐ 7,0711 d > o1 d = π⋅ D = 3,1416⋅ 14,1421 ≐ 44,42 88=0 см
Вы найти ошибку или неточность? Не стесняйтесь
напишите нам . Спасибо!
Спасибо!
Советы по использованию связанных онлайн-калькуляторов
См. также наш калькулятор прямоугольного треугольника.
См. также наш калькулятор тригонометрического треугольника.
Для решения этой математической задачи необходимо знать следующие знания:
- арифметика
- сравнение
- планиметрия
- Теорема Пифагора
- Прямоугольный треугольник
- Окружность
- Периметр
- треугольник
- квадрат
- диагональ
Уровень задачи:
- практика для 12-летних
- практика для 13-летних
- практика для 14-летних
Рекомендуем посмотреть это обучающее видео по этой математической задаче: видео1 видео2
- Прямоугольник
Прямоугольник имеет длину 21 см и ширину 38 см. Найдите радиус окружности, описанной вокруг прямоугольника. - Фоторамка
Фотография квадратной формы со стороной 20 см обрамлена полосой шириной 4 см. Найдите внешний размер рамки этой фотографии (рамка со всех сторон)
Найдите внешний размер рамки этой фотографии (рамка со всех сторон) - Описанная окружность
Найдите радиус описанной окружности к прямоугольному треугольнику со сторонами 6 см и 3 см. - Десятиугольник
Вычислите площадь и длину окружности правильного десятиугольника, когда его радиус описанной окружности равен R = 1 м - Найдите
Найдите длину стороны квадрата ABCD, вписанного в окружность радиусом k 10 см. - Квадратные круги
Вычислите длину описанного и вписанного круга до квадрата ABCD со стороной 5см. - Конус 3
Конус имеет диаметр x см и наклонную высоту y см. Квадратная пирамида имеет длину стороны основания x см и высоту наклона y см. У кого больше площадь поверхности? Объяснять. - Окруженный 36661
Вычислите длину круга, который окружает квадрат со стороной 3 см - 6 правильный многоугольник
Правильный шестиугольник имеет длину стороны 5 см. Вычислите его площадь. Сравните, на сколько еще см² (квадратных сантиметров) окружность вписана в 6-угольник.

 Найдите внешний размер рамки этой фотографии (рамка со всех сторон)
Найдите внешний размер рамки этой фотографии (рамка со всех сторон)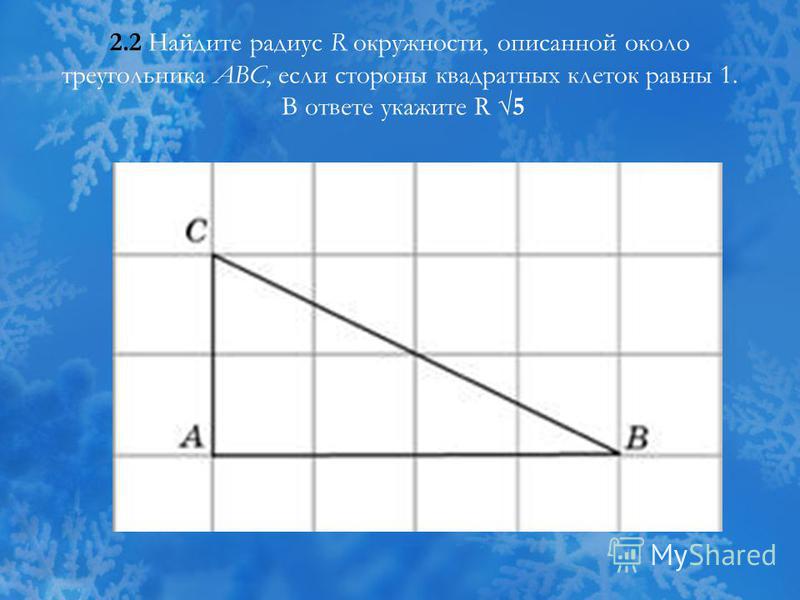
Leave A Comment