Геометрия 7-9 класс. Площадь трапеции — math200.ru
Skip to contentГеометрия 7-9 класс. Площадь трапецииadmin2022-12-21T20:06:20+03:00
Скачать файл в формате pdf.
Геометрия 7-9 класс. Площадь трапеции
Площадь трапеции равна произведению полусуммы оснований на высоту, \(S = \frac{{a + b}}{2}h\).
| Задача 1. Найдите площадь трапеции, основания которой равны 6 и 10, а её высота равна 4. Ответ ОТВЕТ: 32. | |
| Задача 2. Найдите высоту трапеции, основания которой равны 3 и 7, а её площадь равна 20. Ответ ОТВЕТ: 4. | |
| Задача 3. По данным на рисунке найдите площадь трапеции ABCD, если меньшее основание BC = 6. Ответ ОТВЕТ: 54. | |
Задача 4. По данным на рисунке найдите площадь трапеции ABCD. Ответ ОТВЕТ: 264. | |
| Задача 5. По данным на рисунке найдите площадь трапеции ABCD. Ответ ОТВЕТ: 96. | |
| Задача 6. По данным на рисунке найдите площадь трапеции ABCD, если AB = 24. Ответ ОТВЕТ: 190. | |
| Задача 7. По данным на рисунке найдите площадь трапеции ABCD, если AD = 14. Ответ ОТВЕТ: 45. | |
| Задача 8. По данным на рисунке найдите площадь трапеции ABCD. Ответ ОТВЕТ: 144. | |
| Задача 9. По данным на рисунке найдите площадь трапеции ABCD, если её периметр равен 44. Ответ ОТВЕТ: 96. | |
Задача 10. По данным на рисунке найдите площадь трапеции ABCD, если её периметр равен 91. Ответ ОТВЕТ: 382,5. | |
| Задача 11. По данным на рисунке найдите площадь равнобедренной трапеции ABCD, если ВК = 3 и KD = 7. Ответ ОТВЕТ: 21. | |
| Задача 12. По данным на рисунке найдите высоту равнобедренной трапеции CH, если AH = 10 и \({S_{ABCD}} = 38.\) Ответ ОТВЕТ: 3,8. | |
| Задача 13. Найдите площадь трапеции ABCD с основаниями AD = 18 и BC = 10, если площадь треугольника ACD равна 45. Ответ ОТВЕТ: 70. | |
| Задача 14. Найдите площадь трапеции ABCD с основаниями AD = 22 и BC = 8, если площадь треугольника AВC равна 40. ОТВЕТ: 150. | |
| Задача 15. В трапеции ABCD основания AD и ВС относятся как 2 : 1, точка М – принадлежит основанию ВС. Найдите площадь трапеции, если площадь треугольника AMD равна 30. Ответ ОТВЕТ: 45. | |
| Задача 16. В равнобедренной трапеции с основаниями AD = 22 и BC = 8 диагонали перпендикулярны. Найдите площадь трапеции ABCD. Ответ ОТВЕТ: 225. | |
| Задача 17. Ответ ОТВЕТ: 37. | |
| Задача 18. По данным на рисунке найдите площадь трапеции ABCD, если известно, что AB : DC = 3 : 1 и \({S_{\Delta \,EOF}} = 11.\) Ответ ОТВЕТ: 88. Ответ ОТВЕТ: 125. | |
Ответ ОТВЕТ: 108. | |
| Задача 23. Основания трапеции AD и ВС делят отрезок ЕР перпендикулярный к ним на три равные части. Площади треугольников ВЕС и APD равны соответственно 12 и 23. Найдите площадь трапеции ABCD. Ответ ОТВЕТ: 35. | |
Задача 24. В трапеции ABCD AD – большее основание. Прямые, проходящие через середины сторон 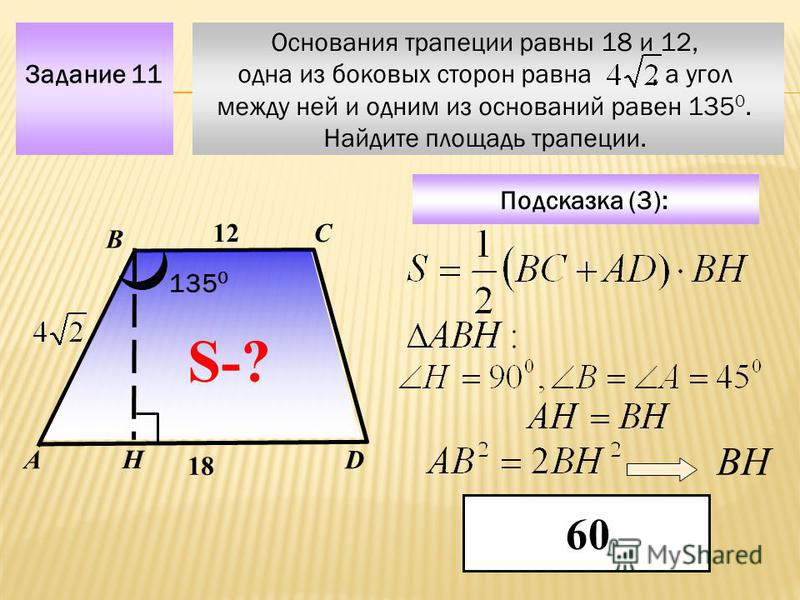 \circ },\) АВ = 8, ВС = 5, AD = 10. Найдите площадь трапеции. \circ },\) АВ = 8, ВС = 5, AD = 10. Найдите площадь трапеции.Ответ ОТВЕТ: 30. | |
Реклама
Мы Вконтакте
Поддержать нас
Как найти площадь трапеции — формулы расчета и онлайн калькуляторы
Формулы для вычисления площади всех видов трапеции, онлайн калькуляторы для расчета. Вывод основной формулы и примеры применения формул в задачах. Удобный справочный материал с подробными объяснениями.
Чему равна площадь трапеции? Трапеция это важная и часто исследуемая геометрическая фигура в курсе геометрии, начиная с 7 класса. В процессе обучения школьники учатся решать задачи по геометрии на нахождение боковых сторон и оснований трапеции, углов и средней линии. Важно уметь находить периметр и площадь трапеции. Рассмотрим чему равна площадь трапеции и решим несколько задач на нахождение площади трапеции.
Содержание
Как найти площадь произвольной трапеции
Площадь трапеции равна произведению полусуммы её оснований на высоту трапеции.
Трапеция ABCD
Единицей измерения площади является квадратная единица длины: м2, см2, кв.ед., км2.
Докажем, что данная формула верна для любой трапеции.
Доказательство 1
Пусть нам дана трапеция , проведем из вершины высоту трапеции на сторону .
Продлим сторону на длину основания получим точку . Продлим сторону трапеции на длину стороны . Получим точку .
Соединим точки и . Трапеция равна трапеции по построению.
Полученный в результате построения четырехугольник — параллелограмм, площадь которого равна двум площадям трапеции :
Отсюда площадь трапеции
так как , то получим:
.
Таким образом, .
Что и требовалось доказать.
Доказательство 2
Достроим трапецию ABCD до прямоугольника, получим прямоугольник .
Площадь трапеции можно получить, если вычесть из площади прямоугольника площади достроенных треугольников.
Построение прямоугольника из трапеции для доказательства
Находим .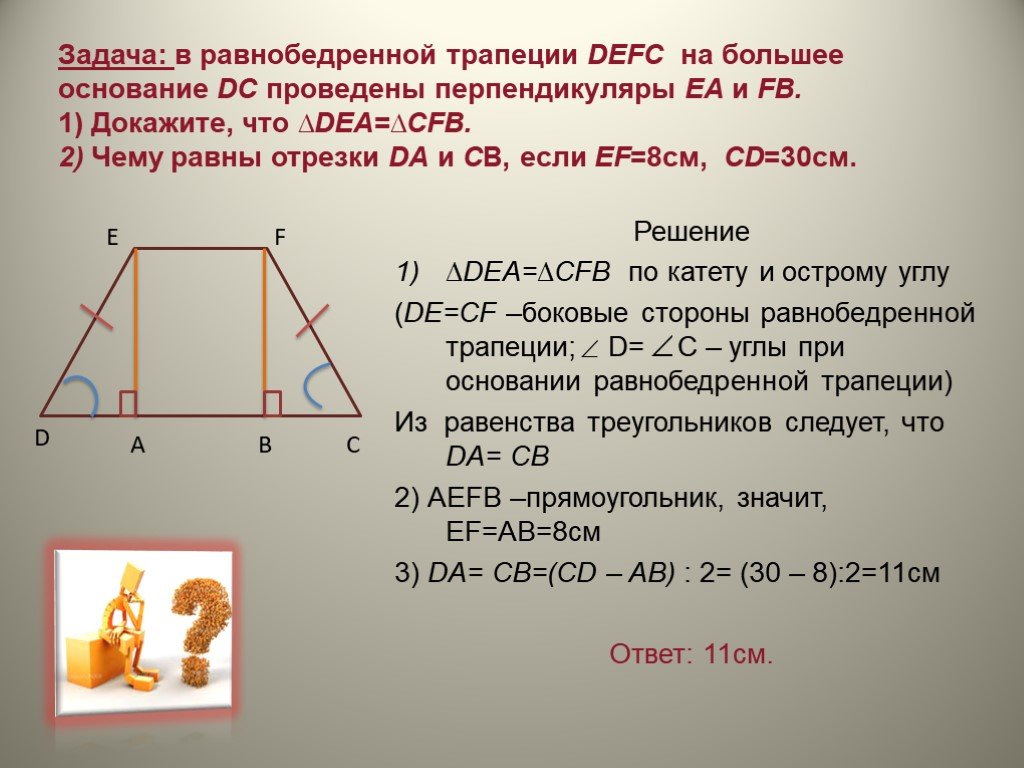
Можно еще привести множество доказательств правильности формулы для площади трапеции, но двух уже достаточно.
Давайте теперь решим несколько задач на нахождение площади трапеции.
Как найти площадь равнобедренной трапеции? Точно также как и площадь любой другой трапеции. Формула одна и та же.
Примеры решения задач
Решим задачи, в которых нужно узнать площадь трапеции.
Задача 1
Вычислить площадь четырехугольника , если известно, что , и боковая сторона перпендикулярна к , а .
Решение.
По последнему условию боковая сторона является высотой трапеции.
Рисунок к задаче 1
Тогда .
Ответ: 30.
Задача 2
Дана трапеция . Известно, что см, , см, а ∠=30°. Найти .
Рисунок к задаче 2 площадь трапеции
Решение:
Для определения площади нам потребуется знать высоту . Определим ее из прямоугольного треугольника . Катет, лежащий напротив угла в 30 градусов равен половине гипотенузы, а, следовательно, см.
Определим . Так как , то получим: см.
Тогда см.
Ответ: 9 см.
Формулы площади трапеции для всех трапеций
Ниже приведем все формулы для определения площади трапеции, которые можно использовать. Однако, многие из них выводятся из основной, приведенной выше и редко используются как самостоятельные. Запоминать их нет необходимости, так как их всегда можно вывести. Однако, если вам дана задача с исходными данными и нужно проверить правильность ее решения, именно с исходными данными (например, даны только длины всех сторон трапеции, а нужно найти ее площадь), то используйте наши онлайн-калькуляторы.
По высоте и основаниям
Проверьте вычисления, используя наш онлайн калькулятор. Десятичные дроби вводите через точку. Ориентируйтесь на обозначения на рисунке.
Введите длину нижнего основания трапеции (на рисунке ) :
Введите длину верхнего основания трапеции (на рисунке ) :
Введите значение высоты трапеции h :
Площадь трапеции
По высоте и средней линии
Если дана высота и средняя линяя трапеции, то ее площадь можно найти по формуле:
где — средняя линия трапеции,
— высота.
Введите высоту трапеции :
Введите длину средней линии :
Площадь трапеции
По известным четырем сторонам
Если известны стороны трапеции , , , , то формула площади:
Вы можете воспользоваться онлайн калькулятором:
Введите сторону :
Введите сторону :
Введите сторону :
Введите сторону :
Площадь трапеции
По известным основаниям и углам при основании
Если известны стороны трапеции , и углы при основании, то формула площади:
Вы можете воспользоваться онлайн калькулятором:
Введите сторону :
Введите сторону :
Введите угол (в градусах) :
Введите угол (в градусах ):
Площадь трапеции
По двум диагоналям и углу между ними
Если известны диагонали трапеции , и угол между ними, то формула площади трапеции:
Если вам известны эти величины, то можно быстро найти площадь, используя наш калькулятор онлайн:
Введите диагональ :
Введите диагональ :
Введите угол (в градусах) :
Площадь трапеции
Площадь прямоугольной трапеции
Если известны основания прямоугольной трапеции , и угол у большего основания, то формула площади трапеции:
Вывод формулы: действительно, для произвольной неравнобедренной и не прямоугольной трапеции площадь по известным основаниям и углам при основании определяется по формуле:
.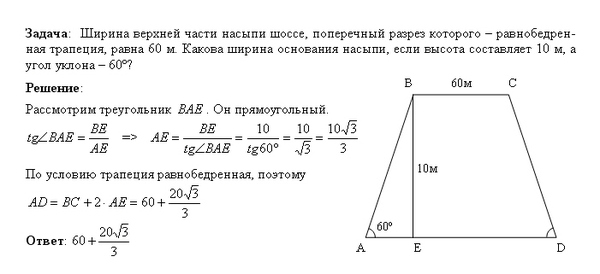
Если угол при основании равен 90 градусов (для прямоугольной трапеции) (пусть это угол ) то получим
.
По формулам приведения
Тогда формула примет вид:
, так как , то окончательно получается:
Если вам известны эти величины, то можно быстро найти площадь, используя наш калькулятор онлайн:
Сторона :
Сторона :
Введите угол (в градусах) :
Площадь трапеции
Площадь равнобедренной трапеции
Площадь равнобедренной трапеции можно найти по любой из вышеприведенных формул, кроме формулы для прямоугольной трапеции, если ввести одинаковые значения для боковых сторон.
Например, формула нахождения площади по известным сторонам, упростится и будет иметь вид:
Сторона :
Сторона :
Сторона :
Площадь трапеции
Таблица формул для определения площади трапеции
Сведем для удобства все формулы в таблицу. Если вам дана прямоугольная или равнобедренная трапеция, вы всегда можете определить ее площадь по любой из формул для неравнобедренной (произвольной) трапеции, просто введите одинаковые значения для боковой стороны.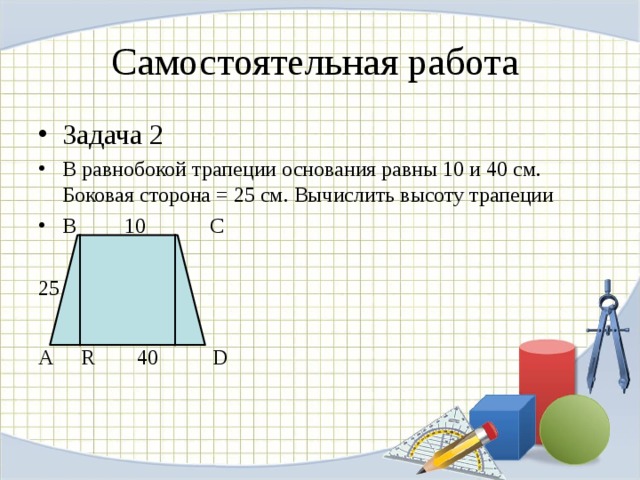
| Известные величины для расчета | Рисунок | Формула |
| Высота и основания | ||
| Высота и средняя линия | ||
| Все стороны | ||
| Основания и углы при основании | ||
| Две диагонали и угол между ними | ||
| Угол при основании 90° (случай прямоугольной трапеции), известен другой угол при основании и основания | ||
| Боковые стороны равны (случай равнобедренной трапеции), известны стороны |
Как найти площадь трапеции
Все математические ресурсы среднего уровня ISEE
6 Диагностические тесты 303 практических теста Вопрос дня Карточки Learn by Concept
Справка по математике среднего уровня ISEE » Геометрия » Плоская геометрия » Четырехугольники » Трапеции » Как найти площадь трапеции
Какова площадь этой трапеции?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы найти площадь трапеции, умножьте одну половину (или 0,5, так как мы работаем с десятичными дробями) на сумму длин ее оснований (параллельных сторон) на ее высоту (перпендикулярное расстояние между основаниями).
Сообщить об ошибке
Найдите площадь трапеции:
Возможные ответы:
Правильный ответ:
Пояснение:
Площадь трапеции можно определить с помощью уравнения .
Сообщить об ошибке
Какова площадь трапеции?
Возможные ответы:
Правильный ответ:
Чтобы найти площадь трапеции, умножьте сумму оснований (параллельных сторон) на высоту (перпендикулярное расстояние между основаниями), а затем разделите на 2.
Сообщить об ошибке
На приведенной выше диаграмме изображен прямоугольник с равнобедренным треугольником. Если является серединой , а площадь оранжевой области равна , то какова длина одной стороны ?
Если является серединой , а площадь оранжевой области равна , то какова длина одной стороны ?
Возможные ответы:
Правильный ответ:
Длина катета равна высоте оранжевой области, которая является трапецией. Назовите эту длину/высоту.
Поскольку треугольник равнобедренный, то , а так как является серединой , . Кроме того, поскольку противоположные стороны прямоугольника конгруэнтны,
Следовательно, оранжевая область представляет собой трапецию с основаниями и высотой . Его площадь равна 72, поэтому мы можем составить и решить это уравнение, используя формулу площади трапеции:
Это длина одной стороны треугольника.
Сообщить об ошибке
Трапеция имеет высоту в дюймах и основания, измеряемые в дюймах и дюймах.
Возможные ответы:
Правильный ответ:
Объяснение:
Используйте следующую формулу с :
Сообщить об ошибке
Найдите площадь трапеции с основаниями 7 и 9 и высотой 2. Пояснение:
Чтобы решить, просто используйте формулу площади трапеции.
Таким образом,
Сообщить об ошибке
Найдите площадь трапеции с основаниями 10 см и 8 см и высотой 4 см.
Возможные ответы:
Правильный ответ:
Объяснение:
Формула для области трапеции:
, где
Следовательно основание в форме равнобедренной трапеции. Если маленькое основание составляет 2 фута, большое основание — 3 фута, а глубина — 8 дюймов, какова площадь основания вашей новой книжной полки?
Если маленькое основание составляет 2 фута, большое основание — 3 фута, а глубина — 8 дюймов, какова площадь основания вашей новой книжной полки?
Возможные ответы:
Невозможно определить по предоставленной информации.
Правильный ответ:
Пояснение:
Недавно вы купили новую книжную полку с основанием в форме равнобедренной трапеции. Если маленькое основание 2 фута, большое основание 3 фута, а глубина 8 дюймов, какова площадь основания вашей новой книжной полки?
Чтобы найти площадь трапеции, нам нужно использовать следующую формулу:
Где a и b — длины оснований, а h — перпендикулярное расстояние от одного основания до другого.
Нам даны a и b, и тогда h будет равно нашей глубине. Сложность заключается в том, чтобы понять, что наша глубина указана в дюймах, а базовая длина — в футах. Нам нужно преобразовать 8 дюймов в футы:
Нам нужно преобразовать 8 дюймов в футы:
Затем подставьте все это в наше уравнение выше.
Итак, наш ответ:
Сообщить об ошибке
На приведенном выше рисунке показан прямоугольник с серединой .
Площадь Четырехугольника равна . Оценивать .
Возможные ответы:
Правильный ответ:
Объяснение:
Самый простой способ увидеть эту задачу — заметить, что площадь четырехугольника равна площади прямоугольника минус площадь прямоугольника.
Площадь прямоугольника равна произведению его длины на ширину:
является серединой , поэтому имеет в качестве основания и высоты и соответственно;
Его площадь — это половина их продукта, или
. Площадь четырехсторонней работы составляет
, так что
Сообщайте о ошибке
Уведомление об авторском праве
Все математические ресурсы среднего уровня Isee
6 60004. Тесты
303 практических теста
Вопрос дня
Карточки
Учитесь по концепции
Тесты
303 практических теста
Вопрос дня
Карточки
Учитесь по концепции
Как найти площадь трапеции (Formula & Video)
Написано
Malcolm McKinsey
, проверенный по факту
Paul Mazzola
Что представляет собой Trapezoid??
Трапеция является четырехугольником с одной парой параллельных сторон. Итак, этот четырехугольник представляет собой плоскую фигуру и замкнутую форму. Он имеет четыре отрезка и четыре внутренних угла. Параллельные стороны — это две 9 трапеции.0315 оснований ; две другие стороны — его ноги.
Обычно трапецию изображают с более длинной параллельной стороной — основанием — горизонтальной.
Перпендикулярная линия от основания к другой параллельной стороне даст вам высоту трапеции или высоту .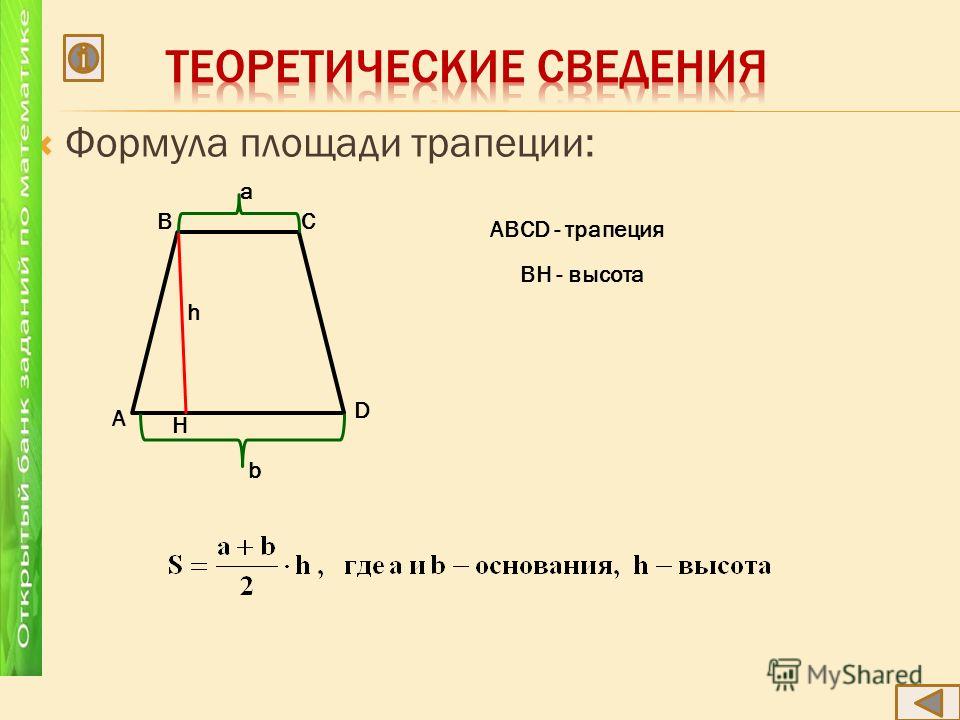
Что такое средний балл по математике?
В математике среднее – это сумма группы чисел, деленная на количество элементов в группе.
Итак, если у вас есть три человека, держащие книги, вы можете найти среднее количество книг, которые они держат, следующим образом:
Мартин держит 5 книг, Мак держит 3 книги, а Мария держит 4 книги. Вместе 12 книг держат 3 человека .
Итак, 12 книг ÷ 3 человека = в среднем по 4 книги у каждого .
Чтобы найти площадь трапеции, нужно найти среднюю длину двух оснований.
Как найти площадь трапеции
Чтобы найти площадь любой трапеции, начните с обозначения ее оснований и высоты. В нашей трапеции обозначьте более длинное основание aa, а более короткое основание b . Отметьте линию, перпендикулярную двум основаниям h для высоты или высоты трапеции.
Площадь трапеции Обратите внимание, мы не обозначили ноги.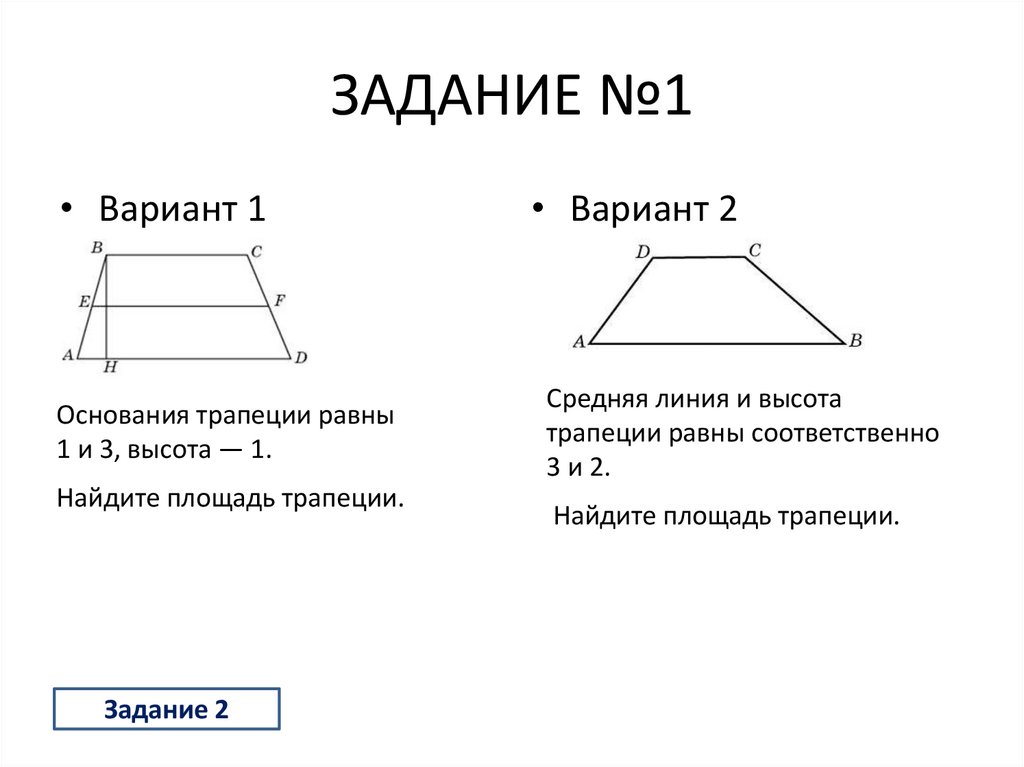 Нам не нужно ничего знать о длине катетов или углах вершин, чтобы найти площадь.
Нам не нужно ничего знать о длине катетов или углах вершин, чтобы найти площадь.
Площадь трапеции формула
Формула площади трапеции представляет собой произведение среднего основания на высоту. В формуле длинные и короткие основания равны a и b , а высота равна h :
. как деление на 222. Мы берем половину суммы длин двух оснований (их среднее значение), а затем умножаем ее на высоту или высоту, чтобы найти площадь в квадратных единицах.
Используя уравнение площади трапеции
Трапеция LMNO имеет параллельные основания LM и NO . Отрезок LM имеет длину 7 см , а отрезок NO имеет длину 13 см . Мы обозначим более длинную сторону NO как a , а более короткую сторону LM как b . Высота ч , 5 см .
Используйте площадь уравнения трапецииСначала подставим эти числа в нашу формулу:
Затем складываем 13 плюс 7 и получаем:
Затем делим на два и получаем:
Наконец, умножаем и получаем ответ:
Площадь этой трапеции 50 квадратных сантиметров .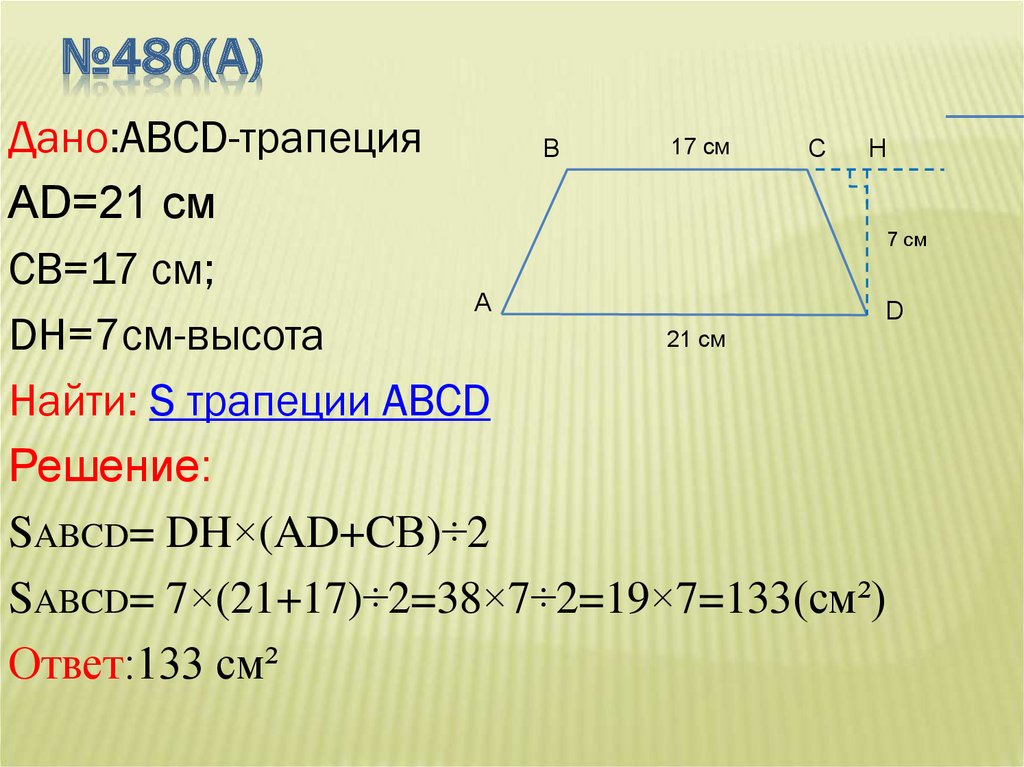
Площадь трапеции примеры
А теперь попробуй! Другая трапеция имеет длинное основание a , 11 метров и более короткое основание б , 7 метров . Его высота ч составляет 9 метров . Какая площадь в квадратных метрах?
Вы получили 81 квадратный метр ? Ваш ответ для площади всегда в квадратных единицах линейного измерения.
Таким образом, трапеция, измеренная в футах, дает площадь в квадратных футах, сантиметры дают квадратные сантиметры и так далее.
Помните, что умножение на ½ равносильно делению на 9.0315 2 , так что вы можете сложить длины оснований, а затем разделить их сумму на два, если вам так проще.
Из-за коммутативного свойства умножения вы можете переставить эти три числа: 12\frac{1}{2}21, высоту h и длину основания a + b в любом порядке для облегчения расчета.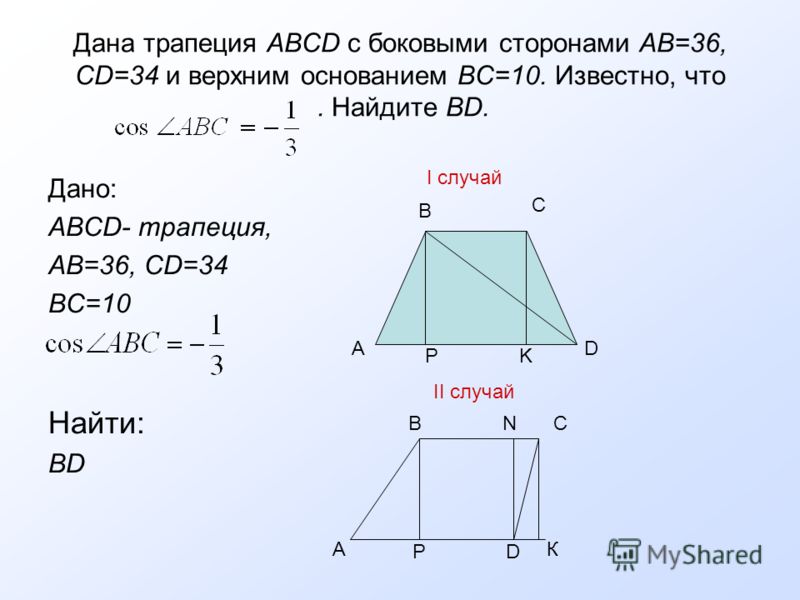

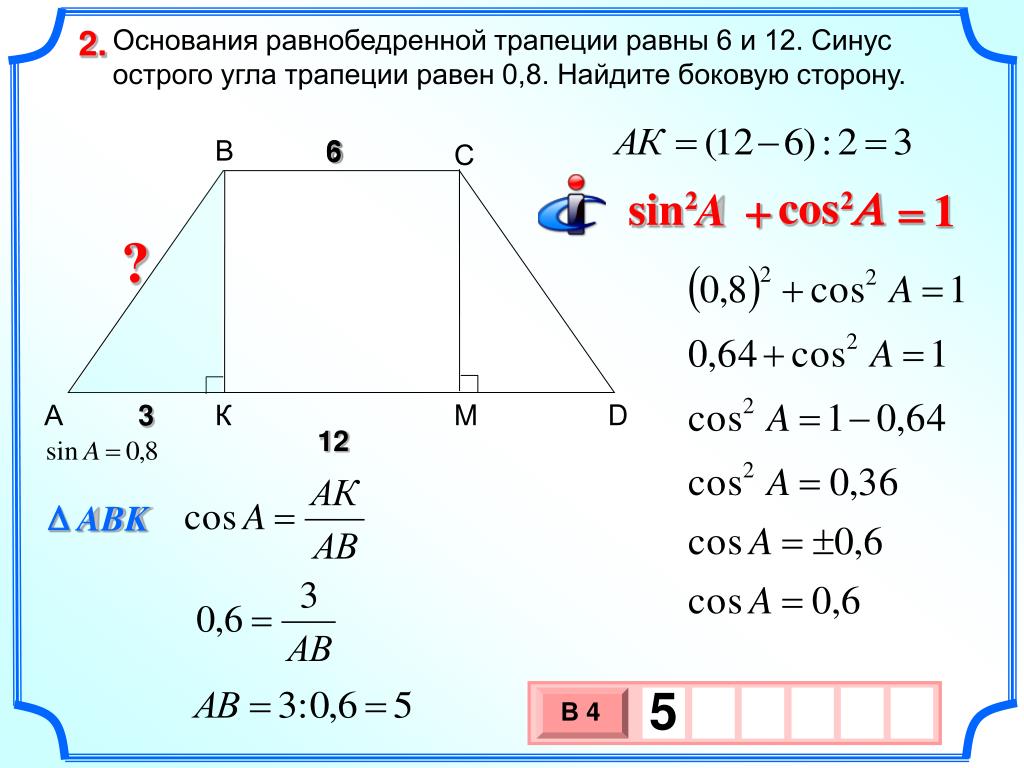
 \circ }.\) Биссектрисы углов С и D пересекаются в точке О, OD = 10, BC = 7, AD = 18. Найдите площадь трапеции.
\circ }.\) Биссектрисы углов С и D пересекаются в точке О, OD = 10, BC = 7, AD = 18. Найдите площадь трапеции.
Leave A Comment