Задание в6
ТРЕУГОЛЬНИК
На клетчатой бумаге с клетками размером
1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
5083.
5085.
5087.
5089.
5093.
5095.
5107.
5113.
5117.
5119.
5123.
5125.
5171.
5173.
5175.
5177.
5179.
5181.
5183.
5185.
5187.
5189.
21337. Найдите площадь треугольника, вершины которого имеют координаты (0;0), (10;8), (8;10).
21339.
21341. Найдите площадь треугольника, изображенного на рисунке.
21863. Найдите площадь треугольника, вершины которого имеют координаты (1;6), (9;6), (7;9).
21865. Найдите площадь треугольника,
вершины которого имеют координаты
(1;6), (9;6), (9;9).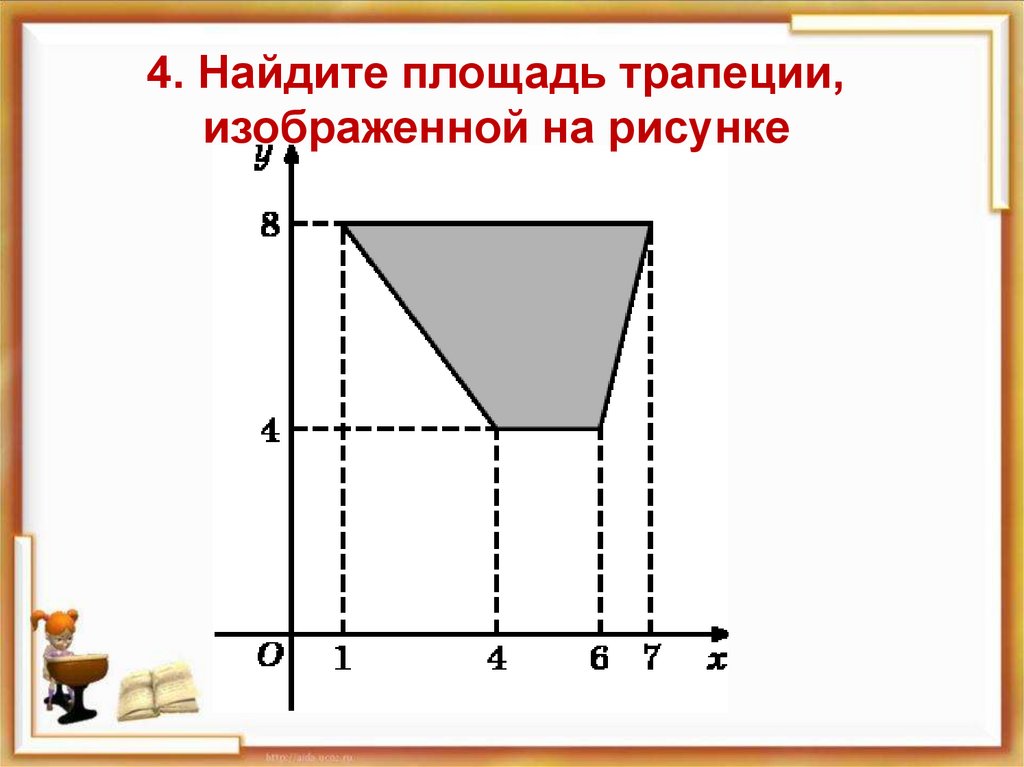
21875. Найдите площадь треугольника, вершины которого имеют координаты (1;6), (10;6), (9;8).
21881. Найдите площадь треугольника, вершины которого имеют координаты (1;7), (3;7), (5;9).
22095. Найдите площадь треугольника, вершины которого имеют координаты (2;7), (6;7), (10;9).
22233. Найдите площадь треугольника, вершины которого имеют координаты (3;7), (5;7), (2;9).
На клетчатой бумаге с клетками размером
1 см 1 см изображена трапеция (см. рисунок). Найдите его площадь в квадратных сантиметрах.
5191.
5193.
5195.
5197.
5199.
5201.
5203.
5205.
5209.
5211.
5215.
5217.
5223.
5241.
5251.
5289.
5291.
22493. Найдите площадь трапеции, вершины которой имеют координаты (1;1), (10;1), (5;7), (1;7).
22495. Найдите площадь трапеции,
вершины которой имеют координаты (1;1),
(10;1), (7;7), (1;7).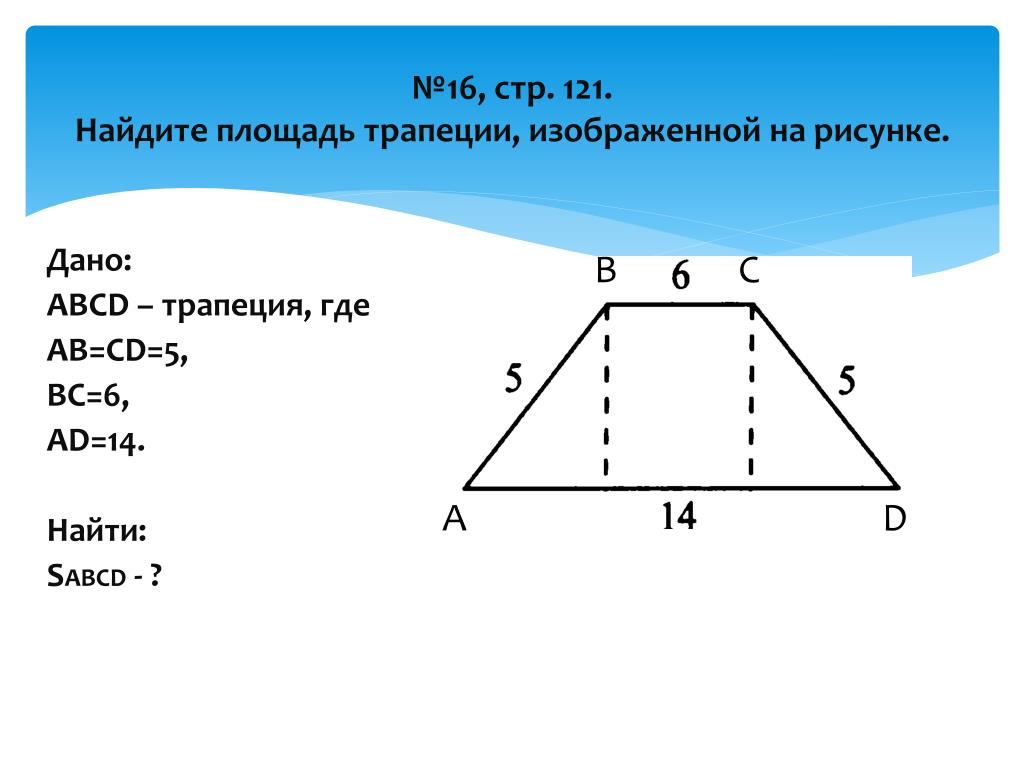
22499. Найдите площадь трапеции, вершины которой имеют координаты (1;1), (10;1), (4;7), (2;7).
22505. Найдите площадь трапеции, вершины которой имеют координаты (1;1), (10;1), (10;7), (2;7).
22533. Найдите площадь трапеции, вершины которой имеют координаты (1;1), (10;1), (9;8), (2;8).
22541. Найдите площадь трапеции, вершины которой имеют координаты (1;1), (10;1), (9;8), (6;8).
22589. Найдите площадь трапеции, изображенной на рисунке.
22601. Найдите площадь трапеции, изображенной на рисунке.
22609. Найдите площадь трапеции, изображенной на рисунке.
22633. Найдите площадь трапеции, изображенной на рисунке.
22785. Найдите площадь трапеции,
изображенной на рисунке.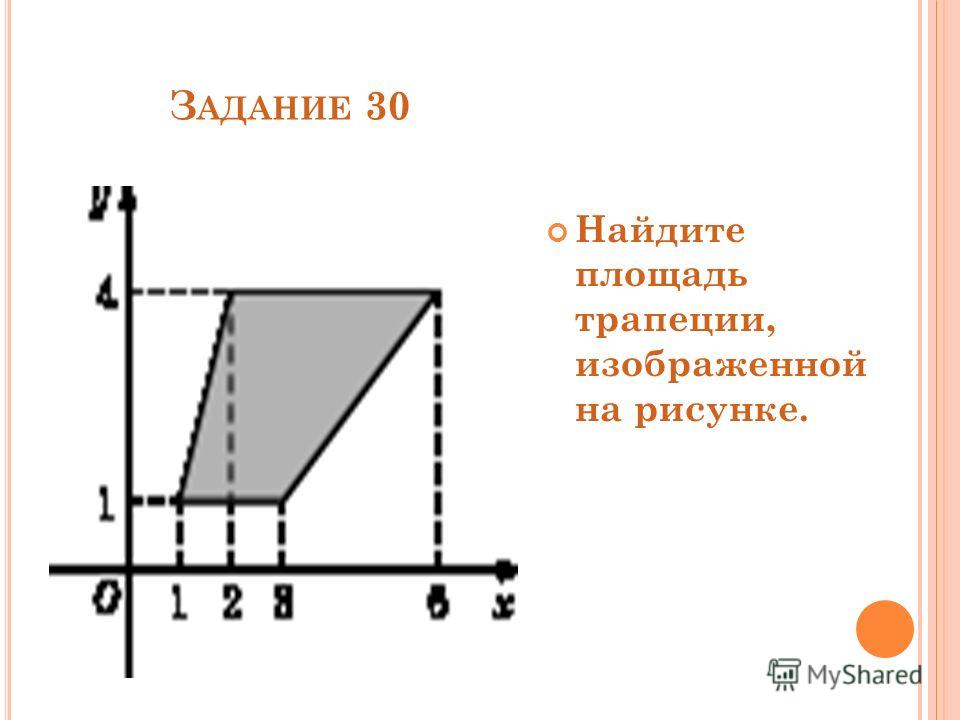
22789. Найдите площадь трапеции, изображенной на рисунке.
23127. Найдите площадь трапеции, изображенной на рисунке.
21343. Найдите площадь четырехугольника, вершины которого имеют координаты (8;0), (9;2), (1;6), (0;4).
21345. Найдите площадь четырехугольника, вершины которого имеют координаты (8;0), (9;1), (1;9), (0;8).
21347. Найдите площадь четырехугольника, вершины которого имеют координаты (9;0), (10;9), (1;10), (0;1).
21351. Найдите площадь четырехугольника, изображенного на рисунке.
21353. Найдите площадь четырехугольника, изображенного на рисунке.
21359. Найдите площадь четырехугольника, вершины которого имеют координаты (1;7), (8;2), (8;4), (1;9).
21361.
21369. Найдите площадь четырехугольника, вершины которого имеют координаты (1;7), (4;4), (4;6), (1;9).
21395. Найдите площадь четырехугольника, вершины которого имеют координаты (1;7), (9;8), (9;10), (1;9).
24223. Найдите площадь четырехугольника, вершины которого имеют координаты (6;3), (9;4), (10;7), (7;6).
24233. Найдите площадь четырехугольника, вершины которого имеют координаты (7;3), (9;4), (10;6), (8;5).
24241. Найдите площадь четырехугольника, изображенного на рисунке.
24243. Найдите площадь четырехугольника, изображенного на рисунке.
РАЗНОЕ
24253. Найдите площадь закрашенной
фигуры на координатной плоскости.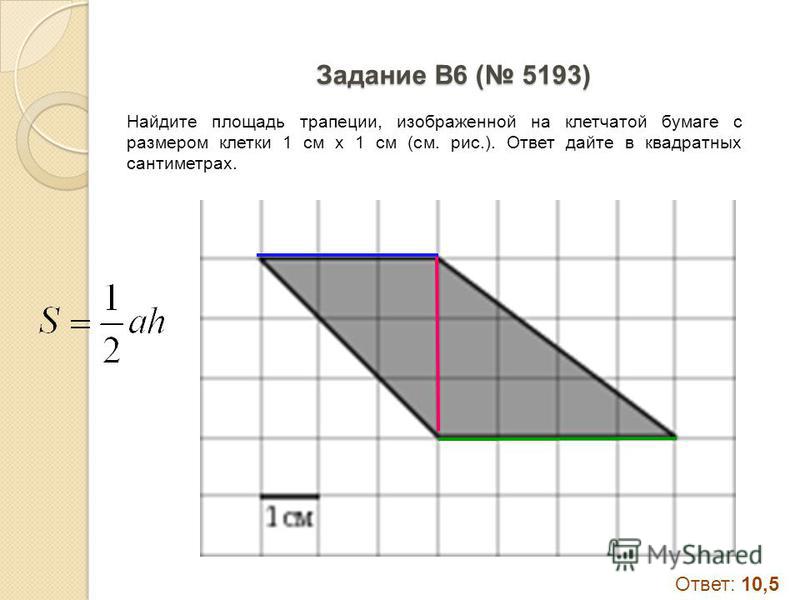
24259. Найдите площадь закрашенной фигуры на координатной плоскости.
24261. Найдите площадь закрашенной фигуры на координатной плоскости.
22267.
Контрольные работы по геометрии 8 класс | Методическая разработка по геометрии (8 класс) по теме:
Опубликовано 12.11.2012 — 17:50 — Захарова Татьяна Александровна
материал соответствует базовому уровню подготовки учащихся
Скачать:
Предварительный просмотр:
Административная контрольная работа по теме «Площадь многоугольника» Вариант 1. 1.Найдите площадь трапеции, изображенной на рисунке: 2. Найдите площадь треугольника, изображенного на рисунке: 3. Найдите площадь параллелограмма, изображенного на рисунке: 4. 5. В треугольнике . Высота делит сторону АС на отрезки и , причем =9см. Найдите площадь | Административная контрольная работа по теме «Площадь многоугольника» Вариант 2. 1.Найдите площадь трапеции, изображенной на рисунке: 2. Найдите площадь треугольника, изображенного на рисунке: 3. Найдите площадь параллелограмма, изображенного на рисунке: 4.Высота , проведенная к стороне параллелограмма, делит эту сторону на два отрезка и . Найдите площадь параллелограмма, если . 5. В треугольнике . Высота . Найдите площадь |
Административная контрольная работа по теме «Площадь многоугольника» Вариант 1. 1.Найдите площадь трапеции, изображенной на рисунке: 2. 3. Найдите площадь параллелограмма, изображенного на рисунке: 4.Смежные стороны параллелограмма равны 22 и 30 см, а острый угол равен 30. Найдите площадь параллелограмма. 5. В треугольнике . Высота делит сторону АС на отрезки и , причем =9см. Найдите площадь | Административная контрольная работа по теме «Площадь многоугольника» Вариант 2. 1.Найдите площадь трапеции, изображенной на рисунке: 2. Найдите площадь треугольника, изображенного на рисунке: 3. Найдите площадь параллелограмма, изображенного на рисунке: 4.Высота , проведенная к стороне параллелограмма, делит эту сторону на два отрезка и . Найдите площадь параллелограмма, если . 5. В треугольнике . Высота . Найдите площадь |
По теме: методические разработки, презентации и конспекты
Контрольные работы по геометрии 8 класс
Готовые контрольные работы для проверки знаний и умений учащихся по геометрии 8 класс по учебнику Атанасяна. …
…
Контрольные работы по геометрии 7 класс
Мною оформлены контрольные работы по геометрии для учащихся 7 класса, занимающихся по учебнику Л.С.Атанасяна.Использовала пособие для учителей общеобразовательных учреждений «Изучение геометрии …
Подготовка к ЕГЭ. Контрольная работа по геометрии, 11 класс.
Итоговое повторение. Контрольная работа по геометрии на 6 вариантов, составленная по материалам «Открытого банка заданий по математике» http://mathege.ru…
Итоговая контрольная работа по геометрии для 10 класса
ИКР расчитана на 2 урока (УМК по учебнику Атанасяна)…
Контрольные работы по геометрии 9 класс
Мною разработаны контрольные работы по геометрии для 9 класса по учебнику Л.С.Атанасяна..Использованная литература: Изучение геометрии в 7-9 классах.Пособие для учителей общеобразоват. учреждений/Л.С….
Контрольная работа по геометрии 8 класс Учебник А.Г.Мерзляк «Геометрия 8 класс»
Это первая контрольная работа по теме «Параллелограм и его виды». ..
..
Контрольная работа по геометрии 8 класс Учебник А.Г.Мерзляк «Геометрия 8 класс»
Первая контрольная работа по теме «Параллелограм и его виды»…
Поделиться:
Площадь трапеции: Формула и примеры
Давайте узнаем, как найти площадь трапеции .
Что такое трапеция?
Трапеция представляет собой четырехстороннюю плоскую фигуру с одной парой параллельных сторон, называемых ее основаниями . Высота (также называемая высотой ) трапеции перпендикулярна ее основаниям. Две другие непараллельные стороны называются ножками . Примерами предметов в форме трапеции являются цветочные горшки, сумки, ведра и другие архитектурные вещи.
См. иллюстрацию трапеции ниже.
Как найти площадь трапеции
Площадь двумерной фигуры относится к общему объему пространства, заключенного внутри этой фигуры. Он измеряется в кубических единицах, таких как м 2 , см 2 , км 2 , а в 2 . Перед вычислением убедитесь, что все единицы одинаковы.
Он измеряется в кубических единицах, таких как м 2 , см 2 , км 2 , а в 2 . Перед вычислением убедитесь, что все единицы одинаковы.
Связанные материалы: Площадь круга – формула и примеры
Чтобы найти площадь трапеции , умножьте среднее значение двух оснований (параллельных сторон) трапеции на ее высоту, как указано в этой формуле:
A = ( a + b ) / 2 • h
Где:
A = площадь трапеции
a = длина основания трапеции 1
b = длина основание трапеции 2
h = высота трапеция
Пример #1: Нахождение площади трапеции при заданных измерениях в одних и тех же единицах измерения
Найдите площадь трапеции при следующих измерениях:
a = 10 см, b = 8 см, h = 6 см
Решение примера №1:
Шаг 1. Запишите данные числа: a = 10 см, b = 8 см, h = 6 см.
Запишите данные числа: a = 10 см, b = 8 см, h = 6 см.
Шаг 2. Подставьте цифры в формулу. Аналог 10см для a , 8 см для b и 6 см для ч .
A = ( a + b ) / 2 • h
= (10 см + 8 см) / 2 • (6 см)
Шаг 3. Упрощение.
A = 18 см / 2 • (6 см)
= 9 см • 6 см
A = 54 см 2
Следовательно, площадь трапеции это 54см 2 .
Пример #2: Нахождение площади трапеции при заданных измерениях в разных единицах измерения
Найдите площадь трапеции, приведенной ниже.
Решение примера №2:
Шаг 1. Запишите данные измерения: a = 5 ярдов, b = 126 дюймов, ч = 4 ярда.
Шаг 2 . Поскольку все единицы измерения должны быть одинаковыми, преобразуйте 126 дюймов в ярды.
Напомним: 1 ярд = 36 дюймов. Запишите преобразование в виде дроби, равной 1: (1 ярд / 36 дюймов) = 1,
126 дюймов • (1 ярд / 36 дюймов) = 126 дюймов • (1 ярд / 36 дюймов ) = 126 ярдов / 36 = 3,5 ярда
Таким образом, преобразованное значение 9000 3 б это 3,5 ярда .
Шаг 3. Подставьте измерения в формулу. Замените 5 ярдов на a , 3,5 ярда на b и 4 ярда на 9004. 0 ч .
А = ( а + б ) / 2 • h
= (5 ярдов + 3,5 ярда) / 2 • (4 ярда)
Шаг 4. Упростить.
A = 8,5 ярда / 2 • (4 ярда)
= 4,25 ярда • 4 ярда
A = 17 ярдов 2 9000 5
Следовательно, площадь трапеции равна 17 ярдов 2 .
Пример №3. Нахождение основания трапеции
Найдите другое основание трапеции площадью 71,5 см 2 , высота 6,5 см, основание 9 см.
Решение примера №3:
Шаг 1. Напишите формулу площади трапеции: A = ( a + b ) / 2 • 9 0040 ч ИЛИ А = ( a + b )h / 2.
Используйте последнее, чтобы найти недостающее основание.
Шаг 2. Пусть a будет недостающим основанием. Подставьте данные измерения в формулу.
Временно удалите юниты, чтобы избежать путаницы.
A = ( a + b )h / 2
71,5 = ( a + 9) (6,5) / 2
Шаг 3. Упростить.
Сначала умножьте 6,5 см на выражение ( a + 9).
71,5 = (6,5 a + 58,5) / 2
Умножьте обе части уравнения на 2. 0178 ]
143 = 6,5 a + 58,5
Вычтите 58,5 с обеих сторон.
143 – 58,5 = 6,5 a + 58,5 – 58,5
85 = 6,5 a
Разделите обе части на 6,5.
85 / 6,5 = 6,5 a / 6,5
13 = a
Следовательно, длина другого основания равна 9000 3 13см .
Проверка решения примера №3:
Подставьте измерения в формулу площади трапеции.
A = ( a + b ) ч / 2
71,5 см 2 = [(13 см + 9 см) (6,5 см)] /2
71,5 см 2 = [(22 см) (6,5 см)] / 2
Упростить.
71,5 см 2 = 143 см 2 / 2
71,5 см 2 = 71,5 см 2
Спасибо для чтения. Мы надеемся, что это эффективно! Всегда не стесняйтесь возвращаться на эту страницу, если у вас возникнут вопросы о площади трапеции .
Ознакомьтесь с некоторыми другими сообщениями в нашем блоге или инвестируйте в свое будущее с помощью одного из наших курсов самообучения!
Нажмите здесь, чтобы ознакомиться с руководством по подготовке к экзамену AP по программе Calculus AB 2021 !Математическое выражение: площадь трапеции
00:00:03. 150
150
В этом уроке мы узнаем о площади трапеции.
00:00:08.030
Во-первых, давайте рассмотрим эту трапецию с высотой «h» и двумя параллельными сторонами, «a» и «b» соответственно.
00:00:17.140
Теперь, чтобы найти площадь трапеции A, сначала мы сложим «a» и «b» и разделим сложенные числа на 2.
00:00:27.010
Это дает (a+b)/2. Затем мы умножаем (a+b)/2 на высоту трапеции «h».
00:00:38.070
Следовательно, теперь у нас есть формула площади трапеции, A = ((a+b)/2)h.
00:00:47.240
Обратите внимание на то, что очень важно включить устройство. Поскольку это формула площади, ее единица измерения будет в виде квадратной единицы.
00:00:57.020
Мы увидим больше пояснений по этому поводу в следующем примере.
00:01:02.040
Теперь давайте рассмотрим несколько примеров использования этой формулы.
00:01:07.030
Найдите площадь этой трапеции, если ее высота равна 4 см, а параллельные стороны равны 5 см и 9 см соответственно.
00:01:17.080
Сначала начнем с формулы площади трапеции A = ((a+b)/2)h.
00:01:26,080
Поскольку более короткая параллельная сторона равна 5 см, мы можем заменить «а» на 5.
00:01:33,150
Аналогично, поскольку длинная параллельная сторона равна 9см, мы можем заменить ‘b’ на 9.
00:01:41.230
Далее мы можем упростить, добавив 5 к 9. Это даст 14.
00:01:48.110
14 разделить на 2, даст 7.
00:01:52.200
Теперь, поскольку высота равна 4 см, мы можем заменить «h» на 4.
00:01:59.120
Умножение 7 на 4 дает 28.
00:02:03. 180
Обратите внимание, что это число не имеет значения, если мы не включим для него единицу измерения.
00:02:08.160
Поскольку стороны трапеции выражены в сантиметрах, единицей измерения площади будет квадрат
сантиметра.
00:02:15.160
Следовательно, площадь этой трапеции равна 28 квадратных сантиметров.
00:02:23.050
Следующий пример, учитывая, что площадь этой трапеции составляет 9 квадратных футов, а ее параллельные стороны равны 2 футам и 4 футам соответственно. Найдите его высоту.
Найдите его высоту.
00:02:34.200
Снова начнем с формулы площади трапеции A = ((a+b)/2)h.
00:02:44.040
Теперь, когда площадь и две параллельные стороны известны, мы можем найти высоту, решив это уравнение относительно h. Вот как.
00:02:53,240
Поскольку площадь равна 9 квадратных футов, мы можем заменить «А» на 9,
00:03:00,100
Аналогично, поскольку более короткая параллельная сторона равна 2 см, мы можем заменить ‘a’ на 2.
00:03:08.100
Опять же, поскольку более длинная параллельная сторона равна 4 см, мы можем заменить ‘b’ на 4.
00:03:16.150
Мы можем упростить это уравнение, сложение 2 с 4. Это дает 6. 6 разделить на 2, дает 3.
00:03:27.130
(3)h равно 3h.
00:03:32.010
Теперь у нас 3h равно 9.
00:03:36.140
Давайте перепишем это уравнение, чтобы оно выглядело аккуратнее.
00:03:40.190
Чтобы найти «h», нам нужно удалить 3. Мы можем сделать это, разделив обе части уравнения на 3.

 Смежные стороны параллелограмма равны 22 и 30 см, а острый угол равен 30. Найдите площадь параллелограмма.
Смежные стороны параллелограмма равны 22 и 30 см, а острый угол равен 30. Найдите площадь параллелограмма. Найдите площадь треугольника, изображенного на рисунке:
Найдите площадь треугольника, изображенного на рисунке:
Leave A Comment