№ 3 ЕГЭ профиль / vivat2.okis.ru
Локация Главная страница Карта сайта
Весомость заданий Шкала перевода баллов Продолжение шкалы перевода
Прототипы задания 3 профиля ЕГЭ — 2021(№ 8,15 базового уровня)
Тема заданий № 3 «Квадратная решетка. Координатная плоскость»
Типы заданий № 3: многоугольники: вычисление длин и углов здесь и здесь и здесь многоугольники: вычисление площадей здесь и здесь и здесь и здесь круг и его элементы здесь и здесь координатная плоскость здесь и здесь
Вид задания: с кратким ответом. Уровень сложности: базовый. Количество баллов: 1. Примерное время на выполнение: 2 минуты. Средний процент выполнения: в 2019 году 93,3%, в 2020 году 89,8%. Ответом к заданию 3 по математике может быть целое число или конечная десятичная дробь. Требования ФИПИ к профильному уровню здесь Соответствие заданий в КИМах базового и профильного уровня здесь
За заданием № 3 негласно закрепилось название «фигура на бумаге в клетку». В этом задании чаще всего представлена какая-либо фигура (круг, четырехугольник, треугольник или угол) на клетчатой бумаге.
Тригонометрические функции острого угла прямоугольного треугольника– это не только часть планиметрических задач №3 и №6, но и ряд задач про геометрический смысл производной (№7), задачи, где требуется вычислить значения тригонометрических функций (№9 и даже №10).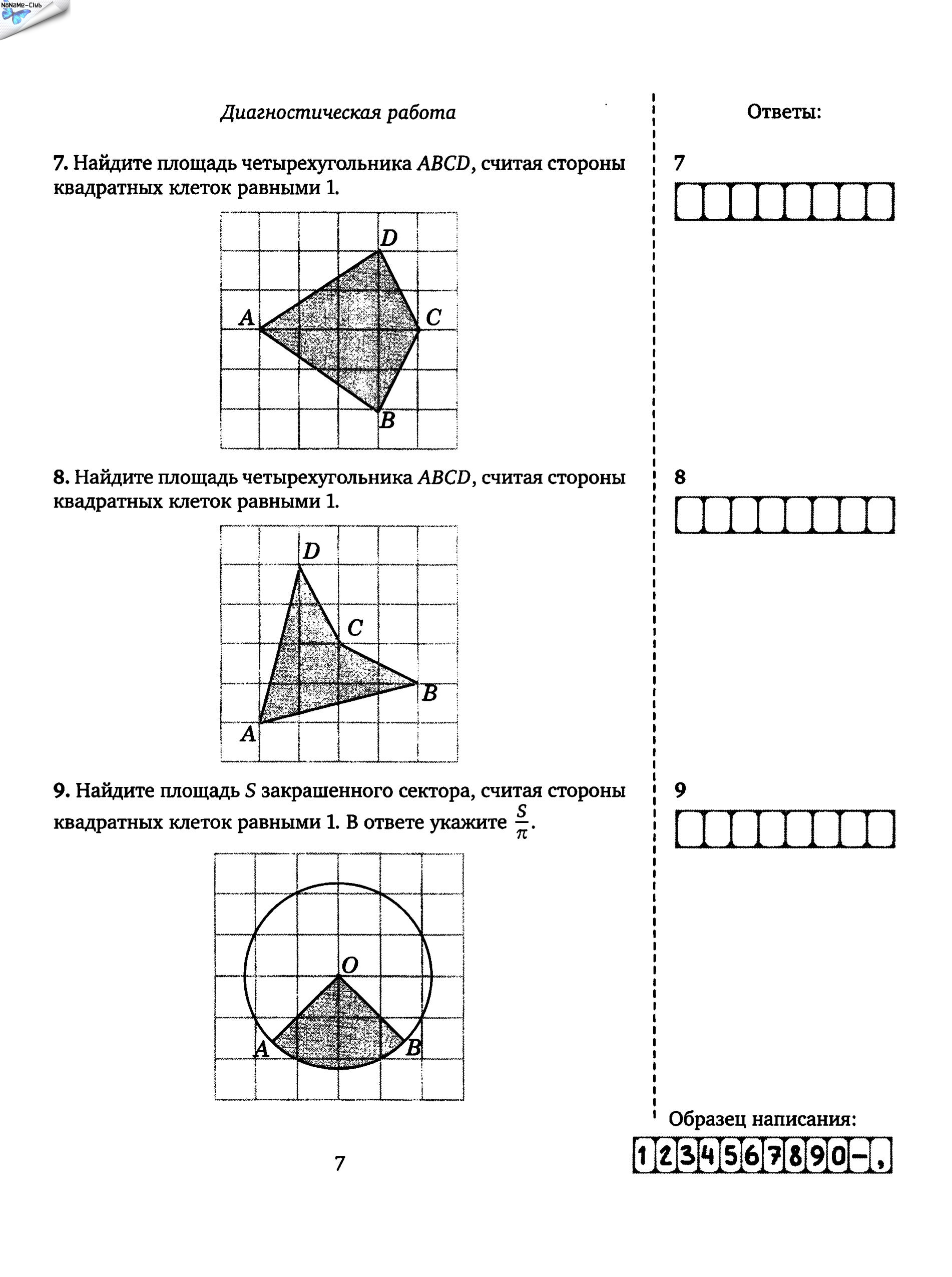
В заданиях №3 встречаются фигуры: угол, все виды треугольников, произвольный выпуклый четырехугольник, трапеция (в том числе равнобедренная и прямоугольная), параллелограмм, прямоугольник, ромб, квадрат, круг. При решении надо учитывать, что размер клетки 1*1см. В заданиях это указано. Очень редко попадаются другие размеры клетки – надо внимательно читать задание. По умолчанию считается, что ученик легко находит на бумаге в клетку углы в 180, 135, 90 и 45 градусов.
Вершины многоугольников и центры окружностей во всех заданиях лежат в вершинах клеток (имеют целые координаты). Однако концы искомых отрезков, например, средней линии трапеции, могут иметь произвольные координаты. Но всё очень легко вычисляется по формулам.
При подготовке полезно пользоваться справочными материалами, даже если вам все это давно и отлично знакомо. В самый ответственный момент эта привычка может оказаться полезной. Во время решения третьего задания на экзамене большинство сдающих еще находятся в состоянии стресса от процедуры начала экзамена. Поэтому навык использования справочных материалов снижает риск ошибки и даже оказывает некоторую психологическую поддержку. Определения, а также свойства фигур и их элементов, в справочных материалах на ЕГЭ не даются. Их надо знать. Все они изучаются в курсе геометрии за 7-8 класс. При подготовке к экзамену полезно выписать из учебника теоремы и время от времени перечитывать их.
Поэтому навык использования справочных материалов снижает риск ошибки и даже оказывает некоторую психологическую поддержку. Определения, а также свойства фигур и их элементов, в справочных материалах на ЕГЭ не даются. Их надо знать. Все они изучаются в курсе геометрии за 7-8 класс. При подготовке к экзамену полезно выписать из учебника теоремы и время от времени перечитывать их.
Сложных вычислений в третьем задании нет. Бывают задания, где достаточно знать определение, а искомую величину можно отсчитать по клеточкам. Если решение получается в несколько действий – ищите способ проще. Большинство задач можно решить несколькими способами.
Чтобы решить задание 3 необходимо: 1. Уметь вычислять площадь фигуры, 2. Уметь вычислять градусные меры углов, 3. Уметь вычислять периметры, 4. Знать, что длина средней линии трапеции находится по формуле l= (a+b)/2 5. Знать, что можно воспользоваться формулой Пика S = В + Г/2 — 1 , где S — площадь многоугольника, В — количество узлов сетки, лежащих внутри многоугольника,
Тесты. Вычисление углов: 1) здесь ответ 2) здесь
ответ 3) здесь решение 4) здесь
решение 5) здесь решение 6) здесь решение 7) здесь решение 8) здесь решение 9) здесь решение 10) здесь решение 11) здесь
решение 12) здесь здесь Вычисление длин: 1) здесь решение 2) здесь
решение 3) здесь решение 4) здесь решение 5) здесь
здесь 6) здесь решение 7) здесь решение Вычисление площадей: 1) здесь решение 2) здесь решение 3) здесь решение 4) здесь решение 5) здесь решение 6) здесь
решение 7) здесь здесь 8) здесь решение 9) здесь решение 10) здесь решение 11) здесь здесь 12) здесь здесь Вычисление элементов круга: 1) здесь решение 2) здесь решение 3) здесь
решение 4) здесь решение 5) здесь решение 6)здесь решение 7) здесь решение 8)здесь решение 9)здесь решение 10) здесь
решение 11) здесь решение 12) здесь здесь 13) здесь решение 14) здесь решение 15) здесь решение 16) здесь решение 17) здесь решение Вычисления на координатной плоскости: 1)здесь решение 2) здесь решение 3) здесь решение 4) здесь
решение 5) здесь
решение 6) здесь решение 7) здесь решение 8) здесь решение 9) здесь решение 10) здесь решение 11) здесь
решение 12) здесь решение 13) здесь решение 14) здесь решение 15) здесь
решение 16) здесь решение
Вычисление углов: 1) здесь ответ 2) здесь
ответ 3) здесь решение 4) здесь
решение 5) здесь решение 6) здесь решение 7) здесь решение 8) здесь решение 9) здесь решение 10) здесь решение 11) здесь
решение 12) здесь здесь Вычисление длин: 1) здесь решение 2) здесь
решение 3) здесь решение 4) здесь решение 5) здесь
здесь 6) здесь решение 7) здесь решение Вычисление площадей: 1) здесь решение 2) здесь решение 3) здесь решение 4) здесь решение 5) здесь решение 6) здесь
решение 7) здесь здесь 8) здесь решение 9) здесь решение 10) здесь решение 11) здесь здесь 12) здесь здесь Вычисление элементов круга: 1) здесь решение 2) здесь решение 3) здесь
решение 4) здесь решение 5) здесь решение 6)здесь решение 7) здесь решение 8)здесь решение 9)здесь решение 10) здесь
решение 11) здесь решение 12) здесь здесь 13) здесь решение 14) здесь решение 15) здесь решение 16) здесь решение 17) здесь решение Вычисления на координатной плоскости: 1)здесь решение 2) здесь решение 3) здесь решение 4) здесь
решение 5) здесь
решение 6) здесь решение 7) здесь решение 8) здесь решение 9) здесь решение 10) здесь решение 11) здесь
решение 12) здесь решение 13) здесь решение 14) здесь решение 15) здесь
решение 16) здесь решение
Вы обязательно завалите задачу № 3, если не читая ее условие, просто посчитаете площадь и запишете полученное число в ответ.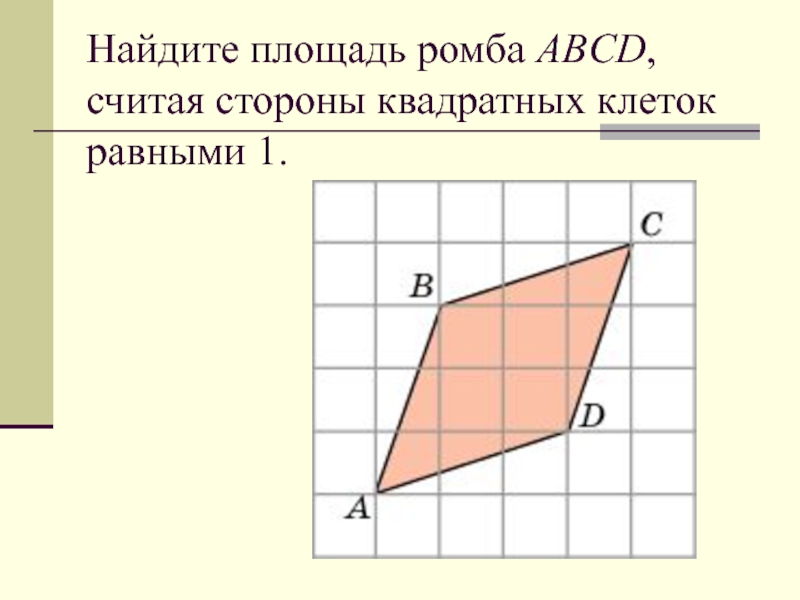 И потом будете недоумевать почему Вам поставили 0 баллов до тех пор, пока не увидите, что в ответе нужно было указать среднюю линию, медиану или тангенс угла.
И потом будете недоумевать почему Вам поставили 0 баллов до тех пор, пока не увидите, что в ответе нужно было указать среднюю линию, медиану или тангенс угла.
Задачи с ответами для самостоятельного решения и самопроверки,
предлагаемые авторами ЕГЭ на экзаменах прошлых лет, а также из открытого банка ФИПИ:
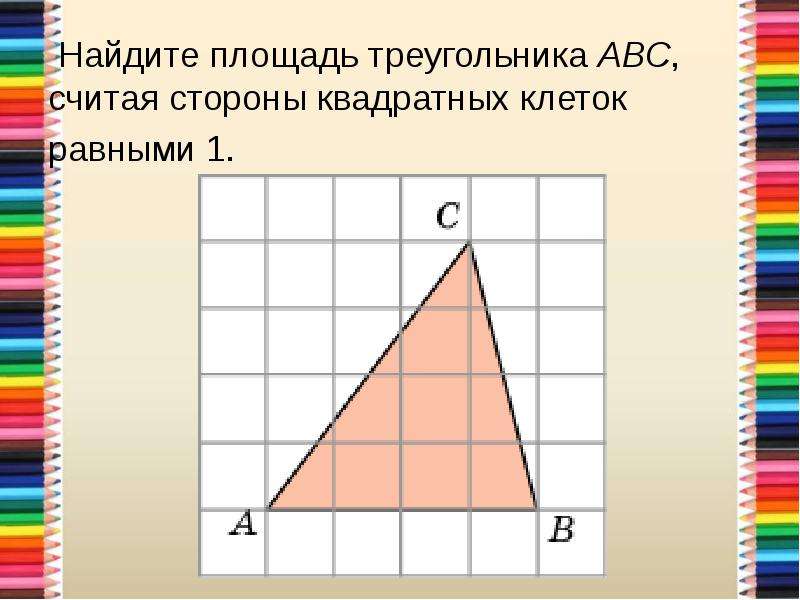
1. 2021 год. Демонстрационный вариант ЕГЭ. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Решение здесь
ИЛИ
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции. Решение здесь
1. 2020 год. Основная волна. Москва. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Решение здесь или здесь Ответ:15.
2. 2020 год. Досрочная волна.
На клетчатой бумаге с размером 1х1 изображён ромб.
Решение 1 здесь Решение 2 здесь
3. 2019 год. Основная волна ЕГЭ. Центр. Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1×1 см. Ответ дайте в квадратных сантиметрах.
Решение здесь
4. 2018 год. Основная волна ЕГЭ. На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите среднюю линию этой трапеции.
Решение здесь
5. 2017 год. Основная волна ЕГЭ. На клетчатой бумаге изображен треугольник ABC. Найдите среднюю линию этого треугольника, параллельную стороне AB.
Решение здесь
6. 2016 год. Основная волна ЕГЭ. Юг. На клетчатой бумаге с размером клетки 1х1 изображен параллелограмм. Найдите его площадь.
Основание параллелограмма 2, высота 5. Ответ: здесь
5. Найдите площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1см х 1 см (см. рис.). В ответе запишите S/п.
Решение здесь
6. Найдите площадь S круга, считая стороны квадратных клеток равными 1 (см. рис.). В ответе укажите S/п.
рис.). В ответе укажите S/п.
Решение здесь
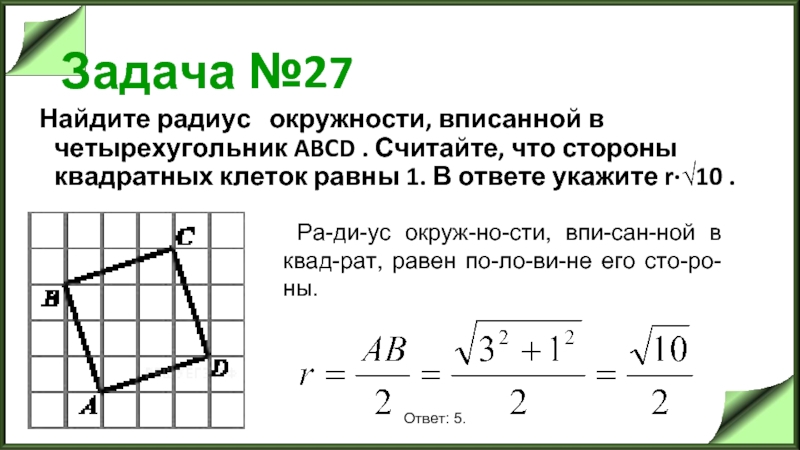
Вероятно, вы привыкли, что в задании № 3 в профильном ЕГЭ необходимо найти площадь или хотя бы периметр. Однако это не всегда так. В последнее время этим заданием стали проверять ваше знание базовых элементов и теорем геометрии, поэтому просят найти медиану, высоту, биссектрису, среднюю линию или радиус окружности. Чтобы выполнить это задание верно, необходимо внимательно читать условие и иметь в голове всю теорию в структурированном виде, чтобы вовремя воспользоваться нужным правилом.
7. На клетчатой бумаге с размером клетки 1х1 изображён равнобедренный прямоугольный треугольник. Найдите длину его медианы, проведенной к гипотенузе.
Решение здесь
8. Найдите большую диагональ ромба.
Решение здесь
9. Найдите площадь треугольника.
Решение здесь
Задачу 5 можно решить и другим способом здесь
10. Найдите площадь многоугольника
Решение здесь
Задачу 6 можно решить и вычитанием из площади прямоугольника здесь
11.
Решение здесь
12. Найдите градусную меру угла АВС.
Решение здесь
13. Найдите тангенс угла.
Решение здесь
14. Найдите площадь трапеции, вершины которой имеют координаты (2; 2), (8; 4), (8; 8), (2; 10). Подсказка здесь Ответ: здесь
15. Тип задания — круг и его элементы. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 1. Найдите площадь заштрихованной фигуры.
Подсказка здесь
16. Тип задания — многоугольники: вычисление длин и углов. Чему равна медиана треугольника АВС, проведенная из вершины В к стороне АС?
Примечание. Все клетки считаем одинаковыми квадратами со стороной 1. Решение здесь
17. На клетчатой бумаге с размером клетки 1х1 изображен четырехугольник. Найдите его площадь.
Решение здесь
18. На клетчатой бумаге с размером клетки 1х1 изображен треугольник. Найдите его площадь.
Решение здесь здесь
19. На клетчатой бумаге с размером клетки 1х1 изображен треугольник. Найдите его площадь.
Найдите его площадь.
Решение здесь здесь
В завершение еще раз напомним: листы с заданиями не проверяются. Можно все необходимые построения и вычисления делать прямо на рисунке. Это позволяет избежать ошибок по невнимательности.
Чтобы продолжить подготовку к ЕГЭ 2021, перейдите по ссылкам на другие страницы сайта:
Локация Главная страница Карта сайта
Нашли опечатку или ошибку? Пожалуйста, сообщите о ней. E-mail: [email protected]
На клетчатой бумаге нарисованы два круга
Бизнес с Oriflame — рост и РАЗВИТИЕ!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2013-10-04
Здравствуйте, друзья! В состав ЕГЭ по математике входят задачи связанные с нахождением площади круга или его частей (сектора, кольцевых элементов). Фигура задаётся на листе в клетку. В одних задачах масштаб клетки задаётся 1×1 сантиметр, в других он не оговаривается – даётся площадь элемента круга или самого круга.
Задания неглубокие, необходимо помнить формулу площади круга, уметь визуально (по клеткам) определить радиус круга, какую долю от круга составляет выделенный сектор. Кстати, на блоге имеется статья о площади сектора. Её содержание к решению представленных ниже задач отношения не имеет, но для тех, кто хочет вспомнить формулу площади круга и площади сектора будет весьма полезна. Рассмотрим задачи (взяты из открытого банка заданий):
Кстати, на блоге имеется статья о площади сектора. Её содержание к решению представленных ниже задач отношения не имеет, но для тех, кто хочет вспомнить формулу площади круга и площади сектора будет весьма полезна. Рассмотрим задачи (взяты из открытого банка заданий):
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см. В ответе запишите S/л.
Для того, чтобы площадь фигуры (кольца) необходимо из площади круга радиусом равным 2 вычесть площадь круга с радиусом 1. Формула площади круга:
Значит,
Разделим результат на число Пи и запишем ответ.
Ответ: 3
На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 51. Найдите площадь заштрихованной фигуры.
Площадь заштрихованной фигуры можно найти вычислив разность между площадью большего круга и площадью меньшего. Определим во сколько раз площадь большего отличается от площади меньшего. Пусть радиус меньшего равен R, тогда его площадь равна:
Радиус большего круга в два раза больше (видно по клеткам).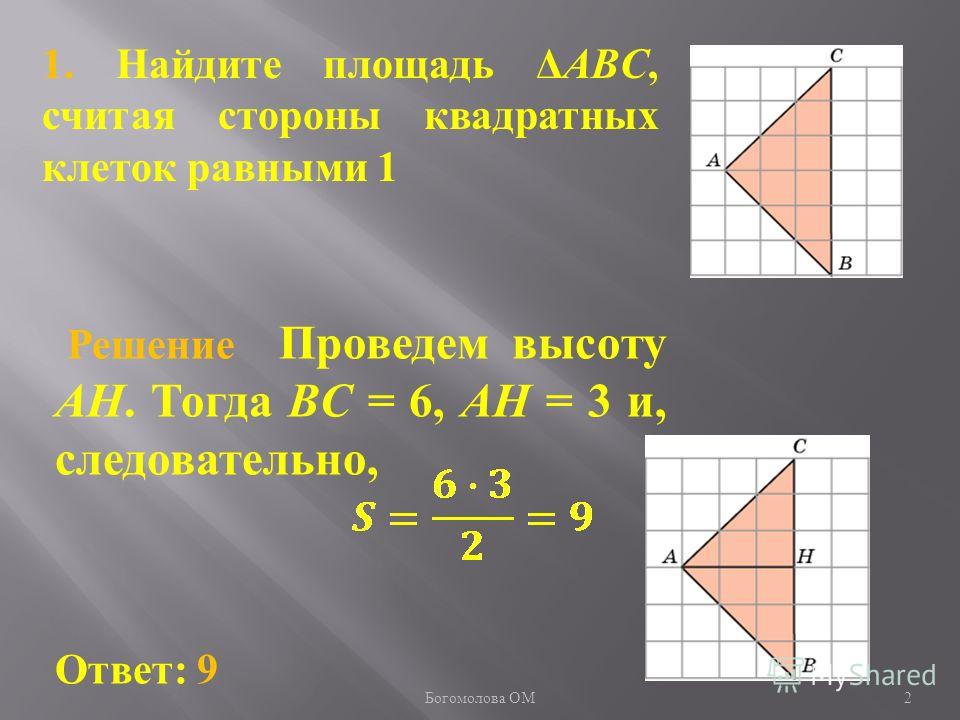 Значит, его площадь равна:
Значит, его площадь равна:
Получили, что его площадь в 4 раза больше.
Следовательно, она равна 51∙4 = 204 см2
Таким образом, площадь заштрихованной фигуры равна 204 – 51 = 153 см2.
*Второй способ. Можно было вычислить радиус малого круга, затем определить радиус большего. Далее найти площадь большего и вычислить площадь искомой фигуры.
На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 1. Найдите площадь заштрихованной фигуры.
Данная задача по ходу решения практически не отличается от предыдущей, разница состоит лишь в том, что круги имеют разные центры.
Несмотря на то, что видно, что радиус большего круга в 2 раза больше радиуса меньшего, советую вам обозначить размер клетки переменной х (икс).
Так же, как и в предыдущей задаче, определим во сколько раз площадь большего отличается от площади меньшего. Выразим площадь меньшего круга, так как его радиус равен 3х:
Выразим площадь большего круга, так как его радиус равен 6х:
Как видно, площадь большего круга в 4 раза больше.
Следовательно, она равна 1∙4 = 4 см2
Таким образом, площадь заштрихованной фигуры равна 4 – 1 = 3 см2.
Ответ: 3
На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 9. Найдите площадь заштрихованной фигуры.
Обозначим размер клетки переменной х (икс).
Определим во сколько раз площадь большего круга отличается от площади меньшего. Выразим площадь меньшего круга. Так как его радиус равен 3∙х, то
Выразим площадь большего круга. Так как его радиус равен 4∙х, то
Разделим площадь большего на площадь меньшего:
То есть, площадь большего круга в 16/9 раза больше площади меньшего, следовательно, она равна:
Таким образом, площадь заштрихованной фигуры равна 16 – 9 = 7 см2.
*Второй способ.
Вычислим радиус меньшего круга. Его площадь равна 9, значит,
Найдём размер клетки и затем сможем определить радиус большего круга. Размер клетки равен:
Размер клетки равен:
Так как радиус большего круга соответствует 4 клеткам, то его радиус будет равен:
Определяем площадь большего круга:
Находим разность: 16 – 9 = 7 см2
Ответ: 7
На клетчатой бумаге нарисован круг площадью 48. Найдите площадь заштрихованного сектора.
В этой задаче очевидно, что заштрихованная часть составляет половину от площади всего круга, то есть равна 24.
Ответ: 24
На клетчатой бумаге изображён круг. Какова площадь круга, если площадь заштрихованного сектора равна 32?
По рисунку видно, что площадь сектора составляет треть от площади круга. Значит, площадь круга будет равна 32∙3 = 96.
Ответ: 96
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см. В ответе запишите S/л.
Посмотреть решение
Найдите площадь S круга, считая стороны квадратных клеток равными 1. В ответе укажите S/л.
В ответе укажите S/л.
Посмотреть решение
Небольшой итог.
В задачах связанных с площадью сектора круга необходимо уметь определять какую долю он составляет от площади круга. Это сделать не сложно, так как в подобных задачах центральный угол сектора кратен 30 либо 45.
В задачах связанных с нахождением площадей кольцевых элементов есть разные пути для решения, оба показаны в решённых заданиях. Способ, в котором размер клетки обозначается через переменную х, и затем определяются радиусы более универсален.
Но самое главное – не запоминать эти способы. Можно найти и третий и четвёртый путь решения. Главное – это знать формулу площади круга и уметь логически рассуждать.
На этом всё. Успеха вам!
С уважением, автор проекта Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Категория: Площади фигур | ЕГЭ-№1Окружность КругПлощадь
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Использование неравенства среднего арифметического и среднего геометрического при решении задач.
Презентация на ежегодном собрании Ассоциации школьной математики и естественных наук, Бирмингем, 8 ноября 2012 г. , была подготовлена с использованием некоторых частей этой статьи.
PDF-версия
Неравенство среднего арифметического и среднего геометрического (неравенство AM-GM) — это фундаментальное соотношение в математике. Это полезный инструмент для решения задач и построения взаимосвязей с другой математикой. Он должен найти больше применения в школьной математике, чем в настоящее время. Далее я представлю введение в теорему, некоторые предыстории и обобщения, альтернативные демонстрации доказательства и примеры задач, которые можно исследовать с помощью неравенства AM-GM. Я буду в значительной степени полагаться на коллекцию задач и эссе на моем веб-сайте:
http://jwilson. coe.uga.edu
coe.uga.edu
и подкаталог моего курса решения задач по математике в Университете Джорджии.
В своих примерах я сосредоточусь на теореме для двух положительных чисел , но упомяну обобщения ниже и иногда использую случай для трех положительных чисел.
Для реальных положительных чисел a и b неравенство AM-GM для двух чисел:
Ясно, что неравенство AM-GM можно обобщить для n положительных чисел. Связь ставит проблему обобщения доказательства в соответствии с аргументами, выдвинутыми Курантом и Роббинсом (1942). То есть
Неравенство AM-GM также можно обобщить, включив его по отношению к другим средствам, таким как гармоническое среднее (HM) или среднеквадратичное значение (RMS, иногда называемое средним квадратичным). В частности, для двух положительных чисел a и b
В частности, для двух положительных чисел a и b
Геометрическая демонстрация неравенства RMS-AM-GM-HM
На более продвинутом уровне (возможно, более фундаментальном?) все эти средства являются экземплярами степенных средних, где параметр мощности p принимает разные значения для разных средних. Их также можно назвать обобщенными средствами.
AM-GM для двух положительных чисел может быть полезным инструментом при изучении некоторых задач оптимизации. Например, хорошо известно, что для прямоугольников с фиксированным периметром максимальная площадь определяется квадратом, имеющим этот периметр.
Изд. Комментарий: Слово «минимум» во втором предложении ниже должно быть «максимум»
.
Возможно, некоторое представление дает график справа. Фиксированный периметр
Фиксированный периметр
2а + 2б = 10.
Красный график представляет функцию площади графика как либо из а или b в диапазоне от 0 до 5. Пусть b представляет длину одной стороны, а 5 — b длину другой.
Площадь = ab = b(5 — b) для 0 < b < 5
Когда применяется неравенство AM-GM, мы получаем Площадь ≤
Точки на синей кривой, площадь = 6,25, всегда больше точек на красной кривой (то есть площадь прямоугольника всегда меньше 6,25), а синяя кривая (горизонтальная линия, представляющая константу) касается красная кривая тогда и только тогда, когда b = (5 — b), т. е. b = 2,5.
Установив это с помощью обычных обозначений функций, пусть периметр прямоугольника равен 10, а одна сторона равна x. Другая сторона 5 — x.
Полезность неравенства AM-GM заключается в том, что замещающая функция после применения неравенства AM-GM представляет собой постоянную прямую, касательную к предыдущей функции. Площадь всегда меньше константы И равна этой константе, когда а = b. В нашем примере для P = 10 a = b = 2,5 когда прямоугольник является квадратом.
Площадь всегда меньше константы И равна этой константе, когда а = b. В нашем примере для P = 10 a = b = 2,5 когда прямоугольник является квадратом.
На моей веб-странице поставлена задача для учащихся:
Вторая задача, в которой ab является константой, а не a + b, хорошо контрастирует с первой и также быстро следует из неравенства AM-GM:
В этом разделе я ограничу исследование простейшим случаем: Среднее арифметическое и среднее геометрическое двух положительных чисел. В моем курсе «Решение проблем» я ставлю В КАЧЕСТВЕ ИССЛЕДОВАНИЯ чтобы студент нашел как минимум 5 демонстраций или доказательств. Увидев несколько подходов к этому отношению, вы сможете понять его, увидеть его важность и найти его полезным в качестве инструмента решения проблем.
Постройте полукруг диаметром a + b.
Радиус будет средним арифметическим значений a и b. Постройте перпендикуляр к диаметру из общих концов отрезков длины a и b. От пересечения этого перпендикуляра с полуокружностью постройте красный отрезок. Этот отрезок всегда будет иметь длину, меньшую или равную радиусу окружности, и он будет равен только в том случае, если a = b.
Этот пример тесно связан с известной геометрической теоремой о том, что высота прямоугольного треугольника от вершины с углом 90 градусов до гипотенузы будет средним геометрическим двух отрезков отрезков на гипотенузе.
Эта демонстрация начинается с идентификатора:
Так как имеем с равенством тогда и только тогда, когда a = b.

Другой пример геометрии
Даны две касательные окружности радиусов a и b. Постройте общую внешнюю касательную к двум окружностям и проведите радиусы каждой окружности к общей касательной. Найдите длину, обозначенную ? вдоль общей касательной через a и b.
Решение. Построив отрезок, параллельный изучаемому, прямоугольный треугольник с катетами длиной ? и a-b, и гипотенуза длины a+b. отрезок общей касательной имеет длину, вдвое превышающую среднее геометрическое a и b.
Больше геометрии
Рассмотрим окружность с хордами AB и CD.
Пусть CD проходит через середину M треугольника AB.
Пусть AM = MB = z и пусть CM = x, MD = y. Все длины являются положительными значениями.
По элементарной теореме геометрии произведения частей хорд равны.
Мы знаем, что x + y ≥ 2z с равенством, только если M — середина CD.
Алгебра
Что-то другое
Задача : Фермер хочет оградить 60 000 квадратных футов земли на прямоугольном участке вдоль прямой дороги.
Забор, который он планирует использовать вдоль шоссе, стоит 2 доллара за фут, а забор с трех других сторон стоит 1 доллар за фут. Сколько заборов каждого типа ему придется купить, чтобы свести расходы к минимуму? Какой минимальный расход?
Решение : (Это типичная задача на вычисления, но расчеты не нужны!)
Задача состоит в том, чтобы найти минимальные значения для этой функции в диапазоне или 0 < x < π. Это требует некоторого изменения формы уравнения, чтобы применить неравенство AM-GM. Однако сначала полезно увидеть график и иметь некоторое представление об уравнении. На графике справа показано, что в диапазоне 0 < x < π может быть два минимальных значения.
Задача состоит в том, чтобы с помощью линейки и циркуля построить квадрат, площадь которого равна площади заданного прямоугольника.
Площадь будет равна ab и поэтому длина стороны квадрата равна среднему геометрическому.
Рассмотрим:
Красный сегмент – это среднее геометрическое значений a и b.
Понимание проблемы. Сектор круга имеет периметр, состоящий из двух радиусов и дуги окружности, соединяющей конечные точки двух радиусов. Сравните площади трех секторов — каждый с P = 100 — центральные углы 45 градусов, 90 градусов и 180 градусов. Это сектора, представляющие собой восьмой круг, четверть круга и полукруг. По мере увеличения углов радиусы становятся короче, потому что большая часть фиксированного периметра находится в дуге. Обратите внимание, что эти углы равны
Когда вычисляются эти три области, мы получаем
Ясно, что при увеличении угла от 45 до 90 и до 180 площадь увеличивается, а затем уменьшается.
Где-то максимальная площадь. Где?
Сектор как часть круга
Некоторые ученики (и учителя) ненавидят работать с радианами. Для них подход может быть следующим:
Пусть k будет частью круга, представленного сектором. 0 < k < 1. Периметр является константой, поэтому мы можем представить его как удвоенный радиус плюс часть длины окружности.
Площадь сектора в дробном обозначении может быть сформирована либо как функция r, либо как функция k, в зависимости от подстановки r или k из уравнения периметра. Любой из них можно использовать с неравенством AM-GM, чтобы решить проблему:
Оглядываясь назад на пример, когда P = 100, максимальная площадь будет, когда r = 25 и, следовательно, длина дуги равна 50.
Угол немного меньше 120 градусов.
Сектор в радианах
Следует отметить параллель этого решения с тем, где квадрат был максимальной площадью для прямоугольников с фиксированным периметром.
Постройте сегменты из концов диаметра, чтобы получить прямоугольный треугольник.
Переписать
Для x > 0, используя среднее арифметическое-среднее геометрическое неравенство,
Следовательно, значение функции всегда меньше или равно 0,5 и равно 0,5 только при x = 1,
Для x < 0 аналогичное рассуждение приводит к нахождению минимума функции при x = -1.
Поскольку среднее арифметическое — неравенство среднего геометрического справедливо только для положительных значений, когда x < 0, мы должны применить неравенство к - x и - 1/x. Мы знаем
Имейте в виду, что это для x < 0, поэтому -x и -1/x положительны. Умножение каждой стороны неравенства на -1 дает
и равенство возникает, когда x = -1. Поэтому значение функции всегда больше или равно -0,5 и равно -0,5 только при x = -1.
См. графики
У нас есть три фактора в функции, и мы хотим знать, когда функция достигает максимума в интервале [0,1].
Чтобы воспользоваться неравенством AM-GM, нам нужно, чтобы сумма этих факторов равнялась константе.
.То есть нам нужно -2x, а не -x. Мы можем получить это по следующему номеру
Функция достигает этого максимального значения для x в [0,1] тогда и только тогда, когда2(1 — x) = 1 + x
2 — 2x = 1 + x
1 = 3xТо есть
При упаковке продукта в банку в форме правильного круглого цилиндра различные факторы, такие как традиции и предполагаемые предпочтения клиентов, могут влиять на решения о том, какая форма (например, низкая и толстая или высокая и худая) может использоваться для фиксированного объема.
. Обратите внимание, например, на все 12 унций. банки из-под газировки имеют такую же форму — высота около 5 дюймов и радиус около 1,25 дюйма. Почему?
Что, если решение было основано на минимизации материала, используемого для изготовления банки? Это будет означать, что для фиксированного объема V форма банки (например, радиус и высота) будет определяться минимальной площадью поверхности банки. Какова связь между радиусом и высотой, чтобы минимизировать площадь поверхности для фиксированного объема?
Какой должна быть форма банки газировки на 12 унций, которая сводит к минимуму количество алюминия в банке?
Объем фиксирован.
Площадь поверхности зависит от r и h.
Каково минимальное значение S?
( Обратите внимание, что мы использовали неравенство AM-GM для трех положительных чисел )
Предположим, у вас есть 100 футов ограждения. Вам нужна прямоугольная ручка с перегородкой, параллельной стороне. 100 футов ограждения должны охватывать четыре стороны и перегородку. Какова форма ручки и какова максимальная площадь?
Покажите, что размеры загона максимальной площади составляют 25 футов на 16,67 футов, а максимальная площадь составляет примерно 417,7 кв.
футов.
Докажите, что максимальная площадь треугольника с фиксированным периметром равна
Найдите на графике точку, ближайшую к началу координат.
(перейти по ссылке на обсуждение)
Дан треугольник, одна сторона которого имеет длину 9 единиц, а отношение двух других сторон равно 40/41.
Найдите максимальную площадь.
(используйте ссылку для обсуждения)
Используйте неравенство среднего арифметического и среднего геометрического, чтобы найти максимальный объем коробки, сделанной из квадратного листа картона 25 на 25, удалив маленький квадрат из каждого угла и сложив стороны, чтобы сформировать коробку без крышки.

Теорема: Произведение n положительных чисел равно 1 тогда сумма чисел больше или равна n.
Очевидно, доказательство 3 подразумевает первые два.
Извлечение квадратного корня
Устанавливает эффективный процесс для получения последовательных оценок с помощью ручного калькулятора, электронной таблицы или бумаги и карандаша. Справа часть таблицы, показывающая расчет для . Процесс быстро сходится к хорошей оценке.
Нажмите ЗДЕСЬ, чтобы открыть файл Excel. Введите в ячейку A1 значение N , для которого требуется извлечь квадратный корень.
как рассчитать периметр многоугольника в python
AlleVideosBilderBücherMapsNewsShoppingsuchoptionen
Программа для нахождения периметра многоугольника в Python
определить функцию get Информация(). …
вернуть квадратный корень из ((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)), который является евклидовым расстоянием.
между (x1, y1) и (x2, y2)
В основном методе выполните следующие действия.
N := размер точек.
(firstx, firsty) := points[0]
(prevx, prevy) := (firstx, firsty)
Программа для нахождения периметра многоугольника в Python — CoderLessons.com 0007
www. tutorialspoint.com › программа для поиска периметра многоугольника в pyth…
Hervorgehobene Фрагменты
Код для вычисления периметра любого многоугольника с использованием классов…
stackoverflow. com › вопросы › код для расчета…
com › вопросы › код для расчета…
Это должно работать class Polygon(): def __init__(self, points) : self.points = points def __len__(self): return len(self.points) def …
Периметр полигона — python — Stack Overflow
периметр многоугольника с заданными координатами — Stack Overflow
Площадь полигона, периметр и длина стороны по кругу с питоном
Многоугольник из $n$ точек: площадь простая, периметр сложный?
Weitere Ergebnisse von stackoverflow.com
Программа для нахождения периметра правильного многоугольника — GeeksforGeeks
www.geeksforgeeks.org › program-to-find-the-peri…
21 .08.2022 · Это представляет собой двухмерную фигуру. Периметр правильного многоугольника = количество сторон * длина каждой стороны. Ниже приведен …
Ähnliche Fragen
Как вычислить периметр многоугольника?
Как найти периметр в Python?
python — Периметр многоугольника по его вершинам
codereview.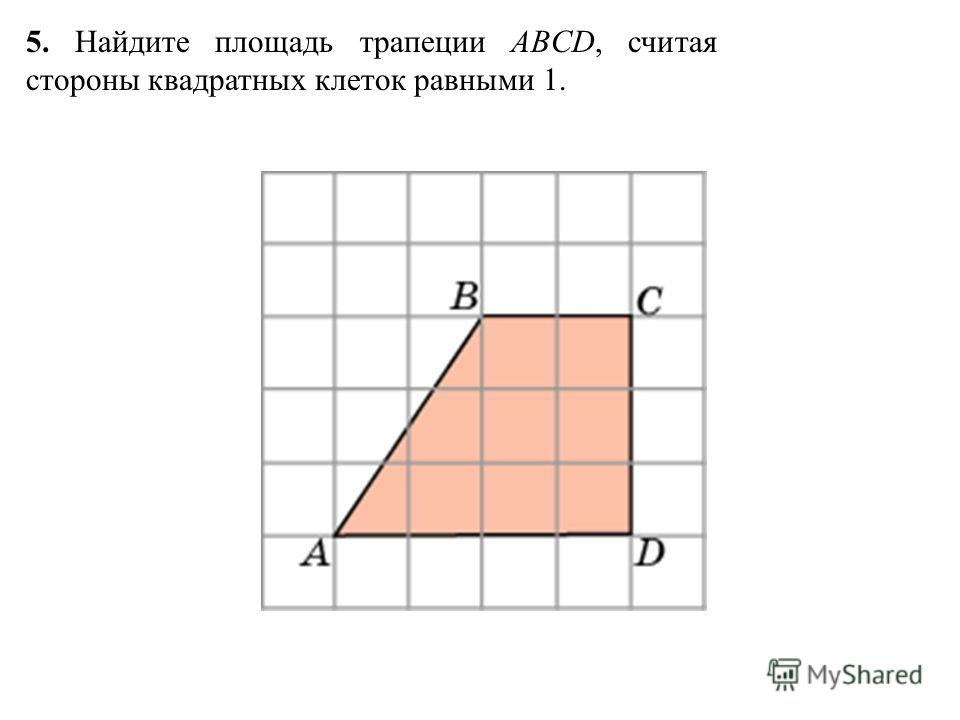 stackexchange.com › questions › perime…
stackexchange.com › questions › perime…
Задача прочитать координаты многоугольника из файла и вычислить периметр, мне предоставили скрипт содержит ошибки и просит исправить …
Как рассчитать периметр многоугольника с помощью python…
gis.stackexchange.com › вопросы › как рассчитать…
Для полигона это периметр. периметр=функция.геометрия().длина(). Делиться.
Расчет длины полигона в геопандах? — GIS Stack Exchange
Вычисление площади и периметра координатных точек в Python
Вычисление площади на поверхности Земли по пересечению…
python — Как найти геометрии всех пересечений в многоугольнике и…
Вызов-I (Площадь и периметр многоугольника) | [ООП в Python]
www.youtube.com › смотреть
30.07.2020 · Это урок номер 19 из серии уроков по объектно-ориентированному программированию (ООП) в …
Дауэр: 14:14
Прислан: 30.07.2020
периметр правильного многоугольника с питоном на Visual Studio код
www.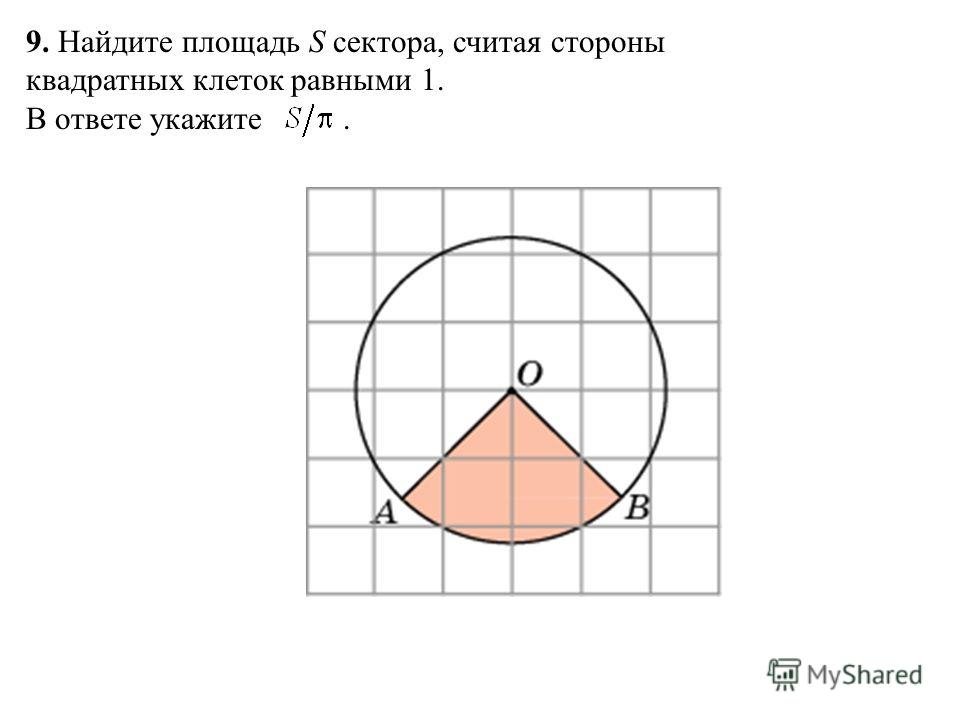 youtube.com › смотреть
youtube.com › смотреть
11.05.2020 · расчет периметра правильного многоугольника с питоном на Visual Studio CodeCode: …
Dauer : 4:37
Прислан: 11.05.2020
как рассчитать периметр неправильного многоугольника — Sololearn
www.sololearn.com › Обсудить › как рассчитать…
На самом деле все зависит от того, какие данные вам предоставлены. Если вам даны вершины, рассчитайте длину линий и добавьте их. вот как вы можете рассчитать …
Python Math: вычислить площадь правильного многоугольника — w3resource
www.w3resource.com › python-упражнения › python-…
28.01.2023 · Упражнения на Python , Практика и решение. Напишите программу на Python для вычисления площади правильного многоугольника.
isennkubilay/Вычисление периметра многоугольника — GitHub
github.com › isennkubilay › Вычисление периметра…
Напишите программу, которая вычисляет периметр многоугольника. Начните с прочтения значений x и y для первой точки по периметру полигона из .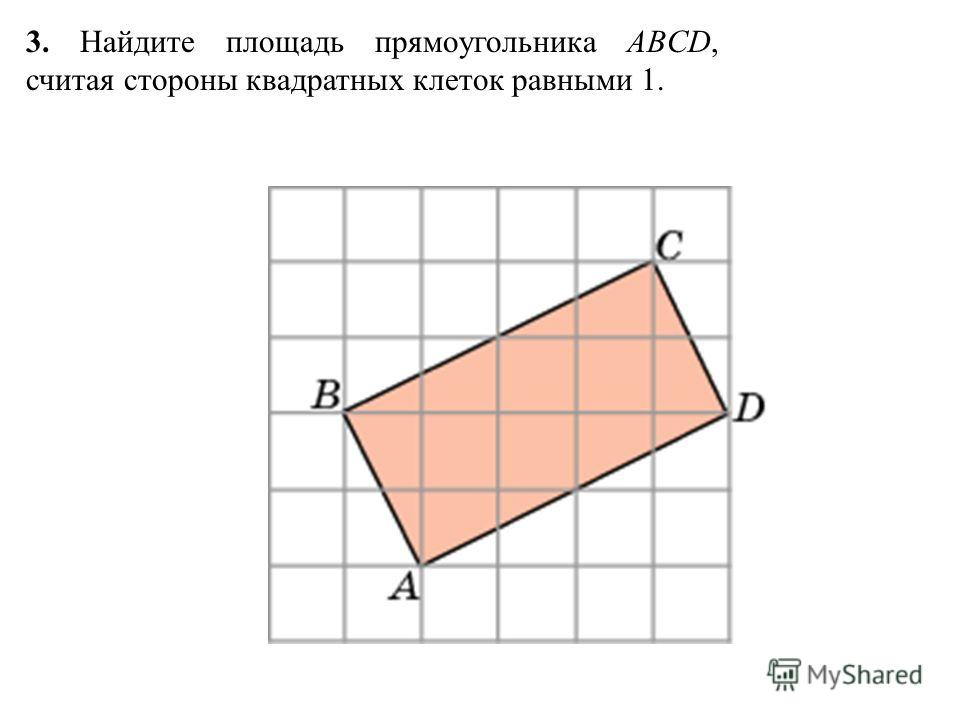

 Радиус будет средним арифметическим значений a и b. Постройте перпендикуляр к диаметру из общих концов отрезков длины a и b. От пересечения этого перпендикуляра с полуокружностью постройте красный отрезок. Этот отрезок всегда будет иметь длину, меньшую или равную радиусу окружности, и он будет равен только в том случае, если a = b.
Радиус будет средним арифметическим значений a и b. Постройте перпендикуляр к диаметру из общих концов отрезков длины a и b. От пересечения этого перпендикуляра с полуокружностью постройте красный отрезок. Этот отрезок всегда будет иметь длину, меньшую или равную радиусу окружности, и он будет равен только в том случае, если a = b.
 Пусть CD проходит через середину M треугольника AB.
Пусть CD проходит через середину M треугольника AB.  Забор, который он планирует использовать вдоль шоссе, стоит 2 доллара за фут, а забор с трех других сторон стоит 1 доллар за фут. Сколько заборов каждого типа ему придется купить, чтобы свести расходы к минимуму? Какой минимальный расход?
Забор, который он планирует использовать вдоль шоссе, стоит 2 доллара за фут, а забор с трех других сторон стоит 1 доллар за фут. Сколько заборов каждого типа ему придется купить, чтобы свести расходы к минимуму? Какой минимальный расход?
 Где-то максимальная площадь. Где?
Где-то максимальная площадь. Где? Угол немного меньше 120 градусов.
Угол немного меньше 120 градусов. Поскольку среднее арифметическое — неравенство среднего геометрического справедливо только для положительных значений, когда x < 0, мы должны применить неравенство к - x и - 1/x. Мы знаем
Поскольку среднее арифметическое — неравенство среднего геометрического справедливо только для положительных значений, когда x < 0, мы должны применить неравенство к - x и - 1/x. Мы знаем  То есть нам нужно -2x, а не -x. Мы можем получить это по следующему номеру
То есть нам нужно -2x, а не -x. Мы можем получить это по следующему номеру  . Обратите внимание, например, на все 12 унций. банки из-под газировки имеют такую же форму — высота около 5 дюймов и радиус около 1,25 дюйма. Почему?
. Обратите внимание, например, на все 12 унций. банки из-под газировки имеют такую же форму — высота около 5 дюймов и радиус около 1,25 дюйма. Почему?
 футов.
футов.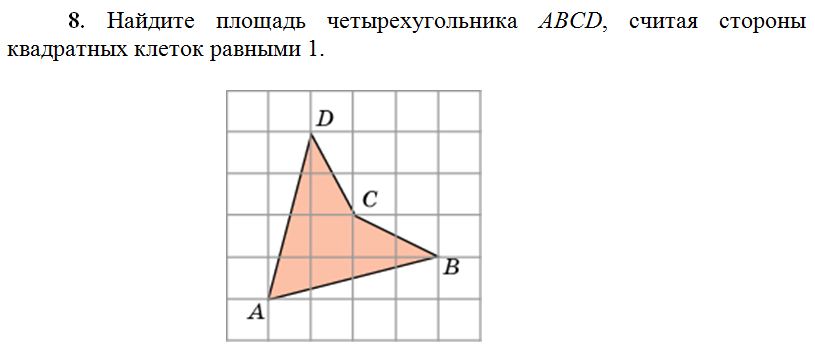
Leave A Comment