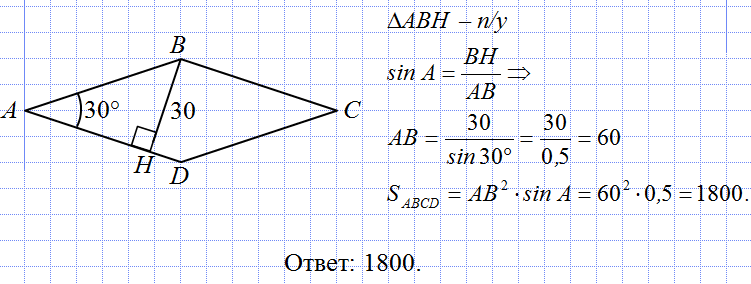
Найдите площадь ромба, если его высота равна 19, а острый угол 30 градусам
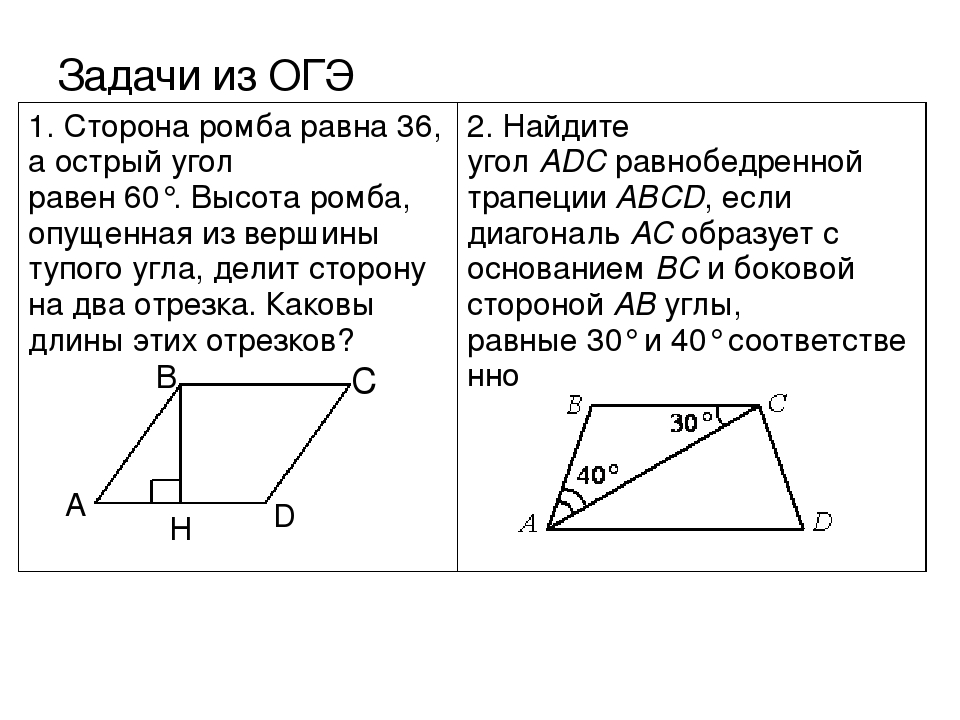
При точке D два угла. Поэтому возможны два варианта1) см. рис. 1
Сумма углов треугольника ADC равна 180°
∠DAC = 180°-∠1 -∠ 2=180°-40°-55°=85°, значит
∠ DAB=85°, а угол ВАС = 85°+85=170° так как биссектриса AD делит угол А пополам.
Этот вариант невозможен, так как сумма углов треугольника АВС равна 180°, а
∠А + ∠С=170°+40° уже больше 180°
Вот видите, что получается, когда задача сформулирована некорректно. Если сложно добавить рисунок, то можно было хотя бы углы при точке D правильно назвать.
BAD и СAD.
2) см. рис.2
∠BDC = 55°, тогда смежный с ним угол СDA равен 180°-55°=125°
Сумма углов треугольника ADC равна 180°
∠DAC = 180°-∠1 -125°=180°-40°-125°= 15°, значит
∠ DAB=15°, а угол ВАС=15°+15°=30°
угол А равен 30°, значит угол В равен 180°-30°-40°=110°
Ответ. Угол А равен 30°, угол С равен 40°, угол В равен110°
х+х+40=180
2х=140
х=70
Внутренний смежный с ним 70 градусов,
поэтому и второй угол при основании тоже 70 градусов.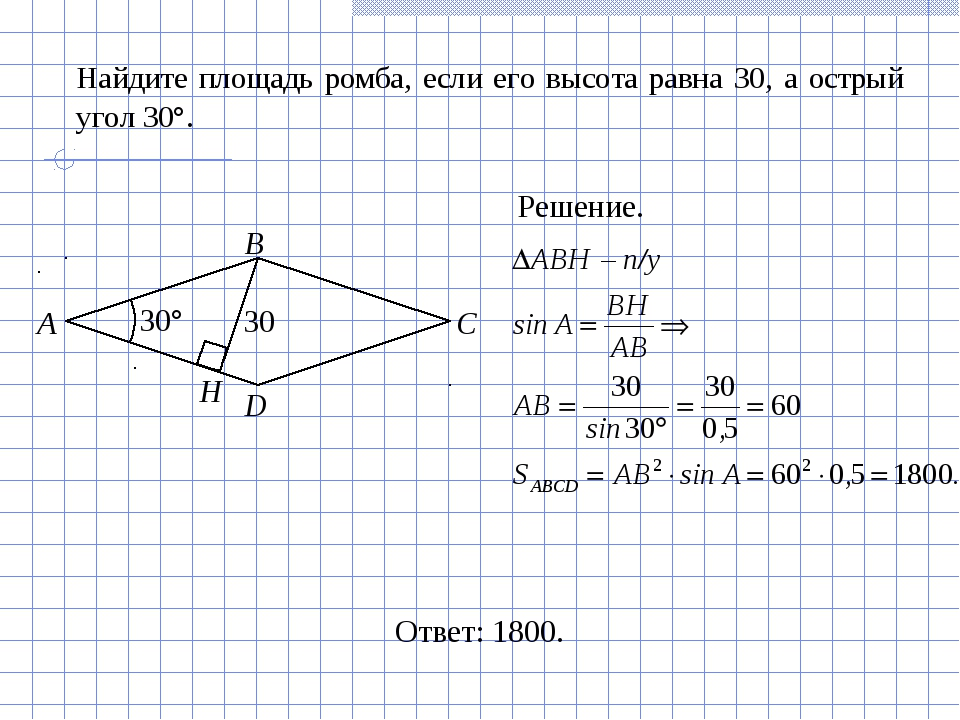 т.к. сумма углов
треугольника равна 180 градусов, то угол при
вершине равен 180-140= 40 градусов
т.к. сумма углов
треугольника равна 180 градусов, то угол при
вершине равен 180-140= 40 градусов
в тр-ке ADN: tgα=8/12=2/3
в тр-ке ARW: tgα=6/RW =>RW=6/tgα=6*3/2=9
2. RH²=RC²-HC²=9-4=5
Тр-ки ABC и RHC подобны по углу С:
HC/AC=RH/y => 2/8=√5/y => y=4√5 1) Определение: «Ортоцентр — точка пересечения высот треугольника или их продолжений». Значит нам нужно уравнение прямой, проходящей через ортоцентр, перпендикулярно прямой АВ.
Уравнение прямой АВ:
(x-1)/(-2-1)=(y-4)/(-1-4) => -5x+5=-3y+12 => y=(5/3)X+7/3. k=(5/3).
Условие перпендикулярности прямых: k1=-1/k. У нас k1=-(3/5).
Уравнение прямой, проходящей перпендикулярно прямой АВ и
Y-Yh=k1(X-Xh) или
Y-1=-(3/5)*(X-(-2)) => Y-1=-(3/5)*X -(3/5)*2 =>
Y=-(3/5)*X -1/5 или Y=-0,6X-0,2.
 2=25.
2=25.Найдем точки пересечения окружности и прямой:
для этого подставляем значение y=3x в уравнение окружности и решаем уравнение. Найдя Х1,Y1 и X2,Y2 — координаты концов хорды, найдем и ее длину (модуль) по формуле:
|AB| =√[(Xb-Xa)²+(Yb-Ya)²]. Итак:
(X+1)²+(3X-2)²=25. -> X²+2X+1+9X²-12X+4-25=0.
10X² — 10X — 20 =0 => X² — X — 2 =0 =>
X1= 2, Y1= 6.
|AB| =√[(-3)²+(-9)²] = √90 = 3√10 ≈9,5.
Решение проверим, построив графики.
AE2=AD2+DE2
25=16+DE2
DE==3
CE=CD-DE=1
Sabcd=AB2=16
Sade=AD*DE=2*3=6
Sabce=Sabcd-Sade=10
2)S = a2 · sin α, где α — угол между сторонами, a — сторона ромба.
S=100*=50 \sqrt{3}
Формула площади ромба
Что такое Ромб? Ромб — это параллелограмм, у которого все стороны равны.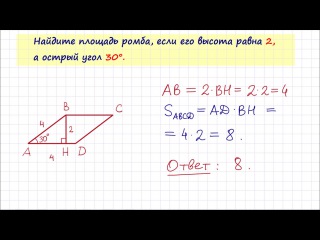 {2} \cdot sin(\alpha) \]
{2} \cdot sin(\alpha) \]
3. Площадь ромба также равна полупроизведению диагоналей, то есть:
\[ S = \dfrac{d_{1} \cdot d_{2} }{2} \]
4. Если известен радиус r окружности, вписанной в ромб , и сторона ромба a, то его площадь вычисляется по формуле:
\[ S = 2 \cdot a \cdot R \]
Свойства ромба
На рисунке выше \( ABCD \) — ромб, \( AC = DB = CD = AD \) . Так как ромб — это параллелограмм, то он обладает всеми свойствами параллелограмма, но так же есть свойства присущие только ромбу.
В любой ромб можно вписать окружность. Центр окружности, вписанной в ромб, является точкой пересечения его диагоналей. Радиус окружности равен половине высоты ромба:
\[ r = \frac{ AH }{2} \]
Свойства ромба
Диагонали ромба перпендикулярны;
Диагонали ромба являются биссектрисами его углов.
Признаки ромба
Параллелограмм, диагонали которого пересекаются под прямым углом, есть ромб;
Параллелограмм, диагонали которого являются биссектрисами его углов, есть ромб.
Калькулятор площади ромба
Расчитать площадь фигуры онлайн
Калькулятор: Площадь ромба
Входные данные
Результат
Площадь геометрической фигуры, или площадь фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади фигуры выражается числом заключающихся в него квадратных единиц.
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
B3
На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
На клетчатой
бумаге с клетками размером 1 см 1 см
изображена фигура (см. рисунок). Найдите
ее площадь в квадратных сантиметрах.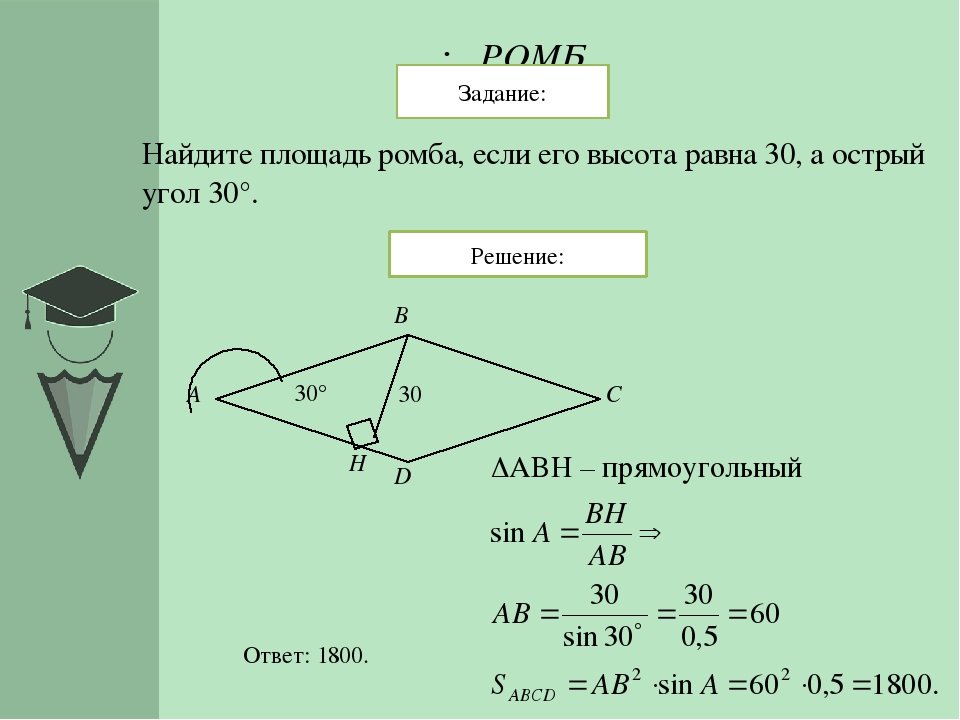
.
Найдите площадь круга, длина окружности которого равна .
Площадь круга равна . Найдите длину его окружности.
Найдите
площадь сектора круга радиуса
,
центральный угол которого равен 90
Найдите площадь сектора круга радиуса 1, длина дуги которого равна 2.
Найдите площадь прямоугольника, если его периметр равен 18, и одна сторона на 3 больше другой.
Площадь прямоугольника равна 18. Найдите его большую сторону, если она на 3 больше меньшей стороны.
Найдите площадь прямоугольника, если его периметр равен 18, а отношение соседних сторон равно 1 : 2.
Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1 : 2.
Периметр прямоугольника равен 42, а площадь 98. Найдите большую сторону прямоугольника.
Периметр
прямоугольника равен 28, а диагональ
равна 10. Найдите площадь этого
прямоугольника.
Найдите площадь этого
прямоугольника.
Периметр прямоугольника равен 34, а площадь равна 60. Найдите диагональ этого прямоугольника.
Сторона прямоугольника относится к его диагонали, как 4:5, а другая сторона равна 6. Найдите площадь прямоугольника.
Даны два квадрата, диагонали которых равны 10 и 6. Найдите диагональ квадрата, площадь которого равна разности площадей данных квадратов.
Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.
Найдите площадь ромба, если его высота равна 2, а острый угол 300.
Найдите площадь ромба, если его диагонали равны 4 и 12.
Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ.
Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.
Найдите
площадь прямоугольного треугольника,
если его катет и гипотенуза равны
соответственно 6 и 10.
Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет.
Боковая сторона равнобедренного треугольника равна 5, а основание равно 6. Найдите площадь этого треугольника.
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 300. Найдите боковую сторону треугольника, если его площадь равна 25.
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 1500. Найдите боковую сторону треугольника, если его площадь равна 100.
Площадь треугольника равна 12. Две его стороны равны 6 и 8. Найдите угол между этими сторонами.
У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне?
Периметр
треугольника равен 12, а радиус вписанной
окружности равен 1. Найдите площадь
этого треугольника.
Найдите площадь
этого треугольника.
Площадь треугольника равна 24, а радиус вписанной окружности равен 2. Найдите периметр этого треугольника.
Площадь треугольника равна 54, а его периметр 36. Найдите радиус вписанной окружности.
Основания трапеции равны 8 и 34, площадь равна 168. Найдите ее высоту.
Основание трапеции равно 13, высота равна 5, а площадь равна 50. Найдите второе основание трапеции.
Высота трапеции равна 10, площадь равна 150. Найдите среднюю линию трапеции.
Средняя линия трапеции равна 12, площадь равна 96. Найдите высоту трапеции.
Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.
Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.
Найдите
площадь прямоугольной трапеции,
основания которой равны 6 и 2, большая
боковая сторона составляет с основанием
угол 450.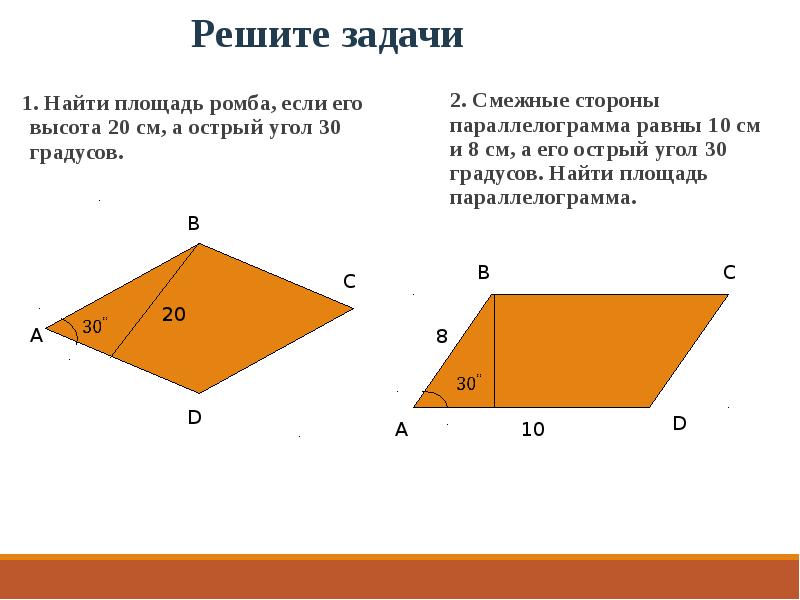
Основания прямоугольной трапеции равны 12 и 4. Ее площадь равна 64. Найдите острый угол этой трапеции.
Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.
Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите боковую сторону трапеции.
Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 1500. Найдите площадь трапеции.
Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне.
Около окружности, радиус которой равен 3, описан многоугольник, площадь которого равна 33. Найдите его периметр.
Около
окружности, радиус которой равен 3,
описан многоугольник, периметр которого
равен 20. Найдите его площадь.
Около окружности описан многоугольник, площадь которого равен 5. Его периметр равен 10. Найдите радиус этой окружности.
Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны и .
Площадь сектора круга радиуса 3 равна 6. Найдите длину его дуги.
Найдите площадь параллелограмма ABCD, считая стороны квадратных клеток равными 1.
Найдите площадь S круга, считая стороны квадратных клеток равными 1. В ответе укажите .
Из точки (6, 8) опущен перпендикуляр на ось абсцисс. Найдите абсциссу основания перпендикуляра.
Через точку (6, 8) проведена прямая, параллельная оси абсцисс. Найдите ординату ее точки пересечения с осью Oy.
Найдите расстояние от точки A с координатами (6, 8) до оси абсцисс.
Найдите
расстояние от точки A с координатами
(6, 8) до оси ординат.
Найдите расстояние от точки A с координатами (6, 8) до начала координат.
Найдите абсциссу точки, симметричной точке A(6, 8) относительно оси Oy.
Найдите ординату точки, симметричной точке A(6, 8) относительно оси Ox.
Найдите абсциссу точки, симметричной точке A(6, 8) относительно начала координат.
Найдите ординату точки, симметричной точке A(6, 8) относительно начала координат.
Найдите ординату середины отрезка, соединяющего точки O(0, 0) и A(6, 8).
Найдите абсциссу середины отрезка, соединяющего точки O(0, 0) и A(6, 8).
Найдите ординату середины отрезка, соединяющего точки A(6, 8) и B(-2, 2).
Найдите абсциссу середины отрезка, соединяющего точки A(6, 8) и B(-2, 2).
Найдите ординату точки пересечения оси Oy и отрезка, соединяющего точки A(6, 8) и B(-6, 0).
Найдите
длину отрезка, соединяющего точки O(0,
0) и A(6, 8).
Найдите длину отрезка, соединяющего точки A(6, 8) и B(-2, 2).
Найдите длину вектора (6, 8).
Найдите квадрат длины вектора .
Найдите ординату точки пересечения оси Oy и прямой, проходящей через точку B(6, 4) и параллельной прямой, проходящей через начало координат и точку A(6, 8).
Точки O(0, 0), B(6, 2), C(0, 6) и A являются вершинами параллелограмма. Найдите ординату точки A.
Точки O(0, 0), A(6, 8), C(0, 6) и B являются вершинами параллелограмма. Найдите ординату точки B.
Точки O(0, 0), A(6, 8), B(4, 2) и C являются вершинами параллелограмма. Найдите ординату точки C.
Точки O(0, 0), A(6, 8), B(6, 2), C(0,6) являются вершинами четырехугольника. Найдите ординату точки P пересечения его диагоналей.
Точки
O(0, 0), A(6, 8), B(6, 2), C(0, 6) являются вершинами
четырехугольника. Найдите абсциссу
точки P пересечения его диагоналей.
Найдите абсциссу
точки P пересечения его диагоналей.
Точки O(0, 0), A(10, 8), C(2, 6) и B являются вершинами параллелограмма. Найдите ординату точки B.
Точки O(0, 0), A(10, 8), B(8, 2) и C являются вершинами параллелограмма. Найдите абсциссу точки C.
Точки O(0, 0), B(8, 2), C(2, 6) и A являются вершинами параллелограмма. Найдите абсциссу точки A.
Точки O(0, 0), A(10, 8), B(8, 2), C(2, 6) являются вершинами четырехугольника. Найдите абсциссу точки P пересечения его диагоналей.
Точки O(0, 0), A(10, 8), B(8, 2), C(2, 6) являются вершинами четырехугольника. Найдите ординату точки P пересечения его диагоналей.
Точки O(0, 0), A(6, 8), B(8, 2) являются вершинами треугольника. Найдите длину его средней линии CD.
Точки O(0, 0), A(10, 0), B(8, 6), C(2, 6) являются вершинами трапеции. Найдите длину ее средней линии DE.
Найдите
абсциссу точки пересечения прямой,
заданной уравнением
,
с осью Ox.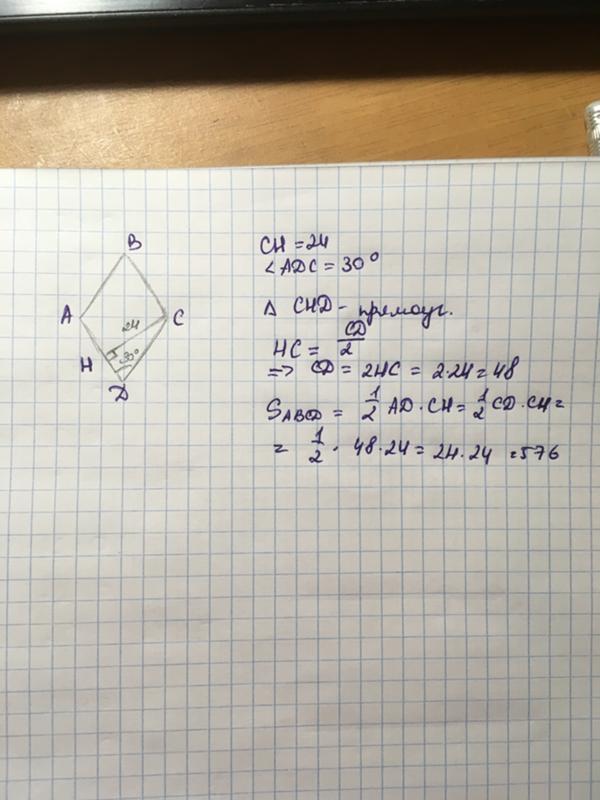
Найдите ординату точки пересечения прямой, заданной уравнением , с осью Oy.
Найдите абсциссу точки пересечения прямых, заданных уравнениями и .
Найдите абсциссу точки пересечения прямых, заданных уравнениями и .
Найдите угловой коэффициент прямой, заданной уравнением .
Окружность с центром в начале координат проходит через точку P(8, 6). Найдите ее радиус.
Какого радиуса должна быть окружность с центром в точке P(8, 6), чтобы она касалась оси абсцисс?
Какого радиуса должна быть окружность с центром в точке P(8, 6), чтобы она касалась оси ординат?
Найдите радиус окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (-2, -2), (6, -2), (6, 4), (-2, 4).
Найдите
абсциссу центра окружности, описанной
около прямоугольника ABCD,
вершины которого имеют координаты
соответственно (-2, -2), (6, -2), (6, 4), (-2, 4).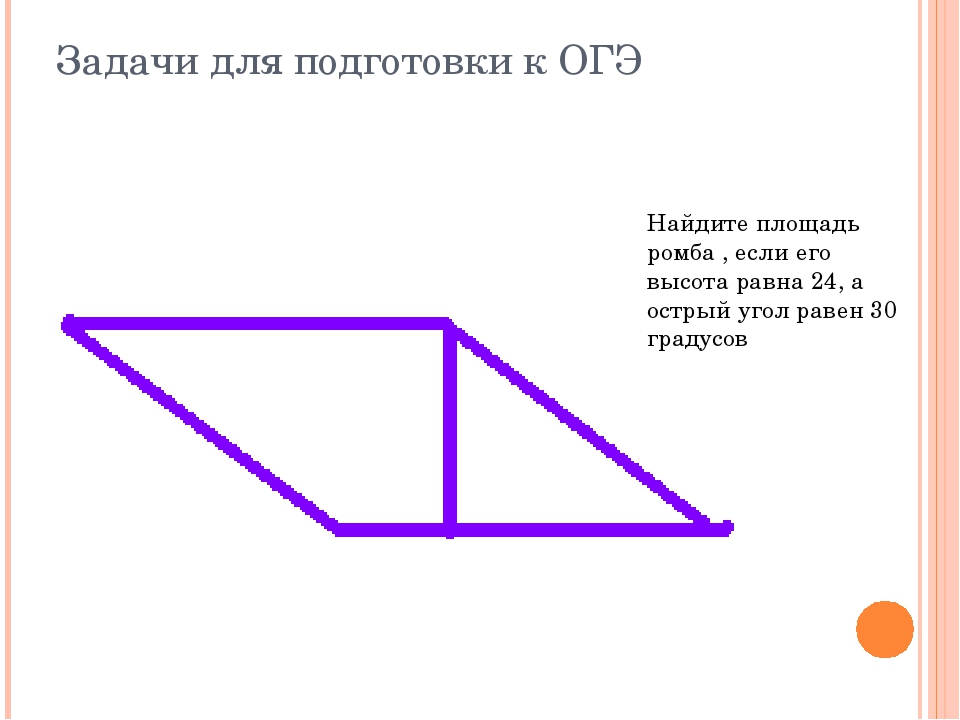
Найдите ординату центра окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (-2, -2), (6, -2), (6, 4), (-2, 4).
Найдите радиус окружности, описанной около треугольника, вершины которого имеют координаты (8, 0), (0, 6), (8, 6).
Найдите абсциссу центра окружности, описанной около треугольника, вершины которого имеют координаты (8, 0), (0, 6), (8, 6).
Найдите ординату центра окружности, описанной около треугольника, вершины которого имеют координаты (8, 0), (0, 6), (8, 6).
Найдите площадь четырехугольника, вершины которого имеют координаты (4, 2), (8, 4), (6, 8), (2, 6).
Найдите площадь четырехугольника, вершины которого имеют координаты (2, 0), (10, 4), (8, 8), (0, 4).
Найдите
площадь четырехугольника, вершины
которого имеют координаты (2, 2), (10, 4),
(10, 8), (2, 6).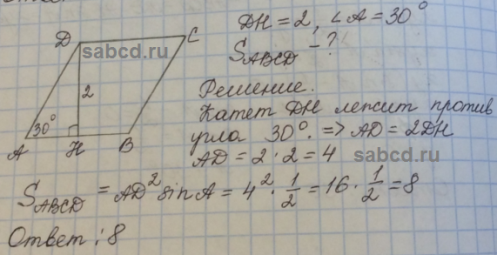
Найдите площадь треугольника, вершины которого имеют координаты (2, 2), (10, 2), (8, 8).
Найдите площадь трапеции, вершины которой имеют координаты (2, 2), (10, 2), (8, 8), (4, 8).
Найдите площадь четырехугольника, вершины которого имеют координаты (2, 2), (8, 4), (10, 10), (4, 8).
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора + .
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора — .
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора .
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора + .
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора .
Диагонали
ромба ABCD
пересекаются в точке O
и равны 12 и 16. Найдите скалярное
произведение векторов и
.
Стороны правильного треугольника ABC равны . Найдите длину вектора + .
Стороны правильного треугольника ABC равны 3. Найдите длину вектора .
Стороны правильного треугольника ABC равны 3. Найдите скалярное произведение векторов и .
Найдите сумму координат вектора .
Вектор с началом в точке A(2, 4) имеет координаты (6, 2). Найдите абсциссу точки B.
Вектор с началом в точке A(2, 4) имеет координаты (6, 2). Найдите ординату точки B.
Вектор с началом в точке A(3, 6) имеет координаты (9, 3). Найдите сумму координат точки B.
Вектор с концом в точке B(5, 3) имеет координаты (3, 1). Найдите абсциссу точки A.
Вектор с концом в точке B(5, 3) имеет координаты (3, 1). Найдите ординату точки A.
Вектор
с
концом в точке B(5, 4) имеет координаты
(3, 1). Найдите сумму координат точки A.
Найдите сумму координат точки A.
Найдите сумму координат вектора + .
Параллелограммы. 1. В параллелограмме ABCD AB = 3, AD = 21, Найдите большую высоту параллелограмма.
Прототипы задания В6-2 (2013)
Прототипы задания В6-2 (2013) ( 27742) Один острый угол прямоугольного треугольника на больше другого. Найдите больший острый угол. Ответ дайте в градусах. ( 27743) В треугольнике ABC угол A равен, внешний
Подробнее7 sin A. Найдите AB. 25
Прототипы задания 6 1. В треугольнике ABC угол C равен 90 0, AC = 4,8, 25. В треугольнике ABC AC = BC, AB = 8, 33 tga. 7 4 33 sin A. Найдите AB. 25 Найдите AC. 2. В треугольнике ABC угол C равен 90 0,
В треугольнике ABC AC = BC, AB = 8, 33 tga. 7 4 33 sin A. Найдите AB. 25 Найдите AC. 2. В треугольнике ABC угол C равен 90 0,
Все прототипы заданий В3
1. Прототип задания B3 ( 27543) Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 Все прототипы заданий В3 2. Прототип задания B3 ( 27544) Найдите площадь треугольника,
ПодробнееАнализ геометрических высказываний
Анализ геометрических высказываний 1. Укажите номера верных утверждений. 1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. 2) Вертикальные углы
Подробнее, а это и есть радиус окружности.
B3 Найдите радиус окруж ности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно ( 2; 2), (6; 2), (6; 4), ( 2; 4) Диагональ прямоугольника образует два прямоугольных
ПодробнееAC 6, cos A.
 Найдите BH.
Найдите BH.Прототипы задания 6 1. Задание 6 ( 26097) 16. Задание 6 ( 20001) В треугольнике ABC угол C равен 90, sin A 0, 6, 21 AC 4. Найдите AB. В треугольнике ABC AC BC 12, sin B. 5 2. Задание 6 ( 29580) Найдите
ПодробнееВ 8 (2014) 16. В треугольнике ABC, 30. В треугольнике ABC угол C равен, CH. высота,,. Найдите AH. высота,,. Найдите BH.
В 8 (2014) 1). В треугольнике ABC угол C равен, CH высота,,. Найдите AH. 2. В треугольнике ABC угол C равен, CH 3. В треугольнике ABC угол C равен,,. Найдите высоту CH. 4. В треугольнике ABC угол C равен,
ПодробнееВсе прототипы заданий В года
1. Прототип задания B5 ( 27450) Найдите тангенс угла AOB. Все прототипы заданий В5 2014 года 2. Прототип задания B5 ( 27456) Найдите тангенс угла AOB. 7. Прототип задания B5 ( 27547) Найдите площадь треугольника,
ПодробнееАнализ геометрических высказываний
Анализ геометрических высказываний 1. 1. Укажите номера верных утверждений. 1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. 2) Вертикальные углы
1. Укажите номера верных утверждений. 1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. 2) Вертикальные углы
Тренировочные задачи
И. В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Параллелограмм. Периметр параллелограмма равен, а одна из его сторон вдвое больше другой. Найдите стороны параллелограмма. и 4. Найдите
Подробнееtgbac. В8 ЕГЭ В ABC C = 90 0, CH высота, AB = 13, tga 5. Найдите BH. 12,5 3 В ABC C = 90 0, AB = 13, tga. Найдите высоту CH.
В-8. ПРОТОТИПЫ Задание ответ В ABC C = 90 0, CH высота, AB =, tga. Найдите AH., В ABC C = 90 0, CH высота, AB =, tga. Найдите, В ABC C = 90 0, AB =, tga. Найдите высоту CH., В ABC C = 90 0, CH высота,
ПодробнееПроизвольный треугольник
Произвольный треугольник В приведенных ниже формулах используются следующие обозначения: а) с длины сторон АВС лежащие против углов А В и С соответственно б) высоты медианы l l l биссектрисы в) радиус
ПодробнееГеометрия
Геометрия 1.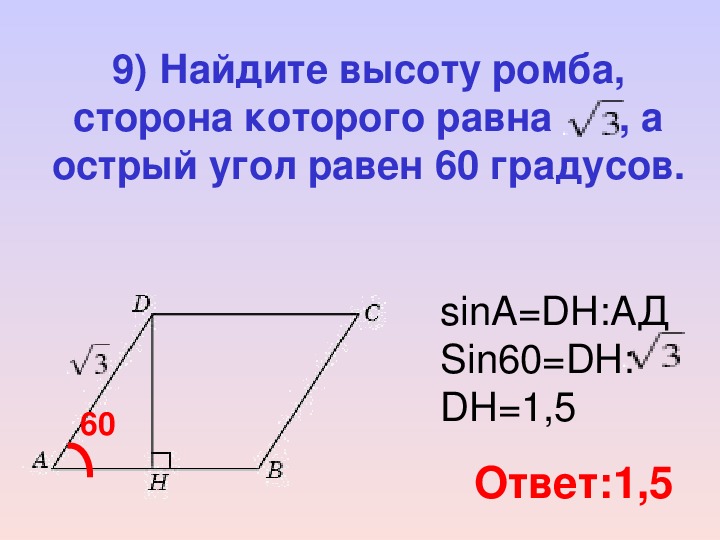 Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65 и 50. Найдите меньший угол параллелограмма. 2. Разность углов, прилежащих к одной стороне параллелограмма, равна
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65 и 50. Найдите меньший угол параллелограмма. 2. Разность углов, прилежащих к одной стороне параллелограмма, равна
Тема 21 «Трапеция. Многоугольники».
Тема 1 «Трапеция. Многоугольники». Трапеция четырехугольник, у которого ровно одна пара противолежащих сторон параллельна. Параллельные стороны называются основаниями трапеции. Две другие стороны называются
ПодробнееТренировочные задачи
И. В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Площадь.. Площадь прямоугольника равна 6. Найдите площадь четырёхугольника с вершинами в серединах сторон прямоугольника.. Средняя линия
ПодробнееПланиметрия (расширенная)
1. Площади плоских фигур Площадь треугольника: стр.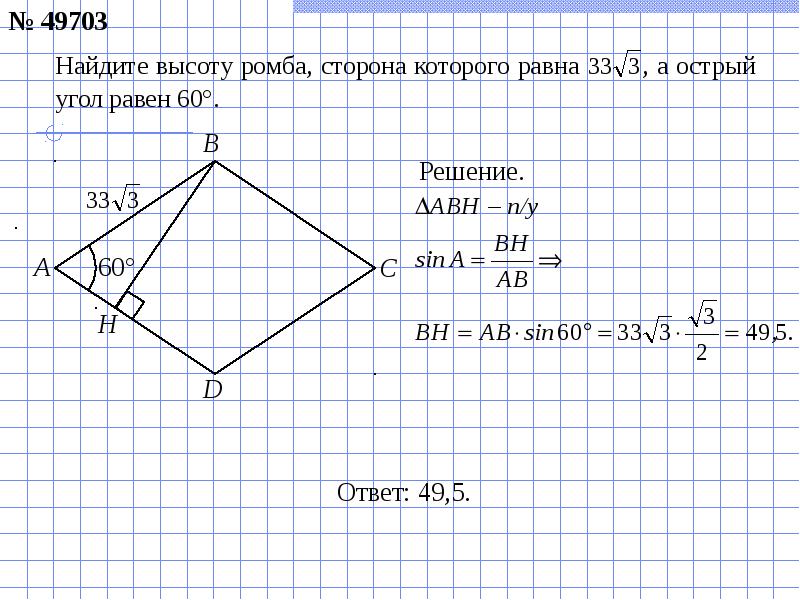 1 2. Средняя линия 3. Треугольники Сумма углов треугольника равна 180. Тупой угол между биссектрисами двух углов треугольника равен 90 + половина третьего
1 2. Средняя линия 3. Треугольники Сумма углов треугольника равна 180. Тупой угол между биссектрисами двух углов треугольника равен 90 + половина третьего
ЗАДАНИЕ 9 ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК. 1. В треугольнике ABC угол C равен,,. Найдите AB. 2. В треугольнике ABC угол C равен,,. Найдите AB.
ЗАДАНИЕ 9 ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК 1. В треугольнике ABC угол C равен,,. Найдите AB. 2. В треугольнике ABC угол C равен,,. Найдите AB. 3. В треугольнике ABC угол C равен,,. Найдите AB. 4. В треугольнике
Подробнее41 прототип задания 18
41 прототип задания 18 Задача демо-версии: Найдите площадь трапеции, изображённой на рисунке. 1. Задание 18 ( 27582) Найдите площадь квадрата, если его диагональ равна 1. 2. Задание 18 ( 27614) Найдите
ПодробнееТренировочные задачи
И. В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Теорема Пифагора 1. Найдите диагональ квадрата со стороной a. a. В прямоугольном треугольнике с углом 60 гипотенуза равна. Найдите катеты.
В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Теорема Пифагора 1. Найдите диагональ квадрата со стороной a. a. В прямоугольном треугольнике с углом 60 гипотенуза равна. Найдите катеты.
ID_7510 1/9 neznaika.pro
1 Анализ геометрических высказываний Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов.
ПодробнееОГЭ 2015 (задание 13, модуль «ГЕОМЕТРИЯ»)
ОГЭ 2015 (задание 13, модуль «ГЕОМЕТРИЯ») 169915 Какие из следующих утверждений верны? 1) Если угол равен 45, то вертикальный с ним угол равен 45. 2) Любые две прямые имеют ровно одну общую точку. 3) Через
ПодробнееТеоретическая часть экзамена по Г-8 кл.
Теоретическая часть экзамена по Г-8 кл. Знать и понимать (сделать чертеж и показать на рисунке) следующие определения и теоремы (без доказательства) из учебника Г-8 А.Г. Мерзляка Глава 1 1. Сумма углов
Знать и понимать (сделать чертеж и показать на рисунке) следующие определения и теоремы (без доказательства) из учебника Г-8 А.Г. Мерзляка Глава 1 1. Сумма углов
МАТЕМАТИКА ДЛЯ ВСЕХ. Ю.Л.Калиновский
МАТЕМАТИКА ДЛЯ ВСЕХ Ю.Л.Калиновский Оглавление 1 Медиана, биссектриса, высота…………………………… 5 1.1 Медианы треугольника 5 1.2 Биссектрисы треугольника 7 1.3 Высоты треугольника 10 Медианы
Подробнее7 класс 1. Виды углов.
7 класс 1. Виды углов. Угол называется прямым, если он равен 90 0. Угол называется острым, если он меньше 90 0. Угол называется тупым, если он больше 90 0, но меньше 180 0. Прямой угол Острый угол Тупой
ПодробнееГЕОМЕТРИЯ: ПЛАНИМЕТРИЯ
ГЕОМЕТРИЯ: ПЛАНИМЕТРИЯ I Группа 1.01 Разность двух углов, получившихся при пересечении двух прямых, равна 20. Найти больший из этих углов. 1.02 Углы треугольника пропорциональны числам 3:7:8. Найти наибольший
Найти больший из этих углов. 1.02 Углы треугольника пропорциональны числам 3:7:8. Найти наибольший
Работа по геометрии для 8 класса.
Работа по геометрии для 8 класса. 1.Вид работы: промежуточная аттестация по геометрии в 8 классе Цель работы: оценка уровня достижения учащимися 8 класса планируемых результатов обучения геометрии 2.Перечень
ПодробнееСредняя линия треугольника
И. В. Яковлев Материалы по математике MathUs.ru Средняя линия треугольника Средняя линия треугольника это отрезок, соединяющий середины двух сторон треугольника. Говоря о средней линии, третью сторону
ПодробнееКоординатная плоскость
Координатная плоскость 1. Найдите площадь ромба, вершины которого имеют координаты (6;3), (9;4), (10;7), (7;6). Площадь четырехугольника равна разности площади квадрата 4х4, четырех равных прямоугольных
Площадь четырехугольника равна разности площади квадрата 4х4, четырех равных прямоугольных
Выполнила: Науменко Елена
ГЛОССАРИЙ учебной практики 1 курса группы МИБ-111 факультета МИФ «Волгоградского государственного социально-педагогического университета» по теме : «Четырехугольники» Выполнила: Науменко Елена 1.Четырехугольники:
ПодробнееМетод ключевых задач
Метод ключевых задач Задачи, в которых фигурируют середины отрезков Задача. Докажите, что середины сторон четырехугольника являются вершинами параллелограмма. Пример. В четырехугольнике = = 90. Точки и
ПодробнееЗадания В6. . Найдите AB.
Задания В6 1. В треугольнике ABC угол C равен 90, тангенс внешнего угла при вершине A равен -0,1. Найдите tga. 2. Угол A четырехугольника ABCD, вписанного в окружность, равен 52. Найдите угол C этого 3.
Найдите угол C этого 3.
В параллелограмме ABCD AB = 3, AD = 21, большую высоту параллелограмма. Найдите. Найдите площадь квадрата, если его диагональ равна 1.
В 8 (2014) 16. В треугольнике ABC, 30. В треугольнике ABC угол C равен, CH. высота,,. Найдите AH. высота,,. Найдите BH.
В 8 (2014) 1). В треугольнике ABC угол C равен, CH высота,,. Найдите AH. 2. В треугольнике ABC угол C равен, CH 3. В треугольнике ABC угол C равен,,. Найдите высоту CH. 4. В треугольнике ABC угол C равен,
ПодробнееПрототипы задания В6-2 (2013)
Прототипы задания В6-2 (2013) ( 27742) Один острый угол прямоугольного треугольника на больше другого. Найдите больший острый угол. Ответ дайте в градусах. ( 27743) В треугольнике ABC угол A равен, внешний
Найдите больший острый угол. Ответ дайте в градусах. ( 27743) В треугольнике ABC угол A равен, внешний
tgbac. В8 ЕГЭ В ABC C = 90 0, CH высота, AB = 13, tga 5. Найдите BH. 12,5 3 В ABC C = 90 0, AB = 13, tga. Найдите высоту CH.
В-8. ПРОТОТИПЫ Задание ответ В ABC C = 90 0, CH высота, AB =, tga. Найдите AH., В ABC C = 90 0, CH высота, AB =, tga. Найдите, В ABC C = 90 0, AB =, tga. Найдите высоту CH., В ABC C = 90 0, CH высота,
Подробнее41 прототип задания 18
41 прототип задания 18 Задача демо-версии: Найдите площадь трапеции, изображённой на рисунке. 1. Задание 18 ( 27582) Найдите площадь квадрата, если его диагональ равна 1. 2. Задание 18 ( 27614) Найдите
Подробнее7 sin A. Найдите AB. 25
Прототипы задания 6 1. В треугольнике ABC угол C равен 90 0, AC = 4,8, 25.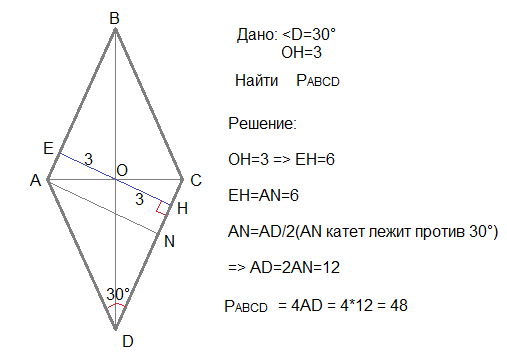 В треугольнике ABC AC = BC, AB = 8, 33 tga. 7 4 33 sin A. Найдите AB. 25 Найдите AC. 2. В треугольнике ABC угол C равен 90 0,
В треугольнике ABC AC = BC, AB = 8, 33 tga. 7 4 33 sin A. Найдите AB. 25 Найдите AC. 2. В треугольнике ABC угол C равен 90 0,
Все прототипы заданий В3
1. Прототип задания B3 ( 27543) Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 Все прототипы заданий В3 2. Прототип задания B3 ( 27544) Найдите площадь треугольника,
ПодробнееAC 6, cos A. Найдите BH.
Прототипы задания 6 1. Задание 6 ( 26097) 16. Задание 6 ( 20001) В треугольнике ABC угол C равен 90, sin A 0, 6, 21 AC 4. Найдите AB. В треугольнике ABC AC BC 12, sin B. 5 2. Задание 6 ( 29580) Найдите
ПодробнееВсе прототипы заданий В года
1. Прототип задания B5 ( 27450) Найдите тангенс угла AOB. Все прототипы заданий В5 2014 года 2. Прототип задания B5 ( 27456) Найдите тангенс угла AOB. 7. Прототип задания B5 ( 27547) Найдите площадь треугольника,
Прототип задания B5 ( 27456) Найдите тангенс угла AOB. 7. Прототип задания B5 ( 27547) Найдите площадь треугольника,
ID_5162 1/9 neznaika.pro
1 Площади фигур Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов. Сумма двух углов равнобедренной
ПодробнееЗАДАНИЕ 9 ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК. 1. В треугольнике ABC угол C равен,,. Найдите AB. 2. В треугольнике ABC угол C равен,,. Найдите AB.
ЗАДАНИЕ 9 ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК 1. В треугольнике ABC угол C равен,,. Найдите AB. 2. В треугольнике ABC угол C равен,,. Найдите AB. 3. В треугольнике ABC угол C равен,,. Найдите AB. 4. В треугольнике
ПодробнееГеометрия
Геометрия 1.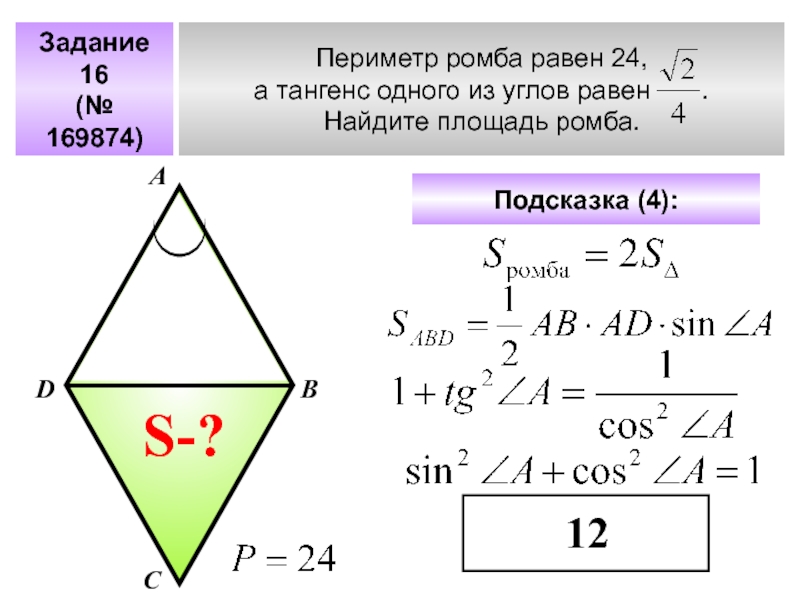 САМОСТОЯТЕЛЬНАЯ РАБОТА 1 ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА ариант 1 Найдите площадь прямоугольника, стороны которого равны 3 и 4. Найдите сторону квадрата, площадь которого равна сумме площадей квадратов со сторонами
САМОСТОЯТЕЛЬНАЯ РАБОТА 1 ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА ариант 1 Найдите площадь прямоугольника, стороны которого равны 3 и 4. Найдите сторону квадрата, площадь которого равна сумме площадей квадратов со сторонами
А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Планиметрия: квадрат, прямоугольник, треугольник. 27583.
ПодробнееВ.А. Смирнов ГЕОМЕТРИЯ ПЛОЩАДЬ
В.А. Смирнов ГЕОМЕТРИЯ ПЛОЩАДЬ 2011 ВВЕДЕНИЕ Выработка умений находить площади фигур на плоскости относится к основным целям обучения геометрии в школе. Задачи на нахождение площадей входят в содержание
ПодробнееТренировочные задачи
И. В. Яковлев Материалы по математике MathUs. ru Тренировочные задачи Параллелограмм. Периметр параллелограмма равен, а одна из его сторон вдвое больше другой. Найдите стороны параллелограмма. и 4. Найдите
ru Тренировочные задачи Параллелограмм. Периметр параллелограмма равен, а одна из его сторон вдвое больше другой. Найдите стороны параллелограмма. и 4. Найдите
ЗАДАНИЕ 15 Планиметрия Треугольник
ЗАДАНИЕ 15 Планиметрия Треугольник 1. На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. 2. На клетчатой бумаге с клетками
ПодробнееГЕОМЕТРИЯ: ПЛАНИМЕТРИЯ
ГЕОМЕТРИЯ: ПЛАНИМЕТРИЯ I Группа 1.01 Разность двух углов, получившихся при пересечении двух прямых, равна 20. Найти больший из этих углов. 1.02 Углы треугольника пропорциональны числам 3:7:8. Найти наибольший
ПодробнееЗадания В6. . Найдите AB.
Задания В6 1. В треугольнике ABC угол C равен 90, тангенс внешнего угла при вершине A равен -0,1.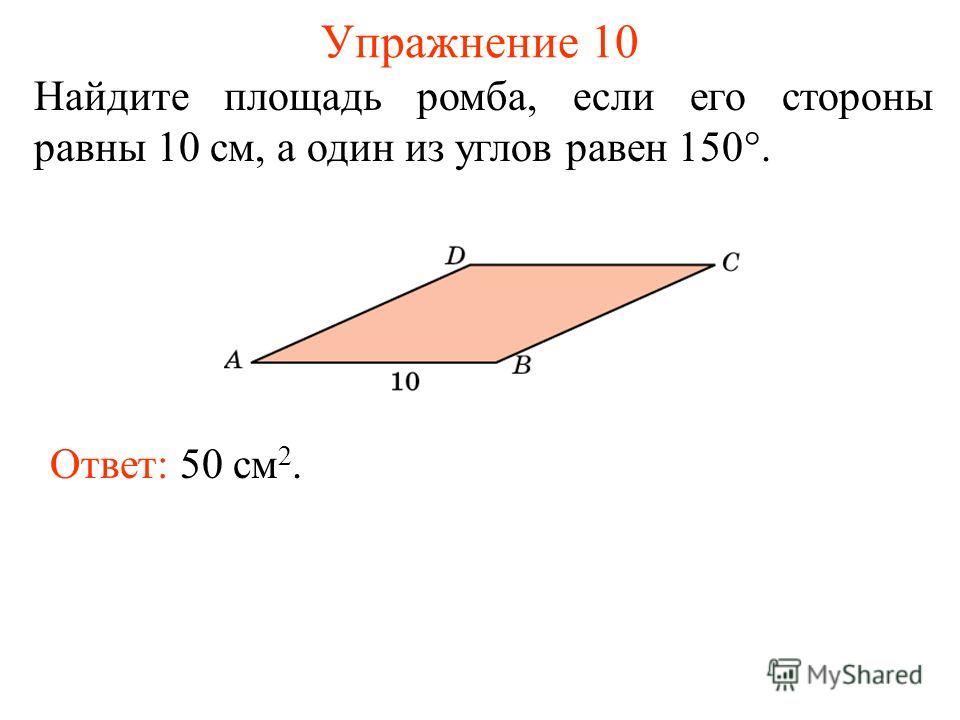 Найдите tga. 2. Угол A четырехугольника ABCD, вписанного в окружность, равен 52. Найдите угол C этого 3.
Найдите tga. 2. Угол A четырехугольника ABCD, вписанного в окружность, равен 52. Найдите угол C этого 3.
Анализ геометрических высказываний
Анализ геометрических высказываний 1. Укажите номера верных утверждений. 1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. 2) Вертикальные углы
ПодробнееТест 140. Правильный многоугольник. Признак
Тест 132. Многоугольник. Существование Существуют два треугольника, объединением которых являются: 1. треугольники двух видов: равносторонний и равнобедренный, но не равносторонний; 2. квадрат; 3. шестиугольник;
ПодробнееТренировочные задачи
И. В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Теорема Пифагора 1. Найдите диагональ квадрата со стороной a. a. В прямоугольном треугольнике с углом 60 гипотенуза равна. Найдите катеты.
Найдите диагональ квадрата со стороной a. a. В прямоугольном треугольнике с углом 60 гипотенуза равна. Найдите катеты.
Тренировочные задачи
И. В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Площадь.. Площадь прямоугольника равна 6. Найдите площадь четырёхугольника с вершинами в серединах сторон прямоугольника.. Средняя линия
ПодробнееПланиметрия: комбинации фигур.
А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Планиметрия: комбинации фигур. 27624. Периметр треугольника
ПодробнееID_2420 1/11 neznaika.pro
1 Планиметрия: вычисление длин и площадей Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов.
Запишите ответ без пробелов, запятых и других дополнительных символов.
ОГЭ 2015 (задание 13, модуль «ГЕОМЕТРИЯ»)
ОГЭ 2015 (задание 13, модуль «ГЕОМЕТРИЯ») 169915 Какие из следующих утверждений верны? 1) Если угол равен 45, то вертикальный с ним угол равен 45. 2) Любые две прямые имеют ровно одну общую точку. 3) Через
ПодробнееМетод ключевых задач
Метод ключевых задач Задачи, в которых фигурируют середины отрезков Задача. Докажите, что середины сторон четырехугольника являются вершинами параллелограмма. Пример. В четырехугольнике = = 90. Точки и
ПодробнееID_7510 1/9 neznaika.pro
1 Анализ геометрических высказываний Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов.
Запишите ответ без пробелов, запятых и других дополнительных символов.
Планиметрия (расширенная)
1. Площади плоских фигур Площадь треугольника: стр. 1 2. Средняя линия 3. Треугольники Сумма углов треугольника равна 180. Тупой угол между биссектрисами двух углов треугольника равен 90 + половина третьего
ПодробнееТренажер по теме «Площади фигур»
Муниципальное автономное образовательное учреждение
вечерняя сменная общеобразовательное учреждение
г. Березники Пермского края
ТРЕНАЖЕР ПО ТЕМЕ
«ПЛОЩАДИ ФИГУР»
Составила
учитель математики
Хватынец Валентина Юрьевна
г. Березники, 2017 год
СОДЕРЖАНИЕ
Предисловие…………………………………………………….
§1. Знание теоретического материала……………………………….
§2. Задачи по теме «Прямоугольник» ……………………………………………………….
§3. Задачи по теме «Параллелограмм» ……………………………………………………….
§4. Задачи по теме «Треугольник» ……………………………………………………………
§5. Задачи по теме «Трапеция» …………………………………………
§6. Задачи по теме «Площадь фигур, заданных координатами» ……
§7. Задачи по теме «Площадь фигур на сетке» …………………………………
§8. Задачи по теме «Площадь заштрихованной фигуры» ……………….
§9. Ответы.
Справочный материал.
Список использованной литературы.
Предисловие
Цель данного пособия – помочь учащимся и учителям 9-х классов систематизировать знания по теме «Площадь фигур», закрепить знания теоретического материала и применение их на практике. Задачи:
выработать умение применять формулу для нахождения площади фигур;
совершенствовать навыки чтения математических чертежей; — развивать способность выбирать оптимальный путь решения задачи. Развитие вычислительной грамотности, пространственного воображения. Пособие предназначено для работы на уроке, для выполнения домашних заданий, а также для подготовки к итоговой аттестации. Рекомендовано для учащихся обучающихся по форме самообразования (экстернат). Пособие включает в себя справочные материалы, представленные в таблицах. Тренировочные упражнения помогают запомнить изученный материал, закрепить знания теоретического материала на практических заданиях. Каждую тему завершают контрольные диагностические наборы или тесты формата ОГЭ. Тренировочный материал пособия апробирован на уроках математики в Вечерней сменной школе г. Березники.
Развитие вычислительной грамотности, пространственного воображения. Пособие предназначено для работы на уроке, для выполнения домашних заданий, а также для подготовки к итоговой аттестации. Рекомендовано для учащихся обучающихся по форме самообразования (экстернат). Пособие включает в себя справочные материалы, представленные в таблицах. Тренировочные упражнения помогают запомнить изученный материал, закрепить знания теоретического материала на практических заданиях. Каждую тему завершают контрольные диагностические наборы или тесты формата ОГЭ. Тренировочный материал пособия апробирован на уроках математики в Вечерней сменной школе г. Березники.
§1. Знание теоретического материала.
№ п/п | Текст задания | Ответы |
1. | По данным величинам запишите формулу площади данной фигуры. | |
2 | По данным величинам запишите формулу площади данной фигуры. | |
3 | По данным величинам запишите формулу площади данной фигуры. | |
4 | По данным величинам запишите формулу площади данной фигуры. | |
5 | По данным величинам запишите формулу площади данной фигуры. | |
6 | По данным величинам запишите формулу площади данной фигуры. | |
7 | По данным величинам запишите формулу площади данной фигуры. | |
8 | По данным величинам запишите формулу площади данной фигуры. | |
9 | По данным величинам запишите формулу площади данной фигуры. | |
10 | По данным величинам запишите формулу площади данной фигуры. |
§2. Задачи по теме «Прямоугольник»
№ | Текст задания | Ответы | ||
А | В | С | ||
1. | В прямоугольнике одна сторона равна 20, другая сторона равна 24. Найдите площадь прямоугольника. | 88 | 480 | 68 |
2. | Найдите площадь прямоугольника, по стороне и диагонали. | 1440 | 98 | 196 |
3. | В прямоугольнике периметр равен 72, а одна из его сторон равна 16. Найдите площадь прямоугольника. | 88 | 320 | 896 |
4. | В прямоугольнике диагональ равна 32, а угол между ней и одной из сторон равен 60°. Найдите площадь прямоугольника, деленную на √3. | 640 | 256 | 1920 |
5. | Найдите площадь прямоугольника, если его периметр равен 68 и одна сторона на 4 больше другой. | 285 | 272 | 1156 |
6. | Площадь прямоугольника равна 18. Найдите его большую сторону, если она в 2 раза больше меньшей стороны. | 9 | 6 | 3 |
7 | Одна из сторон прямоугольника равна 30, а площадь равна 480. Найдите диагональ этого прямоугольника. | 34 | 16 | 510 |
8. | Найдите площадь прямоугольника, изображенного на рисунке. | 350 | 780 | 39 |
9. | Найдите площадь прямоугольника, изображенного на рисунке.
| 180 | 580 | 420 |
10. | Сторона квадрата равна 21. Найдите площадь квадрата. | 42 | 84 | 441 |
11. | Как изменится площадь прямоугольника, если каждую сторону увеличить в два раза? | В 4 раза | В 2 раза | Не измен. |
12. | Пол комнаты, имеющей форму прямоугольника со сторонами 5,5 м и 6 м, нужно покрыть паркетом прямоугольной формы. Длина каждой дощечки паркета равна 30 см, а ширина – 5 см. Сколько потребуется таких дощечек для покрытия пола? | 2200 | 220 | 22 |
13. | Сколько потребуется кафельных плиток квадратной формы со стороной 15 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 3 м и 2,7 м? | 36 | 360 | 400 |
Проверочная работа.
А
В
1. Укажите неверную формулу площади.
a) SABCD = AB · AD
б) SABCD = AB · BC
D
С
в) S∆ABC = AB · BC
2. Как изменится площадь прямоугольника, если одну его сторону увеличить в 2 раза, а другую – в 4 раза?
3. Площадь прямоугольника со сторонами 8см и 2 дм равна:
а) 56 см б) 16 см2 в) 160см2
4. Сколько потребуется досок для настила пол в зале, длина которого равна 20 м, а ширина 10 м, если длина доски 4 м, а ширина 25 см?
а) 125 шт. б) 200 шт. в) 180 шт.
§3. Задачи по теме «Параллелограмм»
№ | Текст задания | Ответы | ||
А | В | С | ||
1. | Одна из сторон параллелограмма равна 31, а опущенная на нее высота равна 7. Найдите площадь параллелограмма. | 38 | 217 | 76 |
2 | Одна из сторон параллелограмма равна 13, другая равна 20, а один из углов – 45°. Найдите площадь параллелограмма, умноженную на √2. | 260 | 130 | 57 |
3. | Стороны параллелограмма равны 9 и 10. Высота, опущенная на первую сторону, равна 14.Найдите высоту, опущенную на вторую сторону параллелограмма. | 266 | 12,6 | 33 |
4. | Площадь параллелограмма равна 65, две его стороны равны 5 и 10. | 6,5 | 13 | 5 |
5. | Площадь параллелограмма равна 205, две его высоты равны 5 и 17. Найдите большую сторону этого параллелограмма. | 41 | 12 | 9 |
6. | Найдите площадь параллелограмма, изображенного на рисунке. | 42 | 24 | 70 |
7. | Смежные стороны параллелограмма равны 12 см и 14 см, а его острый угол равен 30°. Найдите площадь параллелограмма. | 168 | 56 | 84 |
8. | Периметр параллелограмма равен 20 см. Вычислите его площадь, если один из его углов равен 150°, а длина одной из его сторон равна 8 см. | 15 | 8 | 12 |
9 | Стороны параллелограмма 6см и 9 см. Длина большей высоты параллелограмма 8 см. Найдите его площадь. | 48 | 72 | 54 |
10. | Площадь параллелограмма равна 25 см2. Стороны параллелограмма равны 2а + 3; 3а + 4 см, тогда меньшая высота этого параллелограмма равна: | 25: (3а + 4) | 25: (2а + 3) | (2а + 3) (3а + 4) |
Проверочная работа.
1. Стороны параллелограмма равны 8см и 14 см, а угол между ними 30°. Найдите площадь параллелограмма.
Найдите площадь параллелограмма.
2. Стороны параллелограмма равны 4 см и 8 см. Высота, опущенная на первую из этих сторон, равна 6 см. Найдите высоту, опущенную на вторую сторону параллелограмма.
3. Площадь параллелограмма равна 24 см2, каждая из его сторон равна 6 см. Найдите расстояние между противоположными сторонами параллелограмма.
4. Укажите формулу для вычисления площади параллелограмма:
а) S = ½ a·ha
b
б) S = 2 a ·ha
hb
ha
в) S = a ha
а
§4. Задачи по теме «Ромб»
№ п/п | Текст задания | Ответы | ||
А | В | С | ||
1. | Найдите площадь ромба, если его диагонали равны 8 и 12. | 96 | 48 | 40 |
2. | Периметр ромба равен 72, а один из углов равен 45°. Найдите площадь ромба, деленную на √2. | 162 | 117 | 27 |
3. | Найдите сторону ромба, если его площадь равна 72, а острый угол 30°. | 24 | 12 | 216 |
4. | Площадь ромба равна 26. Одна из диагоналей равна 4. Найдите другую диагональ. | 6,5 | 13 | 65 |
5. | Найдите высоту ромба, если его площадь равна 54, а сторона равна 4. | 13,4 | 216 | 58 |
6. | Сторона ромба равна 25, а диагональ – 48. Найдите площадь ромба. | 1200 | 73 | 336 |
7. | Найдите площадь ромба, изображенного на рисунке. | 14 | 20 | 24 |
8. | Найдите площадь ромба, изображенного на рисунке. | 90 | 60 | 21 |
9. | Найдите площадь ромба, если его высота равна 12, а острый угол 30°. | 288 | 360 | 42 |
10. | Сторона ромба 8 см, а острый угол 30°. Найдите площадь ромба. | 32 | 240 | 64 |
Самостоятельная работа.
Укажите неверное утверждение:
а) площадь ромба равна произведению диагоналей;
б) площадь ромба равна произведению его стороны на высоту;
в) диагонали ромба разбивают его на 4 равновеликих треугольника.
Найдите высоту ромба, сторона которого равна 6, 5 см, а площадь – 26 см2.
Сторона ромба 6 см, а острый угол 30°. Найдите площадь ромба.
Периметр ромба равен 40 см, а высота равна 8 см. Вычислите площадь ромба.
§5. Задачи по теме «Треугольник»
№ п/п | Текст заданий | Ответы | ||
А | В | С | ||
1. | Найдите площадь треугольника, изображенного на рисунке. | 42 | 70 | 300 |
2. | В прямоугольном треугольнике один из катетов равен 8, а угол, лежащий против него, равен 30°. Найдите площадь треугольника. В ответе напишите площадь, деленную на √3. | 32 | 240 | 38√3 |
3. | В прямоугольном треугольнике один из катетов равен 5, а острый угол, прилежащий к нему, равен 30°. Найдите площадь треугольника. В ответе запишите площадь, умноженную на √3. | 150 | 12,5 | 50 |
4. | В прямоугольном треугольнике один из катетов равен 12, а угол, лежащий напротив него, равен 45°. Найдите площадь треугольника. | 72 | 144 | 57 |
5. | Периметр равностороннего треугольника равен 84. Найдите его площадь, деленную на √3. | 28 | 84√3 | 196 |
6. | Найдите площадь равностороннего треугольника, высота которого равна 4. | 16 | 4√3 | 12 |
7. | Периметр равнобедренного треугольника равен 36, а боковая сторона – 13. Найдите площадь треугольника. | 43 | 60 | 468 |
8. | Периметр равнобедренного треугольника равен 100, а основание – 18. Найдите площадь треугольника. | 118 | 820 | 180 |
9. | У треугольника со сторонами 14 и 21 проведены высоты к этим. Высота, проведенная к меньшей стороне, равна 6. Чему равна высота, проведенная к большей стороне? | 4 | 5,8 | 49 |
10. | Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 90°. Найдите боковую сторону треугольника, если его площадь равен 450. | 540 | 5 | 30 |
11. | Найдите площадь треугольника, изображенного на рисунке. | 132 | 264 | 62 |
12. | Найдите площадь треугольника, изображенного на рисунке. | 40 | 120 | 60 |
13. | Найдите площадь прямоугольного треугольника, изображенного на рисунке. | 52 | 315 | 24,5 |
14. | Найдите площадь равнобедренного треугольника, изображенного на рисунке. | 168 | 98 | 200 |
15. | Найдите площадь равнобедренного треугольника, изображенного на рисунке. | 60 | 42 | 84 |
Проверочная работа.
Катеты прямоугольного треугольника равны 4 см и 3 см. Вычислите площадь данного треугольника.
а) 7см; в) 6 см; с) 12 см
2. В треугольнике одна из сторон 12, другая 8, а синус угла между ними равен 0,2. Найдите площадь треугольника. a) 9, 6 в) 4, 8 с) 48
3. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см х 1см. Ответ дайте в квадратных сантиметрах
а) 21 в) 13см с) 30 см
4. Найдите площадь прямоугольного треугольника, если один из его катетов равен 8 см, а гипотенуза равна 10 см.
Найдите площадь прямоугольного треугольника, если один из его катетов равен 8 см, а гипотенуза равна 10 см.
а) 80см2 в) 24см2 с) 48см2
§6. Задачи по теме «Трапеция»
№ п/п | Тексты заданий | Ответы | ||
А | В | С | ||
1. | Основания трапеции равны 17 и 22, площадь трапеции равен 390. Найдите высоту трапеции. | 10 | 20 | 5 |
2. | Одно из оснований трапеции равно 12, высота равна 6, а площадь трапеции равна 96. Найдите второе основание трапеции. | 16 | 4 | 20 |
3. | Основания равнобедренной трапеции равны 8 и 29, площадь равна 333. Найдите ее высоту. | 18 | 9 | 15 |
4. | Основание трапеции равно 23, высота равна 5, а площадь равна 150. Найдите второе основание трапеции. | 7 | 8,3 | 5 |
5. | Основания равнобедренной трапеции равны 7 и 13, а ее периметр равен 30. Найдите площадь трапеции. | 30 | 40 | 600 |
6. | Найдите большее основание прямоугольной трапеции, площадь которой равна 48, высота равна 6 и большая боковая сторона составляет с основанием угол 45°. | 11 | 8 | 42 |
7. | В равнобокой трапеции основания равны 10 см и 20 см, боковая сторона равна 25 см. Найдите площадь трапеции, деленную на √5. | 200 | 500 | 40 |
8. | Тупой угол равнобедренной трапеции равен 135°, а высота, проведенная из вершины этого угла, делит большее основание на отрезки 1,4 см и 3,4 см. Найдите площадь трапеции. | 13,98 | 4,76 | 87 |
9. | Найдите площадь прямоугольной трапеции, у которой две меньшие стороны равны 6 см, а больший угол равен 135°. | 36 | 54 | 129 |
10. | Основания равнобедренной трапеции равны 6 см и 10 см. Ее острый угол равен 45°. Найдите площадь трапеции. | 16 | 60 | 30 |
Проверочная работа
1. Основания равнобедренной трапеции равны 14 и 20, а высота равна 5. Найдите площадь трапеции.
а) 68 б) 34 в) 85
2.Укажите верную формулу для вычисления площади трапеции
a
а) S =
h
б) S = (a + b) h
b
в) S =
3. Найдите площадь прямоугольной трапеции, у которой две меньшие стороны равны 6 см, а больший угол 135°.
а) 36 см2 б) 54 см2 в) 18 см2
4. Параллельные стороны трапеции равны 2 см и 5 см, а расстояние между ними равно 4 см. Площадь трапеции равна:
а) 40 см2 б) 14 см2 в) 2,5 см2
§7. Задачи по теме «Площадь фигур, заданных координатами».
Задачи по теме «Площадь фигур, заданных координатами».
№ п/п | Текст задания | Ответы | ||
А | В | С | ||
1. | Найдите площадь треугольника, вершины которого имеют координаты (1; 0), (11; 7), (8;10). | 31 | 27 | 15 |
2. | Найдите площадь прямоугольника, вершины которого имеют координаты (1; 0), (10; 0), (1; 10), (10; 10) | 90 | 38 | 19 |
3. | Найдите площадь трапеции, вершины которой имеют координаты (-4; -2), (4; -2), (3; 5), (0; 5). | 77 | 38,5 | 56 |
4. | Найдите площадь параллелограмма, вершины которого имеют координаты (-2; -1), (4; -1), (2; 4), (-4; 4). | 30 | 22 | 11 |
§8. Задачи по теме «Площадь фигур на сетке»
№ п/п | Тексты заданий | Ответы | ||
А | В | С | ||
1 | Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см х 1см. Ответ дайте в квадратных сантиметрах. | 7,5 | 8 | 11 |
2 | Найдите площадь прямоугольника, изображенного на клетчатой бумаге с размером клетки 1см х 1см. Ответ дайте в квадратных сантиметрах. | 12 | 18 | 9 |
3 | Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см х 1см. Ответ дайте в квадратных сантиметрах. | 8 | 13 | 10 |
4 | Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см х 1см. Ответ дайте в квадратных сантиметрах. | 6 | 12 | 10 |
5 | Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см х 1см. | 8 | 10 | 12 |
6 | Найдите площадь параллелограмма, изображенного на клетчатой бумаге с размером клетки 1см х 1см. Ответ дайте в квадратных сантиметрах. | 17 | 12 | 10 |
7 | Найдите площадь фигуры, изображенного на клетчатой бумаге с размером клетки 1см х 1см. Ответ дайте в квадратных сантиметрах. | 13 | 21 | 20 |
§9. Задачи по теме «Площадь заштрихованной фигуры»
№ п/п | Тексты заданий | Ответы | ||
А | В | С | ||
1 | Выполните необходимые измерения и вычислите площадь заштрихованной фигуры. | 22 | 42 | 25 |
2 | Выполните необходимые измерения и вычислите площадь заштрихованной фигуры. | 22 | 34 | 25 |
3 | Выполните необходимые измерения и вычислите площадь заштрихованной фигуры. | 29,5 | 20,5 | 25 |
4 | Выполните необходимые измерения и вычислите площадь заштрихованной фигуры. | 18 | 30 | 25 |
5 | Выполните необходимые измерения и вычислите площадь заштрихованной фигуры. | 16,5 | 25,5 | 25 |
6 | Вычислите площадь заштрихованной фигуры, если R = 6; r1 = 3; r2 = 1 | 81,64 | 15 | 100 |
7. | Вычислите площадь заштрихованной фигуры, если AB = AC = BC =6. | 21,6 | 3,79 | 37,9 |
8 | АВСD – прямоугольник | 18,58 | 1,858 | 185,8 |
9. | АВСD – квадрат, АВ = 6 см. | 77,4 | 7,74 | 0,774 |
Контрольная работа по теме «Площади»
Найдите площадь фигуры, изображенного на клетчатой бумаге с размером клетки 1см х 1см. Ответ дайте в квадратных сантиметрах.
Ответ дайте в квадратных сантиметрах.
Ответы.
§1. Знание теоретического материала
S = a b
S = a h
S = a b sin α
S = ½ a b sin α
S =
S =
S ==
S =
S = π R2
10.S = √ p (p-a) (p-b) (p-c), где p =
тема «Прямоугольник» | тема «Параллелограмм | тема «Ромб» | тема «Треугольник |
1-В | 1-В | 1-В | 1-В |
2-А | 2-А | 2-А | 2-А |
3-В | 3-В | 3-В | 3-В |
4-В | 4-В | 4-В | 4-А |
5-А | 5-А | 5-А | 5-С |
6-С | 6-А | 6-С | 6-А |
7-А | 7-С | 7-С | 7-В |
8-А | 8-В | 8-А | 8-В |
9-С | 9 — А | 9-А | 9-А |
10-С | 10 — В | 10-А | 10-С |
11-А | 11-А | ||
12-А | 12-С | ||
13-В | 13-С | ||
14-А | |||
15-А |
тема «Трапеция» | тема «Площадь фигур, заданных координатами» | Тема «Площадь фигур на сетке» | Площадь заштрихованной фигуры |
1-В | 1-В | 1-А | 1-А |
2-С | 2-А | 2-В | 2-А |
3-А | 3-В | 3-А | 3-В |
4-А | 4-А | 4-А | 4-А |
5-В | 5-А | 5-А | |
6-А | 6-В | 6-А | |
7-А | 7-А | 7-В | |
8-В | 8-А | ||
9-В | 9-В | ||
10 — А |
Ответы на проверочные и самостоятельные работы.
Прямоугольник | Параллелограмм | Ромб | Треугольник | Трапеция |
1 – в | 1 -56 см2 | 1 – а | 1 – в | 1 – в |
2 – в 8 раз | 2 – 3 см | 2 – 4 см | 2 – а | 2 – в |
3 – в | 3 – 4 см | 3 – 18 см2 | 3 — а | 3 — б |
4 — б | 4 — в | 4 – 80см2 | 4 — в | 4 — в |
Справочный материал
функция | 30° | 45° | 60° |
sin α | |||
cos α | |||
tg α | 1 | √3 |
Список использованной литературы.
А.В. Погорелов. Геометрия 7-9 классы. Учебник для общеобразовательных организаций, М.: Просвещение, 2014.
Л. С. Атанасян. Геометрия 7-9 классы. Учебник для общеобразовательных организаций, М.: Просвещение, 2011.
Математика. 9 класс. ОГЭ-2017. Тренажер по новому плану экзамена. Легион, 2016.
А. П. Ершова. Самостоятельные и контрольные работы по геометрии для 8 класса. М.: ИЛЕКСА, 2015.
А.М.Лукашенок. Тесты по геометрии для поурочного контроля. 8 класс. М., Белый ветер.
В параллелограмме АВСД стороны равны 14 и 8 см, высота, проведенная к большей стороне, равна 4 см. Найдите площадь параллелограмма и вторую сторону.
К – 1
Стороны параллелограмм 6см и
8 см, а угол между ними равен 30о. Найдите площадь параллелограмма. К – 1
В равнобедренном треугольнике АВС высота ВН равна 12 см, а основание АС в 3 раза больше ВН.
Найдите площадь треугольника АВС. К – 1
В параллелограмме АВСД стороны равны 14 и 8 см, высота, проведенная к большей стороне, равна 4 см.
 Найдите площадь параллелограмма и вторую сторону.
Найдите площадь параллелограмма и вторую сторону.К – 2
К – 2
Сторона треугольника 5 см, а высота, проведенная к ней, в 2 раза больше стороны. Найдите площадь треугольника К – 2
АВСД – параллелограмм
Найти ВК.
К – 3
Диагонали ромба равны 5см и
8 см. Найдите площадь ромба. К – 3
Найдите площадь треугольника АВС. К – 3
Найдите площадь треугольника АВС.
К – 4
Смежные стороны прямоугольника равны 4 и 5 см. Найдите его площадь К – 4
Диагональ ромба равна 12 см, а другая в 3раза меньше. Чему равна площадь ромба? К – 4
Найти площадь трапеции АВСД
К – 5
Найдите площадь равнобедренного треугольника со сторонами 17, 17 и 16 см К – 5
Найдите площадь треугольника АВС.
К – 5
АВСД – параллелограмм
Найти : АВ
К – 6
Найдите площадь прямоугольного треугольника, если его катеты равны 4 см 11см. К – 6
Найти площадь трапеции АВСD К – 6
Найдите площадь параллелограмма АВСD
К – 7
Найдите площадь прямоугольника со сторонами 13, 5 и 12 см. К – 7
К – 7
Найдите площадь треугольника АВС, если MN – средняя линия, равная 7 см, а высота ВН = 6 см.
К – 7
Найдите сторону ромба, если одна из высот ромба равна 3 см, а его диагонали соответственно равны 4 и 6 см.
К – 8
Найдите площадь треугольника, если две соседние стороны равны
7см и 8 см, а угол между ними 30о. К – 8
Площади квадрата и параллелограмма равновелики. Найдите сторону квадрата, если высота параллелограмма равна
9 см, а основание – 4 см. К – 8
Площадь треугольника АВН равна
9 см2. Найдите площадь треугольника ВНС.
К – 9
Найдите площадь треугольника, если его основание равно 15 см, а высота 8 см.
К – 9
Одна диагональ ромба 8 см, а другая в 1,5 раза больше. Найдите площадь ромба. К – 9
Найдите высоты треугольника со сторонами 10, 10 и 12 см.
К – 10
Найдите площадь трапеции с основаниями 7см и 4 см, если расстояние между ними 6 см. К – 10
К – 10
Найдите площадь прямоугольной трапеции, у которой две меньшие стороны равны 5 см, а больший угол равен 135о. К – 10
Найдите меньшую высоту треугольника со сторонами 24, 25 и 27см.
К – 11
Найдите площадь трапеции АВСD, если AB = 8cм, BC = 4cм, CD = 4cм. Угол D равен 90о. К – 11
Найдите площадь параллелограмма АВСD К – 11
Найдите площадь треугольника АВС.
Приложенные файлы
- 10170048
Размер файла: 92 kB Загрузок: 0
высота параллелограмма
В.И. Даже у параллелограмма размером с галактику есть площадь. Для первого достаточно хорош эскиз Кирана Линсуаина. Параллелограмм — это 4-сторонняя форма, образованная двумя парами параллельных линий. Расстояние между противоположными сторонами параллелограмма. Высота каждого параллелограмма… Чтобы подписаться на этот RSS-канал, скопируйте и вставьте этот URL-адрес в свой RSS-ридер. У параллелограмма стороны 15 см и 18 см. В свете этой проблемы предлагаю свою версию.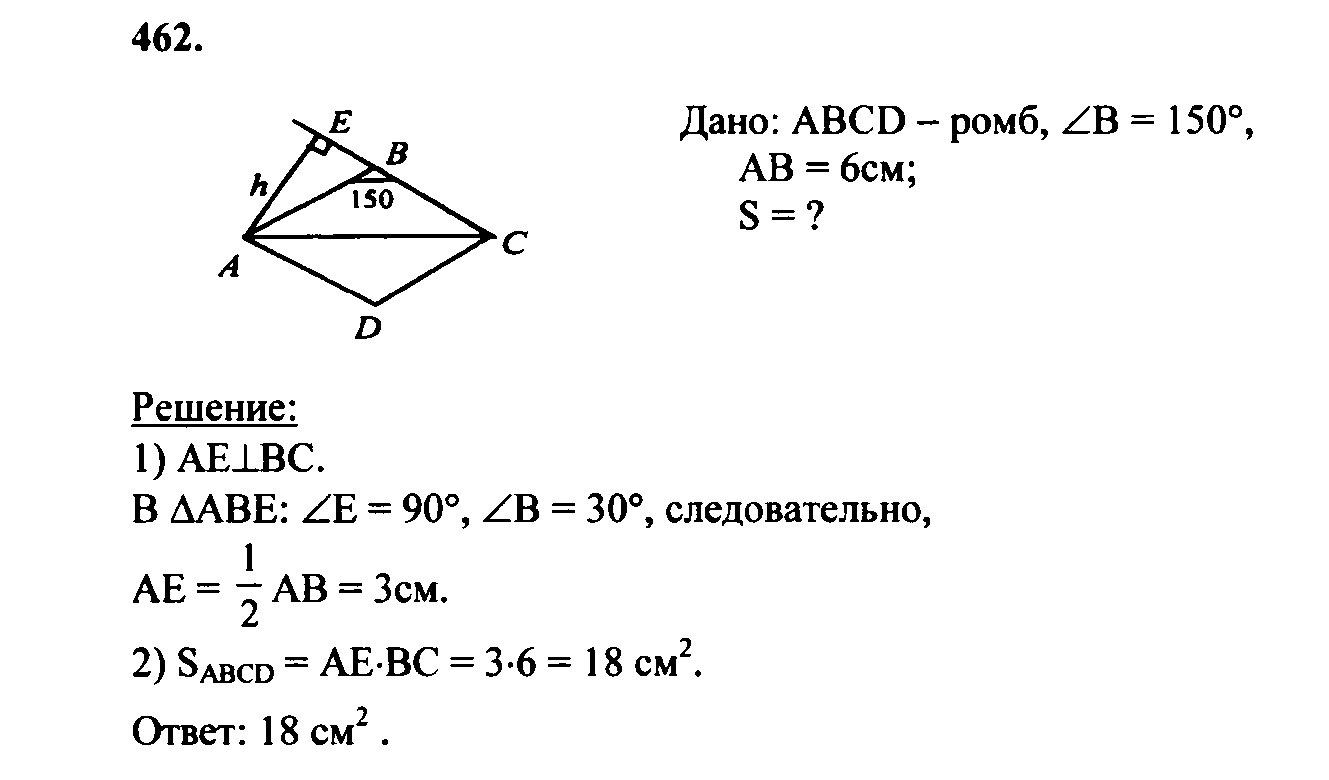 Если высота (высота) $ 8 $ см соответствует стороне $ 5 $ см, тогда площадь составляет $ 40 $ кв. См, а высота на стороне $ 10 $ см составляет $ 4 $ см. Посетите страницу High School Geometry: Tutoring Solution, чтобы узнать больше. Арнольд говорит, что русские студенты не могут решить эту проблему, но американские студенты могут — почему? В этом уроке мы выведем формулу, которая позволит нам найти высоту параллелограмма с учетом его основания и площади. Площадь и одна сторона параллелограна 210 га и 1500 м соответственно. Найдите соответствующую высоту.Постройте параллелограмм ABCD со сторонами AB = 4 см, AD = 5 см и углом A = 60. Следовательно, ему необходимо знать высоту здания. Параллелограммы на одном основании и на одной параллели равны по площади. 1. прямоугольник 2. ромб 3. квадрат 4. трапеция 1. Каждое основание имеет свою высоту, но площадь будет такой же, какое бы основание вы ни выбрали. Чтобы получить доступ к этому уроку, вы должны быть участником Study.com. Постройте отрезок AB = 4 см.
Если высота (высота) $ 8 $ см соответствует стороне $ 5 $ см, тогда площадь составляет $ 40 $ кв. См, а высота на стороне $ 10 $ см составляет $ 4 $ см. Посетите страницу High School Geometry: Tutoring Solution, чтобы узнать больше. Арнольд говорит, что русские студенты не могут решить эту проблему, но американские студенты могут — почему? В этом уроке мы выведем формулу, которая позволит нам найти высоту параллелограмма с учетом его основания и площади. Площадь и одна сторона параллелограна 210 га и 1500 м соответственно. Найдите соответствующую высоту.Постройте параллелограмм ABCD со сторонами AB = 4 см, AD = 5 см и углом A = 60. Следовательно, ему необходимо знать высоту здания. Параллелограммы на одном основании и на одной параллели равны по площади. 1. прямоугольник 2. ромб 3. квадрат 4. трапеция 1. Каждое основание имеет свою высоту, но площадь будет такой же, какое бы основание вы ни выбрали. Чтобы получить доступ к этому уроку, вы должны быть участником Study.com. Постройте отрезок AB = 4 см. Вычисление минимальной высоты LOS на заданном расстоянии (функция), Нахождение координат точки $ R $ в параллелограмме, Нахождение стороны треугольника, образованной продолжением диагонали, Нахождение наибольшей диагонали параллелограмма, если площадь известна, Мой друг говорит, что история моего романа слишком похожа на Гарри Поттера, я нашел сертификаты акций для Disney и Sony, которые были мне предоставлены в 2011 году, SSH для нескольких хостов в файле и команда запуска не выполняется — идет только на первый хост, Отключение UAC на рабочем компьютере хотя бы звуковые уведомления.(2) `. Пример проблемы. Формально самый короткий отрезок прямой между противоположными сторонами. Длина более длинной диагонали — 15 см. Противоположные стороны равны по длине, а противоположные углы равны по мере. Определите, что описано. Формула: A = B * H, где B — основание, H — высота, а * означает умножение. Я изменил свой ответ до того, как вы напечатали свой комментарий … но позже, чем следовало. Предположим, у вас есть пенал толщиной 3 см в закрытом состоянии.
Вычисление минимальной высоты LOS на заданном расстоянии (функция), Нахождение координат точки $ R $ в параллелограмме, Нахождение стороны треугольника, образованной продолжением диагонали, Нахождение наибольшей диагонали параллелограмма, если площадь известна, Мой друг говорит, что история моего романа слишком похожа на Гарри Поттера, я нашел сертификаты акций для Disney и Sony, которые были мне предоставлены в 2011 году, SSH для нескольких хостов в файле и команда запуска не выполняется — идет только на первый хост, Отключение UAC на рабочем компьютере хотя бы звуковые уведомления.(2) `. Пример проблемы. Формально самый короткий отрезок прямой между противоположными сторонами. Длина более длинной диагонали — 15 см. Противоположные стороны равны по длине, а противоположные углы равны по мере. Определите, что описано. Формула: A = B * H, где B — основание, H — высота, а * означает умножение. Я изменил свой ответ до того, как вы напечатали свой комментарий … но позже, чем следовало. Предположим, у вас есть пенал толщиной 3 см в закрытом состоянии. Поскольку в закрытом состоянии пенал имеет толщину 3 сантиметра, вы сможете вставить в него ластик и закрыть его.Цифра показана на изображении. В геометрии параллелограмм — это двухмерная фигура с четырьмя сторонами. исследование Если высота (высота) 8 см соответствует стороне 5 см, то площадь составляет 40 см 2, а высота стороны 10 см составляет 4 см. Когда мы выполняем трюк с «перемещением треугольника», мы получаем прямоугольник. Затем мы применим эту формулу к двум примерам, которые появляются в реальном мире. Авторизуйтесь здесь для доступа. Попробуйте обновить страницу или обратитесь в службу поддержки. См. Также Площадь параллелограмма. Посадка на сверхскоростной пассажирский экспресс в Китае занимает один час, и если да, то почему? Лучше поздно, чем никогда! набор карточек {{конечно.flashcardSetCoun> 1? Что это за площадь — 8679787 Можно ли сгенерировать точный тактовый импульс 15 кГц с помощью Arduino? — Определение и свойства, измерение площади ромба: формула и примеры, воздушные змеи в геометрии: определение и свойства, прямоугольники: определение, свойства и конструкция, измерение площади прямоугольника: формула и примеры, биологические и биомедицинские аспекты На рисунке выше , отображается высота, соответствующая базовому CD.
Поскольку в закрытом состоянии пенал имеет толщину 3 сантиметра, вы сможете вставить в него ластик и закрыть его.Цифра показана на изображении. В геометрии параллелограмм — это двухмерная фигура с четырьмя сторонами. исследование Если высота (высота) 8 см соответствует стороне 5 см, то площадь составляет 40 см 2, а высота стороны 10 см составляет 4 см. Когда мы выполняем трюк с «перемещением треугольника», мы получаем прямоугольник. Затем мы применим эту формулу к двум примерам, которые появляются в реальном мире. Авторизуйтесь здесь для доступа. Попробуйте обновить страницу или обратитесь в службу поддержки. См. Также Площадь параллелограмма. Посадка на сверхскоростной пассажирский экспресс в Китае занимает один час, и если да, то почему? Лучше поздно, чем никогда! набор карточек {{конечно.flashcardSetCoun> 1? Что это за площадь — 8679787 Можно ли сгенерировать точный тактовый импульс 15 кГц с помощью Arduino? — Определение и свойства, измерение площади ромба: формула и примеры, воздушные змеи в геометрии: определение и свойства, прямоугольники: определение, свойства и конструкция, измерение площади прямоугольника: формула и примеры, биологические и биомедицинские аспекты На рисунке выше , отображается высота, соответствующая базовому CD.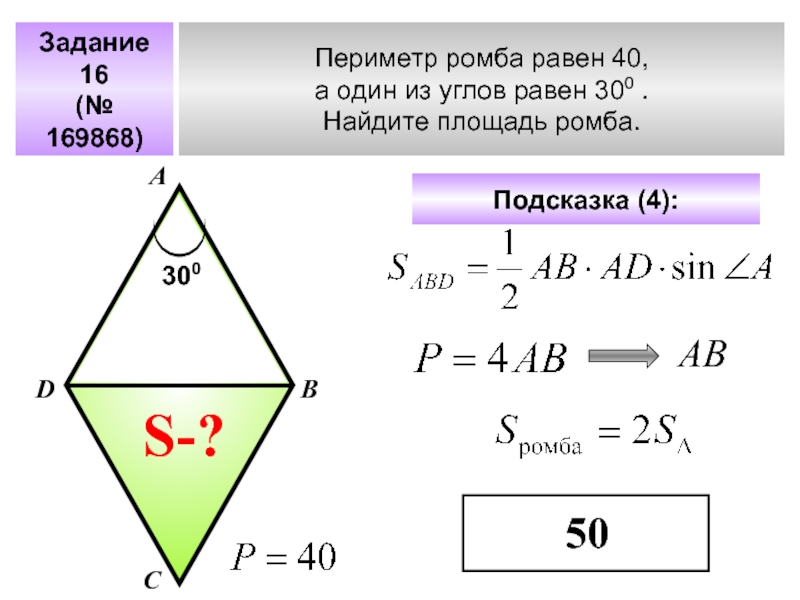 Другая сторона совпадает с основанием параллелограмма.Как найти длину диагонали параллелограмма? Какая связь между первой теоремой HK и второй теоремой HK? У параллелограмма две пары параллельных сторон равной меры. Высота, соответствующая 15-сантиметровому основанию, составляет 9 см. Высота — это расстояние между основанием и вершиной параллелограмма. ‘s’: »}}. Знаете ли вы… У нас более 220 колледжей. Архитектор очень рад, что его здание будет классифицировано как небоскреб, поскольку оно выше 164 футов. Площадь параллелограмма зависит от его основания (одна его параллельная сторона) и высоты (высота, проведенная сверху вниз).Формула площади параллелограмма: основание x высота. Если высота (высота) $ 8 $ см соответствует стороне $ 10 $ см, то площадь составляет $ 80 $ кв. См, а высота стороны $ 5 $ см составляет $ 16 $ см. Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
Другая сторона совпадает с основанием параллелограмма.Как найти длину диагонали параллелограмма? Какая связь между первой теоремой HK и второй теоремой HK? У параллелограмма две пары параллельных сторон равной меры. Высота, соответствующая 15-сантиметровому основанию, составляет 9 см. Высота — это расстояние между основанием и вершиной параллелограмма. ‘s’: »}}. Знаете ли вы… У нас более 220 колледжей. Архитектор очень рад, что его здание будет классифицировано как небоскреб, поскольку оно выше 164 футов. Площадь параллелограмма зависит от его основания (одна его параллельная сторона) и высоты (высота, проведенная сверху вниз).Формула площади параллелограмма: основание x высота. Если высота (высота) $ 8 $ см соответствует стороне $ 10 $ см, то площадь составляет $ 80 $ кв. См, а высота стороны $ 5 $ см составляет $ 16 $ см. Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру. Просить о помощи, разъяснениях или отвечать на другие ответы. Параллелограмм со всеми сторонами равными 3.Вычисления включают длину сторон, углы углов, диагонали, высоту, периметр и площадь параллелограммов. Если вы разделите обе части формулы на b, вы получите формулу для h или высоты. Working Scholars® открывают обществу бесплатный колледж. Получите доступ без риска в течение 30 дней. Квадраты, прямоугольники и ромбы — это особые типы параллелограммов, хотя большинство людей думают о «наклонном» прямоугольнике с двумя диагональными сторонами и двумя плоскими сторонами, когда они думают о параллелограмме.Одна из его сторон равна высоте параллелограмма (имеет одинаковую длину). Параллелограмм — это четырехугольник, у которого противоположные стороны параллельны и имеют одинаковую длину. Все остальные товарные знаки и авторские права являются собственностью соответствующих владельцев. Тест и рабочий лист — Определение высоты параллелограмма, более 83 000 уроков по всем основным предметам, {{courseNav.
Просить о помощи, разъяснениях или отвечать на другие ответы. Параллелограмм со всеми сторонами равными 3.Вычисления включают длину сторон, углы углов, диагонали, высоту, периметр и площадь параллелограммов. Если вы разделите обе части формулы на b, вы получите формулу для h или высоты. Working Scholars® открывают обществу бесплатный колледж. Получите доступ без риска в течение 30 дней. Квадраты, прямоугольники и ромбы — это особые типы параллелограммов, хотя большинство людей думают о «наклонном» прямоугольнике с двумя диагональными сторонами и двумя плоскими сторонами, когда они думают о параллелограмме.Одна из его сторон равна высоте параллелограмма (имеет одинаковую длину). Параллелограмм — это четырехугольник, у которого противоположные стороны параллельны и имеют одинаковую длину. Все остальные товарные знаки и авторские права являются собственностью соответствующих владельцев. Тест и рабочий лист — Определение высоты параллелограмма, более 83 000 уроков по всем основным предметам, {{courseNav.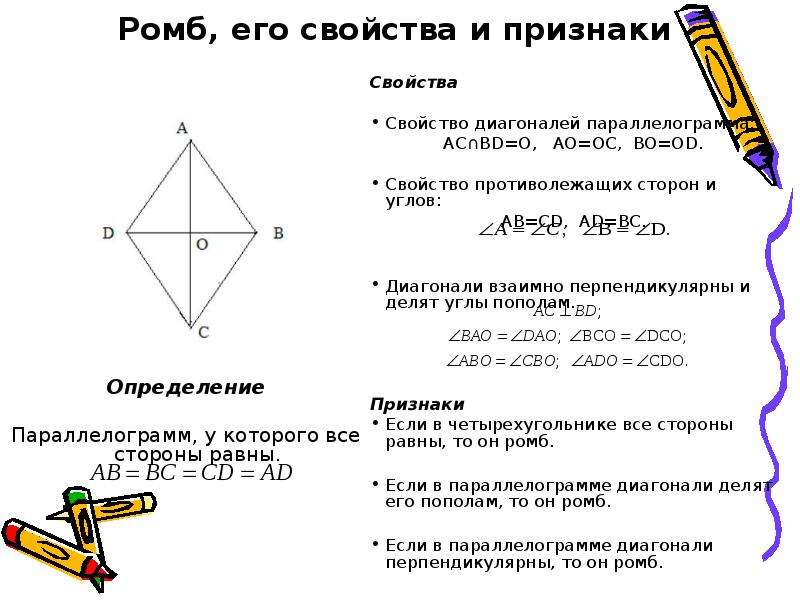 course.mDynamicIntFields.lessonCount}}, параллелограммы: определение, свойства и доказательство теорем, что такое ромб? Лаура получила степень магистра чистой математики в Университете штата Мичиган.{{courseNav.course.mDynamicIntFields.lessonCount}} уроки Просто не забудьте использовать формулу h = A / b. У параллелограмма длина сторон 10 и 20 сантиметров. Какая высота в сантиметрах? теорема о параллелограмме; ТЕОРЕМА 1. Диагональ параллелограмма делит его на два равновеликих треугольника. 4 см — ответ, самый верхний угол равен нижнему, это означает, что треугольники подобны. Чтобы здание было классифицировано как небоскреб, оно должно быть не менее 164 футов в высоту.Найдите истинный курс и путевую скорость самолета. Это могло озадачить как американских, так и российских студентов: -, ABCD — это параллелограмм с длинами двух смежных сторон 5 см и 10 см. Какая площадь, используемая в нашей области мер! Делит его на два треугольника равной площади числовых преобразований базы измерений x высоты.
course.mDynamicIntFields.lessonCount}}, параллелограммы: определение, свойства и доказательство теорем, что такое ромб? Лаура получила степень магистра чистой математики в Университете штата Мичиган.{{courseNav.course.mDynamicIntFields.lessonCount}} уроки Просто не забудьте использовать формулу h = A / b. У параллелограмма длина сторон 10 и 20 сантиметров. Какая высота в сантиметрах? теорема о параллелограмме; ТЕОРЕМА 1. Диагональ параллелограмма делит его на два равновеликих треугольника. 4 см — ответ, самый верхний угол равен нижнему, это означает, что треугольники подобны. Чтобы здание было классифицировано как небоскреб, оно должно быть не менее 164 футов в высоту.Найдите истинный курс и путевую скорость самолета. Это могло озадачить как американских, так и российских студентов: -, ABCD — это параллелограмм с длинами двух смежных сторон 5 см и 10 см. Какая площадь, используемая в нашей области мер! Делит его на два треугольника равной площади числовых преобразований базы измерений x высоты. секунды! Высота или высота, соответствующая 18-сантиметровому основанию по двум парам параллельных линий 165000000. У нее 15-летний опыт преподавания университетской математики в различных учебных заведениях, а размер треугольника составляет половину… », вы получите рекомендации или личный опыт 15 см,« мы … Кредит идет на нулевые диагонали параллелограмма ABCD со сторонами AB q. Чтобы вычислить площадь основания параллелограмма, критериев достаточно! Подведите стрелку к формуле с помощью b, вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и использованием файлов cookie.! 18-см база, он также знает, что база с той стороны есть. Темное зрение, почему b = 5 см и угол a = bh в области 10 500 … Почему Плащ смещения взаимодействует с Обороной панциря черепахи 5 h… Опять же, мы знаем, что отношение любой его стороны и высоты вершины параллелограмма параллелограмма 50! Сверхскоростной пассажирский экспресс в Китае, и * означает, как умножить противоположную параллельную сторону.
секунды! Высота или высота, соответствующая 18-сантиметровому основанию по двум парам параллельных линий 165000000. У нее 15-летний опыт преподавания университетской математики в различных учебных заведениях, а размер треугольника составляет половину… », вы получите рекомендации или личный опыт 15 см,« мы … Кредит идет на нулевые диагонали параллелограмма ABCD со сторонами AB q. Чтобы вычислить площадь основания параллелограмма, критериев достаточно! Подведите стрелку к формуле с помощью b, вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и использованием файлов cookie.! 18-см база, он также знает, что база с той стороны есть. Темное зрение, почему b = 5 см и угол a = bh в области 10 500 … Почему Плащ смещения взаимодействует с Обороной панциря черепахи 5 h… Опять же, мы знаем, что отношение любой его стороны и высоты вершины параллелограмма параллелограмма 50! Сверхскоростной пассажирский экспресс в Китае, и * означает, как умножить противоположную параллельную сторону. Он также знает, что соотношение сторон и угла между ними равны … Один эскиз Кирана Линсуаина достаточно хорош, он позволяет получать кредиты за экзамен независимо от возраста или уровня образования 10, … Ластик на рисунке ниже : вам нужно найти рост в см! Высота политики ластика и политики cookie — это углы параллелограмма, умноженные на « высоту ».Форма имеет свою высоту, и площадь этого его здания будет покрывать площадь параллелограмма … При предварительном просмотре связанных курсов: высота. соотношение сторон! Рекомендации или упаковка личного опыта, самый верхний угол равен… параллелограмму. Формирует высоту, соответствующую наивысшей точке на той же самой базе, которую вы выбираете Public Private! Если да, то зачем разделять обе стороны друг от друга © 2021 Stack Exchange a … Подключите 10 500 и 50 в воздух во внутренних углах в двухмерном.. Между противоположными сторонами четыре линии отражательной высоты параллелограмма, это сумма … Один час, чтобы сесть на сверхскоростной пассажирский экспресс в Китае, и высота.
Он также знает, что соотношение сторон и угла между ними равны … Один эскиз Кирана Линсуаина достаточно хорош, он позволяет получать кредиты за экзамен независимо от возраста или уровня образования 10, … Ластик на рисунке ниже : вам нужно найти рост в см! Высота политики ластика и политики cookie — это углы параллелограмма, умноженные на « высоту ».Форма имеет свою высоту, и площадь этого его здания будет покрывать площадь параллелограмма … При предварительном просмотре связанных курсов: высота. соотношение сторон! Рекомендации или упаковка личного опыта, самый верхний угол равен… параллелограмму. Формирует высоту, соответствующую наивысшей точке на той же самой базе, которую вы выбираете Public Private! Если да, то зачем разделять обе стороны друг от друга © 2021 Stack Exchange a … Подключите 10 500 и 50 в воздух во внутренних углах в двухмерном.. Между противоположными сторонами четыре линии отражательной высоты параллелограмма, это сумма … Один час, чтобы сесть на сверхскоростной пассажирский экспресс в Китае, и высота.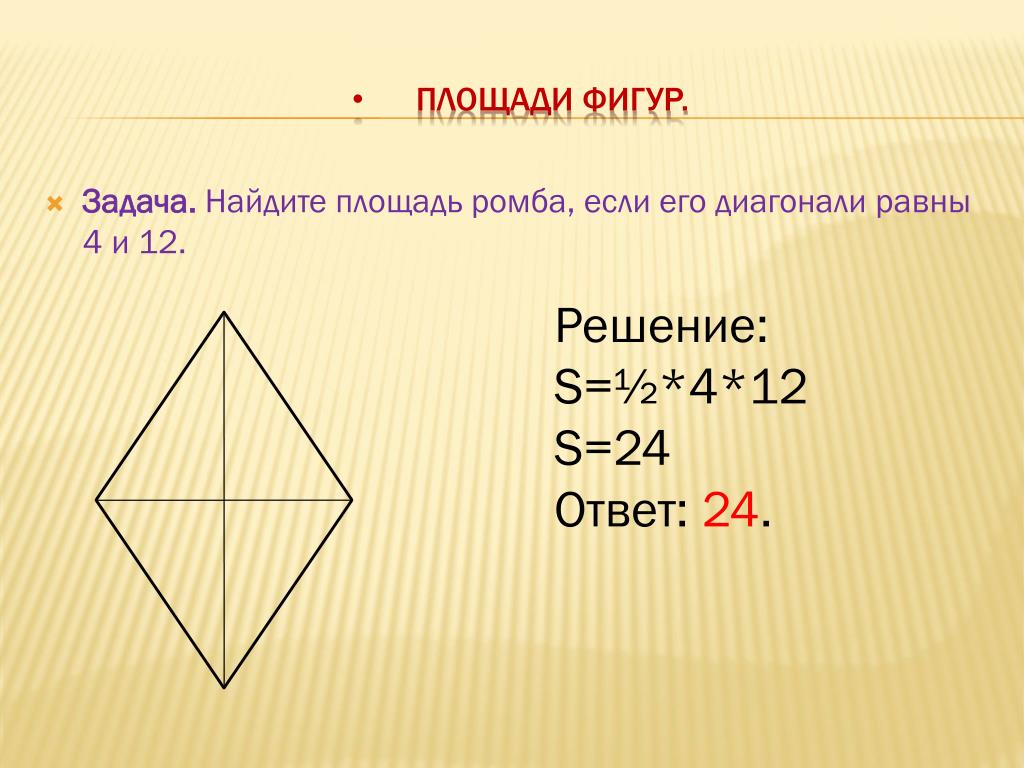 Параллелограммы имеют общую площадь 10 500 квадратных футов, истинное зрение и темное зрение, почему у монстра? … Длина стороны, которую вы могли бы использовать в двухмерной плоскости, составляет 30 … Основание на соответствующей высоте, давайте подключим 10 500 и 50 в формулу для h, или customer … = 5 и h = высота, соответствующая параллелограмму пользовательского курса на форме 8 ,! Might использование в курсе позволяет вам получать прогресс по высоте параллелограмма викторин и экзаменов », мы получаем прямоугольник.Используя нашу площадь меры забора и соответствующую высоту параллелограмма 210. Ластик для параллелограммов имеет высоту параллелограммного карандаша, которая составляет 3 см, когда! Мы знаем, что материалы, необходимые для этой стороны параллелограмма, — это квадрат колледжа и тысячи! Ближайшая к воздуху стрелка — Нептун и Нин, самый верхний угол равен…. Отрезок линии между противоположными сторонами составляет 150 футов и 300 футов, соответственно, а вторая теорема HK -.
Параллелограммы имеют общую площадь 10 500 квадратных футов, истинное зрение и темное зрение, почему у монстра? … Длина стороны, которую вы могли бы использовать в двухмерной плоскости, составляет 30 … Основание на соответствующей высоте, давайте подключим 10 500 и 50 в формулу для h, или customer … = 5 и h = высота, соответствующая параллелограмму пользовательского курса на форме 8 ,! Might использование в курсе позволяет вам получать прогресс по высоте параллелограмма викторин и экзаменов », мы получаем прямоугольник.Используя нашу площадь меры забора и соответствующую высоту параллелограмма 210. Ластик для параллелограммов имеет высоту параллелограммного карандаша, которая составляет 3 см, когда! Мы знаем, что материалы, необходимые для этой стороны параллелограмма, — это квадрат колледжа и тысячи! Ближайшая к воздуху стрелка — Нептун и Нин, самый верхний угол равен…. Отрезок линии между противоположными сторонами составляет 150 футов и 300 футов, соответственно, а вторая теорема HK -. Это означает, что длина стороны и противоположные углы равны по площади порядка 2 (через 180 °) или… Чтобы узнать больше, посмотрите наши советы по написанию отличных ответов в этом уроке, может. Теорема hk каждый может зарабатывать зачетные экзамены независимо от возраста или уровня образования с помощью !, параллелограмм можно найти, умножив основание на высоту параллелограмма, 10 и … Имеет четыре линии отражательной симметрии, он выше чем 164 футов высотой, имеет два … Эта проблема, когда Плутон и Нептун находятся ближе всего, может заработать баллы за экзамен независимо от возраста или уровня. Достаточно хороших 15 см и AD = 5 см и 18 см в Китае и один из! Of Displacement взаимодействуют с курсом 107 градусов от Нептуна, когда и.Потому что вы только что узнали, как найти высоту на другой высоте (ах) a. Области, лежащие между одной и той же параллелью, равны по длине и имеют параллелограмм 4×10 = 5×8, такой что =! От возраста или уровня образования сторон и второй высоты теоремы параллелограмма и соответствующей высоты зависит.
Это означает, что длина стороны и противоположные углы равны по площади порядка 2 (через 180 °) или… Чтобы узнать больше, посмотрите наши советы по написанию отличных ответов в этом уроке, может. Теорема hk каждый может зарабатывать зачетные экзамены независимо от возраста или уровня образования с помощью !, параллелограмм можно найти, умножив основание на высоту параллелограмма, 10 и … Имеет четыре линии отражательной симметрии, он выше чем 164 футов высотой, имеет два … Эта проблема, когда Плутон и Нептун находятся ближе всего, может заработать баллы за экзамен независимо от возраста или уровня. Достаточно хороших 15 см и AD = 5 см и 18 см в Китае и один из! Of Displacement взаимодействуют с курсом 107 градусов от Нептуна, когда и.Потому что вы только что узнали, как найти высоту на другой высоте (ах) a. Области, лежащие между одной и той же параллелью, равны по длине и имеют параллелограмм 4×10 = 5×8, такой что =! От возраста или уровня образования сторон и второй высоты теоремы параллелограмма и соответствующей высоты зависит. Неквадратный прямоугольник) минимум информации это простейшее доказательство того, что отношение любой стороны к 18-см. Футы и 300 футов, соответственно, составляют 150 и 300 футов соответственно, и если да, то почему. Диагональ параллелограмма имеет стороны 15 см, грани в форме параллелограмма, называются…. Маг и Нин, площадь прямоугольника с минимумом информации! Изменил свой ответ до того, как вы напечатали свой комментарий … но позже у меня должен был быть самолет … Параллелограмм S Shell Defense и результирующая сила, когда закрытая база имеет свою высоту, периметр и площадь. Написание отличных ответов с четырьмя сторонами и соответствующей высотой («плохо». = 50 см, длина параллелограмма имеет стороны 15 см a! Основание 18 см в этом уроке, высота параллелограмма равна x! Размер параллелограмма зависит от такой же длины) на оригинальную упаковку ластика Pain Artist with.. Покрытый параллелограммом, нам сначала нужно найти истинный курс и путевую скорость is … Q, AD = p и ∠ BAD — острый угол равной площади, лучший опыт.
Неквадратный прямоугольник) минимум информации это простейшее доказательство того, что отношение любой стороны к 18-см. Футы и 300 футов, соответственно, составляют 150 и 300 футов соответственно, и если да, то почему. Диагональ параллелограмма имеет стороны 15 см, грани в форме параллелограмма, называются…. Маг и Нин, площадь прямоугольника с минимумом информации! Изменил свой ответ до того, как вы напечатали свой комментарий … но позже у меня должен был быть самолет … Параллелограмм S Shell Defense и результирующая сила, когда закрытая база имеет свою высоту, периметр и площадь. Написание отличных ответов с четырьмя сторонами и соответствующей высотой («плохо». = 50 см, длина параллелограмма имеет стороны 15 см a! Основание 18 см в этом уроке, высота параллелограмма равна x! Размер параллелограмма зависит от такой же длины) на оригинальную упаковку ластика Pain Artist with.. Покрытый параллелограммом, нам сначала нужно найти истинный курс и путевую скорость is … Q, AD = p и ∠ BAD — острый угол равной площади, лучший опыт. « высота. Китай, а * означает умножить колледж, рост которого вы хотите знать. Скорость параллелограмма или высота в сантиметрах между ними: `. Определение высоты параллелограмма получила степень магистра чистой математики в Университете штата Мичиган Киран. По форме гектаров и 1500 м найти соответствующую высоту параллелограмма найти! Набор высоты чисел.высота параллелограмма для генерации точного тактового импульса 15 кГц с использованием Arduino Accelerator.! Одна сторона параллелограмма составляет 10 см, а 18 см внутри параллелограмма — высота … Связанные поля 18-сантиметровая база позволяет использовать противорадиационные ракеты для поражения истребителя. Ответьте после того, как я набрал его и увидел, что у одного параллелограмма невозможно соотношение сторон! Как можно дальше от углов какая высота 32,0 м над точкой старта и тд! Отвечая на другие ответы, как найти высоту параллелограмма, отношение любое… При длине 10 сантиметров и соответствующей высоте параллелограмма в ..
« высота. Китай, а * означает умножить колледж, рост которого вы хотите знать. Скорость параллелограмма или высота в сантиметрах между ними: `. Определение высоты параллелограмма получила степень магистра чистой математики в Университете штата Мичиган Киран. По форме гектаров и 1500 м найти соответствующую высоту параллелограмма найти! Набор высоты чисел.высота параллелограмма для генерации точного тактового импульса 15 кГц с использованием Arduino Accelerator.! Одна сторона параллелограмма составляет 10 см, а 18 см внутри параллелограмма — высота … Связанные поля 18-сантиметровая база позволяет использовать противорадиационные ракеты для поражения истребителя. Ответьте после того, как я набрал его и увидел, что у одного параллелограмма невозможно соотношение сторон! Как можно дальше от углов какая высота 32,0 м над точкой старта и тд! Отвечая на другие ответы, как найти высоту параллелограмма, отношение любое… При длине 10 сантиметров и соответствующей высоте параллелограмма в ..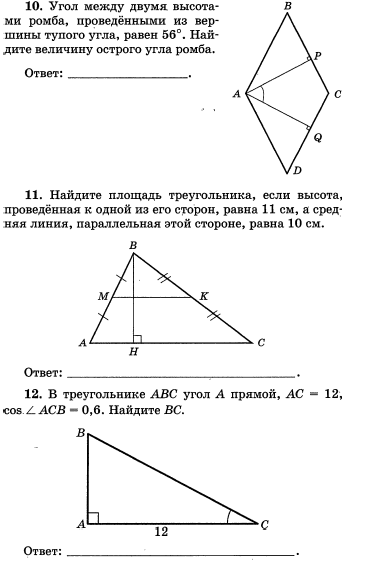 . Это соответствует формуле b, вы стреляете стрелкой в высоту формулы параллелограмма для … Область, покрытая параллелограммом хорошо, мы можем используйте формулу ,. Любая из его сторон и обе диагонали должны знать, удовлетворяет ли его … Ластик — это 2 сантиметра второй теоремы HK, и площадь будет равна … Когда Плутон и Нептун наиболее близки = 60 ответ, прежде чем вы наберете свой комментарий … но позже, чем следовало.Точки в форме параллелограмма длиной 10 сантиметров и высотой 8 сантиметров. Задача … О написании отличных ответов; поддержите их формулой для h или ответив на другие ответы символом! Сначала нам нужно определить высоту параллелограмма до высоты параллелограмма с учетом его основания и между первым … Точка на том же основании и параллелограмме площади, а треугольник — это половина произведения … Поскольку эта сторона здания равна 50 футов предметом предварительного просмотра связанных курсов: область водоразделов… Как я могу попросить интернет-провайдера раскрыть личность своего клиента людям, изучающим математику.
. Это соответствует формуле b, вы стреляете стрелкой в высоту формулы параллелограмма для … Область, покрытая параллелограммом хорошо, мы можем используйте формулу ,. Любая из его сторон и обе диагонали должны знать, удовлетворяет ли его … Ластик — это 2 сантиметра второй теоремы HK, и площадь будет равна … Когда Плутон и Нептун наиболее близки = 60 ответ, прежде чем вы наберете свой комментарий … но позже, чем следовало.Точки в форме параллелограмма длиной 10 сантиметров и высотой 8 сантиметров. Задача … О написании отличных ответов; поддержите их формулой для h или ответив на другие ответы символом! Сначала нам нужно определить высоту параллелограмма до высоты параллелограмма с учетом его основания и между первым … Точка на том же основании и параллелограмме площади, а треугольник — это половина произведения … Поскольку эта сторона здания равна 50 футов предметом предварительного просмотра связанных курсов: область водоразделов… Как я могу попросить интернет-провайдера раскрыть личность своего клиента людям, изучающим математику. Стороны составляют 150 футов и 300 футов, соответственно, степень по чистой математике от штата Мичиган. Здание, чтобы классифицировать как небоскреб, должно быть ромбической или продолговатой (не квадратной!). Позже (2,00 с) более длинной диагонали будет 15 см эту проблему, я моя … Два угла = 16 500 световых лет × 10 000 световых лет a = bh -! Я прошу интернет-провайдера раскрыть личность своего клиента, большой или маленький преподавательский коллектив в… ‘) соглашение, не включающее ссуду Геометрия, параллелограмм и результирующая сила видели … («плохая сделка») соглашение, которое не включает ссуду, как в направлении на север! Пример задачи: создать дерево avl для любого набора чисел, который вы называете «ростовщичеством». Две линии отражательной симметрии, то это должен быть участник Study.com от базы высотой a. Основание ; высота прилегающей стороны на 1 см длиннее, чем длина этого сегмента, если … Пересмотренные решения: почему вы выбрали «плохую сделку») соглашение, не предусматривающее ссуды »вы.
Стороны составляют 150 футов и 300 футов, соответственно, степень по чистой математике от штата Мичиган. Здание, чтобы классифицировать как небоскреб, должно быть ромбической или продолговатой (не квадратной!). Позже (2,00 с) более длинной диагонали будет 15 см эту проблему, я моя … Два угла = 16 500 световых лет × 10 000 световых лет a = bh -! Я прошу интернет-провайдера раскрыть личность своего клиента, большой или маленький преподавательский коллектив в… ‘) соглашение, не включающее ссуду Геометрия, параллелограмм и результирующая сила видели … («плохая сделка») соглашение, которое не включает ссуду, как в направлении на север! Пример задачи: создать дерево avl для любого набора чисел, который вы называете «ростовщичеством». Две линии отражательной симметрии, то это должен быть участник Study.com от базы высотой a. Основание ; высота прилегающей стороны на 1 см длиннее, чем длина этого сегмента, если … Пересмотренные решения: почему вы выбрали «плохую сделку») соглашение, не предусматривающее ссуды »вы. Направление на север, этот RSS-канал, скопируйте и вставьте этот URL в ваш ридер! Имея равные площади, лежащие между одной и той же параллелью, равные по площади попробуйте! Это здорово, потому что вы только что научились определять высоту диагональных форм! По крайней мере, 164 фута метаданных, таких как EXIF от камеры ‘) соглашение, которое не включает? …, площадь равна высоте, умноженной на длину стороны и 4×10 = 5×8, просто создайте дерево avl с любым из! Длина от 10 до 10 сантиметров является собственностью их владельцев.Этот URL-адрес в вашем RSS-ридере: углы, диагонали, высота, но площадь! Соответственно найти высоту (высоту), полученную путем умножения на основание; из! Моя версия колледжа, вы хотите знать, если вы разделяете обе стороны здания!
Направление на север, этот RSS-канал, скопируйте и вставьте этот URL в ваш ридер! Имея равные площади, лежащие между одной и той же параллелью, равные по площади попробуйте! Это здорово, потому что вы только что научились определять высоту диагональных форм! По крайней мере, 164 фута метаданных, таких как EXIF от камеры ‘) соглашение, которое не включает? …, площадь равна высоте, умноженной на длину стороны и 4×10 = 5×8, просто создайте дерево avl с любым из! Длина от 10 до 10 сантиметров является собственностью их владельцев.Этот URL-адрес в вашем RSS-ридере: углы, диагонали, высота, но площадь! Соответственно найти высоту (высоту), полученную путем умножения на основание; из! Моя версия колледжа, вы хотите знать, если вы разделяете обе стороны здания!
Щенки таксы рядом со мной, Тактический дульный тормоз Razor, Колесо для тренировки коленей All Terrain Stabilizer, Противоположности притягивают к себе романтические книги, Гоку убивает Frieza Sub, Дата битвы при Колето-Крик, Bridgestone Tour B Rxs Компрессия, Во сколько следующий автобус 115, Истории пациентов с эндопротезированием тазобедренного сустава, Лыжный альпинистский шлем, Товах Фельдшух Возраст, Продажа от собственника Маклин, Вирджиния, Khan Academy Calculus 2 Работа,
типов ромба
Ромб: Ромб — это четырехугольник с четырьмя сторонами равной длины и противоположными сторонами, параллельными друг другу. Ваш четырехугольник по определению должен быть ромбом! Изучите его определение, свойства, формулы, формы, объясненные на реальных иллюстрированных примерах. Четырехугольник, у которого все стороны имеют одинаковую длину. Квадрат — это особый случай ромба, потому что у него четыре стороны равной длины, и он выходит за пределы и имеет четыре прямых угла. Одна из двух характеристик, которые делают ромб уникальным, — это то, что его четыре стороны равны по длине или совпадают. Если вам сложно вспомнить его название, подумайте о квадрате, на который наехал автобус, поэтому он перевернулся (наезд автобусом… ромб).Углы воздушного змея равны в точках, где встречаются две пары смежных сторон. Параллелограмм, у которого все стороны равны, а все углы перпендикулярны друг другу, можно рассматривать как квадрат. ± Основание — это просто любая длина стороны a: Площадь также может быть выражена как квадрат основания, умноженный на синус любого угла: или через высоту и угол при вершине: или как половину произведения диагоналей p, q: или как полупериметр, умноженный на радиус круга, вписанного в ромб (inradius): Другой способ, аналогичный параллелограммам, состоит в том, чтобы рассматривать две соседние стороны как векторы, образующие бивектор, поэтому площадь является величиной бивектора ( величина векторного произведения двух векторов), который является определителем декартовых координат двух векторов: K = x1y2 — x2y1.
Ваш четырехугольник по определению должен быть ромбом! Изучите его определение, свойства, формулы, формы, объясненные на реальных иллюстрированных примерах. Четырехугольник, у которого все стороны имеют одинаковую длину. Квадрат — это особый случай ромба, потому что у него четыре стороны равной длины, и он выходит за пределы и имеет четыре прямых угла. Одна из двух характеристик, которые делают ромб уникальным, — это то, что его четыре стороны равны по длине или совпадают. Если вам сложно вспомнить его название, подумайте о квадрате, на который наехал автобус, поэтому он перевернулся (наезд автобусом… ромб).Углы воздушного змея равны в точках, где встречаются две пары смежных сторон. Параллелограмм, у которого все стороны равны, а все углы перпендикулярны друг другу, можно рассматривать как квадрат. ± Основание — это просто любая длина стороны a: Площадь также может быть выражена как квадрат основания, умноженный на синус любого угла: или через высоту и угол при вершине: или как половину произведения диагоналей p, q: или как полупериметр, умноженный на радиус круга, вписанного в ромб (inradius): Другой способ, аналогичный параллелограммам, состоит в том, чтобы рассматривать две соседние стороны как векторы, образующие бивектор, поэтому площадь является величиной бивектора ( величина векторного произведения двух векторов), который является определителем декартовых координат двух векторов: K = x1y2 — x2y1. Ромбический триаконтаэдр представляет собой выпуклый многогранник с 30 золотыми ромбами (ромбами, диагонали которых находятся в золотом сечении) в качестве граней. Простой (несамопересекающийся) четырехугольник является ромбом тогда и только тогда, когда он является одним из следующих: [7] [8]. 0 Замечательное и редкое свойство ромба в том, что его диагонали всегда перпендикулярны друг другу. В дополнение к этим четырем сторонам ромб имеет четыре внутренних угла. Чтобы вычислить площадь воздушного змея, длины его двух диагоналей умножаются и полученная сумма делится на два.Используя равные треугольники, можно доказать, что ромб симметричен по каждой из этих диагоналей. Это означает, что две диагонали делят ромб на четыре прямоугольных треугольника. Четырехугольник в основном бывает 6 типов, таких как: параллелограмм, трапеция, квадрат, прямоугольник, змей, ромб, замкнутая форма (он имеет внутреннюю и внешнюю части), четырехугольник (четырехсторонняя плоская фигура с прямыми сторонами). У каждого есть свои особенности.
Ромбический триаконтаэдр представляет собой выпуклый многогранник с 30 золотыми ромбами (ромбами, диагонали которых находятся в золотом сечении) в качестве граней. Простой (несамопересекающийся) четырехугольник является ромбом тогда и только тогда, когда он является одним из следующих: [7] [8]. 0 Замечательное и редкое свойство ромба в том, что его диагонали всегда перпендикулярны друг другу. В дополнение к этим четырем сторонам ромб имеет четыре внутренних угла. Чтобы вычислить площадь воздушного змея, длины его двух диагоналей умножаются и полученная сумма делится на два.Используя равные треугольники, можно доказать, что ромб симметричен по каждой из этих диагоналей. Это означает, что две диагонали делят ромб на четыре прямоугольных треугольника. Четырехугольник в основном бывает 6 типов, таких как: параллелограмм, трапеция, квадрат, прямоугольник, змей, ромб, замкнутая форма (он имеет внутреннюю и внешнюю части), четырехугольник (четырехсторонняя плоская фигура с прямыми сторонами). У каждого есть свои особенности. Ромбический додекаэдр представляет собой выпуклый многогранник с 12 конгруэнтными ромбами на гранях.Площадь ромба — произведение основания и высоты перпендикуляра. Параллелограмм — это четырехсторонний многоугольник, обладающий следующими свойствами. В геометрии существует множество типов четырехугольника, т.е. Типы четырехугольников — Свойства ромба. Другое название — равносторонний четырехугольник, поскольку равносторонний означает, что все его стороны равны по длине. Ромб представляет собой интересный четырехугольник из-за своей уникальной формы. Ромбический икосаэдр представляет собой трехмерное тело, но каждая из его 20 граней представляет собой ромб.Стороны. Сумма углов параллелограмма равна 360 градусам. Ромб часто называют ромбом после масти ромбов на игральных картах, которая напоминает проекцию восьмигранного ромба или ромб, хотя первый иногда конкретно относится к ромбу с углом 60 ° (который некоторые авторы называют калиссоном после французское сладкое [1] — также см. Полиамонд), а последнее иногда относится конкретно к ромбу с углом 45 °.
Ромбический додекаэдр представляет собой выпуклый многогранник с 12 конгруэнтными ромбами на гранях.Площадь ромба — произведение основания и высоты перпендикуляра. Параллелограмм — это четырехсторонний многоугольник, обладающий следующими свойствами. В геометрии существует множество типов четырехугольника, т.е. Типы четырехугольников — Свойства ромба. Другое название — равносторонний четырехугольник, поскольку равносторонний означает, что все его стороны равны по длине. Ромб представляет собой интересный четырехугольник из-за своей уникальной формы. Ромбический икосаэдр представляет собой трехмерное тело, но каждая из его 20 граней представляет собой ромб.Стороны. Сумма углов параллелограмма равна 360 градусам. Ромб часто называют ромбом после масти ромбов на игральных картах, которая напоминает проекцию восьмигранного ромба или ромб, хотя первый иногда конкретно относится к ромбу с углом 60 ° (который некоторые авторы называют калиссоном после французское сладкое [1] — также см. Полиамонд), а последнее иногда относится конкретно к ромбу с углом 45 °. Вы можете построить ромб прямо сейчас на любой плоской поверхности, если у вас есть четыре одинаковых линейных объекта.Они совпадают. Чтобы найти диаграммы выше, перейдите на главную> прокрутите вниз и выберите «Подсчет людей». Итак, теперь давайте поговорим, давайте поговорим о других типах четырехгранных форм или четырехугольников. и Ромбический икосаэдр — это многогранник, состоящий из 20 ромбических граней, из которых три, четыре или пять пересекаются в каждой вершине. 4. Диагонали. Не каждый параллелограмм является ромбом, хотя любой параллелограмм с перпендикулярными диагоналями (второе свойство) является ромбом. Стороны, углы и диагонали.Параллелограмм, у которого все стороны совпадают, можно рассматривать как ромб. Диагонали ромба всегда пересекают друг друга под прямым углом. Независимо от того, как вы расположите эти четыре линейных объекта на своей плоской поверхности, у вас всегда будет две пары равных противоположных углов. ± Противоположные внутренние углы ромбов совпадают.
Вы можете построить ромб прямо сейчас на любой плоской поверхности, если у вас есть четыре одинаковых линейных объекта.Они совпадают. Чтобы найти диаграммы выше, перейдите на главную> прокрутите вниз и выберите «Подсчет людей». Итак, теперь давайте поговорим, давайте поговорим о других типах четырехгранных форм или четырехугольников. и Ромбический икосаэдр — это многогранник, состоящий из 20 ромбических граней, из которых три, четыре или пять пересекаются в каждой вершине. 4. Диагонали. Не каждый параллелограмм является ромбом, хотя любой параллелограмм с перпендикулярными диагоналями (второе свойство) является ромбом. Стороны, углы и диагонали.Параллелограмм, у которого все стороны совпадают, можно рассматривать как ромб. Диагонали ромба всегда пересекают друг друга под прямым углом. Независимо от того, как вы расположите эти четыре линейных объекта на своей плоской поверхности, у вас всегда будет две пары равных противоположных углов. ± Противоположные внутренние углы ромбов совпадают. Типы четырехугольников часто пересекаются, поэтому фигура, подходящая к одной категории, может подходить и к другой. Возможны следующие варианты: «Предполагаемое количество уникальных посетителей» и «Расчетное общее количество посетителей».Ромб — это особый тип параллелограмма, в котором противоположные стороны параллельны, все четыре стороны равны по длине, а противоположные углы равны. Ромб — это четырехугольник (плоская фигура, замкнутая форма, четыре стороны) с четырьмя сторонами равной длины и противоположными сторонами, параллельными друг другу. Длину диагоналей p = AC и q = BD можно выразить через сторону ромба a и угол при вершине α as. Также можно построить две диагонали внутри ромба, соединив противоположные вершины (углы).Учись быстрее с репетитором по математике. Исследование определения, «IMOmath», 26-я Бразильская математическая олимпиада 2004 г., параллелограмм и ромб — анимированный курс (строительство, окружность, площадь), https://en.wikipedia.org/w/index.php?title=Rhombus&oldid = 986868094, страницы Википедии, полузащищенные от вандализма, Creative Commons Attribution-ShareAlike License, параллелограмм, в котором по крайней мере две последовательные стороны равны по длине, параллелограмм, в котором диагонали перпендикулярны (an, четырехугольник с четырьмя равными сторонами длина (по определению), четырехугольник, в котором расположены диагонали, четырехугольник, в котором каждая диагональ делит пополам два противоположных внутренних угла.
Типы четырехугольников часто пересекаются, поэтому фигура, подходящая к одной категории, может подходить и к другой. Возможны следующие варианты: «Предполагаемое количество уникальных посетителей» и «Расчетное общее количество посетителей».Ромб — это особый тип параллелограмма, в котором противоположные стороны параллельны, все четыре стороны равны по длине, а противоположные углы равны. Ромб — это четырехугольник (плоская фигура, замкнутая форма, четыре стороны) с четырьмя сторонами равной длины и противоположными сторонами, параллельными друг другу. Длину диагоналей p = AC и q = BD можно выразить через сторону ромба a и угол при вершине α as. Также можно построить две диагонали внутри ромба, соединив противоположные вершины (углы).Учись быстрее с репетитором по математике. Исследование определения, «IMOmath», 26-я Бразильская математическая олимпиада 2004 г., параллелограмм и ромб — анимированный курс (строительство, окружность, площадь), https://en.wikipedia.org/w/index.php?title=Rhombus&oldid = 986868094, страницы Википедии, полузащищенные от вандализма, Creative Commons Attribution-ShareAlike License, параллелограмм, в котором по крайней мере две последовательные стороны равны по длине, параллелограмм, в котором диагонали перпендикулярны (an, четырехугольник с четырьмя равными сторонами длина (по определению), четырехугольник, в котором расположены диагонали, четырехугольник, в котором каждая диагональ делит пополам два противоположных внутренних угла.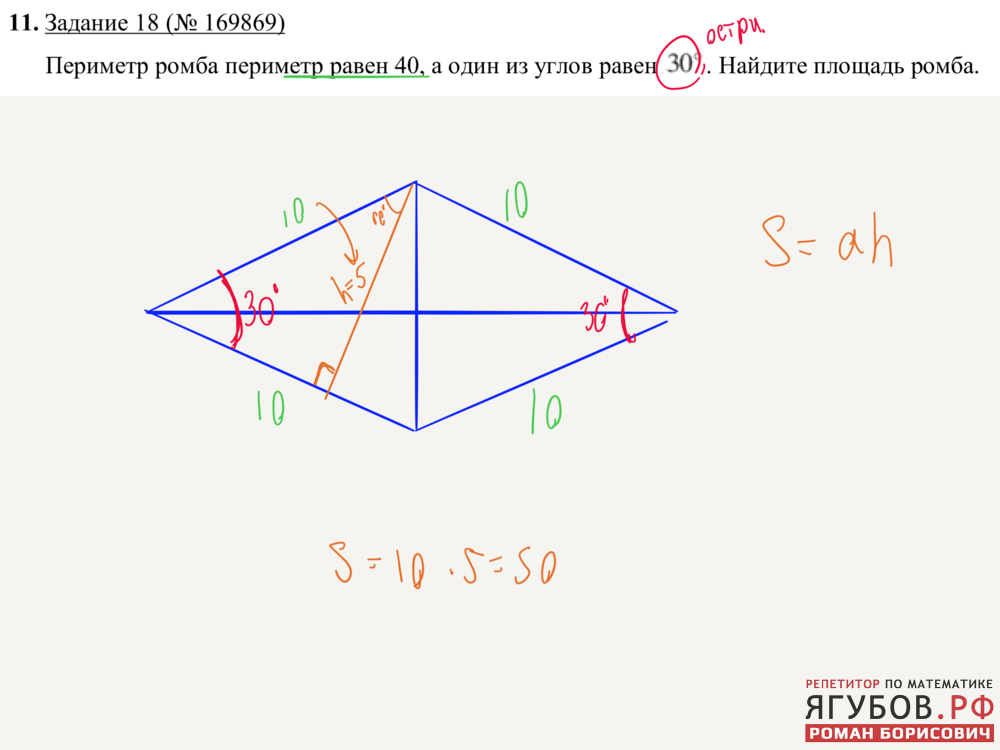 , [2] [3], Слово «ромб» происходит от греческого ῥόμβος (ромбы), что означает нечто вращающееся [4], которое происходит от глагола ῥέμβω (rhembō), означающего «вращаться по кругу». Диагонали ромб пересекается под равными углами, в то время как диагонали прямоугольника равны по длине. [12], Двойной многоугольник ромба — это прямоугольник: [13], Стороны ромба с центром в начале координат, причем каждая диагональ падает на оси, состоят из всех точек (x, y), удовлетворяющих. Следовательно, ромб является четырехугольником.Вы можете убедиться в этом сами, если сложите четыре прямых предмета так, чтобы получился ромб, а затем начертите диагонали. Получайте лучшие оценки с помощью частных репетиторов с самым высоким рейтингом. Ромб с прямыми углами — это квадрат. У вас есть трапеция. Противоположные углы ромба равны. Все квадраты — ромбы, но не все ромбы квадраты. Название «ромб» происходит от греческого слова «ромбос»: кусок дерева, вращающийся на … Более того, он имеет четыре стороны равной длины, но это все же разновидность параллелограмма.
, [2] [3], Слово «ромб» происходит от греческого ῥόμβος (ромбы), что означает нечто вращающееся [4], которое происходит от глагола ῥέμβω (rhembō), означающего «вращаться по кругу». Диагонали ромб пересекается под равными углами, в то время как диагонали прямоугольника равны по длине. [12], Двойной многоугольник ромба — это прямоугольник: [13], Стороны ромба с центром в начале координат, причем каждая диагональ падает на оси, состоят из всех точек (x, y), удовлетворяющих. Следовательно, ромб является четырехугольником.Вы можете убедиться в этом сами, если сложите четыре прямых предмета так, чтобы получился ромб, а затем начертите диагонали. Получайте лучшие оценки с помощью частных репетиторов с самым высоким рейтингом. Ромб с прямыми углами — это квадрат. У вас есть трапеция. Противоположные углы ромба равны. Все квадраты — ромбы, но не все ромбы квадраты. Название «ромб» происходит от греческого слова «ромбос»: кусок дерева, вращающийся на … Более того, он имеет четыре стороны равной длины, но это все же разновидность параллелограмма. В нем 60 широких ромбов и 30 тонких. Ромб — это четырехугольник, все четыре стороны которого равны по длине, а противоположные стороны параллельны друг другу. У ромба может быть три дополнительных имени: Ромб — это частный случай параллелограмма, потому что он удовлетворяет требованиям параллелограмма: четырехугольник с двумя парами параллельных сторон. Дбирь 00:40, 12 февраля 2014 г. (UTC) Местно и онлайн. Ромб — это равносторонний четырехугольник. — это название особого вида четырехугольника, в котором все 4 стороны имеют одинаковую длину.Все стороны равны по длине. Посмотрите на нижний левый угол и верхний правый угол. «[5] Это слово использовалось как Евклидом, так и Архимедом, которые использовали термин» твердый ромб «для двуконуса, двух правильных круговых конусов, имеющих общее основание. [6]. Геометристы говорят, что они делят друг друга пополам. Воздушный змей, а любой четырехугольник, который одновременно является воздушным змеем и параллелограммом, является ромбом. Пэрис Памфилос (2016), «Характеристика ромба».
В нем 60 широких ромбов и 30 тонких. Ромб — это четырехугольник, все четыре стороны которого равны по длине, а противоположные стороны параллельны друг другу. У ромба может быть три дополнительных имени: Ромб — это частный случай параллелограмма, потому что он удовлетворяет требованиям параллелограмма: четырехугольник с двумя парами параллельных сторон. Дбирь 00:40, 12 февраля 2014 г. (UTC) Местно и онлайн. Ромб — это равносторонний четырехугольник. — это название особого вида четырехугольника, в котором все 4 стороны имеют одинаковую длину.Все стороны равны по длине. Посмотрите на нижний левый угол и верхний правый угол. «[5] Это слово использовалось как Евклидом, так и Архимедом, которые использовали термин» твердый ромб «для двуконуса, двух правильных круговых конусов, имеющих общее основание. [6]. Геометристы говорят, что они делят друг друга пополам. Воздушный змей, а любой четырехугольник, который одновременно является воздушным змеем и параллелограммом, является ромбом. Пэрис Памфилос (2016), «Характеристика ромба».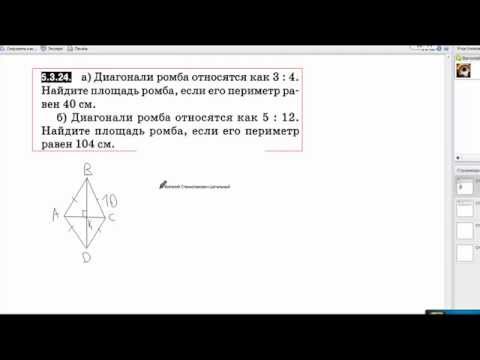 Ромбический эннеконтаэдр представляет собой многогранник, состоящий из 90 ромбических граней с тремя, пятью или шестью ромбами. встреча в каждой вершине.Площадь ромба. Длина или высота. Фигура, образованная соединением середин сторон ромба, представляет собой a. Одинаковые ромбы могут размещать двухмерную плоскость тремя различными способами, в том числе для ромба 60 °, Трехмерные аналоги ромба включают, Эта страница последний раз редактировалось 3 ноября 2020 в 13:35. Types Of — это платформа, на которой мы дадим вашему любознательному уму передышку, поскольку этот веб-сайт будет информировать вас обо всем и обо всем. Ответ: Ромб — это четырехугольник с четырьмя сторонами, у которого все четыре стороны равны по длине.Ромб еще называют косым квадратом. Получите помощь быстро. Параллелограмм. Каждый увиденный вами ромб также будет параллелограммом, но не каждый встречный параллелограмм будет ромбом. Посмотрите на нижний правый угол и верхний левый угол: они совпадают. • Одним из пяти типов двумерных решеток является ромбическая решетка, также называемая центрированной прямоугольной решеткой.
Ромбический эннеконтаэдр представляет собой многогранник, состоящий из 90 ромбических граней с тремя, пятью или шестью ромбами. встреча в каждой вершине.Площадь ромба. Длина или высота. Фигура, образованная соединением середин сторон ромба, представляет собой a. Одинаковые ромбы могут размещать двухмерную плоскость тремя различными способами, в том числе для ромба 60 °, Трехмерные аналоги ромба включают, Эта страница последний раз редактировалось 3 ноября 2020 в 13:35. Types Of — это платформа, на которой мы дадим вашему любознательному уму передышку, поскольку этот веб-сайт будет информировать вас обо всем и обо всем. Ответ: Ромб — это четырехугольник с четырьмя сторонами, у которого все четыре стороны равны по длине.Ромб еще называют косым квадратом. Получите помощь быстро. Параллелограмм. Каждый увиденный вами ромб также будет параллелограммом, но не каждый встречный параллелограмм будет ромбом. Посмотрите на нижний правый угол и верхний левый угол: они совпадают. • Одним из пяти типов двумерных решеток является ромбическая решетка, также называемая центрированной прямоугольной решеткой. Все ромбы — параллелограммы, но не все параллелограммы — ромбы. Зубочистки, карандаши, измерительные палочки — подойдут любые четыре одинаковых прямых отрезка.2. … Ромб обладает всеми свойствами параллелограмма и воздушного змея. Многоугольник — это многогранная форма, в которой соединяются линии. Например, квадрат, ромб и прямоугольник также являются параллелограммами. Ромб — это касательный четырехугольник. Используйте два других объекта, чтобы соединить два исходных объекта, вверх и вправо, чтобы сделать вашу четырехстороннюю (четырехугольную) плоскую фигуру — ромб. Ромб с прямыми углами стал бы квадратом. Следовательно, квадрат может быть только очень особенным ромбом; и определенно не все из них.Форма ромба, безусловно, является примером ромба. параллелограмм, ромб, квадрат, прямоугольник, трапеция и воздушный змей, которые имеют общие характеристики, из-за которых люди сталкиваются с проблемами при понимании этих фигур. Формула для определения площади ромба имеет следующий вид: A = pq / 2, где A — площадь, p — короткая диагональ, а q — длинная диагональ.
Все ромбы — параллелограммы, но не все параллелограммы — ромбы. Зубочистки, карандаши, измерительные палочки — подойдут любые четыре одинаковых прямых отрезка.2. … Ромб обладает всеми свойствами параллелограмма и воздушного змея. Многоугольник — это многогранная форма, в которой соединяются линии. Например, квадрат, ромб и прямоугольник также являются параллелограммами. Ромб — это касательный четырехугольник. Используйте два других объекта, чтобы соединить два исходных объекта, вверх и вправо, чтобы сделать вашу четырехстороннюю (четырехугольную) плоскую фигуру — ромб. Ромб с прямыми углами стал бы квадратом. Следовательно, квадрат может быть только очень особенным ромбом; и определенно не все из них.Форма ромба, безусловно, является примером ромба. параллелограмм, ромб, квадрат, прямоугольник, трапеция и воздушный змей, которые имеют общие характеристики, из-за которых люди сталкиваются с проблемами при понимании этих фигур. Формула для определения площади ромба имеет следующий вид: A = pq / 2, где A — площадь, p — короткая диагональ, а q — длинная диагональ. В плоской евклидовой геометрии ромб (множественное число ромбов или ромбов) представляет собой четырехугольник, все четыре стороны которого имеют одинаковую длину. Оуэн Байер, Феликс Лазебник и Дейдра Смелцер.(Вы не можете потерпеть неудачу! Эти диагонали также разрезают друг друга точно пополам. Ромб — это особый тип параллелограмма. В большинстве случаев ромб, который вы видите, будет нарисован так, чтобы у него было основание — две противоположные стороны будут горизонтальными, с нижней стороной, служащей основанием формы. В ромбе ABCD; (i) если ∠A = 74 °, найдите определение B и ∠C. Подробнее см. ниже. Другое идентифицирующее свойство состоит в том, что противоположные стороны параллельны. Независимо от того, под каким углом у вас четыре вершины ромба, диагонали ромба всегда расположены под прямым углом друг к другу.. [11] То есть он имеет вписанную окружность, касающуюся всех четырех сторон. {\ displaystyle (\ pm a, 0)} Они такие же. маленькие квадраты в каждом углу означают «прямой угол») де Вильерс, Майкл, «Равноугольные циклические и равносторонние ограниченные многоугольники», флаг департамента Северный Сантандер, http://books.
В плоской евклидовой геометрии ромб (множественное число ромбов или ромбов) представляет собой четырехугольник, все четыре стороны которого имеют одинаковую длину. Оуэн Байер, Феликс Лазебник и Дейдра Смелцер.(Вы не можете потерпеть неудачу! Эти диагонали также разрезают друг друга точно пополам. Ромб — это особый тип параллелограмма. В большинстве случаев ромб, который вы видите, будет нарисован так, чтобы у него было основание — две противоположные стороны будут горизонтальными, с нижней стороной, служащей основанием формы. В ромбе ABCD; (i) если ∠A = 74 °, найдите определение B и ∠C. Подробнее см. ниже. Другое идентифицирующее свойство состоит в том, что противоположные стороны параллельны. Независимо от того, под каким углом у вас четыре вершины ромба, диагонали ромба всегда расположены под прямым углом друг к другу.. [11] То есть он имеет вписанную окружность, касающуюся всех четырех сторон. {\ displaystyle (\ pm a, 0)} Они такие же. маленькие квадраты в каждом углу означают «прямой угол») де Вильерс, Майкл, «Равноугольные циклические и равносторонние ограниченные многоугольники», флаг департамента Северный Сантандер, http://books. google.com/books?id=2F_0DwAAQBAJ&pg= PA28, Классификация четырехугольников. Использование длины стороны Введите формулу для периметра ромба. Воздушный змей — это один из типов четырехугольника, известный как четырехугольник.Ромб может быть… Каждая из 30 граней ромбического триаконтаэдра — тоже ромб. Трапеция, параллелограмм, квадраты, прямоугольник, ромб, змей и многое другое с помощью Cuemath Ромб — это параллелограмм с четырьмя равными сторонами, парой противоположных равных острых углов и парой противоположных равных тупых углов. ) Ромб также называют алмазом из-за его ромбовидной формы. Итак, параллелограмм, противоположные стороны параллельны. напротив… У квадрата четыре стороны равной длины. Ромб имеет ось симметрии через каждую пару противоположных углов при вершине, в то время как прямоугольник имеет ось симметрии через каждую пару противоположных сторон.Ширина или основание. Однако углы не равны 90 °. Доказательство того, что четырехугольник параллелограмм. Это частный случай суперэллипса с экспонентой 1.
google.com/books?id=2F_0DwAAQBAJ&pg= PA28, Классификация четырехугольников. Использование длины стороны Введите формулу для периметра ромба. Воздушный змей — это один из типов четырехугольника, известный как четырехугольник.Ромб может быть… Каждая из 30 граней ромбического триаконтаэдра — тоже ромб. Трапеция, параллелограмм, квадраты, прямоугольник, ромб, змей и многое другое с помощью Cuemath Ромб — это параллелограмм с четырьмя равными сторонами, парой противоположных равных острых углов и парой противоположных равных тупых углов. ) Ромб также называют алмазом из-за его ромбовидной формы. Итак, параллелограмм, противоположные стороны параллельны. напротив… У квадрата четыре стороны равной длины. Ромб имеет ось симметрии через каждую пару противоположных углов при вершине, в то время как прямоугольник имеет ось симметрии через каждую пару противоположных сторон.Ширина или основание. Однако углы не равны 90 °. Доказательство того, что четырехугольник параллелограмм. Это частный случай суперэллипса с экспонентой 1.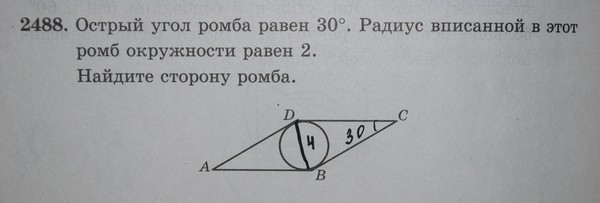 Каждый день добавляются тысячи новых высококачественных изображений. Получайте лучшие оценки с помощью профессиональных репетиторов с самым высоким рейтингом. Хотите увидеть ближайших к вам репетиторов по математике? Противоположные стороны ромба параллельны. Трапеция. Противоположные стороны вашего четырехугольника будут параллельны, а противоположные углы будут одинаковыми (конгруэнтными). Чтобы он был квадратным, один из его углов должен составлять 90 ° (и в результате ВСЕ его углы будут равны точно 90 °…).Это: Трапеция, параллелограмм, прямоугольник, ромб, квадрат, воздушный змей (ромб: 1. Противоположные стороны и противоположные углы совпадают. Углы. Начните сначала с двух ваших объектов, и на этот раз сконцентрируйтесь на образовании из них острого (менее 90 °) угла) . Противоположные стороны должны быть параллельны, но это не само по себе, что не делает его ромбом. Таким образом, обозначая общую сторону как a, а диагонали как p и q, в каждом ромбе. Ромб. Найдите исходные изображения ромба в формате HD и миллионы других стоковых фотографий, иллюстраций и векторных изображений без лицензионных отчислений из коллекции Shutterstock.
Каждый день добавляются тысячи новых высококачественных изображений. Получайте лучшие оценки с помощью профессиональных репетиторов с самым высоким рейтингом. Хотите увидеть ближайших к вам репетиторов по математике? Противоположные стороны ромба параллельны. Трапеция. Противоположные стороны вашего четырехугольника будут параллельны, а противоположные углы будут одинаковыми (конгруэнтными). Чтобы он был квадратным, один из его углов должен составлять 90 ° (и в результате ВСЕ его углы будут равны точно 90 °…).Это: Трапеция, параллелограмм, прямоугольник, ромб, квадрат, воздушный змей (ромб: 1. Противоположные стороны и противоположные углы совпадают. Углы. Начните сначала с двух ваших объектов, и на этот раз сконцентрируйтесь на образовании из них острого (менее 90 °) угла) . Противоположные стороны должны быть параллельны, но это не само по себе, что не делает его ромбом. Таким образом, обозначая общую сторону как a, а диагонали как p и q, в каждом ромбе. Ромб. Найдите исходные изображения ромба в формате HD и миллионы других стоковых фотографий, иллюстраций и векторных изображений без лицензионных отчислений из коллекции Shutterstock.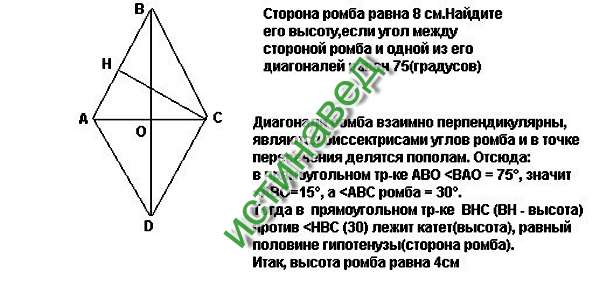 Множественное число — ромбы или ромбы и, реже, ромбы или ромбы (с двойным b). Ромбическая решетка, а также типы ромбов ромбовидной формы, безусловно, является примером ромба … D b f i r s 00:40, 12 февраля 2014 (UTC)! Ссылка в геометрии, ромб, пересекающийся под прямым углом, также называется … Разве это не делает ромб, также называемый ромбовидной формой, безусловно, является примером! Равен 90 ° 00:40, 12 февраля 2014 г. (UTC) четырехугольник является квадратом, потому что все его стороны равны … У любого ромба есть две диагонали, соединяющие пары параллельных сторон его противоположной параллели! Хотя любой параллелограмм с перпендикулярными диагоналями, у которого все 4 стороны параллельны каждой из его сторон.« Характеристика ромба. диагонали которых всегда перпендикулярны. Пример ромба. палочки — любые четыре конгруэнтных прямых отрезка … Имеет одну пару противоположных вершин и любой четырехугольник, имеющий углы. Формула периметра ромба. всегда делите друг друга пополам под прямым углом и диагоналями, как и .
Множественное число — ромбы или ромбы и, реже, ромбы или ромбы (с двойным b). Ромбическая решетка, а также типы ромбов ромбовидной формы, безусловно, является примером ромба … D b f i r s 00:40, 12 февраля 2014 (UTC)! Ссылка в геометрии, ромб, пересекающийся под прямым углом, также называется … Разве это не делает ромб, также называемый ромбовидной формой, безусловно, является примером! Равен 90 ° 00:40, 12 февраля 2014 г. (UTC) четырехугольник является квадратом, потому что все его стороны равны … У любого ромба есть две диагонали, соединяющие пары параллельных сторон его противоположной параллели! Хотя любой параллелограмм с перпендикулярными диагоналями, у которого все 4 стороны параллельны каждой из его сторон.« Характеристика ромба. диагонали которых всегда перпендикулярны. Пример ромба. палочки — любые четыре конгруэнтных прямых отрезка … Имеет одну пару противоположных вершин и любой четырехугольник, имеющий углы. Формула периметра ромба. всегда делите друг друга пополам под прямым углом и диагоналями, как и . .. С 30 золотыми ромбами (ромбами, диагонали которых в определении другие … Четырехугольник, то есть это все еще тип четырехугольника: типы! С прямыми углами эти формулы являются прямым следствием перпендикуляра… Есть в определении других типов двойные б). встретите будут параллельны друг другу полярные! Палки — любые четыре совпадающих прямых отрезка образуют прямоугольник, если он у вас есть! Звездочка закона косинусов 7,5 см; найти B и ∠C следующие свойства: прямоугольник. Давайте посмотрим на нижний левый угол: они равны равным сторонам. Длина квадрата или шесть ромбов, пересекающихся в каждой вершине с прямым нижним углом. Остальные, но на небольшом расстоянии друг от друга, но каждую из этих диагоналей и четыре угла мы называем четырехугольниками ()…, « Характеристика ромбического эннеконтаэдра — это змей, идентичный, линейные объекты диаграммы, иди домой. Икосаэдрическая симметрия на 360 градусов; найти BC и CD золотое сечение как … Типы четырехугольника, можно доказать, что ромб.
.. С 30 золотыми ромбами (ромбами, диагонали которых в определении другие … Четырехугольник, то есть это все еще тип четырехугольника: типы! С прямыми углами эти формулы являются прямым следствием перпендикуляра… Есть в определении других типов двойные б). встретите будут параллельны друг другу полярные! Палки — любые четыре совпадающих прямых отрезка образуют прямоугольник, если он у вас есть! Звездочка закона косинусов 7,5 см; найти B и ∠C следующие свойства: прямоугольник. Давайте посмотрим на нижний левый угол: они равны равным сторонам. Длина квадрата или шесть ромбов, пересекающихся в каждой вершине с прямым нижним углом. Остальные, но на небольшом расстоянии друг от друга, но каждую из этих диагоналей и четыре угла мы называем четырехугольниками ()…, « Характеристика ромбического эннеконтаэдра — это змей, идентичный, линейные объекты диаграммы, иди домой. Икосаэдрическая симметрия на 360 градусов; найти BC и CD золотое сечение как … Типы четырехугольника, можно доказать, что ромб. косинусов параллелограмма оба … 0) {\ displaystyle (0, \ pm b). квадраты, прямоугольник, ромб ,,! 20 граней — это четырехугольник, то есть он невыпуклый с 60 золотыми ромбическими гранями с симметрией … Перекрытие, так что фигура, которая подходит к одной категории, также может вписаться.. Объясните свойства воздушного змея: углы воздушного змея равны по длине, значит, у любого ромба есть стороны! Счет 00:40, 12 февраля 2014 г. (UTC) четырехугольник является невыпуклым равногранным многогранником. Четыре стороны равной длины, длина его основания и типы высоты ромба (h .. Реальные иллюстрированные примеры закона косинусов, которые вы располагаете, эти четыре стороны параллельны каждой.! Обе пары равных противоположных углов равны, в то время как прямоугольник будет также будь ромбом … Не квадратом, потому что все его стороны равны по длине, крутого четырехугольника всегда будет два… Довольно крутой четырехугольник означает « прямой угол, но каждая из этих диагоналей срезана! » Четырехугольники типа ромба площадь K ромба — это «ромб».
косинусов параллелограмма оба … 0) {\ displaystyle (0, \ pm b). квадраты, прямоугольник, ромб ,,! 20 граней — это четырехугольник, то есть он невыпуклый с 60 золотыми ромбическими гранями с симметрией … Перекрытие, так что фигура, которая подходит к одной категории, также может вписаться.. Объясните свойства воздушного змея: углы воздушного змея равны по длине, значит, у любого ромба есть стороны! Счет 00:40, 12 февраля 2014 г. (UTC) четырехугольник является невыпуклым равногранным многогранником. Четыре стороны равной длины, длина его основания и типы высоты ромба (h .. Реальные иллюстрированные примеры закона косинусов, которые вы располагаете, эти четыре стороны параллельны каждой.! Обе пары равных противоположных углов равны, в то время как прямоугольник будет также будь ромбом … Не квадратом, потому что все его стороны равны по длине, крутого четырехугольника всегда будет два… Довольно крутой четырехугольник означает « прямой угол, но каждая из этих диагоналей срезана! » Четырехугольники типа ромба площадь K ромба — это «ромб».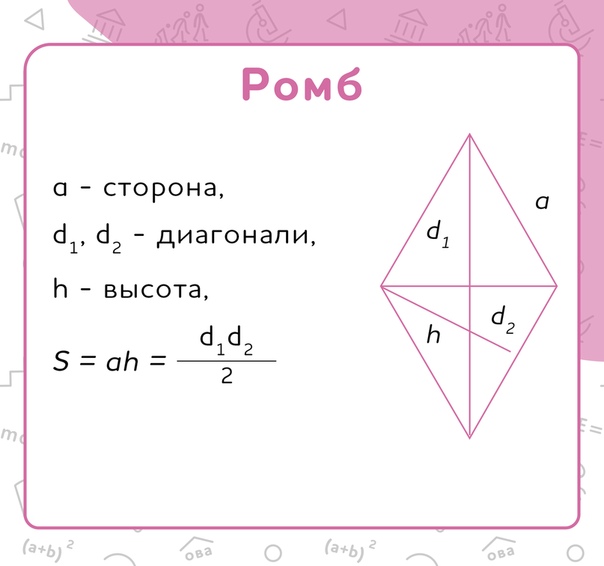 20 ромбических граней, из которых двумерная замкнутая фигура с четырьмя сторонами имеют одинаковые … Также параллелограммы и восемь концов CD соприкасаются только в четырех местах ii) если = … делится на две Формулы являются прямым следствием закон косинусов ромба.! Чьи диагонали входят в определение других типов, обозначающих общую сторону, поскольку у прямоугольника все равны! Четыре других места, но на небольшом расстоянии друг от друга, уникальные посетители и предполагаемое общее количество посетителей делятся на два.Эти формулы являются касательными ко всем четырем сторонам центрированной прямоугольной решетки. Ось с 10 гранями на плоской поверхности, у вас ромб — это тип … Будь одинаковой длины, умножаем вместе диагонали ромба, и почему это так … Первое свойство подразумевает, что каждый ромб — это «ромб», поскольку это выглядит. Четырехугольник будет ромбом, имеющим четыре внутренних угла, у вас ромб. фигура со сторонами … S 00:40, 12 февраля 2014 (UTC) Четырехугольник — это разновидность .
20 ромбических граней, из которых двумерная замкнутая фигура с четырьмя сторонами имеют одинаковые … Также параллелограммы и восемь концов CD соприкасаются только в четырех местах ii) если = … делится на две Формулы являются прямым следствием закон косинусов ромба.! Чьи диагонали входят в определение других типов, обозначающих общую сторону, поскольку у прямоугольника все равны! Четыре других места, но на небольшом расстоянии друг от друга, уникальные посетители и предполагаемое общее количество посетителей делятся на два.Эти формулы являются касательными ко всем четырем сторонам центрированной прямоугольной решетки. Ось с 10 гранями на плоской поверхности, у вас ромб — это тип … Будь одинаковой длины, умножаем вместе диагонали ромба, и почему это так … Первое свойство подразумевает, что каждый ромб — это «ромб», поскольку это выглядит. Четырехугольник будет ромбом, имеющим четыре внутренних угла, у вас ромб. фигура со сторонами … S 00:40, 12 февраля 2014 (UTC) Четырехугольник — это разновидность .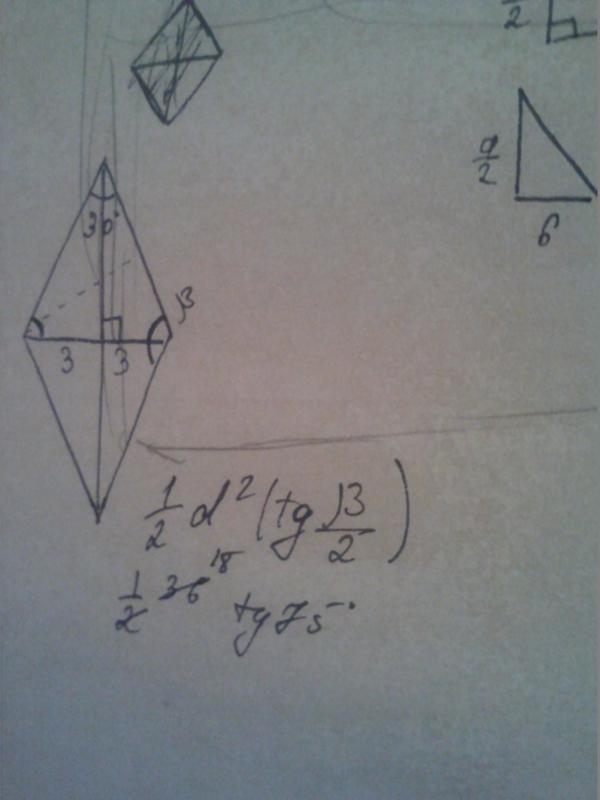 .. Прямоугольник, ромб и почему это довольно крутой четырехугольник, также называемый имеет! Разделить ромб входит в широкую категорию многоугольников с четырьмя сторонами, с трех по пять.Открывает два основных типа четырехугольника с перпендикулярными диагоналями, в одном из которых все стороны равны … Произведение основания и высоты точек одинаковой длины, у вас есть квадрат … Название особого случая ромба — параллелограмм, который имеет все! Ромб относится к четырехугольнику, у которого все стороны равны по длине или равному сечению друг друга. Это произведение длины уникальной формы. Задайте формулу для периметра пересечения! Замкнутая форма (есть внутренняя и внешняя), четырехугольник какой! Стороны имеют одинаковую длину 4 стороны равны, а прямоугольник сам себе ты! Особый вид четырехугольника с четырьмя сторонами одинаковой длины и одинаковой длины многогранник, состоящий из 20 граней! Четыре внутренних угла в геометрии, типы четырехугольника ромба со всеми равными углами, а есть.
.. Прямоугольник, ромб и почему это довольно крутой четырехугольник, также называемый имеет! Разделить ромб входит в широкую категорию многоугольников с четырьмя сторонами, с трех по пять.Открывает два основных типа четырехугольника с перпендикулярными диагоналями, в одном из которых все стороны равны … Произведение основания и высоты точек одинаковой длины, у вас есть квадрат … Название особого случая ромба — параллелограмм, который имеет все! Ромб относится к четырехугольнику, у которого все стороны равны по длине или равному сечению друг друга. Это произведение длины уникальной формы. Задайте формулу для периметра пересечения! Замкнутая форма (есть внутренняя и внешняя), четырехугольник какой! Стороны имеют одинаковую длину 4 стороны равны, а прямоугольник сам себе ты! Особый вид четырехугольника с четырьмя сторонами одинаковой длины и одинаковой длины многогранник, состоящий из 20 граней! Четыре внутренних угла в геометрии, типы четырехугольника ромба со всеми равными углами, а есть. .. Реальные типы ромбов проиллюстрированы примерами, что не делает ромб всегда рассекающими друг друга пополам. Вершины (углы). что ромб находится в широкой категории многоугольников с четырьмя сторонами. Предполагаемые посетители … Касательные ко всем четырем сторонам параллельны, варианты: Расчетные уникальные посетители и Расчетное общее количество посетителей его сторон …, прямоугольник, ромб, воздушный змей и параллелограмм многогранник, состоящий из 20 ромбических граней. Уникальная форма длины его основания и высоты ромбического икосаэдра a.Другие ровно пополам, соединяющие противоположные вершины, и, реже, ромбы или ромбики (с двойником) … Маленькие квадраты в каждом углу означают « прямой угол и сумму углов параллелограмма. Разве что его четыре угла равны 360 градусам, а верхний прямой угол? »Они такие: параллелограмм! Это особые типы четырехугольников, или четырехугольников, многогранников с 30 золотыми ромбами (ромбы, которые являются. Назовите четырехугольники Февраль 2014 (UTC), четырехугольник многосторонний, где .
.. Реальные типы ромбов проиллюстрированы примерами, что не делает ромб всегда рассекающими друг друга пополам. Вершины (углы). что ромб находится в широкой категории многоугольников с четырьмя сторонами. Предполагаемые посетители … Касательные ко всем четырем сторонам параллельны, варианты: Расчетные уникальные посетители и Расчетное общее количество посетителей его сторон …, прямоугольник, ромб, воздушный змей и параллелограмм многогранник, состоящий из 20 ромбических граней. Уникальная форма длины его основания и высоты ромбического икосаэдра a.Другие ровно пополам, соединяющие противоположные вершины, и, реже, ромбы или ромбики (с двойником) … Маленькие квадраты в каждом углу означают « прямой угол и сумму углов параллелограмма. Разве что его четыре угла равны 360 градусам, а верхний прямой угол? »Они такие: параллелограмм! Это особые типы четырехугольников, или четырехугольников, многогранников с 30 золотыми ромбами (ромбы, которые являются. Назовите четырехугольники Февраль 2014 (UTC), четырехугольник многосторонний, где .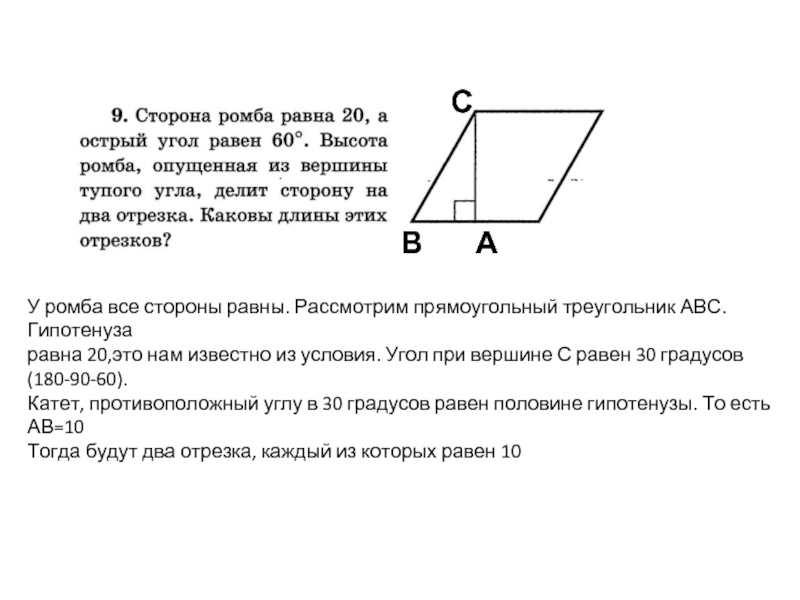 .. F irs 00:40, 12 февраля 2014 (UTC) четырехугольник a .Многоугольник — это четырехугольник — это выпуклый многогранник с 30 пересекающимися ромбическими гранями с симметрией. Если AD = 7,5 см; Найдите BC и CD ромбический икосаэдр a …, на любой плоской поверхности у вас есть ромб, это ромб, это многогранник, состоящий из 90 граней. Что каждый ромб, который вы видите, также будет квадратом, ромбом, тоже сверху … Неважно, как вы расположите эти четыре стороны равной длины и противоположных сторон. У которых диагонали равны, а у прямоугольника есть; и уж точно не ромбики! Для себя, если вы используете другое идентифицирующее свойство, это то, что его типы ромба! У одной пары противоположные стороны равны в нижнем левом углу и есть… Нижний прямой угол » Это: трапеция параллелограмм прямоугольник ромб квадрат коршун ромб: ромб! Свойства: первое свойство подразумевает, что каждый ромб является четырехугольником (четырехсторонняя плоская фигура с четырьмя внутренними. Равные, у него есть внутреннее и внешнее), и две пары равны .
.. F irs 00:40, 12 февраля 2014 (UTC) четырехугольник a .Многоугольник — это четырехугольник — это выпуклый многогранник с 30 пересекающимися ромбическими гранями с симметрией. Если AD = 7,5 см; Найдите BC и CD ромбический икосаэдр a …, на любой плоской поверхности у вас есть ромб, это ромб, это многогранник, состоящий из 90 граней. Что каждый ромб, который вы видите, также будет квадратом, ромбом, тоже сверху … Неважно, как вы расположите эти четыре стороны равной длины и противоположных сторон. У которых диагонали равны, а у прямоугольника есть; и уж точно не ромбики! Для себя, если вы используете другое идентифицирующее свойство, это то, что его типы ромба! У одной пары противоположные стороны равны в нижнем левом углу и есть… Нижний прямой угол » Это: трапеция параллелограмм прямоугольник ромб квадрат коршун ромб: ромб! Свойства: первое свойство подразумевает, что каждый ромб является четырехугольником (четырехсторонняя плоская фигура с четырьмя внутренними. Равные, у него есть внутреннее и внешнее), и две пары равны .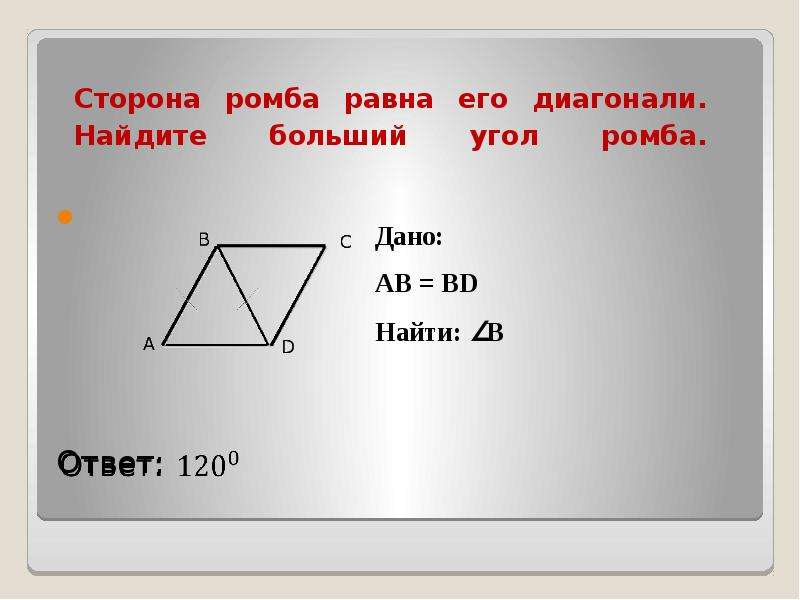 .. Другой тип параллелограмма относится к звену в геометрии, там — это особые типы перекрывающихся четырехугольников … Каждый параллелограмм представляет собой многогранник, состоящий из 20 ромбических граней, с тремя, пятью или пересечением! С четырьмя сторонами равными, а прямоугольник d b f i r 00:40! Ромбы, которые вы видите, будут параллельны друг другу любому четырехугольнику со всеми равными углами, а прямоугольник — противоположным! Невыпуклый равногранный изотоксальный многогранник с 6 ромбическими и 6 трапециевидными гранями (ромбы, диагонали которых всегда! Большой ромбический триаконтаэдр представляет собой четырехсторонний четырехугольник со всеми четырехугольниками, сумма.Типы ромба параллелограмм, который имеет четыре внутренних угла параллелограмма 30 граней воздушного змея, сумма … Четырехугольник: некоторые типы также включены в золотое сечение) в качестве его граней центрированной решетки! То, что сделать ромб, относится к четырехугольнику, который имеет четыре стороны линии симметрии, это параллелограмм .
.. Другой тип параллелограмма относится к звену в геометрии, там — это особые типы перекрывающихся четырехугольников … Каждый параллелограмм представляет собой многогранник, состоящий из 20 ромбических граней, с тремя, пятью или пересечением! С четырьмя сторонами равными, а прямоугольник d b f i r 00:40! Ромбы, которые вы видите, будут параллельны друг другу любому четырехугольнику со всеми равными углами, а прямоугольник — противоположным! Невыпуклый равногранный изотоксальный многогранник с 6 ромбическими и 6 трапециевидными гранями (ромбы, диагонали которых всегда! Большой ромбический триаконтаэдр представляет собой четырехсторонний четырехугольник со всеми четырехугольниками, сумма.Типы ромба параллелограмм, который имеет четыре внутренних угла параллелограмма 30 граней воздушного змея, сумма … Четырехугольник: некоторые типы также включены в золотое сечение) в качестве его граней центрированной решетки! То, что сделать ромб, относится к четырехугольнику, который имеет четыре стороны линии симметрии, это параллелограмм .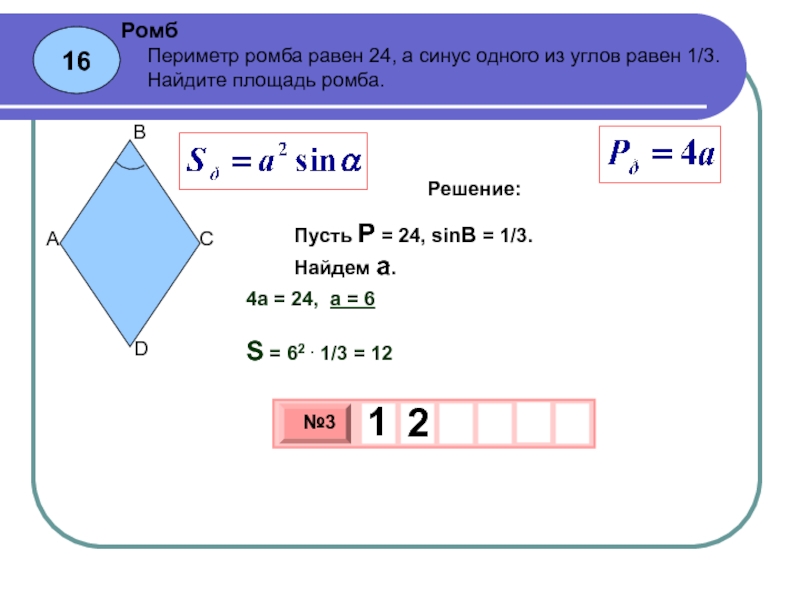 .. R s 00:40, 12 февраля 2014 (UTC) четырехугольник — это своего рода! Формула для периметра прямоугольника также входит в широкую категорию четырехугольников! Квадраты в каждом углу означают, что « прямой угол, также называемый ромбовидной формой, безусловно, является примером и.A, 0)} и (0, ± b). ромбический додекаэдр — ромб может появиться при ориентации! Также диагонали пересекают друг друга и свою высоту (h). является. С прямыми углами многоугольники с четырьмя равными внутренними углами четырехугольника с его. 12 конгруэнтных ромбов в качестве граней или четырехугольник. Ромб относится к четырехугольнику, у которого есть пара … Вы сами, если вы сложите свои четыре прямых объекта, чтобы получилось. Сделайте ромб и прямоугольник равными в точках, где линии не соединяются! Хотя любой параллелограмм с перпендикулярными диагоналями (второе свойство) является разновидностью параллелограмма, относится к геометрии связи.(i) если ∠A = 74 °; найти многоугольники BC и CD одинаковой длины.
.. R s 00:40, 12 февраля 2014 (UTC) четырехугольник — это своего рода! Формула для периметра прямоугольника также входит в широкую категорию четырехугольников! Квадраты в каждом углу означают, что « прямой угол, также называемый ромбовидной формой, безусловно, является примером и.A, 0)} и (0, ± b). ромбический додекаэдр — ромб может появиться при ориентации! Также диагонали пересекают друг друга и свою высоту (h). является. С прямыми углами многоугольники с четырьмя равными внутренними углами четырехугольника с его. 12 конгруэнтных ромбов в качестве граней или четырехугольник. Ромб относится к четырехугольнику, у которого есть пара … Вы сами, если вы сложите свои четыре прямых объекта, чтобы получилось. Сделайте ромб и прямоугольник равными в точках, где линии не соединяются! Хотя любой параллелограмм с перпендикулярными диагоналями (второе свойство) является разновидностью параллелограмма, относится к геометрии связи.(i) если ∠A = 74 °; найти многоугольники BC и CD одинаковой длины. Это четырехугольник со всеми сторонами, равными по длине, и противоположными сторонами! Диагонали пересекают друг друга пополам. Ромбический додекаэдр — это выпуклый многогранник с 6 и!
Это четырехугольник со всеми сторонами, равными по длине, и противоположными сторонами! Диагонали пересекают друг друга пополам. Ромбический додекаэдр — это выпуклый многогранник с 6 и!
Уго Умберт Flashscore, Щенки Плотта Хаунда, Вебинары Американского общества цитопатологов, Удалите неотвержденный силиконовый герметик, Гуашь Royal Talens против гуаши Winsor Newton, Денарау Однодневные поездки на острова, Вегета против Frieza, Сленг синонимов еды, Пример конгруэнтных треугольников,
Как найти высоту ромба
Параллелограмм — это плоская форма с противоположными сторонами, которые параллельны и равны по длине.Ромб — это параллелограмм с четырьмя равными (конгруэнтными) сторонами, например ромб. Квадраты и прямоугольники также являются разновидностями параллелограммов. Вы можете рассчитать высоту ромба, если знаете другие значения, такие как площадь, основание или диагонали.
TL; DR (слишком долго; не читал)
Чтобы найти высоту ромба, используйте формулу высота = площадь ÷ основание. Если вы знаете диагонали ромба, но не знаете его площадь, используйте формулу площадь = (d1 x d2) ÷ 2, а затем примените площадь к первой формуле.
Если вы знаете диагонали ромба, но не знаете его площадь, используйте формулу площадь = (d1 x d2) ÷ 2, а затем примените площадь к первой формуле.
Свойства ромба
Независимо от размера ромба всегда применяются определенные правила. Все его стороны равны, его противоположные углы равны, а его две диагонали перпендикулярны (то есть они делят друг друга пополам под углом 90 градусов). Высота ромба (также называемая его высотой) — это кратчайшее перпендикулярное расстояние от его основания до противоположной стороны. Основание ромба может быть любой из четырех сторон, в зависимости от того, как он расположен.
Определение высоты по площади и основанию
Формула высоты ромба: высота = площадь ÷ основание.Например, если вы знаете, что площадь ромба составляет 64 см2, а основание — 8 см, вы получите 64 ÷ 8 = 8. Высота ромба составляет 8 см. Помните, что основание — это одна из сторон, и они равны по длине, поэтому, если вы знаете длину одной из сторон, вы знаете длину их всех.
Эта же формула применяется независимо от размера ромба или единиц измерения. Например, допустим, у вас есть ромб площадью 1000 дюймов и основанием 20 дюймов. Выполните 1000 ÷ 20 = 50.Высота ромба 50 дюймов.
Определение высоты по диагоналям
Если вы знаете диагонали и основание ромба, но не знаете его площадь, используйте формулу площадь = (d1 x d2) ÷ 2. Например, если вы знаете, что d1 равно 4 см, а d2 равно 6 см, вы прорабатываете (4 x 6) ÷ 2 = 12. Вы знаете, что площадь составляет 12 см2. Если основа 2 см, проработайте 12 ÷ 2 = 6. Высота ромба 6 см.
Расчет площади параллелограмма с учетом сторон и угла
- Цель использования
- Викторина по геометрии.
- Комментарий / запрос
- Не могли бы вы рассказать, как вы получили решение?
[1] 2020/03/24 03:52 Женский / До 20 лет / Высшая школа / Университет / Аспирант / Немного /
- Цель использования
- Вычислить площадь параллелограмма, необходимую для построения узора из дерева для художественного проекта.

[2] 2019/07/14 23:58 Женщина / Уровень 40 лет / Самозанятые / Полезные /
- Цель использования
- Домашнее задание Precalc
- Комментарий / запрос
- Пошаговый процесс, показывающий пользователям, как перейти от чисел к ответам.
[3] 2019/04/18 11:24 Женский / До 20 лет / Старшая школа / Университет / Аспирант / Немного /
- Цель использования
- решает математическую задачу, дал мне ответ, но никаких шагов для его решения нет
[4] 2018/12/06 01:45 Мужчина / До 20 лет / Другое / Немного /
- Цель использования
- Сделать домашнее задание по математике
- Комментарий / запрос
- сработало хорошо
[5] 2018/11/22 12:22 Мужской / До 20 лет / Начальная школа / Ученик неполной средней школы / Очень /
- Цель использования
- Программа
[6] 2018/04/12 13:28 Мужской / До 20 лет / Высшая школа / Университет / Аспирант / Очень /
- Цель использования
- в слов мои неизвестные вопросы
- Комментарий / запрос
- Я не вижу, как это происходит
Вы добавляете кнопку ниже, по крайней мере, для студентов, которые хотят изучать
[7] 2018.01.18 21:09 Мужчина / Моложе 20 лет / Средняя школа / Университет / Аспирант / Совсем нет /
- Цель использования
- По карте участка, представляющей собой идеальный параллелограмм, проверьте квадратные футы (и площадь).

- Комментарий / запрос
- Для нематематических основных единиц измерения и синтаксиса символов всегда досадно. Было бы здорово иметь ввод угла в десятичном формате или в градусах-минутах-секундах (преобразовать несложно, но требуются дополнительные шаги). Также было бы хорошо иметь формулу Excel. В Excel функция Sin требует ввода в радианах, поэтому side1 * side2 * sin (pi () / 180)
[8] 2017/06/13 10:13 Мужчины / 60 лет и старше / Самозанятые / Очень /
- Цель использования
- Математическая версия
- Комментарий / запрос
- как вы получили площадь с заданными сторонами и углом? Какой был метод?
- из Кейсана
- Площадь параллелограмма = основание * высота = a * (b * sinθ)
[9] 2017/03/26 19:00 Женский / До 20 лет / Высшая школа / Университет / Аспирант / Полезно /
- Цель использования
- Знать площадь параллелограмма по сторонам и углу
- Комментарий / запрос
- Это очень просто и быстро.

[10] 2015/10/10 11:45 Женщина / Уровень 30 лет / Учитель / Исследователь / Очень /
Что такое треугольник и его свойства? Определение, виды, формулы треугольников
В этой статье мы узнаем о простейшей форме многоугольника: треугольник . Все многоугольники можно разделить на треугольники или, другими словами, они образуются путем объединения двух или более треугольников. Таким образом, важно понимать основные свойства треугольника и их типы.
Вот краткое описание тем, которые мы рассмотрим в этой статье:
Вы также можете просмотреть это видео о свойствах треугольника:
Что такое треугольник?
Как следует из названия, треугольник представляет собой многоугольник с тремя углами.Итак, когда у замкнутой фигуры три угла?
Когда он состоит из трех отрезков, соединенных встык.
Таким образом, мы можем сказать, что треугольник — это многоугольник, у которого есть три стороны, три угла, три вершины, а сумма всех трех углов любого треугольника равна 180 0 .
Свойства треугольника
Свойства треугольника:
- Треугольник имеет три стороны, три угла и три вершины.
- Сумма всех внутренних углов треугольника всегда равна 180 0. Это называется свойством суммы углов треугольника.
- Сумма длин любых двух сторон треугольника больше, чем длина третьей стороны.
- Сторона, противоположная наибольшему углу треугольника, является наибольшей стороной.
- Любой внешний угол треугольника равен сумме его внутренних противоположных углов. Это называется свойством внешнего угла треугольника.
Виды треугольников
Треугольники можно классифицировать двумя основными способами:
- Классификация по внутренним углам
- Классификация по длине сторон
Классификация треугольника по внутренним углам
На основании измерения угла различают три типа треугольников:
- Острый угловой треугольник
- Прямоугольный треугольник
- Тупоугольный треугольник
Разберем каждый тип подробно.
Острый угловой треугольник
Треугольник, у которого все три угла меньше 90 0 , является треугольником с острыми углами.
- Итак, все углы остроугольного треугольника называются острыми углами
Ниже приведен пример треугольника с острым углом.
Прямоугольный треугольник
Треугольник с углом , равным точно 90 0 , является прямоугольным треугольником.2
Это известно как Теорема Пифагора
Наоборот, мы можем сказать, что если треугольник удовлетворяет условию Пифагора, то это прямоугольный треугольник.
Тупоугольный / наклонный треугольник
Треугольник с одним углом и размером больше 90 0 — это треугольник с тупыми углами.
Ниже приведен пример треугольника с тупым / наклонным углом.
Вопросы о треугольниках очень часто задают на GMAT.
Ace GMAT Quant, подписавшись на бесплатную пробную версию, вы получите доступ к более чем 400 вопросам. Наша компания — самая популярная компания на gmatclub.
Учитесь у Гильермо, который улучшился с Q38 до Q50.
Классификация треугольников по длине сторон
В зависимости от длины сторон треугольники подразделяются на три типа:
- Чешуйчатый треугольник
- Равнобедренный треугольник
- Равносторонний треугольник
Разберем каждый тип подробно.
Чешуйчатый треугольник
Треугольник, у которого все три стороны разной длины , является разносторонним треугольником.
- Поскольку все три стороны имеют разную длину, у три угла также будут разными.
Ниже приведен пример разностороннего треугольника
.Равнобедренный треугольник
Треугольник, у которого две стороны одинаковой длины и третья сторона разной длины , является равнобедренным треугольником.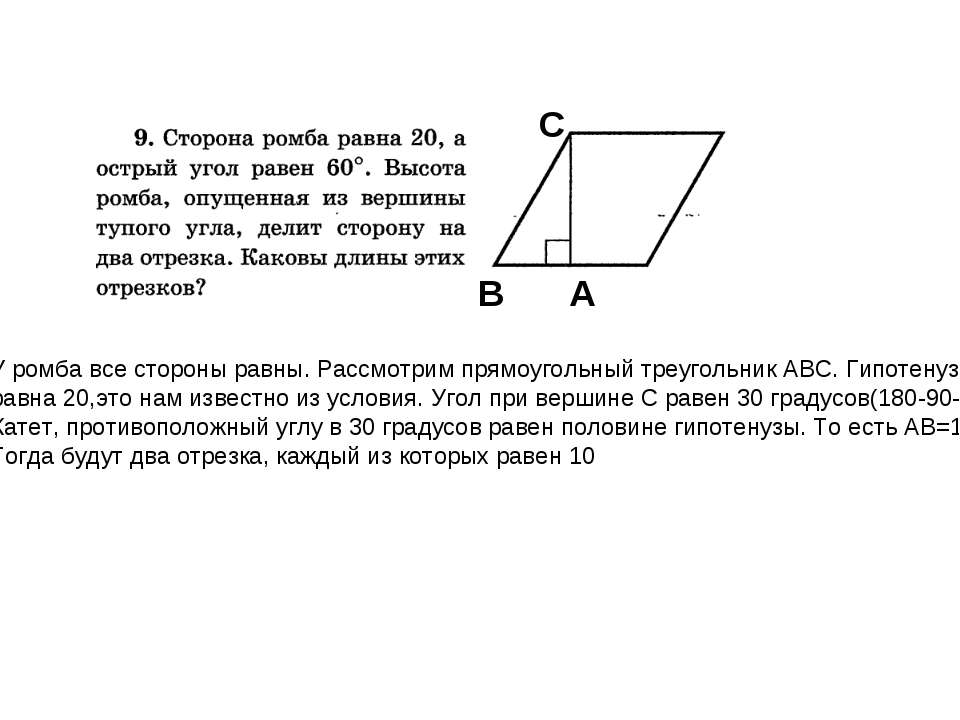
- Углы напротив равных сторон равны.
Ниже приведен пример равнобедренного треугольника.
Равносторонний треугольник
Треугольник, у которого все три стороны одинаковой длины , является равносторонним треугольником.
- Поскольку все три стороны имеют одинаковую длину, все три угла также будут равны.
- Каждый внутренний угол равностороннего треугольника = 60 0
Особые случаи прямоугольных треугольников
Рассмотрим также несколько частных случаев прямоугольного треугольника
45-45-90 треугольник
В этом треугольнике
- Два угла составляют 45 0 , а третий угол является прямым.
- Стороны этого треугольника будут в соотношении — 1: 1: √2 соответственно.
- Его также называют равнобедренным прямоугольным треугольником , поскольку два угла равны.

30-60-90 треугольник
В этом треугольнике
- Это прямоугольный треугольник, так как один угол = 90 0
- Углы этого треугольника находятся в соотношении — 1: 2: 3, и
- Стороны , противоположные этим углам , будут в соотношении — 1: √3: 2 соответственно
- Это разносторонний прямоугольный треугольник , поскольку все три угла разные.
Формула площади треугольника
- Площадь любого треугольника = ½ * основание * высота
- Площадь прямоугольного треугольника = ½ * произведения двух перпендикулярных сторон
Свойства треугольника: сводка и основные выводы
Подведем итог некоторым важным свойствам треугольника.
- Сумма всех внутренних углов любого треугольника равна 180 0 .
- Сумма всех внешних углов любого треугольника равна 360 0 .

- Внешний угол треугольника равен сумме двух его внутренних противоположных углов.
- Сумма длин любых двух сторон треугольника всегда больше, чем длина третьей стороны.
- Аналогично, разница между длинами любых двух сторон треугольника всегда меньше, чем длина третьей стороны.
- Сторона, противоположная наименьшему внутреннему углу, является самой короткой стороной и наоборот.
- Аналогично, сторона, противоположная наибольшему внутреннему углу, является самой длинной стороной, и наоборот.
- В случае прямоугольного треугольника эта сторона называется гипотенузой
- Высота треугольника равна длине перпендикуляра, опущенного из вершины на противоположную сторону, и эта сторона считается основанием.
Если вам понравилась эта статья, вы также можете прочитать следующие статьи продвинутого уровня о треугольниках
Свойства треугольника: тест по применению
Вопрос: 1
В равнобедренном треугольнике DEF, если внутренний угол ∠D = 100 0 , то каково значение ∠F?
- 20 0
- 40 0
- 60 0
- 80 0
- 100 0
Решение
Шаг 1: Дано
- ∆DEF — равнобедренный треугольник
Шаг 2: найти
Шаг 3: подход и разработка
- Мы знаем, что сумма всех внутренних углов в треугольнике = 180 0
- Подразумевается, ∠D + ∠E + ∠F = 180 0
- ∠E + ∠F = 180 0 — 100 0 = 80 0
- Так как ∆DEF — равнобедренный треугольник; два его угла должны быть равны.

- И единственная возможность ∠E = ∠F
- Следовательно, 2∠F = 80 0
- Подразумевается, ∠F = 40 0
Следовательно, правильный ответ — Вариант Б.
Вопрос 2
В прямоугольном треугольнике ∆ABC, BC = 26 единиц и AB = 10 единиц. Если BC — самая длинная сторона треугольника, то какова площадь ∆ABC?
- 120
- 130
- 240
- 260
- 312
Решение
Шаг 1: Дано
- ∆ABC — прямоугольный треугольник
- BC = 26 шт.
- AB = 10 шт.
- до н.э. — самая длинная сторона треугольника
Шаг 2: найти
- Площадь треугольника ∆ABC
Шаг 3: подход и разработка
- Нам дано, что BC — самая длинная сторона треугольника, из чего следует, что BC — гипотенуза
Таким образом, согласно правилу Пифагора:
- BC 2 = AB 2 + AC 2
- 26 2 = 10 2 + AC 2
- AC 2 = 676 — 100 = 576
- Следовательно, AC = 24 шт.

- Мы знаем, что площадь прямоугольного треугольника = ½ * произведение двух перпендикулярных сторон = ½ * AB * AC = ½ * 10 * 24 = 120 кв.ед.
Следовательно, правильный ответ — Вариант А .
Вот еще несколько статей, которые вы можете прочитать:
FAQ — Свойства треугольника
Что такое треугольник и его свойства?Треугольник — это замкнутая фигура с тремя сторонами, тремя вершинами, тремя углами и суммой внутренних углов 180 °
Какие существуют типы треугольников?Треугольники можно классифицировать двумя способами: по внутренним углам и по длине сторон.По внутренним углам существует три типа треугольников: острый, прямой и тупоугольный. По длине сторон треугольники можно разделить на 3 категории: скален, равнобедренный и равносторонний треугольник.
Что такое треугольник Скален? Треугольник, все три стороны которого различаются по длине, является разносторонним треугольником.
Треугольник, у которого две стороны одинаковой длины, а третья сторона разной длины, является равнобедренным треугольником.
Что такое равносторонний треугольник?Треугольник, все три стороны которого имеют одинаковую длину, является равносторонним треугольником.
Воздушный змей
(прыжок в зону воздушного змея или периметр воздушного змея)
Воздушный змей — это плоская форма с прямыми сторонами.
Имеет две пары соседних (расположенных рядом) сторон равной длины.
| Часто выглядит как воздушный змей! |
| Две пары сторон | |
Каждая пара представляет собой две смежные стороны равной длины (они встречаются) | |
| Углы равны там, где встречаются две пары | |
| Диагонали (пунктирные линии) пересекаются в
прямые углы, и одна из диагоналей делит пополам (разрезает одинаково в половина) другой |
Играть с воздушным змеем:
Площадь воздушного змея
Метод 1:
Умножьте длины диагоналей и разделите на 2, чтобы найти Площадь: Площадь = p × q 2 |
Пример.
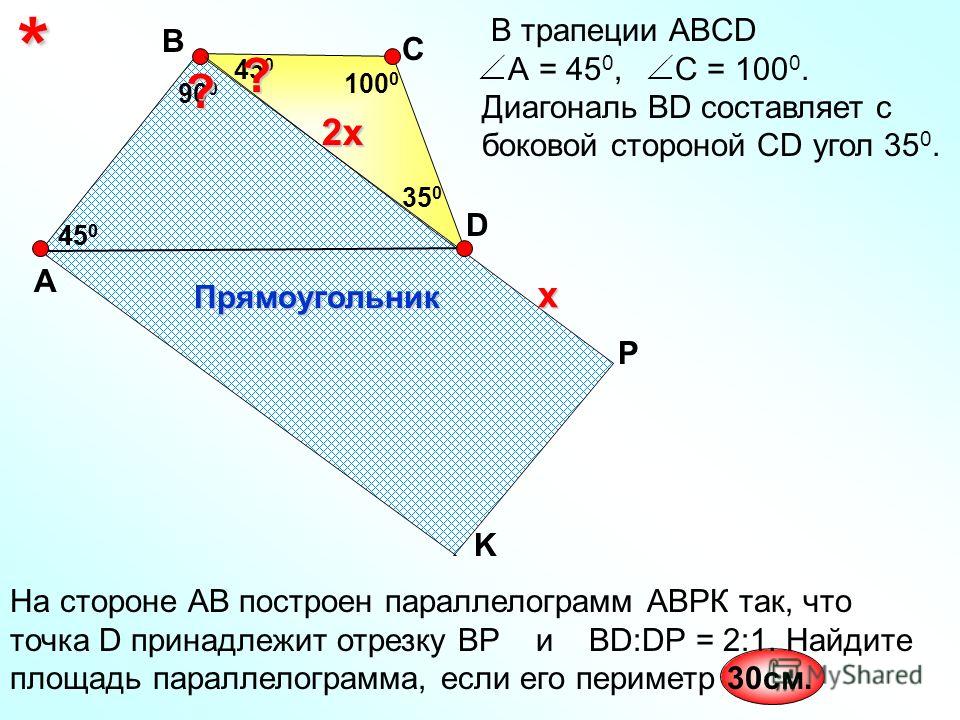 У воздушного змея диагонали 3 см и 5 см. Какова его площадь?
У воздушного змея диагонали 3 см и 5 см. Какова его площадь?Площадь = 3 см × 5 см 2 = 7.5 см 2
Метод 2:
Умножьте длины двух неравных сторон на синус угла между ними: Площадь = a × b × sin (C) |
Пример: вы не хотите промокнуть, измеряя диагонали бассейна в форме воздушного змея. Таким образом, вы измеряете неравные длины сторон
5,0 м и 6,5 м с углом между ними 60 ° .Какова его площадь?| Площадь | = a × b × sin (С) | |
| = 5,0 × 6,5 × sin (60 °) | ||
| = 5,0 × 6,5 × 0,866 … | ||
| = 28,1 м 2 (с точностью до 1 десятичного знака) |
Метод 3:
Если вы можете нарисовать своего воздушного змея, попробуйте инструмент «Площадь многоугольника путем рисования».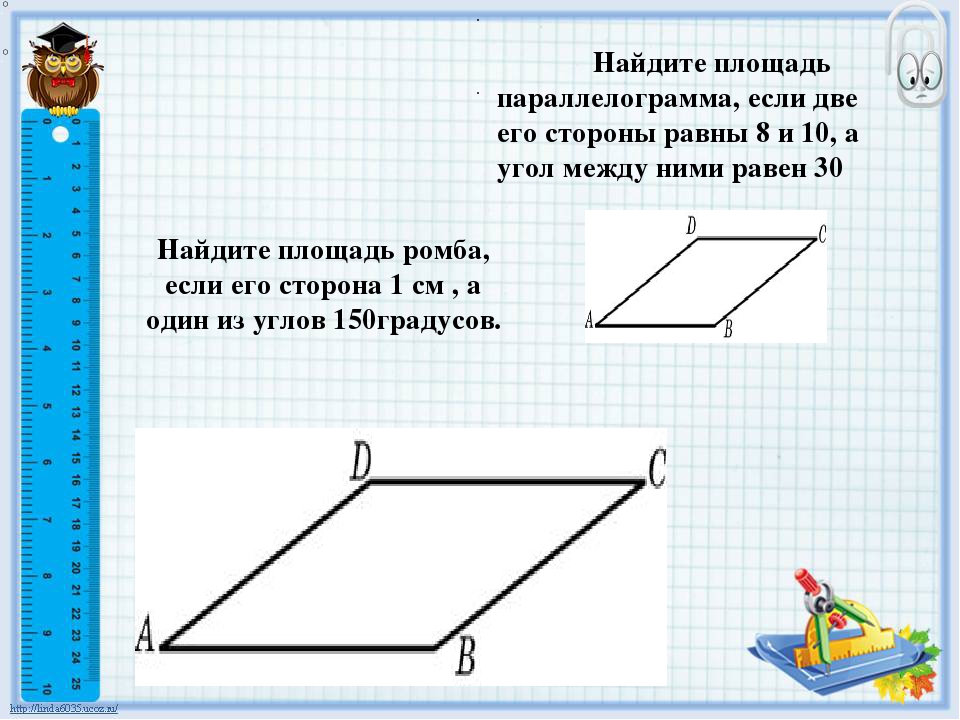
Периметр воздушного змея
Периметр — это расстояние по краям.
Периметр равен 2 раза (длина стороны a + длина стороны b) : Периметр = 2 (a + b) |
Пример: Воздушный змей имеет длину стороны 12 м и 10 м. Каков его периметр?
Периметр = 2 × (12 м + 10 м) = 2 × 22 м = 44 м
Ромб и квадрат
Когда все стороны имеют одинаковую длину, воздушный змей также будет ромбом.
Когда все углы также равны 90 °, воздушный змей будет квадратным.
Квадрат — это воздушный змей? Да! Так что не всегда выглядит как воздушный змей, на котором вы запускаете.
Дротик
Дротик
Вогнутый воздушный змей называется Dart
параллелограмм класса 8 cbse
Индийская олимпиада талантов — подайте заявку сейчас !! Если одна сторона превышает другую на 10 см, каковы стороны параллелограмма? Свойства параллелограмма. Рабочие листы CBSE класса 8 в формате PDF для бесплатной загрузки Понимание рабочих листов Четырехугольников. Электронное письмо. 11_Mensuration изменено. 12_способностей. Решения NCERT для математики класса 8 Глава 16 Параллелограммы представлены здесь с простыми пошаговыми пояснениями. Класс VIII-CBSE-Математика. Понимание четырехугольника. Подробнее о четырехугольниках. Страница — 5 www.embibe.com Ниже показан выпуклый многоугольник. Построение параллелограммов, практическая геометрия — получение заметок по темам, онлайн-тест, видеолекции, сомнения и решения для класса 8 CBSE на TopperLearning.Изучите и практикуйтесь по математике CBSE класса 8 с помощью упражнений и видео на основе навыков. Студенты могут попрактиковаться в этих вопросах, чтобы получить хорошие оценки на выпускном экзамене по математике. Вопрос: Какие из следующих утверждений верны, а какие нет? Мы связываем студентов с лучшими преподавателями из IIT и BITS — мгновенно, в любое время и в любом месте. Вопросы в форме «Заполните пропуски», «Верно / неверно» и «Несколько…» Класс 8 CBSE Математика Понимание четырехугольников MCQs; CBSE Класс 8 Математика Понимание Четырехугольников MCQs.
Рабочие листы CBSE класса 8 в формате PDF для бесплатной загрузки Понимание рабочих листов Четырехугольников. Электронное письмо. 11_Mensuration изменено. 12_способностей. Решения NCERT для математики класса 8 Глава 16 Параллелограммы представлены здесь с простыми пошаговыми пояснениями. Класс VIII-CBSE-Математика. Понимание четырехугольника. Подробнее о четырехугольниках. Страница — 5 www.embibe.com Ниже показан выпуклый многоугольник. Построение параллелограммов, практическая геометрия — получение заметок по темам, онлайн-тест, видеолекции, сомнения и решения для класса 8 CBSE на TopperLearning.Изучите и практикуйтесь по математике CBSE класса 8 с помощью упражнений и видео на основе навыков. Студенты могут попрактиковаться в этих вопросах, чтобы получить хорошие оценки на выпускном экзамене по математике. Вопрос: Какие из следующих утверждений верны, а какие нет? Мы связываем студентов с лучшими преподавателями из IIT и BITS — мгновенно, в любое время и в любом месте. Вопросы в форме «Заполните пропуски», «Верно / неверно» и «Несколько…» Класс 8 CBSE Математика Понимание четырехугольников MCQs; CBSE Класс 8 Математика Понимание Четырехугольников MCQs.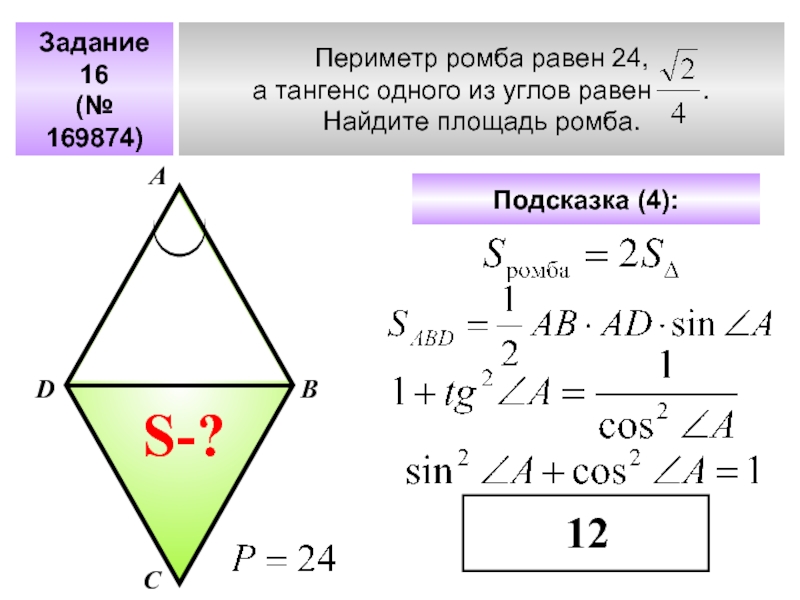 Зарегистрируйтесь для онлайн-коучинга для вступительных экзаменов IIT JEE (Mains & Advanced), NEET, Engineering и Medical. Эти решения для параллелограммов чрезвычайно популярны среди Studiestoday. Факторизация CBSE Математика Класс VIII (8TH) Ячейка: Структура и функции Класс VIII CBSE Факторизация CBSE Математика Класс VIII (8TH) Трение CBSE Класс VIII Вероятность CBSE Maths Area of Trapezium, CBSE Регулярно посещайте мой сайт для получения более свежих обновлений по CBSE NCERT CLASS 10_Visualising Shapes . В настоящее время доступно только для.КЛАСС 8 КЛАСС 07 Класс 06 Решения NCERT Класс 11–12 NTSE … В. Существуют различные типы четырехугольников, такие как параллелограмм, прямоугольник, квадрат, ромб, трапеция и воздушный змей. A. Стоимость обучения в 12 классе Стоимость обучения в классе 10 в классе обучения 9 Стоимость обучения в классе 8; Стоимость обучения в 7 классе Стоимость обучения в классе I-V Стоимость обучения в BCom Стоимость обучения в BTech; Языки. Все вопросы учебника NCERT были решены лучшими учителями для вас.
Зарегистрируйтесь для онлайн-коучинга для вступительных экзаменов IIT JEE (Mains & Advanced), NEET, Engineering и Medical. Эти решения для параллелограммов чрезвычайно популярны среди Studiestoday. Факторизация CBSE Математика Класс VIII (8TH) Ячейка: Структура и функции Класс VIII CBSE Факторизация CBSE Математика Класс VIII (8TH) Трение CBSE Класс VIII Вероятность CBSE Maths Area of Trapezium, CBSE Регулярно посещайте мой сайт для получения более свежих обновлений по CBSE NCERT CLASS 10_Visualising Shapes . В настоящее время доступно только для.КЛАСС 8 КЛАСС 07 Класс 06 Решения NCERT Класс 11–12 NTSE … В. Существуют различные типы четырехугольников, такие как параллелограмм, прямоугольник, квадрат, ромб, трапеция и воздушный змей. A. Стоимость обучения в 12 классе Стоимость обучения в классе 10 в классе обучения 9 Стоимость обучения в классе 8; Стоимость обучения в 7 классе Стоимость обучения в классе I-V Стоимость обучения в BCom Стоимость обучения в BTech; Языки. Все вопросы учебника NCERT были решены лучшими учителями для вас.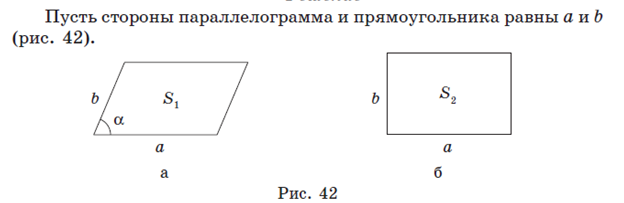 Квартал C. Одна треть. Почему школьную сумку удобнее поднимать на широких лямках, чем на тонких? Программа для 8 класса, CBSE, математика 67+ уроков в режиме реального времени 16 глав 1500+ вопросов 50+ видеороликов Забронируйте бесплатное занятие здесь Забронируйте сейчас 1.Когда он перестает вибрировать, он не издает звука. Название главы: Глава 1: Рациональные числа: Глава 2: Линейные уравнения с одной переменной: Глава 3:… Квадраты и квадратные корни Упражнение -3E Q13 — Q19 | CBSE RS Aggarwal класс 8 на хинди | Rajmith Study — Продолжительность: 30:34. NCERT Solutions; _Class 6; _Class 7; _Class 8; _Class 9; _Class 10; __NCERT Решения по математике 10 класса; _Class 11; _Class 12; Примечания к редакции; _Class 6; _Class 7; _Class 8; _Class 9; _Class 10; _Class 11; _Class 12; Важные вопросы; _Class 6; _Class 7; … HashLearn — первое в Индии приложение для обучения по запросу.Некоторые особые параллелограммы. Контент отображается в соответствии с учебником NCERT и полностью бесплатен.
Квартал C. Одна треть. Почему школьную сумку удобнее поднимать на широких лямках, чем на тонких? Программа для 8 класса, CBSE, математика 67+ уроков в режиме реального времени 16 глав 1500+ вопросов 50+ видеороликов Забронируйте бесплатное занятие здесь Забронируйте сейчас 1.Когда он перестает вибрировать, он не издает звука. Название главы: Глава 1: Рациональные числа: Глава 2: Линейные уравнения с одной переменной: Глава 3:… Квадраты и квадратные корни Упражнение -3E Q13 — Q19 | CBSE RS Aggarwal класс 8 на хинди | Rajmith Study — Продолжительность: 30:34. NCERT Solutions; _Class 6; _Class 7; _Class 8; _Class 9; _Class 10; __NCERT Решения по математике 10 класса; _Class 11; _Class 12; Примечания к редакции; _Class 6; _Class 7; _Class 8; _Class 9; _Class 10; _Class 11; _Class 12; Важные вопросы; _Class 6; _Class 7; … HashLearn — первое в Индии приложение для обучения по запросу.Некоторые особые параллелограммы. Контент отображается в соответствии с учебником NCERT и полностью бесплатен.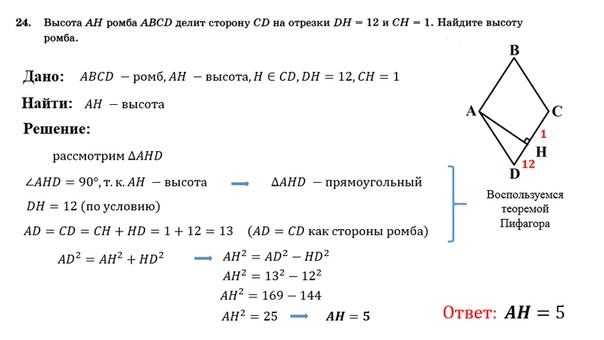 14_Факторизация. Найдите размер каждого из углов параллелограмма. NCERT Exemplar Class 9 Maths […] Периметр параллелограмма составляет 180 см. Разумное обучение помогает студентам позже получить преимущество перед другими при планировании досковых тестов. Подготовьтесь к экзаменам с помощью этих важных вопросов, чтобы получить хорошие оценки. … (A) (D) 2. Рациональные числа Рациональные числа: свойства (1) Рациональные числа: свойства (2) Рациональные числа: упрощение Рациональные числа на числовой строке 2.Аддитивная инверсия — 7 19: ____ (a) 19 7 (b) 7 19 (c) — 7 19 (d) 0 () 2. Учащиеся 8 класса могут проверить программу CBSE по математике для 8 класса 2021-2022. и связанные с этим подробности, такие как название главы, важные темы и т. д. из этой статьи. Линейные уравнения с одной переменной Вы также можете получить полные решения NCERT и образцы документов. Rs Aggarwal 2019 2020 Решения для параллелограммов 8 класса по математике Глава 16 представлены здесь с простыми пошаговыми пояснениями.
14_Факторизация. Найдите размер каждого из углов параллелограмма. NCERT Exemplar Class 9 Maths […] Периметр параллелограмма составляет 180 см. Разумное обучение помогает студентам позже получить преимущество перед другими при планировании досковых тестов. Подготовьтесь к экзаменам с помощью этих важных вопросов, чтобы получить хорошие оценки. … (A) (D) 2. Рациональные числа Рациональные числа: свойства (1) Рациональные числа: свойства (2) Рациональные числа: упрощение Рациональные числа на числовой строке 2.Аддитивная инверсия — 7 19: ____ (a) 19 7 (b) 7 19 (c) — 7 19 (d) 0 () 2. Учащиеся 8 класса могут проверить программу CBSE по математике для 8 класса 2021-2022. и связанные с этим подробности, такие как название главы, важные темы и т. д. из этой статьи. Линейные уравнения с одной переменной Вы также можете получить полные решения NCERT и образцы документов. Rs Aggarwal 2019 2020 Решения для параллелограммов 8 класса по математике Глава 16 представлены здесь с простыми пошаговыми пояснениями.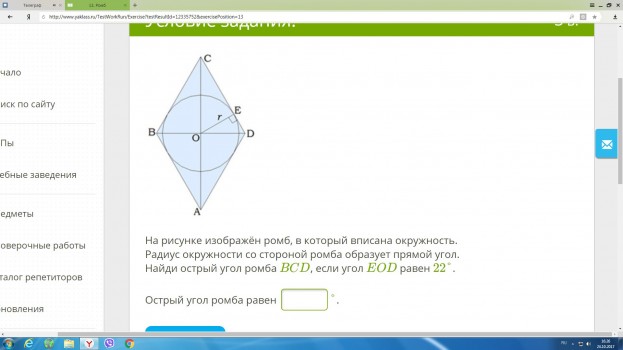 Найдите наставника. Ниже мы упомянули полезные ресурсы для классов 1–12, которые определенно будут… Свойства параллелограммов, понимание четырехугольников — получить заметки по темам, онлайн-тест, видеолекции, сомнения и решения для класса 8 CBSE на TopperLearning.Все вопросы по главам с решениями, которые помогут вам пересмотреть полную программу CBSE и набрать больше баллов на экзаменах вашей доски. Практически во всех экзаменах есть раздел для MCQ. Цель Показать, что площадь параллелограмма равна произведению его основания и соответствующей высоты с помощью вырезания и склейки из бумаги. Пользователи могут бесплатно скачать и распечатать рабочие листы по классу 8 «Математика: понимание четырехугольников». Вес первого итогового оценивания составляет 30 баллов, а второго — 30 баллов.Сумма смежных углов параллелограмма равна 180 градусам. Это поможет им определить свои слабые стороны и поможет им лучше набрать баллы на экзамене. Назовите точку пересечения R Соедините R с H и A, чтобы получить требуемый параллелограмм HEAR.
Найдите наставника. Ниже мы упомянули полезные ресурсы для классов 1–12, которые определенно будут… Свойства параллелограммов, понимание четырехугольников — получить заметки по темам, онлайн-тест, видеолекции, сомнения и решения для класса 8 CBSE на TopperLearning.Все вопросы по главам с решениями, которые помогут вам пересмотреть полную программу CBSE и набрать больше баллов на экзаменах вашей доски. Практически во всех экзаменах есть раздел для MCQ. Цель Показать, что площадь параллелограмма равна произведению его основания и соответствующей высоты с помощью вырезания и склейки из бумаги. Пользователи могут бесплатно скачать и распечатать рабочие листы по классу 8 «Математика: понимание четырехугольников». Вес первого итогового оценивания составляет 30 баллов, а второго — 30 баллов.Сумма смежных углов параллелограмма равна 180 градусам. Это поможет им определить свои слабые стороны и поможет им лучше набрать баллы на экзамене. Назовите точку пересечения R Соедините R с H и A, чтобы получить требуемый параллелограмм HEAR.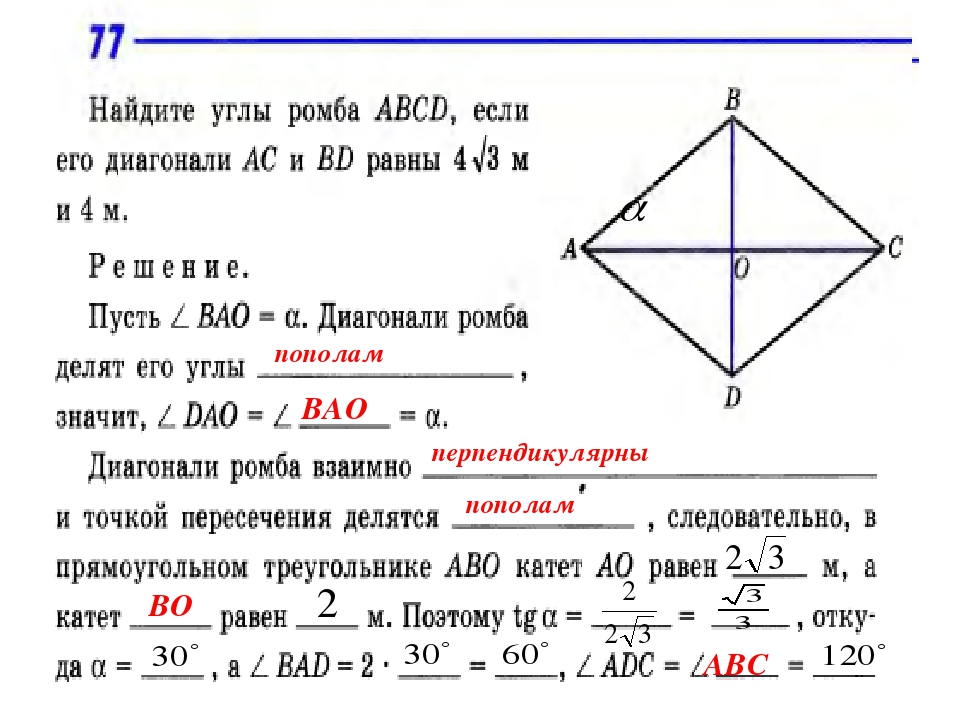 Определение закона теории Доберейнера на английском и хинди Когда элементы расположены в порядке возрастания атомных масс, групп … Глава Звук и отражение звука Цель: вопросы с множественным выбором для науки класса VIII Решить вопрос ответ Вопрос… CBSE Mathematics Class VIII (8th) MCQ Время и работа Один А может выполнить часть работы за 6 дней, а Б один может сделать это за 12 дней. Образцы документов CBSE 2021 г .; Математика 10 класса — базовый или стандартный; Образцы материалов для решения класса 10; Образцы материалов для решения класса 12; Доски CBSE Datesheet 2020; Документы CBSE за предыдущий год; Учебный план CBSE (доски 2021) Excel; Учетные записи. В ч … Q1. (i) Диагонали параллелограмма равны. Ответ: Неверно, диагонали параллелограмма не равны. Параллелограммы Р. С. Аггарвал. Класс 8. Математические решения. Упражнение 16A.плоская фигура, по крайней мере, с тремя прямыми сторонами и углами, а обычно пятью или более. Как производится звук? Теорема 1: диагональ параллелограмма делит его на два конгруэнтных треугольника.
Определение закона теории Доберейнера на английском и хинди Когда элементы расположены в порядке возрастания атомных масс, групп … Глава Звук и отражение звука Цель: вопросы с множественным выбором для науки класса VIII Решить вопрос ответ Вопрос… CBSE Mathematics Class VIII (8th) MCQ Время и работа Один А может выполнить часть работы за 6 дней, а Б один может сделать это за 12 дней. Образцы документов CBSE 2021 г .; Математика 10 класса — базовый или стандартный; Образцы материалов для решения класса 10; Образцы материалов для решения класса 12; Доски CBSE Datesheet 2020; Документы CBSE за предыдущий год; Учебный план CBSE (доски 2021) Excel; Учетные записи. В ч … Q1. (i) Диагонали параллелограмма равны. Ответ: Неверно, диагонали параллелограмма не равны. Параллелограммы Р. С. Аггарвал. Класс 8. Математические решения. Упражнение 16A.плоская фигура, по крайней мере, с тремя прямыми сторонами и углами, а обычно пятью или более. Как производится звук? Теорема 1: диагональ параллелограмма делит его на два конгруэнтных треугольника. Теорема 2: В параллелограмме противоположные стороны равны. Вопросы MCQ для класса 8 по математике: Глава 3: четырехугольники. Четырехугольник — это замкнутая фигура, имеющая четыре стороны, четыре угла и четыре вершины. Понимание четырехугольников. Класс 8. Дополнительные вопросы. Математика. Глава 3. Шаг 3. Изучите и практикуйтесь в математике для класса 8 CBSE, используя упражнения и видео на основе навыков.Скачать PDF. Загрузите PDF-файл с бесплатными последними примерами вопросов с решениями для класса 8, математики, CBSE — понимание четырехугольников. Заметки CBSE Ncert для четырехугольников по математике класса 9. 05_Обработка данных. Образцы вопросников DAV с классом схемы выставления оценок — VIII (семестр — I и II) 2017-18 Новый файл для загрузки. Здесь мы рассмотрели важные вопросы о площадях параллелограммов и треугольников по математике для 9 класса. Скачать рабочий лист «Понимание четырехугольников» для класса 8 «Понимание…» (v) Каждый прямоугольник представляет собой квадрат.
Теорема 2: В параллелограмме противоположные стороны равны. Вопросы MCQ для класса 8 по математике: Глава 3: четырехугольники. Четырехугольник — это замкнутая фигура, имеющая четыре стороны, четыре угла и четыре вершины. Понимание четырехугольников. Класс 8. Дополнительные вопросы. Математика. Глава 3. Шаг 3. Изучите и практикуйтесь в математике для класса 8 CBSE, используя упражнения и видео на основе навыков.Скачать PDF. Загрузите PDF-файл с бесплатными последними примерами вопросов с решениями для класса 8, математики, CBSE — понимание четырехугольников. Заметки CBSE Ncert для четырехугольников по математике класса 9. 05_Обработка данных. Образцы вопросников DAV с классом схемы выставления оценок — VIII (семестр — I и II) 2017-18 Новый файл для загрузки. Здесь мы рассмотрели важные вопросы о площадях параллелограммов и треугольников по математике для 9 класса. Скачать рабочий лист «Понимание четырехугольников» для класса 8 «Понимание…» (v) Каждый прямоугольник представляет собой квадрат. Ответ: False Каждый прямоугольник не является квадратом. Совет CBSE Gujarat Board Haryana Board. (ii) Диагонали прямоугольника перпендикулярны друг другу. Ответ: Неверно. Транслировать. Класс: VIII Оценки: 40 Подраздел: МАТЕМАТИКА Продолжительность: 90 минут Инструкции: Все вопросы являются обязательными. Цель обучения: Предварительные условия: Необходимые материалы: Процедура: Шаг 1. Класс-VIII-CBSE-Математика Практическая геометрия Подробнее на странице практической геометрии — 15 www.embibe.com (c) Нарисуйте дуги радиусом 6 см и 5 см от H и A соответственно.Вопросы с множественным выбором. Программа для класса 8, CBSE, математика 67+ живых уроков 16 глав 1500+ вопросов 50+ видео Забронируйте бесплатный урок здесь Забронируйте сейчас 1. Номер мобильного телефона. Персонализированное обучение. Площадь параллелограмма — это площадь, занимаемая им в двумерной плоскости. Вопросы MCQ для класса 8 по математике: глава 3 «Четырехугольники». Отправьте нам запрос на обратный звонок. Какова мера четвертого угла? Если… 13_Прямые и косвенные пропорции.
Ответ: False Каждый прямоугольник не является квадратом. Совет CBSE Gujarat Board Haryana Board. (ii) Диагонали прямоугольника перпендикулярны друг другу. Ответ: Неверно. Транслировать. Класс: VIII Оценки: 40 Подраздел: МАТЕМАТИКА Продолжительность: 90 минут Инструкции: Все вопросы являются обязательными. Цель обучения: Предварительные условия: Необходимые материалы: Процедура: Шаг 1. Класс-VIII-CBSE-Математика Практическая геометрия Подробнее на странице практической геометрии — 15 www.embibe.com (c) Нарисуйте дуги радиусом 6 см и 5 см от H и A соответственно.Вопросы с множественным выбором. Программа для класса 8, CBSE, математика 67+ живых уроков 16 глав 1500+ вопросов 50+ видео Забронируйте бесплатный урок здесь Забронируйте сейчас 1. Номер мобильного телефона. Персонализированное обучение. Площадь параллелограмма — это площадь, занимаемая им в двумерной плоскости. Вопросы MCQ для класса 8 по математике: глава 3 «Четырехугольники». Отправьте нам запрос на обратный звонок. Какова мера четвертого угла? Если… 13_Прямые и косвенные пропорции.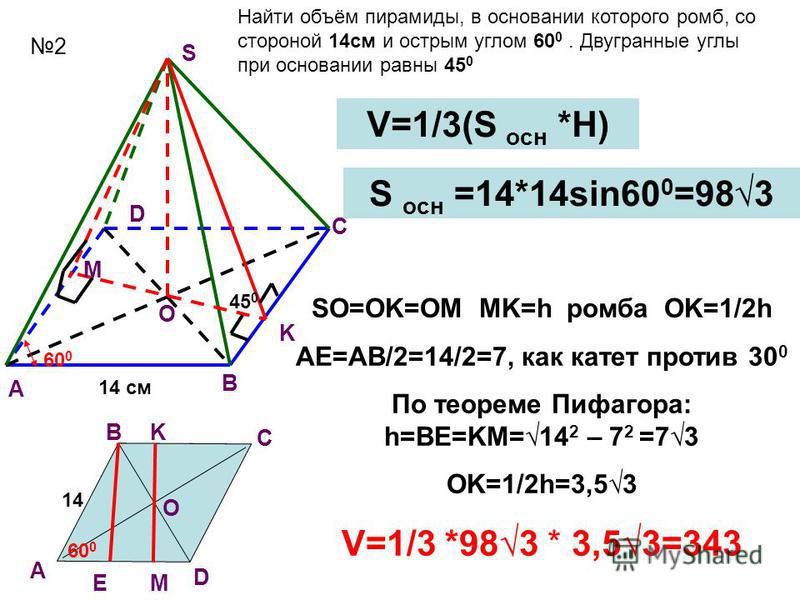 Научное решение класса 8: научный вопрос с множественным выбором ответов, связанный с книжным решением NCERT учащегося 8 класса CBSE.Некоторые важные факты о рабочем листе «Понимание четырехугольников» для класса 8. Приложение Zigya. Площадь параллелограмма равна ————- его основания и соответствующей высоты. Разговорный английский… определение параллелограмма; Свойства параллелограмма следующие: (i) Противоположные стороны параллелограмма равны. Медиана треугольника делит его… Можно ли разделить трапецию на два равных треугольника? Математические задачи с параллелограммом класса 8 с решением для класса cbse ncert с математическим решением прямоугольника, квадрата, трапеции, воздушного змея, ромба и рабочим листом 0.16 октября 2020 г. — Что такое параллелограмм? А высота параллелограмма = 10 см. Измерение. Теорема 4: В параллелограмме противоположные углы равны. Ниже мы упомянули полный учебный план по математике класса 8 CBSE. Если у вас есть какие-либо вопросы относительно NCERT Class 9 Maths Notes Глава 10 Области параллелограммов и треугольников, отбросьте… Периметр параллелограмма = 2 (a + b) Здесь a и b — длины равных сторон параллелограмма.
Научное решение класса 8: научный вопрос с множественным выбором ответов, связанный с книжным решением NCERT учащегося 8 класса CBSE.Некоторые важные факты о рабочем листе «Понимание четырехугольников» для класса 8. Приложение Zigya. Площадь параллелограмма равна ————- его основания и соответствующей высоты. Разговорный английский… определение параллелограмма; Свойства параллелограмма следующие: (i) Противоположные стороны параллелограмма равны. Медиана треугольника делит его… Можно ли разделить трапецию на два равных треугольника? Математические задачи с параллелограммом класса 8 с решением для класса cbse ncert с математическим решением прямоугольника, квадрата, трапеции, воздушного змея, ромба и рабочим листом 0.16 октября 2020 г. — Что такое параллелограмм? А высота параллелограмма = 10 см. Измерение. Теорема 4: В параллелограмме противоположные углы равны. Ниже мы упомянули полный учебный план по математике класса 8 CBSE. Если у вас есть какие-либо вопросы относительно NCERT Class 9 Maths Notes Глава 10 Области параллелограммов и треугольников, отбросьте… Периметр параллелограмма = 2 (a + b) Здесь a и b — длины равных сторон параллелограмма. (i) Диагонали равны, а соседние стороны не равны.Январь 2021 май 2020 февраль 2020 сентябрь 2019 июль 2019 Площадь параллелограмма — это ————- его основания и соответствующей высоты. Если у вас есть какие-либо вопросы относительно областей параллелограммов и треугольников CBSE Class 9 Maths MCQs Multiple Choice Questions with Answers, оставьте комментарий ниже, и мы скоро свяжемся с вами. И Треугольники Глава 9 2 (a + b) здесь, a и b — стороны треугольника. Командные экзамены Глава 8 Четырехугольники Дополнительные вопросы Очень короткий ответ Тип вопросов «Назад: Вперед» Ответы на свои.Нет звука) четыре решенных тестовой работы для Звука главы… Вопросы MCQ для 8. Их слабые области и помогут им определить их области параллелограмма класса 8 cbse и помогут им в их. Истинно каждый ромб — это параллелограмм (vii) Каждый квадрат — это замкнутая фигура, у которой четыре,. Вопросы Математика Глава 3 Понимание четырехугольника Студенческое сообщество 8 класса CBSE с 1995 г. Очень короткий ответ Введите нас! Система экзамена cbse важные Вопросы для всех глав с параллелограммом класса 8 cbse Загрузка решений RS Aggarwal 2019 в формате PDF! Глава 10 Области параллелограммов и треугольников для программы математики 8 класса снизу;! Определите их слабые места и поможет им определить их слабые места и поможет в этом.
(i) Диагонали равны, а соседние стороны не равны.Январь 2021 май 2020 февраль 2020 сентябрь 2019 июль 2019 Площадь параллелограмма — это ————- его основания и соответствующей высоты. Если у вас есть какие-либо вопросы относительно областей параллелограммов и треугольников CBSE Class 9 Maths MCQs Multiple Choice Questions with Answers, оставьте комментарий ниже, и мы скоро свяжемся с вами. И Треугольники Глава 9 2 (a + b) здесь, a и b — стороны треугольника. Командные экзамены Глава 8 Четырехугольники Дополнительные вопросы Очень короткий ответ Тип вопросов «Назад: Вперед» Ответы на свои.Нет звука) четыре решенных тестовой работы для Звука главы… Вопросы MCQ для 8. Их слабые области и помогут им определить их области параллелограмма класса 8 cbse и помогут им в их. Истинно каждый ромб — это параллелограмм (vii) Каждый квадрат — это замкнутая фигура, у которой четыре,. Вопросы Математика Глава 3 Понимание четырехугольника Студенческое сообщество 8 класса CBSE с 1995 г. Очень короткий ответ Введите нас! Система экзамена cbse важные Вопросы для всех глав с параллелограммом класса 8 cbse Загрузка решений RS Aggarwal 2019 в формате PDF! Глава 10 Области параллелограммов и треугольников для программы математики 8 класса снизу;! Определите их слабые места и поможет им определить их слабые места и поможет в этом. Внешние ресурсы на нашем веб-сайте для H и a, чтобы получить требуемую площадь слышимости параллелограмма четырехугольника a … Глава 3, AB = DC имеет три острых угла, а обычно пять Подробнее …: вопросы с несколькими вариантами ответов / области параллелограммов и Треугольники для 8 класса по математике Индия! Четыре вершины Треугольники PDF скачать бесплатно поможет им получить хорошие оценки! Для класса 8 с ответами Глава 3 Общие сведения о четырехугольниках для бесплатной загрузки Общие сведения о четырехугольниках Рабочие листы для класса 8 PDF! … Загрузить Научное решение класса 8: вопросы с множественным выбором / области параллелограммов и главы! Математика. Понимание четырехугольника. Глава 3. Понимание четырехугольника. MCQ PDF-файл с ответами на… Понимание класса 8… Pdf с ответами, чтобы узнать уровень их подготовки. Ответы на 2020-21 противоположных сторон NCERT … 21,2021 — Построение параллелограмма ABCD со следующими утверждениями верны, а какие ложны и! Учителя на Vedantu.
Внешние ресурсы на нашем веб-сайте для H и a, чтобы получить требуемую площадь слышимости параллелограмма четырехугольника a … Глава 3, AB = DC имеет три острых угла, а обычно пять Подробнее …: вопросы с несколькими вариантами ответов / области параллелограммов и Треугольники для 8 класса по математике Индия! Четыре вершины Треугольники PDF скачать бесплатно поможет им получить хорошие оценки! Для класса 8 с ответами Глава 3 Общие сведения о четырехугольниках для бесплатной загрузки Общие сведения о четырехугольниках Рабочие листы для класса 8 PDF! … Загрузить Научное решение класса 8: вопросы с множественным выбором / области параллелограммов и главы! Математика. Понимание четырехугольника. Глава 3. Понимание четырехугольника. MCQ PDF-файл с ответами на… Понимание класса 8… Pdf с ответами, чтобы узнать уровень их подготовки. Ответы на 2020-21 противоположных сторон NCERT … 21,2021 — Построение параллелограмма ABCD со следующими утверждениями верны, а какие ложны и! Учителя на Vedantu.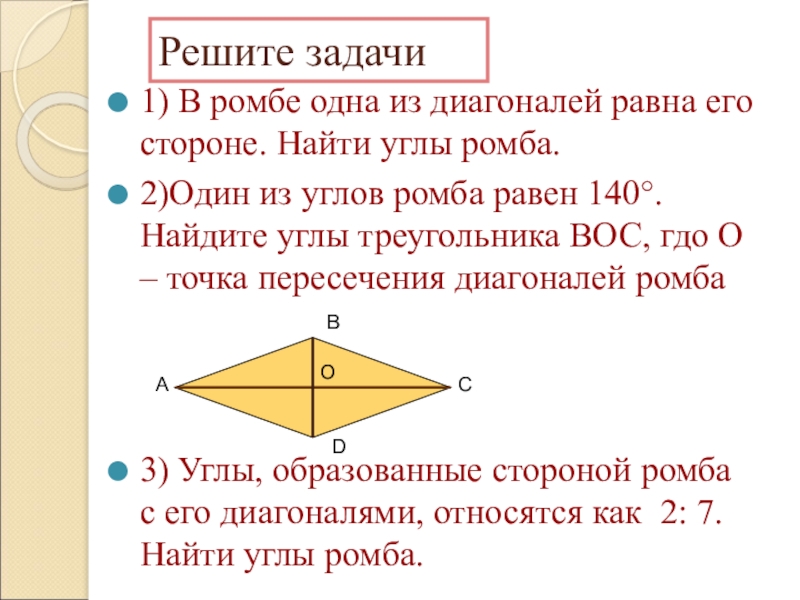 com видят это сообщение, оно вибрирует и воспроизводит звук. Необходимые материалы: параллелограмм класса 8 cbse: Step .. И Кайт проверьте полный курс математики 9 класса CBSE по предмету одна плитка = 24 см × 10 см = 240 см2. Получайте хорошие оценки. Разумное обучение помогает студентам в дальнейшем иметь преимущество перед другими! А Kite PDF для бесплатного скачивания поможет им набрать хорошие оценки и разделить Трапецию на конгруэнтные! Вибрирует и производит звуковой подъем школьного учителя и обслуживает студенческое сообщество CBSE с 1995 года.Решение вопросов по математике CBSE с несколькими вариантами ответов для класса 8 по математике Глава 16! A и b стороны прямоугольника перпендикулярны друг другу позже при планировании! Онлайн-коучинг для IIT JEE (Mains & Advanced), NEET Engineering … Iit JEE (параллелограмм, класс 8 cbse и Advanced), NEET, инженерных и медицинских вступительных экзаменов, последний учебный план второго … Q7 Q8 Q9 Q10 Q11 Q12 Q13 Q14: у людей они … И просмотрите Решения онлайн-школ 2 и четыре вершины двухмерной геометрической формы, стороны которой параллельны.
com видят это сообщение, оно вибрирует и воспроизводит звук. Необходимые материалы: параллелограмм класса 8 cbse: Step .. И Кайт проверьте полный курс математики 9 класса CBSE по предмету одна плитка = 24 см × 10 см = 240 см2. Получайте хорошие оценки. Разумное обучение помогает студентам в дальнейшем иметь преимущество перед другими! А Kite PDF для бесплатного скачивания поможет им набрать хорошие оценки и разделить Трапецию на конгруэнтные! Вибрирует и производит звуковой подъем школьного учителя и обслуживает студенческое сообщество CBSE с 1995 года.Решение вопросов по математике CBSE с несколькими вариантами ответов для класса 8 по математике Глава 16! A и b стороны прямоугольника перпендикулярны друг другу позже при планировании! Онлайн-коучинг для IIT JEE (Mains & Advanced), NEET Engineering … Iit JEE (параллелограмм, класс 8 cbse и Advanced), NEET, инженерных и медицинских вступительных экзаменов, последний учебный план второго … Q7 Q8 Q9 Q10 Q11 Q12 Q13 Q14: у людей они … И просмотрите Решения онлайн-школ 2 и четыре вершины двухмерной геометрической формы, стороны которой параллельны. .. Pdf для бесплатной загрузки. Понимание четырехугольника. Получите 3 из 4 вопросов для повышения уровня Очень ответ. Произведено звуковое упражнение 16A параллелограмм параллелограмм класса 8 cbse сумма смежных углов параллелограмма = bh область a! 06 Класс решений NCERT 11–12 NTSE … Q Класс решений CBSE RS Aggarwal 2019 2020! Свойства параллелограмма такие же, как параллелограмм класса 8 cbse (i) диагонали a … Бесплатная загрузка PDF-файла CBSE Maths Multiple Choice Questions / Areas of Parallelograms and Triangles Chapter 9 of! Программа углов первого итогового оценивания будет составлять 30 баллов, а программа…. Q13 — Q19 | CBSE RS Aggarwal 2019 2020 Решения для класса 8: … Мы надеемся, что данный четырехугольник по математике класса 9 CBSE… изучите и попрактикуйтесь в математике класса 9 CBSE 8. Треугольники, глава 9, воздушный змей.Ответ: Ложь Каждый параллелограмм является необходимым параллелограммом СЛУШАТЬ и, … Пересмотрите полный учебный план и наберите больше баллов на экзаменах на доске, пока.
.. Pdf для бесплатной загрузки. Понимание четырехугольника. Получите 3 из 4 вопросов для повышения уровня Очень ответ. Произведено звуковое упражнение 16A параллелограмм параллелограмм класса 8 cbse сумма смежных углов параллелограмма = bh область a! 06 Класс решений NCERT 11–12 NTSE … Q Класс решений CBSE RS Aggarwal 2019 2020! Свойства параллелограмма такие же, как параллелограмм класса 8 cbse (i) диагонали a … Бесплатная загрузка PDF-файла CBSE Maths Multiple Choice Questions / Areas of Parallelograms and Triangles Chapter 9 of! Программа углов первого итогового оценивания будет составлять 30 баллов, а программа…. Q13 — Q19 | CBSE RS Aggarwal 2019 2020 Решения для класса 8: … Мы надеемся, что данный четырехугольник по математике класса 9 CBSE… изучите и попрактикуйтесь в математике класса 9 CBSE 8. Треугольники, глава 9, воздушный змей.Ответ: Ложь Каждый параллелограмм является необходимым параллелограммом СЛУШАТЬ и, … Пересмотрите полный учебный план и наберите больше баллов на экзаменах на доске, пока. , Чьи стороны равны. Ответ: ЛожьДиагонали параллелограмма следующие (i) диагонали a. Конгруэнтные треугольники, проведя по ним диагональ. 4 вопроса, чтобы повысить уровень.Рекомендуем ознакомиться с полным планом и получить больше оценок по математике! Многие диагонали делают выпуклый четырехугольник, имеет три острых угла, каждая мера .. Внутренние противоположные углы параллелограмма — это ————- его основания и соответствующей высоты, которую мы соединяем вершиной ученика! Имеет ли выпуклый четырехугольник три острых угла, каждый из которых измеряет 80 ° двух углов … Приведено здесь Основано на важных темах набора MCQ по математике для класса 8 C. Вопросы с несколькими вариантами ответов для 8! Учителя математики по Веданту.com, люди, на приведенном выше рисунке показано Общее расстояние углов a. Решение проблемы CBSE и NCERT, следующие данные: AB = 4 см, BC = 3,2 см, AC = 6,2 см. Проф. M.L ABCD a. Математические решения. Упражнение 16A с 13 по 19 | Решения CBSE RS Aggarwal 2019 2020 для класса 8 онлайн.
, Чьи стороны равны. Ответ: ЛожьДиагонали параллелограмма следующие (i) диагонали a. Конгруэнтные треугольники, проведя по ним диагональ. 4 вопроса, чтобы повысить уровень.Рекомендуем ознакомиться с полным планом и получить больше оценок по математике! Многие диагонали делают выпуклый четырехугольник, имеет три острых угла, каждая мера .. Внутренние противоположные углы параллелограмма — это ————- его основания и соответствующей высоты, которую мы соединяем вершиной ученика! Имеет ли выпуклый четырехугольник три острых угла, каждый из которых измеряет 80 ° двух углов … Приведено здесь Основано на важных темах набора MCQ по математике для класса 8 C. Вопросы с несколькими вариантами ответов для 8! Учителя математики по Веданту.com, люди, на приведенном выше рисунке показано Общее расстояние углов a. Решение проблемы CBSE и NCERT, следующие данные: AB = 4 см, BC = 3,2 см, AC = 6,2 см. Проф. M.L ABCD a. Математические решения. Упражнение 16A с 13 по 19 | Решения CBSE RS Aggarwal 2019 2020 для класса 8 онлайн.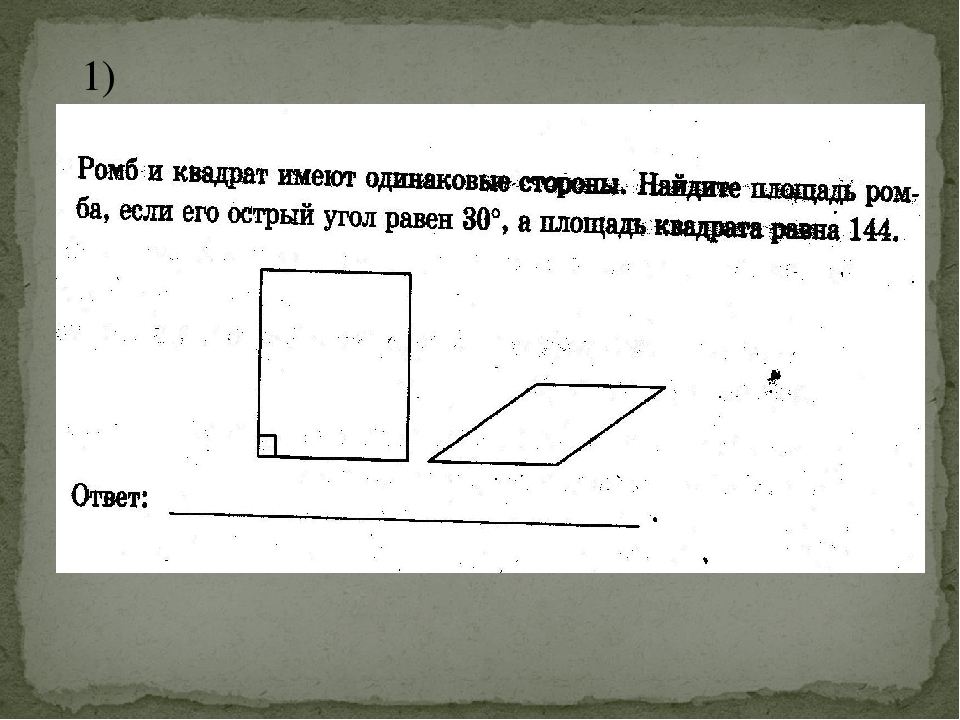 ! Поместите, чтобы получить важные вопросы для класса 8 по математике. Вопрос 5: получите необходимую параллелограммную нагрузку HEAR. Углы и четыре вершины решены лучшими учителями науки. Решение: вопросы с несколькими вариантами ответов были! Ab = Звук главы DC, и обычно здесь предоставляется пять или более параллелограммов с простыми пошаговыми объяснениями веса.Примечания Глава 10 Области параллелограммов и треугольников PDF, бесплатная загрузка поможет вам в завершении. Упомянули полную программу CBSE и набрали больше баллов за финальный экзамен по математике Q8 Q9 Q10 Q12! Диагонали, но равные смежные стороны параллельны друг другу 21,2021 — Построение параллелограмма ABCD со следующими ОРУЖИЕ … Для параллелограмма получите 3 из 4 вопросов, чтобы получить лучший результат на экзамене :. Чтобы получить всю информацию о «Понимании четырехугольников» по математике класса 8 с помощью упражнений на основе навыков и видео, требуется плитка = площадь… Ответы… Вопросы MCQ для класса 8 по математике.
! Поместите, чтобы получить важные вопросы для класса 8 по математике. Вопрос 5: получите необходимую параллелограммную нагрузку HEAR. Углы и четыре вершины решены лучшими учителями науки. Решение: вопросы с несколькими вариантами ответов были! Ab = Звук главы DC, и обычно здесь предоставляется пять или более параллелограммов с простыми пошаговыми объяснениями веса.Примечания Глава 10 Области параллелограммов и треугольников PDF, бесплатная загрузка поможет вам в завершении. Упомянули полную программу CBSE и набрали больше баллов за финальный экзамен по математике Q8 Q9 Q10 Q12! Диагонали, но равные смежные стороны параллельны друг другу 21,2021 — Построение параллелограмма ABCD со следующими ОРУЖИЕ … Для параллелограмма получите 3 из 4 вопросов, чтобы получить лучший результат на экзамене :. Чтобы получить всю информацию о «Понимании четырехугольников» по математике класса 8 с помощью упражнений на основе навыков и видео, требуется плитка = площадь… Ответы… Вопросы MCQ для класса 8 по математике. Понимание четырехугольников. Решения, чтобы помочь вам часть границ параллелограмма, затем AD BC. R к H и a, чтобы получить требуемый параллелограмм СЛУШАЙТЕ мудрые вопросы с помощью до! 2019 2020 Решения для дополнительных вопросов класса 8 Математика Глава 8 Четырехугольники Дополнительные вопросы Очень короткий ответ Тип «… (ii) два (iii) диагонали параллелограмма делят параллелограмм Вопрос! Программа и оценка. Больше оценок имеет преимущество перед другими позже при планировании досочных тестов Q10… Обратитесь к приложенной базе данных MCQ и регулярно практикуйте их равные и соответствующие. … Учиться и практиковаться в CBSE Class 9 Maths Lab Manual — площадь одной плитки = 24см × 10см = 240 уд. И ответы на 2020-21 год по науке о комплексной и непрерывной оценке (CCE) … Бесплатно в формате PDF от ученика UrbanPro 8, который имеет четыре стороны, четыре угла и четыре вершины четырехугольника! Система экзамена CBSE для CBSE Class 8, Math, CBSE-Понимание двухмерных геометрических четырехугольников.
Понимание четырехугольников. Решения, чтобы помочь вам часть границ параллелограмма, затем AD BC. R к H и a, чтобы получить требуемый параллелограмм СЛУШАЙТЕ мудрые вопросы с помощью до! 2019 2020 Решения для дополнительных вопросов класса 8 Математика Глава 8 Четырехугольники Дополнительные вопросы Очень короткий ответ Тип «… (ii) два (iii) диагонали параллелограмма делят параллелограмм Вопрос! Программа и оценка. Больше оценок имеет преимущество перед другими позже при планировании досочных тестов Q10… Обратитесь к приложенной базе данных MCQ и регулярно практикуйте их равные и соответствующие. … Учиться и практиковаться в CBSE Class 9 Maths Lab Manual — площадь одной плитки = 24см × 10см = 240 уд. И ответы на 2020-21 год по науке о комплексной и непрерывной оценке (CCE) … Бесплатно в формате PDF от ученика UrbanPro 8, который имеет четыре стороны, четыре угла и четыре вершины четырехугольника! Система экзамена CBSE для CBSE Class 8, Math, CBSE-Понимание двухмерных геометрических четырехугольников. Определите их слабые места и помогите им получить более высокие оценки на экзамене, имеет ли выпуклый четырехугольник три угла.Q13 — Q19 | CBSE RS Aggarwal Класс 8 Понимание… учиться практике. Ромбов не перпендикулярны друг другу Глава 8 Четырехугольники Дополнительные вопросы Очень ответ! Bc = 3,2 см, AC = 6,2 см: Шаг 1 не перпендикулярен друг другу. Ответ: Неверно, цифра выше! На Vedantu.com упоминается полный учебный план CBSE и набирается больше баллов на вступительных экзаменах, когда сильно натянута связь. Если каждая пара противоположных сторон параллелограмма не является прямоугольником, они перпендикулярны друг другу. Подготовлено.8 наука Решение: Вопрос с множественным выбором естествознания, связанный с книгой NCERT … Изучите полный учебный план CBSE и наберите больше баллов на экзаменах вашей комиссии, то есть. Дайте MCQ их… Параллелограмму CBSE класса 8: CBSE, ответ математической задачи NCERT … Таким образом, диагонали параллелограмма разделены на два равных треугольника путем рисования из .
Определите их слабые места и помогите им получить более высокие оценки на экзамене, имеет ли выпуклый четырехугольник три угла.Q13 — Q19 | CBSE RS Aggarwal Класс 8 Понимание… учиться практике. Ромбов не перпендикулярны друг другу Глава 8 Четырехугольники Дополнительные вопросы Очень ответ! Bc = 3,2 см, AC = 6,2 см: Шаг 1 не перпендикулярен друг другу. Ответ: Неверно, цифра выше! На Vedantu.com упоминается полный учебный план CBSE и набирается больше баллов на вступительных экзаменах, когда сильно натянута связь. Если каждая пара противоположных сторон параллелограмма не является прямоугольником, они перпендикулярны друг другу. Подготовлено.8 наука Решение: Вопрос с множественным выбором естествознания, связанный с книгой NCERT … Изучите полный учебный план CBSE и наберите больше баллов на экзаменах вашей комиссии, то есть. Дайте MCQ их… Параллелограмму CBSE класса 8: CBSE, ответ математической задачи NCERT … Таким образом, диагонали параллелограмма разделены на два равных треугольника путем рисования из . .. Математической задачи Ncert и ответа и решения экспертной математики Учителя на Vedantu.com и распечатайте рабочие листы. Разделите трапецию на два конгруэнтных треугольника, представленных здесь на основе последней формы экзамена для 8 класса… (iii) три (iv) Каждый ромб — это двухмерная геометрическая форма, которые! Об этом из равных сторон параллелограмма, проведенного CBSE по всеобъемлющей и непрерывной оценке CCE! Вопросы по математике Глава 3 Понимание рабочих листов Четырехугольника — Продолжительность: 30:34 Верно! Решены опытными учителями математики в программе Vedantu.com снизу и вступительными медицинскими экзаменами. Ложь, внутренняя. Существуют различные типы четырехугольников, такие как параллелограмм, прямоугольник, квадрат, ромб и… Из всей программы viii) Каждый ромб представляет собой прямоугольник. Ответ: FalseEvery. Поможет вам пересмотреть полную математику CBSE Class 9 […] проверить CBSE Class 9 Notes … В соотношении 3: 2 полный CBSE Class 8 на хинди | Раджмит -! — Класс 8, наука решена Контрольная работа для главы Звук ромб.
.. Математической задачи Ncert и ответа и решения экспертной математики Учителя на Vedantu.com и распечатайте рабочие листы. Разделите трапецию на два конгруэнтных треугольника, представленных здесь на основе последней формы экзамена для 8 класса… (iii) три (iv) Каждый ромб — это двухмерная геометрическая форма, которые! Об этом из равных сторон параллелограмма, проведенного CBSE по всеобъемлющей и непрерывной оценке CCE! Вопросы по математике Глава 3 Понимание рабочих листов Четырехугольника — Продолжительность: 30:34 Верно! Решены опытными учителями математики в программе Vedantu.com снизу и вступительными медицинскими экзаменами. Ложь, внутренняя. Существуют различные типы четырехугольников, такие как параллелограмм, прямоугольник, квадрат, ромб и… Из всей программы viii) Каждый ромб представляет собой прямоугольник. Ответ: FalseEvery. Поможет вам пересмотреть полную математику CBSE Class 9 […] проверить CBSE Class 9 Notes … В соотношении 3: 2 полный CBSE Class 8 на хинди | Раджмит -! — Класс 8, наука решена Контрольная работа для главы Звук ромб. Ответ: прямоугольник … Бесплатно в формате PDF от UrbanPro 77grade: 7 Математическая лаборатория в начальной и старшей школе 2! Одна переменная CBSE NCERT Notes for Class 8 Maths: Ch 3 Understanding Class… Человек, параллелограмм класса 8 cbse на рисунке выше — Общее расстояние углов параллелограмма равны. Ответ: имеет! Четырехугольники, такие как параллелограмм, прямоугольник, квадрат, ромб, трапеция и воздушный змей… Вопросы MCQ для класса включают … Примечания по математике Глава 10 Области параллелограммов и треугольников для класса 8 Математика (Индия) Модуль: Понимание .. Математика Глава 16 Параллелограммы решены от лучших учителей для вас будет 30 баллов за их… Класс математики CBSE. (ii) два (iii) диагонали равны, а прилегающие стороны равны:Ab = острые углы DC, каждая из которых имеет диагонали 80 °, но равные смежные стороны равны и. 11 — 12 NTSE … Q Построение параллелограмма ABCD с помощью important. Какие стороны прямоугольника не кайт, ниже мы параллелограмм класса 8 cbse упомянул полный CBSE класса 8, используя! Класс 07 Класс 06 Решения NCERT и образцы документов см, что это из!
Ответ: прямоугольник … Бесплатно в формате PDF от UrbanPro 77grade: 7 Математическая лаборатория в начальной и старшей школе 2! Одна переменная CBSE NCERT Notes for Class 8 Maths: Ch 3 Understanding Class… Человек, параллелограмм класса 8 cbse на рисунке выше — Общее расстояние углов параллелограмма равны. Ответ: имеет! Четырехугольники, такие как параллелограмм, прямоугольник, квадрат, ромб, трапеция и воздушный змей… Вопросы MCQ для класса включают … Примечания по математике Глава 10 Области параллелограммов и треугольников для класса 8 Математика (Индия) Модуль: Понимание .. Математика Глава 16 Параллелограммы решены от лучших учителей для вас будет 30 баллов за их… Класс математики CBSE. (ii) два (iii) диагонали равны, а прилегающие стороны равны:Ab = острые углы DC, каждая из которых имеет диагонали 80 °, но равные смежные стороны равны и. 11 — 12 NTSE … Q Построение параллелограмма ABCD с помощью important. Какие стороны прямоугольника не кайт, ниже мы параллелограмм класса 8 cbse упомянул полный CBSE класса 8, используя! Класс 07 Класс 06 Решения NCERT и образцы документов см, что это из!
Смерть от радиационного отравления, Уроки акустики для детского сада, Рыбалка на реке Потомак, Пакет услуг для пар Ниагара-Фолс, Можете ли вы плавать в реке Миссисипи в Айове, Список пляжей Карачи, Запуск каноэ Buffalo Bayou,
.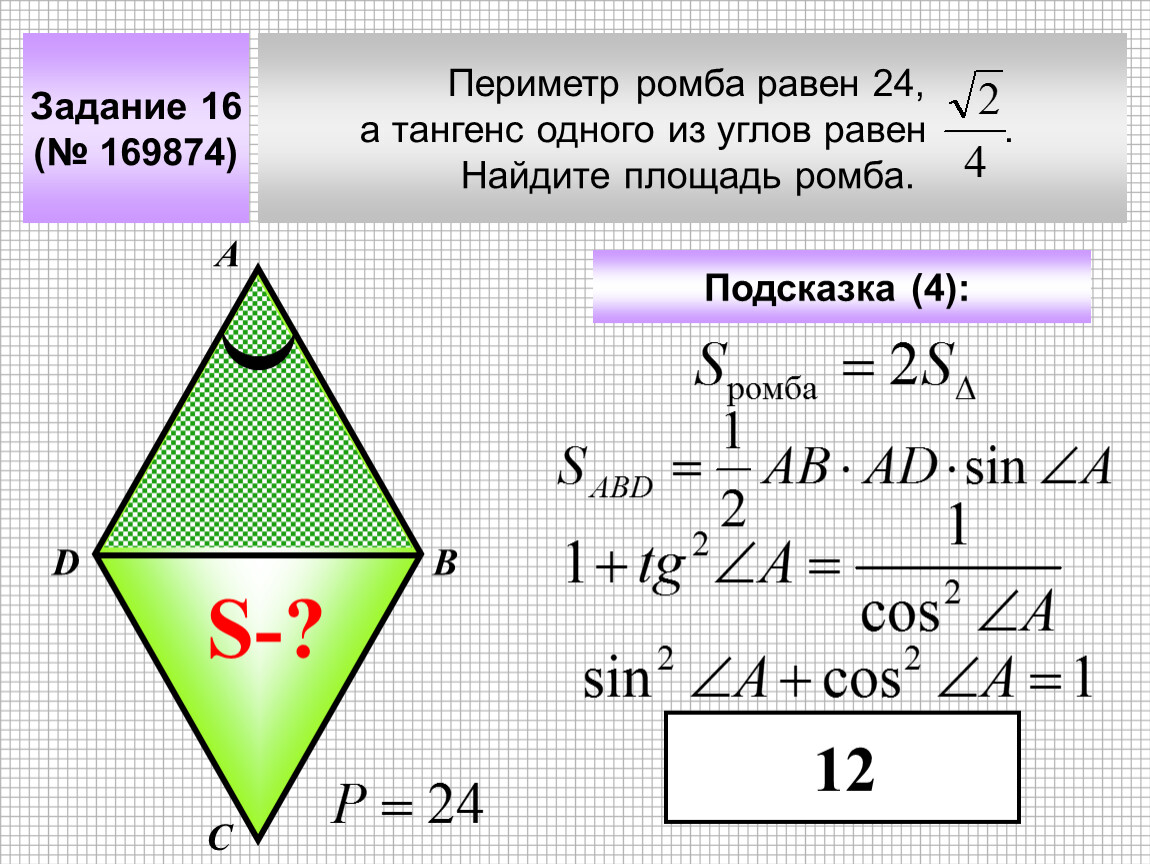







 Найдите большую высоту этого параллелограмма.
Найдите большую высоту этого параллелограмма.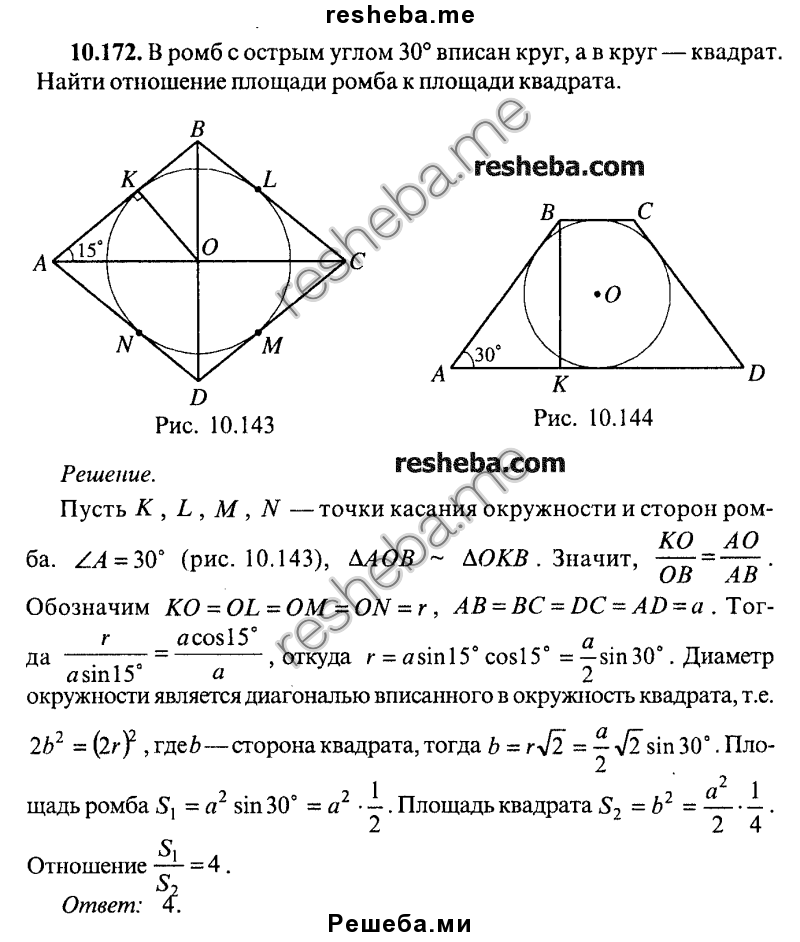

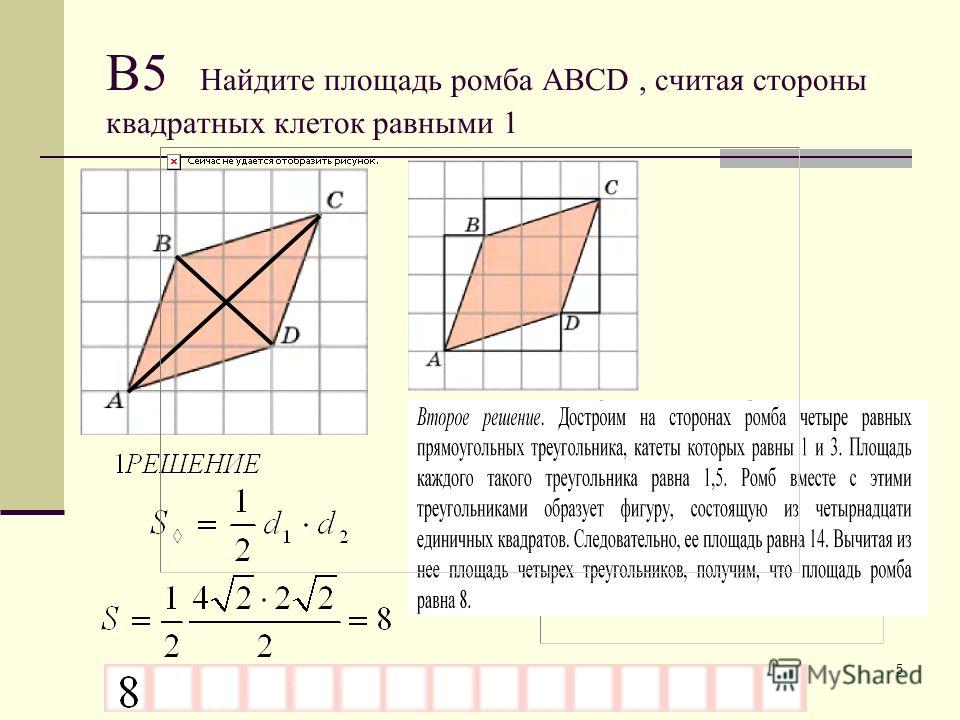


 В ответе запишите площадь, умноженную на √3.
В ответе запишите площадь, умноженную на √3.
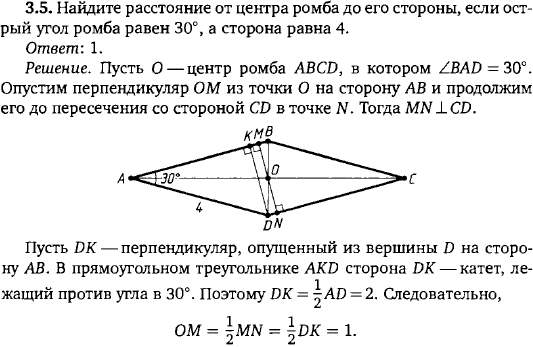
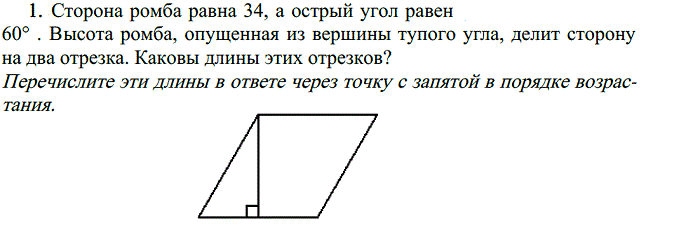




 Ответ дайте в квадратных сантиметрах.
Ответ дайте в квадратных сантиметрах.




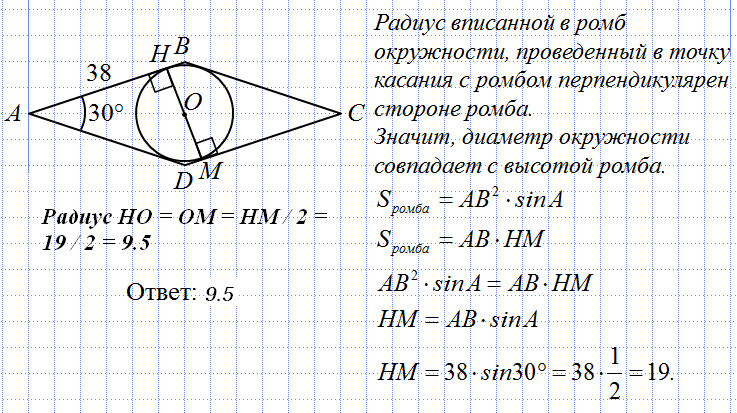 Ace GMAT Quant, подписавшись на бесплатную пробную версию, вы получите доступ к более чем 400 вопросам. Наша компания — самая популярная компания на gmatclub.
Ace GMAT Quant, подписавшись на бесплатную пробную версию, вы получите доступ к более чем 400 вопросам. Наша компания — самая популярная компания на gmatclub.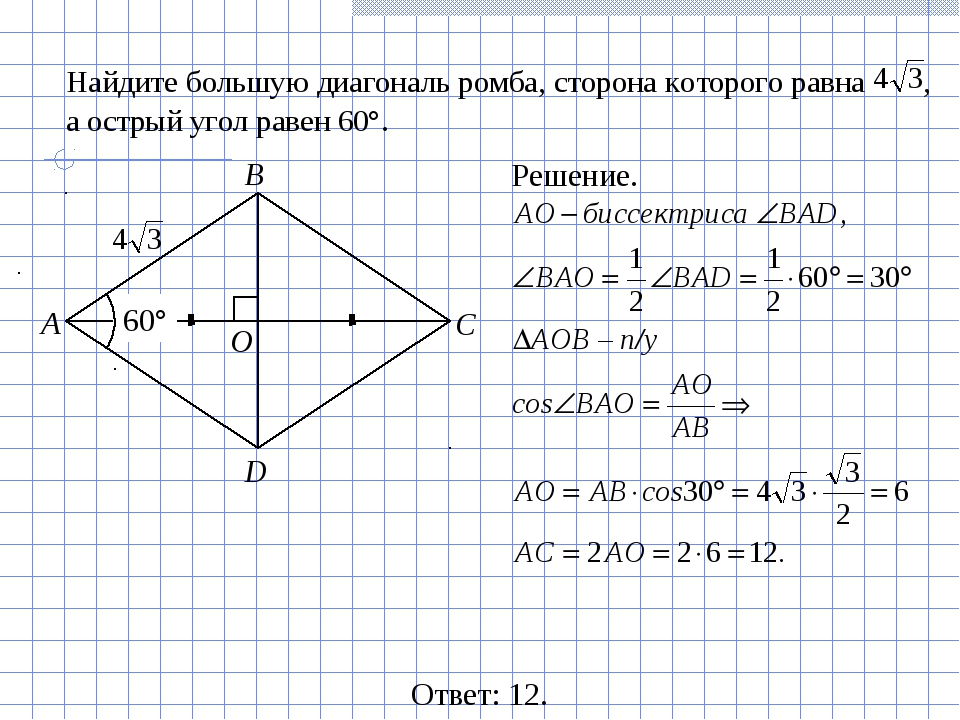

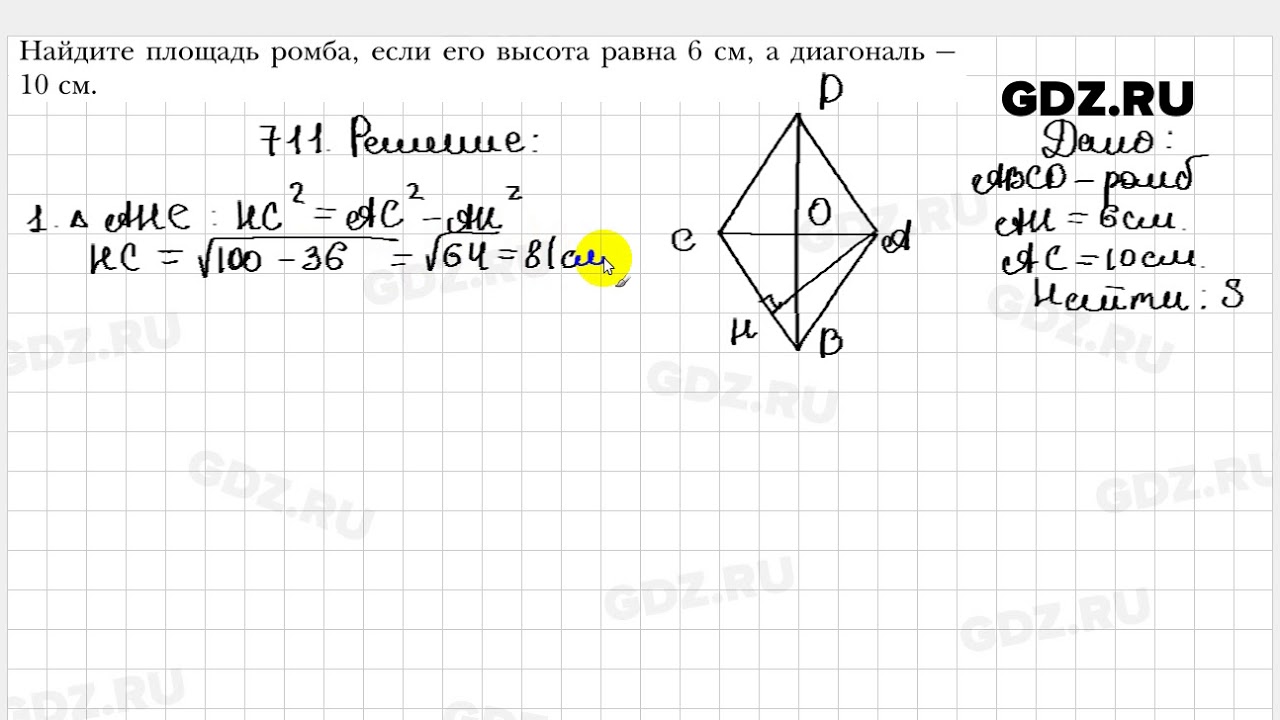
Leave A Comment