Геометрия в ГИА
Квадрат
Сторона квадрата равна 10. Найдите его площадь.
Периметр квадрата равен 40. Найдите площадь квадрата.
Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
Периметр квадрата равен 160. Найдите площадь квадрата.
Найдите площадь квадрата, если его диагональ равна 1.
Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
В прямоугольнике одна сторона равна 10, другая сторона равна 12. Найдите площадь прямоугольника.
Прямоугольник
Найдите площадь прямоугольника, если его периметр равен 44 и одна сторона на 2 больше другой
Найдите площадь прямоугольника, если его периметр равен 60, а отношение соседних сторон равно 4:11.

Найдите площадь прямоугольника, если его периметр равен 58 и одна сторона на 5 больше другой.
В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
Прямоугольный треугольник
В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен 45°. Найдите площадь треугольника.
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.
В прямоугольном треугольнике один из катетов равен 4, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
Равнобедренный треугольник
Периметр равнобедренного треугольника равен 16, а боковая сторона — 5. Найдите площадь треугольника.

В равнобедренном треугольнике . Найдите , если высота .
Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
Периметр равнобедренного треугольника равен 216, а боковая сторона — 78. Найдите площадь треугольника.
Трапеция
Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке
Найдите площадь трапеции, изображённой на рисунке.
Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°.

Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
Основания равнобедренной трапеции равны 5 и 17, а ее боковые стороны равны 10. Найдите площадь трапеции.
В трапеции ABCD AD = 3, BC = 1, а её площадь равна 12. Найдите площадь треугольника ABC.
Треугольники общего вида
В треугольнике одна из сторон равна 10, а опущенная на нее высота — 5. Найдите площадь треугольника.
Найдите площадь треугольника, изображённого на рисунке.
Параллелограмм
Найдите площадь параллелограмма, изображённого на рисунке.
Сторона ромба равна 5, а диагональ равна 6. Найдите площадь ромба.

Одна из сторон параллелограмма равна 12, а опущенная на нее высота равна 10. Найдите площадь параллелограмма.
Площадь параллелограмма ABCD равна 56. Точка E — середина стороны CD. Найдите площадь трапеции AECB.
Найдите площадь ромба, если его диагонали равны 14 и 6.
Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
Сторона ромба равна 50, а диагональ равна 80. Найдите площадь ромба.
Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 1 и HD = 28. Диагональ параллелограмма BD равна 53. Найдите площадь параллелограмма.
Высота BH ромба ABCD делит его сторону AD на отрезки AH = 5 иHD = 8. Найдите площадь ромба.

Теорема Пифагора
От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.
От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м.
Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
Мальчик прошел от дома по направлению на восток 800 м. Затем повернул на север и прошел 600 м. На каком расстоянии (в метрах) от дома оказался мальчик?
Девочка прошла от дома по направлению на запад 500 м. Затем повернула на север и прошла 300 м.

Мальчик и девочка, расставшись на перекрестке, пошли по взаимно перпендикулярным дорогам, мальчик со скоростью 4 км/ч, девочка — 3 км/ч. Какое расстояние (в километрах) будет между ними через 30 минут?
Глубина крепостного рва равна 8 м, ширина 5 м, а высота крепостной стены от ее основания 20 м. Длина лестницы, по которой можно взобраться на стену, на 2 м больше, чем расстояние от края рва до верхней точки стены (см. рис.). Найдите длину лестницы.
Девочка прошла от дома по направлению на запад 20 м. Затем повернула на север и прошла 800 м. После этого она повернула на восток и прошла ещё 200 м. На каком расстоянии (в метрах) от дома оказалась девочка?
Лестница соединяет точки A и B и состоит из 35 ступеней.
 Высота каждой ступени
равна 14 см, а длина — 48 см. Найдите
расстояние между точками A и B (в
метрах).
Высота каждой ступени
равна 14 см, а длина — 48 см. Найдите
расстояние между точками A и B (в
метрах).От столба к дому натянут провод длиной 17 м, который закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 15 м.
Девочка прошла от дома по направлению на запад 880 м. Затем повернула на север и прошла 900 м. После этого она повернула на восток и прошла ещё 400 м. На каком расстоянии (в метрах) от дома оказалась девочка?
Длина стремянки в сложенном виде равна 1,85 м, а её высота в разложенном виде составляет 1,48 м. Найдите расстояние (в метрах) между основаниями стремянки в разложенном виде.
Длина стремянки в сложенном виде равна 1,11 м, а расстояние между её основаниями в разложенном виде составляет 0,72 м.

Лестница соединяет точки A и B и состоит из 20 ступеней. Высота каждой ступени равна 16,5 см, а длина — 28 см. Найдите расстояние между точками A и B(в метрах).
Лестница соединяет точки A и B . Высота каждой ступени равна 14 см, а длина — 48 см. Расстояние между точками A и B составляет 10 м. Найдите высоту, на которую поднимается лестница (в метрах).
. Пожарную лестницу длиной 13 м приставили к окну пятого этажа дома. Нижний конец лестницы отстоит от стены на 5 м. На какой высоте расположено окно? Ответ дайте в метрах
.Пожарную лестницу приставили к окну, расположенному на высоте 12 м от земли. Нижний конец лестницы отстоит от стены на 5 м. Какова длина лестницы? Ответ дайте в метрах
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 5,5 м от земли.
 Расстояние
от основания флагштока
до места крепления троса на земле
равно 4,8 м. Найдите длину троса.
Ответ дайте в метрах.
Расстояние
от основания флагштока
до места крепления троса на земле
равно 4,8 м. Найдите длину троса.
Ответ дайте в метрах.Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 6,3 м от земли. Длина троса равна 6,5 м. Найдите расстояние от точки основания флагштока до места крепления троса на земле. Ответ дайте в метрах.
Расстояние от основания флагштока до места крепления троса на земле равно 1,6 м. Длина троса равна 3,4 м. Найдите расстояние от земли до точки крепления троса, удерживающего флагшток в вертикальном положении. Ответ дайте в метрах.
Зачет №2 Площади 8 класс | Материал для подготовки к ЕГЭ (ГИА, 8 класс):
Опубликовано 28.08.2019 — 12:10 — Цветкова Ольга Валентиновна
Тренировочные задания по геометрии для подготовки обучающихся к ОГЭ
Скачать:
Предварительный просмотр:
Вариант 1
- Периметр квадрата равен 40.
 Найдите площадь квадрата
Найдите площадь квадрата - Найдите площадь прямоугольника, если его периметр равен 60, а отношение соседних сторон равно 4:11.
- Найдите площадь треугольника, изображённого на рисунке
- Найдите площадь параллелограмма, изображённого на рисунке.
- Найдите площадь ромба, если его диагонали равны 14 и 6.
- Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
- Найти площадь прямоугольного треугольника, если его катеты равны 6 и 11.
- Площадь прямоугольного треугольника равна 28. Один из его катетов равен 14. Найти другой катет.
- Найдите площадь трапеции, изображённой на рисунке.
- Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен 30° . Найдите площадь трапеции, если её основания равны 2 и 7.
- На клетчатой бумаге с размером клетки 1см × 1см изображена трапеция.
 Найдите её площадь. Ответ дайте в квадратных сантиметрах.
Найдите её площадь. Ответ дайте в квадратных сантиметрах. - На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
- На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.
- На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите его площадь
- Стороны параллелограмма равны 12 и 4. Высота, опущенная на первую сторону равна 5. Найти высоту, опущенную на вторую сторону.
Вариант 2
- Периметр квадрата равен 24. Найдите площадь квадрата.
- Найдите площадь прямоугольника, если его периметр равен 102, а отношение соседних сторон равно 2:15.
- Найдите площадь треугольника, изображённого на рисунке
- Найдите площадь параллелограмма, изображённого на рисунке.

- Найдите площадь ромба, если его диагонали равны 27 и 4.
- Сторона ромба равна 10, а расстояние от центра ромба до неё равно 3. Найдите площадь ромба.
- Найти площадь прямоугольного треугольника, если его катеты равны 5 и 10.
- Площадь прямоугольного треугольника равна 38. Один из его катетов равен 19. Найти другой катет.
- Найдите площадь трапеции, изображённой на рисунке.
- Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
- На клетчатой бумаге с размером клетки 1см × 1см изображена трапеция. Найдите её площадь. Ответ дайте в квадратных сантиметрах
- На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
- На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.
- На клетчатой бумаге с размером клетки 1×1 изображён ромб.
 Найдите его площадь
Найдите его площадь - Стороны параллелограмма равны 10 и 6. Высота, опущенная на первую сторону равна 3. Найти высоту, опущенную на вторую сторону.
По теме: методические разработки, презентации и конспекты
Урок зачет в 5 классе по немецкому языку
Урок зачет в 5 классе по немецкому языку 1 полугодие…
Сборник текстов и упражнений для подготовки к устному зачету в 7 классе
Этот сборник тем может помочь вам в подготовке к экзамену по английскому языку.В нем собраны устные темы, предусмотренные школьной программой для изучения английского языка учащимися 7-х классов.Кажда…
Интерактивный урок-зачет в 5 классе » Морфемика»
урок групповой работы по проверке знаний по теме….
Вопросы для зачета №1 6 класс
Зачет №1 6 класс (1 полугодие)…
Вопросы для зачета №1 6 класс
Зачет №1 6 класс (1 полугодие)…
Вопросы для зачета №2 6 класс
Зачет №2 6 класс (2 полугодие)…
Зачет №8 Площади 9 класс
Тренировочные задания по геометрии для подготовки обучающихся к ОГЭ. ..
..
Поделиться:
Математическая задача: Периметр 3
Периметр прямоугольника равен 35 см. Отношение длины к ширине 3:2. Вычислите размеры прямоугольника.
Правильный ответ:
l = 10,5 смw = 7 см
Пошаговое объяснение:
p=35 см n=3+2+3+2=10 d=p/n= 35/10=27=3,5 см l=3⋅d=3⋅ 3,5=10,5 см
w=2⋅d=2⋅ 3,5=7=7 см Проверочное решение: o=2⋅ (w+l)= 2⋅ (7+10,5)=35 см
Нашли ошибку или неточность? Не стесняйтесь
напишите нам. Спасибо!
Советы по использованию связанных онлайн-калькуляторов
Воспользуйтесь нашим калькулятором коэффициентов.
Вы хотите преобразовать единицы длины?
Для решения данной словесной задачи по математике необходимо знать следующие знания:
- алгебра
- выражение переменной из формулы
- планиметрика 900 35
- периметр
- прямоугольник
- основные функции
- соотношение
- прямая связь
Единицы физических величин:
- длина
Степень словесной задачи:
- практика на 1 1-летние
- практика для 12-летних
Мы Предлагаем вам посмотреть это обучающее видео по этой математической задаче: video1
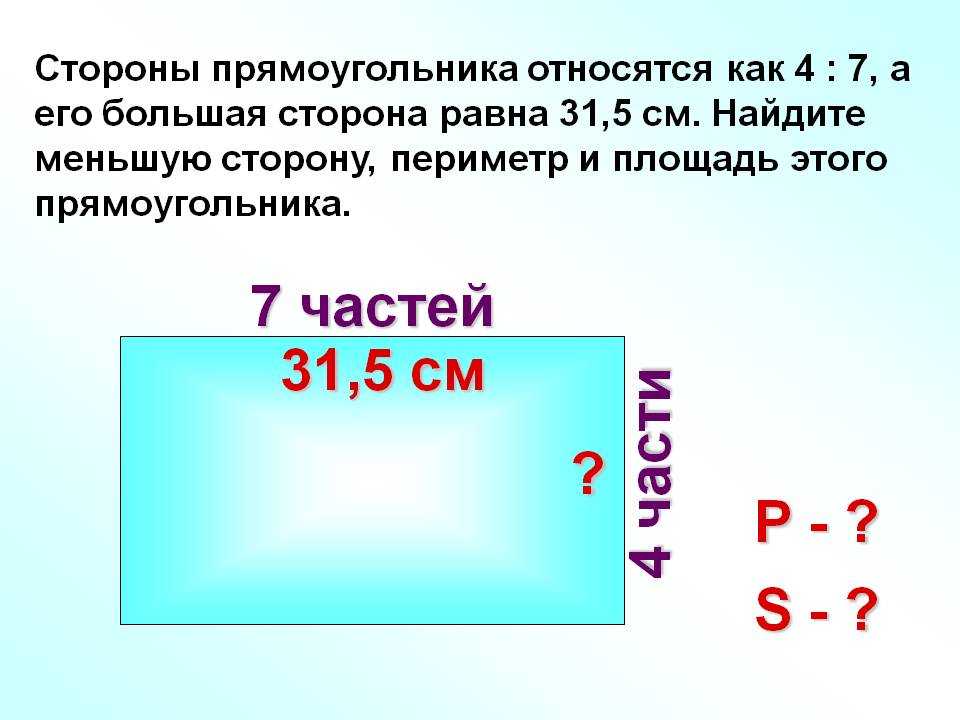
- Прямоугольник 81776
Длина прямоугольника на 5 см больше, чем его ширина. Определите размеры прямоугольника, если известно, что его периметр равен 22 см.
Определите размеры прямоугольника, если известно, что его периметр равен 22 см. - Окружность 47903
Длина прямоугольника на 35% больше его ширины, а длина окружности равна 188 см. Вычислите его площадь. - Стол
Окружность прямоугольного стола 420 см. Соотношение длины к ширине 5:2. Вычислить размеры таблицы и размеры уменьшить в соотношении 3:5 - Прямоугольник 81596
Периметр прямоугольника 30 см. Отношение его сторон a:b=2:3. Вычислите длины сторон и площадь прямоугольника. - Прямоугольник
Периметр прямоугольника равен 48 см. Вычислите его размеры, если они находятся в соотношении 5:3 (ширина: высота) - Прямоугольник
Длина прямоугольника в три раза больше его ширины. Предположим, что периметр прямоугольника равен 60 футам. Какова длина прямоугольника? - Длина окружности 70984
Длина прямоугольника составляет 12 см. Вычислите его длину окружности, если отношение длины к ширине равно 4:3 - Прямоугольник
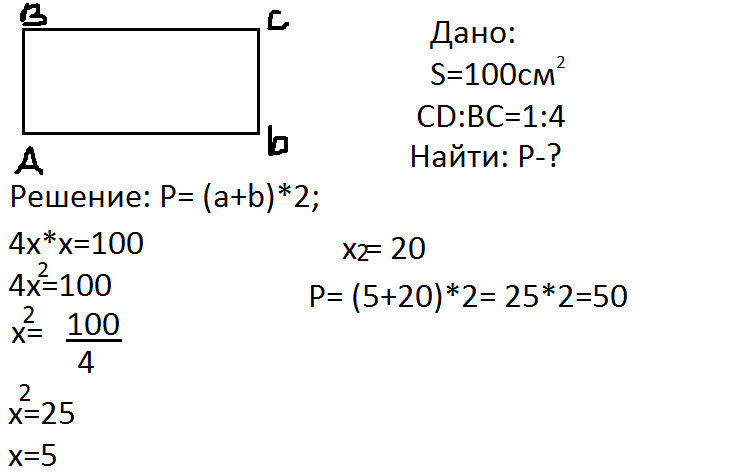
Ширина прямоугольника составляет 65% его длины. Периметр прямоугольника равен 132 см. Определить размеры прямоугольника.
Периметр прямоугольника равен 132 см. Определить размеры прямоугольника. - Сантиметры 4162
Вычислите для меня длину диагонали прямоугольника, размер которого на 7 см больше его ширины, а периметр равен 34 сантиметрам. Размеры прямоугольника выражаются в натуральных числах. - Прямоугольник — desc окружность
Длина сторон прямоугольника находится в соотношении 1:3. Радиус окружности, описанной вокруг прямоугольника, равен 10 см. Вычислите периметр прямоугольника. - Размеры прямоугольника
Найдите размеры прямоугольника, если его периметр равен 110 см. Его длина составляет 1 см, что более чем в два раза превышает его ширину. - Размеры 4118
Ширина прямоугольника на 17 см меньше его длины. Периметр прямоугольника равен 0,9 м. Найдите остальные размеры и вычислите их площадь. - Два прямоугольника 2
Из квадрата площадью 36 см² вырезаны два прямоугольника – А и В. Отношение площадей А к В составляет 2:1. Найдите размеры прямоугольников A и B.
- Длина
Длина прямоугольника 6 метров, что в два раза меньше ширины. Найдите площадь прямоугольника, если его площадь 216 м. - Размеры 20513
Стороны прямоугольника 6,6 см и 4,2 см. Изменяем его размеры в соотношении 5:2. Во сколько раз изменилась площадь прямоугольника по сравнению с исходным прямоугольником? - Угол диагоналей
Вычислите периметр и площадь прямоугольника, если его диагональ равна 14 см, а диагонали образуют угол 130°. - Размеры 3
Периметр прямоугольного поля равен 96 метрам. Длина на четыре метра меньше ширины в три раза. Найдите длину и ширину (его размеры).
Сколько различных прямоугольников можно составить с периметром 24 см?
Прямоугольник — замкнутая двумерная фигура, состоящая из четырех сторон и четырех вершин. Все углы прямоугольника равны 90 градусов. Прямоугольник, у которого все стороны равны, эквивалентен квадрату. Прямоугольник состоит из двух пар параллельных сторон, длины и ширины соответственно.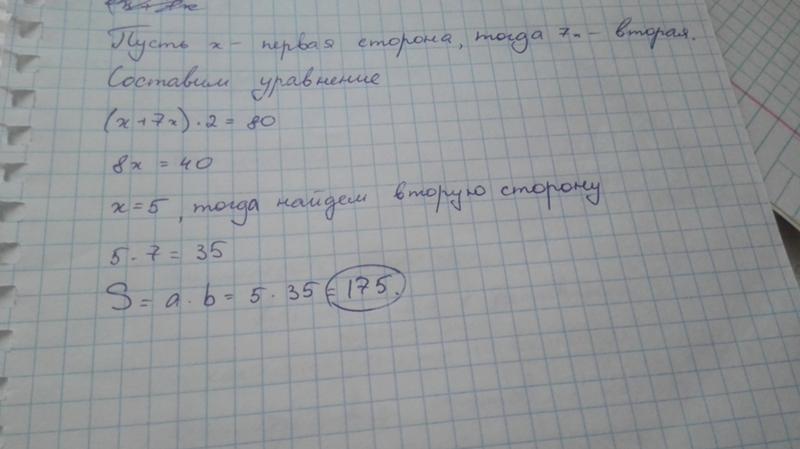
Периметр прямоугольника — это длина внешней границы прямоугольника. Он также рассчитывается путем суммирования общей меры длины и ширины прямоугольника.
Периметр прямоугольника Формула
Предположим, есть прямоугольник с периметром P, длина и ширина которого равны «l» и «w» соответственно равны 2(l + w).
Периметр прямоугольника Формула = 2 (длина + ширина) единиц
Сколько различных прямоугольников можно составить с периметром 24 см?
Решение:
Может быть несколько прямоугольников с периметром, равным 24 см. Например, один прямоугольник со сторонами 5 см и 7 см имеет периметр 24, аналогично прямоугольник со сторонами 4 см и 8 см имеет периметр 24. Таким образом, может быть много прямоугольников таких размеров, как (5,7), (4, 8), (3,9), (3.6,8.4) и т. д.
Если a и b — стороны прямоугольника, то периметр равен 2a+2b.
Вам дана нить длиной 24 см (это будет периметр), из которой нужно составить прямоугольники. Итак,
2a + 2b = 24
2(a + b) = 24
a + b = 12
Если стороны должны быть целыми числами, то возможны следующие варианты:
a = 1, b = 11
a = 2, b = 10
a = 3, b = 9
a = 4, b = 8
a = 5, b = 7
a = 6, b = 6
Если a=7, то b=5, что совпадает с пятым указанным прямоугольником, т. е. a=5, b=7.
Итак, есть только 6 возможных прямоугольников (квадраты a=6 и b=6, являющиеся частным случаем прямоугольника).
Полное пошаговое решение:
Мы знаем,
Длина нити, образующей прямоугольник, составляет 24 см. Следовательно, можно сделать вывод, что периметр прямоугольника равен 24 см.
Периметр прямоугольника равен 2(a+b)=P, что означает, что периметр равен удвоенной сумме сторон прямоугольника.
Подставляя, получаем
∴ 2(a+b) = 24
Следовательно,
(a+b) = 12
Начиная с a = 6, b = 6.
По возрастанию значение по 1, заключаем, что следующие стороны прямоугольника
a = 7, b = 5
a = 8, b = 4
a = 9, b = 3
a = 10, b = 2
a = 11, b = 1
Таким образом, все, что мы можем сказать, возможны 6 прямоугольников, и вот эти прямоугольники:
- 6, 6, 6, 6
- 5, 7, 5, 7
- 4, 8, 4, 8
- 3, 9, 3, 9
- 2, 10, 2, 10
- 1, 11, 1, 11
Примеры вопросов
Вопрос 1. Предположим, что стороны прямоугольника относятся как 6:4, а его периметр равен 100 см. Тогда найдите его размеры?
Решение:
Здесь имеем
Периметр прямоугольника = 100 см
Отношение длины к ширине равно 6 : 4
Нам нужно найти длину и ширину прямоугольника
Предположим, что знаменатель равен х
Таким образом, стороны будут 6х и 4х
Как мы знаем,
Периметр прямоугольника = 2(длина + ширина )
Периметр прямоугольника = 2(6x + 4x)
Периметр прямоугольника = 2 × 10x
Периметр прямоугольника = 20x
100 = 20x
x = 100/20
х = 5
Следовательно,
Длина = 6x = 6 × 5 = 30 см
Ширина = 4x = 4 × 5 = 20 см
Следовательно,
Длина 30 см, а ширина 20 см.
Вопрос 2. Если стороны прямоугольника относятся как 4:2, а его периметр равен 600 см, то найдите его размеры?
Решение:
Здесь имеем
Периметр прямоугольника = 600 м
Отношение длины к ширине равно 4 : 2 ширина прямоугольника
Предположим, что знаменатель x
Таким образом, стороны будут 4x и 2x
Как мы знаем,
Периметр прямоугольника = 2(длина + ширина)
Периметр прямоугольника = 2(4x + 2x)
Периметр прямоугольника = 2 × 6x
Периметр прямоугольника = 12x
600 = 12x
x = 600/12
x = 50
9001 3 Следовательно,Длина = 4x = 4 × 50 = 200 м
Ширина = 2x = 2 × 50 = 100 м
Следовательно,
Длина 200 м, а ширина 100 м.
Вопрос 3. Найдите, сколько плиток размером 26 см в длину и 14 см в ширину потребуется для покрытия прямоугольного пола размером 1040 см в длину и 280 см в ширину?
Площадь прямоугольника = длина × ширина 6 × 14
Площадь прямоугольной плитки = 364 см 2
Площадь прямоугольника по низу = 1040 × 280
Площадь прямоугольника по низу = 291200 см 2
Сейчас, 900 03
Определение необходимого количества плиток
Количество плитки = площадь поддона / площадь плитки
Количество плиток = 291200/364
Количество плиток = 800 плиток
Следовательно,
Нам понадобится 800 плиток, чтобы покрыть пол подвала.







 Высота каждой ступени
равна 14 см, а длина — 48 см. Найдите
расстояние между точками A и B (в
метрах).
Высота каждой ступени
равна 14 см, а длина — 48 см. Найдите
расстояние между точками A и B (в
метрах).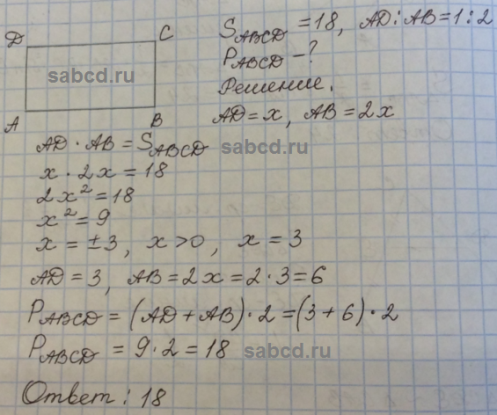
 Расстояние
от основания флагштока
до места крепления троса на земле
равно 4,8 м. Найдите длину троса.
Ответ дайте в метрах.
Расстояние
от основания флагштока
до места крепления троса на земле
равно 4,8 м. Найдите длину троса.
Ответ дайте в метрах. Найдите площадь квадрата
Найдите площадь квадрата Найдите её площадь. Ответ дайте в квадратных сантиметрах.
Найдите её площадь. Ответ дайте в квадратных сантиметрах. 
 Найдите его площадь
Найдите его площадь  Определите размеры прямоугольника, если известно, что его периметр равен 22 см.
Определите размеры прямоугольника, если известно, что его периметр равен 22 см. Периметр прямоугольника равен 132 см. Определить размеры прямоугольника.
Периметр прямоугольника равен 132 см. Определить размеры прямоугольника.
 Вам дана нить длиной 24 см (это будет периметр), из которой нужно составить прямоугольники. Итак,
Вам дана нить длиной 24 см (это будет периметр), из которой нужно составить прямоугольники. Итак,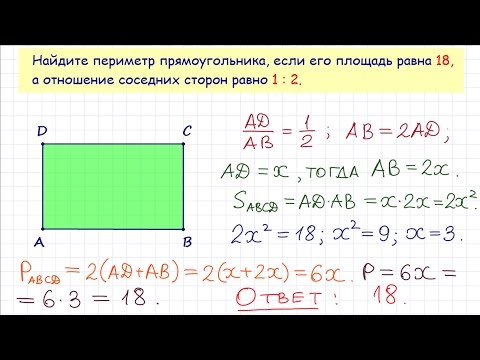

Leave A Comment