Задания №15 базового уровня (прямоугольник)

Практикум №6
по решению
планиметрических задач
( базового уровня)
Задания №15
базового уровня
(прямоугольник)

3. Содержание

• Задача №1
• Задача №2
• Задача №3
• Задача №4
• Задача №5
• Задача №6
• Задача №7
•Задача №8
• Задача №9
• Задача №10
• Задача №11
• Задача №12
• Задача №13
• Задача №14
•Задача №15
• Задача №16
• Задача №17
• Задача №18
• Задача №19
• Задача №20
• Задача №21
•Задача №22
• Задача №23
• Задача №24
• Задача №25
• Задача №26
• Задача №27
•Задачи для самостоятельного решения

4. Задача №1

Найдите площадь прямоугольника, вершины которого
имеют координаты (1;1), (10;1), (10;7), (1;7).

5. Задача №2

Найдите площадь квадрата, если его диагональ
равна 1.
Площадь квадрата равна половине
произведения
его
диагоналей.
Поэтому она равна 0,5.

6. Задача №3

Найдите диагональ квадрата, если его площадь равна 2.
Площадь квадрата равна половине
произведения его диагоналей. Поэтому
произведение диагоналей равно 4, а
каждая из них равна 2.

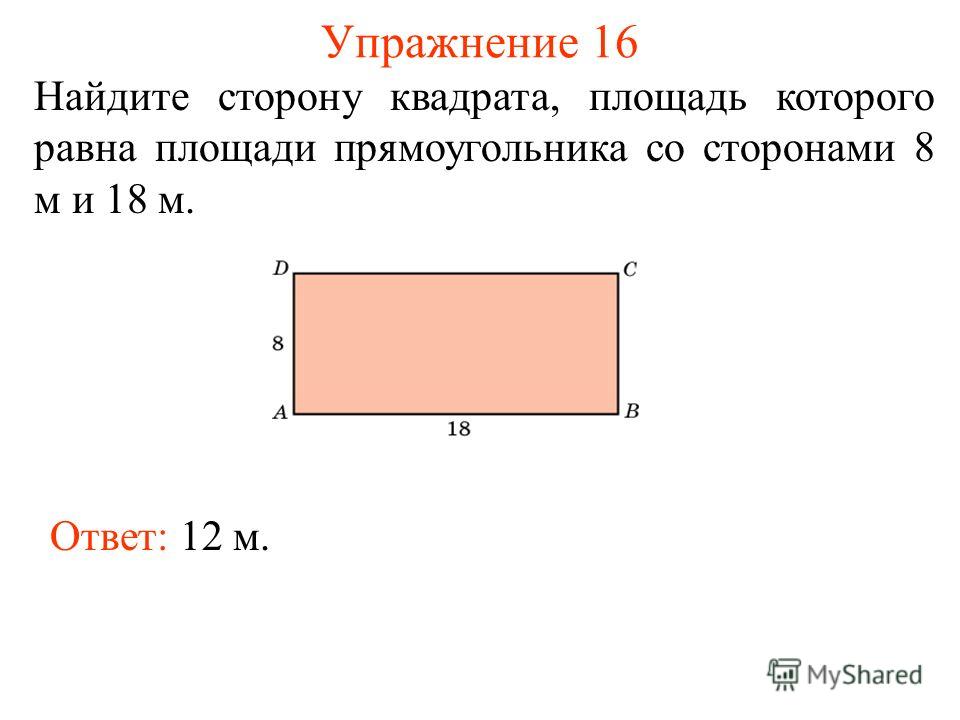
7. Задача №4

Найдите сторону квадрата, площадь которого
равна площади прямоугольника со сторонами 4 и
9.
Поэтому сторона квадрата, площадь
которого равна 36, равна 6.

8. Задача №5

Найдите площадь прямоугольника, если его
периметр равен 18, и одна сторона на 3 больше
другой.
Пусть одна из сторон прямоугольника
равна a, тогда вторая равна a+3.
P = 2a + 2(a + 3) = 18;
S = 3 · 6 = 18.
2а+2а +6=18; 4а=12; а=3

9. Задача №6

Найдите площадь прямоугольника, если его
периметр равен 18, а отношение соседних сторон
равно 1:2.
Пусть одна из сторон прямоугольника равна a,
тогда вторая равна 2a.
Периметр
будет
соответственно
равен P = 2a + 2; 2a = 18, тогда одна из сторон
равна 3, а другая 6. Поэтому S = 3 ·6 = 18.

10. Задача №7

Найдите периметр прямоугольника, если его
площадь равна 18, а отношение соседних сторон
равно 1:2.
Пусть одна из сторон прямоугольника
равна a, тогда вторая равна 2a. Площадь
прямоугольника будет равна S = 2a2 = 18,
тогда одна из сторон равна 3, а другая 6.
Поэтому P = 2 ·3 + 2·6 = 18.

11. Задача №8

Периметр прямоугольника равен 42, а площадь 98.
Найдите большую сторону прямоугольника.
Пусть одна из сторон прямоугольника равна a,
вторая равна b. Площадь и периметр
прямоугольника
будут
соответственно
равны S = a·b = 98, P = 2·a + 2·b = 42. Решая
систему из этих уравнений, получаем, что
a1 = 7, a2 = 14, b1 = 14, b2 = 7. Значит большая
сторона равна 14.

12. Задача №9

Периметр прямоугольника равен 34, а площадь
равна 60. Найдите диагональ этого
прямоугольника.
Диагональ разбивает прямоугольник на два
прямоугольных треугольника, в которых она
является гипотенузой. Пусть длина диагонали
равна с, тогда по теореме Пифагора

13. Задача №10

Сторона прямоугольника относится к его
диагонали, как 4:5, а другая сторона равна 6.
Найдите площадь прямоугольника.
Пусть одна из сторон прямоугольника равна 4a, тогда
диагональ равна 5a. Диагональ образует в
прямоугольнике два прямоугольных треугольника. По
теореме Пифагора 16a2 + 36 = 25a2, тогда 9a2 = 36,
откуда a = 2. Значит S = 8·6 = 48.

14. Задача №11

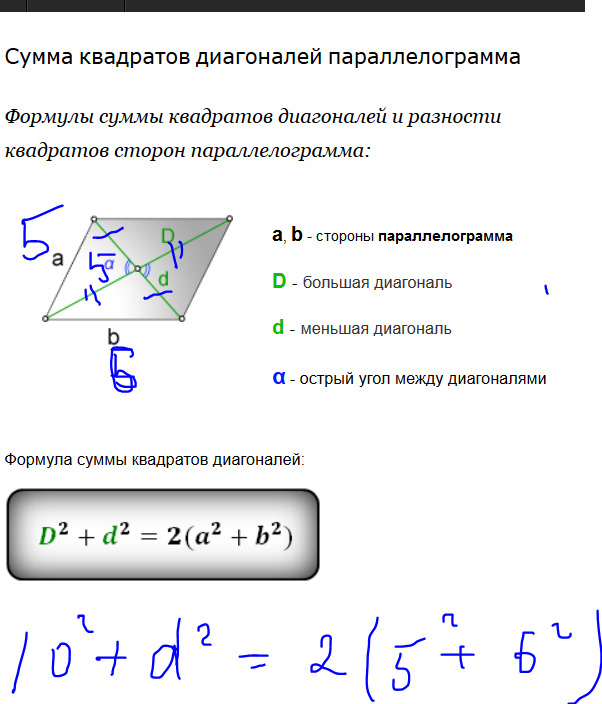
Даны два квадрата, диагонали которых равны 10 и
6. Найдите диагональ квадрата, площадь
которого равна разности площадей данных
квадратов.
Площадь квадрата равна половине квадрата
его диагонали. Поэтому площадь первого
квадрата равна 50, а площадь второго
квадрата равна 18. Разность найденных
площадей равна 32, значит, квадрат искомой
диагонали равен 64, а сама она равна 8.

15. Задача №12

Во сколько раз площадь квадрата, описанного около
окружности, больше площади квадрата, вписанного в
эту окружность? Пусть радиус окружности равен R. Тогда
сторона описанного вокруг нее квадрата
равна 2R, а его площадь, равная квадрату
стороны, равна 4R². Диагональ вписанного
квадрата также равна 2R, поэтому его
площадь, равная половине произведения
диагоналей, равна 2R². Значит, отношение
площади описанного квадрата к площади
вписанного равно 2.

16. Задача №13

Две стороны прямоугольника АВСD равны 6 и 8.
Найдите длину вектора АС .
Вектор АС образует в прямоугольнике
два прямоугольных треугольника.
Поэтому по теореме Пифагора

17. Задача № 14

Две стороны прямоугольника АВСD равны 6 и 8.
Найдите сумму векторов АВ и АD.
Сумма векторов АВ и АD равна вектору АС.
Вектор АС образует в прямоугольнике два
прямоугольных треугольника.
Поэтому по теореме Пифагора

18. Задача №15

Две стороны прямоугольника АВСD равны 6 и 8.
Найдите разность векторов
Разность векторов АВ и АD равна вектору DВ.
Вектор DВ образует в прямоугольнике два
прямоугольных треугольника.
Поэтому

19. Задача №16

Две стороны прямоугольника АВСD равны 6 и 8.
Найдите скалярное произведение векторов АВ и
АD.
Скалярное произведение двух векторов
равно произведению их длин на косинус
угла между ними. Так как косинус
прямого угла равен нулю, то и
скалярное произведение тоже равно
нулю.

20. Задача №17

Две стороны прямоугольника АВСD равны 6 и 8.
Диагонали пересекаются в точке О. Найдите
длину суммы векторов АО и ВО.
Сумма векторов АО и ВО равна вектору
АD. Значит его длина равна 6.

21. Задача №18

Две стороны прямоугольника АВСD равны 6 и 8.
Диагонали пересекаются в точке О. Найдите
длину разности векторов АО и ВО.
Разность векторов АО и ВО равна
вектору АВ. Значит длина вектора равна
8.

22. Задача №19

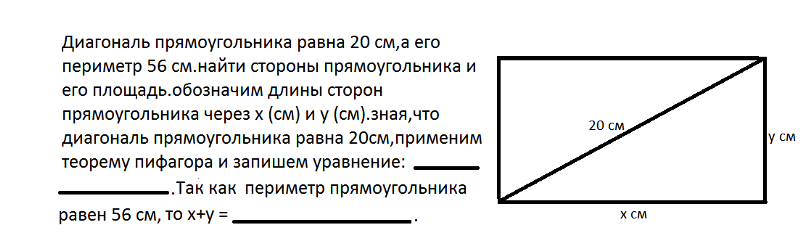
Найдите диагональ прямоугольника, если его периметр
равен 28, а периметр одного из треугольников, на
которые диагональ разделила прямоугольник, равен 24.
Сумма двух периметров треугольников
отличается
от
периметра
прямоугольника
на
две
длины
диагонали, значит

23.

Задача №20Середины сторон прямоугольника, диагональ которого
равна 5, последовательно соединены отрезками.
Найдите периметр образовавшегося четырехугольника.
Четырехугольник EHGF ромб, значит, его
периметр равен
4·EF. Стороны искомого
четырехугольника
равны
средним
линиям
треугольников,
образуемых
диагоналями
и
сторонами данного четырехугольника. Значит
стороны
искомого
четырехугольника
равны
половинам диагоналей. Значит, имеем:

24. Задача №21

В прямоугольнике расстояние от точки пересечения
диагоналей до меньшей стороны на 1 больше, чем
расстояние от нее до большей стороны. Периметр
прямоугольника равен 28. Найдите меньшую сторону
прямоугольника.
=>

25. Задача №22

Найдите периметр четырехугольника АВСD, если
стороны квадратных клеток равны √10.
по теореме Пифагора найдем сторону
четырехугольника:

26. Задача №23

Меньшая сторона прямоугольника равна 6,
диагонали пересекаются под углом 60°. Найдите
диагонали прямоугольника.
значит, треугольник DОА – равносторонний
.

27. Задача №24

Диагональ прямоугольника вдвое больше одной из его
сторон. Найдите больший из углов, который образует
диагональ со сторонами прямоугольника? Ответ
выразите в градусах.
Диагональ
прямоугольника
является
гипотенузой прямоугольного треугольника. Так
как она вдвое больше одной из сторон
прямоугольника, являющейся катетом того же
треугольника, то угол, лежащий против этой
стороны, равен
30°. Больший угол будет
равен 90° — 30° = 60°

28. Задача №25

В прямоугольнике диагональ делит угол в
отношении 1 : 2 , меньшая его сторона равна 6.
Найдите диагональ данного прямоугольника.
Т.к. диагональ делит угол в отношении 1 : 2, значит, углы
равны 30°и 60°. Диагональ тогда равна удвоенной длине
катета, лежащего против угла в 30°, то есть 12.

29. Задача №26

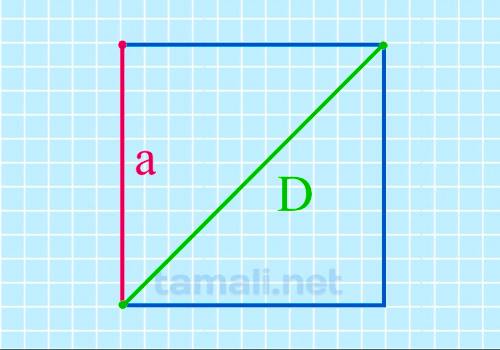
Найдите сторону квадрата, диагональ которого
равна √8 .

30. Задача №27

В квадрате расстояние от точки пересечения
диагоналей до одной из его сторон равно 7.
Найдите периметр этого квадрата.
В квадрате расстояние от точки
пересечения диагоналей до стороны
равно половине стороны. Поэтому
сторона квадрата равна 14, а тогда
его периметр 56.
Задачи
для самостоятельного
решения

32. Задача №1 Решите самостоятельно

1) Найдите площадь прямоугольника, вершины которого
имеют координаты (1;2), (10;2), (10;7), (1;7). Ответ:
2) Найдите площадь прямоугольника, вершины которого
имеют координаты (2;2), (10;2), (10;9), (2;9) . Ответ:
3) Найдите площадь прямоугольника, вершины которого
имеют координаты (4;1), (10;1), (10;8), (4;8) . Ответ:

33. Задача №2 Решите самостоятельно

1) Найдите площадь квадрата, если его диагональ
равна 38.
Ответ: 722
2) Найдите площадь квадрата, если его диагональ
равна 30.
Ответ:
3) Найдите площадь квадрата, если его диагональ
равна 16.
Ответ:

34. Задача №5 Решите самостоятельно

1) Найдите площадь прямоугольника, если его периметр
равен 80, и одна сторона на 6 больше другой. Ответ:
2) Найдите площадь прямоугольника, если его периметр
равен 12, и одна сторона на 2 больше другой. Ответ:
3) Найдите площадь прямоугольника, если его периметр
равен 88, и одна сторона на 6 больше другой. Ответ:

35. Задача №6 Решить самостоятельно

1) Найдите площадь прямоугольника, если его периметр
равен 140, а отношение соседних сторон равно 4:31.
Ответ:496
2) Найдите площадь прямоугольника, если его периметр
равен 126, а отношение соседних сторон равно 2:19.
3) Найдите площадь прямоугольника, если его периметр
равен 64, а отношение соседних сторон равно 3:13.

36. Задача №7 Решить самостоятельно

1) Найдите периметр прямоугольника, если его площадь
равна 176, а отношение соседних сторон равно 4:11.
Ответ:60
2) Найдите периметр прямоугольника, если его площадь
равна 272, а отношение соседних сторон равно 4:17.
3) Найдите периметр прямоугольника, если его площадь
равна 432, а отношение соседних сторон равно 4:27.

37. Задача №8 Решить самостоятельно

1) Периметр прямоугольника равен 42, а площадь 108.
Найдите большую сторону прямоугольника. Ответ:
2) Периметр прямоугольника равен 90, а площадь 234.
Найдите большую сторону прямоугольника. Ответ:
3) Периметр прямоугольника равен 30, а площадь 36.
Найдите большую сторону прямоугольника. Ответ:

38. Задача №10 Решить самостоятельно

1) Сторона прямоугольника относится к его диагонали,
как 12:13, а другая сторона равна 35. Найдите
площадь прямоугольника. Ответ:
2) Сторона прямоугольника относится к его диагонали,
как 21:29, а другая сторона равна 80. Найдите
площадь прямоугольника. Ответ:
3) Сторона прямоугольника относится к его диагонали,
как 15:17, а другая сторона равна 48. Найдите
площадь прямоугольника. Ответ:

39. Задача №11 Решить самостоятельно

1) Даны два квадрата, диагонали которых равны 196 и
261. Найдите диагональ квадрата, площадь которого
равна разности площадей данных квадратов.
2) Даны два квадрата, диагонали которых равны 72 и 75.
Найдите диагональ квадрата, площадь которого равна
разности площадей данных квадратов.
3) Даны два квадрата, диагонали которых равны 192 и
200. Найдите диагональ квадрата, площадь которого
равна разности площадей данных квадратов.

40. Задача №19 Решить самостоятельно

1) Найдите диагональ прямоугольника, если его
периметр равен 42, а периметр одного из
треугольников, на которые диагональ разделила
прямоугольник, равен 37.
2) Найдите диагональ прямоугольника, если его
периметр равен 100, а периметр одного из
треугольников, на которые диагональ разделила
прямоугольник, равен 87.

41. Задача №20 Решить самостоятельно

1) Середины сторон прямоугольника, диагональ
которого равна 24, последовательно соединены
отрезками. Найдите периметр образовавшегося
четырехугольника.
Ответ: 48
2) Середины сторон прямоугольника, диагональ
которого равна 46, последовательно соединены
отрезками. Найдите периметр образовавшегося
четырехугольника.

42. Задача №21 Решить самостоятельно

1) В прямоугольнике расстояние от точки пересечения
диагоналей до меньшей стороны на 2 больше, чем
расстояние от нее до большей стороны. Периметр
прямоугольника равен 52. Найдите меньшую сторону
прямоугольника.
2) В прямоугольнике расстояние от точки пересечения
диагоналей до меньшей стороны на 3 больше, чем
расстояние от нее до большей стороны. Периметр
прямоугольника равен 124. Найдите меньшую
сторону прямоугольника.

43. Задача №22 Решить самостоятельно

1) Найдите периметр четырехугольника АВСD, если
стороны квадратных клеток равны √5.
Ответ: 30.

44. Задача №23 Решить самостоятельно

1) Меньшая сторона прямоугольника равна 59,
диагонали пересекаются под углом 60°. Найдите
диагонали прямоугольника.
2) Меньшая сторона прямоугольника равна 1, диагонали
пересекаются под углом 60°. Найдите диагонали
прямоугольника.
3) Меньшая сторона прямоугольника равна18,
диагонали пересекаются под углом 60°. Найдите
диагонали прямоугольника.

45. Задача №25 Решить самостоятельно

1) В прямоугольнике диагональ делит угол в отношении
1 : 2 , меньшая его сторона равна 57. Найдите диагональ
данного прямоугольника.
2) В прямоугольнике диагональ делит угол в отношении
1 : 2 , меньшая его сторона равна 39. Найдите диагональ
данного прямоугольника.
3) В прямоугольнике диагональ делит угол в отношении
1 : 2 , меньшая его сторона равна 23. Найдите диагональ
данного прямоугольника.

46. Задача №26Решите самостоятельно

1) Найдите сторону квадрата, диагональ которого
равна 5√2 .
Ответ: 5
2) Найдите сторону квадрата, диагональ которого
равна 14√2 .
3) Найдите сторону квадрата, диагональ которого
равна 9√2 .

47.

Интернет ресурсы• https://img-fotki.yandex.ru/get/15509/83186431.80f/0_a284a_ce0b20bd_S
• Шаблон подготовила учитель русского языка и литературы Тихонова Надежда Андреевна
http://sch-53.ru/files/director/GIA/2016/%D0%95%D0%93%D0%AD%202016.jpg
•«Решу ЕГЭ» Образовательный портал для подготовки к ЕГЭ и ОГЭ. Режим доступа:
http://mathb.reshuege.ru
Автор и источник заимствования неизвестен

Решебник по геометрии за 8 класс к учебнику Геометрия. 7-9 класс Л.С.Атанасян и др.Глава VI. Площадь. Дополнительные задачи

Решебники и ГДЗ

    Начните вводить часть условия (например, могут ли, чему равен или найти):

    • 500 Докажите, что площадь квадрата, построенного на катете равнобедренного прямоугольного треугольника, вдвое больше площади квадрата, построенного на высоте, проведенной к гипотенузе.
    • 501 Площадь земельного участка равна 27 га. Выразите площадь этого же участка: а) в квадратных метрах; б) в квадратных километрах.
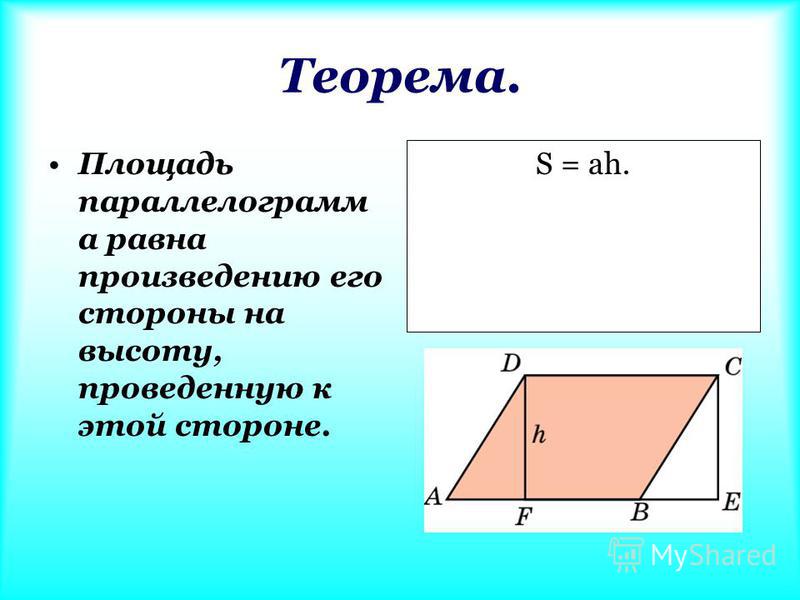
    • 502 Высоты параллелограмма равны 5 см и 4 см, а периметр равен 42 см. Найдите площадь параллелограмма.
    • 503 Найдите периметр параллелограмма, если его площадь равна 24 см2, а точка пересечения диагоналей удалена от сторон на 2 см и 3 см.
    • 504 Меньшая сторона параллелограмма равна 29 см. Перпендикуляр, проведенный из точки пересечения диагоналей к большей стороне, делит ее на отрезки, равные 33 см и 12 см. Найдите площадь параллелограмма.
    • 505 Докажите, что из всех треугольников, у которых одна сторона равна a, а другая — b, наибольшую площадь имеет тот, у которого эти стороны перпендикулярны.
    • 506 Как провести две прямые через вершину квадрата, чтобы разделить его на три фигуры, площади которых равны?
    • 507* Каждая сторона одного треугольника больше любой стороны другого треугольника. Следует ли из этого, что площадь первого треугольника больше площади второго треугольника?
    • 508* Докажите, что сумма расстояний от точки на основании равнобедренного треугольника до боковых сторон не зависит от положения этой точки.
    • 509 Докажите, что сумма расстояний от точки, лежащей внутри равностороннего треугольника, до его сторон не зависит от положения этой точки.
    • 510* Через точку D, лежащую на стороне ВС треугольника ABC, проведены прямые, параллельные двум другим сторонам и пересекающие стороны АВ и АС соответственно в точках Е и F. Докажите, что треугольники CDE и BDF имеют равные площади.
    • 511 В трапеции ABCD с боковыми сторонами АВ и CD диагонали пересекаются в точке О. а) Сравните площади треугольников ABD и ACD. б) Сравните площади треугольников АВО и СDO. в) Докажите, что выполняется равенство ОА • ОВ = ОС • OD.
    • 512* Основания трапеции равны а и b. Отрезок с концами на боковых сторонах трапеции, параллельный основаниям, разделяет трапецию на две трапеции, площади которых равны. Найдите длину этого отрезка.
    • 513 Диагонали ромба равны 18 м и 24 м. Найдите периметр ромба и расстояние между параллельными сторонами.
    • 514 Площадь ромба равна 540 см2, а одна из его диагоналей равна 4,5 дм. Найдите расстояние от точки пересечения диагоналей до стороны ромба.
    • 515 Найдите площадь равнобедренного треугольника, если: а) боковая сторона равна 20 см, а угол при основании равен 30°; б) высота, проведенная к боковой стороне, равна 6 см и образует с основанием угол в 45°.
    • 516 В треугольнике ABC ВС = 34 см. Перпендикуляр MN, проведенный из середины ВС к прямой АС, делит сторону АС на отрезки AN= 25 см и NC= 15 см. Найдите площадь треугольника ABC.
    • 517 Найдите площадь четырехугольника ABCD, в котором АВ = 5 см, ВС = 13 см, CD = 9 см, DA =15 см, АС = 12 см.
    • 518 Найдите площадь равнобедренной трапеции, если: а) ее меньшее основание равно 18 см, высота — 9 см и острый угол равен 45°; б) ее основания равны 16 см и 30 см, а диагонали взаимно перпендикулярны.
    • 519 Найдите площадь равнобедренной трапеции, у которой высота равна h, а диагонали взаимно перпендикулярны.
    • 520 Диагонали равнобедренной трапеции взаимно перпендикулярны, а сумма ее оснований равна 2а. Найдите площадь трапеции.
    • 521 Докажите, что если диагонали четырехугольника ABCD взаимно перпендикулярны, то AD2 +ВС2 =AB2+CD2.
    • 522 В равнобедренной трапеции ABCD с основаниями AD=17 см, ВС=5 см и боковой стороной АВ=10 см через вершину В проведена прямая, делящая диагональ АС пополам и пересекающая основание AD в точке М. Найдите площадь треугольника BDM.
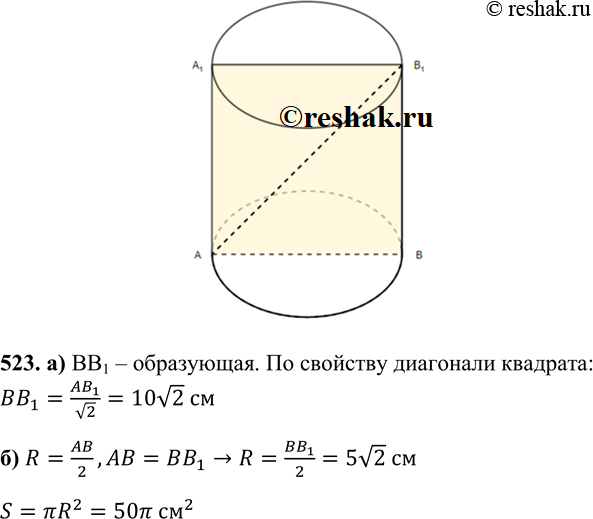
    • 523 Два квадрата со стороной а имеют одну общую вершину, причем сторона одного из них лежит на диа-гонали другого. Найдите площадь общей части этих квадратов.
    • 524 Докажите, что площадь S треугольника со сторонами a, b, c выражается формулой
    • 525 Расстояние от точки М, лежащей внутри треугольника ABC, до прямой АВ равно 6 см, а до прямой АС равно 2 см. Найдите расстояние от точки М до прямой BC, если АВ = 13 см, ВС =14 см, АС =15 см.
    • 526 В ромбе высота, равная см, составляет большей диагонали. Найдите площадь ромба.
    • 527 В равнобедренной трапеции диагональ равна 10 см, а высота равна 6 см. Найдите площадь трапеции.
    • 528 В трапеции ABCD диагонали пересекаются в точке О. Найдите площадь треугольника АОВ, если боковая сторона CD трапеции равна 12 см, а расстояние от точки О до прямой CD равно 5 см.
    • 529 Диагонали четырехугольника равны 16 см и 20 см и пересекаются под углом в 30°. Найдите площадь этого четырехугольника.
    • 530 В равнобедренном треугольнике ABC с основанием ВС высота AD равна 8 см. Найдите площадь треугольника ABC, если медиана DM треугольника ADC равна 8 см.
    • 531 Стороны AB и ВС прямоугольника ABCD равны соответственно 6 см и 8 см. Прямая, проходящая через вершину С и перпендикулярная к прямой BD, пересекает сторону AD в точке М, а диагональ BD — в точке К. Найдите площадь четырехугольника АВКМ.
    • 532 В треугольнике ABC проведена высота ВН. Докажите, что если:

    Поиск по сайту

    Видео-урок: Площадь квадрата по диагоналям

    Стенограмма видео

    В этом видео мы найдем площадь квадрата по длине диагонали. Мы также посмотрим, как мы можем найти длина диагонали с учетом площади. Начнем с краткого обзора то, что мы уже должны знать. Во-первых, мы знаем, что квадрат четырехугольник или четырехугольник со всеми четырьмя сторонами одинаковой длины. В квадрате весь интерьер углы тоже будут 90 градусов. Если нам известна длина стороны квадрат, назовем его 𝑙, тогда мы знаем, что каждая сторона также будет стороной длина 𝑙.

    Чтобы найти площадь квадрата, мы умножит длину на длину, что будет 𝑙 раз 𝑙. Мы могли бы также написать это как 𝑙 в квадрате. Но что будет, если вместо нам дана длина квадрата, нам дана длина диагонали, которую мы мог позвонить 𝑑? Как же тогда мы можем выработать область? Начнем с того, что мы можем вычислить длину стороны этого квадрата, а затем использовать эту формулу, чтобы найти другая формула площади квадрата с использованием диагоналей.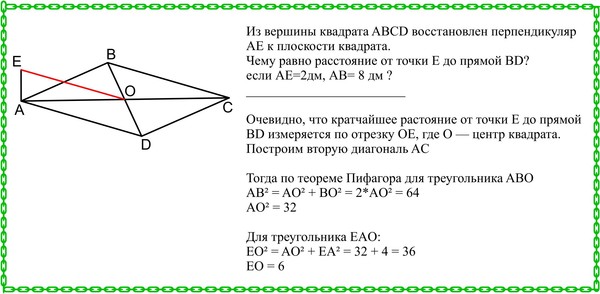

    Вспомним, что квадрат имеет получил четыре угла по 90 градусов. Это означает, что мы можем создать право треугольник внутри нашего квадрата и, следовательно, мы могли бы применить пифагорейский теорема. Эта теорема применима к правому только треугольники. И это говорит о том, что площадь гипотенуза равна сумме квадратов двух других сторон.

    Применение теоремы Пифагора к тогда в нашем треугольнике гипотенуза будет 𝑑, поэтому мы начнем с 𝑑 в квадрате равно 𝑙 в квадрате плюс 𝑙 в квадрате. Это, конечно, упростит до 𝑑 квадрат равен двум 𝑙 в квадрате. И тогда помните, что мы пытаемся чтобы найти длину 𝑙 через диагональ. Это означает, что нам нужно разделить обе части уравнения на два. Следовательно, 𝑑 в квадрате над двумя равно 𝑙 в квадрате. Итак, чтобы найти 𝑙, мы берем квадрат корень из обеих сторон, в результате чего 𝑙 равен квадратному корню из 𝑑 в квадрате больше двух.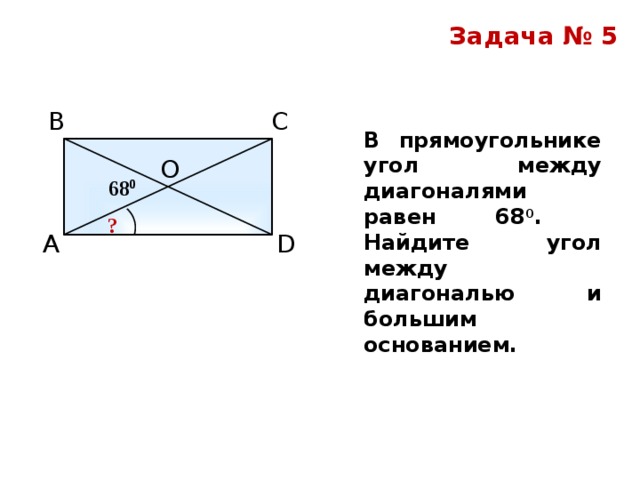

    Давайте помнить, что мы пытаемся найдите площадь квадрата, что мы можем сделать теперь, когда у нас есть 𝑙 по диагонали длина 𝑑. Мы возьмем нашу формулу и заполним в значениях для 𝑙, чтобы дать нам, что площадь квадрата равна квадрату корень из 𝑑 в квадрате, умноженный на квадратный корень из 𝑑 в квадрате два.

    Когда у нас есть квадратный корень из число, умноженное само на себя, мы просто остаемся с этим числом. В этом случае у нас останется 𝑑 в квадрате над двумя. Теперь мы нашли формулу для площадь квадрата через длину диагонали. То есть площадь квадрата равно 𝑑 в квадрате над двумя, где 𝑑 — длина диагонали. Когда мы пройдем остальную часть этого видео, мы в основном будем смотреть на квадраты, где нам дана длина диагонали. Но, конечно, всегда Важно помнить формулу площади через длину стороны.

    Давайте посмотрим на нашу первую вопрос.

    Найдите площадь квадрата, диагональ равна девяти сантиметрам.

    Давайте начнем с моделирования нашего квадрат. Мы знаем, что у него будет четыре равные стороны и четыре угла по 90 градусов. Мы можем вспомнить, что легко найдите площадь квадрата, если известна длина одной из сторон. Однако здесь нам дается длина диагонали. Итак, нам нужно запомнить другая формула, то есть площадь квадрата равна 𝑑 в квадрате над два, где 𝑑 — длина диагонали.

    Нам дано, что диагональ составляет девять сантиметров. Таким образом, мы можем заполнить это в формулу так, чтобы площадь была равна девяти в квадрате на два. Как девять в квадрате девять умножить к девяти мы получим ответ 81 больше двух. Наши подразделения здесь будут возведены в квадрат сантиметры. Итак, мы нашли площадь квадрат с диагональю девять сантиметров, что составляет 81 на два квадрата сантиметры. Конечно, мы могли бы также дать наш ответ в виде десятичных 40,5 квадратных сантиметров.

    До сих пор в этом видео мы видели как найти площадь квадрата по длине диагонали. Но можем ли мы найти способ найти длина диагонали, если нам известна площадь? Что ж, на самом деле мы можем сделать это, переставляя формулу площади квадрата по диагонали. Если принять площадь равной буква 𝐴, то что нам действительно нужно сделать, так это переставить ее так, чтобы у нас была 𝑑 в качестве предметом этого уравнения. Когда мы умножаем обе части уравнение на два, мы получим два 𝐴 равно 𝑑 в квадрате. Чтобы найти 𝑑, мы возьмем квадратный корень из обеих частей уравнения, что дает нам квадратный корень из двух 𝐴 равно 𝑑.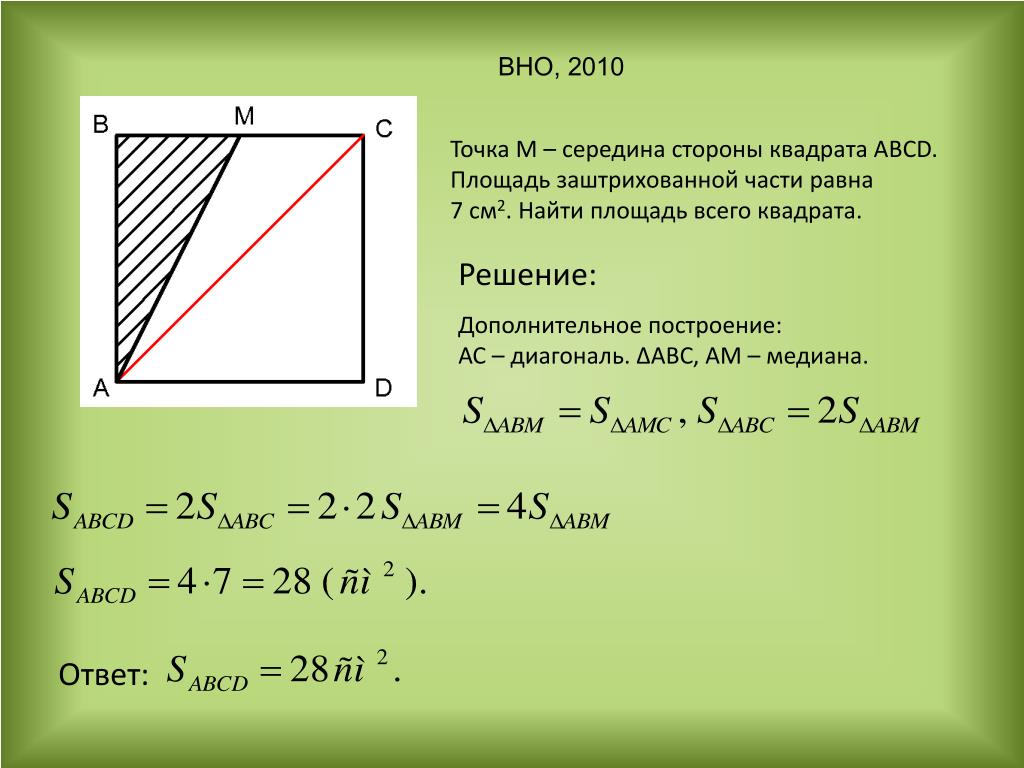

    Теперь у нас есть еще одна формула для найдите длину диагонали 𝑑, зная площадь 𝐴 квадрата. Давайте посмотрим, как мы можем поместить это в практика в следующем вопросе.

    Учитывая, что площадь каждого квадрата на шахматной доске 81 квадратный сантиметр, найдите длину диагонали шахматная доска.

    Здесь нам говорят, что площадь каждый из этих меньших квадратов на шахматной доске будет равен 81 квадратному сантиметру. Это не просто включает все черные квадраты, например, но он также будет включать каждый белый квадрат как хорошо. Нам нужно узнать диагональ длина шахматной доски. И мы должны помнить, что существует Формула, связывающая длину диагонали квадрата с его площадью. Формула состоит в том, что 𝑑, длина диагонали равна квадратному корню из двух 𝐴, где 𝐴 — площадь. Мы можем получить эту формулу перестановка площади квадрата по формуле. Эта площадь равна 𝑑 в квадрате больше двух, где 𝑑 — диагональ.

    Прежде чем мы сможем использовать формулу, которая 𝑑 равно квадратному корню из двух 𝐴, нам сначала нужно найти площадь целая шахматная доска. Вместо того, чтобы считать каждый квадрат, чтобы увидеть, сколько полей на этой шахматной доске, мы могли бы просто посчитать что в каждой строке восемь квадратов и в каждом столбце восемь квадратов. Это также подтвердит, что мы делаем действительно есть квадратная шахматная доска. Поскольку у нас есть восемь квадратов в каждом ряд и восемь в каждом столбце, то общее количество квадратов будет 64 квадраты. Чтобы найти общую площадь всех этих квадратов, мы знаем, что есть 64 квадрата, и каждый из них будет иметь площадь 81 квадратных сантиметров. Оценка этого даст нам общая площадь 5184 квадратных сантиметра.

    В качестве альтернативного метода подсчитайте это, если представить, что один квадрат имеет площадь 81 квадратный сантиметр, это означало бы, что длина каждого из этих квадратов будет девять сантиметры. Так как у нас есть восемь квадратов вдоль длина каждой из сторон квадрата и восемь умножить на девять равно 72, то мы могли бы проработайте площадь. Площадь здесь будет длиной на длину, которая будет 72 умножить на 72, что также даст нам площадь площадью 5184 квадратных сантиметра. Мы можем заполнить значение, которое площадь 𝐴 равна 5184 в нашей формуле, учитывая, что квадратный корень также включает в себя это значение площади, а не только два. Мы можем упростить это, чтобы получить 𝑑 равен квадратному корню из 10368.

    Вместо того, чтобы тянуться к нашему калькулятор, давайте посмотрим, сможем ли мы упростить это значение 10368, посмотрев, есть ли квадратный множитель его. Мы могли бы написать, что это равно до квадратного корня из 144, умноженного на 72. Разбив это на два отдельных квадратных корней, мы можем вычислить квадратный корень из 144 как 12. Но, конечно, 72 также имеет квадратный коэффициент. Мы можем выписать квадратный корень из 72 как квадратный корень из 36, умноженный на два. Тогда мы могли бы упростить нашу расчет 12 раз шесть раз квадратный корень из двух до 72 корень из двух. Тогда мы можем дать наш ответ, что длина диагонали шахматной доски равна 72 корням из двух. А единицами будут сантиметры поскольку мы работаем с длиной, а не с площадью.

    Посмотрим на другой вопрос.

    Найдите длину диагонали квадрат, площадь которого равна площади прямоугольника, имеющего размеры 10 см и 35 сантиметров.

    Здесь лучше всего начать с моделируем две наши фигуры, квадрат и прямоугольник. Прямоугольник имеет длину и ширина 10 сантиметров и 35 сантиметров. И нам нужно найти диагональ длина квадрата. Информация, которую нам дают позволяют нам вычислить длину диагонали в том, что площадь наших двух четырехугольников та же. У нас нет длины информацию о квадрате, поэтому давайте посмотрим, сможем ли мы вычислить площадь этого прямоугольник.

    Мы можем вспомнить, что площадь прямоугольник равен произведению длины на ширину. Затем мы заполним наши два значения 35 и 10, и вычисление 35, умноженное на 10, легко и просто, 350 квадратных сантиметров. Итак, площадь нашего квадрата будет также быть 350 квадратных сантиметров. Нам нужно запомнить формулу которая соединяет площадь квадрата с его диагональю. Площадь квадрата равна диагональ 𝑑 в квадрате над двумя. Так как мы хотим найти диагональ учитывая площадь, то мы можем использовать переставленную форму этой формулы, чтобы получить, что 𝑑 равно квадратному корню из двух 𝐴, где 𝐴 — площадь квадрата.

    Мы можем ввести значение для область, которую мы знаем, сохраняя букву 𝑑, поскольку это неизвестное, которое мы хотим найти вне. 𝑑 равно квадратному корню из два умножить на 350, что упрощает до 𝑑 равно квадратному корню из 700. Предположим, что мы используем метод без калькулятора, нам нужно еще больше упростить этот квадратный корень. Мы должны это заметить хороший квадратный коэффициент 100. И, следовательно, мы можем разбить наш расчет в квадратный корень из 100, умноженный на квадратный корень из семи, что упрощается до 𝑑 равно 10 корень семь. Поскольку 𝑑 — длина диагонали, то мы можем дать окончательный ответ из 10 корней из семи сантиметров.

    Давайте посмотрим на последний вопрос где нам нужно будет использовать обе формулы площади квадрата.

    Найдите разницу между площадь квадрата со стороной 17 см и площадь квадрата со стороной длина диагонали 20 сантиметров.

    В этом вопросе нам говорят, что есть два квадрата. Нам дана длина стороны одного и длина диагонали другого. Итак, давайте начнем с рисования этих квадраты. Но не волнуйтесь, если они не вполне в масштабе. Предположим, что этот первый квадрат тот, у которого длина стороны 17 сантиметров. И, конечно же, потому что это квадрат, мы знаем, что все стороны будут 17 сантиметров. И второй квадрат, мы могли бы сделать с диагональю 20 сантиметров.

    Нас спрашивают о районах эти квадраты. На самом деле, нам нужно отработать разница между областями. Но давайте для начала подумаем, как мы найти площадь каждого квадрата. В первом квадрате у нас есть длина стороны, так что давайте вспомним нашу первую формулу. Площадь квадрата равна длина, умноженная на длину, или, альтернативно, длина в квадрате.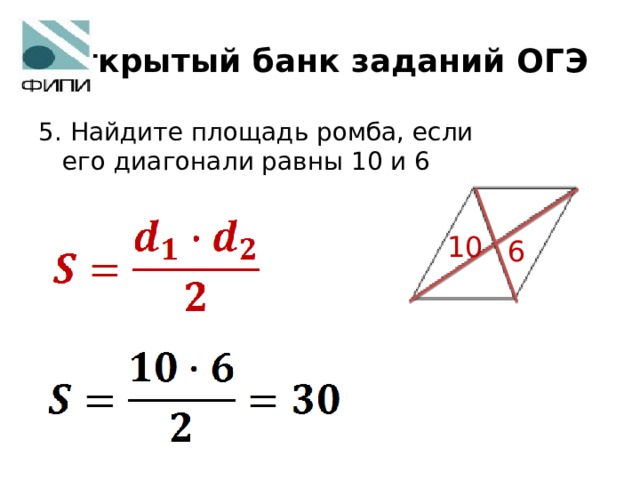 Мы можем заполнить длину стороны 𝑙 в нашу формулу, поэтому мы будем вычислять 17, умноженное на 17. Используя любое умножение метод, мы получим ответ 289. И поскольку это область, мы будем имеют единицы площади квадратные сантиметры.

    Теперь, когда мы нашли площадь этого первого квадрата, давайте посмотрим, как мы можем найти площадь второго квадрата, где нам дана длина диагонали вместо длины стороны. Мы можем вспомнить вторую формулу для площади квадрата, который говорит, что он равен 𝑑 в квадрате над двумя, где 𝑑 длина диагонали. Подставляем длину диагонали 𝑑 как 20 сантиметров, у нас есть формула, что площадь равна 20 в квадрате над два. 20 умножить на 20 даст нам 400 и деление на два дает нам площадь 200 квадратных сантиметров.

    Мы не должны забывать в этот момент что мы не ответили на вопрос. Нам еще нужно найти разница. Поэтому берем большую площадь из 289 и вычесть 200, что дает нам окончательный ответ, что разница между площадь этих двух квадратов равна 89 квадратных сантиметров.

    Давайте теперь подведем итог тому, что мы узнал в этом видео. Мы начали с повторения того, что следует быть знакомой формулой, что площадь квадрата равна 𝑙 умножить на 𝑙, где 𝑙 это длина стороны. Затем мы увидели, как можно использовать Теорема Пифагора, позволяющая вывести еще одну формулу площади квадрата. учитывая длину диагонали 𝑑, то есть площадь квадрата равна 𝑑 в квадрате над двумя. Затем мы увидели, как мы можем переставить что формула 𝐴, площадь, равна 𝑑 в квадрате над двумя, что дает нам формулу 𝑑 равно квадратному корню из двух 𝐴. Эта формула позволяет нам более быстро найти длину диагонали, зная площадь квадрата.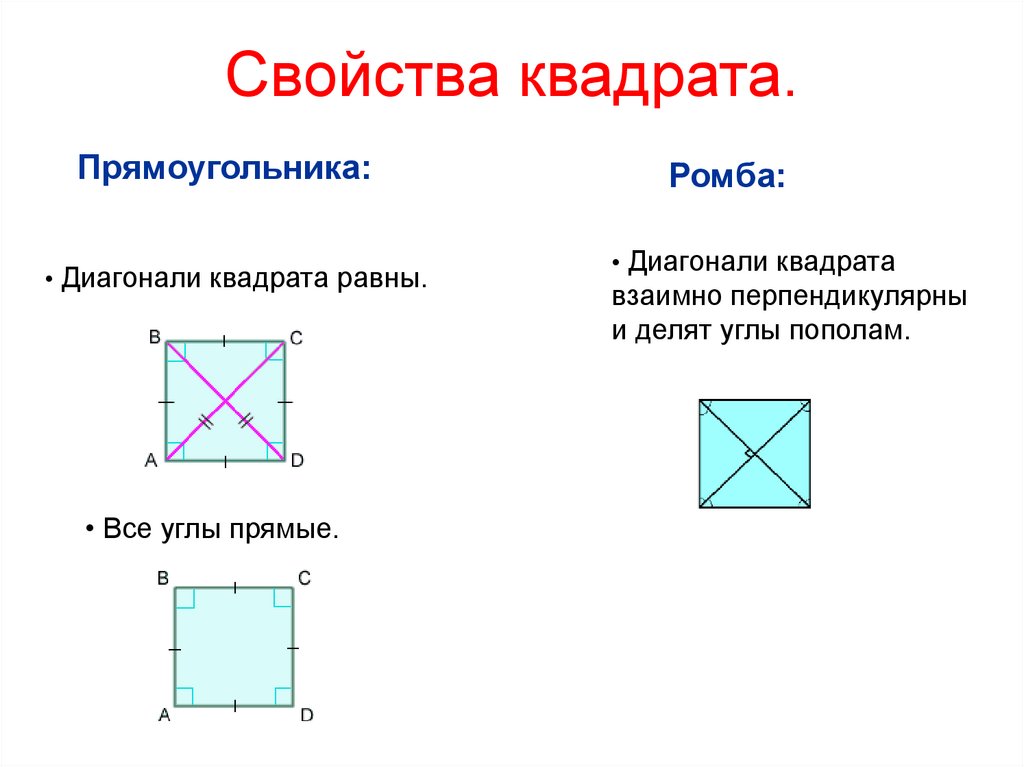

    Диагональ квадратного калькулятора

    Автор: Ханна Памула, доктор философии

    Рецензию сделали Богна Шик и Адена Бенн

    Последнее обновление: 31 января 2023 г.

    Содержание:
    • Диагональ квадрата

      диагональ квадрата?
    • Как использовать эту диагональ квадратного калькулятора?
    • FAQ

    Узнайте длину диагонали квадрата с помощью нашего калькулятора диагонали квадрата. Посмотрите ниже, как найти диагональ квадрата по формуле, или просто попробуйте наш инструмент — вы не будете разочарованы.

    Диагональ квадрата

    Диагональ — это отрезок, соединяющий две несмежные вершины. Каждый четырехугольник имеет две диагонали, квадрат тоже. Его диагонали:

    • Одинаковая длина;
    • Перпендикулярные биссектрисы друг друга; и
    • Биссектрисы квадратных углов.

    Каждая диагональ делит квадрат на два конгруэнтных равнобедренных прямоугольных треугольника — по ним мы сделали калькулятор треугольника 45 45 90.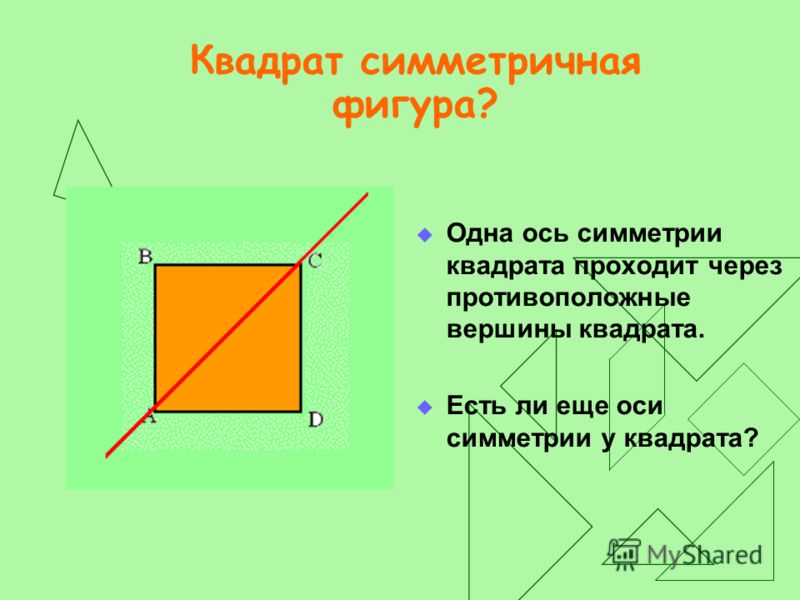 Такой треугольник имеет половину площади квадрата, его катеты являются квадратными сторонами, а гипотенуза равна длине диагонали квадрата.

    Какова формула диагонали квадрата?

    Чтобы вычислить длину диагонали квадрата, умножьте длину стороны на квадратный корень из 2 : диагональ = √2 × сторона . Внедрите эту взаимосвязь в свой мозг и сердце, чтобы никогда больше не задумываться о том, как найти диагональ квадрата.

    Разберем пример. Если сторона квадрата равна 5 дюймам, то диагональ равна 52 дюйма≈7,071 дюйма5\sqrt{2}\ \text{дюйм} \приблизительно 7,071\ \text{дюйм}52​ дюйма≈7,071 дюйма. Введите это значение в поле диагональ квадрата калькулятор, чтобы проверить это самостоятельно! 92}\\ &\text{диагональ}=a\cdot\sqrt{2} \end{split}​a2+a2=diagonal2diagonal=a2+a2

    ​=2⋅a2

    ​diagonal=a⋅2

    Это то же самое, что вычисление гипотенузы в прямоугольном треугольнике.

    Если сторона квадрата не указана, используйте другие формулы:

    d=2⋅aread = \sqrt{2\cdot\text{площадь}}d=2⋅площадь

    ​

    Если площадь дана, и:

    d=периметр4⋅2d = \frac{\text{периметр}}{4}\cdot\sqrt{2}d=4периметр​⋅2

    ​

    Если мы знаем периметр квадрата.

    🙋 Мы также можем научить вас, как найти диагональ прямоугольника с помощью нашего калькулятора диагонали прямоугольника!

    Как использовать эту диагональ квадратного калькулятора?

    С нашим калькулятором это проще простого!

    1. Введите заданное значение в соответствующее поле . Допустим, мы знаем, что сторона квадрата равна 8 дюймам.
    2. Диагональ квадрата Калькулятор выводит результат! В нашем случае диагональ составляет 15,556 дюйма15,556\ \text{дюйм}15,556 дюйма.
    3. Если вы хотите проверить результат в другом блоке, нажмите на название блока и выберите тот, который соответствует вашим потребностям. Например, 15,556 дюйма15,556\ \text{дюйм}15,556 дюйма составляет 39,51 см39,51\ \text{см}39,51 см и около 1 фута 3 дюйма1\ \text{фута}\ 3\ \text{дюйма}1 фута. 3 дюйма
    4. Калькулятор диагонали квадрата работает и наоборот — зная диагональ, можно вычислить сторону квадрата.

    Теперь вы эксперт и точно знаете, как найти диагональ квадрата по сторонам квадрата. Однако, если у вас его нет, используйте этот общий квадратный калькулятор, где вы можете ввести площадь или периметр, и инструмент также найдет диагональ.

    Часто задаваемые вопросы

    Как найти сторону квадрата по диагонали?

    Чтобы вычислить длину стороны квадрата:

    1. Запишите длину диагонали квадрата d .
    2. Разделите d на √2 или, если приближения достаточно, на 1,4142 или просто на 1,41 .
    3. Вот оно! Если вы затрудняетесь с расчетами, воспользуйтесь онлайн-калькулятором квадратов.