Задача 2.15 Гольфарб — Школьная физика — Спроси!
SnUS (Жирослав Метонов) 1
Найти ускорения a1 и a2 грузов массами m1 и m2 и силу натяжения T нити в системе, изображенной на рис. 15. Массой блоков и нити и трением пренебречь. Я дошел до определенного момента, но не понял что делать дальше:
Для тела с массой m1:
T1 — m1g = m1a1
Для тела с массой m2:
m2g — T2 = m2a2
На второй блок с двух сторон вниз действует сила упругости нити, равная T1, тогда T2 = 2T1
1 лайк
AnsarYesma (Ансар) 2
https://znanija.com/task/3474621
SnUS (Жирослав Метонов) 3
Я видел это решение, но не получилось разобраться, почему именно так сделано (т.е. почему первый блок вниз движется, а второй вверх, сила упругости по другому направлена)
ernur045 (Yernur Kairollayev) 4
Сначала разберёмся с твоим решением:
Для начала тут сила натяжения, а не сила упругости. Разница в том, что нить не сжимается, то есть все точки нити имеют одинаковый модуль линейной скорости, и поэтому справедливо равенство x_1 = 2x_2.
Теперь рассмотрим кинематические уравнения: Уравнения
v = \frac {\Delta x} {\Delta t}\\ a = \frac {\Delta v}{\Delta t}
Начни уменьшать промежутки \Delta t и посмотри, к чему это приведёт (Спойлер: к недостающему уравнению)
Теперь про решение на знаниях.

В общем, не имеет значения, куда направлено итоговое ускорение, потому что знаки потом встанут на места, и можешь брать уравнения как хочешь, главное чтобы со знаками проблем потом не вышло. Такой вариант встречается чаще, потому что на второй груз действует вдвое большая сила натяжения
3 лайка
SnUS (Жирослав Метонов) 5
Заранее извиняюсь за такой глупый вопрос, но почему силы натяжения x1 и x2 расставлены именно так? С x1 у левой части первого блока понятно, а вот почему справа она направлена вверх, вроде бы нить должна растягиваться вниз? Такой же вопрос и по x2 в правой части второго блока
1 лайк
ernur045 (Yernur Kairollayev) 6
Прошу перечитать первые предложения моего ответа. Через иксы я обозначал не растяжения нити, а то, куда движутся кусочки нити. В случае, когда правый груз движется вниз, он тянет за собой всю нить. Отсюда и выходят такие вот направления.
- Справа x_1 нить поднимается, чтобы возместить ушедший вслед за m_1 участок нити.
- Самый правый конец нити закреплён, значит после того, как x_1 ушла, длина нити справа от неподвижного блока не меняется, поэтому длина возмещается за счёт перераспределения нити
4 лайка
SnUS (Жирослав Метонов) 7
Спасибо, теперь понял!
3 лайка
Sigvegutt 8
Yernur Kairollayev:Для начала тут сила натяжения, а не сила упругости. Разница в том, что нить не сжимается, то есть все точки нити имеют одинаковый модуль линейной скорости, и поэтому справедливо равенство x1=2×2 x_1 = 2x_2x1=2×2.
Привет. Извините, что поднимаю эту тему, но хотел узнать, откуда именно такое соотношение x1 = 2*x_2? И почему на рисунке движение вниз происходит у груза m1, а не у m2 (или это здесь не так важно?)?
2 лайка
ernur045 (Yernur Kairollayev) 9
Добро пожаловать на форум!
x_1 = 2 x_2 мы получаем за счёт кинематических связей системы. Длина верёвки постоянна, поэтому она слева от неподвижного блока увеличивается настолько, насколько уменьшается справа.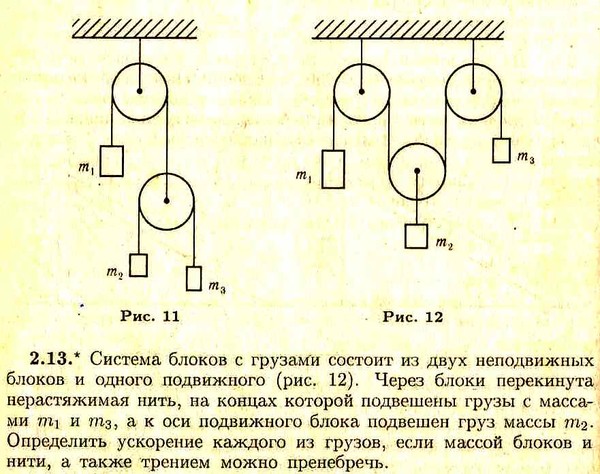 Ну и там два, потому что справа верёвка делится на 2.
Ну и там два, потому что справа верёвка делится на 2.
И почему на рисунке движение вниз происходит у груза m1, а не у m2
Нить невесомая, поэтому сила натяжения вдоль нити не меняется. Получается, если на m_1 действует натяжение T, то на m_2 действует натяжение 2T.
Sigvegutt:Извините, что поднимаю эту тему
Всё хорошо, совершенно нормально задавать дополнительные вопросы, если у тебя они есть
3 лайка
Повторение динамики. 9-10 | Quizizz
Browse from millions of quizzesQUIZ
Physics
83%accuracy
3plays
Alevtina Lebedeva3 years
Physics
Alevtina Lebedeva
plays
7 questions
No student devices needed. Know more
Know more
7 questions
Show AnswersSee Preview
1. Multiple-choice
5 minutes
1 pt
Два бруска массами m1= 1 кг и m2= 3 кг, связанные лёгкой нерастяжимой нитью, находятся на гладкой горизонтальной плоскости (см. рисунок). К ним приложены силы F1= 2 Н и F2= 10 Н. Найдите модуль ускорения системы этих тел. Ответ запишите в м/c2.
2. Multiple-choice
5 minutes
1 pt
Через неподвижный лёгкий блок перекинута невесомая нерастяжимая нить, к концам которой подвешены два груза.

3. Multiple-choice
1 minute
1 pt
В инерциальной системе отсчёта брусок из состояния покоя начинает скользить с ускорением вниз по наклонной плоскости. Равнодействующая всех сил, действующих на брусок, сонаправлена вектору
4. Multiple-choice
5 minutes
1 pt
Два связанных нитью друг с другом бруска массой соответственно m 1 = 200 г и m 2 = 300 г движутся равноускоренно под действием силы F = 2 Н, направленной под углом 60° к горизонту (см.
 рисунок). Чему равна сила натяжения нити между брусками? Трение пренебрежимо мало.
рисунок). Чему равна сила натяжения нити между брусками? Трение пренебрежимо мало.5. Multiple-choice
3 minutes
1 pt
Мальчик стоит на напольных весах в лифте. Лифт начинает движение вверх с ускорением 1 м/с 2 . Что покажут весы в этот момент времени, если в покоящемся лифте они показывали 40 кг? Ответ запишите в кг.
6. Multiple-choice
1 minute
1 pt
В инерциальной системе отсчёта брусок массой m начинает скользить с ускорением вниз по наклонной плоскости (см. рисунок). Модуль равнодействующей сил, действующих на брусок, равен
7.
 Multiple-choice
Multiple-choice1 minute
1 pt
На горизонтальной плоскости находится брусок массой 1 кг. Если к бруску прикладывают горизонтальную силу F = 10 Н, как показано на рисунке а , то он движется по плоскости с ускорением. Коэффициент трения между поверхностью бруска и плоскостью равен 0,5.
Как изменятся вес бруска и модуль действующей на брусок силы трения если, не изменяя модуля силы, изменить её направление так, как показано на рисунке б?
P — увеличится, Fтр — не изменится
P — увеличится, Fтр — увеличится
P — не изменится, Fтр — не изменится
P — уменьшится, Fтр — не изменится
P — уменьшится, Fтр — уменьшится
Expore all questions with a free account
Already have an account?
Натяжение струн: уравнение, размеры и расчет
Сила натяжения — это сила, развиваемая в веревке, струне или кабеле при растяжении под действием приложенной силы.
Сила, возникающая при приложении нагрузки к концам объекта, обычно к его поперечному сечению. Его также можно назвать тянущей силой, напряжением или напряжением.
Этот тип силы проявляется только при контакте между кабелем и объектом. Натяжение также позволяет передавать силу на относительно большие расстояния.
Натяжение при отсутствии ускорения
Предположим, у нас есть тело массой (m) на нити, как показано ниже. Сила тяжести тянет ее вниз, что составляет ее вес:
Натяжение струны
Чтобы струна не разгонялась вниз из-за своей массы, ее нужно тянуть обратно вверх с равной силой. Это то, что мы называем напряжением. Если он не ускоряется, мы можем сказать, что T = mg.
Напряжение при ускорении
Когда у нас есть напряжение в объекте, который ускоряется вверх, т.е. в лифте, поднимающем людей на верхние этажи здания, напряжение не может быть таким же, как вес груза — оно обязательно будет больше. Итак, откуда берется дополнение? Напряжение = усилие для балансировки + дополнительная сила для ускорения. Математически это моделируется следующим образом:
Итак, откуда берется дополнение? Напряжение = усилие для балансировки + дополнительная сила для ускорения. Математически это моделируется следующим образом:
\[T = mg + ma\]
\[T = m (g + a)\]
Другой сценарий, когда лифт опускается вниз. Натяжение не будет равно 0, что приведет к свободному падению. Он будет немного меньше веса предмета. Итак, если выразить это уравнение словами, напряжение = сила, необходимая для баланса, — сила сбрасывается. Математически это будет \(T = mg — ma\), \(T = m (g — a)\).
Примеры работы
Давайте посмотрим на пару примеров работы.
Когда частицы высвобождаются из состояния покоя на приведенной ниже диаграмме, каково натяжение удерживающей их струны?
Пример натяжения струны
Ответ:
В такой ситуации упадет частица с наибольшей массой, а поднимется частица с наименьшей массой. Возьмем частицу массой 2 кг за частицу a, а частицу массой 5 кг за частицу b.
Чтобы уточнить вес каждой частицы, мы должны умножить ее массу на силу тяжести.
Вес a = 2 г
Вес b = 5 г
Теперь вы можете смоделировать уравнение для ускорения и напряжения каждой частицы.
T -2g = 2a [Частица a] [Уравнение 1]
5g -T = 5a [Частица b] [Уравнение 2]
Теперь вы решаете это одновременно. Добавьте оба уравнения, чтобы исключить переменную T.
3g = 7a
Если взять 9,8 мс -2 9{-2}\)
Вы можете подставить ускорение в любое из уравнений, чтобы получить напряжение.
Подставьте ускорение в уравнение 1.
\(T = -2g = 2 \cdot 4,2 \rightarrow T -19,6 = 8,4 \rightarrow T = 28 Н\) гладкий стол и другой с массой 20 кг, висящей сбоку от стола над шкивом, соединяющим обе частицы — показано ниже. Эти частицы удерживались на месте все это время, и теперь они высвобождаются. Что будет дальше? Чему равны ускорение и натяжение струны?
Что будет дальше? Чему равны ускорение и натяжение струны?
Натяжение струны с одной частицей на гладком столе
Ответ: Дополним диаграмму, чтобы увидеть, с чем мы работаем.
Натяжение нити с одной частицей на гладком столе
Примем частицу массой 2 кг за частицу А.
А частицу массой 20 кг за частицу В.
Теперь разложим частицу А по горизонтали.
T = ma [уравнение 1]
Разделение частицы B по вертикали
mg -T = ma [уравнение 2] 9{-2}\)
Теперь учтите ускорение в любом из уравнений. Мы бы сделали первое.
\(T = 2 \cdot \frac{98}{11} = 17,8 Н\)
Натяжение под углом
Мы можем рассчитать натяжение веревки, прикрепленной к грузу под углом. Давайте возьмем пример, чтобы увидеть, как это делается.
Найдите натяжение каждой части струны на диаграмме ниже.
Растяжение под углом
Ответ: нам нужно будет составить два уравнения из всей диаграммы – одно для вертикальных сил, а другое для горизонтальных. Итак, что мы собираемся сделать, так это разделить натяжение обеих струн на их соответствующие вертикальную и горизонтальную составляющие.
Итак, что мы собираемся сделать, так это разделить натяжение обеих струн на их соответствующие вертикальную и горизонтальную составляющие.
Натяжение под углом
\(T_1 \cos 20 =T_2 \cos 30 = 50 \space [Уравнение \space 1] [Vertical]\)\(T_1 \sin 20 = T_2 \sin 30 \space [ Уравнение \пробел 2] [Горизонтальное]\)
Поскольку здесь у нас есть два уравнения и два неизвестных, мы собираемся использовать процедуру одновременного уравнения, чтобы сделать это путем замены.
Теперь перестроим второе уравнение и подставим его в первое уравнение.
\(T_1 = \frac{T_2 \sin 30}{\sin 20}\)
\((\frac{0.5T_2}{0.342}) = \cos 20 + T_2 \cos 30 = 50\)
\((\frac{0.5T_2}{0.342})0.94 + 0.866 \space T_2 = 50 \)
\(1,374 \space T_2 + 0,866 \space T_2 = 50\)
\(2,24 T_2 = 50\)
\(T_2 = 22,32 N\)
Теперь, когда у нас есть значение для 9013 7 т 2 , мы можем подставить это в любое из уравнений. Воспользуемся вторым.
Воспользуемся вторым.
\(T_1 \sin 20 = 22,32 \пробел \sin 30\)
\(T_1 = \frac{11,16}{0,342} = 32,63\)
Натяжение струн. Ключевые выводы
- Сила натяжения — это сила, возникающая в веревке, струне или кабеле при растяжении под действием приложенной силы.
- При отсутствии ускорения напряжение равно весу частицы.
- Натяжение также можно назвать тянущей силой, напряжением или натяжением.
- Этот тип силы проявляется только при контакте между кабелем и объектом.
- При наличии ускорения натяжение равно силе, необходимой для равновесия, плюс дополнительная сила, необходимая для ускорения.
5.6 Common Forces — University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Определение нормальной силы и силы растяжения
- Различать реальные и фиктивные силы
- Применение законов движения Ньютона для решения задач с участием различных сил
Силам дается много названий, например, толкание, тяга, тяга и вес. Традиционно силы были сгруппированы в несколько категорий и получили имена, относящиеся к их источнику, способу их передачи или их воздействию. Некоторые из этих категорий обсуждаются в этом разделе вместе с некоторыми интересными приложениями. Дальнейшие примеры сил обсуждаются далее в этом тексте.
Традиционно силы были сгруппированы в несколько категорий и получили имена, относящиеся к их источнику, способу их передачи или их воздействию. Некоторые из этих категорий обсуждаются в этом разделе вместе с некоторыми интересными приложениями. Дальнейшие примеры сил обсуждаются далее в этом тексте.
Каталог сил: нормальные силы, силы растяжения и другие примеры сил
Каталог сил будет полезен для справки при решении различных задач, связанных с силой и движением. Эти силы включают в себя нормальную силу, натяжение, трение и силу пружины.
Нормальная сила
Вес (также называемый силой тяжести) — это всепроникающая сила, действующая постоянно, и ей необходимо противодействовать, чтобы объект не упал. Вы должны поддерживать вес тяжелого предмета, отталкиваясь от него, удерживая его неподвижно, как показано на рис. 5.21(а). Но как неодушевленные предметы, такие как стол, выдерживают вес размещенного на них груза, как показано на рис.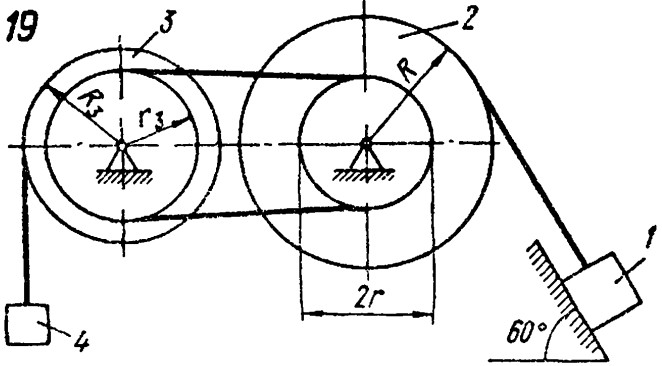 5.21(b)? Когда пакет с собачьим кормом кладут на стол, стол немного прогибается под нагрузкой. Это было бы заметно, если бы груз был помещен на карточный стол, но даже крепкий дубовый стол деформируется при приложении к нему силы. Если объект не деформируется сверх своих пределов, он будет оказывать восстанавливающую силу подобно деформированной пружине (или батуту, или трамплину). Чем больше деформация, тем больше восстанавливающая сила. Таким образом, когда груз помещается на стол, стол прогибается до тех пор, пока восстанавливающая сила не станет равной весу груза. В этот момент чистая внешняя сила, действующая на груз, равна нулю. Это ситуация, когда груз неподвижен на столе. Стол проседает быстро и провисание незначительное, поэтому мы его не замечаем. Но это похоже на провисание батута, когда на него забираешься.
5.21(b)? Когда пакет с собачьим кормом кладут на стол, стол немного прогибается под нагрузкой. Это было бы заметно, если бы груз был помещен на карточный стол, но даже крепкий дубовый стол деформируется при приложении к нему силы. Если объект не деформируется сверх своих пределов, он будет оказывать восстанавливающую силу подобно деформированной пружине (или батуту, или трамплину). Чем больше деформация, тем больше восстанавливающая сила. Таким образом, когда груз помещается на стол, стол прогибается до тех пор, пока восстанавливающая сила не станет равной весу груза. В этот момент чистая внешняя сила, действующая на груз, равна нулю. Это ситуация, когда груз неподвижен на столе. Стол проседает быстро и провисание незначительное, поэтому мы его не замечаем. Но это похоже на провисание батута, когда на него забираешься.
Рисунок
5.21
(a) Человек, держащий пакет с собачьим кормом, должен приложить восходящую силу F→рукаF→рука, равная по величине и противоположная по направлению весу корма w→w→, чтобы он не упал на землю. (b) Карточный стол прогибается, когда на него кладут корм для собак, как жесткий батут. Упругие восстанавливающие силы в столе возрастают по мере его провисания, пока не создадут силу N→N→, равную по величине и противоположную по направлению весу груза.
(b) Карточный стол прогибается, когда на него кладут корм для собак, как жесткий батут. Упругие восстанавливающие силы в столе возрастают по мере его провисания, пока не создадут силу N→N→, равную по величине и противоположную по направлению весу груза.
Мы должны заключить, что все, что поддерживает груз, одушевленное оно или нет, должно создавать направленную вверх силу, равную весу груза, как мы предполагали в нескольких предыдущих примерах. Если сила, поддерживающая вес объекта или груза, перпендикулярна поверхности контакта между грузом и его опорой, эта сила определяется как нормальная сила и здесь обозначается символом N→.N→. (Это не ньютон для силы или Н.) Слово нормальный означает перпендикулярно поверхности. Это означает, что нормальная сила, действующая на объект, покоящийся на горизонтальной поверхности, может быть выражена в векторной форме следующим образом:
N→=−мг→,N→=−мг→,
Объект лежит на горизонтальной поверхности.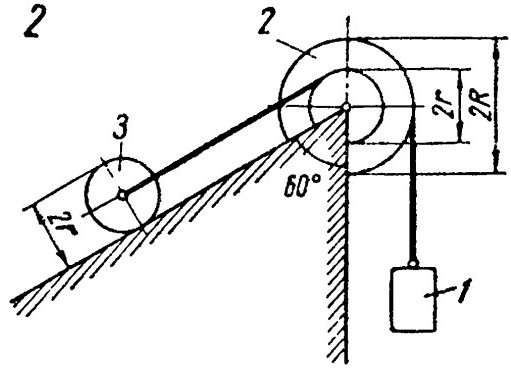 В скалярной форме это становится
В скалярной форме это становится
Н=мг, Н=мг,
Объектлежит на горизонтальной поверхности. Нормальная сила может быть меньше веса объекта, если объект находится под наклоном.
Пример 5.12
Груз на склоне
Рассмотрим лыжника на склоне на рис. 5.22. Ее масса с оборудованием составляет 60,0 кг. а) Чему равно ее ускорение, если трением можно пренебречь? б) Чему равно ее ускорение, если трение равно 45,0 Н? Рисунок
5.22
Поскольку ускорение параллельно склону и действует вниз по склону, все силы удобнее всего спроецировать на систему координат, где одна ось параллельна склону, а другая перпендикулярна ему (оси показаны слева от лыжника). ). N→N→ перпендикулярно склону, а f→f→ параллельно склону, но w→w→ имеет компоненты по обеим осям, а именно, wywy и wxwx. Здесь w→w→ имеет волнистую линию, показывающую, что она была заменена этими компонентами. Сила N→N→ равна по модулю wywy, поэтому ускорение перпендикулярно склону отсутствует, а f меньше, чем wxwx, поэтому имеет место ускорение вниз по склону (вдоль оси, параллельной склону).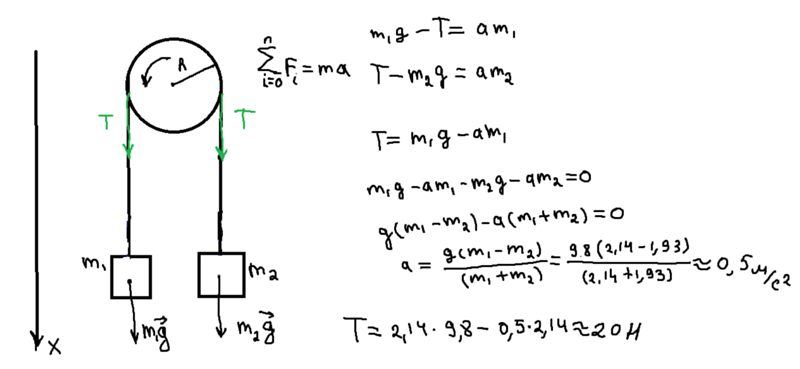
Стратегия
Это двумерная задача, поскольку не все силы, действующие на лыжника (исследуемую систему), параллельны. Здесь также хорошо работает подход, который мы использовали в двумерной кинематике. Выберите удобную систему координат и спроецируйте векторы на ее оси, создав две одномерные задачи для решения. Наиболее удобной системой координат для движения по склону является та, которая имеет одну координату, параллельную склону, и одну, перпендикулярную склону. (Движения вдоль взаимно перпендикулярных осей независимы.) Используем x и y для параллельного и перпендикулярного направлений соответственно. Такой выбор осей упрощает задачу такого типа, поскольку движение перпендикулярно склону отсутствует, а ускорение направлено вниз по склону. Что касается сил, то трение рисуется против движения (трение всегда препятствует движению вперед) и всегда параллельно склону, wxwx рисуется параллельно склону и вниз по склону (вызывает движение лыжника вниз по склону) и wywy изображается как составляющая веса, перпендикулярная уклону. Затем мы можем рассмотреть отдельные задачи о силах, параллельных склону, и силах, перпендикулярных склону.
Затем мы можем рассмотреть отдельные задачи о силах, параллельных склону, и силах, перпендикулярных склону.Решение
Величина составляющей веса, параллельной наклону, равнаwx=wsin25°=mgsin25°,wx=wsin25°=mgsin25°,
и модуль веса, перпендикулярный наклону, равен
wy=wcos25°=mgcos25°.wy=wcos25°=mgcos25 °.
а. Трением пренебречь. Поскольку ускорение параллельно наклону, нам нужно рассматривать только силы, параллельные наклону. (Силы, перпендикулярные склону, складываются в ноль, так как ускорение в этом направлении отсутствует.) Силы, параллельные склону, представляют собой составляющую веса лыжника, параллельную склону, wxwx и силы трения 9.0189 ф . Используя второй закон Ньютона с нижними индексами для обозначения величин, параллельных наклону,
ax=Fnetxmax=Fnetxm
, где Fnetx=wx=mgsin25°, Fnetx=wx=mgsin25°, при условии отсутствия трения в этой части. Следовательно,
ax=Fnetxm=mgsin25°m=gsin25°(9,80 м/с2)(0,4226)=4,14 м/с2ax=Fnetxm=mgsin25°m=gsin25°(9,80 м/с2)(0,4226)=4,14 м/ s2
— ускорение.
б. Включите трение. У нас есть заданное значение трения, и мы знаем, что его направление параллельно склону и оно препятствует движению между соприкасающимися поверхностями. Таким образом, чистая внешняя сила равна
Fnetx=wx-f.Fnetx=wx-f.
Подставив это во второй закон Ньютона, ax=Fnetx/m,ax=Fnetx/m, получим
ax=Fnetxm=wx-fm=mgsin25°-fm.ax=Fnetxm=wx-fm=mgsin25°-fm.
Подставляем известные значения, чтобы получить 0кг.
Это дает нам
ax=3,39 м/с2, ax=3,39 м/с2,
, что является ускорением, параллельным наклону, когда имеется 45,0 Н противодействующего трения.
Значение
Поскольку трение всегда препятствует движению между поверхностями, ускорение при наличии трения меньше, чем при его отсутствии. Общий результат состоит в том, что если трением на склоне можно пренебречь, то ускорение вниз по склону равно a=gsinθa=gsinθ, независимо от массы. Как обсуждалось ранее, все объекты падают с одинаковым ускорением при отсутствии сопротивления воздуха. Точно так же все объекты, независимо от массы, скользят по склону без трения с одинаковым ускорением (если угол одинаков).
Точно так же все объекты, независимо от массы, скользят по склону без трения с одинаковым ускорением (если угол одинаков).Когда объект покоится на наклонной плоскости, составляющей угол θθ с горизонтом, сила тяжести, действующая на объект, делится на две составляющие: силу, действующую перпендикулярно плоскости, wywy, и силу, действующую параллельно плоскости, wxwx (рис. 5.23). Нормальная сила N→N→ обычно равна по величине и противоположна по направлению перпендикулярной составляющей веса wywy. Сила, действующая параллельно плоскости, wxwx, заставляет объект ускоряться вниз по склону.
Рисунок 5.23 Объект лежит на склоне, который составляет угол θθ с горизонтом.
Будьте осторожны при разложении веса объекта на составляющие. Если наклон составляет угол θθ к горизонту, то величины компонентов веса равны
wx=wsinθ=mgsinθwx=wsinθ=mgsinθ
и
wy=wcosθ=mgcosθ.wy=wcosθ=mgcosθ.
Воспользуемся вторым уравнением, чтобы записать нормальную силу, действующую на объект, покоящийся на наклонной плоскости:
N=мгcosθ, N=мгcosθ,
объект в состоянии покоя или скользящий по наклонной плоскости. Вместо того, чтобы запоминать эти уравнения, полезно уметь определять их разумом. Для этого мы рисуем прямой угол, образованный тремя весовыми векторами. Угол наклона θθ такой же, как угол, образованный между w и wywy. Зная это свойство, мы можем с помощью тригонометрии определить величину составляющих веса:
Вместо того, чтобы запоминать эти уравнения, полезно уметь определять их разумом. Для этого мы рисуем прямой угол, образованный тремя весовыми векторами. Угол наклона θθ такой же, как угол, образованный между w и wywy. Зная это свойство, мы можем с помощью тригонометрии определить величину составляющих веса:
cosθ=wyw,wy=wcosθ=mgcosθsinθ=wxw,wx=wsinθ=mgsinθ.cosθ=wyw,wy=wcosθ=mgcosθsinθ=wxw,wx=wsinθ=mgsinθ.
Проверьте свое понимание 5,8
Сила 1150 Н, действующая параллельно пандусу, вталкивает 250-килограммовый оружейный сейф в движущийся фургон. Пандус не имеет трения и наклонен под углом 17°.17°. а) Каково ускорение сейфа вверх по пандусу? б) Если в этой задаче рассмотреть трение при силе трения 120 Н, каково ускорение сейфа?
Напряжение
Натяжение — это сила по длине среды; в частности, это тяговое усилие, действующее вдоль натянутого гибкого соединителя, такого как канат или трос. Слово «напряжение» происходит от латинского слова, означающего «растягивать». Не случайно гибкие шнуры, передающие мышечные силы к другим частям тела, называются 9.0189 сухожилия .
Слово «напряжение» происходит от латинского слова, означающего «растягивать». Не случайно гибкие шнуры, передающие мышечные силы к другим частям тела, называются 9.0189 сухожилия .
Любой гибкий соединитель, такой как веревка, веревка, цепь, проволока или кабель, может оказывать натяжение только параллельно своей длине; таким образом, сила, переносимая гибким соединителем, представляет собой натяжение с направлением, параллельным соединителю. Напряжение — это натяжение в соединителе. Рассмотрим фразу: «Вы не можете толкнуть веревку». Вместо этого сила натяжения тянет наружу вдоль двух концов веревки.
Рассмотрим человека, держащего груз на веревке, как показано на рис. 5.24. Если масса 5,00 кг на рисунке неподвижна, то ее ускорение равно нулю и результирующая сила равна нулю. Единственными внешними силами, действующими на массу, являются ее вес и натяжение веревки. Таким образом,
Fnet=T−w=0,Fnet=T−w=0,
, где T и w — величины натяжения и веса, соответственно, а их знаки указывают направление, причем вверх положительно. Как мы доказали с помощью второго закона Ньютона, натяжение равно весу поддерживаемой массы:
Как мы доказали с помощью второго закона Ньютона, натяжение равно весу поддерживаемой массы:
Т=вес=мг, Т=вес=мг,
Объектвисит в состоянии покоя. Таким образом, для массы 5,00 кг (без учета массы веревки) получаем, что
T=мг=(5,00 кг)(9,80 м/с2)=49,0 Н.Т=мг=(5,00 кг)(90,80 м/с2)=49,0 Н.
Если мы разрежем веревку и вставим пружину, пружина растянется на длину, соответствующую силе 49,0 Н, что обеспечит прямое наблюдение и измерение силы натяжения веревки.
Рисунок
5.24
Когда совершенно гибкий соединитель (не требующий усилия для его изгиба), такой как эта веревка, передает силу T→,T→, эта сила должна быть параллельна длине веревки, как показано на рисунке. По третьему закону Ньютона веревка тянет с одинаковой силой, но в противоположных направлениях, на руку и поддерживаемую массу (без учета веса веревки). Веревка — это среда, которая переносит равные и противоположные силы между двумя объектами. Натяжение в любом месте веревки между рукой и грузом одинаково. Как только вы определили натяжение в одном месте, вы определили натяжение во всех точках веревки.
Как только вы определили натяжение в одном месте, вы определили натяжение во всех точках веревки.
Гибкие соединители часто используются для передачи сил на поворотах, например, в больничной системе вытяжения, сухожилии или велосипедном тормозном тросе. Если нет трения, передача натяжения не уменьшается; меняется только его направление, и он всегда параллелен гибкому соединителю, как показано на рис. 5.25.
Рисунок 5,25 (а) Сухожилия в пальце переносят силу T от мышц к другим частям пальца, обычно изменяя направление силы, но не ее величину (сухожилия относительно свободны от трения). (b) Тормозной трос на велосипеде выдерживает натяжение T от рычага тормоза на руле к тормозному механизму. Снова изменилось направление, но не величина T .
Пример 5.13
Что такое натяжение каната?
Рассчитайте натяжение троса, поддерживающего канатоходца массой 70,0 кг, показанного на рис. 5.26.
5.26.Рисунок 5.26 Вес канатоходца заставляет проволоку прогибаться на 5,0°5,0°. Исследуемая система представляет собой точку на проводе, в которой стоит канатоходец.
Стратегия
Как видно на рис. 5.26, проволока изгибается под весом человека. Таким образом, напряжение с обеих сторон человека имеет направленный вверх компонент, способный выдержать его вес. Как обычно, силы представляют собой векторы, представленные графически стрелками, которые имеют то же направление, что и силы, и длины, пропорциональные их величине. Система представляет собой канатоходца, и единственными внешними силами, действующими на него, являются его вес w→w→ и два напряжения T→LT→L (левое натяжение) и T→RT→R (правое натяжение). Весом провода разумно пренебречь. Чистая внешняя сила равна нулю, потому что система статична. Мы можем использовать тригонометрию, чтобы найти напряжения. Вначале возможен один вывод — из рис. 5.26(б) видно, что величины натяжений TLTL и TRTR должны быть равны. Мы знаем это, потому что в веревке нет горизонтального ускорения, и единственными силами, действующими влево и вправо, являются TLTL и TRTR. Таким образом, величина этих горизонтальных составляющих сил должна быть равна, чтобы они уравновешивали друг друга.
Мы знаем это, потому что в веревке нет горизонтального ускорения, и единственными силами, действующими влево и вправо, являются TLTL и TRTR. Таким образом, величина этих горизонтальных составляющих сил должна быть равна, чтобы они уравновешивали друг друга.Всякий раз, когда у нас есть двумерные векторные задачи, в которых нет двух параллельных векторов, самый простой способ решения — выбрать удобную систему координат и спроецировать векторы на ее оси. В этом случае наилучшая система координат имеет одну горизонтальную ось ( x ) и одну вертикальную ось ( y ).
Раствор
Во-первых, нам нужно разложить векторы натяжения на их горизонтальную и вертикальную составляющие. Это помогает взглянуть на новую диаграмму свободного тела, показывающую все горизонтальные и вертикальные компоненты каждой силы, действующей на систему (рис. 5.27). Рисунок
5.27
При проецировании векторов на вертикальную и горизонтальную оси их составляющие по этим осям должны в сумме равняться нулю, так как канатоходец неподвижен. Малый угол приводит к тому, что T намного больше, чем w .
Малый угол приводит к тому, что T намного больше, чем w .
Рассмотрим горизонтальные компоненты сил (обозначенные нижним индексом x ):
Fnetx=TRx-TLx.Fnetx=TRx-TLx.
Суммарная внешняя горизонтальная сила Fnetx=0,Fnetx=0, так как человек неподвижен. Таким образом,
Fnetx=0=TRx-TLxTLx=TRx.Fnetx=0=TRx-TLxTLx=TRx.
Теперь обратите внимание на рисунок 5.27. Вы можете использовать тригонометрию для определения величины TLTL и TRTR:
cos5.0°=TLxTL,TLx=TLcos5.0°cos5.0°=TRxTR,TRx=TRcos5.0°.cos5.0°=TLxTL,TLx =TLcos5.0°cos5.0°=TRxTR,TRx=TRcos5.0°.
Эквивалент T L x и T R x :
TLcos5.0°=TRcos5. 0°.TLcos5.0°=TRcos5.0°.
Таким образом,
TL=TR=T,TL=TR=T,
как и предполагалось. Теперь, рассматривая вертикальные компоненты (обозначенные нижним индексом y ), мы можем найти T . Опять же, поскольку человек неподвижен, второй закон Ньютона подразумевает, что Fnety=0Fnety=0. Таким образом, как показано на диаграмме свободного тела,
Теперь, рассматривая вертикальные компоненты (обозначенные нижним индексом y ), мы можем найти T . Опять же, поскольку человек неподвижен, второй закон Ньютона подразумевает, что Fnety=0Fnety=0. Таким образом, как показано на диаграмме свободного тела,
Fnety=TLy+TRy-w=0.Fnety=TLy+TRy-w=0.
Мы можем использовать тригонометрию, чтобы определить отношения между TLy, TRy, TLy, TRy и T . Как мы определили из анализа в горизонтальном направлении, TL=TR=TTL=TR=T:
sin5.0°=TLyTL,TLy=TLsin5.0°=Tsin5.0°sin5.0°=TRyTR,TRy=TRsin5.0°=Tsin5.0°.sin5.0°=TLyTL,TLy=TLsin5. 0°=Tsin5.0°sin5.0°=TRyTR,TRy=TRsin5.0°=Tsin5.0°.
Теперь мы можем подставить значения для TlyTLy и TRyTRy в уравнение общей силы в вертикальном направлении:
Fnety=TLy+TRy−w=0Fnety=Tsin5.0°+Tsin5.0°−w=02Tsin5.0 °−w=02Tsin5.0°=wFnety=TLy+TRy−w=0Fnety=Tsin5.0°+Tsin5.0°−w=02Tsin5.0°−w=02Tsin5.0°=w
и
T =w2sin5. 0°=mg2sin5.0°,T=w2sin5.0°=mg2sin5.0°,
0°=mg2sin5.0°,T=w2sin5.0°=mg2sin5.0°,
, поэтому
T=(70,0 кг)(9,80 м/с2)2(0,0872),T=(70,0 кг)(9,80 м/с2)2(0,0872),
и натяжение
T=3930 Н .Т=3930Н.
Значение
Вертикальное натяжение троса действует как сила, поддерживающая вес канатоходца. Натяжение почти в шесть раз превышает вес 686 Н канатоходца. Поскольку проволока почти горизонтальна, вертикальная составляющая ее натяжения составляет лишь часть натяжения проволоки. Большие горизонтальные компоненты направлены в противоположные стороны и компенсируются, поэтому большая часть натяжения проволоки не используется для поддержки веса канатоходца.Если мы хотим создать большое натяжение, все, что нам нужно сделать, это приложить усилие, перпендикулярное натянутому гибкому соединителю, как показано на рис. 5.26. Как мы видели в примере 5.13, вес канатоходца действует как сила, перпендикулярная веревке. Мы видели, что натяжение веревки связано с весом канатоходца следующим образом:
T=w2sinθ. T=w2sinθ.
T=w2sinθ.
Мы можем расширить это выражение, чтобы описать натяжение T , создаваемое перпендикулярной силой (F⊥)(F⊥) к середине гибкого соединителя:
Т=F⊥2sinθ.T=F⊥2sinθ.
Угол между горизонталью и изогнутым соединителем обозначается θθ. В этом случае T становится большим, когда θθ приближается к нулю. Даже относительно небольшой вес любого гибкого соединителя вызовет его провисание, так как если бы он был горизонтальным (т. е. θ=0θ=0 и sin θ=0θ=0), возникло бы бесконечное натяжение). Например, на рис. 5.28 показана ситуация, когда мы хотим вытащить автомобиль из грязи, когда эвакуатора нет. Каждый раз, когда автомобиль движется вперед, цепь натягивается, чтобы он оставался как можно более прямым. Натяжение в цепи определяется как T=F⊥2sinθ,T=F⊥2sinθ, а поскольку θθ мало, T большой. Эта ситуация аналогична ситуации с канатоходцем, за исключением того, что показанные здесь напряжения передаются машине и дереву, а не действуют в точке приложения F⊥F⊥.
Рисунок 5,28 Мы можем создать сильное натяжение в цепи — и, возможно, большой беспорядок — надавив на нее перпендикулярно ее длине, как показано на рисунке.
Проверьте свое понимание 5,9
Один конец 3,0-метровой веревки привязан к дереву; другой конец привязан к застрявшей в грязи машине. Автомобилист тянет вбок за середину веревки, смещая ее на расстояние 0,25 м. Если он приложит в этих условиях силу 200,0 Н, определите силу, действующую на автомобиль.
В «Применении законов Ньютона» мы расширяем обсуждение натяжения троса, включив в него случаи, когда показанные углы не равны.
Трение
Трение – это сила сопротивления, противодействующая движению или его тенденции. Представьте себе объект, покоящийся на горизонтальной поверхности. Суммарная сила, действующая на объект, должна быть равна нулю, что приводит к равенству веса и нормальной силы, действующих в противоположных направлениях. Если поверхность наклонена, нормальная сила уравновешивает составляющую веса, перпендикулярную поверхности. Если предмет не скользит вниз, то часть веса, параллельная наклонной плоскости, уравновешивается трением. Трение обсуждается более подробно в следующей главе.
Если предмет не скользит вниз, то часть веса, параллельная наклонной плоскости, уравновешивается трением. Трение обсуждается более подробно в следующей главе.
Сила пружины
Пружина – это особая среда со специфической атомарной структурой, обладающая способностью восстанавливать свою форму при деформации. Чтобы восстановить свою форму, пружина прикладывает восстанавливающую силу, которая пропорциональна и направлена в противоположном направлении, в котором она растягивается или сжимается. Это формулировка закона, известного как закон Гука, который имеет математическую форму
. F→=−kx→.F→=−kx→.5.11
Константа пропорциональности k является мерой жесткости пружины. Линия действия этой силы параллельна оси пружины, а направление силы противоположно направлению вектора смещения (рис. 5.29).). Смещение должно быть измерено из расслабленного положения; x=0x=0, когда пружина ослаблена.
Рисунок
5. 29
Сила пружины пропорциональна смещению независимо от того, сжата она или растянута. (а) Пружина находится в расслабленном состоянии и не оказывает никакого действия на блок. (b) Пружина сжимается перемещением Δx→1Δx→1 объекта и оказывает восстанавливающую силу −kΔx→1.−kΔx→1. (c) Пружина растягивается за счет смещения Δx→2Δx→2 объекта и оказывает восстанавливающую силу −kΔx→2.−kΔx→2.
29
Сила пружины пропорциональна смещению независимо от того, сжата она или растянута. (а) Пружина находится в расслабленном состоянии и не оказывает никакого действия на блок. (b) Пружина сжимается перемещением Δx→1Δx→1 объекта и оказывает восстанавливающую силу −kΔx→1.−kΔx→1. (c) Пружина растягивается за счет смещения Δx→2Δx→2 объекта и оказывает восстанавливающую силу −kΔx→2.−kΔx→2.
Реальные силы и инерциальные системы координат
Есть еще одно различие между силами: одни силы реальны, а другие нет. Реальные силы имеют физическое происхождение, например гравитационное притяжение. Напротив, фиктивные силы возникают просто потому, что наблюдатель находится в ускоряющейся или неинерциальной системе отсчета, такой как та, которая вращается (как карусель) или подвергается линейному ускорению (например, автомобиль замедляется). Например, если спутник движется строго на север над северным полушарием Земли, то наблюдателю на Земле будет казаться, что он испытывает на западе силу, не имеющую физического происхождения. Вместо этого Земля вращается на восток и движется на восток под спутником. В системе Земли это выглядит как западная сила, действующая на спутник, или это можно интерпретировать как нарушение первого закона Ньютона (закона инерции). Мы можем идентифицировать фиктивную силу, задав вопрос: «Что такое сила реакции?» Если мы не можем назвать силу реакции, то рассматриваемая нами сила является фиктивной. В примере со спутником сила реакции должна быть направлена на восток на Земле. Напомним, что инерциальная система отсчета — это система, в которой все силы реальны, и, что эквивалентно, система, в которой законы Ньютона имеют простую форму, приведенную в этой главе.
Вместо этого Земля вращается на восток и движется на восток под спутником. В системе Земли это выглядит как западная сила, действующая на спутник, или это можно интерпретировать как нарушение первого закона Ньютона (закона инерции). Мы можем идентифицировать фиктивную силу, задав вопрос: «Что такое сила реакции?» Если мы не можем назвать силу реакции, то рассматриваемая нами сила является фиктивной. В примере со спутником сила реакции должна быть направлена на восток на Земле. Напомним, что инерциальная система отсчета — это система, в которой все силы реальны, и, что эквивалентно, система, в которой законы Ньютона имеют простую форму, приведенную в этой главе.
Вращение Земли настолько медленное, что Земля представляет собой почти инерциальную систему отсчета. Обычно вы должны проводить точные эксперименты, чтобы наблюдать фиктивные силы и небольшие отклонения от законов Ньютона, такие как только что описанный эффект. В больших масштабах, таких как вращение погодных систем и океанских течений, эффекты можно легко наблюдать (рис. 5.30).
5.30).
Рисунок 5.30 Ураган Фрэн направляется к юго-восточному побережью США 19 сентября.96. Обратите внимание на характерную форму «глаза» урагана. Это результат эффекта Кориолиса, который представляет собой отклонение объектов (в данном случае воздуха) во вращающейся системе отсчета, подобно вращению Земли. Этот ураган показывает вращение против часовой стрелки, потому что это шторм низкого давления. (кредит «бегун»: модификация работы «Greenwich Photography»/Flickr)
Решающим фактором в определении того, является ли система отсчета инерциальной, является ее ускорение или вращение относительно известной инерциальной системы отсчета. Если не указано иное, все явления, обсуждаемые в этом тексте, находятся в инерциальных системах отсчета.
Силы, обсуждаемые в этом разделе, являются реальными силами, но не единственными реальными силами. Подъемная сила и тяга, например, являются более специализированными реальными силами. Есть ли в длинном списке сил более основные, чем другие? Являются ли различные проявления одной и той же основной силы? Ответ на оба вопроса положительный, как вы увидите в трактовке современной физики далее в тексте.


 рисунок). Чему равна сила натяжения нити между брусками? Трение пренебрежимо мало.
рисунок). Чему равна сила натяжения нити между брусками? Трение пренебрежимо мало. Multiple-choice
Multiple-choice
Leave A Comment