Ядерные реакции (задачи)

Ядерные реакции

1. Перечислить несколько ядерных реакций, в которых может образоваться изотоп 8Be.

2. Какую минимальную кинетическую энергию в лабораторной системе Tmin должен иметь нейтрон, чтобы стала возможной реакция 16O(n,α)13C?

3. Является ли реакция 6Li(d,α)4He эндотермической или экзотермической? Даны удельные энергии связи ядер в МэВ: ε(d) = 1.11; ε() = 7.08; ε(6Li) = 5.33.

4. Определить пороги Tпор реакций фоторасщепления 12С.

  1. γ + 12С → 11С + n
  2. γ + 12С → 11В + р
  3. γ + 14С → 12С + n + n

5. Определить пороги реакций: 7Li(p,α)4He и 7Li(p,γ)8Be.

6. Определить, какую минимальную энергию должен иметь протон, чтобы стала возможной реакция p + d → p + p + n. Даны избытки масс. Δ(1H) = 7.289 МэВ, Δ(2H) = 13.136 МэВ,
Δ(n) = 8.071 МэВ. 

7. Возможны ли реакции:

  1. α + 7Li → 10B + n;
  2. α + 12C → 14N + d

под действием α-частиц с кинетической энергией T = 10 МэВ?

8. Идентифицировать частицу X и рассчитать энергии реакции Q в следующих случаях:

1. 35Сl + X→ 32S + α;4. 23Na + p→
20Ne + X;
2. 10B + X→ 7Li + α;5. 23Na + d→ 24Mg + X;
3. 7Li + X →7Be + n;6. 23Na + d→ 24Na + X.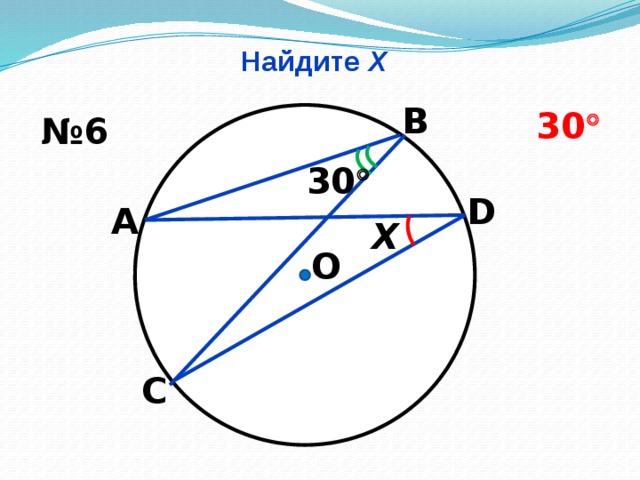

9. Какую минимальную энергию Tmin должен иметь дейтрон, чтобы в результате неупругого рассеяния на ядре 10B возбудить состояние с энергией Eвозб = 1.75 МэВ?

10. Вычислить порог реакции: 14

N + α→17О + p, в двух случаях, если налетающей частицей является:
1) α-частица,
2) ядро 14N. Энергия реакции Q = 1.18 МэВ. Объяснить результат.

11. Рассчитать энергии и пороги следующих реакций:

1. d( p,γ)3He;5. 32S(γ,p )31P;
2. d( d,3He )n;  6. 32 (γ,n )31S;
3. 7Li( p,n )7Be;7. 32S(γ,α)28Si;
4. 3He(α,γ)
7Be;		8. 4He(α,p)7Li;

 

12. Какие ядра могут образовываться в результате реакций под действием: 1) протонов с энергией 10 МэВ на мишени из 7Li; 2) ядер 7Li с энергией 10 МэВ на водородной мишени?

13. Ядро 7LI захватывает медленный нейтрон и испускает γ-квант. Чему равна энергия γ-кванта?

14. Определить в лабораторной системе кинетическую энергию ядра 9Ве, образующегося при пороговом значении энергии нейтрона в реакции

12C(n,α)9Be.

15. При облучении мишени из натурального бора наблюдалось появление радиоактивных изотопов с периодами полураспада 20.4 мин и 0.024 с. Какие образовались изотопы? Какие реакции привели к образованию этих изотопов?

16. Мишень из натурального бора бомбардируется протонами. После окончания облучения детектор -частиц зарегистрировал активность 100 Бк.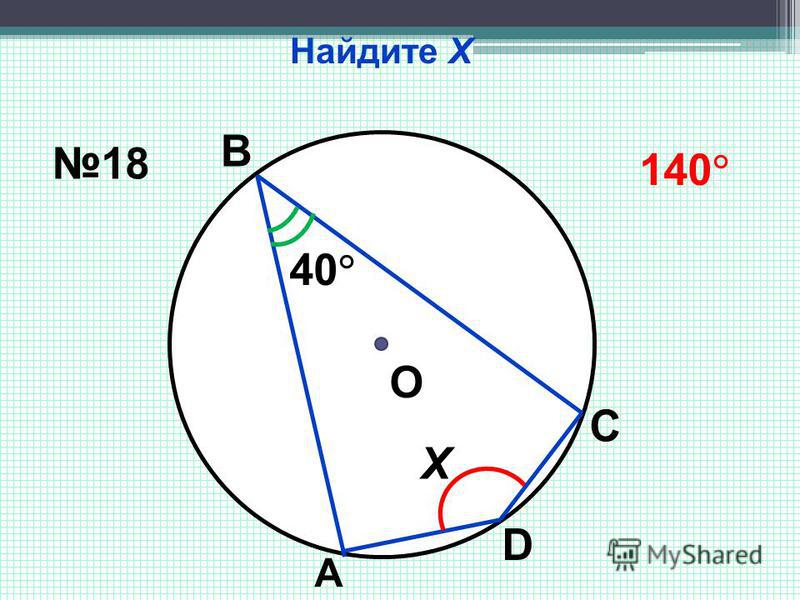 Через 40 мин активность образца снизилась до ~25 Бк. Каков источник активности? Какая ядерная реакция происходит?

17. α-Частица с кинетической энергией T = 10 МэВ испытывает упругое лобовое столкновение с ядром 12С. Определить кинетическую энергию в л.с. ядра 12C TC после столкновения.

18. Определить максимальную и минимальную энергии ядер 7Ве, образующихся в реакции
7Li(p,n)7Be (Q = -1,65 МэВ) под действием ускоренных протонов с энергией Tp = 5 МэВ.

19. -Частицы, вылетающие под углом θнеупр = 300 в результате реакции неупругого рассеяния с возбуждением состояния ядра 12C с энергией Eвозб = 4.44 МэВ, имеют такую же энергию в л.с., что и упруго рассеянные на том же ядре α-частицы под углом θ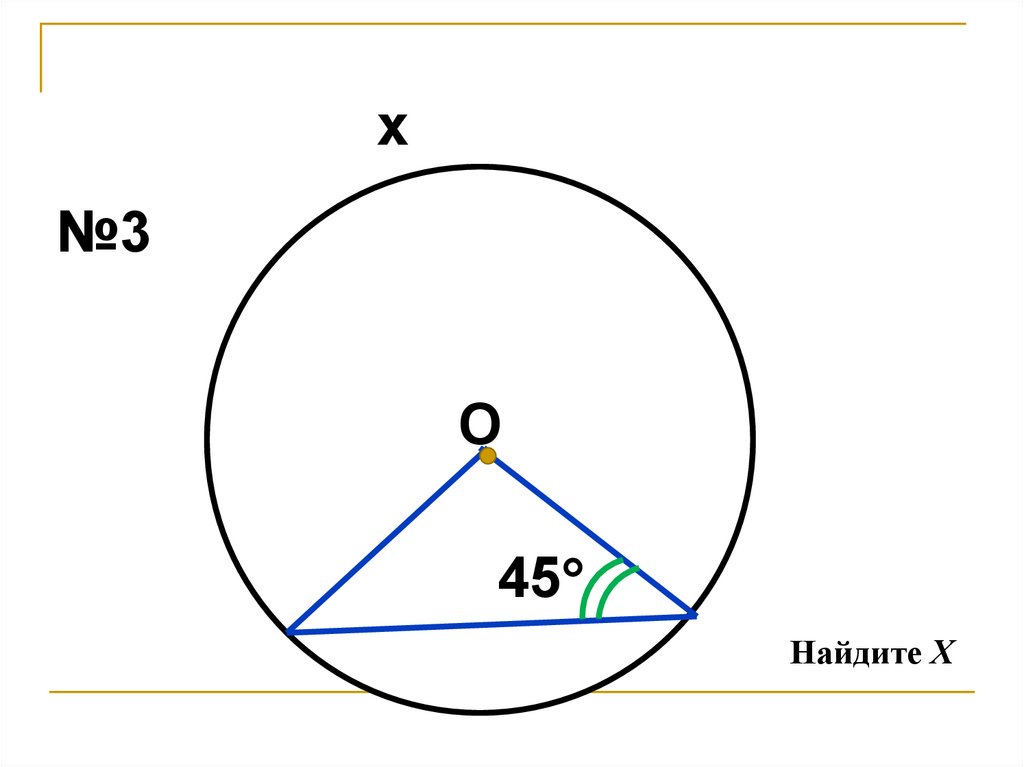

упр = 450. Определить энергию α-частиц, падающих на мишень .

20. α-Частицы с энергией T = 5 МэВ взаимодействуют с неподвижным ядром 7Li. Определить величины импульсов в с.ц.и., образующихся в результате реакции 7Li(α,n)10B нейтрона pα и ядра 10B pBe.

21. С помощью реакции 32S(α,p)35Cl исследуются низколежащие возбужденные состояния

35Cl (1.219; 1.763; 2.646; 2.694; 3.003; 3.163 МэВ). Какие из этих состояний будут возбуждаться на пучке α-частиц с энергией 5.0 МэВ? Определить энергии протонов, наблюдаемых в этой реакции под углами 00 и 900 при Е =5.0 МэВ.

22. Используя импульсную диаграмму получить связь между углами в л.с. и с.ц.и.

23. Протон с кинетической энергией Тa= 5 МэВ налетает на ядро 1Н и упруго рассеивается на нем. Определить энергию TB и угол рассеяния θB ядра отдачи 1Н, если угол рассеяния протона θb = 30

0.

24. Для получения нейтронов широко используется реакция t(d,n)α. Определить энергию нейтронов Tn, вылетающих под углом 900 в нейтронном генераторе, использующем дейтроны, ускоренные до энергии Тd = 0.2 МэВ.

25. Для получения нейтронов используется реакция 7Li(p,n)7Be. Энергия протонов Tp = 5 МэВ. Для эксперимента необходимы нейтроны с энергией Tn = 1.75 МэВ. Под каким углом θn относительно направления протонного пучка будут вылетать нейтроны с такой энергией? Какой будет разброс энергий нейтронов ΔT, если их выделять с помощью коллиматора размером 1 см, расположенного на расстоянии 10 см от мишени.

26. Определить орбитальный момент трития lt, образующегося в реакции 27Al(,t)28Si, если орбитальный момент налетающей α-частицы lα = 0.

27.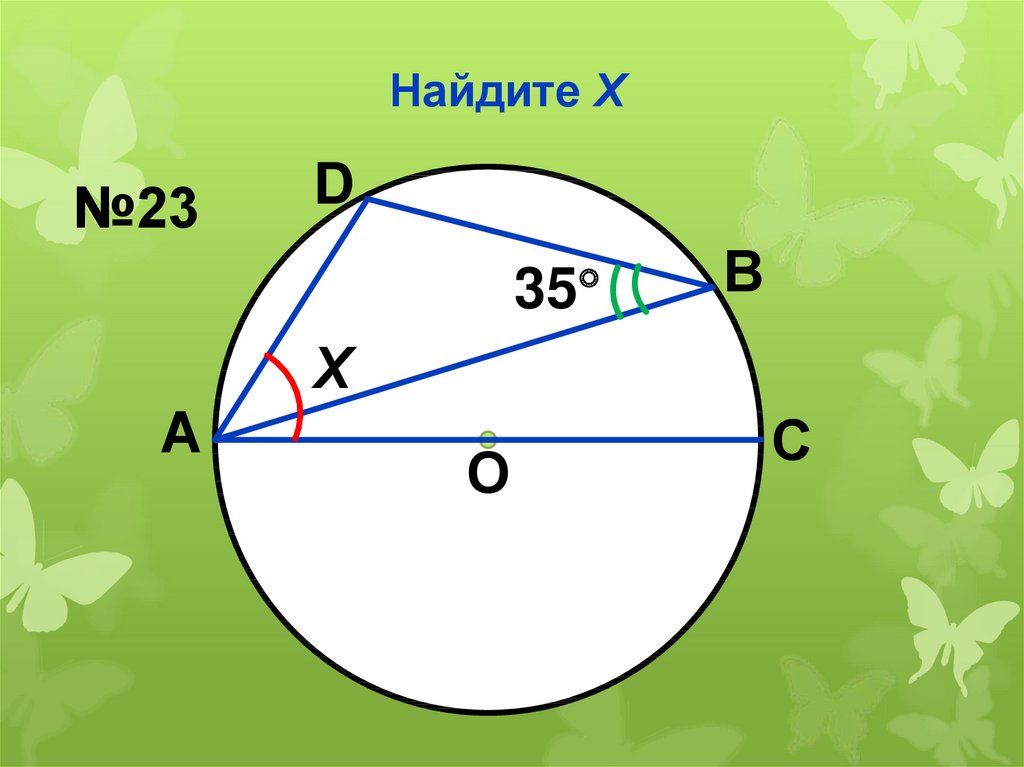 При каких относительных орбитальных моментах количества движения протона возможна ядерная реакция p + 7Li → 8Be*→  α + α?

28. С какими орбитальными моментами lp могут вылетать протоны в реакции 12C(,p)11B, если: 1) конечное ядро образуется в основном состоянии, а поглотился Е2- фотон; 2) конечное ядро образуется в состоянии 1/2+, а поглотился М1- фотон; 3) конечное ядро образуется в основном состоянии, а поглотился Е1- фотон?

29. В результате поглощения ядром -кванта вылетает нейтрон с орбитальным моментом ln = 2. Определить мультипольность -кванта, если конечное ядро образуется в основном состоянии.

30. Ядро 12C поглощает γ-квант, в результате чего вылетает протон с орбитальным моментом l = 1. Определить мультипольность поглощенного γ-кванта, если конечное ядро образуется в основном состоянии?

31.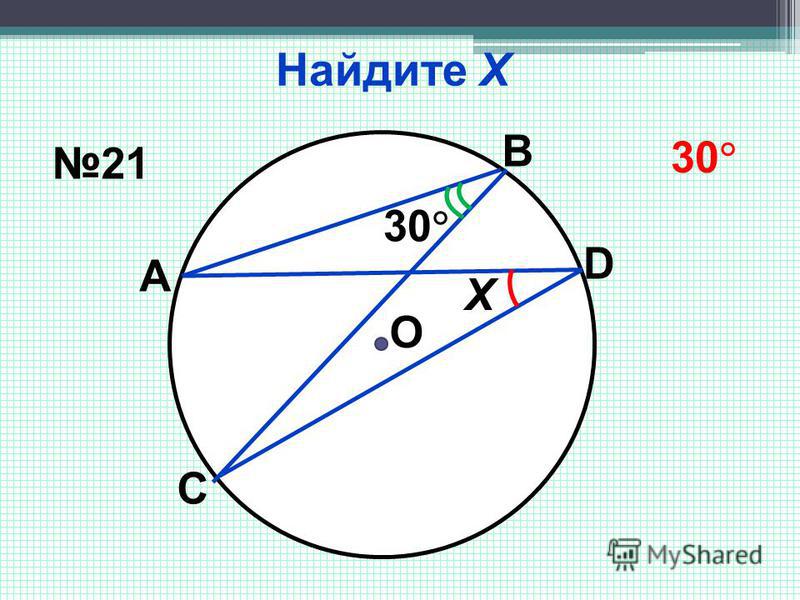 Определить орбитальный момент дейтрона ld в реакции подхвата 15N(n,d)14C, если орбитальный момент нейтрона ln = 0.

33. Ядро 40Cа поглощает Е1 γ-квант. Какие одночастичные переходы возможны?

34. Ядро 12C поглощает Е1 γ-квант. Какие одночастичные переходы возможны ?

35. Можно ли в реакции неупругого рассеяния дейтронов на ядре

10В возбудить состояние с характеристиками JP = 2+ , I = 1?

36. Вычислить сечение рассеяния -частицы с энергией 3 МэВ в кулоновском поле ядра 238U в интервале углов от 1500 до 1700.

37. Золотая пластинка толщиной d = 0.1 мм облучается пучком α-частиц с интенсивностью N0 = 103 частиц/c. Кинетическая энергия -частиц T = 5 МэВ. Сколько α-частиц на единицу телесного угла падает в секунду на детектор, расположенный под углом = 1700? Плотность золота ρ = 19.3 г/см3.

38. Коллимированный пучок α-частиц с энергией T = 10 МэВ падает перпендикулярно на медную фольгу толщиной δ = 1 мг/см2. Частицы, рассеянные под углом = 30, регистрируются детектором площадью S = 1см2, расположенным на расстоянии l = 20 см от мишени. Какая доля от полного числа рассеянных α-частиц будет зарегистрирована детектором?

39. При исследовании реакции 27Al(p,d)26Al под действием протонов с энергией Tp = 62 МэВ в спектре дейтронов, измеренном под углом θd = 90 с помощью детектора с телесным углом
dΩ = 2·10-4 ср, наблюдались пики с энергиями Td = 45,3; 44,32; 40.91 МэВ. При суммарном заряде протонов q = 2.19 мКл, упавших на мишень толщиной δ = 5 мг/см2, количество отсчетов в этих пиках N составило 5180, 1100 и 4570 соответственно.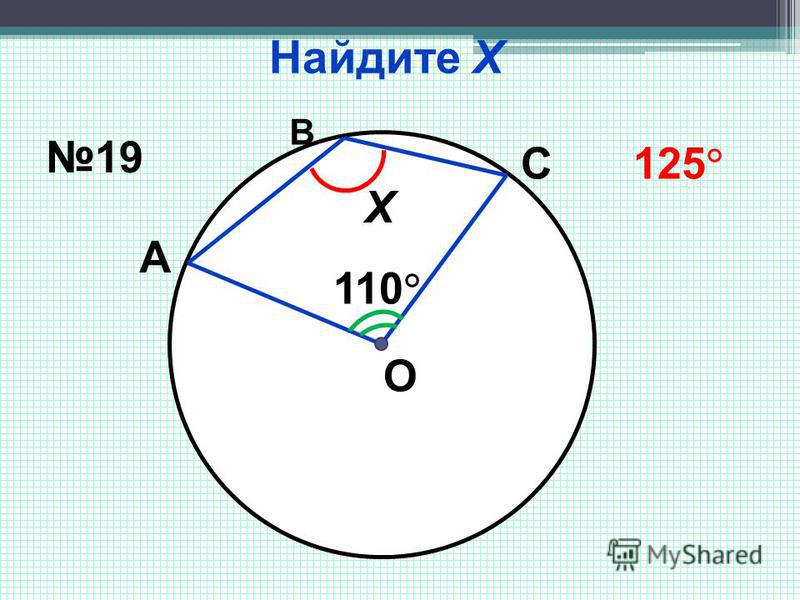 Определить энергии уровней ядра 26Al, возбуждение которых наблюдалось в этой реакции. Рассчитать дифференциальные сечения dσ/dΩ этих процессов.

40. Интегральное сечение реакции 32S(γ,p)31P с образованием конечного ядра 31P в основном состоянии при энергии падающих γ-квантов, равной 18 МэВ, составляет 4 мб. Оценить величину интегрального сечения обратной реакции 31P(p,γ)32S, отвечающей той же энергии возбуждения ядра 32S, что и в реакции 32S(γ,p)31P. Учесть, что это возбуждение снимается за счет γ-перехода в основное состояние.

41. Рассчитать интенсивность пучка нейтронов J, которым облучали пластинку 55Mn толщиной d = 0.1 см в течении tакт = 15 мин, если спустя tохл = 150 мин после окончания облучения ее активность I составила 2100 Бк. Период полураспада 56Mn 2.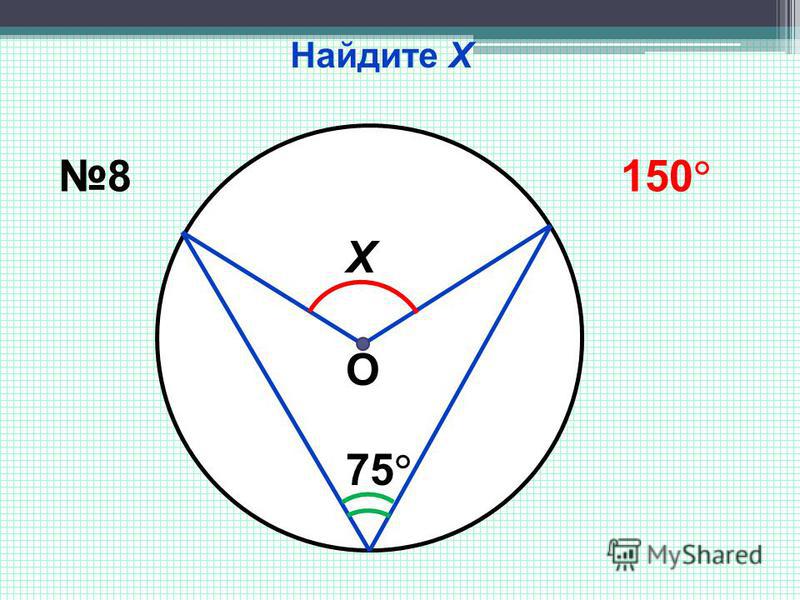 58 ч, сечение активации σ = 0.48 б, плотность вещества пластины ρ = 7.42 г/см3.

42. Дифференциальное сечение реакции dσ/dΩ под углом 900 составляет 10 мб/ср. Рассчитать величину интегрального сечения, если угловая зависимость дифференциального сечения имеет вид 1+2sinθ.

43. Рассеяние медленных (Tn1 кэВ) нейтронов на ядре изотропно. Как можно объяснить этот факт?

44. Определить энергию возбуждения составного ядра, образующегося при захвате α-частицы с энергией T = 7 МэВ неподвижным ядром 10В.

45. В сечении реакции 27Аl (α,р) 30Si наблюдаются максимумы при энергиях α-частиц T 3.95; 4.84 и 6.57 МэВ. Определить энергии возбуждения составного ядра, соответствующие максимумам в сечении.

46. С каким орбитальным моментом могут рассеиваться протоны с Тр = 2 МэВ на ядре 112Sn?

47.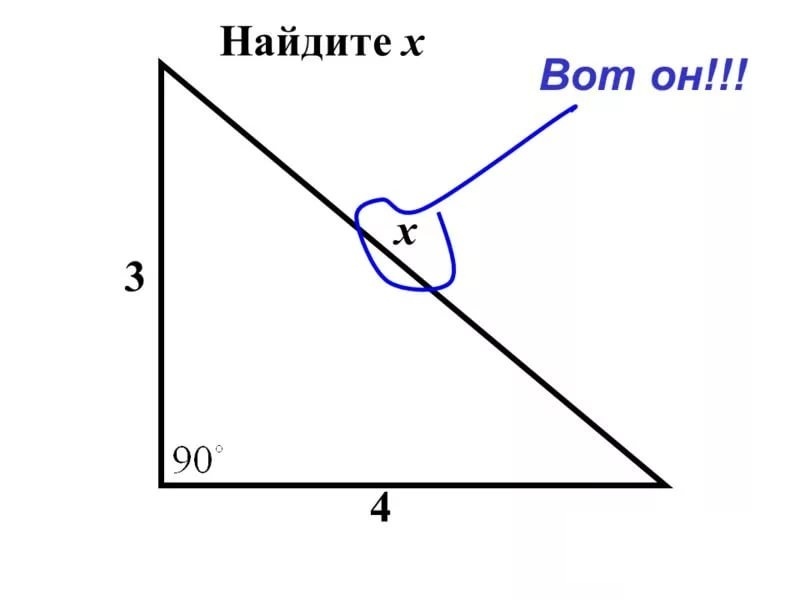 Оценить сечение образования составного ядра при взаимодействии нейтронов с кинетической энергией Tn = 1 эВ с ядрами золота 197Au.

48. Оценить сечение образования составного ядра при взаимодействии нейтронов с кинетической энергией Tn = 30 МэВ с ядрами золота 197Au.

49. Сравнить полные сечения реакции для α-частиц с энергией 20 Мэв на ядрах 56Fe и 197Au.

50. Оценить сечение реакции 63Cu(p,n)63Zn, если известны сечения реакций, идущих с образованием того же составного ядра с той же энергией возбуждения:
60Ni(α,p)63Zn — 0.7 б; 63Cu(p,pn)62Cu — 0.87 б; 60Ni(α,pn)62Cu — 0.97 б.

51. Оценить нейтронную ширину Гn изолированного уровня 0+ ядра 108Rh (энергия уровня E0 = 1.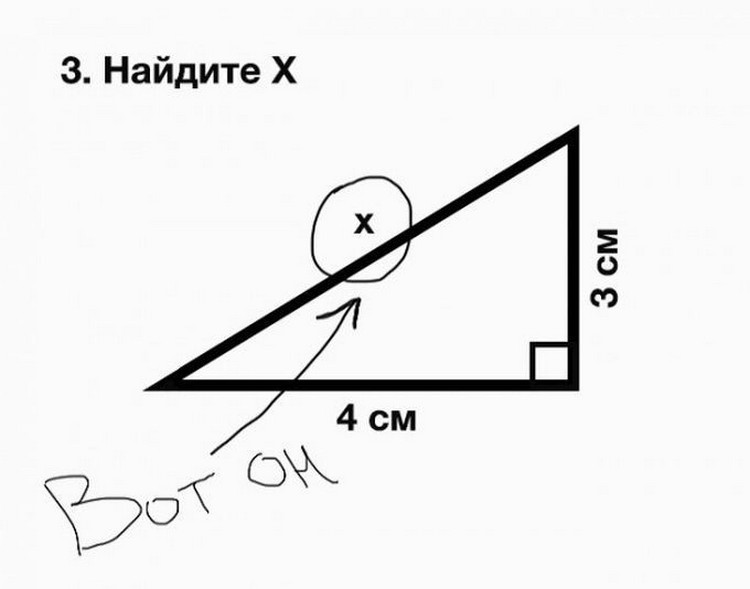 21 эВ, полная ширина Г = 0.21 эВ), если при резонансном поглощении нейтронов с образованием этого уровня составного ядра сечение поглощения для энергии нейтронов Tn = 1 эВ  σ = 2700 б. Спин ядра-мишени I(107Rh) = 1/2.

52. Получить, исходя из модели оболочек, отношение сечений реакций подхвата 16O(p,d)15O, с образованием конечного ядра 15Oв основном состоянии (JP =1/2—) и в состоянии (JP =3/2—).

53. Для реакции срыва 35Cl(d,p)36Cl найти возможные значения орбитального момента ln захваченного ядром нейтрона. Указать, исходя из простейшей оболочечной модели, какое из значений ln реализуется, если ядро 36Cl образуется в основном состоянии.

54. Оценить спин и четность состояния ядра 24Mg с энергией 1.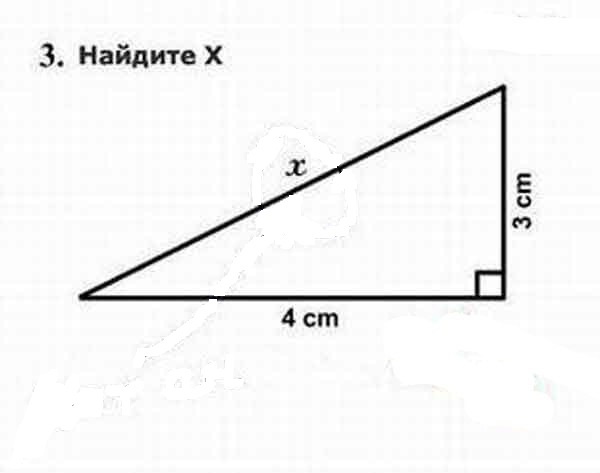 37 МэВ, если при возбуждении этого состоянии в реакции неупругого рассеяния α-частиц с энергией T = 40 Мэв, первый максимум в угловом распределении α-частиц наблюдается под углом 100.

55. Найти угол , под которым должен быть максимум углового распределения протонов в реакции (d,p) на ядре 58Ni, вызванной дейтронами с энергией T=15 МэВ, с образованием ядра 59Ni в основном состоянии.

56. Показать, что в реакции неупругого рассеяния дейтронов на ядре 10B, идущей за счёт сильного взаимодействия, невозможно возбуждение уровней этого ядра с изоспином I = 1.


Спектр нижних уровней ядра

57. Какие состояния из приведенного на рисунке спектра ядра могут возбуждаться в реакциях неупругого рассеяния (α,α’), (d,d’) и (p,p’)?

 

 

 

 

 

58.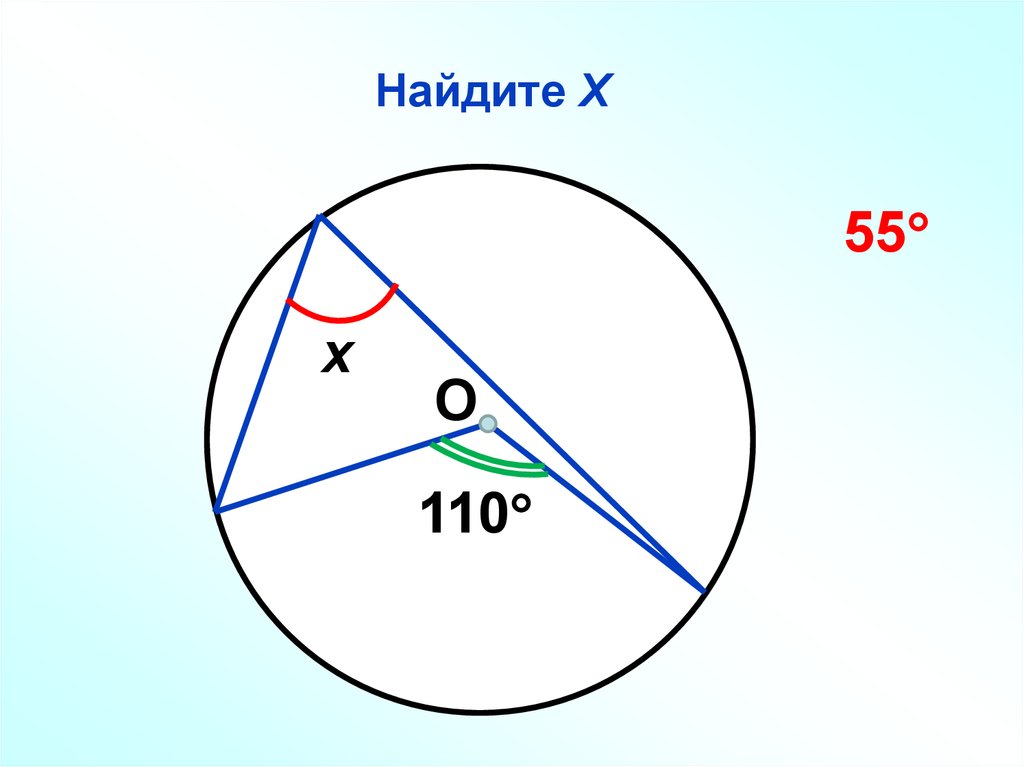 Оценить отношение сечений двух каналов реакции фоторасщепления ядра 16O:

γ + 16O → 15Ngs + p,                   (а)
γ + 16O → 15N*(JP = 3/2−) + p.    (б)

59. При изучении дифракционного рассеяния протонов с кинетической энергией Т = 20 ГэВ на ядрах свинца первый дифракционный минимум наблюдается при θmin = 0.3о. Оценить радиус ядра свинца.

60. Оценить радиус ядра меди, если известно, что при прохождении высокоэнергетичных нейтронов через пластинку меди толщиной 2 см поток нейтронов уменьшился в 1.1 раза. Размером нейтрона пренебречь. ρ(Cu) = 9 г/см3.

Калькулятор Интегралов • По шагам!

Поддержка

Вам помог мой калькулятор? Расскажите своим друзьям об этом Калькуляторе и Вы тоже сможете мне помочь!

Наверху страницы введите функцию, которую Вы хотите проинтегрировать. Переменная интегрирования, пределы интегрирования и другие параметры могут быть изменены в разделе «Настройки«. Нажмите «=» чтобы запустить интегрирование/нахождение первообразной функции. Результат будет показан ниже на этой странице.

Как работает Калькулятор Интегралов

Для тех кому интересны технические подробности, в этой части рассказывается как устроен и работает Калькулятор Интегралов.

Сначала синтаксический анализатор (па́рсер) анализирует исходное математическое выражение. Он преобразует его в форму более удобную для компьютера, а именно в форму дерева (см. картинку ниже). В процессе такого преобразования, Интегральный Калькулятор должен соблюдать порядок операций с учетом их приоритета. Так же, как и то, что в математических выражениях знак умножения часто опускается, например, мы обычно пишем «5x» вместо «5*x». Калькулятор Интегралов должен уметь понимать такие случаи и сам добавлять знак умножения.

Па́рсер написан на JavaScript, и основывается на алгоритме сортировочной станции, поэтому может исполняться прямо в браузере. Это дает возможность генерировать удобочитаемое выражение на ходу, преобразуя получающееся дерево в код для LaTeX (Ла́тех). С помощью MathJax происходит генерация картинки и ее отображение в браузере.

По нажатию кнопки «=», Калькулятор Интегралов отправляет математическое выражение вместе с параметрами (переменной интегрирования и пределами интегрирования) на сервер, где оно анализируется еще раз. В этот раз выражение преобразуется в форму которая будет понятна системе компьютерной алгебры Maxima (Ма́ксима).

Ма́ксима вычисляет интеграл математической функции. Результат Ма́ксимы снова преобразуется в Ла́тех а затем показывается пользователю. Первообразная вычисляется с помощью алгоритма Ри́ша, который достаточно замысловат для понимания человеком. Именно поэтому задача показывать промежуточные шаги решения интегралов является такой сложной.

Для того чтобы всё-таки показать пошаговое решение, Калькулятор Интегралов использует такие же методы, которыми бы воспользовался человек. Алгоритм, который это осуществляет, разрабатывался в течении нескольких лет и был написан на собственном языке программирования Ма́ксимы. Программа содержит более чем 17000 строк кода. Если интегрируемое выражение совпадает по форме с уже известным, алгоритм применяет заранее определённые правила для решения интеграла (например, метод неопределённых коэффициентов для рациональных функций, тригонометрическую подстановку в интегралах с квадратным корнем из квадратичной функции или интегрирование по частям для продуктов определенных функций). Если же оно не совпадает с уже известным, тогда алгоритм пробует разные подстановки и преобразования пока интеграл не будет решен или пока не закончится отведённое для этого время или же пока не кончатся все возможные варианты. С одной стороны, у Калькулятора нет математической интуиции, которая бы очень помогла в поисках первообразной, но зато, с другой стороны, Калькулятор в состоянии перепробовать большое количество разных вариантов за очень короткое время. Такое пошаговое вычисление первообразной по правилам, зачастую, более компактно и элегантно чем вычисленное Ма́ксимой.

Еще один режим работы «Проверка  решения» должен решить сложную задачу по определению являются ли два математических выражения равными друг другу. Разница между выражениями вычисляется и упрощается с помощью Ма́ксимы настолько, насколько это возможно. К примеру, это может быть переписывание тригонометрических/гиперболических функций в их экспоненциальные формы. Если удается упростить разницу до нуля — задача выполнена. В противном случае, применяется вероятностный алгоритм, который вычисляет и сравнивает оба выражения в случайно выбранных местах. В случае с первообразной, вся процедура повторяется для каждой производной, т.к. первообразная может отличаться константой.

Интерактивные графики функций вычисляются в браузере и отрисовываются на Сanvas («Холст») из HTML5. Для каждой математической функции, которая должна быть отрисована, Калькулятор создает функцию JavaScript, которая затем вычисляется с шагом, необходимым для правильного отображения графика. Все сингулярности (например  полюса) функции обнаруживаются в процессе отрисовки и обрабатываются отдельно. Управление жестами для мобильных устройств сделано на основе hammer.js.

Если у Вас есть вопросы или пожелания, а так же идеи как улучшить Калькулятор Интегралов, пожалуйста пишите мне на e-mail.

Калькулятор решения для x — MathCracker.com

Решатели Алгебра

Инструкции: Используйте этот пошаговый калькулятор, чтобы найти x из предложенного вами линейного уравнения. Пожалуйста, введите допустимое линейное уравнение в поле предоставлено ниже.

Введите линейное уравнение (пример: 3x — 2y = 3, x — y = 2/3 x и т. д.)

Подробнее об этом калькуляторе решения для x

Традиционно вам приходится решать уравнения, и чаще всего приходится решать уравнения, когда есть только одна переменная.

Но также может быть случай, когда вы хотите решить уравнение, когда присутствует более одной переменной. В таком случае, вы говорите, что решаете для этой переменной, в отличие от решения для любой другой присутствующей переменной.

Случай линейного уравнения с двумя переменными \(x\) и \(y\) является одним из самые простые случаи, которые вы можете иметь, в которых вы можете найти одну из переменных, \(x\) в этом случае.

Как использовать этот решатель x

Это очень просто:

Шаг 1: Первое, что вам нужно сделать, это ввести линейное уравнение, например, «2x — 3y = 3» или что-то вроде «x — 2y = 4»

Шаг 2: Одно верное линейное уравнение, калькулятор попытается найти значение x и, если возможно, решит для x, показывая все шаги

Шаг 3: Окончательный результат: выражение x как функции y, если это возможно, или прийти к выводу, что для x нет решения

Как вы решаете для X?

Идея проста: вам нужно манипулировать уравнением, используя алгебраически правильные шаги, чтобы получить \(x\) только с одной стороны уравнения. В общем случае это не всегда просто, но это для линейных уравнений.

Например, у вас может быть уравнение \(2x + 3y = 2\), вам нужно, чтобы \(x\) помещался один в левой части, поэтому вы вычитаете \(3y\) из обеих частей уравнения, что приводит к отмене \(3y\) с левой стороны и появлению \(-3y\) с правой стороны уравнения.

Вот что происходит, когда мы говорим «переходим \(3y\) на другую сторону со знаком минус».

Этот метод «передачи термина на другую сторону с измененным знаком» представляет собой способ перемещения переменных, чтобы решить для искомой переменной.

Как решить для x с помощью шагов

Чтобы получить шаги для решения для \(y\) для данного линейного уравнения, вам просто нужно ввести уравнение в соответствующем поле. Все это требуется, чтобы представленное линейное уравнение было действительным.

Вместо этого вас может заинтересовать \(y\), и в этом случае вы можете использовать это решение для калькулятора y если вы хотите найти \(y\) вместо \(x\), если это то, что вам нужно.

Пример: Решение для x:

Найдите \(x\) для данного уравнения \(2x + 3y = 2\).

Ответ:

Мы получили следующее уравнение:

\[\displaystyle 2x+4y=4\]

Положив \(x\) в левую часть, а \(y\) и константу в правую, получим

\[\displaystyle 2x = -4y +4\]

Теперь, решая \(x\), получаем следующее

\[\displaystyle x=-\frac{4}{2}y+\frac{4}{2}\]

и упрощая все термины, которые нуждаются в упрощении, окончательно получаем следующее

\[\displaystyle х=-2у+2\]

Решить для x калькулятор Решение For x Calculator Линейные уравнения Решите линейные уравнения Решение для калькулятора переменных

Нахождение точек пересечения функции по оси х

Для графика любой функции точкой пересечения по оси х является просто точка или точки, в которых график пересекает ось абсцисс. Может быть только одна такая точка, может не быть такой точки или их может быть много, что означает, что функция может иметь несколько пересечений по оси x. Как вы увидите ниже, мы можем использовать график или простое алгебраическое правило, чтобы найти точку пересечения по оси x или точку пересечения по оси x любой функции. Вы также можете прокрутить вниз до примера видео ниже.

Оглавление

  1. Использование графика для поиска пересечений по оси x
  2. Использование алгебры для поиска точек пересечения по оси x
  3. Пример видео (в том числе при отсутствии x-перехватов)
  4. Дальнейшее чтение


[adsenseWide]

Нахождение точки пересечения по оси x или точек пересечения по оси x с помощью графика

Как упоминалось выше, функции могут иметь один, ноль или даже несколько точек пересечения по оси x. Их можно найти, посмотрев, где график функции пересекает ось x, которая является горизонтальной осью в плоскости координат xy. Вы можете увидеть это на графике ниже. Эта функция имеет единственный x-перехват.

На приведенном ниже графике функция имеет два пересечения по оси x. Обратите внимание, что форма точки всегда \((c, 0)\) для некоторого числа \(c\).

Наконец, на следующем графике показана функция без пересечений по оси x. Вы можете видеть это, потому что он ни в какой точке не пересекает ось X.

Вы можете увидеть более подробное обсуждение этих идей здесь: Нули многочлена.

Нахождение точки пересечения или точек пересечения с помощью алгебры

Общее правило для нахождения точки пересечения по оси x или точек пересечения любой функции состоит в том, чтобы положить \(y = 0\) и найти \(x\). Это может быть несколько легко или очень сложно, в зависимости от функции. Давайте рассмотрим несколько примеров, чтобы понять, почему это может быть так.

Пример

Найдите точку пересечения функции по оси x: \(y = 3x – 9\)

Решение

Пусть \(y = 0\) и решить для \(x\).