Нахождение средней линии треугольника: Как находить среднюю линию треугольника? Основные свойства, определения и способы :: SYL.ru

Как находить среднюю линию треугольника? Основные свойства, определения и способы :: SYL.ru

Порой темы, которые объясняют в школе, могут быть не всегда понятны с первого раза. Особенно это касается такого предмета, как математика. Но все становится намного сложнее, когда эта наука начинает подразделяться на две части: алгебру и геометрию.

Каждый ученик может обладать способностью к одному из двух направлений, но особенно в начальных классах важно понять базу и алгебры, и геометрии. В геометрии одной из главных тем принято считать раздел о треугольниках.

Как находить среднюю линию треугольника? Давайте разбираться.

Основные понятия

Для начала чтобы разобраться, как находить среднюю линию треугольника, важно понимать, что же это.

Для проведения средней линии нет ограничений: треугольник может быть любым (равнобедренным, равносторонним, прямоугольным). И все свойства, которые относятся к средней линии, будут действовать.

Средняя линия треугольника является отрезком, соединяющим середины 2-х его сторон. Следовательно, любой треугольник может иметь 3 таких линии.

Свойства

Чтобы знать, как находить среднюю линию треугольника, обозначим ее свойства, которые необходимо запомнить, иначе без них будет невозможным решение задач с необходимостью обозначить длину средней линии, поскольку все полученные данные необходимо обосновать и аргументировать теоремами, аксиомами или свойствами.

1. Средняя линия параллельна стороне данной геометрической фигуры и равна ее 1/2. Это говорит о том, что если, к примеру, сторона равна 8, то средняя линия будет равна 4.
2. Проводя в данной геометрической фигуре всевозможные средние линии, мы получим 4 треугольника, равных и подобных друг другу. Также их коэффициент подобия будет равен 1/2.
3. И последнее свойство о том, что одна проведенная средняя линия делит основной треугольник на трапецию и треугольник.

Таким образом, чтобы ответить на вопрос: «Как найти среднюю линию треугольника АВС?», достаточно знать одну из сторон треугольника.

Приведем пример

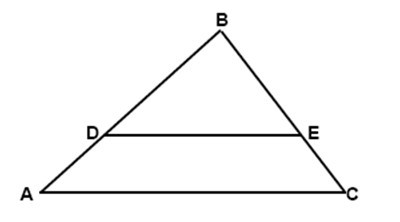
Взгляните на рисунок. На нем представлен треугольник ABC со средней линией DE. Обратим внимание, что она параллельна основанию AC в треугольнике. Следовательно, каким бы ни было значение AC, средняя линия DE будет в два раза меньше. К примеру, AC=20, значит DE=10 и т. д.

Вот такими несложными способами можно понять, как находить среднюю линию треугольника. Запомните ее основные свойства и определение, и тогда у вас никогда не возникнет проблем с нахождением ее значения.

Конспект «Средняя линия треугольника» — УчительPRO

«Средняя линия треугольника + Задачи по теме»

---

---

Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.

Свойства средней линии треугольника:
1. Средняя линия параллельна третьей стороне и равна ее половине.
2. Средняя линия трeугольника отсекает от него треугольник, подобный данному (с коэффициентом подобия 1/2 ).
3. Три средние линии треугольника делят его на 4 равных треугольника, подобных данному, с коэффициентом подобия 1/2.

Свойство средней линии треугольника является следствием теоремы Фалеса.

ПРИМЕРЫ РЕШЕНИЯ КЛЮЧЕВЫХ ЗАДАЧ

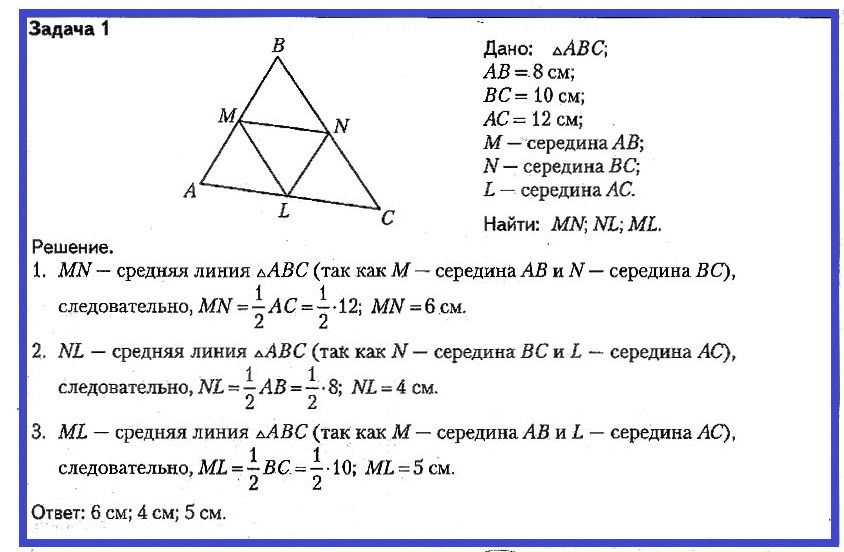
Задача № 1. Дано: ΔABC; AB = 8 см; BC = 10 см; AC = 12 см; M — середина AB; N — середина BC; L — середина AC.  Найти: MN, NL, ML.

Задача № 2.

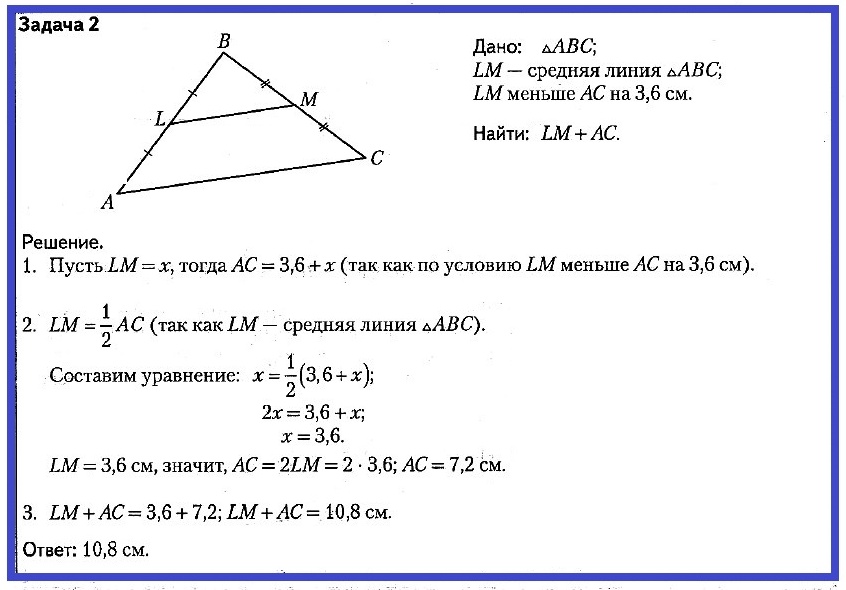
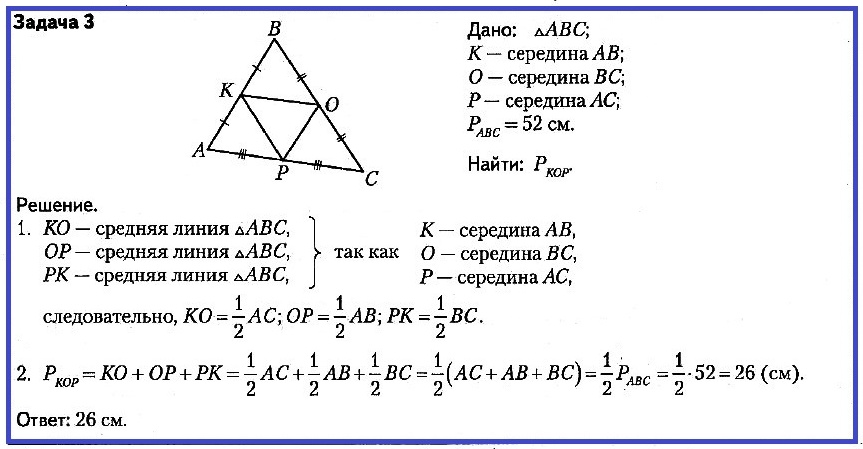
Задача № 3. ΔABC; K — середина AB; O — середина BC; P — середина AC; P_ABC = 52 см.   Найти: P_КOР

Задача № 4.

---

Это конспект по теме «Средняя линия треугольника + Задачи по теме». Выберите дальнейшие действия:

 

Средняя линия треугольника на клетчатой бумагеТреугольники

Рассмотрим, как может быть найдена средняя линия треугольника по рисунку на клетчатой бумаге.

Задача 1

На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC.

Найдите длину его средней линии, параллельной стороне AB.

Решение:

Как правило, в таких заданиях на чертеже треугольник расположен таким образом, что по клеточкам посчитать длину средней линии невозможно.

Но задача легко разрешима с применением свойства средней линии треугольника:

средняя линия треугольника, соединяющая середины двух его сторон, параллельна третьей стороне и равна её половине.

Следовательно, чтобы найти длину средней линии, параллельной стороне AB, надо найти длину отрезка AB.

Длина искомой средней линии равна её половине.

 

1) AB=6,

   

   

   

   

 

А как быть, если длину стороны треугольника посчитать по клеточкам не получается?

Возможно, в этом случае сторону треугольника можно найти с помощью теоремы Пифагора.

 

Задача 2

На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC.

Найдите длину его средней линии, параллельной стороне AB.

 

 

Решение:

1)В прямоугольном треугольнике ABC AB — гипотенуза.

AC=4, BC=3.

По теореме Пифагора

   

   

Средняя линия MN равна половине гипотенузы:

   

2)Достроим по клеточкам прямоугольный треугольник ABD с гипотенузой AB.

По теореме Пифагора

   

   

   

Уравнение средней линииТреугольники | Треугольники

Как составить уравнение средней линии треугольника по координатам его вершин? Как записать уравнение средней линии трапеции?

Для решения этих задач используем свойства средней линии треугольника и средней линии трапеции.

1 способ

Найти координаты середин двух сторон и составить уравнение прямой, проходящей через две найденные точки.

Пример.

1) Написать уравнение прямой, содержащей среднюю линию треугольника с вершинами в точках A(-2;-4), B(1;6), C(7;0), пересекающей стороны AB и BC в точках M и N.

Решение:

М — середина отрезка AB, N — середина BC.

По формулам координат середины отрезка

   

   

   

   

Таким образом,

   

Составим уравнение прямой MN, например, в виде y=kx+b:

   

Отсюда

   

   

2 способ

Найти координату одной из точек средней линии и составить уравнение прямой, параллельной стороне треугольника.

Решение:

   

— середина отрезка AB. Составим уравнение прямой AC:

   

   

Составим уравнение прямой MN как уравнение прямой, проходящей через точку M и параллельной прямой AC.

Угловой коэффициент прямой MN равен угловому коэффициенту прямой AC:

   

то есть уравнение прямой MN ищем в виде

   

Поскольку точка M принадлежит прямой, её координаты удовлетворяют этому уравнению. Отсюда находим значение b:

   

Таким образом, уравнение прямой MN

   

или

   

Аналогичные рассуждения применимы и при составлении уравнения средней линии трапеции.

Написать уравнение прямой, содержащей среднюю линию трапеции с вершинами в точках A(-2;1), B(1;5), C(4;-1), D(0;-3).

Решение:

1 способ

Сначала следует определить основания данной трапеции.

Составим уравнения сторон AD и BC. Если эти прямые параллельны, то AD и BC — основания трапеции. Если эти прямые не параллельны, то основания трапеции — AB и CD.

A(-2;1), D(0;-3), отсюда

   

Значит, уравнение прямой AD:  y= -2k-3.
B(1;5), C(4;-1),

   

Уравнение прямой BC: y= -2k+7.

Поскольку угловые коэффициенты прямых равны:

   

то AD ∥BC, то есть AD и BC являются основаниями трапеции ABCD. Значит AB и CD — боковые стороны. Найдём координаты точек M и N — середины  AB и CD соответственно.

   

   

   

   

Составим уравнение прямой MN, M(-1/2;3), N(2;-2):

   

то есть y=-2k+2.

2 способ

Уравнение AD — y= -2k-3, середина AB — M(-1/2;3). Составляем уравнение прямой MN, параллельной прямой AD.

   

Значит уравнение MN ищем в виде y= -2x+b.

Так как прямая проходит через точку M, её координаты удовлетворяют уравнению прямой:

   

Следовательно, уравнение средней линии трапеции ABCD имеет вид y=-2x+2 или 2x+y-2=0.

Средняя линия треугольника

Понятие средней линии треугольника

Введем понятие средней линии треугольника.

Определение 1

Средняя линия треугольника — это отрезок, соединяющий середины двух сторон треугольника (Рис. 1).

Рисунок 1. Средняя линия треугольника

Теорема о средней линии треугольника

Теорема 1

Средняя линия треугольника параллельна одной из его сторон и равна её половине.

Доказательство.

Пусть нам дан треугольник $ABC$. $MN$ — средняя линия (как на рисунке 2).

Рисунок 2. Иллюстрация теоремы 1

Так как $\frac{AM}{AB}=\frac{BN}{BC}=\frac{1}{2}$, то треугольники $ABC$ и $MBN$ подобны по второму признаку подобия треугольников. Значит

Также, отсюда следует, что $\angle A=\angle BMN$, значит $MN||AC$.

Теорема доказана.

Следствия из теоремы о средней линии треугольника

Следствие 1: Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении $2:1$ начиная с вершины.

Доказательство.

Рассмотрим треугольник $ABC$, где ${AA}_1,\ {BB}_1,\ {CC}_1$ его медианы. Так как медианы делят стороны пополам. Рассмотрим среднюю линию $A_1B_1$ (Рис. 3).

Готовые работы на аналогичную тему

Рисунок 3. Иллюстрация следствия 1

По теореме 1, $AB||A_1B_1$ и $AB=2A_1B_1$, следовательно, $\angle ABB_1=\angle BB_1A_1,\ \angle BAA_1=\angle AA_1B_1$. Значит треугольники $ABM$ и $A_1B_1M$ подобны по первому признаку подобия треугольников. Тогда

Аналогично доказывается, что

Теорема доказана.

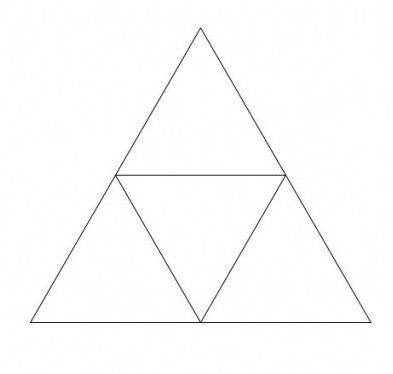
Следствие 2: Три средние линии треугольника делят его на 4 треугольника, подобных исходному треугольнику с коэффициентом подобия $k=\frac{1}{2}$.

Доказательство.

Рассмотрим треугольник $ABC$ со средними линиями $A_1B_1,\ {\ A}_1C_1,\ B_1C_1$ (рис. 4)

Рисунок 4. Иллюстрация следствия 2

Рассмотрим треугольник $A_1B_1C$. Так как $A_1B_1$ — средняя линия, то

Угол $C$ — общий угол этих треугольников. Следовательно, треугольники $A_1B_1C$ и $ABC$ подобны по второму признаку подобия треугольников с коэффициентом подобия $k=\frac{1}{2}$.

Аналогично доказывается, что треугольники $A_1C_1B$ и $ABC$, и треугольники $C_1B_1A$ и $ABC$ подобны с коэффициентом подобия $k=\frac{1}{2}$.

Рассмотрим треугольник $A_1B_1C_1$. Так как $A_1B_1,\ {\ A}_1C_1,\ B_1C_1$ — средние линии треугольника, то

Следовательно, по третьему признаку подобия треугольников, треугольники $A_1B_1C_1$ и $ABC$ подобны с коэффициентом подобия $k=\frac{1}{2}$.

Теорема доказана.

Примеры задачи на понятие средней линии треугольника

Пример 1

Дан треугольник со сторонами $16$ см, $10$ см и $14$ см. Найти периметр треугольника, вершины которого лежат в серединах сторон данного треугольника.

Решение.

Так как вершины искомого треугольника лежат в серединах сторон данного треугольника, то его стороны — средние линии исходного треугольника. По следствию 2, получим, что стороны искомого треугольника равны $8$ см, $5$ см и $7$ см.

\[P=8см+5см+7см=20\ см\]

Ответ: $20$ см.

Пример 2

Дан треугольник $ABC$. Точки $N\ и\ M$ — середины сторон $BC$ и $AB$ соответственно (Рис. 5).

Рисунок 5.

Периметр треугольника $BMN=14$ см. Найти периметр треугольника $ABC$.

Решение.

Так как $N\ и\ M$ — середины сторон $BC$ и $AB$, то $MN$ — средняя линия. Значит

\[AB=2MB,\ BC=2BN\]

По теореме 1, $AC=2MN$. Получаем:

\[P_{ABC}=AB+BC+AC=2MB+2BN+2MN=2P_{BMN}=28\ см\]

Ответ: $28$ см.

Средняя линия треугольника — это… Что такое Средняя линия треугольника?



Средняя линия треугольника

Средняя линия треугольника

Средняя линия треугольника — отрезок, соединяющий середины двух сторон этого треугольника.^[1]

Свойства средней линии треугольника:

1. средняя линия параллельна основанию треугольника и равна его половине;
2. при проведении всех трёх средних линий образуются 4 равных треугольника, подобных (даже гомотетичных) исходному с коэффициентом 1/2.

Средняя линия трапеции

Средняя линия трапеции — отрезок, соединяющий середины боковых сторон этой трапеции.

Свойство средней линии трапеции: средняя линия параллельна основаниям трапециии равна их полусумме.

Примечания

Wikimedia Foundation. 2010.

• Реддлы
• Бег на длинные дистанции

Смотреть что такое «Средняя линия треугольника» в других словарях:

• Средняя линия — фигур в планиметрии отрезок, соединяющий середины двух сторон этой фигуры. Понятие употребляется для следующих фигур: треугольник, четырехугольник, трапеция. Содержание 1 Средняя линия треугольника 1.1 Свойства …   Википедия

• СРЕДНЯЯ ЛИНИЯ — (1) трапеции отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции параллельна её основаниям и равна их полусумме; (2) треугольника отрезок, соединяющий середины двух сторон этого треугольника: третья сторона при этом… …   Большая политехническая энциклопедия

• СРЕДНЯЯ ЛИНИЯ — треугольника (трапеции) отрезок, соединяющий середины двух сторон треугольника (боковых сторон трапеции) …   Большой Энциклопедический словарь

• средняя линия — треугольника (трапеции), отрезок, соединяющий середины двух сторон треугольника (боковых сторон трапеции). * * * СРЕДНЯЯ ЛИНИЯ СРЕДНЯЯ ЛИНИЯ треугольника (трапеции), отрезок, соединяющий середины двух сторон треугольника (боковых сторон трапеции) …   Энциклопедический словарь

• СРЕДНЯЯ ЛИНИЯ — треугольника отрезок, соединяющий середины двух сторон треугольника. Третья сторона треугольника при этом наз. основанием треугольника. С. л. треугольника параллельна основанию и равна половине его длины. Во всяком треугольнике С. л. отсекает от… …   Математическая энциклопедия

• СРЕДНЯЯ ЛИНИЯ — треугольника (трапеции), отрезок, соединяющий середины двух сторон треугольника (боковых сторон трапеции) …   Естествознание. Энциклопедический словарь

• Средняя линия —         1) С. л. треугольника, отрезок, соединяющий середины двух сторон треугольника (третью сторону называют основанием). С. л. треугольника параллельна основанию и равна его половине; площади частей треугольника, на которые делит его с. л.,… …   Большая советская энциклопедия

• Площадь треугольника — Стандартные обозначения Треугольник  простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, не лежащими на одной прямой, и тремя отрезками, попарно соединяющими эти точки. Вершины треугольника …   Википедия

• Словарь терминов планиметрии — Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И К Л М Н О П Р С …   Википедия

• Коллинеарные точки — Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф …   Википедия

Нахождение угла в прямоугольном треугольнике

Угол с любых двух сторон

Мы можем найти неизвестный угол в прямоугольном треугольнике, если нам известны длины двух его сторон .

Пример

Лестница прислонена к стене, как показано.

Какой угол между лестницей и стеной?

Ответ — использовать синус, косинус или тангенс!

Но какой использовать? У нас есть специальная фраза «SOHCAHTOA», чтобы помочь нам, и мы используем ее так:

Шаг 1 : найдите имен двух известных нам сторон

• Соседний примыкает к углу
  
• Напротив напротив угла
  
• , а самая длинная сторона — Гипотенуза .

Пример: в нашем примере лестницы нам известна длина:

• сторона Напротив угол «х», который равен 2,5
• самая длинная сторона, называемая Гипотенуза , что составляет 5

Шаг 2 : теперь используйте первые буквы этих двух сторон ( O pposite и H ypotenuse) и фразу «SOHCAHTOA», чтобы найти, какой из синуса, косинуса или тангенса использовать:

SOH…	S ine: sin (θ) = O pposite / H ypotenuse
… CAH …	C осин: cos (θ) = A djacent / H ypotenuse
… TOA	T Угол: tan (θ) = O pposite / A djacent

В нашем примере это O pposite и H ypotenuse, что дает нам « SOH cahtoa», что говорит нам, что нам нужно использовать Sine .

Шаг 3 : Поместите наши значения в уравнение синуса:

S дюйм (x) = O pposite / H ypotenuse = 2,5 / 5 = 0,5

Шаг 4 : Теперь решите это уравнение!

грех (х) = 0,5

Далее (поверьте мне на данный момент) мы можем преобразовать это в это:

х = грех ^-1 (0,5)

Затем возьмите наш калькулятор, введите 0,5 и используйте кнопку sin ^-1 , чтобы получить ответ:

х = 30 °

И у нас есть ответ!

Но что означает sin ^-1 …?

Итак, функция синуса «sin» принимает угол и дает нам соотношение «противоположность / гипотенуза»,

Но sin ^-1 (так называемый «обратный синус») идет другим путем…
… это принимает соотношение «противоположная сторона / гипотенуза» и дает нам угол.

Пример:

• Функция синуса: sin ( 30 ° ) = 0,5
• Функция обратной синусоиды: sin ^-1 ( 0,5 ) = 30 °

На калькуляторе нажмите одну из следующих кнопок (в зависимости от от вашей марки калькулятора): либо «2ndF sin», либо «shift sin».

На своем калькуляторе попробуйте использовать sin и sin ^-1 , чтобы увидеть, какие результаты вы получите!

Также попробуйте cos и cos ^-1 . И tan и tan ^-1 .
Давай, попробуй.

Шаг за шагом

Вот четыре шага, которые нам нужно выполнить:

• Шаг 1 Найдите две известные нам стороны — противоположную, смежную и гипотенузу.
• Шаг 2 Используйте SOHCAHTOA, чтобы решить, какой из синусов, косинусов или касательных использовать в этом вопросе.
• Шаг 3 Для синуса вычислить противоположное / гипотенузу, для косинуса вычислить смежное / гипотенузу или для касательного вычислить противоположное / смежное.
• Шаг 4 Найдите угол на своем калькуляторе, используя один из следующих значений: sin ^-1 , cos ^-1 или tan ^-1

Примеры

Давайте рассмотрим еще пару примеров:

Пример

Найдите угол подъема плоскости из точки А на земле.

• Step 1 Две известные нам стороны — это O pposite (300) и A djacent (400).
• Шаг 2 SOHCAH TOA сообщает нам, что мы должны использовать T angent.
• Шаг 3 Вычислить Противоположный / Соседний = 300/400 = 0,75
• Шаг 4 Найдите угол с помощью калькулятора, используя tan ^-1

Tan x ° = напротив / рядом = 300/400 = 0.75

tan ^-1 из 0,75 = 36,9 ° (с точностью до 1 знака после запятой)

Если не указано иное, углы обычно округляются до одного десятичного знака.

Пример

Найдите величину угла a °

• Step 1 Две известные нам стороны: A djacent (6750) и H ypotenuse (8100).
• Step 2 SOH CAH TOA сообщает нам, что мы должны использовать осин C .
• Шаг 3 Вычислить прилегающее / гипотенузу = 6,750 / 8,100 = 0,8333
• Шаг 4 Найдите угол с помощью калькулятора, используя cos ^-1 из 0,8333:

cos a ° = 6,750 / 8,100 = 0,8333

cos ^-1 из 0,8333 = 33,6 ° (с точностью до 1 знака после запятой)

.

В поисках стороны в прямоугольном треугольнике

Найдите сторону, когда мы знаем другую сторону и угол

Мы можем найти неизвестную сторону в прямоугольном треугольнике, если знаем:

• одной длины и
• один угол (то есть кроме прямого).

Пример: Глубина до дна

Судно стоит на якоре на морском дне.

Мы знаем:

• длина кабеля (30 м) и
• угол, под которым кабель образует дно

Значит, мы сможем найти глубину!

Но как?

Ответ — использовать синус, косинус или тангенс !

Но какой?

Какой из синус, косинус или тангенс использовать?

Чтобы узнать какие, сначала даем имен сторонам:

• Соседний находится рядом (рядом) с углом,
  
• Напротив напротив угла,
  
• , а самая длинная сторона — Гипотенуза .

Теперь для стороны, которую мы уже знаем и стороны , которую мы пытаемся найти , мы используем первые буквы их имен и фразу «SOHCAHTOA», чтобы решить, какая функция:

SOH …		S In: sin (θ) = O pposite / H ypotenuse
…CAH …		C осин: cos (θ) = A djacent / H ypotenuse
… TOA		T angent: tan (θ) = O pposite / A djacent

Как это:

Пример: Глубина до дна (продолжение)

Найдите имен двух сторон, над которыми мы работаем:

• известная нам сторона — это Гипотенуза
• сторона, которую мы хотим найти, — это Угол, противоположный (убедитесь, что буква d находится напротив угла 39 °)

Теперь используйте первые буквы этих двух сторон ( O, pposite и H ypotenuse) и фразу «SOHCAHTOA», которая дает нам « SOH cahtoa», которая говорит нам, что нам нужно использовать Sine :

S In: sin (θ) = O pposite / H ypotenuse

Теперь введите известные нам значения:

sin (39 °) = d / 30

И решите это уравнение!

Но как вычислить sin (39 °) …?

Воспользуйтесь калькулятором. Введите 39 и затем используйте клавишу «грех». Это просто!

sin (39 °) = 0,6293 …

Итак, теперь у нас:

0,6293 … = d / 30

Теперь немного переставляем, и решаем:

Начать с: 0,6293 … = d / 30

Поменять местами стороны: d / 30 = 0.6293 …

Умножаем обе стороны на 30: d = 0,6293 … x 30

Вычислить: d = 18,88 до 2 знаков после запятой

Глубина залегания анкерного кольца под скважиной 18,88 м

Шаг за шагом

Вот четыре шага, которые необходимо выполнить:

• Шаг 1 Найдите названия двух сторон, которые мы используем: одну, которую мы пытаемся найти, и другую, которую мы уже знаем, из Противоположной, Смежной и Гипотенузы.

• Шаг 2 Используйте SOHCAHTOA, чтобы решить, какой из синуса, косинуса или касательного использовать в этом вопросе.

• Шаг 3 Для синуса запишите Противоположный / Гипотенуза, для косинуса запишите Соседний / Гипотенуза или для Касательного запишите Противоположный / Соседний. Одно из значений — неизвестная длина.

• Step 4 Решите, используя калькулятор и свои навыки алгебры.

Примеры

Рассмотрим еще несколько примеров:

Пример: найти высоту плоскости.

Мы знаем, что расстояние до плоскости 1000
А угол 60 °

Какая высота у самолета?

Осторожно! Угол 60 °, находится вверху, поэтому сторона «h» равна , примыкает к углу !

• Step 1 Мы используем две стороны: A djacent (h) и H ypotenuse (1000).

• Step 2 SOH CAH TOA говорит нам использовать осин C .

Начать с: cos 60 ° = h / 1000

Замена: ч / 1000 = cos 60 °

Рассчитать cos 60 °: ч / 1000 = 0,5

Умножить обе стороны на 1000: h = 0,5 x 1000

ч = 500

Высота самолета = 500 метров

Пример: найти длину стороны y :

• Step 1 Мы используем две стороны: O pposite (y)
  и A djacent (7).

• Шаг 2 SOHCAH TOA говорит нам использовать угол T .

Начать с: tan 53 ° = y / 7

Поменять местами: y / 7 = tan 53 °

Умножаем обе стороны на 7: y = 7 tan 53 °

Вычислить: y = 7 x 1.32704 …

y = 9,29 (с точностью до 2 знаков после запятой)

Сторона y = 9,29

Пример: радиомачта

Есть мачта высотой 70 метров.

Трос идет к вершине мачты под углом 68 °.

Какова длина провода?

• Step 1 Мы используем две стороны: O pposite (70) и H ypotenuse (w).

• Step 2 SOH CAHTOA говорит нам использовать S ine.

• Шаг 3 Запишите:

  sin 68 ° = 70 / w

Неизвестная длина указана внизу (знаменателю) дроби!

Таким образом, нам нужно использовать несколько иной подход при решении:

Начать с: sin 68 ° = 70 / w

Умножаем обе стороны на w: w × (sin 68 °) = 70

Разделим обе части на «sin 68 °»: w = 70 / (sin 68 °)

Вычислить: w = 70/0.9271 …

w = 75,5 м (на 1 место)

Длина провода = 75,5 м

.

Соотношение длин сторон и углов треугольника

Связь длин сторон и углов треугольника — Math Open Reference В любом треугольнике:

1. Самая короткая сторона всегда противоположна самой маленькой внутренний угол
2. Самая длинная сторона всегда противоположна наибольшему внутреннему углу

Попробуй это Перетащите оранжевые точки на треугольник ниже.

Напомним, что в неравносторонний треугольник, все стороны имеют разную длину и все внутренние углы имеют разные меры.В таком треугольнике самая короткая сторона всегда противоположна самому маленькому углу. (Они выделены жирным шрифтом выше) Точно так же самая длинная сторона противоположна наибольшему углу.

На рисунке выше перетащите любой вершина треугольника и увидишь, какая сторона самая короткая, противоположный угол тоже самый маленький. Затем нажмите «Показать самый большой» и увидите, что, как бы вы ни изменили форму треугольника, самая длинная сторона всегда противоположна наибольшему внутреннему углу.

Средние детали

Если наименьшая сторона противоположна наименьшему углу, а наибольшая — противоположна наибольшему углу, то из этого следует, что так как треугольник имеет только три стороны, средняя сторона противоположна среднему углу.

Равносторонние треугольники

Равносторонний треугольник все стороны равны по длине и все внутренние углы равны. Следовательно, в данном случае нет «наибольшего» или «наименьшего».

Равнобедренные треугольники

Равнобедренные треугольники имеют две стороны одинаковой длины и два равных внутренних угла. Следовательно, могут быть две стороны и углы, которые могут быть «самыми большими» или «самыми маленькими». Если вы будете осторожны с мышью, вы можете создать такую ​​ситуацию на рисунке выше.

Другие темы треугольника

Общие

Периметр / Площадь

Типы треугольников

Центры треугольника

Конгруэнтность и сходство

Решение треугольников

Треугольник викторины и упражнения

(C) Открытый справочник по математике, 2011 г.
Все права защищены.

.

Решение треугольников SSS

«SSS» означает «Сторона, Сторона, Сторона»

« SSS » — это когда мы знаем три стороны треугольника и хотим найти отсутствующих углов .

Мы используем «угловую» версию закона косинусов:

cos (Кл) = а ² + б ² — с ² 2ab

cos (А) = б ² + с ² — а ² 2bc

cos (B) = в ² + а ​​ ² — б ² 2ca

(все они одинаковые формулы, просто разные лейблы)

Пример 1

В этом треугольнике мы знаем три стороны:

Сначала используйте Закон косинусов, чтобы найти один из углов.Неважно, какой именно. Давайте сначала найдем угол A :

cos A = (b ² + c ² — a ² ) / 2bc

cos A = (6 ² + 7 ² — 8 ² ) / (2 × 6 × 7)

cos A = (36 + 49 — 64) / 84

cos A = 0,25

A = cos ⁻¹ (0,25)

А = 75,5224 … °

A = 75,5 ° с точностью до одного десятичного знака.

Далее мы найдем другую сторону.Мы снова используем Закон косинусов, на этот раз для угла B:

.

cos B = (c ² + a ² — b ² ) / 2ca

cos B = (7 ² + 8 ² — 6 ² ) / (2 × 7 × 8)

cos B = (49 + 64 — 36) / 112

cos B = 0,6875

B = cos ⁻¹ (0,6875)

В = 46,5674 … °

B = 46,6 ° с точностью до одного десятичного знака

Наконец, мы можем найти угол C, используя «углы треугольника складываются с 180 °»:

С = 180 ° — 75.5224 … ° — 46,5674 … °

C = 57,9 ° с точностью до одного десятичного знака

Теперь мы полностью решили треугольник, то есть нашли все его углы.

Треугольник может содержать буквы, отличные от ABC:

Пример 2

Это тоже треугольник SSS.

В этом треугольнике нам известны три стороны x = 5,1, y = 7,9 и z = 3,5. Используйте закон косинусов, чтобы сначала найти угол X:

cos X = (y ² + z ² — x ² ) / 2yz

cos X = ((7.9) ² + (3,5) ² — (5,1) ² ) / (2 × 7,9 × 3,5)

cos X = (62,41 + 12,25 — 26,01) /55,3

cos X = 48,65 / 55,3 = 0,8797 …

X = cos ⁻¹ (0,8797 …)

X = 28,3881 … °

X = 28,4 ° с точностью до одного десятичного знака

Далее мы снова воспользуемся законом косинусов, чтобы найти угол Y:

cos Y = (z ² + x ² — y ² ) / 2zx

cos Y = -24.15 / 35,7 = -0,6764 …

cos Y = (12,25 + 26,01 — 62,41) / 35,7

cos Y = -24,15 / 35,7 = -0,6764 …

Y = cos ⁻¹ (−0,6764 …)

Y = 132,5684 … °

Y = 132,6 ° с точностью до одного десятичного знака.

Наконец, мы можем найти угол Z, используя «углы треугольника добавить к 180 °»:

Z = 180 ° — 28,3881 … ° — 132,5684 … °

Z = 19,0 ° с точностью до одного десятичного знака

Другой метод

Наибольший угол?

Почему мы сначала пытаемся найти наибольший угол? Таким образом, два других угла должны быть острых (менее 90 °), и закон синуса даст правильные ответы.

Закон синуса трудно использовать с углами выше 90 ° . По обе стороны от 90 ° может быть два ответа (например, 95 ° и 85 °), но калькулятор даст вам только меньший.

Таким образом, если сначала вычислить наибольший угол с помощью закона косинусов, остальные углы будут меньше 90 °, и закон синусов можно без труда использовать для любого из них.

Пример 3

B — наибольший угол, поэтому сначала найдите B, используя закон косинусов:

cos B = (a ² + c ² — b ² ) / 2ac

cos B = (11.6 ² + 7,4 ² — 15,2 ² ) / (2 × 11,6 × 7,4)

cos B = (134,56 + 54,76 — 231,04) / 171,68

cos B = -41,72 / 171,68

cos B = −0,2430 …

B = 104,1 ° с точностью до одного десятичного знака

Используйте закон синусов sinC / c = sinB / b, чтобы найти угол A:

sin C / 7,4 = sin 104,1 ° / 15,2

sin C = 7,4 × sin 104,1 ° / 15,2

грех C = 0.4722 …

C = 28,2 ° с точностью до одного десятичного знака

Найдите угол A, используя «углы треугольника добавить к 180»:

А = 180 ° — (104,1 ° + 28,2 °)

А = 180 ° — 132,3 °

A = 47,7 ° с точностью до одного десятичного знака

Итак, A = 47,7 °, B = 104,1 ° и C = 28,2 °

.