Тело на наклонной плоскости | Физика

1. Тело на гладкой наклонной плоскости

Напомним: когда говорят о гладкой поверхности, подразумевают, что трением между телом и этой поверхностью можно пренебречь.

На тело массой m, находящееся на гладкой наклонной плоскости, действуют сила тяжести m и сила нормальной реакции (рис. 19.1).

Удобно ось x направить вдоль наклонной плоскости вниз, а ось y – перпендикулярно наклонной плоскости вверх (рис. 19.1). Угол наклона плоскости обозначим α.

Уравнение второго закона Ньютона в векторной форме имеет вид

? 1. Объясните, почему справедливы следующие уравнения:


? 2. Чему равна проекция ускорения тела на ось x?

? 3. Чему равен модуль силы нормальной реакции?

? 4. При каком угле наклона ускорение тела на гладкой плоскости в 2 раза меньше ускорения свободного падения?

? 5. При каком угле наклона плоскости сила нормальной реакции в 2 раза меньше силы тяжести?

При выполнении следующего задания полезно заметить, что ускорение тела, находящегося на гладкой наклонной плоскости, не зависит от направления начальной скорости тела.

? 6. Шайбу толкнули вверх вдоль гладкой наклонной плоскости с углом наклона α. Начальная скорость шайбы v0.
а) Какой путь пройдет шайба до остановки?
б) Через какой промежуток времени шайба вернется в начальную точку?
в) С какой скоростью шайба вернется в начальную точку?

? 7. Брусок массой m находится на гладкой наклонной плоскости с углом наклона α.
а) Чему равен модуль силы, удерживающей брусок на наклонной плоскости, если сила направлена вдоль наклонной плоскости? Горизонтально?
б) Чему равна сила нормальной реакции, когда сила направлена горизонтально?

2. Условие покоя тела на наклонной плоскости

Будем теперь учитывать силу трения между телом и наклонной плоскостью.

Если тело покоится на наклонной плоскости, на него действуют сила тяжести m, сила нормальной реакции и сила трения покоя тр.пок (рис. 19.2).

Сила трения покоя направлена вдоль наклонной плоскости вверх: она препятствует соскальзыванию бруска.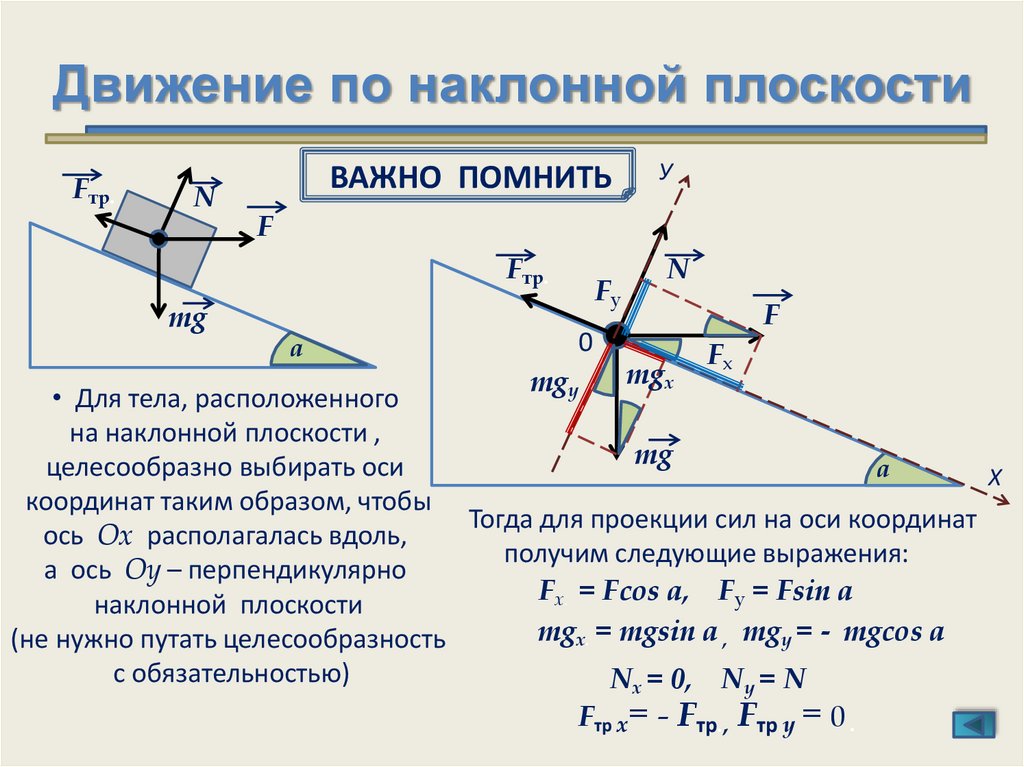 Следовательно, проекция этой силы на ось x, направленную вдоль наклонной плоскости вниз, отрицательна:

Fтр.пок x = –Fтр.пок

? 8. Объясните, почему справедливы следующие уравнения:


? 9. На наклонной плоскости с углом наклона α покоится брусок массой m. Коэффициент трения между бруском и плоскостью равен μ. Чему равна действующая на брусок сила трения? Есть ли в условии лишние данные?

? 10. Объясните, почему условие покоя тела на наклонной плоскости выражается неравенством

μ ≥ tgα.

Подсказка. Воспользуйтесь тем, что сила трения покоя удовлетворяет неравенству Fтр.пок ≤ μN.

Последнее неравенство можно использовать для измерения коэффициента трения: угол наклона плоскости плавно увеличивают, пока тело не начинает скользить по ней (см. лабораторную работу 4).

? 11.Лежащий на доске брусок начал скользить по доске, когда ее угол наклона к горизонту составил 20º. Чему равен коэффициент трения между бруском и доской?

? 12. Кирпич массой 2,5 кг лежит на доске длиной 2 м. Коэффициент трения между кирпичом и доской равен 0,4.
а) На какую максимальную высоту можно поднять один конец доски, чтобы кирпич не сдвинулся?
б) Чему будет равна при этом действующая на кирпич сила трения?

Сила трения покоя, действующая на тело, находящееся на наклонной плоскости, не обязательно направлена вдоль плоскости вверх. Она может быть направлена и вниз вдоль плоскости!

? 13. Брусок массой m находится на наклонной плоскости с углом наклона α. Коэффициент трения между бруском и плоскостью равен μ, причем и μ < tg α. Какую силу надо приложить к бруску вдоль наклонной плоскости, чтобы сдвинуть его вдоль наклонной плоскости:

а) вниз? б) вверх?

3. Движение тела по наклонной плоскости с учетом трения

Пусть теперь тело скользит по наклонной плоскости вниз (рис. 19.3). При этом на него действует сила трения скольжения, направленная противоположно скорости тела, то есть вдоль наклонной плоскости вверх.

? 15. Изобразите на чертеже в тетради силы, действующие на тело, и объясните, почему справедливы следующие уравнения:

? 16. Чему равна проекция ускорения тела на ось x?

? 17. Брусок скользит по наклонной плоскости вниз. Коэффициент трения между бруском и плоскостью равен 0,5. Как изменяется со временем скорость бруска, если угол наклона плоскости равен:
а) 20º? б) 30º? в) 45º? г) 60º?

? 18. Брусок начинает скользить по доске, когда ее наклоняют на угол 20º к горизонту. Чему ранен коэффициент трения между бруском и доской? С каким по величине и направлению ускорением будет скользить брусок вниз по доске, наклоненной на угол 30º? 15º?

Пусть теперь начальная скорость тела направлена вверх (рис. 19.4).

? 19. Изобразите на чертеже в тетради силы, действующие на тело, и объясните, почему справедливы следующие уравнения:


? 20. Чему равна проекция ускорения тела на ось x?

? 21. Брусок начинает скользить по доске, когда ее наклоняют на угол 20º к горизонту. Брусок толкнули вверх по доске. С каким ускорением он будет двигаться, если доска наклонена на угол: а) 30º? б) 15º? В каком из этих случаев брусок остановится в верхней точке?

? 22.Шайбу толкнули вверх по наклонной плоскости с начальной скоростью v0. Угол наклона плоскости α, коэффициент трения между шайбой и плоскостью μ. Спустя некоторое время шайба вернулась в начальное положение.
а) Сколько времени двигалась шайба вверх до остановки?

б) Какой путь прошла шайба до остановки?
в) Сколько времени после этого шайба возвращалась в начальное положение?

? 23. После толчка брусок двигался в течение 2 с вверх по наклонной плоскости и затем в течение 3 с вниз до возвращения в начальное положение. Угол наклона плоскости 45º.
а) Во сколько раз модуль ускорения бруска при движении вверх больше, чем при движении вниз?
б) Чему равен коэффициент трения между бруском и плоскостью?

Зацените!! Езда Электро-Велосипеда по воде

Дополнительные вопросы и задания

24. Брусок соскальзывает без начальной скорости с гладкой наклонной плоскости высотой h (рис. 19.5). Угол наклона плоскости равен α. Какова скорость бруска в конце спуска? Есть ли здесь лишние данные?

25. (Задача Галилея) В вертикальном диске радиуса R просверлен прямолинейный гладкий желоб (рис. 19.6). Чему равно время соскальзывания бруска вдоль всего желоба из состояния покоя? Угол наклона желоба α, в начальный момент брусок покоится.

26. По гладкой наклонной плоскости с углом наклона α скатывается тележка. На тележке установлен штатив, на котором на нити подвешен груз. Сделайте чертеж, изобразите силы, действующие на груз. Под каким углом к вертикали расположена нить, когда груз покоится относительно тележки?

27. Брусок находится на вершине наклонной плоскости длиной 2 м и высотой 50 см.

Коэффициент трения между бруском и плоскостью 0,3.
а) С каким по модулю ускорением будет двигаться брусок, если толкнуть его вниз вдоль плоскости?
б) Какую скорость надо сообщить бруску, чтобы он достиг основания плоскости?

28. Тело массой 2 кг находится на наклонной плоскости. Коэффициент трения между телом и плоскостью 0,4.
а) При каком угле наклона плоскости достигается наибольшее возможное значение силы трения?
б) Чему равно наибольшее значение силы трения?
в) Постройте примерный график зависимости силы трения от угла наклона плоскости.
Подсказка. Если tg α ≤ μ, на тело действует сила трения покоя, а если tg α > μ – сила трения скольжения.

для студентов гл.7-10 — Стр 2

664.Постройте сечение правильной треугольной призмы ABCA1B1C1 плоскостью, проходящей через:

а) середины рёбер АВ, ВС и А1В1; б) середину ребра АС и вершины А1 и В1; в) середины рёбер АА1, ВВ1 и А1С1;

г) середину ребра АС и вершины В и В1; д) середину ребра А1С1 и вершины А и В.

665.Постройте сечение правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1 плоскостью, проходящей через:

а) вершины А, D и С1; б) вершины А, С и D1; в) вершины А, В и D1; г) вершины B, D и Е1; д) вершины С, F и E1.

§ 3. Углы и расстояния в пространстве.

. Угол между прямыми.

Угол между параллельными прямыми считается равным 00.

Определение. Углом между

 

 

b

пересекающимися прямыми называется

a

 

 

 

наименьший из углов, образованных

 

 

пересечением прямых.

 

 

 

Определение. Две прямые называются

a

 

b

перпендикулярными, если угол между

 

 

 

 

ними равен 900.

 

 

 

Определение. Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, параллельными данным скрещивающимся прямыми.

Пример. Дан куб ABCDA1B1C1D1 . Найти угол между скрещивающимися прямыми

A1B и C1D.

В грани CDD1C1 проводим диагональ CD1;

CD1|| BA1 ( A1B;C1D) = ( CD1;C1D) =900(угол между диагоналями квадрата).

. Угол между прямой и плоскостью.

В1

 

С1

А1

D1

 

 

В

 

С

А

 

D

 

 

 

Если прямая параллельна плоскости или лежит в ней, то угол между данными прямыми и плоскостью считается равным 00.

Определение. Прямая называется перпендикулярной к плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости. В этом случае угол между прямой и плоскостью считается равным 900.

11

Определение. Прямая называется наклонной к некоторой плоскости, если она пересекает эту плоскость, но не перпендикулярна ей.

MK

MN – наклонная к

KN – проекция MN на

M

K N a

Определение. Углом между наклонной к плоскости и этой плоскостью называется угол между наклонной и её проекцией на данную плоскость.

( MN; ) = (MN;KN) = MNK=

Теорема 7 (о трех перпендикулярах). Наклонная к плоскости перпендикулярна прямой, лежащей в плоскости тогда и только тогда, когда проекция этой наклонной на эту плоскость, перпендикулярна данной прямой.

 

 

 

M

 

MK

 

 

 

 

 

MN – наклонная к

 

K

 

 

m

 

 

 

KN – проекция MN на

 

 

 

 

 

 

N

 

 

 

m

 

a

 

MN m KN m

 

 

 

 

 

 

 

 

. Расстояния в пространстве.

Определение. Расстоянием от точки до прямой, не содержащей эту точку,

называется длина отрезка перпендикуляра, проведённого из этой точки к данной плоскости.

Определение. Расстоянием от точки до плоскости, не содержащей эту точку,

называется длина перпендикуляра, проведённого из этой точки к данной плоскости.

Расстояние между параллельными прямыми равно расстоянию от любой точки одной из этих прямых до другой прямой.

Расстояние между параллельными плоскостями равно расстоянию от произвольной точки одной из плоскостей до другой плоскости.

Расстояние между прямой и параллельной ей плоскостью равно расстоянию от любой точки этой прямой до плоскости.

Определение. Расстоянием между двумя скрещивающимися прямыми называется длина их общего перпендикуляра.

Расстояние между скрещивающимися прямыми равно расстоянию от любой точки одной из этих прямых до плоскости, проходящей через вторую прямую параллельно первой прямой (другими словами: расстоянию между двумя параллельными плоскостями, содержащими эти прямые).

V. Угол между плоскостями. Двугранный угол.

Если плоскости параллельны, то угол между ними считается равным 00.

12

Определение. Двугранным углом называется геометрическая фигура, образованная двумя полуплоскостями с общей границей не лежащими в одной плоскости. Полуплоскости называются гранями, а их общая граница ребром двугранного угла.

Определение. Линейным углом двугранного угла называется угол, полученный при пересечении данного двугранного угла плоскостью, перпендикулярной его ребру. Все линейные углы данного двугранного угла равны между собой. Величина двугранного угла равна величине его линейного угла.

Пример. Дана пирамида MABCD , основание которой – M квадрат ABCD со стороной 2, MA ABC, MA = 2. Найдите угол

наклона грани MBC плоскости основания.

 

(по признаку перпендикулярности прямой и

плоскости).

 

Таким образом, плоскость MAB пересекает двугранный угол с ребром BC и перпендикулярна ему. Следовательно, по определению линейного угла: MBA – линейный угол данного двугранного угла.

MBA – равнобедренный прямоугольный MBA = 450. Ответ: 450.

Определение. Две плоскости называются перпендикулярными, если при пересечении они образуют прямой двугранный угол.

Теорема 8 (признак перпендикулярности плоскостей): Если плоскость содержит перпендикуляр к другой плоскости, то эти плоскости перпендикулярны

А В

D С

2

 

M

 

 

 

 

 

 

 

А

 

 

 

В

 

 

2

 

 

 

 

β

b

α

a

§ 5. Некоторые теоремы о параллельности и перпендикулярности в пространстве.

Теорема 9. Если одна из двух

a

b

 

 

параллельных прямых пересекает

 

α

плоскость, то и другая прямая пересекает

M

 

эту плоскость.

 

 

13

Теорема 10.Если две прямые параллельны

 

 

третьей, то они параллельны между собой.

 

α

 

 

 

c

 

 

a

b

 

 

Теорема 11. Если плоскость проходит

 

 

α

через данную прямую, параллельную

 

 

 

 

 

 

другой плоскости, и пересекает эту

 

 

 

 

плоскость, то линия пересечения

 

 

a

 

 

плоскостей параллельна данной прямой.

 

 

 

 

 

 

 

β

 

 

b

 

 

 

 

 

 

 

 

 

Теорема 12. Если одна из двух

 

 

параллельных прямых параллельна

 

 

данной плоскости, то другая прямая либо

 

 

также параллельна данной плоскости,

 

 

либо лежит в этой плоскости.

a

α

 

b

 

 

Теорема 13. Если каждая из двух

 

пересекающихся плоскостей проходит

α

через одну из двух параллельных прямых,

 

то прямая пересечения плоскостей

 

параллельна этим прямым.

a

 

β

с b

Теорема 14. Если две параллельные плоскости пересечены третьей плоскостью, то линии их пересечения параллельны.

Теорема 15. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.

Теорема 16. Если прямая пересекает одну

 

a

 

 

из двух параллельных прямых, то она

α

M

пересекает и вторую.

 

 

14

 

β

 

 

Теорема 17. Через точку, не лежащую на плоскости, можно провести одну и только одну плоскость, параллельную данной плоскости.

Теорема 18. Если одна из двух

 

 

параллельных прямых перпендикулярна к

a

b

плоскости, то и другая прямая

 

 

перпендикулярна к этой плоскостью.

α

 

 

 

Теорема 19. Если две прямые перпендикулярны к плоскости, то эти прямые параллельны.

Теорема 20. Через любую точку пространства проходит единственная плоскость, перпендикулярная данной прямой.

Теорема 21. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.

Теорема 22. Если прямая перпендикулярна одной из параллельных плоскостей, то она перпендикулярна и другой.

Теорема 23. Если две плоскости перпендикулярны одной и той же прямой, то эти плоскости параллельны.

Вопросы и задачи

666.Отметьте верные утверждения а) если прямая перпендикулярна плоскости, то она перпендикулярна любой

прямой, лежащей в этой плоскости.

б) если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, параллельной этой плоскости.

в) прямая, перпендикулярная каким-нибудь двум прямым, лежащим в плоскости, перпендикулярна этой плоскости.

г) прямая, пересекающая круг в центре и перпендикулярная его диаметру, перпендикулярна плоскости круга.

д) прямая, пересекающая круг в центре и перпендикулярная двум его радиусам, перпендикулярна плоскости круга.

е) прямая, перпендикулярная двум не параллельным хордам круга, перпендикулярна его плоскости.

667.Отметьте верные утверждения

15

а) если плоскость перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.

б) если прямая перпендикулярна одной из параллельных плоскостей, то она перпендикулярна и другой.

в) если две плоскости перпендикулярны одной и той же прямой, то они параллельны.

г) если две прямые, перпендикулярны одной и той же плоскости, то они параллельны.

668. Дан куб ABCDA1B1C1D1. Точка М – середина ребра B1C1, N – середина C1D1, K – середина DC, О – точка пересечения диагоналей основания ABCD. Найдите угол между следующими прямыми:

а) АA1 и CС1; б) A1C1 и B1D1; в) A1C1 и C1D1; г) A1М и CC1; д) A1D и DC1; е)A1C1 и BD;

ё) A1C и АС; ж) A1B и D1С; з) A1C и ВB1;

и) A1D и АВ ; й) A1М и ВС; к) A1М и ВК ;

л) C1К и B1N ; м) C1О и AB1 ; н) A1О и B1D.

669.Прямые ОВ и CD параллельные, а ОА и CD – скрещивающиеся прямые. Найдите угол между прямыми ОА и CD, если:

а) АОВ = 40°; б) АОВ = 135°; в) АОВ = 90°.

670.Прямая a параллельна стороне ВС параллелограмма ABCD и не лежит в плоскости параллелограмма. Докажите, что а и CD – скрещивающиеся прямые, и найдите угол между ними, если один из углов параллелограмма равен: а) 50°; б) 121°.

671.Прямая m параллельна диагонали BD ромба ABCD и не лежит в плоскости ромба. Докажите, что: а) m и АС – скрещивающиеся прямые – и найдите угол между ними; б) m и AD — скрещивающиеся прямые – и найдите угол между ними, если угол АВС равен

128°.

672.Рёбра основания прямоугольного параллелепипеда имеют длину 4 см и 3 см, высота параллелепипеда равна 5 см. Определите угол между диагональю и плоскостью основания параллелепипеда.

673.В правильной четырёхугольной пирамиде боковые рёбра наклонены к основанию под углом 30°. Высота пирамиды 5 см. Найдите длины рёбер пирамиды.

674.Образующая конуса наклонена к плоскости основания под углом 60°. Найдите длину образующей, если высота конуса 2 см.

675.Прямая КВ перпендикулярна плоскости равностороннего треугольника АВС. ВК = АВ, М — середина АС. Определите угол между прямой и плоскостью и найдите его величину:

а) КА и АВС; б) КМ и АВС; в) АС и ВМК; г) АВ и ВМК; д) АС и АВК; е) ВМ и АВК; ё) АК и ВМК; ж) ВК и АКС; з) ВМ и АКС.

676. Дан куб ABCDA1B1C1D1. Точка М – середина B1C1, N – середина D1С1, К – середина DC, О – точка пересечения диагоналей квадрата ABCD. Определите угол между прямой и плоскостью и найдите его величину:

а) AB1 и АВС; б) АС и АA1В; в) MN и DD1C;

г) MN и DD1B; д) АМ и АВС; е) АС и MKN;

16

ё) АК и МКN; ж) АC1 и ВСC1; з) DC1 и АСC1; и) В1D и АСC1; й) АА1 и AMN; к) DD1 и AMN.

677.MABCD – четырёхугольная пирамида, основание которой квадрат ABCD. МD перпендикулярно плоскости АВС, MD = AB, O – точка пересечения диагоналей квадрата ABCD. Определите угол между прямой и плоскостью и найдите его величину:

а) МС и АВС; б) МВ и АВС; в) МА и АВС; г) МО и АВС; д) АС и МDС; е) АD и MDC; ё) АВ и MDC; ж) АС и ОАМ; з) АО и ВСМ.

678.Дана треугольная пирамида МАВС, все рёбра которой равны а. О – центр основания АВС. МО перпендикулярно плоскости основания. N – середина ВС. Определите угол между прямой и плоскостью и найдите его величину:

а) МС и АВС; б) MN и АВС; в) СВ и AMN; г) СА и AMN; д) ОС и AMN; е) СМ и AMN; ё) ОМ и МВС; ж) AN и МВС.

679.Расстояние от точки до каждой из двух параллельных плоскостей равно 6. Найдите расстояние между данными плоскостями.

680.Расстояние между двумя параллельными плоскостями равно 8. Точка удалена от одной из этих плоскостей на 3. На какое расстояние эта точка удалена от второй плоскости?.

681.Расстояние между двумя параллельными плоскостями равно 5. Точка удалена от одной из этих плоскостей на 10. На какое расстояние эта точка удалена от второй плоскости?

682.Расстояния от точки до каждой из двух параллельных плоскостей равны соответственно 3 и 7. Найдите расстояние между этими плоскостями.

683.Из вершины прямого угла прямоугольного треугольника с катетами, равными 15 и 20, проведён перпендикуляр к плоскости треугольника длиной 16. Найдите расстояние от концов перпендикуляра до гипотенузы.

684.Стороны треугольника равны 51, 30 и 27. Из вершины меньшего угла треугольника проведён к его плоскости перпендикуляр длиной 10. Найдите расстояние от концов перпендикуляра до противоположной стороны треугольника.

685.Диагонали ромба равны 60 и 80. В точке пересечения диагоналей к плоскости ромба проведён перпендикуляр длиной 45. Найдите расстояние от конца перпендикуляра до стороны ромба.

686.Точка М находится на расстоянии 11 см от каждой стороны равнобедренной трапеции с основаниями, равными 16 см и 30 см. Найдите расстояние от точки М до плоскости трапеции.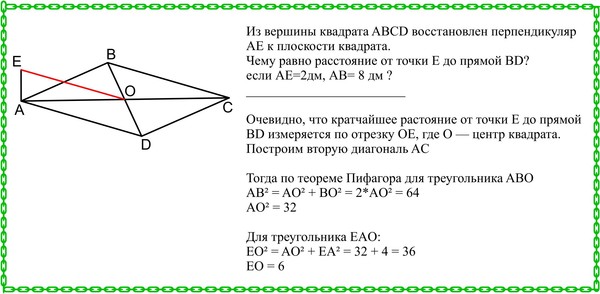

687.Из точки, отстоящей от плоскости на расстояние а, проведены две наклонные под углом 45° к плоскости, а их проекции составляют между собой угол 120°. Найдите расстояние между концами наклонных.

688.На грани двугранного угла, равного 60°, дана точка, удалённая от ребра на расстояние m. Найдите расстояние от этой точки до другой грани.

689.Внутри двугранного угла, равного 120°, дана точка М, удалённая от каждой из граней на расстояние m. Найдите расстояние от этой точки до ребра двугранного угла.

690.Выразите диагональ d куба через его ребро a.

17

691.Найдите расстояние от вершины куба со стороной а до его диагонали.

692.Отрезок AD перпендикулярен к плоскости равнобедренного треугольника АВС. АВ = АС = 5 см, ВС = 6 см, AD = 12 см. Найдите расстояния от концов отрезка AD до прямой ВС.

693.Через вершину А прямоугольника ABCD проведена прямая АК, перпендикулярная к плоскости прямоугольника. KD = 6 см, КВ = 7 см, КС = 9 см. Найдите: а) расстояние от точки К до плоскости прямоугольника ABCD; б) расстояние между АК и CD.

694.Через вершину В квадрата ABCD проведена прямая BF, перпендикулярная к его плоскости. Найдите расстояния от точки F до прямых, содержащих стороны и диагонали квадрата, если BF = 8 дм, АВ = 4 дм.

695.Прямая BD перпендикулярна к плоскости треугольника АВС. BD = 9 см, АС = 10 см, ВС = ВА = 13 см. Найдите: а) расстояние от точки D до прямой АС; б) площадь треугольника ACD.

696.Через вершину прямого угла С равнобедренного прямоугольного треугольника АВС проведена прямая СМ, перпендикулярная к его плоскости. Найдите расстояние от

точки М до прямой АВ, если АС = 4 см, а СМ = 2 см.

697.Один из катетов прямоугольного треугольника АВС равен m, а острый угол, прилежащий к этому катету, равен φ. Через вершину прямого угла С проведена прямая СD, перпендикулярная к плоскости этого треугольника, CD = n. Найдите расстояние от точки D до прямой АВ.

698.Через вершину В ромба ABCD проведена прямая ВМ, перпендикулярная к его плоскости. Найдите расстояние от точки М до прямых, содержащих стороны ромба, если АВ = 25 см, угол ВАD равен 60°, ВМ = 12,5 см.

699.Дан куб ABCDA1B1C1D1. Точка М делит ребро АВ на отрезки АМ = 3 и ВМ = 5. Найдите расстояние от точки М до плоскостей:

а) ADA1 б) ВСB1; в) A1B1C1; г) DCC1.

700.SABC – тетраэдр. Ребро SA перпендикулярно плоскости АВС, АВ

перпендикулярно АС, АВ = АС = 1, SA = 2. Найдите расстояние от точки S до прямой ВС.

701.SABC – тетраэдр. Ребро SA перпендикулярно плоскости АВС, АВ = АС = 10, ВС = 16, SA = 8. Найдите расстояние от точки S до прямой ВС.

702.К плоскости прямоугольника ABCD через его вершину В проведен перпендикуляр ВР. Найдите расстояния от точки Р до сторон прямоугольника, если они равны 4 см и 5 см, а ВР равно 3 см.

703.К плоскости ромба ABCD из вершины его тупого угла В проведён перпендикуляр ВР, равный 3 см. Найдите расстояние от точки Р до сторон ромба, если их длина 4 см, а угол В равен 120°.

704.К плоскости ромба из точки О пересечения его диагоналей проведён перпендикуляр ОР, равный 3 см. Найдите расстояние от точки Р до сторон ромба, если диагонали ромба равны 6 см и 8 см.

705.Прямая АК перпендикулярна к плоскости квадрата ABCD. Докажите, что: а) KD перпендикулярна CD; б) ВС перпендикулярна ВК; в) КС перпендикулярна BD.

706.Прямая АК перпендикулярна к плоскости параллелограмма ABCD. KD перпендикулярна BD. Докажите, что ABCD – ромб.

18

707.Прямая ВМ перпендикулярна к плоскости треугольника АМС, а прямая ВС перпендикулярна АС. Докажите, что треугольник АМС – прямоугольный и укажите его прямой угол.

708.Прямая ВМ перпендикулярна к плоскости треугольника АМС, а прямая ВК перпендикулярна прямой АС. Точка К – середина отрезка АС. Докажите, что треугольник АМС – равнобедренный и укажите его равные углы.

709.SABC – правильный тетраэдр. Точка М – середина ребра SA. Докажите, что угол ВМС – линейный угол двугранного угла между плоскостями SBA и SCA.

710.ABCDA1B1C1D1 – параллелепипед, такой, что ABCD – прямоугольник, AA1 = A1B. Точка М – середина ребра АВ, О – точка пересечения диагоналей прямоугольника ABCD. Докажите, что угол ОМA1 – линейный угол двугранного угла между плоскостями АВС и A1ВА.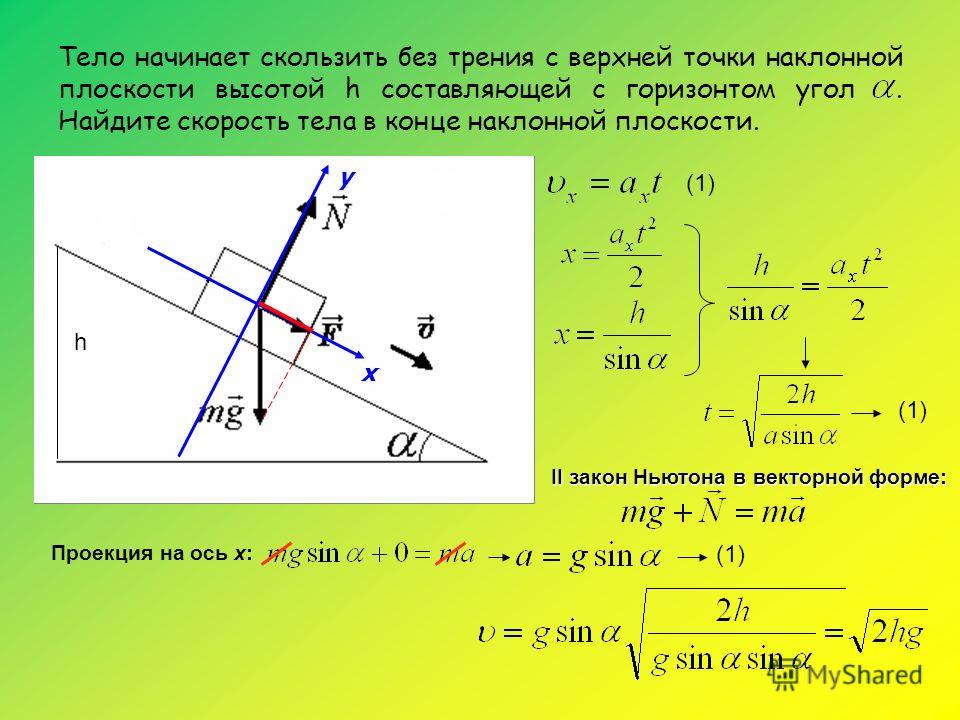

711.Дан куб ABCDA1B1C1D1. Точка М – середина ребра D1С1. Укажите взаимное расположение плоскостей и найдите угол между ними:

а) A1BА и D1СD; б) A1B1C1 и DD1С; в) A1BD и B1D1С; г) B1АС и ADC; д) A1BD и C1DВ; е) A1BD и СC1А;

ё) АB1C1 и ADC; ж) A1МА и B1C1С; з) A1МА и ВB1D;

и) МA1D и СA1D.

712.В правильной пирамиде SABC высота SM равна 3, сторона основания АВ равна 18. Найдите угол между боковой гранью и основанием.

713.В прямоугольном параллелепипеде ABCDA1B1C1D1 ребро АВ равно 2, ребро АA1 равно 4. Найдите тангенс угла наклона диагонального сечения AB1C1D к основанию.

714.SABCD – правильная четырёхугольная пирамиды, в которой сторона основания равна 2, а угол между боковой гранью и основанием равен 45°. Найдите высоту пирамиды.

715.Точка А лежит на одной из граней двугранного угла, равного 30°, и удалена от ребра двугранного угла на 8. Найдите расстояние от точки А до плоскости второй грани двугранного угла.

716.Точки А и В лежат на разных гранях двугранного угла. Прямая АВ перпендикулярна ребру двугранного угла, а точки А и В удалены от этого ребра соответственно на 3 и 4. Найдите величину двугранного угла, если АВ = 5. 90°

717.Точки А и В лежат на разных гранях двугранного угла, величина которого равна 60°. А1 и В1 – проекции точек А и В на ребро двугранного угла. АА1 = А1В1 = ВВ1 = 2. Найдите длину отрезка АВ.

718.Точка А лежит внутри острого двугранного угла величины α и удалена от граней на расстояние h. Найдите расстояние от А до ребра этого угла.

719.Точка А лежит внутри двугранного угла и удалена от его граней на расстояния 1 и

, а от ребра на 2. Найдите величину двугранного угла.

720. Точка А лежит внутри двугранного угла. Угол между перпендикулярами, опущенными из А на его грани, равен 131°. Найдите величину двугранного угла.

19

Глава 8. Многогранники.

Определение. Многогранником называется поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело. Тело, ограниченное многогранником, также называют многогранником.

Многоугольники, из которых составлен многогранник, называются его гранями. Стороны граней называются его рёбрами, а концы рёбер – вершинами многогранника. Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.

Определение. Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани (известные нам тетраэдр, пирамиды, параллелепипед и т.п. – выпуклые многогранники).

Подробно рассмотрим два вида выпуклых многогранников: призмы и пирамиды.

§ 1. Призма.

. Призма. Правильная призма.

Определение. Призмой называется многогранник, две грани которого равные многоугольники (основания призмы) с соответственно параллельными сторонами, а остальные грани (боковые) – параллелограммы.

Определение. Высотой призмы называется перпендикуляр, проведённый из какойлибо точки одного основания призмы к плоскости другого основания.

Определение. Диагональю призмы называется отрезок, соединяющий две вершины призмы, не лежащие в одной грани.

Определение. Прямой призмой называется призма, боковые рёбра которой перпендикулярны основаниям. В противном случае призма называется наклонной.

 

 

 

B1

 

 

 

 

A1

 

A1

 

C1

B1

C1

 

 

 

 

 

 

 

B

 

A

 

C

A

 

 

B

C

 

 

 

 

 

прямая треугольная призма

 

наклонная треугольная призма

 

Для прямой призмы справедливы следующие утверждения:

20

5.

4 Наклонные плоскости — физика

Раздел Цели обучения

К концу этого раздела вы сможете делать следующее:

  • Различать статическое и кинетическое трение
  • Решение задач на наклонные плоскости

Поддержка учителей

Поддержка учителей

Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:

  • (4) Научные концепции. Учащийся знает и применяет законы, управляющие движением в двух измерениях, в различных ситуациях. Ожидается, что студент:
    • (D) рассчитать действие сил на объекты, включая закон инерции, связь между силой и ускорением и характер пар сил между объектами.

Основные термины раздела

кинетическое трение статическое трение

Статическое трение и кинетическое трение

Напомним из предыдущей главы, что трение — это сила, противодействующая относительному движению параллельно поверхности контакта взаимодействующих объектов и постоянно присутствующая вокруг нас. Трение позволяет нам двигаться, в чем вы убедились, если когда-нибудь пробовали ходить по льду.

Существуют разные виды трения — кинетическое и статическое. Кинетическое трение действует на объект в относительном движении, а статическое трение действует на объект или систему, покоящиеся друг относительно друга. Максимальное статическое трение обычно больше, чем кинетическое трение между объектами.

Поддержка учителей

Поддержка учителей

[BL][OL] Повторить понятие трения.

[AL] Начните обсуждение двух видов трения: статического и кинетического. Спросите учащихся, какая из них, по их мнению, будет больше для двух заданных поверхностей. Объясните понятие коэффициента трения и значение этого числа на практике. Посмотрите на таблицу статического и кинетического трения и попросите учащихся угадать, какие другие системы будут иметь более высокие или более низкие коэффициенты.

Представьте, например, что вы пытаетесь сдвинуть тяжелый ящик по бетонному полу. Вы можете давить на ящик все сильнее и сильнее и вообще не двигать его. Это означает, что статическое трение реагирует на то, что вы делаете — оно увеличивается, чтобы быть равным вашему толчку и в противоположном направлении. Но если вы, наконец, нажмете достаточно сильно, ящик, кажется, внезапно соскользнет и начнет двигаться. Начав движение, его легче поддерживать в движении, чем было запустить, потому что кинетическая сила трения меньше, чем статическая сила трения. Если бы вы добавили массу к ящику (например, поместив на него коробку), вам пришлось бы толкать его еще сильнее, чтобы он начал двигаться, а также чтобы он продолжал двигаться. Если, с другой стороны, вы смазали бетон маслом, вам будет легче запустить ящик и поддерживать его в рабочем состоянии.

На рис. 5.33 показано, как возникает трение на границе раздела двух объектов. Увеличение этих поверхностей показывает, что они являются шероховатыми на микроскопическом уровне. Поэтому, когда вы нажимаете, чтобы заставить объект двигаться (в данном случае ящик), вы должны поднимать объект до тех пор, пока он не сможет прыгать вместе с ударами только кончиками поверхности, отламывать точки или делать и то, и другое. Чем сильнее прижимаются поверхности друг к другу (например, если на ящик кладут еще одну коробку), тем больше усилий требуется для их перемещения.

Рисунок 5.33 Силы трения, такие как f , всегда препятствуют движению или попытке движения между соприкасающимися объектами. Трение возникает отчасти из-за шероховатости соприкасающихся поверхностей, как видно на увеличенном виде.

Величина силы трения имеет две формы: одна для статического трения, другая для кинетического трения. Когда между объектами нет движения, величина статического трения f s равна

fs≤μsNs,fs≤μsNs,

где μsμs — коэффициент трения покоя, а Н — величина нормальной силы. Напомним, что нормальная сила действует перпендикулярно поверхности и не дает ящику провалиться сквозь пол. В этом примере она противостоит силе тяжести, но так будет не всегда.

Поскольку символ ≤≤ означает меньше или равно, это уравнение говорит о том, что трение покоя может иметь максимальное значение мксН. мксН. То есть

fs(max)=µsN.fs(max)=µsN.

Статическое трение представляет собой реактивную силу, которая увеличивается, чтобы быть равной и противоположной любой прилагаемой силе, вплоть до ее максимального предела. Как только приложенная сила превысит f с (макс.), объект начнет двигаться. Когда объект движется, величина кинетического трения f k определяется выражением

fk=µkN.fk=µkN.

где μkμk — коэффициент кинетического трения.

Трение варьируется от поверхности к поверхности, потому что разные вещества более шероховатые, чем другие. В таблице 5.2 сравниваются значения статического и кинетического трения для различных поверхностей. Коэффициент трения зависит от двух соприкасающихся поверхностей.

Система Статическое трение мксмкс Кинетическое трение μkμk
Резина на сухом бетоне 1,0 0,7
Резина на мокром бетоне 0,7 0,5
Дерево на дереве 0,5 0,3
Вощеная древесина на мокром снегу 0,14 0,1
Металл на дереве 0,5 0,3
Сталь по стали (сухая) 0,6 0,3
Сталь по стали (промасленный) 0,05 0,03
Тефлон на стали 0,04 0,04
Кость, смазанная синовиальной жидкостью 0,016 0,015
Туфли на дереве 0,9 0,7
Обувь на льду 0,1 0,05
Лед на льду 0,1 0,03
Сталь на льду 0,4 0,02

Стол 5. 2 Коэффициенты статического и кинетического трения

Поскольку трение всегда препятствует относительному движению, направление трения вверх по плоскости, если объект покоится или скользит по склону. Например, если ящик, который вы пытаетесь толкнуть (с усилием, параллельным полу), имеет массу 100 кг, то нормальная сила будет равна его весу

Вт=мг=(100 кг)(9,80 м/с2)=980 Н, Вт=мг=(100 кг)(9,80 м/с2)=980 Н,

перпендикулярно полу. Если бы коэффициент статического трения был равен 0,45, вам пришлось бы приложить параллельную полу силу, превышающую

.

фс(макс)=мксN=(0,45)(980 Н)=440 Нфс(макс)=мксN=(0,45)(980 Н)=440 Н

для перемещения ящика. Когда есть движение, трение меньше, а коэффициент кинетического трения может быть равен 0,30, так что сила всего 290 Н

fk=µkN=(0,30)(980 N)=290 Nfk=µkN=(0,30)(980 N)=290 N

будет поддерживать его движение с постоянной скоростью. Если бы пол был смазан, оба коэффициента были бы намного меньше, чем без смазки. Коэффициент трения не имеет единиц измерения и обычно представляет собой число от 0 до 1,0, но теоретического верхнего предела его значения не существует.

Работа с наклонными плоскостями

Ранее мы обсуждали, что когда объект лежит на горизонтальной поверхности, на него действует нормальная сила, равная по величине его весу. До сих пор мы имели дело только с нормальной силой в одном измерении, с гравитацией и нормальной силой, действующими перпендикулярно поверхности в противоположных направлениях (гравитация вниз, а нормальная сила вверх). Теперь, когда у вас есть навыки работы с силами в двух измерениях, мы можем исследовать, что происходит с весом и нормальной силой на наклонной поверхности, такой как наклонная плоскость. Для задач с наклонной плоскостью легче разбить силы на составляющие, если мы повернем систему координат, как показано на рис. 5.34. Первым шагом при постановке задачи является разложение силы веса на составляющие.

Рисунок 5. 34 На диаграмме показаны перпендикулярная и горизонтальная составляющие веса на наклонной плоскости.

Поддержка учителей

Поддержка учителей

[BL] Повторить понятия массы, веса, гравитации и нормальной силы.

[OL] Обзор векторов и компонентов векторов.

Когда объект лежит на наклонной плоскости, составляющей угол θθ с горизонтом, сила тяжести, действующая на объект, делится на две составляющие: сила, действующая перпендикулярно плоскости, w⊥w⊥, и сила, действующая параллельно плоскости плоскость, w||w|| . Перпендикулярная сила веса w⊥w⊥ обычно равна по величине и противоположна по направлению нормальной силе Н.Н. Сила, действующая параллельно плоскости, w||w||, заставляет объект ускоряться вниз по склону. Сила трения ff противодействует движению тела, поэтому она действует вверх по плоскости.

Важно соблюдать осторожность при разложении веса объекта на составляющие. Если угол наклона составляет угол θθ к горизонту, то величины компонентов веса равны

w||=wsin(θ)=mgsin(θ) и w||=wsin(θ)=mgsin(θ) и

w⊥=wcos(θ)=mgcos(θ). w⊥=wcos(θ) = мгкос(θ).

Вместо того, чтобы запоминать эти уравнения, полезно уметь определять их разумом. Для этого нарисуйте прямоугольный треугольник, образованный тремя весовыми векторами. Обратите внимание, что угол наклона такой же, как угол, образованный между ww и w⊥w⊥. Зная это свойство, можно с помощью тригонометрии определить величину весовых составляющих

cos(θ)=w⊥ww⊥=wcos(θ)=mgcos(θ)cos(θ)=w⊥ww⊥=wcos(θ)=mgcos(θ)

sin(θ)=w||ww ||=wsin(θ)=mgsin(θ).sin(θ)=w||ww||=wsin(θ)=mgsin(θ).

Поддержка учителей

Поддержка учителей

[BL][OL][AL] Поэкспериментируйте со скольжением различных объектов по наклонным плоскостям, чтобы понять статическое и кинетическое трение. Каким объектам нужен больший угол, чтобы скользить вниз? Что это говорит о коэффициентах трения этих систем? Требуется ли большая сила, чтобы начать движение объекта, чем для поддержания его в движении? Что это говорит о статическом и кинетическом трении? Когда тело скользит вниз с постоянной скоростью? Что это говорит о трении и нормальной силе?

Смотреть физику

Компоненты силы наклонной плоскости

В этом видеоролике показано, как вес объекта на наклонной плоскости разбивается на составляющие, перпендикулярные и параллельные поверхности плоскости. Он объясняет геометрию для нахождения угла более подробно.

В этом видео показано, как вес объекта на наклонной плоскости разбивается на составляющие, перпендикулярные и параллельные поверхности плоскости. Он объясняет геометрию для нахождения угла более подробно.

Когда поверхность плоская, можно сказать, что одна из составляющих гравитационной силы равна нулю; Который из? Что происходит с величинами перпендикулярной и параллельной составляющих гравитационной силы по мере увеличения угла наклона?

  1. Когда угол равен нулю, параллельная составляющая равна нулю, а перпендикулярная составляющая максимальна. По мере увеличения угла параллельная составляющая уменьшается, а перпендикулярная составляющая увеличивается. Это связано с тем, что косинус угла уменьшается, а синус угла увеличивается.

  2. Когда угол равен нулю, параллельная составляющая равна нулю, а перпендикулярная составляющая максимальна. По мере увеличения угла параллельная составляющая уменьшается, а перпендикулярная составляющая увеличивается. Это связано с тем, что косинус угла увеличивается, а синус угла уменьшается.

  3. Когда угол равен нулю, параллельная составляющая равна нулю, а перпендикулярная составляющая максимальна. По мере увеличения угла параллельная составляющая увеличивается, а перпендикулярная составляющая уменьшается. Это связано с тем, что косинус угла уменьшается, а синус угла увеличивается.

  4. Когда угол равен нулю, параллельная составляющая равна нулю, а перпендикулярная составляющая максимальна. По мере увеличения угла параллельная составляющая увеличивается, а перпендикулярная составляющая уменьшается. Это связано с тем, что косинус угла увеличивается, а синус угла уменьшается.

Советы для успеха

Нормальная сила представлена ​​переменной N.N. Его не следует путать с символом ньютона, который также обозначается буквой N. Важно различать эти символы, тем более что единицами измерения нормальной силы (NN) являются ньютоны (Н). Например, нормальная сила NN, с которой пол действует на стул, может составлять N=100 N.N=100 Н. Одно важное отличие состоит в том, что нормальная сила — это вектор, а ньютон — это просто единица измерения. Будьте осторожны, чтобы не перепутать эти буквы в своих вычислениях!

Для обзора, процесс решения задач наклонной плоскости выглядит следующим образом:

  1. Нарисуйте схему задачи.
  2. Определите известные и неизвестные количества и определите интересующую систему.
  3. Нарисуйте диаграмму свободного тела (это эскиз, показывающий все силы, действующие на объект) с системой координат, повернутой под тем же углом, что и наклонная плоскость. Разделите векторы на горизонтальную и вертикальную составляющие и нарисуйте их на диаграмме свободного тела.
  4. Запишите второй закон Ньютона в горизонтальном и вертикальном направлениях и сложите силы, действующие на объект. Если объект не ускоряется в определенном направлении (например, в направлении x ), то F net x = 0. Если объект ускоряется в этом направлении, F net x = м и .
  5. Проверьте свой ответ. Разумный ли ответ? Единицы правильные?

Рабочий пример

Нахождение коэффициента кинетического трения на наклонной плоскости

Лыжник, изображенный на рис. 5.35(а), массой 62 кг скользит по заснеженному склону под углом 25 градусов. Найдите коэффициент кинетического трения лыжника, если известно, что трение равно 45,0 Н.

Рисунок 5,35 Используйте диаграмму, чтобы найти коэффициент кинетического трения для лыжника.

Стратегия

Величина кинетического трения равна 45,0 Н. Кинетическое трение связано с нормальной силой N как fk=µkNfk=µkN . Следовательно, мы можем найти коэффициент кинетического трения, сначала найдя нормальную силу лыжника на склоне. Нормальная сила всегда перпендикулярна поверхности, а поскольку движение перпендикулярно поверхности отсутствует, нормальная сила должна равняться составляющей веса лыжника, перпендикулярной склону.

То есть

N=w⊥=w cos(25∘)=mg cos(25∘).N=w⊥=w cos(25∘)=mg cos(25∘).

Подставляя это в выражение для кинетического трения, получаем

fk=µkmg cos 25∘,fk=µkmg cos 25∘,

, которое теперь можно решить для коэффициента кинетического трения µ k .

Решение

Решение для µkµk дает

µk=fkw cos 25∘=fkmg cos 25∘.µk=fkw cos 25∘=fkmg cos 25∘.

Подставляя известные значения в правую часть уравнения,

мкк=45,0 Н(62 кг)(9,80 м/с2)(0,906)=0,082,мкк=45,0 Н(62 кг)(9,80 м/с2 )(0,906)=0,082.

Обсуждение

Этот результат немного меньше, чем коэффициент, указанный в таблице 5.2 для вощеной древесины на снегу, но все же приемлем, поскольку значения коэффициентов трения могут сильно различаться. В подобных ситуациях, когда объект массой м скользит вниз по склону, составляющему угол θ с горизонтом, трение определяется формулой fk=µkmg cosθ.fk=µkmg cosθ.

Рабочий пример

Вес на склоне, двумерная задача

Масса лыжника, включая снаряжение, 60,0 кг. (См. рис. 5.36(b).) (a) Каково ее ускорение, если трением можно пренебречь? б) Чему равно ее ускорение, если сила трения равна 45,0 Н?

Рисунок 5,36 Теперь используйте диаграмму, чтобы найти ускорение лыжника, если трением можно пренебречь и если сила трения равна 45,0 Н.

Стратегия

Наиболее удобной системой координат для движения по склону является та, в которой одна координата параллельна склону, а другая перпендикулярна склону. Помните, что движения вдоль перпендикулярных осей независимы. Мы используем символ ⊥⊥ для обозначения перпендикуляра, а |||| значит параллельно.

Единственными внешними силами, действующими на систему, являются вес лыжника, трение и нормальная сила, действующая на лыжный склон, обозначенные ww, ff и NN на диаграмме свободного тела. NN всегда перпендикулярен склону, а ff параллелен ему. Но ww не направлен ни по одной из осей, поэтому мы должны разбить его на составляющие по выбранным осям. Определим w||w|| быть компонентом веса, параллельным склону, и w⊥w⊥ компонентом веса, перпендикулярным склону. Как только это будет сделано, мы можем рассмотреть две отдельные проблемы сил, параллельных склону, и сил, перпендикулярных склону.

Решение

Величина составляющей веса, параллельной наклону, равна w||=wsin(25°)=mgsin(25°)w||=wsin(25°)=mgsin(25°), а величина составляющей веса, перпендикулярной наклону, равна w⊥=wcos(25°)=mgcos(25°). w⊥=wcos(25°)=mgcos(25°).

(a) Пренебрегая трением: поскольку ускорение параллельно наклону, нам нужно учитывать только силы, параллельные наклону. Силы, перпендикулярные склону, складываются в ноль, так как в этом направлении нет ускорения. Силы, параллельные склону, равны сумме веса лыжника, параллельного склону, w||w|| и трение ff . При отсутствии трения по второму закону Ньютона ускорение, параллельное склону, равно

a||=Fnet ||m,a||=Fnet ||m,

Где результирующая сила, параллельная склону, Fnet ||=w||=mgsin(25°)Fnet ||=w|| =mgsin(25°), так что

a||=Fnet ||m=mgsin(25°)m=gsin(25°)=(9,80 м/с2)(0,423)=4,14 м/с2a||= Fnet ||m=mgsin(25°)m=gsin(25°)=(9,80 м/с2)(0,423)=4,14 м/с2

— ускорение.

(b) Включая трение: Теперь у нас есть заданное значение трения, и мы знаем, что его направление параллельно склону и оно препятствует движению между контактирующими поверхностями. Таким образом, чистая внешняя сила теперь равна 9.0005

Fnet ||=w||−f,Fnet ||=w||–f,

и подставляя это во второй закон Ньютона, a||=Fnet ||ma||=Fnet ||m дает

a||=Fnet ||m=w||-fm=mgsin(25°)-fm. a||=Fnet ||m=w||-fm=mgsin(25°)-fm.

Подставляем известные значения и получаем )−45,0 N60,0 кг,

или

a||=3,39 м/с2, a||=3,39 м/с2,

, что представляет собой ускорение, параллельное наклону, при наличии противодействующего трения 45 Н.

Обсуждение

Поскольку трение всегда препятствует движению между поверхностями, ускорение при наличии трения меньше, чем при его отсутствии.

Практические задачи

15.

Когда объект находится на наклонной плоскости, составляющей угол θ с горизонтом, как выражается составляющая силы веса объекта, параллельная наклону?

  1. w||=wcosθw||=wcosθ
  2. w||=wsinθw||=wsinθ 9\круг\! от горизонтального. Какая составляющая силы веса параллельна наклону?

    1. 4. 33\,\текст{N}

    2. 5.0\,\текст{N}

    3. 24,5\,\текст{N}

    4. 42.43\,\текст{N}

    Снап Лаборатория

    Трение под углом: скольжение монеты

    Объект будет скользить по наклонной плоскости с постоянной скоростью, если результирующая сила, действующая на объект, равна нулю. Мы можем использовать этот факт для измерения коэффициента кинетического трения между двумя объектами. Как показано в первом рабочем примере, кинетическое трение на склоне fk=µkmg cosθfk=µkmg cosθ, а составляющая веса вниз по склону равна mg sinθmg sinθ . Эти силы действуют в противоположных направлениях, поэтому, когда они имеют одинаковую величину, ускорение равно нулю. Написание этих

    fk=Fgxμkmg cosθ=mg sinθ.fk=Fgxμkmg cosθ=mg sinθ.

    Решая μkμk, поскольку tanθ=sinθ/cosθtanθ=sinθ/cosθ, мы находим, что

    μk=mg sinθmg cosθ= tanθ.μk=mg sinθmg cosθ= tanθ.

    5,10

    • 1 монета
    • 1 книга
    • 1 транспортир
      1. Положите монету плоской стороной на книгу и наклоняйте ее, пока монета не будет скользить по книге с постоянной скоростью. Возможно, вам придется слегка постучать по книге, чтобы заставить монету двигаться.
      2. Измерьте угол наклона относительно горизонтали и найдите μkμk .

    Проверка захвата

    Верно или неверно — если известны только углы двух векторов, мы можем найти угол их результирующего вектора сложения.

    1. Правда
    2. Ложь

    Проверьте свое понимание

    17.

    Что такое трение?

    1. Трение — это внутренняя сила, противодействующая относительному движению объекта.

    2. Трение — это внутренняя сила, которая ускоряет относительное движение объекта.

    3. Трение — это внешняя сила, противодействующая относительному движению объекта.

    4. Трение — это внешняя сила, увеличивающая скорость относительного движения объекта.

    18.

    Какие существуют две разновидности трения? На что действует каждый?

    1. Кинетическое и статическое трение действуют на движущийся объект.

    2. Кинетическое трение действует на движущийся объект, а статическое трение действует на покоящийся объект.

    3. Кинетическое трение действует на неподвижный объект, а статическое трение действует на движущийся объект.

    4. Кинетическое и статическое трение действуют на покоящийся объект.

    19.

    Какое значение статического и кинетического трения между двумя поверхностями больше? Почему?

    1. Кинетическое трение имеет большее значение, потому что трение между двумя поверхностями больше, когда две поверхности находятся в относительном движении.

    2. Статическое трение имеет большее значение, потому что трение между двумя поверхностями больше, когда две поверхности находятся в относительном движении.

    3. Кинетическое трение имеет большее значение, потому что трение между двумя поверхностями меньше, когда две поверхности находятся в относительном движении.

    4. Статическое трение имеет большее значение, потому что трение между двумя поверхностями меньше, когда две поверхности находятся в относительном движении.

    Поддержка учителей

    Поддержка учителей

    Используйте вопросы Проверьте свое понимание , чтобы оценить, достигают ли учащиеся целей обучения в этом разделе. Если учащиеся не могут справиться с определенной задачей, Check Your Understanding поможет определить, какая цель вызывает проблему, и направит учащихся к соответствующему контенту.

    Наклонные плоскости

    Объект, помещенный на наклонную поверхность , будет часто скользить по поверхности. Скорость, с которой объект скользит по поверхности, зависит от того, насколько наклонена поверхность; чем больше наклон 90 577 90 305 поверхности, тем выше скорость, с которой объект будет скользить по ней. В физике наклонных поверхностей называется наклонной плоскостью. Известно, что объекты ускоряются вниз по наклонным плоскостям из-за неуравновешенной силы. Чтобы понять этот тип движения, важно проанализировать силы, действующие на объект на наклонной плоскости. На диаграмме справа показаны две силы, действующие на ящик, расположенный на наклонной плоскости (предполагается, что трение отсутствует). Как показано на диаграмме, всегда

    по крайней мере две силы

    действуют на любой объект, расположенный на наклонной плоскости, — сила тяжести и нормальная сила. Сила тяжести (также известная как вес) действует в направлении вниз; однако нормальная сила действует в направлении, перпендикулярном поверхности (фактически нормальный означает «перпендикулярный»).


    Аномальная нормальная сила

    Первая особенность задач с наклонной плоскостью состоит в том, что нормальная сила , а не направлена ​​в привычном нам направлении. До этого момента в курсе мы всегда видели нормальные силы, действующие в восходящем направлении, противоположном направлению силы тяжести. Но это только потому, что объекты всегда находились на горизонтальных поверхностях, а не на наклонных плоскостях. Правда о нормальных силах заключается не в том, что они всегда направлены вверх, а в том, что они всегда направлены перпендикулярно поверхности, на которой находится объект.

     

    Компоненты силы тяжести

    Задача определения результирующей силы, действующей на объект на наклонной плоскости, является сложной задачей, поскольку две (или более) силы не направлены в противоположные стороны. Таким образом, одну (или несколько) сил придется разложить на перпендикулярные составляющие, чтобы их можно было легко добавить к другим силам, действующим на объект. Обычно любую силу, направленную под углом к ​​горизонтали, разлагают на горизонтальную и вертикальную составляющие. Однако это не тот процесс, который мы будем проводить с наклонными плоскостями. Вместо этого процесс анализа сил, действующих на объекты на наклонных плоскостях, будет включать определение весового вектора (F грав ) на две перпендикулярные составляющие. Это вторая особенность задач наклонной плоскости. Сила тяжести будет разложена на две составляющие силы — одну, направленную параллельно наклонной поверхности, и другую, направленную перпендикулярно наклонной поверхности. На приведенной ниже диаграмме показано, как сила тяжести была заменена двумя составляющими — параллельной и перпендикулярной составляющей силы.

     

    Перпендикулярная составляющая силы тяжести направлена ​​против нормальной силы и, таким образом, уравновешивает нормальную силу. Параллельная составляющая силы тяжести не уравновешивается никакой другой силой. Этот объект впоследствии будет ускоряться вниз по наклонной плоскости из-за наличия неуравновешенной силы. Именно параллельная составляющая силы тяжести вызывает это ускорение. Параллельная составляющая силы тяжести является чистой силой.

    Задача определения величины двух составляющих силы тяжести — это простой способ использования уравнений. Уравнения для параллельной и перпендикулярной составляющих:

    При отсутствии трения и других сил (растяжения, приложенных и т. д.) ускорение объекта на наклонной поверхности равно значению параллельной составляющей (м *g*синус угла), деленное на массу (m). Это дает уравнение

    (при отсутствии сил трения и других сил)


    Упрощение задачи о наклонной плоскости

    При наличии трения или других сил (приложенной силы, силы натяжения и т. д.) ситуация несколько усложняется. Рассмотрим схему, показанную справа. Перпендикулярная составляющая силы по-прежнему уравновешивает нормальную силу, поскольку объекты не ускоряются перпендикулярно наклону. Тем не менее, сила трения также должна учитываться при определении чистой силы. Как и во всех задачах о чистой силе, чистая сила представляет собой векторную сумму всех сил. То есть все отдельные силы складываются вместе как 9.0577 векторов . Перпендикулярная составляющая и нормальная сила в сумме дают 0 Н. Параллельная составляющая и сила трения в сумме дают 5 Н. Суммарная сила равна 5 Н и направлена ​​вдоль наклона к полу.

    Приведенную выше задачу (и все задачи с наклонной плоскостью) можно упростить с помощью полезного приема, известного как «наклон головы». Задача о наклонной плоскости во всех отношениях подобна любой другой задаче о результирующей силе, за исключением того, что поверхность была наклонена 90 577 90 305 . Таким образом, чтобы преобразовать проблему обратно в более удобную для вас форму, достаточно наклонить голову в том же направлении, в котором был наклон наклонить . Или, еще лучше, просто наклоните 90 577 90 305 страницу бумаги (надежное лекарство от TNS — «синдром перекошенной шеи» или «синдром тако-шейки»), чтобы поверхность перестала казаться ровной. Это показано ниже.

    После того, как сила тяжести будет разделена на две составляющие и наклонена наклонная плоскость, задача должна выглядеть очень знакомо. Просто игнорируйте силу гравитации (поскольку она была заменена двумя ее компонентами) и найдите результирующую силу и ускорение.

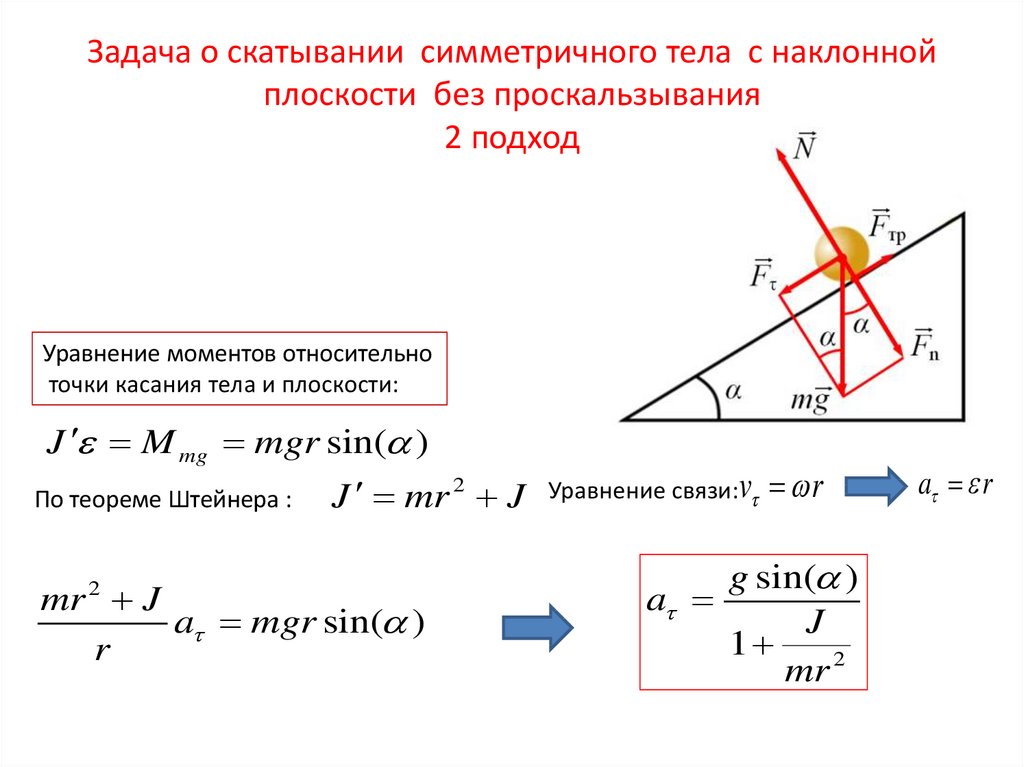
    В качестве примера рассмотрим ситуацию, изображенную на диаграмме справа. На диаграмме свободного тела показаны силы, действующие на 100-килограммовый ящик, скользящий по наклонной плоскости. Плоскость наклонена под углом 30 градусов. Коэффициент трения между обрешеткой и склоном равен 0,3. Определить результирующую силу и ускорение ящика.

    Начнем с вышеуказанной задачи, найдя силу тяжести, действующую на ящик, и компоненты этой силы, параллельные и перпендикулярные наклону. Сила тяжести равна 980 Н, а компоненты этой силы равны F параллельно = 490 Н (980 Н • sin 30 градусов) и F перпендикулярно = 849 Н (980 Н • cos30 градусов). Теперь нормальную силу можно определить равной 849 Н (она должна уравновешивать перпендикулярную составляющую вектора веса). Силу трения можно определить по величине нормальной силы и коэффициента трения; F трение составляет 255 Н (F трение = «mu»*F норма = 0,3 • 849 Н). Чистая сила представляет собой векторную сумму всех сил. Силы, направленные перпендикулярно наклону, уравновешивают; силы, направленные параллельно наклону, не уравновешиваются. Чистая сила составляет 235 Н (490 Н — 255 Н). Ускорение составляет 2,35 м/с/с (F net /м = 235 Н/100 кг).

     

    Практика

    На двух приведенных ниже диаграммах показана диаграмма свободного тела для 1000-килограммовых американских горок при первом падении двух разных аттракционов на американских горках. Используйте приведенные выше принципы векторного разрешения, чтобы определить результирующую силу и ускорение автомобилей американских горок. Предположим, что влияние трения и сопротивления воздуха пренебрежимо мало. Когда закончите, нажмите кнопку, чтобы просмотреть ответы.

     

     

     

    Влияние угла наклона на ускорение американских горок (или любого объекта на склоне) можно наблюдать в двух вышеприведенных практических задачах. С увеличением угла увеличивается ускорение объекта. Объяснение этого относится к компонентам, которые мы рисовали. По мере увеличения угла составляющая силы, параллельная наклону, увеличивается, а составляющая силы, перпендикулярная наклону, уменьшается. Именно параллельная составляющая вектора веса вызывает ускорение. Таким образом, ускорения больше при больших углах наклона. На приведенной ниже диаграмме показано это соотношение для трех различных углов возрастающей величины.

     

     

    Немного физики американских горок

    Американские горки вызывают два острых ощущения, связанных с начальным падением по крутому склону. Острые ощущения от ускорения создаются за счет использования больших углов наклона при первом падении; такие большие углы увеличивают значение параллельной составляющей вектора веса (составляющей, вызывающей ускорение). Ощущение невесомости производится за счет уменьшения величины нормальной силы до значений, меньших их обычных значений. Важно признать, что ощущение невесомости — это чувство, связанное с более низкой, чем обычно, нормальной силой. Как правило, человек весом 700 Н испытывает нормальную силу 700 Н, когда сидит на стуле. Однако, если кресло движется с ускорением вниз по наклону в 60 градусов, то человек будет испытывать нормальную силу в 350 ньютонов. Это значение меньше нормального и способствует ощущению, что вес меньше нормального, т. е. 9.0059 невесомость .

     

    Больше практики

    Используйте виджет ниже, чтобы исследовать другие ситуации с наклонной плоскостью. Просто введите массу, угол наклона и коэффициент трения (используйте 0 для случаев отсутствия трения). Затем нажмите кнопку Отправить , чтобы просмотреть ускорение.

    Проверьте свое понимание

    Следующие вопросы предназначены для проверки вашего понимания математики и концепций наклонных плоскостей. После того, как вы ответили на вопрос, нажмите кнопку, чтобы увидеть ответы.

    1. Два мальчика играют в хоккей на соседней улице. Бродячая шайба движется по льду без трения , а затем поднимается по наклонной дороге без трения. Какая из следующих бегущих лент (A, B или C) точно изображает движение шайбы, когда она движется по ровной улице, а затем вверх по подъездной дорожке?

    Объясните свой ответ.

     

     

    2. Маленький Джонни стоит внизу подъездной дорожки и пинает футбольный мяч. Мяч катится на север по подъездной дорожке, а затем возвращается к Джонни. Какой из следующих графиков зависимости скорости от времени (A, B, C или D) наиболее точно отображает движение мяча, когда он катится вверх по подъездной дорожке и обратно?

    Объясните свой ответ.

     

     

     

    3. Мяч для гольфа катится по горизонтальному участку грина на 18-й лунке. Затем он сталкивается с крутым нисходящим уклоном (см. Диаграмму). Участвует трение. Какой из следующих шаблонов бегущей строки (A, B или C) может быть подходящим представлением движения мяча?

    Объясните, почему неуместные шаблоны неуместны.

     

     

     

    4. Восьмой фрейм Мисси де Пенн в боулинг-лиге по средам стал катастрофой. Мяч скатился с полосы, прошел через грузовой люк в задней части здания, а затем по подъездной дорожке. Милли Митер (товарищ по команде Мисси), которая проводила каждую свободную минуту за подготовкой к экзамену по физике, начала визуализировать график зависимости скорости от времени для движения мяча. Какой из графиков зависимости скорости от времени (A, B, C или D) будет подходящим представлением движения мяча, когда он катится по горизонтальной поверхности, а затем вниз по склону? Рассмотрим силы трения.

     

     

     

     

    5. Три партнера по лаборатории — Олив Н. Гленво, Глен Брук и Уоррен Пис — обсуждают задачу о наклоне (см. схему). Они спорят о значении нормальной силы. Олив утверждает, что нормальная сила равна 250 Н; Глен утверждает, что нормальная сила равна 433 Н; а Уоррен утверждает, что нормальная сила равна 500 Н. Хотя все три ответа кажутся разумными, правильным является только один. Укажите, какие два ответа неверны, и объясните, почему они неверны.

     

     

     

    6. Лон Скейпер возится с газоном, когда из его тачки вырывается 2-килограммовая шина, которая начинает катиться вниз по крутому холму (уклон 30°) в Сан-Франциско. Нарисуйте параллельные и перпендикулярные компоненты этого весового вектора.