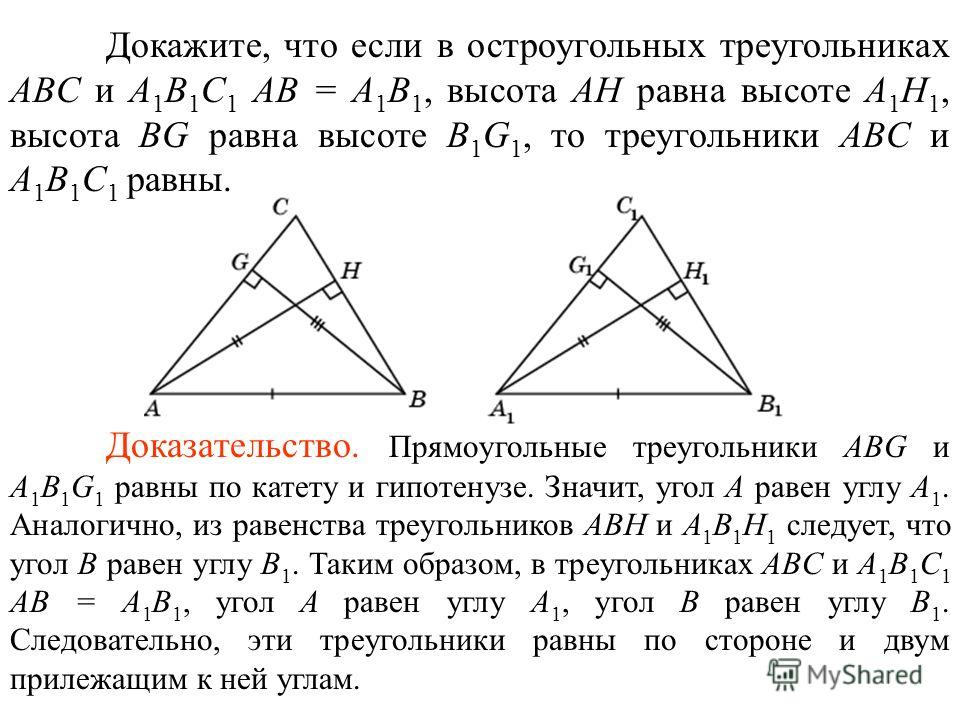
31 января 2023 Математика 9 класс статград ответы и задания МА2290301-МА2290304
Вариант МА2290301, МА2290302, МА2290303, МА2290304
Скачать ответы и решения
Автомобильное колесо, как правило, представляет из себя металлический диск с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине. Для маркировки автомобильных шин применяется единая система обозначений. Например, 195/65 R15 (рис. 1).
Первое число (число 195 в приведённом примере) обозначает ширину шины в миллиметрах (параметр B на рис. 2). Второе число (число 65 в приведённом примере) — процентное отношение высоты боковины (параметр H на рис. 2) к ширине шины, то есть 100 H B ⋅ .
Последующая буква обозначает тип конструкции шины. В данном примере буква R означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции.
За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса d в дюймах (в одном дюйме 25,4 мм).
Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины. Возможны дополнительные маркировки, обозначающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие параметры. Завод производит легковые автомобили определённой модели и устанавливает на них колёса с шинами маркировки 245/45 R18.
1.Завод допускает установку шин с другими маркировками. В таблице показаны разрешённые размеры шин. Шины какой наименьшей ширины можно устанавливать на автомобиль, если диаметр диска равен 20 дюймам? Ответ дайте в миллиметрах.
2. Найдите диаметр колеса автомобиля, выходящего с завода. Ответ дайте в миллиметрах.
3. На сколько миллиметров радиус колеса с шиной маркировки 215/60 R17 меньше, чем радиус колеса с шиной маркировки 265/50 R17?
4. На сколько миллиметров увеличится диаметр колеса, если заменить колёса, установленные на заводе, колёсами с шинами маркировки 265/35 R20?
5.
На сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить колёса, установленные на заводе, колёсами с шинами маркировки 265/45 R18? Результат округлите до десятых.
9. Решите уравнение 6×2=36x. Если уравнение имеет больше одного корня, в ответе запишите меньший из корней.
10. В магазине канцтоваров продаётся 100 ручек: 37 красных, 8 зелёных, 17 фиолетовых, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или чёрной.
11.
12.
13.
14.В ходе распада радиоактивного изотопа его масса уменьшается вдвое каждые 9 минут. В начальный момент масса изотопа составляла 400 мг. Найдите массу изотопа через 36 минут. Ответ дайте в миллиграммах.
15. В треугольнике ABC известно, что AB = 7 , BC = 8 , AC =13. Найдите cos∠ABC.
16. Хорды AC и BD окружности пересекаются в точке P , BP =10 , CP = 8, DP =12.
Найдите длину отрезка AP.
17. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30° . Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
18. На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
19. Какое из следующих утверждений верно? 1) Средняя линия трапеции равна полусумме её оснований. 2) Диагонали любого прямоугольника делят его на четыре равных треугольника. 3) Косинус острого угла прямоугольного треугольника равен отношению гипотенузы к прилежащему к этому углу катету.
21. Моторная лодка прошла против течения реки 77 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 4 км/ч.
23. Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD , если AB 40 , CD 42 , а расстояние от центра окружности до хорды AB равно 21.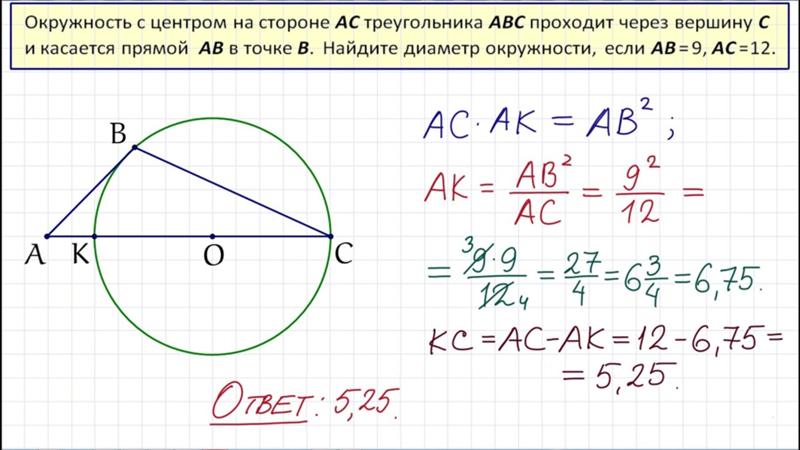
24. Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AD и BC четырёхугольника пересекаются в точке K . Докажите, что треугольники KAB и KCD подобны.
25. На стороне BC остроугольного треугольника ABC как на диаметре построена полуокружность, пересекающая высоту AD в точке M , AD 15 , MD 12, H — точка пересечения высот треугольника ABC . Найдите AH .
Скачать ответы и решения
Задание №16. Планиметрия с доказательством. ЕГЭ. Математика. 1
1. Планиметрия
2. Стереометрия
3. Начала теории вероятностей
4. Теория вероятностей
5. Простейшие уравнения
6. Преобразование выражений
7. Производная функции
8. Практические задачи
9. Текствые задачи
10. Графики функций
11.
Исследование функций
12. Уравнения
13. Стереометрия с доказ-вом
14. Неравенства
15. Финансовая математика
16. Планиметрия с доказ-вом
17. Задачи с параметром
18. Задачи на логику
БАЗА ЗАДАНИЙ
Задание № 16. Планиметрия с доказательством.
1. Прямая, проходящая через вершину B прямоугольника ABCD перпендикулярно диагонали AC, пересекает сторону AD в точке M, равноудалённой от вершин B и D.
а) Докажите, что ∠ABM =∠DBС = 30°.
б) Найдите расстояние от центра прямоугольника до прямой CM, если BC = 9.
2. К окружности, вписанной в квадрат ABCD, проведена касательная, пересекающая стороны AB и AD в точках M и N соответственно.
а) Докажите, что периметр треугольника AMN равен стороне квадрата.
б) Прямая MN пересекает прямую CD в точке P. В каком отношении делит сторону BC прямая, проходящая через точку P и центр окружности, если AM : MB = 1 : 3?
Ответ: б) 1:3
3. Диагонали AC и BD четырёхугольника ABCD, вписанного в окружность, пересекаются в точке P, причём BC=CD.
а) Докажите, что AB:BC = AP:PD.
б) Найдите площадь треугольника COD, где O— центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD — диаметр описанной около четырёхугольника
Ответ: б) 18√3
4. В треугольнике ABC точки A1, B1, C1 — середины сторон BC, AC и AB соответственно, AH— высота, ∠BAC = 60°, ∠BCA = 45°.
а) Докажите, что точки A1, B1, C1, H— лежат на одной окружности.
б) Найдите A1 H, если BC = 2√3.
Ответ: б)
5. Две окружности касаются внутренним образом в точке A, причём меньшая проходит через центр большей. Хорда BC большей окружности касается меньшей в точке P. Хорды AB и AC пересекают меньшую окружность в точках K и M соответственно.
а) Докажите, что прямые KM и BC параллельны.
б) Пусть L— точка пересечения отрезков KM и AP. Найдите AL, если радиус большей окружности равен 10, а BC = 16.
Ответ: б) √10
6. Две окружности касаются внутренним образом в точке A, причём меньшая окружность проходит через центр O большей. Диаметр
Лучи AO и AM вторично пересекают большую окружность в точках P и Q соответственно. Точка C лежит на дуге AQ большей окружности, не содержащей точку P.
а) Докажите, что прямые PQ и BC параллельны.
б) Известно, что sin ∠AOC=√15/4. Прямые PC и AQ пересекаются в точке K. Найдите отношение QK:KA.
Ответ: б) 1:4
7. Две окружности касаются внутренним образом в точке K, причём меньшая проходит через центр большей. Хорда
а) Докажите, что CN:CM = LB:LA.
б) Найдите MN, если LB:LA = 2:3, а радиус малой окружности равен √23.
Ответ: б) 115/6
8.
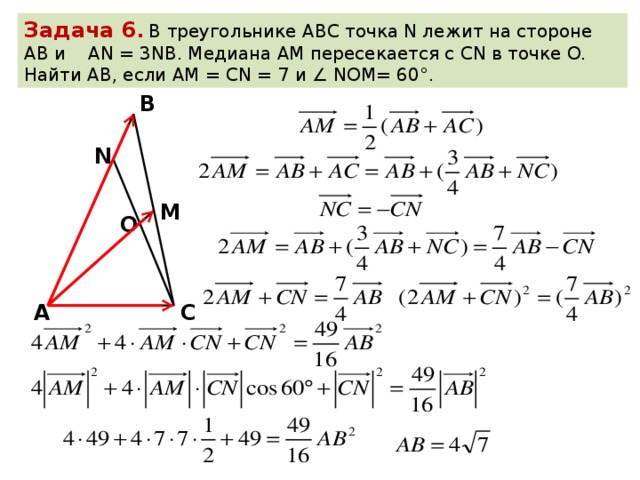Дан прямоугольный треугольник ABC с прямым углом C. На катете AC взятаточка M. Окружность с центром O и диаметром CM касается гипотенузы в точке
а) Докажите, что прямые MN и BO параллельны.
б) Найдите площадь четырёхугольника BOMN, если CN = 4 и AM:MC = 1:3.
Ответ: б) 7
9. Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MB пересекает окружность с диаметром AB в точке D.
а) Докажите, что прямые AD и MC параллельны.
б) Найдите площадь треугольника DBC, если AK = 3 и MK = 12.
Ответ: б) 30
10. Точка M лежит на стороне BC выпуклого четырёхугольника ABCD, причём B и C — вершины равнобедренных треугольников с основаниями AM и DM соответственно, а прямые AM и MD перпендикулярны.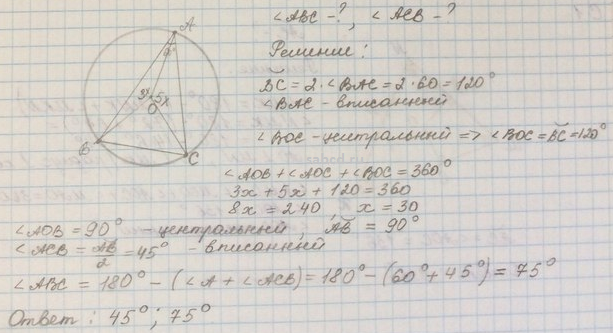
а) Докажите, что биссектрисы углов при вершинах B и C четырёхугольника ABCD пересекаются на стороне AD.
б) Пусть N— точка пересечения этих биссектрис. Найдите площадь четырёхугольника ABCD, если известно, что BM:MC=1:3, а площадь четырёхугольника, стороны которого лежат на прямых
Ответ: б) 96
11. В равнобедренном тупоугольном треугольнике ABC на продолжение боковой стороны BC опущена высота AH. Из точки H на сторону AB и основание AC опущены перпендикуляры HK и HM соответственно.
а) Докажите, что отрезки AM и MK равны.
б) Найдите MK, если AB = 5, AC = 8.
Ответ: б) 2,88
12. Точка O — центр окружности, описанной около остроугольного треугольника ABC, I — центр вписанной в него окружности,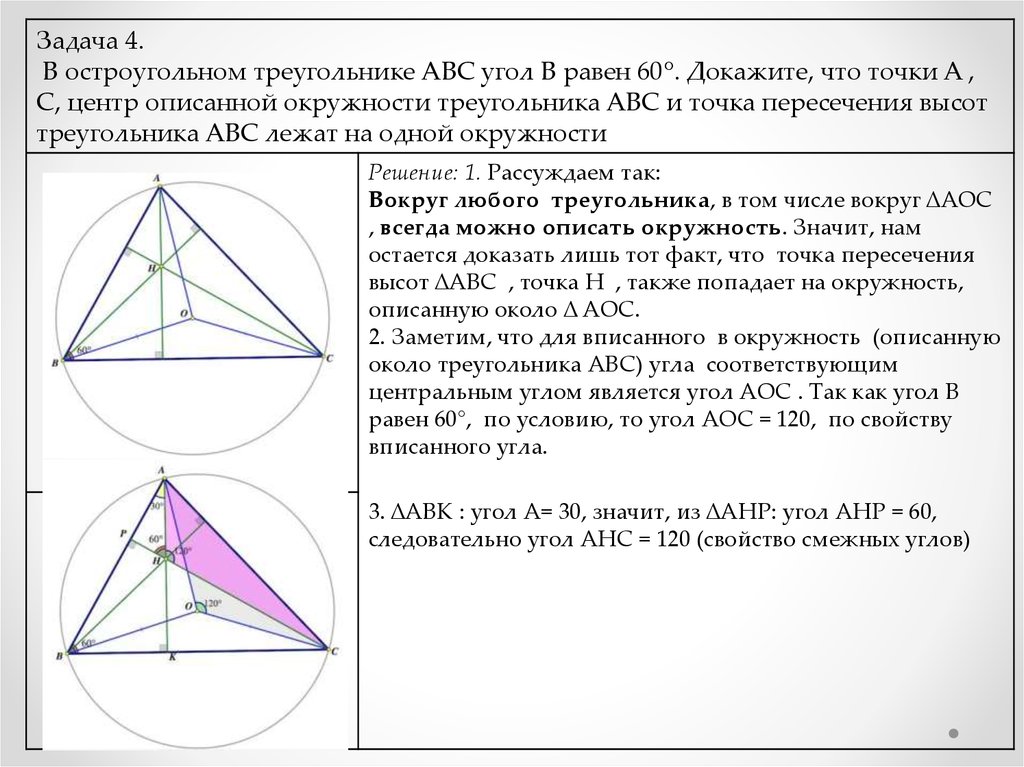 
Известно, что ∠BAC = ∠OBC+∠OCB.
а) Докажите, что точка H лежит на окружности, описанной около треугольника BOC.
б) Найдите угол OIH, если ∠ABC = 55°.
Ответ: б) 175
13. Точки P, Q, W делят стороны выпуклого четырёхугольника ABCD в отношении AP:PB = CQ:QB = CW:WD = 3:4, радиус окружности, описанной около треугольника PQW, равен 10, PQ = 16, QW = 12, угол PWQ— острый.
а) Докажите, что треугольник
б) Найдите площадь четырёхугольника ABCD.
Ответ: б) 392
14. Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках C1, B1 соответственно.
а) Докажите, что треугольник АВC подобен треугольнику AB1C1.
б) Вычислите длину стороны ВС и радиус данной окружности, если ∠ А = 45°, B1C1=6 и площадь треугольника AB1C1 в восемь раз меньше площади четырёхугольника
15. Дана трапеция ABCD с основаниями AD и BC. Диагональ BD разбивает её на два равнобедренных треугольника с основаниями AD и CD.
а) Докажите, что луч AC— биссектриса угла BAD.
б) Найдите CD, если известны диагонали трапеции: AC = 15 и BD = 8,5.
Ответ: б) 8
16. В прямоугольном треугольнике АВС с прямым углом С точки М и N –середины катетов АС и ВС соответственно, СН – высота.
а) Докажите, что прямые MH и NH
б) Пусть Р – точка пересечения прямых АС и NH, а Q – точка пересечения прямых ВС и MH.
Найдите площадь треугольника PQM, если АН = 12 и ВН = 3.Ответ: б) 50
17. В треугольнике АВС угол АВС равен 60°. Окружность, вписанная в треугольник, касается стороны AC в точке M.
а) Докажите, что отрезок BM не больше утроенного радиуса вписанной в треугольник окружности.
б) Найдите sin ∠BMC если известно, что отрезок ВМ в 2,5 раза больше радиуса вписанной в треугольник окружности.
Ответ: б) 0,65
18. В треугольнике АВС проведены высоты АК и СМ. На них из точек М и К опущены перпендикуляры МЕ и КН соответственно.
а) Докажите, что прямые ЕН и АС параллельны.
б) Найдите отношение ЕН:АС, если угол АВС равен 30.
Ответ: б) 3:4
19. Окружность, вписанная в треугольник KLM, касается сторон KL, LM, MK в точках A, B и C соответственно.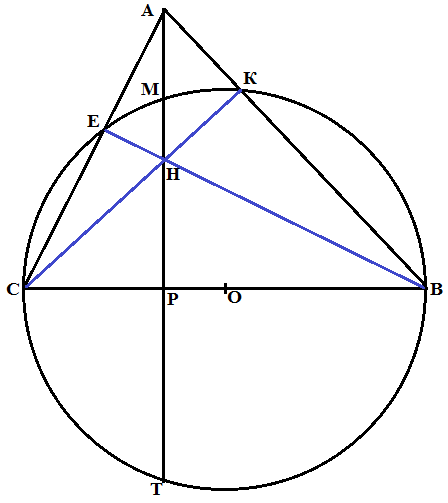
а) Докажите, что KC = (KL+KM-LM)/2 .
б) Найдите отношение LB:BM, если известно, что KC:CM = 3:2 и ∠ MKL = 60.
Ответ: б) 5:2
20. Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром O, построенная на боковой стороне AB как на диаметре, касается боковой стороны CD и второй раз пересекает большее основание AD в точке H, точка Q — середина CD.
а) Докажите, что четырёхугольник DQOH — параллелограмм.
б) Найдите AD, если ∠BAD = 75° и BC =1.
Ответ: б) 3
21. Квадрат ABCD вписан в окружность. Хорда CE пересекает его диагональ BD в точке K.
а) Докажите, что CK*CE = AB*CD.
б) Найдите отношение CK к KE, если ∠ ECD = 15.
Ответ: б) 2:1
22. В прямоугольном треугольнике ABC точки M и N – середины гипотенузы AB и катета BC соответственно.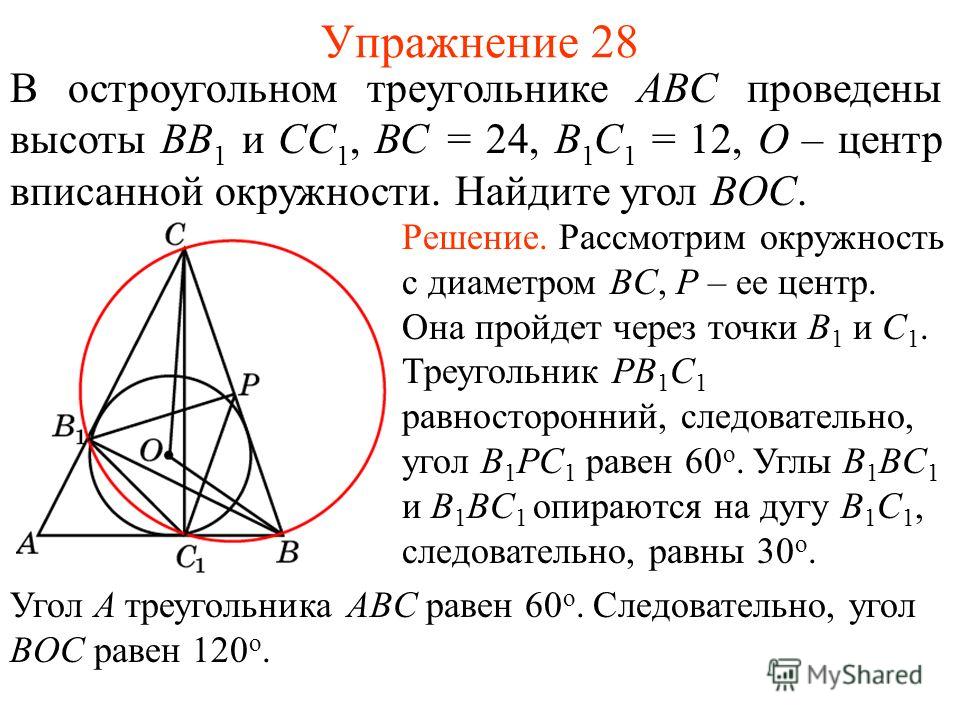
Биссектриса ∠ BAC пересекает прямую MN в точке L
а) Докажите, что треугольники AML и BLC подобны.
б) Найдите отношение площадей этих треугольников, если cos ∠BAC = 7/25.
Ответ: б) 25:36
23. Окружность касается стороны AC остроугольного треугольника ABC и делит каждую из сторон AB и BC на три равные части.
а) Докажите, что треугольник ABC равнобедренный.
б) Найдите, в каком отношении высота этого треугольника делит сторону BC.
Ответ: б) 5:4
24. На катетах AC и BC прямоугольного треугольника ABC как на диаметрах построены окружности, второй раз пересекающиеся в точке M. Точка Q лежит на меньшей дуге MB окружности с диаметром BC. Прямая CQ второй раз пересекает окружность с диаметром AC в точке P.
а) Докажите, что прямые PM и QM перпендикулярны.
б) Найдите PQ, если AM = 1, BM = 3, а Q – середина дуги MB.
Ответ: б) 2
25. Окружность, построенная на медиане BM равнобедренного треугольника ABC как на диаметре, второй раз пересекает основание BC в точке K.
а) Докажите, что отрезок BK втрое больше отрезка CK.
б) Пусть указанная окружность пересекает сторону AB в точке N. Найдите AB, если BK = 24 и BN = 23.
26. В прямоугольной трапеции ABCD с прямым углом при вершине A расположены две окружности. Одна из них касается боковых сторон и большего основания AD, вторая – боковых сторон, меньшего основания BC и первой окружности.
а) Прямая, проходящая через центр окружностей, пересекает основание AD в точке P. Докажите, что AP/PD = sin ∠D.
б) Найдите площадь трапеции, если радиусы окружностей равны 3 и 1.
27. В трапецию ABCD с основаниями AD и BC вписана окружность с центром O.
а) Докажите, что sin ∠AOD = sin ∠ BOS.
б) Найдите площадь трапеции, если ∠ BAD = 90, а основания равны 5 и 7.
Ответ: б) 35
28. Дана трапеция с диагоналями равными 8 и 15. Сумма оснований равна 17.
а) Докажите, что диагонали перпендикулярны.
б) Найдите площадь трапеции.
Ответ: б) 60
1 2 3
Главная
На фигуре «треугольник ABC» — прямой угол. ‘(##VPUTTTMATXP01C02E02004Q01##)’ a) Если окружность нарисована с AC в качестве диаметра, найти положение ‘B’ b) если круг нарисован с ‘BC’ в качестве диаметра, найти положение ‘A’.
V ПУБЛИКАЦИИ-КРУГИ-БАНК ВОПРОСОВ
20 видеоРЕКЛАМА
Ab Padhai каро бина объявления ке
Khareedo DN Про и дехо сари видео бина киси ад ки рукаават ке!
Ответить
Пошаговое решение, разработанное экспертами, чтобы помочь вам в решении вопросов и получении отличных оценок на экзаменах.
Похожие видео
Нарисованы две окружности со сторонами AB и AC треугольника ABC в качестве диаметров
На рисунке ABC — прямоугольный треугольник, ∠B=900,AB=28см и ВС=21см. Диаметром АС начерчена полуокружность, а радиусом ВС — а. нарисована четверть круга. Найдите площадь заштрихованной области с точностью до двух десятичные знаки.
Если в прямоугольный треугольник ABC с прямым углом при вершине B вписана окружность, докажите, что диаметр окружности равен AB+BC−AC.
8493354
समकोण त्रिभुज abc क़ि भुजा ab को व्यास मानक выполнительный
415194024
Текст Решение
В прямоугольном треугольнике ABC есть окружность со стороной. AB как диаметр пересекает гипотенузу AC в P. Докажите, что касательная к окружности в точке P делит сторону BC пополам.
515795955
В прямоугольном треугольнике ABC есть окружность со стороной. AB как диаметр пересекает гипотенузу AC в P. Докажите, что касательная к окружности в точке P делит сторону BC пополам.
516945168
На рис. 12.58 ABC представляет собой треугольник с прямым углом в точке A. Полуокружности нарисованы на AB и AC как диаметры. Найдите площадь заштрихованной области.
544310602
ABC — прямоугольный треугольник с вершиной A. Полуокружности, проведенные через AB, AC и BC в качестве диаметров. Найдите площадь заштрихованной области.
544313033
В прямоугольном треугольнике ABC, в котором ∠B=90∘, начерчена окружность диаметром AB, пересекающим гипотенузу AC в точке P. Докажите, что касательная к окружности в точке P делит BC пополам.
608077677
В прямоугольном треугольнике ΔABC, у которого ∠B=90∘, проведена окружность с диаметром AB, пересекающая гипотенузу AC в точке P. Докажите, что касательная к окружности в точке PQ делится пополам с BC.
642506055
На рисунке ABC – прямоугольный треугольник, ∠B=900,AB=28 см
и ВС=21 см
Диаметром АС начерчена полуокружность, а радиусом ВС — а.
нарисована четверть круга. Найдите площадь заштрихованной области с точностью до двух
десятичные знаки.
642565574 9(@) Is, нарисована окружность, принимая диаметр AB, который пересекает гипотенузу AC в точке P. Докажите, что касательная к окружности в точке P делит BC пополам.
642838104
На рисунке □P=90o. Стороны треугольника APC продолжены до B и D.
Если начертить окружность с AC в качестве диаметра, где будет положение P по отношению к этой окружности?
.
643262733
ਚਿੱਤਰ 12,33 ਵਿੱਚ, ABC ਅਰਧ ਵਿਆਸ 14cm ਵਾਲੇ ਇੱਕ ਚੱਕਰ ਦਾ ਹਿੱਸਾ ਹੈ ਅਤੇ ਅਤੇ ਅਤੇ ਵਿਆਸ ਕੇ ਇੱਕ ਅਰਧ ਚੱਕਰ ਗਿਆ ਹੈ।ਰੰਗੀਨ ਭਾਗ ਦਾ ਪਤਾ ਕਰੋ ਮੰਨ ਇੱਕ ਅਰਧ ਚੱਕਰ ਗਿਆ ਭਾਗ ਦਾ ਖੇਤਰਫਲ ਕਰੋ। ਕੇ ਚੱਕਰ ਖਿੱਚਿਆ ਗਿਆ ਭਾਗ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ਕਰੋ ਕਰੋ
643582726
В треугольнике ABC AB = 8 см, BC = 6 см, AC = 10 см. Каково положение B на основе круга с AC в качестве диаметра? Почему?
645091430
В прямоугольном треугольнике ABC проведена окружность с диаметром AB, пересекающая гипотенузу AC в P.
Докажите, что касательная в точке P делит сторону BC пополам.ICSE-КАСАТЕЛЬНЫЕ И ПЕРЕСЕКАЮЩИЕСЯ ХОРДЫ-УПРАЖНЕНИЕ 18 (C)
21 видеоРЕКЛАМА
Ab Padhai karo bina ads ke
Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!
Обновлено: 27-06-2022
Текстовое решение
Ответ
Правильный ответ CQ=BQ Экзамены.
Видео по теме
Нарисованы две окружности со сторонами AB и AC треугольника ABC в качестве диаметров
В прямоугольном треугольнике Delta ABC равен /_B=9(@) нарисована окружность с диаметром AB, пересекающим гипотенузу AC в точке P. Докажите, что касательная к окружности в точке PQ делит BC пополам.
Докажи, что окружность, проведенная на любой из равных сторон равнобедренного треугольника как диаметр делит основание пополам. Дано: Азбука в котором АВ=АС и круг рисуется взятием AB как диаметр которая пересекает сторону BC треугольника в Д Доказать: BD=DC Строительство : Присоединяйтесь к
1414987
समकोण त्रिभुज ABC क़ि भुजा ab को व्यास मानकर खींचा वृता वृत्त क क को प प पve कvить सिद क़िшить सिद कшить सिद कvить सिद कшить सिद कшить सिद कшить सिद कvvреди सिद= सिदvvреди है= क ेखvvреди सिद= सिद कvvреди है= सिद सिदvvреди सिद हैvvреди सिद हैvvреди है हैvvить सिद हैvvреди है हैvvреди सिद हैvvреди है हैvvить सिद क़ि हैvvреди सिद सिद हैvvреди सिद क़ि हैvvреди सिद सिद है्ध है वृत है्ध=
415194024
Текст Решение
ABC — прямой угол в прямоугольном треугольнике ABC.
Если прямая, проведенная параллельно ВС через гипотенузу АВ в знаменателе М, пересекает АС в точке D, то докажите, что середина точки АС D
443418728
ABC является прямым углом в прямоугольном треугольнике ABC. Докажите следующее, если прямая, проведенная параллельно BC через середину M гипотенузы AB, пересекает AC в точке D. ДО Н.Э. Если AC и DB пересекаются в точке P, то:
449929972
В точке ABC проведен прямоугольный треугольник с окружностью диаметра AB, обозначающей AC, обозначающей P, в точке P. Докажите, что касательная, проведенная к окружности через точку P, равнобедренна с плечом BC.
469254635
В прямоугольном треугольнике ABC есть окружность со стороной. AB как диаметр пересекает гипотенузу AC в P. Докажите, что касательная к окружности в точке P делит сторону BC пополам.
515795955
В прямоугольном треугольнике ABC есть окружность со стороной. AB как диаметр пересекает гипотенузу AC в P. Докажите, что касательная к окружности в точке P делит сторону BC пополам.
Leave A Comment