14. На рисунке изображены график функции и касательные, проведённые к нему в точках… Математика Ященко И. В. ЕГЭ-2017 ГДЗ. Вариант 10.
14. На рисунке изображены график функции и касательные, проведённые к нему в точках… Математика Ященко И. В. ЕГЭ-2017 ГДЗ. Вариант 10. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
14.
На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами А, В, С и D.
В правом столбце указаны значения производной функции в точках А, В, С и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
ответы
ответ
2413
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
ГИА
ОГЭ
Экзамены
Выпускной
похожие вопросы 5
Здравствуйте! Помогите найти значение выражения:
(Подробнее…)
ГДЗЭкзаменыМатематикаЯщенко И.В.
Объясните, пожалуйста, зачем нужно итоговое сочинение в школах, если есть ЕГЭ?
Как ребенок может успеть подготовиться и к ЕГЭ и к итоговому сочинению? Не слишком ли это большая нагрузка? (Подробнее.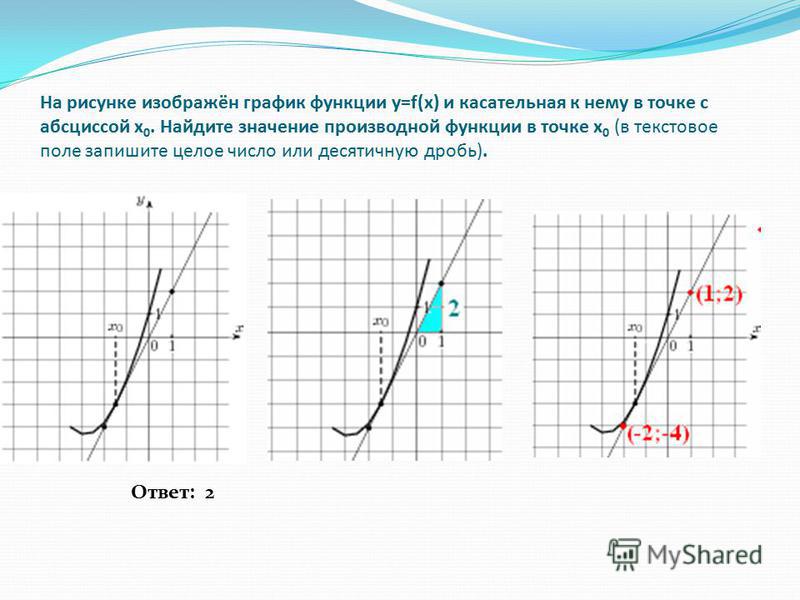 ..)
..)
ШколаНовостиЕГЭСочинения
Сколько марок № 131 ГДЗ Математика 6 класс Никольский С.М.
У Алёши 80 марок, у Бори на 20 %
меньше, чем у Алёши. Сколько марок (Подробнее…)
ГДЗМатематика6 классНикольский С.М.
влияет ли спинер на мозг?
влияет ли спинер на человеческий мозг ?
9 классГДЗВыпускнойАнглийский языкЭкзаменыЕГЭШкола11 классГИАДосуг
9. Установите соответствие между величинами и их возможными значениями… ЕГЭ-2017 Математика Ященко И. В. ГДЗ. Вариант 10.
9.
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите (Подробнее…)
ГДЗЕГЭМатематикаЯщенко И.В.
Банк ЕГЭ | Открытый банк заданий
Банк ЕГЭ Банк решенных | ЕГЭ по математике В1 ● В2 ● В3 ● В4 ● В5 ● В6 ● В7 |
Полезные советы | Лента задачек | |
| С4Дан параллелограмм $ABCD$, сторона которого $AB=13$. Из углов $А$ и $В$ проведены биссектрисы, которые пересекаются в точке $O$. Расстояние от точки $O$ до отрезка АВ равно $\frac{60}{13}$. В7$$\frac{8\cos\alpha+2\sin\alpha+6}{\sin\alpha+4\cos\alpha+3}$$ |
Как график тангенсной функции
BY: Мэри Джейн Стерлинг и
Обновлено: 07-09-2021
Из книги: Pre-Calculus для Dummies
Pre-Calculus for Dummies
6669
. Исследуйте книгу Купить на Amazon
Как и у любой другой функции, у функции тангенса есть родительский график. Используя график этой функции, вы можете сделать тот же тип преобразования, который применяется к родительскому графику любой функции.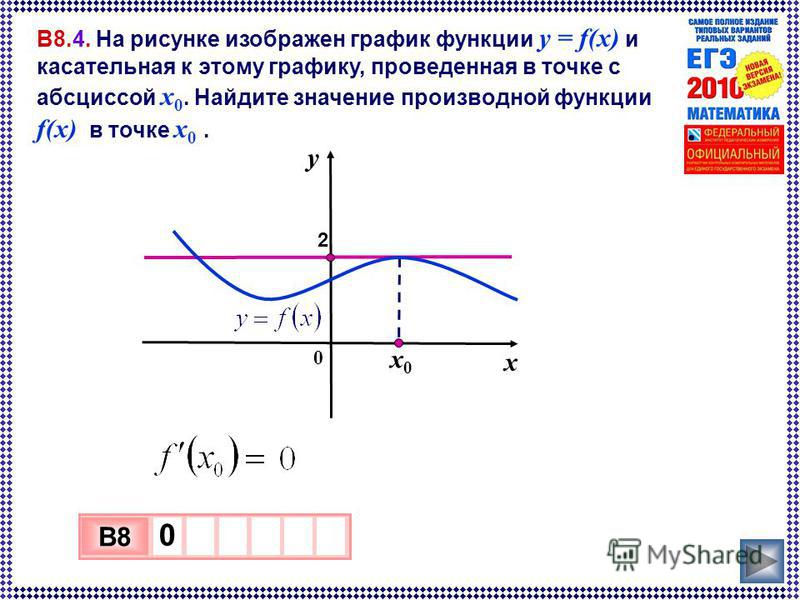 Самый простой способ запомнить, как построить график функции тангенса, это вспомнить, что
Самый простой способ запомнить, как построить график функции тангенса, это вспомнить, чтоС графиком касательной происходят интересные вещи. Когда знаменатель дроби равен 0, дробь
Показывает корни (или нули), асимптоты (где функция не определена) и поведение графика между определенными ключевыми точками на единичной окружности.
Для построения исходного графика касательной функции f ( x ) = tan x , где x представляет собой угол в радианах, вы начинаете с нахождения вертикальных асимптот. Эти асимптоты дают вам некоторую структуру, из которой вы можете заполнить недостающие точки.
Найдите вертикальные асимптоты, чтобы найти домен.
В этих шагах используется
 Первая асимптота возникает, когда угол
Первая асимптота возникает, когда угол( Примечание: Период касательной
, которое отличается от синуса и косинуса.) Иными словами, тангенс имеет асимптоты, когда
Самый простой способ написать это
, где n — целое число. Вы пишете
, так что если асимптота равна
, вы автоматически найдете следующую асимптоту.
Напомним, что функция тангенса может быть определена как
Чем ближе вы подходите к значениям, где
, чем меньше становится число внизу дроби и тем больше становится значение общей дроби — в положительном или отрицательном направлении.
Диапазон тангенса не имеет ограничений; вы не застряли между 1 и –1, как с синусом и косинусом. На самом деле отношения — это любые числа. Диапазон
Вычислить x- точек пересечения графика.
Родительский график касательной имеет корни (пересекает ось x-) на
Вы можете найти эти значения, установив
равно 0, а затем решение.

Выясните, что происходит с графиком между точками пересечения и асимптотами.
График f ( x ) = tan x положителен для углов в первом квадранте (относительно единичной окружности) и указывает вверх к асимптоте на пи / 2, потому что все значения синуса и косинуса положительны для углов в первой четверти.
График f ( x ) = tan x является отрицательным для углов в квадранте II, потому что синус положительный, а косинус отрицательный для углов в этом квадранте.
График f ( x ) = tan x положителен для углов в квадранте III, потому что и синус, и косинус отрицательны.
Наконец, график f ( x ) = tan x положителен для углов в квадранте IV, потому что синус отрицателен, а косинус положителен для углов в этом квадранте.

Примечание: Касательный график не имеет точек максимума или минимума.
. Эта статья взята из книги:
- Предварительное исчисление для чайников,
Об авторе книги:
Мэри Джейн Стерлинг алгебра, деловое исчисление, геометрия и конечная математика в Университете Брэдли в Пеории, штат Иллинойс, более 30 лет. Она является автором нескольких книг «Для чайников», , в том числе «Рабочая тетрадь по алгебре для чайников», «Алгебра II для чайников», и 9.0019 Рабочая тетрадь по алгебре II для чайников.
Эту статью можно найти в категории:
- Предварительное вычисление,
Расчет I — касательные линии и скорости изменения
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 2.1: Касательные линии и скорости изменения
В этом разделе мы рассмотрим две довольно важные проблемы в изучении исчисления. Есть две причины обратить внимание на эти проблемы сейчас.
Во-первых, обе эти проблемы приведут нас к изучению пределов, что, в конце концов, является темой этой главы. Рассмотрение этих проблем здесь позволит нам начать понимать, что такое предел и что он может рассказать нам о функции.
Во-вторых, проблема скорости изменения, которую мы собираемся рассмотреть, является одним из наиболее важных понятий, с которыми мы столкнемся во второй главе этого курса. На самом деле, это, наверное, одна из самых важных концепций, с которыми мы столкнемся на протяжении всего курса. Итак, глядя на это сейчас, мы начинаем думать об этом с самого начала.
На самом деле, это, наверное, одна из самых важных концепций, с которыми мы столкнемся на протяжении всего курса. Итак, глядя на это сейчас, мы начинаем думать об этом с самого начала.
Касательные линии
Первая задача, которую мы собираемся рассмотреть, — это задача касательной линии. Прежде чем приступить к этой проблеме, вероятно, было бы лучше определить касательную линию.
Касательной к функции \(f(x)\) в точке \(x = a\) называется прямая, которая касается графика функции в рассматриваемой точке и является «параллельной» (в некоторых путь) к графику в этой точке. Взгляните на график ниже.
На этом графике линия является касательной в указанной точке, потому что она только касается графика в этой точке, а также «параллельна» графику в этой точке. Точно так же во второй показанной точке линия просто касается графика в этой точке, но она не «параллельна» графику в этой точке и, следовательно, не является касательной к графику в этой точке.
Во второй показанной точке (точке, где линия не является касательной) мы иногда будем называть линию секущей линией .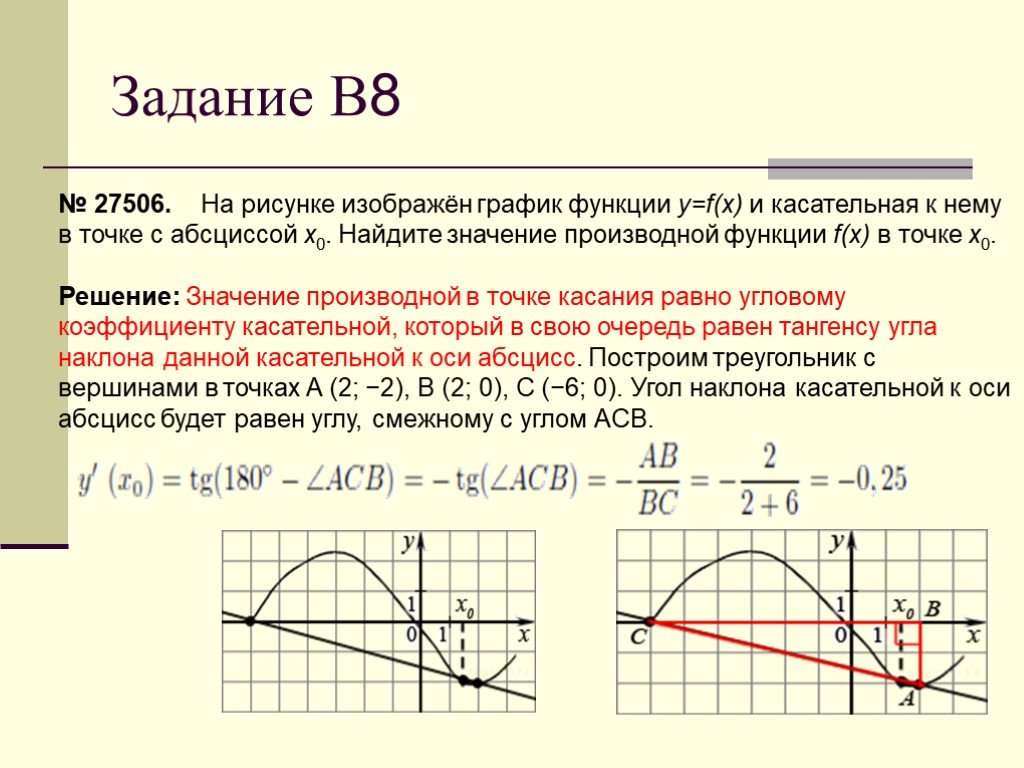
Мы уже несколько раз использовали слово «параллельный», и нам, вероятно, следует быть с ним немного осторожнее. В общем, мы будем думать о линии и графике как о параллельных в точке, если они оба движутся в одном направлении в этой точке. Итак, в первой точке выше график и линия движутся в одном направлении, поэтому мы будем говорить, что они параллельны в этой точке. С другой стороны, во второй точке линия и график не движутся в одном направлении, поэтому в этой точке они не параллельны. 92}\) в \(х=1\).
Показать решение
Из алгебры мы знаем, что для нахождения уравнения прямой нужны либо две точки на прямой, либо одна точка на прямой и наклон прямой. Поскольку мы знаем, что находимся после касательной, у нас есть точка, которая находится на этой линии. Касательная и график функции должны соприкасаться в точке \(x\) = 1, поэтому точка \(\left( {1,f\left( 1 \right)} \right) = \left( {1,13 } \right)\) должен быть в строке.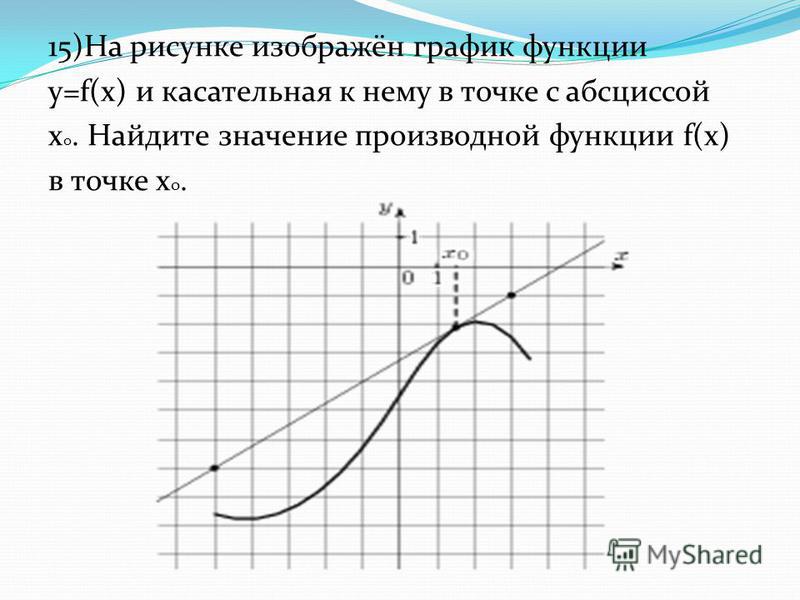
Теперь мы подошли к проблеме. Это все, что мы знаем о касательной. Чтобы найти касательную, нам нужна либо вторая точка, либо наклон касательной. Поскольку единственная причина, по которой нам нужна вторая точка, состоит в том, чтобы позволить нам найти наклон касательной, давайте просто сконцентрируемся на том, сможем ли мы определить наклон касательной.
На данный момент все, что мы можем сделать, это получить оценку наклона касательной, но если мы сделаем это правильно, мы сможем получить оценку, которая на самом деле является фактический наклон касательной. Мы сделаем это, начав с точки, которая нам нужна, назовем ее \(P = \left({1,13} \right)\). Затем мы выберем другую точку, лежащую на графике функции, назовем ее \(Q = \left( {x,f\left( x \right)} \right)\).
Для аргументации возьмем \(x = 2\) и тогда вторая точка будет \(Q = \left( {2,7} \right)\). Ниже приведен график функции, касательная и секущая, соединяющая \(P\) и \(Q\).
Из этого графика видно, что секущая и касательная в чем-то похожи, поэтому наклон секущей должен быть несколько близок к фактическому наклону касательной.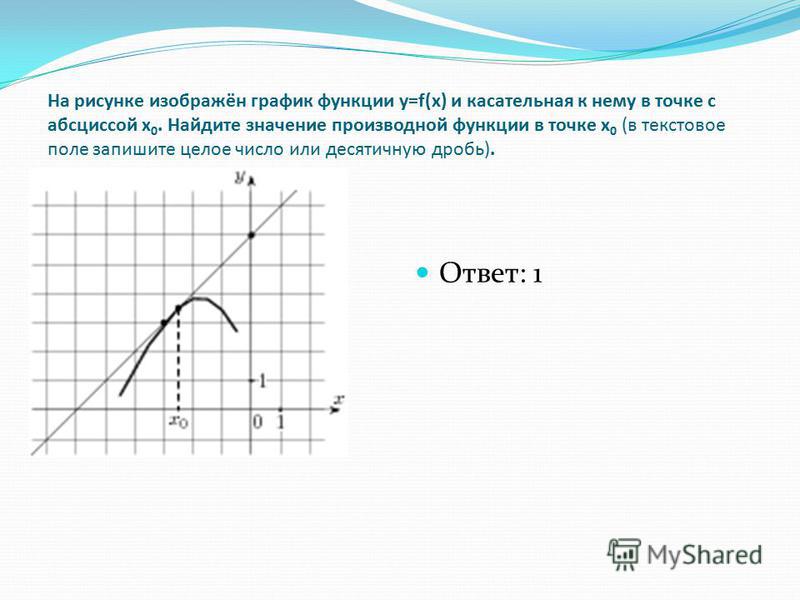 Итак, в качестве оценки наклона касательной мы можем использовать наклон секущей, назовем его \({m_{PQ}}\), то есть
Итак, в качестве оценки наклона касательной мы можем использовать наклон секущей, назовем его \({m_{PQ}}\), то есть
\[{m_{PQ}} = \frac{{f\left( 2 \right) — f\left( 1 \right)}}{{2 — 1}} = \frac{{7 — 13}}{ 1} = — 6\]
Теперь, если бы нас не слишком интересовала точность, мы могли бы сказать, что этого достаточно, и использовать это как оценку наклона касательной. Однако хотелось бы, чтобы оценка была хоть как-то близка к фактическому значению. Таким образом, чтобы получить лучшую оценку, мы можем взять \(x\), который ближе к \(x = 1\), и повторить вышеописанную работу, чтобы получить новую оценку наклона. Затем мы могли бы взять третье значение \(x\) еще ближе и получить еще лучшую оценку.
Другими словами, по мере того, как мы приближаем \(Q\) к \(P\), наклон секущей, соединяющей \(Q\) и \(P\), должен становиться все ближе и ближе к наклону касательной линии. Если вы просматриваете это в Интернете, на изображении ниже показан этот процесс.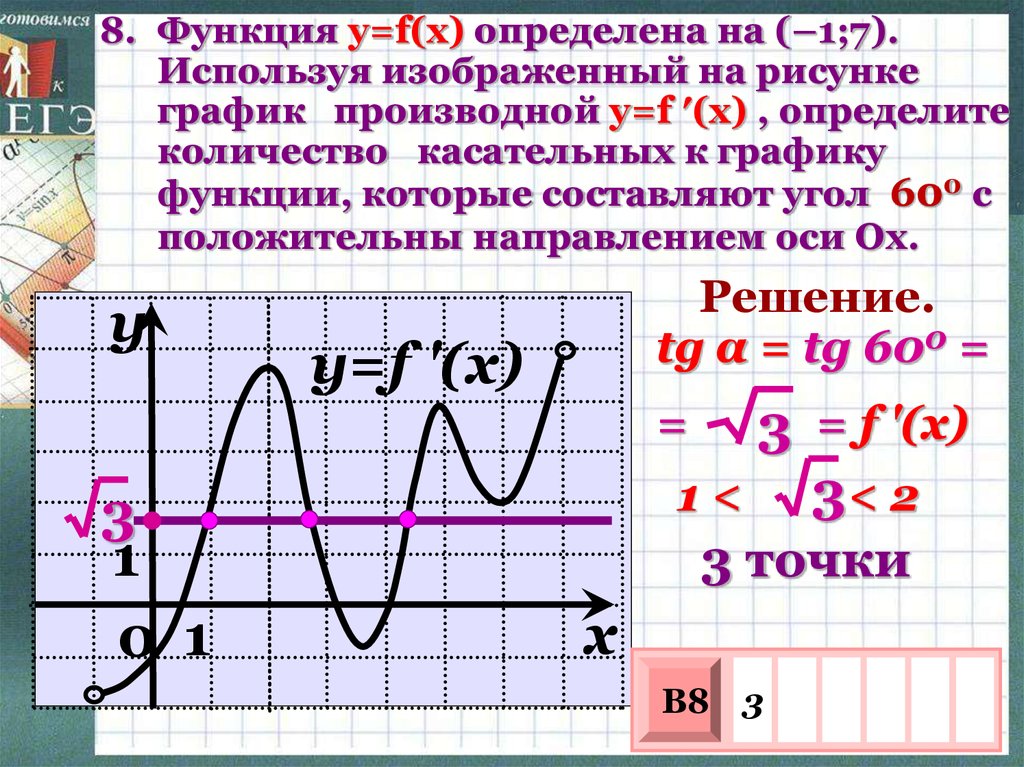
Как видите (к сожалению, анимация не будет работать на всех программах просмотра PDF), по мере того, как мы перемещали \(Q\) все ближе и ближе к \(P\), секущие линии начинают все больше и больше походить на касательную и поэтому приблизительные наклоны ( т.е. наклоны секущих) все ближе и ближе к точному наклону. Кроме того, не беспокойтесь о том, как я получил точные или приблизительные наклоны. Вскоре мы вычислим приблизительные наклоны и сможем вычислить точный наклон на нескольких участках.
На этом рисунке мы рассматривали только \(Q\), которые были справа от \(P\), но мы могли бы так же легко использовать \(Q\), которые были слева от \ (P\), и мы получили бы такие же результаты. На самом деле, мы всегда должны смотреть на \(Q\), которые находятся по обе стороны от \(P\). В этом случае одно и то же происходит по обе стороны от \(P\). Однако в конечном итоге мы увидим, что этого не должно произойти. Следовательно, мы всегда должны смотреть на то, что происходит по обе стороны от рассматриваемой точки при выполнении такого рода процесса. 2}}}{{х — 1}}\]
2}}}{{х — 1}}\]
Теперь давайте выберем некоторые значения \(x\), все ближе и ближе к \(x = 1\), подключим и получим наклоны.
| \(х\) | \({м_{PQ}}\) | \(х\) | \({м_{PQ}}\) |
|---|---|---|---|
| 2 | -6 | 0 | -2 |
| 1,5 | -5 | 0,5 | -3 |
| 1.1 | -4,2 | 0,9 | -3,8 |
| 1,01 | -4.02 | 0,99 | -3,98 |
| 1,001 | -4.002 | 0,999 | -3,998 |
| 1,0001 | -4. 0002 0002 | 0,9999 | -3,9998 |
Итак, если мы возьмем \(x\) справа от 1 и переместим их очень близко к 1, окажется, что наклон секущих приближается к -4. Точно так же, если мы возьмем \(x\) слева от 1 и переместим их очень близко к 1, наклон секущих снова окажется приближающимся к -4.
Основываясь на этом свидетельстве, кажется, что наклоны секущих приближаются к -4, когда мы приближаемся к \(x = 1\), поэтому мы оценим, что наклон касательной также равен -4. Как отмечалось выше, это правильное значение, и в конечном итоге мы сможем это доказать.
Теперь уравнение прямой, проходящей через \[\left( {a,f\left( a \right)} \right)\] задается как
\[y = f\left( a \right) + m\left( {x — a} \right)\] 92}\) в \(x=1\) равно
\[y = 13 — 4\влево( {x — 1} \вправо) = — 4x + 17\]
Следует отметить несколько важных моментов в нашей работе. Во-первых, мы рассмотрели точки, находящиеся по обе стороны от \(x = 1\). В такого рода процессах важно никогда не предполагать, что то, что происходит на одной стороне точки, будет происходить и на другой стороне. Мы всегда должны смотреть на то, что происходит по обе стороны от точки. В этом примере мы могли бы нарисовать график и, исходя из этого, предположить, что то, что происходит с одной стороны, будет происходить и с другой, но обычно у нас не будет графиков перед собой или мы не сможем легко их получить.
Во-первых, мы рассмотрели точки, находящиеся по обе стороны от \(x = 1\). В такого рода процессах важно никогда не предполагать, что то, что происходит на одной стороне точки, будет происходить и на другой стороне. Мы всегда должны смотреть на то, что происходит по обе стороны от точки. В этом примере мы могли бы нарисовать график и, исходя из этого, предположить, что то, что происходит с одной стороны, будет происходить и с другой, но обычно у нас не будет графиков перед собой или мы не сможем легко их получить.
Далее, обратите внимание, что когда мы говорим, что собираемся приблизиться к рассматриваемой точке, мы имеем в виду, что собираемся приблизиться очень близко, и мы также использовали больше, чем пару точек. Мы никогда не должны пытаться определить тренд, основываясь на паре точек, которые на самом деле не так уж близки к рассматриваемой точке.
Следующее, на что следует обратить внимание, — это скорее предупреждение, чем что-либо еще. Значения \({m_{PQ}}\) в этом примере были довольно «хорошими», и было довольно ясно, к какому значению они приближаются после пары вычислений. В большинстве случаев этого не будет. Большинство значений будут гораздо «беспорядочнее», и вам часто потребуется довольно много вычислений, чтобы получить оценку. Вы всегда должны использовать не менее четырех точек с каждой стороны, чтобы получить оценку. Двух баллов никогда не бывает достаточно для получения хорошей оценки, и трех баллов также часто недостаточно для получения хорошей оценки. Как правило, вы выбираете точки все ближе и ближе к точке, на которую смотрите, пока изменение значения между двумя последовательными точками не станет очень маленьким.
В большинстве случаев этого не будет. Большинство значений будут гораздо «беспорядочнее», и вам часто потребуется довольно много вычислений, чтобы получить оценку. Вы всегда должны использовать не менее четырех точек с каждой стороны, чтобы получить оценку. Двух баллов никогда не бывает достаточно для получения хорошей оценки, и трех баллов также часто недостаточно для получения хорошей оценки. Как правило, вы выбираете точки все ближе и ближе к точке, на которую смотрите, пока изменение значения между двумя последовательными точками не станет очень маленьким.
Наконец, нам нужно было выяснить, что происходило при \(x = 1\), и мы не могли подставить \(x = 1\) в нашу формулу для наклона. Несмотря на это ограничение, мы смогли получить некоторую информацию о том, что происходит в точке \(x = 1\), просто взглянув на то, что происходит вокруг точки \(x = 1\). Это важнее, чем вы можете себе представить на первый взгляд, и мы подробно обсудим этот момент в следующих разделах.
Прежде чем двигаться дальше, давайте кратко рассмотрим, что мы сделали в приведенном выше примере. Мы хотели, чтобы касательная шла к \(f\left( x \right)\) в точке \(x = a\). Во-первых, мы знаем, что точка \(P = \left( {a,f\left( a \right)} \right)\) будет на касательной. Затем мы возьмем вторую точку на графике функции, назовем ее \(Q = \left( {x,f\left( x \right)} \right)\) и вычислим наклон кривой линия, соединяющая \(P\) и \(Q\) следующим образом,
Мы хотели, чтобы касательная шла к \(f\left( x \right)\) в точке \(x = a\). Во-первых, мы знаем, что точка \(P = \left( {a,f\left( a \right)} \right)\) будет на касательной. Затем мы возьмем вторую точку на графике функции, назовем ее \(Q = \left( {x,f\left( x \right)} \right)\) и вычислим наклон кривой линия, соединяющая \(P\) и \(Q\) следующим образом,
\[{m_{PQ}} = \frac{{f\left( x \right) — f\left( a \right)}}{{x — a}}\]
Затем мы берем значения \(x\), которые все ближе и ближе к \(x = a\) (убедившись, что мы смотрим на \(x\) по обе стороны от \(x = a\) и используйте этот список значений для оценки наклона касательной \(m\)
Тогда касательная будет иметь вид
\[y = f\left( a \right) + m\left( {x — a} \right)\]
Скорость изменения
Следующая проблема, на которую нам нужно обратить внимание, — это проблема скорости изменения. Как упоминалось ранее, это окажется одной из самых важных концепций, которые мы будем рассматривать на протяжении всего курса.
Как упоминалось ранее, это окажется одной из самых важных концепций, которые мы будем рассматривать на протяжении всего курса.
Здесь мы собираемся рассмотреть функцию \(f\left( x \right)\), представляющую некоторую величину, которая изменяется при изменении \(x\). Например, возможно, \(f\left( x \right)\) представляет собой количество воды в накопительном баке через \(x\) минут. Или, может быть, \(f\left( x \right)\) — это расстояние, пройденное автомобилем за \(x\) часов. В обоих этих примерах мы использовали \(x\) для представления времени. Конечно, \(x\) не обязательно должно представлять время, но это дает примеры, которые легко визуализировать.
Здесь мы хотим определить, насколько быстро \(f\left( x \right)\) меняется в какой-то момент, скажем, \(x = a\). Это называется мгновенной скоростью изменения или иногда просто скоростью изменения \(f\left( x \right)\) в \(x = a\).
Как и в случае с задачей о касательной линии, все, что мы сейчас можем сделать, — это оценить скорость изменения. Итак, давайте продолжим с приведенными выше примерами и будем думать о \(f\left( x \right)\) как о чем-то, что изменяется во времени, а \(x\) является измерением времени. Опять же, \(x\) не обязательно представляет время, но это немного облегчит объяснение. Хотя мы не можем вычислить мгновенную скорость изменения, мы можем найти среднюю скорость изменения.
Итак, давайте продолжим с приведенными выше примерами и будем думать о \(f\left( x \right)\) как о чем-то, что изменяется во времени, а \(x\) является измерением времени. Опять же, \(x\) не обязательно представляет время, но это немного облегчит объяснение. Хотя мы не можем вычислить мгновенную скорость изменения, мы можем найти среднюю скорость изменения.
Чтобы вычислить среднюю скорость изменения \(f\left( x \right)\) в \(x = a\), все, что нам нужно сделать, это выбрать другую точку, скажем, \(x\), а затем средняя скорость изменения будет
\[\begin{align*}А.Р.К. & = \frac{{{\mbox{изменение}}f\left( x \right)}}{{{\mbox{изменение}}x}}\\ & = \frac{{f\left( x \right) — f\left( a \right)}}{{x — a}}\end{align*}\]
Затем, чтобы оценить мгновенную скорость изменения при \(x = a\), все, что нам нужно сделать, это выбрать значения \(x\), все ближе и ближе к \(x = a\) (не забывайте чтобы выбрать их по обе стороны от \(x = a\)) и вычислить значения \(A. R.C.\). Затем мы можем оценить мгновенную скорость изменения на основе этого. 92} + 25}}{{т — 5}}\]
R.C.\). Затем мы можем оценить мгновенную скорость изменения на основе этого. 92} + 25}}{{т — 5}}\]
Чтобы оценить мгновенную скорость изменения объема при \(t = 5\), нам просто нужно выбрать значения \(t\), которые все ближе и ближе к \(t = 5\). Вот таблица значений \(t\) и средней скорости изменения этих значений.
| \(т\) | \(АРК\) | \(т\) | \(АРК\) |
|---|---|---|---|
| 6 | 25,0 | 4 | 7,0 |
| 5,5 | 19,75 | 4,5 | 10,75 |
| 5.1 | 15,91 | 4,9 | 14.11 |
| 5.01 | 15.0901 | 4,99 | 14. 9101 9101 |
| 5,001 | 15.009001 | 4,999 | 14.991001 |
| 5.0001 | 15.000 | 4,9999 | 14.99910001 |
Итак, из этой таблицы видно, что средняя скорость изменения приближается к 15, и поэтому мы можем оценить, что мгновенная скорость изменения на данный момент равна 15.
Итак, что же это говорит нам об объеме в точке \(t = 5\)? Положим несколько единиц на ответ сверху. Это может помочь нам увидеть, что происходит с томом в этот момент. Предположим, что единицы объема были в см 3 . Тогда единицы скорости изменения (как средней, так и мгновенной) равны см 3 /час.
Мы подсчитали, что при \(t = 5\) объем изменяется со скоростью 15 см 3 /час. Это означает, что при \(t = 5\) объем изменяется так, что, если бы скорость была постоянной, то через час в баллоне было бы на 15 см 3 больше воздуха, чем было при \( т = 5\).
Однако здесь нужно быть осторожным. На самом деле через час в воздушном шаре, вероятно, не будет больше 15 см 3 воздуха. Скорость, с которой изменяется объем, как правило, непостоянна, поэтому мы не можем реально определить, каким будет объем через следующий час. Что мы можем сказать, так это то, что объем увеличивается, поскольку мгновенная скорость изменения положительна, и если бы у нас были скорости изменения для других значений \(t\), мы могли бы сравнить числа и посмотреть, быстрее ли скорость изменения или медленнее в других точках.
Например, при \(t = 4\) мгновенная скорость изменения равна 0 см 3 /час, а при \(t = 3\) мгновенная скорость изменения равна -9 см 3 /час. Мы предоставим вам проверить эти скорости изменения. На самом деле, это было бы хорошим упражнением, чтобы увидеть, сможете ли вы построить таблицу значений, которая подтвердит наши утверждения об этих темпах изменений.
Итак, вернемся к примеру. При \(t = 4\) скорость изменения равна нулю, поэтому в этот момент времени объем вообще не меняется. Это не значит, что он не изменится в будущем. Это просто означает, что ровно при \(t = 4\) громкость не меняется. Точно так же в точке \(t = 3\) объем уменьшается, поскольку скорость изменения в этой точке отрицательна. Мы также можем сказать, что, независимо от аспектов увеличения/уменьшения скорости изменения, объем воздушного шара изменяется быстрее при \(t = 5\), чем при \(t = 3\), поскольку 15 больше чем 9.
Это не значит, что он не изменится в будущем. Это просто означает, что ровно при \(t = 4\) громкость не меняется. Точно так же в точке \(t = 3\) объем уменьшается, поскольку скорость изменения в этой точке отрицательна. Мы также можем сказать, что, независимо от аспектов увеличения/уменьшения скорости изменения, объем воздушного шара изменяется быстрее при \(t = 5\), чем при \(t = 3\), поскольку 15 больше чем 9.
В следующей главе мы еще поговорим о скорости изменений.
Задача о скорости
Давайте кратко рассмотрим задачу о скорости. Многие книги по математическому анализу рассматривают это как отдельную проблему. Однако нам нравится думать об этом как о частном случае проблемы скорости изменения. В задаче о скорости нам дана функция положения объекта \(f\left( t \right)\), которая дает положение объекта в момент времени \(t\). Затем, чтобы вычислить мгновенную скорость объекта, нам просто нужно вспомнить, что скорость — это не что иное, как скорость изменения положения.
Другими словами, чтобы оценить мгновенную скорость, мы должны сначала вычислить среднюю скорость,
\[\begin{align*}А.В. & = \frac{{{\mbox{изменение положения}}}}{{{\mbox{пройденное время}}}}\\ & \\ & = \frac{{f\left( t \right) — f \left( a \right)}}{{t — a}}\end{align*}\]
, а затем брать значения \(t\) все ближе и ближе к \(t = a\) и использовать эти значения для оценки мгновенной скорости.
Изменение обозначения
Последнее, что нам нужно сделать в этом разделе, прежде чем двигаться дальше. Основная цель этого раздела состояла в том, чтобы познакомить нас с парой ключевых концепций и идей, которые мы увидим в первой части этого курса, а также помочь нам начать путь к ограничениям.
Прежде чем мы официально перейдем к ограничениям, давайте вернемся назад и проделаем небольшую работу, которая свяжет обе (или все три, если включить скорость как отдельную проблему) проблемы в более общую концепцию.
Во-первых, обратите внимание, что независимо от того, нужна ли нам касательная, мгновенная скорость изменения или мгновенная скорость, каждый из них сводился к использованию одной и той же формулы. А именно,
\begin{equation}\frac{{f\left( x \right) — f\left( a \right)}}{{x — a}} \label{eq:eq1}\end{equation}
Это должно означать, что все три проблемы на самом деле являются одной и той же проблемой. На самом деле это так, как мы увидим в следующей главе. Мы действительно работаем над одной и той же проблемой в каждом из этих случаев, единственная разница заключается в интерпретации результатов.
При подготовке к следующему разделу, где мы обсудим это более подробно, нам нужно быстро изменить обозначения. Это проще сделать здесь, так как мы уже потратили изрядное количество времени на эти проблемы.
Во всех этих задачах мы хотели определить, что происходит в точке \(x = a\). Для этого мы выбрали другое значение \(x\) и подключили его к \(\eqref{eq:eq1}\). Для того, что мы делали здесь, это, вероятно, самый интуитивный способ сделать это. Однако, когда мы начнем рассматривать эти проблемы как одну проблему, \(\eqref{eq:eq1}\) не будет лучшей формулой для работы.
Для того, что мы делали здесь, это, вероятно, самый интуитивный способ сделать это. Однако, когда мы начнем рассматривать эти проблемы как одну проблему, \(\eqref{eq:eq1}\) не будет лучшей формулой для работы.
Вместо этого мы сначала определим, как далеко от \(x = a\) мы хотим двигаться, а затем определим нашу новую точку на основе этого решения. Итак, если мы хотим переместиться на расстояние \(h\) от \(x = a\), новая точка будет \(x = a + h\). Это показано на эскизе ниже.
Как мы видели в нашей работе выше, важно брать значения \(x\), которые являются обеими сторонами \(x = a\). Этот способ выбора нового значения \(x\) сделает это за нас, как мы можем видеть на скетче выше. Если \(h > 0\), мы получим значение \(x\), которое находится справа от \(x = a\), а если \(h < 0\), мы получим значения \(x\) которые находятся слева от \(x = a\), и оба задаются как \(x = a + h\).
Теперь, с этим новым способом получения второго значения \(x\) \(\eqref{eq:eq1}\) станет
\[\frac{{f\left( x \right) — f\left( a \right)}}{{x — a}} = \frac{{f\left( {a + h} \right) — f\left( a \right)}}{{a + h — a}} = \frac{{f\left( {a + h} \right) — f\left( a \right)}}{h} \]
Теперь это для конкретного значения \(x\), т.

 wolframalpha.com/. На этом сайте вы можете: решать не слишком сложные уравнения и системы уравнений (неравенств), брать производные от функций, стоить графики этих функций и так далее. Во время подготовки к ЕГЭ, этот сайт можно использовать для:
wolframalpha.com/. На этом сайте вы можете: решать не слишком сложные уравнения и системы уравнений (неравенств), брать производные от функций, стоить графики этих функций и так далее. Во время подготовки к ЕГЭ, этот сайт можно использовать для: 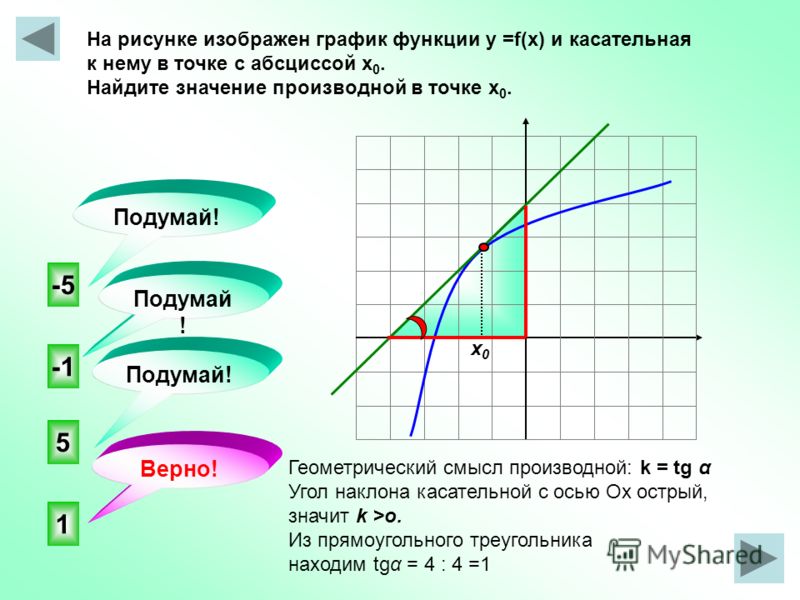
 {\circ}$ больше вписанного угла ACB, опирающегося на ту же дугу. Ответ дайте в градусах. [посмотреть решение]
{\circ}$ больше вписанного угла ACB, опирающегося на ту же дугу. Ответ дайте в градусах. [посмотреть решение] Первая асимптота возникает, когда угол
Первая асимптота возникает, когда угол
Leave A Comment