Самостоятельная работа по теме: Графики
Самостоятельная работа по теме: Графики. 1 вариант
1 . При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, за сколько часов работы фонарика напряжение упадёт с 1 В до 0,6 В.
2 .Мощность отопителя в автомобиле регулируется дополнительным сопротивлением, которое можно менять, поворачивая рукоятку в салоне машины. При этом меняется сила тока в электрической цепи электродвигателя — чем меньше сопротивление, тем больше сила тока и тем быстрее вращается мотор отопителя. На рисунке показана зависимость силы тока от величины сопротивления. На оси абсцисс откладывается сопротивление (в омах), на оси ординат — сила тока в амперах. Ток в цепи электродвигателя уменьшился с 12 до 8 ампер. На сколько ом при этом увеличилось сопротивление цепи?
Ток в цепи электродвигателя уменьшился с 12 до 8 ампер. На сколько ом при этом увеличилось сопротивление цепи?
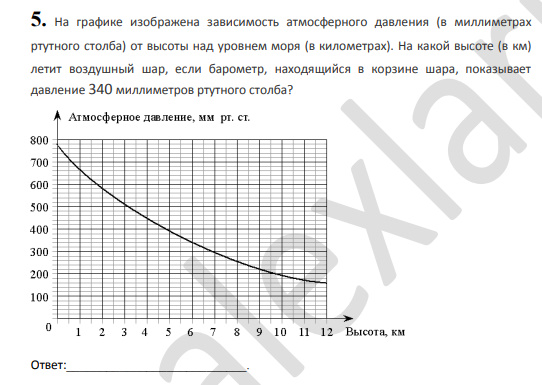
3.На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 220 миллиметров ртутного столба?
4 . На рисунке изображен график изменения силы тока при подключении цепи, содержащей реостат, к источнику тока. По вертикальной оси откладывается сила тока (в A), по горизонтальной — время (в сек). По рисунку определите силу тока через 6 секунд с момента подключения данной цепи.
С амостоятельная работа по теме: Графики.2 вариант
1.При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, за сколько часов работы фонарика напряжение упадёт с 1,4 В до 0,8 В.
На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, за сколько часов работы фонарика напряжение упадёт с 1,4 В до 0,8 В.
2. На графике показано изменение температуры в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя, на вертикальной оси — температура двигателя в градусах Цельсия. Определите по графику, на сколько градусов Цельсия нагреется двигатель с 3-й по 8-ю минуту с момента запуска.
3 . На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 280 миллиметров ртутного столба?
4. На рисунке изображен график изменения силы тока при подключении цепи, содержащей реостат, к источнику тока.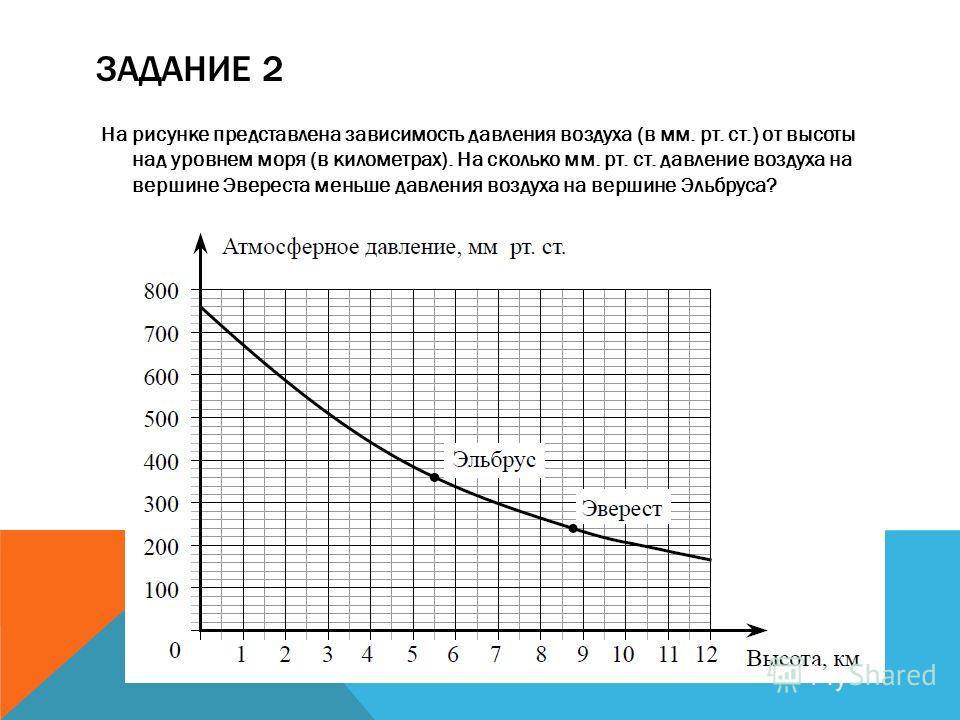 По вертикальной оси откладывается сила тока (в A), по горизонтальной — время (в сек). По рисунку определите силу тока через 4 секунды с момента подключения данной цепи.
По вертикальной оси откладывается сила тока (в A), по горизонтальной — время (в сек). По рисунку определите силу тока через 4 секунды с момента подключения данной цепи.
С амостоятельная работа по теме: Графики.3 вариант
1.На графике показано изменение температуры в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя, на вертикальной оси -температура двигателя в градусах Цельсия. Определите по графику, через сколько минут с момента запуска двигатель нагреется до 60°С.
2 .При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, за сколько часов работы фонарика напряжение упадёт с 1,2 В до 1 В.
3. На рисунке изображен график зависимости амплитуды вынужденных колебаний от частоты колебаний. По вертикальной оси откладывается амплитуда (в м), по горизонтальной — частота колебаний (в Гц). По рисунку определите частоту колебаний, если амплитуда была равна 1 м.
На рисунке изображен график зависимости амплитуды вынужденных колебаний от частоты колебаний. По вертикальной оси откладывается амплитуда (в м), по горизонтальной — частота колебаний (в Гц). По рисунку определите частоту колебаний, если амплитуда была равна 1 м.
4.На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 260 миллиметров ртутного столба?
С амостоятельная работа по теме: Графики 4 вариант
1.На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Сколько часов температура превышала 19°C?
2. На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 580 миллиметров ртутного столба?
На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 580 миллиметров ртутного столба?
3. На рисунке изображен график зависимости амплитуды вынужденных колебаний от частоты колебаний. По вертикальной оси откладывается амплитуда (в м), по горизонтальной — частота колебаний (в Гц). По рисунку определите частоту колебаний, если амплитуда была равна 3 м.
4. На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Найдите наименьшее значение температуры. Ответ дайте в градусах Цельсия.
С амостоятельная работа по теме: Графики 5 вариант
1.На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты местности над уровнем моря (в километрах). На сколько миллиметров ртутного столба атмосферное давление на высоте Эвереста ниже атмосферного давления на высоте Большого Шелома?
На сколько миллиметров ртутного столба атмосферное давление на высоте Эвереста ниже атмосферного давления на высоте Большого Шелома?
2. На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наименьшее значение атмосферного давления во вторник.
3 . При резком торможении расстояние, пройденное автомобилем до полной остановки (тормозной путь), зависит от скорости, с которой автомобиль двигался. На рисунке показан график этой зависимости. По горизонтальной оси откладывается скорость (в км/ч), по вертикальной – тормозной путь (в метрах). Определите по графику, каким будет тормозной путь автомобиля, который двигается со скоростью 70 км/ч. Ответ дайте в метрах.
4. На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Найдите наименьшее значение температуры. Ответ дайте в градусах Цельсия.
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/259098-samostojatelnaja-rabota-po-teme-grafiki
Разбор и решение задания №5 ОГЭ по математике
Анализ графиков
Перейдем к рассмотрению пятого задания. В данном случае нам необходимо соотнести значения на графике. По значению одной оси определить значение на второй оси. Задание также выполнено не в абстрактной форме, а на конкретных примерах, например соотнести значение температуры с днями в месяце.
Разбор типовых вариантов задания ОГЭ по математике
Первый вариант задания
На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Найдите наименьшее значение температуры в первой половине суток. Ответ дайте в градусах Цельсия.
По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Найдите наименьшее значение температуры в первой половине суток. Ответ дайте в градусах Цельсия.
Решение:
Смотрим на график и ищем первую половину суток: это график до 12 часов. Значит, будем искать минимум в первой половине:
Находим минимум — смотрим на значение по оси y, на которой откладывается температура. Это значение 7.
Ответ: 7
Второй вариант задания
На графике изображена зависимость крутящего момента двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту, на оси ординат — крутящий момент в Н*м. Чему равен крутящий момент (в Н-м), если двигатель делает 2500 оборотов в минуту?
Решение:
Ищем значение 2500 оборотов в минуту и смотрим, чему равно значение y.
Ответ: 140
Третий вариант задания
При работе фонарика батарейка постепенно разряжается, и напряжение в электрической цепи фонарика падает. На рисунке показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечается время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по рисунку, на сколько вольт упадёт напряжение с 6-го по 56-й час работы фонарика.
На рисунке показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечается время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по рисунку, на сколько вольт упадёт напряжение с 6-го по 56-й час работы фонарика.
Решение:
Найдем значения напряжения в 6 и 56 час работы:
В 6 часов значение напряжения 1,4В , в 56 — 1 В. Разница в значениях — 0,4.
Ответ: 0,4
Четвертый вариант задания (демонстрационный вариант 2017)
На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). На какой высоте (в километрах) давление составит 540 миллиметров ртутного столба?
Решение:
Данное задание демонстрирует нам, как функции и графики функций встречаются нам в повседневной жизни, и демонстрируют нам необходимость умения работать с ними. Зависимость давления от высоты — это не что иное, как функция y (давление) от x (высота).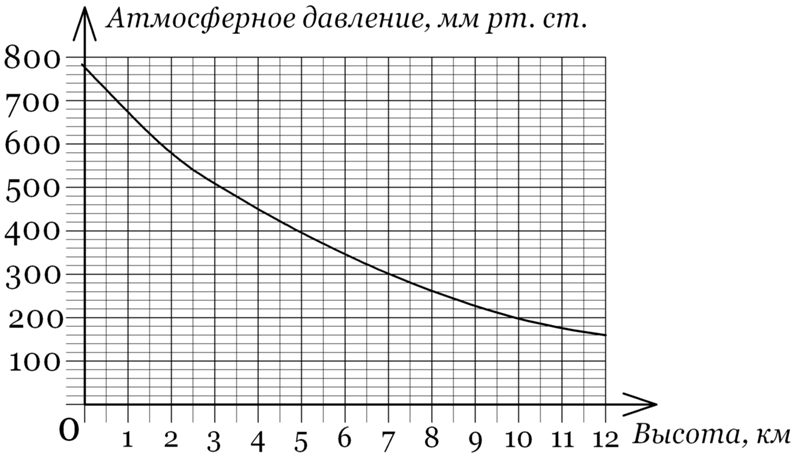
Для решения этой задачи, нужно сопоставить значению функции ее аргумент: значению давления — высоту.
Находим значение 540 на вертикальной оси (y). Мы не видим точной отметки, однако можем посчитать, что деления между 500 и 600 разделены на 5 дополнительных делений, если основное деление — 100, а дополнительных 5, то одно дополнительное это:
100 / 5 = 20 мм.
Значит, значению 540 соответствуют два деления выше 500 — 2 по 20 мм.
Далее ищем аргумент функции (высоту) следующим образом:
Видим, что значение высоты находится ровно между 2 и 3 километрами, значит высота равна 2,5 км. Ответ: 2,5 км.Пятый вариант задания
На рисунке жирными точками показана среднесуточная температура воздуха в Калининграде с 9 по 28 апреля 2018 года. По горизонтали указываются числа месяца, по вертикали — температура в градусах Цельсия. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку разность между наибольшей и наименьшей среднесуточными температурами в Калининграде за данный период. ответ дайте в градусах Цельсия.
ответ дайте в градусах Цельсия.
Решение:
Ищем на графике самую нижнюю точку. Условно проводим от нее горизонтальную линию до пересечения с вертикальной шкалой температур (обозначено красной линией). Получаем значение, равное 11 0С. Это – наименьшая среднесуточная темп-ра за период. Ищем на графике самую верхнюю его точку. И аналогично находим наибольшую среднесуточную темп-ру. Она составляет 22 0С. Определяем разницу найденных значений как разность большего и меньшего чисел: 22–11=11 0С. Ответ: 11Седьмой вариант задания
На рисунке жирными точками показана среднесуточная температура воздуха в Калининграде с 9 по 28 апреля 2018 года. По горизонтали указываются числа месяца, по вертикали — температура в градусах Цельсия. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода среднесуточная температура в Калининграде была больше 16 градусов Цельсия.
Решение:
Находим на вертикальной шкале значений число 16. Проводим условную горизонтальную – параллельную оси, отображающей дни апреля – линию (обозначена красным). Поскольку требуется найти все значения температур, большие 16, фиксируем все точки графика, расположенные выше красной линии. Их количество и есть конечный результат. На рисунке искомых точек 8 (обозначены красными точками). Значит, дней со среднесуточной температурой, большей 160С в период 9–28 апреля было 8. Ответ: 8
Проводим условную горизонтальную – параллельную оси, отображающей дни апреля – линию (обозначена красным). Поскольку требуется найти все значения температур, большие 16, фиксируем все точки графика, расположенные выше красной линии. Их количество и есть конечный результат. На рисунке искомых точек 8 (обозначены красными точками). Значит, дней со среднесуточной температурой, большей 160С в период 9–28 апреля было 8. Ответ: 8Подготовка к ОГЭ по математике | Материал для подготовки к ЕГЭ (ГИА, 9 класс):
Слайд 1
Задание №5. Графики Реальная математикаСлайд 2
На графике изображена зависимость атмосферного давления от высоты над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в километрах, на вертикальной — давление в миллиметрах ртутного столба. Определите по графику, на какой высоте атмосферное давление равно 780 миллиметрам ртутного столба. Ответ дайте в километрах.
Слайд 3
При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, за сколько часов работы фонарика напряжение упадёт с 1,4 В до 1,2 В.
На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, за сколько часов работы фонарика напряжение упадёт с 1,4 В до 1,2 В.
Слайд 4
На графике показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали — значение температуры в градусах Цельсия. Определите по графику наименьшую температуру воздуха 15 октября. Ответ дайте в градусах Цельсия.
Слайд 5
На графике изображена зависимость атмосферного давления от высоты над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в километрах, на вертикальной — давление в миллиметрах ртутного столба. Определите по графику, на какой высоте атмосферное давление равно 660 миллиметрам ртутного столба. Ответ дайте в километрах.
Слайд 6
На графике изображена зависимость атмосферного давления от высоты над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в километрах, на вертикальной — давление в миллиметрах ртутного столба. Определите по графику, на какой высоте атмосферное давление равно 580 миллиметрам ртутного столба. Ответ дайте в километрах.
На горизонтальной оси отмечена высота над уровнем моря в километрах, на вертикальной — давление в миллиметрах ртутного столба. Определите по графику, на какой высоте атмосферное давление равно 580 миллиметрам ртутного столба. Ответ дайте в километрах.
Слайд 7
На графике изображена зависимость атмосферного давления от высоты над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в километрах, на вертикальной — давление в миллиметрах ртутного столба. Определите по графику, чему равно атмосферное давление на высоте 12 км над уровнем моря. Ответ дайте в миллиметрах ртутного столба.
Слайд 8
На графике изображена зависимость атмосферного давления от высоты над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в километрах, на вертикальной — давление в миллиметрах ртутного столба. Определите по графику, чему равно атмосферное давление на высоте 0,5 км над уровнем моря. Ответ дайте в миллиметрах ртутного столба.
Слайд 9
При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, на сколько вольт упадёт напряжение за первый час работы фонарика .
На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, на сколько вольт упадёт напряжение за первый час работы фонарика .
Слайд 10
При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, на сколько вольт упадёт напряжение за первые 6 часов работы фонарика.
Слайд 11
При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, на сколько вольт упадёт напряжение с 1-го по 6-й час работы фонарика.
Слайд 12
При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, на сколько вольт упадёт напряжение с 1-го по 11-й час работы фонарика.
Слайд 13
При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, на сколько вольт упадёт напряжение с 28-го по 54-й час работы фонарика.
Слайд 14
При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, на сколько вольт упадёт напряжение с 28-го по 58-й час работы фонарика .
На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, на сколько вольт упадёт напряжение с 28-го по 58-й час работы фонарика .
Слайд 15
При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, за сколько часов работы фонарика напряжение упадёт с 1,6 В до 1,2 В.
Слайд 16
На графике показано изменение температуры в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя, на вертикальной оси — температура двигателя в градусах Цельсия. Определите по графику, за сколько минут двигатель нагреется с 30 ° C до 40 ° C .
Слайд 17
На графике показано изменение температуры в процессе разогрева двигателя легкового автомобиля.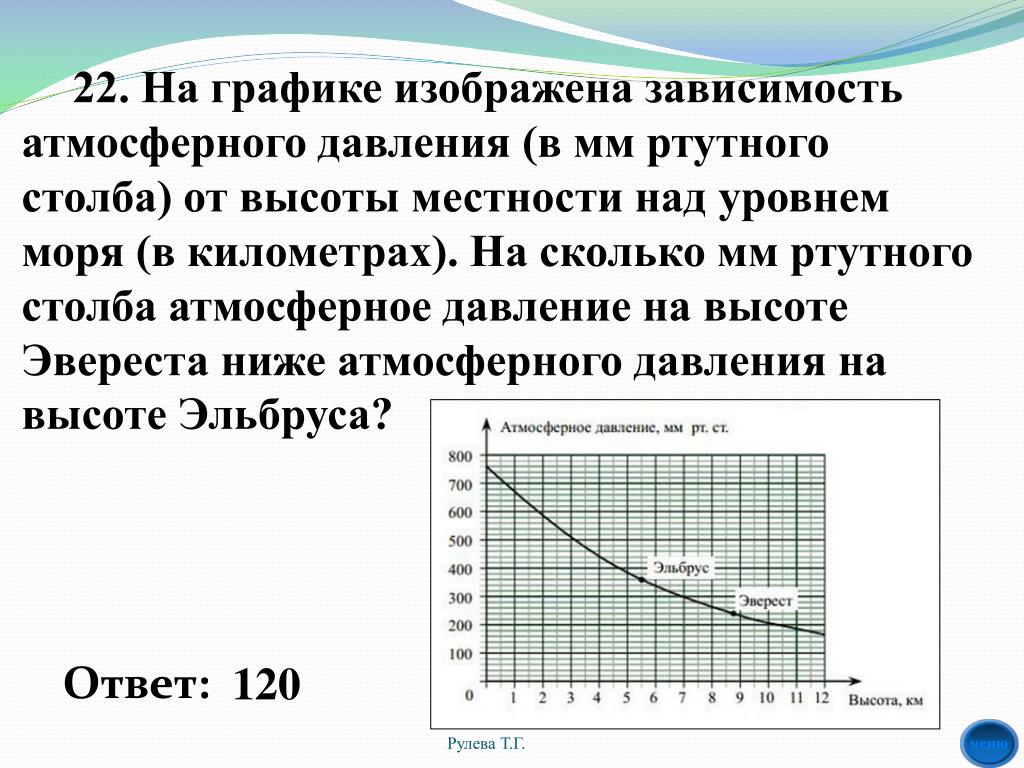 На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя, на вертикальной оси — температура двигателя в градусах Цельсия. Определите по графику, за сколько минут двигатель нагреется с 30 ° C до 50 ° C .
На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя, на вертикальной оси — температура двигателя в градусах Цельсия. Определите по графику, за сколько минут двигатель нагреется с 30 ° C до 50 ° C .
Слайд 18
На графике показано изменение температуры в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя, на вертикальной оси — температура двигателя в градусах Цельсия. Определите по графику, через сколько минут с момента запуска двигатель нагреется до 30 ° C .
Слайд 19
На графике показано изменение температуры в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя, на вертикальной оси — температура двигателя в градусах Цельсия. Определите по графику, через сколько минут с момента запуска двигатель нагреется до 40 ° C
Слайд 20
На графике показано изменение температуры воздуха на протяжении трёх суток.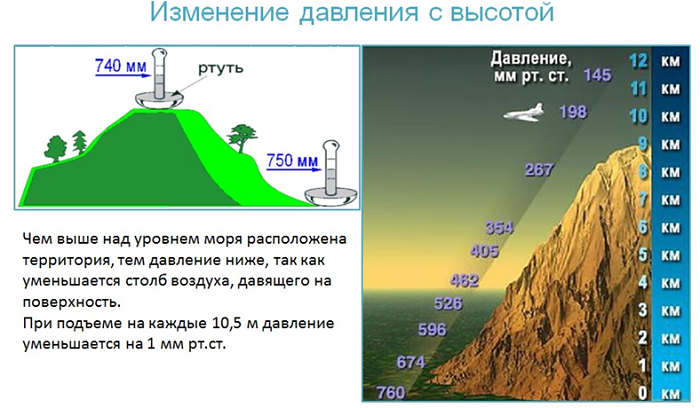 По горизонтали указывается дата и время, по вертикали — значение температуры в градусах Цельсия. Определите по графику наибольшую температуру воздуха 7 августа. Ответ дайте в градусах Цельсия .
По горизонтали указывается дата и время, по вертикали — значение температуры в градусах Цельсия. Определите по графику наибольшую температуру воздуха 7 августа. Ответ дайте в градусах Цельсия .
Слайд 21
На графике показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали — значение температуры в градусах Цельсия. Определите по графику наибольшую температуру воздуха 13 июля. Ответ дайте в градусах Цельсия .
Слайд 22
На графике показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали — значение температуры в градусах Цельсия. Определите по графику наименьшую температуру воздуха 9 августа. Ответ дайте в градусах Цельсия.
Слайд 23
На рисунке жирными точками показано суточное количество осадков, выпадавших в Казани с 3 по 15 февраля 1909 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа из данного периода в Казани выпало ровно 2 миллиметра осадков.
Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа из данного периода в Казани выпало ровно 2 миллиметра осадков.
Слайд 24
На рисунке жирными точками показано суточное количество осадков, выпадавших в Казани с 3 по 15 февраля 1909 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода в Казани не выпадало осадков.
Слайд 25
На рисунке жирными точками показано суточное количество осадков, выпадавших в Казани с 3 по 15 февраля 1909 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода в Казани выпадало более 3 миллиметров осадков .
Слайд 26
На рисунке жирными точками показано суточное количество осадков, выпадавших в Казани с 3 по 15 февраля 1909 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какое наибольшее суточное количество осадков выпадало в Казани в данный период. Ответ дайте в миллиметрах.
По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какое наибольшее суточное количество осадков выпадало в Казани в данный период. Ответ дайте в миллиметрах.
Столбчатые диаграммы, графики | |||||||||
1. На диаграмме представлены семь крупнейших по площади территории (в млн км2) стран мира.Какое из следующих утверждений неверно? 1) Площадь территории Индии составляет 3,3 млн км2 2) Площадь Китая больше площади Австралии. 3) Россия — крупнейшая по площади территории страна мира. 4) площадь Канады больше площади США на 1,5 млн км2. В ответ запишите номер выбранного утверждения. | |||||||||
2. На диаграмме показано количество SMS, присланных слушателями за каждый час четырёхчасового эфира программы по заявкам на радио. Определите разность между наибольшим и наименьшим количеством СМС за эти часы. | |||||||||
3. На рисунке изображена зависимость температуры (в градусах Цельсия) от высоты (в метрах) над уровнем моря. Определите по графику, на сколько градусов температура на высоте 200 метров выше, чем на высоте 650 метров. | |||||||||
4. На диаграмме представлены семь крупнейших по площади территории (в млн км2) стран мира. Какое из следующих утверждений верно? 1) Казахстан входит в семёрку крупнейших по площади территории стран мира. 2) Площадь территории Бразилии составляет 8,5 млн км2. 3) Площадь Австралии больше площади Китая. 4) Площадь Бразилии больше площади Индии более чем в три раза. В ответе запишите номер выбранного утверждения. | |||||||||
5. На диаграмме представлены некоторые из крупнейших по численности населения стран мира. Численность населения какого государства примерно в 6 раз меньше численности населения Индии? В ответе напишите численность населения этой страны в млн чел. | |||||||||
6. На диаграмме представлены некоторые из крупнейших по площади территории стран мира. Во сколько примерно раз площадь России больше площади США? (Ответ округлите до целых.) | |||||||||
7. Рок-магазин продаёт значки с символикой рок-групп. В продаже имеются значки пяти цветов: чёрные, синие, зелёные, серые и белые. Данные о проданных значках представлены на столбчатой диаграмме. Определите по диаграмме, значков какого цвета было продано меньше всего. Сколько примерно процентов от общего числа значков составляют значки этого цвета? 1) 5; 2) 10; 3) 15; 4) 20. | |||||||||
8.
Закончите построение столбчатой диаграммы. | |||||||||
9. Пешеход вышел из пункта А в пункт В. Через 1 час он сделал первый привал у озера, где провёл 1 час, затем отправился в пункт В, где провёл 3 часа. Ответьте на вопросы: 1) Сколько часов двигался пешеход? 2) На каком расстоянии от пункта А находится в пункт В? 3) С какой скоростью пешеход двигался на каждом участке пути: до озера, до пункта В и на мотоцикле?
| |||||||||
Давление газов и жидкостей
37.1. Домашний эксперимент.
1. Надуйте резиновый шарик.
2. Пронумеруйте фразы в таком порядке, чтобы получился связный рассказ о проделанном эксперименте.
37.2. В сосуде под поршнем заключен газ (рис. а), объем которого меняется при постоянной температуре. На рисунке б представлен график зависимости расстояния h, на котором относительно дна находится поршень, от времени t. Заполните пропуски в тексте, используя слова: увеличивается; не меняется; уменьшается.
37.3.На рисунке показана установка для изучения зависимости давления газа в закрытом сосуде от температуры.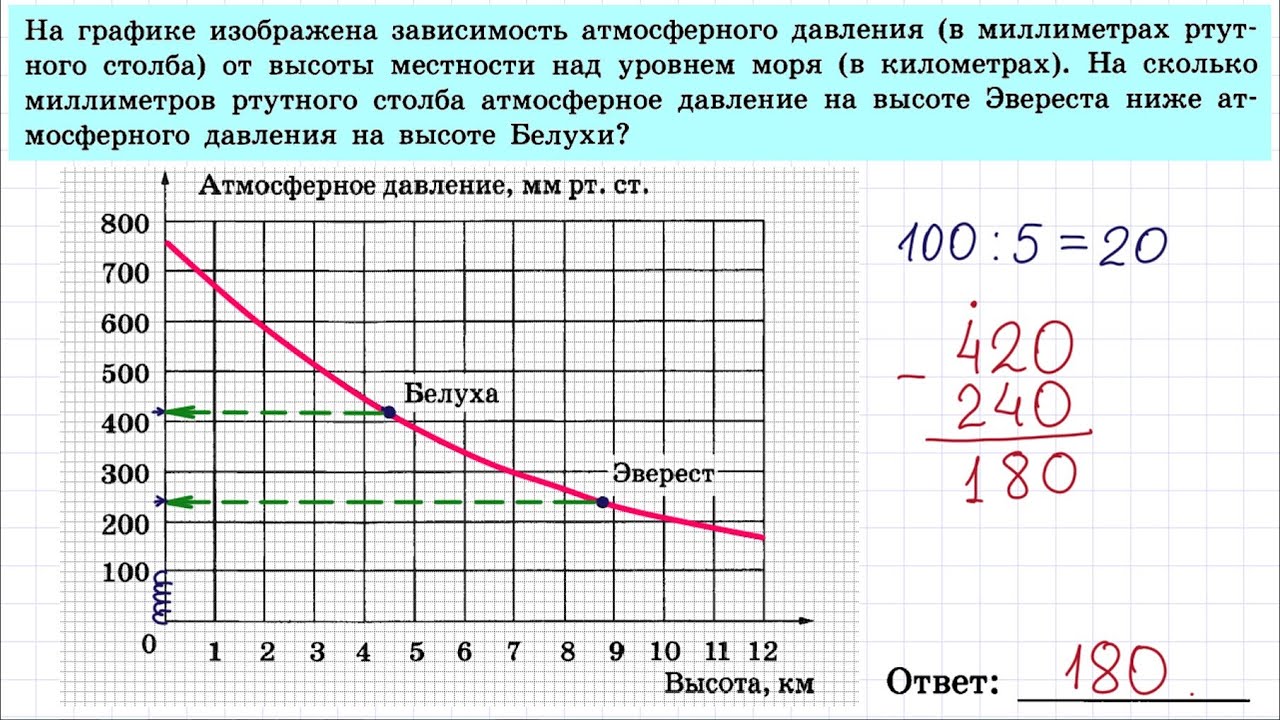 Цифрами обозначены: 1 – пробирка с воздухом; 2 – спиртовка; 3 – резиновая пробка; 4 – стеклянная трубка; 5 – цилиндр; 6 – резиновая мембрана. Поставьте знак «+» около верных утверждений и знак «» около неверных.
Цифрами обозначены: 1 – пробирка с воздухом; 2 – спиртовка; 3 – резиновая пробка; 4 – стеклянная трубка; 5 – цилиндр; 6 – резиновая мембрана. Поставьте знак «+» около верных утверждений и знак «» около неверных.
37.4. Рассмотрите графики зависимости давления p от времени t, соответствующие различным процессам в газах. Вставьте недостающие слова в предложение.
38.1. Домашний эксперимент.
Возьмите полиэтиленовый пакет, сделайте в нем четыре дырочки одинакового размера в разных местах нижней части пакета, используя, например, толстую иглу. Над ванной налейте в пакет воды, зажмите его сверху рукой и выдавливайте воду через дырочки. Меняйте положение руки с пакетом, наблюдая, какие изменения происходят со струйками воды. Зарисуйте опыт и опишите свои наблюдения.
38.2. Отметьте галочкой утверждения, которые отражают суть закона Паскаля.
38.3. Допишите текст.
38.4. На рисунке показана передача давления твердым и жидким телом, заключенным под диском в сосуде.
а) Отметьте верное утверждение.
После установки гири на диск возрастает давление … .
б) Ответьте на вопросы, записав необходимые формулы и проводя соответствующие расчеты.
С какой силой будет давить на диск площадью 100 см2 установленная на него гиря массой 200 г?
Как изменится при этом и на сколько давление:
на дно сосуда 1
на дно сосуда 2
на боковую стенку сосуда 1
на боковую стенку сосуда 2
39.1. Отметьте верное окончание фразы.
Нижнее и боковое отверстия трубки затянуты одинаковыми резиновыми мембранами. В трубку наливают воду и медленно опускают ее в широкий сосуд с водой до тех пор, пока уровень воды в трубке не совпадет с уровнем воды в сосуде. В этом положении мембраны … .
39.2. На рисунке показан опыт с сосудом, дно которого может отпадать.
В ходе опыта были сделаны три наблюдения.
1. Дно пустой бутылки прижато, если трубка погружена в воду на некоторую глубину Н.
2. Дно по-прежнему прижато к трубке, когда в нее начинают наливать воду.
3. Дно начинает отходить от трубки в тот момент, когда уровень воды в трубке совпадет с уровнем воды в сосуде.
а) В левом столбце таблицы запишите номера наблюдений, которые позволяют прийти к выводам, обозначенным в правом столбце.
б) Запишите свои гипотезы о том, что может измениться в описанном выше опыте, если:
в сосуде будет находиться вода, а в трубку будут наливать подсолнечное масло дно трубки начнет отходить когда уровень масла будет выше уровня воды в сосуде;
в сосуде будет находиться подсолнечное масло, а в трубку будут наливать воду дно трубки начнет отходить раньше, чем совпадут уровни воды и масла.
39.3. В закрытом баллоне с площадью основания 0,03 м2 и высотой 1,2 м находится воздух плотностью 1,3 кг/м3. Определите «весовое» давление воздуха на дно баллона.
40.1. Запишите, какие из опытов, изображенных на рисунке, подтверждают, что давление в жидкости с глубиной увеличивается.
Поясните, что демонстрирует каждый из опытов.
40.2. Кубик помещен в жидкость плотностью p, налитую в открытый сосуд. Поставьте в соответствие указанным уровням жидкости формулы для вычисления давления, созданного столбом жидкости на этих уровни.
40.3. Отметьте знаком «+» верные утверждения.
Сосуды различной формы заполнили водой. При этом … .
+ давление воды на дно всех сосудов одинаково, поскольку давление жидкости на дно определяется только высотой столба жидкости.
40.4. Выберите пару слов, пропущенных в тексте. «Дном сосудов 1, 2 и 3 служит резиновая пленка, укрепленная в стойке прибора».
40.5. Чему равно давление воды на дно прямоугольного аквариума длиной 2 м, шириной 1 м и глубиной 50 см, доверху заполненного водой.
40.6. Используя рисунок, определите:
а) давление, созданное столбом керосина на поверхность воды:
б) давление на дно сосуда, созданное только столбом воды:
в) давление на дно сосуда, созданное двумя жидкостями:
41. 1. В одну из трубок сообщающихся сосудов налита вода. Что произойдет, если зажим с пластиковой трубки убрать?
1. В одну из трубок сообщающихся сосудов налита вода. Что произойдет, если зажим с пластиковой трубки убрать?
41.2. В одну из трубок сообщающихся сосудов налита вода, а в другую – бензин. Если зажим с пластиковой трубки убрать, то:
41.3. Впишите в текст подходящие по смыслу формулы и сделайте вывод.
Сообщающиеся сосуды заполнены одной и той же жидкостью. Давление столба жидкости
41.4. Какова высота столба воды в U-образном сосуде относительно уровня АВ, если высота столба керосина 50 см?
41.5. В сообщающиеся сосуды налиты машинное масло и вода. Рассчитайте, на сколько сантиметров уровень воды находится ниже уровня масла, если высота столба масла относительно границы раздела жидкостей Нм = 40 см.
42.1. На весах уравновесили стеклянный шар объемом 1 л. Шар закрыт пробкой, в которую вставлена резиновая трубка. Когда из шара при помощи насоса откачали воздух и зажали трубку зажимом, равновесие весов нарушилось.
а) Груз какой массы придется положить на левую чашу весов, чтобы их уравновесить? Плотность воздуха 1,3 кг/м3.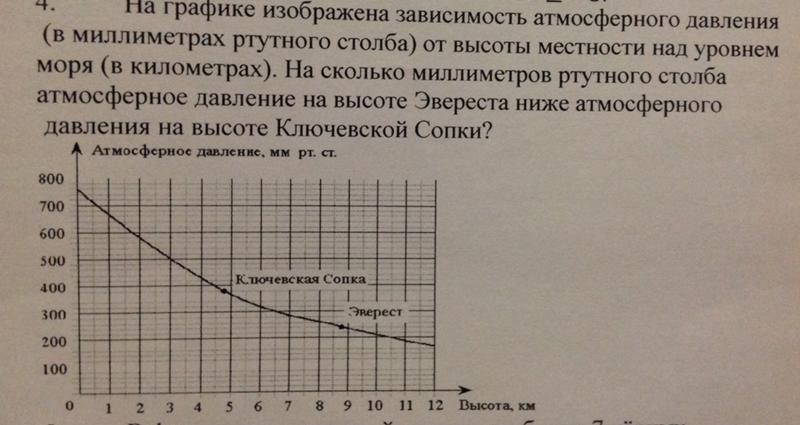
б) Каков вес воздуха, находившегося в колбе до откачивания?
42.2. Опишите, что произойдет, если конец резиновой трубки шара, из которого откачали воздух (см. задание 42.1), опустить в стакан с водой, а затем снять зажим. Объясните явление.
42.3. На асфальте начерчен квадрат со стороной 0,5 м. Рассчитайте массу и вес столба воздуха высотой 100 м, расположенного над квадратом, считая, что плотность воздуха не меняется с высотой и равна 1,3 кг/м3.
42.4. При движении поршня вверх внутри стеклянной трубки вода поднимается за ним. Отметьте правильное объяснение этого явления. Вода поднимается за поршнем … .
43.1. В кружках А, В, С схематично изображен воздух разной плотности. Отметьте на рисунке места, где следует расположить каждый кружок, чтобы в целом получилась картина, иллюстрирующая зависимость плотности воздуха от высоты над уровнем моря.
43.2. Выберите правильный ответ.
Для того чтобы покинуть Землю, любая молекула воздушной оболочки Земли должна обладать скоростью, большей чем … .
43.3. На Луне, масса которой примерно в 80 раз меньше массы Земли, отсутствует воздушная оболочка (атмосфера). Чем это можно объяснить? Запишите вашу гипотезу.
44.1. Выберите правильное утверждение.
В опыте Торричелли в стеклянной трубке над поверхностью ртути … .
44.2. В трех отрытых сосудах находится ртуть: в сосуде А высота столба ртути 1 м, в сосуде В – 1 дм, в сосуде С – 1 мм. Вычислите, какое давление на дно сосуда оказывает столб ртути в каждом случае.
44.3. Запишите значения давления в указанных единицах по приведенному образцу, округлив результат до целых.
44.4. Найдите давление на дно цилиндра, заполненного подсолнечным маслом, если атмосферное давление равно 750 мм рт. ст.
44.5. Какое давление испытывает аквалангист на глубине 12 м под водой, если атмосферное давление 100 кПа? Во сколько раз это давление больше атмосферного?
45.1. На рисунке показана схема устройства барометра-анероида. Отдельные детали конструкции прибора обозначены цифрами. Заполните таблицу.
Отдельные детали конструкции прибора обозначены цифрами. Заполните таблицу.
45.2. Заполните пропуски в тексте.
На рисунках изображен прибор, который называется __барометр-анероид_.
Этим прибором измеряют ___атмосферное давление__.
Запишите показание каждого прибора с учетом погрешности измерения.
45.3. Заполните пропуски в тексте. «Разница атмосферного давления в разных слоях атмосферы Земли вызывает движение воздушных масс».
45.4. Запишите значения давления в указанных единицах, округляя результат до целых.
46.1. На рисунке а изображена трубка Торричелли, расположенная на уровне моря. На рисунках б и в отметьте уровень ртути в трубке, помещенной соответственно на горе и в шахте.
46.2. Заполните пропуски в тексте, используя слова, приведенные в скобках.
Измерения показывают, что давление воздуха быстро (уменьшается, увеличивается) с увеличением высоты. Причиной тому служит не только (уменьшение, увеличение) плотности воздуха, но и (понижение, повышение) его температуры при удалении от поверхности Земли на расстояние до 10 км.
46.3. Высота Останкинской телебашни достигает 562 м. Чему равно атмосферное давление около вершины телебашни, если у ее основания атмосферное давление равно 750 мм рт. ст.? Давление выразите в мм рт. ст. и в единицах СИ, округлив оба значения до целых.
46.4. Выберите на рисунке и обведите график, который наиболее правильно отражает зависимость атмосферного давления p от высоты h над уровнем моря.
46.5. У кинескопа телевизора размеры экрана составляют l = 40 см и h = 30 см. С какой силой давит атмосфера на экран с наружной стороны (или какова сила давления), если атмосферное давление pатм = 100 кПа?
47.1. Постройте график зависимости давления p, измеряемого под водой, от глубины погружения h, заполнив предварительно таблицу. Считайте g = 10 Н/кг, pатм = 100 кПа.
47.2. На рисунке изображен открытый жидкостный манометр. Цена деления и шкалы прибора 1 см.
а) Определите, на сколько давление воздуха в левом колене манометра отличается от атмосферного.
б) Определите давление воздуха в левом колене манометра с учетом того, что атмосферное давление 100 кПа.
47.3. На рисунке показана U-образная трубка, заполненная ртутью, правый конец которой закрыт. Чему равно атмосферное давление, если разность уровней жидкости в коленах U-образной трубки равна 765 мм, а мембрана погружена в воду на глубину 20 см?
47.4. а) Определите цену деления и показание металлического манометра (рис. а).
б) Опишите принцип действия прибора, используя цифровые обозначения деталей (рис. б).
48.1. а) Зачеркните ненужные из выделенных слов, чтобы получилось описание работы поршневого насоса, изображенного на рисунке.
б) Опишите, что происходит при движении рукоятки насоса вверх.
48.2. Поршневым насосом, схема которого приведена в задании 48.1, при нормальном атмосферном давлении можно поднять воду на высоту не более 10 м. Объясните почему.
48.3. Вставьте в текст пропущенные слова, чтобы получилось описание работы поршневого насоса с воздушной камерой.
49.1. Допишите формулы, показывающие правильные соотношения между площадями покоящихся поршней гидравлической машины и массами грузов.
49.2. Площадь малого поршня гидравлической машины равна 0,04 м2, площадь большого – 0,2 м2. С какой силой следует действовать на малый поршень, чтобы равномерно поднять груз массой 100 кг, находящийся на большом поршне?
49.3. Заполните пропуски в тексте, описывающем принцип действия гидравлического пресса, схема устройства которого показана на рисунке.
49.4. Опишите принцип действия отбойного молотка, схема устройства которого показана на рисунке.
49.5. На рисунке показана схема устройства пневматического тормоза железнодорожного вагона.
Барометрические формулы: различные выводы и сравнения с экологическими наблюдениями
Общие соображения
Из опыта хорошо известно, что температура воздуха изменяется с высотой. Поэтому при поиске более реалистичной барометрической формулы этот факт необходимо как-то учитывать. Прежде всего следует отметить, что в этом случае следует полностью отказаться от соображений, основанных на статистической механике, поскольку их основополагающий принцип — это концепция теплового равновесия.
Поэтому при поиске более реалистичной барометрической формулы этот факт необходимо как-то учитывать. Прежде всего следует отметить, что в этом случае следует полностью отказаться от соображений, основанных на статистической механике, поскольку их основополагающий принцип — это концепция теплового равновесия.
С другой стороны, механический образ мышления не нуждается в корректировке, поэтому уравнение. 4 все еще действует, с той лишь разницей, что температура T становится функцией высоты h в нем, что означает, что простое решение в уравнении. 5 больше использовать нельзя. Смешанное термодинамико-механическое мышление не лишено помощи, но оно будет обсуждено в отдельном подразделе.
Существует две стратегии решения проблемы изменения температуры: первая состоит в том, чтобы просто измерить ее и подставить эмпирическую температурную зависимость в уравнение.4. Этот метод, вероятно, менее удовлетворителен в интеллектуальном плане, чем альтернатива, которая будет представлена более подробно, поскольку использование наблюдаемой зависимости даже не пытается объяснить полученные результаты.
В качестве первого подхода следует подумать о том, что разница температур в атмосфере с высотой сохраняется, несмотря на то, что теплопроводность стремится их уравнять.Хотя температура воздуха действительно изменяется даже на данной высоте, это довольно медленно по сравнению с обычной скоростью теплопроводности и в первую очередь вызвано изменениями в облучении (например, дневные и ночные циклы). Итак, это хорошая отправная точка — думать, что постоянная температура на заданной высоте поддерживается, несмотря на то, что теплопроводность происходит вертикально. Короче говоря, здесь необходимо уравнение переноса. Формулы, описывающие перенос тепла, полностью аналогичны первому и второму законам Фика (которые описывают перенос вещества).{2}}} \ sqrt {\ frac {2RT \ left (h \ right)} {{{\ uppi} M}}} $$
(17)
Ранее неопределенные величины в этом уравнении равны ν (греческая буква ню), что составляет половину числа степеней свободы молекулы (безразмерных) и диаметра d молекулы. {2}}} = 0 $$
{2}}} = 0 $$
(19)
Это возможно, только если первая частная производная постоянна.Эта величина обозначается α (греческая буква альфа) и называется температурным градиентом атмосферы (единица измерения: кельвин на метр). Известно, что температура уменьшается с высотой, поэтому из-за нашего обычного человеческого предпочтения положительных чисел
$$ — \ alpha = \ frac {{{\ text {d}} T}} { {{\ text {d}} h}} $$
(20)
Интегрирующее уравнение. 20 с введением T 0 (температура на уровне моря) и T ( h ) (температура на высоте h ) дает:
$$ T \ left (h \ right) = T_ {0} — \ alpha h $$
(21)
Суть этого уравнения заключается в том, что атмосфера может находиться в стационарном состоянии только в том случае, если температура уменьшается линейно с высотой (или изотермически, что означает α = 0).
Здесь следует отметить, что рисунок, сделанный до сих пор для интерпретации профиля температуры атмосферы, является весьма неполным. Уравнение теплопроводности, показанное в формуле. 16 не включает так называемый источник, что означает, что предполагается, что тепло не производится в атмосфере. На самом деле это происходит из-за поглощения солнечного света. Кроме того, потеря тепла также происходит из-за теплового излучения, что также исключается из рассмотрения. В следующих разделах будут представлены теоретические соображения для интерпретации значения теплового градиента
Уравнение теплопроводности, показанное в формуле. 16 не включает так называемый источник, что означает, что предполагается, что тепло не производится в атмосфере. На самом деле это происходит из-за поглощения солнечного света. Кроме того, потеря тепла также происходит из-за теплового излучения, что также исключается из рассмотрения. В следующих разделах будут представлены теоретические соображения для интерпретации значения теплового градиента
Вместо того, чтобы пытаться определить значение α теоретическим способом, уравнение. 21 сначала подставляется обратно в формулу. 4, справедливость которого уже была доказана независимо от изменений температуры. Результат:
$$ \ frac {{{\ text {d}} p}} {{{\ text {d}} h}} \, = — \ frac {Mg} {{R \ left ({ T_ {0} — \ alpha h} \ right)}} p \ left (h \ right) $$
(22)
Таким образом, эта мысль устраняет проблемы, связанные с изменениями температуры и давления.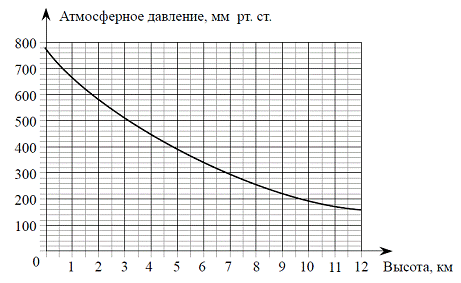 {{\ frac {Mg} {{\ alpha R}}}} $$
{{\ frac {Mg} {{\ alpha R}}}} $$
(23)
Уравнение 23 — это улучшенная барометрическая формула, так как она также учитывает изменение температуры.
Теперь можно обратить внимание на теоретические оценки температурного градиента атмосферы.
Простое сохранение энергии
Возможно, самый простой подход состоит в том, чтобы включить потенциальную энергию в гравитационное поле как часть общей энергии молекулы.Средняя внутренняя энергия одиночной молекулы идеального газа при температуре
$$ \ nu kT_ {0} = mgh + \ nu kT \ left (h \ right) $$
(24)
После умножения на константу Авогадро и некоторых дополнительных перегруппировок получается прямое выражение для
$$ T \ left (h \ right) = T_ {0} — \ frac {Mg } {{\ nu R}} h $$
(25)
Уравнение 25 полностью согласуется с уравнением. 21. Теоретически полученный температурный градиент:
21. Теоретически полученный температурный градиент:
$$ \ alpha = \ frac {Mg} {{\ nu R}} $$
(26)
Это даст оценку 0,0137 км -1 = 13,7 км -1 для градиента температуры. Экспериментальное значение (как обсуждается ниже) составляет 0,00649 км -1 = 6,49 км -1 для самых нижних 10 км атмосферы.
Обратимое адиабатическое расширение идеального газа
В пояснениях к формуле.21 уже упоминалось, что модель, предсказывающая линейное изменение температуры в зависимости от высоты, была основана на стационарном состоянии уравнения теплопроводности, что подразумевает, что одинаковое количество тепла входит и выходит из атмосферы в разных местах. Таким образом, в целом теплообмен с окружающей средой равен нулю (конечно, поглощение и излучение излучения в этой модели все еще не учитываются, и возможная роль испарения и конденсации воды также исключена). В этой модели снижение температуры с увеличением высоты легко объяснить адиабатическим расширением идеального газа.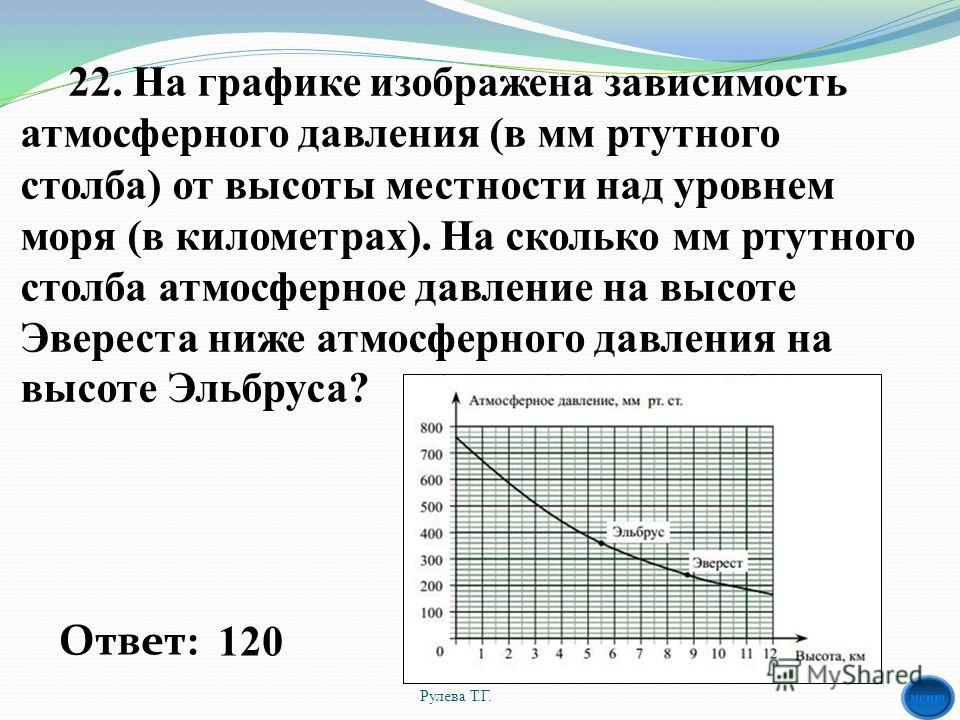
(27)
Новая величина γ (греческая буква гамма) — это отношение двух молярных теплоемкостей (измеренных при постоянном давлении и постоянном объеме) идеального газа:
$$ \ gamma = \ frac {{C_ {p }}} {{C_ {v}}} = \ frac {\ nu R + R} {{\ nu R}} = \ frac {\ nu + 1} {\ nu} $$
(28)
Из закона идеального газа можно получить другое уравнение:
$$ V = V_ {0} \ frac {{p_ {0} T}} {{pT_ {0}}} $$
(29)
Сравнение уравнений.{1 / \ gamma — 1} $$
(30)
Теперь это уравнение, которое связывает изменение давления с изменением температуры, вместо того, чтобы напрямую давать зависимость изменения температуры от высоты. Итак, теперь уравнения. 4 и 30 вместе образуют систему двух одновременных уравнений с двумя неизвестными функциями. Вычисление производной уравнения.
(31)
Теперь выгодно заменить уравнения.4 и 28 в приведенную выше формулу:
$$ \ frac {{{\ text {d}} T}} {{{\ text {d}} h}} = — \ left ({1 — \ frac {\ nu} {\ nu + 1}} \ right) \ frac {T} {p \ left (h \ right)} \ frac {Mg} {{RT}} p \ left (h \ right) = — \ frac { Mg} {{\ left ({\ nu + 1} \ right) R}} $$
(32)
Эта формула все еще полностью согласуется с уравнениями. 20 и 21, но дает теоретическую оценку градиента температуры атмосферы, которая немного отличается от уравнения. 26:
$$ \ alpha = \ frac {Mg} {{\ left ({\ nu + 1} \ right) R}} $$
(33)
Числовое значение: α = 0. 00978 км −1 = 9,78 км −1 из этого уравнения.
00978 км −1 = 9,78 км −1 из этого уравнения.
Спасение смешанного термодинамического и механического мышления
Здесь следует отметить, что до сих пор все соображения относительно температуры, зависящей от высоты, основывались на механическом подходе к проблеме. Поскольку мы рассматриваем воздух как единый идеальный газ, его химический потенциал совпадает с молярной энергией Гиббса ( G m ) и зависит как от температуры, так и от давления.Тогда термодинамическая сила будет задана как:
$$ F _ {{{\ text {td}}}} = \ frac {{{\ text {d}} \ mu}} {{{\ text {d}} h}} = — \ left ({\ frac {{\ partial G _ {{\ text {m}}}}} {\ partial p}} \ right) _ {T} \ frac {{{\ text {d} } p}} {{{\ text {d}} h}} — \ left ({\ frac {{\ partial G _ {{\ text {m}}}}} {\ partial T}} \ right) _ { p} \ frac {{{\ text {d}} T}} {{{\ text {d}} h}} \ quad ??? $$
(34)
Три вопросительных знака в конце этого уравнения означают, что позже будет показано, что оно неверно. Первый член можно упростить, используя уравнение, согласно которому частная производная функции Гиббса по давлению представляет собой объем системы [11]:
Первый член можно упростить, используя уравнение, согласно которому частная производная функции Гиббса по давлению представляет собой объем системы [11]:
$$ \ left ({\ frac {{\ partial G _ {{\ текст {m}}}}} {\ partial p}} \ right) _ {T} = V _ {{\ text {m}}} = \ frac {RT} {p} $$
(35)
Второй член в уравнении. 34 — это частная производная функции Гиббса по температуре, которая является энтропией [11]:
$$ \ left ({\ frac {{\ partial G _ {{\ text {m}}}}}} {\ частичный T}} \ right) _ {p} = — S _ {{\ text {m}}} $$
(36)
Итак, уравнение, задающее термодинамическую силу, теперь примет следующий вид:
$$ F _ {{{\ text {td}}}} = — \ frac {RT} {p} \ frac {{{\ text {d}} p}} {{{\ text {d}} h}} — \ left ({- S _ {{\ text {m}}}} \ right) \ frac {{{\ text {d}} T}} {{{\ text {d}} h}} = — \ frac {RT} {p} \ frac {{{\ text {d}} p}} {{{\ text {d}} h} } + S _ {{\ text {m}}} \ frac {{{\ text {d}} T}} {{{\ text {d}} h}} \ quad ??? $$
(37)
Три вопросительных знака снова означают, что это уравнение окажется неверным.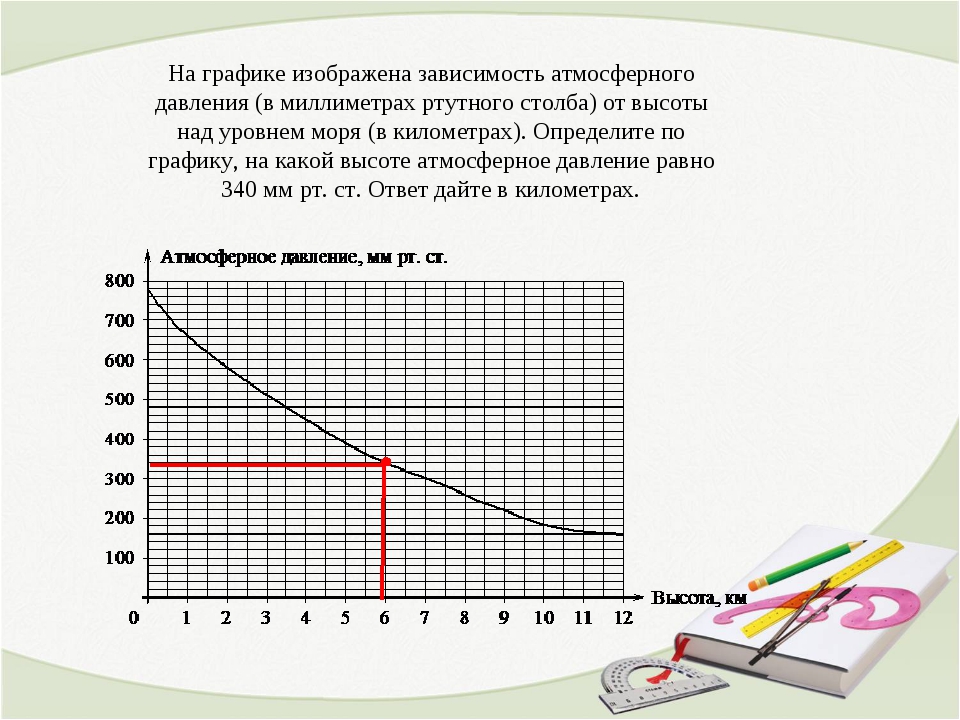
Здесь кроется загадка: если эта сила используется для уравновешивания гравитации аналогично уравнению. 11, получается следующая формула (производная температуры по температуре уже обозначена как α ):
$$ \ frac {{{\ text {d}} p}} {{{\ text {d} } h}} = — \ frac {Mg} {{RT}} p — \ frac {{pS _ {{\ text {m}}}}} {RT} \ alpha \ quad ??? $$
(38)
Уравнение 4, основанное на механической мысли, уже было объявлено справедливым даже при наличии температурного градиента.Третий закон термодинамики гарантирует, что молярная энтропия S m всегда положительна (примечание: обратимое адиабатическое расширение является изэнтропическим, поэтому S m не будет зависеть от высоты в сценарии, описанном в предыдущем примере. подраздел). Итак, единственный способ привести уравнения. 4 и 38, означает, что α = 0, так что случай изотермический. Но этот сценарий уже рассматривался в разд. 2. 2. Как избежать этого противоречия?
2. Как избежать этого противоречия?
Чтобы разрешить это противоречие, нужно сделать большой крюк в царство неравновесной термодинамики.Последовательный взгляд на природу и расчет термодинамических сил был важной частью научной работы, за которую американский физик-химик и физик-теоретик норвежского происхождения Ларс Онсагер (1903–1976) был удостоен Нобелевской премии по химии в 1968 году [17]. Не вдаваясь в подробности, оказалось, что уравнение. 34 имеет две проблемы. Во-первых, градиент химического потенциала — не единственный источник термодинамической силы в неизотермических условиях. Во-вторых, конечным источником термодинамической силы является не изменение химического потенциала ( μ ) или температуры ( T ), а изменение соотношения химического потенциала и температуры ( μ / T ). и обратная температура (1/ T ).Следовательно, правильная формула, которая дает термодинамическую силу, следующая:
$$ F _ {{{\ text {td}}}} = — T \ frac {{{\ text {d}} \ left ({\ mu / T} \ right)}} {{{\ text {d}} h}} + TH _ {{\ text {m}}} \ frac {{{\ text {d}} \ left ({1 / T} \ справа)}} {{{\ text {d}} h}} $$
(39)
Здесь H m — молярная энтальпия системы. {2}}} \ frac {{{\ text { dT}}}} {{{\ text {d}} h}} $$
{2}}} \ frac {{{\ text { dT}}}} {{{\ text {d}} h}} $$
(40)
Первый член можно упростить, используя уравнение, в котором частная производная функции Гиббса по давлению представляет собой объем системы, а затем подставив закон идеального газа:
$$ \ left ({\ frac {{ \ partial \ left ({G _ {{\ text {m}}} / T} \ right)}} {\ partial p}} \ right) _ {T} = \ frac {1} {T} \ left ({ \ frac {{\ partial G _ {{\ text {m}}}}} {\ partial p}} \ right) _ {T} = \ frac {1} {T} V _ {{\ text {m}}} = \ frac {1} {T} \ frac {RT} {p} = \ frac {R} {p} $$
(41)
Второй член в уравнении.{2}}}} \ right) \ frac {{{\ text {d}} T}} {{{\ text {d}} h}} — \ frac {{H _ {{\ text {m}}} }} {T} \ frac {{{\ text {dT}}}} {{{\ text {d}} h}} = — \ frac {RT} {p} \ frac {{{\ text {d} } p}} {{{\ text {d}} h}} $$
(43)
Итак, приложив много усилий, формула, уже приведенная в Ур. 10, но теперь в неизотермических условиях. Следовательно, уравнение. 4 следует из термодинамико-механического мышления и в неизотермических условиях.
10, но теперь в неизотермических условиях. Следовательно, уравнение. 4 следует из термодинамико-механического мышления и в неизотермических условиях.
Слои атмосферы | NIWA
Атмосфера состоит из слоев в зависимости от температуры.Эти слои — тропосфера, стратосфера, мезосфера и термосфера. Еще одна область на высоте около 500 км над поверхностью Земли называется экзосферой.
Различные слои атмосферы
Атмосферу можно разделить на слои в зависимости от ее температуры, как показано на рисунке ниже. Эти слои — тропосфера, стратосфера, мезосфера и термосфера. Дальнейшая область, начинающаяся примерно на 500 км над поверхностью Земли, называется экзосферой.
Красная линия на рисунке ниже показывает, как температура изменяется с высотой (шкала температур приведена в нижней части диаграммы). Шкала справа показывает давление. Например, на высоте 50 км давление составляет всего одну тысячную от давления у земли.
Тропосфера
Это самая нижняя часть атмосферы — та часть, в которой мы живем. Она содержит большую часть нашей погоды — облака, дождь, снег. В этой части атмосферы температура становится ниже по мере увеличения расстояния над землей примерно на 6 градусов.5 ° C на километр. Фактическое изменение температуры с высотой меняется день ото дня в зависимости от погоды.
Она содержит большую часть нашей погоды — облака, дождь, снег. В этой части атмосферы температура становится ниже по мере увеличения расстояния над землей примерно на 6 градусов.5 ° C на километр. Фактическое изменение температуры с высотой меняется день ото дня в зависимости от погоды.
Тропосфера содержит около 75% всего воздуха в атмосфере и почти весь водяной пар (который образует облака и дождь). Снижение температуры с высотой является результатом падения давления. Если воздушный шарик движется вверх, он расширяется (из-за более низкого давления). Когда воздух расширяется, он охлаждается. Таким образом, воздух вверху холоднее, чем воздух внизу.
Самая нижняя часть тропосферы называется пограничным слоем.Здесь движение воздуха определяется свойствами поверхности Земли. Турбулентность возникает, когда ветер дует над поверхностью Земли, и термиками, поднимающимися с земли, когда она нагревается солнцем. Эта турбулентность перераспределяет тепло и влагу в пограничном слое, а также загрязняющие вещества и другие составляющие атмосферы.
Верхняя часть тропосферы называется тропопаузой. Это самый низкий уровень на полюсах, где он находится примерно на 7-10 км над поверхностью Земли.Самый высокий (около 17-18 км) у экватора.
Стратосфера
Он простирается вверх от тропопаузы примерно до 50 км. Он содержит много озона в атмосфере. Повышение температуры с высотой происходит из-за поглощения этим озоном ультрафиолетового (УФ) излучения солнца. Температуры в стратосфере самые высокие над летним полюсом и самые низкие над зимним.
Поглощая опасное УФ-излучение, озон в стратосфере защищает нас от рака кожи и других повреждений здоровья.Однако химические вещества (называемые ХФУ или фреоны и галоны), которые когда-то использовались в холодильниках, аэрозольных баллончиках и огнетушителях, уменьшили количество озона в стратосфере, особенно в полярных широтах, что привело к так называемой «озоновой дыре в Антарктике».
Сейчас люди перестали производить большую часть вредных ХФУ, мы ожидаем, что озоновая дыра в конечном итоге восстановится в течение 21 -го века, но это медленный процесс.
Мезосфера
Область над стратосферой называется мезосферой.Здесь температура снова понижается с высотой, достигая минимума около -90 ° C в «мезопаузу».
Термосфера и ионосфера
Термосфера находится выше мезопаузы и представляет собой область, в которой температура снова увеличивается с высотой. Это повышение температуры вызвано поглощением энергичного ультрафиолетового и рентгеновского излучения от солнца.
Область атмосферы выше 80 км также вызвана «ионосферой», так как энергичное солнечное излучение сбивает электроны с молекул и атомов, превращая их в «ионы» с положительным зарядом.Температура термосферы колеблется между днем и ночью и между сезонами, как и количество присутствующих ионов и электронов. Ионосфера отражает и поглощает радиоволны, что позволяет нам принимать коротковолновые радиопередачи в Новой Зеландии из других частей мира.
Экзосфера
Область выше 500 км называется экзосферой. Он содержит в основном атомы кислорода и водорода, но их так мало, что они редко сталкиваются — они следуют по «баллистическим» траекториям под действием силы тяжести, а некоторые из них уходят прямо в космос.
Магнитосфера
Земля ведет себя как огромный магнит. Он улавливает электроны (отрицательный заряд) и протоны (положительный), концентрируя их в двух полосах на высоте около 3000 и 16000 км над земным шаром — «радиационных» поясах Ван Аллена. Эта внешняя область, окружающая Землю, где заряженные частицы вращаются по спирали вдоль силовых линий магнитного поля, называется магнитосферой.
Дополнительная информация
Посетите наш Национальный научный центр атмосферы
Узнайте о наших исследованиях УФ-излучения и озона
изменений за 56- и 20-летний рекорд
Abstract
Определение масштаба моделей изменения климата по градиентам высот имеет важное значение для лучшего понимания более широких моделей изменения климата и для прогнозирования гидрологических и экосистемных изменений.Мы представляем температурные тренды с пяти долгосрочных метеорологических станций на 2077-метровой высоте разреза в Хребте Скалистых гор в Колорадо, США. Эти тенденции измерялись в двух временных периодах: полный 56-летний рекорд (1953–2008) и более короткий 20-летний (1989–2008) период, представляющий период ускоряющихся изменений, о которых широко сообщалось. Скорость изменения биологических индикаторов, продолжительности сезона и накопленных дней роста также измерялась за 56 и 20 лет. Наконец, мы сравнили, насколько хорошо интерполированные наборы данных «Параметрическая регрессия по модели независимых откосов» (PRISM) соответствуют данным с контролем качества и погодным данным с каждой станции.Наши результаты показывают, что сигналы потепления были наиболее сильными на средних высотах в обоих временных масштабах. За 56-летний период на большинстве участков наблюдается потепление, происходящее в основном за счет повышения максимальных температур, в то время как 20-летний рекорд свидетельствует о потеплении, связанном с повышением максимальных температур на более низких высотах и повышением минимальных температур на более высоких высотах.
Эти тенденции измерялись в двух временных периодах: полный 56-летний рекорд (1953–2008) и более короткий 20-летний (1989–2008) период, представляющий период ускоряющихся изменений, о которых широко сообщалось. Скорость изменения биологических индикаторов, продолжительности сезона и накопленных дней роста также измерялась за 56 и 20 лет. Наконец, мы сравнили, насколько хорошо интерполированные наборы данных «Параметрическая регрессия по модели независимых откосов» (PRISM) соответствуют данным с контролем качества и погодным данным с каждой станции.Наши результаты показывают, что сигналы потепления были наиболее сильными на средних высотах в обоих временных масштабах. За 56-летний период на большинстве участков наблюдается потепление, происходящее в основном за счет повышения максимальных температур, в то время как 20-летний рекорд свидетельствует о потеплении, связанном с повышением максимальных температур на более низких высотах и повышением минимальных температур на более высоких высотах. В последние десятилетия также наблюдается переход от потепления в весенний период к потеплению в июле и ноябре. Потепление вдоль градиента способствовало увеличению количества дней с возрастанием, хотя и в разной степени, в обоих временных масштабах.Однако продолжительность вегетационного периода осталась неизменной. Наконец, фактические и интерполированные годовые темпы PRISM редко демонстрировали сильную корреляцию и предполагают различные тенденции потепления и похолодания на большинстве участков. Интерпретация климатических тенденций и их сезонных отклонений в хребте Скалистых гор зависит как от высоты, так и от временного масштаба анализа. Учитывая несоответствия между интерполированными данными и данными прямых измерений станций, мы предостерегаем от чрезмерного использования методов интерполяции для документирования местных закономерностей климатических изменений.
В последние десятилетия также наблюдается переход от потепления в весенний период к потеплению в июле и ноябре. Потепление вдоль градиента способствовало увеличению количества дней с возрастанием, хотя и в разной степени, в обоих временных масштабах.Однако продолжительность вегетационного периода осталась неизменной. Наконец, фактические и интерполированные годовые темпы PRISM редко демонстрировали сильную корреляцию и предполагают различные тенденции потепления и похолодания на большинстве участков. Интерпретация климатических тенденций и их сезонных отклонений в хребте Скалистых гор зависит как от высоты, так и от временного масштаба анализа. Учитывая несоответствия между интерполированными данными и данными прямых измерений станций, мы предостерегаем от чрезмерного использования методов интерполяции для документирования местных закономерностей климатических изменений.
Образец цитирования: McGuire CR, Nufio CR, Bowers MD, Guralnick RP (2012) Зависимые от высоты температурные тенденции в хребте Скалистых гор: изменения за 56- и 20-летний рекорд. PLoS ONE 7 (9):
e44370.
https://doi.org/10.1371/journal.pone.0044370
PLoS ONE 7 (9):
e44370.
https://doi.org/10.1371/journal.pone.0044370
Редактор: Хуан А. Аньель, Оксфордский университет, Великобритания
Поступила: 07.11.2011; Одобрена: 3 августа 2012 г .; Опубликован: 6 сентября 2012 г.
Авторские права: © McGuire et al.Это статья в открытом доступе, распространяемая в соответствии с условиями лицензии Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии указания автора и источника.
Финансирование: Этот проект поддержан грантом Национального научного фонда № 1543813, исследовательским грантом Уокера Ван Рипера, предоставленным Музеем естественной истории Университета Колорадо, и стипендией канцлера Университета Колорадо в Боулдере.Финансирующие организации не играли никакой роли в дизайне исследования, сборе и анализе данных, принятии решения о публикации или подготовке рукописи.
Конкурирующие интересы: Авторы заявили, что никаких конкурирующих интересов не существует.
Введение
Горные районы, особенно альпийские, относятся к числу сред, наиболее уязвимых к последствиям изменения климата [1] — [3]. Климатические изменения в горах имели и, вероятно, будут продолжать оказывать сильное влияние на гидрологические циклы [4], [5], время биологических событий [6] — [8] и биоразнообразие [9], [10].Для биологических систем, адаптированных к узко распределенным и экстремальным условиям окружающей среды, даже небольшие изменения климатических условий могут иметь пропорционально большие воздействия на флору и фауну [11]. Важным первым шагом к прогнозированию гидрологических и экосистемных изменений в отдельных горных системах является документирование климатических тенденций на различных высотах в пределах этих систем.
Несмотря на большую работу по документированию температурных трендов в горных системах мира за последние полвека, последовательный сигнал о зависимости от высоты или систематического изменения климата не стал очевидным [12] — [14]. Например, в то время как тенденции потепления в Европейских Альпах [15], [16] и на Тибетском плато [17] усиливаются с повышением, было обнаружено, что тенденции потепления в тропических Андах ослабевают с повышением [18]. Учитывая эти различия, ключевой вопрос заключается в том, появятся ли общие положения, которые могут объяснить эту изменчивость, по мере появления новых тематических исследований в различных регионах мира. Кроме того, изменчивость климатических тенденций, зависящих от высоты, указывает на необходимость развития мониторинга климата вдоль горных разрезов, который может контролировать региональную неоднородность и широтное влияние при улучшении пространственного разрешения.
Например, в то время как тенденции потепления в Европейских Альпах [15], [16] и на Тибетском плато [17] усиливаются с повышением, было обнаружено, что тенденции потепления в тропических Андах ослабевают с повышением [18]. Учитывая эти различия, ключевой вопрос заключается в том, появятся ли общие положения, которые могут объяснить эту изменчивость, по мере появления новых тематических исследований в различных регионах мира. Кроме того, изменчивость климатических тенденций, зависящих от высоты, указывает на необходимость развития мониторинга климата вдоль горных разрезов, который может контролировать региональную неоднородность и широтное влияние при улучшении пространственного разрешения.
В Северной Америке единственная известная долгосрочная климатическая трансекта, представляющая континентальный горный хребет, расположена в Хребте Роки-Маунтин-Фронт непосредственно к западу от Боулдера, штат Колорадо. Расположенный вдоль 40-й параллели, трансекта Рокки Маунтин Фронт Хребет (далее трансекта RMFR) проходит от 1672 м на высоких равнинах до 3749 м в альпийской тундре на расстоянии менее 30 км. База этого разреза в Боулдере, штат Колорадо, собирала данные о температуре в течение последних 100 лет и в настоящее время обслуживается Национальным управлением океанических и атмосферных исследований Министерства торговли США (NOAA).Четыре горных станции к западу от Боулдера собирают ежедневные данные о температуре в районе Колорадского переднего хребта с 1952 года [19] и обслуживаются в рамках проекта долгосрочных экологических исследований Нивот-Ридж (NWT LTER) Университета Колорадо в Боулдере.
База этого разреза в Боулдере, штат Колорадо, собирала данные о температуре в течение последних 100 лет и в настоящее время обслуживается Национальным управлением океанических и атмосферных исследований Министерства торговли США (NOAA).Четыре горных станции к западу от Боулдера собирают ежедневные данные о температуре в районе Колорадского переднего хребта с 1952 года [19] и обслуживаются в рамках проекта долгосрочных экологических исследований Нивот-Ридж (NWT LTER) Университета Колорадо в Боулдере.
Исследования, моделирующие последствия изменения климата в районе Скалистых гор, обычно предсказывают, что тенденции к потеплению будут наибольшими на более высоких высотах, причем альпийские горы покажут наибольшее относительное изменение [20] — [22].Напротив, исследования, включающие гидрологические изменения вблизи переднего хребта Колорадо, предсказывают похолодание на средних и больших высотах [23]. Оба набора исследований контрастируют с предыдущими исследованиями климатических данных разреза RMFR (1952–1998), которые выявили потепление, связанное со станциями ниже 3000 м, и, вопреки ожиданиям, что альпийские горы были связаны со значительным похолоданием [24], [25].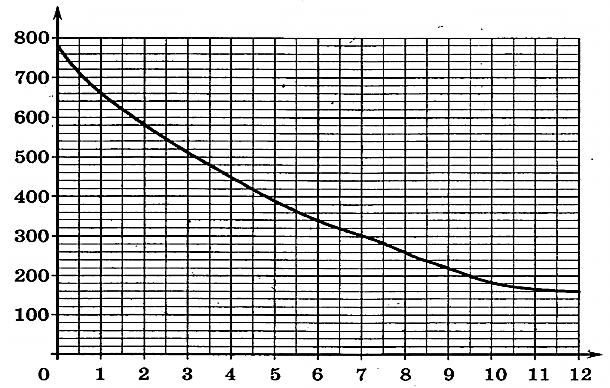 Эти исследования показывают, что изменение климата на обширной территории, такой как Скалистые горы, может быть более сложным, чем ожидалось.Однако более детальному пониманию этой сложности препятствует отсутствие полного современного анализа тенденций изменения температуры, такого как тот, который предоставляется по разрезу RMFR. Трансекта RMFR содержит лучшие неинтерполированные и контролируемые по широте данные, доступные для хребта Фронт Скалистых гор, и, следовательно, его анализ и интерпретация важны для улучшения пространственного разрешения трендов в Скалистых горах. Ускорение темпов потепления в северном полушарии в последние десятилетия [26] дополнительно требует тщательного изучения температурных данных, связанных с трансектом RMFR.
Эти исследования показывают, что изменение климата на обширной территории, такой как Скалистые горы, может быть более сложным, чем ожидалось.Однако более детальному пониманию этой сложности препятствует отсутствие полного современного анализа тенденций изменения температуры, такого как тот, который предоставляется по разрезу RMFR. Трансекта RMFR содержит лучшие неинтерполированные и контролируемые по широте данные, доступные для хребта Фронт Скалистых гор, и, следовательно, его анализ и интерпретация важны для улучшения пространственного разрешения трендов в Скалистых горах. Ускорение темпов потепления в северном полушарии в последние десятилетия [26] дополнительно требует тщательного изучения температурных данных, связанных с трансектом RMFR.
Целью данного исследования является анализ и сравнение температурных трендов вдоль 2077-метрового перепада высот разреза RMFR как за 56-летний (1953–2008), так и за 20-летний (1989–2008) период. Мы описываем тенденции за все доступные данные (56 лет; 1953–2008) и за последние 20 лет (1989–2008), чтобы сравнить долгосрочные (> 50 лет) температурные тенденции с температурными тенденциями в течение недавнего периода ускорения роста. глобальное изменение климата [26]. Сравниваемые данные включают тенденции среднегодовых и месячных максимальных, минимальных и средних температур.Месячные тренды температуры в обоих временных масштабах были изучены, чтобы определить более мелкомасштабную сезонную основу для обнаруженных изменений.
глобальное изменение климата [26]. Сравниваемые данные включают тенденции среднегодовых и месячных максимальных, минимальных и средних температур.Месячные тренды температуры в обоих временных масштабах были изучены, чтобы определить более мелкомасштабную сезонную основу для обнаруженных изменений.
Поскольку интерполяция климатических данных в пределах горных систем может быть затруднена из-за сложной топологии и низкой плотности доступных метеостанций [27], [28], доступ к 56-летним данным RMFR позволил нам проверить способность Parameter-elevation Модель регрессии на независимых склонах (PRISM; http://www.prism.oregonstate.edu/) для точной интерполяции годовых значений температуры (макс., Мин., Среднее) и их расчетной скорости изменения климата за последние 56 лет для каждого участок вдоль трансекты РМФР.Низкая корреляция между интерполированными и фактическими наборами данных и значительные различия в их измеренных темпах изменения климата за последние 56 лет подчеркнут ценность наборов долгосрочных данных и предостерегают от чрезмерного доверия к интерполированным данным для понимания изменения климата вдоль градиентов. особенно в Скалистых горах, где было предложено множество различных моделей будущего изменения климата [22], [23]. Наконец, поскольку существует большой интерес к тому, как изменение климата влияет на биологические индикаторы (например,грамм. [6] — [8]), мы также исследовали, как изменение температуры повлияло на продолжительность вегетационного периода и доступные дни градуса роста (GDD) вдоль высотного разреза.
особенно в Скалистых горах, где было предложено множество различных моделей будущего изменения климата [22], [23]. Наконец, поскольку существует большой интерес к тому, как изменение климата влияет на биологические индикаторы (например,грамм. [6] — [8]), мы также исследовали, как изменение температуры повлияло на продолжительность вегетационного периода и доступные дни градуса роста (GDD) вдоль высотного разреза.
Методы
Трансект Хребта Скалистых гор
Четыре из пяти станций, составляющих трансекту RMFR, были созданы в 1952 году Джоном Марром из Университета Колорадо [19], [29], [30]. Данные для этих станций были предоставлены проектом долгосрочных экологических исследований хребта Нивот (NWT LTER) и Горной исследовательской станцией Университета Колорадо.Целью создания этих метеостанций было предоставление подробной климатической информации об отдельных экологических зонах восточного склона хребта Скалистых гор. Станции обозначаются как A1 (2185 м), B1 (2591 м), C1 (3048 м) и D1 (3749 м), и они отражают климат, связанный с региональными нижними горами (предгорьями), верхними горами, субальпийская и альпийская тундровая жизненная зона соответственно (таблица 1; рисунок 1). Чтобы свести к минимуму возможные ошибки, связанные с размещением этих метеостанций, и гарантировать, что они отражают климат, связанный с экологическими зонами, которые они должны были представлять, Марр разместил эти станции в районах с умеренными для своего типа почвами и топографическими условиями, которые были близки к центр каждой обозначенной зоны жизни, и они были вдоль единой системы хребтов, которые следовали за 40 -й параллелью [31].Поскольку мы не могли объединить другие местные метеостанции по сходству в топографии, используемом оборудовании, временном масштабе сбора данных и широте, данные с других станций использовались, чтобы помочь исправить аномальные события данных, но, как это было сделано в предыдущих исследованиях [24], они не были включены в наши меры по локальному изменению климата. Трансекта RMFR расширяет первоначальную трансекту Марра, включая пятую метеостанцию, которая в настоящее время находится в здании Национального института стандартов и технологий (NIST) на западной окраине Боулдера, к югу от кампуса Министерства торговли США в Боулдере, Колорадо.
Чтобы свести к минимуму возможные ошибки, связанные с размещением этих метеостанций, и гарантировать, что они отражают климат, связанный с экологическими зонами, которые они должны были представлять, Марр разместил эти станции в районах с умеренными для своего типа почвами и топографическими условиями, которые были близки к центр каждой обозначенной зоны жизни, и они были вдоль единой системы хребтов, которые следовали за 40 -й параллелью [31].Поскольку мы не могли объединить другие местные метеостанции по сходству в топографии, используемом оборудовании, временном масштабе сбора данных и широте, данные с других станций использовались, чтобы помочь исправить аномальные события данных, но, как это было сделано в предыдущих исследованиях [24], они не были включены в наши меры по локальному изменению климата. Трансекта RMFR расширяет первоначальную трансекту Марра, включая пятую метеостанцию, которая в настоящее время находится в здании Национального института стандартов и технологий (NIST) на западной окраине Боулдера, к югу от кампуса Министерства торговли США в Боулдере, Колорадо.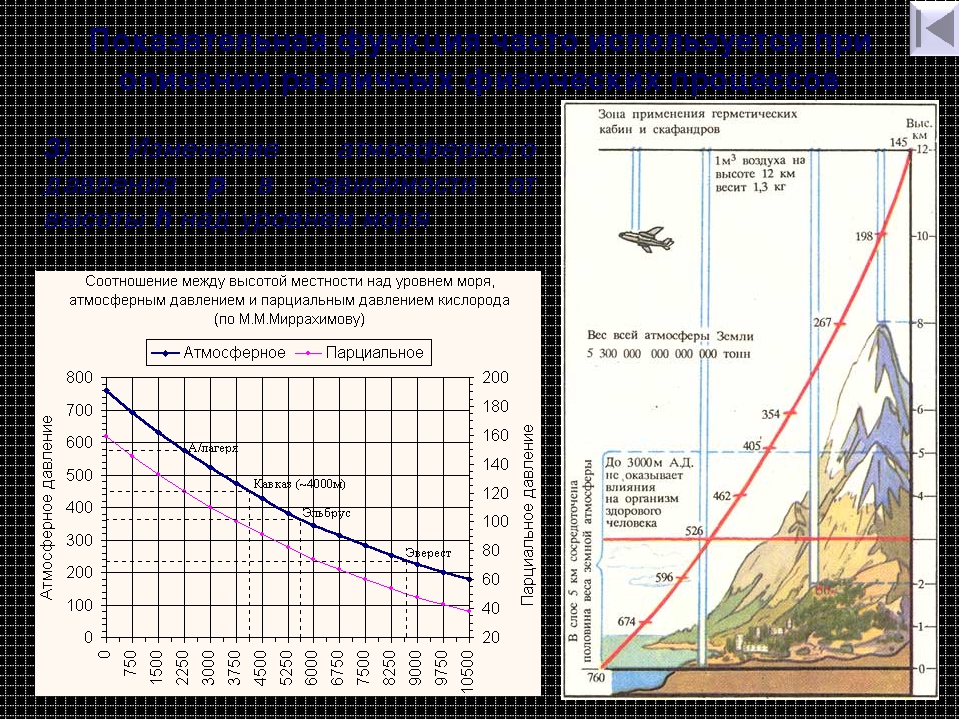 Эта метеостанция обслуживается Национальным управлением океанических и атмосферных исследований (NOAA; 1672 м) и отражает климат, связанный с местным экотоном высокогорных равнин и предгорий. Данные для NOAA (кооперативный идентификатор 050848) были получены из Национального центра климатических данных Министерства торговли США.
Эта метеостанция обслуживается Национальным управлением океанических и атмосферных исследований (NOAA; 1672 м) и отражает климат, связанный с местным экотоном высокогорных равнин и предгорий. Данные для NOAA (кооперативный идентификатор 050848) были получены из Национального центра климатических данных Министерства торговли США.
Ежедневные минимальные и максимальные температуры регистрировались на станциях A1, B1, C1 и D1 с 1953 года. При необходимости эти данные были нормализованы и скорректированы для смены приборов (см. [24]).Кроме того, замена гигротермографов электронными модулями данных в точках A1 и B1 в 1987 году привела к необходимости установить нижние температурные пределы для общих максимальных и минимальных записей (1953–2008 гг.) Для этих двух точек на уровне -17,8 ° C, поскольку датаподы не могли регистрировать температуру ниже этого порога. Суточные минимальные и максимальные температуры для Боулдера, штат Колорадо, непрерывно регистрировались с 1897 года, за исключением периода с 1989 по 1990 год. С 1947 по 1989 год данные о температуре регистрировались пожарной службой Боулдера с помощью приборов, расположенных на территории пожарной части.Начиная с 1990 года, данные наблюдений за погодой в Боулдере собирались в здании NIST и управлялись NOAA. Предыдущий анализ данных разреза RMFR [24] включал анализ наблюдений из Лонгмонт, Колорадо (идентификатор кооператива 055116). Наше исследование не включает анализ данных Longmont из-за бездействия станции с 2004 года. Однако стабильность местоположения станции Longmont по сравнению с ее историческими записями позволяет контролировать изменение местоположения инструмента, связанное с данными Boulder.Используя станцию Лонгмонт в качестве стабильного ориентира, данные о температуре для Боулдера за период 1952–1989 гг. Были скорректированы, чтобы отразить стабильное положение в NIST в записи данных (методы, обсуждаемые ниже).
С 1947 по 1989 год данные о температуре регистрировались пожарной службой Боулдера с помощью приборов, расположенных на территории пожарной части.Начиная с 1990 года, данные наблюдений за погодой в Боулдере собирались в здании NIST и управлялись NOAA. Предыдущий анализ данных разреза RMFR [24] включал анализ наблюдений из Лонгмонт, Колорадо (идентификатор кооператива 055116). Наше исследование не включает анализ данных Longmont из-за бездействия станции с 2004 года. Однако стабильность местоположения станции Longmont по сравнению с ее историческими записями позволяет контролировать изменение местоположения инструмента, связанное с данными Boulder.Используя станцию Лонгмонт в качестве стабильного ориентира, данные о температуре для Боулдера за период 1952–1989 гг. Были скорректированы, чтобы отразить стабильное положение в NIST в записи данных (методы, обсуждаемые ниже).
Как отмечено и подробно описано в других исследованиях, в температурных записях станций разреза RMFR имеется несколько пробелов [24], [32].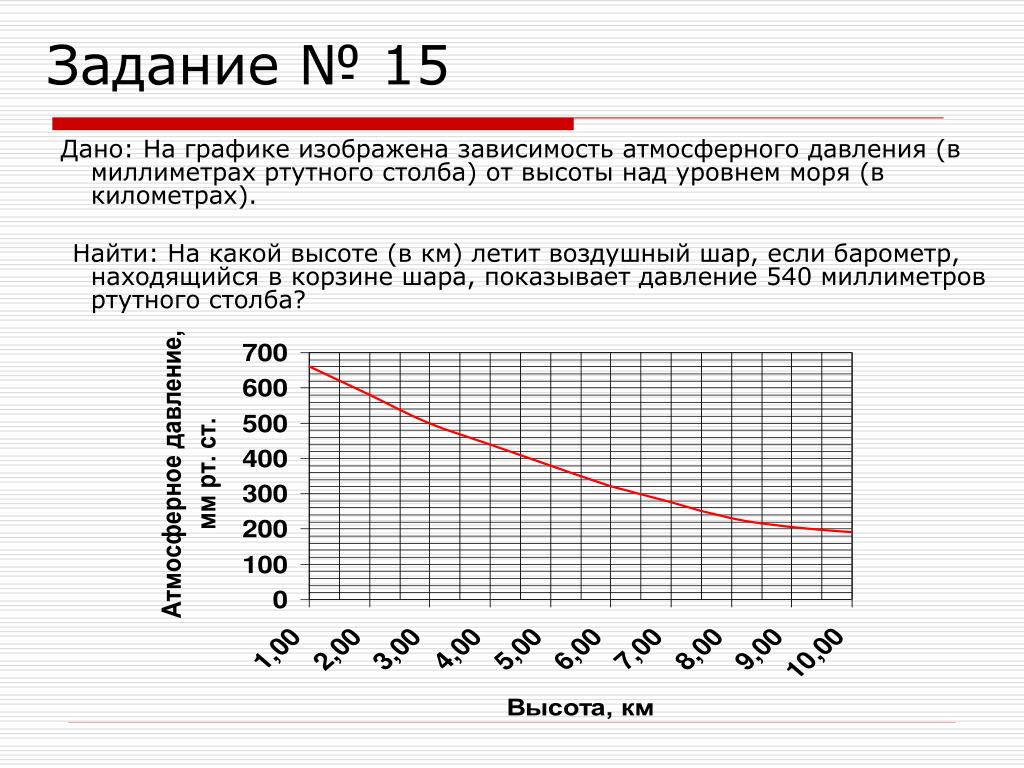 Заполнение этих пробелов, которые варьировались от дней до (в редких случаях) месяцев, было необходимо для определения дат заморозков и расчета сезонных GDD.Помимо заполнения пробелов, мы дополнительно проверили отдельные климатические записи на предмет аномальных значений температуры. Ниже представлен протокол заполнения пробелов и исправления аномальных значений. Поскольку данные о погоде для участков A1 и B1 между 1970 и 1986 годами содержали большие многомесячные пробелы (с адекватными погодными данными только для 59 из 204 месяцев в A1 и только для 88 из 204 месяцев в B1), и потому что нет данные, доступные для NOAA за несколько месяцев в 1989 и 1990 годах, эти годы были исключены из всех анализов соответствующих станций.Большие пробелы за несколько лет в точках A1 и B1 не были заполнены, чтобы избежать чрезмерной зависимости от независимых данных, которые могли бы замаскировать потенциальные различия в климатических тенденциях на каждой высоте. Хотя исключение данных за 1970–1986 гг.
Заполнение этих пробелов, которые варьировались от дней до (в редких случаях) месяцев, было необходимо для определения дат заморозков и расчета сезонных GDD.Помимо заполнения пробелов, мы дополнительно проверили отдельные климатические записи на предмет аномальных значений температуры. Ниже представлен протокол заполнения пробелов и исправления аномальных значений. Поскольку данные о погоде для участков A1 и B1 между 1970 и 1986 годами содержали большие многомесячные пробелы (с адекватными погодными данными только для 59 из 204 месяцев в A1 и только для 88 из 204 месяцев в B1), и потому что нет данные, доступные для NOAA за несколько месяцев в 1989 и 1990 годах, эти годы были исключены из всех анализов соответствующих станций.Большие пробелы за несколько лет в точках A1 и B1 не были заполнены, чтобы избежать чрезмерной зависимости от независимых данных, которые могли бы замаскировать потенциальные различия в климатических тенденциях на каждой высоте. Хотя исключение данных за 1970–1986 гг. Из NOAA, C1 и D1 не повлияло сколько-нибудь заметным образом на интерпретацию их температурных трендов (см. Ниже), эти годы были включены на этих участках, чтобы повысить статистическую мощность и уменьшить вероятность ошибка II типа. Все нескорректированные, исправленные и заполненные метеорологические данные RMFR, использованные в этом исследовании, а также описание методов, используемых для корректировки или заполнения данных, доступны в Приложении S1.
Из NOAA, C1 и D1 не повлияло сколько-нибудь заметным образом на интерпретацию их температурных трендов (см. Ниже), эти годы были включены на этих участках, чтобы повысить статистическую мощность и уменьшить вероятность ошибка II типа. Все нескорректированные, исправленные и заполненные метеорологические данные RMFR, использованные в этом исследовании, а также описание методов, используемых для корректировки или заполнения данных, доступны в Приложении S1.
Как обсуждается ниже и резюмируется в таблицах 1 и 2, в процессе корректировки данных использовались данные о температуре от соседних климатических станций за пределами разреза RMFR. Данные для седловины хребта Нивот (3525 м) были предоставлены проектом NWT LTER и Горной исследовательской станцией Университета Колорадо. Данные для Лонгмонт, Колорадо (идентификатор кооператива 055116), Денвера, Колорадо (идентификатор кооператива 052220) и Алленспарка, Колорадо (идентификатор кооператива 050183), были получены из Национального центра климатических данных Министерства торговли США.
Заполнение пропусков и исправление данных
Пробелы в записи температуры от C1 и D1 были первоначально заполнены менеджером данных NWT LTER с использованием методов линейной регрессии, разработанных Гренландией [32]. Вкратце, 14 дней до и после пробелов в данных были регрессированы на соответствующие значения с соседних метеостанций. Полученное уравнение регрессии затем использовалось для интерполяции недостающих значений температуры для фокальной станции. Подробная методология и иерархия соседних станций, используемых для этого процесса, изложены на веб-сайте СЗТ LTER (http: // culter.colorado.edu/exec/nwtdatas.cgi). Этот метод заполнения использовался только для заполнения данных для C1 и D1, когда значение регрессии r 2 превышало 0,6. Из-за отсутствия данных для опорных станций данные для пяти дат в C1 не могли быть заполнены с использованием этого метода, и вместо этого были заполнены с использованием среднего значения температур для даты до и даты после отсутствующей точки данных (см.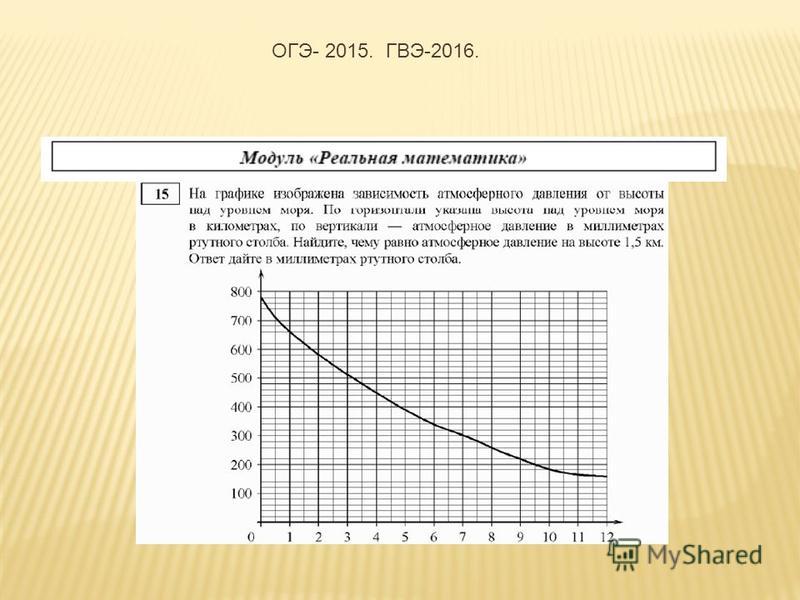 Приложение S1).
Приложение S1).
Был завершен дополнительный уровень заполнения данных в рамках подготовки к анализу в этой рукописи.Это связано с тем, что в записях данных для A1, B1 и NOAA остались пробелы, которые ранее не заполнялись менеджерами данных NWT LTER, а на станциях C1 и D1 осталось несколько пробелов из-за низкой корреляции между температурами этих станций и соседние станции в течение 14 дней до и после определенного перерыва. Чтобы устранить низкую корреляцию станций и облегчить и ускорить процесс заполнения, мы разработали метод заполнения по месяцам. Соотношение температур между любыми двумя соседними участками не является постоянным в течение года, а, скорее, меняется в зависимости от сезона из-за синоптических (таких как направление ветрового потока и термическая инверсия) и орографических условий, а также множества других переменных.Соответственно, использование 14-дневных постов и предыдущих окон, которые растекаются на несколько месяцев, может способствовать снижению значений регрессии r 2 , что снижает предсказательную силу по мере увеличения размера промежутка.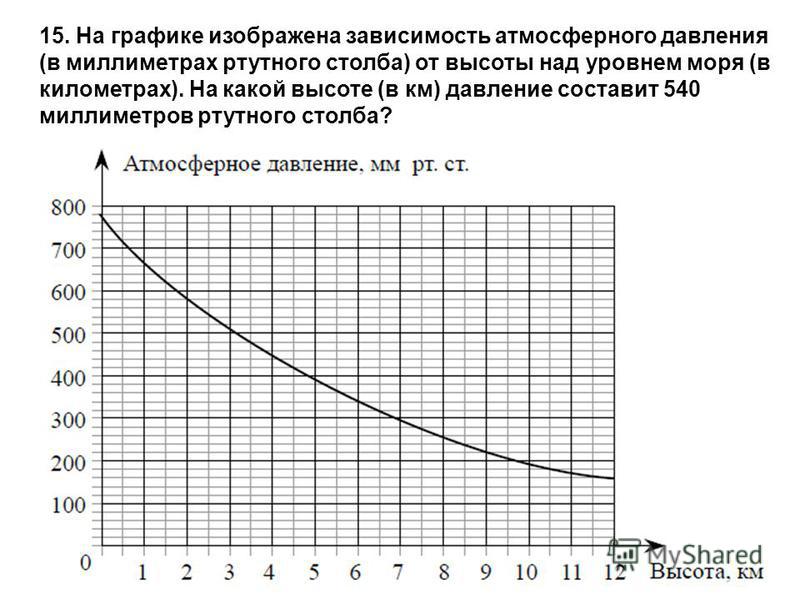 Регрессия, ограниченная одним месяцем, но включающая несколько лет, позволяет избежать этого ограничения, предлагая гораздо больший объем данных для определения статистической взаимосвязи температур между участками в течение интересующего месяца. Кроме того, в то время как окно в ± 14 дней требует отдельного расчета регрессии для каждого пробела, метод регрессии по месяцам дает только 12 формул регрессии (по одной для каждого месяца на каждом участке), которые используются для заполнения пробелов, попадающих в данный месяц).
Регрессия, ограниченная одним месяцем, но включающая несколько лет, позволяет избежать этого ограничения, предлагая гораздо больший объем данных для определения статистической взаимосвязи температур между участками в течение интересующего месяца. Кроме того, в то время как окно в ± 14 дней требует отдельного расчета регрессии для каждого пробела, метод регрессии по месяцам дает только 12 формул регрессии (по одной для каждого месяца на каждом участке), которые используются для заполнения пробелов, попадающих в данный месяц).
Методология регрессии по месяцам заключается в следующем: доступные значения температуры с центральной станции для каждой даты в пределах календарного месяца по всей записи данных были регрессированы на соответствующие значения с соседней метеостанции. Используя полученную формулу регрессии для данного месяца, известные значения температуры с соседней станции использовались для прогнозирования и заполнения отсутствующих данных о температуре для центральной станции. Иерархия соседних станций-предсказателей, используемых для каждой целевой станции, показана в таблице 2.Эта иерархия следует общей схеме от ближайшего к самому дальнему по высоте и расстоянию до фокусной станции и, соответственно, от наивысшей к наименьшей корреляции с температурами между фокусной станцией и станциями-предсказателями для данного месяца. В большинстве случаев самая высокая корреляция была со станциями трансекты RMFR, ближайшими к фокальной станции.
Иерархия соседних станций-предсказателей, используемых для каждой целевой станции, показана в таблице 2.Эта иерархия следует общей схеме от ближайшего к самому дальнему по высоте и расстоянию до фокусной станции и, соответственно, от наивысшей к наименьшей корреляции с температурами между фокусной станцией и станциями-предсказателями для данного месяца. В большинстве случаев самая высокая корреляция была со станциями трансекты RMFR, ближайшими к фокальной станции.
В случаях, когда пропуски превышают один месяц или когда сравнения отдельных сайтов в течение данного месяца давали регрессию r 2 значений меньше 0.60, вместо одного использовались два соседних сайта-предсказателя. Использование двух участков прогнозирования компенсировало различия в соотношении между температурами окружающей среды на двух участках, которые могли быть вызваны изменениями синоптических условий (например, направления ветрового потока) в разные периоды года. Иерархия станций-предикторов, использованная в этих случаях, была такой же, как и иерархия, использованная для сайтов-предикторов (таблица 2). Две результирующие формулы регрессии были использованы для создания двух независимых значений для одной и той же отсутствующей точки данных.Значение, используемое для заполнения отсутствующей точки данных, представляло собой средневзвешенное значение этих двух предсказанных значений, при этом вес каждого был пропорционален их индивидуальной регрессии r 2 значений.
Две результирующие формулы регрессии были использованы для создания двух независимых значений для одной и той же отсутствующей точки данных.Значение, используемое для заполнения отсутствующей точки данных, представляло собой средневзвешенное значение этих двух предсказанных значений, при этом вес каждого был пропорционален их индивидуальной регрессии r 2 значений.
В зависимости от станции, данные, полученные для заполнения пробелов ранее СЗТ LTER и в рамках этого исследования, составили от одного до шести процентов их общих данных (см. Таблицу 2 и Приложение S1). Из 738 минимальных и максимальных значений температуры, которые были заполнены в NOAA, 0,04% этих значений были заполнены с использованием двух сайтов прогнозирования, в то время как два сайта прогнозирования были использованы для заполнения 78% из 1347 значений температуры заполнения в A1 и 81% из 1245. заполненные значения в B1.Все остальные данные на этих сайтах были заполнены с использованием единого сайта-предсказателя.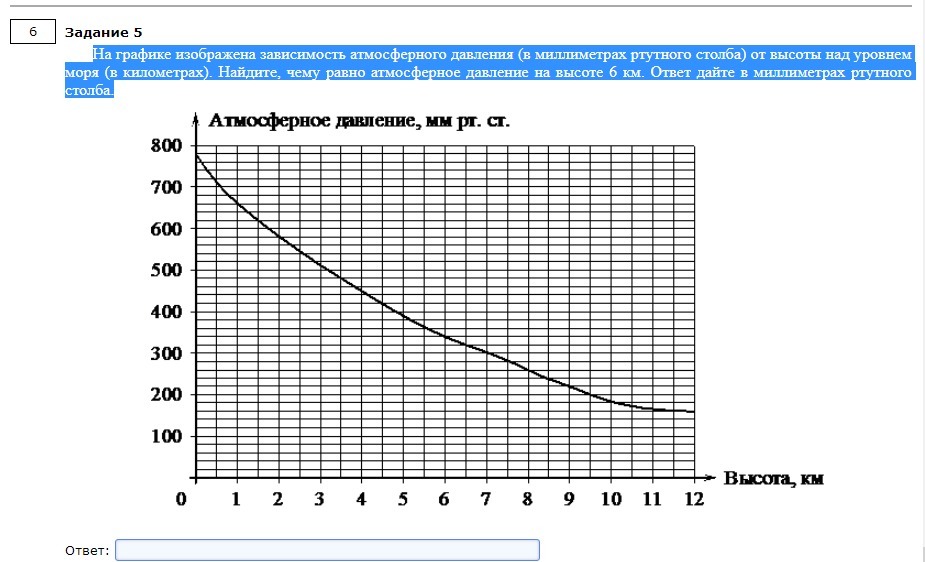 Для всех заполненных значений температуры в C1 и D1, которые составляли 1024 и 2546 значений температуры соответственно, использовался только один сайт прогнозирования.
Для всех заполненных значений температуры в C1 и D1, которые составляли 1024 и 2546 значений температуры соответственно, использовался только один сайт прогнозирования.
Хотя заполнение может повлиять на результаты анализа тенденций или создать проблемы отсутствия независимости, включение данных, созданных с помощью этой модели, было важным для измерения изменений в годовых накопленных GDD и продолжительности вегетационного периода. Поскольку включение этих заполненных данных составило относительно небольшой объем суточных данных о температуре, связанных с каждой метеостанцией, и поскольку эти дополнения были распределены по месяцам и годам (Приложение S1, Таблица 2), это включение не изменило интерпретацию каких-либо величины или значимость тенденций в нашем исследовании при сравнении с тенденциями, полученными с использованием наборов данных с незаполненными пробелами.Например, для D1, участка с наибольшим количеством заполненных данных (6,2% минимальных и максимальных значений температуры, таблица 2), наклон изменения (° C / год) за 56-летний рекорд максимальной температуры составил -0,005 ( оставшиеся промежутки; Тау Кендалла p = 0,745) и 0,007 (промежутки заполнены; p = 0,276), а наклон изменения для min составил -0,016 (оставшиеся промежутки; p = 0,467) и -0,005 (промежутки заполнены; p = 0,7238). В обоих случаях соответствующие минимальные и максимальные уклоны существенно не различались независимо от того, остались ли зазоры или были заполнены (P> 0.10). Поэтому предполагалось, что среднемесячные и годовые средние значения в значительной степени не зависят от материала и используются в качестве независимых точек данных при анализе тенденций температуры.
В обоих случаях соответствующие минимальные и максимальные уклоны существенно не различались независимо от того, остались ли зазоры или были заполнены (P> 0.10). Поэтому предполагалось, что среднемесячные и годовые средние значения в значительной степени не зависят от материала и используются в качестве независимых точек данных при анализе тенденций температуры.
Климатические данные NOAA, A1, B1 и C1 также были проверены на наличие аномальных значений. При контроле высоты данные считались аномальными, если средняя разница температур между центральной станцией и ее тремя опорными станциями была больше 10 ° C или меньше -10 ° C [24]. Эти аномальные значения данных были удалены, а образовавшиеся пробелы были заполнены в соответствии с методологией регрессии по месяцам, описанной выше.В зависимости от участка от нуля до двух процентов общих данных о температуре были признаны аномальными и впоследствии были скорректированы (Таблица 2). Как правило, опорные станции для каждого участка состояли из станций разреза RMFR, расположенных непосредственно над и сразу под координационной станцией, а также одной станции за пределами разреза RMFR, расположенной в Алленспарке, Колорадо (Таблица 1). Станция NOAA сравнивалась с тремя метеорологическими станциями, внешними по отношению к разрезу RMFR: две станции примерно одинаковой высоты (Лонгмонт, Колорадо и Денвер, Колорадо) плюс станция в Алленспарке, Колорадо.Данные с D1 не могли быть проверены на аномальные значения из-за отсутствия соответствующих опорных станций на аналогичных высотах в хребте Роки-Маунтин-Фронт.
Станция NOAA сравнивалась с тремя метеорологическими станциями, внешними по отношению к разрезу RMFR: две станции примерно одинаковой высоты (Лонгмонт, Колорадо и Денвер, Колорадо) плюс станция в Алленспарке, Колорадо.Данные с D1 не могли быть проверены на аномальные значения из-за отсутствия соответствующих опорных станций на аналогичных высотах в хребте Роки-Маунтин-Фронт.
Чтобы определить, повлияло ли изменение местоположения станции NOAA в 1990 году на зарегистрированные температуры, данные с этого места сравнивались с данными стабильной станции в Лонгмонт, штат Колорадо, которая постоянно регистрировала температуры в период с 1960 по 2004 год. Разница в среднемесячной температуре между NOAA и Longmont была рассчитана для периодов 1960–1987 и 1991–2004 годов, и был использован t-тест, чтобы определить, изменились ли эти различия между двумя периодами.Мы обнаружили, что на температуру, зарегистрированную в январе, феврале, марте и апреле, значительно повлияло изменение местоположения (p <0,05).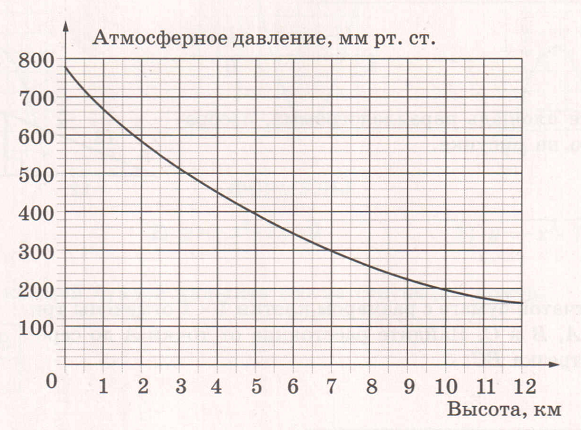 Чтобы исправить это, температура в NOAA с января по апрель для дат до 1987 года была скорректирована для поддержания постоянной разницы температур между Лонгмонтом и Боулдером в оба периода времени. Максимальные температуры NOAA до 1987 г. были скорректированы в сторону понижения на 1,17, 0,91, 0,99 и 0,84 ° C для января, февраля, марта и апреля соответственно.Минимальные температуры были увеличены на 0,64, 0,76, 0,81 и 0,72 ° C для января, февраля, марта и апреля соответственно.
Чтобы исправить это, температура в NOAA с января по апрель для дат до 1987 года была скорректирована для поддержания постоянной разницы температур между Лонгмонтом и Боулдером в оба периода времени. Максимальные температуры NOAA до 1987 г. были скорректированы в сторону понижения на 1,17, 0,91, 0,99 и 0,84 ° C для января, февраля, марта и апреля соответственно.Минимальные температуры были увеличены на 0,64, 0,76, 0,81 и 0,72 ° C для января, февраля, марта и апреля соответственно.
Анализ тенденций за 20 и 56 лет
Для анализа тенденций изменения температуры (т. Е. Наклона изменения во времени) за 20- и 56-летний период средние годовые и месячные средние, максимальные и минимальные температуры были регрессированы по годам для всех участков. Для анализа индексов вегетационного периода время последних весенних заморозков, первых осенних заморозков, продолжительность вегетационного периода и годовые GDD были регрессированы по годам для всех участков.Из-за потенциальных проблем автокорреляции, общих для данных временных рядов окружающей среды, мы использовали непараметрический метод Тау Кендалла для проверки уровней значимости тренда во всех регрессионных анализах. Однако наклоны, измеряющие средние изменения во времени, были определены с использованием моделей линейной регрессии. Все статистические анализы были выполнены с использованием JMP 8.02 [33].
Однако наклоны, измеряющие средние изменения во времени, были определены с использованием моделей линейной регрессии. Все статистические анализы были выполнены с использованием JMP 8.02 [33].
Исключение пропущенного периода 1970–1986 гг. В точках A1 и B1 в анализе 56-летних трендов температуры создало возможность несоизмеримости трендов на этих двух станциях и на остальных станциях разреза RMFR.Чтобы рассмотреть эту возможность, мы сравнили 56-летние ежегодные максимальные и минимальные наклоны из полных записей данных NOAA, C1 и D1 с максимальными и минимальными наклонами, которые возникли, когда годы с 1970 по 1986 были удалены из записи данных. Наклоны (° C / год) и значения p-значения Кендалла, связанные с полным 56-летним климатическим отчетом и наборами данных с удаленным климатом 1970–1986 годов, составляли 0,009 (p = 0,118) против 0,007 (p = 0,160) для NOAA. max, -0,025 (p <0,0001) против -0,028 (p <0,0001) для NOAA min, и 0.045 (p <0,0001) против 0,042 (p <0,0001) для C1 max, -0,027 (p = 0,572) против -0,004 (p = 0,458) для C1 min, и, наконец, 0,007 (p = 0,276) против 0,007 (p = 0,414) для D1 max и -0,005 (p = 0,724) против -0,005 (p = 0,773) для D1 min. Во всех случаях максимальные и минимальные наклоны, рассчитанные за 56-летний период для каждого из этих участков, существенно не различались, были ли удалены или сохранены данные 1970–1986 годов (p> 0,10). В свою очередь, относительная значимость каждого тренда также не различалась. То, что это было верно на высотах выше (C1 и D1) и ниже (NOAA), чем станции A1 и B1, предполагает, что период с 1970 по 1986 год может не оказывать заметного влияния на расчет 56-летних трендов по разрезу.Таким образом, мы сочли, что отсутствие данных о температуре на А1 и В1 в период с 1970 по 1986 год не препятствовало сравнению 56-летних трендов на А1 и В1 с трендами трех других станций. Наконец, мы решили не восстанавливать такой обширный временной рекорд за все эти годы, чтобы минимизировать степень независимости между станциями.
Во всех случаях максимальные и минимальные наклоны, рассчитанные за 56-летний период для каждого из этих участков, существенно не различались, были ли удалены или сохранены данные 1970–1986 годов (p> 0,10). В свою очередь, относительная значимость каждого тренда также не различалась. То, что это было верно на высотах выше (C1 и D1) и ниже (NOAA), чем станции A1 и B1, предполагает, что период с 1970 по 1986 год может не оказывать заметного влияния на расчет 56-летних трендов по разрезу.Таким образом, мы сочли, что отсутствие данных о температуре на А1 и В1 в период с 1970 по 1986 год не препятствовало сравнению 56-летних трендов на А1 и В1 с трендами трех других станций. Наконец, мы решили не восстанавливать такой обширный временной рекорд за все эти годы, чтобы минимизировать степень независимости между станциями.
Интерполяция климатических данных по разрезу RMFR
Чтобы проверить способность PRISM интерполировать климатические данные вдоль разреза RMRF за последние 56 лет, мы сравнили годовые максимальные, минимальные и средние значения температуры наших данных с годовыми значениями температуры, интерполированными PRISM для 2.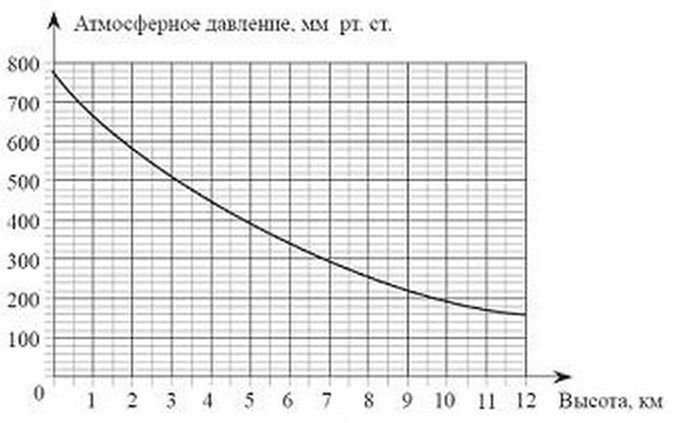 5-минутная (~ 4 км) ячейка сетки, связанная с географическими координатами каждой из метеостанций RMFR (http://www.prism.oregonstate.edu/; данные по состоянию на сентябрь 2011 г.). Интерполированные средние годовые значения были определены путем усреднения соответствующих годовых максимальных и минимальных температур PRISM. Модель линейной регрессии использовалась для определения степени корреляции максимальных, минимальных и средних значений PRISM и RMFR за 56 лет на каждом участке. Интерполированные годовые максимальные, минимальные и средние значения также подвергались регрессии с течением времени для определения расчетных темпов (наклонов) изменения климата за последние 56 лет на каждой метеостанции.Затем наклоны PRISM сравнивались с соответствующими наклонами, связанными с каждой из метеостанций RMFR. Различия в скорости изменения климата, оцененные с использованием интерполированных наборов данных PRISM и фактических климатических данных, сравнивались путем определения того, совпадают ли 95% доверительные интервалы вокруг склонов, полученные с помощью моделей линейной регрессии.
5-минутная (~ 4 км) ячейка сетки, связанная с географическими координатами каждой из метеостанций RMFR (http://www.prism.oregonstate.edu/; данные по состоянию на сентябрь 2011 г.). Интерполированные средние годовые значения были определены путем усреднения соответствующих годовых максимальных и минимальных температур PRISM. Модель линейной регрессии использовалась для определения степени корреляции максимальных, минимальных и средних значений PRISM и RMFR за 56 лет на каждом участке. Интерполированные годовые максимальные, минимальные и средние значения также подвергались регрессии с течением времени для определения расчетных темпов (наклонов) изменения климата за последние 56 лет на каждой метеостанции.Затем наклоны PRISM сравнивались с соответствующими наклонами, связанными с каждой из метеостанций RMFR. Различия в скорости изменения климата, оцененные с использованием интерполированных наборов данных PRISM и фактических климатических данных, сравнивались путем определения того, совпадают ли 95% доверительные интервалы вокруг склонов, полученные с помощью моделей линейной регрессии.
Расчет индексов вегетационного периода
Продолжительность вегетационного периода обычно определяется как период между последними весенними заморозками и первыми осенними заморозками [34].В нашем исследовании мы рассчитали последние весенние заморозки и первые осенние заморозки, используя среднее значение дневных минимальных температур за семь дней. Последние заморозки, ведущие к весне, рассчитывались как последняя дата, когда семидневное скользящее среднее дневных минимальных температур переходило в положительные градусы Цельсия, тогда как первые осенние заморозки рассчитывались как первая дата, когда семидневное скользящее среднее дневных минимальные температуры перешли на отрицательные градусы Цельсия. Семидневное окно было использовано для того, чтобы обеспечить устойчивость к ложным значениям и четко разграничить переходы в периоды отрицательных температур и выхода из них.Годовые градусо-дни роста (GDD) были рассчитаны как Σ [(T max + T min ) / 2] — T base , где T max и T min — дневные максимальные и минимальные температуры, соответственно, и T base составляет 10 ° C. Любая минимальная или максимальная температура ниже T base была установлена на 10 ° C. Эта базовая температура (10 ° C) является температурой, наиболее часто используемой для расчетов GDD, и использовалась в нашем исследовании для прямого сравнения с другими исследованиями [35], [36].Хотя существуют разные способы оценки GDD [37] — [39], используемый нами метод обычно используется в литературе по изменению климата [40] — [42].
Любая минимальная или максимальная температура ниже T base была установлена на 10 ° C. Эта базовая температура (10 ° C) является температурой, наиболее часто используемой для расчетов GDD, и использовалась в нашем исследовании для прямого сравнения с другими исследованиями [35], [36].Хотя существуют разные способы оценки GDD [37] — [39], используемый нами метод обычно используется в литературе по изменению климата [40] — [42].
Результаты
Среднегодовая, максимальная и минимальная температура
Анализ 56-летних тенденций среднегодовой температуры показывает, что наибольшее потепление испытали промежуточные высоты (участки B1 и C1, 2591–3048 м). То есть, с точки зрения средней температуры по градиенту, значительное потепление было обнаружено на участках B1 (0.17 ° C / десятилетие) и C1 (0,20 ° C / десятилетие), в то время как более низкие возвышенности (NOAA и A1) и альпийский (D1) не показали значительных тенденций к потеплению (Рисунок 2A). Однако, когда учитывается только недавний 20-летний климатический рекорд (1989–2008 гг.), Влияние возвышения менее очевидно. Скорость среднего потепления за последние 20 лет была почти одинаковой на 0,4 ° C за десятилетие по всей трансекте (рис. 2A), хотя тенденции были значительными только на B1 (0,39 ° C / десятилетие). Незначительные тренды потепления на NOAA, A1, C1 и D1 были равны 0.43 ° C, 0,34 ° C, 0,35 ° C и 0,41 ° C / декаду соответственно.
Однако, когда учитывается только недавний 20-летний климатический рекорд (1989–2008 гг.), Влияние возвышения менее очевидно. Скорость среднего потепления за последние 20 лет была почти одинаковой на 0,4 ° C за десятилетие по всей трансекте (рис. 2A), хотя тенденции были значительными только на B1 (0,39 ° C / десятилетие). Незначительные тренды потепления на NOAA, A1, C1 и D1 были равны 0.43 ° C, 0,34 ° C, 0,35 ° C и 0,41 ° C / декаду соответственно.
Рис. 2. Годовые тренды температуры, полученные с помощью линейной регрессии для периодов 1953–2008 (56 лет) и 1989–2008 (20 лет) по разрезу RMFR.
Тенденции показаны как изменения среднегодовой (A) средней, (B) максимальной и (C) минимальной температуры (° C) за год. Уровень значимости регрессий обозначен * p <0,05, ** p <0,01.
https://doi.org/10.1371/journal.pone.0044370.g002
56-летние тенденции среднегодовых максимумов показывают тенденцию к потеплению на трех промежуточных отметках (A1, B1 и C1), в то время как обе самые низкие ( NOAA) и самые высокие (D1) возвышения не показывают значительного потепления (Рисунок 2B).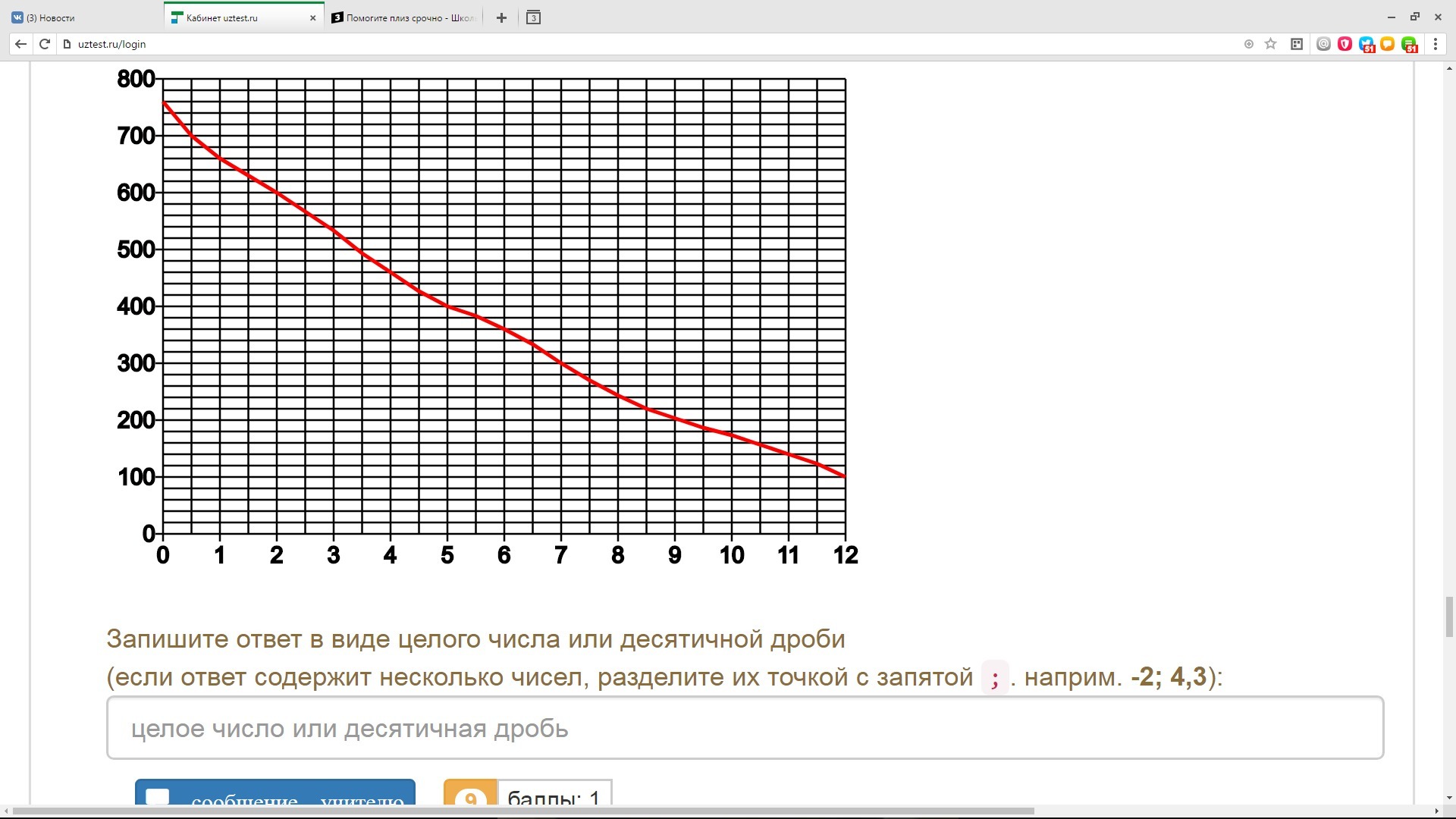 Величина 56-летних тенденций среднегодовых максимумов согласуется с тенденциями среднегодовых значений за этот период, при этом участки B1 и C1 демонстрируют наибольшее и наиболее значительное потепление. Среднегодовые максимальные температуры за 56-летний рекорд увеличились в точке A1 на 0,15 ° C / десятилетие, в то время как средние максимальные температуры в B1 и C1 увеличились на 0,42 ° C и 0,44 ° C / десятилетие, соответственно. Незначительные тенденции потепления на NOAA и D1 были связаны с повышением на 0,09 ° C и 0,07 ° C / десятилетие, соответственно.
Величина 56-летних тенденций среднегодовых максимумов согласуется с тенденциями среднегодовых значений за этот период, при этом участки B1 и C1 демонстрируют наибольшее и наиболее значительное потепление. Среднегодовые максимальные температуры за 56-летний рекорд увеличились в точке A1 на 0,15 ° C / десятилетие, в то время как средние максимальные температуры в B1 и C1 увеличились на 0,42 ° C и 0,44 ° C / десятилетие, соответственно. Незначительные тенденции потепления на NOAA и D1 были связаны с повышением на 0,09 ° C и 0,07 ° C / десятилетие, соответственно.
За последние 20 лет значительное максимальное повышение температуры было ограничено более низкими высотами (NOAA, A1 и B1), в то время как положительные наклоны в C1 и D1 были незначительными (рис. 2B). Среднегодовые максимумы за период 1989–2008 гг. Увеличивались в NOAA и A1 со скоростью 0,60 ° C / десятилетие, а в B1 — примерно на 0,85 ° C / десятилетие. Незначительные тенденции потепления в точках C1 и D1 были связаны с повышением на 0,21 ° C и 0,39 ° C за десятилетие, соответственно.
56-летние тенденции среднегодовых минимумов показывают значительное похолодание примерно до 0.25 ° C за десятилетие в NOAA, в то время как на более высоких высотах тенденции не проявляются (рис. 2C). Напротив, 20-летние тенденции среднегодовых минимумов показывают значительное потепление на 0,50 ° C и 0,43 ° C / десятилетие в точках C1 и D1, соответственно, в то время как на более низких высотах не обнаруживается никаких значительных тенденций (рис. 2C).
Таким образом, потепление за 56 и 20-летние рекорды для всех высот ниже субальпийского (C1) преимущественно является функцией увеличения среднегодовых максимумов. 56-летний рекорд показывает, что субальпийский (C1) потеплел из-за повышения максимальных температур, 20-летний рекорд показывает, что недавнее потепление в альпийском (D1) и субальпийском (C1) произошло за счет значительного увеличения среднегодовые минимальные температуры и заметное, но незначительное увеличение годовых максимумов.Однако, в отличие от увеличения максимальных температур в C1 за 56-летний рекорд, такой тенденции к потеплению в D1 за этот период не наблюдается.
Максимальные и минимальные температуры за месяц
За последние 56 лет наблюдалась тенденция к увеличению среднемесячных максимумов в марте на всех высотах ниже альпийского (D1), а также в июле и августе на участках B1 и выше (Рисунок 3A). В целом, тенденции к потеплению наиболее заметны в точках B1 и C1. Кроме того, B1 и C1 демонстрируют значительное увеличение максимумов в течение большей части года с февраля по сентябрь.На D1 наблюдаются осенние и ранние зимние похолодания, хотя только в декабре наблюдался значительный отрицательный тренд месячных максимальных температур (рис. 3A). Тенденции среднемесячных минимальных температур в основном незначительны за 56-летний рекорд, за исключением наличия значительного тренда похолодания с мая по октябрь в NOAA, значительного потепления в D1 в течение июля и похолодания в декабре в B1 и D1 (Рисунок 3B. ).
Рис. 3. Месячные тренды температуры, полученные путем линейной регрессии за пятидесятишестилетний период (1953–2008 гг. ) На разрезе RMFR.
) На разрезе RMFR.
Тенденции показаны как изменения среднемесячной (A) максимальной и (B) минимальной температуры (° C) за год. Уровень значимости регрессии обозначен * p <0,05.
https://doi.org/10.1371/journal.pone.0044370.g003
За последние 20 лет величина и направление месячных максимальных и минимальных температурных трендов на всем разрезе RMFR очень согласованы. Самые сильные сигналы потепления возникают в июле и ноябре как для максимальных, так и для минимальных температур (рис. 4AB), хотя тенденции в ноябре обычно незначительны.В среднем, довольно однородные 20-летние тенденции потепления в июле максимальных и минимальных температур составляют примерно 2,0 ° C и 1,5 ° C за десятилетие, соответственно, в то время как тенденции максимумов и минимумов ноября составляют примерно 1,5 ° C и 1,0 ° C за одно десятилетие. десятилетие соответственно. Тенденции в остальное время года менее выражены и, за редким исключением, незначительны (Рисунок 4).
Рис.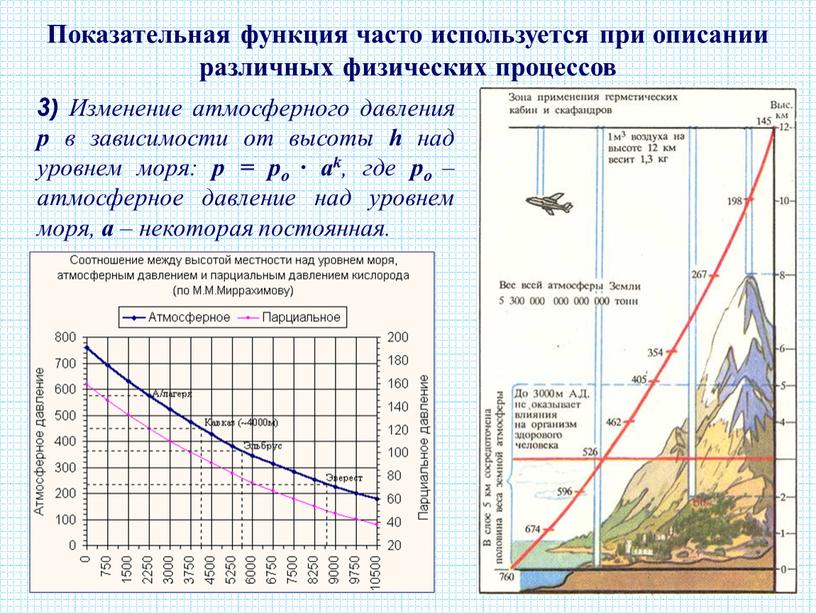 4. Месячные тренды температуры, полученные путем линейной регрессии за двадцатилетний период (1989–2008 гг.) На разрезе RMFR.
4. Месячные тренды температуры, полученные путем линейной регрессии за двадцатилетний период (1989–2008 гг.) На разрезе RMFR.
Тенденции показаны как изменения среднемесячной (A) максимальной и (B) минимальной температуры (° C) за год. Уровень значимости регрессии обозначен * p <0,05.
https://doi.org/10.1371/journal.pone.0044370.g004
Таким образом, наиболее значительные ежемесячные тенденции потепления за 56-летний рекорд наблюдались ниже альпийского (D1) весной (март-апрель) до увеличивается при максимальных температурах. Дальнейшее увеличение максимумов наблюдалось в течение большей части года на станциях B1 и C1.За последние 20 лет было обнаружено существенное повышение максимальных и минимальных температур в июле и, что менее важно, в ноябре, примерно на 1-2 ° C за десятилетие на разрезе RMFR. Тем не менее, скорость потепления, обнаруженная за 56 и 20 лет, различалась не только по месяцам, температурам (максимальным, средним) и участкам, временами они также различались по обнаруженному масштабу изменений. Например, за последние 56 лет скорость максимального потепления в июле на B1 и C1, соответственно, была равна 0.30 и 0,60 ° C за десятилетие, тогда как за последние 20 лет скорость максимального потепления в июле на B1 и C1 увеличилась на 1,9 и 1,7 ° C за десятилетие, соответственно (рис. 3 и 4).
Например, за последние 56 лет скорость максимального потепления в июле на B1 и C1, соответственно, была равна 0.30 и 0,60 ° C за десятилетие, тогда как за последние 20 лет скорость максимального потепления в июле на B1 и C1 увеличилась на 1,9 и 1,7 ° C за десятилетие, соответственно (рис. 3 и 4).
Интерполяция климатических данных по разрезу RMFR
Сравнение интерполированных годовых максимальных, минимальных и средних значений PRISM с 56-летним отчетом RMFR показало переменную и часто поразительно низкую корреляцию между наборами данных (Таблица 3). В NOAA и A1 мы обнаружили относительно сильные положительные связи между интерполированными годовыми максимальными значениями и значениями, непосредственно записанными на метеостанциях (r 2 > 0.75). Хотя корреляции также были значительными на других участках, отношения были намного слабее (r 2 <0,30). Данные PRISM слабо коррелировали с минимальными годовыми значениями на всех участках (r 2 <0,20), а линейные зависимости не были значимыми в B1 и D1. Среднемесячные значения температуры, полученные при усреднении интерполированных максимальных и минимальных температур PRISM, имели значительную положительную корреляцию со средними значениями температуры RMFR на каждом участке, причем более сильная взаимосвязь наблюдалась в NOAA, A1 и B1 (диапазон r 2 = 0.48–0,57) и более слабые корреляции в точках C1 и D1 (r 2 <0,15) (таблица 3).
Среднемесячные значения температуры, полученные при усреднении интерполированных максимальных и минимальных температур PRISM, имели значительную положительную корреляцию со средними значениями температуры RMFR на каждом участке, причем более сильная взаимосвязь наблюдалась в NOAA, A1 и B1 (диапазон r 2 = 0.48–0,57) и более слабые корреляции в точках C1 и D1 (r 2 <0,15) (таблица 3).
Относительно низкая корреляция между интерполированными 56-летними данными о климате вдоль разреза RMFR и фактическими данными метеостанции, особенно в высокогорных районах, привела к различиям в степени, а иногда и в направлении воспринимаемого изменения климата на протяжении тот же период времени, что и данные метеостанций (Таблица 4). Например, максимальные температуры C1, основанные на данных станции, показывают сильное увеличение годовых температур по сравнению с 56-летним рекордом, в то время как данные PRISM предсказывают явное снижение температуры в тот же период времени. Для пятнадцати измерений уклонов (по три измерения температуры на пяти участках) восемь из них показывают тенденцию PRISM и данных станций в разных направлениях.
Для пятнадцати измерений уклонов (по три измерения температуры на пяти участках) восемь из них показывают тенденцию PRISM и данных станций в разных направлениях.
Продолжительность вегетационного периода и накопление степеней роста
Анализ 56-летнего рекорда показывает значительное сокращение вегетационного периода в субальпийском (C1) примерно на четыре дня в десятилетие (Таблица 5), и эта тенденция сопровождается значительным увеличением первых осенних заморозков. На других высотах наблюдается незначительная, но устойчивая тенденция к сокращению вегетационного периода и продвижению первых осенних заморозков на всей трансекте.Анализ 20-летнего рекорда не выявляет ни тенденций, ни устойчивых тенденций в отношении продолжительности вегетационного периода, первых осенних заморозков или последних весенних заморозков (Таблица 6).
Анализ 56-летнего отчета выявил значительное увеличение GDD на участках с B1 по D1 (таблица 5). Это увеличение составило 35, 33 и 15 GDD за десятилетие для B1, C1 и D1 соответственно. За 20-летний период наибольшее и наиболее значительное увеличение GDD произошло на более низких высотах: NOAA, A1 и B1 вызвали увеличение GDD на 114, 110 и 88 за десятилетие, соответственно (Таблица 6).Незначительные тенденции в C1 и D1 за этот период показали увеличение примерно на 45 GDD за десятилетие на обоих участках.
За 20-летний период наибольшее и наиболее значительное увеличение GDD произошло на более низких высотах: NOAA, A1 и B1 вызвали увеличение GDD на 114, 110 и 88 за десятилетие, соответственно (Таблица 6).Незначительные тенденции в C1 и D1 за этот период показали увеличение примерно на 45 GDD за десятилетие на обоих участках.
Обсуждение
Результаты этих анализов показывают несколько общих закономерностей: 1) Все пять исследовательских центров продемонстрировали значительное увеличение средней или максимальной температуры (или обоих), хотя не все сайты показали значительное увеличение как за 20-летний, так и за 56-летний периоды. годовые записи; 2) Минимальные температуры обычно показывают менее драматические изменения, но субальпийские и альпийские минимумы явно потеплели за последние 20 лет, в то время как минимумы в NOAA значительно снизились за 56-летний рекорд; 3) Анализ месячных графиков за 56 и 20 лет показывает, что наибольшее потепление вдоль разреза RMFR произошло весной и летом; 4) Продолжительность и сроки вегетационного периода мало изменились, в то время как годовые GDD увеличились на всех высотах, наиболее резко ниже субальпийских за последние 20 лет; 5) Тенденции, основанные на данных станций и данных PRISM, часто показывают только слабую корреляцию и могут отличаться по направлению изменения. Ниже мы дополнительно исследуем эти общие закономерности и даем сравнение с другими региональными и внутриконтинентальными исследованиями.
Ниже мы дополнительно исследуем эти общие закономерности и даем сравнение с другими региональными и внутриконтинентальными исследованиями.
Среднегодовые тенденции изменения температуры в период с 1953 по 2008 год показывают, что значительное потепление вдоль разреза RMFR ограничивается верхними горными (B1, 2591 м) и субальпийскими (C1, 3048 м) участками, а средние температуры в альпийской тундре (D1 , 3749 м) остались без изменений. Аналогичная картина потепления на средних высотах, в сочетании с отсутствием потепления в альпийских горах, ранее была зафиксирована в Хребте Скалистых гор в исследовании периода 1953–1997 годов [24].Тем не менее, это предыдущее исследование зафиксировало абсолютное похолодание в альпийских горах, которое не было восстановлено здесь после включения дополнительных 11-летних климатических данных. Утрата сигнала об охлаждении в альпийских горах с добавлением данных за период с 1998 по 2008 гг. Предполагает, что в последние годы в альпийских горах наблюдается потепление. Действительно, анализ среднегодовых температур за последние 20 лет указывает на значительную тенденцию к потеплению в альпийских горах, которая не очевидна при анализе 56-летних тенденций (Рисунок 3).
Действительно, анализ среднегодовых температур за последние 20 лет указывает на значительную тенденцию к потеплению в альпийских горах, которая не очевидна при анализе 56-летних тенденций (Рисунок 3).
В отличие от тенденций, зависящих от высоты над уровнем моря, выявленных за последние 56 лет, тенденции среднегодовых температур за последние 20 лет (1989–2008 гг.) Демонстрируют почти однородное (хотя в целом незначительное) потепление примерно на 0,4 ° C. за десятилетие на всех высотах трансекты RMFR, предполагая, что потепление за последние 20 лет не было смещено в сторону какой-либо конкретной высоты в Переднем хребте, и что современное и будущее потепление может быть в меньшей степени зависеть от высоты, чем предполагает 56-летний рекорд .
Когда тенденции в средних годовых максимумах и минимумах исследуются независимо друг от друга, возникают более сложные закономерности. Четкое разделение тренда максимальной и минимальной температуры было обнаружено как за 20, так и за 56 лет анализа. В 56-летнем масштабе значительные сигналы потепления присутствуют в среднегодовых максимумах, но не в среднегодовых минимумах. Эти данные предполагают, что трансекта RMFR может не отражать глобальные [43] — [45] или даже региональные [46] тенденции, которые связывают обнаруженные закономерности потепления с повышением минимальных температур, а не (или более чем) с повышением максимальных температур.
В 56-летнем масштабе значительные сигналы потепления присутствуют в среднегодовых максимумах, но не в среднегодовых минимумах. Эти данные предполагают, что трансекта RMFR может не отражать глобальные [43] — [45] или даже региональные [46] тенденции, которые связывают обнаруженные закономерности потепления с повышением минимальных температур, а не (или более чем) с повышением максимальных температур.
Модели потепления вдоль разреза RMFR не следуют общей тенденции Северного полушария к повышению зимних температур за последнюю половину двадцатого века [47], хотя повышение весенних температур ранее было зарегистрировано в западной части Северной Америки [48]. Тем не менее, многочисленные исследования отметили снижение летних температур в Северо-Восточном Колорадо [23], [49], а точнее в июле [49]. В то время как температуры на нашей самой низкой высоте (NOAA) в целом соответствуют этой региональной тенденции похолодания, более высокие высоты демонстрируют значительное летнее потепление, особенно в июле. Этот вывод предполагает, что местные факторы воздействия на климат вдоль разреза Рокки Маунтин Хребет могут преобладать над глобальными или даже региональными климатическими тенденциями.
Этот вывод предполагает, что местные факторы воздействия на климат вдоль разреза Рокки Маунтин Хребет могут преобладать над глобальными или даже региональными климатическими тенденциями.
Значительное снижение среднегодовой минимальной температуры было обнаружено на участке NOAA (1672 м) по сравнению с 56-летним рекордом. Присутствие регионального сигнала похолодания вдоль Переднего хребта было ранее задокументировано и в значительной степени связано с изменениями в региональных и местных практиках землепользования за последнее столетие, наиболее значительные из которых произошли за последние 50 лет [23], [ 50].В период с мая по октябрь в NOAA были обнаружены значительные тенденции к похолоданию, что согласуется с предположениями о том, что расширение орошаемого земледелия способствует региональным тенденциям похолодания летом и в начале осени [51]. Из-за атмосферной циркуляции тенденции к похолоданию, связанные с орошаемым земледелием, часто становятся очевидными в соседних регионах [23], хотя такой сигнал охлаждения не был очевиден ни на одной из метеостанций над NOAA. В свою очередь, 50-летнее похолодание температуры в NOAA в летние и осенние месяцы исчезает, если рассматривать только 20-летний рекорд.Потеря минимальной охлаждающей температуры в эти месяцы свидетельствует о том, что другие факторы, такие как усиление урбанизации и / или общее повышение низких температур земли (как предполагают более высокие летние и осенние максимальные 20-летние температуры), могут уменьшать охлаждающее влияние орошения. .
В свою очередь, 50-летнее похолодание температуры в NOAA в летние и осенние месяцы исчезает, если рассматривать только 20-летний рекорд.Потеря минимальной охлаждающей температуры в эти месяцы свидетельствует о том, что другие факторы, такие как усиление урбанизации и / или общее повышение низких температур земли (как предполагают более высокие летние и осенние максимальные 20-летние температуры), могут уменьшать охлаждающее влияние орошения. .
Наконец, роль, которую накопление снега и время таяния снега сыграли в отношении изменений сезонных температур в течение последних 20 лет, неясна, потому что в Скалистых горах Колорадо было зарегистрировано уменьшение количества осадков с октября по апрель (когда снегопад накапливается) и повышение соответствующих месячных температур [52], а также потому, что относительные изменения этих переменных, по-видимому, зависят от высоты и широты [5], [52].В свою очередь, в течение более крупных 50-летних изменений во временном масштабе снег-водный эквивалент (мера доступной воды, удерживаемой в виде снега) в начале сезона снизился с 1950 по 1997 год, и это снижение было связано с потеплением температур и более ранним таянием снега.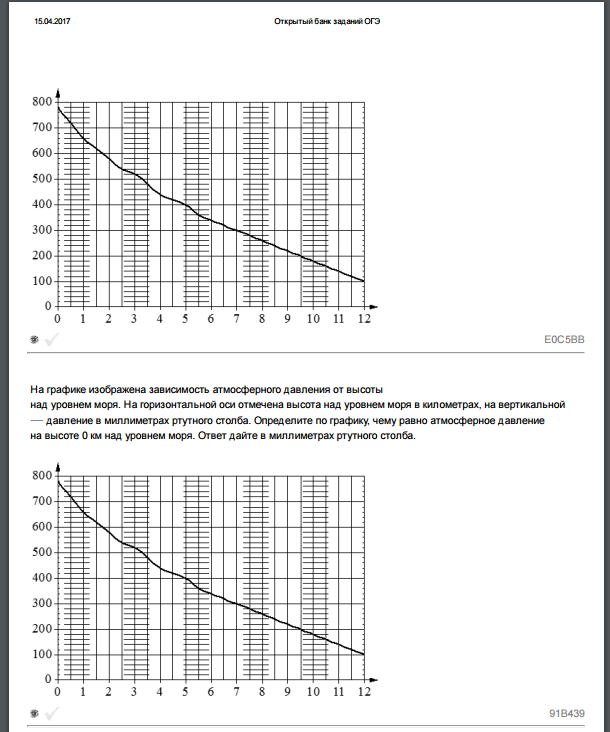 а не к изменению количества осадков [5], [53].
а не к изменению количества осадков [5], [53].
В будущих исследованиях следует изучить взаимосвязь между записями о выпадении снега и таянием снега и моделями потепления в NOAA, C1 и D1 (местах, где доступны такие записи), чтобы определить, как связаны температуры и осадки в начале и даже в конце сезона и как изменения синоптических условия могут влиять на эти модели.
Интерполяция климатических данных по разрезу RMFR
Наборы пространственных климатических данных пользуются большим спросом у исследователей и политиков, заинтересованных в увязке данных географической информационной системы с различными моделями и инструментами принятия решений [27], [54]. Целью нашего сравнения 56-летних климатических данных разреза RMFR и данных PRISM за тот же период было не проведение экспертной оценки PRISM, а определение ценности наборов долгосрочных данных в свете одного из самые современные, высококачественные и часто используемые модели интерполяции.В целом, сравнения интерполированных и измеренных метеорологических данных RMFR показали переменную и часто низкую корреляцию между наборами данных.
Кроме того, оценочные темпы изменения климата вдоль разреза RMFR за последние 56 лет часто различались между двумя наборами данных по измеренным скоростям изменения, направлению изменения и тому, была ли скорость изменения значительной (Таблица 4). Здесь важен вывод о том, что от A1 до D1, PRISM (в отличие от данных по разрезу RMFR) предполагает, что за последние 56 лет максимальные и средние температуры все больше и больше снижаются с высотой.Эта закономерность, без сомнения, может повлиять на представление о том, что горные системы могут быть более защищены от изменения климата, чем низменные районы [5], [52], хотя на самом деле долгосрочные данные для этого района предполагают, что средние высоты нагреваются сильнее, чем самые низкие и самые высокие отметки.
Несмотря на большие статистические и вычислительные достижения, интерполяция климатических данных с высоким разрешением в горных системах может быть затруднена [27]. Эти трудности могут быть результатом многих факторов, влияющих на климат в меньших масштабах (сложная топология, температурные инверсии, тени дождя и т. Д.) или может быть результатом отсутствия доступных метеостанций как в пространстве, так и во времени [28]. Приведенные здесь сравнения показывают большую ценность тщательно развернутых долгосрочных метеорологических станций, таких как предоставленные на разрезе RMFR, для понимания закономерностей изменения климата.
Д.) или может быть результатом отсутствия доступных метеостанций как в пространстве, так и во времени [28]. Приведенные здесь сравнения показывают большую ценность тщательно развернутых долгосрочных метеорологических станций, таких как предоставленные на разрезе RMFR, для понимания закономерностей изменения климата.
Продолжительность вегетационного периода и накопление степеней роста
Наше исследование не продемонстрировало последовательного изменения продолжительности вегетационного периода в хребте Рокки Маунтин Фронт. Этот результат контрастирует с большинством исследований, в том числе сосредоточенных на Западной Северной Америке, которые последовательно сообщают об увеличении продолжительности вегетационного периода во второй половине 90–149-х годов века [34], что объясняется более ранним наступлением весны. [34], [55] — [60].Однако расхождения в форме повышения температуры и отсутствия изменений [59] или сокращения [46] вегетационного периода были ранее зарегистрированы для региона Скалистых гор. Возможное объяснение несоответствия в нашем исследовании заключается в том, что границы вегетационного периода определяются минимальными температурами, которые оставались относительно неизменными в Переднем хребте за последние 56 лет и контрастируют с максимальными температурами потепления.
Возможное объяснение несоответствия в нашем исследовании заключается в том, что границы вегетационного периода определяются минимальными температурами, которые оставались относительно неизменными в Переднем хребте за последние 56 лет и контрастируют с максимальными температурами потепления.
За последние 56 лет произошло значительное увеличение накопления GDD в верхнем горном лесу (B1) и над ним.Увеличение GDD на этих высотах за последние 56 лет отражает повышение весенних и летних максимальных температур. Хотя отсутствие значительных тенденций в GDD за 56-летний рекорд на высотах ниже верхнего горного леса (то есть в NOAA и A1) в целом согласуется с тенденциями, обнаруженными в западной части США [59], анализ 20-летнего рекорда обнаружили значительное и существенное увеличение накопления градусо-дней к нижнему концу разреза RMFR. Тенденции на NOAA, A1 и B1 имеют значительные положительные наклоны, примерно 100 GDD за десятилетие за последние 20 лет.
В заключение, наше исследование предполагает, что расчетные тренды температуры вдоль RMFR зависят как от а) высоты, так и б) от временного масштаба анализа. То, что предполагаемые закономерности изменения климата в горных системах могут зависеть от временного масштаба имеющихся климатических данных, предполагает, что отсутствие временной стандартизации и доступность долгосрочных климатических данных может повлиять на нашу способность понимать и сравнивать общие закономерности и скорости климатических изменений в горных системах. .Хотя температурные записи последних двух десятилетий предполагают повышенную скорость потепления на разрезе RMFR, важно отметить, что продолжение этого потепления может зависеть от более масштабных моделей колебаний, таких как Эль-Ниньо — Южное колебание и Тихий океан. Десятилетние колебания, которые, как было показано, влияют на периоды относительного потепления и похолодания в Скалистых горах [61]. Постоянный мониторинг и анализ данных по этому разрезу RMFR имеют решающее значение для понимания долгосрочных тенденций, а дальнейшие исследования разрезов на других участках дадут более четкое представление о том, как изменение климата оказывает и будет продолжать влиять на горные регионы мира.
То, что предполагаемые закономерности изменения климата в горных системах могут зависеть от временного масштаба имеющихся климатических данных, предполагает, что отсутствие временной стандартизации и доступность долгосрочных климатических данных может повлиять на нашу способность понимать и сравнивать общие закономерности и скорости климатических изменений в горных системах. .Хотя температурные записи последних двух десятилетий предполагают повышенную скорость потепления на разрезе RMFR, важно отметить, что продолжение этого потепления может зависеть от более масштабных моделей колебаний, таких как Эль-Ниньо — Южное колебание и Тихий океан. Десятилетние колебания, которые, как было показано, влияют на периоды относительного потепления и похолодания в Скалистых горах [61]. Постоянный мониторинг и анализ данных по этому разрезу RMFR имеют решающее значение для понимания долгосрочных тенденций, а дальнейшие исследования разрезов на других участках дадут более четкое представление о том, как изменение климата оказывает и будет продолжать влиять на горные регионы мира.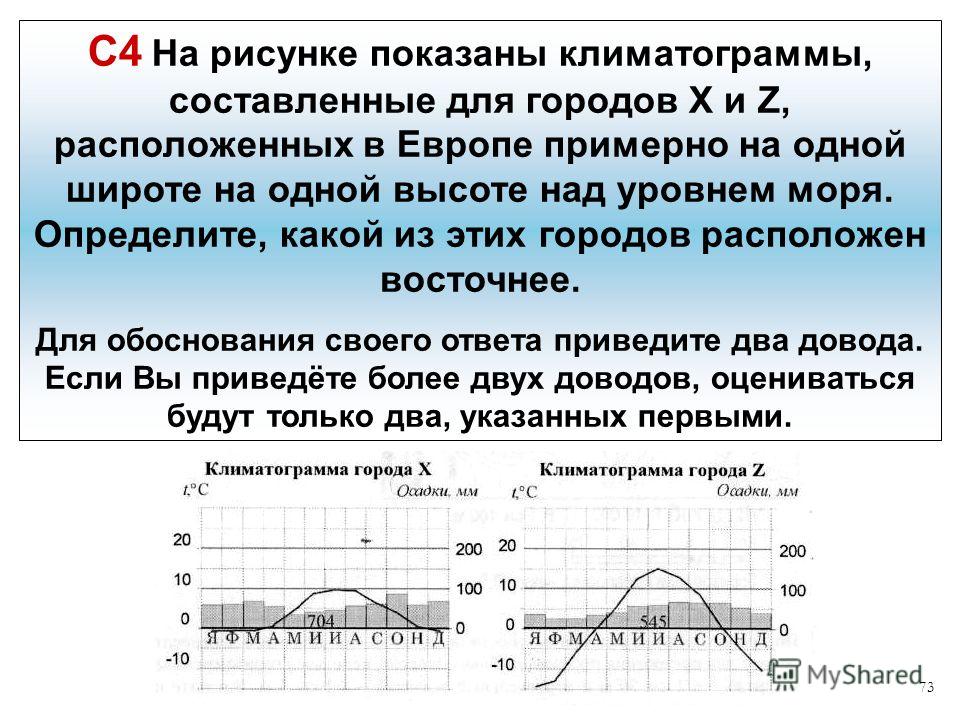
Благодарности
Мы благодарим Тодда Акермана, Тима Киттеля и Марка Уильямса за их критические идеи и техническую помощь. Материально-техническая поддержка и данные были предоставлены Национальным научным фондом при поддержке проекта долгосрочных экологических исследований Niwot Ridge и Горной исследовательской станции Университета Колорадо. Мы также благодарим Сьюзан Битти, Билла Боумена, Эвана Лэмперта, Каролину Кинтеро и Натали Робинсон за обзоры более ранних версий этой рукописи.
Вклад авторов
Задумал и разработал эксперименты: CRM CRN MDB RPG. Проведены эксперименты: CRM. Проанализированы данные: CRM CRN MDB RPG. Предоставленные реагенты / материалы / инструменты анализа: CRM CRN. Написал статью: CRM CRN MDB RPG.
Список литературы
- 1. Паундс Дж. А., Фогден М. П., Кэмпбелл Дж. Х. (1999) Биологическая реакция на изменение климата на тропической горе. Природа 398: 611–615.
- 2.
Стилл С.
 Дж., Фостер П.Н., Шнайдер С.Х. (1999) Моделирование воздействия изменения климата на тропические горные облачные леса.Природа 398: 608–610.
Дж., Фостер П.Н., Шнайдер С.Х. (1999) Моделирование воздействия изменения климата на тропические горные облачные леса.Природа 398: 608–610. - 3. Диас Х. Ф., Эйшайд Дж. К., Дункан С., Брэдли Р. С. (2003) Изменчивость уровней замерзания, показателей сезона таяния и снежного покрова для отдельных высокогорных и континентальных регионов за последние 50 лет. Изменение климата 59: 33–52.
- 4. Бенистон М. (2003) Изменение климата в горных регионах: обзор возможных воздействий. Изменение климата 59: 5–31.
- 5. Mote PW, Hamlet AF, Clark MP, Lettenmaier DP (2005) Уменьшение снежного покрова в горах в западной части Северной Америки.Бюллетень Американского метеорологического общества 86: 39–49.
- 6. Walther GR, Post E, Convey P, Menzel A, Parmesan C и др. (2002) Экологические реакции на недавнее изменение климата. Природа 416: 389–395.
- 7.
Parmesan C, Yohe G (2003) Глобально согласованный отпечаток воздействия изменения климата на природные системы.
 Природа 421: 37–42.
Природа 421: 37–42. - 8. Root TL, Price JT, Hall KR, Schneider SH, Rosenzweig C и др. (2003) Отпечатки глобального потепления на диких животных и растениях.Природа 421: 57–60.
- 9. Guisan A, Theurillat J-P (2000) Оценка уязвимости альпийских растений к изменению климата: перспективы моделирования. Комплексная оценка 1: 307–320.
- 10. Энглер Р., Рэндин С.Ф., Туиллер В., Дуллингер С., Циммерманн Н.Э. и др. (2011) Изменение климата в 21 веке угрожает горной флоре в неравной степени по всей Европе. Биология глобальных изменений 17: 2330–2341.
- 11. Сала О.Е., Чапин Ф.С., Арместо Дж. Дж., Берлоу Э., Блумфилд Дж. И др.(2000) Биоразнообразие — Сценарии глобального биоразнообразия на 2100 год. Science 287: 1770–1774.
- 12. Pepin NC, Seidel DJ (2005) Глобальное сравнение температуры поверхности и атмосферного воздуха на больших высотах. Журнал геофизических исследований атмосферы 110.
- 13.
 Nogues-Bravo D, Araujo MB, Errea MP, Martinez-Rica JP (2007) Подверженность глобальных горных систем климатическому потеплению в 21 веке. Глобальное изменение окружающей среды — человеческие и политические аспекты 17: 420–428.
Nogues-Bravo D, Araujo MB, Errea MP, Martinez-Rica JP (2007) Подверженность глобальных горных систем климатическому потеплению в 21 веке. Глобальное изменение окружающей среды — человеческие и политические аспекты 17: 420–428. - 14. Пепин NC, Lundquist JD (2008) Температурные тенденции на больших высотах: закономерности по всему миру. Письма о геофизических исследованиях 35.
- 15. Beniston M, Rebetez M (1996) Региональное поведение минимальных температур в Швейцарии за период 1979–1993 гг. Теоретическая и прикладная климатология 53: 231–243.
- 16. Giorgi F, Hurrell JW, Marinucci MR, Beniston M (1997) Зависимость от высоты сигнала изменения климата на поверхности: модельное исследование.Journal of Climate 10: 288–296.
- 17. Чен Б., Чао В. К., Лю Х (2003) Усиленное потепление климата на Тибетском плато из-за удвоения выбросов CO2: модельное исследование. Климатическая динамика 20: 401–413.
- 18.
 Vuille M, Bradley RS (2000) Тенденции среднегодовых температур и их вертикальная структура в тропических Андах. Письма о геофизических исследованиях 27: 3885–3888.
Vuille M, Bradley RS (2000) Тенденции среднегодовых температур и их вертикальная структура в тропических Андах. Письма о геофизических исследованиях 27: 3885–3888. - 19. Marr JW (1967) Данные о горной среде I: Фронт-хребет, Колорадо, шестнадцать участков.1952–1953: 110.
- 20. Файф Дж. К., Флато Г. М. (1999) Усиленное изменение климата и его обнаружение над Скалистыми горами. Журнал климата 12: 230–243.
- 21. Снайдер М.А., Белл Д.Л., Слоан Л.К., Даффи П.Б., Говиндасами Б. (2002) Реакция климата на удвоение концентрации углекислого газа в атмосфере для климатически уязвимого региона. Письма о геофизических исследованиях 29.
- 22. Диас Х. Ф., Эйшайд Дж. К. (2007) Исчезающий климатический тип «альпийская тундра» Коппена на западе США.Письма о геофизических исследованиях 34.
- 23.
Stohlgren TJ, Chase TN, Pielke RA, Kittel TGF, Baron JS (1998) Доказательства того, что местные методы землепользования влияют на региональный климат, растительность и режимы стока в прилегающих природных территориях.
 Биология глобальных изменений 4: 495–504.
Биология глобальных изменений 4: 495–504. - 24. Пепин Н. (2000) Изменение климата в ХХ веке для Переднего хребта, Колорадо, США. Исследования Арктики, Антарктики и Альп 32: 135–146.
- 25. Пепин Н., Лослебен М. (2002) Изменение климата в Скалистых горах Колорадо: тенденции изменения температуры свободного воздуха в зависимости от температуры поверхности.Международный журнал климатологии 22: 311–329.
- 26. IPCC (2007) Climate Change 2007: The Physical Science Basis. Вклад Рабочей группы I в Четвертый доклад об оценке Межправительственной группы экспертов по изменению климата. Кембридж.
- 27. Daly C (2006) Руководство по оценке пригодности наборов пространственных климатических данных. Международный журнал климатологии 26: 707–721.
- 28.
Дэйли С., Халблейб М., Смит Дж. И., Гибсон В. П., Доггетт М.К. и др.(2008) Физиографически чувствительное картографирование температуры и осадков на территории Соединенных Штатов.
 Международный журнал климатологии 28: 2031–2064.
Международный журнал климатологии 28: 2031–2064. - 29. Марр Дж. У., Джонсон А. В., Осберн В. С., Кнорр О. А. (1968) Данные о горной среде II: Передний хребет, Колорадо, четыре региона кульминации. 1953–1958: 169.
- 30. Марр Дж. У., Кларк Дж. М., Осберн В. С., Паддок М. В. (1968) Данные о горных условиях III: Передний хребет, Колорадо, четыре региона кульминации. 1959–1964: 181.
- 31. Марр Дж. В. (1961) Экосистемы восточного склона Переднего хребта в Колорадо. 124.
- 32. Гренландия D (1989) Климат хребта Нивот, Передний хребет, Колорадо, США, Арктические и альпийские исследования. 21: 380–391.
- 33. Институт SAS (1989–2008) СПМ, версия 8.02. Кэри, Северная Каролина.
- 34. Робсон С.М. (2002) Увеличение продолжительности вегетационного периода в Иллинойсе в 20 веке. Изменение климата 52: 219–238.
- 35.Trudgill DL, Honek A, Li D, Van Straalen NM (2005) Тепловое время — концепции и полезность.
 Анналы прикладной биологии 146: 1–14.
Анналы прикладной биологии 146: 1–14. - 36. Bonhomme R (2000) Основы и ограничения использования единиц «градус.день». Европейский журнал агрономии 13: 1–10.
- 37. Брайант С.Р., Бейл Дж.С., Томас С.Д. (1998) Модификация треугольного метода накопления градус-день, чтобы учесть терморегуляцию поведения у насекомых. Журнал прикладной экологии 35: 921–927.
- 38.ДеГаэтано А.Т., Кнапп В.В. (1993) Стандартизация еженедельно растущих накоплений градус-день на основе времени наблюдения разницы температур и метода сельскохозяйственной и лесной метеорологии. 66: 1–19.
- 39. McMaster GS, Wilhelm WW (1997) Растущие градусо-дни: одно уравнение, две интерпретации. Сельскохозяйственная и лесная метеорология 87: 291–300.
- 40.
Ричи Дж. Т., НеСмит Д. С. (1991) Температура и развитие сельскохозяйственных культур. В: Хэнкс Дж., Ричи Дж. Т., редакторы.Моделирование растений и почвенных систем Монография Американского агрономического общества № 31.
 Мэдисон, Висконсин: Американское агрономическое общество. 5–29.
Мэдисон, Висконсин: Американское агрономическое общество. 5–29. - 41. Шленкер В., Ханеманн В.М., Фишер А.С. (2007) Наличие воды, градусо-дни и потенциальное влияние изменения климата на орошаемое земледелие в Калифорнии. Изменение климата 81: 19–38.
- 42. Mix K, Rast W, Lopes VL (2010) Увеличивается количество дней роста в альпийской пустыне долины Сан-Луис, Колорадо. Вода, загрязнение воздуха и почвы 205: 289–304.
- 43. Диаз Х.Ф., Брэдли Р.С. (1997) Температурные колебания в течение последнего столетия на возвышенностях. Изменение климата 36: 253–279.
- 44. Истерлинг Д. Р., Хортон Б., Джонс П. Д., Петерсон Т. К., Карл Т. Р. и др. (1997) Тенденции максимальных и минимальных температур для земного шара. Science 277: 364–367.
- 45. Истерлинг Д.Р. (2002) Недавние изменения морозных дней и безморозного сезона в США. Бюллетень Американского метеорологического общества 83: 1327–1332.
- 46.
 Пилке Р.А., Штольгрен Т., Шелл Л., Партон В., Доскен Н. и др. (2002) Проблемы оценки региональных и местных тенденций изменения температуры: пример Восточного Колорадо, США. Международный журнал климатологии 22: 421–434.
Пилке Р.А., Штольгрен Т., Шелл Л., Партон В., Доскен Н. и др. (2002) Проблемы оценки региональных и местных тенденций изменения температуры: пример Восточного Колорадо, США. Международный журнал климатологии 22: 421–434. - 47. Serreze MC, Walsh JE, Chapin FS, Osterkamp T, Dyurgerov M, et al. (2000) Наблюдательные свидетельства недавних изменений в северной среде высоких широт. Изменение климата 46: 159–207.
- 48. IPCC (2001) Изменение климата 2001: научная основа.Вклад рабочей группы I в Третий доклад об оценке Межправительственной группы экспертов по изменению климата. Кембридж. 881 с.
- 49. Chase TN, Pielke RA, Kittel TGF, Baron JS, Stohlgren TJ (1999) Потенциальные воздействия на погоду в Скалистых горах в Колорадо из-за изменений в землепользовании на прилегающих Великих равнинах. Журнал геофизических исследований атмосферы 104: 16673–16690.
- 50.
Пилке Р.А., Истман Дж., Чейз Т.Н., Кнафф Дж.
 , Киттель TGF (1998) Тенденции 1973–1996 гг. В усредненной по глубине температуре тропосферы Журнал геофизических исследований атмосферы.103: 16927–16933.
, Киттель TGF (1998) Тенденции 1973–1996 гг. В усредненной по глубине температуре тропосферы Журнал геофизических исследований атмосферы.103: 16927–16933. - 51. Сегал М., Шрайбер В.Е., Каллос Г., Гарратт Дж. Р., Роди А. и др. (1989) Влияние посевных площадей в Северо-Восточном Колорадо на мезомасштабные тепловые циркуляции в середине лета. Ежемесячный обзор погоды. 117: 809–825.
- 52. Clow DW (2010) Изменения в сроках таяния снега и речного стока в Колорадо: ответ на недавнее потепление. Journal of Climate 23: 2293–2306.
- 53. Гамлет А.Ф., Моте П.В., Кларк М.П., Леттенмайер Д.П. (2005) Влияние изменчивости температуры и осадков на тенденции снежного покрова в западной части Соединенных Штатов.Журнал климата 18: 4545–4561.
- 54.
Ди Лузио М., Джонсон Г.Л., Дейли С., Эйшайд Дж.К., Арнольд Дж.Г. (2008) Построение ретроспективных наборов данных о суточных осадках и температуре с привязкой к сетке для приграничных Соединенных Штатов.
 47: 475–497.
47: 475–497. - 55. Schwartz MD, Reiter BE (2000) Изменения весны в Северной Америке. Международный журнал климатологии 20: 929–932.
- 56. Cayan DR, Kammerdiener SA, Dettinger MD, Caprio JM, Peterson DH (2001) Изменения наступления весны в западных Соединенных Штатах.Бюллетень Американского метеорологического общества 82: 399–415.
- 57. Менцель А., Эстрелла Н., Фабиан П. (2001) Пространственная и временная изменчивость фенологических сезонов в Германии с 1951 по 1996 год. Биология глобальных изменений 7: 657–666.
- 58. Ахас Р., Ааса А., Мензель А., Федотова В.Г., Шайфингер Х. (2002) Изменения в фенологии европейской весны. Международный журнал климатологии 22: 1727–1738.
- 59. Feng S, Hu Q (2004) Изменения агрометеорологических показателей в сопредельных Соединенных Штатах: 1951–2000 гг.Теоретическая и прикладная климатология 78: 247–264.
- 60.
Linderholm HW (2006) Изменения вегетационного периода в прошлом веке.
 Сельскохозяйственная и лесная метеорология 137: 1–14.
Сельскохозяйственная и лесная метеорология 137: 1–14. - 61. Kittel TGF, Thornton PE, Royle JA, Chase TN (2002) Климат Скалистых гор: исторические и будущие модели. В: Baron JS, редактор. Будущее Скалистых гор: экологическая перспектива. Вашингтон, округ Колумбия, США: Island Press.
Мах и калькулятор скорости звука
Воздух — это газ, и очень важный свойство любого газа скорость звука через газ.Почему нас интересует скорость звука? Скорость «звука» на самом деле скорость передачи небольшого возмущения через средний. Звук сам по себе является ощущением, созданным в человеческом мозг в ответ на сенсорные сигналы от внутреннего уха. (Мы не будем комментировать старые обсуждение «падение дерева в лесу»!)
Помехи передаются через газ в результате
столкновения
между беспорядочно движущимися молекулами газа.Передача небольшого возмущения через газ — это
изоэнтропический процесс.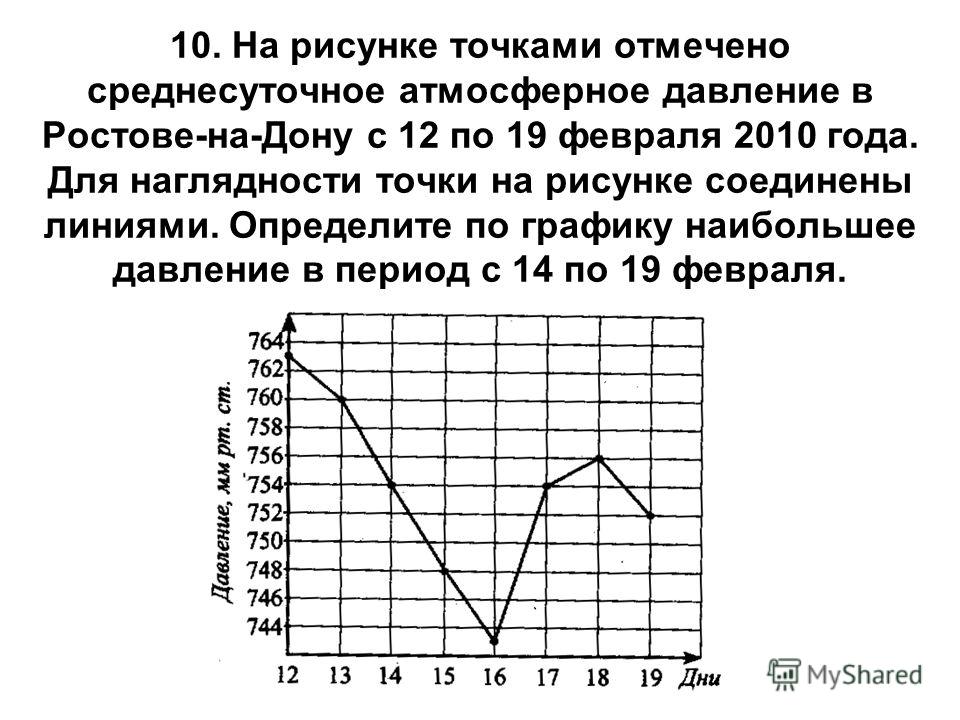 Условия в
газы одинаковы до и после прохождения возмущения.
Поскольку скорость передачи зависит от молекулярных столкновений,
скорость звука зависит от состояния
газа. Скорость звука в данном газе постоянна.
а значение постоянной зависит от типа газа (воздух, чистый кислород,
углекислый газ и др.) и температуры газа.An
анализ
на основе сохранения
масса
и
импульс
показывает, что скорость звука a равна квадратному корню из
соотношение
удельные плавки г раз больше газовой постоянной R раз больше
температура Т .
Условия в
газы одинаковы до и после прохождения возмущения.
Поскольку скорость передачи зависит от молекулярных столкновений,
скорость звука зависит от состояния
газа. Скорость звука в данном газе постоянна.
а значение постоянной зависит от типа газа (воздух, чистый кислород,
углекислый газ и др.) и температуры газа.An
анализ
на основе сохранения
масса
и
импульс
показывает, что скорость звука a равна квадратному корню из
соотношение
удельные плавки г раз больше газовой постоянной R раз больше
температура Т .
a = sqrt [g * R * T]
Обратите внимание, что температура должно быть указано в абсолютной шкале (Кельвина или Ренкин).Зависимость от типа газа включена в газовая постоянная R . который равен универсальной газовой постоянной, деленной на молекулярная масса газа и отношение удельных теплоемкостей.
Скорость звука в воздухе зависит от типа газа и
температура газа. На
Земля,
атмосфера
состоит из
в основном двухатомный азот и кислород, а температура
зависит от высоты довольно сложным образом.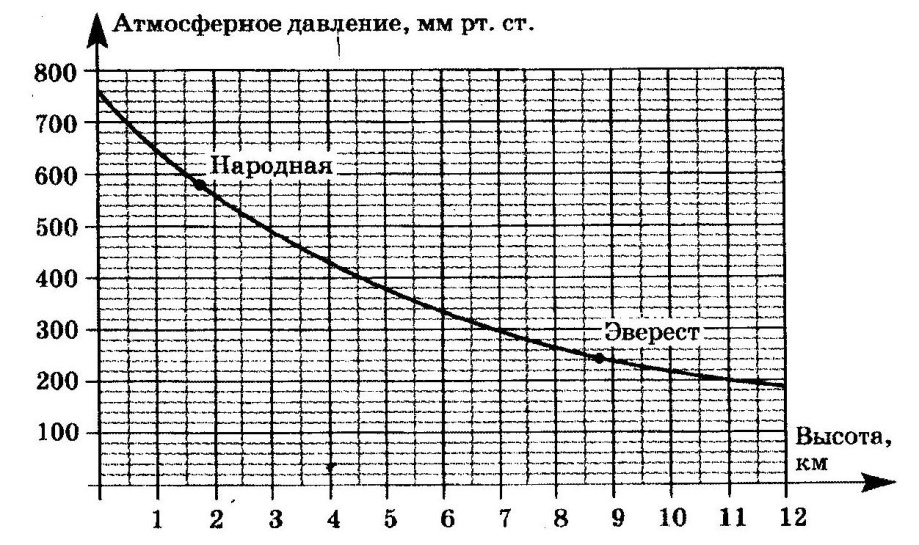 Ученые и инженеры создали
математическая модель атмосферы в помощь
они объясняют изменение температуры с высотой.
Марс также имеет атмосферу, состоящую из
в основном углекислый газ. Есть похожий
математическая модель марсианской атмосферы.
Мы создали
атмосферный калькулятор
чтобы вы могли изучить изменение скорости звука с планетой и
высота.
Ученые и инженеры создали
математическая модель атмосферы в помощь
они объясняют изменение температуры с высотой.
Марс также имеет атмосферу, состоящую из
в основном углекислый газ. Есть похожий
математическая модель марсианской атмосферы.
Мы создали
атмосферный калькулятор
чтобы вы могли изучить изменение скорости звука с планетой и
высота.
Вот программа на JavaScript для расчета скорости звука и число Маха для разных планет, высот и скоростей.Вы можете использовать этот калькулятор для определения числа Маха ракеты на заданной скорости и высоте на Земле или Марсе.
Пресс->
Выход
Скорость
Скорость звука
Мах
На этой странице показан интерактивный Java-апплет, который вычисляет скорость звука. и число Маха для входной скорости и высоты.
Чтобы изменить входные значения, щелкните поле ввода (черный на белом),
пробел над входным значением, введите новое значение и нажмите клавишу Enter на клавиатуре (это отправит новое значение программе). Вы увидите поля вывода (желтый на черном)
изменить значение. Вы можете использовать английские или метрические единицы, а также ввести число Маха.
или скорость с помощью кнопок меню. Просто нажмите кнопку меню и нажмите
на ваше
выбор.Существует
гладкая версия
этой программы для опытных пользователей, которым эти инструкции не нужны.
Вы увидите поля вывода (желтый на черном)
изменить значение. Вы можете использовать английские или метрические единицы, а также ввести число Маха.
или скорость с помощью кнопок меню. Просто нажмите кнопку меню и нажмите
на ваше
выбор.Существует
гладкая версия
этой программы для опытных пользователей, которым эти инструкции не нужны.
Вы также можете загрузить свою собственную копию этой программы для работы в автономном режиме, нажав на этой кнопке:
Когда объект движется через атмосферу, воздух нарушается и беспорядки передается по воздуху со скоростью звука. Вы можете изучить, как помехи передаются с помощью интерактивный симулятор звуковой волны.Если мы рассмотрим атмосферу на стандартный день в статических условиях на уровне моря скорость звука составляет около 761 миль / ч , или 1100 футов / сек . Мы можем использовать эти знания примерно для определять как далеко произошел удар молнии.
Скорость звука в атмосфере — постоянная величина, которая зависит от
высоту, но самолет может двигаться по воздуху на любом желаемом
скорость. Отношение скорости самолета к скорости звука.
влияет на силы самолета.Авиационные инженеры называют отношение скорости самолета к
скорость звука
Число Маха, M .
Если летательный аппарат движется намного медленнее скорости звука,
условия называются
дозвуковой, 0,
и сжимаемость
эффекты незначительны, и ими можно пренебречь.
Если самолет движется со скоростью, близкой к скорости звука,
условия называются
трансзвуковой, M ~ 1 ,
и эффекты сжимаемости, такие как
подавление потока
становится очень важным.Для самолетов, скорость которых превышает скорость звука,
условия называются
сверхзвуковой, 1,
и эффекты сжимаемости важны.
В зависимости от конкретной формы и скорости самолета,
ударные волны
может образоваться в сверхзвуковом потоке газа. За
высокие сверхзвуковые скорости, 3,
аэродинамический обогрев становится очень важным.
Если летательный аппарат движется со скоростью более чем в пять раз превышающей скорость звука,
условия называются
гиперзвуковой, M> 5 ,
и высокая энергия, связанная с этими
условия оказывают значительное влияние на сам воздух.
Отношение скорости самолета к скорости звука.
влияет на силы самолета.Авиационные инженеры называют отношение скорости самолета к
скорость звука
Число Маха, M .
Если летательный аппарат движется намного медленнее скорости звука,
условия называются
дозвуковой, 0,
и сжимаемость
эффекты незначительны, и ими можно пренебречь.
Если самолет движется со скоростью, близкой к скорости звука,
условия называются
трансзвуковой, M ~ 1 ,
и эффекты сжимаемости, такие как
подавление потока
становится очень важным.Для самолетов, скорость которых превышает скорость звука,
условия называются
сверхзвуковой, 1,
и эффекты сжимаемости важны.
В зависимости от конкретной формы и скорости самолета,
ударные волны
может образоваться в сверхзвуковом потоке газа. За
высокие сверхзвуковые скорости, 3,
аэродинамический обогрев становится очень важным.
Если летательный аппарат движется со скоростью более чем в пять раз превышающей скорость звука,
условия называются
гиперзвуковой, M> 5 ,
и высокая энергия, связанная с этими
условия оказывают значительное влияние на сам воздух. Спейс шаттл снова входит в атмосферу в
высокие гиперзвуковые скорости, М ~ 25 .
В этих условиях нагретый воздух превращается в ионизированную плазму.
газа и космический корабль должен быть изолирован от высоких температур.
Спейс шаттл снова входит в атмосферу в
высокие гиперзвуковые скорости, М ~ 25 .
В этих условиях нагретый воздух превращается в ионизированную плазму.
газа и космический корабль должен быть изолирован от высоких температур.
Деятельность:
Экскурсии с гидом
Навигация ..
- Руководство для начинающих Домашняя страница
Оценка зависимости между температурой и осадками для лучшей оценки рисков одновременных экстремальных погодных явлений
Осадки и температура являются одними из основных климатических переменных, которые используются для характеристики экстремальных погодных явлений, которые могут иметь глубокое влияние на экосистемы и общество.Точное моделирование этих переменных в местном масштабе необходимо для адаптации городских систем и политики к будущим климатическим изменениям. Однако точное моделирование этих климатических переменных затруднено из-за возможной взаимозависимости и обратной связи между ними. В этой статье концепция копул была использована для моделирования сезонной зависимости между осадками и температурой. Пять функций копул были приспособлены к сетке (приблизительно 10 км × 10 км) климатических данных с 1960 по 2013 год в южном Онтарио, Канада.Затем теоретические и эмпирические связки сравнивали друг с другом, чтобы выбрать наиболее подходящее семейство связок для этой области. Результаты показали, что из протестированных связок ни одна из них не показывала стабильно лучших показателей во всем регионе в течение всех сезонов. Тем не менее, копула Гамбела была лучшей в зимний сезон, а Клейтон — летом. Большая изменчивость по лучшей связке была обнаружена в весенний и осенний сезоны. Изучая вероятность одновременных периодов экстремальных температур и осадков, включая влажные / прохладные зимой и сухие / жаркие летом, мы обнаружили, что игнорирование совместного распределения и смешанных воздействий осадков и температуры приводит к недооценке вероятности возникновения этих два одновременных экстремальных режима.
В этой статье концепция копул была использована для моделирования сезонной зависимости между осадками и температурой. Пять функций копул были приспособлены к сетке (приблизительно 10 км × 10 км) климатических данных с 1960 по 2013 год в южном Онтарио, Канада.Затем теоретические и эмпирические связки сравнивали друг с другом, чтобы выбрать наиболее подходящее семейство связок для этой области. Результаты показали, что из протестированных связок ни одна из них не показывала стабильно лучших показателей во всем регионе в течение всех сезонов. Тем не менее, копула Гамбела была лучшей в зимний сезон, а Клейтон — летом. Большая изменчивость по лучшей связке была обнаружена в весенний и осенний сезоны. Изучая вероятность одновременных периодов экстремальных температур и осадков, включая влажные / прохладные зимой и сухие / жаркие летом, мы обнаружили, что игнорирование совместного распределения и смешанных воздействий осадков и температуры приводит к недооценке вероятности возникновения этих два одновременных экстремальных режима. Эта недооценка также может привести к неправильным выводам и ошибочным решениям с точки зрения серьезности этих экстремальных явлений.
Эта недооценка также может привести к неправильным выводам и ошибочным решениям с точки зрения серьезности этих экстремальных явлений.
1. Введение
Экстремальные погодные явления могут иметь серьезные физические и экономические последствия для городских и сельских общин [1–3]. Согласно Пятому оценочному докладу Межправительственной группы экспертов по изменению климата [4], ожидается, что экстремальные высокие температуры будут увеличиваться, а экстремальные низкие температуры будут уменьшаться в течение следующих нескольких десятилетий [5].Кроме того, значительный рост количества экстремальных осадков прогнозируется во многих областях в течение 21 века, но с сильной изменчивостью по годам [6]. Estrella и Menzel [7] обнаружили, что взаимозависимость климатических переменных может иметь более серьезное влияние на пространственное изменение климата, чем влияние какой-либо отдельной климатической переменной, например, комбинированное воздействие на изменение температуры и количества осадков на возникновение и степень засухи. Канадские прерии [8].В других исследованиях также оценивалась зависимость между климатическими переменными и экстремальными явлениями. AghaKouchak et al. [9] обнаружили, что последствия засухи и жары в Соединенных Штатах значительно усилились, когда они произошли одновременно. Little et al. [10] обнаружили, что повышение уровня моря и изменения частоты и интенсивности тропических циклонов увеличат риск наводнений в будущем на восточном побережье США.
Канадские прерии [8].В других исследованиях также оценивалась зависимость между климатическими переменными и экстремальными явлениями. AghaKouchak et al. [9] обнаружили, что последствия засухи и жары в Соединенных Штатах значительно усилились, когда они произошли одновременно. Little et al. [10] обнаружили, что повышение уровня моря и изменения частоты и интенсивности тропических циклонов увеличат риск наводнений в будущем на восточном побережье США.
В большинстве исследований воздействия изменения климата колебания температуры и осадков рассматриваются независимо.Однако эти две переменные физически зависят через несколько механизмов. Например, осадки влияют на влажность почвы, которая, в свою очередь, может оказывать влияние на поверхность и температуру воздуха на низком уровне за счет эффектов диабатических потоков и разделения потоков явного и скрытого тепла или более низкого / более высокого отношения Боуэна [11, 12]. Взаимодействие экстремальных температур и осадков может привести к сильным погодным явлениям и связанным с ними стихийным бедствиям со значительными последствиями для сельского хозяйства и других секторов экономики [13]. Например, засуха, сопровождающая аномальную жару, может повлиять на доступность воды для производства продуктов питания [14, 15], а также на ресурсы питьевой воды. Кроме того, взаимозависимость температуры и количества осадков в моделях может влиять на распределение снежного покрова и продолжительность моделирования [16, 17], а также на возникновение и продолжительность паводков весной во многих регионах, особенно в Канаде [18]. В результате следует обратить внимание на комбинированные эффекты изменения температуры и осадков и их смешанные воздействия.Недавний анализ зависимости между температурой и осадками становится центром исследований в области метеорологии и предотвращения стихийных бедствий [19, 20].
Например, засуха, сопровождающая аномальную жару, может повлиять на доступность воды для производства продуктов питания [14, 15], а также на ресурсы питьевой воды. Кроме того, взаимозависимость температуры и количества осадков в моделях может влиять на распределение снежного покрова и продолжительность моделирования [16, 17], а также на возникновение и продолжительность паводков весной во многих регионах, особенно в Канаде [18]. В результате следует обратить внимание на комбинированные эффекты изменения температуры и осадков и их смешанные воздействия.Недавний анализ зависимости между температурой и осадками становится центром исследований в области метеорологии и предотвращения стихийных бедствий [19, 20].
Многие исследования показали, что связи между температурой и осадками различаются как в пространстве, так и в зависимости от сезона [21–24]. Johns et al. [25] использовали диаграммы разброса среднегодовых осадков и аномалий температуры, чтобы показать глобальную линейную корреляцию, которая моделировалась большинством климатических моделей за период 1980–1990 гг.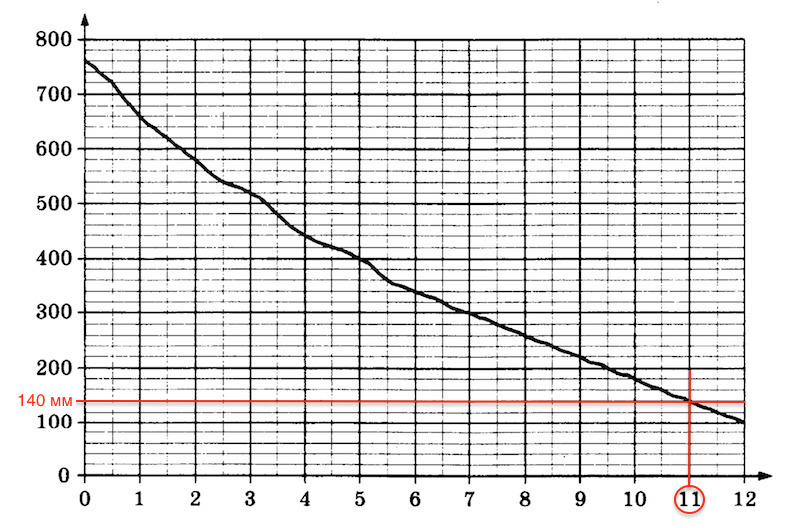 Основываясь на модели HadGEM2, Цезарь и Лоу [26] проанализировали корреляцию между среднегодовой температурой и экстремальными осадками.Они обнаружили пропорционально высокую корреляцию между ними. Dai et al. [27] обнаружили сильную отрицательную корреляцию между осадками, максимальной температурой (Tmax) и дневным диапазоном температур в короткие сроки в теплый сезон во всем мире. Отрицательная корреляция между летними осадками и температурой была обнаружена на большей части континентальной части Соединенных Штатов, что указывает на то, что теплое лето, как правило, более сухое, а более холодное — более влажное [24]. В Канаде взаимозависимость между температурой и осадками имеет тенденцию увеличиваться с широтой и особенно сильна в Северо-Западных территориях и относительно слаба в Прериях [21], но эти модели корреляции различаются между зимними и летними месяцами [28].Юго-восточный Онтарио и Квебек почти не показывают зависимости количества осадков от температуры летом (например, июль), но существует общая отрицательная корреляция между среднемесячными аномалиями температуры и количеством осадков для групп месяцев, происходящих в период май / июнь / июль.
Основываясь на модели HadGEM2, Цезарь и Лоу [26] проанализировали корреляцию между среднегодовой температурой и экстремальными осадками.Они обнаружили пропорционально высокую корреляцию между ними. Dai et al. [27] обнаружили сильную отрицательную корреляцию между осадками, максимальной температурой (Tmax) и дневным диапазоном температур в короткие сроки в теплый сезон во всем мире. Отрицательная корреляция между летними осадками и температурой была обнаружена на большей части континентальной части Соединенных Штатов, что указывает на то, что теплое лето, как правило, более сухое, а более холодное — более влажное [24]. В Канаде взаимозависимость между температурой и осадками имеет тенденцию увеличиваться с широтой и особенно сильна в Северо-Западных территориях и относительно слаба в Прериях [21], но эти модели корреляции различаются между зимними и летними месяцами [28].Юго-восточный Онтарио и Квебек почти не показывают зависимости количества осадков от температуры летом (например, июль), но существует общая отрицательная корреляция между среднемесячными аномалиями температуры и количеством осадков для групп месяцев, происходящих в период май / июнь / июль. / Август / Сентябрь [28]. В целом, в теплые летние / зимние месяцы выпадает меньше / больше осадков. В восточной части региона Скалистых гор Исаак и Стюарт [21] обнаружили, что больше осадков выпадает, когда температура обычно ниже, независимо от времени года, как показано также в исследовании Тренбета и Ши [28].Это может быть связано с тем, что обычные системы низкого давления (например, наличие Alberta Clippers) движутся с запада в сторону области Альберты.
/ Август / Сентябрь [28]. В целом, в теплые летние / зимние месяцы выпадает меньше / больше осадков. В восточной части региона Скалистых гор Исаак и Стюарт [21] обнаружили, что больше осадков выпадает, когда температура обычно ниже, независимо от времени года, как показано также в исследовании Тренбета и Ши [28].Это может быть связано с тем, что обычные системы низкого давления (например, наличие Alberta Clippers) движутся с запада в сторону области Альберты.
Большинство исследований, в которых анализируется зависимость между температурой и осадками, предполагают линейную зависимость и нормальное распределение обеих переменных (например, [21, 24, 28]). Следовательно, соответствующие результаты, вероятно, будут неточными, если одна или обе переменные не удовлетворяют условию нормального распределения, особенно если осадки не распределяются нормально, а также низкие температуры воздуха в зимние месяцы из-за нелинейных обратных связей, вызванных присутствием снег на земле.Кроме того, линейная корреляция игнорирует высокие пиковые флуктуации и структуру зависимости [29]. В этом исследовании мы применяем подход на основе связок для анализа значимости взаимосвязи между осадками и температурой, чтобы преодолеть проблему нормальности нераспределенных данных. Взаимозависимость количества осадков и температуры с использованием копулы не была широко исследована в литературе, особенно для южного Онтарио [11, 30]. Конг и Брэди [11] использовали связки для изучения зависимости между температурой и количеством осадков в Скании (самая южная провинция Швеции).Они обнаружили значительную отрицательную корреляцию с апреля по сентябрь. С точки зрения связки, Студент был выбран как более подходящий для этого региона. Они заявили, что их результаты сильно связаны с изучаемым регионом, и эти результаты различаются в пространстве (от региона к региону) и во времени. В этом исследовании использовался подход, основанный на связках, для определения внутренней взаимосвязи между среднесуточной температурой и общим количеством осадков (осадки> 0,1 мм). Пять функций копул, принадлежащих к трем разным семействам, были сконструированы для выявления совместного распределения или взаимозависимости осадков и температуры (см.
В этом исследовании мы применяем подход на основе связок для анализа значимости взаимосвязи между осадками и температурой, чтобы преодолеть проблему нормальности нераспределенных данных. Взаимозависимость количества осадков и температуры с использованием копулы не была широко исследована в литературе, особенно для южного Онтарио [11, 30]. Конг и Брэди [11] использовали связки для изучения зависимости между температурой и количеством осадков в Скании (самая южная провинция Швеции).Они обнаружили значительную отрицательную корреляцию с апреля по сентябрь. С точки зрения связки, Студент был выбран как более подходящий для этого региона. Они заявили, что их результаты сильно связаны с изучаемым регионом, и эти результаты различаются в пространстве (от региона к региону) и во времени. В этом исследовании использовался подход, основанный на связках, для определения внутренней взаимосвязи между среднесуточной температурой и общим количеством осадков (осадки> 0,1 мм). Пять функций копул, принадлежащих к трем разным семействам, были сконструированы для выявления совместного распределения или взаимозависимости осадков и температуры (см. Следующий раздел).Предлагаемый подход был применен к климатическим данным с координатной привязкой (0,0833 градуса или ∼ 10 км × 10 км), доступным по всей Канаде, но использовался для конкретного региона на юге Онтарио, Канада. Это первое исследование, посвященное изучению и количественной оценке нелинейной зависимости между осадками и температурой с использованием копул в южном Онтарио.
Следующий раздел).Предлагаемый подход был применен к климатическим данным с координатной привязкой (0,0833 градуса или ∼ 10 км × 10 км), доступным по всей Канаде, но использовался для конкретного региона на юге Онтарио, Канада. Это первое исследование, посвященное изучению и количественной оценке нелинейной зависимости между осадками и температурой с использованием копул в южном Онтарио.
2. Методы
2.1. Исследуемый регион и наборы данных
Исследуемый регион расположен на юге Онтарио, Канада (рис. 1).Район исследования расположен между 42 ° 18′N 83 ° 01′W и 45 ° 31′N 74 ° 06′W и ограничен на юге международной границей с США. Площадь области составляет около 100 000 км 2 . В этом регионе проживает около 11 миллионов человек (по данным переписи населения Канады 2016 г.), он составляет почти треть населения Канады и примерно 75% населения провинции Онтарио. Климат в восточной части Канады, включая район исследования, частично зависит от топографических эффектов, Ниагарского откоса и крупных озер [31]. Ниагарский откос пересекает исследуемую территорию от залива Джорджиан на северо-западе до озера Эри на востоке и влияет на характер осадков в регионе. Кроме того, Великие Лаврентийские озера оказывают серьезное влияние на климат в регионе, включая следующее: (1) снижение экстремальных температур в любое время года, (2) увеличение облачности и количества осадков зимой (эффект снежного озера). и (3) уменьшение количества летних конвективных облаков и дождевых осадков. Эти эффекты обусловлены различиями в теплоемкости воды и поверхности суши и коэффициентом Боуэна между двумя поверхностями, а также большими различиями в источнике влаги, особенно в Великих озерах [32, 33].
Ниагарский откос пересекает исследуемую территорию от залива Джорджиан на северо-западе до озера Эри на востоке и влияет на характер осадков в регионе. Кроме того, Великие Лаврентийские озера оказывают серьезное влияние на климат в регионе, включая следующее: (1) снижение экстремальных температур в любое время года, (2) увеличение облачности и количества осадков зимой (эффект снежного озера). и (3) уменьшение количества летних конвективных облаков и дождевых осадков. Эти эффекты обусловлены различиями в теплоемкости воды и поверхности суши и коэффициентом Боуэна между двумя поверхностями, а также большими различиями в источнике влаги, особенно в Великих озерах [32, 33].
Наборы данных о наблюдаемых суточных осадках и максимальной и минимальной 2-метровой температуре воздуха, использованные для этого исследования, были извлечены из исторических данных метеостанции с привязкой к сетке (CanGrid), произведенных Natural Resources Canada с использованием интерполированных станций наблюдений Environment Canada по всей Канаде. Этот набор данных [34] охватывает Канаду (к югу до 60 ° с.ш.) и содержит дневные переменные с 1951 по 2013 год на конформной конической проекции Ламберта с шагом 5 угловых минут (что эквивалентно разрешению примерно 10 км).Эти климатические данные были получены с помощью программы «ANUSPLIN» [35]. Этот набор данных использовался во многих исследованиях изменения климата в недавнем прошлом (например, [36–38] и [8, 39, 40]). В этом исследовании использовались данные с привязкой к канадской сетке из 1699 точек сетки CanGrid, расположенных в южной части Онтарио, соответствующих границам исследуемого участка за период 1951–2013 гг. (Рисунок 1). Основываясь на информации о точках сетки, общее годовое количество осадков за этот период колеблется от самого низкого зарегистрированного значения 725 мм до 1162 мм.
Этот набор данных [34] охватывает Канаду (к югу до 60 ° с.ш.) и содержит дневные переменные с 1951 по 2013 год на конформной конической проекции Ламберта с шагом 5 угловых минут (что эквивалентно разрешению примерно 10 км).Эти климатические данные были получены с помощью программы «ANUSPLIN» [35]. Этот набор данных использовался во многих исследованиях изменения климата в недавнем прошлом (например, [36–38] и [8, 39, 40]). В этом исследовании использовались данные с привязкой к канадской сетке из 1699 точек сетки CanGrid, расположенных в южной части Онтарио, соответствующих границам исследуемого участка за период 1951–2013 гг. (Рисунок 1). Основываясь на информации о точках сетки, общее годовое количество осадков за этот период колеблется от самого низкого зарегистрированного значения 725 мм до 1162 мм.
2.2. Copula Concepts
Copula — это статистическое понятие, используемое для описания нелинейной зависимости между случайными величинами и для установления совместного распределения этих переменных с использованием их маргинальных функций. Он также описывается как функция, которая связывает одномерные распределения с многомерным распределением, описывающим зависимость между коррелированными переменными. Основными преимуществами использования подхода копулы являются следующие: (1) гибкость в выборе произвольной маргинальной и структуры зависимости, (2) расширение до более чем двух переменных и (3) раздельный анализ маргинальных распределений и структуры зависимости [41, 42 ].Совместное распределение подбирается путем отдельной оценки предельных распределений переменных и их соответствия, что не ограничивается каким-либо параметрическим распределением (например, распределением Гаусса). Метод Copula широко использовался для изучения взаимодействий и связей между гидрологическими и / или климатологическими переменными. Де Микеле и Сальвадори [43] определили связь между интенсивностью и продолжительностью ливневых дождей в Италии с помощью копулы Франка. Hao и AghaKouchak [44] использовали набор параметрических связок, чтобы получить многомерный стандартизованный индекс засухи на основе векторов осадков и влажности почвы.
Он также описывается как функция, которая связывает одномерные распределения с многомерным распределением, описывающим зависимость между коррелированными переменными. Основными преимуществами использования подхода копулы являются следующие: (1) гибкость в выборе произвольной маргинальной и структуры зависимости, (2) расширение до более чем двух переменных и (3) раздельный анализ маргинальных распределений и структуры зависимости [41, 42 ].Совместное распределение подбирается путем отдельной оценки предельных распределений переменных и их соответствия, что не ограничивается каким-либо параметрическим распределением (например, распределением Гаусса). Метод Copula широко использовался для изучения взаимодействий и связей между гидрологическими и / или климатологическими переменными. Де Микеле и Сальвадори [43] определили связь между интенсивностью и продолжительностью ливневых дождей в Италии с помощью копулы Франка. Hao и AghaKouchak [44] использовали набор параметрических связок, чтобы получить многомерный стандартизованный индекс засухи на основе векторов осадков и влажности почвы.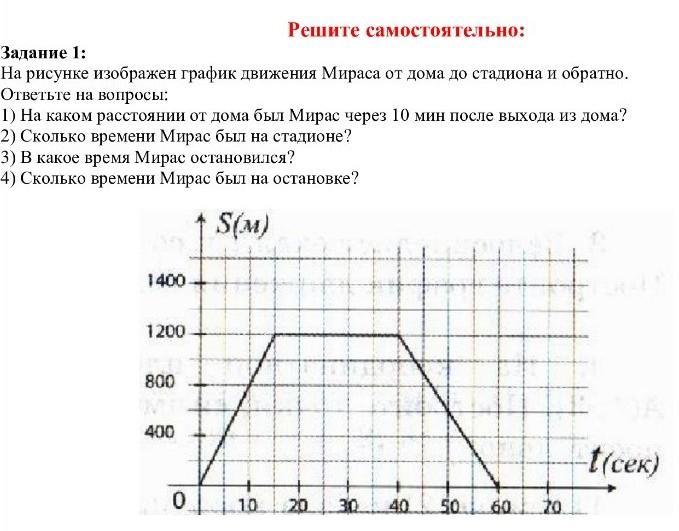 Ли и др. [45] изучали влияние формы хвоста различных функций связок (например, Гамбеля, Фрэнка, Клейтона и Гаусса) на двумерный частотный анализ засухи. Ренар и Ланг [46] предложили применение гауссовой связки для смягчения последствий наводнений во Франции. Гримальди и Серинальди [47] доказали адекватность двух связок (Фрэнка и Гамбеля) по анализируемым характеристикам паводков для реки Канава в Западной Вирджинии (США). Чебана и Уарда [48, 49] представили региональный многомерный анализ паводков с использованием связки и многомерных L-моментов, которые также использовались в исследовании Saad et al.[18], которые разработали трехфакторную связку для анализа наводнений над рекой Ришелье, расположенной в южной части Квебека. Копула Гамбеля была использована Леонардом, Меткалфом и Ламбертом [50] для связывания предельных распределений сезонных максимумов дождевых осадков в бассейне Мюррей-Дарлинг, Австралия. Адлуни и Уарда [51] предложили применение копулы для анализа зависимости уровня воды в озере Сен-Луи от максимального потока на реке Шатоге в Квебеке (Канада).
Ли и др. [45] изучали влияние формы хвоста различных функций связок (например, Гамбеля, Фрэнка, Клейтона и Гаусса) на двумерный частотный анализ засухи. Ренар и Ланг [46] предложили применение гауссовой связки для смягчения последствий наводнений во Франции. Гримальди и Серинальди [47] доказали адекватность двух связок (Фрэнка и Гамбеля) по анализируемым характеристикам паводков для реки Канава в Западной Вирджинии (США). Чебана и Уарда [48, 49] представили региональный многомерный анализ паводков с использованием связки и многомерных L-моментов, которые также использовались в исследовании Saad et al.[18], которые разработали трехфакторную связку для анализа наводнений над рекой Ришелье, расположенной в южной части Квебека. Копула Гамбеля была использована Леонардом, Меткалфом и Ламбертом [50] для связывания предельных распределений сезонных максимумов дождевых осадков в бассейне Мюррей-Дарлинг, Австралия. Адлуни и Уарда [51] предложили применение копулы для анализа зависимости уровня воды в озере Сен-Луи от максимального потока на реке Шатоге в Квебеке (Канада). Роза и Лейте [52] показали, что связки Фрэнка и Клейтона хорошо подходят для изучения взаимосвязи между максимальным потоком и объемом в Португалии.Чтобы установить связь между различными характеристиками паводков, Salarpour et al. [53] применили т-копулу на реке Джохор в Малайзии. Копула Гамбеля была выбрана в качестве наиболее подходящей модели для трехфакторного частотного анализа пиковых расходов, объемов гидрографов и концентраций взвешенных наносов в работе Безака и др. [54]. Также связка использовалась для описания пика и объема наводнения, пика и продолжительности наводнения, а также объема и продолжительности наводнения [55, 56]; интенсивность и продолжительность засухи [45]; волны тепла и засуха [57].Таким образом, функция связки оказалась очень полезным и эффективным инструментом для многомерного гидрологического и климатологического анализа и моделирования.
Роза и Лейте [52] показали, что связки Фрэнка и Клейтона хорошо подходят для изучения взаимосвязи между максимальным потоком и объемом в Португалии.Чтобы установить связь между различными характеристиками паводков, Salarpour et al. [53] применили т-копулу на реке Джохор в Малайзии. Копула Гамбеля была выбрана в качестве наиболее подходящей модели для трехфакторного частотного анализа пиковых расходов, объемов гидрографов и концентраций взвешенных наносов в работе Безака и др. [54]. Также связка использовалась для описания пика и объема наводнения, пика и продолжительности наводнения, а также объема и продолжительности наводнения [55, 56]; интенсивность и продолжительность засухи [45]; волны тепла и засуха [57].Таким образом, функция связки оказалась очень полезным и эффективным инструментом для многомерного гидрологического и климатологического анализа и моделирования.
Математически копула — это многомерное распределение вероятностей, связывающее стандартные равномерно распределенные маргиналы. Предполагая, что X и Y являются парами случайных величин с кумулятивными функциями распределения (CDF), и. Согласно теореме Склара [58], совместная функция двумерного распределения X и Y , обозначенная как совокупная совместная вероятность, может быть затем сгенерирована следующим образом: определяется как функция копулы.
Предполагая, что X и Y являются парами случайных величин с кумулятивными функциями распределения (CDF), и. Согласно теореме Склара [58], совместная функция двумерного распределения X и Y , обозначенная как совокупная совместная вероятность, может быть затем сгенерирована следующим образом: определяется как функция копулы.
Здесь C (u, v) — произвольная двумерная функция копулы. Функция C имеет следующие элементарные свойства [59]: (1) Для каждых u и, (2) (3) Для каждых u 1, u 2 ,, и, если u 1 ≤ u 2 и ≤,
В литературе описано множество семейств связок (например, [59, 60]. Семейства копул различаются номерами параметров и структурой зависимости , которые имеют отношение к их сложности.Параметры связок контролируют силу зависимости. Эти параметры обычно оцениваются с использованием алгоритмов локальной оптимизации (например, [61–63], байесовского (например, [64, 65]), подхода L-моментов (например, [66]) и методов точного максимального правдоподобия) [ 67]). В этом исследовании для описания взаимозависимости между осадками и температурными переменными использовались пять функций копул: Гаусса, Стьюдента, Фрэнка, Клейтона и Гамбеля (Таблица 1). Эти связки принадлежат к семействам эллиптических (гауссово и t -копулы) [60] и архимедовых (копулы Франка, Клейтона и Гамбеля) [59].Обратите внимание, что эллиптические связки часто используются для простой структуры зависимостей [68, 69]. Следовательно, архимедово семейство связок более желательно для гидрологического анализа, потому что оно может быть легко построено и может применяться независимо от того, является ли корреляция между переменными положительной или отрицательной [56]. Эти связки были выбраны для анализа, потому что они обычно использовались для оценки взаимозависимости климатических переменных в гидрологических и климатологических исследованиях.
В этом исследовании для описания взаимозависимости между осадками и температурными переменными использовались пять функций копул: Гаусса, Стьюдента, Фрэнка, Клейтона и Гамбеля (Таблица 1). Эти связки принадлежат к семействам эллиптических (гауссово и t -копулы) [60] и архимедовых (копулы Франка, Клейтона и Гамбеля) [59].Обратите внимание, что эллиптические связки часто используются для простой структуры зависимостей [68, 69]. Следовательно, архимедово семейство связок более желательно для гидрологического анализа, потому что оно может быть легко построено и может применяться независимо от того, является ли корреляция между переменными положительной или отрицательной [56]. Эти связки были выбраны для анализа, потому что они обычно использовались для оценки взаимозависимости климатических переменных в гидрологических и климатологических исследованиях.
| ||||||||||||||||||
2.3. Процедура анализа
Доступные климатические данные сначала обрабатывались по следующим критериям: дни без осадков (<0,10 мм) были исключены из анализа, а все остальные дни были сгруппированы по сезонам (декабрь-январь-февраль (DJF), март-апрель- Май (MAM), июнь-июль-август (JJA) и сентябрь-октябрь-ноябрь (SON)).Чтобы соответствовать совместному распределению между температурой и осадками с использованием метода копул, была использована следующая процедура: (1) На первом этапе анализа выбирается адекватное маргинальное распределение (функция распределения вероятностей, PDF) для каждой из исследуемых переменных. Фактически, было выявлено маргинальное распределение среднесуточной температуры и суммы суточных осадков в исследуемом регионе. Определение подобранного распределения вероятностей позволяет прогнозировать вероятность превышения для определенной величины (квантиля) или величины, связанной с конкретной вероятностью превышения.Теоретических оснований для выбора распределения вероятностей и метода оценки параметров нет. В этом исследовании было подобрано двенадцать распределений вероятности для каждой сетки и сезона. Подгоняемые PDF-файлы: бета, экспонента, экстремальное значение, гамма, обобщенное экстремальное значение, обобщенное Парето, обратное гауссово, логистическое, лог-логистическое, логнормальное, нормальное и Вейбулла (см. Таблицу 2). В литературе представлено несколько методов оценки параметров, связанных с этими распределениями, то есть метод максимального правдоподобия (например, метод максимального правдоподобия).g., [70, 71]), метод моментов (например, [72]) и метод L-моментов (например, [73]).
Фактически, было выявлено маргинальное распределение среднесуточной температуры и суммы суточных осадков в исследуемом регионе. Определение подобранного распределения вероятностей позволяет прогнозировать вероятность превышения для определенной величины (квантиля) или величины, связанной с конкретной вероятностью превышения.Теоретических оснований для выбора распределения вероятностей и метода оценки параметров нет. В этом исследовании было подобрано двенадцать распределений вероятности для каждой сетки и сезона. Подгоняемые PDF-файлы: бета, экспонента, экстремальное значение, гамма, обобщенное экстремальное значение, обобщенное Парето, обратное гауссово, логистическое, лог-логистическое, логнормальное, нормальное и Вейбулла (см. Таблицу 2). В литературе представлено несколько методов оценки параметров, связанных с этими распределениями, то есть метод максимального правдоподобия (например, метод максимального правдоподобия).g., [70, 71]), метод моментов (например, [72]) и метод L-моментов (например, [73]). В данном исследовании использовался метод максимального правдоподобия. Выбор наиболее подходящего распределения для каждой переменной (то есть наилучшего соответствия предельного распределения данных сетки) основан на байесовском информационном критерии (BIC), предложенном Шварцем (1978). Наименьшие значения BIC определяют наиболее подходящее распределение [74]. (2) На втором этапе анализа кумулятивная функция распределения (CDF) этих распределений используется для вычисления предельных кумулятивных вероятностей и.Это вычисление предполагает, что F i и G i являются выбранными PDF для общего количества осадков и среднесуточной температуры для сетки и , соответственно. Обратите внимание, что и являются строго возрастающими функциями и находятся в пределах интервала [0, 1]. (3) На третьем этапе анализа пять функций копул (как определено в таблице 1) подгоняются к предельным кумулятивным вероятностям среднесуточной температуры. и общее количество осадков.
В данном исследовании использовался метод максимального правдоподобия. Выбор наиболее подходящего распределения для каждой переменной (то есть наилучшего соответствия предельного распределения данных сетки) основан на байесовском информационном критерии (BIC), предложенном Шварцем (1978). Наименьшие значения BIC определяют наиболее подходящее распределение [74]. (2) На втором этапе анализа кумулятивная функция распределения (CDF) этих распределений используется для вычисления предельных кумулятивных вероятностей и.Это вычисление предполагает, что F i и G i являются выбранными PDF для общего количества осадков и среднесуточной температуры для сетки и , соответственно. Обратите внимание, что и являются строго возрастающими функциями и находятся в пределах интервала [0, 1]. (3) На третьем этапе анализа пять функций копул (как определено в таблице 1) подгоняются к предельным кумулятивным вероятностям среднесуточной температуры. и общее количество осадков.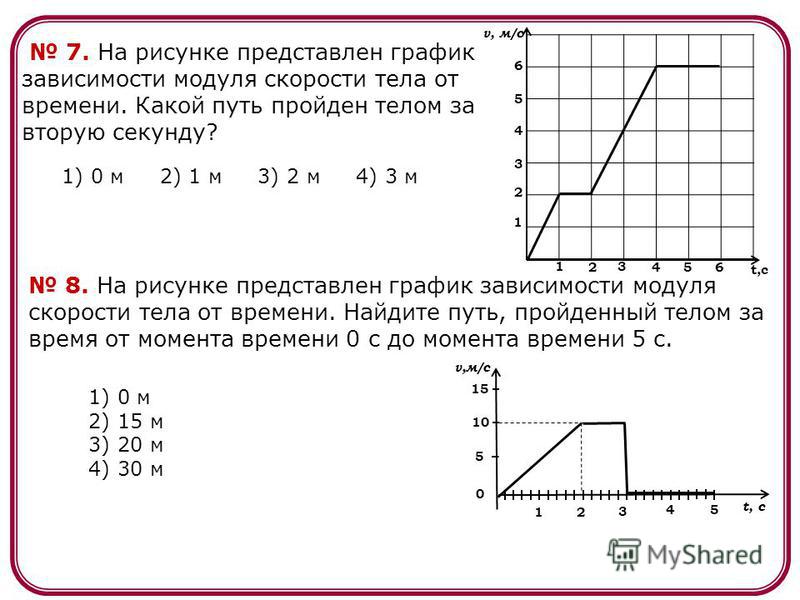 Для выбора подходящей (наиболее подходящей) функции копулы использовался метод, основанный на сравнении теоретических и эмпирических функций копулы.Подробно для каждой функции копул была рассчитана среднеквадратичная ошибка, определяемая как среднее квадратное расстояние между теоретической и эмпирической связками. Соответствующая копула каждой сетки — та, которая имеет наименьшую среднеквадратичную ошибку. Отметим, что параметры копулы оценивались с использованием метода точного максимального правдоподобия (EML) [67].
Для выбора подходящей (наиболее подходящей) функции копулы использовался метод, основанный на сравнении теоретических и эмпирических функций копулы.Подробно для каждой функции копул была рассчитана среднеквадратичная ошибка, определяемая как среднее квадратное расстояние между теоретической и эмпирической связками. Соответствующая копула каждой сетки — та, которая имеет наименьшую среднеквадратичную ошибку. Отметим, что параметры копулы оценивались с использованием метода точного максимального правдоподобия (EML) [67].
| ||||||||||||||||||||||||||||||||
После того, как совместное распределение каждой сетки установлено (включая поля, связку и их параметры), его можно использовать, например, для расчета совместного риска (вероятности). Совместная вероятность осадков и средняя температура очень важны для управления и оценки рисков, связанных с экстремальными метеорологическими и гидрологическими явлениями.Это помогает в управлении ресурсами, такими как производительность сельскохозяйственного сектора. Как правило, в двумерном случае могут быть интересны четыре одновременных события: (1) одновременное превышение { P ≥ p , T ≥ t }, (2) превышение-непревышение { P ≥ p , T ≤ t }, (3) непревышение-превышение { P ≤ p , T ≥ t }, и (4) одновременное непревышение { P ≤ p , T ≤ t }.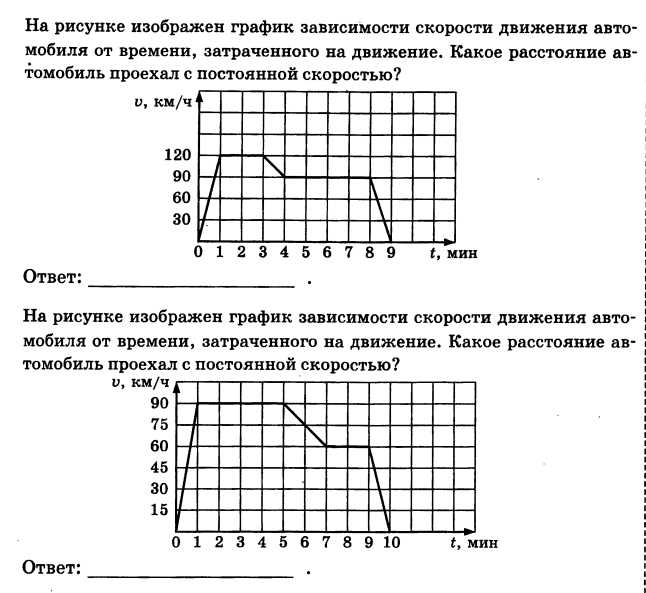 В этом исследовании мы в основном сосредоточились на вычислении вероятности одновременных экстремальных температурных явлений и осадков, включая влажные / прохладные (обозначается P w / c ) зимой (DJF) и сухие / жаркие (обозначается ). П д / ч ) летом (JJA). Следуя Чжоу и Лю [75], чтобы уловить большое количество событий, мы использовали квантильные пороги 25 th и 75 th T и P для определения этих двух вероятностей: где, соответственно , 25 -е и 75 -е квантильные пороги осадков и температуры.Чтобы количественно оценить полезность введения зависимости между осадками и температурой, эти две вероятности были рассчитаны для каждой сетки, предполагая, что P и T являются независимыми (обозначены как и) и зависимыми (обозначены как и) переменными. Следовательно, используя некоторые вероятностные манипуляции, они могут быть определены как где F и G — выбранные PDF для суточного общего количества осадков и среднесуточной температуры, а C представляет собой наиболее подходящие связки для выбранной сетки.
В этом исследовании мы в основном сосредоточились на вычислении вероятности одновременных экстремальных температурных явлений и осадков, включая влажные / прохладные (обозначается P w / c ) зимой (DJF) и сухие / жаркие (обозначается ). П д / ч ) летом (JJA). Следуя Чжоу и Лю [75], чтобы уловить большое количество событий, мы использовали квантильные пороги 25 th и 75 th T и P для определения этих двух вероятностей: где, соответственно , 25 -е и 75 -е квантильные пороги осадков и температуры.Чтобы количественно оценить полезность введения зависимости между осадками и температурой, эти две вероятности были рассчитаны для каждой сетки, предполагая, что P и T являются независимыми (обозначены как и) и зависимыми (обозначены как и) переменными. Следовательно, используя некоторые вероятностные манипуляции, они могут быть определены как где F и G — выбранные PDF для суточного общего количества осадков и среднесуточной температуры, а C представляет собой наиболее подходящие связки для выбранной сетки.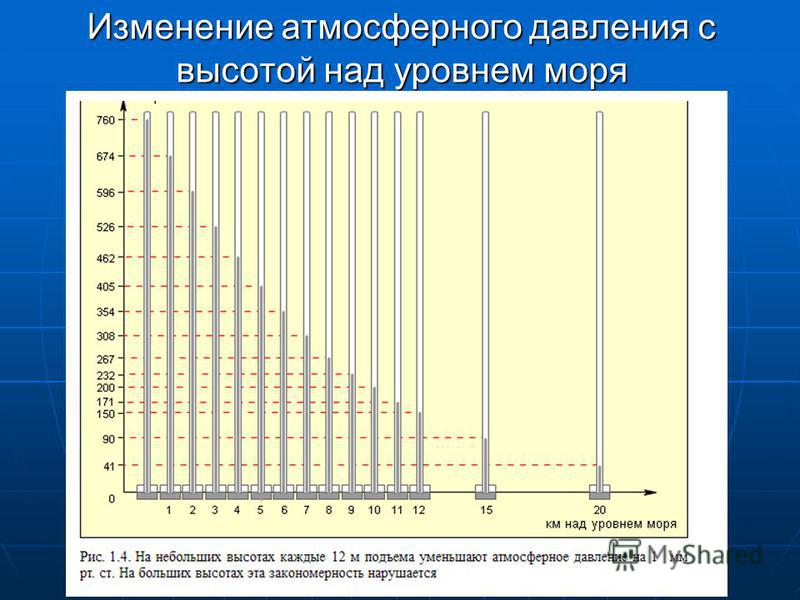 После вычисления этих вероятностей для каждой сетки изучаемого региона были разработаны две карты, показывающие различия вероятностей между зависимыми и независимыми (т. Е. Карта для и одна для). Эти карты показали наличие риска, не учтенного при оценке этих одновременных экстремальных явлений, путем игнорирования зависимости между температурой и осадками. Более подробная информация представлена в разделе «Результаты».
После вычисления этих вероятностей для каждой сетки изучаемого региона были разработаны две карты, показывающие различия вероятностей между зависимыми и независимыми (т. Е. Карта для и одна для). Эти карты показали наличие риска, не учтенного при оценке этих одновременных экстремальных явлений, путем игнорирования зависимости между температурой и осадками. Более подробная информация представлена в разделе «Результаты».
3. Результаты
Пространственная изменчивость среднемесячной температуры, которая была усреднена за период исследования для всех четырех сезонов, показана на Рисунке 2 (а).Высокая изменчивость температур между сезонами демонстрирует необходимость сезонного анализа копул для этого исследования, чтобы зафиксировать изменчивость и экстремальные явления. Среднемесячная температура колебалась от −20 до 3 ° C зимой (DJF), от −10 до 19 ° C весной (MAM), от 13 до 26 ° C летом (JJA) и от −5 до 20 ° C осенью (СЫН). В течение всех сезонов самые высокие температуры были обнаружены в юго-западной части (городские центры) недалеко от озера Онтарио и озера Эри в западной части области исследования. Самая низкая температура была обнаружена в северных (сельских) районах и на возвышенностях в северо-западной части исследуемой области. В целом, что касается пространственной изменчивости, мы наблюдали градиент примерно + 5 ° C с юго-запада на север по всему исследуемому региону.
Самая низкая температура была обнаружена в северных (сельских) районах и на возвышенностях в северо-западной части исследуемой области. В целом, что касается пространственной изменчивости, мы наблюдали градиент примерно + 5 ° C с юго-запада на север по всему исследуемому региону.
Пространственная изменчивость общего количества осадков по сезонам и усредненная по времени за исследуемый период показана на Рисунке 2 (b). Сумма месячных осадков варьировала от 178 до 285 мм для DJF, от 185 до 240 мм для MAM, от 195 до 265 мм для JJA и от 208 до 315 мм для SON.Изменчивость общего сезонного количества осадков была пространственно более сложной, чем средняя температура, что отражало комбинированное воздействие на состояние поверхности и топографию. Наименьшее количество осадков выпало в восточной и южной частях исследуемого региона рядом с озером Онтарио и озерами Эри, но с максимумом осадков в западной части, недалеко от озера Гурон и залива Джорджиан, с осени до весны (т. Е. Снег- эффект озера).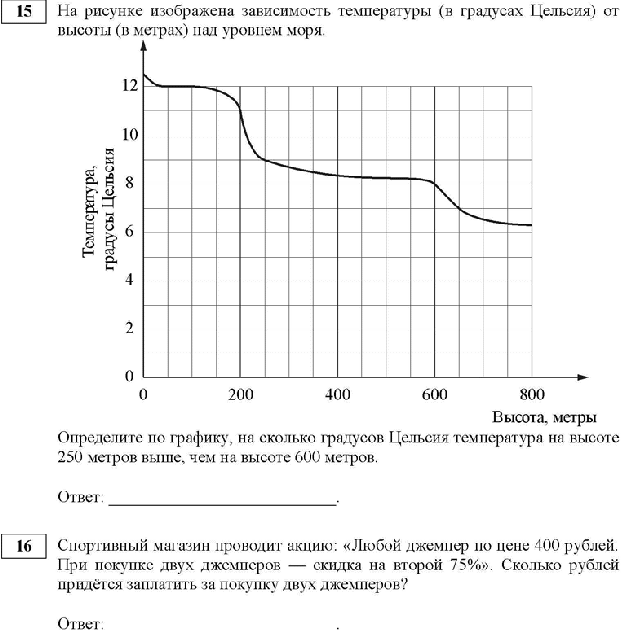 Дневное отопление / охлаждение и режим ветра у озер был более изменчивым по сравнению с районами, расположенными дальше от суши.Повышенная изменчивость этих береговых ветров могла способствовать более низкому / большему количеству осадков рядом с озерами в самом южном / крайнем западном Онтарио. Районы с наибольшим ежемесячным количеством осадков наблюдались в западной и северной частях исследуемого региона к востоку от залива Джорджиан Бэй, и озеро Гурон также является высокогорным сектором по сравнению с южной частью исследуемого участка и более высоким лесным покровом. На погодные условия в этой области также больше повлияли осадки или известные снежные полосы, простирающиеся к востоку от озера Гурон и залива Джорджиан на западе.Эти региональные влияния, возможно, способствовали увеличению количества осадков в этой части исследуемой области. В целом, высокая сезонная изменчивость (стандартное отклонение не показано) была обнаружена в течение осеннего и зимнего сезонов по сравнению с изменчивостью весной и летом.
Дневное отопление / охлаждение и режим ветра у озер был более изменчивым по сравнению с районами, расположенными дальше от суши.Повышенная изменчивость этих береговых ветров могла способствовать более низкому / большему количеству осадков рядом с озерами в самом южном / крайнем западном Онтарио. Районы с наибольшим ежемесячным количеством осадков наблюдались в западной и северной частях исследуемого региона к востоку от залива Джорджиан Бэй, и озеро Гурон также является высокогорным сектором по сравнению с южной частью исследуемого участка и более высоким лесным покровом. На погодные условия в этой области также больше повлияли осадки или известные снежные полосы, простирающиеся к востоку от озера Гурон и залива Джорджиан на западе.Эти региональные влияния, возможно, способствовали увеличению количества осадков в этой части исследуемой области. В целом, высокая сезонная изменчивость (стандартное отклонение не показано) была обнаружена в течение осеннего и зимнего сезонов по сравнению с изменчивостью весной и летом.
На рис. 3 (а) показана пространственная изменчивость ранговой корреляции Спирмена между дневными данными с общим количеством осадков и среднесуточной температурой для всех четырех сезонов. Значения p соответствующего критерия значимости показаны на рисунке 3 (b).Два основных преимущества теста ранговой корреляции Спирмена по сравнению с простым тестом линейной корреляции заключаются в следующем: (1) его можно вычислить без каких-либо предположений о нормальном распределении данных и (2) он имеет низкую чувствительность для неоднородных временных рядов. Эта корреляция использовалась для анализа тенденций в климатологических и гидрологических временных рядах [76]. Обнаружена положительная ранговая корреляция между суточной суммой осадков и средней температурой на исследуемой территории для всех четырех сезонов.В пространственном отношении корреляция находилась в наиболее значимой точке сетки на всей территории исследования. Наибольшая корреляция наблюдалась в западных районах весной и осенью. Также высокая корреляция наблюдалась в центральных частях исследуемой области, прилегающей к озерам Эри и Гурон летом, но с низкими значениями корреляции за пределами этой области. Этот центральный и южный регион был пропорционально теплее, и количество туманов было выше, чем в других местах исследуемой области. Исаак и Стюарт [21] показывают, что в 90% дней, когда возникал туман, также сообщалось об осадках.Поэтому ожидалось, что в части исследуемого участка с обычными туманными днями будет большое количество дней с осадками. В целом, как предположили Исаак и Стюарт [21] из исследования в масштабе станции, больше осадков выпадает в теплые погодные условия зимой над южным Онтарио и Квебеком.
Также высокая корреляция наблюдалась в центральных частях исследуемой области, прилегающей к озерам Эри и Гурон летом, но с низкими значениями корреляции за пределами этой области. Этот центральный и южный регион был пропорционально теплее, и количество туманов было выше, чем в других местах исследуемой области. Исаак и Стюарт [21] показывают, что в 90% дней, когда возникал туман, также сообщалось об осадках.Поэтому ожидалось, что в части исследуемого участка с обычными туманными днями будет большое количество дней с осадками. В целом, как предположили Исаак и Стюарт [21] из исследования в масштабе станции, больше осадков выпадает в теплые погодные условия зимой над южным Онтарио и Квебеком.
На рис. 4 (а) показано наиболее подходящее распределение (PDF) для сезонной среднесуточной температуры с 1951 по 2013 год для исследуемой области. Чтобы показать пространственное и временное изменение PDF, которое может существовать на крайних концах исследуемой области, были выбраны две сетки: одна на самом дальнем северо-востоке (сетка 1), а другая на самом дальнем юго-западе (сетка 1699) (рис. (б)).Было обнаружено, что отобранное распределение варьируется в зависимости от времени года и пространства между двумя краями исследуемой области. В течение зимнего сезона, исходя из средней температуры, исследуемая территория была сгруппирована в два разных региона на основе временного распределения данных: (1) юго-западная часть, которая следовала кривой нормального распределения, и (2) северо-восточная часть, которая следовала кривой распределения GEV. с высоким отрицательным параметром формы (тип III ГЭВ). Параметр формы принадлежал узкому диапазону, примерно от -8 до -10.Экстремально низкие температуры зимой в северо-восточной части исследуемого региона могут объяснить использование GEV III (рис. 4 (b), красная кривая). ГЭВ с положительным параметром формы (тип II ГЭВ) показал наилучшее распределение ГЭВ для весеннего и осеннего сезонов. Параметр формы варьировался в пространстве от 2 до 5 весной и от 5,5 до 9,5 осенью. Наблюдаемое изменение параметров формы можно объяснить большой временной изменчивостью среднесуточной температуры в течение этих двух сезонов с нелинейными обратными связями в зависимости от снежного покрова и мерзлых условий земли, что влияет на диабатические потоки и лежащий в основе процесс нагрева / охлаждения. (Рисунок 4 (б)).Положительное значение параметра формы подразумевает распределение с тяжелым хвостом. Распределение данных весной и осенью показывает, что экстремальные значения встречались чаще по сравнению с другими значениями. Двухпараметрическое распределение Вейбулла с большой положительной формой наблюдалось для летних данных (рис. 4 (b)).
На рис. 5 показано наиболее подходящее распределение общего сезонного количества осадков с 1951 по 2013 год для исследуемой области (5A) и PDF суточных сумм осадков в сетках 1 и 1699 для разных сезонов (5B).Было обнаружено, что наиболее подходящее распределение изменялось пространственно и сезонно с высокой пространственной изменчивостью весной и летом. Это был ожидаемый результат из-за высокой пространственной изменчивости процессов выпадения осадков в эти сезоны. Было обнаружено, что логнормальное (LN) и обобщенное Парето (GP) распределения являются наилучшими для соответствия ежедневным данным в течение всех четырех сезонов. Распределение LN предполагает, что логарифм суточного общего количества осадков распределен нормально и полезно, когда интересующая переменная смещена вправо.Было обнаружено, что LN является наилучшим распределением в сетках для соответствия с пропорционально низким количеством осадков. Кроме того, было обнаружено, что GP является лучшим распределением для соответствия данным в сетках с большим суточным количеством осадков.
На рисунке 6 показана среднеквадратичная ошибка (MSE) между теоретическими и эмпирическими функциями копулы для всех 1699 сеток. Для каждой сетки лучшая функция копулы, которая соответствует совместному распределению осадков и температуры, — это та, которая минимизирует MSE. В общем, ни одна связка не подходила для всех сезонов и / или сеток.Это ожидалось из-за различий в географических и геофизических условиях в регионе, которые влияют на колебания температуры и количества осадков. Менее изменчивость лучшей связки наблюдалась зимой и летом по сравнению с изменчивостью лучшей связки весной и осенью. Вариации копулы можно объяснить тем фактом, что температура имеет один и тот же положительный знак для всех сеток зимой и летом (т.е. положительный для лета и отрицательный для зимы), чего не происходит весной и осенью (тогда как положительный знак температуры зависит от выбранную сетку).Гамбель оказалась лучшей связкой зимой, а копула Клейтона — лучшей связкой летом. Эти две связки асимметричны и принадлежат к семейству Архимедов. Копула Гамбеля используется для моделирования сильных зависимостей в правом хвосте, а это означает, что больше осадков зимой обычно связано с теплой погодой в этом регионе. Фактически, более теплый воздух может содержать больше водяного пара, чем более холодный воздух, что может привести к более высокой вероятности более интенсивных осадков (например, соотношение Клаузиуса-Клапейрона).Следовательно, копула Клейтона используется для моделирования сильных зависимостей в левом хвосте, объясняя зависимость между небольшим количеством осадков и экстремальной температурой летом. Из-за механизмов, упомянутых ранее в этом разделе, большая изменчивость температуры и осадков в весенний и осенний сезоны приводит к большей изменчивости с точки зрения лучших связок в течение этих двух сезонов.
В этом разделе представлено приложение, демонстрирующее влияние игнорирования зависимости между температурой и осадками на оценку рисков экстремальных явлений, таких как влажно / прохладно зимой и сухо / жарко летом.На рисунке 7 показаны различия между вероятностями одновременных экстремальных значений, вычисленные путем принятия P и T в качестве зависимых и независимых переменных. Мы обнаружили, что в целом различия положительные (варьируются от 8 до 14%), что означает, что игнорирование зависимости приводит к недооценке вероятности возникновения событий влажный / прохладный и сухой / жаркий до 14% в южном Онтарио. Кроме того, мы заметили, что вероятность различий выше в случае события влажный / холодный по сравнению с случаем сухого / горячего события.Это можно объяснить тем, что в этом регионе количество осадков и температуры больше коррелировано зимой, чем летом. В частности, различия более значительны в городских центрах вблизи озера Онтарио. В заключение, этот анализ показывает, что корреляции между P и T имеют прямое влияние на оценку риска возникновения одновременных климатических явлений.
Другой пример полезности моделирования риска экстремального явления на основе совместного распределения температуры и осадков, в отличие от модели, основанной на этих двух переменных по отдельности, показан на рисунке 8.Фактически, этот рисунок показывает пространство между температурой и осадками по сетке 1682 (т. Е. Область Торонто) для четырех сезонов. Контуры представляют собой двумерную квантильную кривую для различных одновременных непревышающих событий. Обратите внимание, что функция квантиля выражает величину события с точки зрения вероятности его превышения или непревышения, что также связано с периодами повторяемости. Кривая квантиля состоит из двух частей: наивной части (хвост) и собственной части (центральной). Наивная часть состоит из двух сегментов, начинающихся на концах правой части.Подробное описание и свойства двумерной квантильной функции можно найти в Chebana and Ouarda [77]. Для примера сетки 1682 зимой, для значения риска p = 0,9, одномерные значения квантилей осадков и температуры составляют 10 мм и 5 ° C, соответственно. Фиолетовая кривая на рисунке 8 представляет двумерный квантиль, извлеченный из совместного распределения. Обратите внимание, что комбинация одномерных значений (осадки = 10 мм и температура = 5 ° C) не относится к двумерной квантильной кривой.Эта комбинация соответствует другому риску ( p ), меньшему, чем фактический риск p = 0,9. Следовательно, неправильный вывод (с точки зрения величины и периода повторяемости) может быть сделан без учета совместного или смешивающего распределения. Общность двумерной квантильной функции, которая может дать несколько возможных сценариев, связанных с одним и тем же риском p , не относится к одномерному квантилю. Одномерный квантиль представляет собой крайние точки соответствующей части двумерной квантильной кривой, обозначенной черным пунктиром на рисунке 8.
4. Обсуждение
В этом исследовании использовался подход, основанный на связках, для определения внутренней сезонной зависимости между средней температурой и общим ненулевым количеством осадков при суточном разрешении на юге Онтарио. Мы обнаружили положительную корреляцию между температурой и количеством осадков во всем регионе. Наши аналитические результаты согласуются с предыдущими исследованиями, опубликованными в литературе, которые указывают на положительную корреляцию между осадками и температурой в этом регионе (например,g., [21, 78]), но с другим выводом, как в работе Тренберта и Ши [28], в которой они объединяют все «более теплые» месяцы с мая по сентябрь. Исаак и Стюарт [21] вычислили индекс температуры-осадков, который вычисляет процент осадков на основе температур ниже средней дневной температуры для 51 канадской метеорологической станции. Они сообщают о положительной корреляции зимой для всех станций, расположенных в южном Онтарио и Квебеке.
Результаты этого исследования являются важным шагом вперед для характеристики и количественной оценки нелинейной зависимости между осадками и температурой в районе, который склонен к возникновению экстремальных погодных явлений и имеет глубокое социальное и экономическое значение для Канады.Предлагаемый подход, продемонстрированный здесь, является гибким и свободным от предположений. Фактически, смоделированная структура зависимости не требует нормальности предельных распределений переменных, что обеспечивает гибкость в коррелирующих переменных, а также предотвращает необходимость подобных предельных распределений.
Мы обнаружили, что копулы Гамбеля и Клейтона являются наиболее подходящими для описания зависимости между температурой и осадками зимой и летом, соответственно. Гамбель и Клейтон представляют собой две асимметричные связки с правой (Гамбель) и левой (Клейтон) хвостовой зависимостью [79].Это объясняет значительную корреляцию между экстремальной температурой и экстремальным количеством осадков в этом регионе в эти сезоны. Механически это показывает, что в целом в холодную погоду зимой выпадает меньше осадков, а осенью в теплую погоду выпадает больше. Асимметричные связки лучше подходят для выявления нелинейной корреляции между температурой и осадками в этой области.
5. Заключение
В этой статье был представлен подход, основанный на связках, для моделирования сезонного совместного или смешанного распределения температуры и осадков.Предлагаемый подход является гибким и свободным от предположений. Пять членов копул, принадлежащих к трем семействам, были приспособлены к 1699 сеткам (разрешение ∼10 км × 10 км) в южном Онтарио. Для каждой сетки был вычислен информационный критерий с использованием эмпирических и теоретических связок, и наиболее подходящая связка была выбрана на основе силы нелинейных корреляций. Моделирование совместного распределения осадков и температуры поможет улучшить моделирование погодных явлений, что может помочь повысить точность оценки рисков.
Результаты показали, что ни одна связка не работала стабильно как лучшая связка для всех четырех сезонов и для всего региона. Гамбель выглядел как наиболее подходящая связка для зимы, а связка Клейтона — как наиболее подходящая связка для лета. Большая изменчивость с точки зрения наилучшей связки была обнаружена весной и осенью, что может быть связано с колебаниями температуры во время определенных событий или пороговых значений (например, около 0 ° C) между точками сетки и смешением типов осадков, которые могут привести к различным связям. с температурой (как отмечено в [28]).Путем извлечения многомерных и одномерных квантилей, связанных с заранее выбранным риском, было обнаружено, что игнорирование совместного или смешивающего / комбинированного распределения осадков и температуры может привести к недооценке риска экстремального события. Такая недооценка может привести к неверному истолкованию и неправильному выводу о сроках возврата. Наше исследование также показывает, что взаимосвязи и физика комбинированного возникновения осадков и температурных явлений должны приниматься во внимание при интерпретации климатических изменений и в анализе климатических рисков.
Экстремальные метеорологические переменные могут оказывать значительное влияние на экосистемы и общество в результате возникновения экстремальных погодных явлений. Оценка потенциального риска экстремальных климатических переменных имеет решающее значение для политики устойчивости и смягчения негативных последствий климатических изменений. Потенциально ценным расширением этого исследования является анализ трехкомпонентной связки, позволяющий связать количество осадков и температуры с планированием растениеводства, экономикой сельского хозяйства и оценкой паводков.Такое исследование может быть использовано при разработке стратегий снижения рисков для фермеров и лиц, принимающих решения, которые будут приобретать все большее значение перед лицом изменения климата и связанных с ним изменений в экстремальных условиях, круговороте воды и гидрометеорологических опасностях.
Доступность данных
Ежедневные данные CanGrid, используемые в этом исследовании, получены со следующего веб-сайта: ftp://ftp.nrcan.gc.ca/pub/outgoing/canada_daily_grids.
Конфликт интересов
Авторы заявляют, что у них нет конфликта интересов.
Благодарности
Финансовая поддержка этого исследования была предоставлена Советом по естественным и инженерным исследованиям (NSERC) Канады в рамках проекта FloodNet. Авторы также благодарят исследователей из Министерства природных ресурсов Канады и Министерства охраны окружающей среды и изменения климата Канады за их вклад в предоставление наборов климатических данных.
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, используйте кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или уточнить у системного администратора.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файлах cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Температурная зависимость поведения упругой и пластической деформации тугоплавкого высокоэнтропийного сплава
Реферат
Однофазные твердорастворные тугоплавкие высокоэнтропийные сплавы (ВЭА) демонстрируют замечательные механические свойства, такие как высокий предел текучести и существенное сопротивление размягчению при повышенных температурах.Следовательно, углубленное изучение поведения при деформации объемно-центрированных кубических (ОЦК) огнеупорных ВЭС является критически важным вопросом для изучения открытых / уникальных механизмов деформации. Мы исследовали упругой и пластической деформации поведение одного ВСС NbTaTiV огнеупорного АЭМ при повышенных температурах с использованием комплексных экспериментальных усилий и теоретических расчетов. Результаты нейтронной дифракции in situ показывают, что упругая анизотропная деформация зависит от температуры. Модули упругости монокристалла и макроскопические модули Юнга, сдвига и объемного сжатия были определены с помощью дифракции нейтронов in situ, что показало хорошее согласие с расчетами из первых принципов, результатами машинного обучения и резонансной ультразвуковой спектроскопией.Более того, поведение краевой дислокации при пластической деформации, которое отличается от обычных ОЦК-сплавов, было количественно описано с помощью моделирования профиля графика Вильямсона-Холла и многоугловой кольцевой сканирующей электронной микроскопии в темном поле.
ВВЕДЕНИЕ
Высокоэнтропийные сплавы (ВЭА) определяются как эквимолярные или неэквимолярные одно- и многофазные твердые растворы, в зависимости от количества и типа основных / вторичных металлических элементов с конфигурационной энтропией больше 1.61 R , (где R — газовая постоянная) ( 1 , 2 ). Минимизация свободной энергии Гиббса за счет увеличения конфигурационной энтропии приводит к образованию одно- или многофазного твердого раствора, такого как объемно-центрированный кубический (ОЦК) ( 3 ), гранецентрированный кубический (ГЦК) ( 4 ) и / или гексагональные плотноупакованные фазы твердых растворов ( 5 ) вместо интерметаллических соединений ( 6 ). Более того, случайное распределение множества элементов с разными атомными радиусами приводит к сильно искаженной решетке с вариациями межатомных расстояний вдоль кристаллографического направления элементарных ячеек ( 3 ).Эти характеристики, в свою очередь, способствуют желаемым механическим свойствам, таким как высокая твердость, прочность, пластичность и сопротивление размягчению при комнатной температуре (RT) и повышенных температурах ( 3 ).
Чтобы определить происхождение этих желаемых механических свойств, были предприняты теоретические усилия по проверке механизмов деформации с учетом упругих и пластических деформаций в огнеупорных HEA BCC ( 7 ). В отличие от обычных ОЦК-сплавов, которые имеют узкое распределение межатомных расстояний, HEA имеют более широкий диапазон длин связей и межатомных взаимодействий в элементарной ячейке, что может играть роль в уникальном поведении упругой и пластической деформации при комнатной температуре и высоких температурах.
Недавно Тиан и др. . ( 7 ) предложил стратегии проектирования сплавов для разработки упруго-изотропных HEA (системы TiZrNbMoV x ) с использованием современного моделирования ab initio. Согласно их расчетам, огнеупорные ВЭЗ TiZrNbMo y V x [где ( x , y ) равны (0, 0,9) и (0,5, 0,8)] демонстрируют упруго-изотропную деформацию. , что сильно коррелирует со значением концентрации валентных электронов (VEC) ( 7 ).Кроме того, эти предыдущие исследования предоставляют критерии для оценки хрупко-пластичного поведения на основе упругих постоянных монокристаллов, предсказывая, что некоторые системы BCC HEA могут быть пластичными ( 7 — 9 ). Однако применимость этих теоретических методов расчета для проектирования упруго-изотропных и пластичных ВСС ОЦК все еще обсуждается и не имеет экспериментальной проверки ( 7 , 10 ), что является критически важным вопросом в сообществе HEA.
Для того, чтобы продемонстрировать эти предсказанные необычное поведение деформации, мы исследовали упругой и пластической деформации поведение для огнеупорного АЭМ NbTaTiV BCC при комнатной температуре и при повышенных температурах, с использованием нейтронных экспериментов на места и теоретических подходов в. В отличие от обычных сплавов BCC ( 11 ), эволюция деформации решетки и измеренные дифракционные модули упругости указывают на упруго-изотропное поведение при комнатной температуре. Величины монокристаллических и макроскопических модулей упругости, полученные с помощью нейтронных экспериментов на месте и резонансной ультразвуковой спектроскопии (RUS), соответственно, сравниваются с теоретическими расчетами, включая вычисления из первых принципов и подходы машинного обучения (ML).Кроме того, обнаружено, что настоящий огнеупорный HEA из NbTaTiV указывает на отсутствие сильной зависящей от температуры упругой анизотропной деформации при повышенных температурах, что является нетипичным поведением при упругой деформации по сравнению с другими традиционными металлическими материалами ( 12 — 15 ).
Отличная пластичность настоящего огнеупорных АЭЙ может быть предсказано соотношением между поликристаллическим упругими модулями, такими как давление Коши ( C 12 — C 44 ) ( 16 ), соотношение Pugh [модуль объемной упругости ( K ) / модуль сдвига ( G )] ( 8 ) и коэффициент Пуассона (ν) ( 9 ).Кроме того, мы исследовали тип подвижных дислокаций с помощью нейтронографического моделирования и анализа уширения пиков с использованием метода графика Вильямсона-Холла ( 17 ), экспериментально подтвержденного с помощью многоугольного кольцевого сканирования темного поля (HAADF). метод просвечивающей электронной микроскопии (STEM). Установлено, что преобладающим типом подвижных дислокаций при пластической деформации могут быть краевые дислокации, в отличие от обычных ОЦК-металлов. Эти новые открытия уникальных упругой и пластической деформации поведения в огнеупорной АЭМ NbTaTiV будет способствовать развитию возможных систем сплавов для структурных материалов приложений.
РЕЗУЛЬТАТЫ
Формирование единого твердого раствора BCC и механические свойства гомогенизации обработанных NbTaTiV АЭМ при повышенных температурах
микроструктура гомогенизируют NbTaTiV огнеупорного АЭМ характеризовался, с использованием сканирующей электронной микроскопии (SEM) обратного рассеяния электронов ( BSE), как показано на рис. 1A. Типичная простая микроструктура твердого раствора HEA с размером зерен от 200 до 400 мкм была идентифицирована без присутствия вторичных фаз или сегрегации элементов.Химический состав образца был подтвержден (с использованием анализа точечной энергодисперсионной рентгеновской спектроскопии) и составлял Nb 23,8 Ta 25,5 Ti 24,9 V 25,8 , что указывает на однородное распределение элементов в почти эквиатомном процентном соотношении. . Измеренные картины ND массивных образцов, как показано на рис. 1B, подтверждают наличие единственного твердого раствора BCC при комнатной температуре и повышенных температурах. Параметры решетки данного сплава при RT, 500 °, 700 ° и 900 ° C, которые были определены методом подгонки одного пика ( 18 ), равны 3.2318, 3,2445, 3,2511 и 3,2588 Å соответственно. Одиночная фаза ОЦК стабильна до 900 ° C, что свидетельствует о превосходной фазовой стабильности при повышенных температурах. На рисунке 1С показаны номинальные кривые истинного напряжения-деформации при сжатии, полученные в результате нейтронного измерения in situ гомогенизирующего сплава NbTaTiV при комнатной температуре, 500 °, 700 ° и 900 ° C с расчетной скоростью деформации 1 × 10 . −4 с −1 , которые были получены непосредственно из нейтронных измерений in situ. Предел текучести (σ y ) и показатель деформационного упрочнения ( N ) настоящего сплава постепенно снижались с 1064 МПа (RT) до 595 МПа (900 ° C) и с 0.От 2732 (RT) до 0,1199 (900 ° C) соответственно. Показатель деформационного упрочнения ( N ) был оценен для различных экспериментальных температур с использованием уравнения Холломона ( 19 ) σt = kεtN (1), где σ t — истинное приложенное напряжение, k — напряжение коэффициент упрочнения, а ε t — истинная пластическая деформация. Во время пластической деформации приложенная нагрузка слегка расслабляется, а время записи нейтронов было установлено примерно на 20 мин с режимом контроля постоянного смещения при 700 ° C.Более того, это релаксационное поведение становится более выраженным при 900 ° C (примерно от 440 до 580 МПа) по сравнению с 700 ° C (примерно от 130 до 260 МПа), представленным на рис. 1C.
Рис. 1. Микроструктуры, фазовые характеристики и механические свойства гомогенизированного сплава NbTaTiV, исследованные с помощью SEM, ND, и кривые номинального напряжения сжатия и истинной деформации во время экспериментов in situ при повышенных температурах.( ) СЭМ-BSE изображение гомогенизации обработанного NbTaTiV огнеупорного HEA.( B ) Картины ND с пиками, индексированными для BCC-структуры при комнатной температуре, 500 °, 700 ° и 900 ° C, соответственно. а.е., условные единицы. ( C ) Истинные кривые напряжение-деформация, записанные во время эксперимента по сжатию на месте при комнатной температуре, 500 °, 700 ° и 900 ° C со скоростью деформации 1 × 10 -4 с -1 .
Эволюция деформации решетки гомогенизированного сплава NbTaTiV при комнатной температуре и повышенных температурах
Для исследования поведения при упругой деформации зерен с различной ориентацией были проведены испытания на сжатие гомогенизированного сплава NbTaTiV на месте с испытанием на сжатие.На рисунке 2 показана эволюция соответствующей деформации решетки (ε hkl ) в осевом и поперечном направлениях плоскостей {110}, {200}, {211} и {310} во время упругой деформации при различных температурах (RT , 500 °, 700 ° и 900 ° C). Деформации решетки были получены из следующего уравнения: hkl = dhkl-dhklidhkli (2), где d hkl — это hkl шаг решетки соответствующего приложенного напряжения, а dhkli — hkl шаг решетки до нагрузки.Наклон эволюции деформации решетки в зависимости от приложенного напряжения во время упругой деформации определяет дифракционные упругие постоянные для конкретных плоскостей { hkl }. Было обнаружено, что изменение дифракционных упругих постоянных среди всех зерен четко не наблюдается, что указывает на упруго-изотропную деформацию, как показано на фиг. 2А.
Рис. 2 Эволюция деформации решетки в HEA огнеупора NbTaTiV в зависимости от приложенного напряжения, полученная в ходе экспериментов in situ ND во время упругой деформации, и графики модулей упругости кристаллов с разной ориентацией как функции фактора упругой анизотропии и соответствия модели Kroner, Voigt и Reuss при комнатной температуре, 500 °, 700 ° и 900 ° C.Соответствующие деформации решетки плоскостей ориентации {110}, {200}, {211} и {310} в осевом и поперечном направлениях во время упругой деформации при ( A ) RT, ( B ) 500 ° C , ( C ) 700 ° C и ( D ) 900 ° C соответственно. Обратные дифракционные упругие модули (1/ E hkl и ν hkl / E hkl ) как функция фактора упругой анизотропии, A hkl (h3k2 + l2 + k2h3 (h3 + k2 + l2) 2), которые получены из экспериментальных (Exp.) упругой деформации решетки (символы) и аппроксимированы моделями Кронера, Фойгта и Ройсса (сплошные линии) при ( E ) RT, ( F ) 500 ° C, ( G ) 700 ° C и () H ) 900 ° С соответственно.
В отличие от эволюции деформации решетки при RT, наблюдаются разные наклоны деформации решетки в зависимости от приложенных напряжений при повышенных температурах из-за повышенной упругой анизотропии, как показано на рис. 2 (от B до D). При более высоких температурах, когда общая жесткость уменьшается, анизотропия увеличивается.Зерно {200} демонстрирует самую большую упругую деформацию решетки при самой низкой жесткости, а зерна {310} испытывают вторую по величине упругую деформацию с почти линейным откликом. Принимая во внимание, что зерна {110} и {211} имеют более низкую деформацию решетки и более высокое отношение прочности к жесткости по направлению, чем другие ориентации, дифракционные упругие модули, E hkl , различных кристаллографических плоскостей при повышенных температурах (перечислены в таблице S1) демонстрируют практически одинаковые значения модулей упругости в разных ориентациях.Эта тенденция указывает на то, что NbTaTiV HEA демонстрирует уникальное поведение при упругой изотропной деформации при комнатной температуре. Более того, упругая анизотропия постепенно увеличивается при повышенных температурах, но изменение увеличения незначительно, что можно отличить от других обычных сплавов ( 12 — 14 ).
Расчеты и измерения монокристаллических модулей упругости для сплава NbTaTiV с помощью модели Кронера и методики RUS
Чтобы лучше понять лежащее в основе упругое деформационное поведение сплава NbTaTiV как функцию температуры, макроскопической упругости, сдвига и Модули объемного сжатия ( E M , G M и K M ) получены из дифракционных модулей упругости ( E hkl ) и коэффициента Пуассона (ν) с помощью теоретических моделей. .Тремя наиболее широко применяемыми теоретическими моделями для определения макроскопических модулей упругости являются модели Фойгта, Рейсса и Кронера соответственно ( 20 , 21 ).
На рисунке 2 (от E до H) показаны модули упругости обратной дифракции (1/ E hkl и ν hkl / E hkl ) как функция коэффициента упругой анизотропии, A hkl , [h3k2 + k2l2 + l2h3 (h3 + k2 + l2) 2], которые получены из экспериментальной упругой деформации решетки и рассчитаны по моделям Фойгта, Рейсса и Кронера при комнатной температуре и повышенных температурах ( 20 , 21 ).Результаты, представленные на рис. 2 (от E до H), показывают, что модель Кронера лучше всего согласуется с экспериментальными данными для всех температурных диапазонов по сравнению с моделями Фойгта и Рейсса. Обратите внимание, что абсолютные процентные значения SE при подгонке модели Кронера составляют 2,46, 6,34, 3,15 и 8,85% для RT, 500 °, 700 ° и 900 ° C, соответственно, что свидетельствует о приемлемой точности расчетных значений упругих постоянных монокристалла. Эти две теоретические модели рассматривают только однородные деформации (Фойгт) или напряжения (Рейсс) во всех зернах во время непрерывного нагружения.С другой стороны, модель Кронера учитывает изменение напряжений и деформаций среди всех зерен. Таким образом, самосогласованная модель Кронера, которая является наиболее подходящим прикладным методом расчета для определения макроскопических модулей упругости по дифракционным модулям упругости для систем HEA ( 20 , 21 ), была применена к результатам эволюции деформации решетки для получения макроскопические модули упругости. Подробные процессы расчета для модели Кронера описаны в разделе S1.
Рассчитанные монокристаллические упругие постоянные, C ij , макроскопическая упругость ( E M ), сдвиг ( G M ), объемные ( K M ) модули и Коэффициент Пуассона (ν) при комнатной температуре и повышенных температурах приведен в таблице 1. При повышении температуры до 700 ° C изменение ° C 11 становится более выраженным по сравнению с ° C 12 и К 44 900 26.Эти результаты предполагают, что продольная деформация в значительной степени вызывает изменение объема. Это изменение объема тесно связано с температурой и, таким образом, соответствует относительно большому изменению ° C 11 . Следовательно, модуль четырехугольного сдвига, C ‘ = [( C 11 — C 12 ) / 2], существенно уменьшается с постепенно уменьшающимися модулями упругости, сдвига и объемного сжатия. Более того, по сравнению с упругими постоянными при 700 ° C, значения C 11 и C 12 резко снижаются при 900 ° C, в то время как C 44 остается почти постоянным при RT, 500 °, 700 ° и 900 ° C, что приводит к небольшому изменению модуля тетрагонального сдвига, C ′ .Этот результат подразумевает упругую устойчивость этого ОЦК ВЭА против деформации тетрагонального сдвига.
Таблица 1 Экспериментально и теоретически полученные монокристаллические и макроскопические модули упругости сплава NbTaTiV при повышенных температурах.Упругие постоянные монокристалла, C 11 , C 12 и C 44 ; макроскопические упругие ( E M ), сдвиговые ( G M ) и объемные ( K M ) модули; и коэффициент Пуассона (ν) при RT, 500 °, 700 ° и 900 ° C получены из дифракционных модулей упругости с использованием модели Кронера, RUS (RT), расчет из первых принципов (−273 ° C и RT), и подход ML (RT).
Дальнейший анализ модулей упругости был выполнен с использованием RUS. Упругие постоянные, C ij , были определены из ~ 45 резонансов, где частоты находились в диапазоне от 100 до 650 кГц, с использованием итеративно обратного процесса подгонки измеренных резонансов. Типичный РУС резонансный спектр, полученный из огнеупорного АЭМ NbTaTiV показано на рис. S1, на вставке которого показан пример подгонки Лоренца одиночного резонансного пика. Полученные значения модулей упругости для сплава NbTaTiV сведены в Таблицу 1, что показывает хорошее согласие с нейтронными данными in situ.
Предсказания модулей упругости для огнеупорных АОГО NbTaTiV через расчеты из первых принципов
На основе экспериментальных наблюдений упругого поведения деформации для сплава NbTaTiV, первые принципы вычисления используется теоретически подтверждают значение монокристалла модули упругости при RT с использованием теории функционала плотности (DFT). Модули Юнга, объемного сжатия и сдвига при -273 ° C и RT для текущего HEA количественно рассчитываются на основе упругих констант, определенных путем подбора напряжений, рассчитанных ab initio, которые соответствуют деформированным структурам.Расчетные и измеренные модули объемной упругости при температуре абсолютного нуля и RT приведены в таблице 1, которая показывает хорошее согласие между экспериментальными и теоретическими результатами. Расчетные модули упругости при RT были меньше экспериментально измеренных значений примерно на -15,9, -16,6 и -6,0% для модулей Юнга, сдвига и объемного сжатия, соответственно. Вышеприведенный результат подтверждает общую тенденцию к снижению жесткости металлов с повышением температуры. Кроме того, рассчитанные значения упругой постоянной для C 11 , C 12 и C ‘ все уменьшаются от абсолютного нуля до RT, в то время как C 44 немного увеличивается с 31.От 6 до 33,5 ГПа.
Упругие свойства NbTaTiV HEA были проанализированы и нанесены на график в зависимости от кристаллографической ориентации, как показано на рис. 3. Чтобы вычислить зависящие от направления упругие свойства, мы применили тензорные операции к тензору упругости четвертого порядка, определенному из Расчеты DFT. Упругости четвертого порядка тензор преобразуется в новом базисе для определения упругих свойств в любом направлении с использованием уравнения belowCαβγδ ‘= λαiλβjλγkλδlCijkl (3) где каждый λ представляет собой направленный косинус угла между повернутой и опорной осью (+ 22 ).
Рис. 3 Направленная зависимость рассчитанных из первых принципов упругих свойств RT.Величина по отношению к направлениям в трех измерениях для ( A ) модуля Юнга в ГПа, ( B ) линейной сжимаемости в TPa −1 , ( C ) модуля сдвига в ГПа и ( D ) коэффициент Пуассона соответственно. Модуль сдвига и коэффициент Пуассона представлены двумя поверхностями для максимального и минимального значений. Величина относительно направлений на плоскостях XY , XZ и YZ для ( E ) модуля Юнга в ГПа, ( F ) линейной сжимаемости в TPa −1 , ( G ) модуль сдвига в ГПа и коэффициент Пуассона ( H ) соответственно.Модуль сдвига и коэффициент Пуассона представлены двумя линиями для максимального и минимального значений.
Более высокая степень изотропных упругих свойств приводит к меньшему изменению величины трехмерных (3D) поверхностей и 2D-контуров. Двухмерные контурные графики соответствуют разрезам трехмерных поверхностей на плоскостях XY , XZ и YZ . Модуль Юнга представлен твердой поверхностью с цветовой картой, на которой более темные цвета обозначают меньшие значения, а более яркие цвета обозначают большие значения.Отношение модуля Юнга от максимального к минимальному составляет 1,16, что указывает на небольшую характеристику анизотропии. Максимальное значение 107,7 ГПа соответствует направлению <100>, а минимальное значение для направления <111> составляет 93,0 ГПа (см. Рис. 3, A и B). Трехмерный поверхностный график для линейной сжимаемости представлен полупрозрачной зеленой сферой, которая демонстрирует пренебрежимо малую анизотропию, поскольку она имеет значение 2,42 ТПа −1 во всех направлениях (рис. 3, C и D). Диапазон минимальных и максимальных значений модулей сдвига и коэффициентов Пуассона для каждого направления приложенного напряжения объясняется изменением направления измерения.На трехмерных поверхностных графиках модуля сдвига и коэффициента Пуассона полупрозрачная зеленая поверхность представляет максимальные значения и охватывает твердую поверхность внутри, что представляет собой минимальные значения. На минимальную поверхность нанесена цветовая карта, так что более темные цвета представляют меньшие значения, чем более яркие цвета, как показано на рис. 3 (E и G). На 2D-графиках максимальные значения представлены зеленой кривой, а минимальные значения обозначены розовой кривой. Отношение максимального к минимальному значениям модуля сдвига равно 1.17. Максимум находится в направлении <111> со значением 39,33 ГПа, тогда как минимум соответствует направлениям <110> со значением 33,51 ГПа. Кроме того, отношение максимального коэффициента Пуассона к минимальному составляет 1,32. И максимальное, и минимальное значения происходят в направлении <110> со значениями 0,44 и 0,33 соответственно (рис. 3, F и H).
Недавно Ранганатан и Остоя-Старзевски ( 23 ) представили метод измерения анизотропии с использованием универсального индекса упругой анизотропии, который обычно можно применять к кристаллическим системам, которые учитывают объемную составляющую тензора упругости.В отличие от других методов измерения анизотропии, таких как индекс анизотропии Зинера, который применим только к кубическим кристаллам, и индекс анизотропии Ледбеттера-Мильори, который учитывает только сдвиговую составляющую тензора упругости, универсальный индекс анизотропии определяется как следующее уравнение: AU = 5GVGR + KVKR-6≥0 (4) где G — модуль сдвига, K — объемный модуль, а надстрочные индексы V и R относятся к оценкам Фойгта и Ройсса соответственно.Для сравнения: значения составляющих элементов A U , полученные из базы данных Materials Project, равны Nb, 2,71; Та 0,07; Ti 0,27; и V, 3,42. В результате значение A U для NbTaTiV HEA равно 0, что определяет упругие свойства монокристалла как изотропные.
Предсказания модулей упругости для огнеупорных АОГО NbTaTiV через модель ML
Множества элементарных и структурных свойства, которые были найдены, чтобы быть хорошее предсказанием в модуле сдвиг модели ML были Держатель средних (четвертые мощности) номера групп из элементы, энергия когезии, среднее значение держателя (вторая степень) атомных радиусов элементов, среднее значение держателя (четвертая степень) электроотрицательности элементов и плотность.Набор элементных и структурных свойств, которые оказались хорошими предсказаниями в модели объемного модуля упругости ML: среднее по Гёльдеру (четвертая степень) групповых номеров элементов, энергия когезии, среднее Гёльдера (первая степень) атомных радиусов. элементов, среднее значение Холдера (отрицательная четвертая степень) электроотрицательности элементов и плотности. Производительность моделей машинного обучения была проверена на 20% набора данных, что никогда не было обнаружено моделью машинного обучения в процессе подбора. Модули объема и сдвига были нормализованы логарифмически для обучения и тестирования модели, чтобы гарантировать, что большие выбросы не окажут чрезмерного влияния на модели.В качестве показателя эффективности модели использовалась среднеквадратическая ошибка. Среднеквадратические ошибки моделей модуля сдвига и объемного модуля были 0,0409 и 0,0284 соответственно. Прогнозы модели ML в сравнении с экспериментальными значениями и значениями, рассчитанными методом DFT, суммированы в таблице 1. Прогнозируемый модуль сдвига составляет 36,6 ГПа, а прогнозируемый модуль объемного сжатия составляет 146,3 ГПа, что дает относительные ошибки 2,5 и 6% соответственно.
Также существует стохастическая изменчивость производительности модели в зависимости от того, как перемешивается обучающий набор данных.Чтобы определить изменчивость производительности модели, которая просто связана с тем, какие обучающие примеры включены в набор обучающих данных, мы построим кривые обучения на рис. 4. Изменчивость прогнозов модели из-за случайного перемешивания данных изучается путем случайного перемешивания данные 20 различными способами. Красные кривые представляют среднеквадратичную ошибку моделей во время обучения, усредненную по 20 различным испытаниям, а зеленые кривые обозначают среднеквадратичную ошибку моделей, рассчитанную на тестовой выборке, усредненную по 20 различным испытаниям.Заштрихованные области представляют 1 стандартное отклонение (SD) вверху и внизу, как определено в 20 различных испытаниях. Ось x кривых обучения показывает, как размер самого обучающего набора данных влияет на производительность модели. Кривые обучения показывают, что производительность прогнозирования модели на тестовом наборе сходится после 3000 обучающих выборок. Небольшая разница в среднеквадратических ошибках обучения и тестирования указывает на то, что модель достаточно хороша для прогнозирования сдвиговых и объемных модулей для соединений, которых не было в наборе обучающих данных.Эта тенденция также демонстрирует возможность обобщения модели в том смысле, что ее можно использовать для соединений, которые не включены в исходный набор данных.
Рис. 4 Кривые обучения для моделей ML сдвига и объемных модулей.Сплошные кривые представляют собой среднеквадратичную ошибку, усредненную по 20 различным испытаниям, а заштрихованные области представляют собой 1 стандартное отклонение выше и ниже. Ось x представляет размер обучающего набора данных. Красная кривая и область соответствуют фазе обучения, а зеленая кривая и область соответствуют фазе тестирования.
ОБСУЖДЕНИЕ
Поведение упругой изотропии и анизотропии при деформации огнеупора HEA
из NbTaTiV Как правило, реакция деформации решетки под действием приложенных напряжений сильно связана с ориентированными зернами из-за эффектов упругой анизотропии в поликристаллических металлических материалах (9401339 11 , 13 ), включая HEA со структурой FCC ( 24 ). Упруго-анизотропные деформации происходят из зависящего от ориентации модуля упругости, который представлен различными наклонами на графиках эволюции деформации решетки как функции приложенных напряжений.В случае материалов со структурой ОЦК зерна {110} и {211}, которые имеют более высокую упругую жесткость, чем другие зерна, имеют больший наклон. Зерна {200} и {310}, с другой стороны, имеют меньшие уклоны и меньшую упругую жесткость ( 11 , 25 ). После этого упругого растяжения последовательность текучести зерна зависит от значения фактора Шмида, показывая различные уровни напряжения для начала текучести в разных зернах, что обычно характеризуется как поведение текучести от зерна к зерну ( 25 ) .Пластическая анизотропия возникает из-за возникновения пластической деформации на определенных зернах ( hkl ), на которых предпочтительно иметь место скольжение. Увеличение наклона указывает на пластическую текучесть определенных зерен, тогда как уменьшение наклона представляет собой передачу межзеренной нагрузки от податливых зерен к соседним зернам, которые все еще находятся в области упругой деформации. При таких тенденциях развития деформации решетки зерна {110} и {211} с наибольшей жесткостью в упругой области имеют тенденцию к деформации на ранней стадии из-за их системы скольжения.Впоследствии нагрузка передается от вышеупомянутых зерен к зернам {200} и {310}, а не происходит передача нагрузки в различных ориентациях ( 11 , 13 , 26 ). Это негармоничное распределение нагрузки может привести к концентрации напряжений на определенных зернах ({200} зерна в сплавах со структурой ОЦК) после большой пластической деформации. В отличие от обычных BCC-сплавов, как обсуждалось выше, огнеупорный HEA NbTaTiV BCC не демонстрирует зависящих от ориентации эволюций деформации решетки во время упругой деформации при комнатной температуре, что приводит к почти одинаковым значениям упругих модулей в разных зернах, как показано на рис.2А. При такой необычной упругой деформации все ориентированные зерна деформируются при одинаковом уровне напряжения (около 1000 МПа), как показано на рис. S2. Кроме того, особенности передачи нагрузки не были четко представлены во время пластической деформации при комнатной температуре, что указывает на снижение пластической анизотропии. Эта тенденция к снижению пластической анизотропной деформации может привести к превосходной пластичности (пластичности) при КТ из-за однородного распределения нагрузки между разными зернами, а не концентрации нагрузки на отдельные зерна во время пластической деформации, как показано на рис.S2.
Упругая изотропия часто количественно описывается отношением анизотропии Зенера ( A z ) и границами Фойгта и Рейсса ( A VR ) AZ = 2C44C11 − C12 (5) AVR = GV − GRGV + GR (6) где G R = [5 ( C 11 — C 12 ) C 44 ] / [4 C 44 + 3 ( C 11 — C 12 )] и G V = ( C 11 — C 12 + 3 C 44 ) / 5 ( 7 ) .Расчетные значения A Z и A VR при повышенных температурах можно найти в таблице S2. В случае идеальных изотропных материалов значение модуля тетрагонального сдвига ( C ′ ) будет идентично кубическому модулю сдвига ( C 44 ), и это приведет к A z = 1 и A VR = 0 ( 7 , 10 ). Как правило, коэффициенты Зенера для большинства обычных конструкционных материалов FCC и BCC намного превышают 2.0 или 3,0, что указывает на значительную упругую анизотропию ( 12 , 24 ). Недавно Тиан и др. . ( 7 ) предложил стратегию проектирования сплава для достижения упругой изотропии в HEA с использованием расчетов ab initio. Сообщалось, что огнеупорные HEA с ОЦК, содержащие Мо, имеют одинаковые поликристаллический сдвиг и модули Юнга при всех ориентациях, что указывает на изотропию упругости. Кроме того, эти изотропные HEA имеют аналогичную VEC около 4,7 (как правило, HEA имеют тенденцию образовывать фазы твердого раствора BCC, когда VEC становится меньше 7.55) ( 7 , 27 ), который аналогичен другим упругим изотропным сплавам, таким как сплав Ti-V (смолистые металлы) ( 28 ). Однако из-за отсутствия экспериментальных подтверждений их опубликованные работы сосредоточены только на теоретических расчетах. Согласно нашим расчетным результатам A Z и A VR в таблице S2, которые в основном получены в нейтронных экспериментах на месте, огнеупорный HEA NbTaTiV демонстрирует почти идеально изотропную упругую деформацию при комнатной температуре ( A Z ≈ 1.2, A VR ≈ 0,0056, VEC ≈ 4,68). Более того, упругая изотропия постепенно увеличивалась при повышенных температурах. Многие традиционные сплавы демонстрируют сильную температурно-зависимую упругую анизотропную деформацию, что указывает на существенное увеличение параметров анизотропии Зенера при более высоких температурах ( 11 — 13 ). Например, наноструктурированный ферритный сплав с ОЦК (NFA) и суперсплав на основе никеля с ГЦК-структурой демонстрируют большой разброс параметров анизотропии от комнатной температуры до высоких температур [от 1 до 1 ° С.От 7 (RT) до 5,3 (800 ° C) для NFA и от 2,8 (RT) до 3,6 (700 ° C) для суперсплава на основе Ni] ( 12 , 13 ). Кроме того, ожидается, что чистое железо и случайный сплав Fe 90 Cr 10 будут иметь заметное увеличение параметра анизотропии при повышенных температурах ( 14 ). Кроме того, было обнаружено, что CoCrFeMnNi HEA демонстрирует сильную температурно-зависимую упругую и пластическую анизотропную деформацию от RT до 527 ° C ( 15 ). В случае нынешнего NbTaTiV HEA параметры анизотропии Зенера постепенно увеличивались при повышенных температурах, но изменение параметров анизотропии в NbTaTiV (1.2 при комнатной температуре и 1,6 при 900 ° C) намного меньше, чем у других обычных сплавов ( 11 — 13 ). Подробные сравнения параметров анизотропии Зенера и пределов текучести при повышенных температурах между NFA ( 13 ) и нынешним огнеупорным HEA из NbTaTiV показаны на рис. S3, демонстрируя, что оба сплава демонстрируют зависящую от температуры упругую анизотропию и меньшее изменение параметров анизотропии Зенера в ВЭА NbTaTiV, чем наноструктурированный ферритный сплав при повышенных температурах.
Механическая стабильность и пластичность (пластичность) огнеупора NbTaTiV HEA
Механическая стабильность огнеупора NbTaTiV HEA может быть оценена с учетом значений упругих постоянных монокристаллов. Борн и Хуанг ( 29 ) предложили критерии оценки упругой устойчивости через условия динамической устойчивости: C 11 > ∣ C 12 ∣, C 11 + 2 C 12 > 0 и C 44 > 0 ( 30 ).Согласно упругим константам, приведенным в таблице 1, настоящий сплав показывает хорошую механическую стабильность во всех диапазонах температур.
Характерное поведение при деформации от хрупкого до пластичного HEA, которое преимущественно состоит из фаз твердого раствора, можно предсказать по взаимосвязи поликристаллических модулей упругости, таких как давление Коши ( C 12 — C 44 ) ( 16 ), коэффициент Пью [модуль объемной упругости ( K ) / модуль сдвига ( G )] ( 8 ) и коэффициент Пуассона (ν) ( 9 ).Давление Коши часто используется для классификации типа атомной связи. Относительно большое положительное значение давления Коши представляет повышенную степень характера металлического связывания с поведением пластичной деформации, тогда как отрицательное давление Коши означает ковалентное связывание с хрупким поведением ( 16 ). Более того, соотношение K / G , которое было предложено Пью, можно применять для прогнозирования пластичности и хрупкости материалов ( 8 ).Модуль объемной упругости ( K ) оценивает сопротивление разрушению, а модуль сдвига ( G ) определяется как сопротивление пластической деформации поликристаллических материалов. Когда сплавы имеют большие значения K с относительно небольшими значениями G , сплавы имеют тенденцию проявлять значительное сопротивление разрушению после начала пластической деформации, что приводит к пластическим характеристикам материалов ( 8 ). Из существующих экспериментальных результатов для большого количества изученных материалов было обнаружено, что точка перехода от хрупкого к пластичному состоянию ( K / G ) 0 равна 1.75 ( 30 ). Следовательно, более высокие значения коэффициентов Пью (> 1,75) указывают на то, что материалы являются пластичными, тогда как более низкие значения связаны с хрупкими свойствами. На основе эмпирических критериев отношения Пью, приведенных выше, предел хрупкости к вязкости также можно оценить с помощью коэффициента Пуассона, учитывая взаимосвязь между ν и ( K / G ) 0 , как ν = (3 K — 2 G ) / [2 (3 K + G )], в случае изотропных поликристаллических материалов.Следовательно, предел перехода от хрупкого состояния к пластическому ( K / G ) 0 > 1,75 соответствует ν> 0,26. Отметим, что критерий хрупкости и пластичности для объемных металлических стекол ν> 0,31 ( 9 ). Значения давления Коши, коэффициента Пью и коэффициента Пуассона (см. Таблицу 1 и таблицу S2), которые получены в нейтронных экспериментах на месте, предполагают, что NbTaTiV по своей природе пластичен.
Определение характеристик подвижных дислокаций для сплава NbTaTiV при повышенных температурах
Для дальнейшего исследования поведения пластической деформации сплава NbTaTiV тщательно выполняются моделирование профиля линии и анализ с учетом эволюции ширины пика НА. макродеформации при повышенных температурах.В целом пластическая деформация часто приводит к значительному уширению дифракционных пиков, что в основном обусловлено образованием неоднородных полей деформации ( 31 ). Хорошо известно, что неоднородность субзеренной структуры обычно больше связана с накоплением дислокаций, чем с вариациями межзеренных деформаций. Таким образом, возникают флуктуации деформации с полем деформации вокруг дислокаций, ответственные за уширение дифракционных пиков ( 32 ). С учетом указанным выше фундаментального пониманием пластического поведения деформации в металлических материалах, эволюция дифракционных пиков ширинов при различных уровнях деформации для огнеупорных АОГО NbTaTiV дополнительно обсуждается в пике анализ уширения подходом Виллиэмсон-Холле ( 17 ).Эволюция ширины пиков полной ширины на полувысоте (FWHM / FWHM 0 ) дифракционных пиков {110}, {200}, {211} и {310} как функция макродеформации при комнатной температуре, 700 ° , и 900 ° C, а подробные процессы анализа уширения пиков Вильямсона-Холла во время пластической деформации описаны в разделе S2.
На рис. 5 показаны модифицированные графики Вильямсона-Холла для сплава NbTaTiV, соответствующие диапазону макродеформации от 0 до 15%. Отклик линейной аппроксимации графика, который получается из предположения о конкретных типах дислокаций, относится к преобладающему характеру подвижных дислокаций во время пластической деформации ( 33 ).Следовательно, если рассматривать значения q и C h 00 как чистые винтовые дислокации ( q = 2,2244 и C h 00 = 0,2415), немонотонное отклонение ∆K как функция K 2 C постепенно увеличивается с увеличением макродеформации, как показано на фиг. 5A. Тем не менее, данные имеют линейный тренд на всех уровнях деформации, когда значения ∆K и K 2 C , полученные с учетом чисто краевой дислокации ( q = 0.0673 и C h 00 = 0,1937), как показано на фиг. 5B. Отклонения от линейно подобранной линии количественно описываются коэффициентами R в квадрате в таблице S4. Эти результаты однозначно указывают на то, что тип подвижных дислокаций тугоплавкого ВЭС NbTaTiV — это краевые дислокации в исходном состоянии (недеформированные) при повышенных температурах. Более того, с увеличением макродеформаций (до 15% деформации) краевая дислокация <111> {110} остается доминирующим характером подвижной дислокации при комнатной температуре и повышенных температурах (рис.5, Б — Г).
Рис. 5 Моделирование профиля линии профиля ND для гомогенизированного сплава NbTaTiV во время пластической деформации с использованием модифицированного графика Вильямсона-Холла при повышенных температурах.Изображения HAADF-STEM сплава NbTaTiV, деформированного в режиме реального времени. Анализ уширения пиков ∆ K 2 как функция K 2 C для образца, сжатого от 0 до 15%, с учетом доминирующего типа дислокаций как чистого ( A ) <111> винтовая дислокация при RT, ( B ) <111> {110} краевая дислокация при RT, ( C ) <111> {110} краевая дислокация при 700 ° C и ( D ) <111> {110} краевая дислокация при 900 ° C соответственно.( E и F ) Видимое исследование присутствия краевых дислокаций для 15% RT-деформированного NbTaTiV HEA с помощью исследования HAADF-STEM.
ОЦК металлические материалы обычно содержат краевые дислокации, которые движутся быстрее винтовых дислокаций из-за их основных свойств дислокаций во время пластической деформации ( 34 ). Критическое напряжение, которое вызывает движение краевой дислокации, довольно мало (<10 МПа для чистого ОЦК Fe), что приводит к легкой аннигиляции краевых дислокаций, что приводит к анизотропии винт / край в кажущемся отклонении подвижности ( 34 ).Следовательно, в ОЦК-металлах оставшиеся дислокации имеют более винтовой характер. Однако недавно Рао и др. . ( 35 ) сообщили об атомистическом моделировании пластической деформации BCC HEA с точки зрения движения дислокаций. Это углубленное исследование предсказывает тенденцию движений дислокаций в ОЦК твердом растворе ВЭА соответствовать случайному элементному распределению, которое значительно отличается от обычных ОЦК металлов. Во время пластической деформации ядро краевой дислокации может отклоняться от своих нейтральных плоскостей дислокаций, создавая волнистые линии дислокации, которые объясняются сильным искажением решетки.Эта особенность вызвана колебаниями состава и, таким образом, приводит не только к упрочнению, но и к заметному затруднению движения краевой дислокации. Эти предсказания поведения пластической деформации для BCC HEA предполагают, что количество краевых дислокаций сопоставимо с количеством винтовых дислокаций, в отличие от обычных низкоэнтропийных BCC-металлов. Подобно вышеприведенному предсказанию, доминирующие подвижные дислокации исследованного тугоплавкого HEA NbTaTiV BCC, который имеет сильно искаженную решетку, близки к краевым дислокациям <111> {110} с увеличением макродеформации, как показано на рис.
Для дальнейшей идентификации и предоставления видимых доказательств типа подвижных дислокаций во время пластической деформации в NbTaTiV HEA наноразмерная микроструктура деформированного образца была тщательно исследована с помощью ПЭМ-исследования. На рисунке 5E показано отфильтрованное изображение HAADF-STEM 15% RT-деформированного NbTaTiV HEA, полученное вдоль оси зоны [110]. Формирование краевых дислокаций четко наблюдается с дополнительными плоскостями на изображении, обозначенными символом «», что согласуется с моделированием профиля линии с использованием результатов графика Вильямсона-Холла (рис.5Б). Обнаружено, что эти краевые дислокации образовывались в разных плоскостях, обозначенных разными цветными символами краевых дислокаций. Изображение с большим увеличением на фиг. 5E проиллюстрировано на фиг. 5F, чтобы обеспечить четкое описание краевых дислокаций.
В целом, это комплексное исследование дает доказательство уникального упругое и пластическое деформации поведение в однофазном твердом растворе ВССА огнеупорных АОМ при повышенных температурах с использованием нейтронных экспериментов на местах в сочетании с теоретическими расчетами в.Результаты ND и характеристики микроструктуры показывают превосходную однофазную стабильность BCC до 900 ° C. Кроме того, настоящий сплав имеет высокий предел текучести и отличную пластичность при комнатной температуре и сопротивление разупрочнению при повышенных температурах. Результаты эволюции деформации решетки показывают характерное поведение упругой деформации в виде упругой изотропии при комнатной температуре и меньшую температурную зависимость поведения упругой анизотропной деформации, чем у традиционных металлических материалов при повышенных температурах.
Модули упругости монокристаллов получены из данных ND in situ в сочетании с подходом модели Кронера, что демонстрирует отличное согласие с экспериментальными значениями, определенными на основе измерений RUS и расчетов из первых принципов. Кроме того, хорошее согласие предсказаний модели ML для модулей сдвига и объемного сжатия несколько неожиданно, учитывая, что база данных Materials Project содержит только упорядоченные соединения и не содержит неупорядоченных сплавов, таких как HEA. Эффект искажения решетки также может привести к тому, что модель ML будет давать менее точные результаты для HEA, но, учитывая отсутствие данных для сравнения, хорошее согласие предполагает, что эти модели могут быть полезны для консервативных оценок.
Сплав NbTaTiV прогнозируется как пластичный по своей природе на основе критериев пластичности с использованием давления Коши, коэффициента Пью и коэффициента Пуассона. Проверка типа подвижной дислокации была количественно исследована с использованием профиля графика Уильямсона-Холла, экспериментально подтвержденного с помощью HAADF-STEM. Установлено, что преобладающей подвижной дислокацией являются краевые дислокации при 15% -ной пластической деформации при повышенных температурах. Считается, что сильно искаженная решетка вызывает отклонение образования дислокаций от их нейтральных дислокационных плоскостей, что, следовательно, приводит к существенному снижению подвижности краевых дислокаций при пластической деформации.Таким образом, краевые дислокации считаются преобладающим типом дислокаций для ОЦК тугоплавкого ВЭА, что нетипично по сравнению с обычными ОЦК-металлами и сплавами. Эти новые открытия уникальных упругой и пластической деформации поведения тугоплавкого АЭМ ВСС NbTaTiV может привести к общей превосходной механической производительности, а также обеспечивают дорожную карту в направлении открытия и производства новой конструкции поликристаллических материалов для конструкционных материалов приложений.
МАТЕРИАЛЫ И МЕТОДЫ
Получение материалов и микроструктурная характеристика
Сплавы были синтезированы дуговой плавкой в атмосфере аргона на водоохлаждаемом медном поде из элементов Nb, Ta, Ti и V из 99.Чистота 99 мас.%. Номинальный состав настоящего сплава: Nb 25 Ta 25 Ti 25 V 25 в атомных%. Слиток был переплавлен более 10 раз, чтобы обеспечить полностью однородное распределение элементов. Из лигатуры были изготовлены образцы с последующим прямым литьем в цилиндрические стержни диаметром 4 мм и длиной 50 мм методом капельного литья. Эти сплавы герметизировали аргоном с тройной откачкой в кварцевых трубках и гомогенизировали при 1200 ° C в течение 3 дней с последующим водяным охлаждением.Микроструктуру исследовали с помощью SEM, используя Zeiss Auriga 40, оборудованный BSE. Химический анализ сплава исследовали методом энергодисперсионной рентгеновской спектроскопии после гомогенизационной обработки.
In situ ND-эксперименты
In situ ND-измерения проводились на инженерном дифрактометре VULCAN на установке источника нейтронов расщепления, расположенной в Национальной лаборатории Oak Ridge (ORNL). В приборе ND используются времяпролетные измерения, что позволяет создавать структуру ND, охватывающую широкий диапазон d-расстояний без вращения детекторов или образцов.Два детектора, обозначенные как блоки 1 и 2 под углом ± 90 °, использовались для сбора дифрагированных нейтронов от поликристаллических зерен с плоскостями решетки, параллельными осевому и поперечному направлениям, соответственно. Эксперименты по сжатию гомогенизирующего сплава NbTaTiV диаметром 4 мм и длиной 8 мм были проведены для исследования поведения при упругой и пластической деформации при комнатной температуре и повышенных температурах с использованием силовой рамы системы механических испытаний. Образцы освещаются падающим пучком нейтронов с размером щели 3 × 3 мм 2 и приемными коллиматорами 2 мм.В течение периода упругой деформации использовалась последовательность ступенчатого управления усилием, собирая данные измерения ND в течение 20 минут на каждом уровне напряжения. Когда уровень напряжения достигал 1030 МПа для RT, 650 МПа для 500 ° C, 585 МПа для 700 ° C и 550 МПа для 900 ° C (близко к макроскопическому пределу текучести), ступенчатое управление перемещением с шагом приращения 0,2 мм. Собранные данные были проанализированы путем подбора одного пика с использованием программы VULCAN Data Reduction and Interactive Visualization software (VDRIVE) ( 18 ).
Расчеты из первых принципов
Расчеты из первых принципов были выполнены с помощью пакета Vienna Ab-initio Simulation Package (VASP) с использованием метода расширенной волны (PAW) проектора ( 36 ). Обменно-корреляционная энергия описывалась с помощью приближения обобщенного градиента в параметризации Пердью-Беке-Эрнцехофа. Для всех расчетов использовалась отсечка плоской волны 700 эВ и сетка Monkhorst-Pack k точек размером 4 × 4 × 4. Химический беспорядок твердого раствора моделировался с помощью 64-атомной специальной квазислучайной структуры (SQS).SQS использовался с помощью метода, основанного на моделированной Монте-Карло петле отжига, в которой атомные конфигурации предлагаются путем случайной перестановки атомных позиций и принятия изменений, когда вычисленные корреляционные функции конфигурации более близки к таковым для неупорядоченного состояния.
Тензор упругости суперячейки SQS был рассчитан с использованием набора искаженных структур на основе методологии, описанной в ( 37 ). Параметры решетки сверхъячейки были зафиксированы на экспериментально определенных значениях RT, а положениям ионов позволяли релаксировать.Набор деформированных структур был создан путем принятия 3 × 3 тензоров деформации Грина-Лагранжа различных величин при ± 0,5 и ± 1%. Для каждой искаженной конструкции тензор напряжений 3 × 3 вычисляется с помощью ДПФ. Линейная аппроксимация методом наименьших квадратов между тензорами напряжений и деформаций была проведена для расчета тензора упругости SQS. Однако, поскольку суперячейка SQS не сохраняет симметрию точечной группы, метод проецирования используется для получения ближайших упругих тензоров с кубической симметрией для сплава NbTaTiV, что эквивалентно кристаллографически усредняющим элементам тензора.Метод проекции эффективен с точки зрения вычислений, а значения упругих постоянных быстро сходятся с размером SQS. Модули упругости текущего HEA рассчитываются с использованием элементов прогнозируемого тензора упругости, как описано ниже. Объемный модуль ( K ) и модуль сдвига ( G ) были получены из упругой постоянной. Затем математически рассчитали модуль Юнга, заменив K и G в простом уравнении (E = 9KG3K + G), в котором учитывалась корреляция между E , K и G K = 5 (s11 + s22 + s33) +2 (s12 + s23 + s31) (7) G = 154 (s11 + s22 + s33) −4 (s12 + s23 + s31) +3 (s − 44 + s55 + s66) + (s11 + s22 + s33) — (s12 + s23 + s31) +3 (s − 44 + s55 + s66) 15 (8) где s ij — тензор жесткости, а тензор упругости, C ij , после их корреляции было вычислено sij = Cij − 1.
ML-модели для модулей объемного сжатия и сдвига
ML-модели, использующие алгоритм градиентно-усиленных деревьев, были разработаны для прогнозирования модулей сдвига и объемного сжатия (по одной модели для каждого). Модели были построены с использованием библиотеки scikit-learn на Python ( 38 ). Модели ML были обучены рассчитанным методом DFT модулям сдвига и объемного сжатия, элементным свойствам и структурным свойствам соединений из базы данных Materials Project ( 37 ). В наборе данных, используемом для обучения и тестирования моделей машинного обучения, было 6826 неорганических соединений.Наиболее общий подход к объединению элементарных свойств для каждого соединения был предпринят путем вычисления взвешенных по составу средних значений Холдера с диапазоном значений от -4 до 4. Средние значения Холдера определены в приведенном ниже уравнении μp (x) = ((∑i = 1nwi ) −1∑i = 1nwixip) 1p, (p ≠ 0) (9) μ0 (x) = exp ((∑i = 1nwi) −1∑i = 1nwiln (xi)), (p = 0) (10) где μ p — среднее значение держателя с мощностью, p ; и w i представляет собой композиционную долю элемента, i , в соединении с n элементами.Среднее значение Холдера со степенями 1, -1 или 2 соответствует среднему арифметическому, среднему гармоническому или среднему евклидову соответственно ( 39 ). Методология выбора признаков, основанная на схеме генетической алгоритмической оптимизации, использовалась для определения того, какие свойства элементов и структурные свойства по Холдеру дают наилучшие модели для прогнозирования модулей сдвига и объема. Модели были обучены с использованием 80% набора данных с использованием пятикратной схемы перекрестной проверки для предотвращения переобучения.Производительность модели определяется на оставшихся 20% набора данных.
Резонансная ультразвуковая спектроскопия
Упругие постоянные также измерялись с помощью RUS. Цилиндрический образец NbTaTiV HEA был установлен в углу между двумя преобразователями. В этой конфигурации один преобразователь возбуждает образец, в то время как приемный преобразователь определяет и передает отклик образца на резонансных частотах. Предполагая, что упругая изотропия и упругие постоянные ( C 11 , C 12 и C 44 ) были определены с использованием размеров образца и наблюдаемых резонансов.В нашем исследовании частота прокручивалась в диапазоне от 100 до 650 кГц, при этом большие отклики обнаруживались, когда частота соответствует собственной частоте образца. Из упругих постоянных определяли объемный модуль ( K ) и модуль сдвига ( G ) с использованием приближений Хилла ( 40 ).
Благодарности: Мы хотели бы поблагодарить J. Brechtl, H. Choo и Y. Chen за помощь в проведении экспериментов, соответственно. Ни правительство США, ни какое-либо его агентство, ни LRST, ни какой-либо из их сотрудников не дают никаких гарантий, явных или подразумеваемых, и не принимают на себя никаких юридических обязательств или ответственности за точность, полноту или полезность любой информации, оборудования, продукта или процесса. раскрывается или представляет, что его использование не нарушает права частной собственности.Ссылка в данном документе на какой-либо конкретный коммерческий продукт, процесс или услугу по торговому наименованию, товарному знаку, производителю или иным образом не обязательно означает или подразумевает его одобрение, рекомендацию или поддержку со стороны правительства США или любого его агентства. Взгляды и мнения авторов, выраженные в данном документе, не обязательно отражают или отражают точку зрения правительства США или его ведомства. Финансирование: Исследование было поддержано Проектом Управления армии США (W911NF-13-1-0438 и W911NF-19-2-0049) с руководителями программ М.П. Бакас, Д. М. Степп и С. Матхаудху, и материал был разработан. П.К.Л. также благодарен за поддержку NSF (DMR-1611180 и 1809640) с руководителями программ Дж. Янгом, Г. Шифлетом и Д. Фаркасом, и нейтронные работы были проведены. C.L. и Б.Л.М. хотел бы выразить признательность за частичную поддержку со стороны Центра обработки материалов с Ч. Роном в качестве директора Центра передового опыта Комиссии по высшему образованию штата Теннесси (THEC), расположенного в Университете Теннесси, Ноксвилл. Часть исследований в источнике нейтронов расщепления ORNL спонсировалась Отделом научного пользователя Управления фундаментальных энергетических наук, U.С. Министерство энергетики. Ссылка в данном документе на какой-либо конкретный коммерческий продукт, процесс или услугу под торговым наименованием, товарным знаком, производителем или иным образом не обязательно означает или подразумевает его одобрение, рекомендацию или поддержку со стороны правительства США или любого его агентства. Взгляды и мнения авторов, выраженные здесь, не обязательно отражают или отражают точку зрения правительства США или любого его ведомства. Y.-C.C. благодаря финансированию Министерства науки и технологий (MOST) Тайваня в рамках гранта №MOST-109-2636-M-009-002, поддержка основного объекта в Национальном университете Цзяо Дун (NCTU) от MOST. Y.-C.C. благодаря частичной поддержке со стороны «Центра исследований полупроводниковых технологий» в рамках программы Центра исследований избранных областей в рамках проекта «Росток высшего образования» Министерства образования (МО) Тайваня и при частичной поддержке Министерства Наука и технологии, Тайвань, по гранту MOST 109-2634-F-009-029. M.C.G. благодарит за поддержку U.S. Программа комплексных технологий использования ископаемых источников энергии Министерства энергетики в Национальной лаборатории энергетических технологий (NETL) в соответствии с контрактом RSS № 89243318CFE000003. Кроме того, настоящая работа была поддержана Программой лаборатории фундаментальных исследований через Министерство образования Республики Корея (2019R1A4A1026125) и грантом Национального исследовательского фонда Кореи (NRF), финансируемым правительством Кореи (MSIT) (№ 2020R1C1C1005553). . ТУАЛЕТ. и Г.К. подтверждаем поддержку со стороны NSF по грантам №OAC-1940114 и DMR-1945380. В этом исследовании использовались ресурсы Национального вычислительного центра энергетических исследований (NERSC), Научно-исследовательского центра Министерства энергетики США, работающего по контракту № DE-AC02-05Ch21231. В этой работе использовалась среда обнаружения экстремальных наук и инженерии (XSEDE), которая поддерживается грантом NSF No. ACI-1548562. Эта работа была частично профинансирована Министерством энергетики, Национальной лабораторией энергетических технологий, агентством правительства США, в рамках контракта на поддержку с Leidos Research Support Team (LRST). Вклад авторов: Все авторы внесли большой вклад в работу, представленную в этой рукописи. C.L., P.K.L., K.A. и G.S. выполнили SEM, нейтронные и механические испытания на месте и написали основные рукописи и дополнительные материалы. M.C.G. разработал HEA, провел расчет фазовой диаграммы и написал части вычислительного прогнозирования в основной рукописи. Г.К. и W.C. провел расчеты из первых принципов и ML и написал расчетные части в основной рукописи.Y.C. и Y.-C.C. выполнил HAADF-STEM и написал части исследования структуры атомного масштаба в основной рукописи. Б.Л.М. и В.К. провели измерение RUS и написали соответствующие части в основной рукописи. Все авторы обсуждали результаты и последствия и комментировали рукопись на всех этапах. Конкурирующие интересы: Авторы заявляют, что у них нет конкурирующих интересов. Доступность данных и материалов: Все данные, необходимые для оценки выводов в статье, представлены в статье и / или дополнительных материалах.




 Результаты выполнения учащимися контрольной работы по математике представлены в таблице.
Результаты выполнения учащимися контрольной работы по математике представлены в таблице. После этого пешеход вернулся домой.
После этого пешеход вернулся домой. Дж., Фостер П.Н., Шнайдер С.Х. (1999) Моделирование воздействия изменения климата на тропические горные облачные леса.Природа 398: 608–610.
Дж., Фостер П.Н., Шнайдер С.Х. (1999) Моделирование воздействия изменения климата на тропические горные облачные леса.Природа 398: 608–610.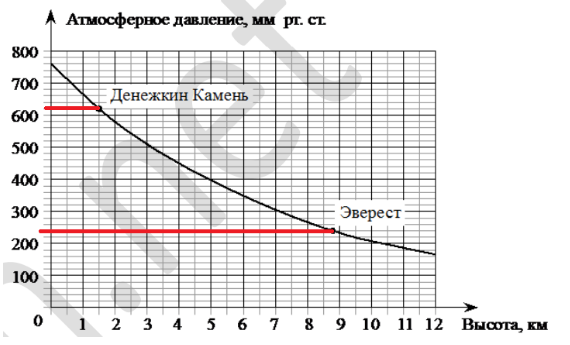 Природа 421: 37–42.
Природа 421: 37–42.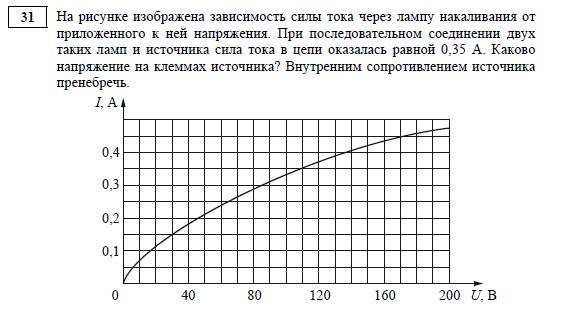 Nogues-Bravo D, Araujo MB, Errea MP, Martinez-Rica JP (2007) Подверженность глобальных горных систем климатическому потеплению в 21 веке. Глобальное изменение окружающей среды — человеческие и политические аспекты 17: 420–428.
Nogues-Bravo D, Araujo MB, Errea MP, Martinez-Rica JP (2007) Подверженность глобальных горных систем климатическому потеплению в 21 веке. Глобальное изменение окружающей среды — человеческие и политические аспекты 17: 420–428. Vuille M, Bradley RS (2000) Тенденции среднегодовых температур и их вертикальная структура в тропических Андах. Письма о геофизических исследованиях 27: 3885–3888.
Vuille M, Bradley RS (2000) Тенденции среднегодовых температур и их вертикальная структура в тропических Андах. Письма о геофизических исследованиях 27: 3885–3888. Биология глобальных изменений 4: 495–504.
Биология глобальных изменений 4: 495–504. Международный журнал климатологии 28: 2031–2064.
Международный журнал климатологии 28: 2031–2064. Анналы прикладной биологии 146: 1–14.
Анналы прикладной биологии 146: 1–14.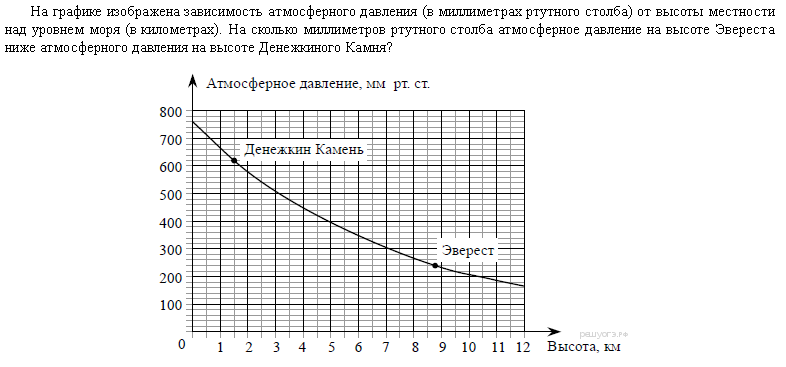 Мэдисон, Висконсин: Американское агрономическое общество. 5–29.
Мэдисон, Висконсин: Американское агрономическое общество. 5–29. , Киттель TGF (1998) Тенденции 1973–1996 гг. В усредненной по глубине температуре тропосферы Журнал геофизических исследований атмосферы.103: 16927–16933.
, Киттель TGF (1998) Тенденции 1973–1996 гг. В усредненной по глубине температуре тропосферы Журнал геофизических исследований атмосферы.103: 16927–16933. 47: 475–497.
47: 475–497. Сельскохозяйственная и лесная метеорология 137: 1–14.
Сельскохозяйственная и лесная метеорология 137: 1–14.


Leave A Comment