На рисунке изображен колодец с журавлем короткое плечо имеет длину 2 м и 7: Колодец с «журавлем», короткое плечо

8. На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо… Математика Ященко И. В. ЕГЭ-2017 ГДЗ. Вариант 22.

8. На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо… Математика Ященко И. В. ЕГЭ-2017 ГДЗ. Вариант 22. – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 5 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?

ответы

ответ
2,5

может, быть ответ 10?

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения

похожие темы

ГИА

ОГЭ

Экзамены

Выпускной

похожие вопросы 5

ГДЗ.Русский язык.7 класс.1 часть.С.И.Львова.§13. Сочетание разных типов речи в тексте.Задание 367.Выпишите слова и словосочетания.

Кто знает так сделать ?
Сначала спишите первые два абзаца,
вставляя пропущенные буквы и раскрывая скобки. (Подробнее…)

ЕГЭРусский язык7 классЛьвова С.И.

ГДЗ. Математика. Базовый уровень ЕГЭ — 2017. Вар.№26. Зад.№9.Под руководством Ященко. Помогите установить соответствие.

Здравствуйте! Помогите установить соответствие между величинами и их возможными значениями: к каждому элементу первого столбца (Подробнее…)

ЕГЭЭкзаменыМатематикаЯщенко И.В.

Задание 38 Однородные члены предложения. Что такое однородные члены предложения? Русский язык.4 класс. Канакина В.П., Горецкий В.Г. ГДЗ

Всем привет, поделитесь ответом на задание
Прочитайте.
Рассмотрите условные обозначения однородных членов. (Подробнее…)

ГДЗРусский языкКанакина В.П.Горецкий В.Г.4 класс

Когда в 2018 году будет проводиться ЕГЭ?

Когда в 2018 году запланировано провести ЕГЭ? (Подробнее…)

ЕГЭШколаНовостиЭкзамены

20. В корзине лежит 45 грибов: рыжики и грузди. Известно, что среди любых 23 грибов… Математика Ященко И.

В. ЕГЭ-2017 ГДЗ. Вариант 19.

20.
В корзине лежит 45 грибов: рыжики и грузди. Известно, что среди любых 23 грибов имеется хотя бы один рыжик, а среди любых 24 (Подробнее…)

ГДЗЕГЭМатематикаЯщенко И.В.

Задачи на повторение по геометрии. Подготовка к ГИА

1. Задачи на повторение по геометрии Подготовка к ГИА

2. Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60°. Найдите длину хорды АВ, если радиус окружности равен 8.

Центральный угол AOB опирается на хорду АВ так,
что угол ОАВ равен 60°. Найдите длину хорды АВ,
если радиус окружности равен 8.

3. Точка О – центр окружности, ∠AOB=84° (см. рисунок). Найдите величину угла ACB(в градусах).

Точка О – центр
окружности, ∠AOB=84° (см. рисунок).
Найдите величину угла ACB(в градусах).

4. Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания

Боковая сторона трапеции равна 3, а один из
прилегающих к ней углов равен 30°.

Найдите
площадь трапеции, если её основания равны 2
и 6.
Какие из данных утверждений верны?
Запишите их номера.
1) Каждая из биссектрис равнобедренного
треугольника является его медианой.
2) Диагонали прямоугольника равны.
3) У любой трапеции боковые стороны
равны.

6. На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?

На каком расстоянии (в метрах) от
фонаря стоит человек ростом 2 м, если
длина его тени равна 1 м, высота фонаря
9 м?

7. Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы,

Найдите больший угол равнобедренной
трапеции ABCD, если диагональ АС образует с
основанием AD и боковой стороной АВ углы,
равные 30° и 45° соответственно.

8. В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 30°. Найдите величину угла ODC.

В окружности с центром в точке О проведены
диаметры AD и BC, угол ABO равен 30°.

Найдите величину угла ODC.

9. Найдите тангенс угла С треугольника ABC, изображённого на рисунке.

Найдите тангенс
угла С треугольника ABC, изображённого
на рисунке.

10. Найдите площадь параллелограмма, изображённого на рисунке.

11. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма.

Диагональ AC параллелограмма ABCD об
разует с его сторонами углы,
равные 30° и 45°. Найдите больший угол
параллелограмма.

12. Втреугольнике ABC угол C прямой, BC=9, sinA=0,3. Найдите AB.

Втреугольнике ABC угол C прямой, BC=
9, sinA=0,3. Найдите AB.

13. Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 12 м от земли. Расстояние от

Точка крепления троса, удерживающего
флагшток в вертикальном положении,
находится на высоте 12 м от земли. Расстояние
от основания флагштока до места крепления
троса на земле равно 9 м.

Найдите длину
троса.

14. Найдите тангенс угла А треугольника ABC, изображённого на рисунке.

Найдите тангенс
угла А треугольника ABC, изображённого
на рисунке.

15. Найдите площадь трапеции, изображённой на рисунке.

16. В треугольнике ABC угол C прямой, BC=3, cosB=0,6. Найдите AB.

В
треугольнике ABC угол C прямой, BC=3,
cosB=0,6. Найдите AB.

17. От столба к дому натянут провод длиной 15 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите

От столба к дому натянут провод длиной 15 м, который
закреплён на стене дома на высоте 3 м от земли (см.
рисунок). Вычислите высоту столба, если расстояние от
дома до столба равно 12 м.

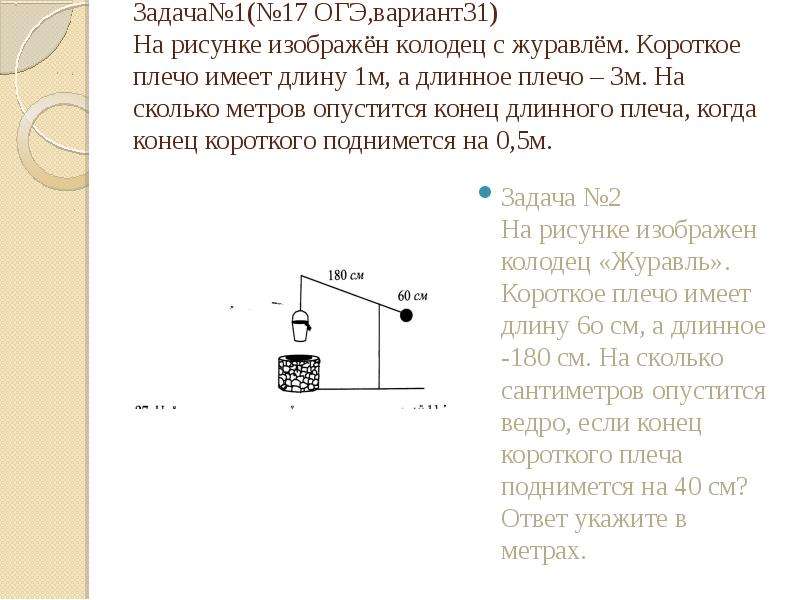
18. На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 4 м. На сколько метров опустится

На рисунке изображён колодец с «журавлём».
Короткое плечо имеет длину 2 м, а длинное
плечо — 4 м. На сколько метров опустится
конец длинного плеча, когда конец короткого
поднимется на 0,5 м?
Укажите номера верных утверждений.

1) Квадрат любой стороны треугольника равен
сумме квадратов двух других его сторон без
удвоенного произведения этих сторон на
синус угла между ними.
2) Площадь ромба равна произведению его
стороны на высоту, проведенную к этой
стороне.
3) Треугольник со сторонами 4, 5, 6 является
прямоугольным

20. На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 3 м, а длинное плечо — 6 м. На сколько метров опустится

На рисунке изображён колодец с «журавлём». Короткое
плечо имеет длину 3 м, а длинное плечо — 6 м. На
сколько метров опустится конец длинного плеча, когда
конец короткого поднимется на 1,5 м?

21. Найдите синус угла АВС , изображенного на рисунке

22. На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 7 м. На сколько метров опустится

На рисунке изображён колодец с «журавлём».
Короткое плечо имеет длину 2 м, а длинное
плечо — 7 м. На сколько метров опустится
конец длинного плеча, когда конец короткого
поднимется на 1 м?

23.

Сторона ромба равна 38, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка.Сторона ромба равна 38, а острый угол
равен 60°. Высота ромба, опущенная из
вершины тупого угла, делит сторону на два
отрезка. Каковы длины этих отрезков?

24. Найдите площадь трапеции.

25. Найдите косинус угла АВС , изображенного на рисунке

• Укажите номера верных утверждений.
• 1) Любые два прямоугольных
равнобедренных треугольника подобны
• 2) В тупоугольном треугольнике сумма
углов больше 180 градусов
• 3) Сумма двух противоположных углов
равнобедренной трапеции равна 180
градусов

27. Найдите АМ

28. Найдите угол ВАD , если AD – касательная к окружности, угол ВОА равен 120 градусов.

29. В равнобедренном треугольнике основание равно 6, боковая сторона равна 5. Из вершины треугольника при основании и вершины,

противолежащей основанию,
проведены высоты.
Длина меньшей из них равна 4, найдите длину
другой высоты.

9.3 Простые машины | Техасский шлюз

Цели обучения: Простые машины. Расчет механических преимуществ и эффективности простых машин. Практические задачи. Проверка понимания.

. Цели обучения.

Расчет механического преимущества и эффективности простых и сложных машин

Основные термины раздела
сложная машина	выход эффективности	идеальное механическое преимущество
наклонная плоскость	входная работа	рычаг
механическое преимущество	выходная работа	шкив
винт	простая машина	клин
колесо и ось

Простые машины

Простые машины облегчают работу, но не уменьшают ее объем.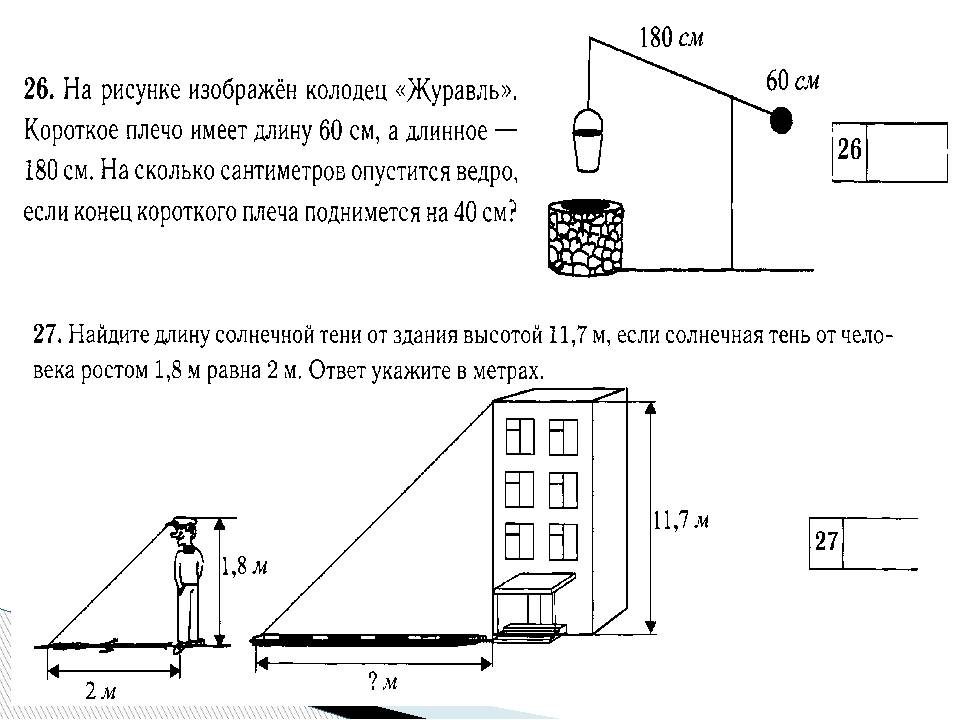 Почему простые машины не могут изменить объем выполняемой вами работы? Напомним, что в закрытых системах общее количество энергии сохраняется. Машина не может увеличить количество энергии, которую вы в нее вкладываете. Итак, чем полезна простая машина? Хотя она не может изменить объем выполняемой вами работы, простая машина может изменить величину силы, которую вы должны приложить к объекту, и расстояние, на котором вы прикладываете силу. В большинстве случаев для уменьшения силы, которую необходимо приложить для выполнения работы, используется простая машина. Обратной стороной является то, что вы должны приложить силу на большее расстояние, потому что произведение силы и расстояния,

f d (что равно работе) не меняется.

На рис. 9.8(b) показано, как математически работает рычаг. Сила усилия, приложенная к точке F _и , поднимает груз (сила сопротивления), которая давит вниз в точке F _р . Треугольный стержень называется точкой опоры; часть рычага между точкой опоры и F _e является усилителем, L _e ; а часть слева — это рычаг сопротивления, L _r . Механическое преимущество — это число, которое говорит нам, во сколько раз простая машина увеличивает силу усилия. Идеальное механическое преимущество, IMA , представляет собой механическое преимущество совершенной машины без потери полезной работы, вызванной трением между движущимися частями. Уравнение для IMA показан на рис. 9.8(b).

Рисунок 9. 8 (a) Монтировка представляет собой тип рычага. (b) Идеальное механическое преимущество равно длине плеча усилия, деленному на длину плеча сопротивления рычага.

В общем, IMA = сила сопротивления, F _r, деленная на силу усилия, F _e. IMA также равняется расстоянию, на котором прилагается усилие, d _e , деленное на расстояние, которое проходит груз, d _r .

IMA=FrFe=dedrIMA=FrFe=dedr

Возвращаясь к сохранению энергии, для любой простой машины работа, вложенная в машину, Вт _i равна работе, производимой машиной,

Вт _или . Объединив это с информацией из предыдущих абзацев, мы можем написать

Wi=WoFede=FrdrIf FeFr, затем de>dr.Wi=WoFede=FrdrIf FeFr, затем de>dr.

Уравнения показывают, как простая машина может производить тот же объем работы, уменьшая величину усилия за счет увеличения расстояния, на котором действует усилие.

Watch Physics

Введение в Mechanical Advantage

В этом видеоролике показано, как рассчитать IMA рычага тремя различными методами: (1) по силе усилия и силе сопротивления; (2) от длин плеч рычагов, и; (3) от расстояния, на котором приложена сила, и расстояния, на которое перемещается груз.

Проверка хватки

Двое детей разного веса катаются на качелях. Как они располагаются относительно точки опоры (точки опоры), чтобы сохранять равновесие?

Более тяжелый ребенок сидит ближе к точке опоры.
Более тяжелый ребенок сидит дальше от точки опоры.
Оба ребенка сидят на равном расстоянии от точки опоры.

Поскольку оба имеют разный вес, они никогда не будут сбалансированы.

Некоторые рычаги прикладывают большое усилие к короткому рычагу. Это приводит к тому, что на конце рычага сопротивления действует меньшая сила на большем расстоянии. Примерами этого типа рычага являются бейсбольные биты, молотки и клюшки для гольфа. В другом типе рычага точка опоры находится на конце рычага, а груз — посередине, как в конструкции тачки.

Простая машина, показанная на рис. 9.9, называется колесом и осью . На самом деле это форма рычага. Разница в том, что рычаг усилия может вращаться по полному кругу вокруг точки опоры, которая является центром оси. Сила, приложенная к внешней стороне колеса, вызывает большее усилие, приложенное к веревке, обернутой вокруг оси. Как показано на рисунке, идеальное механическое преимущество рассчитывается путем деления радиуса колеса на радиус оси. Любое устройство с кривошипным приводом является примером колеса и оси.

Рисунок 9.9 Сила, приложенная к колесу, действует на его ось.

Наклонная плоскость и клин — две формы одной и той же простой машины. Клин — это просто две наклонные плоскости, расположенные спиной к спине. На рис. 9.10 показаны простые формулы для расчета IMA s этих машин. Все наклонные мощеные поверхности для ходьбы или вождения представляют собой наклонные плоскости. Ножи и головки топоров являются примерами клиньев.

Рис. 9.10 Слева показана наклонная плоскость, справа — клин.

Винт, показанный на рис. 9.11, на самом деле представляет собой рычаг, прикрепленный к круглой наклонной плоскости. Шурупы по дереву (конечно) также являются примерами шурупов. Рычажная часть этих винтов представляет собой отвертку. В формуле для IMA расстояние между витками резьбы называется шагом и имеет символ P .

Рисунок 9.11 Показанный здесь винт используется для подъема очень тяжелых предметов, например, угла автомобиля или дома на небольшое расстояние.

На рис. 9.12 показаны три различные системы шкивов. Из всех простых машин механическое преимущество легче всего рассчитать для шкивов. Просто посчитайте количество канатов, поддерживающих груз. Это IMA . И снова мы должны применять силу на более длинном расстоянии, чтобы умножить силу. Чтобы поднять груз на 1 метр с помощью шкивной системы, вам нужно потянуть N метров веревки. Системы шкивов часто используются для подъема флагов и оконных жалюзи и являются частью механизма строительных кранов.

Рисунок 9.12 Здесь показаны три системы шкивов.

Watch Physics

Механические преимущества наклонных плоскостей и шкивов

В первой части этого видео показано, как рассчитать IMA систем шкивов. В последней части показано, как рассчитать IMA наклонной плоскости.

Щелкните, чтобы просмотреть содержание

Проверка захвата

Как можно использовать систему шкивов, чтобы поднять легкий груз на большую высоту?

Уменьшить радиус шкива.
Увеличить количество шкивов.
Уменьшите количество канатов, поддерживающих груз.
Увеличьте количество канатов, поддерживающих груз.

Сложная машина представляет собой комбинацию двух или более простых машин. Кусачки на рис. 9.13 сочетают в себе два рычага и два клина. Велосипеды включают в себя колеса и оси, рычаги, винты и шкивы. Автомобили и другие транспортные средства представляют собой комбинации многих машин.

Рис. 9.13 Кусачки для проволоки — обычное сложное оборудование.

Расчет механических преимуществ и эффективности простых машин

В общем, IMA = сила сопротивления, F _r, деленная на силу усилия, F _e. IMA также равно расстоянию, на которое прикладывается усилие, d _e , деленному на расстояние, которое проходит груз, d _r .

IMA=FrFe=dedrIMA=FrFe=dedr

Вернитесь к обсуждениям каждой простой машины для конкретных уравнений для IMA для каждого типа машины.

Никакие простые или сложные машины не обладают реальными механическими преимуществами, рассчитанными по уравнениям IMA . В реальной жизни часть прикладной работы всегда заканчивается напрасной тратой тепла из-за трения между движущимися частями. И входная работа ( W _i ), и выходная работа ( W _o ) являются результатом действия силы, F , действующей на расстоянии, d .

Wi=Fidi Wo=FodoWi=Fidi and Wo=Fodo

Выходная эффективность машины — это просто работа на выходе, деленная на работу на входе, и обычно умножается на 100, так что это выражается в процентах.

% эффективности=WoWi×100% эффективности=WoWi×100

Посмотрите на изображения простых машин и подумайте, какая из них будет иметь наибольшую эффективность. Эффективность связана с трением, а трение зависит от гладкости поверхностей и от площади соприкасающихся поверхностей. Как смазка повлияет на эффективность простой машины?

Рабочий пример

Эффективность рычага

Входная сила в 11 Н, действующая на плечо рычага, перемещается на 0,4 м, что поднимает груз массой 40 Н, опирающийся на плечо сопротивления, на расстояние 0,1 м. Каков КПД машины?

Стратегия

Укажите уравнение для эффективности простой машины, %эффективность = WOWI × 100, %эффективность = WOWI × 100 и рассчитывайте W _O и W _I . _{Оба рабочих значения являются продуктом Fd .}

Решение

Wi=FidiWi=Fidi = (11)(0,4) = 4,4 Дж и Wo=FodoWo=Fodo = (40)(0,1) = 4,0 Дж, тогда % эффективности=WoWi×100=4,04,4×100 =91% % efficiency=WoWi×100=4,04. 4×100=91%

Обсуждение

КПД реальных машин всегда будет меньше 100 процентов из-за работы, которая преобразуется в недоступное тепло за счет трения и сопротивления воздуха. W _o и W _i всегда можно вычислить как силу, умноженную на расстояние, хотя эти величины не всегда так очевидны, как в случае с рычагом.

Практические задачи

Какова IMA наклонной плоскости длиной 5 м и высотой 2 м?

0,4
2,5
0,4 м
2,5 м

Если система шкивов может поднять груз 200 Н с усилием 52 Н и имеет КПД почти 100 %, сколько канатов поддерживает груз?

Требуется 1 веревка, поскольку фактическое механическое преимущество составляет 0,26.
Требуется 1 веревка, потому что фактическое механическое преимущество составляет 3,80.
Требуется 4 веревки, потому что фактическое механическое преимущество составляет 0,26.
Требуется 4 веревки, потому что фактическое механическое преимущество составляет 3,80.

Проверьте свое понимание

Упражнение 6

Правда или ложь — КПД простой машины всегда меньше 100 %, потому что некоторая малая часть вложенной работы всегда преобразуется в тепловую энергию за счет трения.

Правда
Ложь

Упражнение 7

Круглая ручка крана прикреплена к стержню, который открывает и закрывает клапан при повороте ручки. Если стержень имеет диаметр 1 см, а IMA машины 6 , каков радиус ручки?

0,08 см
0,17 см
3,0 см
6,0 см

Печать
Поделиться

9.

3 Простые машины — физика

Раздел Цели обучения

К концу этого раздела вы сможете делать следующее:

Описывать простые и сложные машины
Расчет механического преимущества и эффективности простых и сложных машин

Поддержка учителей

Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:

(6) Научные концепции. Учащийся знает, что изменения происходят в физической системе, и применяет законы сохранения энергии и импульса. Ожидается, что студент:
- (C) описывать простые и сложные механизмы и решать задачи, связанные с простыми механизмами;
- (D) определяют входную работу, выходную работу, механическое преимущество и эффективность машин.

Кроме того, в Руководстве по физике для средней школы рассматривается содержание этого раздела лабораторной работы под названием «Работа и энергия», а также следующие стандарты:

(6) Научные концепции. Учащийся знает, что изменения происходят в физической системе, и применяет законы сохранения энергии и импульса. Ожидается, что студент:
- (Д) продемонстрировать и применить законы сохранения энергии и сохранения импульса в одном измерении.

Основные термины раздела

сложная машина	выход эффективности	идеальное механическое преимущество	наклонная плоскость	входная работа
рычаг	механическое преимущество	выходная работа	шкив	винт
простая машина	клин	колесо и ось

Поддержка учителей

В этом разделе вы примените то, что узнали о работе, чтобы найти механические преимущества и эффективность простых машин.

[BL][OL] Спросите учащихся, что они знают о машинах и работе. Развейте любые заблуждения о том, что машины сокращают объем работы. Следите за тем, чтобы учащиеся не приравнивали машины и двигатели, запрашивая (и, при необходимости, предоставляя) примеры машин без двигателя. Объясните, что простые машины часто держат в руках и что они снижают силу, а не работают.

[AL] Запросить напоминание формулы W = f d . Объясните, что произведение силы на расстояние имеет решающее значение для понимания простых механизмов. Поскольку объем работы не меняется, срок f d не меняется, но сила может уменьшаться при увеличении расстояния. Это основной принцип всех простых машин.

Простые машины

Давайте посмотрим, как это работает на практике. На рис. 9.8(а) рабочий использует своего рода рычаг, чтобы приложить небольшое усилие на большом расстоянии, в то время как монтировка тянет гвоздь с большой силой на небольшом расстоянии. На рис. 9.8(b) показано, как математически работает рычаг. Сила усилия, приложенная к точке F _и , поднимает груз (сила сопротивления), которая давит вниз в точке F _р . Треугольный стержень называется точкой опоры; часть рычага между точкой опоры и F _e является усилителем, L _e ; а часть слева — это рычаг сопротивления, L _r . Механическое преимущество — это число, которое говорит нам, во сколько раз простая машина увеличивает силу усилия. Идеальное механическое преимущество, IMA , представляет собой механическое преимущество совершенной машины без потери полезной работы, вызванной трением между движущимися частями. Уравнение для IMA показан на рис. 9.8(b).

Рисунок 9,8 а) Рычаг представляет собой разновидность рычага. (b) Идеальное механическое преимущество равно длине плеча усилия, деленному на длину плеча сопротивления рычага.

IMA=FrFe=dedrIMA=FrFe=dedr

Возвращаясь к сохранению энергии, для любой простой машины работа, вложенная в машину, Вт _i равна работе, производимой машиной, Вт _или . Объединив это с информацией из предыдущих абзацев, мы можем написать

Wi=WoFede=FrdrIf Fedr.Wi=WoFede=FrdrIf Fedr.

Смотреть физику

Введение в механические преимущества

Поддержка учителей

Начало этого видео может вызвать больше путаницы, чем просветления. Он показывает вывод с использованием триггерных функций, который выходит за рамки этой главы. Заинтересованные студенты могут захотеть пройти через это. Большинству студентов следует пропустить последние две или три минуты, которые объясняют основы расчета IMA рычага из различных соотношений. Обзор W = f d .

Физика часов: введение в механические преимущества. В этом видео представлены простые машины, механическое преимущество и моменты.

Нажмите, чтобы просмотреть содержимое

Более тяжелый ребенок сидит ближе к точке опоры.
Более тяжелый ребенок сидит дальше от точки опоры.
Оба ребенка сидят на равном расстоянии от точки опоры.
Поскольку оба имеют разный вес, они никогда не будут сбалансированы.

Поддержка учителей

[AL]Скажите учащимся, что есть еще два класса рычагов с различным расположением нагрузки, точки опоры и усилия. Попросите их сначала попытаться нарисовать их. После того, как они с вашей помощью или без вас обнаружат три типа, спросите, могут ли они придумать примеры типов, не показанных на рис. 9.8.

Рисунок 9,9 Сила, приложенная к колесу, действует на его ось.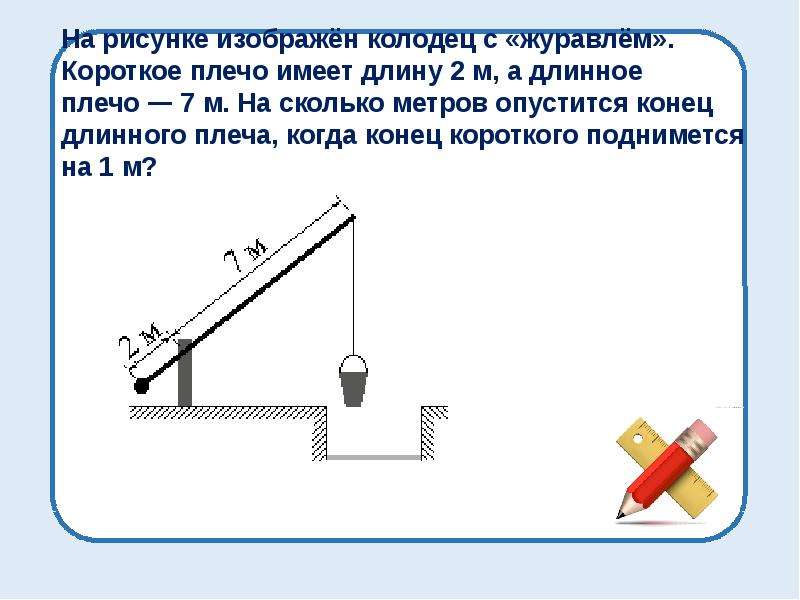

Поддержка учителей

[BL][OL] Посмотрите, уловили ли учащиеся идею о том, что колесо и ось на самом деле являются разновидностью рычага. Покажите им, что это больше похоже на рычаг, если колесо заменить рукояткой. Приведите несколько примеров: лебедка с ручным приводом, рулевое колесо, дверная ручка и т. д. Спросите их, почему рулевые колеса имели больший диаметр до изобретения гидроусилителя руля.

[AL] Объясните, что колеса транспортных средств на самом деле не являются простыми механизмами в том смысле, в каком они показаны на рис. 9.9. Ось транспортного средства не работает под нагрузкой. Потери энергии на трение уменьшаются, но ничего не поднимается.

Рисунок 9.10 Слева показана наклонная плоскость, справа – клин.

Поддержка учителей

[BL][OL] Расскажите о сходстве и различиях наклонных плоскостей и клиньев. Обратите внимание, что при использовании наклонной плоскости груз перемещается, а при использовании клина груз неподвижен, а машина движется. Объясните, почему в этих машинах на трение обычно теряется больше энергии, чем в других простых машинах.

Поддержка учителей

[BL][OL] Предложите выделить винт в отдельный тип простой машины, возможно, потому, что он выглядит совсем иначе, чем он есть на самом деле — наклонная плоскость, которую иногда поворачивает рычаг. Объясните, что комбинированное механическое преимущество может быть большим. Устройства, подобные показанному на рис. 9.10, используются для подъема автомобилей и даже домов. Предложите учащимся сравнить этот шуруп с шурупом для дерева и круглой лестницей.

[AL] Спросите учащихся, чем сила, прикладываемая шурупом, отличается от силы, приложенной шурупом на рис. 9..10. Попросите объяснить 2 ππ в уравнении для IMA .

Рисунок 9.12 Здесь показаны три системы шкивов.

Поддержка учителей

[BL][OL] Расчет для IMA шкива кажется слишком простым, чтобы быть правдой, но это так. Попросите учащихся попытаться понять, почему IMA — это просто N . Скажите им, что просмотр видео должен прояснить этот момент. Шкивы когда-то видели на парусных кораблях и фермах, где они использовались для подъема тяжелых грузов. Выступ, который вы, возможно, видели на конце старых крыш сарая, — это место, где когда-то был прикреплен шкив. Таким образом, тюки сена можно было поднять на сеновал, не промокнув. Шкивы все еще можно увидеть в использовании, чаще всего на больших строительных кранах.

Смотреть физику

Механические преимущества наклонных плоскостей и шкивов

Поддержка учителей

Прежде чем смотреть видео, ознакомьтесь с тем, что вы узнали о IMA наклонных плоскостей и систем шкивов. Напомните учащимся, что для идеальной машины работа в = работа и что Вт = ж д . На видео показано, как найти f s и d s.

Проверка захвата

Как можно использовать систему шкивов, чтобы поднять легкий груз на большую высоту?

Уменьшить радиус шкива.
Увеличить количество шкивов.
Уменьшите количество канатов, поддерживающих груз.
Увеличьте количество канатов, поддерживающих груз.

Сложная машина представляет собой комбинацию двух или более простых машин. Кусачки на рис. 9.13 соединить два рычага и два клина. Велосипеды включают в себя колеса и оси, рычаги, винты и шкивы. Автомобили и другие транспортные средства представляют собой комбинации многих машин.

Рисунок 9.13 Кусачки для проволоки — это обычная сложная машина.

Поддержка учителей

[BL][OL] Убедитесь, что учащиеся понимают, что сложная машина представляет собой просто комбинацию простых машин и все еще довольно проста . Не позволяйте им путать этот термин со сложными машинами, такими как компьютеры. Обратите внимание, что IMA отдельных простых машин в сложной машине обычно умножаются, потому что выходная сила одной машины становится входной силой другой машины. В качестве дополнительного развлечения предложите учащимся найти в Интернете Машина Руба Голдберга .

Расчет механических преимуществ и эффективности простых машин

В общем, IMA = сила сопротивления, F _r, деленная на силу усилия, F _e. IMA также равно расстоянию, на котором прилагается усилие, d _e , деленному на расстояние, которое проходит груз, d _r .

IMA=FrFe=dedrIMA=FrFe=dedr

Вернитесь к обсуждениям каждой простой машины для конкретных уравнений для IMA для каждого типа машины.

Никакие простые или сложные машины не обладают реальными механическими преимуществами, рассчитанными по уравнениям IMA . В реальной жизни часть прикладной работы всегда заканчивается напрасной тратой тепла из-за трения между движущимися частями. И входная работа ( W _i ), и выходная работа ( W _o ) являются результатом действия силы 9.0061 F , действующий на расстоянии, d .

Wi=FidianandWo=FodoWi=FidianandWo=Fodo

% эффективности=WoWi×100% эффективности=WoWi×100

Поддержка учителей

[BL][OL] Повторить материал о переходе механической энергии в теплоту и законе сохранения энергии. Объясните, как потери тепла из-за трения гарантируют, что Вт _o всегда будет меньше, чем Вт _i , предотвращая достижение КПД 100%.

Рабочий пример

Эффективность рычага

Входная сила в 11 Н, действующая на плечо усилия рычага, перемещается на 0,4 м, что поднимает груз массой 40 Н, опирающийся на плечо сопротивления, на расстояние 0,1 м. Каков КПД машины?

Стратегия

Составьте уравнение для эффективности простой машины, % КПД = WoWi × 100, % КПД = WoWi × 100, и рассчитайте Вт _o и Вт _i .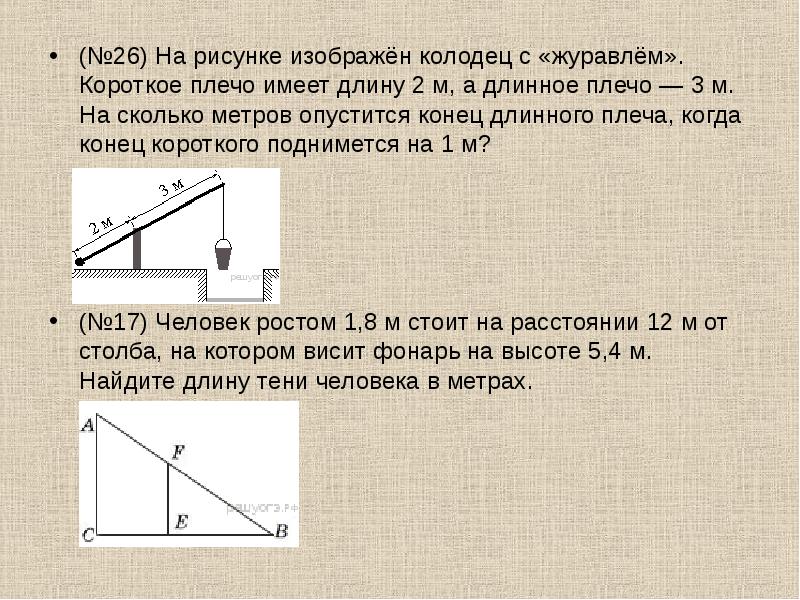 _{Оба рабочих значения являются продуктом Fd .}

Решение

Wi=FidiWi=Fidi = (11)(0,4) = 4,4 Дж и Wo=FodoWo=Fodo = (40)(0,1) = 4,0 Дж, тогда % эффективности=WoWi×100=4,04,4×100= 91% % эффективность=WoWi×100=4,04,4×100=91%

Обсуждение

Поддержка учителей

Совет для преподавателя. При расчете эффективности достаточно легко понять, что такое сила входа и выхода: сила, которую вы прикладываете, — это сила входа, а вес поднимаемого объекта — сила выхода. Входное и выходное расстояния легче увидеть для рычага, наклонной плоскости и клина. Остальные три не так очевидны. Для системы шкивов входное расстояние — это расстояние, на которое вы тянете веревку, а выходное расстояние — это расстояние, на которое поднимается груз. Для колеса и оси входное расстояние — это окружность колеса, а выходное расстояние — это окружность оси. Для винта входное расстояние — это длина окружности, к которой приложена сила, а выходное расстояние — это расстояние между витками резьбы.

Практические задачи

11.

(кредит: модификация работы OdysseyWare Inc.)

Рисунок 9.14

Наклонная плоскость длиной 5 м и высотой 2 м используется для загрузки большого ящика в кузов грузовика. Что такое IMA наклонной плоскости?

0,4
2,5
0,4\,\текст{м}
2,5\,\текст{м}

12.

Требуется 1 веревка, поскольку фактическое механическое преимущество составляет 0,26.
Требуется 1 веревка, потому что фактическое механическое преимущество составляет 3,80.
Требуется 4 веревки, потому что фактическое механическое преимущество составляет 0,26.
Требуется 4 веревки, потому что фактическое механическое преимущество составляет 3,80.

Проверьте свое понимание

13.

Правда
Ложь

14.

Круглая ручка крана прикреплена к стержню, который открывает и закрывает клапан при повороте ручки.