Задание № 7. Производная функции. ЕГЭ . Математика. 1
ПОДГОТОВКА К ЕГЭ ПО МАТЕМАТИКЕ
1. Планиметрия
2. Стереометрия
3. Начала теории вероятностей
4. Теория вероятностей
5. Простейшие уравнения
6. Преобразование выражений
7. Производная функции
8. Практические задачи
9. Текствые задачи
10. Графики функций
11. Исследование функций
12. Уравнения
13. Стереометрия с доказ-вом
14. Неравенства
15. Финансовая математика
16. Планиметрия с доказ-вом
17. Задачи с параметром
18. Задачи на логику
БАЗА ЗАДАНИЙ
Задание № 7.
1. На рисунке изображены график дифференцируемой функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Ответ: 1
2. На рисунке изображены график дифференцируемой функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
3. На рисунке изображены график дифференцируемой функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Ответ: -0,5
4. На рисунке изображены график дифференцируемой функции y=f(x) и касательная к нему в точке с абсциссой x0.
Ответ: 2
5. На рисунке изображены график дифференцируемой функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0..
Ответ: -0,75
6. На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x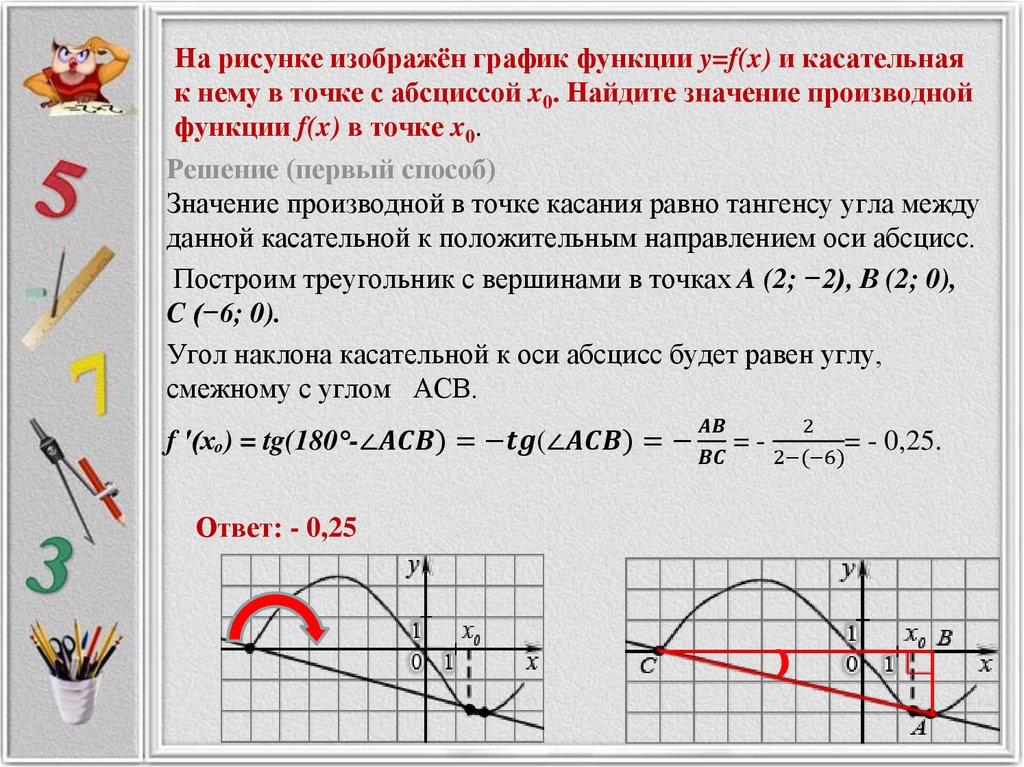
Ответ: 1,4
7. На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Ответ: -0,25
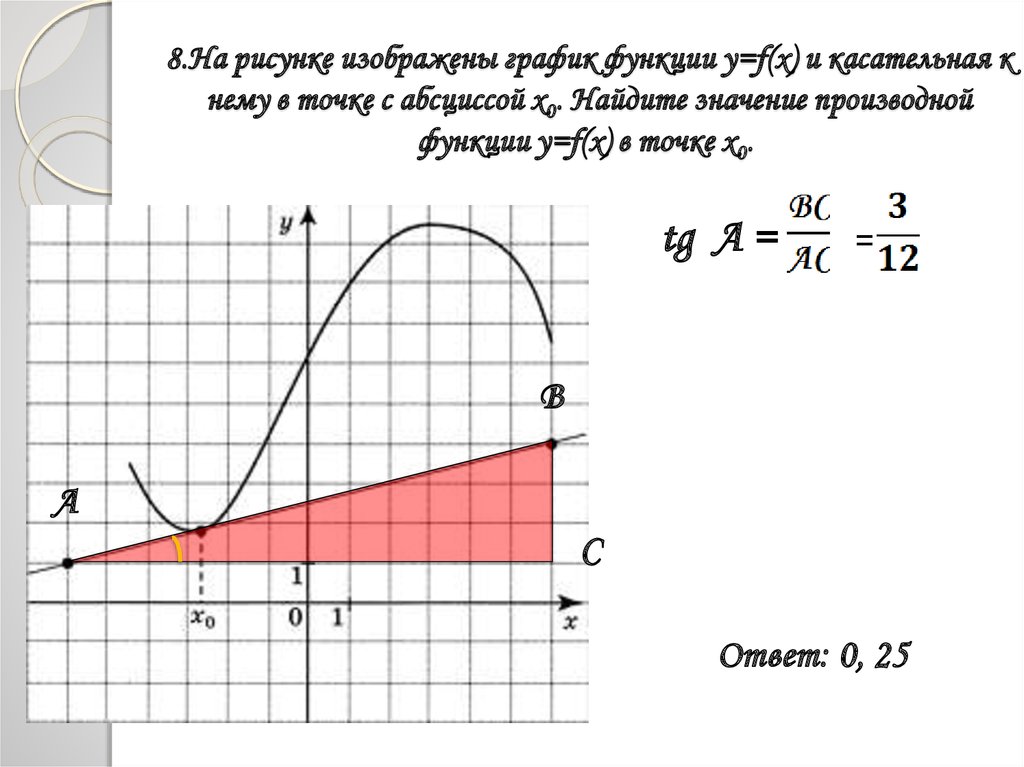
8. На рисунке изображены график функции
Ответ: 0,4
9. На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Ответ: -0,8
10. На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Ответ: -1,25
11. На рисунке изображен график функции y=f(x). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 8. Найдите значение производной в точке 8.
Ответ: 1,25
12. На рисунке изображён график дифференцируемой функции y=
Ответ: 1
13. На рисунке изображён график дифференцируемой функции y=f(x), определённой на интервале (1; 10). Найдите точку из отрезка [2; 6], в которой производная функции f(x) равна 0.
На рисунке изображён график дифференцируемой функции y=f(x), определённой на интервале (1; 10). Найдите точку из отрезка [2; 6], в которой производная функции f(x) равна 0.
Ответ: 3
Ответ: -7
15. На рисунке изображён график дифференцируемой функции y=f(x), определённой на интервале (− 11; − 1). Найдите точку из отрезка [− 7; − 2], в которой производная функции f(x) равна 0.
Ответ: -4
16. На рисунке изображён график функции 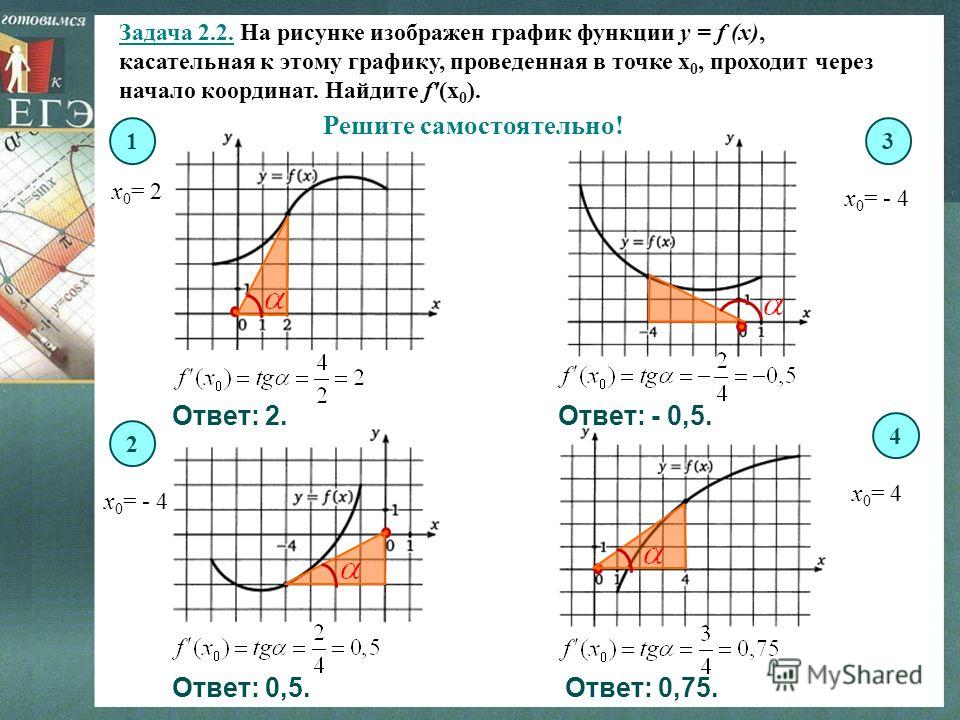 Найдите количество точек, в которых производная функции f(x) равна 0.
Найдите количество точек, в которых производная функции f(x) равна 0.
Ответ: 6
17. На рисунке изображён график функции y=f(x), определённой на интервале (− 5; 8). Найдите количество точек, в которых производная функции f(x) равна 0.
Ответ: 8
18. На рисунке изображён график функции y=f(x), определённой на интервале
Ответ: 7
19. На рисунке изображён график функции y=f(x), определённой на интервале (− 6; 6). Найдите количество решений уравнения f '(x)=0 на отрезке [− 4,5; 2,5].
Ответ: 4
20. На рисунке изображён график функции y=f '(x) — производной функции f(x), определённой на интервале (2; 13).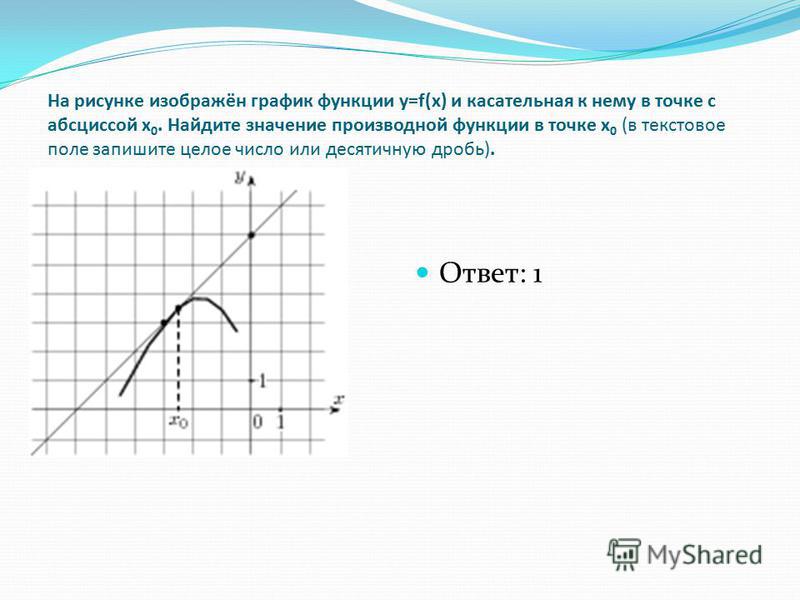 Найдите точку максимума функции
Найдите точку максимума функции
Ответ: 9
21. На рисунке изображён график функции y=f '(x) — производной функции f(x), определённой на интервале (− 6; 3). Найдите точку минимума функции f(x).
Ответ: -2
22. На рисунке изображён график функции y=f '(x) — производной функции f(x), определённой на интервале (1; 10). Найдите точку минимума функции f(x).
Ответ: 9
23. На рисунке изображён график функции y=f '(x)
Ответ: -1
24. На рисунке изображён график функции y=f(x), определённой на интервале (− 7; 7).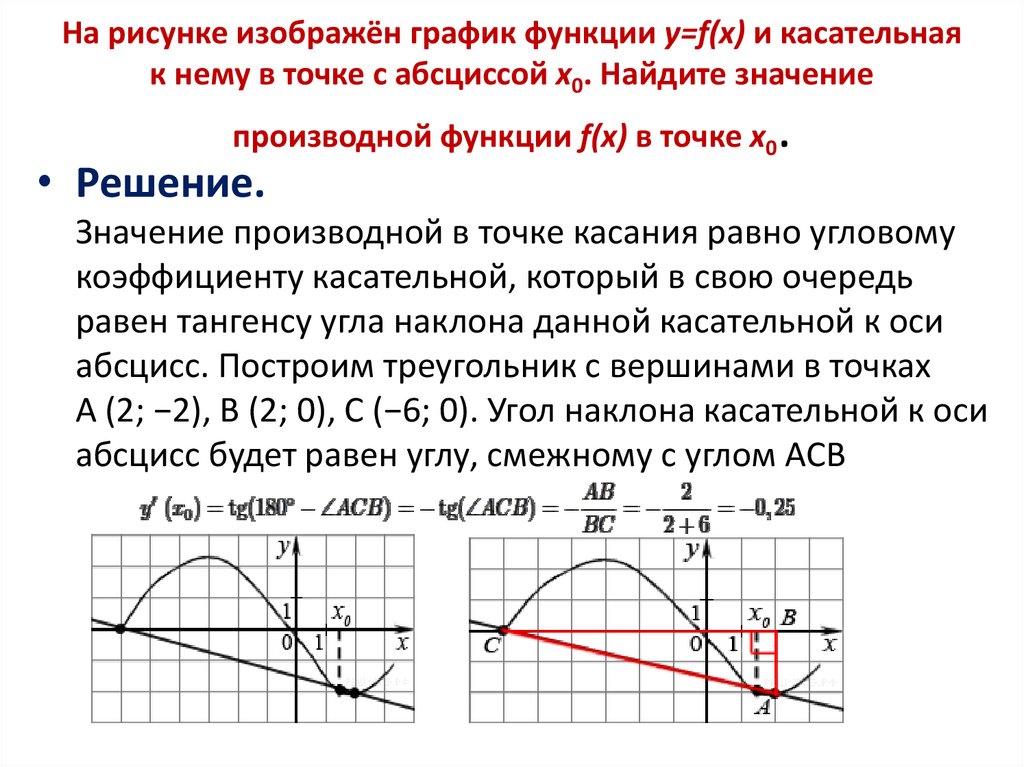 Определите количество целых точек, в которых производная функции положительна.
Определите количество целых точек, в которых производная функции положительна.
Ответ: 8
25. На рисунке изображён график функции y=f(x), определённой на интервале (− 7; 7)
Ответ: 5
1 2 3
Главная
@ 2017- 2023
База заданий сформирована из Официального Банка заданий ФИПИ,
Открытого банка заданий ЕГЭ, а также из реальных вариантов ЕГЭ прошлых лет.
Репетитор
по математике
WhatsApp: 8-913-866-07-50
Готовимся к ЕГЭ. Задания В 8 и В 14
Similar presentations:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Готовимся к ЕГЭ
Задания В 8 и В 142. На рисунке изображены график функции y=f(x) и касательная к этому графику, проведённая в точке с абсциссой x₀.
• Найдите значениепроизводной
функции f(x)в точке
x₀
2
3. На рисунке изображен график производной функции f(x), определенной на интервале (−6;5)
В какой точкеотрезка
[−5;−1] f(x)
принимает
наименьшее
значение?
-5
4. На рисунке изображен график производной функции y=f(x), определенной на интервале (–9;4)
Найдите количество точек, в которыхкасательная к графику функции
у=f(x)параллельна прямой y=2x−17
или совпадает с ней.

2
5. На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x₀.
Найдите значениепроизводной
функции f(x) в точке
x₀
0,5
В8
Найдите точку касания прямой
y=3x+8 и графика функции
y=xᵌ+x²−5x−4. В ответе укажите
абсциссу этой точки.
-2
7. На рисунке изображён график функции y=f(x), определенной на интервале (−7;5)
Определите количество целочисленныхзначений аргумента, при которых
производная функции f(x) отрицательна
4
8. На рисунке изображён график функции y=f′(x), определенной на интервале (−8;8)
2Найдите количество точек экстремума
функции f(x), принадлежащих отрезку [−4;6].
9. На рисунке изображён график функции y=f′(x), определенной на интервале (−8;4)
На рисунке изображён график функцииy=f′(x), определенной на интервале (−8;4)
3
Найдите количество точек, в которых касательная к
графику функции f(x) параллельна прямой y=5–x
или совпадает с ней.
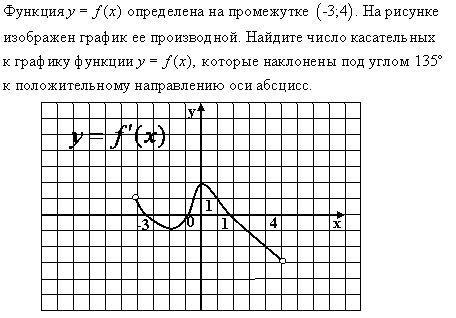
• Найдите наибольшее значение функции
y=12sinx− 102 x+20 на отрезке [ 56 ;0].
99
11. На рисунке изображен график производной функции y=f(x), определенной на интервале (−8;3)
2Найдите количество точек, в которых касательная к
графику функции параллельна прямой y=−20
12. На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x₀
Найдитезначение
производной
функции f(x) в
точке x₀
-0,5
• Найдите наименьшее значение функции
y=6cosx−7x+8 на отрезке [−3/2π;0]
14
14. На рисунке изображён график производной функции f(x), определенной на интервале (−9;9)
Найдите количество точек минимумафункции f(x) на отрезке [−6;8]
1
• Найдите наибольшее значение
функции y=xᵌ+4x²−3x−12 на отрезке
[−4;−1]
6
16. На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x₀
Найдитезначение
производной
функции f(x) в
точке x₀
0,5
• Найдите наибольшее значение
функции y=9tgx−9x+4 на отрезке
[ ;0]
4
4
• Найдите наибольшее значение функции
на отрезке 1;10
х 2 25
у
х
26
English Русский Rules
На следующем рисунке показан график непрерывной функции y = f(x) на отрезке [1, 3].
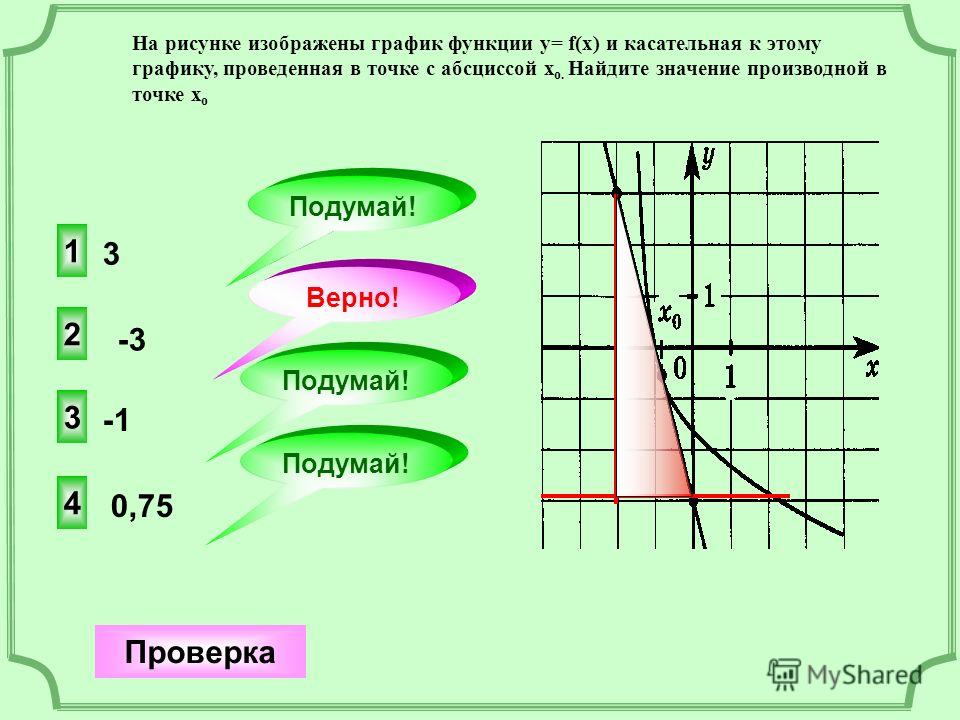 Точки A, B, C имеют координаты (1,1), (3,2),(2,3) соответственно, а прямые L(1) и L(2) параллельны, причем L(1) касательной к кривой в точке C. Если площадь под графиком y = f(x) от x = 1 до x = 3 равна 4 квадратным единицам, то площадь заштрихованной области равна
Точки A, B, C имеют координаты (1,1), (3,2),(2,3) соответственно, а прямые L(1) и L(2) параллельны, причем L(1) касательной к кривой в точке C. Если площадь под графиком y = f(x) от x = 1 до x = 3 равна 4 квадратным единицам, то площадь заштрихованной области равнаCENGAGE-AREA-Единственный правильный ответ Тип
20 видеоРЕКЛАМА
Ab Padhai karo bina ads ke
Khareedo DN Про и дехо сари видео бина киси ад ки рукаават ке!
Ответить
Пошаговое решение, разработанное экспертами, чтобы помочь вам в решении вопросов и получении отличных оценок на экзаменах.
Похожие видео
График функции y=f(x) показан на соседнем рисунке. Четыре предела l_(1),l_(2),l_(3) и I_(4) задаются как:
9391947
Ниже показан график непрерывной функции y=f(x) на интервале [1,3]. Точки A, B, C имеют координаты (1,1),(3,2),(2,3) соответственно, а прямые L1 и L2 параллельны, причем L1 касается кривой в точке C.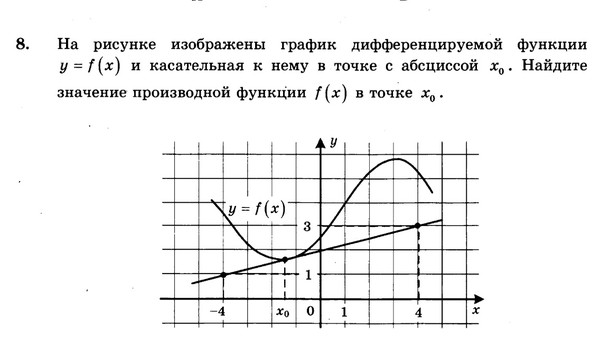 Если площадь под графиком y=f(x) от x=1 до x=3 составляет 4 квадратных единицы, то площадь заштрихованной области равна —
Если площадь под графиком y=f(x) от x=1 до x=3 составляет 4 квадратных единицы, то площадь заштрихованной области равна —
28828078
Текстовое решение
L1:x+1−3=y−32=z+21,L2:x1=y−7−3=z+72
Строки L1 и L2 равны —
121711480
L1:x+1−3=y−32=z+21,L2:x1=y−7−3=z+72
Прямые L1 и L2 пересекаются в точке
121711481
L1:x+ 1−3=y−32=z+21,L2:x1=y−7−3=z+72
Уравнение плоскости, содержащей L1 и L2, равно —
121711484
Прямая L1:x5+yb=1 проходит через точку (13, 32) и параллелен L2:xc+y3=1. Тогда расстояние между L1 и L2 равно
327463484
Рассмотрим строки
L1:x+y=10, L2:x+y=60
L3:x=40, L4:y=40.
L1 совпадает с осью x и y в точках A и B соответственно.
L4 пересекается с осью y в точке C и L2 в точке D
L3 пересекается с L2 в точке E и с осью x в точке F.
Периметр шестиугольника ABCDEF равен
621728211
(x) на отрезке [1, 3].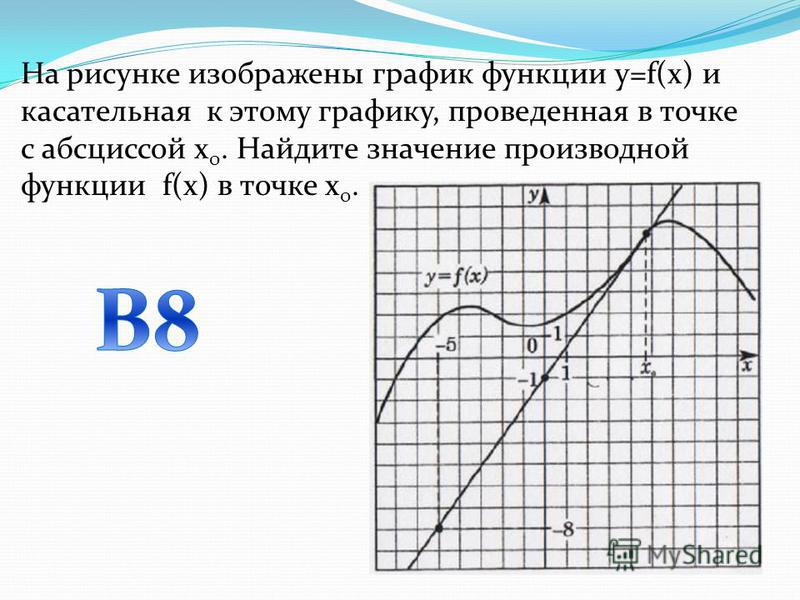 Точки A, B, C имеют координаты (1,1), (3,2),(2,3) соответственно, а прямые L1 и L2 параллельны, причем L1 касается кривой в точке C. Если площадь под график y = f(x) от x = 1 до x = 3 равен 4 квадратным единицам, тогда площадь заштрихованной области равна
Точки A, B, C имеют координаты (1,1), (3,2),(2,3) соответственно, а прямые L1 и L2 параллельны, причем L1 касается кривой в точке C. Если площадь под график y = f(x) от x = 1 до x = 3 равен 4 квадратным единицам, тогда площадь заштрихованной области равна
642553325
На следующей диаграмме показана непрерывная функция y = f (x) на интервале [1,3]. Координаты A, B, C равны (1, 1), (3, 2) и (2, 3) соответственно: L_1 И L_2 Линии параллельны, L_1 Является касательной, которая касается кривой в точке C. Если y = f (x) площадь под графиком равна 4 квадратным единицам от x = 1 до x = 3, то какова площадь покрытой области?
642682416
एक रेखा L1:x5+yb=1 , बिन्दु M(13, 32) से गुजरतै है रेखा L2:xc+y3=1 रेखा L1 के समान्तर है, तो L1 एवं L2 के मध्य दी र0003
643094887
L1: x+1–3 = y — 32 = z+21
L2: x1 = y — 7 — 3 = z+72
रेखाएँ L1 व L2 है
643227138
СМОТ x3+y4=1,L2:x4+y3=1,L3:x3+y4=2andL4:x4+y3=2 .Найдите соотношение между этими линиями.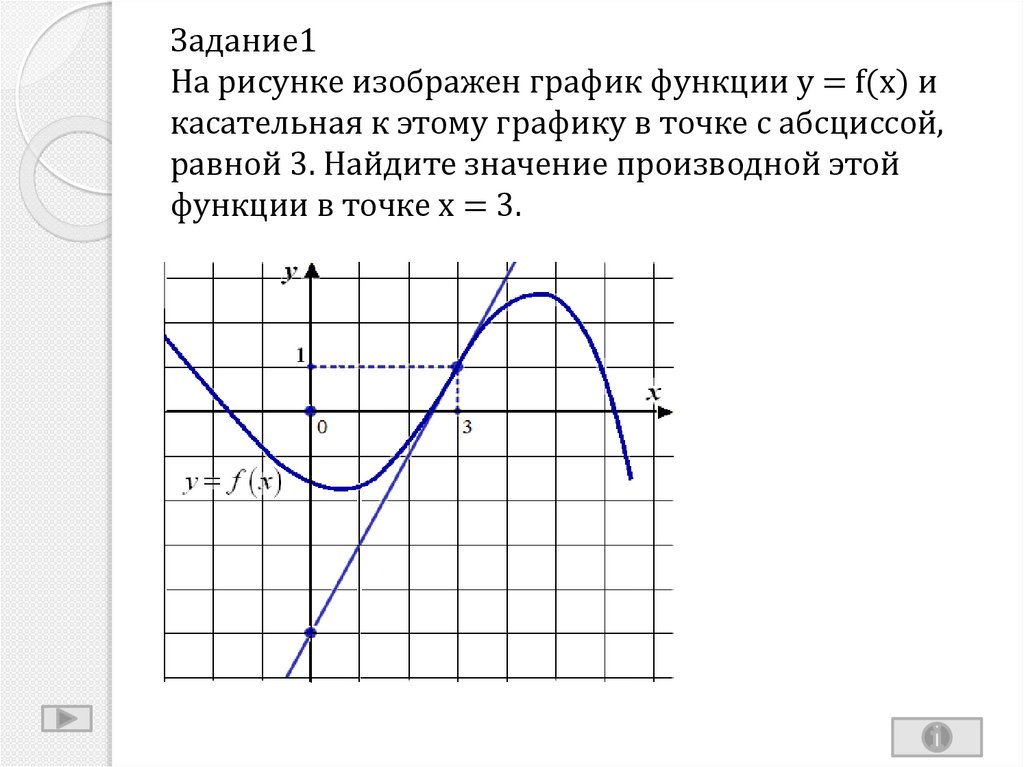
644013777
यदि 000 ेख ेख ेख13 = y — 21 = z — 32 और l2: x — 31 = y -12 = z — 23 समतलीय हैं, तब l1 और l2 प प wher प प प प प Как प समीक क क क समतल क क 3 , जो मूल बिंदु से अधिकतम दूरी पर है,
644157562
two=Dx9=x30022 L1 : x=a,L2:x=1(a≠0) — две прямые.
ЕСЛИ линия L1 пересекает параболу C в точке B на линии L2, отличной от A, то a может быть равно
644360996
L1:x+1−3=y−32=z+21,L2 :x1=y−7−3=z+72
Прямые L1 и L2 равны —
644637183
Прямая L1:x5+yb=1 проходит через точку (13, 32) и параллельна L2:xc +у3=1. Тогда расстояние между L1 и L2 равно
645080850
Производные, касательные и скорости изменения
Производные, касательные и скорости изменения Исчисление с одной переменной можно разделить на дифференциальное исчисление и интегральное
исчисление . Дифференциальное исчисление производные и их применение. Исследования интегрального исчисления интегралы и их приложения.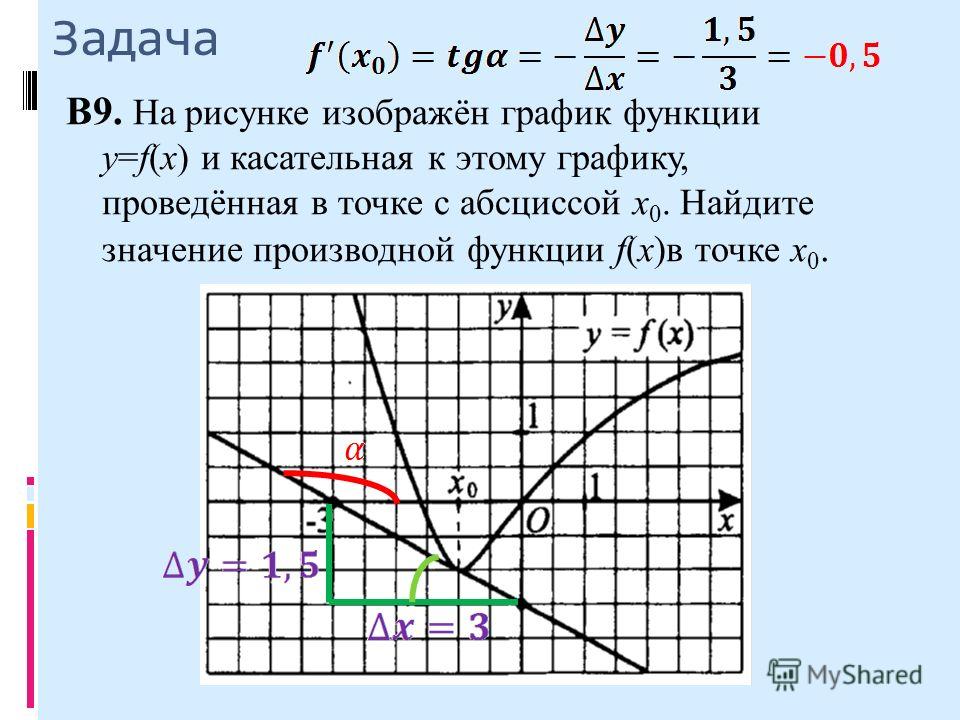 Два
части связаны основной теоремой Расчет ; грубо говоря, что производные и интегралы равны
«противоположности».
Два
части связаны основной теоремой Расчет ; грубо говоря, что производные и интегралы равны
«противоположности».
Я начну обсуждение производных с геометрического вопроса. Учитывая функцию, как найти наклон касательная к графику в точке ?
(Я думаю о касательной линии как о линии который просто просматривает график в , не переходя через график в этой точке. Это расплывчатое описание, но оно пока сделаю)
Вот идея. Выберите точку поблизости и нарисуйте линия, соединяющая с. (А Линия, соединяющая две точки на графике, называется секущая линия .)
Таким образом, h представляет, сколько вы «переместились» в x-направление. Линия имеет наклон
Если сдвинуть вторую точку по графику по направлению к P секущая линия становится все ближе и ближе к касательной. Алгебраически это равносильно принятию предела как . Таким образом, наклон касательной при
Пример.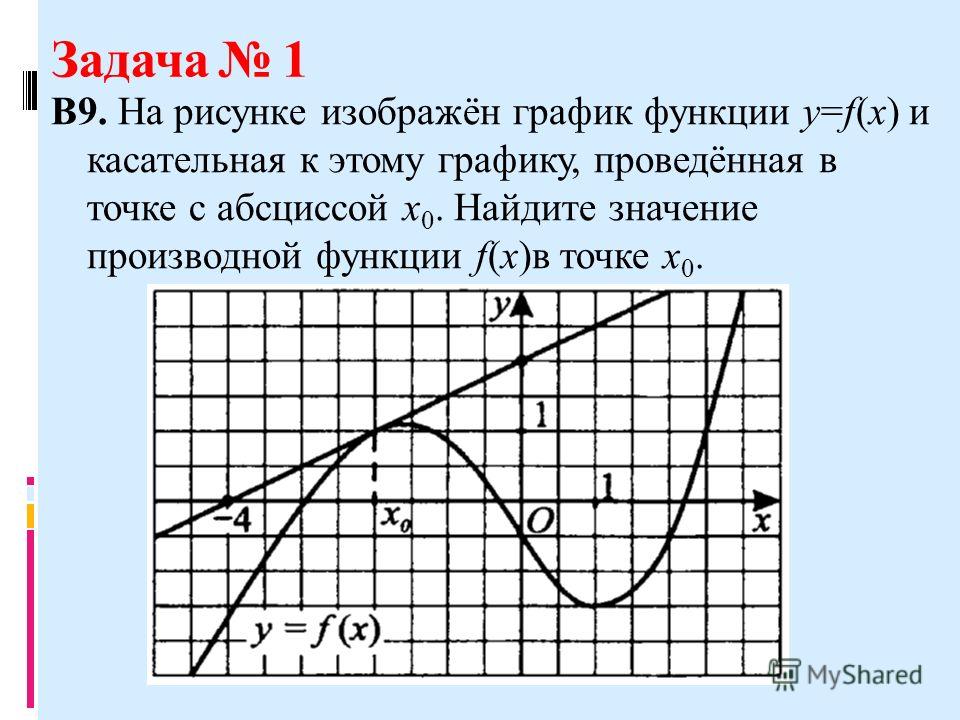 Пусть .
Пусть .
а) Найдите наклон секущей, соединяющей .
(b) Найдите наклон касательной к точке .
(а)
(b) В этом случае я ввожу уравнение для и вычисляю предел:
Другая форма формулы касательной линии:
Вы можете получить эту формулу из предыдущей, поставив . Тогда, так дает.
Пример. Найдите наклон касательной к в .
График представляет собой прямоугольную гиперболу. Уведомление что, не введя конкретный номер для a, я получил формула, которую я могу использовать для любого a. Например, наклон касательная в (т.е. в точке ) равна
Существует и другая интерпретация наклонов секущей и касательная линия. Наклон секущей, соединяющейся с
Это изменение в f разделить на изменить в x,
поэтому он представляет среднюю скорость изменения f при переходе x от a к b (т.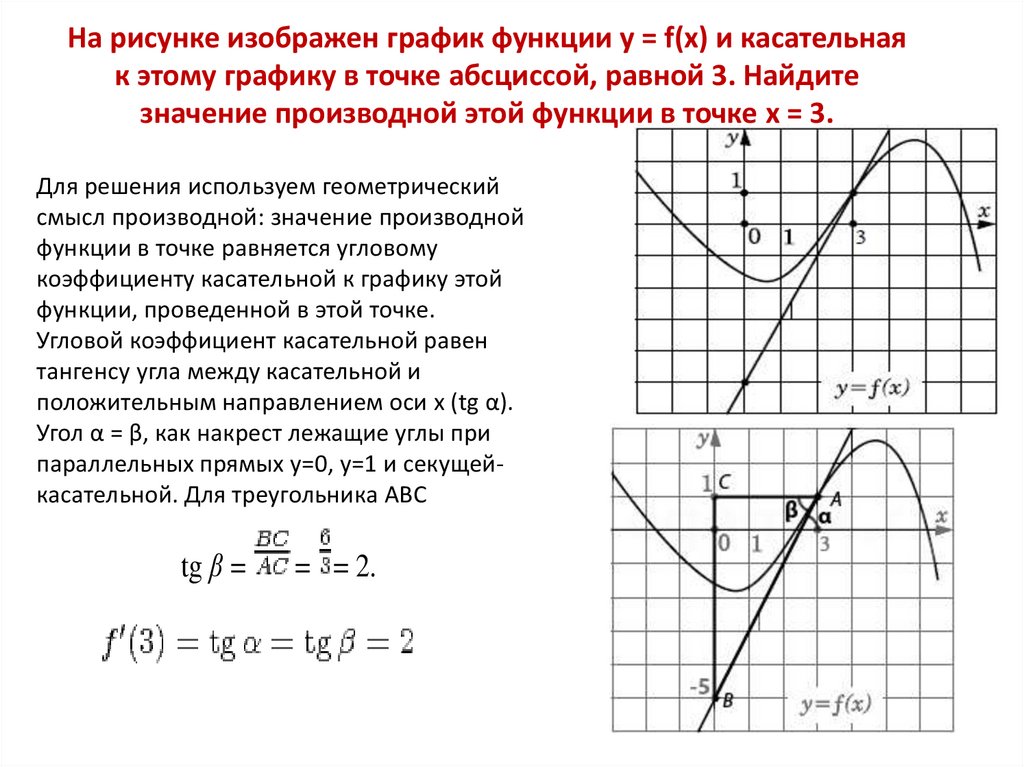 е. на интервале ).
е. на интервале ).
Каков наклон касательной в точке а? Он представляет мгновенную скорость изменения при . (Иногда люди ленятся и просто говорят «оцените изменения» означает » мгновенную скорость изменять».)
Пример. Пусть
а) Найдите среднюю скорость изменения на интервале .
б) Найдите мгновенную скорость изменения при .
(а)
(b) Мгновенная скорость изменения at равна at . я буду использовать вторая формула для:
Я устанавливаю и вычисляю предел:
Таким образом, мгновенная скорость изменения at равна . Это означает что если бы f продолжало изменяться с той же скоростью, то для каждых 4 единиц, что x увеличилось, функция увеличилась бы на 1 единицу.
Конечно, функция , а не продолжает изменяться в
такая же ставка. На самом деле меняется скорость изменения функции! —
скорость изменения функции сама по себе является функцией.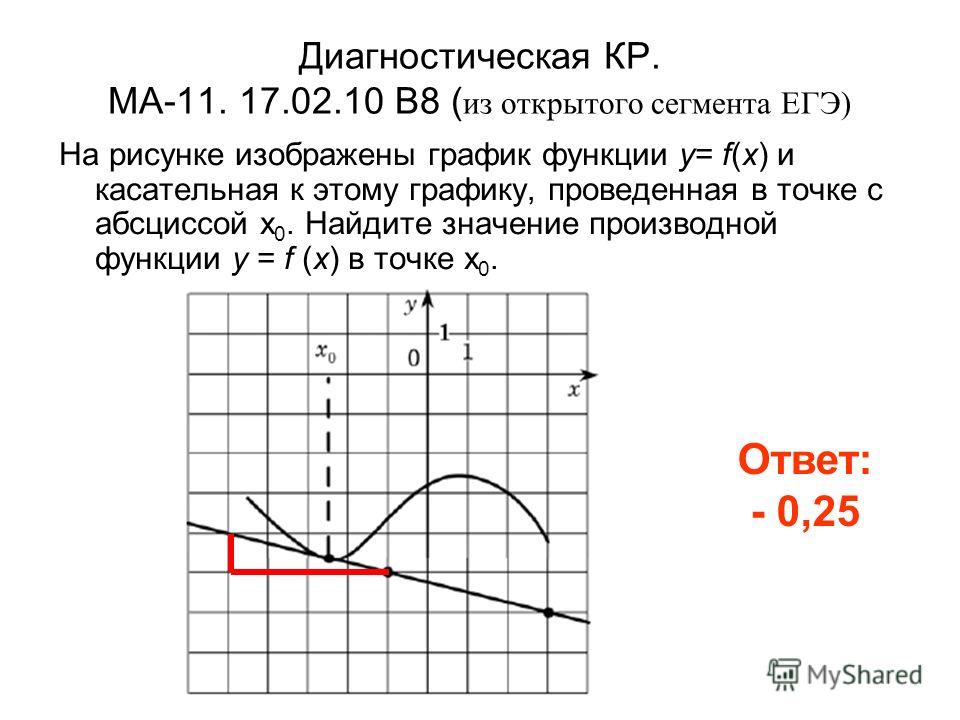
Предположим, что исследуемая функция дает положение объекта, движущегося в одном измерении. (Представьте, что что-то движется влево или вправо по оси x или предмет, который подбрасывают прямо вверх и который в конце концов падает обратно на землю.) Например, предположим, что это положение объекта в момент времени t.
средняя скорость объекта от до представляет собой изменение положения, деленное по прошедшему времени:
Обратите внимание, что это то же самое, что и наклон секущей к кривая, или средняя скорость изменения.
Мгновенная скорость at равна
Это наклон касательной к кривой или мгновенная скорость изменения. Вы также можете использовать вторую формулу
Грубо говоря, мгновенная скорость показывает, насколько быстро объект движется в определенный момент.
Пример. Положение объекта в момент времени t является
а) Найдите среднюю скорость от до .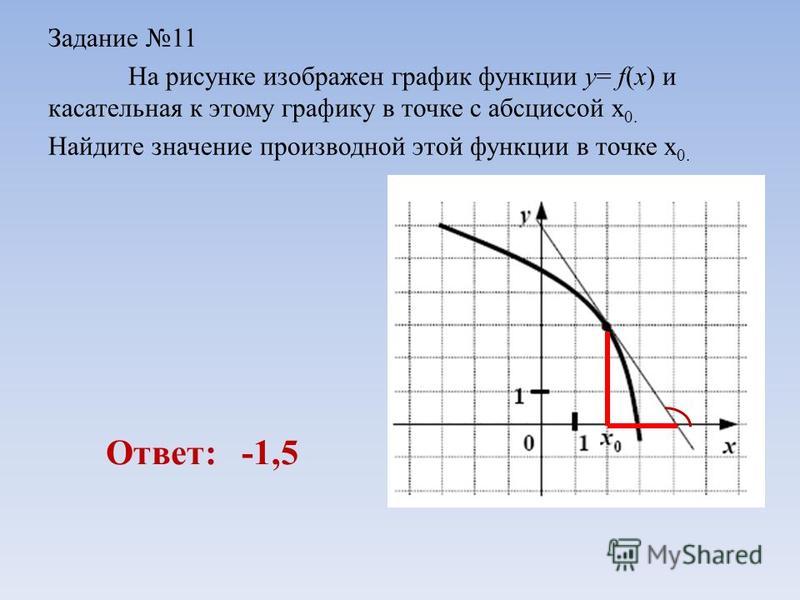
б) Найдите среднюю скорость от до .
в) Найдите мгновенную скорость при .
(а)
(б)
Что это значит? Обратите внимание на это и . Другими словами, объект перемещался из в в , но возвращался туда, где находился. начал. Поскольку чистое изменение позиции на равно 0, среднее скорость была 0.
(с) я вошел
я получил
Люди, которые видели исчисление раньше, знают, что это обычно называется . производная от а. Он обозначается
То есть производная от at определяется выражением
дает мгновенную скорость изменения f при a, или наклон касательной к графику при .
Производная является функцией сама по себе. Поскольку х обычно используется для обозначения входной переменной для функции, это обычно для запишите определение производной в таком виде:
f дифференцируемая в точке x, если существует — то есть, если указанный выше предел определен.
Пример. Вычислить для .
Пример. Предположим
Является ли f дифференцируемым в ?
Однако определение зависит от того, является ли h положительное или отрицательное. Мне нужно взять левый и правый пределы в 1.
Правый предел равен
Левый предел равен
Поскольку левый и правый пределы совпадают, двусторонний предел существует. Таким образом,
Это показывает, что f дифференцируема при .
В этом примере функция была построена путем «склейки» две части и вместе в . Тот факт, что был определен, означает что кусочки были «гладко склеены». По аналогии, если две части функции подобны двум кускам дерева, склеены, можно было провести рукой по стыку и не почувствовать «угол» или «конек».
Геометрически дифференцируемая функция имеет касательную в каждой
точка его графика.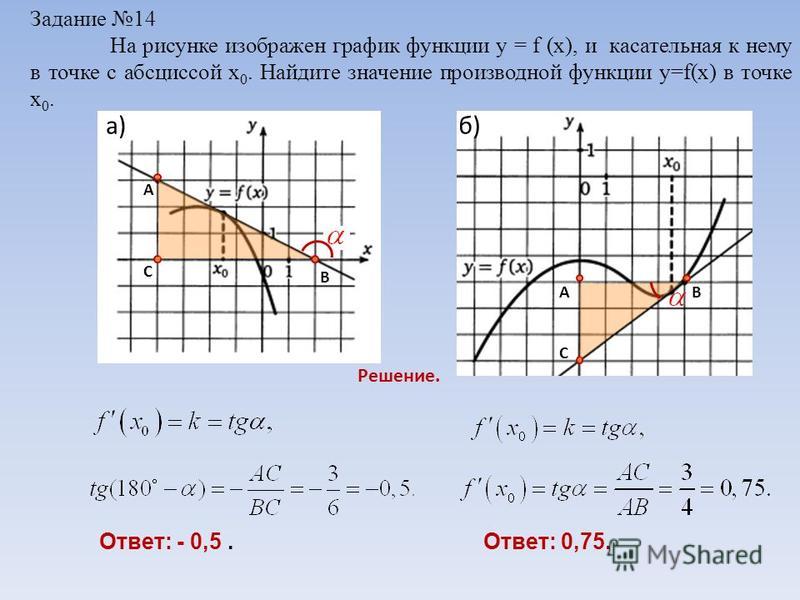 Вы подозреваете, что это исключит пробелы,
скачки, или вертикальные асимптоты — типичные разрывы. Фактически,
требование, чтобы дифференцируемая функция имела касательную в точке
каждая точка означает, что ее график не имеет «углов» — все
кривые и повороты «гладкие».
Вы подозреваете, что это исключит пробелы,
скачки, или вертикальные асимптоты — типичные разрывы. Фактически,
требование, чтобы дифференцируемая функция имела касательную в точке
каждая точка означает, что ее график не имеет «углов» — все
кривые и повороты «гладкие».
Теорема. Дифференцируемая функция непрерывный.
Доказательство. Предположим, дифференцируем в точка в. По определению,
Затем
С одной стороны, так левая сторона равна 0. С другой стороны, произведение пределов равно предел произведения, поэтому
Я могу переписать это как
Это говорит о том, что f непрерывна в точке c.
Пример. На рисунке ниже показан график функция . Нарисуйте график.
Я буду делать каждую часть отдельно слева направо. Часть левой руки
начинается с небольшого положительного наклона.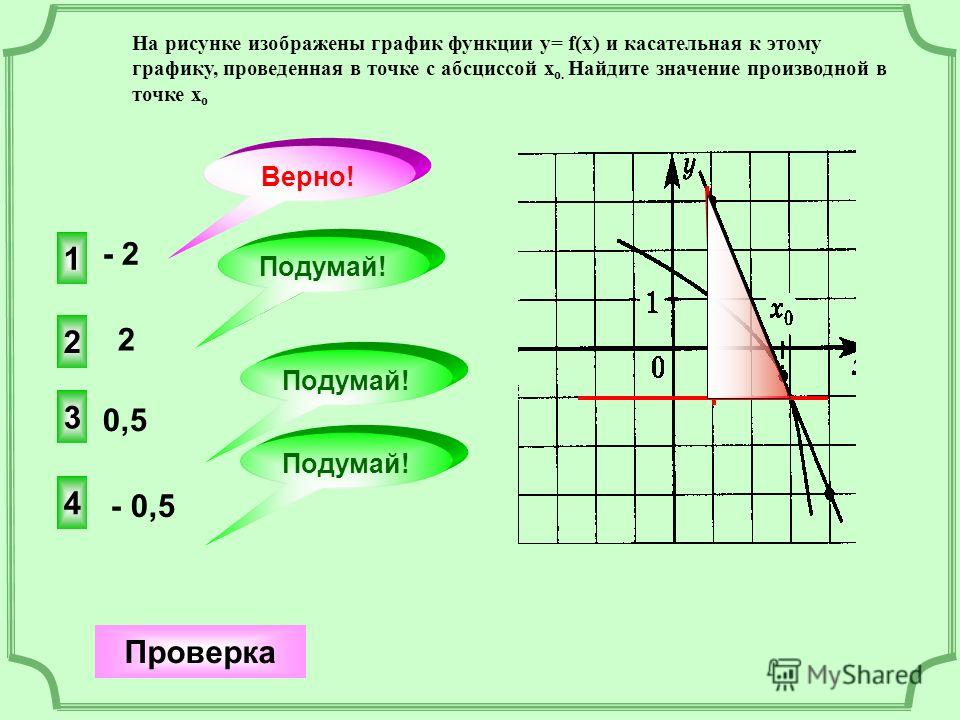 Наклон увеличивается до тех пор, пока
велика и положительна на асимптоте.
Наклон увеличивается до тех пор, пока
велика и положительна на асимптоте.
Кусок в середине начинается с большого положительного наклона в конце. левая асимптота. Уменьшается до 0 — есть горизонталь касательная в верхней части «выпуклости». Продолжает снижаться, становится большим и отрицательным в правой асимптоте.
Наконец, правая часть начинается с большого отрицательного наклона. вблизи асимптоты. По мере того, как вы уходите вправо, наклон продолжается быть отрицательным, но кривая выравнивается — то есть наклон приближается к 0.
Если сложить эти наблюдения вместе, получится такая картина:
Предшествующее обсуждение предлагает следующее эмпирическое правило: если граф непрерывен в точке, но имеет там «угол», производная в углу не определена.
Это не единственный случай, когда производная может быть неопределенной:
Например, производная не определена в точке, где график имеет вертикальная касательная .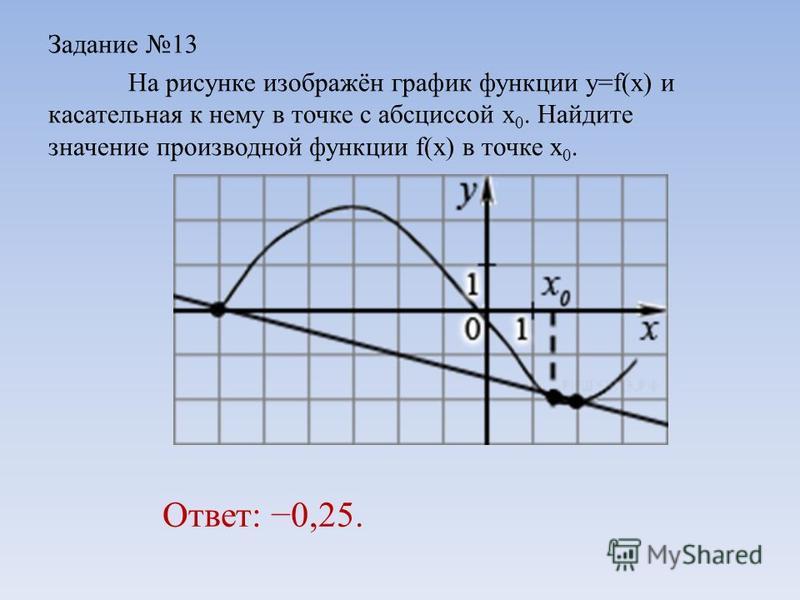

Leave A Comment