Равномерное прямолинейное движение.
Двигаясь прямолинейно, одно тело за каждую секунду проходит путь 5 м. Другое тело, двигаясь по прямой в одном направлении, за каждую секунду проходит путь 10 м. Движения этих тел
1) равномерные
2) неравномерные
3) первого — неравномерное, второго — равномерное
4) нельзя сказать о характере движения тел
П о графику зависимости пройденного пути от времени определите скорость велосипедиста в момент времени t = 2 с.
1) 2 м/с 2) 3 м/с 3) 6 м/с 4) 18 м/с
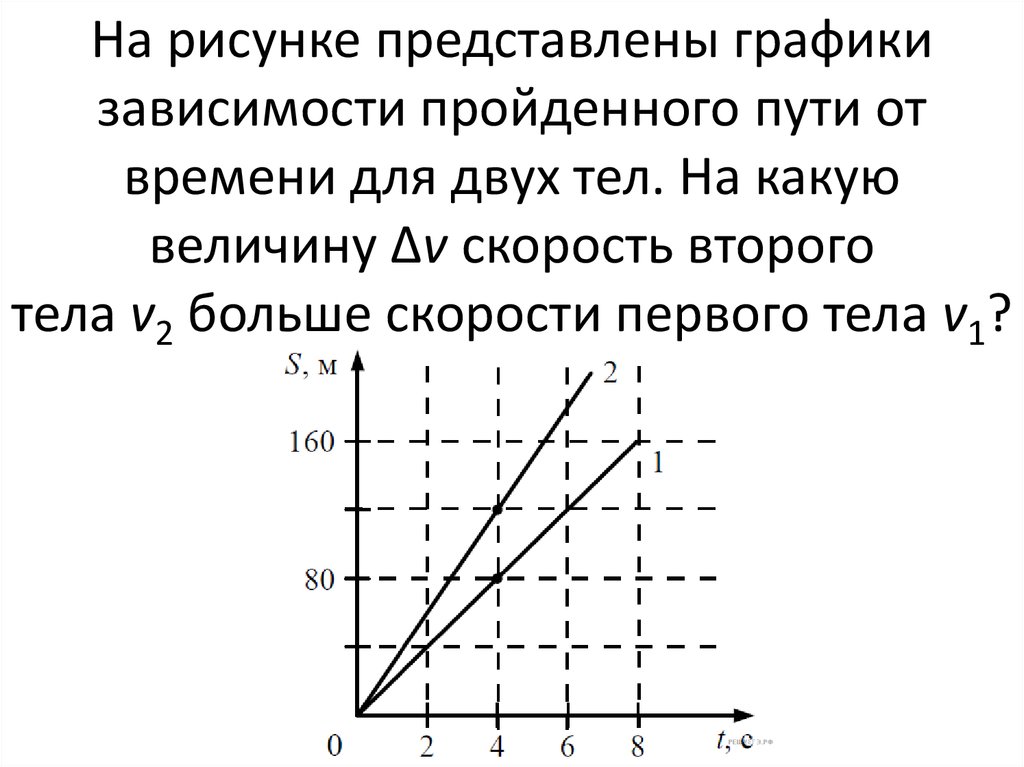
Н а рисунке представлены графики зависимости пройденного в одном направлении пути от времени для трех тел. Какое из тел двигалось с большей скоростью?
1) 1 2) 2 3) 3 4) скорости всех тел одинаковы
Н а рисунке представлены графики зависимости координаты х от времени для трех тел.
 Какое из тел
двигалось с большей скоростью?
Какое из тел
двигалось с большей скоростью?
На рисунке представлен график зависимости координаты х от времени для трех тел. В каком из нижеприведенных соотношений между собой находятся скорости этих тел?
1) 2) 3) 4)
Координата тела меняется с течением времени согласно формуле в единицах СИ. Чему равна координата тела через 5 с после начала движения?
1) -20 м 2) -10 м 3) 10 м 4) 30 м
Тело движется равномерно в сторону, противоположную оси ОX, величина скорости тела равна 28,8 км/ч, начальная координата 40 м. Координата тела и пройденный им путь через 5 с после начала движения равны
1)184 м, 144 м 2) -104 м, 144 м 3) 80 м, 40 м 4) 0 м, 40 м
Т ело движется в соответствии с уравнением .
 Определите скорость этого тела через
3 с.
Определите скорость этого тела через
3 с.
1) 5 м/с 2) 29 м/с 3) 8 м/с 4) 19 м/с
На графике изображена зависимость координаты х тела, движущегося вдоль оси ОХ, от времени. Каковы начальная координата и скорость тела?
1) 1 м, 2 м/с 2) 0 м, 1 м/с
3) -1 м, 1 м/с 4) — 2 м, 3/4 м/с
Н а рисунке показан график зависимости координаты х тела, движущегося прямолинейно, от времени. Определите координату и скорость тела в момент времени 5 с.
1) 4 м, 2,4 м/с 2) 12 м, 2,4 м/с
3) 12 м, 1,6 м/с 4) 4 м, 1,6 м/с
Н а графике изображена зависимость координаты х тела, движущегося вдоль оси ОХ, от времени. Каковы скорость тела и уравнение движения?
1) 0,1 м/с, х = 30 + 0,1 t
2) 0,1 м/с, х = 30 — 0,1 t
3) 10 м/c, х = 30 + 10 t
4) 10 м/c, х = 30 — 10 t
Н а рисунке приведен график зависимости проекции скорости некоторого тела от времени.

1) 5 м 2) 13 м 3) -1 м 4) 9 м
а) Тело, двигаясь прямолинейно и равномерно в плоскости, перемещается из точки А с координатами (1; 2) в точку В с координатами (4; -2) за время 10 с. Модуль скорости тела равен
1) 0,3 м/с 2) 0,5 м/с 3) 0,7 м/с 4) 2,5 м/с
б) Тело, двигаясь прямолинейно и равномерно в плоскости, перемещается из точки А с координатами (1; 2) в точку В с координатами (4; -1) за время 10 с. Скорость тела направлена к оси ОХ под углом
1) 30º 2) 45º 3) 60º 4) 135º
Поезд длиной 200 м въезжает в тоннель длиной 300 м, двигаясь равномерно со скоростью 10 м/с. Через какое время поезд выйдет полностью из тоннеля?
1) 10 с 2) 20 с 3) 30 с 4) 50 с
а) Материальная точка движется в плоскости равномерно прямолинейно по закону: , где х, y—координаты тела, в м, t — время, в с.
 Каково значение скорости тела?
Каково значение скорости тела?
б) Материальная точка движется в плоскости ОХY так, что ее координаты х и y меняются по закону (м), время t выражено в секундах. Чему равна скорость тела?
1) 10 м/с 2) 6 м/с 3) 8 м/с 4) 14 м/с
а) Координаты материальной точки, движущейся в плоскости, изменяются в зависимости от времени по закону , где a, b, c – числа, не равные нулю. Траектория точки выражается уравнением
1) 2) 3) 4)
б) Тело движется в плоскости так, что все время находится на прямой, идущей через начало системы координат. Какое из уравнений правильно описывает его траекторию (
1) 2) 3) 4)
Какая функция υ(t) описывает зависимость скорости от времени t при равномерном прямолинейном движении?
1) υ = 5t 2) υ = 5/t 3) υ = 5 4) υ = -5
Две материальные точки движутся по оси ОХ по законам: х1= 5 + 5t, х2
 Чему равно расстояние
между ними через 2 с?
Чему равно расстояние
между ними через 2 с?
1) 5 м 2) 10 м 3) 15 м 4) 20 м
а) По оси ОХ движутся две точки: первая по закону х1(t) = 5+2t, вторая – по закону х2(t) = 2 — t. В какой момент времени они встретятся?
1) 1 с 2) 2 с 3) 3 с 4) точки не встретятся
б) По оси ОХ движутся
две точки: первая по закону х1(t) = 10+2t,
вторая – по закону х
1) 2 с 2) 4 с 3) 6 с 4) точки не встретятся
Н а рисунке изображен график зависимости координаты тела, движущегося по прямой, от времени. На основании графика можно утверждать, что
на участке 1 тело покоится, на участке 2 – движется равномерно
на участке 1 движение является равномерным, на участке 2 – скорость тела меняется
на участке 1 тело движется равномерно, на участке 2 – покоится
на участке 1 тело движется равномерно, на участке 2 – также равномерно
Из двух пунктов, расстояние между которыми 100 м одновременно навстречу друг другу начали двигаться два тела.
 Скорость
одного из них 20 м/с. Какова скорость второго тела, если тела
встретились через 4 с?
Скорость
одного из них 20 м/с. Какова скорость второго тела, если тела
встретились через 4 с?
1) 5 м/с 2) 10 м/с 3) 15 м/с 4) 20 м/с
Товарный поезд, двигаясь со скоростью 36 км/ч, проехал станцию. Через 0,5 ч в том же направлении начал движение скорый поезд со скоростью 72 км/ч. Через какое время после выхода товарного поезда его нагонит скорый?
1) 1,33 ч 2) 0,5 ч 3) 1,17 ч 4) 1 ч
Цель летит горизонтально на высоте 10 км с постоянной скоростью 600 м/с. Ее засекли, когда она была в зените и пустили ракету в упреждающую точку. Через какое время цель будет сбита, если скорость ракеты постоянна и равна 1 км/с?
1) 11,5 с 2) 12,5 с 3) 13,5 с 4) 14,5 с
Вражеский корабль движется по прямому курсу со скоростью 5 м/с.
 Кратчайшее расстояние между
торпедным катером и курсом корабля
6000 м. Какое расстояние должно быть
между кораблем и катером при выстреле,
чтобы поразить корабль торпедой,
движущейся со скоростью 12 м/с по
кратчайшему расстоянию?
Кратчайшее расстояние между
торпедным катером и курсом корабля
6000 м. Какое расстояние должно быть
между кораблем и катером при выстреле,
чтобы поразить корабль торпедой,
движущейся со скоростью 12 м/с по
кратчайшему расстоянию?
1) 8000 м 2) 7500 м 3) 7000 м 4) 6500 м
Прямолинейное равноускоренное движение — презентация онлайн
Похожие презентации:
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Газовая хроматография
Геофизические исследования скважин
Искусственные алмазы
Трансформаторы тока и напряжения
Транзисторы
Воздушные и кабельные линии электропередач
Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса
Магнитные аномалии
Нанотехнологии
1. Равноускоренное прямолинейное движение
• При неравномерном• Примеры:
движении скорость тела с
Торможение
или
течением времени
разгон автомобиля
изменяется.
• Такое прямолинейное
движение, при котором
• Движение по наклонной
скорость тела за любые
плоскости
равные промежутки
времени изменяется
одинаково, называют
равноускоренным
• Свободное падение
прямолинейным
движением.
3. Ускорение
• Быстроту изменения скорости характеризуютвеличиной, обозначаемой а и называемой ускорением.
• Ускорением называют векторную величину, равную
отношению изменения скорости тела v-v0 к
промежутку времени t, в течение которого это
изменение произошло:
4. Скорость
• При равноускоренном движении с начальнойскоростью v0 мгновенная скорость равна
• Если начальная скорость тела равна нулю, т. е. в
начальный момент времени оно покоилось, то эта
формула приобретает вид:
5. Закон движения
• Кинематический законпрямолинейного
равноускоренного движения x
• Следует помнить, что в
формуле v0x и аx могут быть
как положительными, так и
отрицательными, так как это
проекции векторов v0 и а на ось
Ох
• Обратите внимание:
зависимость координаты от
времени квадратичная,
значит, графиком является парабола
2
x0 v0 t
at
2
6.
 Перемещение• Формула перемещения
Перемещение• Формула перемещенияпри прямолинейном
равноускоренном
движении в векторном
виде:
• Формула для расчета
перемещения в
проекциях:
• Еще одна формула для
расчета перемещения при
равноускоренном
движении:
7. Частные случаи
• В случае равенствапроекции
начальной
скорости нулю (v0
= 0) получаем
выражение:
• Из этого выражения
можно найти
проекции скорости
• или ускорения :
8. Определение перемещения по графику скорости
vv2
v
v2
Δv
v1
v1
t1
Δt
t2
t
Δt
Площадь фигуры под графиком
скорости равна пройденному пути
t`
t
9. Сравнение графиков движения
Прямолинейноеравномерное движение
x
x0 vx t
Закон прямолинейного равномерного
движения
Прямолинейное
равнопеременное движение
2
x x0 v0 t
at
2
Закон прямолинейного
равноускоренного движения
10. Итоги:
11.
 Рассмотрим задачи:
Рассмотрим задачи:12. 1. На рисунках представлены графики зависимости координаты от времени для четырех прямолинейно движущихся тел. Какое из тел
движется с наибольшей скоростью?13. 2. Используя график зависимости скорости движения тела от времени, определите скорость тела в конце 5-ой секунды, считая, что
характер движения тела неизменяется.
1.
2.
3.
4.
9 м/с
10 м/с
12 м/с
14 м/с
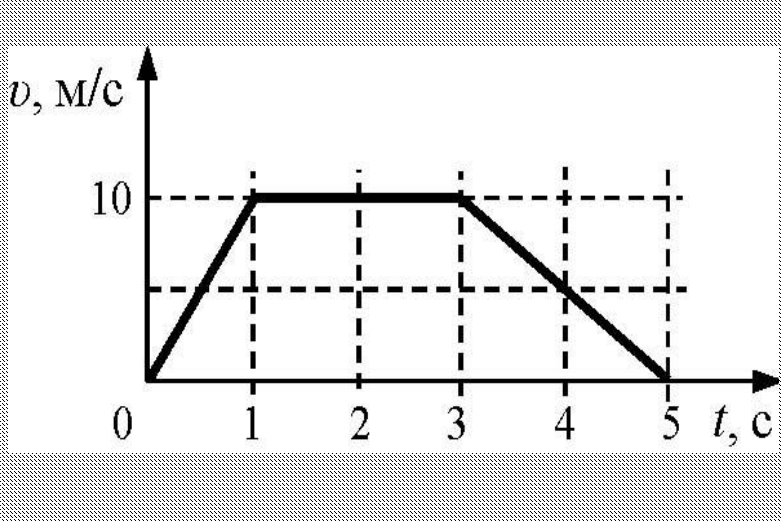
14. 3. По графику скорости, изображенному на рисунке, определите путь, пройденный телом за 5 с.
•1) 25м•2) 5 м
•3)7,5 м
•4) 12,5 м
15. 4. По графику зависимости скорости движения тела от времени. Найдите скорость тела в момент времени t = 4 с.
1) 0 м/с2) 2 м/с
3) — 4м/с
4) 16 м/с
16. 5. На рисунке изображен график зависимости скорости движения материальной точки от времени. Определите скорость тела в момент
времени t = 12 с, считая, что характердвижения тела не изменяется.
1) 30 м/с
2) 40 м/с
3) 50 м/с
4) 36 м/с
17.
 6. На рисунке приведен график скорости некоторого тела. Определите скорость тела в момент времени t = 2 с.1) 5 м/с
6. На рисунке приведен график скорости некоторого тела. Определите скорость тела в момент времени t = 2 с.1) 5 м/с2) 0 м/с
3) 7,5 м/с
4) 4 м/с
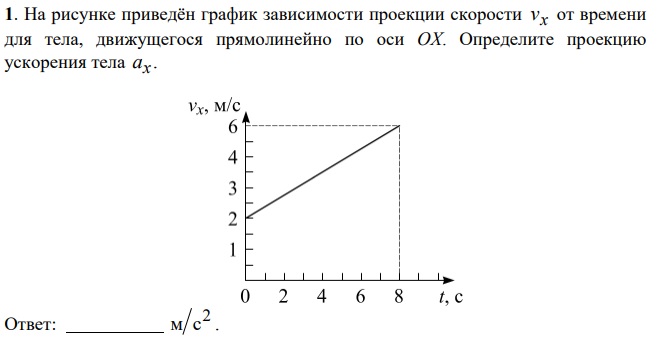
18. 7. На рисунке представлен график зависимости проекции скорости грузовика на ось х от времени. Проекция ускорения грузовика на
эту ось в момент t=3 с равна1) 5 м/с2
2) 10 м/с2
3) 15 м/с2
4) 20 м/с2
Движение равноускоренное,
ускорение постоянно
19. 8. Сани начинают прямолинейное равноускоренное движение по склону горы из состояния покоя и за первую секунду движения проходят
расстояние 1 м. Какое расстояние притаком движении они пройдут за третью секунду
движения?
1. 1м.
2. 3 м.
3. 4 м.
4. 5 м.
5. 9 м.
—
20. 9. Брусок скользит по наклонной плоскости равноускоренно из состояния покоя. За вторую секунду движения он прошел путь 60 см.
Какой путь был пройденбруском за первую секунду движения?
1. 5 см.
2. 10 см.
3. 15 см.
4.
 20 см.
20 см.5. 30 см.
21. 10.Тело начинает прямолинейное движение из состояния покоя, и его ускорение меняется со временем так, как показано на графике.
Через 6 с после начала движениямодуль скорости тела будет равен
1.
2.
3.
4.
0 м/с
12 м/с
8 м/с
16 м/с
22. 11. Зависимость координаты материальной точки от времени задается уравнением x(t)=At2 + Bt + С, где А, В и С — числовые
коэффициенты. Скоростьи ускорение тела в момент времени t = 0 равны
соответственно
1) А и С
2) В и А
3) В и С
4) В и 2А
12. Одной из характеристик автомобиля является
время t его разгона с места до скорости 100 км/ч.
Сколько времени потребуется автомобилю, имеющему
время разгона t = 3 с, для разгона до скорости 50 км/ч
при равноускоренном движении?
2) 1,5 с
V=at
a = v/t = 1000 / (36 м/с ∙ 3 с) = 250/ 27м/с2
t1 = V1 / a = 500 / 36 м/с : ( 125 / 3 м/с2 )= 1.5 c
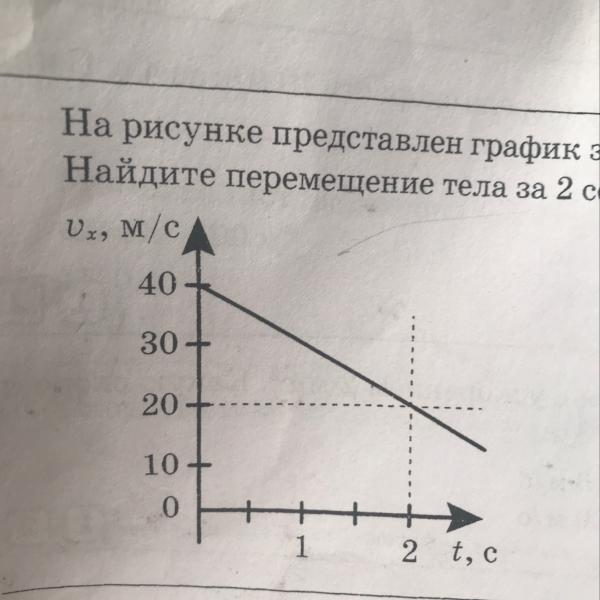
13. На рисунке представлен
график зависимости скорости
υ автомобиля от времени t.
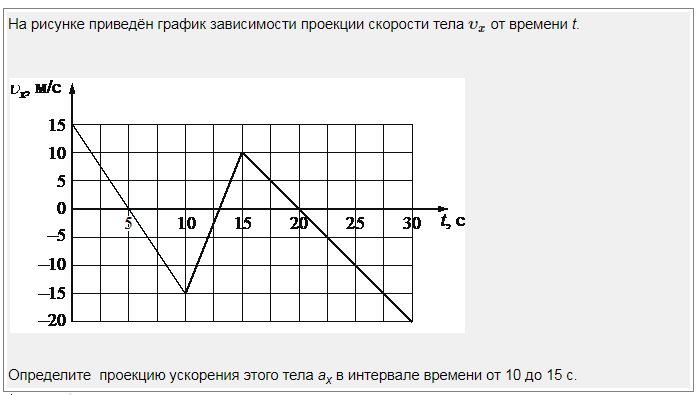
Найдите путь, пройденный
автомобилем за 5 с. На
рисунке представлен график
зависимости скорости υ
автомобиля от времени t.
Найдите путь, пройденный
автомобилем за 5 с.
Трапеция
1) 0 м; 2) 20 м; 3) 30 м; 4) 35 м
• Пройденный путь равен
площади фигуры под
графиком скорости
English Русский Правила
Точка движется вдоль оси x со скоростью, проекция которой vx представлена как функция времени графиком на рисунке. Принимая координату точки x=0 в момент t=0, начертите приближенные графики зависимости от времени ускорения wx, координаты x и пройденного пути s.
Вопрос
Обновлено: 27/05/2019
И.Е. ИРОДОВ, Л.А. СЕНА И С.С. КРОТОВ-ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ-Релятивистская механика
21 видеоРЕКЛАМА
Текст Решение
Ответ
Правильный ответ (##IRODV01C01E01018_S01##)
Решение
) на пять сегментов (для детального анализа), как показано на рисунке.
Для части oa:wx=1 и vx=t=v
Таким образом, Δx1(t)=∫vxdt−t∫0dt−t22−s1(t)
Полагая t=1, получаем, Δx1=s=12unit
Для части ab:
wx=O и νx=ν=constant=1
Таким образом, Δx2(t)=∫vxdt=t∫1dt=(t−1)=s2(t)
Полагая t=3, Δx2=s2=2единицы
Для части b4:wx=1 и vx=1−(t−3)=4−t)=v
Таким образом, Δx3(t)=t∫3(4−t )dt=4t−t22−152=s3(t)
Полагая t=4,Δx3=x3=12unit
Для части 4d:vx=−1 и vx=−(1−4)=4−1
Итак, v=|vx|=t−4 для t>4
Таким образом, ∆x4(t)=t∫4(1−t)dt=4t−t22−8
Полагая t=6,∆x4=−1
Аналогично s4(t )=∫|vx|dt=t∫4(t−4)dt=t22−4t+8
Положив t=6,s4=2unit
Для части d7:wx=2 и vx=−2+2(t −6)=2(t−7)
v=|vx|=2(7−t) для t ←7
Теперь Δx(t)=6∫t2(t−7)dt=t2−14t+48
Полагая t=4, Δx5=−1
Аналогично s5(t)=6∫t2(7−t)dt=14t−t2−48
Полагая t=7,s5=1
На основании этих полученных выражений wx Графики (t),x(t) и s(t) можно легко построить, как показано на рисунке листа ответов.
Ответить
Пошаговое решение от экспертов, которое поможет вам в разрешении сомнений и получении отличных оценок на экзаменах.
Ab Padhai каро бина объявления ке
Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!
92) В момент времени t=0, x=0. Найти (a) ускорение частицы при t = 2 с и (b) координату x частицы при t = 3 с10955413
График ускорения модели железнодорожного локомотива, движущегося по оси x. Постройте график его скорости и координаты как функции времени, если x=0 и v_(x)=0 при t=0 . .
11296251
Точка колеблется вдоль оси x по закону x=a cos (омегат-пи//4) . Нарисуйте приблизительные графики (а) смещения x , проекции скорости upsilon_(x) и проекции ускорения w_(x) как функции времени t , (b) проекции скорости upsilon_(x) и проекции ускорения w_(x) как функции координата х.
12307033
Точка движется вдоль оси ex по закону x=asin2(ωt−π/4) Найти.
(а) амплитуда и период колебаний, изобразите график x(t),
(б) проекцию скорости υx как функцию координации x, изобразите график υx(x).
12307034
Зависимость ускорения тела от времени представлена на рис. При t=0 скорость тела равна -3 м/с, а положение x=0 м.
При t=0 скорость тела равна -3 м/с, а положение x=0 м.
15219524
На рисунке показан график зависимости координаты x частицы, движущейся вдоль оси x, от времени. Средняя скорость в период от 0 до 4 с и мгновенная скорость при t = 4,113 с соответственно будут равны
69127457
На данном рисунке показан график зависящей от времени силы F_(x), действующей на частицу, движущуюся вдоль оси x. Каков полный импульс, сообщаемый этой силой частице с момента времени t = 0 до t = 2 секунды?
209197006
Начертите координатную плоскость и нанесите следующие точки:
x=6
243136681
Начертите координатную плоскость и нанесите следующие точки:
x=0
2 43136684
Текстовое решение
На рисунке показан график зависимости х — координаты частицы, движущейся по оси х, от времени. Средняя скорость в период от 0 до 6 с и мгновенная скорость при t = 3 с соответственно будут равны
304589275
Скорость частицы, движущейся вдоль положительного направления оси x, равна v= Asqrt(x) , где А — положительная константа. В момент времени t = 0 смещение частицы принимается равным x = 0 . (i) Выразите скорость и ускорение как функции времени и (ii) найдите среднюю скорость частицы за период, когда она проходит расстояние s ? 92) В момент времени t=0, x=0. Найти (а) ускорение частицы при t = 2 с и (б) координату x частицы при t = 3 с
В момент времени t = 0 смещение частицы принимается равным x = 0 . (i) Выразите скорость и ускорение как функции времени и (ii) найдите среднюю скорость частицы за период, когда она проходит расстояние s ? 92) В момент времени t=0, x=0. Найти (а) ускорение частицы при t = 2 с и (б) координату x частицы при t = 3 с
643180916
время. Средняя скорость в период от 0 до 4 с и мгновенная скорость при t = 4,113 с соответственно будут
644356022
13.5 к:
- Описать конические сечения и их связь с орбитальным движением
- Опишите, как орбитальная скорость связана с сохранением углового момента
- Определить период эллиптической орбиты от ее большой оси
Используя точные данные, собранные Тихо Браге, Иоганн Кеплер тщательно проанализировал положение на небе всех известных планет и Луны, нанеся их положение через равные промежутки времени. На основе этого анализа он сформулировал три закона, которые мы рассмотрим в этом разделе.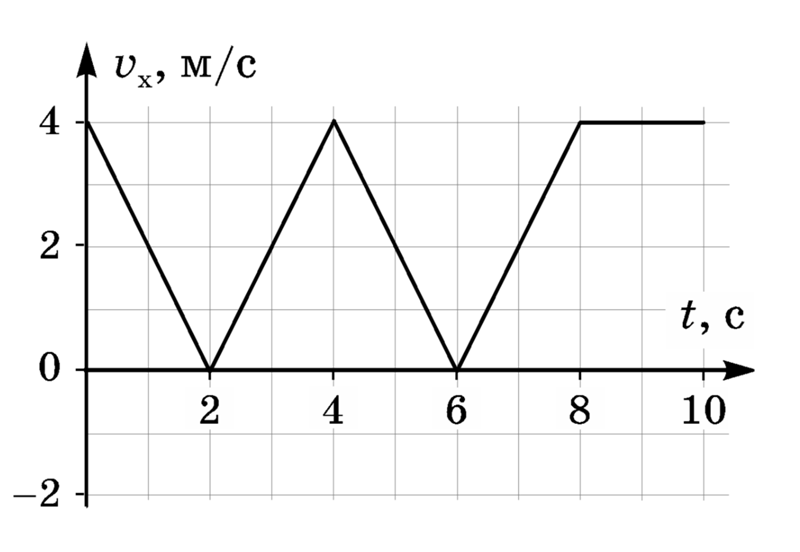
Первый закон Кеплера
Во времена Кеплера преобладало мнение, что орбиты всех планет были круговыми. Данные для Марса представляли наибольший вызов этой точке зрения, и это в конечном итоге побудило Кеплера отказаться от популярной идеи. Первый закон Кеплера гласит, что каждая планета движется по эллипсу, а Солнце находится в фокусе эллипса. Эллипс определяется как множество всех точек, для которых сумма расстояний от каждой точки до двух фокусов является постоянной величиной. (Рисунок) показывает эллипс и описывает простой способ его создания.
. Рис. 13.16. {f}_{2}) [/latex] — константа. Из этого определения видно, что эллипс можно создать следующим образом. Поместите булавку в каждый фокус, затем наденьте петлю из нити на карандаш и булавки. Удерживая нить, двигайте карандаш по кругу. Если два фокуса занимают одно и то же место, получается круг — частный случай эллипса. (b) Для эллиптической орбиты, если [латекс] m\ll M [/латекс], то m движется по эллиптической траектории с М в одном фокусе. Точнее, оба m и M движутся по собственному эллипсу вокруг общего центра масс.
Точнее, оба m и M движутся по собственному эллипсу вокруг общего центра масс.
Для эллиптических орбит точка наибольшего сближения планеты с Солнцем называется перигелием . Он обозначен точкой A на (рис.). Самая дальняя точка — это афелий , она обозначена на рисунке точкой B . Для орбиты Луны вокруг Земли эти точки называются соответственно перигеем и апогеем.
Эллипс имеет несколько математических форм, но все они являются частным случаем более общего уравнения для конических сечений. Есть четыре различных конических сечения, все они задаются уравнением
[латекс] \frac{\alpha }{r}=1+e\text{cos}\theta . [/latex]
Переменные r и [latex] \theta [/latex] показаны на (Рисунок) в случае эллипса. Константы [латекс]\альфа[/латекс] и и определяются полной энергией и угловым моментом спутника в данной точке. Константа e называется эксцентриситетом. Значения [латекс] \альфа [/латекс] и и определяют, какая из четырех конических секций представляет путь спутника. 9Рис. 13.17 .
9Рис. 13.17 .
Одним из настоящих триумфов закона всемирного тяготения Ньютона с силой, пропорциональной обратной величине квадрата расстояния, является то, что в сочетании с его вторым законом решение для траектории любого спутника представляет собой коническое сечение. Каждый путь, пройденный м — одно из четырех конических сечений: круг или эллипс для ограниченных или замкнутых орбит или парабола или гипербола для неограниченных или открытых орбит. Эти конические сечения показаны на (рис.).
Рисунок 13.18 Все движения, вызванные силой обратного квадрата, являются одним из четырех конических сечений и определяются энергией и направлением движущегося тела.
Если полная энергия отрицательна, то [латекс] 0\le e<1 [/латекс], а (Рисунок) представляет собой связанную или замкнутую орбиту эллипса или окружности, где [латекс] е=0 [ /латекс]. [Из (рис.) видно, что для [латекса] e=0 [/латекс], [латекс] r=\альфа [/латекс], и, следовательно, радиус постоянен. ] Для эллипсов эксцентриситет связан с тем, как появляется продолговатый эллипс. У круга эксцентриситет равен нулю, тогда как у очень длинного вытянутого эллипса эксцентриситет близок к единице.
] Для эллипсов эксцентриситет связан с тем, как появляется продолговатый эллипс. У круга эксцентриситет равен нулю, тогда как у очень длинного вытянутого эллипса эксцентриситет близок к единице.
Если полная энергия точно равна нулю, то [латекс] e=1 [/латекс] и путь является параболой. Напомним, что спутник с нулевой полной энергией имеет в точности космическую скорость. (Парабола образуется только путем разрезания конуса параллельно касательной вдоль поверхности.) Наконец, если полная энергия положительна, то [латекс] e>1 [/латекс] и путь является гиперболой. Эти два последних пути представляют собой неограниченные орбиты, где м проходят через м один и только один раз. Эта ситуация наблюдалась для нескольких комет, которые приближаются к Солнцу, а затем удаляются, чтобы никогда не вернуться.
Мы ограничились случаем, когда меньшая масса (планета) вращается вокруг гораздо большей и, следовательно, стационарной массы (Солнца), но (рисунок) также применим к любым двум гравитационно взаимодействующим массам. Каждая масса очерчивает точно такое же коническое сечение, как и другая. Эта форма определяется полной энергией и угловым моментом системы, при этом центр масс системы находится в фокусе. Отношение размеров двух путей обратно пропорционально отношению их масс.
Каждая масса очерчивает точно такое же коническое сечение, как и другая. Эта форма определяется полной энергией и угловым моментом системы, при этом центр масс системы находится в фокусе. Отношение размеров двух путей обратно пропорционально отношению их масс.
Вы можете увидеть анимацию двух взаимодействующих объектов на странице My Solar System в Phet. Выберите предустановленный вариант «Солнце и планета». Вы также можете просмотреть более сложные проблемы с несколькими телами. Вы можете найти реальный путь Луны довольно удивительным, но он подчиняется простым законам движения Ньютона.
Орбитальные перелеты
Люди мечтали о путешествиях на другие планеты нашей Солнечной системы с момента их открытия. Но как нам лучше всего это сделать? Самый эффективный метод был открыт в 1925 Вальтера Хоманна, вдохновленного популярным научно-фантастическим романом того времени. Этот метод теперь называется переносом Хохмана . В случае путешествия между двумя круговыми орбитами переход осуществляется по эллипсу «перехода», который идеально пересекает эти орбиты в афелии и перигелии эллипса. (Рисунок) показывает случай путешествия с орбиты Земли на орбиту Марса. Как и прежде, Солнце находится в фокусе эллипса.
(Рисунок) показывает случай путешествия с орбиты Земли на орбиту Марса. Как и прежде, Солнце находится в фокусе эллипса.
Для любого эллипса большая полуось определяется как половина суммы перигелия и афелия. На (рисунке) большая полуось — это расстояние от начала координат до любой стороны эллипса вдоль x -ось, или только половина самой длинной оси (называемой главной осью). Следовательно, для перехода с одной круговой орбиты радиуса [латекс] {r}_{1} [/латекс] на другую круговую орбиту радиусом [латекс] {r}_{2} [/латекс] афелий перехода эллипс будет равен значению большей орбиты, а перигелий будет меньшей орбитой. Большая полуось, обозначенная a , поэтому задается как [latex] a=\frac{1}{2}({r}_{1}+{r}_{2}) [/latex].
Рисунок 13.19 Эллипс перехода имеет перигелий на орбите Земли и афелий на орбите Марса.
Возьмем случай путешествия с Земли на Марс. На данный момент мы игнорируем планеты и предполагаем, что мы одни на орбите Земли и хотим переместиться на орбиту Марса. Из (Рисунок) выражения для полной энергии видно, что полная энергия космического корабля на большей орбите (Марс) больше (менее отрицательна), чем на меньшей орбите (Земля). Для перехода на переходный эллипс с земной орбиты нам потребуется увеличить нашу кинетическую энергию, то есть нужен прирост скорости. Наиболее эффективным методом является очень быстрое ускорение по круговой орбитальной траектории, которая также проходит по траектории эллипса в этой точке. (На самом деле ускорение должно быть мгновенным, чтобы круговая и эллиптическая орбиты во время ускорения совпадали. На практике конечное ускорение достаточно короткое, чтобы разница не имела существенного значения.) Как только вы достигнете орбиты Марса, вам понадобится еще одно ускорение, чтобы выйти на эту орбиту, или вы останетесь на эллиптической орбите и просто вернетесь к перигелию, с которого начали. Для обратной поездки вы просто обращаете процесс вспять с помощью ретро-ускорения в каждой точке пересадки.
Из (Рисунок) выражения для полной энергии видно, что полная энергия космического корабля на большей орбите (Марс) больше (менее отрицательна), чем на меньшей орбите (Земля). Для перехода на переходный эллипс с земной орбиты нам потребуется увеличить нашу кинетическую энергию, то есть нужен прирост скорости. Наиболее эффективным методом является очень быстрое ускорение по круговой орбитальной траектории, которая также проходит по траектории эллипса в этой точке. (На самом деле ускорение должно быть мгновенным, чтобы круговая и эллиптическая орбиты во время ускорения совпадали. На практике конечное ускорение достаточно короткое, чтобы разница не имела существенного значения.) Как только вы достигнете орбиты Марса, вам понадобится еще одно ускорение, чтобы выйти на эту орбиту, или вы останетесь на эллиптической орбите и просто вернетесь к перигелию, с которого начали. Для обратной поездки вы просто обращаете процесс вспять с помощью ретро-ускорения в каждой точке пересадки.
Чтобы совершить переход на переходный эллипс, а затем обратно, нам необходимо знать скорость каждой круговой орбиты и скорости переходных орбит в перигелии и афелии. Требуемый прирост скорости — это просто разница между скоростью круговой орбиты и скоростью эллиптической орбиты в каждой точке. Мы можем найти круговые орбитальные скорости из (Рисунок). Чтобы определить скорости для эллипса, мы утверждаем без доказательства (поскольку это выходит за рамки этого курса), что полная энергия для эллиптической орбиты равна
Требуемый прирост скорости — это просто разница между скоростью круговой орбиты и скоростью эллиптической орбиты в каждой точке. Мы можем найти круговые орбитальные скорости из (Рисунок). Чтобы определить скорости для эллипса, мы утверждаем без доказательства (поскольку это выходит за рамки этого курса), что полная энергия для эллиптической орбиты равна
[латекс] E=-\frac{Gm{M}_{\text{S}}}{2a} [/latex]
, где [латекс] {M}_{\text{S}} [/ латекс] — масса Солнца, а a — большая полуось. Примечательно, что это то же самое, что и (Рисунок) для круговых орбит, но со значением большой полуоси, заменяющим радиус орбиты. Поскольку мы знаем потенциальную энергию из (рис.), мы можем найти кинетическую энергию и, следовательно, скорость, необходимую для каждой точки эллипса. Мы оставляем в качестве сложной задачи поиск этих скоростей переноса для полета с Земли на Марс.
Мы закончим это обсуждение, указав на несколько важных деталей. Во-первых, мы не учли ни гравитационную потенциальную энергию Земли и Марса, ни механику приземления на Марс. На практике это должно быть частью расчетов. Во-вторых, время решает все. Вы же не хотите выйти на орбиту Марса, чтобы узнать, что его там нет. Мы должны покинуть Землю точно в нужное время, чтобы Марс находился в афелии нашего переходного эллипса, когда мы прибудем. Такая возможность появляется каждые 2 года. И возвращение также требует правильного выбора времени. Всего поездка займет чуть менее 3 лет! Есть и другие варианты, обеспечивающие более быстрый транзит, в том числе гравитационный облет Венеры. Но эти другие варианты требуют дополнительных затрат энергии и опасности для астронавтов.
На практике это должно быть частью расчетов. Во-вторых, время решает все. Вы же не хотите выйти на орбиту Марса, чтобы узнать, что его там нет. Мы должны покинуть Землю точно в нужное время, чтобы Марс находился в афелии нашего переходного эллипса, когда мы прибудем. Такая возможность появляется каждые 2 года. И возвращение также требует правильного выбора времени. Всего поездка займет чуть менее 3 лет! Есть и другие варианты, обеспечивающие более быстрый транзит, в том числе гравитационный облет Венеры. Но эти другие варианты требуют дополнительных затрат энергии и опасности для астронавтов.
Посетите этот сайт, чтобы узнать больше о планировании полета на Марс.
Второй закон Кеплера
Второй закон Кеплера утверждает, что планета за равное время заметает равные площади, то есть площадь, деленная на время, называемая площадной скоростью, постоянна. Рассмотрим (рисунок). Время, которое требуется планете, чтобы переместиться из положения A в положение B , заметая область [латекс] {A}_{1} [/latex], равно времени, которое требуется для перемещения из положения C в положение 9. 0153 D , подметание [латекс] {A}_{2} [/latex], и для перехода с E на F , подметание [латекс] {A}_{3} [/latex] . Эти области одинаковы: [латекс] {A}_{1}={A}_{2}={A}_{3} [/latex].
0153 D , подметание [латекс] {A}_{2} [/latex], и для перехода с E на F , подметание [латекс] {A}_{3} [/latex] . Эти области одинаковы: [латекс] {A}_{1}={A}_{2}={A}_{3} [/latex].
Рисунок 13.20 Показанные заштрихованные области имеют одинаковую площадь и представляют один и тот же временной интервал.
Сравнивая площади на рисунке и пройденное расстояние по эллипсу в каждом случае, мы видим, что для того, чтобы площади были равны, планета должна ускоряться по мере приближения к Солнцу и замедляться по мере своего движения прочь. Такое поведение полностью согласуется с нашим уравнением сохранения (рисунок). Но мы покажем, что второй закон Кеплера на самом деле является следствием сохранения углового момента, справедливого для любой системы только с радиальными силами.
Напомним определение углового момента из «Угловой момент», [латекс] \overset{\to }{L}=\overset{\to }{r}\,×\,\overset{\to }{p} [/ латекс]. Для случая орбитального движения [latex] \overset{\to }{L} [/latex] — это угловой момент планеты относительно Солнца, [latex] \overset{\to }{r} [/latex] — вектор положения планеты, отсчитываемый от Солнца, а [latex] \overset{\to }{p}=m\overset{\to }{v} [/latex] — мгновенный линейный импульс в любой точке орбита. Так как планета движется по эллипсу, [латекс] \overset{\to }{p} [/латекс] всегда касается эллипса.
Так как планета движется по эллипсу, [латекс] \overset{\to }{p} [/латекс] всегда касается эллипса.
Мы можем разложить линейный импульс на две составляющие: радиальную составляющую [латекс] {\overset{\to }{p}}_{\text{рад}} [/латекс] вдоль линии, ведущей к Солнцу, и компонент [латекс] {\overset{\to }{p}}_{\text{perp}} [/latex] перпендикулярно [латексу] \overset{\to }{r} [/latex]. Тогда перекрестное произведение для углового момента можно записать как
[латекс] \overset{\to }{L}=\overset{\to }{r}\,×\,\overset{\to }{p}= \ overset {\ to {r} \, × \, ({\ overset {\ to {p}} _ {\ text {rad}} + {\ overset {\ to {p}} _ {\ text {perp}}) = \ overset {\ to {r} \, × \, {\ overset {\ to {p}} _ {\ text {rad}} + \ overset {\ to {r} \ ,×\,{\overset{\to}}{p}}_{\text{perp}} [/latex].
Первый член справа равен нулю, потому что [латекс] \overset{\to }{r} [/latex] параллелен [латексу] {\overset{\to }{p}}_{\text{rad }} [/latex], а во втором слагаемом [латекс] \overset{\to }{r} [/latex] перпендикулярно [латексу] {\overset{\to }{p}}_{\text{ perp}} [/latex], поэтому величина векторного произведения сводится к [latex] L=r{p}_{\text{perp}}=rm{v}_{\text{perp}} [/latex ]. Обратите внимание, что угловой момент , а не зависит от [латекс] {р} _ {\ текст {рад}} [/латекс]. Поскольку гравитационная сила действует только в радиальном направлении, она может изменяться только [латекс] {р} _ {\ текст {рад}} [/латекс], но не [латекс] {р} _ {\ текст {перп}} [ /латекс]; следовательно, угловой момент должен оставаться постоянным.
Обратите внимание, что угловой момент , а не зависит от [латекс] {р} _ {\ текст {рад}} [/латекс]. Поскольку гравитационная сила действует только в радиальном направлении, она может изменяться только [латекс] {р} _ {\ текст {рад}} [/латекс], но не [латекс] {р} _ {\ текст {перп}} [ /латекс]; следовательно, угловой момент должен оставаться постоянным.
Теперь рассмотрим (Рисунок). Небольшая треугольная область [латекс] \text{Δ}A [/латекс] заметается во времени [латекс] \текст{Δ}t [/латекс]. Скорость движется вдоль пути и составляет угол [латекс] \тета [/латекс] с радиальным направлением. Следовательно, перпендикулярная скорость определяется как [латекс] {v}_{\text{perp}}=v\text{sin}\theta[/latex]. Планета перемещается на расстояние [латекс] \text{Δ}s=v\text{Δ}t\text{sin}\theta [/latex], спроецированное вдоль направления, перпендикулярного r . Так как площадь треугольника равна половине основания ( r ), умноженная на высоту [латекс] (\text{Δ}s) [/латекс], для небольшого смещения площадь определяется как [латекс] \text{Δ}A=\frac{1}{2 }r\text{Δ}s [/латекс]. Подставляя вместо [латекс] \text{Δ}s [/латекс], умножая на m в числителе и знаменателе и переставляя, получаем
Подставляя вместо [латекс] \text{Δ}s [/латекс], умножая на m в числителе и знаменателе и переставляя, получаем
[латекс] \text{Δ}A=\frac{1}{ 2}r\text{Δ}s=\frac{1}{2}r(v\text{Δ}t\text{sin}\theta)=\frac{1}{2m}r(mv\text{ sin} \ theta \ text {Δ} t) = \ frac {1} {2m} r (m {v} _ {\ text {perp}} \ text {Δ} t) = \ frac {L} {2m} \text{Δ}т. [/латекс]
. текст {Δ}\varphi [/латекс]. Угол между радиальным направлением и [латекс] \overset{\to }{v} [/латекс] равен [латекс] \тета [/латекс].
Поверхностная скорость — это просто скорость изменения площади со временем, поэтому мы имеем
[латекс] \text{поверхностная скорость}=\,\frac{\text{Δ}A}{\text{Δ}t }=\frac{L}{2м}. [/латекс]
Так как угловой момент постоянен, площадная скорость также должна быть постоянной. Это и есть второй закон Кеплера. Как и в случае с первым законом Кеплера, Ньютон показал, что это естественное следствие его закона всемирного тяготения.
Вы можете просмотреть анимированную версию (Рисунок) и множество других интересных анимаций на сайте Школы физики (Университет Нового Южного Уэльса).
Третий закон Кеплера
Третий закон Кеплера утверждает, что квадрат периода пропорционален кубу большой полуоси орбиты. В разделе «Спутниковые орбиты и энергия» мы вывели третий закон Кеплера для особого случая круговой орбиты. (Рисунок) дает нам период круговой орбиты радиуса 9{3} [/latex]
Мы изменили массу Земли на более общую M , поскольку это уравнение применимо к спутникам, вращающимся вокруг любой большой массы.
Пример
Орбита кометы Галлея
Определите большую полуось орбиты кометы Галлея, учитывая, что она достигает перигелия каждые 75,3 года. Если перигелий равен 0,586 а.е., что такое афелий?
Стратегия
Нам дан период, поэтому мы можем переставить (Рисунок), находя большую полуось. Поскольку мы знаем значение перигелия, мы можем использовать определение большой полуоси, данное ранее в этом разделе, чтобы найти афелий. Отметим, что 1 астрономическая единица (а.е.) является средним радиусом орбиты Земли и определяется как [латекс] 1\,\text{AU}=1,50\,×\,{10}^{11}\,\text {м} [/латекс]. 9{12}\,\text{m} [/latex] или 17,8 а.е. для большой полуоси.
9{12}\,\text{m} [/latex] или 17,8 а.е. для большой полуоси.
Большая полуось составляет половину суммы афелия и перигелия, поэтому мы имеем
[латекс] \begin{array}{}\\ \hfill a& =\hfill & \frac{1}{2 }(\text{афелий}+\text{перигелий})\hfill \\ \hfill \text{афелий}& =\hfill & 2a-\text{перигелий}.\hfill \end{массив} [/latex]
Подставляя значения, которые мы нашли для большой полуоси, и значение, данное для перигелия, мы находим значение афелия равным 35,0 а.е.
Значение
Эдмонд Галлей , современник Ньютона, первым заподозрил, что три кометы, о которых сообщалось в 1531, 1607 и 1682 годах, на самом деле были одной и той же кометой. До того, как Тихо Браге провел измерения комет, считалось, что это были разовые события, возможно, возмущения в атмосфере, и что на них не влияло Солнце. Галлей использовал новую механику Ньютона, чтобы предсказать возвращение своей одноименной кометы в 1758 году.
Проверьте свое понимание
Почти круговая орбита Сатурна имеет средний радиус около 9,5 а. е. и период 30 лет, тогда как средний радиус Урана составляет около 19 а.е. и период 84 года. Согласуется ли это с нашими результатами для кометы Галлея?
е. и период 30 лет, тогда как средний радиус Урана составляет около 19 а.е. и период 84 года. Согласуется ли это с нашими результатами для кометы Галлея?
Показать решение
Резюме
- Все орбитальное движение происходит по траектории конического сечения. Связанные или замкнутые орбиты представляют собой круг или эллипс; неограниченные или открытые орбиты являются либо параболой, либо гиперболой.
- Площадная скорость любой орбиты постоянна, что является отражением сохранения углового момента.
- Квадрат периода эллиптической орбиты пропорционален кубу большой полуоси этой орбиты.
Концептуальные вопросы
Являются ли законы Кеплера чисто описательными или они содержат информацию о причинно-следственных связях?
На приведенной ниже диаграмме для спутника на эллиптической орбите вокруг гораздо большей массы укажите, где его скорость наибольшая, а где наименьшая. Какой закон сохранения диктует такое поведение? Укажите направления силы, ускорения и скорости в этих точках. Нарисуйте векторы для этих же трех величин в двух точках, где 9{30}\,\text{кг} [/латекс].
Нарисуйте векторы для этих же трех величин в двух точках, где 9{30}\,\text{кг} [/латекс].
Показать решение
Ио вращается вокруг Юпитера со средним радиусом 421 700 км и периодом 1,769 дня. Основываясь на этих данных, какова масса Юпитера?
«Средний» радиус орбиты, указанный для астрономических объектов, вращающихся вокруг Солнца, как правило, не является интегрированным средним значением, а рассчитывается таким образом, чтобы он давал правильный период при применении к уравнению для круговых орбит. Учитывая это, каков средний радиус орбиты с точки зрения афелия и перигелия? 9{11}\,\text{m} [/latex])? ( Подсказка: Вы можете использовать либо закон сохранения энергии, либо угловой момент, но последнее гораздо проще.)
Перигелий кометы Лагерквиста равен 2,61 а.е., а период ее составляет 7,36 года. Покажите, что афелий этой кометы равен 4,95 а.е.
Показать решение
Каково отношение скорости в перигелии к скорости в афелии для кометы Лагерквиста в предыдущей задаче?
Эрос имеет эллиптическую орбиту вокруг Солнца с расстоянием в перигелии 1,13 а.

 Какое из тел
двигалось с большей скоростью?
Какое из тел
двигалось с большей скоростью?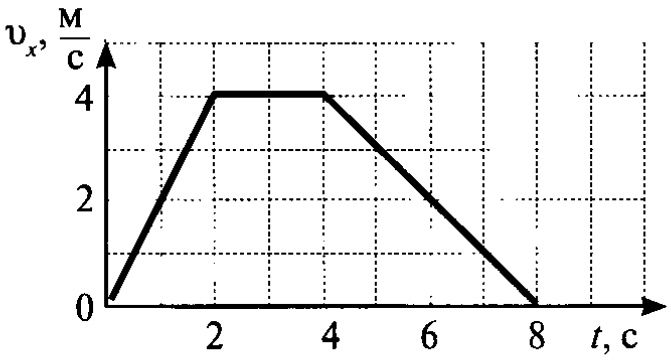 Определите скорость этого тела через
3 с.
Определите скорость этого тела через
3 с.
 Каково значение скорости тела?
Каково значение скорости тела? Чему равно расстояние
между ними через 2 с?
Чему равно расстояние
между ними через 2 с? Скорость
одного из них 20 м/с. Какова скорость второго тела, если тела
встретились через 4 с?
Скорость
одного из них 20 м/с. Какова скорость второго тела, если тела
встретились через 4 с? Кратчайшее расстояние между
торпедным катером и курсом корабля
6000 м. Какое расстояние должно быть
между кораблем и катером при выстреле,
чтобы поразить корабль торпедой,
движущейся со скоростью 12 м/с по
кратчайшему расстоянию?
Кратчайшее расстояние между
торпедным катером и курсом корабля
6000 м. Какое расстояние должно быть
между кораблем и катером при выстреле,
чтобы поразить корабль торпедой,
движущейся со скоростью 12 м/с по
кратчайшему расстоянию?
Leave A Comment