На продолжении стороны ad квадрата abcd за вершину a взята точка m: На продолжении стороны AD квадрата ABCD за вершину А взята точка М, МС=20 дм, угол…

Многоугольники и их свойства

1.В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину Вперпендикулярно АМ, пересекает сторону АС в точке N. АВ = 6; ВС = 5; АС = 9.

а) докажите, что биссектриса угла С делит отрезок МN пополам

б) пусть Р — точка пересечения биссектрис треугольника АВС. Найдите отношение АР : РN.

2.Диагональ AC прямоугольника ABCD с центром O образует со стороной AB угол 30°. Точка Eлежит вне прямоугольника, причём ∠BEC = 120°.

а) Докажите, что ∠CBE = ∠COE.

б) Прямая OE пересекает сторону AD прямоугольника в точке K. Найдите EK, если известно, что BE = 40 и CE = 24.

3.Медианы AA₁, BB₁ и CC₁ треугольника ABC пересекаются в точке M. Точки A₂, B₂ и C₂ — середины отрезков MA, MB и MC соответственно.

а) Докажите, что площадь шестиугольника A₁B₂C₁A₂B₁C₂ вдвое меньше площади треугольника ABC.

б) Найдите сумму квадратов всех сторон этого шестиугольника, если известно, что AB = 5, BC = 8 и AC = 10.

4.Медианы AA₁, BB₁ и CC₁ треугольника ABC пересекаются в точке M. Известно, что AC = 3MB.

а) Докажите, что треугольник ABC прямоугольный.

б) Найдите сумму квадратов медиан AA₁ и CC₁, если известно, что AC = 12.

5.На отрезке BD взята точка C. Биссектриса BL равнобедренного треугольника ABC с основанием BC является боковой стороной равнобедренного треугольника BLD с основанием BD.

а) Докажите, что треугольник DCL равнобедренный.

б) Известно, что В каком отношении прямая DL делит сторону AB?

6.На сторонах AC и BC треугольника ABC вне треугольника построены квадраты ACDE и BFKC. Точка M — середина стороны AB.

а) Докажите, что

б) Найдите расстояние от точки M до центров квадратов, если AC = 10, BC = 32 и ∠ACB = 30°.

7.На гипотенузу AB прямоугольного треугольника ABC опустили высоту CH. Из точки H на катеты опустили перпендикуляры HK и HE.

а) Докажите, что точки A, B, K и E лежат на одной окружности.

б) Найдите радиус этой окружности, если AB = 12, CH = 5.

8.На диагонали параллелограмма взяли точку, отличную от её середины. Из неё на все стороны параллелограмма (или их продолжения) опустили перпендикуляры.

а) Докажите, что четырёхугольник, образованный основаниями этих перпендикуляров, является трапецией.

б) Найдите площадь полученной трапеции, если площадь параллелограмма равна 16, а один из его углов равен 60°.

9.В равнобедренном треугольнике ABC с углом 120° при вершине A проведена биссектриса BD. В треугольник ABC вписан прямоугольник DEFH так, что сторона FH лежит на отрезке BC, а вершина E — на отрезке AB.

а) Докажите, что FH = 2DH.

б) Найдите площадь прямоугольника DEFH, если AB = 4.

10.Дан выпуклый четырёхугольник ABCD.

а) Докажите, что отрезки LN и KM, соединяющие середины его противоположных сторон, делят друг друга пополам.

б) Найдите площадь четырёхугольника ABCD, если ,

11.Высоты BB₁ и CC₁ остроугольного треугольника ABC пересекаются в точке H.

а) Докажите, что ∠AHB₁ = ∠ACB.

б) Найдите BC, если и ∠BAC = 60°.

12.В остроугольном треугольнике ABC провели высоту BH, из точки H на стороны AB и BCопустили перпендикуляры HK и HM соответственно.

а) Докажите, что треугольник MBK подобен треугольнику ABC.

б) Найдите отношение площади треугольника MBK к площади четырёхугольника AKMC, если BH = 2, а радиус окружности, описанной около треугольника ABC равен 4.

13.Медианы AA₁, BB₁ и CC₁ треугольника ABC пересекаются в точке M. Известно, что AC = 3MB.

а) Докажите, что треугольник ABC прямоугольный.

б) Найдите сумму квадратов медиан AA₁ и CC₁, если известно, что AC = 10.

14.На сторонах AD и BC параллелограмма ABCD взяты соответственно точки M и N, причём M — середина AD, а BN : NC = 1 : 3.

а) Докажите, что прямые AN и AC делят отрезок BM на три равные части.

б) Найдите площадь четырёхугольника, вершины которого находятся в точках С, N и точках пересечения прямой BM c прямыми AN и AC, если площадь параллелограмма ABCD равна 48.

15.Точка M — середина стороны AD параллелограмма ABCD . Из вершины A проведены два луча, которые разбивают отрезок BM на три равные части.

а) Докажите, что один из лучей содержит диагональ параллелограмма.

б) Найдите площадь четырёхугольника, ограниченного двумя проведёнными лучами и прямыми BD и BC , если площадь параллелограмма ABCD равна 40.

16.Медианы AA₁, BB₁ и CC₁ треугольника ABC пересекаются в точке M. Точки A₂, B₂ и C₂ — середины отрезков MA, MB и MC соответственно.

а) Докажите, что площадь шестиугольника A₁B₂C₁A₂B₁C₂ вдвое меньше площади треугольника ABC.

б) Найдите сумму квадратов всех сторон этого шестиугольника, если известно, что AB = 4, BC = 7 и AC = 8.

17.Прямая, проходящая через вершину В, прямоугольника ABCD, перпендикулярная диагонали АСи пересекает сторону АD в точке M, равноудаленной от вершин В и D.

а) Докажите, что BM и ВD делят угол В на три равных угла.

б) Найдите расстояние от точки пересечения диагоналей прямоугольника ABCDдо прямой СМ, если

18. Диагональ AC разбивает трапецию ABCD с основанием AD и BC, из которых AD большее, на два подобных треугольника.

а) Докажите, что ∠ABC = ∠ACD.

б) Найдите отрезок, соединяющий середины оснований трапеции, если известно, что BC = 18, AD = 50 и

19.Точка M лежит на стороне BC выпуклого четырёхугольника ABCD, причём B и C — вершины равнобедренных треугольников с основаниями AM и DM соответственно, а прямые AM и MDперпендикулярны.

а) Докажите, что биссектрисы углов при вершинах B и C четырёхугольника ABCD, пересекаются на стороне AD.

б) Пусть N — точка пересечения этих биссектрис. Найдите площадь четырёхугольника ABCD, если известно, что BM : MC = 3 : 4, а площадь четырёхугольника, стороны которого лежат на прямых AM, DM, BN и CN, равна 24.

20.В треугольнике АВС проведены высоты АК и СМ. На них из точек М и К опущены перпендикуляры МЕ и КН соответственно.

а) Докажите, что прямые ЕН и АС параллельны;

б) Найдите отношение ЕН : АС, если угол АВС равен 30°.

21.В трапеции ABCD точка E — середина основания AD, точка M — середина боковой стороны AB. Отрезки CE и DM пересекаются в точке O.

а) Докажите, что площади четырёхугольника AMOE и треугольника COD равны.

б) Найдите, какую часть от площади трапеции составляет площадь четырёхугольника AMOE, если BC = 3, AD = 4.

22.В остроугольном треугольнике ABC проведены высоты AK и CM. На них из точек M и Kопущены перпендикуляры ME и KH соответственно.

а) Докажите, что прямые EH и AC параллельны.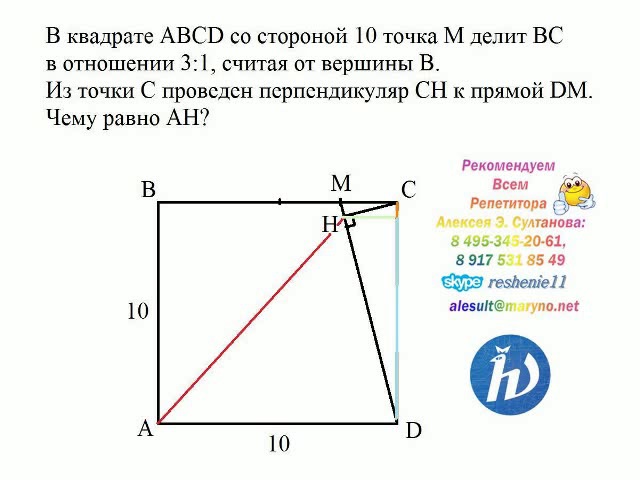

б) Найдите отношение EH и AC, если

23.Дана трапеция ABCD с боковой стороной AB, которая перпендикулярна основаниям. Из точки Ана сторону CD опущен перпендикуляр AH. На стороне AB взята точка E так, что прямые СЕ и СDперпендикулярны.

а) Доказать, что прямые BH и ED параллельны.

б) Найти отношение BH к ED, если

24.В прямоугольном треугольнике АВС с прямым углом С точки М и N — середины катетов АС и ВС соответственно, СН — высота.

а) Докажите, что прямые МН и NH перпендикулярны.

б) Пусть Р — точка пересечения прямых АС и NH, а Q — точка пересечения прямых BC и МН. Найдите площадь треугольника PQM, если АН = 12 и ВН = 3.

25.На продолжении стороны АС за вершину А треугольника АВС отмечена точка D так, что AD = AB. Прямая, проходящая через точку А, параллельно BD, пересекает сторону ВС в точке M.

а) Докажите, что AM — биссектриса треугольника АВС.

б) Найти S_AMBD, если AC = 30, BC = 18 и AB = 24.

26.На отрезке BD взята точка C. Биссектриса BL равнобедренного треугольника ABC с основанием BC является боковой стороной равнобедренного треугольника BLD с основанием BD.

а) Докажите, что треугольник DCL равнобедренный.

б) Известно, что В каком отношении прямая DL делит сторону AB?

27.В прямоугольном треугольнике ABC точки M и N — середины гипотенузы AB и катета BCсоответственно. Биссектриса угла BAC пересекает прямую MN в точке L.

а) Докажите, что треугольники AML и BLC подобны.

б) Найдите отношение площадей этих треугольников, если

28.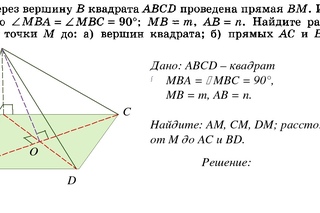 Точки B₁ и C₁ лежат на сторонах соответственно AC и AB треугольника ABC, причём AB₁ : B₁C = AC₁ : C₁B. Прямые BB₁ и CC₁ пересекаются в точке O.

а) Докажите, что прямая AO делит пополам сторону BC.

б) Найдите отношение площади четырёхугольника AB₁OC₁ к площади треугольника ABC, если известно, что AB₁ : B₁C = AC₁ : C₁B = 1 : 4.

29.На катетах AC и BC прямоугольного треугольника ABC вне треугольника построены квадраты ACDE и BFKC. Точка M — середина гипотенузы AB, H — точка пересечения прямых CM и DK.

а) Докажите, что CM DK.

б) Найдите MH, если известно, что катеты треугольника ABC равны 130 и 312.

30.На сторонах AC и BC треугольника ABC вне треугольника построены квадраты ACDE и BFKC. Точка M — середина стороны AB.

а) Докажите, что

б) Найдите расстояния от точки M до центров квадратов, если и

31.Медианы AA₁, BB₁, и CC₁ треугольника ABC пересекаются в точке M. Точки A₂, B₂ и C₂ — середины отрезков MA, MB и MC соответственно.

а) Докажите, что площадь шестиугольника A₁B₂C₁A₂B₁C₂ вдвое меньше площади треугольника ABC.

б) Найдите сумму квадратов всех сторон этого шестиугольника, если известно, что AB = 5, BC = 8 и AC = 10.

32.Дана трапеция ABCD с основаниями AD и BC. Диагональ BD разбивает её на два равнобедренных треугольника с основаниями AD и CD.

а) Докажите, что луч AC — биссектриса угла BAD .

б) Найдите CD, если известны диагонали трапеции: AC = 15 и BD = 8,5.

33.Прямая, проходящая через вершину B прямоугольника ABCD перпендикулярно диагонали AC, пересекает сторону AD в точке M, равноудалённой от вершин B и D.

а) Докажите, что ∠ABM = ∠DBC = 30°.

б) Найдите расстояние от центра прямоугольника до прямой CM, если BC = 9.

34.Прямая, проходящая через середину M гипотенузы AB прямоугольного треугольника ABC, перпендикулярна CM и пересекает катет AC в точке K. При этом AK : KC = 1 : 2.

а) Докажите, что

б) Пусть прямые MK и BC пресекаются в точке P, а прямые AP и BK — в точке Q. Найдите KQ, если BC =

35.Точка E — середина боковой стороны CD трапеции ABCD. На стороне AB взяли точку K, так, что прямые CK и AE параллельны. Отрезки CK и BE пересекаются в точке O.

а) Докажите, что CO = KO.

б) Найти отношение оснований трапеции BC и AD, если площадь треугольника BCK составляет площади трапеции ABCD.

36.Точки E и K — соответственно середины сторон CD и AD квадрата ABCD. Прямая BEпересекается с прямой CK в точке O.

а) Докажите, что вокруг четырёхугольника ABOK можно описать окружность.

б) Найдите AO, если сторона квадрата равна 1.

37.Известно, что АBCD трапеция, АD = 2BC, AD, BC — основания. Точка M такова, что углы АBMи MCD прямые.

а) Доказать, что MA = MD.

б) Расстояние от M до AD равно BC, а угол АDC равен 55°. Найдите угол BAD.

38.Дана равнобедренная трапеция, в которой AD = 3BC, CM — высота трапеции.

а) Доказать, что M делит AD в отношении 2 : 1.

б) Найдите расстояние от точки C до середины BD, если AD = 18, AC =

39.Дана трапеция с диагоналями равными 8 и 15. Сумма оснований равна 17.

а) Докажите, что диагонали перпендикулярны.

б) Найдите площадь трапеции.

40.Дана трапеция ABCD с основаниями AD и ВС, причем и точка M внутри трапеции, такая, что

а) Докажите, что АM = DM.

б) Найдите угол BAD, если угол CDA равен 50°, а высота, проведённая из точки M к АD, равна BC.

41.В треугольник ABC, в котором длина стороны AC меньше длины стороны BC, вписана окружность с центром O. Точка B₁ симметрична точке B относительно CO.

а) Докажите, что A, B, O и B₁ лежат на одной окружности.

б) Найдите площадь четырёхугольника AOBB₁, если AB = 10, AC = 6 и BC = 8.

42.В треугольнике ABC угол ABC тупой, H — точка пересечения продолжений высот, угол AHCравен 60°.

а) Докажите, что угол ABC равен 120°.

б) Найдите BH, если

43.В трапеции ABCD с основаниями ВС и AD углы ABD и ACD прямые.

а) Докажите, что АВ = CD.

б) Найдите AD, если AB = 2, BC = 7.

44.Точка Е — середина стороны BС квадрата АВСD. Серединные перпендикуляры к отрезкам АЕ и ЕС пересекаются в точке O.

а) Докажите, что .

б) Найдите .

45. Четырехугольник ABCD вписан в окружность с центром в точке О. Радиус АО перпендикулярен радиусу ОВ, а радиус ОС перпендикулярен радиусу OD.

а) Докажите, что ВС||AD.

б) Найдите площадь треугольника АОВ, если длина перпендикуляра, опущенного из точки С на AD, равна 9, а длина отрезка ВС в два раза меньше длины отрезка AD.

46.Из вершин А и В тупоугольного треугольника АВС проведены высоты BQ и AH. Известно, что угол В — тупой, BC : CH = 4 : 5, BH = BQ.

А) Докажите, что диаметр описанной вокруг треугольника ABQ окружности в раз больше BQ.

Б) Найдите площадь четырехугольника AHBQ, если площадь треугольника HQC равна 25.

47.Дана трапеция ABCD с основаниями AD и ВС. Диагонали АС и BD пересекаются в точке О, а прямые АВ и CD — в точке К.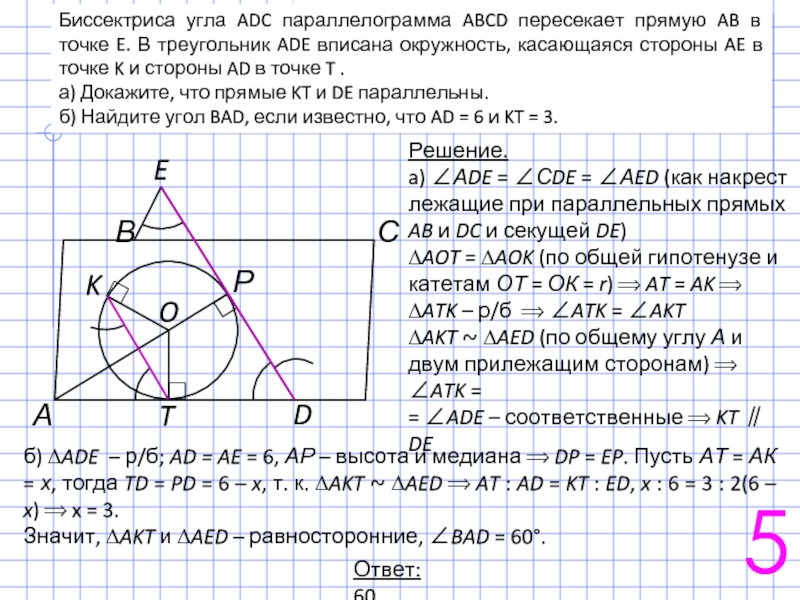 Прямая КО пересекает стороны ВС и AD в точках М и N соответственно, и угол BAD равен 30°. Известно, что в трапеции ABMN и NMCD можно вписать окружность.

а) Докажите, что треугольник AKD тупоугольный.

б) Найти отношение площадей треугольника ВКС и трапеции ABCD.

48.На сторонах AC и BC треугольника ABC вне его построены квадраты ACDE и CBFG. Точка M— середина стороны AB.

а) Докажите, что точка M равноудалена от центров квадратов.

б) Найдите площадь треугольника DMG, если

49.Дана трапеция ABCD с основаниями BC и AD. Точки M и N являются серединами сторон AB и CD соответственно. Окружность, проходящая через точки B и С, пересекает отрезки BM и CN в точках P и Q (отличных от концов отрезков).

а) Докажите, что точки M, N, P и Q лежат на одной окружности.

б) Найдите QN, если отрезки DP и PC перпендикулярны, AB = 21, BC = 4, CD = 20, AD = 17.

50.Дана трапеция ABCD с основаниями BC и AD. Точки M и N являются серединами сторон AB и CD соответственно. Окружность, проходящая через точки B и С, пересекает отрезки BM и CN в точках P и Q (отличных от концов отрезков).

а) Докажите, что точки M, N, P и Q лежат на одной окружности.

б) Найдите радиус окружности, описанной около треугольника MPQ, если прямая DPперпендикулярна прямой PC, AB = 25, BC = 3, CD = 28, AD = 20.

51.Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AKпересекает вторую окружность в точке C.

а) Докажите, что прямые AD и BC параллельны.

б) Найдите радиус окружности, описанной около треугольника BCD, если известно, что радиус первой окружности равен 4, а радиус второй окружности равен 1.

Домашнее задание с решениями к уроку 32 «Многоугольники» по книге В.В Ткачук «Математика

Урок 32. Многоугольники

Домашнее задание из В.В. Ткачук «Математика — абитуриенту»

1. В выпуклом четырехугольнике ABCD углы ABD и ACD равна . Известно, что AD = 2, расстояние от точки пересечения биссектрис в треугольнике ABD до точки пересечения биссектрис в треугольнике ACD равно . Найдите длину стороны BC.
2. Известно, что в выпуклом четырехугольнике ABCD угол ACD равен 60^о, AD = 7, BC = 3. Точки A, B, C, D лежат на одной окружности. Перпендикуляр из точки А на прямую CD делит угол BAD пополам. Найдите длину диагонали AC.
3. Четырехугольник ABCD вписан в окружность. Продолжение стороны AB за точку B пересекает продолжение стороны DC за точку C в точке E. Известно, что AB = 2, BD = , CD = 5, BE:EC=4:3. Найдите угол BAD.
4. В выпуклом четырехугольнике NPQM сторона NP равна b. Точка А лежит на стороне PQ, а точка B — на стороне NM. Отрезок AB разбивает четырехугольник NPQM на два четырехугольника, в каждый из которых можно вписать окружность. Известно, что разность периметров четырехугольников BAQM и ABNP равна 2p. Найдите сторону MQ.
5. В выпуклом четырехугольнике ABCD диагонали пересекаются в точке О. Площади треугольников BOC, COD и AOD равны соответственно 20, 40 и 60. Кроме того, AO = 8, AB = 15, угол BOA больше 31^о. Найдите угол BAO.
6. Диагонали выпуклого четырехугольника ABCD пересекаются в точке Е. Площади треугольников ABE и DCE равны 1, а площадь четырехугольника ABCD не превосходит 4. Найдите BC, если AD = 3.
7. В выпуклом четырехугольнике ABCD имеем AB = 3, BD = , причем угол BCD равен 120^о. Кроме того,. площадь четырехугольника ABCD равна (ABCD+BCAD)/2. Найдите длину стороны AD.
8. В окружность радиуса 7 вписан четырехугольник ABCD, для которого AB = BC,  S_ABD=2S_BCD, угол ADC равен 120^о. Найдите все стороны четырехугольника ABCD.
9. В выпуклом четырехугольнике ABCD биссектриса угла ABC пересекает сторону AD в точке M, AM = 2MD. Перпендикуляр, опущенный из вершины А на прямую BC, делит отрезок BC пополам. Найдите все стороны и площадь четырехугольника ABCD, если его периметр равен , угол BAD прямой и угол ABC равен 60^о.
10. В окружность радиуса 2 вписан правильный шестиугольник ABCDEF. Из точки К, лежащей на продолжении AF (KA<KF), KA = , проведена секущая KH, пересекающая окружность в точках N и H. Ее внешняя часть KN равна 2, и угол NFH тупой. Найдите угол HKF.
11. Выразите сторону правильного десятиугольника через радиус описанной окружности.
12. Один правильный шестиугольник вписан в окружность, другой описан около нее. Найдите радиус окружности, если разность их периметров равна а.
13. В круг радиуса R вписан шестиугольник ABCDEF. Известно, что углы BAF, BCD, DEF равны, AB = a, CD = b, EF = c. Найдите площадь шестиугольника.
14. Найдите площадь пятиугольника, ограниченного прямыми BC, CD, AN и MA, где A, B, D — три вершины квадрата ABCD со стороной а, N — середина BC, точка M лежит на стороне CD, причем CM:MD=2:1.
15. Правильный шестиугольник ABCDEK вписан в окружность радиуса R. Найдите радиус круга, вписанного в треугольник ACD.
16. Пятиугольник ABCDE вписан в окружность, причем BD параллельно AE, угол CAE в два раза больше угла CEA, угол CBD на  градусов превосходит угол CDB. Для треугольника ACE найдите отношение радиуса вписанной окружности к периметру.
17. Семиугольник A₁A₂A₃A₄A₅A₆A₇ вписан в окружность, центр которой лежит внутри него. Докажите, что сумму углов A₁, A₃, A₅ меньше 450^о.
18. В правильном шестиугольнике со стороной 5 на одной из сторон взята точка А на расстоянии 1 от ближайшей вершины шестиугольника. Найдите расстояние от точки А до центра шестиугольника.
19. Дан правильный шестиугольник ABCDEF. Точки А₁, B₁, C₁, D₁, E₁, F₁ лежат соответственно на сторонах AB, BC, CD, DE, EF, FA. Сторона шестиугольника равна а, причем AA₁=A₁B, B₁C=2BB₁, C₁D=3CC₁, D₁E=4DD₁, E₁F=5EE₁, F₁A=6FF₁. Найдите площадь шестиугольника A₁B₁C₁D₁E₁F₁.
20. [3] Прямая проходит через центр правильного n-угольника. Докажите, что сумма квадратов расстояний от вершин многоугольника до этой прямой не зависит от выбора прямой (проходящей через центр) и найдите эту сумму.

Ответы к домашнему заданию урока 32 из В.В. Ткачук «Математика — абитуриенту»

2. 4
4. p+b
5. 30^o
6. 3
7. 1 или 2
8. AB = BC = , CD = , AD = 
9. AB = BC = 2, CD = 1, AD = , 

МАТЕМАТИКА ЕГЭ 2011 (типовые задания С4)

Корянов А.Г., Прокофьев А.А.

отрезка этой прямой, заключенного внутри треугольника.

Ответ: 97 или 57 .

9. В треугольник АВС со сторонами AB 18 и BC 12 вписан параллелограмм BKLM, причем точки К, L, M лежат на сторонах АВ, АС и ВС соответственно. Известно, что площадь параллелограмма

составляет 4 площади треугольника

9

АВС. Найдите стороны параллелограмма.

Ответ: 6; 8 или 4; 12.

10. Высоты треугольника АВС пересекаются в точке Н. Известно, что отрезок СН равен радиусу окружности, описанной около треугольника. Найдите угол АСВ.

Ответ: 60 или 120 .

11. Высоты треугольника АВС пересекаются в точке Н. Известно, что CH AB. Найдите угол АСВ.

Ответ: 45 или 135 .

12. В треугольнике АВС проведены высоты ВМ и CN, О – центр вписанной окружности. Известно, что BC 24, MN 12. Найдите радиус окружности, описанной около треугольника ВОС.

Ответ: 83 или 24.

13. Окружность описана около равностороннего треугольника АВС. На дуге ВС, не содержащей точку А, расположена точка М, делящая градусную меру этой дуги в отношении 1:2. Найдите углы треугольника АМВ.

Ответ: 40 ; 80 ; 60 или 60 ; 20 ; 100 .

14. Треугольник АВС равнобедренный. Радиус ОА описанного круга образует с основанием АС угол ОАС, равный 20 . Найдите угол ВАС.

Ответ: 35 или 55 .

15. Пусть АВ и АС – равные хорды, MAN

– касательная, градусная мера дуги ВС, не содержащей точки А, равна 200 . Найдите углы МАВ и NAC.

Ответ: MAB NAC 40 илиMAB NAC 140 .

16. Через точку М проведены две прямые. Одна из них касается некоторой окружности в точке А, а вторая пересекает эту

05.01.2011.

окружность в точках В и С, причем BC 7 и BM 9. Найдите АМ.

Ответ: 12 или 32 .

17. Пусть О – центр окружности, описанной около треугольника АВС,AOC 60 . Найдите угол АМС, где М – центр окружности, вписанной в треугольник АВС.

Ответ: 165 или 105 .

18. Точка В – середина отрезка АС, причем AC 6. Проведены три окружности радиуса 5 с центрами А, В и С. Найдите радиус четвертой окружности, касающейся всех трех данных.

Ответ: 9 или 9 . 20 10

19. Одна окружность описана около равностороннего треугольника АВС, а вторая вписана в угол А и касается первой окружности. Найдите отношение радиусов окружностей.

Ответ: 3:2 или 1:2.

20. Один из смежных углов с вершиной А вдвое больше другого. В эти углы вписаны окружности с центрами O1 и O2 .

Найдите углы треугольника O1 AO2 , если отношение радиусов окружностей равно

3.

Ответ: 90 ; 45 ; 45 или 90 ; arctg3; arcctg3.

21. В прямоугольном треугольнике АВС катет АС равен 16 и катет ВС равен 12. Из центра В радиусом ВС описана окружность и к ней проведена касательная, параллельная гипотенузе. Катет ВС продолжен до пересечения с проведенной касательной. Определите, на какое расстояние продолжен катет.

Ответ: 15 или 3.

22. Дана трапеция ABCD, диагонали АС и BD которой пересекаются под прямым углом, а продолжения боковых сторон АВ и DC пересекаются в точке К под углом 30 . Известно, что BAC CDB, а площадь трапеции равна S. Найдите площадь треугольника AKD.

Ответ: 3S или S . 2 2

23. Дана трапеция ABCD с боковыми сторонами AB 27, CD 28 и основанием

Задание №16. Планиметрия. ЕГЭ. Математика.

      БАЗА ЗАДАНИЙ

Задание № 16. Планиметрия с доказательством.

29. Дана равнобедренная трапеция, в которой AD = 3BC, CM — высота трапеции.
а) Доказать, что M делит AD в отношении 2:1.
б) Найдите расстояние от точки C до середины BD, если AD = 18, AC =4√13.

30. В трапеции АBCD ∠BAD прямой. Окружность, построенная на большем основании АD как на диаметре, пересекает меньшее основание BC в точке C и M.
а) Докажите, что ∠BАM равен ∠CАD.
б) Диагонали трапеции АBCD пересекаются в точке O. Найдите площадь треугольника АOB, если АB = 6, а BC = 4BM.

31. Известно, что АBCD трапеция, АD = 2BC, AD, BC — основания. Точка M такова, что ∠ АBM и ∠MCD прямые.
а) Доказать, что MA = MD.
б) Расстояние от M до AD= BC, а ∠АDC равен 55. Найдите ∠BAD.
Ответ: б) 80

32. Точка E — середина боковой стороны CD трапеции ABCD. На стороне AB взяли точку K, так, что прямые CK и AE параллельны. Отрезки CK и BE пересекаются в точке O.
а) Докажите, что CO = KO.
б) Найти отношение оснований трапеции BC и AD, если площадь треугольника BCK составляет 9/64 от площади трапеции ABCD.
Ответ: б) 3:5

33. Окружность, вписанная в трапецию ABCD, касается ее боковых сторон AB и CD в точках M и N соответственно. Известно, что AM = 8MB и DN = 2CN.
а) Докажите, что AD = 4BC.
б) Найдите длину отрезка MN, если радиус окружности равен √6.

34. В трапеции ABCD точка E — середина основания AD, точка M — середина боковой стороны AB. Отрезки CE и DM пересекаются в точке O.
а) Докажите, что площади четырёхугольника AMOE и треугольника COD равны.
б) Найдите, какую часть от площади трапеции составляет площадь четырёхугольника AMOE, если BC = 3, AD=4.
Ответ: б) 2/9

35. Две окружности с центрами O₁ и O₂ и радиусами 3 и 4 пересекаются в точках A и B. Через точку A проведена прямая MK пересекающая обе окружности в точках M и K, причем точка A находится между ними.
а) Докажите, что треугольники BMK и O₁AO₂ подобны.
б) Найдите расстояние от точки B до прямой MK, если O₁O₂ = 5, MK = 7.
Ответ: б) 84/25

36. Две окружности с центрами O₁ и O₂ пересекаются в точках A и B, причём точки O₁ и O₂ лежат по разные стороны от прямой AB. Продолжения диаметра CA первой окружности и хорды CB этой окружности пересекают вторую окружности в точках D и E соответственно.
а) Докажите, что треугольники CBD и O₁AO₂ подобны.
б) Найдите AD, если ∠ DAE = ∠BAC радиус второй окружности в четыре раза больше радиуса первой и AB=2.
Ответ: б) 8

37. В прямоугольном треугольнике ABC проведена высота CH из вершины прямого угла. В треугольники ACH и BCH вписаны окружности с центрами O₁ и O₂ соответственно, касающиеся прямой CH в точках M и N соответственно.
а) Докажите, что прямые AO₁ и CO₂ перпендикулярны.
б) Найдите площадь четырёхугольника MO₁NO₂, если AC = 20 и BC = 15.
Ответ: б) 3,5

38. Дана трапеция ABCD с боковой стороной AB, которая перпендикулярна основаниям. Из точки А на сторону CD опущен перпендикуляр AH. На стороне AB взята точка E так, что прямые СЕ и СD перпендикулярны.
а) Доказать, что прямые BH и ED параллельны.
б) Найти отношение BH к ED, если ∠ BCD=135.
Ответ: б) 1:2

39. Один из двух отрезков, соединяющих середины противоположных сторон четырехугольника, делит его площадь пополам, а другой в отношении 11:17.
а) Докажите, что данный четырехугольник ‐ трапеция.
б) Найдите отношение оснований этой трапеции.
Ответ: б) 2:5

40. Точки E и K — соответственно середины сторон CD и AD квадрата ABCD. Прямая BE пересекается с прямой CK в точке O.
а) Докажите, что вокруг четырёхугольника ABOK можно описать окружность.
б) Найдите AO, если сторона квадрата равна 1.

41. На продолжении стороны АС за вершину А треугольника АВС отмечена точка D так, что AD = AB. Прямая, проходящая через точку А, параллельно BD, пересекает сторону ВС в точке M.
а) Докажите, что AM — биссектриса треугольника АВС.
б) Найти площадь SAMBD, если AC = 30, BC = 18 и AB = 24.
Ответ: б) 268,8

42. В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину В перпендикулярно АМ, пересе­кает сторону АС в точке N. АВ = 6; ВС = 5; АС = 9.
а) Докажите, что биссектриса угла С делит отрезок МN пополам
б) Пусть Р — точка пересечения биссектрис треугольника АВС. Найдите отношение АР : РN.
Ответ: б) 3:1

43. Диагональ AC разбивает трапецию ABCD с основанием AD и BC, из которых AD большее, на два подобных треугольника.
а) Докажите, что ∠ABC = ∠ACD.
б) Найдите отрезок, соединяющий середины оснований трапеции, если известно, что BC = 18, AD = 50 и cos ∠ CAD=3/5.
Ответ: б) 8√13

44. К двум непересекающимся окружностям равных радиусов проведены две параллельные общие касательные. Окружности касаются одной из этих прямых в точках A и B. Через точку C, лежащую на отрезке AB, проведены касательные к этим окружностям, пересекающие вторую прямую в точках D и E, причём отрезки CA и CD касаются одной окружности, а отрезки CB и CE — другой.
а) Докажите, что периметр треугольника CDE вдвое больше расстояния между центрами окружностей.
б) Найдите DE, если радиусы окружностей =5, расстояние между их центрами =18, а AC = 8.
Ответ: б) 12,375

45. Высоты BB₁ и CC₁ остроугольного треугольника ABC пересекаются в точке H.
а) Докажите, что ∠AHB₁ = ∠ACB.
б) Найдите BC, если AH = 21 и ∠BAC = 30°.
Ответ: б) 7√3

46. В равнобедренном треугольнике ABC с углом 120° при вершине A проведена биссектриса BD. В треугольник ABC вписан прямоугольник DEFH так, что сторона FH лежит на стороне BC, а вершина E — на стороне AB.
а) Докажите, что FH = 2DH.
б) Найдите площадь прямоугольника DEFH, если AB = 2.
Ответ: б) 6-3√3

47. Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Ответ: б) 3,2

48. Точки A₁, B₁, C₁ — середины сторон соответственно BC, AC и AB остроугольного треугольника ABC.
а) Докажите, что отличная от A₁ точка пересечения окружностей, описанных около треугольников A₁CB₁ и A₁BC₁, лежит на окружности, описанной около треугольника B₁AC_1.
б) Известно, что AB = AC = 10 и BC = 12. Найдите радиус окружности, вписанной в треугольник, вершинами которого являются центры окружностей, описанных около треугольников A₁CB₁, A₁BC₁ и B₁AC_1.
Ответ: б) 1,5

49. В треугольник ABC, в котором длина стороны AC меньше длины стороны BC, вписана окружность с центром O. Точка B₁ симметрична точке B относительно CO.
а) Докажите, что A, B, O и B₁ лежат на одной окружности.
б) Найдите площадь четырёхугольника AOBB₁, если AB = 10, AC = 6 и BC = 8.
Ответ: б) 18

50. Диагонали равнобедренной трапеции ABCD с основаниями BC и AD перпендикулярны. Окружность с диаметром AD пересекает боковую сторону CD в точке M, а окружность с диаметром CD пересекает основание AD в точке N. Отрезки AM и CN пересекаются в точке P.

а) Докажите, что в четырёхугольник ABCP можно вписать окружность.

б) Найдите радиус этой окружности, если BC=7, AD=17.
Ответ: б) 4,2

51. Прямая, проходящая через середину M гипотенузы AB прямоугольного треугольника ABC, перпендикулярна CM и пересекает катет AC в точке K. При этом AK:KC=1:2.
а) Докажите, что ∠BAC=30°.
б) Пусть прямые MK и BC пересекаются в точке P, а прямые AP и BK — в точке Q. Найдите KQ, если BC=√21.
Ответ: б) 14

52. В выпуклом четырёхугольнике ABCD точки K, L, M и N — середины сторон AB, BC, CD и AD соответственно. Площади четырёхугольников ABLN и NLCD равны, а площади четырёхугольников KBCM и AKMD относятся как 11:17.
а) Докажите, что прямые BC и AD параллельны.
б) Найдите отношение BC к AD.
Ответ: б) 0,4

53. Точка О — центр окружности, описанной около остроугольного треугольника ABC. На продолжении отрезка AO за точку О отмечена точка K так, что ∠BAC+∠AKC=90°.
а) Докажите, что четырехугольник OBKC вписанный.
б) Найдите радиус окружности, описанной около треугольника KBC, если известно, что радиус окружности, описанной около треугольника АBC равен 12, а cos∠BAC=0,6.
Ответ: б) 10

54. В остроугольном треугольнике ABC провели высоту BH из точки H на стороны AB и BC опустили перпендикуляры HK и HM соответственно.
а) Докажите, что треугольник MBK подобен треугольнику ABC.
б) Найдите отношение площади треугольника MBK к площади четырёхугольника AKMC, если BH = 2, а радиус окружности, описанной около треугольника ABC равен 4.
Ответ: б) 1:15

55. Около равнобедренного треугольника ABC с основанием BC описана окружность. Через точку C провели прямую, параллельную стороне AB. Касательная к окружности, проведённая в точке B, пересекает эту прямую в точке K.
а) Докажите, что треугольник BCK — равнобедренный.
б) Найдите отношение площади треугольника ABC к площади треугольника BCK, если cos∠BAC=3/4.
Ответ: б) 2

56. Прямая, проходящая через вершину В, прямоугольника ABCD, перпендикулярная диагонали АС и пересекает сторону АD в точке M, равноудаленной от вершин В и D.

а) Докажите, что BM и ВD делят угол В на три равных угла.
б) Найдите расстояние от точки пересечения диагоналей прямоугольника ABCD

до прямой СМ, если BC=6√21.
Ответ: б) 3

Применение теорем Чевы и Менелая

Отрезок, соединяющий вершину треугольника с некоторой точкой на противоположной стороне, называется чевианой. Таким образом, если в треугольнике АВС X, Y и Z- точки, лежащие на сторонах ВС, СА, АВ соответственно, то отрезки АX, ВY, СZ являются чевианами. Этот термин происходит от имени итальянского математика Джованни Чевы, который в 1687 году опубликовал следующую очень полезную теорему:

Если три чевианы АX, ВY, СZ ( по одной из каждой вершины ) треугольнка АВС конкурентны, то

Когда мы говорим, что три прямые ( или отрезка ) конкурентны, то мы имеем в виду, что все они проходят через одну точку, которую обозначим через Р.

Для доказательства теоремы Чевы вспомним, что площади треугольников с равными высотами пропорциональны основаниям треугольников.

( Ссылаясь на рисунок, мы имеем

Теперь, если мы перемножим их, то получим

Теорема Менелая:

Пусть точка А1 лежит на стороне ВС треугольника АВС, точка С1 – на стороне АВ, точка В1 – на продолжении стороны АС за точку С. Точки А1,В1 иС1 лежат на одной прямой тогда и только тогда, когда выполняется равенство

Эта теорема Входит в золотой фонд древнегреческой математики. Она дошла до нас в арабском переводе книги «Сферика» Менелая Александрийского. Равенство Менелая можно записывать, начиная с любой вершины треугольника, в любом направлении ( по часовой стрелке, против часовой стрелки ).

Задача 1.

В треугольнике АВС на стороне ВС взята точка N так, что NC = 3BN; на продолжении стороны АС за точку А взята точка М так, что МА=АС. Прямая MN пересекает сторону АВ в точке F. Найдите: отношение

Решение. По условию задачи МА = АС, NC = 3BN. Пусть МА = АС = b,

BN = k, NC = 3k. Прямая MN пересекает две стороны треугольника АВС и продолжение третьей. По теореме Менелая

Ответ:2:3.

Задача 2.

Пусть AD – медиана треугольника АВС. На стороне AD взята точка K так, что AK:KD=3:1. Прямая ВК разбивает треугольник АВС на два. Найдите отношение площадей этих треугольников.

Решение. Пусть BD = DC = a, KD = m; тогда AK = 3m. Пусть Р – точка пересечения прямой ВК со стороной АС.

Необходимо найти отношение

Так как треугольники АВР и РВС имеют равные высоты, проведенные из вершины В, то

По теореме Менелая для треугольника ADC и секущей PB имеем:

Ответ: 3:2.

Задача 3.

В треугольнике АВС, описанном около окружности, АВ = 8, ВС = 5, АС = 4.

А1 ,В1и С1 – точки касания, принадлежащие соответственно сторонам ВС,АС и ВА. Р – точка пересечения отрезков АА1 и СС1. Точка Р лежит на биссектрисе ВВ1. Найдите АР:РА1.

Решение. Пусть С1В = x, тогда, используя свойство касательных, проведённых к окружности из одной точки, введем обозначения : ВА1=ВС1=х, А1С = СВ1= 5-х, АВ1= АС1= 8-х.

Так как АС=4

8-x+5-x=4,

Значит,

В треугольнике АВА1 прямая С1С пересекает две его стороны и продолжение третьей стороны. По теореме Менелая

Ответ: 70:9.

Задача 4.

В треугольник АВС, описанном около окружности, АВ = 8, ВС = 12, АС = 9, А1 и С1 – точки касания, лежащие соответственно на сторонах ВС и АВ. Q – точка пересечения отрезков АА1 и ВВ1. Q лежит на высоте ВВ1. Найдите отношение ВQ:QB1.

Решение. Треугольник АВС – разносторонний, значит, точка В1 не совпадает с точкой касания.

1. Пусть С1В = x,тогда, используя свойство касательных, проведённых к окружности из одной точки, введём обозначения:

( 13-x ) + ( 12-x ) = 9, x = 8.

Значит, С1В = 8, АС1 = 5.

2. По формуле Герона

3. Из треугольника АВВ1( прямоугольного ) по теореме Пифагора АВ1 =

4. В треугольнике АВВ1 прямая СС1 пересекает две его стороны и продолжение третьей. По теореме Менелая

Ответ: 162:35.

Задача 5.

Стороны треугольника 5,6 и 7. Найдите отношение отрезков, на которые биссектриса большего угла этого треугольника разделена центром окружности, вписанной в треугольник.

Решение. Пусть в треугольнике АВС, АВ = 5, ВС = 7, АС = 6. Угол ВАС лежит против большей стороны в треугольнике АВС, значит, угол ВАС – больший угол треугольника. Центр вписанной окружности треугольника лежит на пересечении биссектрис. Необходимо найти АО:ОD. Так как AD – биссектриса треугольника АВС, то то есть BD = 5k, DC = 6k.

Так как BF – биссектриса треугольника АВС, то то есть AF = 5m, FC = 7m.

Прямая BF пересекает две стороны и продолжение третьей треугольника ADC. По теореме Менелая

Ответ: 11:7.

Задача 6.

Биссектрисы BF и AD треугольника АВС пересекаются в точке Q. Найдите площадь треугольника АВС, если

Решение. Пусть АВ = a, тогда АС =

АD- биссектриса треугольника АВС, тогда то есть BD = 2p,DC = 3p.

ВЕ – биссектриса треугольника АВС, тогда

В треугольнике ВЕС прямая АD пересекает две его стороны и продолжение третьей стороны. По теореме Менелая то есть EQ = 9m,QB = 14m.

Треугольники QBD и EBC имеют общий угол, значит,

Треугольники АВС и ВЕС имеют равные высоты, проведённые из вершины В, значит, тогда

Ответ: 115:16.

Задача 7.

В треугольнике АВС, площадь которого равна 6, на стороне АВ взята точка К, делящая эту сторону в отношении АК:ВК = 2:3, а на стороне АС – точка L, делящая АС в отношении AL:LC = 5:3. Точка Q пересечения прямых CK и BL удалена от прямой АВ на расстояние. Найдите длину стороны АВ.

Решение. 1. Треугольники ABL и ABC имеют одинаковую высоту, проведённую из вершины В. тогда

2. Прямая КС пересекает в треугольнике ABL две стороны и продолжение третьей. По теореме Менелая то есть BQ = 4p, QL = p.

3. Треугольники KBQ и ABL имеют общий угол, значит, тогда

4. тогда

Итак, АВ = 4.

Ответ: 4.

Задача 8.

В треугольнике АВС точки К и L принадлежат соответственно сторонам АВ и ВС. АК:ВК = 1:2, CL:BL = 2:1. Q – точка пересечения отрезков AL и CK. Найдите площадь треугольника АВС.

Решение. В треугольнике МВС прямая AL пересекает две стороны треугольника и продолжение третьей стороны. По теореме Менелая 1)

В треугольнике АВМ прямая КС пересекает две стороны треугольника и продолжение третьей стороны. По теореме Менелая 2) то есть МС = 4p, AM =p.

2. Ещё раз перепишем равенство (1):

то есть MQ = 2l, QB = 5l.

3. Треугольники BQC и MBC имею общий угол, значит, тогда

4. Треугольники АВС и МВС имеют равные высоты, проведённые из вершины В, значит,

Ответ: 1,75.

Задача 9.

На стороне АС в треугольнике АВС взята точка К, АК = 1, КС = 3.

На стороне АВ взята точка L. AL:LB = 2:3. Q – точка пересечения прямых ВК и CL. Найдите длину высоты треугольника АВС, опущенной из вершины В.

Решение. Прямая ВК пересекает две стороны и продолжение третьей треугольника ALC. По теореме Менелая то есть LQ = 1p, QC = 5p.

1) Треугольники ALC и AQC имеют общий угол, значит,

2) Треугольники АВС и ALC имеют общую высоту, проведённую из вершины С, значит,

Ответ: 1,5.

Задача 10.

Через середину М стороны ВС параллелограмма АВСD, площадь которого 1, и вершину А проведена прямая, пересекающая диагональ BD в точке Q. Найдите площадь четырёхугольника QMCD.

Решение. так как СО – медиана треугольника BCD, значит, делит треугольник BCD на два равновеликих треугольника.

1) МА пересекает две стороны и продолжение третьей треугольника ВОС, значит, по теореме Менелая откуда

2) Треугольники BQM и BOC имеют общий угол, значит

Задача 11.

В трапеции ABCD с основанием AD и ВС через середину А проведена прямая, которая пересекает диагональ BD в точке Е и боковую сторону CD в точке К, причем BE:ED = 1:2 и CK:KD = 1:4. Найдите отношение длин оснований трапеции.

Решение. Пусть ВC = a, AD = b. Необходимо найти

Пусть Q – точка пересечения прямых ВС и АК.

1) По теореме Менелая для треугольника BCD и секущей AQ имеем

2) ( по двум углам ), тогда

Так как a =BC, b = AD,то

Ответ: 1:4.

Задача 12.

На стороне NP квадрата MNPQ взята точка А, а на стороне PQ – точка В так, что NA:AP=PB:BQ=2:3. Точка L является точкой пересечения отрезков МА и NB. В каком отношении точка L делит отрезок MA?

Решение. Проведём прямую Ав. Пусть она пересекает MQ в точке F. Пусть прямая NB пересекает прямую MQ в точке D.

тогда откуда тогда откуда

Из треугольника APB ( прямоугольного ) по теореме Пифагора АВ =

Из треугольника QBF (прямоугольного ) по теореме Пифагора BF =

Из треугольника AFM по теореме Менелая

Ответ: 25:4.

Основные выводы:

1. Для решения задач необходимо научиться находить на рисунке треугольник, удовлетворяющий теореме Менелая.

2. При составлении равенства надо переходить от вершины к вершине через точку пересечения секущей линии с этой стороной или ее продолжением; заканчивать необходимо в той же вершине, с которой начали.

Значимость данной работы:

При решении задач ( в работе их представлено 12 ) мы пришли вывод, что:

А) теоремы Чевы и Менелая позволяют легко и изящно решать целый класс задач;

Б) наша работа может быть использована для проведение практических занятий на элективных курсах с учащимися выпускных классов и при подготовке к Единому Государственному Экзамену.

Задач по геометрии

Задача 1 [BMOTC] Проблемы в геометрии Prithwijit De ICFAI Bus в школе ess, Калькутта, Республика Индия, электронная почта : [email protected] Докажите, что медианы из вершин A и B треугольника ABC взаимно перпендикулярны тогда и только тогда, когда | BC | 2 + | AC | 2 = 5 | AB | 2. Задача 2 [BMOTC] Предположим, что ∠A — наименьший из трех углов треугольника ABC.Пусть D — точка в t на дуге BC описанной окружности треугольника ABC, которая не входит в в A. Пусть серединные перпендикуляры к AB, AC в < / strong> tersect AD в точках M и N соответственно. Пусть BM и CN пересекаются в точке T. Докажите, что BT + CT ≤ 2R, где R — радиус описанной окружности треугольника ABC. Задача 3 [BMOTC] Пусть треугольник ABC, как обычно, имеет стороны a, b и c. Po в ts P и Q лежат в стороне этого треугольника и обладают такими свойствами, что ∠BP C = ∠CP A = ∠AP B = 120 ◦ и ∠BQC = 60 ◦. + ∠A, ∠CQA = 60 ◦ + ∠B, ∠AQB = 60 ◦ + ∠C.Докажите, что Задача 4 [BMOTC] (| AP | + | BP | + | CP |) 3. | AQ |. | BQ |. | CQ | = (abc) 2. Точки in ts M и N являются точками касания in окружности равнобедренного треугольника ABC, которые находятся на сторонах AC. и до н.э. Стороны равной длины — это AC и BC. Касательная l in e t проводится к m in или дуге MN. Предположим, что t в пересекает AC и BC в точках Q и P соответственно.Предположим, что l in es AP и BQ встречаются в точке T. (a) Докажите, что T лежит на l in e отрезке MN. (б) Докажите, что сумма площадей треугольников AT Q и BT P равна m , когда t параллельна AB. Задача 5 [BMOTC] В шестиугольнике с равными углами длины четырех последовательных ребер равны 5, 3, 6 и 7 ( в указанном порядке). F in d длина оставшихся in in g двух краев.1

% PDF-1.5 % 1 0 объект > эндобдж 4 0 obj (Постулаты Евклида) эндобдж 5 0 obj > эндобдж 8 0 объект (Современные системы аксиом) эндобдж 9 0 объект > эндобдж 12 0 объект (Геометрия падения) эндобдж 13 0 объект > эндобдж 16 0 объект (Модели систем аксиом) эндобдж 17 0 объект > эндобдж 20 0 объект (Свойства систем аксиом) эндобдж 21 0 объект > эндобдж 24 0 объект (Исторические заметки: независимость постулата евклидовой параллели) эндобдж 25 0 объект > эндобдж 28 0 объект (Исторические заметки: современные аксиоматизации евклидовой геометрии) эндобдж 29 0 объект > эндобдж 32 0 объект (Аксиомы нейтральной геометрии: постулаты и леммы линейки) эндобдж 33 0 объект > эндобдж 36 0 объект (Сегменты, средние точки и лучи) эндобдж 37 0 объект > эндобдж 40 0 объект (Аксиомы нейтральной геометрии: разделение плоскостей, углы и меры) эндобдж 41 0 объект > эндобдж 44 0 объект (Аксиомы нейтральной геометрии: треугольники и конгруэнтность) эндобдж 45 0 объект > эндобдж 48 0 объект (Удивительные нейтральные теоремы: угловые дефекты и четырехугольники Саккери) эндобдж 49 0 объект > эндобдж 52 0 объект (Евклидова геометрия: треугольники и прямоугольники) эндобдж 53 0 объект > эндобдж 56 0 объект (Евклидова геометрия: примечания к площади) эндобдж 57 0 объект > эндобдж 60 0 объект (Евклидова геометрия: подобие треугольника) эндобдж 61 0 объект > эндобдж 64 0 объект (Евклидова геометрия: теоремы Менелая и Чевы) эндобдж 65 0 объект > эндобдж 68 0 объект (Евклидова геометрия: центры треугольников) эндобдж 69 0 объект > эндобдж 72 0 объект (Евклидова геометрия: девятиконечный круг) эндобдж 73 0 объект > эндобдж 76 0 объект (Эквивалентные формулировки постулата евклидовой параллели) эндобдж 77 0 объект > эндобдж 80 0 объект (Модели гиперболической геометрии) эндобдж 81 0 объект > эндобдж 84 0 объект (Гиперболическая геометрия: угол параллельности) эндобдж 85 0 объект > эндобдж 88 0 объект (Краткая аналитическая интерлюдия: непрерывность расстояния и площади) эндобдж 89 0 объект > эндобдж 92 0 объект (Гиперболическая геометрия: вырезание и вставка многоугольников) эндобдж 93 0 объект > эндобдж 96 0 объект (Гиперболическая геометрия: непрерывность дефекта) эндобдж 97 0 объект > эндобдж 100 0 объект (Гиперболическая геометрия: гиперболическая область) эндобдж 101 0 объект > эндобдж 104 0 объект> поток x ڭ Y [۶ ~ _K / C

Проблемы и запросы в Math Central