Главная → Видеоуроки → ОГЭ (ГИА) по математике. Задача 10. Описание видеоурока: Решите задачу: На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что угол ∠NBA=63 градуса. Найдите угол NMB. Ответ дайте в градусах. 00:07:54 Валерий Волков 32 24.01.2015 Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями! Новости образования | ЕГЭ по математике Профильный уровень Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 10 Задание 11 Задание 12 Задание 13 Задание 14 Задание 15 Задание 16 Задание 17 Задание 18 Задание 19 Задание 20 Задание 21 ГИА по математике Задача 1 Задача 2 Задача 3 Задача 4 Задача 5 Задача 6 Задача 7 Задача 8 Задача 9 Задача 10 Задача 11 Задача 12 Задача 13 Задача 14 Задача 15 Задача 16 Задача 17 Задача 18 Задача 19 Задача 20 Задача 21 Задача 22 Задача 23 Задача 24 Задача 25 Задача 26 Демонстрационные варианты ОГЭ по математике Математика. Натуральные числа Обыкновенные дроби Десятичные дроби Проценты Математика. 6 класс. Делимость чисел Умножение и деление обыкновенных дробей Отношения и пропорции Положительные и отрицательные числа Измерение величин Математика. 7 класс. Преобразование выражений Многочлены Формулы сокращенного умножения Математика. 8 класс. Модуль числа. Уравнения и неравенства. Квадратные уравнения Квадратные неравенства Уравнения с параметром Задачи с параметром Математика. 9 класс. Функции и их свойства Прогрессии Векторы Комбинаторика, статистика и теория вероятностей Математика. Числовые функции Тригонометрические функции Тригонометрические уравнения Преобразование тригонометрических выражений Производная Степенные функции Показательная функция Логарифмические функции Первообразная и интеграл Уравнения и неравенства Комбинаторика Создаёте видеоуроки? Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала. Актуально Физкультминутки для школьников и дошкольников Подготовка к ЕГЭ Подготовка к ОГЭ |
Геометрия 7-9 класс. Окружность — math200.ru
Skip to contentГеометрия 7-9 класс. Окружностьadmin2022-12-14T21:48:52+03:00
Скачать файл в формате pdf.
Геометрия 7-9 класс. Окружность
Задача 1. Из точки окружности проведены радиус и равная ему хорда. Найдите угол между этим радиусом и хордой. Ответ дайте в градусах. Из точки окружности проведены радиус и равная ему хорда. Найдите угол между этим радиусом и хордой. Ответ дайте в градусах.Ответ ОТВЕТ: 60. | |
| Задача 2. Из точки окружности проведены две хорды, каждая из которых равна радиусу. Найдите угол между этими хордами. Ответ дайте в градусах. Ответ ОТВЕТ: 120. | |
| Задача 3. Из точки окружности проведены диаметр и хорда, равная половине диаметра. Найдите угол между диаметром и хордой. Ответ дайте в градусах. Ответ ОТВЕТ: 60. | |
| Задача 4. В окружности проведен диаметр AB. Из точки C, лежащей на окружности, опущен перпендикуляр CH на диаметр. Найдите \(\angle \,ABC,\) если AC = 2 CH. Ответ дайте в градусах. Ответ ОТВЕТ: 60. | |
Задача 5. Треугольник ABC вписан в окружность так, что AC – диаметр, вершина B лежит на окружности. Ответ ОТВЕТ: 10,4. | |
| Задача 7. Из конца диаметра AB проведены равные хорды AC и AD по разные стороны от диаметра. Докажите, что CB = DB. | |
| Задача 8. Из концов диаметра AB проведены равные хорды AC и BD по одну стороны от диаметра. Докажите, что AD = BC. | |
| Задача 9. Дана окружность с центром в точке O. Из конца диаметра AB проведена хорда BC. Докажите, что \(\angle \,AOC\) в два раза больше \(\angle \,ABC.\) | |
Задача 10. Дана окружность с центром в точке O, AB – хорда окружности, AC – касательная к окружности. Докажите, что \(\angle \,AOB\) в два раза больше \(\angle \,BAC.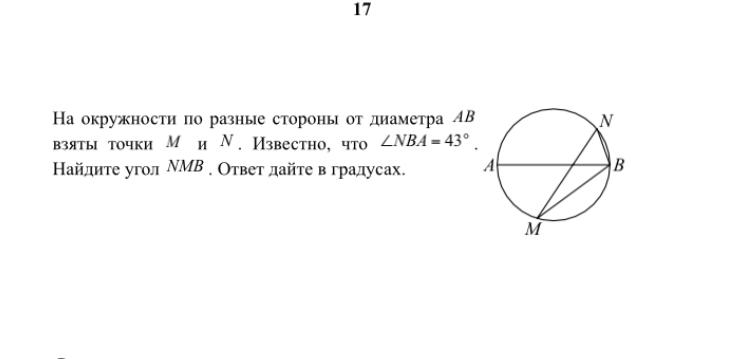 \) \) | |
| Задача 11. Известно, что BK = Ответ ОТВЕТ: 135. | |
Реклама
Мы Вконтакте
Поддержать нас
Две хорды АВ и АС окружности с центром О лежат по разные стороны от ОА Тогда ОАВ ОАС …
Перейти к
- Круги — упражнение 10.1
- Круги — упражнение 10.2
- Круги — упражнение 10.3
- Круги — упражнение 10.
 4
4
- Системы счисления
- Полиномы
- Координатная геометрия
- Введение в геометрию Евклида
- Линии и углы
- Треугольники
- Площади параллелограммов и треугольников
- Круги
- Конструкции
- Формула Герона
- Площади поверхности и объемы
- Статистика и вероятность
Главная >
Образцовые решения NCERT
Класс 9
Математика
>
Глава 10 — Круги
>
Круги — упражнение 10. 2
>
Вопрос 3
2
>
Вопрос 3
Вопрос 3 Окружности — Упражнение 10.2
Две хорды АВ и АС окружности с центром О лежат на противоположных сторонах стороны ОА. Тогда ∠OAB = ∠OAC.
Ответ:
Неверно
Обоснование:
Пусть AB и AC — хорда окружности с центром О на противоположной стороне ОА.
Рассмотрим треугольники AOC и AOB:
AO = AO (общая сторона в обоих треугольниках)
OB = OC (оба OB и OC равны радиусу окружности)
Но мы не можем показать, что равны ни третьи стороны обоих треугольников, ни любой угол равен.
Следовательно, ΔAOB не конгруэнтно ΔAOC.
∴ ∠OAB ≠ ∠OAC.
Стенограмма видео
«привет студент
добро пожаловать обратно на лидера вниз
решение сессии снова
и снова сегодня мы придумываем один
новая проблема математики правильно
в основном это проблема
связано с геометрией правильно хорошо
так быстро я прочитаю заявление для
вы два аккорда
a b и c окружностей с центром o
находятся на противоположной стороне волны
тогда угол o a b равен углу
oac, так что в основном нам нужно проверить
правильно ли это утверждение или
неправильный
правильно и понять это то, что у меня есть
Готово, я нарисовал эту фигуру. можно увидеть рисунок здесь
хорошо хорошо сейчас быстро мы будем
решить эту проблему правильно
эта фигура
Хорошо, у нас здесь два треугольника
правильно, так что один треугольник является треугольником
aoc и еще один треугольник, который мы получаем
треугольник а
хорошо, хорошо, так что в основном мы
получение
два треугольника здесь хорошо хорошо сейчас
Давайте обсудим
хорошо стороны треугольника правильно так
в этом конкретном треугольнике хорошо
сторона хорошо ао
равно стороне хорошо
ао правильно, потому что оба треугольника имеют
общая сторона
правильно, так что ao является общей стороной общей стороны
верно
хорошо, вот почему ао равно ао
сейчас хорошо что мы будем делать мы будем
проверять
хорошо, снова мы можем видеть, что нормальная длина
из
oc длина oc
равно длине ob
правильно хорошо, потому что ob и oc
радиус круга правильный ладно радиус
принадлежащий
обведи вправо поэтому ладно
ob и oc эквивалентны
стороны правы, хорошо, что у них есть
эквивалентно хорошо
но если внимательно понаблюдать то ладно
ac для стороны ac и
ладно б ладно мы не можем сказать что ли
эти стороны
равно или не правильно снова мы не можем сказать
что
любой из углов равен или нет
вот почему
мы не можем предсказать угол
o a b и o a c или равные или неправильные
и поэтому угол о
а б нормально это
не равно или не совпадает с
и
ладно угол o a c ладно
так что в основном это не те
параллельный угол
вот и все о сегодняшней сессии
пожалуйста, прокомментируйте, если у вас есть какие-либо сомнения
и, пожалуйста, подпишитесь на этот канал
так что мы получим обновление для
предстоящее видео
пока
ты»
можно увидеть рисунок здесь
хорошо хорошо сейчас быстро мы будем
решить эту проблему правильно
эта фигура
Хорошо, у нас здесь два треугольника
правильно, так что один треугольник является треугольником
aoc и еще один треугольник, который мы получаем
треугольник а
хорошо, хорошо, так что в основном мы
получение
два треугольника здесь хорошо хорошо сейчас
Давайте обсудим
хорошо стороны треугольника правильно так
в этом конкретном треугольнике хорошо
сторона хорошо ао
равно стороне хорошо
ао правильно, потому что оба треугольника имеют
общая сторона
правильно, так что ao является общей стороной общей стороны
верно
хорошо, вот почему ао равно ао
сейчас хорошо что мы будем делать мы будем
проверять
хорошо, снова мы можем видеть, что нормальная длина
из
oc длина oc
равно длине ob
правильно хорошо, потому что ob и oc
радиус круга правильный ладно радиус
принадлежащий
обведи вправо поэтому ладно
ob и oc эквивалентны
стороны правы, хорошо, что у них есть
эквивалентно хорошо
но если внимательно понаблюдать то ладно
ac для стороны ac и
ладно б ладно мы не можем сказать что ли
эти стороны
равно или не правильно снова мы не можем сказать
что
любой из углов равен или нет
вот почему
мы не можем предсказать угол
o a b и o a c или равные или неправильные
и поэтому угол о
а б нормально это
не равно или не совпадает с
и
ладно угол o a c ладно
так что в основном это не те
параллельный угол
вот и все о сегодняшней сессии
пожалуйста, прокомментируйте, если у вас есть какие-либо сомнения
и, пожалуйста, подпишитесь на этот канал
так что мы получим обновление для
предстоящее видео
пока
ты»
Связанные вопросы
AD — диаметр окружности, AB — хорда. Если AD = 34 см, AB = 30 см, то расстояние AB от t…
Если AD = 34 см, AB = 30 см, то расстояние AB от t…
Две хорды AB и CD окружности находятся на расстоянии 4 см от центра каждая. Тогда АВ=CD
Две конгруэнтные окружности с центрами O и O’ пересекаются в двух точках A и B. Тогда ∠AOB = ∠AO’B.
Через три коллинеарные точки можно провести окружность.
Через две точки А и В можно провести окружность радиусом 3 см так, что АВ = 6 см.
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Круги — Упражнение 10. 1
1
Круги — Упражнение 10.2
Круги — Упражнение 10.3
Круги — Упражнение 10.4 0003
Координатная геометрия
Линейные уравнения с двумя переменными
Введение в геометрию Евклида
Прямые и углы
Треугольники
Четырехугольники
Площади параллелограммов и треугольников
Окружности
Построения
Формула Герона
Площади поверхностей и объемы
Статистика и вероятность
Курсы
Быстрые ссылки
Условия и политика
Условия и политика
2022 © Quality Tutorials Pvt Ltd Все права защищены
Две хорды AB и CD длиной 5 см и 11 см соответственно параллельны друг другу. и находятся по разные стороны от его центра. Если расстояние между АВ и CD равно 6 см, найдите радиус окружности 9 см.0001
Решение:
Проведите две параллельные хорды AB и CD длиной 5 см и 11 см. Пусть центр круга будет O. Соедините один конец каждой хорды с центром.
Проведите два перпендикуляра OM и ON к AB и CD соответственно, которые делят хорды пополам.
Таким образом, MB = 2,5 см и ND = 5,5 см [Перпендикуляр, проведенный из центра окружности к хордам, делит ее пополам.]
Пусть OM = x и ON = 6 — x
Рассмотрим ΔOMB
По теореме Пифагора,
OM 2 + MB 2 = OB 2
x 2 + 2,5 2 07 2 = 1OB 90
x 2 + 6,25 = ОВ 2 ………………(1)
Рассмотрим ΔOND
По теореме Пифагора,
ON 2 + ND 2 = OD 2
( 6 — x)² + 5,5 2 = НД 2
36 + x 2 — 12x + 30,25 = НД 2
x 2 — 12x + 66,25 = OD 2 …………… (2)
OB и OD — радиусы окружности. Следовательно, ОБ = ОД.
Таким образом, ОБ 2 = ОД 2
Приравнивая (1) и (2) получаем, 002 12x = 60
x = 5
Подставляя значение x в (1),
OB 2 = x 2 + 6,25
OB 2 = 5 2 + 6,25
ОВ 2 = 31,25
ОВ = 5,59 (приблизительно)
Таким образом, получаем радиус окружности = 5,59 см.
☛ Проверка: Класс 9 Математика NCERT Решения Глава 10
Видео Решение:
Две хорды AB и CD окружности длиной 5 см и 11 см соответственно параллельны друг другу и лежат на противоположных сторонах его центра. Если расстояние между АВ и CD равно 6 см, найдите радиус окружности 9 см.0274
Математика NCERT Решения Класс 9 Глава 10 Упражнение 10.6 Вопрос 2
Резюме:
Две хорды AB и CD длиной 5 см и 11 см соответственно параллельны друг другу и лежат на противоположных сторонах его центр, если расстояние между AB и CD равно 6 см, радиус окружности равен 5,59 см.

 5 класс.
5 класс.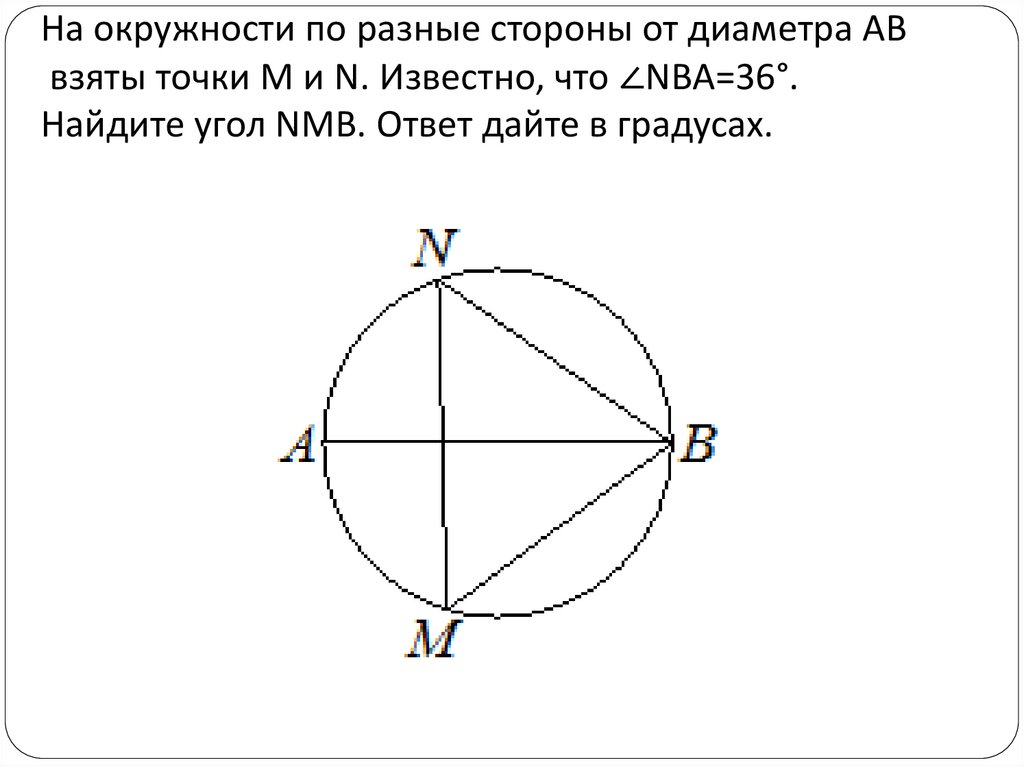 10 — 11 класс.
10 — 11 класс.
 4
4
Leave A Comment