| ||||||||||||
| Специальный поиск | ||||||||||||
|
Физика Теория вероятностей и мат. статистика Гидравлика Теор. механика Прикладн. механика Химия Электроника Витамины для ума |
Главная Поиск по сайту Формулы Все задачи Помощь Контакты Билеты |
|||||||||||
наклонная плоскость образует горизонтом угол Задача 13136 Сплошной однородный диск скатывается без скольжения с наклонной плоскости, образующей угол α с горизонтом. Определите линейное ускорение а центра диска.
Задача 14198 Блок массой m = 1 кг укреплен в вершине наклонной плоскости, образующей с горизонтом угол 30°. Тела массой m1 = 2 кг и m2 = 1 кг соединены нитью, перекинутой через блок. Определить ускорение, с которым движутся тела и силы натяжения нити. Трением тела 2 о наклонную плоскость и трением в блоке пренебречь.
Задача 17414 На разных склонах наклонной плоскости, образующих с горизонтом углы α1 = 32° и α2 = 48°, находятся грузы m1 = 3,3 кг и m2. Нить, связывающая грузы, перекинута через легкий блок, укрепленный на вершине наклонной плоскости. Коэффициент трения между грузами и наклонной плоскостью равен 0,1, ускорение грузов а = –1,2 м/с
Задача 17415 На разных склонах наклонной плоскости, образующих с горизонтом углы α1 = 65° и α2 = 35°, находятся грузы m1 = 4,8 кг и m2 = 5,6 кг. Нить, связывающая грузы, перекинута через легкий блок, укрепленный на вершине наклонной плоскости. Коэффициент трения между грузами и наклонной плоскостью равен 0,12, ускорение грузов а (а > 0, если система движется в сторону груза m
Задача 17440 На разных склонах наклонной плоскости, образующих с горизонтом углы α1 и α2, находятся грузы m1 и m2. Нить, связывающая грузы, перекинута через легкий блок, укрепленный на вершине наклонной плоскости. Коэффициент трения между грузами и плоскостью равен k, ускорение грузов a, (a>0, если система движется в сторону груза m
Задача 17441 На разных склонах наклонной плоскости, образующих с горизонтом углы α1 и α2, находятся грузы m1 и m2. Нить, связывающая грузы, перекинута через легкий блок, укрепленный на вершине наклонной плоскости. Коэффициент трения между грузами и плоскостью равен k, ускорение грузов a, (a>0, если система движется в сторону груза m
Задача 17442 На разных склонах наклонной плоскости, образующих с горизонтом углы α1 и α2, находятся грузы m1 и m2.
Задача 17443 На разных склонах наклонной плоскости, образующих с горизонтом углы α1 и α2, находятся грузы m1 и m2. Нить, связывающая грузы, перекинута через легкий блок, укрепленный на вершине наклонной плоскости. Коэффициент трения между грузами и плоскостью равен k, ускорение грузов a, (a>0, если система движется в сторону груза m2). Определить неизвестную величину. Дано: α
Задача 17444 На разных склонах наклонной плоскости, образующих с горизонтом углы α1 и α2, находятся грузы m1 и m2.
Задача 21538 Невесомый блок укреплен в вершине наклонной плоскости, образующей с горизонтом угол α = 30°. Гири 1 и 2 одинаковой массой m1 = m2 = 1 кг соединены нитью и перекинуты через блок. Найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Коэффициент трения гири о наклонную плоскость k = 0,1.
Задача 23731 В вагоне укреплен отвес (шарик массой m на нити). Какое направление примет отвес, когда вагон будет скатываться без трения с наклонной плоскости, образующей с горизонтом угол α (рис.
Задача 24138 На верхнем краю гладкой наклонной плоскости укреплен легкий блок, через который перекинута нить. На одном ее конце привязан груз с массой m1 = 0,2 кг, лежащий на наклонной плоскости. На другом конце висит груз с массой m2 = 1,0 кг. С каким ускорением а движутся грузы и каково натяжение Т нити? Наклонная плоскость образует с горизонтом угол α = 30°.
| ||||||||||||
7419. Верхний конец стального стержня длины l = 1 м и радиуса г = 0,5 см закреплен (рис. 41). Модуль Юнга стали Е = 196 ГПа. Найти удлинение А/ стержня, если к его середине и нижнему концу с помощью специального подвеса прикрепить грузы массы m = 400 кг каждый. Массой стержня пренебречь. 3 кг/м3. Какую силу давления испытывает каждый человек, если все несущие держат плиту за вершины треугольника? 3 кг/м3. Какую силу давления испытывает каждый человек, если все несущие держат плиту за вершины треугольника?
|
| 7424. Однородный полушар массы m1, имеющий радиус r, выпуклой стороной лежит на горизонтальной плоскости. На край полушара положен небольшой груз массы m2. Под каким углом к горизонту наклонен ограничивающий полушар круг? Расстояние от центра масс полушара до геометрического центра равно 3r/8. |
7425. Однородная пластина имеет форму полукруга радиуса r, соединенного с прямоугольником, имеющим основание, равное диаметру полукруга, и высоту h (рис. 39). Найти отношение h/r, если центр масс всей пластины совпадает с геометрическим центром полукруга (точкой С). Расстояние от центра масс полукруга C1 до его геометрического центра С равно 4r/3п.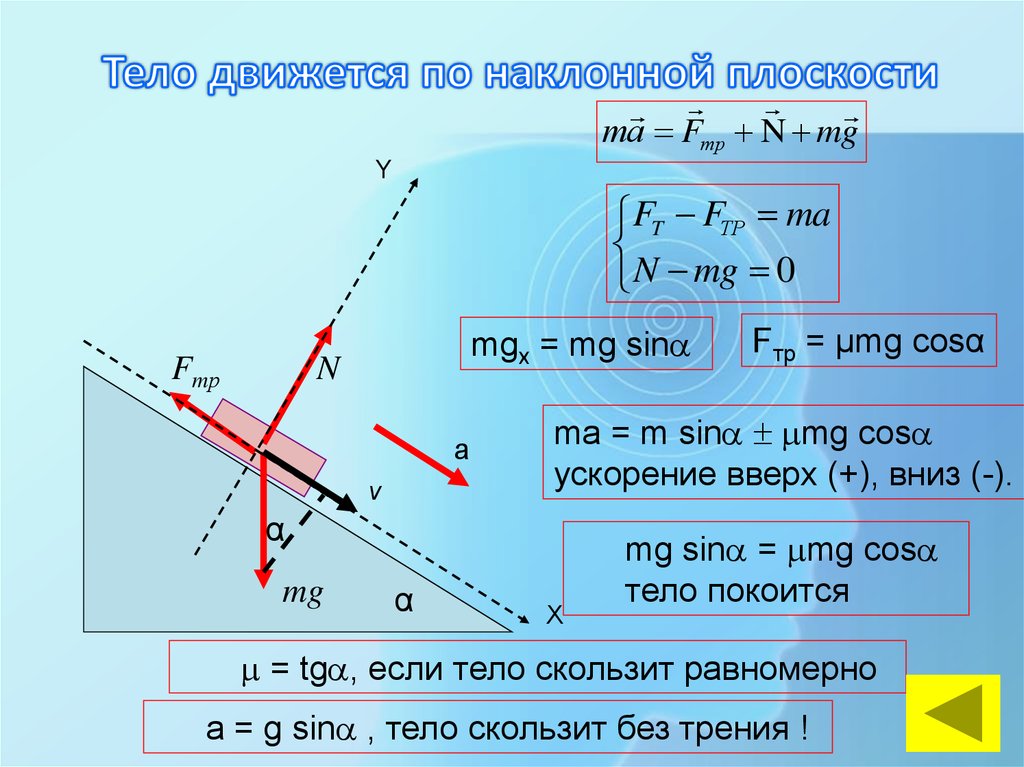 |
| 7429. Четыре однородных шара с массами m1 = 1 кг, m2 = 5 кг, m3 = 7 кг, m4 = 3 кг укреплены на невесомом стержне так, что их центры находятся на равных расстояниях d = 0,2 м друг от друга. На каком расстоянии х от центра третьего шара находится центр масс системы? |
| 7430. Два однородных кубика с массами m1 = 0,3 кг и m2 = 1,2 кг и длинами ребер l1 =0,08 м и l2 = 0,12 м соединены при помощи однородного стержня, имеющего массу m = 0,6 кг и длину d = 0,1 м. Концы стержня прикреплены к серединам граней кубиков, а центры кубиков лежат на продолжении оси стержня. Найти положение центра масс системы. |
| 7431. Две параллельные и противоположно направленные силы F1 = 10 Н и F2 = 25 Н приложены в точках А и В стержня, расположенных на расстоянии d=l,5 м друг от друга. Найти силу F, уравновешивающую силы F1 и F2, и точку ее приложения. |
7432.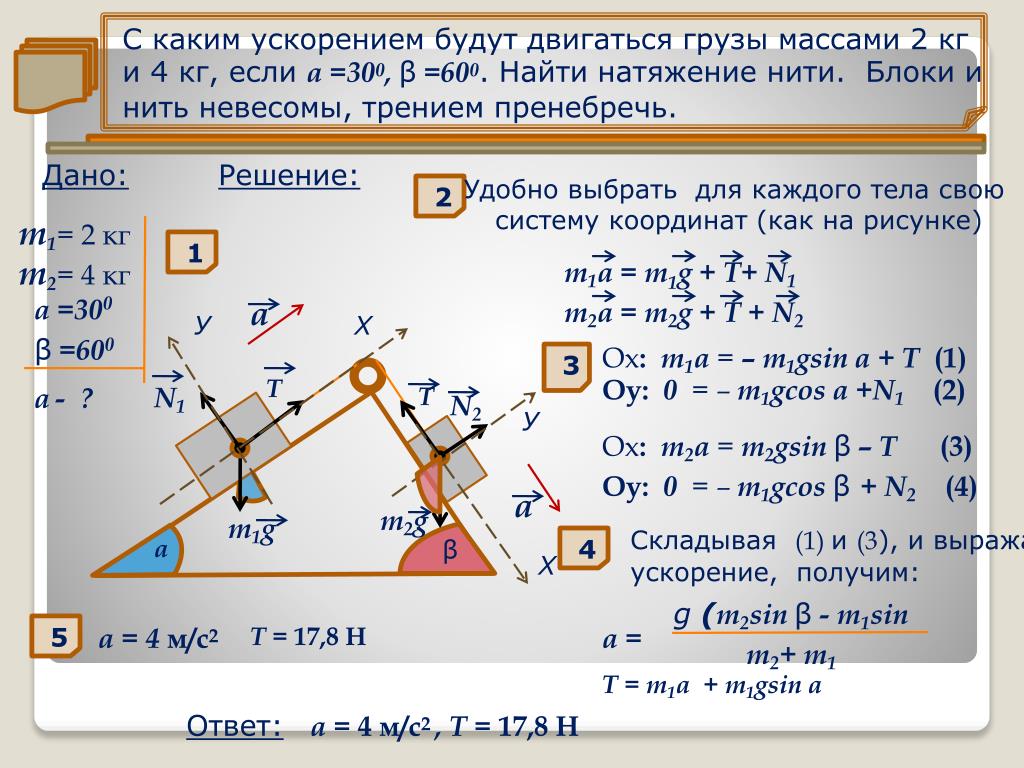 Две тонкие палочки с массами М и m соединены в систему, изображенную на рис. 38. Палочки могут вращаться без трения вокруг осей A и В, проходящих через нижние концы палочек. Верхние концы палочек сходятся под прямым углом так, что конец одной палочки лежит на торце другой (последний закруглен). Верхняя палочка массы М образует с горизонтом угол a. При каком минимальном коэффициенте трения к между палочками нижняя не упадет? Две тонкие палочки с массами М и m соединены в систему, изображенную на рис. 38. Палочки могут вращаться без трения вокруг осей A и В, проходящих через нижние концы палочек. Верхние концы палочек сходятся под прямым углом так, что конец одной палочки лежит на торце другой (последний закруглен). Верхняя палочка массы М образует с горизонтом угол a. При каком минимальном коэффициенте трения к между палочками нижняя не упадет?
|
| 7433. На плоском дне ящика находится шар. Дно ящика образует некоторый угол с горизонтом. Шар удерживается в равновесии нитью, параллельной дну (рис. 37). На какой максимальный угол а можно наклонить дно ящика, чтобы шар оставался в равновесии? Коэффициент трения между шаром и ящиком равен k. |
| 7434. К гладкой вертикальной стене на веревке длины l = 4 см подвешен шар массы m = 300 г и радиуса r = 2,5 см. Найти силу давления шара на стену. |
7435. Конец однородного стержня АС, имеющего массу m1, шарнирно закреплен на доске в точке А (рис. 36). К другому концу стержня привязана переброшенная через блок нить, на конце которой находится груз. Какова должна быть масса груза m2, для того чтобы отрезок нити ВС был горизонтальным, а стержень образовывал с доской угол а? Будет ли равновесие устойчивым? 36). К другому концу стержня привязана переброшенная через блок нить, на конце которой находится груз. Какова должна быть масса груза m2, для того чтобы отрезок нити ВС был горизонтальным, а стержень образовывал с доской угол а? Будет ли равновесие устойчивым?
|
| 7436. Дифференциальный ворот состоит из двух цилиндров с радиусами r1 = 0,2 м и r2 = 0,1 м, закрепленных на общей оси (рис. 35). На цилиндрах укреплен канат, который при вращении ворота наматывается на цилиндр большего диаметра и сматывается с цилиндра меньшего диаметра. На образуемой канатом петле подвешен блок. Какую силу F нужно приложить к рукоятке ворота длины l = 1 м, чтобы удерживать или равномерно поднимать груз массы m = 10 кг? |
7437. Тяжелый цилиндрический каток массы m необходимо поднять на ступеньку высоты h (рис. 34). Найти минимальную силу F, которую необходимо для этого приложить к центру масс катка в горизонтальном направлении, если радиус катка r больше высоты ступеньки h.
|
| 7438. Стержень массы m = 1,5 кг и длины l = 1 м одним концом шарнирно прикреплен к потолку. Стержень удерживается в отклоненном положении вертикальным шнуром, привязанным к свободному концу стержня. Найти силу натяжения Т шнура, если центр масс стержня находится на расстоянии а = 0,4 м от шарнира. |
| 7439. Две одинаковые тонкие дощечки с гладкими закругленными краями поставлены на стол и опираются друг на друга. Каждая дощечка образует с вертикалью угол а (рис. 33). Каким должен быть коэффициент трения к между дощечкой и столом, чтобы дощечки не падали? |
| 7440. Под каким минимальным углом а к горизонту может стоять лестница, прислоненная к гладкой вертикальной стене, если центр масс ее находится в середине? Коэффициент трения между лестницей и полом равен k. |
7441. К стене прислонена лестница массы m под углом а к вертикали. Центр масс лестницы находится на расстоянии 1/3 длины от ее верхнего конца. Какую горизонтальную силу F нужно приложить к середине лестницы, чтобы верхний конец ее не оказывал давления на стену? Какую горизонтальную силу F нужно приложить к середине лестницы, чтобы верхний конец ее не оказывал давления на стену?
|
| 7442. Два человека несут трубу массы m = 80 кг и длины l = 5 м. Первый человек поддерживает трубу на расстояний а = 1 м от ее конца, а второй держит противоположный конец трубы. Найти силу давления трубы, испытываемую каждым человеком. |
| 7443. Однородная балка лежит на платформе так, что один ее конец на 1/4 длины свешивается с. платформы. К свешивающемуся концу прилагают силу, направленную вертикально вниз. Когда эта сила становится равной F = 2000 Н, противоположный конец балки начинает подниматься. Найти массу балки. |
| 7444. Однородный стержень с прикрепленным на одном из его концов грузом массы m = 1,2 кг находится в равновесии в горизонтальном положении, если его подпереть на расстоянии 1/5 длины стержня от груза. Найти массу стержня М. |
7445. При взвешивании на неравноплечих рычажных весах масса тела (по сумме масс уравновешивающих гирь) на одной чаше весов оказалась равной m1 = 2,2 кг, а на другой — m2 = 3,8 кг. Найти истинную массу тела m. При взвешивании на неравноплечих рычажных весах масса тела (по сумме масс уравновешивающих гирь) на одной чаше весов оказалась равной m1 = 2,2 кг, а на другой — m2 = 3,8 кг. Найти истинную массу тела m.
|
| 7446. На кронштейне, изображенном на рис. 32, висит груз массы m = 100 кг. Найти силы натяжения стержней АВ и ВС, если они образуют угол а = 60°, а в точках A, В и С — шарниры. |
| 7447. К тросу длины l = 3 м, концы которого закреплены на одной высоте, на расстояниях а = 1 м от точек закрепления подвешены два груза массы m = 1 кг каждый. Провисание троса в средней части составило dl = 10 см. Найти силы натяжения Т1 Т2 и Т3 троса на каждом из трех участков. |
| 7448. Фонарь массы m = 20 кг подвешен на двух одинаковых тросах, образующих угол а = 120°. Найти силу натяжения T тросов. |
7449. Тонкая доска с двумя низкими опорными выступами на концах лежит на наклонной плоскости (рис. 31). При каком минимальном значении угла наклона а плоскости к горизонту доска начнет скользить по наклонной плоскости? Коэффициенты трения между нижней и верхней опорами и наклонной плоскостью равны k1 и k2. 31). При каком минимальном значении угла наклона а плоскости к горизонту доска начнет скользить по наклонной плоскости? Коэффициенты трения между нижней и верхней опорами и наклонной плоскостью равны k1 и k2.
|
| 7450. Деревянный брусок массы m = 2 кг лежит на наклонной плоскости, образующей с горизонтом угол а = 60°. С какой силой F, направленной перпендикулярно к плоскости, необходимо прижать брусок, чтобы он не соскользнул? Коэффициент трения между бруском и плоскостью k = 0,4. |
| 7451. Однородная линейка массы m на 1/3 длины выступает за край стола. Какую силу F нужно приложить, чтобы сдвинуть линейку вдоль ее длинной стороны? Коэффициент трения между линейкой и столом равен k. |
| 7452. С какой минимальной силой F, направленной горизонтально, нужно прижать плоский брусок массы m = 5 кг к стене, чтобы он не соскользнул вниз? Коэффициент трения между бруском и стеной k = 0,1. |
7453. Цилиндр двигателя внутреннего сгорания имеет внутренний диаметр D = 0,16 м. Число болтов, крепящих крышку цилиндра, n = 8. При сгорании горючей смеси развивается давление Р = 6 МПа. Найти диаметр d болтов, обеспечивающих десятикратный запас прочности. Допустимое напряжение в стали Р0 =150 МПа. Цилиндр двигателя внутреннего сгорания имеет внутренний диаметр D = 0,16 м. Число болтов, крепящих крышку цилиндра, n = 8. При сгорании горючей смеси развивается давление Р = 6 МПа. Найти диаметр d болтов, обеспечивающих десятикратный запас прочности. Допустимое напряжение в стали Р0 =150 МПа.
|
| 7454. В одном случае два человека тянут в противоположные стороны за концы канат с равными по модулю силами F. В другом случае один конец каната привязан к неподвижной опоре, а за другой его конец тянут два человека с теми же по модулю силами F. Какую силу натяжения испытывает канат в обоих случаях? |
| 7455. Снаряд летит по параболе и разрывается в верхней точке траектории на два разных осколка. Первый осколок упал вертикально вниз, второй — на расстоянии s по горизонтали от места разрыва. Найти скорость снаряд перед разрывом, если известно, что взрыв произошел на высоте h и время падения первого осколка равно t0. |
7456.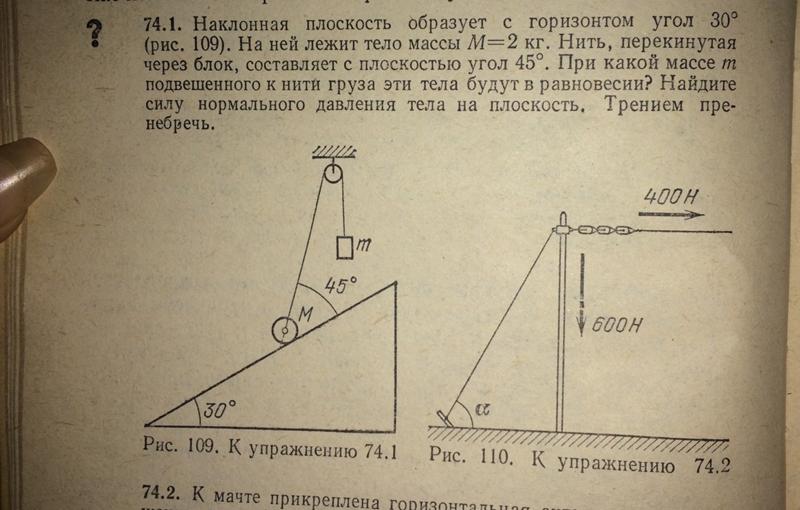 Снаряд вылетает из орудия со скоростью v0 под углом а к горизонту. В верхней точке траектории снаряд разрывается на два разных осколка, причем скорости осколков непосредственно после взрыва горизонтальны и лежат в плоскости траектории. Первый осколок упал на расстоянии s от орудия в направлении выстрела. Найти место падения второго осколка, если известно, что он упал дальше первого. Снаряд вылетает из орудия со скоростью v0 под углом а к горизонту. В верхней точке траектории снаряд разрывается на два разных осколка, причем скорости осколков непосредственно после взрыва горизонтальны и лежат в плоскости траектории. Первый осколок упал на расстоянии s от орудия в направлении выстрела. Найти место падения второго осколка, если известно, что он упал дальше первого.
|
| 7457. Человек массы m = 60 кг переходит с носа на корму лодки. На какое расстояние s переместится лодка длины l = 3 м, если ее масса М = 120 кг? |
| 7458. Поезд массы М = 500 т шел равномерно по горизонтальному пути. От поезда отцепился последний вагон массы m = 20 т. В момент, когда вагон остановился, расстояние между ним и поездом было s = 500 м. Какой путь l прошел вагон до остановки, если известно, что сила сопротивления движению пропорциональна силе тяжести и не зависит от скорости движения? |
7459. Три лодки массы М каждая движутся по инерции друг за другом с одинаковыми скоростями v. Из средней лодки в крайние одновременно перебрасывают грузы массы т каждый со скоростью и относительно лодок. Какие скорости v1, v2 и v3 будут иметь лодки после перебрасывания грузов? Три лодки массы М каждая движутся по инерции друг за другом с одинаковыми скоростями v. Из средней лодки в крайние одновременно перебрасывают грузы массы т каждый со скоростью и относительно лодок. Какие скорости v1, v2 и v3 будут иметь лодки после перебрасывания грузов?
|
| 7460. Две лодки движутся по инерции параллельными курсами навстречу друг другу. Когда лодки поравнялись, с одной из них на другую осторожно переложили груз массы m = 25 кг. После этого лодка с грузом остановилась, а лодка без груза продолжала двигаться со скоростью v = 8 м/с. С какими скоростями v1 и v2 двигались лодки до встречи, если масса лодки, в которую переложили груз, М = 1 т? |
7461. Ядро, летевшее горизонтально со скоростью v = 20 м/с, разорвалось на два осколка с массами m1 = 10 кг и m2 = 5 кг. Скорость меньшего осколка v2 = 90 м/с и направлена так же, как и скорость ядра до разрыва. Найти скорость v1 и направление движения большого осколка.
|
| 7462. С платформы массы М = 20 т, движущейся со скоростью u = 9 км/ч, производится выстрел из пушки. Снаряд массы m = 25 кг вылетает из орудия со скоростью v = 700 м/с. Найти скорости платформы непосредственно после выстрела: если направления движения платформы и выстрела совпадают; если эти направления противоположны. |
| 7463. По горизонтальным рельсам со скоростью v = 20 км/ч движется платформа массы М = 200 кг. На нее вертикально падает камень массы m = 50 кг и движется в дальнейшем вместе с платформой. Через некоторое время в платформе открывается люк, и камень проваливается вниз. С какой скоростью и движется после этого платформа? Трением пренебречь. |
7464. Ракета, имеющая вместе с зарядом массу М = 250 г, взлетает вертикально вверх и достигает высоты h — 150 м. Масса заряда m = 50 г. Найти скорость v истечения газов из ракеты, считая, что сгорание заряда происходит мгновенно.
|
| 7465. Навстречу платформе с песком, движущейся со скоростью v, по гладкому наклонному желобу соскальзывает без начальной скорости тело массы m и застревает в песке. Желоб длины l образует с горизонтом угол а. Найти скорость u платформы после попадания в нее тела, если масса платформы равна М. |
| 7466. Тело массы М = 990 г лежит на горизонтальной поверхности. В него попадает пуля массы m = 10 г и застревает в нем. Скорость пули v = 700 м/с и направлена горизонтально. Какой путь s пройдет тело до остановки? Коэффициент трения между телом и поверхностью k = 0,05. |
7467. Два человека с массами m1 = 70 кг и m2 = 80 кг стоят на роликовых коньках друг против друга. Первый бросает второму груз массы m = 10 кг со скоростью, горизонтальная составляющая которой v = 5 м/с относительно земли. Найти скорость v1 первого человека после бросания груза и скорость v2 второго после того, как он поймает груз. Трением пренебречь. Трением пренебречь.
|
| 7468. Человек, стоящий на коньках на гладком льду реки, бросает камень массы m = 0,5 кг. Спустя время t = 2 с камень достигает берега, пройдя расстояние s = 20 м. С какой скоростью и начинает скользить конькобежец, если его масса М = 60 кг? Трением пренебречь. |
| 7469. Снаряд массы m = 50 кг, летящий со скоростью v = 800 м/с под углом а = 30° к вертикали, попадает в платформу с песком и застревает в нем. Найти скорость платформы и после попадания снаряда, если ее масса М = 16 т. |
| 7470. Орудие, имеющее массу ствола М = 500 кг, стреляет в горизонтальном направлении. Масса снаряда m = 5 кг, его начальная скорость v = 460 м/с. При выстреле ствол откатывается на расстояние s = 40 см. Найти среднюю силу торможения f, возникающую в механизме, тормозящем ствол. |
7471. Пушка, стоящая на гладкой горизонтальной площадке, стреляет под углом а = 30° к горизонту. Масса снаряда m = 20 кг, его начальная скорость v = 200 м/с. Какую скорость u приобретает пушка при выстреле, если ее масса М = 500 кг? Масса снаряда m = 20 кг, его начальная скорость v = 200 м/с. Какую скорость u приобретает пушка при выстреле, если ее масса М = 500 кг?
|
| 7472. Снаряд массы m = 20 кг, летевший горизонтально со скоростью v = 50 м/с, попадает в платформу с песком и застревает в песке. С какой скоростью u начнет двигаться платформа, если ее масса М = 10т? |
| 7473. Из орудия массы М = 3 т, не имеющего противооткатного устройства (ствол жестко скреплен с лафетом), вылетает в горизонтальном направлении снаряд массы m = 15 кг со скоростью v = 650 м/с. Какую скорость u получает орудие при отдаче? |
| 7474. Падающий вертикально шарик массы m = 200 г ударился об пол со скоростью v = 5 м/с и подпрыгнул на высоту h = 46 см. Найти изменение dр импульса шарика при ударе. |
7475. Мяч массы m = 150 г ударяется о гладкую стенку под углом а = 30° к ней и отскакивает без потери скорости. Найти среднюю силу F, действующую на мяч со стороны стенки, если скорость мяча v = 10 м/с, а продолжительность удара dt = 0,1 с. Найти среднюю силу F, действующую на мяч со стороны стенки, если скорость мяча v = 10 м/с, а продолжительность удара dt = 0,1 с.
|
| 7476. Какова средняя сила давления F на плечо при стрельбе из автомата, если масса пули m = 10 г, а скорость пули при вылете из ствола v = 300 м/с? Число выстрелов из автомата в единицу времени n = 300 мин-1. |
| 7477. С каким ускорением а должен ехать грузовик, чтобы бревно длины l и канат длины b, которым оно привязано к грузовику, составляли прямую линию (рис. 30)? Канат привязан к грузовику на высоте h от поверхности земли. |
| 7478. По тросу, образующему с горизонтом угол a, катится без трения блок, к которому подвешено ведро с водой. Высота воды в ведре равна h. Каково давление воды на дно ведра во время движения? |
7479. На наклонной плоскости, образующей с горизонтом угол а, находится бак с водой, имеющий массу m. С какой силой F, параллельной наклонной плоскости, нужно двигать бак, для того чтобы поверхность воды в баке была параллельна наклонной плоскости? Коэффициент трения между баком и наклонной плоскостью равен k. С какой силой F, параллельной наклонной плоскости, нужно двигать бак, для того чтобы поверхность воды в баке была параллельна наклонной плоскости? Коэффициент трения между баком и наклонной плоскостью равен k.
|
| 7480. На тележке, скатывающейся без трения с наклонной плоскости, установлен стержень с подвешенным на нити шариком массы m = 2 г. Найти силу натяжения Т нити, если плоскость образует с горизонтом угол а = 60°. |
| 7481. Доска массы М может двигаться без трения по наклонной плоскости, образующей с горизонтом угол а. С каким ускорением а и в каком направлении должен бежать по доске человек массы m, чтобы доска не соскальзывала с наклонной плоскости? |
| 7482. На наклонной плоскости, образующей угол а с горизонтом, стоит кубик массы m. Плоскость находится в лифте, движущемся с ускорением а, направленным вверх. Найти силу нормального давления кубика на плоскость. При каком коэффициенте трения k между кубиком и плоскостью кубик не будет соскальзывать вниз? |
7483. Шар массы m лежит в ящике, соскальзывающем без трения с наклонной плоскости. Плоскость образует с горизонтом угол ос. Найти силы, с которыми шар давит на переднюю стенку и на дно ящика. Шар массы m лежит в ящике, соскальзывающем без трения с наклонной плоскости. Плоскость образует с горизонтом угол ос. Найти силы, с которыми шар давит на переднюю стенку и на дно ящика.
|
| 7484. Три груза с массами m1, m2 и m3 связаны нитью, перекинутой через блок, установленный на наклонной плоскости (рис. 29). Плоскость образует с горизонтом угол а. Начальные скорости грузов равны нулю. Найти силу натяжения Т нити, связывающей грузы, находящиеся на наклонной плоскости. Коэффициент трения между грузами и плоскостью равен k. |
| 7485. Два тела с массами m1 = 10 г и m2 = 15 г связаны нитью, перекинутой через блок, установленный на наклонной плоскости (рис. 28).Плоскость образует с горизонтом угол а = 30°. Найти ускорение, скоторым будут двигаться эти тела. |
7486. На гладкой наклонной плоскости, образующей угол а = 30° с горизонтом, находится тело массы m = 50 кг, на которое действует горизонтально направленная сила F = 294 Н (рис. 27). Найти ускорение а тела и силу Fн.д., с которой тело давит на плоскость. 27). Найти ускорение а тела и силу Fн.д., с которой тело давит на плоскость.
|
| 7487. По склону горы, имеющей длину l = 50 м и высоту h — 10 м, на веревке спускают без начальной скорости санки массы m = 60 кг. Найти силу натяжения Т веревки, если санки у основания горы имеют скорость v = 5 м/с, а сила трения f между санками и поверхностью горы составляет 10% силы тяжести, действующей на санки. |
| 7488. Тело начинает движение с начальной скоростью v0 вверх по наклонной плоскости, образующей с горизонтом угол a. Через какой промежуток времени t тело вернется в точку, из которой оно начало двигаться вверх? Коэффициент трения между телом и плоскостью k < tg а. |
7489. С вершины наклонной плоскости, имеющей длину l = 10 м и высоту h = 5м, начинает двигаться без начальной скорости тело. Какое время l будет продолжаться движение тела до основания наклонной плоскости и какую скорость v оно будет иметь при этом? Коэффициент трения между телом и плоскостью k = 0,2.
|
| 7490. Найти ускорение а тела, соскальзывающего с наклонной плоскости, образующей с горизонтом угол а = 30°. Коэффициент трения между телом и плоскостью k = 0,3. |
| 7491. Найти силу натяжения Т нити в устройстве, изображенном на рис. 26, если массы тел m1 = 100 г и m2 = 300 г. |
| 7492. С каким ускорением a и b каком направлении будет перемещаться центр масс двух грузов с массами m1 и m2 (m1 < m2), если эти грузы связаны нитью, перекинутой через блок? |
| 7493. Два тела массы m = 100 г каждое подвешены на концах нити, перекинутой через блок. На одно из тел положен груз массы m0 = 50 г. С какой силой Fн.д. будет давить груз на тело, на котором он лежит, когда вся система придет в движение? |
| 7494. Два тела массы m = 240 г каждое подвешены на концах нити, перекинутой через блок. Какую массу m0 должен иметь груз, положенный на одно из тел, чтобы каждое из них прошло за время t = 4 с путь h = 160 см? |
7495. Две гири с массами m1 = 3 кг и m2 = 6,8 кг висят на концах нити, перекинутой через блок. Первая гиря находится на 2 м ниже второй. Гири пришли в движение без начальной скорости. Через какое время t они окажутся на одной высоте? Две гири с массами m1 = 3 кг и m2 = 6,8 кг висят на концах нити, перекинутой через блок. Первая гиря находится на 2 м ниже второй. Гири пришли в движение без начальной скорости. Через какое время t они окажутся на одной высоте?
|
| 7496. На одном конце нити, перекинутой через блок, подвешено тело массы m1 = 30 г. Другой конец нити соединен с легкой пружиной, к концу которой прикреплено тело массы m2 = 50 г. Длина пружины в нерастянутом состоянии l0 = 10 см. Под действием силы F = 0,1 Н пружина удлиняется; ее деформация dl = 2 см. Найти длину l пружины во время движения грузов, считая, что колебания в системе отсутствуют. |
| 7497. На одном конце нити, перекинутой через блок, подвешен груз массы m = 500 г. Известно, что нить не обрывается, если на другом ее конце закрепить груз массы М = 1 т и осторожно отпустить его. Какую силу натяжения Т выдерживает в этом случае нить? |
7498. Через блок, подвешенный к динамометру, перекинут шнур, на концах которого укреплены грузы с массами m1 = 2 кг и m2 = 8 кг. Что показывает динамометр при движении грузов? Что показывает динамометр при движении грузов?
|
| 7499. К одному концу веревки, перекинутой через блок, подвешен груз массы m = 10 кг (рис. 25). С какой силой F нужно тянуть вниз за другой конец веревки, чтобы груз поднимался с ускорением а = 1 м/с2? |
| 7500. На брусок массы m1 = 0,18 кг поставлена гиря массы m2 = 2 кг (рис. 24). С помощью нити, перекинутой через блок , брусок с гирей скользит с постоянной скоростью на доске, когда на чашку массы m3 = 0,18 кг положена гиря массы m4 = 0,5 кг. Найти коэффициент трения к между бруском и доской. |
| 7501. Три тела связаны нитью и лежат на гладкой горизонтальной поверхности. К телу массы m1 приложена сила F1, направленная вдоль поверхности, а к телу массы m3 — сила F2 > Fu направленная в противоположную сторону (рис. 23). Найти силу натяжения Т нити между телами с массами m1 и m2. |
7502. Два тела связаны нитью и лежат на гладкой горизонтальной поверхности. К телу массы m1 приложена сила F1, направленная вдоль поверхности, а к телу массы m2 — сила F2<F1, направленная в противоположную сторону. Найти силу натяжения Т нити при движении тел. К телу массы m1 приложена сила F1, направленная вдоль поверхности, а к телу массы m2 — сила F2<F1, направленная в противоположную сторону. Найти силу натяжения Т нити при движении тел.
|
| 7503. Два тела с массами m1 = 50 г и m2 = 100 г связаны нитью и лежат на гладкой горизонтальной поверхности (рис. 22). С какой р силой F можно тянуть первое тело,чтобы нить, способная выдержать силу натяжения Tmах = 5 Н, не оборвалась? Изменится ли результат, если силу приложить ко второму телу? |
| 7504. Сила сопротивления f, действующая на раскрытый парашют, пропорциональна квадрату скорости (коэффициент пропорциональности к = 20 Н • с2/м2). Масса парашютиста m = 72 кг. С какой высоты h должен спрыгнуть человек без парашюта, чтобы скорость его приземления равнялась скорости приземления парашютиста, прыгнувшего с большой высоты? |
| 7505. Какая минимальная сила сопротивления f воздуха действует на парашютиста и парашют общей массы m = 75 кг при полностью раскрытом парашюте? |
7506. Акробат массы m = 70 кг прыгнул с трапеции на натянутую сетку, которая при этом прогнулась на расстояние dh = 1 м. Высота трапеции над сеткой h = 6 м. С каким ускорением а двигался акробат, прогибая сетку, и с какой силой реакции N сетка действовала на тело акробата? Акробат массы m = 70 кг прыгнул с трапеции на натянутую сетку, которая при этом прогнулась на расстояние dh = 1 м. Высота трапеции над сеткой h = 6 м. С каким ускорением а двигался акробат, прогибая сетку, и с какой силой реакции N сетка действовала на тело акробата?
|
| 7507. Тело массы m = 40 г, брошенное вертикально вверх с начальной скоростью v0 = 30 м/с, достигло высшей точки подъема спустя время t = 2,5 с. Найти среднюю силу сопротивления f воздуха, действовавшую на тело во время полета. |
| 7508. Какой путь s за время t пройдет «юзом» воз массы m, если щука и рак тянут его в противоположные стороны по горизонтали с силами F1 и F2, лебедь тянет с силой F3 в ту же сторону, что и рак, но под углом а к горизонту? Коэффициент трения между колесами и поверхностью земли равен k. Начальная скорость воза v0 = 0. |
7509. Тело массы m движется вверх по вертикальной стене под действием силы F, направленной под углом а к вертикали (рис. 21). Найти ускорение а тела. Коэффициент трения между телом и стеной равен k. 21). Найти ускорение а тела. Коэффициент трения между телом и стеной равен k.
|
| 7510. Тело массы т движется по горизонтальной поверхности под действием силы F, направленной под углом а к горизонту (рис. 20). Найти ускорение а тела. При какой силе F0 движение будет равномерным? Коэффициент трения между телом и плоскостью равен k. |
| 7511. На горизонтальной доске лежит груз. Какое ускорение а в горизонтальном направлении следует сообщить доске, чтобы груз соскользнул с нее? Коэффициент трения между грузом и доской k = 0,2. |
| 7512. На горизонтальной поверхности лежит доска массы М = 10 кг, а на доске — брусок массы m = 1 кг. Какую минимальную силу F в горизонтальном направлении надо приложить к доске, чтобы брусок соскользнул с нее? Коэффициент трения между бруском и доской k = 0,1. |
7513. Камень, скользящий по горизонтальной поверхности, остановился, пройдя расстояние s = 20,4 м.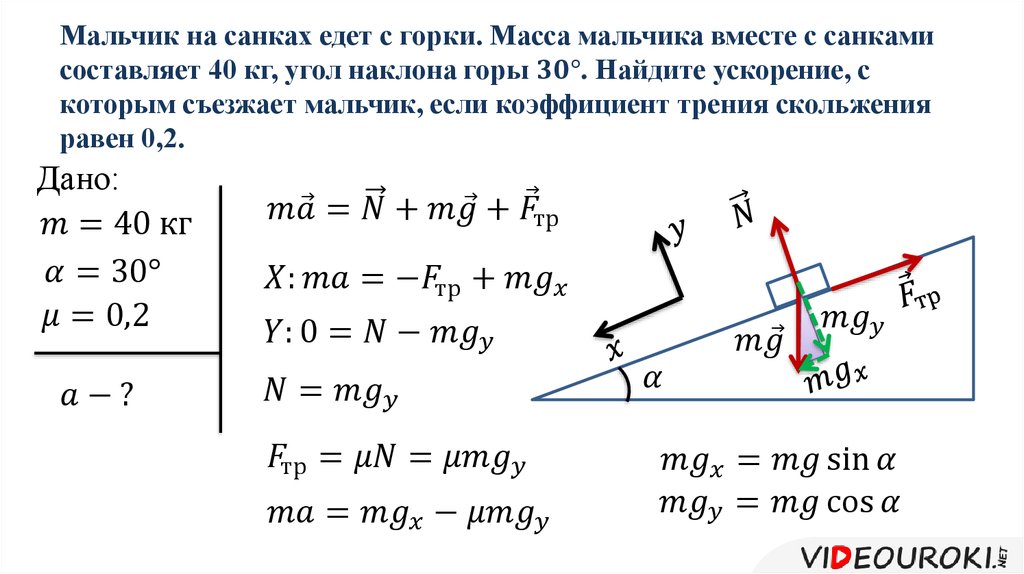 Найти начальную скорость камня v. Сила трения f между камнем и поверхностью составляет 6% силы тяжести, действующей на камень. Найти начальную скорость камня v. Сила трения f между камнем и поверхностью составляет 6% силы тяжести, действующей на камень.
|
| 7514. При быстром торможении трамвай, имевший скорость v = 25 км/ч, начал двигаться «юзом» (заторможенные колеса, не вращаясь, начали скользить по рельсам). Какой участок пути s пройдет трамвай с момента начала торможения до полной остановки? Коэффициент трения между колесами и рельсами k = 0,2. |
| 7515. Какая горизонтальная сила F требуется, чтобы тело массы т = 2 кг, лежащее на горизонтальной поверхности, начало скользить по ней с ускорением а = 0,2 м/с2? Коэффициент трения между телом и поверхностью k = 0,02. |
| 7516. В лифте установлен динамометр, на котором подвешено тело массы m = 1 кг. Что будет показывать динамометр, если: 1) лифт движется вверх с ускорением a1 = 4,9 м/с2; 2) лифт движется вверх замедленно с ускорением a2 = 4,9 м/с2; 3) лифт движется вниз с ускорением a3 = 2,45 м/с2; 4) лифт движется вниз замедленно с ускорением a4 = 2,45 м/с2? |
7517. Груз массы m = 140 кг, лежащий на полу кабины опускающегося лифта, давит на пол с силой Fн.д. = 1440 Н. Найти ускорение лифта и его направление. Груз массы m = 140 кг, лежащий на полу кабины опускающегося лифта, давит на пол с силой Fн.д. = 1440 Н. Найти ускорение лифта и его направление.
|
| 7518. С какой силой Fн.д. будет давить на дно шахтной клети груз массы m = 100 кг, если клеть поднимается с ускорением а = 24,5 м/с2? |
Шестигранный карандаш, помещенный на наклонную плоскость с наклоном α под прямым углом к образующей — Sarthaks eConnect
← Предыдущий вопрос Следующий вопрос →
1 ответ
+1 голос
ответил к Санскар (34,1 тыс. баллов)выбрано Викаш Кумар
Лучший ответ
По условию коэффициент трения скольжения между карандашом и наклонной плоскостью удовлетворяет условию μ ≥ tan α Действительно, карандаш, поставленный под прямым углом к образующей, находится в равновесии, а это означает, что mg sin α = F fr , где mg — сила тяжести, а F fr — сила притяжения трение.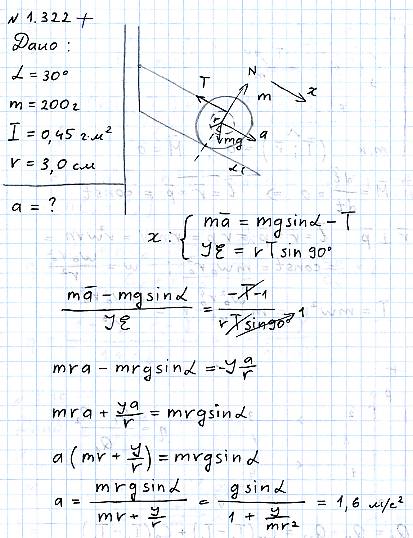 Но F fr ≤ мкм g cos α. Следовательно, mg sin α ≤ μ mg cos α, откуда μ ≥ tan α. Таким образом, карандаш не будет скользить по наклонной плоскости ни при каком значении угла φ.
Но F fr ≤ мкм g cos α. Следовательно, mg sin α ≤ μ mg cos α, откуда μ ≥ tan α. Таким образом, карандаш не будет скользить по наклонной плоскости ни при каком значении угла φ.
Карандаш может начать скатываться под углом φ таким, что вектор силы тяжести
«выходит» из области контакта карандаша с наклонной плоскостью (заштрихованная область на рис. 183). Чтобы найти этот угол, проецируем центр масс карандаша (точка А) на наклонную плоскость и отмечаем точку пересечения вертикали, проходящей через центр масс, и наклонной плоскости (точка В). Очевидно, что точки А и В будут покоиться при разных ориентациях карандаша, если его центр масс остается неподвижным. В этом случае AB = 2l cos 30° tan α, где 2l — сторона шестиугольного сечения карандаша, а 2l cos 30° — радиус окружности, вписанной в шестиугольное сечение.
Пока точка B находится в заштрихованной области, карандаш не будет скатываться по плоскости. Запишем условие начала скатывания
Таким образом, если угол φ удовлетворяет условию
, карандаш остается в равновесии. Выражение для угла φ 0 имеет смысл при условии, что tan α > 1/√3. Тот факт, что карандаш, поставленный параллельно образующей, скатывается вниз, указывает на то, что tan α > 1/√3 (докажите это).
Выражение для угла φ 0 имеет смысл при условии, что tan α > 1/√3. Тот факт, что карандаш, поставленный параллельно образующей, скатывается вниз, указывает на то, что tan α > 1/√3 (докажите это).
← Предыдущий вопрос Следующий вопрос →
Похожие вопросы
Утверждение I: Работа, совершаемая при перемещении тела по гладкой наклонной плоскости, не зависит от наклона наклонной плоскости, если ее высота одинакова.
спросил 31 июля 2019 г. в свойствах твердых тел и жидкостей к Нисуб (71,3 тыс. баллов)
- механика
- джи
- электросеть
Частица брошена по линии наибольшего наклона на шероховатую плоскость, наклоненную под углом 45º
спросил 30 июля 2019 г. в свойствах твердых тел и жидкостей к пия (79,6 тыс. баллов)
- механика
- джи
- электросеть
Тонкий обод массой m и радиусом r скатывается по наклонной плоскости с уклоном a, наматывая при этом тонкую ленту
спросил
8 января 2019 г. в свойствах твердых тел и жидкостей
к
Сахилк
(23,8 тыс. баллов)
в свойствах твердых тел и жидкостей
к
Сахилк
(23,8 тыс. баллов)
- механика
- джи
- электросеть
Утверждение I: Если тела скользят по наклонной плоскости без качения, то все тела достигают дна одновременно.
спросил 31 июля 2019 г. в свойствах твердых тел и жидкостей к Нисуб (71,3 тыс. баллов)
- механика
- джи
- электросеть
Катушка с намотанной на нее нитью уложена на гладкую наклонную плоскость, поставленную под углом 30°
спросил 31 июля 2019 г. в свойствах твердых тел и жидкостей к Нисуб (71,3 тыс. баллов)
- механика
- джи
- электросеть
Категории
- Все категории
- JEE
(30,8к)
- Физика
(8,5к)
- Физика и измерения (40)
- Кинематика (727)
- Законы движения (513)
- Работа, энергия и сила (307)
- Вращательное движение (215)
- Гравитация (569)
- Свойства твердых тел и жидкостей (301)
- Термодинамика (111)
- Кинетическая теория газов (10)
- Колебания и волны (45)
- Электростатика (593)
- Текущее электричество (618)
- Магнитные эффекты тока и магнетизма (45)
- Электромагнитная индукция и переменные токи (29)
- Оптика (71)
- Двойственная природа материи и излучения (8)
- Атомы и ядра (9)
- Электронные устройства (45)
- Система связи (102)
- Экспериментальные навыки (2)
- Химия (8,4к)
- Математика (12,8к)
- Физика
(8,5к)
- NEET
(8.
 6к)
6к) - Наука (761к)
- Математика (247к)
- Статистика (2,9к)
- Наука об окружающей среде (5,2к)
- Биотехнология (660)
- коммерция (71,7к)
- Электроника (3,8к)
- Компьютер (19,5к)
- Искусственный интеллект (ИИ) (1,4к)
- Информационные технологии (14,2к)
- Программирование (10,2к)
- Политическая наука (7,7к)
- Домашняя наука (7,7к)
- Психология (3,9к)
- Социология (6,7к)
- Английский (63,6к)
- хинди (25,7к)
- Способность (23,7к)
- Рассуждение (14,6к)
- ГК (25,7к)
- Олимпиада (530)
- Советы по навыкам (84)
- CBSE (756)
- РБСЭ (49,1к)
- Общий (63,8к)
- МСБШСЭ (1,8к)
- Совет Тамилнаду (59,3к)
- Совет Кералы (24,5к)
5.4 Наклонные плоскости | Техасский шлюз
Цели обученияСтатическое и кинетическое трениеРабота с наклонными плоскостямиПроверьте свое понимание
Цели обучения
К концу этого раздела вы сможете делать следующее:
- Различать статическое трение и кинетическое трение
- Решение задач на наклонные плоскости
Статическое и кинетическое трение
Вспомним из предыдущей главы, что трение — это сила, противодействующая движению и постоянно присутствующая вокруг нас. Трение позволяет нам двигаться, в чем вы убедились, если когда-нибудь пробовали ходить по льду.
Существуют различные виды трения — кинетическое и статическое. Кинетическое трение действует на движущийся объект, а статическое трение действует на объект или систему в состоянии покоя. Максимальное статическое трение обычно больше, чем кинетическое трение между объектами.
Представьте, например, что вы пытаетесь сдвинуть тяжелый ящик по бетонному полу. Вы можете давить на ящик все сильнее и сильнее и вообще не двигать его. Это означает, что статическое трение реагирует на то, что вы делаете — оно увеличивается, чтобы быть равным вашему толчку и в противоположном направлении. Но если вы, наконец, нажмете достаточно сильно, ящик, кажется, внезапно соскользнет и начнет двигаться. Начав движение, его легче поддерживать в движении, чем было запустить, потому что кинетическая сила трения меньше, чем статическая сила трения. Если бы вы добавили массу к ящику (например, поместив на него коробку), вам пришлось бы толкать его еще сильнее, чтобы он начал двигаться, а также чтобы он продолжал двигаться. Если, с другой стороны, вы смазали бетон маслом, вам будет легче запустить ящик и поддерживать его в рабочем состоянии.
Но если вы, наконец, нажмете достаточно сильно, ящик, кажется, внезапно соскользнет и начнет двигаться. Начав движение, его легче поддерживать в движении, чем было запустить, потому что кинетическая сила трения меньше, чем статическая сила трения. Если бы вы добавили массу к ящику (например, поместив на него коробку), вам пришлось бы толкать его еще сильнее, чтобы он начал двигаться, а также чтобы он продолжал двигаться. Если, с другой стороны, вы смазали бетон маслом, вам будет легче запустить ящик и поддерживать его в рабочем состоянии.
На рис. 5.35 показано, как возникает трение на границе раздела двух объектов. Увеличение этих поверхностей показывает, что они являются шероховатыми на микроскопическом уровне. Поэтому, когда вы нажимаете, чтобы заставить объект двигаться (в данном случае ящик), вы должны поднимать объект до тех пор, пока он не сможет прыгать вместе с ударами только кончиками поверхности, отламывать точки или делать и то, и другое. Чем сильнее прижимаются поверхности друг к другу (например, если на ящик кладут еще одну коробку), тем больше усилий требуется для их перемещения.
Рисунок 5.35 Силы трения, такие как f , всегда препятствуют движению или попытке движения между соприкасающимися объектами. Трение возникает отчасти из-за шероховатости соприкасающихся поверхностей, как видно на увеличенном виде.
Величина силы трения имеет две формы: одна для статического трения, другая для кинетического трения. Когда между объектами нет движения, величина трения покоя f с равна
fs≤μsNs,fs≤μsNs,
, где μs μs — коэффициент трения покоя, а Н — величина нормальной силы. Напомним, что нормальная сила противодействует силе тяжести и действует перпендикулярно поверхности в этом примере, но не всегда.
Поскольку символ ≤ ≤ означает меньше или равно, это уравнение говорит, что трение покоя может иметь максимальное значение мксН. мксН. То есть
fs(max)=µsN.fs(max)=µsN.
Статическое трение представляет собой реактивную силу, которая увеличивается, чтобы быть равной и противоположной любой прилагаемой силе, вплоть до ее максимального предела. Когда приложенная сила превышает f с(макс.), объект будет двигаться. Когда объект движется, величина кинетического трения f k определяется выражением
Когда приложенная сила превышает f с(макс.), объект будет двигаться. Когда объект движется, величина кинетического трения f k определяется выражением
fk=µkN.fk=µkN.
где μkμk — коэффициент кинетического трения.
Трение варьируется от поверхности к поверхности, потому что разные вещества более шероховатые, чем другие. В таблице 5.2 сравниваются значения статического и кинетического трения для различных поверхностей. Коэффициент трения зависит от двух соприкасающихся поверхностей.
| Система | Статическое трение мкс мкс | Кинетическое трение мкк мкк |
| Резина на сухом бетоне | 1,0 | 0,7 |
| Резина на мокром бетоне | 0,7 | 0,5 |
| Дерево на дереве | 0,5 | 0,3 |
| Вощеная древесина на мокром снегу | 0,14 | 0,1 |
| Металл на дереве | 0,5 | 0,3 |
| Сталь по стали (сухая) | 0,6 | 0,3 |
| Сталь по стали (промасленный) | 0,05 | 0,03 |
| Тефлон на стали | 0,04 | 0,04 |
| Кость, смазанная синовиальной жидкостью | 0,016 | 0,015 |
| Туфли на дереве | 0,9 | 0,7 |
| Обувь на льду | 0,1 | 0,05 |
| Лед на льду | 0,1 | 0,03 |
| Сталь на льду | 0,4 | 0,02 |
Таблица 5.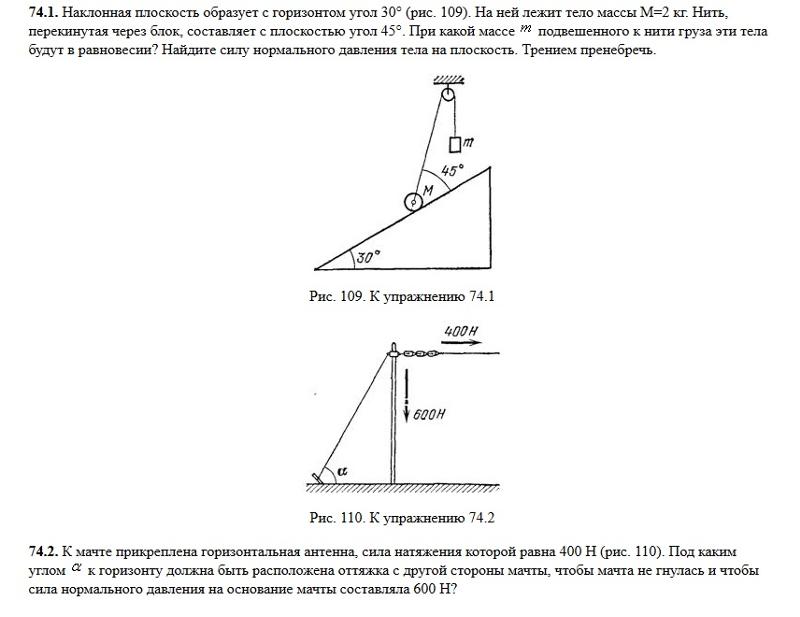 2 Коэффициенты статического и кинетического трения
2 Коэффициенты статического и кинетического трения
Поскольку направление трения всегда противоположно направлению движения, трение происходит параллельно поверхности между объектами и перпендикулярно нормальной силе. Например, если ящик, который вы пытаетесь толкнуть (с усилием, параллельным полу), имеет массу 100 кг, то нормальная сила будет равна его весу
Вт=мг=(100 кг)(9,80 м/с2)=980 Н, Вт=мг=(100 кг)(9,80 м/с2)=980 Н,
перпендикулярно полу. Если бы коэффициент статического трения был равен 0,45, вам пришлось бы приложить параллельную полу силу, превышающую
.фс(макс)=мксN=(0,45)(980 Н)=440 Нфс(макс)=мксN=(0,45)(980 Н)=440 Н
для перемещения ящика. Когда есть движение, трение меньше, а коэффициент кинетического трения может быть 0,30, так что сила всего 290 Н
fk=µkN=(0,30)(980 N)=290 Nfk=µkN=(0,30)(980 N)=290 N
будет поддерживать его движение с постоянной скоростью. Если бы пол был смазан, оба коэффициента были бы намного меньше, чем без смазки. Коэффициент трения не имеет единиц измерения и обычно представляет собой число от 0 до 1,0.
Коэффициент трения не имеет единиц измерения и обычно представляет собой число от 0 до 1,0.
Работа с наклонными плоскостями
Ранее мы обсуждали, что когда объект лежит на горизонтальной поверхности, на него действует нормальная сила, равная по величине его весу. До сих пор мы имели дело только с нормальной силой в одном измерении, с гравитацией и нормальной силой, действующими перпендикулярно поверхности в противоположных направлениях (гравитация направлена вниз, а нормальная сила направлена вверх). Теперь, когда у вас есть навыки работы с силами в двух измерениях, мы можем исследовать, что происходит с весом и нормальной силой на наклонной поверхности, такой как наклонная плоскость. Для задач с наклонной плоскостью легче разбить силы на составляющие, если мы повернем систему координат, как показано на рис. 5.36. Первым шагом при постановке задачи является разложение силы веса на составляющие.
Рис. 5.36 На диаграмме показаны перпендикулярная и горизонтальная составляющие веса на наклонной плоскости.
Когда объект покоится на наклонной плоскости, составляющей угол θ θ с горизонталью, сила тяжести, действующая на объект, делится на две составляющие: сила, действующая перпендикулярно плоскости, w⊥ w⊥, и сила, действующая параллельно на плоскость, w|| ш||. Перпендикулярная сила веса, w⊥ w⊥, обычно равна по величине и противоположна по направлению нормальной силе, N. N. Сила, действующая параллельно плоскости, w|| w||, заставляет объект ускоряться вниз по склону. Сила трения f f противодействует движению объекта, поэтому она действует вверх по плоскости.
Важно соблюдать осторожность при разложении веса объекта на составляющие. Если угол наклона находится под углом θ θ к горизонтали, то величины компонентов веса равны
w||=wsin(θ)=mgsin(θ) и w||=wsin(θ)=mgsin(θ) и
w⊥=wcos(θ)=mgcos(θ).w⊥=wcos(θ) = мгкос(θ).
Вместо того, чтобы запоминать эти уравнения, полезно уметь определять их разумом. Для этого нарисуйте прямоугольный треугольник, образованный тремя весовыми векторами. Обратите внимание, что угол наклона такой же, как угол, образованный между w w и w⊥ w⊥. Зная это свойство, можно с помощью тригонометрии определить величину весовых составляющих
Обратите внимание, что угол наклона такой же, как угол, образованный между w w и w⊥ w⊥. Зная это свойство, можно с помощью тригонометрии определить величину весовых составляющих
cos(θ)=w⊥ww⊥=wcos(θ)=mgcos(θ)cos(θ)=w⊥ww⊥=wcos(θ)=mgcos(θ)
sin(θ)=w||ww ||=wsin(θ)=mgsin(θ).sin(θ)=w||ww||=wsin(θ)=mgsin(θ).
Watch Physics
Компоненты силы в наклонной плоскости
В этом видео показано, как вес объекта на наклонной плоскости разбивается на составляющие, перпендикулярные и параллельные поверхности плоскости. Он объясняет геометрию для нахождения угла более подробно.
Нажмите, чтобы просмотреть содержимое
Проверка захвата
В этом видеоролике показано, как вес объекта на наклонной плоскости разбивается на составляющие, перпендикулярные и параллельные поверхности плоскости. Он объясняет геометрию для нахождения угла более подробно.
Когда поверхность плоская, можно сказать, что одна из составляющих гравитационной силы равна нулю; Который из? Что происходит с величинами перпендикулярной и параллельной составляющих гравитационной силы по мере увеличения угла наклона?
- Когда угол равен нулю, параллельная составляющая равна нулю, а перпендикулярная составляющая максимальна. По мере увеличения угла параллельная составляющая уменьшается, а перпендикулярная составляющая увеличивается. Это связано с тем, что косинус угла уменьшается, а синус угла увеличивается.
- Когда угол равен нулю, параллельная составляющая равна нулю, а перпендикулярная составляющая максимальна. По мере увеличения угла параллельная составляющая уменьшается, а перпендикулярная составляющая увеличивается. Это связано с тем, что косинус угла увеличивается, а синус угла уменьшается.
- Когда угол равен нулю, параллельная составляющая равна нулю, а перпендикулярная составляющая максимальна.
 По мере увеличения угла параллельная составляющая увеличивается, а перпендикулярная составляющая уменьшается. Это связано с тем, что косинус угла уменьшается, а синус угла увеличивается.
По мере увеличения угла параллельная составляющая увеличивается, а перпендикулярная составляющая уменьшается. Это связано с тем, что косинус угла уменьшается, а синус угла увеличивается. - Когда угол равен нулю, параллельная составляющая равна нулю, а перпендикулярная составляющая максимальна. По мере увеличения угла параллельная составляющая увеличивается, а перпендикулярная составляющая уменьшается. Это связано с тем, что косинус угла увеличивается, а синус угла уменьшается.
Tips For Success
Нормальная сила представлена переменной N. N. Не следует путать с символом ньютона, который также обозначается буквой N. Важно различать эти символы, тем более что единицами нормальной силы (NN) являются ньютоны (N). Например, нормальная сила, Н Н, с которой пол действует на стул, может быть Н=100 Н. Н=100 Н. Одно важное отличие состоит в том, что нормальная сила — это вектор, а ньютон — это просто единица измерения. Будьте осторожны, чтобы не перепутать эти буквы в своих вычислениях!
Будьте осторожны, чтобы не перепутать эти буквы в своих вычислениях!
Для обзора, процесс решения задач наклонной плоскости выглядит следующим образом:
- Нарисуйте эскиз задачи.
- Определите известные и неизвестные величины и определите интересующую систему.
- Нарисуйте диаграмму свободного тела (это эскиз, показывающий все силы, действующие на объект) с системой координат, повернутой под тем же углом, что и наклонная плоскость. Разделите векторы на горизонтальную и вертикальную составляющие и нарисуйте их на диаграмме свободного тела.
- Запишите второй закон Ньютона в горизонтальном и вертикальном направлениях и сложите силы, действующие на объект. Если объект не ускоряется в определенном направлении (например, в направлении x ), то F net x = 0. Если объект ускоряется в этом направлении, F net x = м и .

- Проверьте свой ответ. Разумный ли ответ? Единицы правильные?
Рабочий пример
Определение коэффициента кинетического трения на наклонной плоскости
Лыжник массой 62 кг, изображенный на рис. 5.37(а), скользит по заснеженному склону под углом 25 градусов. Найдите коэффициент кинетического трения лыжника, если известно, что трение равно 45,0 Н.
Рис. 5.37 Используйте диаграмму, чтобы найти коэффициент кинетического трения для лыжника.
Стратегия
Величина кинетического трения равна 45,0 Н. Кинетическое трение связано с нормальной силой N как fk=µkN fk=µkN. Следовательно, мы можем найти коэффициент кинетического трения, сначала найдя нормальную силу лыжника на склоне. Нормальная сила всегда перпендикулярна поверхности, а поскольку движение перпендикулярно поверхности отсутствует, нормальная сила должна равняться составляющей веса лыжника, перпендикулярной склону.
То есть
N=w⊥=w cos(25∘)=mg cos(25∘).N=w⊥=w cos(25∘)=mg cos(25∘).
Подставляя это в выражение для кинетического трения, получаем
fk=µkmg cos 25∘,fk=µkmg cos 25∘,
, которое теперь можно решить для коэффициента кинетического трения µ k .
Решение
Решение для µk µk дает
µk=fkw cos 25∘=fkmg cos 25∘.µk=fkw cos 25∘=fkmg cos 25∘.
Подставив известные значения в правую часть уравнения,
мкк=45,0 Н(62 кг)(9,80 м/с2)(0,906)=0,082,мкк=45,0 Н(62 кг)(9,80 м/с2 )(0,906)=0,082.
Обсуждение
Этот результат немного меньше, чем коэффициент, указанный в таблице 5.1 для вощеной древесины на снегу, но все же разумен, так как значения коэффициентов трения могут сильно различаться. В подобных ситуациях, когда объект массой м скользит вниз по склону, который составляет угол θ с горизонтом, трение определяется формулой fk=μkmg cosθ. fk=мкмг cosθ.
fk=мкмг cosθ.
Рабочий пример
Вес на склоне, двумерная задача
Масса лыжника, включая снаряжение, составляет 60,0 кг. (См. рис. 5.38(b).) (a) Каково ее ускорение, если трением можно пренебречь? б) Чему равно ее ускорение, если сила трения равна 45,0 Н?
Рисунок 5.38 Теперь используйте диаграмму, чтобы найти ускорение лыжника, если трением можно пренебречь и если сила трения равна 45,0 Н.
Стратегия
Наиболее удобной системой координат для движения по склону является та, в которой одна координата параллельна склону, а другая перпендикулярна склону. Помните, что движения вдоль перпендикулярных осей независимы. Мы используем символ ⊥ ⊥ для обозначения перпендикуляра и || || значит параллельно.
Единственными внешними силами, действующими на систему, являются вес лыжника, трение и нормальная сила, действующая на лыжный склон, обозначенные на диаграмме свободного тела w w, f f и N N . N N всегда перпендикулярно склону, а f f параллельно ему. Но w w не направлен ни по одной из осей, поэтому мы должны разбить его на составляющие вдоль выбранных осей. Определим w|| ш|| быть компонентом веса, параллельным наклону, и w⊥ w⊥ компонентом веса, перпендикулярным наклону. Как только это будет сделано, мы можем рассмотреть две отдельные проблемы сил, параллельных склону, и сил, перпендикулярных склону.
Но w w не направлен ни по одной из осей, поэтому мы должны разбить его на составляющие вдоль выбранных осей. Определим w|| ш|| быть компонентом веса, параллельным наклону, и w⊥ w⊥ компонентом веса, перпендикулярным наклону. Как только это будет сделано, мы можем рассмотреть две отдельные проблемы сил, параллельных склону, и сил, перпендикулярных склону.
Решение
Величина составляющей веса, параллельной наклону, равна w||=wsin(25°)=mg sin(25°) w||=wsin(25°)=mg sin(25°) , а величина составляющей веса, перпендикулярной наклону, равна w⊥=wcos(25°)=mg cos(25°). w⊥=wcos(25°)=mg cos(25°).
(a) Пренебрегая трением: поскольку ускорение параллельно склону, нам нужно учитывать только силы, параллельные наклону. Силы, перпендикулярные склону, складываются в ноль, так как в этом направлении нет ускорения. Силы, параллельные склону, представляют собой вес лыжника, параллельный склону w|| ш|| и трение f f. При отсутствии трения по второму закону Ньютона ускорение, параллельное склону, равно
a||=Fnet ||m,a||=Fnet ||m,
Где результирующая сила, параллельная склону Fnet ||=w||=mgsin(25°) Fnet ||=w|| =mgsin(25°), так что
a||=Fnet ||m=mg sin(25°)m=g sin(25°)=(9,80 м/с2)(0,423)=4,14 м/с2a| |=Fnet ||m=mg sin(25°)m=g sin(25°)=(9,80 м/с2)(0,423)=4,14 м/с2
— ускорение.
(b) Включая трение: Теперь у нас есть заданное значение трения, и мы знаем, что его направление параллельно склону и оно препятствует движению между контактирующими поверхностями. Таким образом, чистая внешняя сила теперь равна 9.0003
Fnet ||=w||−f,Fnet ||=w||–f,
и подставляя это во второй закон Ньютона, a||=Fnet ||m a||=Fnet ||m , дает
a||=Fnet ||m=w||−fm=mg sin(25°)−fm.a||=Fnet ||m=w||−fm=mg sin(25°)−fm.
Подставляем известные значения и получаем )−45,0 N60,0 кг,
или
a||=3,39 м/с2, a||=3,39 м/с2,
, что представляет собой ускорение, параллельное наклону, при наличии противодействующего трения 45 Н.
Обсуждение
Поскольку трение всегда препятствует движению между поверхностями, ускорение при наличии трения меньше, чем при его отсутствии.
Практические задачи
Когда объект находится на наклонной плоскости, образующей с горизонтом угол θ , как выражается составляющая силы веса объекта, параллельная наклону?
Тело массой 5 кг лежит на плоскости, наклоненной под углом 30∘ к горизонтали. Какая составляющая силы веса параллельна наклону?
Какая составляющая силы веса параллельна наклону?
- 4.33Н
- 5,0 Н
- 24,5Н
- 42.43С
Snap Lab
Трение под углом: скольжение монеты
Объект будет скользить по наклонной плоскости с постоянной скоростью, если результирующая сила, действующая на объект, равна нулю. Мы можем использовать этот факт для измерения коэффициента кинетического трения между двумя объектами. Как показано в первом рабочем примере, кинетическое трение на склоне fk=µkmg cosθ fk=µkmg cosθ, а составляющая веса вниз по склону равна mg sinθ mg sinθ. Эти силы действуют в противоположных направлениях, поэтому, когда они имеют одинаковую величину, ускорение равно нулю. Написание этих
fk=Fgxμkmg cosθ=mg sinθ.fk=Fgxμkmg cosθ=mg sinθ.
Решая для µk µk, поскольку tanθ=sinθ/cosθ tanθ=sinθ/cosθ мы находим, что
Материалы:
- 1 монета
- 1 книга
- 1 транспортир
- Положите монету плоской стороной на книгу и наклоняйте ее, пока монета не будет скользить по книге с постоянной скоростью.
 Возможно, вам придется слегка постучать по книге, чтобы заставить монету двигаться.
Возможно, вам придется слегка постучать по книге, чтобы заставить монету двигаться. - Измерьте угол наклона относительно горизонтали и найдите µk µk.
- Положите монету плоской стороной на книгу и наклоняйте ее, пока монета не будет скользить по книге с постоянной скоростью.
Проверка захвата
Верно или неверно — если известны только углы двух векторов, мы можем найти угол их результирующего вектора сложения.
- Правда
- Ложь
Проверьте свое понимание
Упражнение 9
Что такое трение?
- Трение — это внутренняя сила, противодействующая относительному движению объекта.
- Трение — это внутренняя сила, которая ускоряет относительное движение объекта.
- Трение — это внешняя сила, противодействующая относительному движению объекта.
- Трение — это внешняя сила, увеличивающая скорость относительного движения объекта.

Упражнение 10
Какие существуют две разновидности трения? На что действует каждый?
- Кинетическое и статическое трение действуют на движущийся объект.
- Кинетическое трение действует на движущийся объект, а статическое трение действует на покоящийся объект.
- Кинетическое трение действует на неподвижный объект, а статическое трение действует на движущийся объект.
- Кинетическое и статическое трение действуют на покоящийся объект.
Упражнение 11
Какое значение между статическим и кинетическим трением между двумя поверхностями больше? Почему?
- Кинетическое трение имеет большее значение, потому что трение между двумя поверхностями больше, когда две поверхности находятся в относительном движении.




 Определить неизвестную величину. Дано: α1 = 55°; α2 = 25°; m1 = 2,2 кг; m2 = 4,3 кг; k = 0,17; a — ?
Определить неизвестную величину. Дано: α1 = 55°; α2 = 25°; m1 = 2,2 кг; m2 = 4,3 кг; k = 0,17; a — ? Нить, связывающая грузы, перекинута через легкий блок, укрепленный на вершине наклонной плоскости. Коэффициент трения между грузами и плоскостью равен k, ускорение грузов a, (a>0, если система движется в сторону груза m
Нить, связывающая грузы, перекинута через легкий блок, укрепленный на вершине наклонной плоскости. Коэффициент трения между грузами и плоскостью равен k, ускорение грузов a, (a>0, если система движется в сторону груза m Нить, связывающая грузы, перекинута через легкий блок, укрепленный на вершине наклонной плоскости. Коэффициент трения между грузами и плоскостью равен k, ускорение грузов a, (a>0, если система движется в сторону груза m2). Определить неизвестную величину. Дано: α
Нить, связывающая грузы, перекинута через легкий блок, укрепленный на вершине наклонной плоскости. Коэффициент трения между грузами и плоскостью равен k, ускорение грузов a, (a>0, если система движется в сторону груза m2). Определить неизвестную величину. Дано: α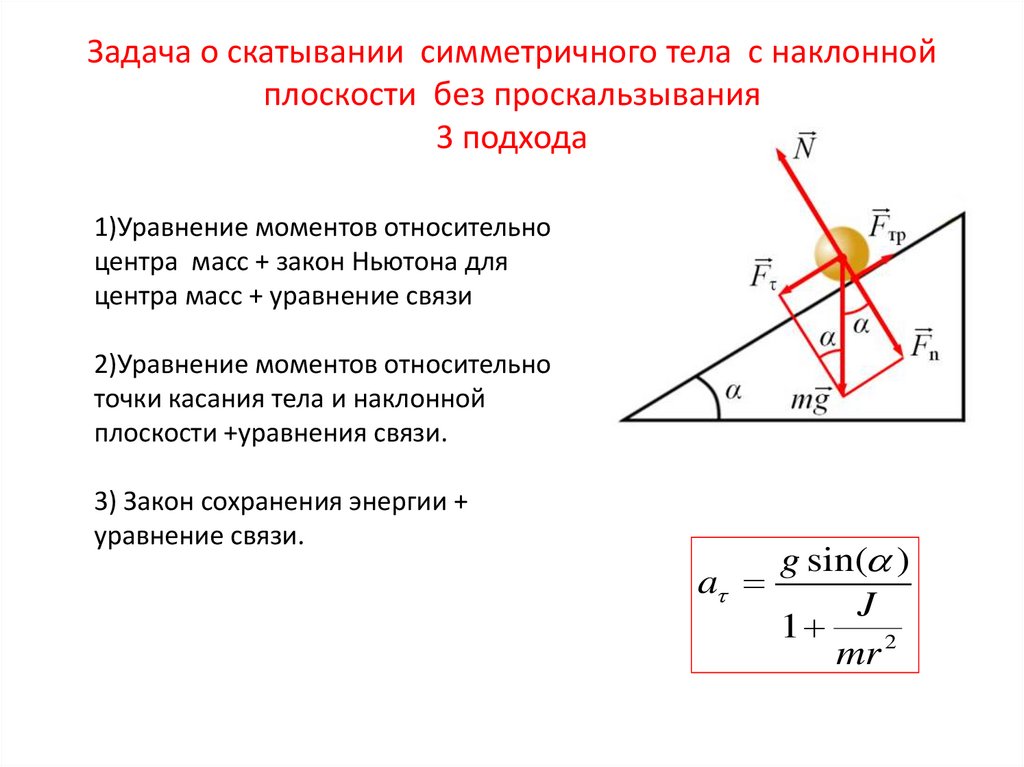
 6к)
6к) По мере увеличения угла параллельная составляющая увеличивается, а перпендикулярная составляющая уменьшается. Это связано с тем, что косинус угла уменьшается, а синус угла увеличивается.
По мере увеличения угла параллельная составляющая увеличивается, а перпендикулярная составляющая уменьшается. Это связано с тем, что косинус угла уменьшается, а синус угла увеличивается.
 Возможно, вам придется слегка постучать по книге, чтобы заставить монету двигаться.
Возможно, вам придется слегка постучать по книге, чтобы заставить монету двигаться.

Leave A Comment