На координатной прямой отмечены числа х и у какое утверждение верно: Решение №3213 На координатной прямой отмечены числа х и у.

Подготовка к ОГЭ по математике. Решение задачи 2. На координатной прямой отмечены числа x и y. Какое из следующих утверждений об этих числах верно?

© 2007 — 2023 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.

---

Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.

Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.

Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.

---

Фотографии предоставлены

Главная → Видеоуроки →  ОГЭ (ГИА) по математике. Задача 2. Описание видеоурока: Тренировочная работа от 6 мая 2014 года по математике в формате ОГЭ (ГИА) для 9 класса. Модуль «Алгебра», задача 2. Условие задачи: На координатной прямой отмечены числа x и y. Какое из следующих утверждений об этих числах верно? 00:04:56 Валерий Волков 13 20.01.2015 Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями! Новости образования

ЕГЭ по математике Профильный уровень Задание 1     Задание 2 Задание 3     Задание 4 Задание 5     Задание 6 Задание 7     Задание 8 Задание 9     Задание 10 Задание 11     Задание 12 Задание 13     Задание 14 Задание 15     Задание 16 Задание 17     Задание 18 Задание 19     Задание 20 Задание 21 ГИА по математике Задача 1     Задача 2 Задача 3     Задача 4 Задача 5     Задача 6 Задача 7     Задача 8 Задача 9     Задача 10 Задача 11     Задача 12 Задача 13     Задача 14 Задача 15     Задача 16 Задача 17     Задача 18 Задача 19     Задача 20 Задача 21     Задача 22 Задача 23     Задача 24 Задача 25     Задача 26 Демонстрационные варианты ОГЭ по математике Математика. 5 класс. Натуральные числа Обыкновенные дроби Десятичные дроби Проценты Математика. 6 класс. Делимость чисел Сложение и вычитание дробей с разными знаменателями Умножение и деление обыкновенных дробей Отношения и пропорции Положительные и отрицательные числа Измерение величин Математика. 7 класс. Преобразование выражений Многочлены Формулы сокращенного умножения Математика. 8 класс. Модуль числа. Уравнения и неравенства. Квадратные уравнения Квадратные неравенства Уравнения с параметром Задачи с параметром Математика. 9 класс. Функции и их свойства Прогрессии Векторы Комбинаторика, статистика и теория вероятностей Математика. 10 — 11 класс. Числовые функции Тригонометрические функции Тригонометрические уравнения Преобразование тригонометрических выражений Производная Степенные функции Показательная функция Логарифмические функции Первообразная и интеграл Уравнения и неравенства Комбинаторика Создаёте видеоуроки? Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала. Актуально Физкультминутки для школьников и дошкольников Подготовка к ЕГЭ Подготовка к ОГЭ

Задание 7 ОГЭ по математике. Числовые неравенства, координатная прямая.

Задание 7 ОГЭ по математике – это решение неравенств, а также выбор верного или неверного утверждения. Тема задания — расположение чисел на координатной прямой.

При выполнении задания 7 ОГЭ по математике необходимо уметь сравнивать числа, включая обыкновенные и десятичные дроби, а также расставлять их на числовой прямой.

Приступим к решению задач.

Пример 1. Какое из следующих чисел заключено между числами  и ?

1) 0,4

2) 0,5

3) 0,6

4) 0,7

Решение. Чтобы ответить на вопрос задачи, преобразуем дроби к виду десятичных:

Между числами 0,58 и 0,625 находится число 0,6. Но в ответ здесь указывается не само число, а номер, под которым оно записано.

Ответ: 3.

Пример 2. Одно из чисел   отмечено на прямой точкой. Укажите это число.

В ответе укажите номер правильного варианта.

2)

3)

4)

Решение. Выделим целую часть в каждой неправильной дроби:

Отметим на числовой прямой числа 2, 3, 4, 5.

Точка, показанная на рисунке, соответствует числу, которое меньше, чем 5, но больше, чем 4,5. Значит, подходит .

Ответ: 1.

Пример 3. Какому промежутку принадлежит число?

В ответе укажите номер правильного варианта.

1) [4; 5]

2) [5; 6]

3) [6; 7]

4) [7; 8]

 

Решение. Составим двойное неравенство:

Ответ очевиден.

Ответ: 4.

Пример 4. На координатной прямой отмечены числа а, b и c.

Из следующих утверждений выберите верное. В ответе укажите номер правильного варианта.

1)

2)

3)

4)

Решение. Заметим, что Проанализируем предложенные утверждения:

1) Неверно. Из меньшего вычитается большее, разность меньше нуля.

2) Неверно. Из большего вычитается меньшее, разность больше нуля.

3) Верно. Из меньшего вычитается большее, разность меньше нуля.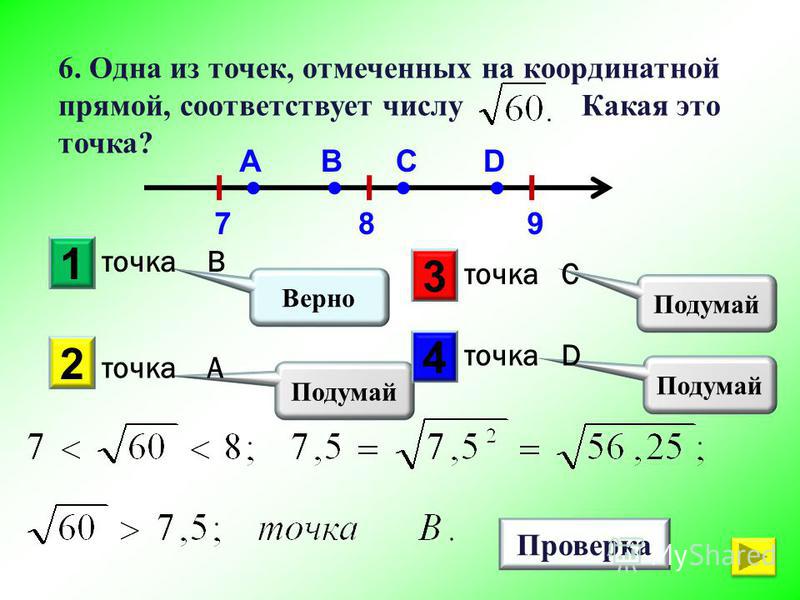

4) Неверно. Из меньшего вычитается большее, разность меньше нуля.
Верно только утверждение 3.
Ответ

: 3.

Пример 5. На координатной прямой отмечены числа а и х.

Какое из следующих чисел наименьшее? В ответе укажите номер правильного варианта.

a+x

2)

3) -a

4) a-x

Решение. Можно решить эту задачу строго математическими рассуждениями. А мы пойдём другим, более наглядным путём. Позволим себе такую вольность, т. к. от нас требуется только правильный ответ. Выберем условную единицу на числовой прямой и оценим приблизительно числа а и х.

Итак, предположим, что Тогда рассчитаем предложенные варианты и выберем наименьшее значение:

1) – наименьшее из всех чисел

2) 

3)

4) 

Ответ: 1.

Замечание. Условную величину -1 можно было отметить в другом месте числовой прямой. Результат вычислений при этом не изменится. Проверьте сами на следующем рисунке:

Пример 6. Известно, что число отрицательное. На каком из рисунков точки с координатами расположены на координатной прямой в правильном порядке?

В ответе укажите номер правильного варианта.

Решение. Используем сначала наглядно-вычислительный способ. Пусть , тогда , . Отсюда понятно, что . Такой ситуации соответствует рисунок под цифрой 2.

Ответ: 2.

Замечание. Значение буквенной переменной выбиралось произвольно. Подставив любое другое отрицательное число, мы придём к тем же самым выводам.

Благодарим за то, что пользуйтесь нашими материалами. Информация на странице «Задание 7 ОГЭ по математике. Числовые неравенства, координатная прямая.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена: 09.03.2023

Что такое оси X и Y? Определение, факты, пример графика и викторина

Ось в математике определяется как линия, которая используется для выполнения или отметки измерений. Оси x и y являются двумя важными линиями координатной плоскости. Ось X — это горизонтальная числовая линия, а ось Y — вертикальная числовая линия. Эти две оси пересекаются перпендикулярно, образуя координатную плоскость. Ось x также называется абсциссой, а ось y — ординатой.

Любая точка на координатной плоскости может быть расположена или представлена ​​с помощью этих двух осей в виде упорядоченной пары вида ( х, у ). Здесь x представляет положение точки относительно оси x, а y представляет положение точки относительно оси y.
Начало координат находится в месте пересечения двух осей и записывается как (0,0).

Нанесение точек на оси X и Y

Давайте узнаем, как наносить точки на график с помощью осей X и Y.

Например: Попробуем нарисовать точку B(3,4) на графике.

Здесь координата x точки B равна 3. Итак, мы начнем с начала координат и переместимся на 3 единицы вправо по оси x.

Теперь координата y B(3,4) равна 4, поэтому мы поднимемся на 4 позиции вверх от этой точки.

Итак, мы начертили нашу точку B(3,4) на графике с помощью осей.

Связанные игры

Представление линейного уравнения по осям X и Y

Чтобы понять, как представить линейное уравнение на графике с использованием осей X и Y,

давайте рассмотрим линейное уравнение, y = x + 1. 

Теперь давайте построим таблицу для представления соответствующих значений y для различных значений x и создадим их упорядоченные пары:

x	y	Ordered pair
0	1	(0,1)
1	2	(1,2)
2	3	(2,3)
3	4	(3,4)

.

В качестве последнего шага мы соединим эти точки, чтобы сформировать прямую линию, которая будет представлением уравнения y = x + 1,

Связанные рабочие листы

Решенные вопросы

Вопрос 1: Какие из следующих точек лежат на оси x?

(0, 1) (4, 0) (7, 7) (−5, 0)       (−4, 4) (0, −5) (8, 0) (6, 0)

Ответ: Поскольку координаты, лежащие на оси x, имеют координату y, равную нулю (0), следующие точки будут лежать на оси x:

(4, 0) (−5, 0) (8, 0) (6 , 0)

Вопрос 2: На график нужно нанести две разные точки. Если заданы точки (3,2) и (2,3), нанесите эти две точки на оси X и Y. Кроме того, найдите точку, где прямая, проходящая через эти точки, пересекает ось x.

Ответ: Для (3,2), как мы видим, точка с координатой x равна 3, а точка с координатой y равна 2.

Аналогичным образом мы можем построить точку (2,3).

Теперь мы можем соединить обе точки прямой линией, когда обе точки нанесены на график. Продлив прямую, мы видим, что эта линия пересекает ось x в точке (5,0).

Вопрос 3: Для линейного уравнения y = 2x + 6 найдите на графике точку пересечения прямой линии с осью y.

Ответ: По оси y координата x точки равна 0. Следовательно, мы можем найти точку пересечения оси y и y = 2x + 6, просто приравняв значение x к 0 и найдя значение у. y = 2(0)+6 = 0 + 6 = 6.

Таким образом, прямая линия уравнения y = 2x + 6 пересекает ось y в точке (0,6).

Практические задачи

1

Как называется ось X?

Ордината

Абсцисса

Аппликация

Ничего из вышеперечисленного

Правильный ответ: Абсцисса
ось x также называется абсциссой.

2

Как правильно изобразить точку на графике?

(координата X, координата X)

(координата Y, координата X)

(координата Y, координата Y)

(координата X, координата Y)

Правильный ответ: (координата X, координата Y)
(координата X, координата Y) — это правильный способ представления точки.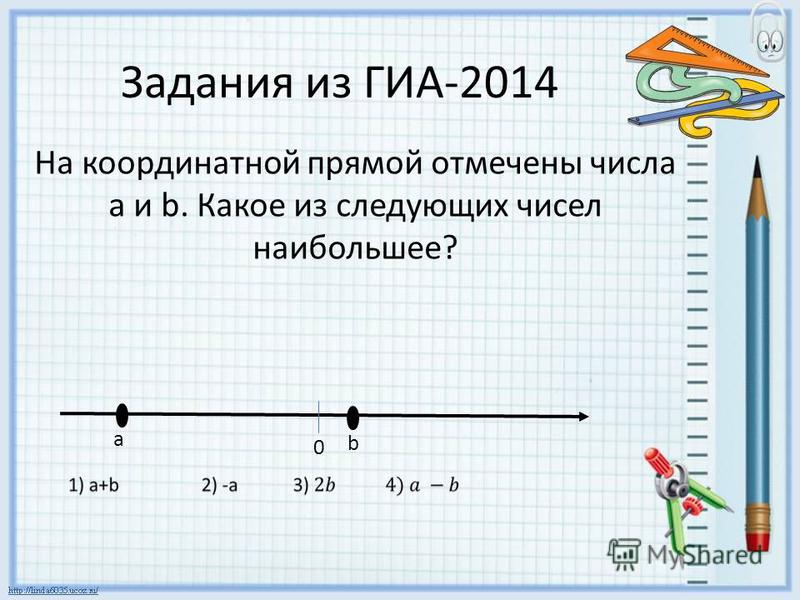

3

Как исходная точка представлена ​​на графике?

(0,0)

(0,x)

(y,0)

(x,y)

Правильный ответ: (0,0)
(0, 0) координаты начала координат на графике.

4

Точка (0,5) будет лежать на

Ось X

Ось Y

Начало

Ничего из вышеперечисленного

Правильный ответ: Ось Y
— координата) равна 0. Итак, данная точка лежит на оси ординат.

Часто задаваемые вопросы

Почему важны оси X и Y?

Ось X и Y необходимы для графического представления данных. Эти оси составляют координатную плоскость. Данные расположены в координатах в соответствии с их расстоянием от осей X и Y. Графическое представление помогает в решении сложных уравнений.

Как формируется координатная плоскость?

Координатная плоскость — это двумерная плоскость, образованная пересечением двух числовых линий. Одна из этих числовых линий представляет собой горизонтальную числовую линию, называемую осью x, а другая числовая линия представляет собой вертикальную числовую линию, называемую осью y (или ординатой). Эти две числовые линии пересекаются друг с другом перпендикулярно и образуют координатную плоскость.

Что такое квадранты на графике?

Две числовые линии делят координатную плоскость на 4 области. Эти области называются квадрантами. Квадранты обозначаются римскими цифрами, и каждый из этих квадрантов имеет свои собственные свойства. X и Y имеют разные знаки в каждом квадранте.

• Квадрант I: (х, у)
• Квадрант II: (-x,y),
• Квадрант III: (-x, -y),
• Квадрант IV: (x,-y).

Чем отличаются оси X и Y?

По оси X указано положение точки по горизонтали, а по оси Y — по вертикали.

1.1: Действительные числа и числовая строка

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

18326

• Анонимный
• LibreTexts

НАВЫКИ ДЛЯ РАЗВИТИЯ

• Постройте числовую прямую и нанесите на нее точки.
• Используйте числовую прямую, чтобы определить порядок действительных чисел.
• Определить противоположное действительному числу.
• Определить абсолютное значение действительного числа.

Определения

Набор представляет собой набор объектов, обычно сгруппированных в фигурных скобках \(\{\) \(\}\), где каждый объект называется элемент . Например, \(\{\text{красный, зеленый, синий}\}\) — это набор цветов. Подмножество — это набор, состоящий из элементов, принадлежащих данному набору. Например, \(\{\text{зеленый, синий}\}\) является подмножеством цвета, установленного выше. Набор без элементов называется пустым набором и имеет собственное специальное обозначение \(\{\) \(\}\) или \(\varnothing\).

Изучая математику, мы фокусируемся на специальных наборах чисел. Набор из натуральных (или счетных) чисел , обозначаемый \(\mathbb{N}\), равен

\( \{1,2,3,4,5 , \dots \} \quad \color{Cerulean}{Natural\: Numbers} \)

Три точки \((\dots)\) называются многоточие и указывает, что числа продолжаются без ограничений. Набор из целых чисел , обозначаемый \(\mathbb{W}\), представляет собой набор натуральных чисел в сочетании с нулем.

\( \{0,1,2,3,4,5 , \dots\} \quad \color{Cerulean}{Whole\: Numbers} \)

Набор из целых чисел , обозначенных \(\ mathbb{Z}\), состоит как из положительных, так и из отрицательных целых чисел, а также нуля.

\( \{\dots, -3,-2,-1,0,1,2,3 , \dots\} \quad \color{Cerulean}{Integers} \)

Обратите внимание, что наборы натуральных и целые числа являются подмножествами множества целых чисел.

Рациональные числа , обозначаемые \(\mathbb{Q}\), определяются как любое число вида \(\dfrac{a}{b}\), где \(a\) и \(b\ ) являются целыми числами, а \(b\) отличен от нуля. Десятичные числа, которые повторяются или заканчиваются, рациональны. Например,

\(0,7= \frac{7}{10} \quad \text{and} \quad 0. \overline{3} =0,3333 \dots = \frac{1}{3}\)

Множество целых чисел является подмножеством множества рациональных чисел, потому что каждое целое число может быть выражено как отношение целого числа и \(1\). Другими словами, любое целое число можно записать над \(1\) и считать рациональным числом. Например,

\(5= \frac{5}{1}\)

Иррациональные числа определяются как любые числа, которые не могут быть записаны как отношение двух целых чисел. Неконечные десятичные дроби, которые не повторяются, иррациональны. Например,

\(\pi =3,14159\dots \quad \text{and} \quad \sqrt{2} = 1.41421 \dots\)

Множество действительных чисел , обозначаемое \(\mathbb{R}\), определяется как множество всех рациональные числа в сочетании с множеством всех иррациональных чисел. Следовательно, все числа, определенные до сих пор, являются подмножествами множества действительных чисел. Таким образом,

Рисунок \(\PageIndex{1}\): Вещественные числа

Числовая строка

Строка действительных чисел или просто числовая строка позволяет визуально отображать действительные числа, связывая их с уникальными точками на линии. . Действительное число, связанное с точкой, называется 9. 0039 координата . Точка на прямой с действительными числами, связанная с координатой, называется ее графиком .

Чтобы построить числовую линию, нарисуйте горизонтальную линию со стрелками на обоих концах, чтобы указать, что она продолжается без границ. Затем выберите любую точку для представления числа ноль; эта точка называется началом координат .

Рисунок \(\PageIndex{2}\)

Отметьте одинаковые длины по обе стороны от исходной точки и пометьте каждую отметку, чтобы определить масштаб. Положительные действительные числа лежат справа от начала координат, а отрицательные — слева. Число ноль \((0)\) не является ни положительным, ни отрицательным. Как правило, каждый тик представляет одну единицу.

Рисунок \(\PageIndex{3}\)

Как показано ниже, шкала не всегда должна быть одной единицей. В первой числовой строке каждая галочка представляет две единицы. Во втором каждая галочка представляет \(\frac{1}{7}\) единицы.

Рисунок \(\PageIndex{4}\)

График каждого действительного числа отображается в виде точки в соответствующей точке на числовой прямой. Ниже приведен частичный график набора целых чисел \(\mathbb{Z}\):

Рисунок \(\PageIndex{5}\)

Пример \(\PageIndex{1}\)

Нарисуйте следующий набор действительных чисел :

Решение

Нарисуйте числа на числовой прямой со шкалой, где каждая галочка представляет \(\frac{1}{2}\) единицы измерения.

Рисунок \(\PageIndex{6}\)

Порядок действительных чисел

При сравнении действительных чисел на числовой прямой большее число всегда будет лежать справа от меньшего. Ясно, что \(15\) больше, чем \(5\), но может быть не так ясно видеть, что \(-1\) больше, чем \(-5\), пока мы не нанесем каждое число на график. числовая строка.

Рисунок \(\PageIndex{7}\)

Мы используем символы, чтобы помочь нам эффективно передать отношения между числами на числовой прямой. Символы, используемые для описания отношения равенства между числами, следующие:

\[\begin{align*} &= \quad \color{Cerulean}{is\ equal\ to} \\ &\neq \quad \color{ Cerulean}{is\ not\ equal\ to} \\ &\ приблизительно \quad \color{Cerulean}{is\ приблизительно\ равно\ to} \end{align*}\]

Эти символы используются и интерпретируются в следующим образом:

\[\begin{align*} &5=5 \qquad &&\color{Cerulean}{5\ is\ equal\ to\ 5} \\ &0 \neq 5 \qquad &&\color{Cerulean}{0\ is \ not\ equal\ to\ 5} \\ &\pi \ приблизительно 3. 14 \quad &&\color{Cerulean}{pi\ is\ приблизительно\ равно\ to\ 3.14} \end{align*}\]

Далее определить символы, которые обозначают отношение порядка между действительными числами.

\[\begin{align*} &< \quad \color{Cerulean}{Меньше\ чем} \\ &> \quad \color{Cerulean}{Больше\ чем} \\ &\leq \quad \color{ Cerulean}{Меньше\ или\ равно\ к} \\ &\geq \quad \color{Cerulean}{Больше\ чем\ или\ равно\ к} \end{align*}\]

Эти символы позволяют сравнивать два числа. Например,

Поскольку график \(−120\) находится слева от графика \(–10\) на числовой прямой, это число меньше \(−10\). Мы могли бы написать эквивалентное утверждение следующим образом:

Точно так же, поскольку график нуля находится справа от графика любого отрицательного числа на числовой прямой, ноль больше любого отрицательного числа.

Символы \(<\) и \(>\) используются для обозначения строгих неравенств , а символы и используются для обозначения включающих неравенств . В некоторых ситуациях можно правильно применить более одного символа. Например, оба следующих утверждения верны:

Кроме того, компонент «или равно» включающего неравенства позволяет нам правильно написать следующее:

Логическое использование слова «или» требует, чтобы только один из условий должны быть истинными: «меньше чем» или «равно».

Пример \(\PageIndex{2}\)

Заполните пробел \(<, =\) или \(>: −2\) ____ \(−12\).

Решение

Используйте >, потому что график \(−2\) находится справа от графика \(−12\) на числовой прямой. Следовательно, \(−2 > −12\), что читается как «минус два больше, чем минус двенадцать».

Рисунок \(\PageIndex{8}\)

Ответ:

\(-2>-12\)

В этом тексте мы часто будем указывать эквивалентную запись, используемую для электронного выражения математических величин с использованием стандарта символы, доступные на клавиатуре. Начнем с эквивалентной текстовой записи неравенств:

\[\begin{align*} &\geq &&»>=» \\ &\leq &&»<=" \\ &\neq &&"!=" \end{align*}\]

Многие калькуляторы , системы компьютерной алгебры и языки программирования используют эту нотацию.

Противоположности

напротив любого действительного числа \(a\) равно \(−a\). Противоположные действительные числа находятся на одинаковом расстоянии от начала координат на числовой прямой, но их графики лежат по разные стороны от начала координат, а числа имеют противоположные знаки.

Рисунок \(\PageIndex{9}\)

Например, мы говорим, что противоположным \(10\) является \(−10\).

Далее рассмотрим противоположное отрицательное число. Учитывая целое число \(−7\), целое число на том же расстоянии от начала координат и с противоположным знаком равно \(+7\) или просто \(7\).

Рисунок \(\PageIndex{10}\)

Следовательно, мы говорим, что противоположным \(−7\) является \(−(−7) = 7\). Эта идея приводит к тому, что часто называют двойным отрицательным свойством . Для любого действительного числа \(a\),

\(-(-a)=a\)

Пример \(\PageIndex{3}\)

Что является противоположностью \(-\frac{3}{4}\)?

Решение

Здесь мы применяем свойство двойного отрицания.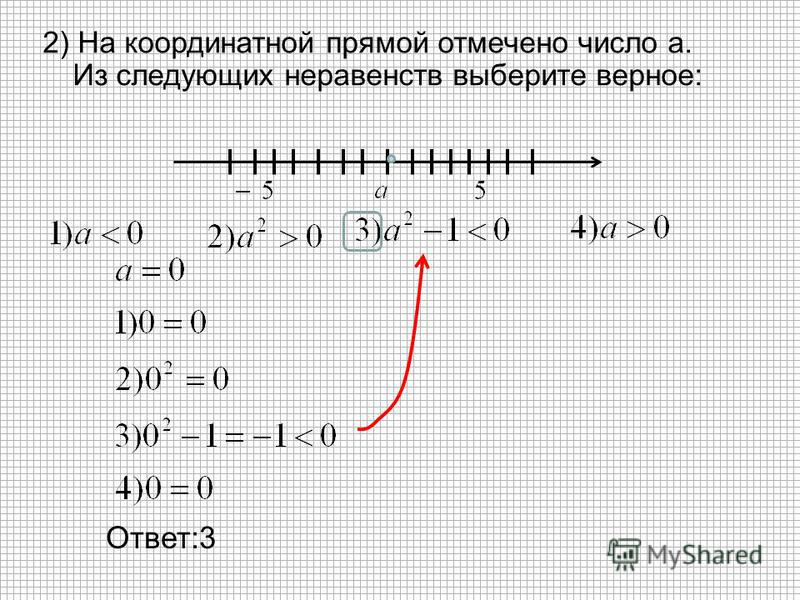

\(-(-\frac{3}{4})=\frac{3}{4}\)

Пример \(\PageIndex{4}\)

Упростить \(-(-(4) )\)

Решение

Начните с самых внутренних скобок, найдя противоположное \(+4\).

\[\begin{align*} -(-(4)) &= -(\color{Cerulean}{-(4)} \color{Black}{)} \\ &= -(\color{Cerulean }{-4} \color{Черный}{)} \\ &=4 \end{align*}\]

Ответ

4

Пример \(\PageIndex{5}\)

Упрощение: \(-(-(-2))\).

Решение

Примените свойство двойного отрицания, начиная с самых внутренних скобок.

\[\begin{align*} -(-(-2)) &= -(\color{Cerulean}{-(-2)} \color{Black}{)} \\ &= -(\color {Cerulean}{2} \color{Black}{)} \\ &=-2 \end{align*}\]

Ответ

-2

tip

Если имеется четное количество последовательных отрицательные знаки, то результат положительный. Если имеется нечетное количество последовательных отрицательных знаков, то результат отрицательный.

Попробуйте!

Упражнение \(\PageIndex{1}\)

Упрощение: \(-(-(-(5)))\).

Ответить

-5

Процедура:

\[\begin{align*} -(-(-(5))) &= -(\color{Cerulean}{-(-(5))} \color{Black}{)}\\ &= — (\color{Cerulean}{-(-5)} \color{Black}{)} \\ &= -(\color{Cerulean}{5} \color{Black}{)} \\&= -5 \ конец{выравнивание*} \]

Видео Решение:

(нажмите, чтобы посмотреть видео)

Абсолютное значение

абсолютное значение действительного числа \(a\), обозначаемое \(|a|\), определяется как расстояние между нулем (начало координат) и графиком этого действительного числа на числовая строка. Поскольку это расстояние, оно всегда положительно. Например,

\(|-4|=4 \quad \text{and} \quad |4|=4\)

И \(4\), и \(−4\) находятся в четырех единицах от начала координат , как показано ниже:

Рисунок \(\PageIndex{11}\)

Пример \(\PageIndex{6}\)

Упрощение:

a. \(|-12|\)

b.\(|12|\)

Решение

И \(−12\), и \(12\) отстоят на двенадцать единиц от начала координат на числовой прямой. Следовательно,

\(|-12|=12 \quad \text{and} \quad |12|=12\)

Ответ

а.\(12\) б.\(12\)

Также стоит отметить, что

\(|0|=0\)

Абсолютное значение может быть выражено в текстовом виде с помощью обозначения abs\((a)\). Мы часто сталкиваемся с отрицательными абсолютными значениями, такими как \(-|3|\) или \(-\) абс\((3)\). Обратите внимание, что перед символом абсолютного значения стоит знак минус. В этом случае сначала обработайте абсолютное значение, а затем найдите противоположный результат.

Не путайте это со свойством двойного отрицания, которое утверждает, что \(-(-7)=+7\).

Пример \(\PageIndex{7}\)

Упрощение: \(-|-(-7)|\).

Решение

Сначала найдите противоположное \(−7\) значение внутри абсолютного значения. Затем найдите противоположный результат.

\[\begin{align*} -|\color{Cerulean}{-(-7)} \color{Black}{|} &= -|\color{Cerulean}{7} \color{Black}{ |} \\ &=-7 \end{align*}\]

Ответ

-7

Теперь мы можем определить, какие действительные числа имеют конкретное абсолютное значение. Например,

\(|?|=5\)

Задумайте реальное число, расстояние до которого до начала координат равно \(5\) единицам. Есть два решения: расстояние справа от начала координат и расстояние слева от начала координат, а именно \(\{\pm 5\}\). Символ \( (\pm) \) читается как «плюс-минус» и указывает на то, что есть два ответа, один положительный и один отрицательный.

\(|-5|=5\ \quad \text{and} \quad |5|=5\)

Теперь рассмотрим следующее:

\(|?|=-5\)

Здесь мы хотим найти значение, для которого расстояние до начала координат отрицательно. Поскольку отрицательное расстояние не определено, это уравнение не имеет решения. Если уравнение не имеет решения, мы говорим, что решением является пустое множество: \(\varnothing\).

Ключевые выводы

• Любое действительное число может быть связано с точкой на прямой.
• Создайте числовую линию, сначала указав начало координат и отметив шкалу, подходящую для данной задачи.
• Отрицательные числа лежат слева от начала координат, а положительные числа — справа.
• Меньшие числа всегда лежат слева от больших чисел на числовой прямой.
• Положительное число является отрицательным, а отрицательное число положительным.
• Абсолютное значение любого действительного числа всегда положительно, поскольку оно определяется как расстояние от нуля (начала координат) на числовой прямой.
• Абсолютное значение нуля равно нулю.

Упражнение \(\PageIndex{2}\)

Используйте нотацию множества для перечисления описанных элементов.

1. Часы на часах.
2. Дни недели.
3. Первые десять целых чисел.
4. Первые десять натуральных чисел.
5. Первые пять положительных четных целых чисел.
6. Первые пять положительных нечетных целых чисел.

Ответить

1. \(\{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12\}\)

3. \(\{0, 1, 2, 3, 4, 5, 6, 7, 8, 9\}\)

5. \(\{2, 4, 6, 8, 10\}\)

Упражнение \(\PageIndex{3}\)

Определите, являются ли следующие действительные числа целыми, рациональными или иррациональными.

1. \(12\)
2. \(−3\)
3. \(4,5\)
4. \(−5\)
5. \(0,3 \overline{6} \)
6. \(0. \overline{3} \)
7. \(1.001000100001 \точки\)
8. \(1.00 \overline{1} \)
9. \(e=2.71828 \точек\)
10. \(\sqrt{7}=2,645751 \точки\)
11. \(−7\)
12. \(3.14\)
13. \(227\)
14. \(1.33\)
15. \(0\)
16. \(8 675 309\)

Ответить

1: целое, рациональное

3: Рационал

5: Рационал

7: Иррациональный

9: Иррациональный

11: целое, рациональное

13: Рационал

15: целое, рациональное

Упражнение \(\PageIndex{4}\)

Верно или неверно.

1. Все целые числа являются рациональными числами.
2. Все целые числа являются целыми числами.
3. Все рациональные числа являются целыми числами.
4. Некоторые иррациональные числа рациональны.
5. Все конечные десятичные числа рациональны.
6. Все иррациональные числа действительны.

Ответить

1: Правда

3: Ложь

5: Правда

Упражнение \(\PageIndex{5}\)

Выберите подходящий масштаб и нарисуйте на числовой прямой следующие наборы действительных чисел.

1. \(\{−3, 0, 3\}\)
2. \(\{−2, 2, 4, 6, 8, 10\}\)
3. \(\{−2, −1/3, 2/3, 5/3\}\)
4. \(\{−5/2, −1/2, 0, 1/2, 2\}\)
5. \(\{−5/7, 0, 2/7, 1\}\)
6. \(\{ –5, –2, –1, 0\}\)
7. \(\{ −3, −2, 0, 2, 5\}\)
8. \(\{−2,5, −1,5, 0, 1, 2,5\}\)
9. \(\{0, 0,3, 0,6, 0,9, 1,2\}\)
10. \(\{−10, 30, 50\}\)
11. \(\{−6, 0, 3, 9, 12\}\)
12. \(\{−15, −9, 0, 9, 15\}\)

Ответить

1. \(\{−3, 0, 3\}\)

Рисунок \(\PageIndex{12}\)

3. \(\{−2, −1/3, 2/3, 5/3\}\)

Рисунок \(\PageIndex{13}\)

5. \(\{−5/7, 0, 2/7 , 1\}\)

Рисунок \(\PageIndex{14}\)

7. \(\{ −3, −2, 0, 2, 5\}\)

Рисунок \(\PageIndex{15}\)

9. \(\{0, 0,3, 0,6, 0,9, 1,2\}\)

Рисунок \(\PageIndex{16}\)

11. \(\{−6, 0, 3, 9, 12\}\)

Рисунок \(\PageIndex{17}\)

Упражнение \(\PageIndex{6}\)

Заполните пробел символом \(<, =\) или \(>\).

1. \(−7\) ___ \(0\)
2. \(30\) ___ \(2\)
3. \(10\) ___ \(−10\)
4. \(−150\) ___ \(−75\)
5. \(−0,5\) ___ \(−1,5\)
6. \(0\) ___ \(0\)
7. \(-500\) ___ \(200\)
8. \(−1\) ___ \(−200\)
9. \(−10\) ___ \(−10\)
10. \(−40\) ___ \(−41\)

Ответить

1. \(<\)

3. \(>\)

5. \(>\)

7. \(<\)

9. \(=\)

Упражнение \(\PageIndex{7}\)

Верно или неверно.

1. \(5≠7\)
2. \(4=5\)
3. \(1≠1\)
4. \(−5>−10\)
5. \(4 \leq 4\)
6. \(−12 \geq 0\)
7. \(−10=−10\)
8. \(3>3\)
9. \(−1000<−20\)
10. \(0=0\)

Ответить

1. Правда

3. Ложь

5. Правда

7. Правда

9. Правда

Упражнение \(\PageIndex{8}\)

Перечислите числа.

1. Укажите три целых числа, меньших \(−5\).
2. Назовите три целых числа больше \(−10\).
3. Назовите три рациональных числа меньше нуля.
4. Назовите три рациональных числа больше нуля.
5. Запишите три целых числа от \(−20\) до \(−5\).
6. Назовите три рациональных числа между \(0\) и \(1\).

Ответить

1. \(−10, −7, −6\) (ответы могут быть разными)

3. \(−1, −2/3, −1/3\) (ответы могут быть разными)

5. \(−15, −10, −7\) (ответы могут быть разными)

Упражнение \(\PageIndex{9}\)

Переведите каждое утверждение в английское предложение.

1. \(10<20\)
2. \(−50 \leq −10\)
3. \(−4 \neq 0\)
4. \(30 \geq −1\)
5. \(0=0\)
6. \(е \около 2,718\)

Ответить

1. Десять меньше двадцати.

3. Минус четыре не равен нулю.

5. Ноль равен нулю.

Упражнение \(\PageIndex{10}\)

Переведите следующее в математическое выражение.

1. Минус семь меньше нуля.
2. Двадцать четыре не равно десяти.
3. Ноль больше или равен отрицательной единице.
4. Четыре больше или равно минус двадцати одному.
5. Минус два равен минус два.
6. Минус две тысячи меньше минус одна тысяча.

Ответить

1. \(−7<0\)

3. \(0 \geq −1\)

5. \(−2=−2\)

Упражнение \(\PageIndex{11}\)

Упрощение.

1. \(-(-9)\)
2. \(-(-35)\)
3. \(−(10)\)
4. \(-(3)\)
5. \(-(5)\)
6. \(−(34)\)
7. \(-(-1)\)
8. \(-(-(-1))\)
9. \(-(-(1))\)
10. \(-(-(-3))\)
11. \(-(-(-(-11)))\)

Ответить

1. \(9\)

3. \(−10\)

5. \(−5\)

7. \(1\)

9. \(1\)

11. \(11\)

Упражнение \(\PageIndex{12}\)

Ответьте на следующие вопросы.

1. Что противоположно \(-12\)
2. Что является противоположностью \(\pi \) ?
3. Что является противоположным \(−0,01\)?
4. Является ли противоположное \(−12\) меньше или больше, чем \(−11\)?
5. Является ли противоположное \(7\) меньше или больше, чем \(−6\)?

Ответить

2. \(-\пи \)

4. Больше

Упражнение \(\PageIndex{13}\)

Заполните пробел символами \(<, =\) или \(>\).

1. \(−7\) ___ \(−(−8)\)
2. \(6\) ___ \(−(6)\)
3. \(13\) ___ \(−(−12)\)
4. \(-(-5)\) ___ \(-(-2)\)
5. \(−100\) ___ \(−(−(−50))\)
6. \(44\) ___ \(−(−44)\)

Ответить

1. \(<\)

3. \(>\)

5. \(<\)

Упражнение \(\PageIndex{14}\)

Упрощение.

1. \(|20|\)
2. \(|−20|\)
3. \(|−33|\)
4. \(|−0,75|\)
5. \(|−\frac{3}{5}|\)
6. \(|38|\)
7. \(|0|\)
8. \(|1|\)
9. \(−|12|\)
10. \(-|-20|\)
11. \(−|20|\)
12. \(-|-8|\)
13. \(−|7|\)
14. \(-|-316|\)
15. \(−(−|\frac{8}{9}|)\)
16. \(|−(−2)|\)
17. \(-|-(-3)|\)
18. \(-(-|5|)\)
19. \(-(-|-45|)\)
20. \(-|-(-21)|\)
21. абс\((6)\)
22. абс\((−7)\)
23. \(−\)абс\((5)\)
24. \(-\)абс\((-19)\)
25. \(−(−\)абс\((9))\)
26. \(-\)абс\((-(-12))\)

Ответить

1. \(20\)

3. \(33\)

5. \(\frac{3}{5}\)

7. \(0\)

9. \(−12\)

11. \(−20\)

13. \(−7\)

15. \(\frac{8}{9}\)

17. \(−3\)

19. \(45\)

21. \(6\)

23. \(−5\)

25. \(9\)

Упражнение \(\PageIndex{15}\)

Определите неизвестное.

1. \(| ? |=9\)
2. \(| ? |=15\)
3. \(| ? |=0\)
4. \(| ? |=1\)
5. \(| ? |=−8\)
6. \(| ? |=−20\)
7. \(|?|−10=−2\)
8. \(|?|+5=14\)

Ответить

1. \(\pm 9\)

3. \(0\)

5. \(\varnothing\), Нет решения

7. \(\pm 8\)

Упражнение \(\PageIndex{16}\)

Заполните пробел символом \(<, =\) или \(>\).

1. \(|−2|\) ____ \(0\)
2. \(|−7|\) ____ \(|−10|\)
3. \(−10\) ____ \(−|−2|\)
4. \(|−6|\) ____ \(|−(−6)|\)
5. \(-|3|\) ____ \(|-(-5)|\)
6. \(0\) ____ \(-|-(-4)|\)

Ответить

1.