Задания для подготовки к ГИА-математика по темам (источник

1. Задание 1 № 314223. Найдите значение выражения   [pic]

2. Задание 1 № 314209. Найдите значение выражения  [pic]

3. Задание 1 № 314196. Найдите значение выражения  [pic]

4. Задание 1 № 314173. Найдите значение выражения  [pic]

5. Задание 1 № 287941. Укажите наибольшее из следующих чисел:

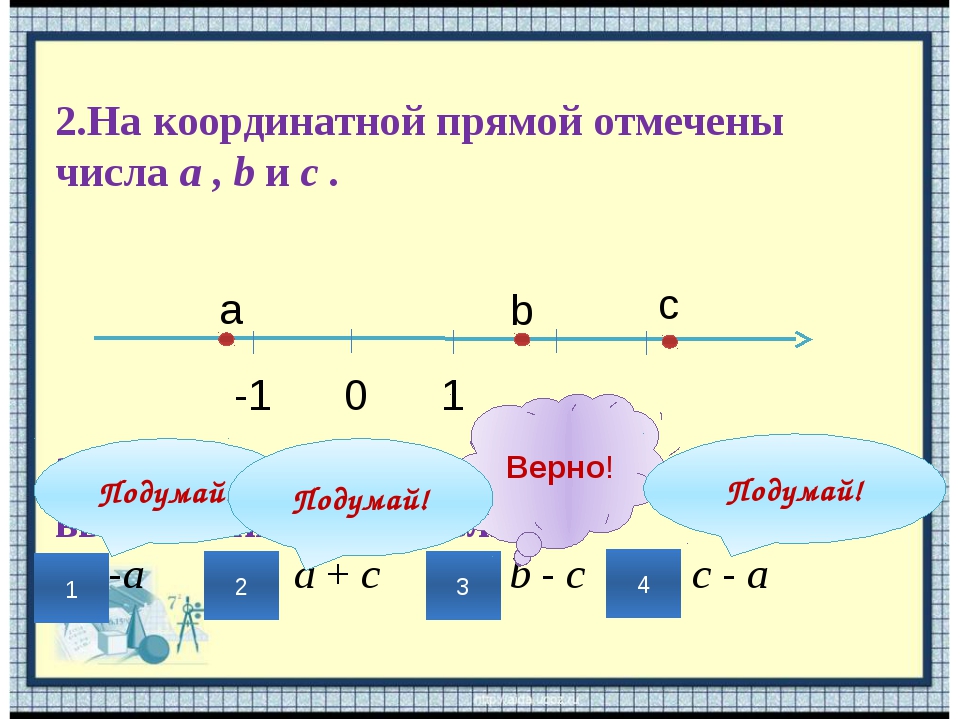
6. Задание 2 № 27. На координатной прямой отмечены числа [pic] и [pic] :

 

[pic]

Какое из следующих чисел наибольшее?

 

1) [pic] 2) [pic] 3) [pic] 4) [pic]

7. Задание 2 № 311902. На координатной прямой отмечены числа a, b и c:

[pic]

Значение какого из следующих выражений отрицательно?

В ответе укажите номер правильного варианта.

 

1) – a 2) a + c 3) b – c 4) c − a

8. Задание 2 № 314156. Одна из точек, отмеченных на координатной прямой, соответствует числу [pic] Какая это точка?

[pic]

 

1) точка M 2) точка N 3) точка P 4) точка Q

9. Задание 2 № 322425. На координатной прямой отмечены числа a, b и c.

 

[pic]

Какая из разностей a − b, a − c, c − b отрицательна?

В ответе укажите номер правильного варианта.

 

1) a – b 2) a – c 3) c − b

4) ни одна из них

10. Задание 2 № 322451. На координатной прямой отмечены числа a и b.

 

[pic]

 

Какое из следующих чисел наибольшее?

В ответе укажите номер правильного варианта.

 

1) a + b 2) –a 3) 2b 4) a − b

1. Задание 1 № 314223. Найдите значение выражения   [pic]

2. Задание 1 № 314209. Найдите значение выражения  [pic]

3. Задание 1 № 314196. Найдите значение выражения  [pic]

4. Задание 1 № 314173. Найдите значение выражения  [pic]

5. Задание 1 № 287941. Укажите наибольшее из следующих чисел:

6. Задание 2 № 27. На координатной прямой отмечены числа [pic] и [pic] :

 

[pic]

Какое из следующих чисел наибольшее?

 

1) [pic] 2) [pic] 3) [pic] 4) [pic]

7. Задание 2 № 311902. На координатной прямой отмечены числа a, b и c:

[pic]

Значение какого из следующих выражений отрицательно?

В ответе укажите номер правильного варианта.

 

1) – a 2) a + c 3) b – c 4) c − a

8. Задание 2 № 314156. Одна из точек, отмеченных на координатной прямой, соответствует числу [pic] Какая это точка?

[pic]

 

1) точка M 2) точка N 3) точка P 4) точка Q

9. Задание 2 № 322425. На координатной прямой отмечены числа a, b и c.

 

[pic]

Какая из разностей a − b, a − c, c − b отрицательна?

В ответе укажите номер правильного варианта.

 

1) a – b 2) a – c 3) c − b

4) ни одна из них

10. Задание 2 № 322451. На координатной прямой отмечены числа a и b.

 

[pic]

 

Какое из следующих чисел наибольшее?

В ответе укажите номер правильного варианта.

 

1) a + b 2) –a 3) 2b 4) a − b

Подготовка к ОГЭ-2020 по математике. Задание 7

Задание 7.

Неравенства

1.  О чис­лах   и   известно, что  . Среди при­ве­ден­ных ниже не­ра­венств вы­бе­ри­те верные:

В ответе укажите номер правильного варианта.

 

1) 

2) 

3) 

4) Верно 1, 2 и 3

2. На ко­ор­ди­нат­ной пря­мой изоб­ра­же­ны числа   и  . Какое из сле­ду­ю­щих не­ра­венств неверно?

 

1) 

2) 

3) 

4) 

3. Какое из сле­ду­ю­щих не­ра­венств не сле­ду­ет из не­ра­вен­ства  ?

В ответе укажите номер правильного варианта.

 

1) 

2) 

3) 

4) 

4.  Известно, что  . Какое из ука­зан­ных утвер­жде­ний верно?

В ответе укажите номер правильного варианта.

 

1) 

2) 

3) 

4) 

5. На ко­ор­ди­нат­ной пря­мой от­ме­че­но число  . Какое из утвер­жде­ний от­но­си­тель­но этого числа яв­ля­ет­ся верным?

В ответе укажите номер правильного варианта.

 

 

1) 

2) 

3) 

4) 

6. На ко­ор­ди­нат­ной пря­мой изоб­ра­же­ны числа   и  . Какое из сле­ду­ю­щих не­ра­венств неверно?

В ответе укажите номер правильного варианта.

 

1) 

2) 

3) 

4) 

7.

 На ко­ор­ди­нат­ной пря­мой от­ме­че­но число а.

Какое из утвер­жде­ний от­но­си­тель­но этого числа яв­ля­ет­ся верным?

В ответе укажите номер правильного варианта.

 1) 

2) 

3) 

4) 

8. На ко­ор­ди­нат­ной пря­мой от­ме­че­но число а.

Какое из утвер­жде­ний от­но­си­тель­но этого числа яв­ля­ет­ся верным?

В ответе укажите номер правильного варианта.

 1) 

2) 

3) 

4) 

9. На ко­ор­ди­нат­ной пря­мой от­ме­че­но число а.

Какое из утвер­жде­ний от­но­си­тель­но этого числа яв­ля­ет­ся верным?

В ответе укажите номер правильного варианта.

 1) 

2) 

3) 

4) 

10.  На ко­ор­ди­нат­ной пря­мой от­ме­че­но число а.

Какое из утвер­жде­ний от­но­си­тель­но этого числа яв­ля­ет­ся верным?

В ответе укажите номер правильного варианта.

 1) 

2) 

3) 

4) 

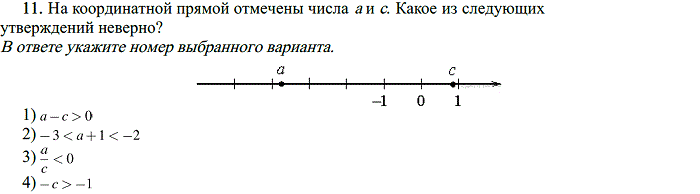
11. На ко­ор­ди­нат­ной пря­мой от­ме­че­ны числа а и с. Какое из сле­ду­ю­щих утвер­жде­ний не­вер­но?

В от­ве­те укажите номер выбранного варианта.

 1) 

2) 

3) 

4) 

12. На ко­ор­ди­нат­ной пря­мой от­ме­че­ны числа а и b. Какое из сле­ду­ю­щих утвер­жде­ний не­вер­но?

В ответе укажите номер правильного варианта.

 1) 

2) 

3) 

4) 

13.  На ко­ор­ди­нат­ной пря­мой от­ме­че­но число 

В ответе укажите номер правильного варианта.

Какое из утвер­жде­ний от­но­си­тель­но этого числа яв­ля­ет­ся верным?

 1) 

2) 

3) 

4) 

14. На ко­ор­ди­нат­ной пря­мой от­ме­че­ны числа a и b.

В ответе укажите номер правильного варианта.

Какое из сле­ду­ю­щих не­ра­венств верно?

 

1) 

2) 

3) 

4) 

15. На ко­ор­ди­нат­ной пря­мой от­ме­че­ны числа a и b.

В ответе укажите номер правильного варианта.

 

 

Какое из при­ве­ден­ных утвер­жде­ний не­вер­но?

 1) 

2) 

3) 

4) 

16.  На ко­ор­ди­нат­ной пря­мой от­ме­че­ны числа a и b.

В ответе укажите номер правильного варианта.

 

 

Какое из сле­ду­ю­щих утвер­жде­ний яв­ля­ет­ся вер­ным?

 1) 

2) 

3) 

4) 

17. На ко­ор­ди­нат­ной пря­мой от­ме­че­ны числа 

a, b, и c.

В ответе укажите номер правильного варианта.

 

 Ука­жи­те номер вер­но­го утвер­жде­ния.

 

1) 

2) 

3) 

4) 

18. На ко­ор­ди­нат­ной пря­мой от­ме­че­ны числа a и b.

В ответе укажите номер правильного варианта.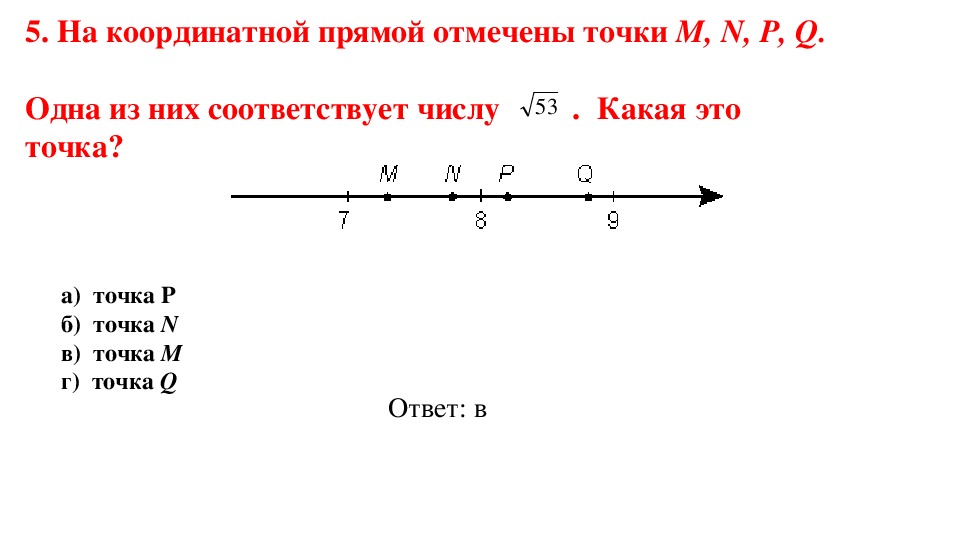

 

 

Какое из сле­ду­ю­щих утвер­жде­ний от­но­си­тель­но этих чисел яв­ля­ет­ся верным?

  1) a3​0

2) a − b  0

3) ab 

4) a + b  1

С равнение чисел

1. На ко­ор­ди­нат­ной пря­мой от­ме­че­ны числа   и  :

 

Какое из сле­ду­ю­щих чисел наибольшее?

 

1) 

2) 

3) 

4) 

2. Сравните числа x и y, если  ,  . В ответ запишите меньшее из чисел

3. О чис­лах  ,  ,   и   известно, что  ,  ,   . Сравнитe числа   и  .

В ответе укажите номер правильного варианта.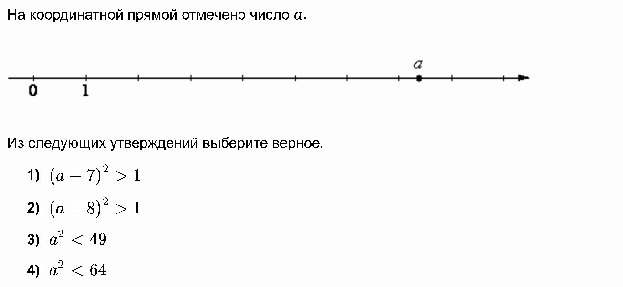

 1) 

2) 

3) 

4) Срав­нить невозможно

4. Известно, что  . Вы­бе­ри­те наи­мень­шее из чисел.

В ответе укажите номер правильного варианта.

 

1) 

2) 

3) 

4) 

5. Известно, что   Вы­бе­ри­те наи­мень­шее из чисел.

В ответе укажите номер правильного варианта.

 

1) 

2) 

3) 

4) 

6. Числа   и   от­ме­че­ны точ­ка­ми на ко­ор­ди­нат­ной пря­мой. Рас­по­ло­жи­те в по­ряд­ке воз­рас­та­ния числа      и 1.

В ответе укажите номер правильного варианта.

 

 

1) 

2) 

3) 

4) 

7.  Ка­ко­му из дан­ных про­ме­жут­ков при­над­ле­жит число  

В ответе укажите номер правильного варианта.

 

1) [0,5;0,6]

2) [0,6;0,7]

3) [0,7;0,8]

4) [0,8;0,9]

8. На ко­ор­ди­нат­ной пря­мой от­ме­че­но число   Рас­по­ло­жи­те в по­ряд­ке убы­ва­ния числа     и 

В от­ве­те укажите номер пра­виль­но­го варианта.

  1) 

2) 

3) 

4) 

9. На ко­ор­ди­нат­ной пря­мой от­ме­че­ны числа a и x.

 Какое из сле­ду­ю­щих чисел наи­мень­шее?

В ответе укажите номер правильного варианта.

 

1) 

2) 

3) 

4) 

10.  На ко­ор­ди­нат­ной пря­мой от­ме­че­ны числа a и b.

 Какое из сле­ду­ю­щих чисел наибольшее?

В ответе укажите номер правильного варианта.

 

1) a + b

2) −a

3) 2b

4) a − b

11. На ко­ор­ди­нат­ной пря­мой от­ме­че­но число a.

 Найдите наи­мень­шее из чисел a2, a3, a4.

В ответе укажите номер правильного варианта.

 

1) a2

2) a3

3) a4

4) не хва­та­ет дан­ных для ответа

12. На ко­ор­ди­нат­ной пря­мой от­ме­че­но число 

 Расположите в по­ряд­ке воз­рас­та­ния числа 

В ответе укажите номер правильного варианта.

 

1) 

2) 

3) 

4) 

13. На ко­ор­ди­нат­ной пря­мой от­ме­че­но число a.

 Найдите наи­боль­ш­ее из чисел a2, a3, a4.

В ответе укажите номер правильного варианта.

 

1) a2

2) a3

3) a4

4) не хва­та­ет дан­ных для ответа

14. Известно, что   и   — по­ло­жи­тель­ные числа и   Срав­ни­те   и 

В ответе укажите номер правильного варианта.

 

1) 

2) 

3) 

4) срав­нить невозможно

15.  На ко­ор­ди­нат­ной пря­мой точ­ка­ми от­ме­че­ны числа 

Какому числу со­от­вет­ству­ет точка B?

1) 

2) 

3) 0,42

4) 0,45

Числа на прямой

1. Какое из чисел от­ме­че­но на ко­ор­ди­нат­ной пря­мой точ­кой A?

 В ответе укажите номер правильного варианта.

 

1) 

2) 

3) 

4) 

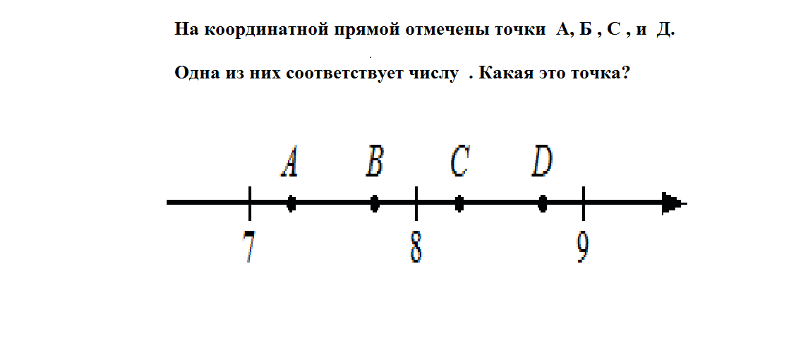
2. Одна из точек, от­ме­чен­ных на ко­ор­ди­нат­ной прямой, со­от­вет­ству­ет числу    Какая это точка?

В ответе укажите номер правильного варианта.

 

1) A

2) B

3) C

4) D

3.  Одно из чисел     от­ме­че­но на ко­ор­ди­нат­ной пря­мой точ­кой   . Ука­жи­те это число.

В от­ве­те укажите номер пра­виль­но­го варианта.

 

1) 

2) 

3) 

4) 

4. Одна из точек, от­ме­чен­ных на ко­ор­ди­нат­ной пря­мой, со­от­вет­ству­ет числу 

 

Какая это точка?

В ответе укажите номер правильного варианта.

 

1) точка A

2) точка B

3) точка C

4) точка D

5. Ка­ко­му из сле­ду­ю­щих чисел со­от­вет­ству­ет точка, от­ме­чен­ная на ко­ор­ди­нат­ной пря­мой?

 

В от­ве­те укажите номер пра­виль­но­го варианта.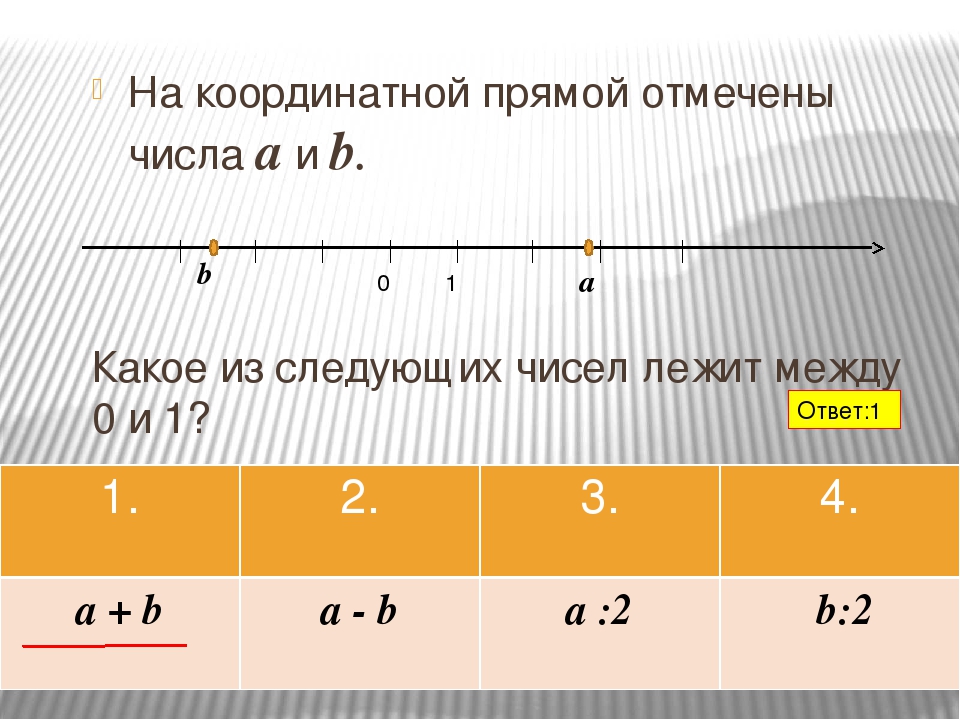

 

1) 

2) 

3) 

4) 

6. На ко­ор­ди­нат­ной пря­мой точ­ка­ми A, B, C и D от­ме­че­ны числа 0,098; −0,02; 0,09; 0,11. Какой точ­кой изоб­ра­жа­ет­ся число 0,09?

В ответе укажите номер правильного варианта.

 

1) A

2) B

3) C

4) D

7. На ко­ор­ди­нат­ной пря­мой от­ме­че­ны точки A, B, C, D. Одна из них со­от­вет­ству­ет числу   Какая это точка?

 

В ответе укажите номер правильного варианта.

 

1) точка A

2) точка B

3) точка C

4) точка D

8.  Известно, что число   отрицательное. На каком из ри­сун­ков точки с ко­ор­ди­на­та­ми   рас­по­ло­же­ны на ко­ор­ди­нат­ной пря­мой в пра­виль­ном порядке?

 

В ответе укажите номер правильного варианта.

 

1) 1

2) 2

3) 3

4) 4

9. На ко­ор­ди­нат­ной пря­мой от­ме­че­на точка А.

Известно, что она со­от­вет­ству­ет од­но­му из че­ты­рех ука­зан­ных ниже чисел. Ка­ко­му из чисел со­от­вет­ству­ет точка А?

 

1) 

2) 

3) 0,6

4) 4

10. На ко­ор­ди­нат­ной пря­мой от­ме­че­но число a.

Какое из утвер­жде­ний от­но­си­тель­но этого числа яв­ля­ет­ся верным?

 

1) a − 8 0

2) 7 − a 

3) a − 3 0

4) 2 − a  0

Выбор верного или неверного утверждения

1.  Известно, что   Какое из сле­ду­ю­щих чисел отрицательно?

В ответе укажите номер правильного варианта.

 1) 

2) 

3) 

4) 

2. Какое из сле­ду­ю­щих чисел за­клю­че­но между чис­ла­ми     и  

В ответе укажите номер правильного варианта.

 1) 0,1

2) 0,2

3) 0,3

4) 0,4

3. На ко­ор­ди­нат­ной пря­мой от­ме­че­ны числа a и b. Какое из сле­ду­ю­щих утвер­жде­ний не­вер­но?

 

1) 

2) 

3) 

4) 

4. Какое из при­ве­ден­ных ниже не­ра­венств яв­ля­ет­ся вер­ным при любых зна­че­ни­ях a и b, удо­вле­тво­ря­ю­щих усло­вию a  b?

В ответе укажите номер правильного варианта.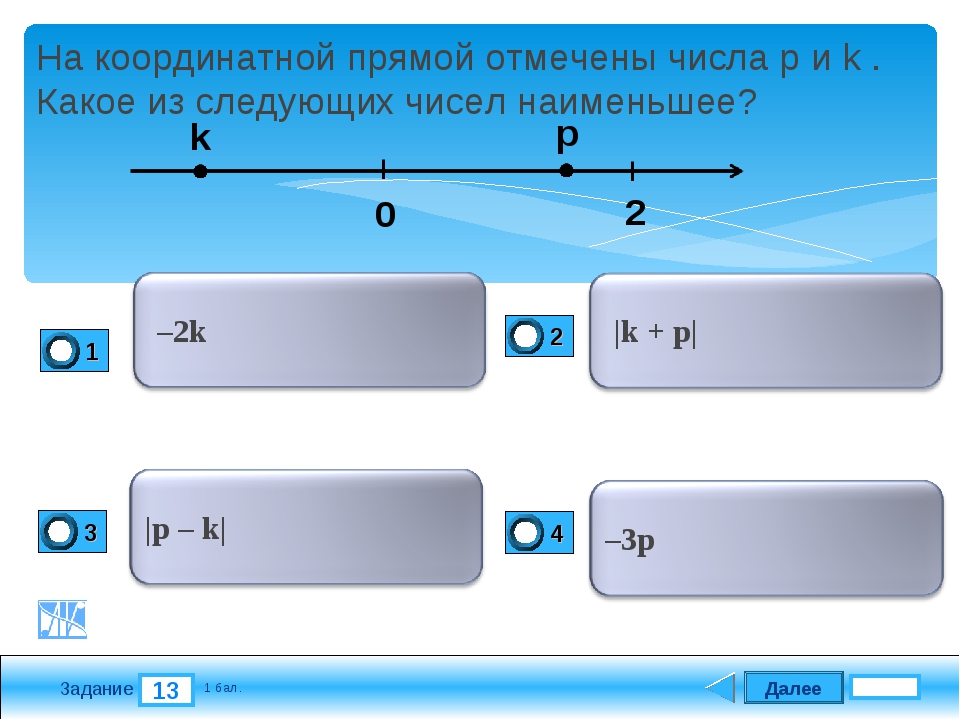

 1) b − a 

2) a − b  −1

3) a − b 

4) b − a  −3

5. На ко­ор­ди­нат­ной пря­мой от­ме­че­но число a.

 

Из сле­ду­ю­щих утвер­жде­ний вы­бе­ри­те вер­ное:

В ответе укажите номер правильного варианта.

 

1) (a − 6)2  1

2) (a − 7)2  1

3) a2  36

4) a2  49

6. На ко­ор­ди­нат­ной пря­мой от­ме­че­ны числа x и y. Какое из сле­ду­ю­щих утвер­жде­ний об этих чис­лах верно?

 

В ответе укажите номер правильного варианта.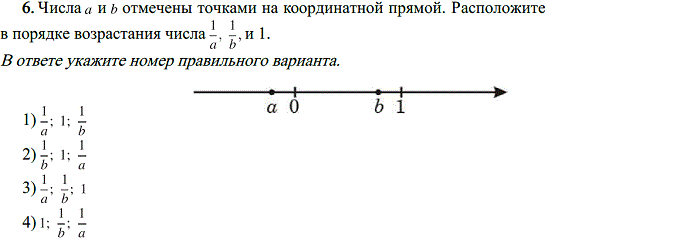

 

1)   и 

2)   и 

3)   и 

4)   и 

7. Ка­ко­му про­ме­жут­ку при­над­ле­жит число 

В ответе укажите номер правильного варианта.

 

1) [4; 5]

2) [5; 6]

3) [6; 7]

4) [7; 8]

8. На ко­ор­ди­нат­ной пря­мой от­ме­че­ны числа p, q и r.

 

Какая из раз­но­стей p − r, p − q, r − q отрицательна?

В ответе укажите номер правильного варианта.

 

1) p − r

2) p − q

3) r − q

4) ни одна из них

9.  На ко­ор­ди­нат­ной пря­мой от­ме­че­ны числа a, b и c.

 

Какая из раз­но­стей a − b, a − c, c − b положительна?

В ответе укажите номер правильного варианта.

 

1) a − b

2) a − c

3) c − b

4) ни одна из них

10. Значение ка­ко­го из дан­ных вы­ра­же­ний положительно, если известно, что x  0, y 

В ответе укажите номер правильного варианта.

 

1) xy

2) (x − y)y

3) (y − x)y

4) (y − x)x

Класс Домашняя работа от 13.

05.15г. — Студопедия

1.За­пи­ши­те в от­ве­те но­ме­ра тех вы­ра­же­ний, зна­че­ние ко­то­рых равно −5.

Но­ме­ра за­пи­ши­те в по­ряд­ке воз­рас­та­ния без про­бе­лов, за­пя­тых и дру­гих до­пол­ни­тель­ных сим­во­лов.

2.На ко­ор­ди­нат­ной пря­мой от­ме­че­ны числа a и b:

Какое из сле­ду­ю­щих чисел наи­боль­шее?

В от­ве­те ука­жи­те номер пра­виль­но­го ва­ри­ан­та.

1) a+b

2) −a

3) 2b

4) a−b

3.Ука­жи­те наи­боль­шее из сле­ду­ю­щих чисел:

В от­ве­те ука­жи­те номер пра­виль­но­го ва­ри­ан­та.

1)

2)

3)

4)

4.Пред­ставь­те вы­ра­же­ние в виде сте­пе­ни с ос­но­ва­ни­ем c.

5.Ре­ши­те урав­не­ние

6.Най­ди­те зна­че­ние вы­ра­же­ния при

7. Ре­ши­те не­ра­вен­ство и опре­де­ли­те, на каком ри­сун­ке изоб­ра­же­но мно­же­ство его ре­ше­ний.

В от­ве­те ука­жи­те номер пра­виль­но­го ва­ри­ан­та.

8.

9.В таб­ли­це при­ве­де­ны рас­сто­я­ния от Солн­ца до четырёх пла­нет Сол­неч­ной си­сте­мы. Какая из этих пла­нет ближе всех к Солн­цу?

Пла­не­та Неп­тун Юпи­тер Уран Ве­не­ра
Рас­сто­я­ние (в км) 4,497 · 109 7,781 · 108 2,871 · 109 1,082 · 108

В от­ве­те ука­жи­те номер пра­виль­но­го ва­ри­ан­та.


1) Неп­тун 2) Юпи­тер 3) Уран 4) Ве­не­ра

10.На ри­сун­ке по­ка­за­но, как из­ме­ня­лась тем­пе­ра­ту­ра воз­ду­ха на про­тя­же­нии одних суток. По го­ри­зон­та­ли ука­за­но время суток, по вер­ти­ка­ли — зна­че­ние тем­пе­ра­ту­ры в гра­ду­сах Цель­сия. Сколь­ко часов в пер­вой по­ло­ви­не дня тем­пе­ра­ту­ра не пре­вы­ша­ла 0° C?

11.На пред­при­я­тии ра­бо­та­ло 240 со­труд­ни­ков. После мо­дер­ни­за­ции про­из­вод­ства их число со­кра­ти­лось до 192. На сколь­ко про­цен­тов со­кра­ти­лось число со­труд­ни­ков пред­при­я­тия?

12.Акции пред­при­я­тия рас­пре­де­ле­ны между го­су­дар­ством и част­ны­ми ли­ца­ми в от­но­ше­нии 3:5. Общая при­быль пред­при­я­тия после упла­ты на­ло­гов за год со­ста­ви­ла 32 млн. р. Какая сумма из этой при­бы­ли долж­на пойти на вы­пла­ту част­ным ак­ци­о­не­рам?

13.Закон Мен­де­ле­е­ва-Кла­пей­ро­на можно за­пи­сать в виде PV = νRT, где P — дав­ле­ние (в пас­ка­лях), V — объём (в м3), ν — ко­ли­че­ство ве­ще­ства (в молях), T — тем­пе­ра­ту­ра (в гра­ду­сах Кель­ви­на), а R — уни­вер­саль­ная га­зо­вая по­сто­ян­ная, рав­ная 8,31 Дж/(К⋅моль). Поль­зу­ясь этой фор­му­лой, най­ди­те тем­пе­ра­ту­ру T (в гра­ду­сах Кель­ви­на), если ν = 68,2 моль, P = 37 782,8 Па, V = 6 м3.

Положительные и отрицательные числа. Числа на координатной прямой.

⇐ ПредыдущаяСтр 2 из 2

 

21.Какие из данных примеров решены верно?

а) -2,7 ∙ = -3,9; в) 3,01 ∙

б) -2,17 ∙ (-1,5) = -3,255; г) .

 

22. Какие из данных примеров решены неверно?

а) -7,112 : (-5,6) = -1,27; в) ;

б) -1,21 : (-1,1) = -1,1; г)

23. Представьте в виде десятичной дроби : ;

24. Выполните действия: -2,5 ∙ (-1,6) + 41,6 : (-4) ;

25. Найдите значение выражения: m2 – 1, 3 , при m = -1,3 ;

26. Выполните действия : ;

27. Выполните действия : ;

28. Вычислите:

а) б) в) г)

д) е) ж) з) и)

 

29. На ко­ор­ди­нат­ной пря­мой от­ме­че­ны числа a и b.

Какое из сле­ду­ю­щих чисел наи­боль­шее?В от­ве­те ука­жи­те номер пра­виль­но­го ва­ри­ан­та.

 

1) a + b 2) –a 3) 2b 4) a − b

30. На ко­ор­ди­нат­ной пря­мой от­ме­че­но число

 

31.Рас­по­ло­жи­те в по­ряд­ке воз­рас­та­ния числа В от­ве­те ука­жи­те номер пра­виль­но­го ва­ри­ан­та.

 

1) 2) 3) 4)

 

32. На ко­ор­ди­нат­ной пря­мой от­ме­че­но число a.

 

Из сле­ду­ю­щих утвер­жде­ний вы­бе­ри­те вер­ное. В от­ве­те ука­жи­те номер пра­виль­но­го ва­ри­ан­та:

1) (a − 6)2 > 1; 2) (a − 7)2 > 1; 3) a2 > 36; 4) a2 > 49

 

33. Зна­че­ние ка­ко­го из дан­ных вы­ра­же­ний по­ло­жи­тель­но, если из­вест­но, что x > 0, y < 0?

В от­ве­те ука­жи­те номер пра­виль­но­го ва­ри­ан­та.

1) xy ; 2) (x − y)y ; 3) (y − x)y ; 4) (y − x)x

_____________________________

Дополнительные задания:

34. Вычислите: а) б)

35. Каж­дую се­кун­ду бак­те­рия де­лит­ся на две новые бак­те­рии. Из­вест­но, что весь объём од­но­го ста­ка­на бак­те­рии за­пол­ня­ют за 1 час. За сколь­ко се­кунд бак­те­рии за­пол­ня­ют по­ло­ви­ну ста­ка­на?

 

⇐ Предыдущая12

Поиск по сайту:

1.1: Действительные числа и числовая строка

НАВЫКИ ДЛЯ РАЗВИТИЯ

  • Постройте числовую линию и точки на ней.
  • Используйте числовую строку, чтобы определить порядок действительных чисел.
  • Определяет противоположность действительного числа.
  • Определите абсолютное значение действительного числа.

Определения

Набор представляет собой набор объектов, обычно сгруппированных в фигурных скобках \ (\ {\) \ (\} \), где каждый объект называется элементом .Например, \ (\ {\ text {красный, зеленый, синий} \} \) — это набор цветов. Подмножество — это набор, состоящий из элементов, которые принадлежат данному набору. Например, \ (\ {\ text {зеленый, синий} \} \) — это подмножество цвета, указанного выше. Набор без элементов называется пустым набором и имеет свои собственные специальные обозначения, \ (\ {\) \ (\} \) или \ (\ varnothing \).

Изучая математику, мы ориентируемся на специальные наборы чисел. Набор из натуральных (или счетных) чисел , обозначенных \ (\ mathbb {N} \), равен

.

\ (\ {1,2,3,4,5, \ dots \} \ quad \ color {Cerulean} {Natural \: Numbers} \)

Три точки \ ((\ точки) \) называются многоточием и указывают на то, что числа продолжаются неограниченно.Набор целых чисел , обозначаемый \ (\ mathbb {W} \), представляет собой набор натуральных чисел в сочетании с нулем.

\ (\ {0,1,2,3,4,5, \ dots \} \ quad \ color {Cerulean} {Whole \: Numbers} \)

Набор из целых чисел , обозначаемый \ (\ mathbb {Z} \), состоит из положительных и отрицательных целых чисел, а также нуля.

\ (\ {\ dots, -3, -2, -1,0,1,2,3, \ dots \} \ quad \ color {Cerulean} {Целые числа} \)

Обратите внимание, что наборы натуральных и целых чисел являются подмножествами набора целых чисел.

Рациональные числа , обозначаемые \ (\ mathbb {Q} \), определяются как любое число в форме \ (\ dfrac {a} {b} \), где \ (a \) и \ (b \) являются целыми числами и \ (b \) не равно нулю. Десятичные дроби, которые повторяются или заканчиваются, рациональны. Например,

\ (0,7 = \ frac {7} {10} \ quad \ text {and} \ quad 0. \ overline {3} = 0,3333 \ dots = \ frac {1} {3} \)

Набор целых чисел является подмножеством набора рациональных чисел, потому что каждое целое число может быть выражено как отношение целого числа к \ (1 \).Другими словами, любое целое число может быть записано над \ (1 \) и может считаться рациональным числом. Например,

\ (5 = \ frac {5} {1} \)

Иррациональные числа — это любое число, которое нельзя записать как отношение двух целых чисел. Неповторяющиеся десятичные дроби, которые не повторяются, иррациональны. Например,

\ (\ pi = 3,14159 \ точек \ quad \ text {и} \ quad \ sqrt {2} = 1,41421 \ точек \)

Набор действительных чисел , обозначаемый \ (\ mathbb {R} \), определяется как набор всех рациональных чисел в сочетании с набором всех иррациональных чисел.Следовательно, все числа, определенные до сих пор, являются подмножествами множества действительных чисел. Таким образом,

Рисунок \ (\ PageIndex {1} \): Действительные числа

Числовая строка

Строка вещественных чисел , или просто числовая линия, позволяет нам визуально отображать действительные числа, связывая их с уникальными точками на линии. Действительное число, связанное с точкой, называется координатой . Точка на линии действительного числа, связанная с координатой, называется ее графиком .

Чтобы построить числовую линию, нарисуйте горизонтальную линию со стрелками на обоих концах, чтобы указать, что она продолжается без границ. Затем выберите любую точку, представляющую число ноль; эта точка называется исходной точкой .

Рисунок \ (\ PageIndex {2} \)

Отметьте одинаковую длину с обеих сторон от исходной точки и пометьте каждую отметку, чтобы определить масштаб. Положительные действительные числа лежат справа от начала координат, а отрицательные действительные числа — слева. Число ноль \ ((0) \) не является ни положительным, ни отрицательным.Обычно каждая отметка представляет собой одну единицу.

Рисунок \ (\ PageIndex {3} \)

Как показано ниже, масштаб не всегда должен быть равным одной единице. В первой числовой строке каждая отметка представляет две единицы. Во втором случае каждая отметка представляет собой \ (\ frac {1} {7} \) единицы.

Рисунок \ (\ PageIndex {4} \)

График каждого действительного числа показан в виде точки в соответствующей точке числовой прямой. Частичный график набора целых чисел \ (\ mathbb {Z} \) следует:

Рисунок \ (\ PageIndex {5} \)

Пример \ (\ PageIndex {1} \)

Изобразите следующий набор действительных чисел:

Решение

Изобразите числа на числовой прямой со шкалой, где каждая отметка представляет собой \ (\ frac {1} {2} \) единицы.

Рисунок \ (\ PageIndex {6} \)

Заказ вещественных чисел

При сравнении действительных чисел в числовой строке большее число всегда будет находиться справа от меньшего. Ясно, что \ (15 \) больше, чем \ (5 \), но может быть не так ясно видеть, что \ (- 1 \) больше, чем \ (- 5 \), пока мы не построим график каждого числа на числовая строка.

Рисунок \ (\ PageIndex {7} \)

Мы используем символы, чтобы помочь нам эффективно передавать отношения между числами в числовой строке. Символы, используемые для описания отношения равенства между числами, следующие:

\ [\ begin {align *} & = \ quad \ color {Cerulean} {is \ equal \ to} \\ & \ neq \ quad \ color {Cerulean} {is \ not \ equal \ to} \\ & \ приблизительно \ quad \ color {Cerulean} {\ приблизительно \ равно \ to} \ end {align *} \]

Эти символы используются и интерпретируются следующим образом:

\ [\ begin {align *} & 5 = 5 \ qquad && \ color {Cerulean} {5 \ is \ equal \ to \ 5} \\ & 0 \ neq 5 \ qquad && \ color {Cerulean} {0 \ is \ не \ равно \ к \ 5} \\ & \ пи \ приблизительно 3.14 \ quad && \ color {Cerulean} {pi \ is \ приблизительно \ equal \ to \ 3.14} \ end {align *} \]

Далее мы определяем символы, которые обозначают отношение порядка между действительными числами.

\ [\ begin {align *} & <\ quad \ color {Cerulean} {Less \ than} \\ &> \ quad \ color {Cerulean} {Greater \ than} \\ & \ leq \ quad \ color {Cerulean } {Меньше \ чем \ или \ равно \ to} \\ & \ geq \ quad \ color {Cerulean} {Больше \ чем \ или \ равно \ to} \ end {align *} \]

Эти символы позволяют сравнивать два числа.Например,

\ (- 120 <-10 \ quad \ color {Cerulean} {Negative \ 120 \ is \ less \ than \ negative \ 10} \)

Поскольку график \ (- 120 \) находится слева от графика \ (- 10 \) на числовой прямой, это число меньше \ (- 10 \). Мы могли бы написать эквивалентное утверждение следующим образом:

\ (- 10> -120 \ quad \ color {Cerulean} {Отрицательное \ 10 \ больше \, чем \ отрицательное \ 120} \)

Аналогичным образом, поскольку график нуля находится справа от графика любого отрицательного числа на числовой прямой, ноль больше любого отрицательного числа.

\ (0> -50 \ quad \ color {Cerulean} {Ноль \ больше \, чем \ negative \ 50} \)

Символы \ (<\) и \ (> \) используются для обозначения строгих неравенств , а символы и используются для обозначения включающих неравенств . В некоторых ситуациях можно правильно нанести более одного символа. Например, оба следующих утверждения верны:

\ (- 10 <0 \ \ text {and} \ -10 \ leq 0 \)

Кроме того, компонент инклюзивного неравенства «или равно» позволяет нам правильно записать следующее:

\ (- 10 \ leq -10 \)

Логическое использование слова «или» требует, чтобы выполнялось только одно из условий: «меньше чем» или «равно».”

Пример \ (\ PageIndex {2} \)

Заполните пустое поле с помощью \ (<, = \) или \ (>: −2 \) ____ \ (- 12 \).

Решение

Используйте>, потому что график \ (- 2 \) находится справа от графика \ (- 12 \) на числовой прямой. Следовательно, \ (- 2> −12 \), что означает «отрицательные два больше, чем отрицательные двенадцать».

Рисунок \ (\ PageIndex {8} \)

Ответ:

\ (- 2> -12 \)

В этом тексте мы часто будем указывать на эквивалентные обозначения, используемые для электронного выражения математических величин с использованием стандартных символов, доступных на клавиатуре.Начнем с эквивалентного текстового обозначения неравенств:

\ [\ begin {align *} & \ geq && «> =» \\ & \ leq && «<=" \\ & \ neq && "! =" \ End {align *} \]

Многие калькуляторы, системы компьютерной алгебры и языки программирования используют эту нотацию.

Противоположности

напротив любого действительного числа \ (a \) есть \ (- a \). Противоположные действительные числа находятся на одинаковом расстоянии от начала координат на числовой прямой, но их графики лежат по разные стороны от начала координат, а числа имеют противоположные знаки.

Рисунок \ (\ PageIndex {9} \)

Например, мы говорим, что противоположностью \ (10 ​​\) является \ (- 10 \).

Затем рассмотрим противоположность отрицательного числа. Учитывая целое число \ (- 7 \), целое число на том же расстоянии от начала координат и с противоположным знаком будет \ (+ 7 \), или просто \ (7 \).

Рисунок \ (\ PageIndex {10} \)

Следовательно, мы говорим, что противоположность \ (- 7 \) есть \ (- (- 7) = 7 \). Эта идея приводит к тому, что часто называют двойным отрицательным свойством . Для любого действительного числа \ (a \),

\ (- (- а) = а \)

Пример \ (\ PageIndex {3} \)

Что противоположно \ (- \ frac {3} {4} \)?

Решение

Здесь мы применяем свойство двойного отрицания.

\ (- (- \ frac {3} {4}) = \ frac {3} {4} \)

Пример \ (\ PageIndex {4} \)

Упростить \ (- (- (4)) \)

Решение

Начните с самых внутренних скобок, найдя противоположность \ (+ 4 \).

\ [\ begin {align *} — (- (4)) & = — (\ color {Cerulean} {- (4)} \ color {Black} {)} \\ & = — (\ color {Cerulean} {-4} \ color {Черный} {)} \\ & = 4 \ end {align *} \]

Ответ

4

Пример \ (\ PageIndex {5} \)

Упростить: \ (- (- (- 2)) \).

Решение

Примените двойное отрицательное свойство, начиная с самых внутренних круглых скобок.

\ [\ begin {align *} — (- (- 2)) & = — (\ color {Cerulean} {- (- 2)} \ color {Black} {)} \\ & = — (\ color { Церулеан} {2} \ color {Черный} {)} \\ & = — 2 \ end {align *} \]

Ответ

-2

подсказка

Если число подряд идущих отрицательных знаков четное, результат положительный. Если число подряд идущих отрицательных знаков нечетное, результат отрицательный.

Попробуй!

Упражнение \ (\ PageIndex {1} \)

Упростить: \ (- (- (- (5))) \).

Ответ

-5

Процедура:

\ [\ begin {align *} — (- (- (5))) & = — (\ color {Cerulean} {- (- (5))} \ color {Black} {)} \\ & = — (\ color {Cerulean} {- (- 5)} \ color {Black} {)} \\ & = — (\ color {Cerulean} {5} \ color {Black} {)} \\ & = -5 \ конец {выравнивание *} \]

Видео решение:

(нажмите, чтобы посмотреть видео)

Абсолютное значение

Абсолютное значение действительного числа \ (a \), обозначенного \ (| a | \), определяется как расстояние между нулем (началом координат) и графиком этого действительного числа на числовой прямой.Поскольку это расстояние, оно всегда положительно. Например,

\ (| -4 | = 4 \ quad \ text {and} \ quad | 4 | = 4 \)

И \ (4 \), и \ (- 4 \) находятся на четыре единицы от начала координат, как показано ниже:

Рисунок \ (\ PageIndex {11} \)

Пример \ (\ PageIndex {6} \)

Упростить:

а. \ (| -12 | \)

б. \ (| 12 | \)

Решение

И \ (- 12 \), и \ (12 \) находятся в двенадцати единицах от начала координат числовой прямой. Следовательно,

\ (| -12 | = 12 \ quad \ text {and} \ quad | 12 | = 12 \)

Ответ

а.\ (12 \) b. \ (12 \)

Также стоит отметить, что

\ (| 0 | = 0 \)

Абсолютное значение может быть выражено в текстовом виде с помощью записи abs \ ((a) \). Мы часто сталкиваемся с отрицательными абсолютными значениями, такими как \ (- | 3 | \) или \ (- \) abs \ ((3) \). Обратите внимание, что знак минуса стоит перед символом абсолютного значения. В этом случае сначала обработайте абсолютное значение, а затем найдите результат, противоположный результату.

\ (\ begin {array} {rrr} {- | 3 |} & {} & {- | — 3 |} \\ {\ color {Cerulean} {\ downarrow}} & {\ text {and}} & {\ color {Cerulean} {\ downarrow}} \\ {= — 3} & {} & {= — 3} \ end {array} \)

Постарайтесь не путать это с двойным отрицательным свойством, которое утверждает, что \ (- (- 7) = + 7 \).

Пример \ (\ PageIndex {7} \)

Simplfy: \ (- | — (- 7) | \).

Решение

Во-первых, найдите в абсолютном значении противоположность \ (- 7 \). Затем найдите результат, противоположный результату.

\ [\ begin {align *} — | \ color {Cerulean} {- (- 7)} \ color {Black} {|} & = — | \ color {Cerulean} {7} \ color {Black} {| } \\ & = — 7 \ end {align *} \]

Ответ

-7

На этом этапе мы можем определить, какие действительные числа имеют конкретное абсолютное значение.Например,

\ (|? | = 5 \)

Представьте себе действительное число, расстояние от которого до начала координат составляет \ (5 \) единиц. Есть два решения: расстояние справа от начала координат и расстояние слева от начала координат, а именно \ (\ {\ pm 5 \} \). Символ \ ((\ pm) \) читается как «плюс или минус» и означает, что есть два ответа, один положительный и один отрицательный.

\ (| -5 | = 5 \ \ quad \ text {and} \ quad | 5 | = 5 \)

Теперь рассмотрим следующее:

\ (|? | = -5 \)

Здесь мы хотим найти значение, для которого расстояние до начала координат отрицательно.Поскольку отрицательное расстояние не определено, это уравнение не имеет решения. Если уравнение не имеет решения, мы говорим, что решение — это пустое множество: \ (\ varnothing \).

Основные выводы

  • Любое действительное число может быть связано с точкой на линии.
  • Создайте числовую линию, сначала указав источник и отметив шкалу, соответствующую данной задаче.
  • Отрицательные числа лежат слева от начала координат, а положительные числа — справа.
  • Меньшие числа всегда лежат слева от больших чисел в числовой строке.
  • Противоположное положительное число отрицательное, а противоположное отрицательному — положительное.
  • Абсолютное значение любого действительного числа всегда положительно, потому что оно определяется как расстояние от нуля (начала координат) на числовой прямой.
  • Абсолютное значение нуля равно нулю.

Упражнение \ (\ PageIndex {2} \)

Используйте обозначение набора для перечисления описанных элементов.

  1. Часы на часах.
  2. Дни недели.
  3. Первые десять целых чисел.
  4. Первые десять натуральных чисел.
  5. Первые пять четных положительных целых чисел.
  6. Первые пять положительных нечетных целых чисел.
Ответ

1. \ (\ {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 \} \)

3. \ (\ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9 \} \)

5.\ (\ {2, 4, 6, 8, 10 \} \)

Упражнение \ (\ PageIndex {3} \)

Определите, являются ли следующие действительные числа целыми, рациональными или иррациональными.

  1. \ (12 \)
  2. \ (- 3 \)
  3. \ (4.5 \)
  4. \ (- 5 \)
  5. \ (0,3 \ overline {6} \)
  6. \ (0. \ Overline {3} \)
  7. \ (1.001000100001 \ точки \)
  8. \ (1.00 \ overline {1} \)
  9. \ (е = 2,71828 \ точек \)
  10. \ (\ sqrt {7} = 2.645751 \ точки \)
  11. \ (- 7 \)
  12. \ (3,14 \)
  13. \ (227 \)
  14. \ (1,33 \)
  15. \ (0 \)
  16. \ (8,675,309 \)
Ответ

1: целое, рациональное

3: Рациональный

5: Рациональный

7: Иррациональное

9: Иррациональное

11: целое число, рациональное

13: Рациональный

15: Целое, рациональное

Упражнение \ (\ PageIndex {4} \)

Верно или неверно.

  1. Все целые числа являются рациональными числами.
  2. Все числа являются целыми числами.
  3. Все рациональные числа являются целыми числами.
  4. Некоторые иррациональные числа рациональны.
  5. Все конечные десятичные числа являются рациональными.
  6. Все иррациональные числа действительны.
Ответ

1: Правда

3: Ложь

5: Правда

Упражнение \ (\ PageIndex {5} \)

Выберите соответствующий масштаб и нанесите на числовую линию следующие наборы действительных чисел.

  1. \ (\ {- 3, 0, 3 \} \)
  2. \ (\ {- 2, 2, 4, 6, 8, 10 \} \)
  3. \ (\ {- 2, −1/3, 2/3, 5/3 \} \)
  4. \ (\ {- 5/2, −1/2, 0, 1/2, 2 \} \)
  5. \ (\ {- 5/7, 0, 2/7, 1 \} \)
  6. \ (\ {–5, –2, –1, 0 \} \)
  7. \ (\ {−3, −2, 0, 2, 5 \} \)
  8. \ (\ {- 2.5, −1.5, 0, 1, 2.5 \} \)
  9. \ (\ {0, 0.3, 0.6, 0.9, 1.2 \} \)
  10. \ (\ {- 10, 30, 50 \} \)
  11. \ (\ {- 6, 0, 3, 9, 12 \} \)
  12. \ (\ {- 15, −9, 0, 9, 15 \} \)
Ответ

1.\ (\ {- 3, 0, 3 \} \)

Рисунок \ (\ PageIndex {12} \)

3. \ (\ {- 2, −1/3, 2/3, 5/3 \} \)

Рисунок \ (\ PageIndex {13} \)

5. \ (\ {- 5/7, 0, 2/7, 1 \} \)

Рисунок \ (\ PageIndex {14} \)

7. \ (\ {−3, −2, 0, 2, 5 \} \)

Рисунок \ (\ PageIndex {15} \)

9. \ (\ {0, 0.3, 0.6, 0.9, 1.2 \} \)

Рисунок \ (\ PageIndex {16} \)

11. \ (\ {- 6, 0, 3, 9, 12 \} \)

Рисунок \ (\ PageIndex {17} \)

Упражнение \ (\ PageIndex {6} \)

Заполните пустое поле с помощью \ (<, = \) или \ (> \).

  1. \ (- 7 \) ___ \ (0 \)
  2. \ (30 \) ___ \ (2 \)
  3. \ (10 ​​\) ___ \ (- 10 \)
  4. \ (- 150 \) ___ \ (- 75 \)
  5. \ (- 0,5 \) ___ \ (- 1,5 \)
  6. \ (0 \) ___ \ (0 \)
  7. \ (- 500 \) ___ \ (200 \)
  8. \ (- 1 \) ___ \ (- 200 \)
  9. \ (- 10 \) ___ \ (- 10 \)
  10. \ (- 40 \) ___ \ (- 41 \)
Ответ

1. \ (<\)

3. \ (> \)

5.\ (> \)

7. \ (<\)

9. \ (= \)

Упражнение \ (\ PageIndex {7} \)

Верно или неверно.

  1. \ (5 ≠ 7 \)
  2. \ (4 = 5 \)
  3. \ (1 ≠ 1 \)
  4. \ (- 5> −10 \)
  5. \ (4 \ leq 4 \)
  6. \ (- 12 \ geq 0 \)
  7. \ (- 10 = −10 \)
  8. \ (3> 3 \)
  9. \ (- 1000 <−20 \)
  10. \ (0 = 0 \)
Ответ

1.Правда

3. Неверно

5. Верно

7. Верно

9. Верно

Упражнение \ (\ PageIndex {8} \)

Перечислите номера.

  1. Перечислите три целых числа меньше \ (- 5 \).
  2. Перечислите три целых числа больше \ (- 10 \).
  3. Перечислите три рациональных числа меньше нуля.
  4. Перечислите три рациональных числа больше нуля.
  5. Перечислите три целых числа от \ (- 20 \) до \ (- 5 \).
  6. Перечислите три рациональных числа между \ (0 \) и \ (1 \).
Ответ

1. \ (- 10, −7, −6 \) (ответы могут отличаться)

3. \ (- 1, −2/3, −1/3 \) (ответы могут отличаться)

5. \ (- 15, −10, −7 \) (ответы могут отличаться)

Упражнение \ (\ PageIndex {9} \)

Переведите каждое утверждение в предложение на английском языке.

  1. \ (10 ​​<20 \)
  2. \ (- 50 \ leq −10 \)
  3. \ (- 4 \ neq 0 \)
  4. \ (30 \ geq -1 \)
  5. \ (0 = 0 \)
  6. \ (е \ около 2.718 \)
Ответ

1. Десять меньше двадцати.

3. Отрицательная четверка не равна нулю.

5. Ноль равен нулю.

Упражнение \ (\ PageIndex {10} \)

Переведите следующее в математическое выражение.

  1. Отрицательная семерка меньше нуля.
  2. Двадцать четыре не равно десяти.
  3. Ноль больше или равен отрицательному.
  4. Четыре больше или равно минус двадцать один.
  5. Отрицательное два равно отрицательному двум.
  6. Отрицательные две тысячи меньше отрицательных одной тысячи.
Ответ

1. \ (- 7 <0 \)

3. \ (0 \ geq −1 \)

5. \ (- 2 = −2 \)

Упражнение \ (\ PageIndex {11} \)

Упростить.

  1. \ (- (- 9) \)
  2. \ (- (- 35) \)
  3. \ (- (10) \)
  4. \ (- (3) \)
  5. \ (- (5) \)
  6. \ (- (34) \)
  7. \ (- (- 1) \)
  8. \ (- (- (- 1)) \)
  9. \ (- (- (1)) \)
  10. \ (- (- (- 3)) \)
  11. \ (- (- (- (- 11))) \)
Ответ

1.\ (9 \)

3. \ (- 10 \)

5. \ (- 5 \)

7. \ (1 \)

9. \ (1 \)

11. \ (11 \)

Упражнение \ (\ PageIndex {12} \)

Ответьте на следующие вопросы.

  1. Что является противоположностью \ (- 12 \)
  2. Что противоположно \ (\ pi \)?
  3. Что наоборот \ (- 0,01 \)?
  4. Противоположность \ (- 12 \) меньше или больше, чем \ (- 11 \)?
  5. Противоположность \ (7 \) меньше или больше, чем \ (- 6 \)?
Ответ

2.\ (- \ пи \)

4. Больше

Упражнение \ (\ PageIndex {13} \)

Заполните пустое поле с помощью \ (<, = \) или \ (> \).

  1. \ (- 7 \) ___ \ (- (- 8) \)
  2. \ (6 \) ___ \ (- (6) \)
  3. \ (13 \) ___ \ (- (- 12) \)
  4. \ (- (- 5) \) ___ \ (- (- 2) \)
  5. \ (- 100 \) ___ \ (- (- (- 50)) \)
  6. \ (44 \) ___ \ (- (- 44) \)
Ответ

1.\ (<\)

3. \ (> \)

5. \ (<\)

Упражнение \ (\ PageIndex {14} \)

Упростить.

  1. \ (| 20 | \)
  2. \ (| -20 | \)
  3. \ (| -33 | \)
  4. \ (| -0,75 | \)
  5. \ (| — \ frac {3} {5} | \)
  6. \ (| 38 | \)
  7. \ (| 0 | \)
  8. \ (| 1 | \)
  9. \ (- | 12 | \)
  10. \ (- | −20 | \)
  11. \ (- | 20 | \)
  12. \ (- | −8 | \)
  13. \ (- | 7 | \)
  14. \ (- | −316 | \)
  15. \ (- (- | \ frac {8} {9} |) \)
  16. \ (| — (- 2) | \)
  17. \ (- | — (- 3) | \)
  18. \ (- (- | 5 |) \)
  19. \ (- (- | −45 |) \)
  20. \ (- | — (- 21) | \)
  21. абс \ ((6) \)
  22. абс \ ((- 7) \)
  23. \ (- \) абс \ ((5) \)
  24. \ (- \) абс \ ((- 19) \)
  25. \ (- (- \) абс \ ((9)) \)
  26. \ (- \) абс \ ((- (- 12)) \)
Ответ

1.\ (20 \)

3. \ (33 \)

5. \ (\ frac {3} {5} \)

7. \ (0 \)

9. \ (- 12 \)

11. \ (- 20 \)

13. \ (- 7 \)

15. \ (\ frac {8} {9} \)

17. \ (- 3 \)

19. \ (45 \)

21. \ (6 \)

23. \ (- 5 \)

25. \ (9 \)

Упражнение \ (\ PageIndex {15} \)

Определить неизвестное.

  1. \ (|? | = 9 \)
  2. \ (|? | = 15 \)
  3. \ (|? | = 0 \)
  4. \ (|? | = 1 \)
  5. \ (|? | = −8 \)
  6. \ (|? | = −20 \)
  7. \ (|? | −10 = −2 \)
  8. \ (|? | + 5 = 14 \)
Ответ

1.\ (\ pm 9 \)

3. \ (0 \)

5. \ (\ varnothing \), решения нет

7. \ (\ pm 8 \)

Упражнение \ (\ PageIndex {16} \)

Заполните пустое поле с помощью \ (<, = \) или \ (> \).

  1. \ (| −2 | \) ____ \ (0 \)
  2. \ (| −7 | \) ____ \ (| −10 | \)
  3. \ (- 10 \) ____ \ (- | −2 | \)
  4. \ (| −6 | \) ____ \ (| — (- 6) | \)
  5. \ (- | 3 | \) ____ \ (| — (- 5) | \)
  6. \ (0 \) ____ \ (- | — (- 4) | \)
Ответ

1.\ (> \)

3. \ (<\)

5. \ (<\)

Упражнение \ (\ PageIndex {17} \)

Темы дискуссионной доски.

  1. Изучите и обсудите историю числа ноль.
  2. Изучите и обсудите различные системы нумерации на протяжении всей истории.
  3. Изучите и обсудите определение и историю \ (\ pi \).
  4. Исследуйте историю иррациональных чисел. Кому приписывают доказательство иррациональности квадратного корня из \ (2 \) и что с ним случилось?
  5. Изучите и обсудите историю абсолютных ценностей.
  6. Обсудите определение абсолютной величины «просто положительно»

дробей, числовых строк и порядка

дробей, числовых строк и порядка

Дроби, числовые строки и порядок

Что не так в следующем примере рекламного заявления?

Только на один день сэкономьте , , и даже больше ‼! Это распродажа, которую нельзя пропустить ‼!

Каждое значение дроби меньше предыдущего значения, но окончание « и даже больше » означает, что значение каждой дроби становится больше.Утверждение — распространенная ошибка, которую допускают многие люди при использовании дробей. Здесь порядок дробей в утверждении основан на значении знаменателя, а не на истинном значении дроби. Выписка должна быть: Только за один день сэкономьте , , и даже больше ‼! , поскольку реклама подразумевает, что на некоторых товарах человек может сэкономить более половины указанной цены.

Мы используем модель числовой линии, чтобы проиллюстрировать порядок дроби для значений от 0 до 1.Мы делим эту длину на две части равного размера и помечаем точку, где сегмент делится, координатой. Расстояние от 0 до представляет собой длину половины всего сегмента от 0 до 1.

Далее мы делим каждую из этих половинок пополам; точки, где каждый сегмент разделен, представлены дробями и. Как и в случае с эквивалентными дробями из предыдущего сеанса, мы можем пометить точку в как, то есть это еще один способ визуализировать эквивалентные дроби.

Следующие диаграммы иллюстрируют расширение отношений порядка дроби до двенадцатой, шестой, четвертой, трети и половины, а также то, как они соотносятся друг с другом в сегменте от 0 до 1.

Мы объединяем эти числовые линии на иллюстрации ниже в одну числовую линию с координатами, обозначенными в упрощенной форме для каждой из дробей на иллюстрации выше.

Когда мы сравниваем значения, то самое левое на числовой строке имеет наименьшее значение.Глядя на диаграмму ниже, мы видим это (значения обведены). Точно так же мы видим это (значения в рамке).

Если бы мы не ссылались на завершенную числовую прямую, мы все равно могли бы определить эти неравенства, заменив каждую пару дробей на дроби с общими знаменателями .

Примеры:

Так как, и, у нас есть. Двенадцатые — это общий знаменатель для четвертей и третей.

Так как и у нас есть.Шестая часть — это общий знаменатель для половин и шестых.

Отметим также, что мы могли бы сравнить все четыре дроби,,, и, заменив их все на общий знаменатель , равный двенадцатым. Поскольку у нас есть. Преобразуя дробные значения в дроби с общими знаменателями, мы можем легко сравнивать их относительные размеры.

Обратите внимание, что наименьший общий знаменатель — это наименьшее общее кратное (НОК) 2, 3, 4 и 6.Значение НОК (2, 3, 4, 6) равно 12, как показано ниже, с заданным методом пересечения для поиска наименьшего общего кратного.

Напоминание: мы также можем найти наименьшее общее кратное (НОК) путем разложения на простые множители в экспоненциальную форму.

2 = 2
3 = 3
4 = 2 2
6 = 2 · 3

Взяв наибольшую экспоненту каждого простого множителя, мы получаем

2 2 · 3 = 4 · 3 = 12.Итак, LCM (2, 3, 4, 6) = 12.

Пятеро студентов принесли формы с плитками одинакового размера для продажи на распродаже выпечки. Все стержни были обрезаны до одинакового размера. К концу продажи были проданы три четверти батончиков Cary’s, две трети батончиков Dana, половина батончиков Джейми, пять восьмых батончиков Линн и семь восьмых батончиков Терри. Чья тарелка слитков была продана в среднем?

Медиана набора дробей может быть найдена с помощью того же метода, который мы использовали для набора целых чисел.Помните, что медиану можно найти, сначала упорядочив набор значений, и что хороший метод упорядочивания дробных значений — это переписать их с общим знаменателем.

Решение указанной выше проблемы: Сначала мы находим наименьший общий знаменатель, находя наименьшее общее кратное для 4, 3, 2, 6 и 8. Мы находим НОК методом разложения на простые множители.

Затем расположите дроби от наименьшей к наибольшей.

Среднее значение — это значение 3 rd . Возьмем самую простую форму, значит, есть медиана.

Мы обнаружили, что Кэри продал среднее количество баров.

Пример: Найдите среднее значение этого списка:

Решение: Сначала нам нужно отсортировать эти значения от наименьшего к наибольшему. Есть много способов сделать это. Мы могли бы использовать числовую строку, как на предыдущей странице. Здесь мы заменим все эти значения на общий знаменатель:

Теперь разместим их в порядке от наименьшего к наибольшему и выберем медианное значение.

Поскольку в списке 10 значений, нам нужно найти значение, которое находится посередине между значениями 5 th и 6 th . Итак, медиана есть.

Мы можем использовать гистограммы для решения некоторых типов проблем. Например, используйте гистограмму для решения следующей задачи:

У Мисси было 45 долларов. На книгу она потратила своих денег. Сколько денег у нее осталось?

Решение: Ответ на вопрос «Сколько стоит 45 долларов?» дает нам сумму, которую она потратила.Сумма, которая у нее останется, будет суммой, оставшейся после того, как потраченная сумма будет удалена.

У нас есть, что 1 единица стоит 9 долларов. Итак, 2 единицы будут стоить 18 долларов, а 3 единицы — 27 долларов.

У Мисси осталось 27 долларов после того, как она потратила 18 из 45 долларов.

Одним из способов оценки решений проблем, связанных с дробями, является использование 0, и 1 в качестве ключевых точек или якорей, чтобы помочь нам визуализировать относительный размер дробей между 0 и 1.Это хорошие ориентиры или ориентиры, которые следует учитывать при оценке решений.

Пример: ближе к 0, или 1?

Решение : Сначала мы замечаем, что это эквивалентно половине, поэтому оно больше по значению, чем. Затем мы замечаем, что числитель 5 максимально приближен к знаменателю 6, но не достигает. Итак, делаем вывод, что ближе к единице.

Пример: ближе к 0, или 1?

Решение: Сначала мы замечаем, что это эквивалентно.Делаем вывод, что чуть больше половины.

Пример: Оцените значение суммы для.

Решение: Мы оцениваем значение суммы в 3, т.к.

Обратите внимание, что символ ≈ означает , примерно равное . Этот символ следует использовать каждый раз, когда во время вычисления делается оценка или приближение.

Шутка или цитата

Порядок — это первый закон Небес.
Очерк о человеке IV — Папа, Александр (1688-1744 )

методов построения графиков

методов построения графиков

Построение графиков — очень важный метод экспериментальной физики. Графики представляют собой компактный и эффективный способ отображения функциональной взаимосвязи между двумя экспериментальными параметрами и обобщения экспериментальных результатов.Некоторые графики в начале этого лабораторного курса должны быть нарисованы от руки , чтобы убедиться, что вы понимаете все, что нужно для построения эффективного научного графика. Вы также узнаете, как использовать компьютер для построения графиков ваших данных. Если в этом руководстве в лабораторных упражнениях требуются графики, вам будет предложено «построить график A против B» (где A и B — переменные). По соглашению, A ( зависимая переменная ) должна быть нанесена вдоль вертикальной оси (ордината), а B ( независимая переменная ) должна быть нанесена вдоль горизонтальной оси (абсцисса).Ниже приводится типичный пример зависимости расстояния от времени для свободно падающего объекта. Внимательно изучите этот график и обратите внимание на следующие важные правила построения графиков:

Рисунок 1

Миллиметровая бумага

Графики, предназначенные для предоставления числовой информации, всегда следует рисовать на миллиметровой бумаге в квадрате или поперечном сечении размером 1 см × 1 см с 10 делениями на см. Используйте острый карандаш (не ручку) для рисования графиков, чтобы можно было легко исправить неизбежные ошибки.

Название

У каждого графика должен быть заголовок, в котором четко указано, какие переменные появляются на графике. Кроме того, напишите свое имя и дату на графике для удобства.

Этикетки осей

Каждая координатная ось графика должна быть помечена словом или символом для переменной, нанесенной вдоль этой оси, и единиц (в скобках), в которых отображается переменная.

Выбор шкалы

Масштаб следует выбирать таким образом, чтобы данные было легко построить и легко прочитать.На координатной бумаге каждая строка 5 -го и / или 10 -го немного тяжелее других строк; такая основная линия деления всегда должна представлять собой десятичное число, кратное 1, 2 или 5 (например, 0, 1, 2, 0,05, 20, 500 и т. д.). Другие варианты (например, 0,3) затрудняют построение и чтение данных. Шкалы не должны быть меньше наименьшего деления на измерительном приборе, с которого были получены данные. Например, данные с измерительной линейки (имеющей деление 1 мм) должны быть нанесены на шкалу не менее 1 деления = 1 мм.Масштаб меньше 1 дел / мм не обеспечит дополнительной точности построения, поскольку данные с измерительной линейки имеют точность только примерно до 0,5 мм. Часто масштаб должен быть значительно грубее этого предела, чтобы уместить весь график на одном листе миллиметровой бумаги. На иллюстрации были выбраны масштабы, чтобы дать графику примерно квадратную границу; вам следует избегать выбора масштаба, из-за которого оси сильно различаются по длине. Обратите внимание в этой связи, что не всегда необходимо указывать начало координат («ноль») на оси графика; во многих случаях необходимо отобразить только ту часть шкалы, которая охватывает данные.

точек данных

Введите точки данных на график, поместив маленькую точку в координаты точки, а затем нарисовав небольшой кружок вокруг точки. Если на одном графике должно отображаться более одного набора данных, используйте другие символы (например, θ , Δ), чтобы различать наборы данных. Для этого пригодится шаблон чертежа.

Кривые

Проведите простую плавную кривую через точки данных. Кривая не обязательно будет проходить через все точки, но должна проходить как можно ближе к каждой точке, примерно по половине точек с каждой стороны кривой; эта кривая предназначена для направления взгляда вдоль точек данных и для указания тенденции данных.Французская кривая полезна для рисования сегментов кривой. Не , а не соединяют точки данных прямыми сегментами точка-точка. Эта кривая теперь показывает средний тренд данных, и любые прогнозируемые значения должны считываться из этой кривой, а не возвращаться к исходным точкам данных.

Прямолинейные графики

Во многих упражнениях в этом руководстве вас попросят построить график ваших экспериментальных результатов таким образом, чтобы между нанесенными на график величинами существовала линейная зависимость.В этих ситуациях вам будет предложено подобрать прямую к точкам данных и определить наклон и интервал y из графика. В приведенном выше примере ожидается, что расстояние до падающего объекта меняется со временем. согласно Трудно сказать, согласуются ли данные, представленные на первом графике выше, с этим прогнозом. Однако, если построено d vs. t 2 , должна быть получена прямая линия с наклоном = g /2 и y -intercept = 0.

Прямой штуцер

Поместите на график прозрачную линейку или чертежный треугольник и отрегулируйте его положение так, чтобы край был как можно ближе ко всем точкам данных. Наилучшая регулировка приведет к тому, что половина точек данных окажется ниже линейки, равномерно распределенных по линии. Нарисуйте линию вдоль края линейки, которая простирается до ближайшей координатной оси на одном конце и немного дальше последней точки данных на другом конце. Степень, в которой данные согласуются с уравнением, отображается тем, насколько близко точки данных находятся к подобранной линии.Построение этой прямой выполняет сглаживание необработанных экспериментальных данных и, таким образом, может быть более надежным индикатором результата эксперимента, чем любая пара точек данных. Следовательно, измерения, взятые из графика, должны выполняться на подогнанной линии, а не на самих точках данных. Не «заставляйте» подобранную линию проходить через начало вашего графика, даже если предполагаемая математическая функция проходит через (0, 0), как в примере функции

d = (g / 2) t 2 .

Рисунок 2

Получение наклона и точки пересечения

Наклон прямой линии вычисляется путем деления «подъема» на «пробег» линии, как показано. Для «пробега» выберите два удобных положения шкалы вдоль горизонтальной оси около концов линии и нарисуйте светлые вертикальные линии, чтобы пересечь нарисованную линию. Считайте положения этих пересечений по вертикальной оси и вычтите, чтобы получить «подъем». Всегда сообщайте рассчитанный уклон на самом графике.Возможно, вам будет полезно пометить точки «подъем» и «бег» и пересечения, как показано в примере, по крайней мере, пока ваша техника построения графиков не будет хорошо развита. Когда вас попросят определить точку пересечения с осью y , отметьте точку пересечения, где нанесенная линия пересекает вертикальную ось (при условии, что вертикальная ось расположена в положении «0» по горизонтальной шкале).

Неопределенность наклона и пересечения

Неопределенность наклона и точки пересечения можно оценить, проведя еще две прямые линии с максимальным и минимальным наклоном, которые по-прежнему позволяют линиям проходить через большинство точек данных.Соответствующий диапазон наклонов и значений пересечения можно затем использовать в качестве разумной оценки неопределенности этих значений.

Аппарат методом наименьших квадратов

Рассмотрим две физические переменные, x и y , которые, как мы ожидаем, связаны линейной зависимостью:

y = a + bx.

График y и x должен быть прямой линией с наклоном b и пересекающей ось y в точке пересечения y = a .

Рисунок 3

Предположим, мы сделали N измерений x и y со значениями (x 1 , y 1 ), (x 2 , y 2 ),, (x N , y N ). Предположим, что измерения x имеют незначительную ошибку, а измерения y имеют стандартные ошибки σ 1 , σ 2 « σ N .График такого набора измерений показан на рисунке 3. Мы хотим найти прямую

y = a + bx,

, которая составляет наилучшие оценки для a и b . В процедуре линейной аппроксимации методом наименьших квадратов наилучшими оценками для a и b являются те, которые минимизируют взвешенную сумму квадратов (хи-квадрат): Обратите внимание, что величина

a + bx i

является ожидаемым значением y , когда

x = x i ,

, таким образом,

y i — (a + bx i )

— это просто отклонение измеренного значения y от ожидаемого значения.Таким образом, метод наименьших квадратов находит значения a и b , которые минимизируют сумму квадратов этих отклонений, взвешенных с учетом их соответствующей неопределенности. В этой лабораторной работе вы будете использовать программное обеспечение для анализа данных, такое как Excel , которое может автоматически вычислять лучшие значения a и b и их соответствующую ошибку,

σ a

и

σ b .

Если ваши точки данных содержат самые разные ошибки, то тем с большими ошибками следует придавать меньший вес.Следовательно, для этих случаев следует использовать версию взвешенного соответствия. Если всем точкам данных необходимо присвоить одинаковый вес, следует использовать невзвешенное соответствие.

чисел с двумя десятичными цифрами

Это полный урок с инструкциями и упражнениями по числам с двумя десятичными цифрами (сотыми), предназначенный для четвертого класса. На числовой строке мы получаем сотые доли, просто разделив каждый интервал одной десятой на 10 новых частей.Или мы можем смотреть на дроби. Видео ниже также включает объяснение того, почему вы можете «пометить» или «добавить» нули в конец десятичной дроби, и ее значение не изменится.


Вы видели эту числовую строку на предыдущем уроке. В нем расстояние от 0,0 до 0,1 равно одна десятая .

Теперь мы нарисуем девять крошечных линий между 0,0 и 0,1, разделив это расстояние на ДЕСЯТЬ новых частей .

Теперь повторите этот процесс между 0,2 и 0,3, разделив это расстояние на ДЕСЯТЬ новых частей.

Если вы повторили этот процесс между От 0,3 до 0,4, а затем от 0,4 до 0,5 и т. Д.
на сколько частей будет вы делите числовую строку от От 0 до 1? ________ части

Эти новые детали поэтому сотки , или сотых .

Числовая строка под цифрой увеличивает масштаб к предыдущей числовой строке от 0 до немного более 0,3. Интервал от 0 до 0,1 разделен на десять частей, и аналогично интервал от От 0,1 до 0,2 и т. Д.

Каждый интервал равен одной сотой. Теперь посмотрите на цифры под отметки.
У них две цифры после десятичной точки — или мы говорим у них две десятичные цифры .

Число 0,28 читается как двадцать восемь сотых и то же, что 28

100		.
Число 0,06 читается как шесть сотых и то же, что 6

100		.
Число 2,34 читается как две и тридцать четыре сотых и совпадает с 2 34

100		.

Мы также можем проиллюстрировать сотые доли деление квадрата на сотка .

1.Раскрасьте части, чтобы показать равенство. Запишите десятичную дробь в (b) и (c).

2. Какие числа изображены на фотографиях? Написать их как дробь и десятичная дробь.

3. Цвет для обозначения десятичных знаков. Затем запишите их дробями.

4. Запишите дроби десятичными знаками.

а.

1

100

 =

1

10

 =
б.

4

100

 =

4

10

 =
с.

31

100

 =

3

10

 =
г. 2

3

100

 =

2

3

10

 =
e. 5

7

10

 =

5

7

100

 =
ф. 10

1

10

 =

10

1

100

 =

5.Пишите дробями.

а. 0,02 г. 1,49 г. 5,5 г. 3,08 e. 10,06

6.Отметьте эти десятичные дроби в числовой строке ниже:

1,55 1,11 1,28 1,39 1,88 1,02 1,67 1,99 1,74 1,43 1,90 1,06 1,20


7. Заполните пропущенные сотые части под галочками на номере. линий.


8. Сделайте числовую черту с делениями сотых долей от 0.С 6 по 0,7.



9. Мы также используем десятичные числа для записи денежных сумм. цент сотая часть доллара.
Итак, 5,12 доллара означает 5 целых долларов и 12 сотых доллара, или 12 центов.

С помощью долларовых центов мы всегда используйте две десятичные цифры после точки.
Итак, как обычно пишут $ 0.6?


10. Сравните. Напишите <,> или = между числами.


Широта Долгота — географические координаты

Географическая система координат

Географическая система координат — это обычная сферическая система координат для определения местоположения пространственных объектов на искривленной поверхности земли. Сеть пересекающихся линий, состоящая из линий долготы с севера на юг и линий широты с востока на запад, создает воображаемую сетку вокруг земного шара.Такая сеть (сетка) позволяет описывать положение любой точки на поверхности земли.

Географические координаты точки — это набор из двух чисел, а именно широты и долготы (часто сокращенно широты ), которые определяют местоположение этой точки. Две координаты представляют собой угловые измерения. Широта представляет собой угловую меру расстояния до точки к северу или югу от экватора, а долгота относится к угловой мере восток-запад относительно нулевого меридиана .

Широта — Линия Широты


Широта и долгота на эллипсоидальной Земле
(геодезическая широта)


Широта и долгота на сферической Земле
(геоцентрическая широта)
Шаг сетки 10 градусов

Широта ( геодезическая широта ) точки — это угол (φ) между плоскостью экватора и линией, проходящей через точку, перпендикулярную поверхности эллипсоидальной земли.Линия, проведенная из точки на поверхности Земли, не проходит через центр Земли, за исключением точек на полюсах и экваторе. Под широтой обычно подразумевается геодезическая широта.

Геоцентрическая широта точки на поверхности Земли — это угол между плоскостью экватора и линией, соединяющей точку с центром сферической Земли.

Широту можно представить как угловое расстояние точки (на поверхности земли) к северу или югу от экватора.Так как плоскость экватора является опорной плоскостью для измерения широты, экватор при 0 ° широты. Экваториальная плоскость делит Землю на два равных полушария. Широты обозначаются буквой N (север) для местоположений к северу от экватора и буквой S (юг) для местоположений к югу от экватора. Углам широты также могут быть присвоены положительные значения для северного полушария и отрицательные значения для южного полушария. Северный полюс находится на 90 ° северной широты, а широта Южного полюса — 90 ° южной широты или -90 °.

Линия (дуга) на земном шаре или на карте, идущая с востока на запад и соединяющая все точки с одним и тем же широтным углом, называется линией широты , параллелью или кругом широты .Линии широты образуют круги вокруг Земли, параллельные экватору и друг другу. Экватор — это большой круг с окружностью, равной земной, с центром в центре Земли. Параллели проходят через равные промежутки от 0 ° на экваторе до 90 ° на полюсах с постепенно уменьшающимися диаметрами, приближающимися к полюсам. За исключением экватора, параллели имеют меньшую окружность, чем Земля, и их центр не совпадает с центром Земли, и поэтому они представляют собой маленькие круги. Параллели на Северном и Южном полюсах представляют собой скорее точки, чем круги.Расстояния между каждым градусом широты более или менее постоянны и составляют около 111 км, 69 статутных миль или 60 морских миль.

Обратите внимание, что широта — это угол; таким образом, точка на 35 ° северной широты относится к углу в 35 ° между плоскостью экватора и линией, соединяющей эту точку с центром Земли. Параллель или линия широты — это линия; линия, соединяющая все точки на широте 35 °, называется 35-й параллелью. Оба относятся к расстоянию в градусах к северу от экватора.

Широта и географические зоны

Градусы широты к северу или югу от экватора и время года влияют на количество солнечной энергии, получаемой в различных регионах Земли. В результате разные географические зоны можно разделить на категории в зависимости от их характерного климата и окружающей среды. Такие широтных географических поясов включают экваториальных и тропических , субтропических , средних широт , субарктических или субантарктических и арктических или антарктических .

Важные линии широты или параллели включают: тропик Рака на 23,5 ° северной параллели, тропик Козерога на 23,5 ° южной параллели, экватор на 0 °, полярный круг на 66,5 ° северной параллели и Южный полярный круг на 66,5 ° параллели.

Долгота — линия долготы

долгота точки на поверхности Земли угловое расстояние (λ) на восток или на запад от линии отсчета называется меридиан , который проходит от Северного полюса до Южного полюса.Будучи опорной линией или происхождения для измерения углов, то главный меридиан имеет долготу 0 °.

Исторически существовало несколько ориентиров для измерения долготы. Нынешний нулевой меридиан был определен международным соглашением 1884 года как воображаемая линия, соединяющая Северный полюс с Южным полюсом и проходящая через Гринвич, Англия. Главный меридиан также называют Гринвичским меридианом.

Линия (дуга) на земном шаре или на карте, проходящая с севера на юг, соединяющая Северный полюс с Южным полюсом и проходящая через все точки с одинаковым продольным углом, называется линией долготы или меридианом .Каждый меридиан образует половину большого круга , считая Землю сферической. Меридианы пересекают линий широты (параллели) под прямым углом. Сферическая земля разделена на 360 градусов с востока на запад. Линии долготы находятся в диапазоне от 0 ° до 180 ° к востоку и от 0 ° до -180 ° к западу от нулевого меридиана. 180 ° восточной или западной долготы — это меридиан, противоположный нулевому меридиану и совпадающий с международной линией перемены дат (IDL имеет некоторые отклонения от прямой линии меридиана).Плоскость, пересекающая Землю в нулевом меридиане и 180 ° меридиане, делит Землю на западное и восточное полушария. Долготы обозначены буквой E (восток) для местоположений к востоку от нулевого меридиана и буквой W (запад) для местоположений к западу от нулевого меридиана. Углам долготы также могут быть присвоены положительные значения для восточного полушария и отрицательные значения для западного полушария.

Подобно широте, долгота — это угол; точка, находящаяся на долготе 122 °, относится к горизонтальному углу в 122 ° между линией, соединяющей точку с центром Земли и плоскостью нулевого меридиана.Меридиан или линия долготы — это линия; таким образом, линия, соединяющая все точки на долготе -122 °, является меридианом 122 ° з.д. Оба относятся к расстоянию в градусах от нулевого меридиана.

На сферической опорной поверхности Земли, такие как земной шар, линия долготы не является параллельной (в отличие от линий широты), а они сходятся по направлению к полюсам. Расстояние до земли в градус долготы является максимальным (около 111 км или 69 миль) на экваторе и уменьшается до 0 на полюсах.На широте 40 ° один градус долготы составляет около 85,4 км, а на широте 60 ° он охватывает расстояние около 55,8 км.

Линии широты и долготы образуют воображаемую сетку, покрывающую земной шар. Такая сеть параллелей и меридианов известна как координатная сетка . Комбинация углов широты и долготы включает географические координаты точки на поверхности земли и позволяет указать ее положение. При указании координат точки перед долготой записывается широта.

Координаты широты и долготы — форматы и преобразование

Чтобы иметь возможность описать положение точки на поверхности земли с приемлемой точностью, следует использовать меньшие участки углового измерения по сравнению с градусами. Например, как уже упоминалось, градус широты составляет около 111 км, такое расстояние не позволяет точно определить положение точки между 35-й и 36-й параллелями над экватором. В результате градусы широты и долготы делятся на более мелкие части.Каждый градус (°) делится на 60 угловых минут (‘), а каждая минута делится на 60 угловых секунд (″). 1 ° = 60 ′ = 3600 ″; и 1 ′ = 60 ″. Координаты широты или долготы могут быть записаны в одном из трех форматов.

Градусов Минут Секунды (DMS) — ddd ° mm ′ ss.s ″:

Как следует из названия, в формате DMS координаты широты и долготы обозначаются значениями в градусах, минутах и ​​секундах. Градусы являются целыми числами и варьируются от 0 ° до 90 ° и от 0 до -90 ° для широты и от 0 ° до 180 ° и от 0 до -180 ° для долготы; минуты также являются целыми числами, а секунды могут быть записаны как целые или действительные числа (десятичные числа).Обратите внимание, что, поскольку 1 ° = 60 ′, если у вас 60 ′, вы можете перенести его и вместо этого добавить 1 ° к градусной части; и точно так же, если у вас 60 дюймов, вы можете перенести их и вместо этого добавить 1 ‘к минутной части. Поэтому минуты и секунды всегда можно записать меньше 60. Пример: 45 ° 36 ′ 23 ″ северной широты 122 ° 46 ′ 18,4 дюйма западной долготы;
46 ° 73 ′ 43 ″ с.ш. 118 ° 36 ′ 83,6 ″ з.д. можно записать как 47 ° 13 ′ 43 ″ с.ш. 118 ° 37 ′ 23,6 ″ з.д. (для координаты 73 ′ широты = 1 ° 13 ′ и координаты долготы 83,6 ″ = 1 ′ 23,6 ″).

Градусы Десятичные Минуты — ддд ° мм.ммм ′:

Здесь градусы представляют собой целые числа, а минуты записываются как действительное (десятичное) число. В десятичной части хранятся доли минуты; поэтому секундной части нет. Пример: 23 ° 34,56 ′ ю.ш. 109 ° 23,72 ′ в.д.

Десятичные градусы — ддд.ddddd °:

В этом формате координаты широты и долготы обозначаются только градусами как действительное (десятичное) число. Любые минуты и секунды можно преобразовать в доли градуса как десятичные дроби. Пример: 46.3678 ° -122,28453 ° (положительная широта — север, отрицательная долгота — запад).

Часто возникает необходимость в преобразовании между различными форматами географических координат. Преобразование между форматами подробно обсуждается ниже. Полезно вспомнить некоторые общие соотношения между градусами, минутами и секундами: 60 ′ = 1 °, 30 ′ = 0,5 °, 15 ′ = 0,25 ° и 45 ′ = 0,75 °; аналогично 60 ″ = 1 ′, 30 ″ = 0,5 ′, 15 ″ = 0,25 ′ и 45 ″ = 0,75 ′.

Преобразовать минуты в градусы : градусы = минуты / 60
Преобразовать градусы в минуты : минуты = градусы x 60
Преобразовать секунды в градусы : градусы = секунды / 3600
Преобразовать градусы в секунды : секунды = градусы x 3600
Преобразовать секунды в минуты : минуты = секунды / 60
Преобразовать минуты в секунды : секунды = минуты x 60

Преобразование градусов минут секунд (DMS) в десятичные градусы

Это преобразование осуществляется путем преобразования минут в градусы, а также преобразования секунд в градусы и последующего добавления результатов к исходным целым градусам.Десятичные градусы = градусы + (минуты / 60) + (секунды / 3600)
Пример — преобразование 38 ° 12 ′ 46 ″ в десятичные градусы: 12 ′ = 0,2 ° и 46 ″ = 0,01278 °
38 ° 12 ′ 46 ″ = 38 ° + (12/60) ° + (46/3600) ° = 38 ° + 0,2 ° + 0,01278 ° = 38,21278 °

Преобразование градусов минут секунд в градусы десятичных минут

Секунды необходимо преобразовать в минуты, а результат прибавить к исходным целым минутам.
Градусы Десятичные Минуты = Градусы и (Минуты + (Секунды / 60))
Пример — преобразовать 38 ° 12 ′ 46 ″ в десятичные градусы: 46 ″ = 0.767 ′
38 ° 12 ′ 46 ″ = 38 ° 12 ′ + (46/60) ′ = 38 ° (12 + 0,767) ′ = 38 ° 12,767 ′

Преобразование десятичных градусов в градусы десятичных минут

В этом преобразовании известно целое число градусов; десятичную часть градуса необходимо преобразовать в минуты. Знак (-) в десятичной координате в градусах обозначает юг, если координата является широтой, или запад, если это долгота.
Пример — преобразование 68,4673 ° в десятичные градусы минут:
Значение целых градусов — 68 °; путем вычитания целого градуса из исходной координаты получается дробная часть градусов (68.4673 ° — 68 ° = 0,4673 °). Умножьте дробную часть градусов на 60, чтобы преобразовать в минуты.
68,4673 ° = 68 ° + 0,4673 ° = 68 ° (0,4673 x 60) ′ = 68 ° 28,038 ′

Преобразование десятичных градусов в градусы минуты секунды (DMS)

Сначала дробная часть градуса преобразуется в десятичные минуты, как указано выше, чтобы получить десятичный формат минут в градусах. Затем десятичные минуты конвертируются в минуты и секунды. Как и в предыдущем шаге, целые минуты и дробная часть разделяются, а дробная минута преобразуется в секунды путем умножения на 60.
Пример — преобразовать 68,4673 ° в градусы минуты секунды:
68,4673 ° = 68 ° + 0,4673 ° = 68 ° (0,4673 x 60) ′ = 68 ° 28,038 ′
68 ° 28,038 ′ = 68 ° (28 + 0,038) ′ = 68 ° 28 ′ (0,038 x 60) ″ = 68 ° 28 ′ 2 ″ (секунды округлены, могут быть сохранены как десятичные)

Преобразовать градусы десятичных минут в десятичные градусы

Минутная часть преобразуется в градусы, а результат добавляется к исходным целым градусам.
Десятичные градусы = градусы + (минуты / 60)
Пример — преобразовать 122 ° 35.483 ′ в десятичных градусах: 35.483 ′ = 0.59138 °
122 ° 35,483 ′ = 122 ° + (35,483 / 60) ° = 122 ° + 0,59138 ° = 122,59138 °

Преобразование градусов десятичных минут в градусы минут секунды (DMS)

Десятичная часть минут преобразуется в минуты и секунды. Целые минуты и дробная часть отделяются, а дробная минута преобразуется в секунды путем умножения на 60.
Пример — преобразовать 43 ° 36,847 ′ в градусы минуты секунды:
43 ° 36.847 ′ = 43 ° (36 + 0,847) ′ = 43 ° 36 ′ (0,847 x 60) ″ = 43 ° 36 ′ 50,8 ″

Широта, долгота и начало отсчета

Система координат может быть основана на разных системах отсчета. Разные карты могут относиться к разным датам, или датум, на который ссылается GPS-приемник, может не соответствовать таковому для карты. Например, более старые карты в Северной Америке основаны на системе координат NAD 27, в то время как последние карты основаны на системе координат NAD 83. Исходной точкой по умолчанию для приемников GPS обычно является Всемирная геодезическая система 1984 года (WGS 84).А интерактивные карты, такие как Google Maps и Bing Maps, используют систему координат WGS 84.


Пример преобразования датума карты и координат

Передача координат между версиями карты, GPS и картой, цифровой и бумажной картами может вызвать ошибки в расположении координат из-за несовпадения датумов. Например, передача координат перекрестка тропы с карты на основе базы данных NAD 27 в GPS, которая установлена ​​на точку привязки WGS 84, может привести к тому, что GPS будет показывать местоположение перекрестка троп в нескольких сотнях метров от фактического местоположения.

Важно указать датум при работе с географическими данными. В путеводителях обычно указывается исходная точка для предоставленных ими координат. Датум в приемниках GPS можно настроить так, чтобы он соответствовал желаемому датуму карты. Датум печатается на полях топографических карт, иногда вместе с информацией для преобразования координат между двумя разными датами путем добавления или вычитания из географических координат широты и долготы; например, пример справа.

Пример изменения датума между версиями карты: http://www.nrcan.gc.ca/earth-sciences/geography-boundary/mapping/topographic-mapping/10129.

Широта и долгота на карте — координаты местонахождения

Значения широты и долготы (долготы) обычно отмечаются на полях карты. Линии широты и долготы также могут отображаться в виде сетки на карте. Обычно помечены только основные подразделения, чтобы не загромождать карту. Подразделы могут быть помечены только частичными значениями координат, такими как минуты или секунды.Не существует единого стандартного способа обозначения линий широты и долготы на карте и ее полях, и могут быть различия в зависимости от масштаба карты, цели карты, а также страны или места производства.

Широта, долгота, значения координат на полях карты или сетка на карте упрощают определение местоположения любой точки с учетом ее значений координат. Аналогичным образом можно получить географические координаты любой точки на карте.

Следует иметь в виду, что крупномасштабные карты могут охватывать области, охватывающие менее одного градуса широты и одного градуса долготы.Полезно проверить четыре угла карты, чтобы найти координаты ограничивающей области, которая покрыта картой, особенно когда значения широты и долготы отмечены частичными числами и на карте нет сетки. Также при чтении значений на полях карты следует знать квадрант или положение относительно экватора и нулевого меридиана. Например, в области в северном и западном полушарии, такой как США или Канада, значения широты увеличиваются от 0 ° на экваторе до 90 ° на северном полюсе, в то время как значения долготы изменяются от 0 до -180 ° (абсолютное число увеличивается) при движении на запад.В южном и восточном полушарии значения широты изменяются от 0 ° на экваторе до -90 ° (абсолютное число увеличивается) на южном полюсе, а значения долготы увеличиваются от 0 ° на нулевом меридиане до 180 ° на международной линии перемены дат.

Карта, использованная в этом примере, представляет собой топографическую карту 1: 50000 региона в Британской Колумбии, Канада. Лист карты охватывает территорию от 49 ° 45 ′ северной широты до 50 ° 00 ′ северной широты и от 122 ° 30 ′ западной долготы до 123 ° западной долготы; изображение принадлежит нижнему правому углу карты.На этой карте синие линии сетки на карте и синие последовательные числа, обозначающие каждую линию сетки, являются координатами UTM. Глядя на поля и черные числа, обозначающие географические координаты, становится очевидно, что не каждый градус или минута обозначены; поэтому важно изучить этикетки, чтобы узнать длину разделов. На этой карте каждая из чередующихся черных и белых полос на полях представляет 1 ′ широты с севера на юг и 1 ′ долготы с востока на запад.

Имейте в виду, что линии сетки или известные деления полей по широте и долготе могут отличаться на разных картах. Например, широты можно разделить на 1 ‘секции, а долготы — на 2’ интервалы.

Найдите координаты широты и долготы места на карте


© Министерство природных ресурсов Канады

На основе определения широты и долготы, чтобы найти географические координаты точки на карте, угловое расстояние (север — юг) точки относительно экватора и ее угловое расстояние (восток — запад) относительно простого числа. меридиан следует определить.

В этом примере желательны географические координаты точки впадения потока в Мисти-Лейк с юга, обозначенной как точка А. Первым шагом является определение ближайших целых значений широты и долготы вокруг точки A по линиям сетки или, в данном случае, на полях карты. Значения широты и долготы точки A на краю можно отметить, поместив линейку из точки A перпендикулярно краям. Из правого поля видно, что точка A находится между 49 ° 48 ′ северной широты и 49 ° 49 ′ северной широты, а нижнее поле показывает, что долгота точки A находится между 122 ° 34 ′ западной долготы и 122 ° 35 ′ западной долготы.

Значения широты и долготы точки A можно легко оценить, взглянув на их относительное положение по сравнению с ближайшими известными значениями широты и долготы. Каждую полоску можно визуально разделить на десять равных частей. Здесь широта точки А находится на полпути между 49 ° 48 ′ северной широты и 49 ° 49 ′ северной широты. Другими словами, его минутное сечение примерно на 0,5 ‘больше 48’. Прибавив это угловое расстояние к нижней широте, широта точки A будет 49 ° 48,5 ′ N. Аналогично, долгота точки A может быть оценена как около 0.На 9 минут больше, чем 122 ° 34 ′ з.д., что может быть указано как 122 ° 34,9 ′ з.д.

Для получения более точных значений координат точки можно использовать линейку. Измерение расстояния между точкой, обозначающей широту точки A, до ближайшего известного значения более низкой широты и деление этого расстояния на расстояние участка между значениями более низкой и нижней широты приводит к пропорциональному расстоянию между точкой A и известным более низким значением. Это расстояние добавляется к нижней широте, чтобы получить широту точки А.

В этом примере с использованием линейки расстояние между точкой A и известной нижней широтой (49 ° 48 ′ N) составляет 2,2 см. Расстояние между нижней (49 ° 48 ′ N) широтой и высокой (49 ° 49 ′ N) широтой составляет 4,4 см. Здесь 1 ′ широты = 4,4 см. Пропорциональное расстояние от широты A до более низкой известной широты составляет 2,2 / 4,4 = 0,5. Преобразование этого значения в угловое расстояние (в этом случае угловое расстояние между нижней и верхней широтой составляет 1 ′ = 60 ″): 0,5 x 1 ′ = 0,5 ′ или 0,5 x 60 ″ = 30 ″. Добавление этого значения к нижней широте дает широту точки A: 49 ° 48.5 ′ северной широты или 49 ° 48 ′ 30 ″ северной широты. Таким же образом рассчитывается долгота точки А. Расстояние долготы А от известной нижней долготы (122 ° 34 ′ з.д.) составляет 2,6 см. Длина участка между нижней (122 ° 34 ′ з.д.) и высшей (122 ° 35 ′ з.д.) долготой составляет 2,7 см. Здесь 1 ′ долготы = 2,7 см. Пропорциональное расстояние 2,6 / 2,7 = 0,963 см. Преобразование этого расстояния в угловое: 0,963 x 1 ′ = 0,963 ′ или 0,963 x 60 ″ = 57,78 ″. Добавление этого значения к нижней долготе дает долготу точки A: 122 ° 34.963 ′ з.д. или 122 ° 34 ′ 57,8 ″ з.д. Географические координаты точки A: 49 ° 48 ′ 30 ″ с.ш. 122 ° 34 ′ 57,8 ″ з.д.

Нанесите точку с известными географическими координатами

Чтобы найти точку на карте по ее географическим координатам, ее значения широты и долготы должны быть отмечены на полях или линиях сетки на карте. Затем точка может быть размещена на поперечном сечении прямых линий, перпендикулярных границе, происходящей от отмеченных долгот широты. В этом примере координаты точки B известны: 49 ° 46′21.8 ″ с.ш. 122 ° 33′40 ″ з.д.

Эти значения могут быть отмечены путем сравнения их относительного положения с ближайшими известными значениями широты и долготы. 21,8 ″ = 0,363 ′, поэтому широту B можно записать как 49 ° 46,363 ′ N. Визуально разделив полосу на десять частей (каждая будет 0,1 ′) и оценив расстояние на полосе в 0,363 ′ или 0,4 ′, получим легко определить положение широты на краю. Аналогично 40 ″ = 0,667 ′, поэтому долгота составляет 122 ° 33,667 ′ з. Д. И 0,667 или 0.7 можно оценить на планке после отметки 122 ° 33 ′.

Для точного определения этих значений на полях можно использовать линейку. 21,8 ″ = 0,363 ′, эту долю минуты можно преобразовать в пропорциональное расстояние в см бара. Столбик равен 1 ‘и равен 4,4 см, следовательно, пропорциональное расстояние составляет 0,363 x 4,4 = 1,597 см. Широту точки B можно обозначить примерно на 1,6 см к северу от точки 49 ° 46 ′ северной широты. Аналогично для долготы 40 ″ = 0,667 ′ и 0,667 x 2,7 = 1,8 см, поэтому долгота B может быть отмечена около 1.8 см западнее точки 122 ° 33 ′ з.д. Перпендикулярные линии к краям карты, проведенные из этих точек, пересекаются в точке B.

Обучающие видео: введение в долгосрочную географическую систему координат

http://www.youtube.com/watch?v=swKBi6hHHMA
http://www.youtube.com/watch?v=-RVsZsK_r1c&feature=related
http://www.youtube.com/watch?v= EPL_e7iQ_Vo & feature = related
Кругосветное плавание по экватору (0 широты): http: // www.youtube.com/watch?v=nQOWOJv3izs&feature=related

VA503242-7470_8Math_RB

% PDF-1.4 % 248 0 объект > endobj 549 0 объект > endobj 3 0 obj > поток Приложение Acrobat Distiller 8.1.0 (Macintosh) / pdf

  • Stacey Driscoll
  • VA503242-7470_8Math_RB
    • 2009-03-27T15: 09: 53-05: 00QuarkXPress: фильтр pictwpstops 1.02009-01-09T07: 09: 35-06: 002009-03-27T15: 09: 53-05: 00uuid: c3fc3faa-fc4b-a442-b5c1- d136a59b7720uuid: 07d9b0f7-1f73-6b46-b57c-a950d067af67 конечный поток endobj 84 0 объект > endobj 357 0 объект > endobj 449 0 объект > endobj 447 0 объект > endobj 458 0 объект > endobj 519 0 объект > endobj 281 0 объект > endobj 77 0 объект > endobj 342 0 объект > / Font> / ProcSet [/ PDF / Text / ImageB / ImageC / ImageI] / Properties> / ExtGState >>> / Type / Page >> endobj 524 0 объект > / ProcSet [/ PDF / Text / ImageB / ImageC / ImageI] / Properties> / ExtGState >>> / Type / Page >> endobj 10 0 obj > / Font> / ProcSet [/ PDF / Text / ImageB / ImageC / ImageI] / Properties> / ExtGState >>> / Type / Page >> endobj 208 0 объект > / Font> / ProcSet [/ PDF / Text / ImageB / ImageC / ImageI] / Properties> / ExtGState >>> / Type / Page >> endobj 429 0 объект > / Font> / ProcSet [/ PDF / Text / ImageB / ImageC / ImageI] / Properties> / ExtGState >>> / Type / Page >> endobj 528 0 объект > / ProcSet [/ PDF / Text / ImageB / ImageC / ImageI] / ExtGState >>> / Type / Page >> endobj 320 0 объект > / ProcSet [/ PDF / Text / ImageB / ImageC / ImageI] / ExtGState >>> / Type / Page >> endobj 394 0 объект > / Тип / Страница >> endobj 324 0 объект > поток HK Ni} P (mB? F1ѝu * ԫ / zdL \ ޲ Y

    Mathematics_ _solutions for Class 8 Math Chapter 1

    Страница № 2:
    Вопрос 1:

    Покажите следующие числа в числовой строке.Нарисуйте отдельную числовую линию для каждого примера.

    (1) 32, 52, -32

    (2) 75, -25, -45

    (3) -58, 118

    (4) 1310, -1710

    Ответ:


    1 32,52, -32 можно представить в числовой строке следующим образом.


    2 75, -25, -45 могут быть представлены в числовой строке следующим образом.


    3 -58,118 можно представить в числовой строке следующим образом.


    4 1310, -1710 можно представить в числовой строке следующим образом.

    Страница № 2:
    Вопрос 2:

    Обратите внимание на числовую строку и ответьте на вопросы.

    (1) Какое число обозначено точкой B?
    (2) Какая точка указывает на число 134?
    (3) Укажите, является ли утверждение «точка D обозначает число 52» истинным или ложным.

    Ответ:

    (1) Мы видим, что каждая единица числовой линии делится на 4 равные части.
    Теперь B — десятая точка слева от 0.
    Итак, B указывает -104 на числовой строке.
    2 134 = 74 = 7 × 14
    Итак, седьмая точка справа от 0 — это C, что означает 134 на числовой прямой.
    (3) Точка D — это десятая точка справа от 0. Итак, D указывает 104 на числовой прямой.
    Итак, 104 = 52
    Итак, D обозначает 52 на числовой прямой. Следовательно, данное утверждение верно.

    Страница № 3:
    Вопрос 1:

    Сравните следующие числа.
    (1) −7, −2

    (2) 0, −95

    (3) 87, 0

    (4) −54, 14

    (5) 4029, 14129

    (6) −1720 , −1320

    (7) 1512, 716

    (8) −258, −94

    (9) 1215, 35

    (10) −711, −34

    Ответ:

    (1) Мы знаем, что 7> 2

    ∴ −7 <−2.

    (2) Мы знаем, что отрицательное число всегда меньше 0.

    ∴ 0> -95.

    (3) Мы знаем, что положительное число всегда больше 0.

    ∴ 87> 0

    (4) Мы знаем, что −5 <1.

    ∴ -54 <14.

    (5) Мы знаем, что 40 <141.

    ∴ 4029 <14129.

    (6) Мы знаем, что −17 <−13.

    ∴-1720 <-1320.

    7 1512 = 15 × 412 × 4 = 6048; 716 = 7 × 316 × 3 = 2148
    Теперь, 6048> 2148
    ∴ 1512> 716.

    (8) Давайте сначала сравним 258 и 94.
    258 = 25 × 18 × 1 = 258; 94 = 9 × 24 × 2 = 188
    Сейчас 258> 188
    ∴ 258> 94
    ∴ -258 <-94.

    9 1215 = 12 × 115 × 1 = 1215; 35 = 3 × 35 × 3 = 915
    Теперь, 1215> 915
    ∴ 1215> 35.

    (10) Давайте сначала сравним 711 и 34.
    711 = 7 × 411 × 4 = 2844; 34 = 3 × 114 × 11 = 3344
    Теперь 2844 <3344
    ∴ 711 <34
    ∴ -711> -34.

    Страница № 4:
    Вопрос 1:

    Запишите следующие рациональные числа в десятичной форме.
    (1) 937

    (2) 1842

    (3) 914

    (4) −1035

    (5) −1113

    Ответ:

    (1) Данный номер — 937.

    ∴ 937 = 0,243243 …. = 0,243
    В десятичной форме числа 937 равно 0,243.

    (2) Заданное число — 1842.

    ∴ 1842 = 0,428571428571 …. = 0,428571
    В десятичной форме 1842 есть 0,428571.

    (3) Данное число — 914.

    ∴ 914 = 0,6428571428571 …. = 0,6428571
    В десятичной форме 914 0,6428571.

    (4) Данное число -1035.

    ∴ 1035 = 20,6
    Десятичная форма -1035 равна -20,6.

    (5) Данное число -1113.

    ∴ 1113 = 0,846153846153 …. = 0,846153
    Десятичная форма -1113 — -0,846153.

    Страница № 5:
    Вопрос 1:

    Число 2 отображается в числовой строке. Даны шаги, чтобы показать 3 в числовой строке с помощью 2. Правильно заполните поля и завершите упражнение.

    Активность:

    ∙ Точка Q на числовой прямой показывает число ……..
    ∙ Прямая, перпендикулярная числовой прямой, проведена через точку Q.Точка R находится на единичном расстоянии от точки Q на линии.
    ∙ Прямоугольный ∆ ORQ получается путем рисования сегмента OR.
    ∙ л (OQ) = 2, л (QR) = 1

    ∴ по теореме Пифагора,
    [ l (OR)] 2 = [ l (OQ)] 2 + [ l (QR)] 2

    = 0 2 + 0 2 = 0 + 0

    = 0

    ∴ l (OR) = 0

    Нарисуйте дугу с центром O и радиусом OR.Отметьте точку пересечения прямой и дуги как C. Точка C показывает числовую прямую 3.


    Ответ:


    ∙ Точка Q на числовой прямой показывает число 2.
    ∙ Прямая, перпендикулярная числовой прямой, проводится через точку Q. Точка R находится на единичном расстоянии от Q на прямой.
    ∙ Прямоугольный ∆ ORQ получается путем рисования сегмента OR.
    ∙ л (OQ) = 2, л (QR) = 1
    ∴ по теореме Пифагора,
    [ л (OR)] 2 = [ л (OQ)] 2 + [ l (QR)] 2
    = 22 + 12 = 2 + 1
    = 3
    ∴ l (OR) = 3
    Нарисуйте дугу с центром O и радиусом OR.Отметьте точку пересечения прямой и дуги как C. Точка C показывает числовую прямую 3.

    Страница № 6:
    Вопрос 2:

    Покажите цифру 5 в числовой строке.

    Ответ:


    Нарисуйте числовую линию, как показано на рисунке. Пусть точка O представляет 0, а точка Q представляет 2. Нарисуйте перпендикуляр QR в точке Q на числовой прямой так, чтобы QR = 1 единица.Присоединяйтесь к OR. Теперь ∆OQR — прямоугольный треугольник.
    По теореме Пифагора имеем
    OR 2 = OQ 2 + QR 2
    = (2) 2 + (1) 2
    = 4 + 1
    = 5
    ∴ OR = 5
    Взяв O за центр и радиус OR = 5, нарисуйте дугу, пересекающую числовую прямую в точке C.
    Очевидно, OC = OR = 5.
    Следовательно, C представляет 5 на числовой прямой.

    Страница № 6:
    Вопрос 3:

    Покажите цифру 7 в числовой строке.

    Ответ:


    Нарисуйте числовую линию, как показано на рисунке, и отметьте на ней точки O, A и B так, чтобы OA = AB = 1 единица. Точка O представляет 0, а B представляет 2. В точке B нарисуйте перпендикуляр CB на числовой прямой так, чтобы BC = 1 единица. Присоединяйтесь к OC. Теперь ∆OBC — прямоугольный треугольник.
    В ∆OBC по теореме Пифагора
    (OC) 2 = (OB) 2 + (BC) 2
    = (2) 2 + (1) 2
    = 4 + 1
    = 5
    ∴ OC = 5
    Принимая O за центр и радиус OC = 5, нарисуйте дугу, пересекающую числовую прямую в точке D.
    Ясно, что OC = OD = 5
    В точке D проведите перпендикуляр ED на числовой прямой так, чтобы ED = 1 единица. Присоединяйтесь к OE. Теперь ∆ODE — прямоугольный треугольник.
    В ∆ODE по теореме Пифагора
    (OE) 2 = (OD) 2 + (DE) 2
    = (5) 2 + (1) 2
    = 5 + 1
    = 6
    ∴ OE = 6
    Взяв O за центр и радиус OE = 6, нарисуйте дугу, пересекающую числовую линию в точке F.
    Ясно, что OE = OF = 6
    В точке F проведите перпендикуляр GF к числовой прямой так, чтобы GF = 1 шт.Присоединяйтесь к OG. Теперь ∆OFG — прямоугольный треугольник.
    В ∆OFG по теореме Пифагора
    (OG) 2 = (OF) 2 + (FG) 2
    = (6) 2 + (1) 2
    = 6 + 1
    = 7
    ∴ OG = 7
    Взяв O за центр и радиус OG = 7, нарисуйте дугу, пересекающую числовую прямую в точке H.
    Очевидно, OG = OH = 7
    Следовательно, H представляет 7 на числовой прямой.

    Просмотреть решения NCERT для всех глав класса 8

    .