На клетчатой бумаге размером 1 на 1 изображен треугольник найдите его площадь: На клетчатой бумаге с размером клетки 1х1 изображен треугольник. Найдите его площадь.

На клетчатой бумаге с размером клетки 1×1 изображен параллелограмм. Найдите его площадь.

Рассмотрим несколько задач на данную тему.

#1

#2

#3

#4

#5

Задача #1

(Номер задачи на fipi.ru — 71E23E). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Прежде чем приступать к решению задачи, вспомним теорию >>

Параллелограмм — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
Площадь параллелограмма вычисляется по формуле:

где a — основание параллелограмма, h — высота параллелограмма.

Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 7, а высота: h = 4.

Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:

Ответ: площадь параллелограмма равна: 28 ед. кв.

Задача #2

(Номер задачи на fipi.ru — 3BD9B6). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Решение:

Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 5. Из рисунка также находим высоту параллелограмма: h = 3.

Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:

Ответ: площадь параллелограмма равна: 15 ед. кв.

Задача #3

(Номер задачи на fipi.ru — 5C5046). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 5.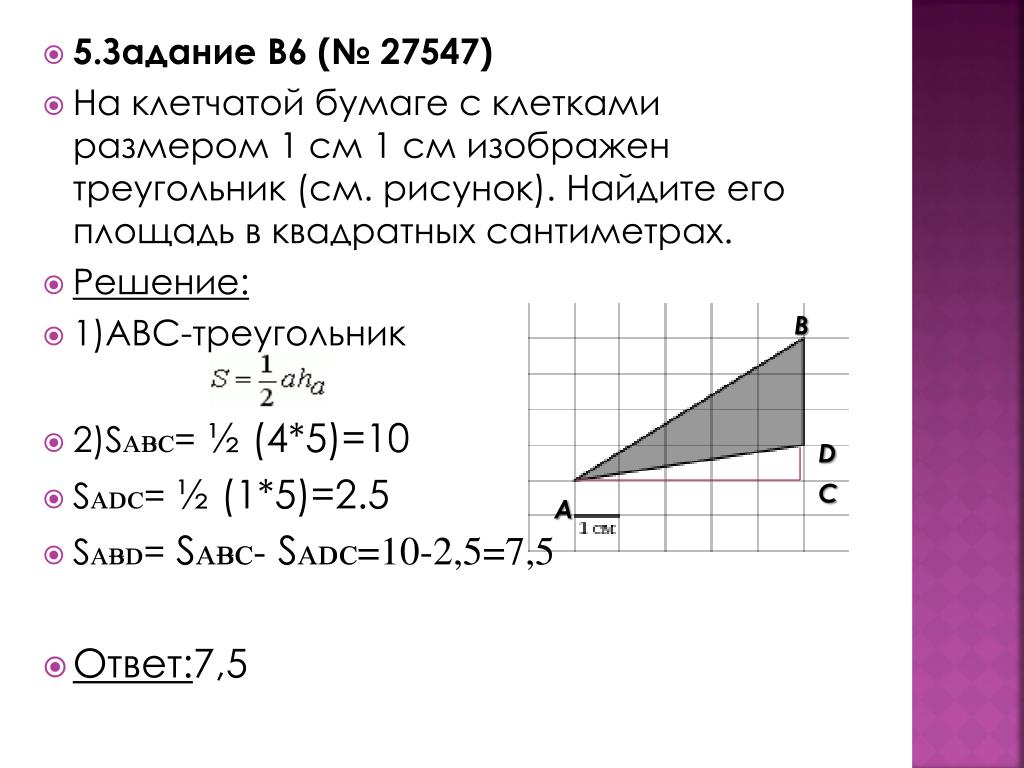 Из рисунка также находим высоту параллелограмма: h = 4.

Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:

Ответ: площадь параллелограмма равна: 20 ед. кв.

Задача #4

(Номер задачи на fipi.ru — 566A4E). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 6. Из рисунка также находим высоту параллелограмма: h = 3.

Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:

Ответ: площадь параллелограмма равна: 18 ед. кв.

Задача #5

(Номер задачи на fipi.ru — 0275CC). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 6. Из рисунка также находим высоту параллелограмма: h = 6.

Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:

Ответ: площадь параллелограмма равна: 36 ед. кв.

Дистанционный репетитор — онлайн-репетиторы России и зарубежья

КАК ПРОХОДЯТ
ОНЛАЙН-ЗАНЯТИЯ?

Ученик и учитель видят и слышат
друг друга, совместно пишут на
виртуальной доске, не выходя из
дома!

КАК ВЫБРАТЬ репетитора

Выбрать репетитора самостоятельно

ИЛИ

Позвонить и Вам поможет специалист

8 (800) 333 58 91

* Звонок является бесплатным на территории РФ
** Время приема звонков с 10 до 22 по МСК

ПОДАТЬ ЗАЯВКУ

Россия +7Украина +380Австралия +61Белоруссия +375Великобритания +44Израиль +972Канада, США +1Китай +86Швейцария +41

Выбранные репетиторы

Заполните форму, и мы быстро и бесплатно подберем Вам дистанционного репетитора по Вашим пожеланиям.
Менеджер свяжется с Вами в течение 15 минут и порекомендует специалиста.

Отправляя форму, Вы принимаете Условия использования и даёте Согласие на обработку персональных данных

Вы также можете воспользоваться
расширенной формой подачи заявки

Как оплачивать и СКОЛЬКО ЭТО СТОИТ

от
800 до 5000 ₽

за 60 мин.

и зависит

ОТ ОПЫТА и
квалификации
репетитора

ОТ ПОСТАВЛЕННЫХ ЦЕЛЕЙ ОБУЧЕНИЯ

(например, подготовка к олимпиадам, ДВИ стоит дороже, чем подготовка к ЕГЭ)

ОТ ПРЕДМЕТА (например, услуги репетиторовиностранных языков дороже)

Оплата непосредственно репетитору, удобным для Вас способом

Почему я выбираю DisTTutor

БЫСТРЫЙ ПОДБОР
РЕПЕТИТОРА И
ИНДИВИДУАЛЬНЫЙ ПОДХОД

ОПТИМАЛЬНОЕ
СООТНОШЕНИЕ ЦЕНЫ И
КАЧЕСТВА

ПРОВЕРЕНЫ ДОКУМЕНТЫ ОБ ОБРАЗОВАНИИ У ВСЕХ РЕПЕТИТОРОВ

НАДЕЖНОСТЬ И ОПЫТ.
DisTTutor на рынке с 2008 года.

ПРОВЕДЕНИЕ БЕСПЛАТНОГО, ПРОБНОГО УРОКА

ЗАМЕНА РЕПЕТИТОРА, ЕСЛИ ЭТО НЕОБХОДИМО

376687 УЧЕНИКОВ ИЗ РАЗНЫХ СТРАН МИРА

уже сделали свой выбор

И вот, что УЧЕНИКИ ГОВОРЯТ
о наших репетиторах

Чулпан Равилевна Насырова

«

Я очень довольна репетитором по химии. Очень хороший подход к ученику,внятно объясняет. У меня появились сдвиги, стала получать хорошие оценки по химии. Очень хороший преподаватель. Всем , кто хочет изучать химию, советую только её !!!

«

Алина Крякина

Надежда Васильевна Токарева

«

Мы занимались с Надеждой Васильевной по математике 5 класса. Занятия проходили в удобное для обоих сторон время. Если необходимо было дополнительно позаниматься во внеурочное время, Надежда Васильевна всегда шла навстречу. Ей можно было позванить, чтобы просто задать вопрос по непонятной задачке из домашнего задания. Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки.

Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.

«

Эльмира Есеноманова

Ольга Александровна Мухаметзянова

«

Подготовку к ЕГЭ по русскому языку мой сын начал с 10 класса. Ольга Александровна грамотный педагог, пунктуальный, ответственный человек. Она всегда старается построить занятие так, чтобы оно прошло максимально плодотворно и интересно. Нас абсолютно все устраивает в работе педагога. Сотрудничество приносит отличные результаты, и мы его продолжаем. Спасибо.

«

Оксана Александровна

Наталья Борисовна Карасева

«

Мы восторге от репетитора. Наталья Борисовна грамотный педагог, она любит свою профессию, любит учеников. Занятия с сыном (2 класс), он находится на домашнем обучении, проходят по скайпу в комфортной обстановке. Репетитор умеет заинтересовать ребенка и выстраивает занятие с учетом его способностей, доступно объясняя предметы русский язык и математику.

По результатам занятий можно сразу заметить повышение уровня успеваемости ученика. Наталья Борисовна хороший педагог, умеет быстро найти общий язык с ребенком, внимательная, легко передающая знания ученику. С большим удовольствием будем продолжать наши занятия, т.к. мы всем довольны.

«

Елена Васильевна

Клиентам

Репетиторы по математике
Репетиторы по русскому языку
Репетиторы по химии
Репетиторы по биологии
Репетиторы английского языка
Репетиторы немецкого языка

Репетиторам

Регистрация
Публичная оферта
Библиотека
Бан-лист репетиторов

Партнеры

ChemSchool
PREPY. RU
Class

Площадь треугольника в координатной геометрии — формула

В геометрии треугольник — это трехсторонний многоугольник, имеющий три ребра и три вершины. Площадь треугольника — это пространство, занимаемое треугольником в двумерной плоскости. Формула площади треугольника: (1/2) × основание × высота. Найдем площадь треугольника в координатной геометрии.

1.	Какова площадь треугольника в координатной геометрии?
2.	Как вычислить площадь треугольника в координатной геометрии?
3.	Площадь треугольника с использованием определителей
4.	Часто задаваемые вопросы о площади треугольника в координатной геометрии

Какова площадь треугольника в координатной геометрии?

Координатная геометрия определяется как изучение геометрии с использованием координатных точек. Площадь треугольника в координатной геометрии можно вычислить, если три вершины треугольника заданы в координатной плоскости. Площадь треугольника в координатной геометрии определяется как площадь или пространство, покрываемое им в двумерной координатной плоскости. Давайте лучше поймем понятие площади треугольника в координатной геометрии на примере, приведенном ниже,

Рассмотрим эти три точки: A(−2,1), B(3,2), C(1,5). Если вы нанесете эти три точки на плоскость, вы обнаружите, что они не лежат на одной прямой, а это означает, что они могут быть вершинами треугольника, как показано ниже:

Площадь, покрытая треугольником ABC в x-y плоскость — область, отмеченная синим цветом. Теперь с помощью координатной геометрии мы можем найти площадь этого треугольника. Давайте узнаем больше об этом в следующем разделе.

Как вычислить площадь треугольника в координатной геометрии?

В координатной геометрии, если нам нужно найти площадь треугольника, мы используем координаты трех вершин.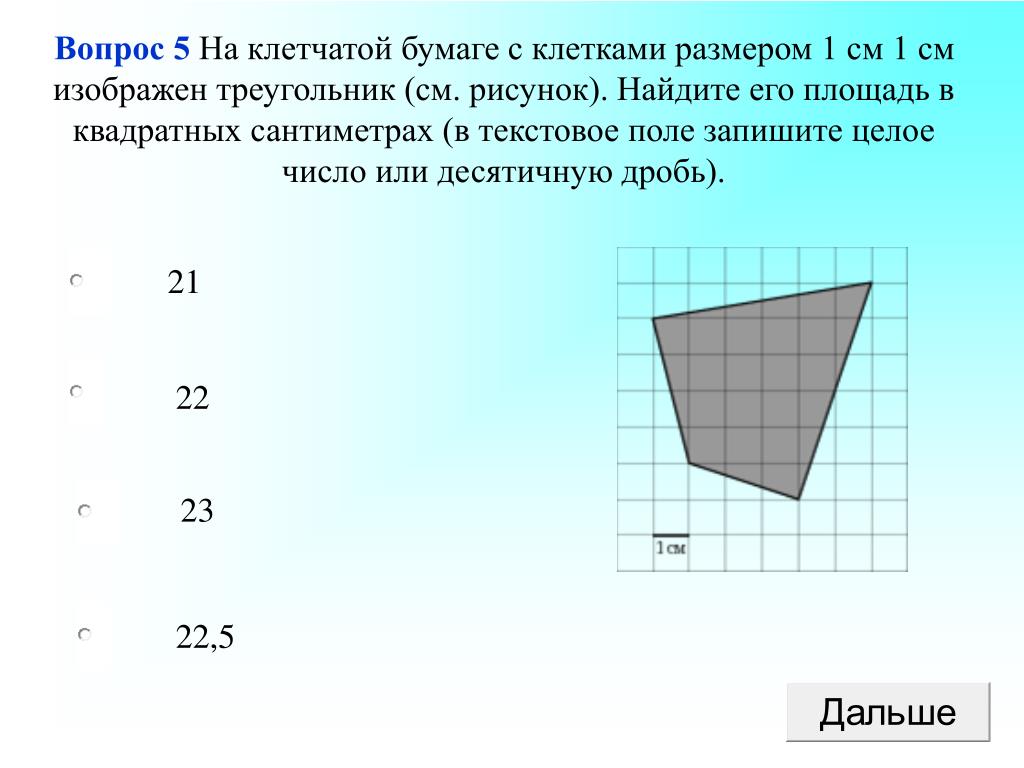 Рассмотрим ▵ABC, как показано на рисунке ниже, с вершинами A(x ₁, y ₁), B(x\(_2\), y\(_2\)) и C(x\(_3\) , у\(_3\)). На этом рисунке мы провели перпендикуляры AE, CF и BD из вершин треугольника к горизонтальной оси. Обратите внимание, что образуются три трапеции: BAED, ACFE и BCFD.

Площадь треугольника можно выразить через площади этих трех трапеций.

Площадь(ΔABC) = Площадь(Trap.BAED) + Площадь(Trap.ACFE) — Площадь(Trap.BCFD)

Теперь площадь трапеции через длины параллельных сторон (основания трапеции) и расстояние между параллельными сторонами (высота трапеции):

Площадь трапеции = (1/2) × сумма оснований × высота

Рассмотрим любую трапецию, скажем, BAED. Его основания BD и AE, а высота DE. Легко видеть, что BD и AE — это координаты y точек B и A, а DE — это разница между x координаты A и B. Точно так же можно легко вычислить основания и высоты двух других трапеций. Таким образом, имеем:

Площадь(Ловушка.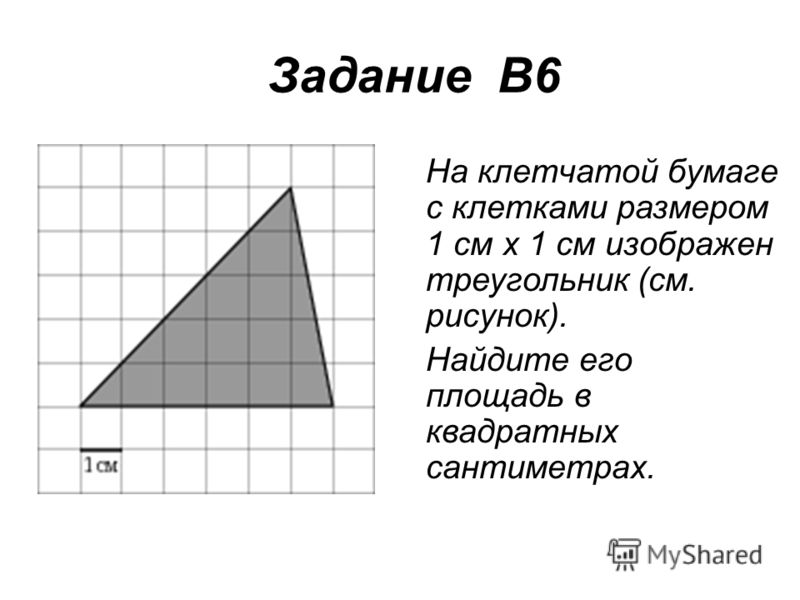 BAED) = (1/2) × (BD + AE) × DE

= (1/2) × (y\(_2\) + y\(_1\) ) × (x\(_1\) − x\(_2\))

Площадь(Ловушка.ACFE) = (1/2) × (AE + CF) × EF

= (1/2) × (y \(_1\) + y\(_3\)) × (x\(_3\) − x\(_1\))

Площадь(Ловушка.BCFD) = (1/2) × (BD + CF) × DF

= (1/2) × (у\(_2\) + у\(_3\)) × (х\(_3\) — х\(_2\))

Выражение для площади треугольника через координаты его вершин может быть таким образом:

= (1/2) × [(у\(_2\) + у\(_1\)) × (х\(_1\) — х\(_2\))] + (1/2) × [ (у\(_1\) + у\(_3\)) × (х\(_3\) — х\(_1\))] — (1/2) × [(у\(_2\) + у\ (_3\)) × (x\(_3\) − x\(_2\))]

Однако мы должны попытаться упростить его, чтобы его было легко запомнить.

Для этого упростим произведение двух скобок в каждом члене:

= (1/2) (х\(_1\)у\(_2\) — х\(_2\)у\(_2\) + х\(_1\)у\(_1\) — х\ (_2\)у\(_1\)) + (1/2) (х\(_3\) у\(_1\) — х\(_1\)у\(_1\) + х\(_3\) у\(_3\) — х\(_1\)у\(_3\)) — (1/2)(х\(_3\)у\(_2\) — х\(_2\)у\(_2 \) + x\(_3\)y\(_3\) − x\(_2\)y\(_3\))

Выносим общий член 1/2 за скобки.

= (1/2) (х\(_1\)у\(_2\) — х\(_2\)у\(_2\) + х\(_1\)у\(_1\) — х\ (_2\)у\(_1\) — х\(_3\) у\(_1\) — х\(_1\)у\(_1\) + х\(_3\)у\(_3\) — х\(_1\)у\(_3\) — х\(_3\)у\(_2\) + х\(_2\)у\(_2\) — х\(_3\)у\(_3\) ) + х\(_2\)у\(_3\))

Таким образом,

Площадь(ΔABC) = (1/2){x\(_1\)(y\(_2\) − y\(_3\)) + x\(_2\)(y\(_3 \) − y\(_1\)) + x\(_3\)(y\(_1\) − y\(_2\))}

Так как площадь всегда положительна.

(ΔABC) = (1/2) |x\(_1\)(y\(_2\) − y\(_3\)) + x\(_2\)(y\(_3\) − y\ (_1\)) + х\(_3\)(у\(_1\) — у\(_2\))|

Это симметричное выражение, и есть простой метод его запоминания, который мы сейчас обсудим как метод детерминантов.

Площадь треугольника с использованием метода определителя

Чтобы вычислить площадь треугольника с помощью определителей, мы используем формулу, показанную ниже:

Площадь = 1/2 \(\begin{bmatrix}{{x_1}}&{{y_1}}&{{1} }\\{{x_2}}&{{y_2}}&{{1}}\\{x_3}&{y_3}&1\end{bmatrix}\)

Решим приведенное выше выражение, чтобы получить формулу для площадь треугольника с помощью координат. Решим определитель по первому столбцу.

Теперь первый член выражения для площади равен \({x_1}\left( {{y_2} — {y_3}} \right)\). Чтобы получить это, мы решаем определители для первого члена в первом столбце. Игнорируйте термины в первой строке и столбце, кроме первого термина, и действуйте в соответствии со следующим визуальным представлением ( поперечные стрелки представляют умножение ). Решая определитель, получаем: x\(_1\)(y\(_2\) — y\(_3\)).

Второй член выражения для площади равен x\(_2\)(y\(_3\) − y\(_1\)). Чтобы получить это, мы решаем определитель для второго члена в первом столбце. Игнорируйте термины во второй строке и первом столбце, кроме первого термина во втором столбце. Решая определитель, получаем -x\(_2\)(y\(_1\) — y\(_3\)) = x\(_2\)(\({y_3} — {y_1}\)):

Далее, третий член выражения для площади равен \({x_3}\left( {{y_1} — {y_2}} \right)\). Чтобы получить это, мы решаем определитель для третьего члена в первом столбце.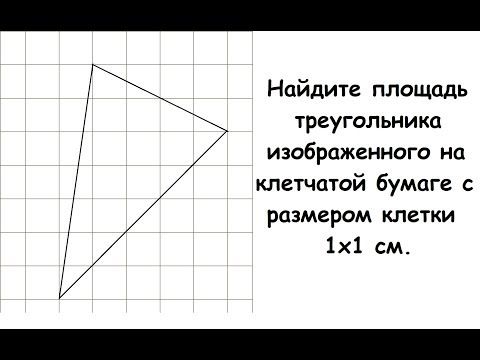 Игнорируйте термины в первой строке и третьем столбце, кроме первого члена в третьем столбце:

Наконец, мы складываем эти три члена, чтобы получить площадь (и делим на коэффициент 2, потому что этот коэффициент исходное выражение, которое мы определили):

Площадь = (1/2) |x\(_1\)(y\(_2\) − y\(_3\)) + x\(_2\)(y\(_3 \) — у\(_1\)) + х\(_3\)(у\(_1\) — у\(_2\))|

Обратите внимание, что мы поставили знак модуля (вертикальные черточки) вокруг нашего алгебраического выражения и удалили отрицательный знак, потому что площадь всегда положительна, что мы и получили в исходном выражении. Таким образом, даже если мы получим отрицательное значение через алгебраическое выражение, знак модуля гарантирует, что оно будет преобразовано в положительное значение.

Приведенное выше выражение для площади можно компактно записать следующим образом:

\(A = \frac{1}{2}\;\left| {\begin{array}{*{20}{c}}{{ x_1}}&{{y_1}}&{{1}}\\{{x_2}}&{{y_2}}&{{1}}\\{x_3}&{y_3}&1\end{массив}} \право|\)

Важные примечания:

Площадь треугольника не может быть отрицательной. В случае, если мы получим отрицательный ответ, мы должны рассматривать числовое значение площади без отрицательного знака.
Чтобы найти площадь треугольника в координатной геометрии, нам нужно найти длину трех сторон треугольника, используя формулу расстояния.
Если три точки A(x\(_1\),y\(_1\)), B(x\(_2\),y\(_2\)), и C(x\(_3\),y\ (_3\)) коллинеарны, то x\(_1\)(y\(_2\) − y\(_3\)) + x\(_2\)(y\(_3\) − y\(_1\ )) + х\(_3\)(у\(_1\) — у\(_2\)) = 0,

Контрольные вопросы

Если расстояние между точками (2, 3) и (1, q) равно 5, найдите значения q.
Какая формула площади четырехугольника в координатной геометрии?

Часто задаваемые вопросы о площади треугольника в координатной геометрии

Как найти длину стороны треугольника, используя координаты?

Формула расстояния используется для нахождения длины треугольника с использованием координат. Формулу расстояния можно использовать для нахождения длины любой стороны по заданным координатам вершин треугольника.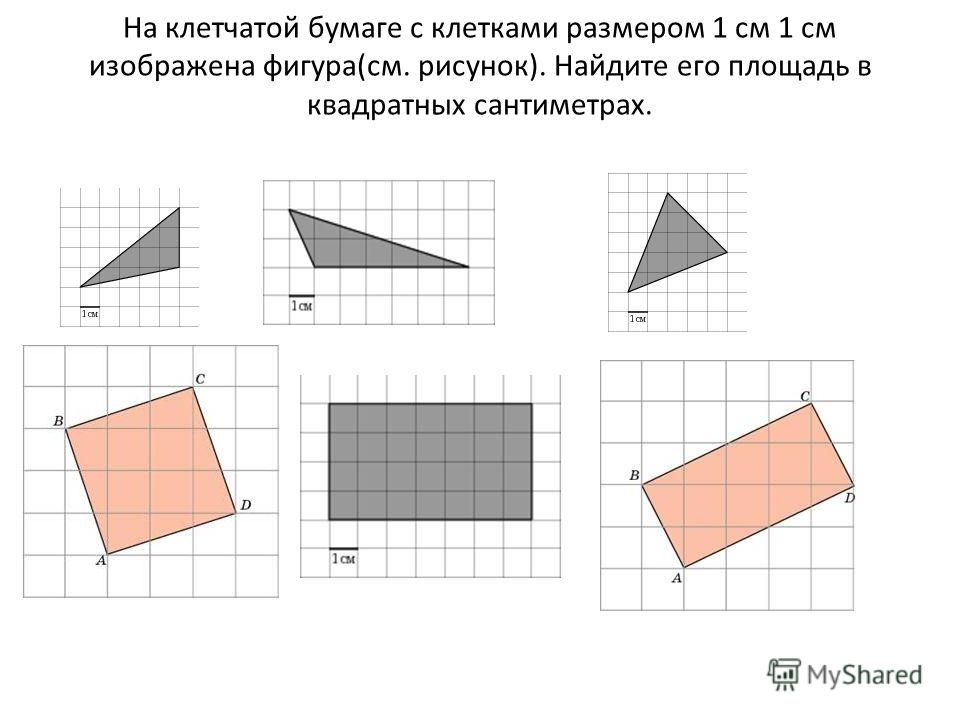

Какая формула площади треугольника в координатной геометрии?

Формула площади треугольника формула в координатной геометрии площадь треугольника в координатной геометрии: A = (1/2) |x\(_1\)(y\(_2\) − y\(_3\)) + x\(_2\)(y\(_3\) — y\(_1\)) + x\(_3\)(y\(_1\) — y\(_2\))|, где (x\ (_1\),y\(_1\)),(x\(_2\),y\(_2\)), и (x\(_3\),y\(_3\)) — координаты вершин треугольника.

Как найти площадь и периметр треугольника с координатами?

Для площади и периметра треугольника с координатами сначала мы должны найти расстояние между каждой парой точек по формуле расстояния, а затем применить формулу площади и периметра.

Как найти площадь треугольника с тремя координатами?

Площадь треугольника с 3 точками: A = (1/2) |x\(_1\)(y\(_2\) − y\(_3\)) + x\(_2\)(y\( _3\) − y\(_1\)) + x\(_3\)(y\(_1\) − y\(_2\))|, где (x\(_1\),y\(_1\) ),(x\(_2\),y\(_2\)), и (x\(_3\),y\(_3\)) — координаты вершин треугольника.

Как найти площадь треугольника, используя вершины?

Формула площади треугольника в координатной геометрии: A = (1/2)|x\(_1\)(y\(_2\) − y\(_3\)) + x\(_2\) (у\(_3\) — у\(_1\)) + х\(_3\)(у\(_1\) — у\(_2\))|, где (х\(_1\),у\ (_1\)), (x\(_2\),y\(_2\)) и (x\(_3\),y\(_3\)) — вершины треугольника.

Как найти площадь равнобедренного треугольника с помощью координат?

Сначала мы используем формулу расстояния, чтобы вычислить длину каждой стороны треугольника. Если две стороны равны, то это равнобедренный треугольник. Мы можем применить формулу площади равнобедренного треугольника, используя длины сторон.

Как найти площадь прямоугольного треугольника с помощью координат?

Сначала мы используем формулу расстояния, чтобы вычислить длину каждой стороны треугольника. Если квадраты двух меньших расстояний равны квадрату наибольшего расстояния, то эти точки являются вершинами прямоугольного треугольника. или мы можем использовать теорему Пифагора. Мы можем применить формулу площади прямоугольного треугольника, используя длины сторон.

Как рассчитать площадь треугольника на графике?

Площадь треугольника на графике рассчитывается по формуле площади: A = (1/2) |x\(_1\)(y\(_2\) − y\(_3\)) + х\(_2\)(у\(_3\) — у\(_1\)) + х\(_3\)(у\(_1\) — у\(_2\))|, где (х\( _1\),y\(_1\)), (x\(_2\),y\(_2\)) и (x\(_3\),y\(_3\)) — вершины треугольника.

Как найти недостающую координату прямоугольного треугольника?

Мы используем формулу расстояния и теорему Пифагора для вычисления недостающей координаты прямоугольного треугольника.

Расчет площади | SkillsYouNeed

Площадь — это мера того, сколько места внутри фигуры. Вычисление площади формы или поверхности может быть полезно в повседневной жизни — например, вам может понадобиться знать, сколько краски нужно купить, чтобы покрыть стену, или сколько семян травы вам нужно, чтобы посеять газон.

На этой странице собрана основная информация, которую вам необходимо знать, чтобы понимать и вычислять площади обычных фигур, включая квадраты и прямоугольники, треугольники и круги.

Расчет площади с использованием метода сетки

Когда фигура рисуется на масштабированной сетке, вы можете найти площадь, подсчитав количество квадратов сетки внутри фигуры.

В этом примере внутри прямоугольника 10 квадратов сетки.

Чтобы найти значение площади с помощью метода сетки, нам нужно знать размер, который представляет квадрат сетки.

В этом примере используются сантиметры, но тот же метод применим для любой единицы длины или расстояния. Например, вы можете использовать дюймы, метры, мили, футы и т. д.

В этом примере каждый квадрат сетки имеет ширину 1 см и высоту 1 см. Другими словами, каждый квадрат сетки равен одному «квадратному сантиметру».

Подсчитайте квадраты сетки внутри большого квадрата, чтобы найти его площадь.

Имеется 16 маленьких квадратов, поэтому площадь большого квадрата составляет 16 квадратных сантиметров.

В математике квадратные сантиметры сокращаются до см ² . ² означает «квадратный».

Каждый квадрат сетки равен 1 см ² .

Площадь большого квадрата 16см ² .

Подсчет квадратов на сетке для нахождения площади работает для всех фигур, если известны размеры сетки. Однако этот метод становится более сложным, когда фигуры не точно соответствуют сетке или когда вам нужно подсчитать доли квадратов сетки.

В этом примере квадрат не вписывается точно в сетку.

Мы все еще можем вычислить площадь, считая квадраты сетки.

Имеется 25 полных квадратов сетки (заштрихованы синим цветом).
10 половинных квадратов сетки (заштрихованы желтым цветом) – 10 половинных квадратов соответствуют 5 полным квадратам.
Существует также 1 четверть квадрата (заштриховано зеленым цветом) – (¼ или 0,25 целого квадрата).
Сложите целые квадраты и дроби вместе: 25 + 5 + 0,25 = 30,25.

Следовательно, площадь этого квадрата равна 30,25 см ² .

Вы также можете записать это как 30¼cm ² .

Хотя использование сетки и подсчет квадратов внутри формы является очень простым способом изучения понятий площади, он менее полезен для нахождения точных площадей с более сложными формами, когда может быть много долей квадратов сетки, которые нужно сложить вместе.

Площадь можно рассчитать с помощью простых формул, в зависимости от типа фигуры, с которой вы работаете.

Оставшаяся часть этой страницы объясняет и дает примеры того, как вычислить площадь фигуры без использования системы сетки.

Площади простых четырехугольников:

Квадраты, прямоугольники и параллелограммы

Простейшие (и наиболее часто используемые) вычисления площадей предназначены для квадратов и прямоугольников.

Чтобы найти площадь прямоугольника, умножьте его высоту на ширину.

Площадь прямоугольника = высота × ширина

Для квадрата вам нужно только найти длину одной из сторон (поскольку каждая сторона имеет одинаковую длину), а затем умножить это само на себя, чтобы найти площадь. Это то же самое, что сказать длину ² или длина в квадрате.

Хорошей практикой является проверка того, что фигура на самом деле является квадратом, путем измерения двух сторон. Например, стена комнаты может выглядеть как квадрат, но когда вы ее измерите, вы обнаружите, что на самом деле это прямоугольник.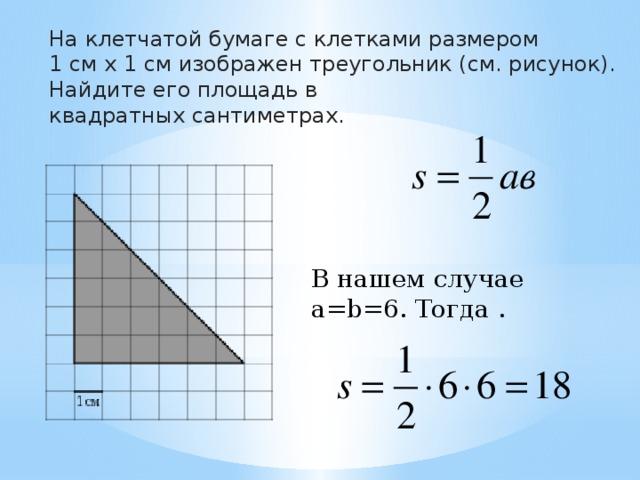

Часто в реальной жизни формы могут быть более сложными. Например, представьте, что вы хотите найти площадь пола, чтобы заказать нужное количество ковра.

Типовой план помещения не может состоять из простого прямоугольника или квадрата:

В этом и других подобных примерах хитрость заключается в том, чтобы разбить фигуру на несколько прямоугольников (или квадратов). Неважно, как вы разделите фигуру — любое из трех решений приведет к одному и тому же ответу.

Решение 1 и 2 требуют, чтобы вы сделали две фигуры и сложили их площади вместе, чтобы найти общую площадь.

Для решения 3 вы делаете большую фигуру (A) и вычитаете из нее меньшую фигуру (B), чтобы найти площадь.

Другая распространенная проблема заключается в нахождении области границы — фигуры внутри другой фигуры.

В этом примере показан путь вокруг поля шириной 2 метра.

Опять же, в этом примере есть несколько способов определить площадь пути.

Вы можете рассматривать путь как четыре отдельных прямоугольника, вычислять их размеры, затем их площадь и, наконец, складывать площади вместе, чтобы получить общую сумму.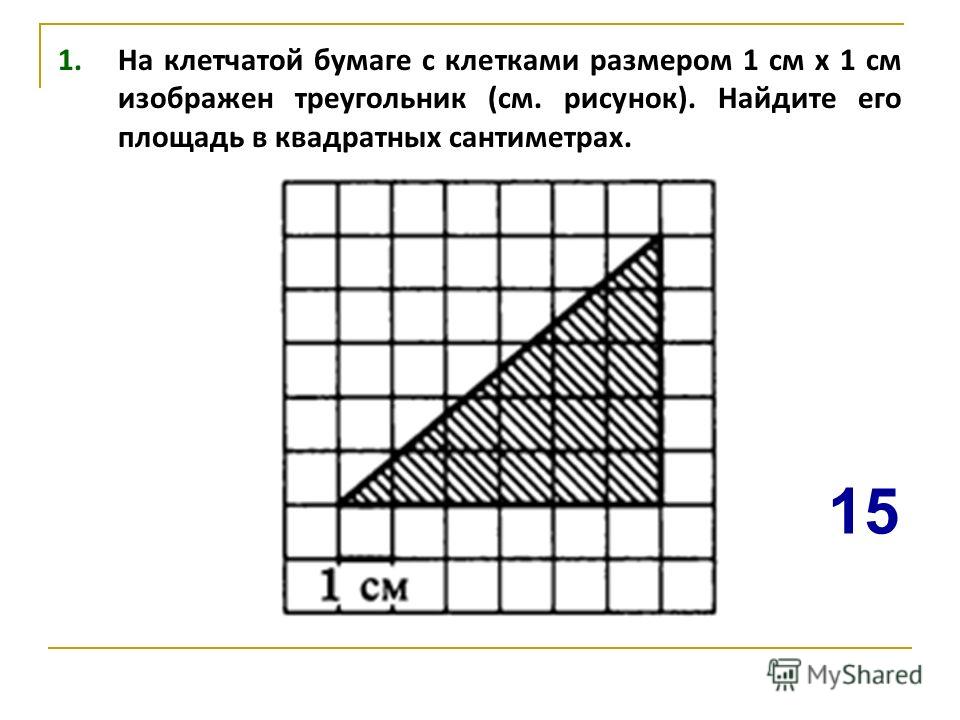

Более быстрым способом было бы определить площадь всей фигуры и площадь внутреннего прямоугольника. Вычтите внутреннюю площадь прямоугольника из целого, оставив площадь пути.

Площадь всей фигуры 16 м × 10 м = 160 м ² .
Мы можем вычислить размеры средней секции, потому что знаем, что путь по краю имеет ширину 2 м.
Ширина всей фигуры 16 м, а ширина пути по всей фигуре 4 м (2 м слева от фигуры и 2 м справа). 16м — 4м = 12м
То же самое можно сделать для высоты: 10 м — 2 м — 2 м = 6 м
Итак, мы подсчитали, что средний прямоугольник имеет размеры 12 м × 6 м.
Таким образом, площадь среднего прямоугольника равна: 12 м × 6 м = 72 м ² .
Наконец, мы отделяем площадь среднего прямоугольника от площади всей фигуры. 160 — 72 = 88м ² .

Площадь пути 88 м ² .

Параллелограмм — это четырехсторонняя фигура с двумя парами сторон одинаковой длины. Прямоугольник по определению является разновидностью параллелограмма. Однако большинство людей склонны думать о параллелограммах как о четырехгранных фигурах с наклонными линиями, как показано здесь.

Площадь параллелограмма вычисляется так же, как и для прямоугольника (высота × ширина), но важно понимать, что под высотой понимается не длина вертикальных (или не вертикальных) сторон, а расстояние между сторонами .

Из диаграммы видно, что высота — это расстояние между верхней и нижней сторонами фигуры, а не длина стороны.

Представьте воображаемую линию под прямым углом между верхней и нижней сторонами. Это высота.

Вычисление площади треугольников

Треугольник можно представить как половину квадрата или параллелограмма.

Предполагая, что вы знаете (или можете измерить) размеры треугольника, вы можете быстро вычислить его площадь, используя следующую формулу:

Площадь треугольника = (высота × ширина) ÷ 2.

Другими словами, вы можете вычислите площадь треугольника так же, как площадь квадрата или параллелограмма, а затем просто разделите ответ на 2.

Высота треугольника измеряется как прямоугольная линия от нижней линии (основания) до «вершины» (верхней точки) треугольника.

Вот несколько примеров:

Площадь трех треугольников на диаграмме выше одинакова.

Каждый треугольник имеет ширину и высоту 3 см.

Площадь вычисляется:

(высота × ширина) ÷ 2

3 × 3 = 9

9 ÷ 2 = 4,5

Площадь каждого треугольника равна 4,5 см ² .

В реальных ситуациях вы можете столкнуться с задачей, требующей нахождения площади треугольника, например:

Вы хотите покрасить фронтон сарая. Вы только хотите посетить отделочный магазин один раз, чтобы получить нужное количество краски. Вы знаете, что литр краски покроет 10м ² стены. Сколько краски нужно, чтобы покрыть фронтон?

Вам нужно три измерения:

A — Общая высота до вершины крыши.

B — Высота вертикальных стен.

C — Ширина здания.

В этом примере размеры:

A — 12,4 м

B — 6,6 м

C — 11,6 м

Следующий этап требует некоторых дополнительных расчетов. Думайте о здании как о двух формах, прямоугольнике и треугольнике. По имеющимся у вас измерениям вы можете рассчитать дополнительные измерения, необходимые для определения площади конца фронтона.

Размер D = 12,4 – 6,6

D = 5,8 м

Теперь можно вычислить площадь двух частей стены:

Площадь прямоугольной части стены: 6,6 × 11,6 = 76,56 м ²

Площадь треугольной части стены: (5,8 × 11,6) ÷ 2 = 33,64 м ²

Сложите эти две площади вместе, чтобы найти общую площадь:

Как известно, один литр краски покрывает 10 м ² стены, чтобы мы могли вычислить, сколько литров нам нужно купить:

110,2 ÷ 10 = 11,02 литра.

На самом деле вы можете обнаружить, что краска продается только в 5-литровых или 1-литровых банках, в результате получается чуть более 11 литров. У вас может возникнуть соблазн округлить до 11 литров, но если мы не разбавим краску водой, этого будет недостаточно. Таким образом, вы, вероятно, округлите до следующего целого литра и купите две 5-литровые банки и две 1-литровые банки, что в сумме составит 12 литров краски. Это позволит избежать любых потерь и оставит большую часть литра для подкрашивания позже. И не забывайте, если вам нужно нанести более одного слоя краски, вы должны умножить количество краски на один слой на необходимое количество слоев!

Площади кругов

Для вычисления площади круга необходимо знать его диаметр или радиус .

Диаметр окружности — это длина прямой линии от одной стороны окружности до другой, проходящей через центральную точку окружности. Диаметр в два раза больше длины радиуса (диаметр = радиус × 2)

Радиус окружности — это длина прямой линии от центральной точки окружности до ее края. Радиус равен половине диаметра. (радиус = диаметр ÷ 2)

Вы можете измерить диаметр или радиус в любой точке окружности – важно измерять с помощью прямой линии, которая проходит через (диаметр) или заканчивается (радиус) в центре окружности.

На практике при измерении окружностей часто бывает проще измерить диаметр, чем разделить его на 2, чтобы найти радиус.

Радиус нужен для вычисления площади круга, формула такова:

Площадь круга = πR ² .

Это означает:

π = Pi — константа, равная 3,142.

R = радиус окружности.

R ² (радиус в квадрате) означает радиус × радиус.

Следовательно, круг с радиусом 5 см имеет площадь:

3,142 × 5 × 5 = 78,55 см ² .

Круг диаметром 3м имеет площадь:

Сначала вычисляем радиус (3м ÷ 2 = 1,5м)

Затем применяем формулу:

πR ²

3,142 × 1,5 × 1,5 = 7,0695.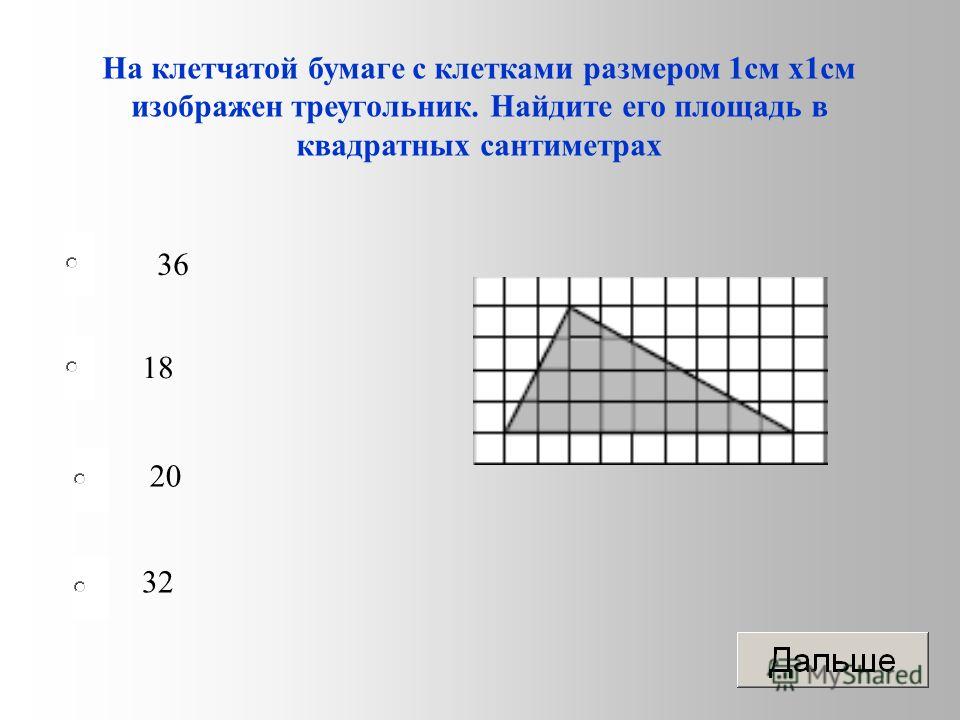

Площадь круга диаметром 3 м равна 7,0695 м ² .

Последний пример

Этот пример использует большую часть содержимого этой страницы для решения простых задач с площадями.

Это дом Рубена М. Бенджамина в Блумингтоне, штат Иллинойс, внесенный в Национальный реестр исторических мест США (регистрационный номер: 376599).

Этот пример включает в себя нахождение площади фасада дома, деревянной решетчатой части, исключая дверь и окна. Вам нужны следующие мерки:

А – 9,7 м	Б – 7,6 м
С – 8,8 м	Г – 4,5 м
В – 2,3 м	Ф – 2,7 м
Г – 1,2 м	В – 1,0 м

Примечания:

Все измерения являются приблизительными.
О бордюре вокруг дома можно не беспокоиться – он не учитывался при измерениях.
Мы предполагаем, что все прямоугольные окна имеют одинаковый размер.
Размер круглого окна — это диаметр окна.
Размеры двери включают ступени.

Какова площадь деревянной решетчатой части дома?

Вычисления и ответы ниже:

Ответы на приведенный выше пример

Во-первых, вычислите площадь основной формы дома, то есть прямоугольника и треугольника, составляющих фигуру.

Основной прямоугольник (В × С) 7,6 × 8,8 = 66,88м ² .

Высота треугольника (A – B) 9,7 – 7,6 = 2,1.

Следовательно, площадь треугольника равна (2,1 × C) ÷ 2,
2,1 × 8,8 = 18,48. 18,48 ÷ 2 = 9,24 м ² .

Суммарная полная площадь фасада дома равна сумме площадей прямоугольника и треугольника:

66,88 + 9,24 = 76,12 м ² .

Затем определите площади окон и дверей, чтобы их можно было вычесть из общей площади.

Площадь двери и ступеней составляет (D × E) 4,5 × 2,3 = 10,35 м ² .

Площадь одного прямоугольного окна составляет (G × F) 1,2 × 2,7 = 3,24 м ² .

Пять прямоугольных окон. Умножьте площадь одного окна на 5.

3,24 × 5 = 16,2 м2. (общая площадь прямоугольных окон).

Круглое окно имеет диаметр 1 м, поэтому его радиус равен 0,5 м.

С помощью πR ² вычислить площадь круглого окна: 3,142 × 0,5 × 0,5 =. 0,7855 м ² .

Затем добавьте площади дверей и окон.

(площадь дверей) 10,35 + (площадь прямоугольных окон) 16,2 + (площадь круглых окон) 0,7855 = 27,3355

Наконец, вычтите общую площадь окон и дверей из полной площади.

76,12 – 27,3355 = 48,7845

Площадь деревянного реечного фасада дома, а ответ на задачу: 48,7845м ² .

Вы можете округлить ответ до 48,8 м ² или 49 м ² .

См. нашу страницу по Оценка, приближение и округление .

Дальнейшее чтение из книги «Навыки, которые вам нужны»

Понимание геометрии
Часть руководства «Навыки, которые вам необходимы для счета»

В этой электронной книге рассматриваются основы геометрии и рассматриваются свойства форм, линий и твердых тел.

Related Posts

Leave A Comment Отменить ответ