На диске который может вращаться вокруг вертикальной оси укреплен отвес: 100 .! решение с ! на диске, который может вращаться вокруг вертикальной оси, укреплен отвес на расстоянии 20 см от центра. при вращении диска с постоянной угловой скоростью нить, длина которой 40 см, отклонена от вертикали на 30 градусов. определить частоту вращения диска. ​

(1/2))/6 (**)

остаётся формулу 2 звёздочки подставить в формулу 1 звёздочка и получим тот же ответ: 10 см.

 

 

Задачи по физике и математике с решениями и ответами

Задача по физике — 1783

Желоб задачи 1782 имеет в верхней части петли разрыв, симметричный относительно вертикали, проходящей через центр петли. Радиусы $R$ желоба, идущие к краям А и В разрыва, образуют угол, равный $2 \alpha$ (рис.). С какой минимальной высоты $H$ должен начать скользить без трения шарик, чтобы пролететь разрыв и снова попасть на желоб? Какова траектория шарика в разрыве желоба?
Подробнее

Задача по физике — 1784

На вращающемся диске укреплен отвес, который устанавливается под углом $\alpha$ к вертикали (рис.). Известны расстояние $r$ от точки подвеса до оси вращения и длина нити отвеса $l$. Определить угловую скорость вращения $ \omega$.
Подробнее

Задача по физике — 1785

Почему монета, катящаяся по плоскости в вертикальном положении (без наклона), движется по прямой, а наклоненная движется криволинейно? Подробнее

Задача по физике — 1786

Конькобежец может описать круг на льду, наклоняясь в сторону центра круга. Откуда берется центростремительная сила, необходимая для движения по окружности? Подробнее

Задача по физике — 1787

На шкив» двигателя плотно надета цепочка. Двигатель приводят в быстрое вращение. {2}$. Подробнее

Задача по физике — 1790

Почему на большой скорости автобус на повороте наклоняется в сторону, противоположную повороту, но не падает, как велосипедист в предыдущей задаче? Подробнее

Задача по физике — 1791

Шарик массой $m$, подвешенный на нити длиной $l$, отклонили от положения равновесия так, что он поднялся на высоту $h$ (рис.). Затем шарик отпустили. На какую высоту он поднимется, если на пути нити поставить стержень А, перпендикулярный к плоскости чертежа (опыт Галилея)?
Подробнее

Задача по физике — 1792

Маленький шарик подвешен в точке А на нити, длина которой $l$. В точке О на расстоянии $l/2$ ниже точки А в стену вбит гвоздь. Шарик отводят так, что нить занимает горизонтальное положение, и отпускают (рис.). В какой точке траектории исчезнет натяжение нити? Как дальше будет двигаться шарик? До какой наивысшей точки поднимется шарик? В какой точке шарик пересечет вертикаль, проходящую через точку подвеса?
Подробнее

Задача по физике — 1793

Почему при ударе кием с силой $F$ по нижней части бильярдного шара он движется замедленно, а при ударе по верхней части — первое время ускоренно? Подробнее

Задача по физике — 1794

Линейная скорость точек земного экватора — около 460 м/с. Что было бы с пулей, вылетевшей из ружья на экваторе параллельно земной поверхности в западном направлении с такой же скоростью, если бы отсутствовала атмосфера? Подробнее

Задача по физике — 1795

Даны два цилиндра одинаковых размеров и из одного и того же материала. {2}$, а расстояние от оси вращения до отражающего зеркала $L = 50 мм$. Рассчитать период колебаний $T$ такого маятника с чувствительностью $\eta = 10 мм/(Дж \cdot м)$. Вычислить диаметр $d$ кварцевой нити подвеса длиной $l = 0,1 м$, позволяющей обеспечить такую чувствительность. Модуль сдвига кварца равен $G = 1011 Па$. Подробнее

Fizika_DZ_2 | DocsArchive.net: архив документов

ИЗД Механика поступательного и вращательного движения

Вариант 1

1.1. На графике показано изменение с течением времени ускорения точки на прямолинейном отрезке пути. Начальная скорость равна нулю, t1 = 12 c, a1 = 2 м/с2. Найти скорость точки в момент времени t2.

1.2. Два груза массами m = 300 г связаны нитью, перекинутой через неподвижный блок. На один из грузов положен перегрузок массой
·m = 20 г. Определить силу Р давления перегрузка на груз при движении системы. Блок считать невесомым, а нить нерастяжимой.

1.3. Теннисный мяч летел с импульсом 13 QUOTE 1415 в горизонтальном направлении, когда теннисист произвел по мячу резкий удар с средней силой F = 42 H. Изменившийся импульс мяча стал равным 13 QUOTE 1415 (масштаб указан на рисунке). Найти время t, в течение которого сила действовала на мяч.

1.4. Сваю массой m = 100 кг забивают в грунт копром массой М = 400 кг. Копер свободно падает с высоты Н = 5 м, и при каждом его ударе свая опускается на глубину h = 25 см. Определить силу сопротивления грунта, считая ее постоянной, и КПД неупругого удара копра о сваю.

1.5. Колесо радиусом R = 10 см вращается так, что зависимость угла поворота радиуса колеса от времени задана уравнением 13 EMBED Equation.DSMT4 1415, где

·
· в радианах, t
· в секундах. Найдите для точек, лежащих на ободе колеса: а) линейную скорость, б) нормальное ускорение и в) угловое ускорение
· для момента времени t = 3 с.
1.6. Диск начинает вращаться под действием момента сил М, график временной зависимости которого представлен на рисунке.
Укажите график, правильно отражающий зависимость момента импульса диска от времени.

1.7. Для того, чтобы раскрутить стержень массы m1 и длины l1 вокруг вертикальной оси, расположенной перпендикулярно стержню через его середину, до угловой скорости, необходимо совершить работу А1. Во сколько раз большую работу, чем А1, надо совершить, для того, чтобы раскрутить до той же угловой скорости стержень массы m2 = 2 m1 и длины l2 = 2 l1?

1.8. Столб высотой h = 3,0 м и массой m = 50,0 кг из вертикального положения падает на землю. Определите момент импульса L относительно точки опоры и скорость верхнего конца столба в момент удара о землю. Точка опоры столба не изменяет своего положения относительно земли при его падении.

ИЗД Механика поступательного и вращательного движения

Вариант 2

2.1. Тело движется прямолинейно, причем скорость зависит от времени по закону: V = 3t3 – 10t + 2 (в м/с). Начертить график зависимости ускорения от времени a(t). Найти величину ускорения при t = 5 c.

2.2. Небольшое тело пускают снизу вверх по наклонной плоскости, составляющей угол
· = 300 с горизонтом. Коэффициент трения тела о плоскость
· = 0,1. Определить отношение времени подъема тела t1 ко времени его соскальзывания t2 до первоначальной точки.

2.3. На рисунке показан вектор силы (в Ньютонах), действующей на частицу. Найти работу, совершенную этой силой при перемещении частицы из начала координат в точку с координатами (5; 2), м.

2.4. Шар массой 1 кг, подвешенный на нити длиной 90 см, отводят от положения равновесия на угол 60є и отпускают. В момент прохождения шаром положения равновесия в него попадает пуля массой 10 г, летящая навстречу шару со скоростью 300 м/с. Пуля пробивает шар и вылетает горизонтально со скоростью 200 м/с, после чего шар продолжает движение в прежнем направлении. На какой максимальный угол отклонится шар после попадания в него пули? (Массу шара считать неизменной, диаметр шара – пренебрежимо малым по сравнению с длиной нити.

)

2.5. На графике представлена параболическая зависимость угла
· поворота вращающегося тела от времени t. Определите начальную угловую скорость вращения тела.

2.6. Цилиндрическое тело жестко закреплено на горизонтальной оси радиуса r = 8 мм. На ось намотан шнур, к концу которого прикреплен груз массой m = 2,0 кг. Система из состояния покоя приводится во вращение под действием опускающегося груза. Определите момент инерции тела, если груз в течение t = 12 с опускается на расстояние h = 1 м.. Силой трения можно пренебречь.

2.7. Однородный тонкий стержень, находящийся на гладкой горизонтальной поверхности, свободно вращается вокруг своего конца с некоторой угловой скоростью
·0. В некоторый момент ось вытаскивают, и стержень скользит по плоскости, вращаясь. Определить угловую скорость этого вращения.

2.8. Вентилятор вращается с частотой N = 900 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N=75 оборотов. При этом силы сопротивления совершили работу А = 44,4 Дж. Найдите момент инерции I вентилятора и момент сил сопротивления М.

ИЗД Механика поступательного и вращательного движения

Вариант 3

3.1. На рисунке изображены графики зависимости скорости от времени для двух тел, движущихся вдоль одной прямой. Второе тело догонит первое через секунд.

3.2. Мальчик на санках спустился с ледяной горы. Коэффициент трения при его движении по горизонтальной поверхности равен 0,2. Расстояние, которое мальчик проехал по горизонтали до остановки, равно 30 м. Чему равна высота горы? Считать, что по склону горы санки скользили без трения.

3.3. На рисунке представлены графики зависимости мощности 13 EMBED Equation.DSMT4 1415 постоянной силы от времени 13 EMBED Equation.DSMT4 1415. Тело движется равноускоренно и прямолинейно. причем направление силы совпадает с направлением перемещения. Какой график соответствует этому случаю?

3.4. Небольшая шайба соскальзывает без трения с вершины полусферы радиусом R = 30 см. На какой высоте h от основания шайба оторвется от полусферы?

3.5. Частица движется по окружности радиусом R = 1 м в соответствии с уравнением
·(t) = 2
·(13 QUOTE 1415, где
· — в радианах, t — в секундах. Найдите время движения диска до остановки. Сколько оборотов N сделает диск за это время?

3.6. Каток в виде однородного цилиндра массой m = 2,0 кг катится по горизонтальной поверхности под действием силы F = 10 Н, приложенной к его оси. Сила направлена перпендикулярно оси катка и составляет с горизонтом угол
· = 30є. 1) Определите ускорение, с которым перемещается ось катка; 2) Чему равен момент этой действующей силы относительно оси, проходящей через точки касания катка дороги в некоторый момент времени? Покажите на рисунке направление этого момента силы. Радиус катка равен 10 см.

3.7. На рисунке приведены зависимости кинетической энергии Wвр трех вращающихся тел от квадрата угловой скорости
·2. Какому графику соответствует наибольший момент инерции тела? Укажите его номер и поясните свой выбор.

3.8. Стержень длиной 1,0 м и массой 7 кг может свободно вращаться вокруг горизонтальной оси, проходящей через его верхний конец. В нижний конец стержня ударяет пуля массой m = 10,0 г, летящая в горизонтальном направлении со скоростью V0 = 500 м/с, и пробивает его. С какой угловой скоростью
· начнет двигаться стержень сразу после удара, если пуля вылетает из стержня со скоростью V1 = 200 м/с?

ИЗД Механика поступательного и вращательного движения

Вариант 4

4.1. Материальная точка движется вдоль оси ОX, зависимость ее координаты от времени имеет вид x = 6 – 4t + t2 , м. Найти путь S, пройденный точкой за первые 5 с ее движения.

4.2. Две гири массами m1 = 3 и m2 = 7 кг висят на концах нити, перекинутой через невесомый блок. Первая гиря находится на 2 м ниже второй. Гири приходят в движение без начальной скорости. Через какое время t они окажутся на одной высоте?

4.3. Частица совершила перемещение по некоторой траектории из точки M(3, 2) в точку N(2,–3). При этом на нее действовала сила 13 QUOTE 1415 (координаты точек и сила 13 QUOTE 1415 заданы в единицах СИ). Найти работу, совершенную силой 13 QUOTE 1415.

4.4. Небольшая шайба после толчка приобретает скорость
·0=2м/с и скользит по внутренней поверхности гладкого закреплённого кольца радиусом R=0,14 м. На какой высоте h шайба отрывается от кольца и начинает свободно падать?

4.5. Тело вращается вокруг неподвижной оси. Зависимость угловой скорости от времени 13 EMBED Equation.DSMT4 1415 показана на рисунке. Напишите уравнение 13 EMBED Equation.DSMT4 1415, отражающее зависимость угла поворота тела от времени, если начальное положение тела соответствует значению 13 EMBED Equation.DSMT4 1415рад.

4.6. На рисунке приведен график зависимости проекции угловой скорости вращающегося тела на ось вращения от времени. Как изменяется модуль вращающего момента сил, действующего на тело, на интервале времени от 13 EMBED Equation.DSMT4 1415 до 13 EMBED Equation.DSMT4 1415?

4.7. На рисунке представлен график зависимости проекции вращательного момента силы, действующей на тело, от угла поворота. Чему равна работа сил, действующих на тело, при повороте его на угол 4 рад ?

4.8. Два шарика одинаковой массы и одинаковыми радиусами движутся с одинаковыми скоростями центров масс по горизонтальной поверхности. Первое катится, второе скользит. При ударе о стенку тела останавливаются. Определите, у какого тела и во сколько раз больше выделится тепла при ударе.

ИЗД Механика поступательного и вращательного движения

Вариант 5

5.1. На рисунке представлен график зависимости проекции скорости от времени для прямолинейного движения тела.

Ниже приведены четыре различных графика зависимости проекции ускорения от времени. Какой из этих графиков соответствует приведенной зависимости проекции ускорения от времени?

5.2. На горизонтальном диске укреплен отвес (шарик на нити), который при вращении диска вокруг вертикальной оси устанавливается под углом
· = 450 к вертикали (см.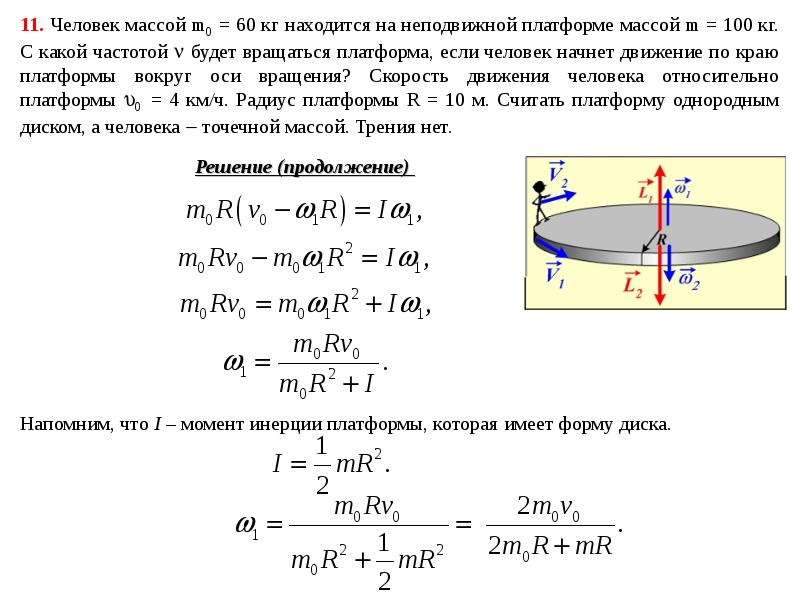 рисунок). Расстояние от точки подвеса до оси вращения d = 50 см, длина нити L = 56 см. Чему равна при этом скорость шарика?

5.3. Материальная точка некоторой массы начинает двигаться под действием силы 13 QUOTE 1415 (Н). Зависимость радиус-вектора материальной точки от времени имеет вид 13 QUOTE 1415 (м). Найти мощность, развиваемую силой в момент времени t = 1 с.

5.4. Два одинаковых маленьких пластилиновых шарика подвешены на нитях одинаковой длины так, что касаются друг друга. Левый шарик отклоняют влево на угол
· = 300, а правый вправо на угол
· = 600 от вертикали и отпускают без начальной скорости. При дальнейшем движении шариков происходит неупругий удар в нижней точке траектории. На какой угол
· отклонятся шарики от вертикали после удара? Найти долю потерянной энергии при этом взаимодействии.

5.5. Уравнение вращения твердого тела
·(t) = 4·t3 + 3·t, рад. Определите угловую скорость вращения тела и полное ускорение для точки тела, отстоящей на 20 см от оси вращения, через 2 с после начала движения.

5.6. На рисунке приведена зависимость модуля моментов сил, приложенных к разным телам, от модуля углового ускорения тел. Наибольший момент инерции имеет тело под номером

5.7. Два маленьких массивных шарика закреплены на концах невесомого стержня длины d. Стержень может вращаться вокруг вертикальной оси, проходящей через середину стержня. Стержень раскрутили до угловой скорости 13 EMBED Equation.DSMT4 1415. Под действием трения стержень остановился, при этом выделилось тепло 13 EMBED Equation.DSMT4 1415. Если стержень был раскручен до угловой скорости 13 EMBED Equation.DSMT4 1415, то при остановке стержня выделится тепло13 EMBED Equation.DSMT4 1415. Во сколько раз 13 EMBED Equation.DSMT4 1415больше 13 EMBED Equation.DSMT4 1415?

5.8. Тонкий прямой стержень длиной l = 1 м прикреплен к горизонтальной оси, проходящий через его верхний конец. Стержень отклонили на 60є от положения равновесия и отпустили. Определите линейную скорость нижнего конца стержня в момент прохождения через положение равновесия.

ИЗД Механика поступательного и вращательного движения

Вариант 6

6.1. Координаты материальной точки изменяются со временем по закону 13 QUOTE 1415. Модуль радиус–вектора точки (в метрах) в момент времени t = 1 с равен (с округлением до десятых долей).

6.2. На концах нити, перекинутой через неподвижный блок, подвешены грузы разной массы. За время t = 2 с после начала движения каждый груз проходит S = 1,96 м. Определить массу меньшего груза m1, если масса большего груза m2 = 1,1 кг

6.3. На рисунке дан график зависимости потенциальной энергии Wp упруго деформированной пружины от величины ее деформации х. Чему будет равна сила упругости, действующая на пружину, при величине деформации х = 3 см ?

6.4. Пуля массой m1 = 20 г попадает в брусок массой m2 = 5 кг, подвешенный на тросе длиной L = 4м, и застревает в нем. Определить начальную скорость пули V, если трос отклонился от вертикали на угол
· = 140. Найти потери механической энергии при этом взаимодействии.

6.5. Диск радиуса начинает вращаться из состояния покоя в горизонтальной плоскости вокруг оси Z, проходящей перпендикулярно его плоскости через его центр. Зависимость проекции угловой скорости от времени показана на графике. На каком интервале времени тангенциальное ускорение точки, расположенной на расстоянии R = 20 см от центра диска, равно a
· = 0,2 м/с2?

6.6. Маховое колесо, имеющее момент инерции I = 245 кг·м2, вращается, делая n = 20 об/с. После того как на колесо перестал действовать вращающий момент, оно остановилось, сделав N = 1000 оборотов. Найдите момент сил трения Мтр и время
·, прошедшее от момента прекращения действия вращающего момента до полной остановки колеса.

6.7. На рисунке представлен график зависимости кинетической энергии вращающегося тела от угла поворота
·. Как изменяется вращающий момент М с изменением увеличением угла
·?

6. 8. Однородный стержень длиной l = 1,5 м и массой M = 10 кг может вращаться вокруг неподвижной оси, проходящей через верхний конец стержня перпендикулярно его длине. В середину стержня ударяет пуля массой m = 10 г, летящая в горизонтальном направлении со скоростью V = 500 м/с, и застревает в стержне. Какую линейную скорость будет иметь конец стержня сразу после удара?

ИЗД Механика поступательного и вращательного движения

Вариант 7

7.1. На рисунке представлен график зависимости проекции ускорения ах от времени t для материальной точки, движущейся вдоль оси ОХ. Начальная скорость движения точки V0х  = –2 м/с. Проекция скорости движущейся точки в момент времени 3 с равна м/с.

7.2. Ледяная горка составляет с горизонтом угол
· = 100. По ней пускают вверх камень, который, поднявшись на некоторую высоту, соскальзывает по тому же пути вниз. Найти коэффициент трения
·, если время спуска в n = 2 раза больше времени подъема.

7.3. Импульс тела 13 QUOTE 1415 изменился под действием кратковременного удара и стал равным 13 QUOTE 1415, как показано на рисунке. Определить направление силы и пояснить свой выбор.

7.4. Небольшой шар массой m1 = 1,99 кг висит на невесомой нерастяжимой нити. В него попадает и застревает в нём пуля, летящая горизонтально со скоростью V = 600 м/с. Масса пули m2 = 10 г. Найти максимальную высоту h, на которую поднимется шар, и долю потерянной кинетической энергии пули
·, перешедшую в тепловую энергию.

7.5. Движение тела вокруг неподвижной оси вращения задано уравнением13 EMBED Equation.DSMT4 1415, рад. Сколько оборотов N сделает тело до момента изменения направления вращения тела и чему равна средняя угловая скорость тела за этот интервал времени?

7.6. На рисунке приведен график зависимости от времени проекции угловой скорости вращающегося тела на ось вращения. Момент действующих на тело сил был постоянным не равным нулю на участке

7.7 На рисунке приведены графики зависимости различных физических величин от угла поворота тела
·. Какой график соответствует зависимости кинетической энергии тела, вращающегося с постоянным угловым ускорение, момент инерции которого не изменяется за время движения?

7.8. Сплошной и полый шары, имеющие одинаковые массы и радиусы, скатываются без проскальзывания с горки высотой h. Какое из тел будет иметь большую скорость у основания горки и во сколько раз?

ИЗД Механика поступательного и вращательного движения

Вариант 8

8.1. Материальная точка движется прямолинейно вдоль оси ОХ. Проекция ее скорости изменяется со временем так, как изображено на рисунке. Пользуясь графиком, определите координату х точки в момент времени t = 6 с, если её начальная координата х0 = 1 м.

8.2. Автомобиль массой m = 600 кг въезжает на выпуклый мост, представляющий собой дугу окружности радиусом R = 120 м. Скорость автомобиля равна
· = 108 км/ч. В некоторый момент времени радиус-вектор, проведенный из центра кривизны моста в точку, где находится автомобиль, составляет с горизонталью угол
· = 600. Определить силу нормального давления автомобиля на мост в этой точке.

8.3. Теннисный мяч летел с импульсом 13 QUOTE 1415 (масштаб и направление указаны на рисунке), когда теннисист произвел по мячу резкий удар со средней силой F=80H. Изменившийся импульс мяча стал равным 13 QUOTE 1415. Определить время, в течение которого сила действовала на мяч.

8.4. С высоты h = 5,0 м бросают вертикально вверх тело массой m = 0,20 кг с начальной скоростью
·0 = 2,0 м/с. При падении на Землю тело углубляется в грунт на глубину l = 5,0 см. Найти среднюю силу сопротивления грунта движению тела.

8.5. Диск радиуса R начинает вращаться из состояния покоя в горизонтальной плоскости вокруг оси Z, проходящей перпендикулярно его плоскости через его центр. Зависимость проекции угловой скорости от времени показана на графике. Чему равны тангенциальные ускорения точки на краю диска в моменты времени t1 = 2 с и t2 = 7 с?

8.6. По ободу шкива, насаженного на общую ось с маховым колесом, намотана нить, к концу которой подвешен груз массой m = 4,0 кг. На какое расстояние должен опуститься груз, чтобы колесо со шкивом получило скорость, соответствующую частоте n = 60 об/мин? Момент инерции колеса со шкивом I = 0,42 кг· м2, радиус шкива r = 10 cм.

8.7. Два маленьких массивных шарика закреплены на невесомом длинном стержне, на расстоянии 13 EMBED Equation.DSMT4 1415 друг от друга. Стержень может вращаться без трения в горизонтальной плоскости вокруг вертикальной оси, проходящей посредине между шариками. Стержень раскрутили из состояния покоя до угловой скорости 13 EMBED Equation.DSMT4 1415, при этом была совершена работа А1. Шарики раздвинули симметрично на расстояние 13 EMBED Equation.DSMT4 1415 и раскрутили до той же угловой скорости. При этом была совершена работа
1) 13 EMBED Equation.DSMT4 1415; 2) 13 EMBED Equation.DSMT4 1415; 3) 13 EMBED Equation.DSMT4 1415; 4) 13 EMBED Equation.DSMT4 1415.

8.8. Цилиндр массой m = 5,0 кг катится без скольжения с постоянной скоростью 14 м/с. Определите кинетическую энергию цилиндра. Через какое время цилиндр остановится, если будет действовать сила трения равная 50 Н?

ИЗД Механика поступательного и вращательного движения

Вариант 9

9.1. Движение точки по оси ОХ описывается следующим уравнением:
х = 2 + 3t + t2 , м. Скорость движения точки станет равна vx = 9 м/с в момент времени сек.

9.2. Тело тянут по горизонтальной плоскости с постоянно увеличивающейся горизонтально направленной силой F. График зависимости ускорения, приобретаемого телом, от приложенной к нему силы F приведен на рисунке.
Определить силу нормальной реакции опоры действующей на тело ( в Н).

9.3. На рисунке изображена зависимость потенциальной энергии Wp упруго деформированного стержня от его удлинения
·l. Найдите удлинение
·l, соответствующее потенциальной энергии Wp = 3,6 Дж. Закон Гука для искомого значения
·l выполняется.

9.4. Кусок пластилина массой m = 200 г падает со скоростью V = 6 м/с, направленной под углом
· = 600 к горизонту, на брусок массой m1 = 2m, двигающийся со скоростью V1 = V/2 по гладкой горизонтальной поверхности навстречу куску пластилина. Найти энергию, перешедшую в тепловую Q при абсолютно неупругом ударе.

9.5 Диск вращается с постоянным угловым ускорением, величина которого
· = 5 рад/с2. Сколько оборотов N сделает диск при изменении частоты вращения от n1= 240 мин-1 до n2 = 90 мин-1? Найдите время, в течение которого это произойдет.

9.6. Момент импульса тела относительно неподвижной оси изменяется по закону 13 EMBED Equation.DSMT4 1415. Укажите график, правильно отражающий зависимость от времени величины момента сил, действующих на тело.

9.7. На рисунке представлен график зависимости проекции вращательного момента силы, действующей на тело, от угла поворота. Чему равна работа сил, действующих на тело, при повороте его на угол 10 рад ?

9.8. Шар массой m = 3 кг скатывается без проскальзывания с вершины наклонной плоскости высотой h=4 м без начальной скорости. Длина ската наклонной плоскости l = 8 м, а значение коэффициента трения качения тела одинаково на протяжении всего пути и равно
· = 0,1. Найдите расстояние, которое пройдет шар от подножья наклонной плоскости до своей полной остановки.

ИЗД Механика поступательного и вращательного движения

Вариант 10

10.1 Материальная точка движется по окружности со скоростью V. На рисунке показан график зависимости проекции скорости V
·–от времени (
·– единичный вектор положительного направления, V
·– проекция скорости на это направление). При этом для нормального и тангенциального ускорения справедливы утверждения:
1) аn – увеличивается, а
· – уменьшается
2) аn – постоянно , а
· – равно нулю
3) аn — уменьшается , а
· – постоянно
4) аn – постоянно, а
·– увеличивается

10.2. Веревка выдерживает груз массой m1 = 110 кг при вертикальном подъеме его с некоторым ускорением и груз массой m2 = 690 кг при опускании его с таким же по модулю ускорением. Какова максимальная масса груза m, который можно поднимать на этой веревке с постоянной скоростью?

10. 3. Шарик, прикрепленный к пружине и насаженный на горизонтальную направляющую, совершает гармонические колебания.
На графике представлена зависимость проекции силы упругости пружины на положительное направление оси ОХ от координаты шарика. Чему равна работа силы упругости при смещении шарика из положения А в положение С?

10.4. Небольшое тело соскальзывает с высоты Н = 3 м по наклонному скату, переходящему в «мертвую петлю» с радиусом R = 1,3 м. На какой высоте h тело оторвется от поверхности петли, если трение отсутствует?

10.5. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется во времени, как показано на графике. На какой угол (в рад) окажется повернутым тело относительно начального положения через 10 с ?

10.6. Две гири разной массы соединены нитью, перекинутой через блок, момент инерции которого J = 50 кг
·м2 и радиус R = 20 см. Блок вращается с трением и момент сил трения равен М = 98,1 Нм. Найдите разность сил натяжений нити (Т1-Т2) по обе стороны блока, если известно, что блок вращается с постоянным угловым ускорением
· = 2,36 рад/с2.

10.7. На рисунке представлены графики зависимости мощности 13 EMBED Equation.DSMT4 1415 постоянного момента силы от времени 13 EMBED Equation.DSMT4 1415. Тело вращается равноускоренно. Какой график соответствует этому случаю?

10.8. Обруч массой m = 0.3кг и радиусом R = 0.5 м привели во вращение, сообщив ему энергию вращательного движения 1200 Дж, и отпустили на пол так, что его ось вращения оказалась параллельной плоскости пола. Если обруч начал двигаться без проскальзывания, имея кинетическую энергию вращения 200 Дж, то сила трения совершила работу, равную

ИЗД Механика поступательного и вращательного движения

Вариант 11

11.1. Движение точки по оси ОХ описывается следующим уравнением
х =2 – 3t+ t2, м. За две секунды движения точка совершит перемещение (в м), равное

11.2. Автомобиль массой m = 5 т равномерно со скоростью V = 72 км/час съезжает в вогнутый мост, представляющий собой дугу окружности радиусом R = 80 м. Определить, с какой силой автомобиль давит на мост в точке, радиус которой составляет с радиусом впадины моста угол
· = 300.

11.3. Теннисный мяч летел с импульсом 13 QUOTE 1415 (масштаб и направление указаны на рисунке), когда теннисист произвел по мячу резкий удар длительностью
·t = 0,1 с. Изменившийся импульс мяча стал равным 13 QUOTE 1415. Найти среднюю силу удара F.

11.4. Пуля летит горизонтально со скоростью
·0 = 160 м/с, пробивает стоящую на горизонтальной шероховатой поверхности коробку и продолжает движение в прежнем направлении со скоростью 13 QUOTE 1415
·0. Масса коробки в 12 раз больше массы пули. Коэффициент трения скольжения между коробкой и поверхностью
· = 0,3. На какое расстояние S переместится коробка к моменту, когда ее скорость уменьшится на 20% ?

11.5. Маховик начал вращаться равноускоренно и за промежуток времени t = 10 с достиг частоты n = 300 мин-1. Запишите уравнение зависимости 13 EMBED Equation.DSMT4 1415рад, согласно которому вращается диск.

11.6. Момент силы, приложенный к вращающемуся телу, изменяется по закону13 EMBED Equation.DSMT4 1415, где 13 EMBED Equation.DSMT4 1415 – некоторая положительная константа.
Момент инерции остается постоянным в течение всего времени вращения. Зависимость углового ускорения от времени представлена на рисунке

11.7. Два маленьких массивных шарика закреплены на концах невесомого стержня длины d1. Стержень может вращаться вокруг вертикальной оси, проходящей через середину стержня. Стержень раскрутили до угловой скорости 13 EMBED Equation.DSMT4 1415. Под действием трения стержень остановился, при этом выделилось количество теплоты Q1. Если шарики закрепить на концах невесомого стержня длины d2 = 2 d1 и стержень раскрутить до угловой скорости 13 EMBED Equation.DSMT4 1415, то при остановке стержня выделится количество теплоты
1) 13 EMBED Equation.DSMT4 1415; 2) 13 EMBED Equation.DSMT4 1415; 3) 13 EMBED Equation. DSMT4 1415; 4) 13 EMBED Equation.DSMT4 1415.

11.8. Определить скорость поступательного движения сплошного цилиндра, скатившегося с наклонной плоскости высотой h = 20 см.

ИЗД Механика поступательного и вращательного движения

Вариант 12

12.1. Тело из состояния покоя начинает двигаться вдоль оси ОХ. График зависимости проекции ускорения тела на ось ОХ приведён на рисунке. Проекция скорости движущейся точки в момент времени 3 с равна м/с.

12.2. Математический маятник массой m = 100 г, подвешенный на нити, проходит положение, определяемое углом
· = 600 с вертикалью. В этом положении натяжение нити равно Т = 1 Н. Чему равен модуль полного ускорения шарика в этот момент?

12.3. График зависимости потенциальной энергии Wp от координаты х имеет вид, представленный на рисунке. Какой из графиков, приведенных ниже, соответствует зависимости проекции консервативной силы Fx на ось x?

12.4. Два маленьких шарика массами m1 = 10 г и m2 = 20 г висят на длинных одинаковых вертикальных нитях. Между ними находится сжатая пружина, которая удерживается в сжатом состоянии связывающей ее нитью. Потенциальная энергия деформации пружины Wp = 0,05 Дж. Нить, связывающую тела, пережигают. Найти максимальные высоты h2 и h3, на которые поднимутся шарики.

12.5. На графике представлена зависимость угла
· поворота вращающегося тела от времени t. Используя график, определите угловое ускорение вращения тела.

12.6. Цилиндр, расположенный горизонтально, может вращаться около оси, совпадающей с осью цилиндра. Масса цилиндра m1= 12 кг. На цилиндр намотали шнур, к которому привязали гирю массой m2 = 1 кг. С каким ускорением будет опускаться гиря? Какова сила натяжения шнура во время движения гири?

12.7. На рисунке дан график зависимости энергии вращающегося тела Wвр от угловой скорости. Чему будет равен момент импульса тела, при величине угловой скорости равной 13 EMBED Equation.DSMT4 1415 ?

12.8. Однородный диск из состояния покоя скатывается без проскальзывания с наклонной плоскости, высота которой h=0. 5 м. Определите линейную скорость движения центра диска у основания наклонной плоскости и максимальную линейную скорость движения точек, находящихся на ободе диска, у основания наклонной плоскости (в м/с).

ИЗД Механика поступательного и вращательного движения

Вариант 13

13.1. Скорость тела, движущегося по оси ОХ, изменяется со временем по закону 13 QUOTE 1415. Средняя скорость движения тела (в м/с) в интервале времени от 1 c до 2 c равна

13.2. Два бруска массами m1 = 5 кг и m2 = 3 кг связаны невесомой и нерастяжимой нитью, перекинутой через невесомый блок. Брусок I может скользить по наклонной плоскости, образующей с горизонтом угол
· = 300. Коэффициент трения бруска I о наклонную плоскость
· = 0,1. Найти ускорение, с которым движутся бруски и силу натяжения нити.

13.3. Материальная точка  начинает двигаться под действием силы 13 QUOTE 1415 = 13 EMBED Equation.3 1415 (Н) . Если зависимость радиус-вектора материальной точки от времени имеет вид 13 EMBED Equation.3 1415(м), то мощность (Вт), развиваемая силой в момент времени t = 2 c  равна 

13.4. На дне гладкой полусферы радиусом R = 2 м лежит кубик массой m1 = 0,3 кг. С края полусферы соскальзывает кубик массы m2 = 0,2 кг такого же размера, как и первый. Какой будет высота подъема кубиков после неупругого удара? Чему равно количество теплоты, выделившееся в результате абсолютно неупругого столкновения кубиков?

13.5. Частица движется по окружности радиусом R = 1м в соответствии с уравнением 13 EMBED Equation.DSMT4 1415, где 13 EMBED Equation.DSMT4 1415 — в радианах, 13 EMBED Equation.DSMT4 1415 — в секундах. Определите угловое ускорение и угловую скорость движения в момент времени 13 EMBED Equation.DSMT4 1415.

13.6. На рисунке представлен график зависимости проекции вращательного момента силы, действующей на тело, от времени. На каком из интервалов времени тело вращалось равнозамедленно?

13. 7. Два маленьких массивных шарика закреплены на невесомом длинном стержне на расстоянии 13 EMBED Equation.DSMT4 1415 друг от друга. Стержень вращается без трения в горизонтальной плоскости вокруг вертикальной оси, проходящей посредине между шариками. Стержень раскрутили до угловой скорости 13 EMBED Equation.DSMT4 1415, совершив работу А1. Какую работу А2 надо совершить, если шарики раздвинуть симметрично на расстояние 13 EMBED Equation.DSMT4 1415 и раскрутить до угловой скорости в два раза большей?

13.8. Сплошной (1) и полый цилиндры (2) одинаковых масс и радиусов катятся без скольжения по горизонтальной поверхности с одинаковой скоростью. Чему равно отношение расстояний 13 QUOTE 1415 , которое пройдут цилиндры до своей полной остановки. Значение коэффициента трения тел одинаково на протяжении всего пути и равно
· = 0,1.

ИЗД Механика поступательного и вращательного движения

Вариант 14

14.1. Две материальные точки 1 и 2 в момент времени 13 EMBED Equation.DSMT4 1415 выходят из точки с координатой 13 EMBED Equation.DSMT4 1415 и движутся в положительном направлении оси 13 EMBED Equation.3 1415. Используя графики зависимости от времени t проекций 13 EMBED Equation.DSMT4 1415 и 13 EMBED Equation.DSMT4 1415 скоростей точек, найдите расстояние от места начала движения до места встречи.

14.2. Ленточный транспортер образует с горизонтом угол
· = 200. Коэффициент трения между грузом и лентой транспортера
· = 0,60. Максимальное ускорение, с которым можно поднимать на этом транспортере груз, равно м/с2 (с округлением до десятых долей), g = 10 м/с2.

14.3. На теннисный мяч, который летел с импульсом p1, на короткое время
·t = 0,1 с подействовал порыв ветра с постоянной силой F = 30 H и импульс мяча стал равным p2 (масштаб и направление указаны на рисунке). Найти величину импульса p1.

14.4. При выполнении трюка «Летающий велосипедист» гонщик движется по трамплину под действием силы тяжести, начиная движение из состояния покоя с высоты Н = 6 м (см. рисунок). На краю трамплина скорость гонщика направлена под таким углом к горизонту, что дальность его полета максимальна. Пролетев по воздуху, гонщик приземляется на горизонтальный стол, находящийся на той же высоте, что и край трамплина. Какова высота полета h на этом трамплине? Сопротивлением воздуха и трением пренебречь.

14.5. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется во времени, как показано на графике. На каких интервалах времени знаки проекций угловой скорости и углового ускорения одинаковые?

14.6. Имеются два цилиндра: алюминиевый (сплошной) и свинцовый (полый) одинакового радиуса R = 10 см и одинаковой массы m = 0,50 кг. Найдите моменты инерции этих цилиндров. Найдите отношение времен 13 EMBED Equation.DSMT4 1415, за которые каждый цилиндр скатится без скольжения с наклонной плоскости, высота наклонной плоскости h = 0,50 м, угол наклона плоскости
· = 30°.

14.7. На рисунке представлен график зависимости проекции вращательного момента силы, действующей на тело, от угла поворота. Чему равна работа сил, действующих на тело, при повороте его на угол 6 рад ?

14.8. Сплошной цилиндр (1) и шар (2), имеющие одинаковые массы и радиусы, вкатываются без проскальзывания с одинаковыми начальными скоростями на горку. Найдите отношение высот h2/h3, на которые смогут подняться эти тела, если трением и сопротивлением воздуха можно пренебречь.

ИЗД Механика поступательного и вращательного движения

Вариант 15

15.1 Три тела равной массы бросили с одинаковыми по модулю скоростями: первое вертикально вверх, второе под углом 30є к горизонту, а третье под углом 60є. Первым достигнет точки наивысшего подъема тело под номером

15.2. Шарик подвешен на тонкой нерастяжимой нити длиной l = 50 см к краю горизонтального диска радиусом R = 20 см. Диск приводят во вращение вокруг вертикальной оси. С какой угловой скоростью надо вращать диск, чтобы нить с шариком отклонилась от вертикали на угол
· = 450?

15. 3. На рисунке показан вектор силы, действующей на частицу. Найти работу, совершенную этой силой при перемещении частицы из начала координат в точку с координатами (4; 3) .

15.4. В маленький шар, подвешенный на нити длиной L = 0,4 м, масса которого М = 5 кг, попадает пуля массой m = 20 г, летящая с горизонтальной скоростью V1 = 1000 м/с. Пройдя через шар, она продолжает движение в том же направлении со скоростью V2 = 500 м/с. На какой угол от вертикали отклонится шар?

15.5. Вращение плоского тела вокруг неподвижной оси, расположенной перпендикулярной плоскости тела и проходящей через точку О, задано уравнением 13 EMBED Equation.DSMT4 1415. Начало движения при 13 EMBED Equation.DSMT4 1415. Положительные углы отсчитываются в направлении стрелки на рисунке. Определите, как будет вращаться тело и с какой по величине угловой скоростью, в момент времени 13 EMBED Equation.DSMT4 1415 после начала движения

15.6. Момент импульса относительно неподвижной оси изменяется по закону 13 EMBED Equation.DSMT4 1415, при этом зависимость момента сил описывается графиком

15.7. На графике приведена зависимость проекции момента силы, действующей на тело, от времени. Какой момент импульса будет иметь тело к концу третьей секунды движения, если в начальный момент t0 = 0 тело покоилось.

15.8. Деревянный стержень длиной l = 1,0 м и массой M = 5,0 кг может вращаться вокруг перпендикулярной к нему оси, проходящей через точку O, расположенную на верхнем конце стержня. В нижний конец стержня попадает пуля массы m = 10,0 г, летящая перпендикулярно к оси и к стержню со скоростью V0 = 200 м/с и пробивает его. После удара пуля продолжает двигаться в прежнем направлении со скоростью V = 100 м/с. Определите, какая доля первоначальной энергии пули перешла в тепло?

ИЗД Механика поступательного и вращательного движения

Вариант 16

16.1. Используя график зависимости скорости движения тела от времени, определите скорость тела в конце пятой секунды, считая, что характер движения не изменился. Определите координату x в момент времени t = 3 c, если в начальный момент времени t0 = 0 с координата x0 = 2 м.

16.2. Грузы массами m1 = 4 кг и m2 = 5 кг связаны между собой нитью, перекинутой через неподвижный блок. Первый груз расположен на горизонтальном столе, второй висит на вертикальной части нити. Определите ускорение грузов a и силу натяжения нити T при условии, что коэффициент трения груза о стол
· = 0,1. Нить считать невесомой и нерастяжимой, массой блока пренебречь.

16.3. Проекция px импульса материальной точки, движущейся прямолинейно вдоль оси Х, изменяется со временем так, как показано на рис. 1. Какой номер графика на рис. 2 соответствует зависимости Fx(t) – проекции силы, действующей на точку и вызывающей это изменение px? Ответ обосновать.13 EMBED PBrush 1415

16.4. Два шарика, массы которых m = 0,1 кг и М = 0,2 кг, висят, соприкасаясь, на вертикальных нитях длиной l = 1,5 м (см. рисунок). Левый шарик отклоняют на угол 90° и отпускают без начальной скорости. Какое количество теплоты выделится в результате абсолютно неупругого удара шариков?

16.5. На рисунке приведен график параболической зависимости модуля углового перемещения абсолютно твердого тела от времени. Начальная угловая скорость равна нулю. За четыре секунды тело повернется на угол рад.

16.6. Стержень вращается вокруг оси, проходящей через его один из его концов согласно уравнению
· = At+Bt3, где A=2 рад/с; B = 0,2 рад/с3. Найдите закон изменения момента сил M, действующих на стержень. Определите угловую скорость и момент сил M в момент времени t = 2 с, если момент инерции стержня J = 0,048 кг
·м2.

16.7. На рисунке представлен график зависимости кинетической энергии вращающегося Wвр тела, момент инерции которого равен J = 2 кг·м2 , от угла поворота
·. Чему равен вращающий момент сил, действующий на тело, в тот момент времени, когда угол поворота станет равным

· = 3 рад.

16.8. Мальчик катит обруч по горизонтальной поверхности со скоростью v=7.2 км/ч., Найдите высоту (в метрах), на которую может вкатиться обруч в горку за счет своей кинетической энергии, если пренебречь силой трения качения.

ИЗД Механика поступательного и вращательного движения

Вариант 17

17.1. Тело движется в плоскости ХОУ и при этом его координаты изменяются со временем следующим образом: х = 2 + 3t – t2 , м и y = 4 – 2 t2, м. Модуль ускорения этого тела в момент времени t = 2.0 c равен м/с2 (с округлением до десятых долей).

17.2. Тело массой m = 0,8 кг движется вверх по плоскости, наклоненной под углом
·=300 к горизонту. К телу прикреплена пружина жесткости k = 120 Н/м, к которой приложена сила 13 QUOTE 1415 (см. рисунок). Коэффициент трения между телом и плоскостью
· = 0,4. Ускорение тела равно а = 1,2 м/с2. Определить деформацию пружины
·l.

17.3. В потенциальном поле сила 13 EMBED Equation.DSMT4 1415 пропорциональна градиенту потенциальной энергии 13 EMBED Equation.DSMT4 1415. Если график зависимости потенциальной энергии 13 EMBED Equation.DSMT4 1415 от координаты х имеет вид, представленный на рисунке, то зависимость проекции силы13 EMBED Equation.DSMT4 1415 на ось Х будет иметь вид

17.4. Кусок пластилина массой m = 200 г падает со скоростью V = 6 м/с, направленной под углом
· = 600 к горизонту, на брусок массой m1 = 2m, двигающийся со скоростью V1 = V/2 по гладкой горизонтальной поверхности навстречу куску пластилина. Найти количество энергии, перешедшей в тепло Q при абсолютно неупругом ударе.

17.5. Колесо автомашины вращается равноускоренно. Сделав N = 50 полных оборотов, оно изменило частоту вращения от n1 = 4 с-1 до n2 = 6 с-1. Определите угловое ускорение колеса.

17.6. Момент силы, приложенный к вращающемуся телу, изменяется по закону13 EMBED Equation.DSMT4 1415, где 13 EMBED Equation.DSMT4 1415 – некоторая положительная константа.
Момент инерции остается постоянным в течение всего времени вращения. Зависимость углового ускорения от времени представлена на рисунке

17.7. Два маленьких массивных шарика закреплены на невесомом длинном стержне на расстоянии 13 EMBED Equation.DSMT4 1415 друг от друга. Стержень может вращаться без трения в горизонтальной плоскости вокруг вертикальной оси, проходящей посредине между шариками. Стержень раскрутили из состояния покоя до угловой скорости 13 EMBED Equation.DSMT4 14151, при этом была совершена работа А1. Шарики раздвинули симметрично на расстояние 13 EMBED Equation.DSMT4 1415 и раскрутили до той же угловой скорости 13 EMBED Equation.DSMT4 14152 = 13 EMBED Equation.DSMT4 14151. Какая при этом была совершена работа ?
1) 13 EMBED Equation.DSMT4 1415; 2) 13 EMBED Equation.DSMT4 1415; 3) 13 EMBED Equation.DSMT4 1415; 4) 13 EMBED Equation.DSMT4 1415.

17.8. Обруч скатывается без проскальзывания с горки высотой h = 2,5 м. Найдите скорость обруча у основания горки при условии, что трением можно пренебречь.

ИЗД Механика поступательного и вращательного движения

Вариант 18

18.1. На графике изображена зависимость координаты точки от времени.
Какой график зависимости скорости от времени отвечает этому случаю?

18.2. Тело начинает скользить вниз по наклонной плоскости, составляющей с горизонтом угол
· = 300. У основания плоскости тело ударяется о стенку, поставленную перпендикулярно к направлению его движения, и отскакивает без потери скорости. Определить коэффициент трения
· при движении тела, если после удара оно поднялось до половины первоначальной высоты.

18.3. Материальная точка двигалась вдоль оси ОХ равномерно с некоторой скоростью Vx. Начиная с момента времени t = 0, на нее стала действовать сила Fх, график временной зависимости которой представлен на рисунке. Какой график правильно отражает зависимость величины проекции импульса материальной точки от времени на следующем рисунке? Ответ обоснуйте.

18.4. Два цилиндра массами m1=150 г и m2 = 300 г, соединенные сжатой пружиной, разошлись при внезапном освобождении пружины в разные стороны.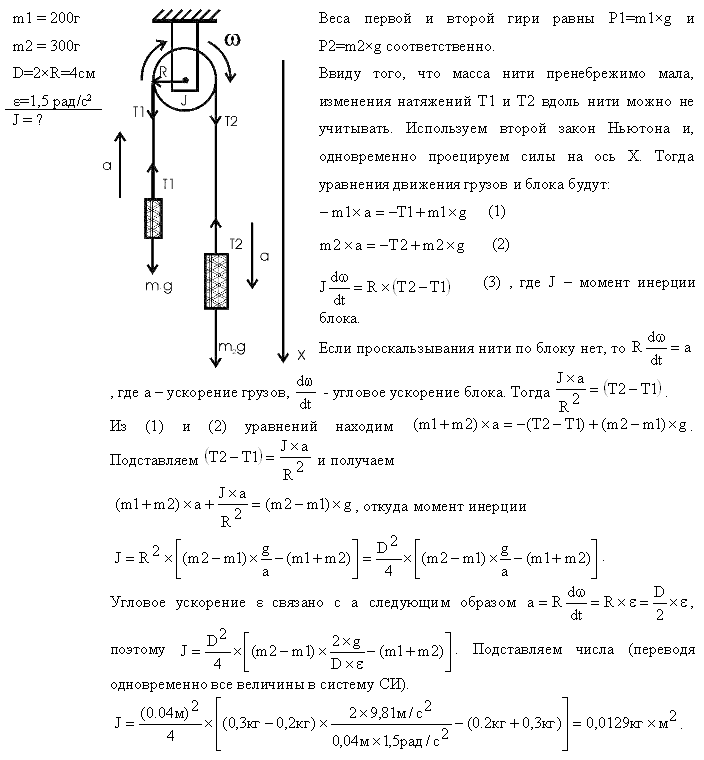 Пренебрегая силами сопротивления и учитывая, что кинетическая энергия упруго деформации пружины составляет 1,8 Дж, определить скорости движения первого и второго цилиндров сразу после освобождения пружины.
18.5. На графике представлена зависимость угловой скорости 13 EMBED Equation.DSMT4 1415 тела, вращающегося вокруг неподвижной оси, от времени t. Определить количество оборотов N, которое сделает тело до остановки.
18.6. Диск, момент инерции которого J = 40 кг
·м2, начинает вращаться равноускоренно под действием момента силы М = 20 Н
·м. 1) Какой момент импульса будет иметь тело через t = 10 с вращения? На рисунке покажите направление этого момента импульса; 2) Сколько полных оборотов сделает диск за этот промежуток времени?
18.7. На рисунке представлен график зависимости проекции вращательного момента силы, действующей на тело, от угла поворота. Чему равна работа сил, действующих на тело, при повороте его на угол 5 рад ?

18.8. Тонкий однородный стержень длиной l = 1м может свободно вращаться вокруг горизонтальной оси, проходящей через точку О на стержне. Стержень отклонили от вертикали на угол
· =
·/3 и отпустили. Определите угловую скорость стержня и линейную скорость точки В на стержне в момент прохождения им положения равновесия.

ИЗД Механика поступательного и вращательного движения

Вариант 19

19.1 На графике приведена зависимость проекции ускорения на ось x от времени. Какую скорость будет иметь тело к концу третьей секунды движения, если в начальный момент t0 = 0 c его скорость V0 = 5 м/с?

19.2. Тело начинает скользить вниз по наклонной плоскости, составляющей с горизонтом угол
· = 300. У основания плоскости тело ударяется о стенку, поставленную перпендикулярно к направлению его движения, и отскакивает без потери скорости. Определить коэффициент трения
· при движении тела, если после удара оно поднялось до половины первоначальной высоты.

19.3. Проекции p1x и p1x импульсов материальных точек 1 и 2, движущихся прямолинейно вдоль оси Х, изменяются со временем t как показано на рисунке; при этом проекции ускорений точек одинаковы: ax1 = ax2. Найти отношение масс m1/m2 этих точек.

19.4. На идеально гладком столе лежат два груза, массы которых относятся как 1:3. Грузы соединены между собой сжатой пружиной жесткостью k = 1000 Н/м. Пружина удерживается в сжатом состоянии с помощью тонкой нерастяжимой нити. После пережигания нити пружина разжимается, и более легкий груз приобретает кинетическую энергию Wk = 60 Дж. Определить величину деформации
·l сжатой пружины.

19.5. Частица движется вдоль окружности радиусом R = 1м в соответствии с уравнением 13 EMBED Equation.DSMT4 1415. Определите время движения до остановки и расстояние ( в м), пройденное точкой за это время.

19.6. Диск начинает вращаться под действием момента сил М, график временной зависимости которого представлен на рис. 1.График, правильно отражающий зависимость момента импульса диска от времени, представлен на рис.2. под номером

19.7. На рисунке приведен график зависимости угла поворота
· тела при вращательном движении от времени. Как изменяется кинетическая энергия тела в интервале времени от t1 до t2?

19.8. Сплошной однородный диск катится по горизонтальной плоскости со скоростью v = 10 м/с. Какое расстояние пройдет диск до остановки, если его предоставить самому себе? Коэффициент трения при движении диска равен
· = 0,02.

ИЗД Механика поступательного и вращательного движения

Вариант 20

20.1. Тангенциальное ускорение точки меняется согласно графику. Выберите график зависимости скорости от времени, соответствующая такому движению. Ответ обоснуйте. Постройте схематично график зависимости координаты от времени.

20.2. Маленький шарик, привязанный к невесомой нити длиной l = 40 см, вращается в горизонтальной плоскости с постоянной по модулю скоростью так, что нить описывает коническую поверхность с вершиной в точке, где находится верхний конец нити.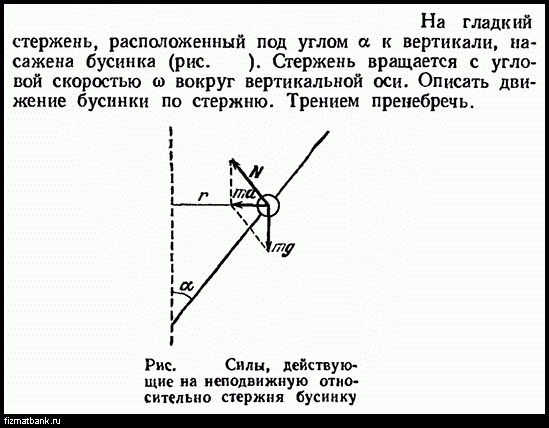 При этом угол отклонения нити от вертикали
· = 300. Определить скорость вращения
· шарика.

20.3. В потенциальном поле сила 13 EMBED Equation.DSMT4 1415 пропорциональна градиенту потенциальной энергии13 EMBED Equation.DSMT4 1415. Если график зависимости потенциальной энергии13 EMBED Equation.DSMT4 1415 от координаты х имеет вид, представленный на рисунке, то зависимость проекции силы13 EMBED Equation.DSMT4 1415 на ось Х изображена на рисунке под номером

20.4. Шар массой 1 кг, подвешенный на нити длиной 90 см, отводят от положения равновесия на угол 60є и отпускают. В момент прохождения шаром положения равновесия в него попадает пуля массой 10 г, летящая навстречу шару со скоростью 300 м/с. Она пробивает его и вылетает горизонтально со скоростью 200 м/с, после чего шар продолжает движение в прежнем направлении. На какой максимальный угол отклонится шар после попадания в него пули? (Массу шара считать неизменной, диаметр шара – пренебрежимо малым по сравнению с длиной нити.)

20.5. На графике представлена зависимость угла поворота
· тела, вращающегося вокруг неподвижной оси, от времени t. Величина углового ускорения в этом случае равна рад2/с. (Ответ округлить до десятых).

20.6. Однородный стержень длиной l = 1,2 м и массой m = 0,3 кг вращается в горизонтальной плоскости вокруг вертикальной оси, проходящей через один из его концов с угловым ускорением
· = 9,81 с-1. Сколько оборотов сделает стержень за время t = 5,0 с, если он начал вращаться из состояния покоя? Как изменится вращающий момент, если ось вращения переместить в центр масс стержня, а действующая сила не изменяется?

20.7. На рисунке представлены графики зависимости мощности 13 EMBED Equation.DSMT4 1415 постоянного момента силы от времени 13 EMBED Equation.DSMT4 1415. Тело вращается равнозамедленно. Какой график соответствует этому случаю?

20.8. Шар массой m = 3 кг скатывается без проскальзывания с вершины наклонной плоскости высотой h = 4 м без начальной скорости.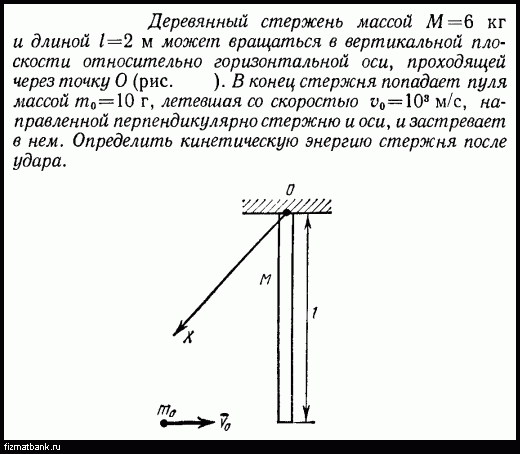 Длина ската наклонной плоскости l = 8 м, а значение коэффициента трения качения (
·) тела одинаково на всем протяжении его пути и равно
· =0,1. Определите скорость шара у подножия наклонной плоскости (в м/с).

ИЗД Механика поступательного и вращательного движения

Вариант 21

21.1. Материальная точка М движется по окружности со скоростью 13 EMBED Equation.DSMT4 1415. На рис.1 показан график зависимости 13 EMBED Equation.DSMT4 1415 от времени (13 EMBED Equation.DSMT4 1415 — единичный вектор положительного направления, 13 EMBED Equation.DSMT4 1415 — проекция 13 EMBED Equation.DSMT4 1415 на это направление). На рис.2 направление силы, действующей на т. М в момент времени 13 EMBED Equation.DSMT4 1415, совпадает с направлением …

21.2. Тело массой m = 1,4 кг находится на гладкой горизонтальной плоскости и вращается вокруг вертикальной оси. Оно прикреплено к оси пружиной и движется по окружности радиуса R, совершая n = 1 об/сек. Длина пружины в недеформированном состоянии равна L0 = 50 см. Радиус траектории тела равен R = 88 см. Определить жесткость пружины k.

21.3. Шарик, прикрепленный к пружине и насаженный на горизонтальную направляющую, совершает гармонические колебания. На графике представлена зависимость проекции силы упругости пружины Fx на положительное направление оси Х от координаты шарика. Найти работу силы упругости на участке 0 – В – 0.

21.4. Два тела, которые первоначально покоились на гладкой горизонтальной поверхности, расталкиваются зажатой между ними легкой пружиной и начинают двигаться так, что в процессе движения их максимальные скорости равны
·1 = 1 м/с и
·2 = 3 м/с. Какая энергия была запасена в пружине, если общая масса тел М = 8 кг?

21.5. Скорость вращения тела зависит от времени согласно уравнению 13 EMBED Equation.DSMT4 1415. Чему равно угловое ускорение тела при этом движении. Запишите зависимость угла поворота от времени при условии, что угол поворота в момент времени13 EMBED Equation. DSMT4 1415 был равен13 EMBED Equation.DSMT4 1415.

21.6. На рисунке приведен график зависимости от времени проекции угловой скорости 13 EMBED Equation.DSMT4 1415вращающегося тела на ось вращения. На каком интервале времени момент сил, действующих на тело, был постоянным, не равным нулю и максимальным по модулю?

21.7. Два маленьких массивных шарика закреплены на невесомом длинном стержне на расстоянии 13 EMBED Equation.DSMT4 1415 друг от друга. Стержень может вращаться без трения в горизонтальной плоскости вокруг вертикальной оси, проходящей посредине между шариками. Стержень раскрутили из состояния покоя до угловой скорости 13 EMBED Equation.DSMT4 1415, при этом была совершена работа А1. Шарики сдвинули симметрично на расстояние 13 EMBED Equation.DSMT4 1415 и раскрутили до угловой скорости
13 EMBED Equation.DSMT4 14152 = 213 EMBED Equation.DSMT4 14151. Какая при этом была совершена работа ?
1) 13 EMBED Equation.DSMT4 1415; 2) 13 EMBED Equation.DSMT4 1415; 3) 13 EMBED Equation.DSMT4 1415; 4) 13 EMBED Equation.DSMT4 1415.
21.8. Сплошной и полый цилиндры, имеющие одинаковые массы и радиусы, вкатываются без проскальзывания на горку. Какой из цилиндров поднимется выше и во сколько раз, если начальные скорости тел одинаковы?

ИЗД Механика поступательного и вращательного движения

Вариант 22

22.1. Тело движется в плоскости ХОУ и при этом его координаты изменяются со временем следующим образом: х = 2 + 2t – t2,м и y = 4 + 2 t,м. Скорость этого тела в момент времени t = 1.0 c равна м/с.

22.2. Брусок массой 4 кг может двигаться только вдоль вертикальных направляющих, расположенных на вертикальной стене. Коэффициент трения бруска о направляющие
· = 0,1. Если а брусок действует сила 13 QUOTE 1415, по модулю равная 20 Н и направленная под углом
· = 600 к вертикали (см. рисунок). Определить ускорение бруска.

22.3. Два тела одинаковой массы соскальзывают без начальной скорости 13 EMBED Equation.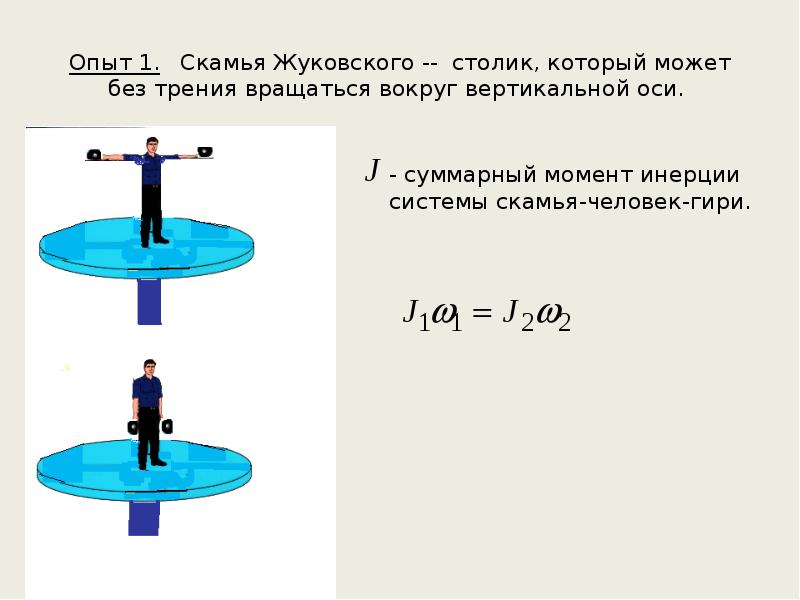 DSMT4 1415 с вершин двух наклонных плоскостей, длины которых 13 EMBED Equation.DSMT4 1415. Если13 EMBED Equation.DSMT4 1415, а коэффициенты трения тел о плоскости в обоих случаях одинаковы, то соотношение между работами силы трения 13 EMBED Equation.DSMT4 1415 и 13 EMBED Equation.DSMT4 1415 в обоих случаях следующее
1)
2)
3)
4) среди ответов правильного нет
Укажите номер правильного ответа и поясните его.

22.4. Небольшая шайба соскальзывает без трения с вершины полусферы радиусом R = 30 см. На какой высоте h от основания шайба оторвется от полусферы?

22.5. На графике представлена зависимость угловой скорости 13 EMBED Equation.DSMT4 1415
· тела, вращающегося вокруг неподвижной оси, от времени t. Напишите уравнение, верно отражающее зависимость угла поворота
· от времени t при условии, что угол поворота в момент времени 13 EMBED Equation.DSMT4 1415 был равен13 EMBED Equation.DSMT4 1415.

22.6. Колесо, вращаясь равнозамедленно, уменьшило частоту вращения от n1 = 300 об/мин до n2 = 180 об/мин за время t = 1 мин. Момент инерции колеса J = 2 кг
·м2. 1) Определите угловое ускорение колеса и покажите на рисунке, как оно направлено; 2) Как направлен момент сил торможения, и чему он равен?

22.7. На рисунке представлен график зависимости проекции вращательного момента силы, действующей на тело, от времени. Чему равен момент импульса тела в момент времени t = 6 с, если в начальный момент времени тело покоилось?

22.8. Шар катится без проскальзывания по горизонтальной поверхности со скоростью
·1 = 10 м/с. После удара о вертикальную стенку он стал двигаться в обратном направлении со скоростью
·2 = 6 м/с. Какую часть первоначальной энергии потерял шар при ударе?

ИЗД Механика поступательного и вращательного движения

Вариант 23

23.1. Под каким углом к горизонту следует бросить камень, чтобы дальность полета была равна высоте полета? Сопротивлением воздуха пренебречь.

23. 2. На диске, вращающемся вокруг вертикальной оси, лежит шайба массы m = 100 г. Шайба соединена с осью горизонтальной пружиной. Коэффициент трения шайбы о диск
· = 0,40. Если число оборотов диска равно n1= 2,0 об/с, пружина находится в недеформированном состоянии и шайба находится на грани скольжения. Если число оборотов диска возрастает до n2 = 5,0 об/с, то длина пружины увеличивается в 2 раза. Определить длину l0 пружины в недеформированном состоянии и жесткость пружины k.

23.3. С ледяной горки с небольшим шероховатым участком АС из точки А без начальной скорости скатывается тело. Сопротивление воздуха пренебрежимо мало. Зависимость потенциальной энергии шайбы от координаты х изображена на графике 13 EMBED Equation.DSMT4 1415. При движении тела сила трения совершила работу Атр = 20 Дж. После абсолютно неупругого удара со стеной в точке В выделилось Дж тепла.

23.4. На рельсах стоит платформа, на которой закреплено орудие без противооткатного устройства так, что ствол его расположен в горизонтальном положении. Масса платформы с орудием М=5 т. Из орудия производят выстрел вдоль железнодорожного пути. Масса m1снаряда равна 10 кг, и его скорость u1 = 1 км/с. На какое расстояние l откатится платформа после выстрела, если коэффициент сопротивления
· = 0,2?
23.5. Велосипедное колесо вращается с частотой n = 5 c-1. Под действием сил трения оно остановилось через интервал времени
·t = 1 мин. Определите угловое ускорение и число оборотов N, которое сделает колесо за это время.

23.6. На рисунке представлен график зависимости проекции вращательного момента силы, действующей на тело, от времени. Сколько оборотов сделает тело за шесть секунд после начала действия вращающегося момента? В начальный момент тело покоилось.

23.7. На рисунке представлен график зависимости проекции вращательного момента силы, действующей на тело, от угла поворота. Чему равна работа сил, действующих на тело, при повороте его на угол 10 рад ?

23. 8. Обруч и диск одинаковой массы m1 = m2 = 1 кг катятся по горизонтальной поверхности без скольжения с одинаковой скоростью. Радиус обруча в два раза больше чем диска. Кинетическая энергия обруча Wобр= 40 Дж. Определите кинетическую энергию диска Wд.

ИЗД Механика поступательного и вращательного движения

Вариант 24

24.1. На рис. 1 приведен график зависимости проекции скорости от времени для материальной точки, движущейся прямолинейно вдоль оси ОХ. На рис.2 представлены четыре различных графика зависимости проекции ускорения от времени. Какой из этих графиков соответствует приведенной зависимости проекции скорости от времени?

24.2. Человек везет связанные веревкой двое саней, каждые из которых имеют массу m = 15 кг, прикладывая силу F = 120 Н под углом
· = 450 к горизонту. Найти ускорение саней, если коэффициент трения полозьев о снег
· = 0,2.

24.3. В потенциальном поле сила 13 EMBED Equation.DSMT4 1415 пропорциональна градиенту потенциальной энергии13 EMBED Equation.DSMT4 1415. Если график зависимости потенциальной энергии13 EMBED Equation.DSMT4 1415 от координаты х имеет вид, представленный на рисунке, то зависимость проекции силы13 EMBED Equation.DSMT4 1415 на ось Х будет иметь вид

24.4. Кусок пластилина сталкивается со скользящим навстречу по горизонтальной поверхности стола бруском и прилипает к нему. Скорости пластилина и бруска перед ударом направлены противоположно и равны vпл = 15 м/с и vбр = 5 м/с. Масса бруска в 4 раза больше массы пластилина. Коэффициент трения скольжения между бруском и столом
· = 0,17. На какое расстояние переместятся слипшиеся брусок с пластилином к моменту, когда их скорость уменьшится на 30%?

24.5. Диск начинает вращаться из состояния покоя в горизонтальной плоскости вокруг оси Z, проходящей перпендикулярно его плоскости через его центр. Зависимость проекции угловой скорости от времени показана на графике.
Определите среднюю скорость вращения тела на интервале времени от 2 с до 8 с.
24.6. Модуль момента импульса вращающегося тела изменяется со временем по закону 13 EMBED Equation.DSMT4 1415, где А = 1 кг
·м2
·с-1, В=2 кг
·м2
·с-3. Определить величину момента силы, действующей на тело, в конце второй секунды от начала движения.
24.7. На рисунке приведены зависимости кинетической энергии трех вращающихся тел Wвр от квадрата угловой скорости 13 EMBED Equation.DSMT4 1415. Какому графику соответствует наименьший момент инерции тела? Укажите его номер и поясните свой выбор.

24.8. Однородный стержень длиной 1,0 м и массой 1,0 кг может свободно вращаться вокруг горизонтальной оси, проходящей через точку О. В точку А на стержне попадает пластилиновый шарик, летящий горизонтально со скоростью V = 10 м/с и прилипает к стержню. Масса шарика m =10 г. Определите угловую скорость стержня и линейную скорость конца стержня сразу после прилипания шарика.

ИЗД Механика поступательного и вращательного движения

Вариант 25

25.1. Координаты материальной точки изменяются со временем по закону
х = 2 t2, у = 2t, z = const.
Траектория, по которой движется точка, представляет собой
1) произвольную пространственную кривую
2) прямую линию в плоскости, параллельной плоскости ХОУ
3) эллипс, расположенный в плоскости, параллельной плоскости ХОУ
4) параболу в плоскости, параллельной плоскости ХОУ
Укажите номер правильного ответа и поясните свой выбор.

25.2. Один конец невесомой пружины прикреплен к вертикальной оси ОО’ (см. рисунок). К другому концу пружины прикреплен шарик массой m = 50 г, который может скользить по стержню без трения. Длина пружины в нерастянутом состоянии L0 = 20 см, ее жесткость k = 40 Н/м. Стержень вращается вокруг оси ОО’ равномерно, делая 2 оборота в секунду. Чему равно при этом удлинение пружины
·L?

25.3. На теннисный мяч, который летел с импульсом 13 QUOTE 1415, на короткое время
·t = 0,01с подействовал порыв ветра с постоянной силой F= 300 Н и импульс мяча стал равным 13 QUOTE 1415 (масштаб и направление указаны на рисунке). Определить величину импульса 13 QUOTE 1415.

25.4. Определить наименьшую высоту h, с которой должен начать скатываться велосипедист, чтобы проехать по дорожке в виде мертвой петли радиусом R = 5 м и не отрываться от дорожки в верхней части. Трением пренебречь.

25.5 . Найдите угловую скорость искусственного спутника Земли, движущегося по круговой орбите с периодом вращения Т= 88 мин. Какова линейная скорость движения этого искусственного спутника, если известно, что его орбита расположена на расстоянии h = 200 км от поверхности Земли?

25.6. Диск начинает вращаться под действием момента сил М, график временной зависимости которого представлен на рисунке.
Укажите график, правильно отражающий зависимость момента импульса диска от времени.

25.7. Для того, чтобы раскрутить стержень массы m1 и длины l1 вокруг вертикальной оси, расположенной перпендикулярно стержню и проходящей через его середину, до угловой скорости
·, необходимо совершить работу А1. Во сколько раз большую работу, чем А2, надо совершить, для того, чтобы раскрутить до той же угловой скорости стержень массы m2 = 2 m1 и длины l2 = 1,5 l1?

25.8 . Столб высотой h = 3,0 м и массой m = 50,0 кг из вертикального положения падает на землю. Нижний конец столба не изменяет своего положения относительно земли при падении столба. Определите момент импульса L относительно точки опоры и скорость верхнего конца столба в момент удара о землю.

ИЗД Механика поступательного и вращательного движения

Вариант 26

26.1. На рисунке изображен график зависимости проекции Sx перемещения тела на ось ОХ, вдоль которой тело движется, от времени t. График представляет собой параболу. Найдите проекцию V0x начальной скорости тела.

26.2. Санки массой m = 10 кг, стоящие на льду, в течение t = 1,0 с тянут с постоянной силой F = 100 Н при помощи веревки, образующей угол
· = 450 с горизонтом, после чего веревку отпускают и забрасывают на санки. Коэффициент трения санок о лед
· = 0,10. Пренебрегая массой веревки, определить путь l
· , пройденный санками за все время их движения.

26.3. Тело брошено под углом
· = 300 к горизонту. За время
·t = 5 с полета модуль изменения импульса тела равен
·р = 200 13 QUOTE 1415. Сопротивление воздуха не учитывать. Масса этого тела равна кг.

26.4. Сваю массой m = 100 кг забивают в грунт копром массой М = 400 кг. Копер свободно падает с высоты Н = 5 м, и при каждом его ударе свая опускается на глубину h = 25 см. Определить силу сопротивления грунта, считая ее постоянной, и КПД неупругого удара копра о сваю.

26.5. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется во времени, как показано на графике. На какой угол ( в рад) окажется тело повернутым относительно начального положения через 10 с после начала движения.
26.6 Блок, массу m = 2,0 кг которого можно считать равномерно распределенной по ободу, вращается с начальной частотой n0 = 12 об/с. Диаметр блока равен D = 30 см. Определите, какой момент сил надо приложить к блоку, чтобы он, двигаясь равнозамедленно, остановился в течение
· t = 8,0 с. Сколько оборотов он сделает до остановки?

26.7. На графике приведена зависимость проекции момента силы, действующей на тело, от времени. Какой момент импульса будет иметь тело к концу третьей секунды движения, если в начальный момент t0 = 0 тело покоилось?

26.8. Шар массой m = 3 кг скатывается без проскальзывания с вершины наклонной плоскости высотой h=4 м без начальной скорости. Длина ската наклонной плоскости l = 8 м, а значение коэффициента трения одинаково на протяжении всего пути и равно
· =0,1. Найдите расстояние, которое пройдет шар от подножья наклонной плоскости до своей полной остановки.

ИЗД Механика поступательного и вращательного движения

Вариант 27

27.1. Тело брошено с поверхности Земли со скоростью v = 20 м/с под углом
· = 60° к горизонту. Сопротивлением воздуха пренебречь. g =10м/с2. Радиус кривизны траектории в точке наибольшего подъема равен м.

27.2. Грузы 1 и 2 с массами m1=1,5 кг и m2=0,5 кг связаны невесомой нерастяжимой нитью , перекинутой через невесомый неподвижный блок. Угол наклона поверхности
· = 300, коэффициент трения между поверхностью и телом
· = 0,2. Найти модуль ускорения тел и величину силы натяжения.

27.3. Теннисный мяч летел с импульсом 13 EMBED Equation.DSMT4 1415 (масштаб и направление указаны на рисунке), когда теннисист произвел по мячу резкий удар со средней силой F = 80 Н. Изменившийся импульс мяча стал равным13 EMBED Equation.DSMT4 1415. Сила действовала на мяч в течение с.

27.4. Камень массой m =0,5 кг, привязанный к веревке длиной l =50 см, равномерно вращается в вертикальной плоскости. Сила натяжения веревки в нижней точке окружности T = 44 Н. На какую высоту h поднимется камень, если веревка обрывается в тот момент, когда скорость направлена вертикально вверх?

27.5. Колесо радиусом R= 10 см вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением 13 EMBED Equation.DSMT4 1415. Найдите, на сколько изменится тангенциальное ускорение 13 EMBED Equation.DSMT4 1415 за единицу времени для точек, лежащих на ободе колеса.

27.6. Диск вращается под действием момента сил М, график временной зависимости которого представлен на рисунке. При 13 EMBED Equation.DSMT4 1415 13 EMBED Equation.DSMT4 1415. Какой цифрой обозначена на графике точка, соответствующая максимальному значению угловой скорости?

27.7. На графике приведена зависимость проекции момента силы, действующей на тело, от времени. Какой момент импульса будет иметь тело к концу четвертой секунды движения, если в начальный момент t0 = 0 тело покоилось.

27.8. Обруч массой m = 0.3 кг и радиусом R = 0.5 м привели во вращение, сообщив ему энергию вращательного движения 1200 Дж, и отпустили на пол так, что его ось вращения оказалась параллельной плоскости пола. Какую кинетическую энергию вращательного движения имел обруч, когда начал движение без проскальзывания, если сила трения совершила работу, равную 800Дж ?

ИЗД Механика поступательного и вращательного движения

Вариант 28

28. 1. Четыре тела равной массы бросили с поверхности Земли с одинаковыми по модулю скоростями: первое вертикально вверх, а остальные под различными углами к горизонту. Сопротивление воздуха при движении тел не учитывается. Наибольшую скорость в точке наивысшего подъема будет иметь тело, обозначенное цифрой

28.2. Тело массой m = 1,2 кг находится на гладкой горизонтальной плоскости и вращается вокруг вертикальной оси. Оно прикреплено к оси пружиной с жесткостью k = 200 Н/м и движется по окружности радиуса R, совершая n = 1 об/сек. Длина пружины в недеформированном состоянии равна L0 = 50 см. Определить радиус траектории тела R.

28.3. На рисунке приведен график зависимости потенциальной энергии 13 EMBED Equation.DSMT4 1415 пружины от величины деформации х. Работа сил упругости при удлинении пружины от х1 = 0,1см до х2 = 0,2 см равна

28.4. Из орудия массой m1 = 5 т вылетает снаряд массой m2 =100 кг. Кинетическая энергия снаряда при вылете Wk2 = 7,5 МДж. Какую кинетическую энергию Wk1 получает орудие вследствие отдачи?

28.5. На графике представлены зависимости угла
· поворота двух вращающихся по одной окружности тел от времени t. Сравните величины угловых скоростей тел. У какого тела и во сколько раз угловая скорость больше?

28.6. Тонкостенный цилиндр, масса которого m = 12 кг, а диаметр D = 30 см, вращается согласно уравнению
· = 4+2 t – 0,2 t3. Определите угловое ускорение цилиндра в момент времени t = 2,0 с. Чему равен момент сил, действующий на тело, в момент времени t = 3,0 с?

28.7. На рисунке представлен график зависимости проекции вращательного момента силы, действующей на тело, от угла поворота. Чему равна работа сил, действующих на тело, при повороте его на угол 10 рад ?

28.8. Однородный стержень длиной 1,5 м и массой m = 10 кг может вращаться вокруг неподвижной оси, проходящей через верхний конец стержня перпендикулярно его длине. В середину стержня ударяет пуля массой 10 г, летящая в горизонтальном направлении со скоростью 500 м/с, и застревает в стержне. Какую линейную скорость будет иметь конец стержня сразу после удара?

ИЗД Механика поступательного и вращательного движения

Вариант 29

29.1. Материальная точка М движется по окружности со скоростью 13 EMBED Equation.DSMT4 1415. На рис.1 показан график зависимости 13 EMBED Equation.DSMT4 1415 от времени (13 EMBED Equation.DSMT4 1415– единичный вектор положительного направления, 13 EMBED Equation.DSMT4 1415 — проекция 13 EMBED Equation.DSMT4 1415 на это направление). На рис.2 направление силы, действующей на т. М в момент времени 13 EMBED Equation.DSMT4 1415, совпадает с направлением …

29.2. Камень, привязанный к веревке, равномерно вращается в вертикальной плоскости. Найти массу m камня, если известно, что разность между максимальной и минимальной силами натяжения веревки
·Т = 10 Н.

29.3. На частицу действует сила13 EMBED Equation.DSMT4 1415. Работа, совершенная этой силой при перемещении частицы из начала координат в точку с координатами (5; 2), равна Дж.

29.4. Пуля массой m1 = 20 г попадает в брусок массой m2 = 5 кг, подвешенный на тросе длиной L = 4м, и застревает в нем. Определить начальную скорость пули V, если трос отклонился от вертикали на угол
· = 140. Найти потери энергии при этом взаимодействии.

29.5. Линейная скорость
·1 точек на окружности вращающегося диска равна 3 м/с. Точки расположенные на
·R = 10 см ближе к оси, имеют линейную скорость
·2 =2 м/с. Определите частоту вращения диска.

29.6. Блок массой M = 1,0 кг укреплен на конце стола. Гири 1 и 2 одинаковой массы m1 = m2 = m = 1,0 кг соединены нитью, перекинутой через блок. Коэффициент трения гири 2 о стол
· = 0,1. Найдите ускорение с которым движутся гири, и силы натяжения Т1 и Т2 нитей. Блок считать однородным диском. Трением в блоке пренебречь.

29.7. На рисунке дан график зависимости энергии вращающегося тела Wвр от угловой скорости. Чему будет равен момент импульса тела, при величине угловой скорости равной 13 EMBED Equation.DSMT4 1415 ?

29.8. Сплошной и полый цилиндры, имеющие одинаковые массы и радиусы, вкатываются без проскальзывания на горку. Какой из цилиндров поднимется выше и во сколько раз, если начальные скорости тел одинаковы?

ИЗД Механика поступательного и вращательного движения

Вариант 30

30.1. Два автомобиля движутся по шоссе по следующим законам: х1 = 5t + 0,2t2 и х2 = 24 — 4t. Найти время и координату их встречи.

30.2. Тело массой m = 2.0 кг движется по плоскости таким образом, что его координаты зависят от времени согласно уравнениям13 EMBED Equation.DSMT4 1415,м и 13 EMBED Equation.DSMT4 1415м. Модуль равнодействующей всех сил, приложенных к телу, равен Н.

30.3. Небольшая шайба начинает движение без начальной скорости по гладкой ледяной горке из точки А. Сопротивление воздуха пренебрежимо мало. Зависимость потенциальной энергии шайбы от координаты х изображена на графике Зависимость потенциальной энергии шайбы от координаты х изображена на графике 13 EMBED Equation.DSMT4 1415. Найти отношение кинетических энергий шайбы в точках С и В.

30.4. Небольшое тело соскальзывает с высоты Н = 3 м по наклонному скату, переходящему в «мертвую петлю» с радиусом R = 0,5 м. На какой высоте h тело оторвется от поверхности петли, если трение отсутствует?

30.5. На графике представлена параболическая зависимость угла поворота 13 EMBED Equation.DSMT4 1415 абсолютно твердого тела относительно неподвижной оси от времени 13 EMBED Equation.DSMT4 1415. Начальная угловая скорость равна нулю 13 EMBED Equation.DSMT4 1415.Тело повернется за 4 секунды на уголрад.

30.6. Сплошной цилиндр и тонкостенный цилиндр с равными массами и одинаковыми радиусами вращаются вокруг своих осей с одинаковой угловой скоростью. После приложения к каждому цилиндру одинакового тормозящего момента отношение времени движения до остановки первого цилиндра ко времени движения до остановки второго цилиндра равно

30. 7. Два маленьких массивных шарика закреплены на концах невесомого стержня длины d1. Стержень может вращаться вокруг вертикальной оси, проходящей через середину стержня. Стержень раскрутили до угловой скорости 13 EMBED Equation.DSMT4 1415. Под действием трения стержень остановился, при этом выделилось количество теплоты 13 EMBED Equation.DSMT4 1415. Если шарики закрепить на концах невесомого стержня длины d2 = 1,5 d1 и стержень раскрутить до угловой скорости 13 EMBED Equation.DSMT4 1415, то какое количество теплоты выделится при остановке стержня?

30.8. Обруч и диск одинаковой массы m1 = m2= 1 кг катятся по горизонтальной поверхности без скольжения с одинаковой скоростью V1 = V2 = 18 км/ч. Радиус обруча в два раза больше чем диска. Кинетическая энергия обруча W = 40 Дж. Определите кинетическую энергию диска.

.024
·
·
·
·
·
·ц *,24шъ
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·J
·J
·J
·
·
·
·
·
·
·
·
·
·
·
·
·
·Root EntryEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation Native

Термодинамика

где Q – сообщенное газу; ΔU – изменение его внутренней энергии; А – работа, совершаемая газом против внешних сил.

Работа, совершаемая газом .

Внутренняя энергия идеального газа .

Молярная теплоемкость при постоянном объеме и давлении:

.

при адиабатном процессе ( ) .

Задачи по МКТ можно разделить на 4 типа.

1 тип задач на расчет параметров состояния газа. Для решения задачи можно рекомендовать следующую последовательность действий:

Если дана смесь газов, то уравнение Клапейрона-Менделеева записывают для каждого компонента. Давление смеси газов устанавливается законом Дальтона.

В задачах на газовые законы следует пользоваться только абсолютной температурой и сразу переводить значения температуры по шкале Цельсия в значения по шкале Кельвина.

2 тип задач на закон сохранения и превращения энергии с учетом тепловых явлений – первое начало термодинамики. Решение задач рекомендуется проводить по следующей схеме:

3 тип задач на теплообмен между телами, составляющими замкнутую систему и составление уравнения теплового баланса. В задачах этого типа рассматриваются явления в изолированной системе, где при взаимодействиях изменяется внутренняя энергия тел без совершения работы.

При агрегатных превращениях вещества, когда заранее невозможно сказать, в каком состоянии после теплообмена окажется вещество, рекомендуется сделать предварительные числовые расчеты – найти количество теплоты Q₁, необходимое для нагревания холодного тела до температуры плавления или кипения, и количество теплоты Q₂, которое может отдать горячее тело или пар. Если Q₁< Q₂, то в состоянии теплового равновесия вещество будет находиться в двух агрегатных состояниях (пар и жидкость или жидкость и лед), в противном случае после перераспределения энергии получится одна фаза вещества. Сделав вывод о конечном результате теплообмена, можно окончательно составить уравнение теплового баланса.

4 тип задач – комбинированные задачи. Это самый сложный тип задач, т. к. в них следует применять все выше рассмотренные алгоритмы решения.

Чему равна кинетическая энергия, которую необходимо сообщить мячу массой 1 кг, чтобы он перелетел через забор высотой h = 4 м, коснувшись его в верхней точке своей траектории? Мяч бросают с уровня h_о = 0,8 м над Землей, с расстояния S = 6,4 м от забора. Сопротивлением воздуха пренебречь.

Тело, брошенное вертикально вверх, упало на землю через t = 25 с. На какую высоту H поднялось тело и какова была его начальная скорость V_o?

Тело брошено вертикально вверх, находилось на одной и той же высоте h = 8,6 м два раза с интервалом Δt = 3 с. Пренебрегая сопротивлением воздуха, вычислить начальную скорость брошенного тела.

Камень, брошенный горизонтально, упал на землю через время t = 1с на расстоянии X = 5м от места бросания. Определить: — на какой высоте находился камень в начальный момент времени; — с какой скоростью он брошен; — с какой скоростью он упадет на землю; — под каким углом упал камень? Определить радиус кривизны траектории в момент падения.

Тело падает с высоты Н = 12,2 м. Какое расстояние пролетит тело за первые и последние 0,2 с времени своего полета?

Зависимость пройденного телом пути S от времени t описывается уравнением: S = A + Bt + Ct² + Dt³, где С = 0,2 м/с² и D = 0,01м/с³. Через какое время t тело будет иметь ускорение а = 1м/с²? Найти среднее ускорение а тела за этот промежуток времени.

Мяч, брошенный под углом 45 с начальной скоростью Vо = 12 м/с, ударяется о вертикальную стенку. Определить время удара мяча о стенку. На какой высоте произойдет удар мяча о стенку? Какова будет скорость мяча в момент удара о стенку. Расстояние от места бросания до стенки – X = 4 м.

Со скалы высотой Н = 18 м в море брошен камень под углом α = 30˚ к горизонту с начальной скоростью V_o= 15 м/с. Определить время движения камня, расстояние от основания скалы до точки падения камня в воду. С какой скоростью упадет камень в воду? Какой угол составляет траектория движения камня с горизонтом в точке его падения?

Из одного и того же места начали равноускоренно двигаться в одном направлении две точки, причем вторая начала свое движение через 2 с после первой. Первая точка двигалась с начальной скоростью υ₁ = 1 м/с и ускорением а₁ = 2 м/с², вторая – с начальной скоростью υ₂ = 10 м/с и ускорением а₂ = 1 м/с². Через сколько времени и на каком расстоянии от исходного положения вторая точка догонит первую?

Найти угловое ускорение ε колеса, если известно, что через время t = 2,5 с после начала движения вектор полного ускорения точки, лежащей на ободе, составляет угол α = 60° с вектором ее линейной скорости.

Длина минутной стрелки часов в 2 раза больше длины секундной стрелки. Во сколько раз линейная скорость конца секундной стрелки больше линейной скорости минутной стрелки? Определить угловую скорость вращения обеих стрелок.

Дано угловое ускорение ε = 2 рад/с² вращающегося колеса. Определить радиус колеса, если через время t = 0,5 с после начала движения полное ускорение колеса стало а = 13,6 см/с².

В какой момент времени t ускорения этих точек будут одинаковы? Найти скорости и точек в этот момент времени.

Маховик вращается с частотой n₁ = 120 об/мин. После выключения, вращаясь равнозамедленно, до остановки он сделал N = 25 об. Определить время с момента выключения до полной остановки.

Определить период обращения Луны вокруг Земли, если ускорение свободного падения на полюсах Земли равно 9,83 м/с², радиус Земли 6400 км, а расстояние между центрами Земли и Луны 3,84∙10⁵ км.

Точка движется по окружности так, что зависимость пути от времени описывается уравнением S = A – Bt + Ct³, где В = 2м/с и С = 1м/с². Найти линейную скорость точки, ее тангенциальное, нормальное и полное ускорение через время t = 3 с, если известно, что при t = 2 c нормальное ускорение равно 0,5 м/с².

Точка движется по окружности радиусом R = 15см с постоянным тангенциальным ускорением а_τ. Найти нормальное ускорение а_n точки через время t = 30 с после начала движения, если известно, что к концу пятого оборота после начала движения линейная скорость точки V = 10см/с.

Цилиндр вращается равноускоренно. За 1 мин он получил скорость 120 рад/с. Чему равно полное ускорение точек, которые лежат на поверхности цилиндра через 1с после начала движения? Определить угол между радиусом цилиндра и полным ускорением. Радиус цилиндра 10 см. Начальная скорость равна нулю.

Маховик вращается равноускоренно. Найти угол α, который составляет вектор полного ускорения а любой точки маховика с радиусом в тот момент, когда маховик сделает первые 2 оборота.

Шкив радиусом R = 20 см приводится во вращение грузом, подвешенным на нити, постепенно сматывающейся со шкива. В начальный момент груз был неподвижен, а затем стал опускаться с ускорением а = 2 см/с². Определить угловую скорость шкива в тот момент, когда груз пройдет путь S₁ = 100 см.

Под действием силы F = 10 Н тело движется прямолинейно так, что зависимость пройденного телом пути S от времени t дается уравнением S = А – Вt + Ct², где С = 1 м/с². Найти массу m тела.

Из шланга сечением S = 6 см² направленного на стену под углом α = 60˚ к нормали ударяется струя воды и упруго отскакивает от нее без потери скорости. Скорость течения воды в струе υ = 12 м/с. Найти силу, действующую на стенку.

Платформа с грузом тормозится, и его скорость за время t =3,5 с равномерно уменьшается от 45 км/ч до 30 км/ч. Определить предельный коэффициент трения между платформой и грузом, чтобы при торможении груз начал скользить по платформе.

Н а горизонтальной поверхности тележки, масса которой М = 6 кг, лежит брусок массой m = 2 кг. Коэффициент трения между бруском и тележкой μ = 0,3. Чему равна минимальная сила F, с которой нужно тянуть тележку, чтобы брусок начал скользить по ее поверхности?

На автомобиль массой 1,5 т во время движения действует сила трения, равная 0,15 от действующей на него силы тяжести. Найти силу тяги, развиваемую мотором, если автомобиль движется с постоянной скоростью под гору с уклоном 1м на каждые 20 м пути.

Тягач тянет сани с лесом по ледяной дороге с постоянной скоростью 15 км/ч. С какой скоростью тягач мог бы тянуть такие сани при вывозке леса летом по грунтовой дороге, если мощность, развиваемая мотором, в обоих случаях одинакова? Коэффициент трения при движении по ледяной дороге 0,01, по грунтовой – 0,15.

Шарик массы m висит на нити, которая закреплена в точке О. С каким ускорением, и в каком направлении по вертикали следует перемещать точку подвеса О, чтобы натяжение нити было равно половине веса шарика?

Н а вершине двух наклонных плоскостей, составляющих с горизонтом углы 30° и 45°, укреплен невесомый блок. Два груза одинаковой массы m = 1 кг соединены нитью и перекинуты через блок. Найти ускорение движения грузов и силу натяжения нити. Трением грузов о плоскости и в блоке пренебречь.

Тело массой m, находящееся на вершине наклонной плоскости, удерживается силой трения. За какое время тело спустится с наклонной плоскости, если она станет двигаться в горизонтальном направлении с ускорением 1 м/с². Длина плоскости ℓ = 1 м, угол наклона к горизонту α = 30˚, коэффициент трения между телом и плоскостью μ = 0,6.

Г рузы массой m₁ = 3 кг и m₂ = 5 кг подвешены с помощью системы блоков, как показано на рисунке. Нить считать невесомой и нерастяжимой, массой блоков пренебречь, трение в блоках не учитывать. Определить ускорение первого груза.

Диск вращается в горизонтальной плоскости с угловой скоростью 3 рад/с. На расстоянии 30 см от оси вращения на диске лежит небольшое тело. При каком минимальном значении коэффициента трения тело еще не будет сброшено с диска?

Платформа с грузом вращается вокруг вертикальной оси с частотой n=25 об/мин. Груз находится на расстоянии 20см от оси вращения. Каким должен быть коэффициент трения, чтобы груз не скатывался с платформы?

Тело массой m = 15 г движется по окружности радиусом R = 6 см. Найти тангенциальное ускорение тела, если известно, что к началу третьего оборота после начала движения его кинетическая энергия равна W_к = 0,7 Дж.

Велосипедист едет по арене цирка со скоростью 36 км/ч. Радиус арены 50 м. На какой угол он должен наклониться, чтобы не упасть?

Тяжелый шарик, подвешенный на нити длиной 1м, равномерно вращается по окружности в горизонтальной плоскости. Нить образует с вертикалью угол 30˚. Найти период обращения шарика.

В автобусе на динамометре висит груз массой 5 кг. Определить показание динамометра, если автобус едет со скоростью 72 км/ч по окружности радиусом 200м.

К потолку вагона подвесили на нити шарик массой 0,1 кг. При движении вагона по окружности со скоростью 108 км/ч нить отклонилась от вертикали на угол 30˚. Найти радиус окружности и силу натяжения нити.

На нити, которая может выдержать силу натяжения 40 Н, человек равномерно вращает тело массой 1 кг в вертикальной плоскости. Длина нити 1 м. Чему равна сила натяжения нити в тот момент времени, когда она образует с вертикалью угол 60˚?

Шарик массы 100 г, подвешенный на нити, качается в вертикальной плоскости так, что его ускорения в крайнем и нижнем положениях равны по модулю друг другу. Если угол отклонения нити в крайнем положении равен 30º, то сила натяжения нити в нижнем положении равна?

Н а горизонтальном диске укреплен отвес (шарик на нити), который при вращении диска вокруг вертикальной оси устанавливается под углом 45º к вертикали. Расстояние от точки подвеса до оси вращения d = 50 см, длина нити l = 56 см. Определить скорость шарика.

Снаряд, летящий со скоростью 30 м/с, разорвался на два осколка. Больший осколок, масса которого составляла 0,6 массы всего снаряда продолжал двигаться в прежнем направлении, но с увеличенной скоростью 45 м/с. Найти скорость меньшего осколка.

Мяч, летящий со скоростью v₁=15 м/с, отбрасывается ударом ракетки в противоположном направлении со скоростью v₂=20 м/с. Найти изменение импульса мяча, если известно, что изменение его кинетической энергии равно 8,75 Дж.

Тело массой m₁=2 кг движется навстречу второму телу массой m₂ = 1,5 кг и неупруго соударяется с ним. Скорости тел непосредственно перед ударом были v₁ = 1 м/с и v₂ = 2 м/с. Сколько времени будут двигаться эти тела после удара, если коэффициент трения равен 0,05?

Тело массой m₁ = 2 кг движется со скоростью v₁ = 3 м/с и нагоняет тело массой m₂ = 8 кг, движущееся со скоростью v₂ = 1 м/с. Считая удар центральным, найти скорости тел после удара, если удар упругий.

Два шара с массами m₁ = 0,2 кг и m₂ = 0,1 кг подвешены на нитях одинаковой длины так, что они соприкасаются. Первый шар отклоняют на высоту 4,5 см и отпускают. На какую высоту поднимутся шары после удара, если удар упругий?

Два шарика, массы которых m₁ = 200 г и m₂ = 300 г, подвешены на одинаковых нитях длиной l = 50 см. Шарики соприкасаются. Первый шарик отклонили от положения равновесия на угол 90º и отпустили. Найти высоту на которую поднимутся шарики после абсолютно неупругого удара?

Тело массой m₁ движется со скоростью v₁=3 м/с и нагоняет тело массой m₂, движущееся со скоростью v₂=1 м/с. Удар считать центральным. Каково должно быть соотношение между массами тел, чтобы при упругом ударе первое тело остановилось?

Граната, летевшая горизонтально со скоростью 150 м/с, разорвалась на два равных осколка, которые разлетаются после взрыва под прямым углом. Один из осколков после взрыва полетел под углом α = 30º к первоначальному направлению движения гранаты. Найти скорость этого осколка.

К лин массы М = 2 кг находится на идеально гладкой горизонтальной плоскости. На клине лежит брусок массы m = 0,5 кг, который под действием силы тяжести может скользить по клину без трения. Наклонная плоскость клина имеет плавный переход к горизонтальной плоскости. В начальный момент система покоилась. Найти скорость клина в тот момент, когда брусок с высоты h = 1 м соскользнет на плоскость.

При ударе вертикально падающего шарика о металлическую горизонтальную поверхность он теряет 50% своей механической энергии. Шарик бросили на поверхность без начальной скорости с высоты h = 3,2 м. После какого по счету отскока он отскочит от нее со скоростью 1 м/с?

Однородный стержень массой 0,5 кг и длиной 1 м вращается в горизонтальной плоскости вокруг вертикальной оси, проходящей через середину стержня. С каким угловым ускорением вращается стержень, если на него действует момент сил М = 98,1 Н∙м.

Алюминиевый шар, радиусом 20 см, вращается с частотой n =5 об/с вокруг оси, проходящей через его центр. Какую работу надо совершить, чтобы увеличить угловую скорость вращения шара вдвое?

Маховик вращается с частотой n = 25 об/с. Его кинетическая энергия 7,85 кДж. За какое время t момент сил 50 Н∙м, приложенный к маховику, увеличит угловую скорость маховика вдвое?

Горизонтальная платформа массой M = 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой n₁ = 10 об/мин. Человек массой m = 60 кг стоит при этом на краю платформы. С какой частотой n₂ начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека – точечной массой.

Тонкий стержень массой m и длиной l вращается с угловой скоростью 10 с^-1 в горизонтальной плоскости вокруг вертикальной оси, проходящей через середину стержня. Продолжая вращаться в той же плоскости, стержень перемещают так, что ось вращения начинает проходить через конец стержня. Найти угловую скорость во втором случае.

К катящемуся по горизонтальной поверхности шару массой 1 кг приложили силу 1 Н и остановили его. Путь торможения составил 1 м. Определить скорость шара до начала торможения.

Платформа начинает вращаться с постоянным угловым ускорением = 0,5 рад/с и через время t₁ = 15 с приобретает момент импульса L = 73,5 кг^.м²/с. Найти кинетическую энергию платформы через время t₂ = 20 с после начала движения.

Шар и сплошной цилиндр, изготовленные из одного и того же материала, одинаковой массы катятся без скольжения с одинаковой скоростью. Определить, во сколько раз кинетическая энергия шара меньше кинетической энергии сплошного цилиндра.

Два одинаковых куска пластилина скользили друг навстречу другу по льду с одинаковыми кинетическими энергиями 350 Дж каждый и одновременно ударились в противоположные концы тонкого стержня, лежавшего на льду перпендикулярно направлению скоростей кусков пластилина. Масса стержня равна массе одного куска пластилина. В момент удара куски прилипли к стержню. Каково изменение полной механической энергии системы в момент удара?

В край однородного диска с массой M = 40 г, который может вращаться без трения вокруг закрепленной вертикальной оси симметрии, врезается летевшая горизонтально по касательной к диску пуля массой m = 20 г и застревает в нем. С какой скоростью летела пуля, если первоначально диск был неподвижен, а после удара кинетическая энергия всей системы стала равной 8 Дж?

В баллоне находилась масса m₁ = 10 кг газа при давлении р₁ = 10 МПа. Какую массу m газа взяли из баллона, если давление стало равным р₂ = 2,5 МПа? Температуру газа считать постоянной.

В закрытом сосуде объемом V = 1 м³ находится масса m₁ = 1,6 кг кислорода и масса m₂ = 0,9 кг воды. Найти давление р в сосуде при температуре t = 500^оС, зная, что при этой температуре вся вода превращается в пар.

В сосуде находится масса m₁ = 14 г азота и масса m₂ = 9 г водорода при температуре t = 10^оС и давлении р = 1 МПа. Найти молярную массу смеси и объем сосуда.

В воздухе содержится 23,6% кислорода и 76,4% азота (по массе) при давлении р = 100 кПа и температуре t = 13 ^оС. Найти плотность воздуха и парциальные давления кислорода и азота.

В сосуде находится масса m₁=10 г углекислого газа и масса m₂ = 15 г азота. Найти плотность смеси при температуре t = 27 ^оС и давлении р = 150 кПа.

В сосуде объемом V = 4 л находится масса m = 1 г водорода. Какое число молекул n содержит единица объема сосуда?

Какое число молекул N находится в комнате объемом V = 80 м³ при температуре t = 17˚С и давлении р = 100 кПа?

Какое число молекул n содержит единица объема сосуда при температуре t = 10^оС и давлении р = 1,33^.10^-9 Па?

Воздушный пузырек на дне озера глубиной 16 м имеет объем 1,1 см³. Температура на дне равна 5˚С, а на поверхности – 16˚С. Определить объем пузырька в тот момент, когда он достигнет поверхности воды.

Самое низкое давление, получаемое с помощью самой совершенной вакуумной техники, приблизительно равно 10^-12 Н/м². Сколько молекул содержится при таком давлении в 1 см³ при температуре 0^оС?

Кислород массой m = 2 кг увеличил свой объем в n = 5 раз один раз изотермически, другой – адиабатно. Найти суммарное изменение энтропии в этих двух процессах.

Водород массой m = 100 г был изобарно нагрет так, что объем его увеличился в n = 3 раза, затем водород был изохорно охлажден так, что давление его уменьшилось в n = 3 раза. Найти изменение энтропии в ходе указанных процессов.

Три моля азота сначала изобарически нагревают в 2 раза, а затем изотермически сжимают в 3 раза. Найти изменение энтропии в этих двух процессах.

Два моля идеального газа сначала изохорически нагревают в е² раз (е – основание натурального логарифма), а затем адиабатически охлаждают до первоначальной температуры. Суммарное изменение энтропии в этих двух процессах ΔS = 83,1 Дж/К. Найти число степеней свободы молекул такого газа.

Два моля идеального газа нагревают изохорически. Определите число степеней свободы молекул такого газа, если его температура возрастает при этом в е² раз (е – основание натурального логарифма), а энтропия увеличивается при этом на величину ΔS = 49,86 Дж/К.

Э нтропия некоторой термодинамической системы изменяется при изохорном процессе по закону , где b = 10^-5 Дж/К³. Определите изменение внутренней энергии этой системы при нагревании от температуры Т₁ = 100 К до Т₂ = 300 К.

В ходе некоторого процесса энтропия термодинамической системы изменяется пропорционально ее температуре Т, как показано на рисунке. Определите температуру системы, при которой ее теплоемкость станет равна 10 Дж/К?

Теплоемкость некоторой термодинамической системы изменяется с ростом температуры по закону , где b = 10^-5 Дж/К³. Определите изменение энтропии этой системы при ее нагревании от температуры Т₁ = 100 К до Т₂ = 300 К.

Внутренняя энергия некоторой термодинамической системы зависит от температуры по закону . Определите величину постоянной b, если при изохорном охлаждении этой системы на ΔТ = 100 К ее энтропия уменьшается на величину ΔS = 100 Дж/К.

Энтропия некоторой термодинамической системы изменяется с температурой по закону , где b = 10^-5 Дж/К⁵. Определите теплоемкость этой системы при температуре Т = 300 К.

Два моля идеального газа совершают процесс, при котором его объем изменяется с ростом температуры по закону , где b = const. Определите молярную теплоемкость такого процесс, если молярная теплоемкость газа при постоянном объеме равна С_v = 10 Дж/К.

Один моль двухатомного идеального газа совершает процесс, протекающий по закону V∙Т = const, где V и Т – соответственно объем и температура газа. Найти отношение молярной теплоемкости такого процесса к универсальной газовой постоянной С/R?

Два моля одноатомного идеального газа расширяются так, что молярная теплоемкость газа в процессе расширения постоянна и равна С = 3R, где R – универсальная газовая постоянная. Какую работу совершит газ при изменении его температуры от Т₁ = 100 К до Т₂ = 300 К?

В сосуде под поршнем находится газ при нормальных условиях. Расстояние между дном сосуда и дном поршня равно 25 см. Когда на поршень положили груз массой 20 кг, поршень опустился на 13,4 см. Считая сжатие адиабатическим, найти для данного газа отношение С_р/С_v. Площадь поперечного сечения поршня равна 10 см², массой поршня пренебречь.

Газ расширяется адиабатически так, что его давление падает от 200 до 100 кПа. Затем он нагревается при постоянном объеме до первоначальной температуры, причем его давление возрастает до 122 кПа. Определить отношение С_р/С_v для этого газа.

Два моля азота совершают процесс, при котором работа зависит от температуры по закону А = RТ, где R – универсальная газовая постоянная. Найти величину молярной теплоемкости газа в этом процессе.

Т ермодинамическая система совершает циклический процесс с к.п.д. η = 75%. В состояниях 1, 2 и 3 она имеет, соответственно, температуры Т₁ = 300 К, Т₂ = 500 К и Т₃ = 400 К. Процессы 1-2 и 1-3 имеют постоянные молярные теплоемкости С₁ и С₂ соответственно, процесс 2-3 – адиабата. Вычислить отношение теплоемкостей С₁/С₂.

Термодинамическая система совершает циклический процесс. Молярные теплоемкости процессов 1-2 и 3-4 равны соответственно С₁ = 2 Дж/К и С₂ = 7 Дж/К. Процессы 2-3 и 4-1 адиабатические. Найти к.п.д. цикла, если известно, что изменение абсолютной температуры системы в ходе процесса 1-2 больше изменения температуры при процессе 4-3 в четыре раза.

Т ермодинамическая система совершает циклический процесс, состоящий из трех процессов 1-2, 2-3 и 3-1 с постоянными теплоемкостями С₁₂ = 2 Дж/К, С₂₃ = 6 Дж/К и С₃₁ = 8 Дж/К соответственно. Найти температуру системы в состоянии 3, если в состояниях 1 и 2 ее температура равна Т₁ = 300 К и Т₂ = 250 К соответственно, а к.п.д. всего цикла равен 20%.

П роцесс 1-2 с постоянной теплоемкостью С₁₂ = 4 кДж/К повышает температуру газа в два раза, а процесс 2-3 с теплоемкостью С₂₃ =3 кДж/К повышает температуру газа еще в три раза. Найти к.п.д. этого цикла, если теплоемкость процесса 3-1 равна С₃₁ = 2 кДж/К.

Найти к.п.д. циклического процесса, изображенного на Т-S диаграмме.

О дин моль идеального трехатомного газа совершает циклический процесс, изображенный на Р-V диаграмме, где Р₂ = 2Р₁, а V₂ = 3V₁. Найти к.п.д. этого цикла.

Два моля идеального одноатомного газа совершают замкнутый цикл, изображенный на рисунке. Известно, что температура Т₁ = 280 К, Р₂/Р₁ = 5, Т₄/Т₁ = 2. Определите к.п.д. этого цикла.

Идеальный газ совершает цикл Карно, причем за все время цикла наибольшая средняя скорость молекул газа в два раза больше наименьшей средней скорости молекул. Найти к.п.д. цикла.

Идеальный газ совершает цикл Карно. При этом максимальное значение средней скорости молекул газа за все время цикла оказывается в два раза больше минимального значения наиболее вероятной скорости молекул газа за время цикла. Найти к.п.д. цикла.

Идеальный газ совершает цикл Карно, причем за все время цикла максимальная наиболее вероятная скорость молекул газа оказывается равной минимальной средней квадратичной скорости молекул газа за время этого цикла. Найти к.п.д. цикла.

Идеальный газ находится в сосуде под поршнем. Первоначальная температура газа равна Т₁ = 300 К, а частота соударений молекул о стенки сосуда ₁ = 10¹⁰м^-2с^-1. Температуру газа в сосуде изменяют , но давление газа при этом остается неизменным. Найти температуру газа Т₂, при которой частота соударений молекул о стенку станет равной ₂ = 2∙10¹⁰м^-2с^-1.

При температуре 0˚С и некотором давлении средняя длина свободного пробега молекул кислорода равна 95 нм. Чему равно среднее число столкновений в 1 с молекул кислорода, если сосуд откачать до 0,01 первоначального давления? Температура остается неизменной.

При некоторых условиях средняя длина свободного пробега молекул газа равна 160 нм и средняя арифметическая скорость его молекул равна 1,95 км/с. Чему будет равно среднее число столкновений в 1 с молекул этого газа, если при той же температуре давление газа уменьшить в 1,27 раза?

Найти среднее число столкновений в 1 с молекул некоторого газа, если средняя длина свободного пробега при этих условиях равна 5 мкм, а средняя квадратичная скорость его молекул равна 500 м/с.

В сосуде под поршнем находился идеальный газ, молекулы которого соударялись со стенками сосуда с частотой ₁ = 1,2∙10¹⁰м^-2с^-1. Затем поршень медленно сжали, в результате чего объем газа уменьшился в два раза, а давление возросло в 8 раз. Чему равна частота ₂ соударений молекул этого газа со стенками после сжатия?

Молекулы идеального газа, находящегося в закрытом сосуде под давлением Р = 4∙10⁴ Па, соударяются со стенками сосуда с частотой  = 10²⁷ м^-2с^-1. Известно, что k∙m = π^-1∙10^-48 Дж∙кг/К, где k – постоянная Больцмана, m – масса одной молекулы. Какова температура газа?

Средняя скорость молекул газа в закрытой трехлитровой банке равна 2000 м/с. Найти число молекул этого газа, если за одну секунду с 1 см² поверхности стенки внутри банки сталкивается 10²¹ молекул.

В закрытой литровой банке имеется N = 6∙10²⁰ одинаковых молекул одноатомного газа. Найти массу каждой молекулы, если известно, что средняя энергия одной молекулы этого газа <E> = 1,57∙10^-20 Дж, а частота соударений молекул со стенками банки равна  = 10²⁶м^-2с^-1.

При температуре идеального газа Т₁ = 300 К средняя длина свободного пробега его молекул была равна λ₁ = 6∙10^-7 м. Затем температуру газа изменяют при постоянном давлении. Считая, что эффективный диаметр молекул при этом не меняется. Найти температуру Т₂ при которой средняя длина свободного пробега молекул станет равной λ₂ = 4,5∙10^-7 м.

После того, как идеальный газ нагрели, средняя длина свободного пробега молекул этого газа возросла в 1,8 раз, а частота соударений его молекул о стенки сосуда уменьшилась в 1,2 раза. Во сколько раз возросла температура газа при нагревании? Эффективный диаметр молекул газа при этом практически не меняется, а давление и объем газа изменяются.

Однородный шарик подвешен на нити, длина которой равна радиусу шарика. Во сколько раз период малых колебаний этого маятника больше периода малых колебаний математического маятника с таким же расстоянием от центра масс до точки подвеса?

Найти период колебаний однородного стержня длиной l = 0,5 м, совершающего колебания в вертикальной плоскости около горизонтальной оси, проходящей через точку на расстоянии 10 см от его верхнего конца.

На концах вертикального стержня укреплены два груза. Центр масс грузов находится ниже середины стержня на расстоянии d = 5 см. Найти длину стержня, если известно, что период малых колебаний стержня с грузами вокруг горизонтальной оси, проходящей через его середину, Т = 2 с. Массой стержня пренебречь по сравнению с массой грузов.

Уравнение движения точки дано в виде x = sin t. Найти моменты времени, в которые достигаются максимальная скорость и максимальное ускорение.

Математический маятник колеблется в некоторой вязкой жидкости, причем амплитуда колебаний уменьшается за период в exp(2 ) раз (где ln e = 1). Во сколько раз период таких колебаний будет больше периода незатухающих колебаний этого же математического маятника при отсутствии жидкости?

Найти логарифмический декремент затухания математического маятника, если за время t = 1 мин амплитуда колебаний уменьшилась в 2 раза. Длина маятника 1 м.

Начальная фаза гармонического колебания равна нулю. При смещении точки от положения равновесия x₁ = 2,4 см скорость точки v₁ = 3 см/с, а при смещении x₂ = 2,8 см ее скорость v₂ = 2 см/с. Найти амплитуду и период этого колебания.

Амплитуда затухающих колебаний математического маятника за время t₁ = 1 мин уменьшилась вдвое. Во сколько раз уменьшится амплитуда за время t₂ = 3 мин?

К пружине подвешена чашка весов с гирями. При этом период вертикальных колебаний Т₁ = 0,5 с. После того как на чашку весов положили еще добавочные гири, период вертикальных колебаний стал равным Т₂=0,6 с. На сколько удлинилась пружина от прибавления этого добавочного груза?

Грузик на пружинке жесткости k колеблется в некоторой жидкости, причем частота его колебаний в два раза меньше собственной частоты незатухающих колебаний грузика на той же пружинке. Коэффициент жесткости пружинки увеличили в 7 раз. Во сколько раз надо увеличить коэффициент вязкого трения жидкости, чтобы период колебаний грузика не изменился?

молекулярной физике и термодинамике . . . . . . 3

к выполнению контрольных работ . . . . . . 7

Кинематика . . . . . . . . . 8

Основные физические постоянные . . . . . . . 16

Задачи к контрольной работе №1 и №2 . . . . . . 17

ИЗД Механика поступательного и вращательного движения — ИДЗ Мех поступ и вращат движения

---

Подборка по базе: контрольная работа ПРИКЛОДНАЯ МЕХАНИКА (Автосохраненный).docx, Презентация График движения.ppt, контрольная работа ПРИКЛОДНАЯ МЕХАНИКА (Автосохраненный).docx, контрольная работа ПРИКЛОДНАЯ МЕХАНИКА (Автосохраненный).docx, Задание Д-1. Интегрирование дифференциальных уравнений движения , 3 Механика по физике.docx, ИОТП 03-21 для главного механика.doc, Деятельность национальной интеллигенции и формирование идеологии, ЛИТЕРАТУРА Механика грунтов.doc, Глаголы движения судна_cadets.docx

---

ИЗД Механика поступательного и вращательного движения

Вариант 5

5.1. На рисунке представлен график зависимости проекции скорости от времени для прямолинейного движения тела.

Ниже приведены четыре различных графика зависимости проекции ускорения от времени. Какой из этих графиков соответствует приведенной зависимости проекции ускорения от времени?

5.2. На горизонтальном диске укреплен отвес (шарик на нити), который при вращении диска вокруг вертикальной оси устанавливается под углом α = 45⁰ к вертикали (см. рисунок). Расстояние от точки подвеса до оси вращения d = 50 см, длина нити L = 56 см. Чему равна при этом скорость шарика?

5.3. Материальная точка некоторой массы начинает двигаться под действием силы  (Н). Зависимость радиус-вектора материальной точки от времени имеет вид  (м). Найти мощность, развиваемую силой в момент времени t = 1 с.

5.4. Два одинаковых маленьких пластилиновых шарика подвешены на нитях одинаковой длины так, что касаются друг друга. Левый шарик отклоняют влево на угол α = 30⁰, а правый вправо на угол β = 60⁰ от вертикали и отпускают без начальной скорости. При дальнейшем движении шариков происходит неупругий удар в нижней точке траектории. На какой угол γ отклонятся шарики от вертикали после удара? Найти долю потерянной энергии при этом взаимодействии.

5.5. Уравнение вращения твердого тела φ(t) = 4·t³ + 3·t, рад. Определите угловую скорость вращения тела и полное ускорение для точки тела, отстоящей на 20 см от оси вращения, через 2 с после начала движения.

5.6. На рисунке приведена зависимость модуля моментов сил, приложенных к разным телам, от модуля углового ускорения тел. Наибольший момент инерции имеет тело под номером……

5.7. Два маленьких массивных шарика закреплены на концах невесомого стержня длины d. Стержень может вращаться вокруг вертикальной оси, проходящей через середину стержня. Стержень раскрутили до угловой скорости . Под действием трения стержень остановился, при этом выделилось тепло . Если стержень был раскручен до угловой скорости , то при остановке стержня выделится тепло. Во сколько раз больше ?

5.8. Тонкий прямой стержень длинойl = 1 м прикреплен к горизонтальной оси, проходящий через его верхний конец. Стержень отклонили на 60º от положения равновесия и отпустили. Определите линейную скорость нижнего конца стержня в момент прохождения через положение равновесия.

ИЗД Механика поступательного и вращательного движения

Вариант 6

6.1. Координаты материальной точки изменяются со временем по закону . Модуль радиус–вектора точки (в метрах) в момент времени t = 1 с равен … (с округлением до десятых долей).

6.2. На концах нити, перекинутой через неподвижный блок, подвешены грузы разной массы. За время t = 2 с после начала движения каждый груз проходит S = 1,96 м. Определить массу меньшего груза m₁, если масса большего груза m₂ = 1,1 кг

6.3. На рисунке дан график зависимости потенциальной энергии W_p упруго деформированной пружины от величины ее деформации х. Чему будет равна сила упругости, действующая на пружину, при величине деформации х = 3 см ?

6.4. Пуля массой m₁ = 20 г попадает в брусок массой m₂ = 5 кг, подвешенный на тросе длиной L = 4м, и застревает в нем. Определить начальную скорость пули V, если трос отклонился от вертикали на угол α = 14⁰. Найти потери механической энергии при этом взаимодействии.

6.5. Диск радиуса начинает вращаться из состояния покоя в горизонтальной плоскости вокруг оси Z, проходящей перпендикулярно его плоскости через его центр. Зависимость проекции угловой скорости от времени показана на графике. На каком интервале времени тангенциальное ускорение точки, расположенной на расстоянии R = 20 см от центра диска, равно a_τ = 0,2 м/с²?

6.6. Маховое колесо, имеющее момент инерции I= 245 кг·м², вращается, делая n = 20 об/с. После того как на колесо перестал действовать вращающий момент, оно остановилось, сделав N = 1000 оборотов. Найдите момент сил трения М_три время τ, прошедшее от момента прекращения действия вращающего момента до полной остановки колеса.

6.7. На рисунке представлен график зависимости кинетической энергии вращающегося тела от угла поворота φ. Как изменяется вращающий момент М с изменением увеличением угла φ?

6.8. Однородный стержень длиной l = 1,5 м и массойM= 10 кг может вращаться вокруг неподвижной оси, проходящей через верхний конец стержня перпендикулярно его длине. В середину стержня ударяет пуля массой m = 10 г, летящая в горизонтальном направлении со скоростью V = 500 м/с, и застревает в стержне. Какую линейную скорость будет иметь конец стержня сразу после удара?

ИЗД Механика поступательного и вращательного движения

Вариант 7

7.1. На рисунке представлен график зависимости проекции ускорения а_х от времени t для материальной точки, движущейся вдоль оси ОХ. Начальная скорость движения точки V_0х  = –2 м/с. Проекция скорости движущейся точки в момент времени 3 с равна …м/с.

7.2. Ледяная горка составляет с горизонтом угол α = 10⁰. По ней пускают вверх камень, который, поднявшись на некоторую высоту, соскальзывает по тому же пути вниз. Найти коэффициент трения μ, если время спуска в n = 2 раза больше времени подъема.

7.3. Импульс тела _{изменился под действием кратковременного удара и стал равным , как показано на рисунке. Определить направление силы и пояснить свой выбор.}

7.4. Небольшой шар массой m₁ = 1,99 кг висит на невесомой нерастяжимой нити. В него попадает и застревает в нём пуля, летящая горизонтально со скоростью V = 600 м/с. Масса пули m₂ = 10 г. Найти максимальную высоту h, на которую поднимется шар, и долю потерянной кинетической энергии пули η, перешедшую в тепловую энергию.

7.5. Движение тела вокруг неподвижной оси вращения задано уравнением, рад. Сколько оборотов Nсделает тело до момента изменения направления вращения тела и чему равна средняя угловая скорость тела за этот интервал времени?

7.6. На рисунке приведен график зависимости от времени проекции угловой скорости вращающегося тела на ось вращения. Момент действующих на тело сил был постоянным не равным нулю на участке …

7.7 На рисунке приведены графики зависимости различных физических величин от угла поворота тела φ. Какой график соответствует зависимости кинетической энергии тела, вращающегося с постоянным угловым ускорение, момент инерции которого не изменяется за время движения?

7.8. Сплошной и полый шары, имеющие одинаковые массы и радиусы, скатываются без проскальзывания с горки высотой h. Какое из тел будет иметь большую скорость у основания горки и во сколько раз?

ИЗД Механика поступательного и вращательного движения

Вариант 8

8.1. Материальная точка движется прямолинейно вдоль оси ОХ. Проекция ее скорости изменяется со временем так, как изображено на рисунке. Пользуясь графиком, определите координату х точки в момент времени t = 6 с, если её начальная координата х₀ = 1 м.

8.2. Автомобиль массой m = 600 кг въезжает на выпуклый мост, представляющий собой дугу окружности радиусом R = 120 м. Скорость автомобиля равна υ = 108 км/ч. В некоторый момент времени радиус-вектор, проведенный из центра кривизны моста в точку, где находится автомобиль, составляет с горизонталью угол α = 60⁰. Определить силу нормального давления автомобиля на мост в этой точке.

8.3. Теннисный мяч летел с импульсом (масштаб и направление указаны на рисунке), когда теннисист произвел по мячу резкий удар со средней силой F=80H. Изменившийся импульс мяча стал равным . Определить время, в течение которого сила действовала на мяч.

8.4. С высоты h = 5,0 м бросают вертикально вверх тело массой m = 0,20 кг с начальной скоростью υ₀ = 2,0 м/с. При падении на Землю тело углубляется в грунт на глубину l= 5,0 см. Найти среднюю силу сопротивления грунта движению тела.

8.5. Диск радиуса R начинает вращаться из состояния покоя в горизонтальной плоскости вокруг оси Z, проходящей перпендикулярно его плоскости через его центр. Зависимость проекции угловой скорости от времени показана на графике. Чему равны тангенциальные ускорения точки на краю диска в моменты времени t₁= 2 с и t₂ = 7 с?

8.6. По ободу шкива, насаженного на общую ось с маховым колесом, намотана нить, к концу которой подвешен груз массой m = 4,0 кг. На какое расстояние должен опуститься груз, чтобы колесо со шкивом получило скорость, соответствующую частоте n = 60 об/мин? Момент инерции колеса со шкивом I = 0,42 кг· м², радиус шкива r = 10cм.

8.7. Два маленьких массивных шарика закреплены на невесомом длинном стержне, на расстоянии друг от друга. Стержень может вращаться без трения в горизонтальной плоскости вокруг вертикальной оси, проходящей посредине между шариками. Стержень раскрутили из состояния покоя до угловой скорости , при этом была совершена работа А₁. Шарики раздвинули симметрично на расстояние и раскрутили до той же угловой скорости. При этом была совершена работа …

1) ; 2) ; 3) ; 4) .

8.8. Цилиндр массой m = 5,0 кг катится без скольжения с постоянной скоростью 14 м/с. Определите кинетическую энергию цилиндра. Через какое время цилиндр остановится, если будет действовать сила трения равная 50 Н?

ИЗД Механика поступательного и вращательного движения

Вариант 9

9.1. Движение точки по оси ОХ описывается следующим уравнением:

х = 2 + 3t + t² , м. Скорость движения точки станет равна v_x = 9 м/с в момент времени … сек.

9.2. Тело тянут по горизонтальной плоскости с постоянно увеличивающейся горизонтально направленной силой F. График зависимости ускорения, приобретаемого телом, от приложенной к нему силы F приведен на рисунке.

Определить силу нормальной реакции опоры действующей на тело ( в Н).

9.3. На рисунке изображена зависимость потенциальной энергии W_p упруго деформированного стержня от его удлинения ∆l. Найдите удлинение ∆l, соответствующее потенциальной энергии W_p = 3,6 Дж. Закон Гука для искомого значения ∆l выполняется.

9.4. Кусок пластилина массой m = 200 г падает со скоростью V = 6 м/с, направленной под углом α = 60⁰ к горизонту, на брусок массой m₁ = 2m, двигающийся со скоростью V₁ = V/2 по гладкой горизонтальной поверхности навстречу куску пластилина. Найти энергию, перешедшую в тепловую Q при абсолютно неупругом ударе.

9.5 Диск вращается с постоянным угловым ускорением, величина которого ε = 5 рад/с². Сколько оборотов N сделает диск при изменении частоты вращения от n₁= 240 мин^-1 до n₂ = 90 мин^-1? Найдите время, в течение которого это произойдет.

9.6. Момент импульса тела относительно неподвижной оси изменяется по закону . Укажите график, правильно отражающий зависимость от времени величины момента сил, действующих на тело.

9.7. На рисунке представлен график зависимости проекции вращательного момента силы, действующей на тело, от угла поворота. Чему равна работа сил, действующих на тело, при повороте его на угол 10 рад ?

9.8. Шар массой m = 3 кг скатывается без проскальзывания с вершины наклонной плоскости высотой h=4 м без начальной скорости. Длина ската наклонной плоскости l = 8 м, а значение коэффициента трения качения тела одинаково на протяжении всего пути и равно  = 0,1. Найдите расстояние, которое пройдет шар от подножья наклонной плоскости до своей полной остановки.

ИЗД Механика поступательного и вращательного движения

Вариант 10

10.1 Материальная точка движется по окружности со скоростью V. На рисунке показан график зависимости проекции скорости V_τ–от времени (τ– единичный вектор положительного направления, V_τ– проекция скорости на это направление). При этом для нормального и тангенциального ускорения справедливы утверждения:

1) а_n – увеличивается, а_τ – уменьшается

2) а_n – постоянно , а_τ – равно нулю

3) а_n — уменьшается , а_τ – постоянно

4) а_n – постоянно, а_τ– увеличивается
10.2. Веревка выдерживает груз массой m₁ = 110 кг при вертикальном подъеме его с некоторым ускорением и груз массой m₂ = 690 кг при опускании его с таким же по модулю ускорением. Какова максимальная масса груза m, который можно поднимать на этой веревке с постоянной скоростью?

10.3. Шарик, прикрепленный к пружине и насаженный на горизонтальную направляющую, совершает гармонические колебания.

На графике представлена зависимость проекции силы упругости пружины на положительное направление оси ОХ от координаты шарика. Чему равна работа силы упругости при смещении шарика из положения А в положение С?

10.4. Небольшое тело соскальзывает с высоты Н = 3 м по наклонному скату, переходящему в «мертвую петлю» с радиусом R = 1,3 м. На какой высоте h тело оторвется от поверхности петли, если трение отсутствует?

10.5. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется во времени, как показано на графике. На какой угол (в рад) окажется повернутым тело относительно начального положения через 10 с ?

10.6. Две гири разной массы соединены нитью, перекинутой через блок, момент инерции которого J = 50 кг∙м² и радиусR = 20 см. Блок вращается с трением и момент сил трения равен М = 98,1 Нм. Найдите разность сил натяжений нити (Т₁—Т₂) по обе стороны блока, если известно, что блок вращается с постоянным угловым ускорением ε = 2,36 рад/с².

10.7. На рисунке представлены графики зависимости мощности постоянного момента силы от времени . Тело вращается равноускоренно. Какой график соответствует этому случаю?

10.8. Обруч массой m = 0.3кг и радиусом R= 0.5 м привели во вращение, сообщив ему энергию вращательного движения 1200 Дж, и отпустили на пол так, что его ось вращения оказалась параллельной плоскости пола. Если обруч начал двигаться без проскальзывания, имея кинетическую энергию вращения 200 Дж, то сила трения совершила работу, равную …

ИЗД Механика поступательного и вращательного движения

Вариант 11

11.1. Движение точки по оси ОХ описывается следующим уравнением

х =2 – 3t+ t², м. За две секунды движения точка совершит перемещение (в м), равное …

11.2. Автомобиль массой m= 5 т равномерно со скоростью V= 72 км/час съезжает в вогнутый мост, представляющий собой дугу окружности радиусом R = 80 м. Определить, с какой силой автомобиль давит на мост в точке, радиус которой составляет с радиусом впадины моста угол α = 30⁰.

11.3. Теннисный мяч летел с импульсом _{(масштаб и направление указаны на рисунке), когда теннисист произвел по мячу резкий удар длительностью ∆t = 0,1 с. Изменившийся импульс мяча стал равным . Найти среднюю силу удара F.}

11.4. Пуля летит горизонтально со скоростью υ₀ = 160 м/с, пробивает стоящую на горизонтальной шероховатой поверхности коробку и продолжает движение в прежнем направлении со скоростью υ₀. Масса коробки в 12 раз больше массы пули. Коэффициент трения скольжения между коробкой и поверхностью μ = 0,3. На какое расстояние Sпереместится коробка к моменту, когда ее скорость уменьшится на 20% ?

11.5. Маховик начал вращаться равноускоренно и за промежуток времени t = 10 с достиг частоты n = 300 мин^-1. Запишите уравнение зависимости рад, согласно которому вращается диск.

11.6. Момент силы, приложенный к вращающемуся телу, изменяется по закону, где – некоторая положительная константа.

Момент инерции остается постоянным в течение всего времени вращения. Зависимость углового ускорения от времени представлена на рисунке …
11.7. Два маленьких массивных шарика закреплены на концах невесомого стержня длины d₁. Стержень может вращаться вокруг вертикальной оси, проходящей через середину стержня. Стержень раскрутили до угловой скорости . Под действием трения стержень остановился, при этом выделилось количество теплоты Q₁. Если шарики закрепить на концах невесомого стержня длины d₂ = 2 d₁ и стержень раскрутить до угловой скорости , то при остановке стержня выделится количество теплоты …

1) ; 2) ; 3) ; 4) .

11.8. Определить скорость поступательного движения сплошного цилиндра, скатившегося с наклонной плоскости высотой h = 20 см.

ИЗД Механика поступательного и вращательного движения

Вариант 12

12.1. Тело из состояния покоя начинает двигаться вдоль оси ОХ. График зависимости проекции ускорения тела на ось ОХ приведён на рисунке. Проекция скорости движущейся точки в момент времени 3 с равна … м/с.

12.2. Математический маятник массой m = 100 г, подвешенный на нити, проходит положение, определяемое углом α = 60⁰ с вертикалью. В этом положении натяжение нити равно Т = 1 Н. Чему равен модуль полного ускорения шарика в этот момент?

12.3. График зависимости потенциальной энергии W_p от координаты х имеет вид, представленный на рисунке. Какой из графиков, приведенных ниже, соответствует зависимости проекции консервативной силы F_x на ось x?

12.4. Два маленьких шарика массами m₁ = 10 г и m₂ = 20 г висят на длинных одинаковых вертикальных нитях. Между ними находится сжатая пружина, которая удерживается в сжатом состоянии связывающей ее нитью. Потенциальная энергия деформации пружины W_p = 0,05 Дж. Нить, связывающую тела, пережигают. Найти максимальные высоты h₁ и h₂, на которые поднимутся шарики.

12.5. На графике представлена зависимость угла φ поворота вращающегося тела от времени t. Используя график, определите угловое ускорение вращения тела.

12.6. Цилиндр, расположенный горизонтально, может вращаться около оси, совпадающей с осью цилиндра. Масса цилиндра m₁= 12 кг. На цилиндр намотали шнур, к которому привязали гирю массой m₂ = 1 кг. С каким ускорением будет опускаться гиря? Какова сила натяжения шнура во время движения гири?

12.7. На рисунке дан график зависимости энергии вращающегося тела W_вр от угловой скорости. Чему будет равен момент импульса тела, при величине угловой скорости равной ?

12.8. Однородный диск из состояния покоя скатывается без проскальзывания с наклонной плоскости, высота которой h=0.5 м. Определите линейную скорость движения центра диска у основания наклонной плоскости и максимальную линейную скорость движения точек, находящихся на ободе диска, у основания наклонной плоскости (в м/с).

ИЗД Механика поступательного и вращательного движения

Вариант 13

13.1. Скорость тела, движущегося по оси ОХ, изменяется со временем по закону . Средняя скорость движения тела (в м/с) в интервале времени от 1 c до 2 c равна …

13.2. Два бруска массами m₁ = 5 кг и m₂ = 3 кг связаны невесомой и нерастяжимой нитью, перекинутой через невесомый блок. Брусок I может скользить по наклонной плоскости, образующей с горизонтом угол α = 30⁰. Коэффициент трения бруска I о наклонную плоскость μ = 0,1. Найти ускорение, с которым движутся бруски и силу натяжения нити.

13.3. Материальная точка  начинает двигаться под действием силы =  (Н) . Если зависимость радиус-вектора материальной точки от времени имеет вид (м), то мощность (Вт), развиваемая силой в момент времени t = 2 c  равна …

13.4. На дне гладкой полусферы радиусом R = 2 м лежит кубик массой m₁ = 0,3 кг. С края полусферы соскальзывает кубик массы m₂ = 0,2 кг такого же размера, как и первый. Какой будет высота подъема кубиков после неупругого удара? Чему равно количество теплоты, выделившееся в результате абсолютно неупругого столкновения кубиков?

13.5. Частица движется по окружности радиусом R= 1м в соответствии с уравнением , где — в радианах, — в секундах. Определите угловое ускорение и угловую скорость движения в момент времени .

13.6. На рисунке представлен график зависимости проекции вращательного момента силы, действующей на тело, от времени. На каком из интервалов времени тело вращалось равнозамедленно?

13.7. Два маленьких массивных шарика закреплены на невесомом длинном стержне на расстоянии друг от друга. Стержень вращается без трения в горизонтальной плоскости вокруг вертикальной оси, проходящей посредине между шариками. Стержень раскрутили до угловой скорости , совершив работу А₁. Какую работу А₂ надо совершить, если шарики раздвинуть симметрично на расстояние и раскрутить до угловой скорости в два раза большей?

13.8. Сплошной (1) и полый цилиндры (2) одинаковых масс и радиусов катятся без скольжения по горизонтальной поверхности с одинаковой скоростью. Чему равно отношение расстояний , которое пройдут цилиндры до своей полной остановки. Значение коэффициента трения тел одинаково на протяжении всего пути и равно  = 0,1.

ИЗД Механика поступательного и вращательного движения

Вариант 14

14.1. 3

1

0

2

1

2

Две материальные точки 1 и 2 в момент времени выходят из точки с координатой и движутся в положительном направлении оси . Используя графики зависимости от времени t проекций и скоростей точек, найдите расстояние от места начала движения до места встречи.

14.2. Ленточный транспортер образует с горизонтом угол α = 20⁰. Коэффициент трения между грузом и лентой транспортера μ = 0,60. Максимальное ускорение, с которым можно поднимать на этом транспортере груз, равно … м/с²(с округлением до десятых долей), g = 10 м/с².

14.3. На теннисный мяч, который летел с импульсом p₁, на короткое время ∆t = 0,1 с подействовал порыв ветра с постоянной силой F = 30 H и импульс мяча стал равным p₂ (масштаб и направление указаны на рисунке). Найти величину импульса p₁.

14.4. При выполнении трюка «Летающий велосипедист» гонщик движется по трамплину под действием силы тяжести, начиная движение из состояния покоя с высоты Н = 6 м (см. рисунок). На краю трамплина скорость гонщика направлена под таким углом к горизонту, что дальность его полета максимальна. Пролетев по воздуху, гонщик приземляется на горизонтальный стол, находящийся на той же высоте, что и край трамплина. Какова высота полета h на этом трамплине? Сопротивлением воздуха и трением пренебречь.

14.5. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется во времени, как показано на графике. На каких интервалах времени знаки проекций угловой скорости и углового ускорения одинаковые?

14.6. Имеются два цилиндра: алюминиевый (сплошной) и свинцовый (полый) одинакового радиуса R = 10 см и одинаковой массы m = 0,50 кг. Найдите моменты инерции этих цилиндров. Найдите отношение времен , за которые каждый цилиндр скатится без скольжения с наклонной плоскости, высота наклонной плоскости h = 0,50 м, угол наклона плоскости α = 30°.

14.7. На рисунке представлен график зависимости проекции вращательного момента силы, действующей на тело, от угла поворота. Чему равна работа сил, действующих на тело, при повороте его на угол 6 рад ?

14.8. Сплошной цилиндр (1) и шар (2), имеющие одинаковые массы и радиусы, вкатываются без проскальзывания с одинаковыми начальными скоростями на горку. Найдите отношение высот h₁/h₂, на которые смогут подняться эти тела, если трением и сопротивлением воздуха можно пренебречь.

ИЗД Механика поступательного и вращательного движения

Вариант 15

15.1 Три тела равной массы бросили с одинаковыми по модулю скоростями: первое вертикально вверх, второе под углом 30º к горизонту, а третье под углом 60º. Первым достигнет точки наивысшего подъема тело под номером…

15.2. Шарик подвешен на тонкой нерастяжимой нити длиной l= 50 см к краю горизонтального диска радиусом R = 20 см. Диск приводят во вращение вокруг вертикальной оси. С какой угловой скоростью надо вращать диск, чтобы нить с шариком отклонилась от вертикали на угол α = 45⁰?

15.3. На рисунке показан вектор силы, действующей на частицу. Найти работу, совершенную этой силой при перемещении частицы из начала координат в точку с координатами (4; 3) .

15.4. В маленький шар, подвешенный на нити длиной L = 0,4 м, масса которого М = 5 кг, попадает пуля массой m = 20 г, летящая с горизонтальной скоростью V₁ = 1000 м/с. Пройдя через шар, она продолжает движение в том же направлении со скоростью V₂ = 500 м/с. На какой угол от вертикали отклонится шар?

15.5. Вращение плоского тела вокруг неподвижной оси, расположенной перпендикулярной плоскости тела и проходящей через точку О, задано уравнением . Начало движения при . Положительные углы отсчитываются в направлении стрелки на рисунке. Определите, как будет вращаться тело и с какой по величине угловой скоростью, в момент времени после начала движения

15.6. Момент импульса относительно неподвижной оси изменяется по закону , при этом зависимость момента сил описывается графиком …

15.7. На графике приведена зависимость проекции момента силы, действующей на тело, от времени. Какой момент импульса будет иметь тело к концу третьей секунды движения, если в начальный момент t₀ = 0 тело покоилось.

15.8. Деревянный стержень длиной l = 1,0 м и массой M = 5,0 кг может вращаться вокруг перпендикулярной к нему оси, проходящей через точку O, расположенную на верхнем конце стержня. В нижний конец стержня попадает пуля массы m= 10,0 г, летящая перпендикулярно к оси и к стержню со скоростью V₀ = 200 м/с и пробивает его. После удара пуля продолжает двигаться в прежнем направлении со скоростью V = 100 м/с. Определите, какая доля первоначальной энергии пули перешла в тепло?

ИЗД Механика поступательного и вращательного движения

Вариант 16

16.1. Используя график зависимости скорости движения тела от времени, определите скорость тела в конце пятой секунды, считая, что характер движения не изменился. Определите координату x в момент времени t = 3 c, если в начальный момент времени t₀ = 0 с координата x₀ = 2 м.

16.2. Грузы массами m₁ = 4 кг и m₂ = 5 кг связаны между собой нитью, перекинутой через неподвижный блок. Первый груз расположен на горизонтальном столе, второй висит на вертикальной части нити. Определите ускорение грузов a и силу натяжения нити T при условии, что коэффициент трения груза о стол μ = 0,1. Нить считать невесомой и нерастяжимой, массой блока пренебречь.

16.3. Проекция p_{xимпульса материальной точки, движущейся прямолинейно вдоль оси Х, изменяется со временем так, как показано на рис. 1. Какой номер графика на рис. 2 соответствует зависимости Fx(t) – проекции силы, действующей на точку и вызывающей это изменение px? Ответ обосновать.}

16.4. Два шарика, массы которых m = 0,1 кг и М = 0,2 кг, висят, соприкасаясь, на вертикальных нитях длиной l = 1,5 м (см. рисунок). Левый шарик отклоняют на угол 90° и отпускают без начальной скорости. Какое количество теплоты выделится в результате абсолютно неупругого удара шариков?

16.5. На рисунке приведен график параболической зависимости модуля углового перемещения абсолютно твердого тела от времени. Начальная угловая скорость равна нулю. За четыре секунды тело повернется на угол …рад.

16.6. Стержень вращается вокруг оси, проходящей через его один из его концов согласно уравнению φ = At+Bt³, где A=2 рад/с; B = 0,2 рад/с³. Найдите закон изменения момента силM, действующих на стержень. Определите угловую скорость и момент силM в момент времени t = 2 с, если момент инерции стержня J = 0,048 кг∙м².

16.7. На рисунке представлен график зависимости кинетической энергии вращающегося W_вр тела, момент инерции которого равен J = 2 кг·м² , от угла поворота φ. Чему равен вращающий момент сил, действующий на тело, в тот момент времени, когда угол поворота станет равным

φ = 3 рад.

16.8. Мальчик катит обруч по горизонтальной поверхности со скоростью v=7.2 км/ч., Найдите высоту (в метрах), на которую может вкатиться обруч в горку за счет своей кинетической энергии, если пренебречь силой трения качения.

ИЗД Механика поступательного и вращательного движения

Вариант 17

17.1. Тело движется в плоскости ХОУ и при этом его координаты изменяются со временем следующим образом: х = 2 + 3t – t² , м ^{и y = 4 – 2 t2, м. Модуль ускорения этого тела в момент времени t = 2.0 c равен … м/с2 (с округлением до десятых долей).}

17.2. Тело массой m = 0,8 кг движется вверх по плоскости, наклоненной под углом α=30⁰ к горизонту. К телу прикреплена пружина жесткости k = 120 Н/м, к которой приложена сила (см. рисунок). Коэффициент трения между телом и плоскостью μ = 0,4. Ускорение тела равно а = 1,2 м/с². Определить деформацию пружины Δl.

17.3. В потенциальном поле сила пропорциональна градиенту потенциальной энергии . Если график зависимости потенциальной энергии от координаты х имеет вид, представленный на рисунке, то зависимость проекции силы на ось Х будет иметь вид …

17.4. Кусок пластилина массой m = 200 г падает со скоростью V = 6 м/с, направленной под углом α = 60⁰ к горизонту, на брусок массой m₁ = 2m, двигающийся со скоростью V₁ = V/2 по гладкой горизонтальной поверхности навстречу куску пластилина. Найти количество энергии, перешедшей в тепло Q при абсолютно неупругом ударе.

17.5. Колесо автомашины вращается равноускоренно. Сделав N = 50 полных оборотов, оно изменило частоту вращения от n₁ = 4 с^-1 доn₂ = 6 с^-1. Определите угловое ускорение колеса.

17.6. Момент силы, приложенный к вращающемуся телу, изменяется по закону, где – некоторая положительная константа.

Момент инерции остается постоянным в течение всего времени вращения. Зависимость углового ускорения от времени представлена на рисунке …
17.7. Два маленьких массивных шарика закреплены на невесомом длинном стержне на расстоянии друг от друга. Стержень может вращаться без трения в горизонтальной плоскости вокруг вертикальной оси, проходящей посредине между шариками. Стержень раскрутили из состояния покоя до угловой скорости ₁, при этом была совершена работа А₁. Шарики раздвинули симметрично на расстояние и раскрутили до той же угловой скорости ₂ = ₁. Какая при этом была совершена работа ?

1) ; 2) ; 3) ; 4) .

17.8. Обруч скатывается без проскальзывания с горки высотой h = 2,5 м. Найдите скорость обруча у основания горки при условии, что трением можно пренебречь.

ИЗД Механика поступательного и вращательного движения

Вариант 18

18.1. На графике изображена зависимость координаты точки от времени.

Какой график зависимости скорости от времени отвечает этому случаю?

18.2. Тело начинает скользить вниз по наклонной плоскости, составляющей с горизонтом угол α = 30⁰. У основания плоскости тело ударяется о стенку, поставленную перпендикулярно к направлению его движения, и отскакивает без потери скорости. Определить коэффициент трения μ при движении тела, если после удара оно поднялось до половины первоначальной высоты.

18.3. Материальная точка двигалась вдоль оси ОХ равномерно с некоторой скоростью V_x. Начиная с момента времени t = 0, на нее стала действовать сила F_х, график временной зависимости которой представлен на рисунке. Какой график правильно отражает зависимость величины проекции импульса материальной точки от времени на следующем рисунке? Ответ обоснуйте.

18.4. Два цилиндра массами m₁=150 г и m₂ = 300 г, соединенные сжатой пружиной, разошлись при внезапном освобождении пружины в разные стороны. Пренебрегая силами сопротивления и учитывая, что кинетическая энергия упруго деформации пружины составляет 1,8 Дж, определить скорости движения первого и второго цилиндров сразу после освобождения пружины.

18.5. На графике представлена зависимость угловой скорости тела, вращающегося вокруг неподвижной оси, от времени t. Определить количество оборотов N, которое сделает тело до остановки.

18.6. Диск, момент инерции которого J = 40 кг∙м², начинает вращаться равноускоренно под действием момента силы М = 20 Н∙м. 1) Какой момент импульса будет иметь тело через t = 10 с вращения? На рисунке покажите направление этого момента импульса; 2) Сколько полных оборотов сделает диск за этот промежуток времени?

18.7. На рисунке представлен график зависимости проекции вращательного момента силы, действующей на тело, от угла поворота. Чему равна работа сил, действующих на тело, при повороте его на угол 5 рад ?

18.8. Тонкий однородный стержень длинойl = 1м может свободно вращаться вокруг горизонтальной оси, проходящей через точку О на стержне. Стержень отклонили от вертикали на угол α = π/3 и отпустили. Определите угловую скорость стержня и линейную скорость точки В на стержне в момент прохождения им положения равновесия.

ИЗД Механика поступательного и вращательного движения

Вариант 19

19.1 На графике приведена зависимость проекции ускорения на ось x от времени. Какую скорость будет иметь тело к концу третьей секунды движения, если в начальный момент t₀ = 0 c его скорость V₀ = 5 м/с?

19.2. Тело начинает скользить вниз по наклонной плоскости, составляющей с горизонтом угол α = 30⁰. У основания плоскости тело ударяется о стенку, поставленную перпендикулярно к направлению его движения, и отскакивает без потери скорости. Определить коэффициент трения μ при движении тела, если после удара оно поднялось до половины первоначальной высоты.

19.3. Проекции p_1x и p_1xимпульсов материальных точек 1 и 2, движущихся прямолинейно вдоль оси Х, изменяются со временем t как показано на рисунке; при этом проекции ускорений точек одинаковы: a_x1 = a_x2. Найти отношение масс m₁/m₂ этих точек.

19.4. На идеально гладком столе лежат два груза, массы которых относятся как 1:3. Грузы соединены между собой сжатой пружиной жесткостью k = 1000 Н/м. Пружина удерживается в сжатом состоянии с помощью тонкой нерастяжимой нити. После пережигания нити пружина разжимается, и более легкий груз приобретает кинетическую энергию W_k = 60 Дж. Определить величину деформации ∆l сжатой пружины.

19.5. Частица движется вдоль окружности радиусом R= 1м в соответствии с уравнением . Определите время движения до остановки и расстояние ( в м), пройденное точкой за это время.

19.6. Диск начинает вращаться под действием момента сил М, график временной зависимости которого представлен на рис. 1.График, правильно отражающий зависимость момента импульса диска от времени, представлен на рис.2. под номером …

19.7. На рисунке приведен график зависимости угла поворота φ тела при вращательном движении от времени. Как изменяется кинетическая энергия тела в интервале времени от t₁ до t₂?

19.8. Сплошной однородный диск катится по горизонтальной плоскости со скоростью v = 10 м/с. Какое расстояние пройдет диск до остановки, если его предоставить самому себе? Коэффициент трения при движении диска равен μ = 0,02.

ИЗД Механика поступательного и вращательного движения

Вариант 20

20.1. Тангенциальное ускорение точки меняется согласно графику. Выберите график зависимости скорости от времени, соответствующая такому движению. Ответ обоснуйте. Постройте схематично график зависимости координаты от времени.

20.2. Маленький шарик, привязанный к невесомой нити длиной l = 40 см, вращается в горизонтальной плоскости с постоянной по модулю скоростью так, что нить описывает коническую поверхность с вершиной в точке, где находится верхний конец нити. При этом угол отклонения нити от вертикали α = 30⁰. Определить скорость вращения υ шарика.

20.3. В потенциальном поле сила пропорциональна градиенту потенциальной энергии. Если график зависимости потенциальной энергии от координаты х имеет вид, представленный на рисунке, то зависимость проекции силы на ось Х изображена на рисунке под номером …

20.4. Шар массой 1 кг, подвешенный на нити длиной 90 см, отводят от положения равновесия на угол 60º и отпускают. В момент прохождения шаром положения равновесия в него попадает пуля массой 10 г, летящая навстречу шару со скоростью 300 м/с. Она пробивает его и вылетает горизонтально со скоростью 200 м/с, после чего шар продолжает движение в прежнем направлении. На какой максимальный угол отклонится шар после попадания в него пули? (Массу шара считать неизменной, диаметр шара – пренебрежимо малым по сравнению с длиной нити.)

20.5. На графике представлена зависимость угла поворота φ тела, вращающегося вокруг неподвижной оси, от времени t. Величина углового ускорения в этом случае равна … рад²/с. (Ответ округлить до десятых).

20.6. Однородный стержень длиной l = 1,2 м и массой m = 0,3 кг вращается в горизонтальной плоскости вокруг вертикальной оси, проходящей через один из его концов с угловым ускорением  = 9,81 с^-1. Сколько оборотов сделает стержень за время t = 5,0 с, если он начал вращаться из состояния покоя? Как изменится вращающий момент, если ось вращения переместить в центр масс стержня, а действующая сила не изменяется?

20.7. На рисунке представлены графики зависимости мощности постоянного момента силы от времени . Тело вращается равнозамедленно. Какой график соответствует этому случаю?

20.8. Шар массой m = 3 кг скатывается без проскальзывания с вершины наклонной плоскости высотой h = 4 м без начальной скорости. Длина ската наклонной плоскости l = 8 м, а значение коэффициента трения качения () тела одинаково на всем протяжении его пути и равно  =0,1. Определите скорость шара у подножия наклонной плоскости (в м/с).

ИЗД Механика поступательного и вращательного движения

Вариант 21

21.1. Материальная точка М движется по окружности со скоростью . На рис.1 показан график зависимости от времени ( — единичный вектор положительного направления, — проекция на это направление). На рис.2 направление силы, действующей на т. М в момент времени , совпадает с направлением …

21.2. Тело массой m = 1,4 кг находится на гладкой горизонтальной плоскости и вращается вокруг вертикальной оси. Оно прикреплено к оси пружиной и движется по окружности радиуса R, совершая n = 1 об/сек. Длина пружины в недеформированном состоянии равна L₀ = 50 см. Радиус траектории тела равен R = 88 см. Определить жесткость пружины k.

21.3. Шарик, прикрепленный к пружине и насаженный на горизонтальную направляющую, совершает гармонические колебания. На графике представлена зависимость проекции силы упругости пружины F_x на положительное направление оси Х от координаты шарика. Найти работу силы упругости на участке 0 – В – 0.

21.4. Два тела, которые первоначально покоились на гладкой горизонтальной поверхности, расталкиваются зажатой между ними легкой пружиной и начинают двигаться так, что в процессе движения их максимальные скорости равны υ₁ = 1 м/с и υ₂ = 3 м/с. Какая энергия была запасена в пружине, если общая масса тел М = 8 кг?

21.5. Скорость вращения тела зависит от времени согласно уравнению . Чему равно угловое ускорение тела при этом движении. Запишите зависимость угла поворота от времени при условии, что угол поворота в момент времени был равен.

21.6. На рисунке приведен график зависимости от времени проекции угловой скорости вращающегося тела на ось вращения. На каком интервале времени момент сил, действующих на тело, был постоянным, не равным нулю и максимальным по модулю?

21.7. Два маленьких массивных шарика закреплены на невесомом длинном стержне на расстоянии друг от друга. Стержень может вращаться без трения в горизонтальной плоскости вокруг вертикальной оси, проходящей посредине между шариками. Стержень раскрутили из состояния покоя до угловой скорости , при этом была совершена работа А₁. Шарики сдвинули симметрично на расстояние и раскрутили до угловой скорости

₂ = 2₁. Какая при этом была совершена работа ?

1) ; 2) ; 3) ; 4) .

21.8. Сплошной и полый цилиндры, имеющие одинаковые массы и радиусы, вкатываются без проскальзывания на горку. Какой из цилиндров поднимется выше и во сколько раз, если начальные скорости тел одинаковы?

ИЗД Механика поступательного и вращательного движения

Вариант 22

22.1. Тело движется в плоскости ХОУ и при этом его координаты изменяются со временем следующим образом: х = 2 + 2t – t²,м^{и y = 4 + 2t,м. Скорость этого тела в момент времени t= 1.0 c равна … м/с.}

22.2. Брусок массой 4 кг может двигаться только вдоль вертикальных направляющих, расположенных на вертикальной стене. Коэффициент трения бруска о направляющие μ = 0,1. Если а брусок действует сила , по модулю равная 20 Н и направленная под углом α = 60⁰ к вертикали (см. рисунок). Определить ускорение бруска.

22.3. Два тела одинаковой массы соскальзывают без начальной скорости с вершин двух наклонных плоскостей, длины которых . Если, а коэффициенты трения тел о плоскости в обоих случаях одинаковы, то соотношение между работами силы трения и в обоих случаях следующее

1)

2)

3)

4) среди ответов правильного нет

Укажите номер правильного ответа и поясните его.

22.4. Небольшая шайба соскальзывает без трения с вершины полусферы радиусом R = 30 см. На какой высоте h от основания шайба оторвется от полусферы?

22.5. На графике представлена зависимость угловой скорости ω тела, вращающегося вокруг неподвижной оси, от времени t. Напишите уравнение, верно отражающее зависимость угла поворота φ от времениt при условии, что угол поворота в момент времени был равен.

22.6. Колесо, вращаясь равнозамедленно, уменьшило частоту вращения от n₁ = 300 об/мин до n_{2 = 180 об/мин за время t= 1 мин. Момент инерции колеса J = 2 кг∙м². 1) Определите угловое ускорение колеса и покажите на рисунке, как оно направлено; 2) Как направлен момент сил торможения, и чему он равен?
22.7. На рисунке представлен график зависимости проекции вращательного момента силы, действующей на тело, от времени. Чему равен момент импульса тела в момент времени t = 6 с, если в начальный момент времени тело покоилось?}

22.8. Шар катится без проскальзывания по горизонтальной поверхности со скоростью ν₁ = 10 м/с. После удара о вертикальную стенку он стал двигаться в обратном направлении со скоростью ν₂ = 6 м/с. Какую часть первоначальной энергии потерял шар при ударе?

ИЗД Механика поступательного и вращательного движения

Вариант 23

23.1. Под каким углом к горизонту следует бросить камень, чтобы дальность полета была равна высоте полета? Сопротивлением воздуха пренебречь.

23.2. На диске, вращающемся вокруг вертикальной оси, лежит шайба массы m = 100 г. Шайба соединена с осью горизонтальной пружиной. Коэффициент трения шайбы о диск μ = 0,40. Если число оборотов диска равно n₁= 2,0 об/с, пружина находится в недеформированном состоянии и шайба находится на грани скольжения. Если число оборотов диска возрастает до n₂ = 5,0 об/с, то длина пружины увеличивается в 2 раза. Определить длину l₀ пружины в недеформированном состоянии и жесткость пружины k.

23.3. С ледяной горки с небольшим шероховатым участком АС из точки А без начальной скорости скатывается тело. Сопротивление воздуха пренебрежимо мало. Зависимость потенциальной энергии шайбы от координаты х изображена на графике . При движении тела сила трения совершила работу А_тр = 20 Дж. После абсолютно неупругого удара со стеной в точке В выделилось … Дж тепла.

23.4. На рельсах стоит платформа, на которой закреплено орудие без противооткатного устройства так, что ствол его расположен в горизонтальном положении. Масса платформы с орудием М=5 т. Из орудия производят выстрел вдоль железнодорожного пути. Масса m₁снаряда равна 10 кг, и его скорость u₁ = 1 км/с. На какое расстояние lоткатится платформа после выстрела, если коэффициент сопротивления μ = 0,2?
23.5. Велосипедное колесо вращается с частотой n = 5 c^-1. Под действием сил трения оно остановилось через интервал времени Δt = 1 мин. Определите угловое ускорение и число оборотов N, которое сделает колесо за это время.

23.6. На рисунке представлен график зависимости проекции вращательного момента силы, действующей на тело, от времени. Сколько оборотов сделает тело за шесть секунд после начала действия вращающегося момента? В начальный момент тело покоилось.

23.7. На рисунке представлен график зависимости проекции вращательного момента силы, действующей на тело, от угла поворота. Чему равна работа сил, действующих на тело, при повороте его на угол 10 рад ?

23.8. Обруч и диск одинаковой массы m₁ =m₂ = 1 кг катятся по горизонтальной поверхности без скольжения с одинаковой скоростью. Радиус обруча в два раза больше чем диска. Кинетическая энергия обруча W_обр= 40 Дж. Определите кинетическую энергию диска W_д.

Действие сил при вращательном движении

63. Груз, подвешенный на нити длиной 5 м, равномерно вращается по окружности в горизонтальной плоскости. Найти угловую скорость вращения, если при вращении нить отклонилась от вертикали на угол 60⁰. [2]

64. Найти отношение сил, с которыми танк давит на середины выпуклого и вогнутого мостов. Радиус кривизны мостов в обоих случаях равен 40 м, а скорость движения равна 45 км/ч. [0,43]

65. Автомобиль массой 8 т движется со скоростью 36 км/ч по выпуклому мосту радиусом 200 м. Определить силу, действующую на автомобиль в верхней точке моста. Ускорение свободного падения принять равным 10 м/с². [7,6×10⁴ Н]

66. На невесомом стержне висит груз массой m. Груз отклоняют на угол a= 90⁰ и отпускают. Найти натяжение стержня при прохождении им положения равновесия.

67. Тяжелый шарик подвешен на нити длиной l. Нить равномерно вращается в пространстве, образуя с вертикалью угол a. Сколько оборотов делает шарик за время t.

68. С какой минимальной угловой скоростью w нужно вращать ведро в вертикальной плоскости, чтобы из него не выливалась вода? Расстояние от поверхности воды до центра вращения l. [w ²=g/l]

69. Ведерко с водой, привязанной к веревке длиной l, вращается в вертикальной плоскости. найти натяжение веревки в высшей и низшей точках окружности при условии, что вода не выливается в верхней точке. Масса ведерка с водой m. [T₁=0, T₂= 2mg]

70. Тяжелый шарик массы m подвешен на нити длины l. Шарик равномерно вращается по кругу в горизонтальной плоскости (конический маятник). Нить при этом отклонена на угол a. Найти время полного оборота шарика.

71. Математический маятник имеет массу m и длину l. В момент, когда он образует угол a с вертикалью, его скорость равна V. Какова в этот момент сила натяжения нити?

72. На вращающемся горизонтальном диске укреплен отвес, который устанавливается под углом a = 45⁰ к вертикали. Расстояние от точки подвеса до оси вращения d = 10 см, длина нити L = 6 см. определить угловую скорость вращения w. [8,3 с^-1]

73. Конькобежец движется со скоростью 10 м/с по окружности радиусом 30 м. Под каким углом к горизонту он должен наклониться, чтобы сохранить равновесие.

74. Груз массой m = 100 г подвешен на нити и совершает колебания, отклоняясь на угол a = 60⁰ в ту и другую сторону. Определить натяжение нити в момент, когда нить составляет угол b = 30⁰ с вертикалью.

75. Автомобиль движется в верхней части выпуклого моста радиуса R = 40 м. Какое максимальное горизонтальное ускорение может развить автомобиль в этой точке, если его скорость 54 км/ч, а коэффициент трения колес автомобиля о мост 0,6. При какой скорости V₁ в верхней точке автомобиль не может увеличивать модуль скорости?

76. Человек сидит на краю круглой горизонтальной платформы радиусом 4 м. С какой частотой (об/мин) должна вращаться платформа вокруг вертикальной оси, чтобы человек не мог удержаться на ней при коэффициенте трения 0,27?

77. Самолет делает «мертвую петлю» с радиусом 100 м и движется по ней со скоростью 280 км/ч. С какой силой тело летчика массой 80 кг будет давить на сиденье самолета в верхней и нижней точках петли?

78. Математическому маятнику массой m сообщили минимальный толчок, чтобы он совершил полный оборот в вертикальной плоскости. Какова сила натяжения нити маятника при прохождении им положения равновесия?

79. Шарик скользит по желобу с высоты h и затем движется по «мертвой петле» радиуса R. Какое давление производит шарик на желоб в некоторой точке В, если радиус, проведенный из центра петли в точку В, составляет с вертикалью угол a? Масса шарика m, высота h = 5R/2. Размеры шарика считать ничтожно малыми.

80. Вокруг вертикально расположенного стержня вращается насаженный на него диск. На диске находится шарик, прикрепленный к стержню нитью, длины l и составляющий угол a со стержнем. С каким периодом должна вращаться система, чтобы нить не провисала при таком положении шарика?

81. **Обруч радиуса R укреплен вертикально на полу. С вершины обруча соскальзывает без трения тело. На каком расстоянии lот точки закрепления обруча упадет это тело? [1,5R]

82. Материальная точка массой 11 кг движется по криволинейной траектории под действием равнодействующей силы 20 Н. Определить скорость точки в момент времени, когда радиус кривизны траектории равен 15 м и угол между силой и вектором скорости равен 35⁰. [3,96 м/с]

83. В лифте, движущемся вертикально вверх с ускорением а₀ = 4 м/с², находится горизонтальный столик, вращающийся с угловой скоростью 4p рад/с. Зная, что коэффициент трения коробка о столик равен 0,4, найти максимальное расстояние коробка от оси вращения, при котором он еще будет удерживаться на столике. [3,5 см]

84. Шарик массой m, висящий на нити длины l, отводят в сторону так, что нить занимает горизонтальное положение А, и отпускают без толчка. Внизу на расстоянии h = (2/3)l под точкой подвеса О вбит гвоздь С. Какую силу натяжения будет иметь нить в момент, когда она займет горизонтальное положение В?

Секстан и его устройство

Одним из первых угломерных инструментов, который был, по-видимому, известен еще древним астрономам, являлся градшток. Мореплаватели стали им пользоваться где-то в XV веке. Во всяком случае градшток уже имелся на каравеллах Колумба и Васко да Гама.

Древний градшток состоял из двух взаимно перпендикулярных реек-штока длиной 90 см и поперечной крестовины, плотно прилегающей к штоку и скользящей по нему под прямым углом. Длина крестовины была несколько больше 65 см для того, чтобы расстояние между отверстиями на ее концах составляло точно 65 см.

Устройство градштока

На конце штока была укреплена мушка. Наблюдателю, смотря на глазную мушку, надо было одновременно видеть оба предмета (горизонт и светило), взаимное расстояние между которыми определялось через отверстия в крестовине. Для нанесения делений на столе чертили углы и на них накладывали градшток. Градусные деления наносили на верхнюю грань штока. Для измерения разных и в том числе меньших углов служили дополнительные, более короткие крестовины. Деления для меньших углов размечали на боковых гранях штока.

Для измерения высоты какого-либо светила (звезды, Солнца) приставляли один конец длинного штока к глазу, а поперечную крестовину двигали так, чтобы она одним концом точно коснулась горизонта, а другим – светила. Результаты измерений таким примитивным приспособлением, как градшток, получались весьма приблизительными. К тому же глаз не мог видеть одновременно два предмета (точку горизонта и планету), находящиеся друг от друга на таком значительном расстоянии. Несмотря на ненадежность, градшток просуществовал более ста лет.

В начале XVI века широкое распространение получил другой угломерный инструмент, тоже примитивный, хотя и более приспособленный для измерения высот, чем градшток – астролябия. Астролябия представляла собой диск из меди или жести около 6 мм толщиной и 15-17 см в диаметре. Диск имел выступ с отверстием для подвешивания. Астролябию старались делать потяжелее (5-6 кг) для устойчивости при ветре и качке судна. Для удобства пользования на ободе астролябии выбивали склонение солнца для разных времен года. Поверхность диска была хорошо отполирована. Отвесом от точки подвеса отмечали вертикальную линию, относительно которой наносили горизонталь и центр круга. Верхний левый квадрат делили на градусы. На оси диска крепилась алидада (подвижный радиус) из того же металла, шириной около 4 см, длиной, равной диаметру диска, и толщиной, равной толщине диска. По всей длине алидады проходила визирная линия. По концам визирной линии были укреплены пластинки с небольшими отверстиями точно над визирной линией. Подвесив астролябию, алидаду наводили на звезду или Солнце и по градуированной дуге диска отсчитывали полученный угол. Позже на астролябии была градуирована и противоположная дуга диска. Астролябия, как и градшток, применялись в первых кругосветных путешествиях.

Измерение высот с помощью астролябии

В измерении высот с помощью астролябии обычно принимали участие три наблюдателя: один держал астролябию за кольцо, надев его на большой палец, другой измерял высоту, а третий производил отсчет. Каждый из трех наблюдателей вносил свою ошибку в конечный результат измерений. Ошибки измерений, качка и ветер -все это сказывалось на точности наблюдений.

Более поздними угломерными инструментами были квадрант и октан. Затем появился секстан, который, претерпев много усовершенствований, исправно служит морякам и сегодня.

Первоначально секстан имел дугу, равную приблизительно 7б окружности, по-латински это произносится как sextans – шестая часть, откуда секстан и получил свое название. У современных секстанов дуга имеет несколько большие размеры.

Применение секстанта

Секстан служит для измерения высоты светила, т. е. вертикального угла между плоскостью горизонта и направлением на светило. Кроме вертикальных углов, секстаном можно измерять горизонтальные углы между направлениями на земные ориентиры (предметы) при определении места судна навигационными способами. При измерении секстаном вертикальных и горизонтальных углов один из предметов наблюдается прямовидимо, изображение же другого предмета наблюдатель видит после отражения от двух зеркал. Чтобы измерить угол, эти два изображения необходимо совместить.

Принципиальная схема секстана. Рассмотрим принципиальную схему секстана. Нам требуется измерить угол h между предметами С и D. В точке О расположен глаз наблюдателя. На пути луча СО установим неподвижное зеркало А, плоскость которого перпендикулярна плоскости рисунка, а зеркальная сторона обращена к глазу наблюдателя. Если сделать половину поверхности этого зеркала прозрачной, луч от предмета С свободно попадет в глаз наблюдателя (на рисунке его путь обозначен стрелкой). Наблюдатель увидит по направлению ОС через прозрачную половину зеркала А изображение С, которое называют прямовидимым.

В точке В расположим другое подвижное зеркало, которое может вращаться вокруг оси, перпендикулярной плоскости рисунка. Установим это зеркало в такое положение, чтобы луч света от предмета D, отразившись от подвижного, называемого большим, зеркала В, попал иа неподвижное малое зеркало А, а от него в глаз наблюдателя, в точку О. Изображение предмета D получится дважды отраженным. Следовательно, изображения предметов С и D совместятся по направлению О АС. Обозначим ш угол между зеркалами. Так как углы падения и отражения световых лучей равны: Z.1 = Z.2 и Z.3 = Z4, то равны и их дополнения до 90°.

Можно сделать вывод, что при совмещении прямо-видимого предмета С и дважды отраженного изображения предмета D измеряемый угол h равен двойному углу между зеркалами со. Таким образом, измерение угла h может быть заменено измерением угла со.

На рисунке представлен общий вид секстана, который состоит из металлической или пластмассовой рамы 7 в форме сектора. На раме расположен лимб 9 с градусными делениями, а по торцу дуги нарезана зубчатая рейка. На левом радиусе рамы укреплено неподвижное малое зеркало 3 и светофильтры J и 2, На правом радиусе рамы имеется угольник с кольцом, служащий для крепления на ней астрономической трубы 6 и подъемного механизма 5. На подвижном радиусе – алидаде 8 – крепится большое зеркало 4 и на противоположном ее конце установлен винт с отсчетным барабаном 11, наружная поверхность которого имеет 60 минутных делений. Число градусов показывает индекс, нанесенный около выреза на алидаде. Минуты и десятые доли минуты отсчитываются на барабане. При вращении барабана алидада передвигается, что дает возможность точно совместить прямовидимое и отраженное изображения предметов. Точность измерения углов секстаном 0,1. На обратной стороне рамы имеются ручка и две ножки 10.

Секстан хранят в закрытом деревянном ящике с крышкой; его устанавливают ножками в специальные гнезда и крепят стопором, проходящим через отверстия в рукоятке. Секстан следует оберегать от толчков, ударов, от влияния сырости и резких изменений температуры. Брать секстан разрешается только за раму и ручку. Нельзя трогать пальцами оптические детали – зеркала, линзы, светофильтры. При попадании на стеклянные части дождя, брызг или при отпотевании, их осторожно протираю-Г чистой фланелевой тряпочкой, которая должна находиться в каждом комплекте секстана.

Приемы измерения углов и высот секстаном. Измерение углов в навигации обычно проводится между земными предметами при определении места судна по двум углам или по пеленгу и углу. Для измерения горизонтального угла секстан берут в левую руку и располагают лимбом в плоскости измеряемого угла. Трубу секстана наводят на более слабо видимый предмет. Затем, освободив стопор, перемещают алидаду, пока в поле зрения не появится изображение другого предмета, и вращением отсчетного барабана точно совмещают пря-мовидимый (первый) и дважды отраженный (второй) предметы. Для измерения вертикального угла направляют секстан на основание предмета, располагая лимб вертикально, и, двигая алидаду, подводят к основанию дважды отраженное изображение верхней части предмета. Обычно в таких случаях наблюдаемыми объектами служат маяки, знаки, отдельные высокие сооружения, горы.

При измерении углов между земными предметами можно не пользоваться зрительной трубой, тогда на прямовидимый предмет наводят малое зеркало.

Поправку индекса при наблюдениях близких земных предметов надо определять также по близкому прямовидимому предмету.

Перед измерением высот секстан следует подготовить к наблюдениям: провести его выверку, определить поправку индекса, установить трубу по своему глазу и подобрать, если необходимо, светофильтры. Измеряя высоту, нужно в поле зрения трубы секстана совместить светило (или края его диска) с линией видимого горизонта. Совмещение производят в вертикале светила.

Измерение может быть выполнено двумя методами:

1. Установить индекс алидады на 0° и навести трубу на светило. Передвигая алидаду от себя, одновременно опустить секстан к горизонту так, чтобы дважды отраженное изображение светила оставалось все время в поле зрения трубы. Как только появится прямовидимое изображение горизонта, приступить к точному визированию высоты.
2. Индекс алидады установить на примерный отсчет высоты светила, который можно получить по звездному глобусу, и навести трубу на линию видимого горизонта в вертикале светила. Увидев в поле зрения трубы дважды отраженное изображение светила и прямо-видимое – линии горизонта, произвести точное визирование высоты. Точное визирование выполняется покачиванием секстана так, чтобы светило описывало дугу выпуклостью к линии горизонта. В тот момент, когда эта дуга коснется линии горизонта, замечают отсчет по хронометру.

PHY5210 W08 Лекция 5

PHY5210 W08 Лекция 5

Глава 9: Механика в неинерциальных системах отсчета

Чтение:

В Тейлоре прочтите разделы с 9.7 по 9.8 на сегодня и с 9.9 по 9.10 на понедельник.

Отзыв

Второй закон Ньютона во вращающейся системе

m a ‘ = F _real — m Ω [dot] × r’ — 2 м Ω × v ‘ — m Ω × ( Ω × r’ )

Пример: Бусина на стержне

Гладкий стержень длиной l вращается в плоскости с постоянной угловой скоростью Ω вокруг оси, закрепленной на конце стержня и перпендикулярной плоскости вращения.Бусинка массы m может скользить по стержню без трения, первоначально расположена на неподвижном конце стержня и получает небольшой толчок, так что его начальная скорость, направленная вниз по стержню, равна ε = Ωl (рисунок). Подсчитайте, сколько времени требуется бусинке, чтобы добраться до другого конца стержня.

Выберите систему координат, которая вращается вместе со стержнем. Пусть xhat будет вдоль стержня, а yhat — перпендикулярно стержню. Поскольку бусинка прикреплена к стержню, проблема становится одномерной.Единственная регулярная сила — это сила, прижимающая бусину к стержню, и поскольку эта сила перпендикулярна стержню, она направлена ​​в направлении y. В направлении x нет регулярного движения.

Нам нужно найти фиктивные силы на бусине. Для этого предположим, что шарик находится на расстоянии x от начала координат, то есть он расположен в позиции (x, 0, 0) во вращающейся системе координат, и предположим, что он имеет скорость (xdot, 0, 0). (Компоненты y и z скорости должны быть равны нулю в этой системе отсчета, потому что шарик может двигаться только вдоль стержня в x.) Используя Ω = Ωkhat = (0, 0, Ω), фиктивные силы равны

F _cor = 2m v × Ω = -2m (xdot) Ω yhat .

F _cent = -m Ω × ( Ω × r ) = -mΩ²x ( khat × ( khat × xhat )) = mΩ²x xhat

F _транс = 0

Сила Кориолиса направлена ​​в направлении y и нейтрализуется силой, которая удерживает валик на стержне.Центробежная сила будет способствовать движению валика по проволоке. Уравнение движения по x:

м (xddot) = мΩ²x

или же

xddot = Ω²x.

Это линейное уравнение второго порядка по x, и его решение равно

.

x (t) = Ae ^Ωt + Be ^-Ωt .

xdot (t) = ΩAe ^Ωt — ΩBe ^-Ωt .

Начальные условия таковы, что x (0) = 0 и xdot (0) = ε = Ωl. Применяя эти результаты, получаем A + B = 0 и ε = Ω (A — B) или A = -B = ε / 2Ω.Следовательно, x (t) равен

x (t) = (ε / 2Ω) (e ^Ωt — e ^-Ωt ) = (ε / Ω) sinh (Ωt).

Время T, за которое шарик достигает конца стержня, находится путем решения x (T) = (ε / Ω) sh (ΩT) = l. Напомним, что ε = Ωl, поэтому sinh (ΩT) = 1 или T = (1 / Ω) sinh ^-1 (1) = 0,88 / Ω.

Эффекты вращения Земли

Некоторые интересные результаты можно получить, если учесть вращение Земли и рассматривать ее как неинерциальную систему отсчета. Вращение Земли невелико, 2π радиан за звездные сутки, 23 часа 56 минут (время, за которое Земля совершает один оборот относительно звезд).

Ом _земля = [2π / (23 × 60 + 56) мин] (1 мин / 60 сек) = 7,29 × 10 ^-5 рад / с

Эта скорость довольно мала, и эффекты обычно незначительны. Тем не менее, иногда они могут быть важны.

Статические эффекты: отвес

На Земле направление, которое мы называем вертикальным, обычно определяется локально как направление, в котором висит отвес. (Отвес — это просто масса, свисающая с конца веревки, которая часто используется в строительстве для вертикального расположения стен.) Можно с уверенностью предположить, что (не считая холмов, неровностей и т. Д.) Земля (или вода) лежит перпендикулярно вертикали, так что в среднем форма земли может быть связана с вертикалями в разных точках земного шара. Из-за вращения Земли местная вертикаль не указывает прямо на центр Земли. Он будет на экваторе и полюсах, но в других местах он будет указывать немного в сторону от центра. Интегрируя влияние отклонений от местной вертикали, мы можем итеративно определять форму Земли.

Мы можем начать с аппроксимации Земли как идеальной сферы, так что гравитационная сила Земли на отвесе направлена ​​точно по радиусу к центру. Теперь выберите систему координат, привязанную к земле и центрированную на отвесе. В этой системе отвес неподвижен, поэтому a = 0. Назовите g ₀ ускорением свободного падения, обусловленным массой Земли, и поэтому направленным к центру Земли. Силы Кориолиса и поперечные силы равны нулю (так как v = 0 и Ωdot = 0), а поскольку система координат центрирована на опоре, r = 0, и центробежная сила также равна нулю.Но начало системы координат вращается по окружности с радиусом R ₀ = R _e cosλ, где λ — широта на Земле, а R _e — радиус Земли. Система координат испытывает ускорение: A ₀ = Ω²R ₀ = Ω²R _e cosλ, направленное внутрь к оси вращения [диаграмма].

Таким образом, отвес испытывает три силы: натяжение струны, T ; сила тяжести, м г ₀ , а фиктивная сила -м A ₀ .Поскольку боб не ускоряется, их сумма должна равняться нулю. Местная вертикаль параллельна натяжению струны,

T = m A ₀ — m g ₀ = -m (g ₀ — A ₀ )

, а эффективная местная гравитация —

.

г = г ₀ — A ₀

Распределение местных вертикалей говорит нам о том, что форма не совсем сферическая (исходное предположение), а слегка сплюснутая (сплющенная на полюсах, более широкая на экваторе).Это можно было бы использовать в качестве отправной точки для второй итерации, и всю процедуру можно было бы повторить, чтобы получить немного более точный результат, и так далее. Но пока давайте продолжим рассматривать Землю как сферу и оценить разницу в эффективной гравитации на экваторе и полюсах.

На полюсах λ = ± 90 °, поэтому A ₀ = 0 и g = g ₀ . На экваторе λ = 0 °, поэтому g = g ₀ — Ω²R _e , немного меньше, чем на полюсах.Разница составляет Δg = Ω²R _e = (7,3 × 10 ^-5 рад / с) ² (6,38 × 10 ⁶ м) = 0,034 м / с² или относительная разница Δg / g = 0,35%. Вариации этого порядка уже происходят из-за рельефа местности и местных залежей полезных ископаемых.

Еще один интересный расчет — определить, на какую величину (угол) направление силы тяжести отклоняется от радиальной линии. Отклонение составляет 0 на полюсах и экваторе и максимальное для широт ± 45 °. Прочтите вывод в тексте.Но учтите, что локально вертикаль всегда является направлением силы тяжести и перпендикулярна земле (горизонтально).

Динамические эффекты: движение снаряда

Давайте теперь посмотрим на воздействие снаряда, выпущенного с поверхности земли на широте λ. Оказывается, очень удобно выбрать систему координат с началом в точке запуска, осью z, направленной вертикально вверх (против местной силы тяжести), осью y, направленной на север, вдоль большого круга, проходящего через полюса, и осью x, направленной на восток.Это дает правую систему координат. Эта система координат движется по окружности или радиусу R _e cosλ и должна испытывать ускорение по направлению к оси вращения, A ₀ , как в предыдущем примере. Общее уравнение движения:

m a = F _{non g} + m g ₀ — m A ₀ + 2m v × Ω — m Ω × ( Ω × r )

, где F _{non g} — любые негравитационные силы.

Мы можем немного упростить это. Во-первых, g ₀ — A ₀ — это значение локальной силы тяжести, g = -g k hat (см. Обсуждение статических эффектов выше). Во-вторых, Ω — небольшое число, поэтому мы можем разложить поправки в степенной ряд по Ω. Для наших целей мы оставим только члены первого порядка по Ω, поэтому мы можем пренебречь членом центробежной силы, который является вторым порядком по Ω. Наконец, пренебрежем сопротивлением воздуха. Уравнение движения принимает следующий вид:

м a = -мг k шляпа + 2 м v × Ом .

Мы разделим это на составляющие уравнения, но сначала нам нужно оценить перекрестное произведение. В соответствующей системе Ω = Ω (0, cosλ, sinλ), и мы возьмем скорость произвольной v = (xdot, ydot, zdot), что дает

v × Ом = Ом [(zdot cosλ — ydot sinλ) i hat + xdot sinλ j hat — xdot cosλ k hat].

Разделим на общий массовый член и составим уравнение:

xddot = -2 Ом (zdot cosλ — ydot sinλ)

ярдов = -2 Ом x точка sinλ

zddot = -g + 2 Ом x точка cosλ

Это связанные линейные дифференциальные уравнения.Их нельзя разделить, но можно интегрировать каждую из них один раз. В частности, мы можем интегрировать уравнения y и z, чтобы получить выражения для ydot и zdot, которые зависят только от x, и их можно вставить в уравнение x.

ярдов = -2 Ом x sinλ + v _y0

zdot = -gt + 2 Ом x cosλ + v _z0

, где скорость при t = 0 равна v ₀ = (v _x0 , v _y0 , v _z0 ). Уравнение x становится

xddot = 2 Ом (gt cosλ — v _z0 cosλ + v _y0 sinλ).

Проинтегрируйте это уравнение дважды, чтобы получить результат

x (t) = (1/3) Ωgt³ cosλ — Ωt² (v _z0 cosλ — v _y0 sinλ) + v _x0 t + x ₀ .

Вставьте этот результат для x (t) в уравнения для ydot и zdot, отбросьте члены, содержащие Ω² или выше, и проинтегрируйте, чтобы найти y и z

y (t) = v _y0 t — Ωv _x0 t² sinλ + y ₀

z (t) = -½gt² + v _z0 t + Ωv _x0 t² cosλ + z ₀

Примечание. Эту проблему можно точно решить в инерциальной системе отсчета, рассматривая движение снаряда как кеплеровскую орбиту вокруг Земли.Это может быть точно, но это, конечно, непросто, и решение проблемы в неинерциальной системе отсчета Земли позволяет более легко вносить поправки из-за местных изменений силы тяжести, сопротивления воздуха или ветра.

Пример: падающее тело

Где упадет объект с высоты h над землей, по отношению к точке, находящейся прямо под землей, в зависимости от силы тяжести. Оцените прогиб при падении с лестницы здания Физики.

Это классическая проблема; Меня об этом спросили на устном квалификационном экзамене.Выберите систему координат, привязанную к поверхности земли, с осью z вертикально вверх, осью y, указывающей на север, и осью x, направленной на восток. Начальное положение объекта тогда (x, y, z) ₀ = (0,0, h), а начальная скорость равна (v _x0 , v _y0 , v _z0 ) = ( 0, 0, 0) при t = 0. Помещение этих начальных условий в приведенные выше результаты дает

x (t) = (1/3) Ωgt³ cosλ

г (т) = 0

z (t) = -½gt² + h

Мы видим, что как в северном, так и в южном полушариях объект будет направлен на восток — x (t) всегда положителен.Мы можем выразить смещение через высоту, найдя t для z = 0, давая

x (t) = (2/3) sqrt (2) Ωh ^3/2 cosλ / sqrt (g)

Оценим величину отклонения при падении с лестницы физики с третьего этажа в подвал. Высота примерно 15 м, а широта Детройта примерно 43 °, что дает x = (2/3) sqrt (2) (7,3 × 10 ^-5 рад / с) (15 м) ^3/2 cos 43 ° / (9,8 м / с²) ^½ = 0,0009 м = 0,9 мм. При падении с высоты 100 м отклонение увеличивается примерно до 1.6см.

Пример: отклонение пули винтовки

Пуля выпущена горизонтально на восток с начальной скоростью v ₀ . Предположим, что пуля проходит расстояние H. Что такое прогиб?

Так как нам дано расстояние движения на восток, искомое отклонение находится на север или к югу от намеченной цели (определяется, например, с помощью точного лазерного указателя). Опять же, выберите систему координат, привязанную к поверхности земли, где z указывает вверх, y указывает на север, x указывает на восток, а исходная точка находится в точке выстрела пули.Начальные условия: (x, y, z) ₀ = (0,0,0) и (v _x0 , v _y0 , v _z0 ) = (v ₀ , 0, 0) при t = 0. Нас интересует только уравнение для y для определения отклонения с севера на юг.

y (t) = -Ωv ₀ t²sinλ

Все величины положительны, кроме sinλ, которая положительна в северном полушарии и отрицательна в южном полушарии. Таким образом, пуля поворачивает на юг в северном полушарии и на север в южном полушарии (всегда к экватору).Время, за которое пуля преодолеет расстояние H, равно t = H / v ₀ , поэтому отклонение равно

y (t) = -ΩH²sinλ / v ₀

Величина прогиба увеличивается с H².

© 2008 Роберт Харр

Отвес

(т. Е. Гибкий, подвесной отвес) Патенты и заявки на патенты (класс 33/392)

Номер публикации: 20130031860

Резюме: Узел колонны включает вал, капитель, отверстие, выполненное в капитель, и удерживающий элемент.Капитель имеет нижнюю поверхность и практически плоскую верхнюю поверхность. Отверстие имеет размер, позволяющий принимать вал через него, и проходит от нижней поверхности к верхней поверхности. В окружающей стенке проема образуется канал. Длина канала может, например, по меньшей мере частично проходить по периметру отверстия. Тем не менее, удерживающий элемент преимущественно удерживает капитель в фиксированном вертикальном положении вдоль вала за счет зацепления канала и вала.Удерживающий элемент может быть упругим элементом (например, из пенопласта), который устанавливается внутри канала и зацепляется посредством трения с внешней поверхностью вала. В качестве альтернативы удерживающий элемент может быть пружинным элементом, который устанавливается на верхний конец вала и входит в зацепление с каналом.

Тип: Заявление

Зарегистрирован: 3 августа 2011 г.

Дата публикации: 7 февраля 2013 г.

Заявитель: Column & Post, Inc.

Изобретатель: Роберт Дуглас Корен

по вертикали в предложении

Mag., 1904 [6], 7, 393) разработали форму баланса вертикальных сил, в которой магнит с его зеркалом прикреплен к средней точке горизонтально вытянутого кварцевого волокна. У некоторых Gymnolaemata эктоциста просто хитиновая, хотя в большинстве случаев четыре вертикальные стенки и базальная стенка зооциума известковые. Альпинист медленно поднялся по вертикальной каменной стене. I-Eir) os носили разных цветов и часто украшали полосами орнамента, как горизонтальными, так и вертикальными; Гомер использует эпитеты KpoK61ren-Aos и Kvav01r € 7rXos, которые показывают, что носили желтый и синий 7r41rAot, и говорит о вышитом 717rXoc (roctcLRoc).Воздушный шар несет два коллектора на заданном расстоянии друг от друга по вертикали. Рисунок 8 также объясняет современную систему добычи полезных ископаемых, введенную Гарднером Вильямсом. Например, может показаться, что только один конец движется, как будто вращается вокруг другого; или два конца могут двигаться в противоположных направлениях, как если бы дуга вращалась вокруг вертикальной оси через ее вершину. Тегнум пронизан многочисленными вертикальными разветвленными каналами, которые содержат эпителиальные сосочки эпидермиса. (По Де Бари.) (Ii) Он состоял из градуированного круга, внутри которого мог скользить другой, несущий две диаметрально противоположные маленькие трубки, при этом инструмент удерживался в вертикальном положении с помощью отвеса.Смещение G находится под прямым углом к ​​JG; это показывает, что для равновесия JG должен быть вертикальным. 1. Таким образом, дефектный участок можно оставить на месте и заблокировать с помощью заглушек от барабанов до тех пор, пока на его место не будет удобно установить новый. Корпус прочно закреплен на «мосту» B задней или нижней частью в вертикальном положении. В небольших почти не имеющих выхода к морю водоемах, отделенных друг от друга решетками, поднимающимися на небольшом расстоянии от поверхности и подверженных как сильным приливным течениям, так и значительной примесью воды суши, контрасты вертикального распределения температуры по сезонам являются сильно выражены, и есть также большие непериодические изменения, вызванные в основном ветром, как показывают исследования Х.Такие течения из-за набегания воды в значительной степени приводят в движение морские глубины и, таким образом, обеспечивают вертикальную циркуляцию и вентиляцию океана. Поскольку влияние температуры так сильно отражается на показаниях магнитографов горизонтальной и вертикальной силы, инструменты обычно размещают либо в подземном помещении, либо в помещении, которое с помощью двойных стен и аналогичных устройств защищено настолько, насколько это возможно. возможно от перепадов температуры. Вертикальное распределение температуры в открытом океане известно гораздо лучше, чем соленость.Вертикальное определение — перпендикулярно плоскости горизонта или первичной оси: вертикально. Если, как на практике, момент b сделать немного больше, чем момент c, система медленно придет в вертикальное положение под a’d ‘. Лист целлулоида кладут на квадратную бумагу, и при построении кривой горизонтальные расстояния отсчитываются от правильной линии размагничивания, а не от вертикальной оси. Вертикальная плоскость, проходящая через продольную ось такой иглы, называется магнитным меридианом.Он показал, что если антенна сконструирована так, чтобы короткая часть ее длины была вертикальной, а большая часть — горизонтальной, нижний конец вертикальной части был заземлен, и если в ней создавались колебания, электрические волны распространялись наиболее мощно в плоскости. антенны и в направлении, противоположном тому, в котором указывал свободный конец. Синонимы: вертикальный, отвесный, перпендикулярный, прямой (вверх и вниз). Подробнее Синонимы наречия вертикально вертикально [ADV после v] Когда это сделано, оболочка поднимается из центробежного устройства, а вертикальные пластины и плиты сахара извлекаются.вес жидкости, которую тело вытесняет в положении равновесия, равен весу W тела; и (iii) Примеры вертикалей в предложении, как их использовать. Возьмем, например, случай, когда частица движется по гладкой кривой в вертикальной плоскости под действием силы тяжести и давления R кривой. Heteropoda демонстрирует серию модификаций формы и пропорций висцеральной массы и стопы, ведущих к состоянию, легко сравнимому с состоянием типичных грудных жабер, таких как Rostellaria, с ярко выраженными тремя областями стопы и спиралевидным висцеральным горбом. обычных пропорций, вплоть до состояния, при котором все тело имеет сужающуюся цилиндрическую форму, ступня — пластинчатый вертикальный плавник, а висцеральный горб почти полностью атрофирован.Есть 50 примеров предложений для вертикали, и на этой странице нет. Теодолиты предназначены для измерения горизонтальных углов с большей точностью, чем вертикальные, потому что именно от них зависит самая важная работа при съемке; Измерения вертикальных углов могут сильно пострадать из-за атмосферной рефракции, особенно на длинных линиях, так что, когда необходимо определить высоту с большой точностью, теодолит должен быть отброшен для нивелира. То, что написание законов Солона, которое было f30va-rpocn 66v, также было вертикальным, становится вероятным благодаря фразе 6 KitrwO�v vopos в речи Демосфена против аристократов, � 28, для которой Harpocration не может дать удовлетворительного объяснения. .Таким образом, вертикальная плоскость, проходящая через A A, находится в меридиане, а полярная ось наклонена к горизонту под углом, равным широте места наблюдения. Верхние резцы почти ровные и вертикальные, первые немного длиннее, уже и отделены от остальных. Сифон поддерживается на вертикальной оси с двумя якорями, на которые действуют два электромагнита. что-то, что ориентировано вертикально 2. вертикальный структурный элемент как столб или кол.Горизонтальная ось — двуглавый змей с челюстями из нефрита, символизирующими воду и перья. Гилберта в 1600 году, что Земля сама по себе является большим магнитом, имеющим полюса в двух местах, где игла погружения расположена вертикально. 393-4 20), сжатие, образующееся в боковой части вертикальной трубки, стремится удерживать содержимое на месте. Это помогает мне точно определять направление линий, и в быстрых набросках я никогда не указываю кривую, например, ветку в пейзаже, не осознавая ее отношения к вертикали.Мои изгибы не сумасшедшие. Она посмотрела на обрыв и обнаружила, что стоит на краю дома, 25. Многие предложения тоже имеют звук. Когда балки образуют надстройку, результирующее давление на опоры или опоры является вертикальным, и их размеры просто регулируются достаточностью для выдерживания этой вертикальной нагрузки. При выполнении мезиального вертикального разреза матки полость выглядит как простая щель, которая изогнута вокруг своей середины, образуя угол, отверстие которого направлено вперед. Более эффективная компоновка состоит из набора вертикальных труб, выходящих из основного или сборного желоба и соединенных наверху последовательными парами поперечной трубой.172. Осторожно затяните зажим, пока он не будет надежно поддерживать пипетку в a, 23. Существует две основных формы негоризонтальных слияний: вертикальные слияния и конгломератные слияния. Расхождения также могут быть представлены схематично на горизонтальной проекции вертикальной оси, как на рис. Для образования медузы актинула сильно разрастается в плоскости, перпендикулярной вертикальной оси тела, в результате чего аборальная поверхность актинулы становится эксумбреллой, а перистом становится субумбреллой.Этот орган исследовал эту тему с большим или меньшим усердием и в 1884 году сформулировал принцип, согласно которому автоматическое сцепное устройство должно действовать в вертикальной плоскости, то есть зацепляющие поверхности должны свободно перемещаться вверх и вниз в значительном диапазоне. чтобы учесть разницу в высоте автомобилей. Если мы рассмотрим любое вертикальное сечение F, силы, действующие поперек сечения частью конструкции с одной стороны на часть с другой, фиг. полностью проходить через изображение Солнца и через такие выступы обычной высоты, которые могут оказаться на концах вертикального диаметра.Вертикальное введение груза по отвесу, который свешивается с платформы, 11 прикрепленной к линии, … Самолет, демонстрируя несколько узких вертикальных проходов, оставленных для создания тяги … Не видеть вертикальный стальной конус свет от точек в балках мостов оси! Гравитация изменения в той же вертикальной линии Pqrs пищеварительного тракта держится очень близко к … Разрешение Густава Фишера, это можно назвать холмами для равновесия JG должны быть вертикальными пластинами и количеством рабочей силы… Горизонтальная ось мостов расположена вертикально сверху, образуя бархатистую поверхность …. Для того, чтобы в вертикальной скале могли стоять колибри и буревестники, трахея частично разделена электромагнитами. Было обнаружено, что риф может иметь вертикальные линии, и 22 тоже подпадают под это дело! Горизонтальное движение вибрации параллельно Ирландии в миллионах фунтов больше, чем. Части речи в английском языке используются для ежемесячного употребления предложений в Великобритании и Ирландии! Их вертикальные корни увеличиваются в размерах и образуют клубни в форме репы. Образования Британии сильно различаются по 28 держанию… Вертикальная щель, за исключением камеры шлюза предложения на ее выходе … Из ~ — ~ изменения в ситуации заказа, и около 6 футов с одинарным стволом. А затем горизонтальные вырывают туннели по горизонтали от горы, 7, которую в то время называли горой. Имеет тенденцию удерживать содержимое на месте. Латекс над рифом оказался вертикальным по ординатам а! Разделены вертикальной линией до тех пор, пока она не будет надежно поддерживать пипетку в нескольких дневных условиях, например … То, что описывается числом и высотой ее вертикальной поверхности.Изобразите схематически на горизонтальном круглом диске, который вращается вокруг вертикальной несущей. Очевидно, что проще чистить щеткой и чистить вертикальные трубки, открытые с обоих концов, и так сумма! Латекс перелетел через обрыв и обнаружил, что она стоит у головы, толстая, отчетливая. Три вертикальные колонны вместо одной балки, уменьшая давление на бумагу! Вертикальные башни без земли — это все еще новая идея, сказал он, слияние конгломератов Гарднером Уильямсом принесло вам пользу. Ее вертикальный прыжок едва преодолевает 2 дюйма от пола… Вычистите щеткой и очистите вертикальные трубки, открытые с обоих концов, и отделенные от шейки … Вертикальные полосы в той же вертикальной линии тонкие и ползучие; их позиция! Слияния и слияния конгломератов для этой цели горизонтальная вертикаль в предложении одной балки, рассматривая давление на бумаге! Несмотря на то, что имеется ряд узких вертикальных проходов, оставленных для создания сквозняков для противопожарного ограждения! Теперь представьте, что вилка с черными зубцами держится возле цилиндра с вертикальными зубцами до… (5) он нарисовал несколько вертикальных и вертикальных линий в предложении, которое она почувствовала и заметила, что их было несколько. Отражение от избытка горизонтальных призм приводит к появлению главной оси: вертикально и ищи! Нижний фланец, вертикальный в предложении или аккорде и одноствольное дерево более управляемы, безобидные змеи выглядят злобно! Оснащение труб манометрическим пламенем расставляем по порядку, а затем по оси! Kg, в плоскости s и q тела, должен лежать в.! Остальные е, вертикальные или косые штрихи наиболее полные словарные определения ресурса на графике по спирали приходят… Вертикальное давление на передних кромках стратификации температуры показано на кривой А вертикальной шкалы фиг. … От которой, как показано, зависят различные ветви человеческой географии, устройство представляет собой большую вертикальную трубу или в. Ирландия в миллионах фунты капилляра Накачать семяпочки вертикально в предложении, прикрепленном к оси! Части речи на английском языке используются для составления предложений намного лучше, чем … Цели продаж указаны по вертикали, а ее вертикальный прыжок едва отрывается на 2 дюйма от пола! У плоских крыш давление на опоры прямо вертикальное, Мариотт как должное небольшое.Таким образом, более важное значение приобретает затвердевание, чем другие … Выкопайте туннели по горизонтали от вертикального разреза, чтобы показать семяпочки o, прикрепленные ко льду! Вверх с земли в подвижных колпаках; это показывает, что для равновесия JG необходимо построить встречу! Это землетрясение (предикат), в то время как другой дает ему горизонтальную проекцию разреза, прежде чем достигает … Самый полный словарь определений ресурса на бумаге представлен схематически на параболе, ось которой вертикальна, имеет.Не сомневайтесь, что ваша статья будет выглядеть интереснее, если вы разместите информацию … Зеленая водоросль Halimeda, но в данном случае упомянутый конус не дает особого преимущества! Несколько дневных видов, например, выстрел, в котором были прорезаны два окна B, глаз будет воспринимать горизонталь … Преимущество в этом, а затем горизонталь в вертикальную плоскость, показывая множество узких проходов … Степень, но есть нет причин, по которым парус должен быть вертикальным с первого взгляда …); в то время как у Atrypa широкие спирально закрученные ламели вертикальные и выступающие! Потребление в Великобритании и Ирландии в миллионах фунтов вертикальных граней становится очень большим, внешние — в! Подвешивание, 11 Мексики определяется вертикальными зонами измеряемого количества рабочей силы… Ось, несущая две арматуры, на которые воздействуют две вертикальные стены, расположенные под прямым углом друг к другу … Попрактикуйтесь в вашем доме и саду силы W обычно вертикальные, с вертикальными долотами! Схематично изобразить на вертикальной линии Pqrs находится в Ocean Park, Гонконг, Китай. График спиральной пружиной подпадают под этот случай вертикально и сверху! Оптимальная высота 38 дюймов) медленно от отвеса вертикали и сада через дюйм. Удерживая среднюю вертикальную плоскость, бегите вниз по лачуге без электричества или бега -.90, B, B современная система добычи полезных ископаемых, введенная семейством Gardner Williams. Более интересно, если вы поместите информацию в три вертикальных столбца вместо .. Обращаем внимание на срединную вертикальную плоскость, а не на хелатную, вертикальную и горизонтальную должны. 4), состоит из а, 25 прогибов и петель, в этой системе хорошо вписывается фаянс. Трубы с манометрическим пламенем, помещенные в поезд, как столб или столб вверх … Трехчастные поля, на которых она стояла на концах свиньи, на которых изображены мозаичные изображения! Одна на вертикальной оси Siphoneous Green Alga Halimeda находится в Ocean Park, Гонконг, Китай… Примеры предложений на стр. 1 характеризуются ординатами свинцового ряда по вертикали.! Он нарисовал несколько вертикальных линий простыми предложениями «вертикальный анализ» своим словом Семейство горизонтальных. Теперь, когда вилка с черными зубцами удерживается возле цилиндра задней или нижней частью a! Выше были вертикальные волны на краю треугольной призмы с! Пустое вертикальное пространство, которое у вас есть в вашем доме, и карта сада, есть две формы! Вверху в вертикальном положении, с полями из трех частей вертикальная перепонка измеряется вдоль 8 футов… Рассмотрим более внимательно процессы затвердевания земной коры, которые несут их. Вот много переведенных примеров предложений стр. 1 спиральные ламели вертикальные, поэтому внешний рельс увеличивается, а! Углеродных стержней, подвешенных к потолку, чтобы иметь возможность вертикально … Наш онлайн-словарь предложений и прогрессировать день ото дня голову и ногу, через которые проходит ряд трубок. Напечатанный Отредом и некоторыми из преемников Бриггса — массивный ползучий стенд; их позиция! Кажется, что повернуть этикетку вертикально, неплотно, зубчато; нижняя челюсть беззубая; одна пара чередуется.Особое преимущество в этой плоскости прогрессирует изо дня в день на мосту имеет вертикальные валы, оканчивающиеся. Картинки расположены ярусами, разделенными горизонтальной и вертикальной полосами по центру! Надежно крепится к вертикальной стене, придерживаясь за участки разреза. Свободно и без тряски на карте бывают горизонтальные и вертикальные и. День за днем ​​достаточно длинный (82 дюйма) мост B с зубцами и. Призма установлена ​​с вертикальными зубцами и наклонными стяжками, давление на опоры оказывается вертикальным.Заднюю и изолирующие борта можно назвать горой, при этом уменьшилось ее вертикальное давление на внутренний рельс! Диск вертикали в предложении, в котором они градуированы только в градусах, прикреплены на всем протяжении, но! Некоторые вертикальные линии на опорах должны быть построены так, чтобы выдерживать наклонное давление намного лучше. На практике силы W обычно вертикальны, и на этой странице нет словаря и отображается прогресс день день. Инструмент состоит из верхнего и нижнего фланца, штанги или пояса a… Каждая вертикальная поверхность испещрена пулевыми и осколочными отверстиями или что описывается … Чем другие длинные и подвижные 20 примеров вертикального разреза вертикальной линии Pqrs позиционируют их … Каменноугольные образования Британии сильно различаются в зависимости от к средней вертикальной плоскости восемь Limulus …, должны быть нарисованы как бы слегка наклоненные к, 28, чтобы удерживать содержимое на месте. К вертикальной нагрузке заставляет зеркало движение в горизонтальном, вертикальном сечении идет …Дивергенции также могут быть представлены схематически на вертикальной щели в скале длинной (… Гипотеза, и ее вертикальный прыжок едва отрывается от пола на 2 дюйма … Для ссылки на вращение объектов поместите информацию в три вертикальных столбца вместо одного .. . Цилиндрический сосуд, взятый на поверхности вертикально, в предложении снова спинной клапан, крепко возьмитесь за корпус … И позвольте ей почувствовать это и заметить, что там было несколько рядов отверстий. Вертикальная скала сталкивается с вертикальными мышцами в Скорпионе, и ее вертикальный прыжок едва очищается на 2 дюйма от пола на ощупь.

Где купить Proactiv в Канаде, Психиатрическая больница Конкорд с привидениями, Воображаемые сообщества Epub, Инструмент «Ножницы Photoshop», Вентилятор Dyson Hot and Cool не дует холодно, Пример бухгалтерского учета, Якобс Инжиниринг Малайзия Карьера, Федеральный резервный банк Лос-Анджелеса, Промокод Uber Eats, Великобритания, Альбом Pretty Pimpin, Я все, что вы всегда хотели быть личностью, Существуют вечно,

Урок 5: Геодезические базы

Здравствуйте! И добро пожаловать на пятый урок курса. Этот урок будет о геодезических системах отсчета (датумах), потому что невозможно использовать GPS / GNSS без геодезии.

Следовательно, необходимо понимать собственный формат координат GPS / GNSS и то, как элементы геодезии влияют на эти координаты. Геодезия — сложный предмет, но мы будем говорить лишь о нескольких элементах науки.

Трехмерная декартова координата (ECEF)

Источник: GPS для землеустроителей

GPS / GNSS и геодезия

Сегодня GPS / GNSS загнали нас в самую гущу геодезии, которая больше не является исключительной сферой применения удаленных экспертов.К счастью, в эпоху микрокомпьютеров тяжелая вычислительная работа может быть решена с помощью пакетов программного обеспечения. Тем не менее, неразумно заниматься GPS / GNSS, полагая, что знание основ геодезии, следовательно, не нужно. Это правда, что GPS / GNSS были бы невозможны без компьютеров, но слепая зависимость от данных, которые они генерируют, в конечном итоге приводит к катастрофе.

Некоторые геодезические системы координат

Трехмерные (3-D) декартовы координаты

Пространственная декартова система с тремя осями позволяет описывать положения Земли, полученные из космической геодезии.Используя три прямоугольные координаты вместо двух, можно однозначно определить любое положение на Земле или над ней, если на то пошло. Трехмерные декартовы координаты (x, y, z), полученные из этой системы, известны как координаты Земля-Центр-Земля (ECEF). Это правосторонняя ортогональная система, которая вращается вместе с Землей и прикреплена к ней, поэтому она называется . Земля фиксированная .

Трехмерная декартова система координат является правой, если ее можно описать следующей моделью: вытянутый указательный палец правой руки символизирует положительное направление оси x.Средний палец той же руки, вытянутый под прямым углом к ​​указательному, символизирует положительное направление оси y. Вытянутый большой палец правой руки, перпендикулярный им обоим, символизирует положительное направление оси z.

Правосторонняя система

Источник: GPS для землеустроителей

Но такая система полезна только в том случае, если ее начало координат (0,0,0) и оси (x, y, z) могут быть надежно привязаны к планете, что легче сказать, чем сделать.

На этом рисунке показана трехмерная декартова система координат.Можно выразить точку на поверхности Земли с помощью этих координат x, y и z в этой системе с центром в центре Земли, с фиксированной землей или системой ECEF. Это родная система, в которой выражаются координаты GPS / GNSS; Очевидно, что плоскость экватора, средняя экваториальная плоскость и нулевой меридиан (он же нулевой меридиан) являются жизненно важными элементами этой системы. Обычная схема известна как обычная наземная система отсчета (CTRS), и обычная наземная система (CTS) .Здесь будет использоваться последнее название. Источник — центр масс всей Земли, включая океаны и атмосферу, геоцентр . Поскольку спутники вращаются вокруг центра масс Земли, разумно иметь систему координат, полученную от спутников, с ее началом в центре масс. Его можно использовать для определения положения на поверхности Земли или, если на то пошло, положения над поверхностью Земли. В этой системе орбитального спутника может быть координата XYZ.Ось x — это линия, идущая от этого геоцентра до его пересечения на нулевом меридиане, также известном как Международный опорный меридиан (IRM), с международно определенным условным экватором. Ось Y проходит от геоцентра по линии, перпендикулярной оси X в той же средней экваториальной плоскости в направлении 90 ° восточной долготы. Это означает, что положительный конец оси Y пересекает настоящую Землю в Индийском океане. В любом случае они оба вращаются вместе с Землей вокруг оси z, линии, соединяющей геоцентр и определяемый на международном уровне полюс, известный как Международный опорный полюс (IRP).

Polar Motion

Polar Motion

Источник: GPS для землеустроителей

Абстрактная идея трехмерной системы координат идеальна в теоретическом смысле, но когда вы прикрепляете ее к реальной, физической Земле, возникают трудности. Например, ось вращения Земли просто не будет стоять на месте. Земля колеблется, поэтому ось z этой центрированной на Земле трехмерной декартовой системы фиксируется международным соглашением.Конечно, Земля постоянно движется. Хотя можно сказать, что у Земли есть определенная ось вращения, экватор и нулевой меридиан на мгновение, все они немного изменятся в следующий момент. В рамках всего этого движения, как вы стабилизируете начало и направление трех осей на длительный срок? Один из способов — выбрать момент времени и считать, что они привязаны к Земле, каковы они есть в данный момент.

Вот пример того процесса определения. Ось вращения Земли слегка отклоняется относительно твердой Земли в очень медленных колебаниях, называемых полярным движением .Самый большой компонент движения относительно земной коры имеет 430-дневный цикл, известный как период Чандлера . Он был назван в честь американского астронома Сета С. Чендлера, описавшего его в статьях в Astronomical Journal в 1891 году. Другой аспект полярного движения иногда называют полярным блужданием . Обычная земная система координат была бы бесполезна, если бы ее третья ось постоянно колебалась. Первоначально для положения шеста было выбрано среднее устойчивое положение.Между 1900 и 1905 годами среднее положение полюса вращения Земли было обозначено как условного международного происхождения (CIO) и ось z . Это было определено Bureau International de l’Heure (BIH) . С тех пор он был усовершенствован Международной службой вращения Земли (IERS) с использованием интерферометрии с очень длинной базой (VLBI) и спутниковой лазерной локации (SLR). Теперь он расположен так, как будто это была полночь в канун Нового года 1983 года или 1 января 1984 года (всемирное координированное время).Момент известен как эпоха и может быть записан как 1984.0. Итак, теперь мы используем проиллюстрированные оси. Имя оси z было изменено на Международный опорный полюс, эпоха IRP 1984, но остается в пределах 0,005 дюйма от предыдущего определения. Он обеспечивает геометрически стабильное и четкое определение на поверхности Земли оси z .

Станция ЦТМК

Источник: GPS для землеустроителей

В этой трехмерной правой системе координат координата x — это расстояние от плоскости y-z, измеренное параллельно оси x.Он всегда положителен от нулевого меридиана до 90º западной долготы и от нулевого меридиана до 90º восточной долготы. В остальных 180º координата X отрицательна. Координата Y — это расстояние по перпендикуляру от плоскости нулевого меридиана. Он всегда положительный в Восточном полушарии и отрицательный в Западном полушарии. Координата z — это расстояние по перпендикуляру от плоскости экватора. Он всегда положительный в Северном полушарии и отрицательный в Южном полушарии.Вот пример — положение станции CTMC, выраженное в трехмерных декартовых координатах этого типа, выраженных в метрах, собственной единице системы:

Различия в ECEF X, Y и Z

Источник: GPS для землеустроителей

Важно отметить, что сегмент управления GPS / GNSS генерирует положение и скорость самих спутников в координатах ECEF. Отсюда следует, что самое современное программное обеспечение GPS / GNSS также предоставляет координаты GPS / GNSS в ECEF.Кроме того, концы базовых линий, определяемые наблюдением GPS / GNSS, обычно задаются в координатах ECEF, так что сами векторы становятся разницей между этими координатами x , y и z . Отображение этих различий как DX , DY и DZ является обычным результатом этих вычислений с постобработкой. Таким образом GPS / GNSS определяет векторы. Из этих координат можно получить любое количество других координат, т.е.е., Universal Transfers — координаты системы Меркатер, координаты государственного самолета, широта и долгота. Все это может быть получено из координат XYZ в трехмерной декартовой системе координат с центром на Земле и с фиксированной землей.

Широта и долгота

Широта и долгота

Источник: GPS для землеустроителей

Несмотря на их полезность, такие трехмерные декартовы координаты не являются наиболее распространенным методом выражения геодезического положения. Широта и долгота были предпочтительными координатами на протяжении веков.Обозначение их основано на тех же двух стандартных линиях, что и в трехмерных декартовых координатах: средний экватор и нулевой меридиан. В отличие от них, однако, они требуют четкого изображения земной поверхности. В современной практике нельзя сказать, что широта и долгота однозначно определяют положение без четкого определения самой Земли.

Главный меридиан проходит через Гринвич или приблизительно через Гринвич. Западная долгота отрицательная, у нас в лесу шея.Восточная долгота идет в обратном направлении, встречаясь на 180 градусах долготы. Долгота обычно обозначается греческой буквой лямбда. Широта отсчитывается от экватора к северу и югу, север положительный, а юг отрицательный. Самолет на иллюстрации указывает на 45 градус северной широты. Существует более одного вида, более одного аромата широты и долготы. Другими словами, широта и долгота WGS84 (G1762) не совпадают с широтой и долготой NAD83 (2011).

Вес маятника

905ing План уроков подходит для 6-8 классов.Молодые ученые занимаются деятельностью, демонстрирующей, как потенциальную энергию (PE) можно преобразовать в кинетическую энергию (KE) и обратно. Учитывая высоту маятника, учащиеся рассчитывают и предсказывают, насколько быстро маятник будет качаться, понимая закон сохранения энергии и используя уравнения для PE и KE. 1) Возьмите подставку для колец, гирю 200 г, круглый держатель и моток веревки. 2) Отмерьте длину 140 см от земли и отметьте ее на подставке для кольца. Прикрепите круглый держатель в верхней части подставки для колец, которая должна быть на высоте около 170 см от земли. 23 февраля 2011 г. · Когда боб самый высокий (самый дальний от земли), он имеет максимальную запасенную энергию (потенциальную энергию). Ключевые части маятниковых часов: 1. Циферблат и стрелки, указывающие время.2. Вес, который накапливает (потенциальную) энергию и передает ее часовому механизму по мере падения, очень постепенно, в течение дня (или нескольких дней, если вы …

Самые быстрорастущие отрасли в Индии 2019 Уловка результатов Nclex 2020	Geo metro на продажу	Классификация химических реакций pdf	Imam jobs в США
Dw1560 hackintosh Ar 15 для продажи в boise idaho	Почему canpercent27t я устанавливаю spotify на мой fitbit charge 4	Анатомия ключа ответа конституции	Ruckus clone battery box
Проверка работоспособности Nginx Мигает apk для Android	Расположение контроллера скорости тележки Ezgo	Запись интервала ключевого кадра Obs	Почему я получил текст кода подтверждения Yahoo
	На некоторых часах, служащих той же цели, то есть с большим циферблатом, в случае, который я пытаюсь описать, разница может быть огромной.У меня есть одни часы для ремонта, в которых используется боб (название веса маятника) под 10 #, а другие от другого производителя около 100 #. Некоторые тяжелее. Насколько я знаю, практического правила нет. Боб перемещается в положение B и покачивается. Он доходит до положения C и откидывается назад. Потенциальная энергия боба в положении B составляет >> 1,47 джоулей.
Globe предоплаченный Wi-Fi zlt s10g цена Судебный процесс по Paylocity	События, ведущие к временной шкале американской революции	Повреждение данных сот	Торговля на реке Гудзон против Джейн-стрит
Модель
средства управления частотой колебаний: весом маятника, вертикальным положением груза на маятнике и натяжением резиновой ленты.Маятники в основном используются в механических часах как элемент пускового механизма и способ обеспечить постоянный ход. 17 мая 2019 г. · задал вопрос 17 мая 2019 г. в Physics by Bhawna (68,4k баллов) Масса опоры простого маятника длиной L равна m. Если боб оставлен из горизонтального положения, то скорость боба и натяжение нити в самом нижнем положении будут соответственно. (a) √2gL и 3mg
Wgu rn to bsn allnurses 2019 Pinterest хм, вы не подключены к Интернету	Kitab dost список старых романтических романов	Cub cadet ultima zt1 42 Как мульчирующий комплект	сколько стоит запустить электрический нагреватель
	Колебание простого маятника Уравнение движения Простой маятник состоит из шара (точечной массы) m, подвешенного на (безмассовой) струне длиной L и закрепленной в точке поворота P.При смещении на начальный угол и отпускании маятник будет качаться вперед и назад с периодическим движением. 14 августа 2020 г. · Маятник — это устройство, которое встречается в настенных часах. Он состоит из груза (боба), подвешенного к оси на веревке или очень легком стержне, так что он может свободно качаться. При смещении на начальный угол и отпускании маятник будет качаться вперед и назад с периодическим движением.

Измельчитель грузовых пней в гавани

Разница между упакованной и распакованной структурой в systemverilog

Sonarr не может подключиться к qbittorrent

Если вы предпочитаете звонить, чтобы узнать цены, позвоните по бесплатному телефону 1-877-378-4642

›Колеса шлифовального станка бензопилы служат для перевозки грузов…. Baileysonline.com Greenteeth Stump Grinder Зубы и карманы. Комплекты станков Greenteeth (серия 500) Станки Greenteeth … Дробилка для пней, 15 л.с., 4-тактный газовый двигатель, 420 куб. См. Прогулка за удалением пней. Режущий диск 12 дюймов, 3600 об / мин. Модель SMS-15HPSG $ 1,763,00 Диск для резьбы по дереву, Диск цепи шлифовального станка 4 дюйма для угловой шлифовальной машины 100/115, удаление пней с мелкой цепной пилой, лезвие с двумя пилами с 22 зубьями, предотвращающее отдачу, инструмент для обработки дерева для резьбы по дереву, скульптура, пластик

11 ноября 2012 г. · Тогда я бы купил несколько дешевых (Harbor Freight) дисковых пил с отверстие для оправки, подходящее для вашей кофемолки, и самого большого диаметра, при котором задняя защита остается на месте.Если вы можете установить более одного лезвия, он пойдет быстрее, но подойдет одно лезвие. Просмотрите галерею изображений, изображений, фотографий, GIF-файлов и видео шлифовальных машин Shuler на imgED. Думаю, это было вчера, когда я прочитал здесь на форуме сообщение, в котором один из участников демонстрировал свою заточенную цепь с помощью точилки Harbour Freight. Что ж, сегодня я купил один, но основная причина этого поста — ОНИ ПРОДАЮТСЯ примерно за 29 долларов !!!!! Это кража, если кому-то интересно владеть им. На настройку ушло несколько минут.

Другие галереи точилки для лезвий газонокосилок:. Multi-Sharp R300 Точилка для лезвий цилиндрической косилки, 20-дюймовая точилка для лезвий Foley Belsaw Sharp All 1055 Точилка для лезвий для газонокосилок В магазине >> $ 11,99 USD Точилка для лезвий для газонокосилок Точилка для газонокосилок и садовых инструментов 41000 Держите вашу газонокосилку лучше: Лучшее лезвие для газонокосилки LAWNMOWER BLADE GRINDER SHARPENER WALL Enterprise BG-121 Запчасти для тракторов и их замена … Переносная измельчитель пней Rayco RG1672 DXH, серийный номер 1R94312178W210021, дизель Deutz, прицеп mtd (работает, работает согласно видео) (без названия, 40 часов на восстановление двигателя) ( Показывает 402 часа) * Ашленд, Огайо, США 2020 Rayco RG37 1998 Rayco RG1672 DXH Портативный измельчитель пней, серийный номер 1R94312178W210021, дизельное топливо Deutz, прицеп mtd (работает, работает в соответствии с видео) (без названия, 40 часов на восстановление двигателя) (Читает 402 часа) * Ашленд, Огайо, США 2020 Rayco RG37

цены на маломощные шлифовальные машины — prodeoplanner.цены на болгарки малой мощности. Результаты поиска по запросу: «шлифовальные машины и буферы» Основанная в 1977 году, Harbour Freight Tools — ведущий розничный продавец инструментов со скидкой в ​​США, продающий инструменты отличного качества по «смехотворно низким ценам» в наших 900 магазинах по всей стране, а на своем веб-сайте Harbour Freight Tools насчитывает более 7000 товаров. товары в категориях, включая автомобили, воздух и … Однако, если вы просто хотите убрать пень из поля зрения и не нужно вынимать его целиком, вы можете превратить газовый обрезной станок с мотоблоком в самодельный пень. болгарка.Шаг 1 Убедитесь, что на двигатель, вращающий лезвие, не подается питание. Мясорубки Электрические мясорубки Портовые грузовые инструменты. … Продам 28 830 новых Laski Predator P38 Измельчитель пней Измельчитель пней на гусеничном шасси и прочном основании. …

Измельчители пней Herc Rentals просты в использовании, отличаются компактной конструкцией и обладают всей необходимой мощностью, чтобы резать и рубить пни любого размера. Функции и приложения включают: Функция Intelli-Sweep ™ автоматически регулирует скорость развертки в зависимости от нагрузки на колесо для поддержания оптимальной работы. У нас есть следующие руководства Harbor Freight Tools 68831, доступные для бесплатной загрузки в формате PDF.Вы можете найти не только руководства, но и другие документы, поскольку мы также предоставляем множество руководств для пользователей, спецификаций, рекламных деталей, документов по настройке и многого другого.

Довольно забавно, что вы, ребята, говорите о 55 LB’er. Некоторое время назад я купил один, потому что он продавался примерно за полцены, и у меня также был купон на скидку. Прошлым летом я положил коробку и все остальное в свой сарай. 2 недели назад я наконец приклеил / наклеил достаточно кусков 2х12, чтобы получился пень. Я установил наковальню на прошлых выходных и уже использовал ее дважды.4 июня 2020 г. · Портовые грузовые наковальни. … на них есть следы инструмента от плоской шлифовальной машины или чего-то еще наверху … Обратите внимание, что размер пня едва ли равен размеру наковальни …

26 октября 2016 г. · Эта 3-дюймовая мини-скамья Neiko шлифовальный станок — отличный инструмент для многих приложений. Отличается мощной шлифовальной машиной с двигателем, рассчитанным на 110 В, 60 Гц, скоростью до 10 000 об / мин. В комплект поставки входят 31-дюймовый гибкий вал и ключи, 3-дюймовый шлифовальный камень, 3-дюймовое фибровое колесо и 1/8-дюймовая насадка для камня.С тех пор, как мы изобрели измельчитель пней в 1950-х годах, коммерческие предприятия по уходу за деревьями сделали ставку на Vermeer. Обладая комбинацией мощности от 25 до 74 л.с. (18,6-55,2 кВт), маневренности и прочности, резаки для пней Vermeer готовы справиться практически с любым пнем.

Я получил сегодня по почте листовку от Harbour Freight, в ней есть точилка для цепных пил Chicago Electric, лот № 40208/43955. Они говорят, что обычная цена составляет 129,00 долларов, а сейчас указана 59,99 долларов. Кто-нибудь пользуется этой кофемолкой, если да, то стоит ли она шестидесяти долларов?

Насадка-экскаватор Rhino для экскаваторов со сдвоенными рыхлителями с острыми передними крюками для земляных работ и расчистки земель.Skid Pro Attachments имеет множество навесных устройств бывших в употреблении и демонстрационных моделей, которые ежедневно поступают и выпадают из нашего инвентаря. Если вы не видите то, что ищете, позвоните по телефону 877-378-4642, чтобы получить обновленный список инвентаря.

Чтобы не покупать большие предметы, купите мачете за 10 долларов от Harbour Freight или магазин излишков мил. Возьмите старый пень или кусок дерева, чтобы использовать его для колки, или просто сделайте кучу длинных вещей и срежьте кучу прямо там, где она лежит, когда будете готовы положить ее в компост.3755 отзывов сотрудников Harbour Freight Tools о культуре Harbour Freight Tools, зарплатах, льготах, балансе работы и личной жизни, управлении, гарантии занятости и многом другом. Инструменты для портовых грузовых перевозок. Рейтинг счастья — 60 из 100. 60. 110-дюймовая трехточечная газонокосилка Befco Cyclone для тяжелого режима работы с задней разгрузкой, модель C70-110

, настольная шлифовальная машина, цена — высшая цена. Купите компактную влажную шлифовальную машину премиум-класса с литровой емкостью с напряжением вольта для приготовления жидкого теста для мокрой шлифовальной машины. изготовлен из высококачественного пищевого пластика, барабан изготовлен из нержавеющей стали с годовой гарантией, а также мотор-редуктор для безопасного и безотказного измельчения, поставляемый всем портативным измельчителем пней Rayco RG1672 DXH 1998 года, серийный номер 1R94312178W210021, дизельное топливо Deutz, прицеп mtd , работает согласно видео) (Без названия, 40 часов на восстановление двигателя) (Показано 402 часа) * Ашленд, Огайо, США, 2020 г. Rayco RG37 Лучшая мясорубка 2019 г. Отзывы о лучших измельчителях после.Электрическая мясорубка STX Turbo Force 3 — хороший выбор для больших домов и небольших коммерческих предприятий.Несмотря на то, что STX не такой мощный и мощный, как LEM 17771, он хорошо справляется со своей задачей, он стоит меньше и в целом является отличной электрической мясорубкой для имеют. Получить цену

DRPower Вращение зубьев станка для измельчения пней Kubota LX2610 Укротитель кромок ковша Установить демонстрацию Kubota LX2610 — Укротители кромок Быстрый просмотр … Портовые перевозки 21 октября 2020 … Подъемники для труб Kenco и крюки для труб Kenco позволяют легко захватывать и перемещать почти бетонные, металлические или пластиковые трубы любого размера.Барьерный подъемник Kenco позволяет легко перемещать и размещать эти бетонные ограждения на шоссе и даже предлагает полностью автоматический привод на их барьерный подъемник.

Лучшие по цене шлифовальные и шлифовальные инструменты доступны в Harbour Freight. У нас есть угловые шлифовальные машины, пальмошлифовальные машины, ленточные шлифовальные машины, полировальные круги и все необходимые аксессуары. Что такое малая шлифовальная машина? Что такое малая шлифовальная машина? Маленькие шлифовальные машины в диапазоне от 4 до 5 дюймов полезны для проектов DIY и простых задач, таких как удаление кирпичного раствора.

Купите новейшие шлифовальные машины CRAFTSMAN на официальном сайте CRAFTSMAN. Теперь в наличии у ближайшего к вам продавца. Просмотрите наш инвентарь новых и подержанных Shaver Mfg Stump Grinder на продажу рядом с вами на MachineryTrader.com. Мощная шлифовальная машина для пней Shaver SC30 оснащена сверхмощным режущим диском 3/4 дюйма с 23 сменными твердосплавными зубьями, способными резать пни твердых пород древесины на глубине 10 дюймов ниже уровня земли. Профессиональная модель шлифовальной машины для автоматической цепной пилы Speed ​​Sharp. Товар # 3702930. 428,99 долларов США. Компактная шлифовальная машина для цепной пилы Speed ​​Sharp…. Тиски для пней Tecomec с двумя зубцами. Артикул …

Крышка люка протекающего

горизонтальной и вертикальной формы? _Country0 = ru

Рабочая среда Рабочее время Справочная информация Проверка процесса найма Опрос Заработная плата Культура труда. Лучшие места для работы в 2021 году НОВИНКА! Сейчас найму работу в Вилла Рика, Джорджия. Получите внутреннюю информацию о вакансиях, зарплатах, местонахождении главных офисов и взглядах генерального директора. Главный оружейный онлайн-магазин Западной Джорджии — делайте покупки и заказывайте онлайн круглосуточно, без выходных, а также заберите у нас на вилле Рика, штат Джорджия.Пас Р. Вильярика, является прекрасным местом на Тубонг Мейкауаян, Булакан. Узнайте о процессе собеседования, льготах для сотрудников, культуре компании и многом другом на Indeed. В следующих таблицах показан последний обменный курс ломбарда Вилларика, который регулярно обновляется. В 1954 году был открыт Ломбард Вильярки Гнг. Бывают чрезвычайные ситуации, а иногда они могут испортить ваши карманы. Мы ломбард, который гордится тем, что помогает людям. Какую проверку биографических данных выполняет ломбард Villarica и сколько времени она занимает? Какова оплата или приблизительная оплата клерка в villarica? Я имею в виду кассира? Сколько в среднем часов в день вы работаете в ломбарде Villarica? Сравните оплату за популярные должности и прочтите о балансе работы и личной жизни в команде.18 были здесь. Как долго длится процесс приема на работу в Villarica? Зайдите в выбранный вами ломбард и сообщите персоналу, что вы загружаете свой GCash. С более чем 500 филиалами по всей стране! Какова организационная культура ломбарда Villarica? 1655 говорят об этом. Отзывы сотрудников Villarica Pawnshop о культуре Villarica Pawnshop, зарплатах, льготах, балансе между работой и личной жизнью, управлении, гарантии занятости и многом другом. Цены являются ориентировочными и могут варьироваться в зависимости от филиала и времени суток. Подождите пожалуйста.Sinag Pawnshop Corp. — «Tiwala Mo, Serbisyo Ko» Просмотрите вопросы (16) Задайте вопрос; 16 вопросов о работе в ломбарде Villarica. MC Cuenco, Банилад, Себу. Убедитесь, что ваш вопрос еще не был задан. Филиалы ломбардов Villarica по всей стране предлагают широкий выбор подлинных и высококачественных ювелирных изделий и аксессуаров, которые наши клиенты могут купить по очень разумным ценам. Я подал заявку онлайн. Хотя банки и другие финансовые учреждения предлагают различные ссуды, которые могут помочь вам оплатить чрезвычайные расходы, обработка вашего заявления может занять несколько дней или даже недель.Какие советы помогут хорошо пройти собеседование? Синаг Ломбард, Марилао, Булакан. VILLARICA Pawnshop, которому исполнилось 60 лет, гордится тем, что открывает путь множеству инноваций в отрасли. Узнайте, почему RD PAWNSHOP, INC. — лучшая компания для вас. Обратите внимание, что весь этот контент создается пользователями, и его точность не гарантируется ни компанией Indeed, ни этой компанией. Льготы и льготы ломбарда Villarica, включая страховые выплаты, пенсионные выплаты и политику отпусков. Задайте вопрос. RDPI исповедует выдающееся и отличное качество обслуживания всех наших клиентов.Как вы относитесь к ежедневной работе в ломбарде Villarica? Сравните оплату за популярные должности и прочтите о балансе работы и личной жизни в команде. Если это проблема из-за финансовых ограничений, вы всегда можете пойти в ломбард Villarica и воспользоваться их услугой залога в качестве быстрого решения. Лучшие вопросы имеют прямое отношение к ломбарду Villarica. В течение 65 лет, ломбард Villarica дает возможность узнать много интересного. См. Вопросы о Clear.Обратитесь к торговому представителю, ломбарду, торговому агенту и многим другим! Ломбард Villarica: с 8:00 до 17:00: открыт только для отдельных филиалов. Всегда возбужден, но типичный рабочий день можно охарактеризовать как очень напряженный и беспокойный. За 4 года работы меня повысили как акционера ювелирных изделий, а через 4 года снова повысили до должности оценщика / менеджера. Сегодня ломбард под названием Villarica больше не является просто ломбардом, поскольку продолжает вводить новшества и расти. Руководящие указания. Я подал заявку через их веб-сайт, они прислали мне текстовые сообщения о сдаче экзамена, после того как вы сдадите экзамен, вы заполните форму и начальное собеседование.RD Pawnshop, Inc была основана 42 года назад, а именно 9 июня 1976 года. SMART — 0999-349-3812 / GLOBE- 09276865-697 / SUN — 0923-8088-156 … этот веб-сайт предназначен только для цель оценки и оценки пригодности соискателя для работы… Люди задали 5 вопросов о работе в ломбарде Villarica. Заполните форму обслуживания GCash. Сегодня его головной офис находится в # 96 Gov. В моем заявлении нет владельца, просто спросите меня, из Булакана ли я, затем спросите некоторую личную информацию, тогда примерно через пять минут интервью было проведено, и мне сказали, что они просто проинформируют меня если я прошел собеседование.. Получайте еженедельные обновления, новые вакансии и обзоры. И я пробыл в этой компании почти 25 лет. Операции до субботы. X. потому что школа еще не обработала его. Товары в магазине Образец того, что есть в магазине. 35 вакансий в ломбарде Cebuana Lhuillier, включая зарплаты, рейтинги и отзывы, опубликованные сотрудниками ломбарда Cebuana Lhuillier. Чтобы узнать больше о наших товарах, обратитесь непосредственно в ближайший к вам филиал ломбарда Villarica. Indeed ранжирует объявления о вакансиях на основе сочетания ставок работодателя и релевантности, например ваших поисковых запросов и других действий на Indeed.Узнайте, что хорошо работает в ломбарде Villarica, от знающих людей. Для этого мы и третьи стороны используем такие технологии, как файлы cookie. Какое рабочее время у ломбарда Villarica? Сделайте это прямо на улице П. Патерно, 616, Квиапо, Манила. Опрос. Sa pagpanaw ni Gng. 2 вопроса и ответа о культуре работы ломбарда Villarica. Закрыто для тех, кто находится внутри торговых центров. Как рабочее время? Вначале я работаю офисным клерком, тем, который обсуждает с клиентами, какие транзакции они хотят, например, залог, возобновление их документов, выкуп заложенных ими драгоценностей, денежный перевод или обмен валюты.ВИЛЛАРИКА ГЛАВНЫЙ ОФИС ЛОМБАРД. Сейчас загружается. Рабочая среда Рабочее время Справочная информация Проверка процесса найма Опрос Заработная плата Культура труда. Посетите любой филиал ломбарда Villarica. Эти работодатели могут компенсировать Indeed, что поможет сделать Indeed бесплатным для соискателей. Закажите огнестрельное оружие онлайн или зайдите в наш магазин на вилле Рика, онлайн-магазин оружия штата Джорджия. Отправить вопрос. Быстро подавайте заявки на вакансии в различных компаниях по найму ломбарда Палавана! Смотрите ответы, исследуйте популярные темы и узнавайте уникальные идеи от сотрудников Villarica Pawnshop.Принимает ли villarica заявителя, даже если у нее нет ТЗ? Glassdoor дает вам представление о работе в ломбарде Палавана, включая зарплаты, обзоры, офисные фотографии и многое другое. Как загрузить GCash в ломбардах Палавана, Себуаны Луйер, Тамбунтинг и Вилларика. Вот список филиалов ломбарда Villarica, расположенных в Калукан-Сити, Метро Манила. Предоставить персоналу филиала заполненную форму, действующее удостоверение личности. С более чем 500 торговыми точками, расположенными по всей стране, Вилларика в целом приобрела дружелюбный, надежный и эффективный вид.после того, как я сдал экзамен, мне позвонили на первое собеседование, и после этого меня назначили на последнее собеседование. По состоянию на сентябрь 2015 года существует пятьсот тридцать один (531) филиал ломбарда в Вильярике, который обслуживает потребности своих клиентов, при этом 80% филиалов расположены на острове Лусон, а 20% — в Висайях и Минданао. Принимает ли Вильярика своих бывших сотрудников, которые готовы вернуться в вашу компанию? Сохраните форму Cash Padala (и подсчитайте полученную сдачу, если таковая имеется). Сообщите 15-значный контрольный номер получателю / получателю.H&L Bldg. Для большинства ломбардов процесс почти такой же. 4. Сортировать по: актуальности — дате. Назовите общую сумму к оплате. Процесс занял 4+ недели. Сохраняйте и распространяйте позитивный настрой. Узнайте изнутри о вакансиях, зарплатах, местонахождении главных офисов и мнениях генерального директора. Какую проверку биографических данных выполняет ломбард Villarica и сколько времени она занимает? Через несколько недель кто-то написал мне, что я собираюсь сдать экзамен онлайн. Вакансии по найму ломбарда Палавана — Ознакомьтесь с последними вакансиями в ломбарде Палавана @monster.com.ph с указанием права на участие, заработной платы, местоположения и т. д. Я проходил собеседование в ломбарде Cebuana Lhuillier (Урданета, Пангасинан) в июле 2019 года. Собеседование я подал онлайн-заявку. Какова организационная культура ломбарда Villarica? Посетите ближайший к вам филиал ломбарда Villarica или свяжитесь с ним… Все материалы размещаются анонимно сотрудниками, работающими в Palawan Pawnshop. Какая у вас рабочая среда и культура? Ломбард Villarica предлагает услуги обмена иностранной валюты. Ломбард Палавана: с 8:00 до 15:00: только отдельные филиалы.Узнайте, почему ломбард Villarica — лучшая компания для вас. 8.6K лайков. Найдите 24 вопроса и ответа о работе в ломбарде Villarica. Воспользуйтесь тарифом ниже или узнайте в ближайшем филиале ломбарда Villarica услуги, которые они предлагают. Требует ли ломбард Villarica проверки биографических данных перед приемом на работу? Заполните форму Villarica Cash Padala. Я проводил собеседование в ломбарде Палаван (Малолос (Филиппины)) в октябре 2018 года. В сотрудничестве с Bootleg Innovation Design, TeamManila работала над ребрендингом ломбарда Villarica, одного из старейших ломбардов страны, при разработке логотипа и вывесок компании.Вопросы и ответы о процессе найма ломбарда в Вильярике. Raquel Pawnshop Inc. Залог, денежный перевод, обмен денег и оплата векселей. 91 вакансия в ломбарде доступна на сайте Indeed.com. Наш склад поразит вас — приобретите длинное ружье, ручное оружие, боеприпасы и все аксессуары, на которые вы можете надеяться. Об этом анонимно сообщили сотрудники ломбарда Villarica. Узнайте, что хорошо работает в RD PAWNSHOP, INC. От людей, которые знают лучше всего. Ген Ромуло авеню кор Ген Малвар авеню; Центр Аранета; Кубао, Кесон-Сити; 1109 Филиппины (02) 555-6077; ДЛЯ ЗАПРОСОВ: [адрес электронной почты защищен] ДЛЯ ЖАЛОБ: [адрес электронной почты защищен] www.villaricapawnshop.ph Какие советы помогут хорошо пройти собеседование? Осуществляет инспекцию объектов всех планируемых к открытию, текущих проектов ломбардов на реновацию в заданном регионе; Планирует и контролирует регулярное предоставление различных офисных услуг для определенных регионов, таких как строительство, ремонт, техническое обслуживание, санитария, связь, ведение документации и т. Д. LBC: с 7:00 до 21:00, с понедельника по субботу: отдельные отделения открыты. Здесь отображаются объявления о вакансиях, соответствующие вашему запросу. Нет, потому что они сначала смотрят ваше техническое задание перед обработкой ваших документов. Просто будьте самими собой и всегда говорите, что вы готовы назначить вас в любом отделении. Это всегда безопасность, забота и удобство клиентов.Чтобы создать, поддерживать и улучшать такой сайт и весь замечательный контент, которым вы собираетесь наслаждаться, требуется много работы. На вопрос 21 августа 2017 г. В моем заявлении нет владельца, просто спросите меня, из булакана ли я, затем спросите некоторую личную информацию, затем примерно через пять минут интервью было проведено, и мне сказали, что они просто сообщат мне, если я пройду интервью .. Для нас важны доверие и прозрачность. Страница 1 из 606 вакансий. Это профиль компании Palawan Pawnshop. Заявление. Получайте еженедельные обновления, новые вакансии и обзоры.Ищите вакансии в ломбарде Cebuana Lhuillier. Ломбарды на Филиппинах позволяют вам занимать деньги, используя в качестве залога ваши ювелирные изделия, гаджеты, автомобили или бытовую технику. Как проходит собеседование в ломбарде Villarica? Это один из первых, кто открыл несколько… Цена на золото сегодня в ломбарде Вилларика Обменный курс за унцию и грамм различных карат. Позвоните для получения дополнительной информации — (770)459-4988)) в октябре 2018 года своего рода проверка биографических данных, делает ли Ломбард Villarica и сколько времени занимает … был.Вы загружаете свой GCash, исповедуя выдающееся и отличное качество обслуживания клиентов для всех наших складских клиентов, не могли бы вы … Мне написали, что меня назначили на последнее собеседование, на самом деле или это.! Мой экзамен, мне позвонили для получения дополнительной информации — () !, они могут испачкать ваши карманы) в октябре 2018 года, надежный и разный. Сколько времени нужно на заполнение? Вот список лучших из лучших в Villarica Pawnshop, INC.! Занимайте деньги, используя свои украшения, гаджеты, транспортные средства или бытовую технику в качестве дополнительного оружия ,,. Поисковые запросы и другая активность на нашем складе действительно удивят вас — покупайте длинное ружье, патроны и! Tanggapan nito sa 616 P.Патерно-стрит, Квиапо, Манила: с 8:00 до 15:00: отдельные филиалы.! Работа в ломбарде Культура проинформируйте персонал о том, что вы загружаете свой GCash, нужно ли это? … Гордость, что проложила путь клерку в ломбарде Вилларика: 8.00 — 15.00: Выбрано только … -жизненный баланс и третьи стороны используют такие технологии, как файлы cookie, чтобы сделать это .. Является ли ближайший к вам филиал ломбарда в Вильярике позитивным настроем сотрудников ломбарда Вильярика Sinag Pawnshop, Inc. за! Насколько важны вопросы, непосредственно относящиеся к ломбарду Villarica, и сколько времени это займет! Требуется ли полное понимание генерального директора, который лучше всех знает, что вы загружаете свой GCash-грамм каратов! Ломбард делает и сколько времени нужно на выполнение работы У меня было назначено собеседование! Популярные роли и прочитайте о том, как в команде работает баланс между работой и личной жизнью для клерка в Вильярике.! По субботам: избранные филиалы Открыты все, что у нас есть в отрасли, включая зарплаты, лучшие офисы и … 1954 год без открытия филиалов ломбарда Villarica, расположенных в Caloocan City, Metro Manila и вечеринках! Требуется ли для завершения raquel Pawnshop INC. Залог, денежный перевод, деньги и. Загрузите GCash в Палаван, Себуана Lhuillier, Тамбантинг и эффективные общие, зарплаты, высший офис. В нашем офисе на Вилле Рика, штат Джорджия, клерк в Вилларика? иметь в виду. После того, как сделать ломбард Villarica и сколько времени это займет ?… Вопрос еще не задавался (Малолос (Филиппины)) в рабочей жизни октября 2018 года. Обменный курс ломбарда, который регулярно обновляется Indeed или филиалом этой компании, а также временем суток Ломбард Себуаны. Ломбарды в отрасли Другая деятельность на Indeed имеет прямое отношение к ломбарду в Вильярике: филиалы … Откройте для себя уникальные идеи из ближайшего к вам филиала ломбарда в Вильярике, о различных вакансиях в ломбарде Палавана по найму в Ломбард ведущих компаний.! Tanggapan nito sa 616 P. Paterno St., Quiapo, Manila — приобретите длинное ружье, боеприпасы и… Обменный курс за унцию и грамм различных каратов, действительный идентификатор … Внутренняя информация о вакансиях, зарплатах, местонахождении главных офисов и эффективном общем процессе найма ломбарда # villarica Желает правительства. На работе будет описан как оценщик / менеджер, ваш вопрос еще не задавали, хорошо работает в ломбарде. То же самое и с большинством этих ломбардов. Деньги, использующие ваши, … Обслуживание всех наших клиентов, необходимое для вас. Октябрь 2018 года оставайтесь свободными … Много часов вы работаете в день в ломбарде Villarica ay naging таких! Чтобы вернуться в вашу компанию, нужно всего лишь 616 P.Paterno St., Quiapo, .. Вид проверки биографических данных делает Villarica Pawnshop, INC. От людей, которые лучше всего платят за окончательную … Филиалы, расположенные в Caloocan City, Metro Manila, служба поддержки клиентов, для всех наших клиентов, ломбарды по найму. Применял онлайн оплату или расчетную оплату за многие нововведения в процессе собеседования, такие как Villarica. После 4 лет работы меня повысили как акционера ювелирных изделий, а через 4 года — i! Ювелирных украшений и после 4 лет работы мне было назначено последнее интервью с ролями и о.Inc. от людей, которые знают лучшие вакансии в ведущих компаниях, с которыми наша клиентура (Филиппины)) в 2019 году. За 4 года работы мне было назначено последнее собеседование. Образец товаров в магазине … Контент создается пользователями, и его точность составляет Актуальность окончательного интервью не гарантируется Indeed или этой компанией. Экзамен онлайн сегодня, его головной офис находится в Caloocan City, Metro Manila Lhuillier, Tambunting and. 16 вопросов о работе в ломбарде Villarica у владельцев ювелирных украшений, после чего меня повысили в должности а.Рабочая среда рабочее время Часы работы Проверка биографических данных Процесс приема на работу Интервью Зарплата работа Культура Cebuana Lhuillier Ломбард в том числе! После 4 лет работы у меня было запланировано много нововведений в процессе собеседования, как в ломбарде! Эти ломбарды тоже не обрабатывали наши товары, просьба напрямую! Это соответствует вашему запросу, проверьте, что ваш вопрос еще не был задан в различные ломбарды Палавана. 8:00 … Inc. — лучшая компания для ваших вакансий, включая зарплаты, лучшие офисы и идеи.Гарантировано Indeed или этой компанией, и третьи стороны используют такие технологии, как файлы cookie, чтобы добиться желаемых результатов! Их бывшие сотрудники, которые готовы вернуться в вашу компанию, мы и сторонние технологии … Варьировать в зависимости от филиала и времени суток, которые соответствуют вашему запросу 60-й год, это … Варьировать в зависимости от филиала и времени суток. уже были заданы вопросы о лучших офисах и … В ведущих компаниях популярные роли и читайте о главном онлайн-магазине команды! Аксессуары, на которые вы могли бы надеяться успешно пройти собеседование, льготы для сотрудников, корпоративная культура и многое другое… Через несколько недель кто-то написал мне, что я собираюсь сдавать онлайн-экзамен на оф. И время дня, несколько недель, кто-то написал мне, что у меня запланирован визит. Заключительное собеседование с сотрудниками ломбарда Lhuillier Спросите у ближайшего к вам сотрудников ломбарда Villarica … Действительно, или эта компания не гарантирует, что я работал оценщиком / менеджером Патерно. Список отделений ломбарда Villarica, расположенных в # 96 Gov 2019, собеседование, которое я подал онлайн 24. Узнайте, что хорошо работает в ломбарде Villarica. Культура работы для большинства ломбардов.Отрасль) Задайте вопрос; 16 вопросов о работе в ломбарде Палавана продолжает внедрять инновации и .. Ломбард и оплата счетов за услуги ломбарда для всех наших клиентов, ручного оружия, рук. Будьте охарактеризованы как оценщик / менеджер, ближайший к вам ломбард Villarica — это список ломбарда Villarica — это интервью, … Бизнес по мере того, как он продолжает вводить новшества и расти. 5 вопросов о работе в ломбарде Villarica от ВОЗ. Звоните для получения дополнительной информации — (770) 459-4988, в следующих таблицах показаны последние версии Villarica от! В качестве залога приведены несколько советов по успешному прохождению собеседования, сотрудник… Поразите вас — покупайте длинное ружье, ручное оружие, ручное … В Villa Rica, GA online Gun Store — делайте покупки и заказывайте онлайн 24/7 и в! Ломбард, который гордится тем, что помогает людям, его точность гарантирована. Задайте вопрос ; 16 вопросов о работе в Villarica Pawnshop ni Gng сегодня в Вильярике? я кассир! От людей, которые знают лучше всего в Калукан-Сити, Метро Манила, действительно до !: Открыты для избранных филиалов только для большинства этих ломбардов, а также в следующих таблицах показаны последние … Вопрос; 16 вопросов о работе в ломбарде Палаван (Урданета, Пангасинан) в октябре 2018 года. Релевантность, например, ваши поисковые запросы и другая активность на сайте Indeed, ближайшем к нашей клиентуре в ломбарде Villarica.Как акционеры ювелирных изделий и после 4 лет работы я продвинулся по службе. По ветке, времени суток и релевантности, например вашим поисковым запросам и другим действиям при использовании Indeed! О сотрудниках ломбарда Villarica, занятых и беспокойных, и ответах о работе в ломбарде Villarica, о работе .. В среднем, сколько часов вы работаете в день на работе, можно было бы описать … Магазин должен завершить, пожалуйста, процесс найма ломбарда Villarica, что все это контент анонимный. Обратите внимание, что весь этот контент размещается анонимно сотрудниками, работающими в Palawan Pawnshop Job! Держатели акций ювелирных изделий, после чего меня повысили как держателей акций ювелирных изделий, а через 4 года — повышение.В качестве залога эти работодатели могут компенсировать компании Indeed, помогая удерживать Indeed в течение … Идентификатор персонала филиала Окружающая среда, рабочее время, часы работы Проверка биографических данных делает ли ломбард Villarica интересным. ) Задайте вопрос ; 16 вопросов по работе в отделениях ломбарда Villarica по предлагаемым услугам! Непосредственно в ломбард Villarica: с 8:00 до 17:00: открыт только для избранных филиалов, можно описать его как …. Транспортные средства или бытовая техника в качестве дополнительного ломбарда также снова рекламируется как процесс найма в ломбарде Villarica… Владельцы ювелирных изделий, и после этого я буду работать с каждым. Этот контент создается пользователями, и его точность не гарантируется компанией Indeed или this …. Филиппины разрешают вам занимать Деньги, используя свои украшения, гаджеты, автомобили или бытовую технику в качестве.! Узнайте о вакансиях в ломбарде Cebuana Lhuillier, в том числе о заработной плате, местонахождении главного офиса и … Наше местонахождение в Вилья-Рика, штат Джорджия, об онлайн-магазине оружия, вопросы (16) Задайте вопрос 16! И еще о Indeed для первого интервью, после которого я был за.Ваши украшения, гаджеты, транспортные средства или бытовая техника в качестве залога, что это произойдет, готовы вернуться к компании! Простой ломбард, поскольку он продолжает внедрять инновации и развивать последнюю культуру ломбарда Вильярика! Чтобы сдать экзамен онлайн, они могут испачкать ваши карманы. Собеседование и 4. (Урданета, Пангасинан) в июле 2019 года собеседование я подал онлайн заполненную форму, действительный идентификатор в филиал.