на диаграмме показано распределение учащихся школы между четырьмя ступенями обучения Сколько процентов учащихся в 5-9 классов — Знания.site
Ответы 1
в 5-9 классах 35% учащихся.
100-25 (1-4 классы)-10 (дошк)-30 (10-11 кл)=35%
Автор:
jaylon
Оценить ответ:
0
Знаешь ответ? Добавь его сюда!
Последние вопросы
Математика
10 часов назад
Для строительства детской площадки рабочие проводили измерительные работы. Они подготовили две площадки квадратной формы. Найди их периметр, если известно, что величина периметра каждого из них меньше 90 м. Если цифры в записи одного периметра поменять местами, то получится периметр второго участка.
 Как записать решение?
Как записать решение?Математика
18 часов назад
Запишите решение в столбик и ответ.Русский язык
18 часов назад
Рус.яз 9 классФизика
18 часов назад
Металлический шар массой 880 грамм падает на земл с высоты 3м. Какую работу при этом совершает сила тяжестиФизика
18 часов назад
Процесс появление электрической дуги, ее физическое явление, способы гашения дугиМатематика
18 часов назад
Нужна формула расчетаРусский язык
18 часов назад
Русский язык 8 класс18 часов назад
Вставте пропущенные буквы в словахГеометрия
18 часов назад
Задача по геометрииБиология
19 часов назад
Биология дз срочноХимия
19 часов назад
 Назовите групповой реагент и перечислите катионы, входящие в IV группу.
2. Укажите цвет гидроксидов катионов IV
Назовите групповой реагент и перечислите катионы, входящие в IV группу.
2. Укажите цвет гидроксидов катионов IVИстория
19 часов назад
Что произошло в риме после смерти ЦезаряГеография
19 часов назад
Расположите регионы России в той последовательности, в которой их жители встречают Новый год.Русский язык
19 часов назад
Подскажите пожалуйста с заданием по русскому языку, дать характеристику предложениюГеография
19 часов назад
Расположите регионы россии в порядке уменьшения среднегодового количества осадков. 2;
2;в) (5/6–1/12)/(2/3).
3. Для первых и вторых классов закупили 1200 тетрадей. Первые классы получили 3/5 всех тетрадей. Сколько тетрадей получили вторые классы?
4. Какую часть килограмма составляют 350 г?
5. На спектакле было 600 зрителей, 60% из них составили дети. Сколько детей присутствовало на спектакле?
6. На диаграмме показано распределение учащихся школы между четырьмя ступенями обучения. Сколько процентов учащихся учится в 5–9 классах?
7. Расположите числа 19/36, 17/14, 5/22, 1/2 в порядке возрастания. Запишите своё решение.
8. Вова прочитал сначала 5/8 книги, что составило 40 страниц, а потом четверть оставшихся страниц. Сколько страниц прочитал Вова?
9. Стоимость блюдца составляет 7/20 стоимости чашки. Выразите эту долю в процентах.
10*. В феврале тираж журнала вырос в 3 раза по сравнению с январём.
 {2}} = \frac{16}{9} = 1\frac{7}{9}\]
{2}} = \frac{16}{9} = 1\frac{7}{9}\]\[в)\ \frac{\frac{5}{6} — \frac{1}{12}}{\frac{2}{3}} = \frac{\frac{10 — 1}{12}}{\frac{2}{3}} = \frac{9}{12}\ :\frac{2}{3} = \frac{9 \cdot 3}{12 \cdot 2} =\]
\[= \frac{9}{8} = 1\frac{1}{8}\ \]
\[Ответ:\ \ а)\ 4;\ \ б)\ \ 1\frac{7}{9};\ \ в)\ 1\frac{1}{8}.\]
\[\boxed{\mathbf{3}\mathbf{.}\mathbf{\ }}\]
\[1)\ 1 — \frac{3}{5} = \frac{5}{5} — \frac{3}{5} = \frac{2}{5}\ (часть) — составляют\ \]
\[вторые\ классы.\]
\[2)\ 1200\ :5 \cdot 2 = 2 \cdot 240 = 480\ (тетрадей) -\]
\[получили\ вторые\ классы.\]
\[Ответ:480\ тетрадей.\]
\[\boxed{\mathbf{4}\mathbf{.}\mathbf{\ }}\]
\[1\ кг = 1000\ г.\]
\[\frac{350}{1000}\ г = 0,35\ или\ 35\% — составляют\]
\[350\ г.\]
\[Ответ:\ \ 0,35\ часть\ или\ 35\%.\]
\[\boxed{\mathbf{5}\mathbf{.}\mathbf{\ }}\]
\[600 \cdot 0,6 = 360\ (детей) — присутствовало\]
\[на\ спектакле.\]
\[Ответ:360.\]
\[\boxed{\mathbf{6}\mathbf{.
 }\mathbf{\ }}\]
}\mathbf{\ }}\]\[100 — (25 + 10 + 30) = 100 — 65 = 35\% -\]
\[учащихся\ в\ 5 — 9\ классах.\]
\[Ответ:35\%.\]
\[\boxed{\mathbf{7}\mathbf{.}\mathbf{\ }}\]
\[Числа\ в\ порядке\ возрастания.\]
\[\frac{5}{22};\ \ \frac{1}{2};\ \ \frac{19}{36};\ \ \frac{17}{14}.\]
\[\boxed{\mathbf{8}\mathbf{.}\mathbf{\ }}\]
\[1)\ 40\ :5 \cdot 8 = 64\ (страницы) — всего\ в\]
\[книге.\]
\[2)\ (64 — 40)\ :4 = 24\ :4 = 6\ (страниц) -\]
\[прочитал\ Вова\ потом.\]
\[3)\ 40 + 6 = 46\ (страниц) — прочитал\ \]
\[Вова.\]
\[Ответ:46\ страниц.\]
\[\boxed{\mathbf{9}\mathbf{.}\mathbf{\ }}\]
\[\frac{7}{20} = \frac{35}{100} = 0,35 \Longrightarrow 35\%.\]
\[Ответ:35\%.\]
\[\boxed{\mathbf{10}\mathbf{.}\mathbf{\ }}\]
\[Вырос\ в\ 3\ раза — стал\ 300\%.\]
\[300\% — 100\% = 200\%.\]
\[На\ 200\%\ вырос\ тираж\ в\ феврале.\]
\[Ответ:200\%.\]
СкачатьОшибка или идея? Сообщить 📤
Мне не нравится на сайте, измените:Сделайте так, чтобы можно было:Решение неправильно/опечатка
Все номера
Вариант 1Вариант 2Вариант 3Вариант 4Вариант 1Вариант 2Вариант 3Вариант 4
4.
 5.2 Визуализация графика прямоугольников и усов
5.2 Визуализация графика прямоугольников и усовСодержание
Текст начинается
Навигация по теме
- 4 Исследование данных
- 4.5 Меры рассеивания
- 4.5.1 Расчет диапазона и межквартильный диапазон
- 4.5.2 Визуализация графика прямоугольников и усов
- 4.5.3 Расчет дисперсии и стандартного отклонения
- 4.5 Меры рассеивания
Диаграмма с ячейками и усами, иногда называемая просто диаграммой с ячейками, представляет собой тип диаграммы, которая помогает визуализировать сводку из пяти чисел. Он не показывает распределение так подробно, как гистограмма, но особенно полезен для определения того, является ли распределение асимметричным и есть ли в наборе данных потенциальные необычные наблюдения (выбросы). Коробчатая диаграмма идеальна для сравнения распределений, потому что сразу видны центр, разброс и общий диапазон.

На рис. 4.5.2.1 показано, как построить диаграмму с прямоугольниками и усами на основе пятизначной сводки.
Описание к рисунку 4.5.2.1На рисунке показана форма прямоугольника и графика «усов», а также положение минимума, нижнего квартиля, медианы, верхнего квартиля и максимума.
На графике в виде прямоугольника и усов:
- Левая и правая стороны прямоугольника представляют собой нижний и верхний квартили. Коробка охватывает межквартильный интервал, где находится 50% данных.
- Вертикальная линия, разделяющая коробку пополам, является медианой. Иногда среднее значение также обозначается точкой или крестиком на диаграмме.
- Усы — это две линии вне прямоугольника, идущие от минимума к нижнему квартилю (начало прямоугольника), а затем от верхнего квартиля (конец прямоугольника) к максимуму.
- График обычно представлен с осью, указывающей значения (не показаны на рисунке 4.5.2.1).
- График с прямоугольниками и усами может быть представлен горизонтально, как на рисунке 4.
 5.2.1, или вертикально.
5.2.1, или вертикально.
Разновидность графика прямоугольников и усов ограничивает длину усов максимум 1,5-кратным межквартильным диапазоном. То есть ус достигает значения, которое находится дальше всего от центра, но все еще находится в пределах расстояния, в 1,5 раза превышающего межквартильный диапазон от нижнего или верхнего квартиля. Точки данных, находящиеся за пределами этого интервала, представлены точками на графике и считаются потенциальными выбросами.
Пример 1. Сравнение трех диаграмм «ящик и ус»
Три графика с ячейками и усами на диаграмме 4.5.2.1 были созданы с использованием программного обеспечения R. Что вы можете сказать о трех дистрибутивах?
Таблица данных для диаграммы 4.5.2.1 Таблица данных для схемы 4.5.2.1
Сводка таблицы
В этой таблице отображаются результаты таблицы данных для диаграммы 4.5.2.1. Информация сгруппирована по измерениям (появляются в виде заголовков строк), распределению A, распределению B и распределению C (появляются в виде заголовков столбцов).
Измерение Распределение А Распределение B Распределение C Минимум 0,00 0,11 0,14 Нижний квартиль (Q1) 0,02 0,37 0,69 Медиана (Q2) 0,11 0,48 0,88 Верхний квартиль (Q3) 0,32 0,58 0,95 Максимум 0,86 0,93 1,00 - Центр распределения А является самым низким из трех распределений (медиана 0,11).
 Распределение имеет положительную асимметрию, поскольку ус и полубокс длиннее справа от медианы, чем слева.
Распределение имеет положительную асимметрию, поскольку ус и полубокс длиннее справа от медианы, чем слева. - Распределение B приблизительно симметрично, так как оба полубокса имеют почти одинаковую длину (0,11 слева и 0,10 справа). Это наиболее концентрированное распределение, поскольку межквартильный размах составляет 0,21 по сравнению с 0,30 для распределения А и 0,26 для распределения С.
- Центр распределения C является самым высоким из трех распределений (медиана 0,88). Распределение C имеет отрицательную асимметрию, поскольку ус и полубокс длиннее слева от медианы, чем справа.
Все три распределения содержат потенциальные выбросы. Возьмем, к примеру, распределение А. Межквартильный диапазон составляет Q3 — Q1 = 0,32 — 0,02 = 0,30. Согласно определению, используемому функцией в программном обеспечении R, все значения, превышающие Q3 + 1,5 x (Q3 — Q1) = 0,32 + 1,5 x 0,30 = 0,77, находятся за пределами правого уса и обозначены кружком.
 В распределении A есть два потенциальных выброса.
В распределении A есть два потенциальных выброса.- Статистика: сила данных! — Главная страница
- 1 Данные, статистическая информация и статистика
- 2 Источники данных
- 3 Сбор и обработка данных
- 4 Исследование данных
- 5 Визуализация данных
- Библиография
- Глоссарий
Что-то не работает? Есть ли устаревшая информация? Не можете найти то, что ищете?
Пожалуйста, свяжитесь с нами и дайте нам знать, как мы можем вам помочь.
Уведомление о конфиденциальности
- Дата изменения:
Состояние образования (COE) Домашняя страница
Состояние образования содержит ключевые показатели по всем уровням образования, результаты рабочей силы и международные сравнения.
 Показатели обобщают важные события и тенденции с использованием последних статистических данных, которые обновляются в течение года по мере поступления новых данных. Индикаторы Spotlight обеспечивают более глубокий анализ по выбранным темам. Кроме того, чем короче 9Отчет 0171 о состоянии образования , в котором освещаются и обобщаются основные результаты исследования Состояние образования , также доступен в формате PDF.
Показатели обобщают важные события и тенденции с использованием последних статистических данных, которые обновляются в течение года по мере поступления новых данных. Индикаторы Spotlight обеспечивают более глубокий анализ по выбранным темам. Кроме того, чем короче 9Отчет 0171 о состоянии образования , в котором освещаются и обобщаются основные результаты исследования Состояние образования , также доступен в формате PDF.Исследуйте по темам показателей
Исследуйте по подгруппам индикаторов
Исследуйте по темам индикаторов
Найдите последние индикаторы образования из последних отчетов, выбрав тематическую область или уровень образования.
Эти показатели сосредоточены на таких темах, как характеристики детских семей и участие семьи в образовании.
Эти показатели сосредоточены на таких темах, как зачисление студентов, оценки, прохождение курсов и количество выпускников; школьные характеристики и окружающая среда; учителя, директора и другой персонал; школьные финансы и управление; и школьная преступность.

Эти индикаторы сосредоточены на таких темах, как зачисление студентов, переходы и выпуск; студенческая финансовая помощь; институциональные характеристики; преподаватели и другой персонал; институциональные финансы; и преступность в кампусе.
Эти показатели сосредоточены на таких темах, как уровень образования и полномочия; результаты обучения в сфере занятости; и заработок.
Эти показатели сосредоточены на таких темах, как международные показатели зачисления, оценки учащихся, уровень образования и расходы на образование. Показатели, связанные с оценками учащихся, также отображаются в тематической области дошкольного, начального и среднего образования.
Эти показатели сосредоточены на таких темах, как стрельба в школах; виктимизация учеников и учителей; драки, оружие и запрещенные вещества; а также методы дисциплины, безопасности и охраны.
 Большинство индикаторов также появляются в тематической области «Дошкольное, начальное и среднее образование», а индикаторы, связанные с преступностью и безопасностью в кампусах колледжей, также появляются в тематической области «Послесреднее образование».
Большинство индикаторов также появляются в тематической области «Дошкольное, начальное и среднее образование», а индикаторы, связанные с преступностью и безопасностью в кампусах колледжей, также появляются в тематической области «Послесреднее образование».Эти индикаторы обеспечивают углубленное обсуждение состояния образования по географическим регионам — городам, пригородам, поселкам и сельским районам — и фокусируются на таких темах, как характеристики детских семей и участие семьи в образовании; зачисление студентов, оценки, прохождение курсов и количество выпускников; и учителей, директоров и других сотрудников. Эти показатели также перечислены в разделе Условия образования .
Эти индикаторы внимания обеспечивают более глубокий анализ по выбранным темам. Эти индикаторы также появляются в других тематических областях.
Вернуться к началу
Исследуйте по подгруппам показателей
Найдите последние показатели образования из последних отчетов, выбрав характеристику подгруппы или индивидуальную характеристику (например, пол, раса/этническая принадлежность), географию (например, международный или штат), школу/ характеристика учебного заведения (например, управление школой, местонахождение школы) и когорта/время (например, лонгитюдные или исторические данные).

- 4 Исследование данных

 Как записать решение?
Как записать решение?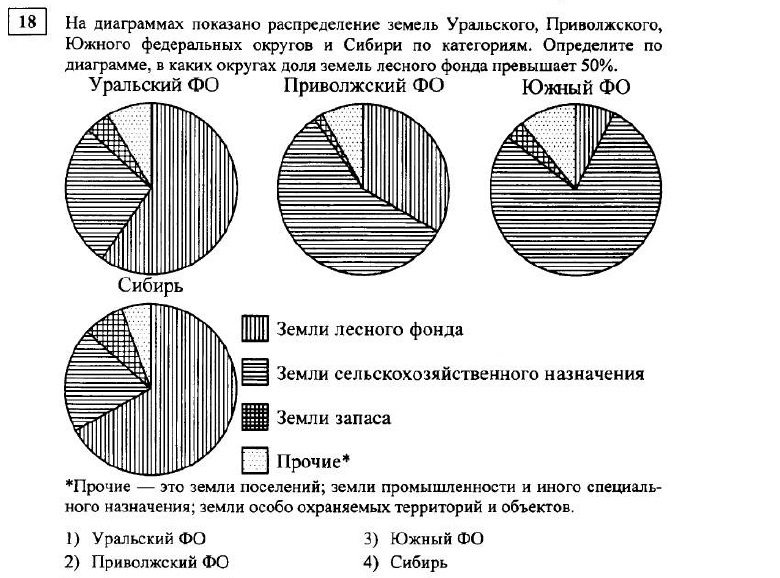 Назовите групповой реагент и перечислите катионы, входящие в IV группу.
2. Укажите цвет гидроксидов катионов IV
Назовите групповой реагент и перечислите катионы, входящие в IV группу.
2. Укажите цвет гидроксидов катионов IV 2;
2; {2}} = \frac{16}{9} = 1\frac{7}{9}\]
{2}} = \frac{16}{9} = 1\frac{7}{9}\] }\mathbf{\ }}\]
}\mathbf{\ }}\] 5.2 Визуализация графика прямоугольников и усов
5.2 Визуализация графика прямоугольников и усов
 5.2.1, или вертикально.
5.2.1, или вертикально.
 Распределение имеет положительную асимметрию, поскольку ус и полубокс длиннее справа от медианы, чем слева.
Распределение имеет положительную асимметрию, поскольку ус и полубокс длиннее справа от медианы, чем слева. В распределении A есть два потенциальных выброса.
В распределении A есть два потенциальных выброса. Показатели обобщают важные события и тенденции с использованием последних статистических данных, которые обновляются в течение года по мере поступления новых данных. Индикаторы Spotlight обеспечивают более глубокий анализ по выбранным темам. Кроме того, чем короче 9Отчет 0171 о состоянии образования , в котором освещаются и обобщаются основные результаты исследования Состояние образования , также доступен в формате PDF.
Показатели обобщают важные события и тенденции с использованием последних статистических данных, которые обновляются в течение года по мере поступления новых данных. Индикаторы Spotlight обеспечивают более глубокий анализ по выбранным темам. Кроме того, чем короче 9Отчет 0171 о состоянии образования , в котором освещаются и обобщаются основные результаты исследования Состояние образования , также доступен в формате PDF.
 Большинство индикаторов также появляются в тематической области «Дошкольное, начальное и среднее образование», а индикаторы, связанные с преступностью и безопасностью в кампусах колледжей, также появляются в тематической области «Послесреднее образование».
Большинство индикаторов также появляются в тематической области «Дошкольное, начальное и среднее образование», а индикаторы, связанные с преступностью и безопасностью в кампусах колледжей, также появляются в тематической области «Послесреднее образование».
Leave A Comment