«Квантик» — журнал для любознательных
Задача 56.
(Григорий Гальперин)На бумаге начертили 130 четырёхугольников. Каждый четырёхугольник – или квадрат, или прямоугольник, или параллелограмм, или ромб, или трапеция. Из них 30 – квадраты, 80 – прямоугольники, 65 – ромбы, и 120 – параллелограммы. Сколько всего трапеций было начерчено? (Напомним, что у трапеции две стороны параллельны, а две – нет.)
Задача 57.
(Александр Грибалко)По кругу лежат 4 одинаковые с виду монеты. Две из них фальшивые – они весят 9 г и 11 г, а две настоящие – весят по 10 г каждая. Известно, что фальшивые монеты соседние. За какое наименьшее число взвешиваний на чашечных весах без гирь можно гарантированно определить вес каждой монеты? (Весы лишь показывают, равны ли чаши по весу, и если нет, то какая тяжелее.)
Задача 58.
(Борис Кордемский)У Квантика на даче есть участок треугольной формы.
Он решил застелить его газоном. Зная третий признак равенства треугольников, он измерил три стороны участка и заказал треугольный газон с такими сторонами. Но когда заказ был доставлен, Квантик не смог наложить газон на свой участок, хотя длины сторон были в точности как в заказе.
а) Как такое могло быть?
б) Как Квантику исправить ситуацию, разрезав газон не более чем на три части?
Задача 59.
(Михаил Евдокимов)Вася расставил по кругу в некотором порядке числа 1, 2, 3, …, 15 и целое число x (не обязательно положительное). Оказалось, что сумма любых двух соседних чисел – квадрат целого числа.
а) Найдите хотя бы одно такое x и нарисуйте соответствующую расстановку.
б) Найдётся ли другое подходящее x?
Задача 60.
(Сергей Костин)Любую ли фигуру пентамино (см. рисунок) можно дополнить доминошками до клетчатого квадрата без дырок и перекрытий?
Задача 51.
(Александр Домашенко)В числовом ребусе
Т×О×П×О×Л×Ь=Т×Ю×Л×Ь×П×А×Н
замените буквы ненулевыми цифрами так, чтобы число ТОПОЛЬ получилось как можно бо́льшим. (Одинаковые буквы заменяйте одинаковыми цифрами, разные – разными.) Не забудьте обосновать ответ.
Задача 52.
(Михаил Евдокимов)Расставьте на шахматной доске несколько белых и чёрных коней так, чтобы каждый белый конь бил ровно четырёх чёрных, а каждый чёрный – ровно четырёх белых.
Задача 53.
(Александр Домашенко)Аня вырезала куклу из бумаги в треугольную сетку. Юра утверждает, что эту фигурку можно свернуть в треугольную пирамидку без просветов и наложений. Прав ли он?
Задача 54.
(Михаил Евдокимов)На отрезке AB построены два различных прилегающих друг к другу квадрата (см. рисунок). Докажите, что диагональ большого квадрата делит отрезок CD пополам.
Задача 55.
(Алексей Воропаев)Петя стреляет по мишени. Табло показывает отношение числа попаданий к числу сделанных выстрелов (до начала стрельбы табло не горит). В какой-то момент число на табло было меньше чем q. Через некоторое время это число стало больше, чем q. Для каких q от 0 до 1 отсюда следует, что в какой-то момент доля попаданий была ровно q?
Задача 46.
(Мария Ахмеджанова)Квантик получил по почте кубическую посылку, запечатанную со всех сторон. Он хочет открыть коробку, разрезав её по рёбрам на две части, но так, чтобы у любой грани было разрезано не более двух рёбер. Удастся ли ему это?
Задача 47.
(Михаил Евдокимов)Два лифта едут вниз с одинаковой скоростью с 95-го этажа офисного небоскрёба. Второй лифт стартовал через 45 секунд после первого. На этажах с номерами, делящимися на 2 или 3, стоит по сотруднику (остальные этажи пустые).
Всем нужно на первый этаж. Лифт, приехавший к сотруднику первым, останавливается на 10 секунд, чтобы его забрать (другой лифт проезжает мимо). Какой лифт раньше попадёт на первый этаж?
Задача 48.
(Михаил Евдокимов)У фокусника есть две копии «хитрой» клетчатой фигуры. Зритель называет любое целое число N от 2 до 100, и фокусник разрезает первую копию на N клетчатых частей, из которых можно сложить квадрат, а вторую копию – на N клетчатых частей, из которых нельзя сложить квадрат. Приведите пример «хитрой» фигуры и объясните, как разрезать её в каждом из случаев, чтобы фокус удавался. (Все части должны использоваться; наложения частей и дырки не допускаются.)
Задача 49.
(Сергей Костин)Каких семизначных натуральных чисел больше: у которых произведение цифр равно 1024, или у которых произведение цифр равно 2048?
Задача 50.
(Джон Конвей)Каждую сторону произвольного треугольника продлили в обе стороны так, как показано на рисунке.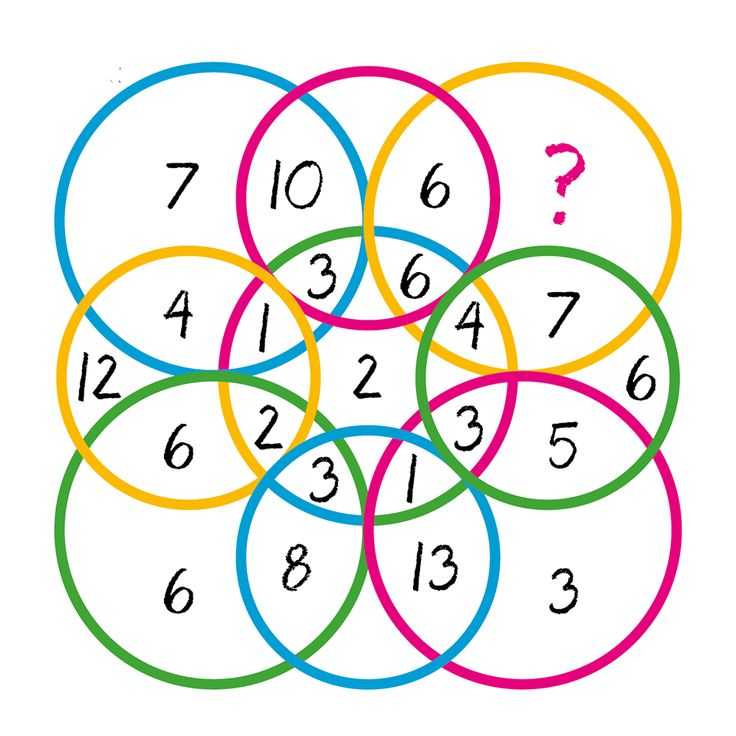
Докажите, что полученные 6 точек лежат на одной окружности.
Задача 41.
(Михаил Евдокимов)Перед игроком стоят в ряд 3 шкатулки, в одной из которых лежит приз. К шкатулкам прикреплены записки с утверждениями, как на рисунке. Известно, что ровно одно из утверждений истинно. Какую шкатулку нужно открыть, чтобы получить приз?
Задача 42.
(Сергей Дворянинов)Толя Втулкин отметил на прямой три точки и заметил, что всевозможных отрезков с концами в этих точках оказалось 3, а всевозможных лучей с началами в этих точках – 6, в два раза больше.
«Интересно, – подумал Толя, – а можно ли отметить столько точек, чтобы получилось наоборот: число всевозможных лучей с началами в этих точках было бы в два раза меньше количества всевозможных отрезков с концами в этих точках?»
Ответьте на вопрос Толи.
Задача 43.
(Михаил Евдокимов)На диагонали и стороне единичного квадрата ABCD построены правильные треугольники AMB и ANC так, как показано на рисунке.
Чему равно расстояние MN?
Задача 44.
(Игорь Акулич и Максим Прасолов)Число 1210 обладает таким свойством: каждая его цифра, кроме последней, показывает, сколько раз в нём встречается следующая цифра. А именно: «12» означает, что в числе одна двойка, «21» – что в числе две единицы, «10» – что в числе один ноль. Существует ли число с таким же свойством, большее миллиарда?
Задача 45.
(Сергей Костин)Можно ли записать в клетках фигуры F натуральные числа так, чтобы сумма чисел в любом горизонтальном прямоугольнике 1×3, целиком лежащем внутри фигуры, равнялась 10, а сумма чисел в любом вертикальном прямоугольнике 3×1, целиком лежащем внутри фигуры, равнялась 11, если фигура F – это
а) квадрат 5 × 5;
б) квадрат 5 × 5, у которого удалили центральную клетку?
Задача 36.
(Григорий Гальперин)Петя решал задачу из книги: «В Канаде __ процентов населения говорит по-английски, а __ процентов – по-французски (на других языках в Канаде не говорят).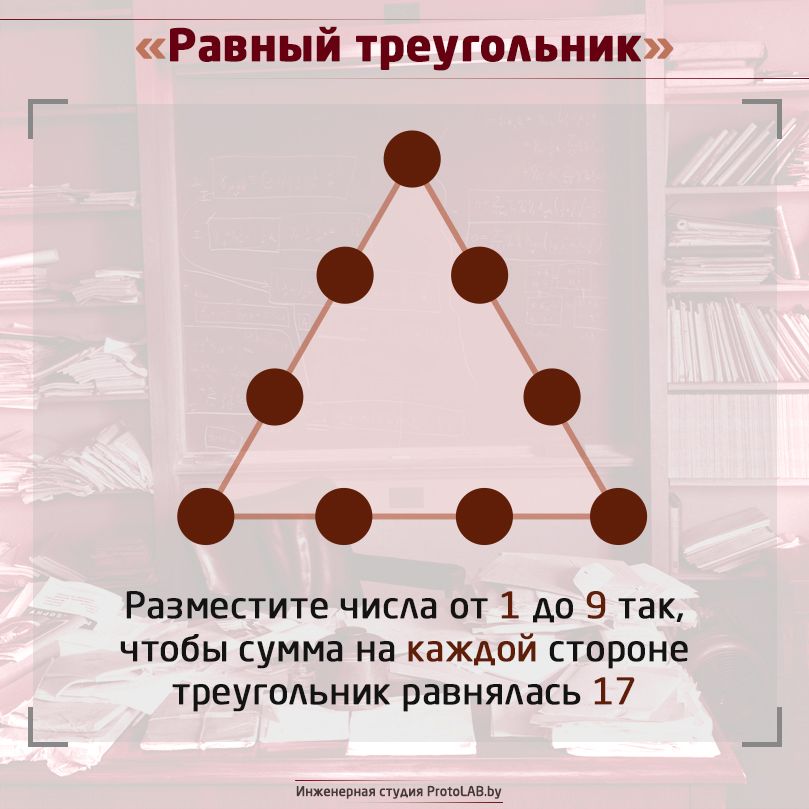
Какой процент населения Канады говорит и по-английски, и по-французски?». (Числа из книги мы заменили пропусками.) «Какая лёгкая задача! – сказал он. – Надо просто вычесть из первого числа второе, вот и всё решение!» Петя посмотрел ответы в конце книги и убедился, что его ответ правильный. Какой процент населения Канады говорит по-французски, по мнению этой книги?
Задача 37.
(Александр Перепечко)Когда родился Квантик, его старшему брату было x месяцев. Число x равно наименьшему общему кратному всех чисел от 1 до 9, кроме одного, а также равно произведению трёх последовательных чисел. Сколько полных лет старшему брату, если Квантику сейчас 100 месяцев?
Задача 38.
(Владимир Расторгуев)Клетчатые квадраты 12×12 и 5×5 разрежьте (один или оба) по линиям сетки так, чтобы всего получилось пять кусков и из этих пяти кусков можно было сложить квадрат 13×13.
Задача 39.
(Сергей Дворянинов)Положительные числа x и y таковы, что в неравенстве ниже левая дробь больше правой. Что больше: x или y?
Задача 40.
(Борис Френкин)В окружность вписан 1000-угольник, его вершины покрашены поочерёдно в красный и синий цвет. Каково наибольшее возможное количество красных вершин, углы при которых меньше 179°?
Задача 31.
(Инесса Раскина)Мимо пассажира «Ласточки», едущей с постоянной скоростью, встречный «Сапсан» пронёсся за 3 секунды, а попутный «Сапсан» – за 7 секунд. Длины и скорости «Сапсанов» были одинаковы. За сколько секунд этот пассажир проедет мимо такого же, но стоящего «Сапсана»?
Задача 32.
(Михаил Евдокимов)На стороне BC квадрата ABCD во внешнюю часть построен равносторонний треугольник BMC. Отрезки AC и MD пересекаются в точке O.
Докажите, что OA = OM.
Задача 33.
(Сергей Дориченко)Три разбойника украли пять алмазов (возможно, разного веса) и решили разделить их между собой поровну по весу, не распиливая на куски. Они отмерили треть, но остальные алмазы нельзя было разделить на две равные части. Докажите, что разбойникам не удастся поделить алмазы, даже если они смогут отмерить треть по-другому.
Задача 34.
(Сергей Костин)Какое наибольшее количество флажков, изображённых на рисунке 1, можно разместить в квадрате а) 8×8; б) 14×14? Флажок должен располагаться по линиям сетки. Никакие два флажка не должны иметь ни одной общей точки. В качестве примера на рисунке 2 показано, как в квадрате 3×3 можно разместить три флажка.
Задача 35.
(Игорь Акулич)В гирлянде n лампочек и n кнопок с номерами. По инструкции, 1-ю кнопку надо соединить с одной лампочкой, 2-ю – с двумя, 3-ю – с тремя, и т.
д., но с какими именно лампочками соединяется каждая кнопка, решает пользователь. Сначала все лампочки погашены. Нажатие на любую кнопку меняет состояние всех соединённых с ней лампочек на противоположное (горящие лампочки гаснут, не горящие – зажигаются).
Коля уверен, что можно так соединить кнопки с лампочками, чтобы, нажав нужные кнопки, можно было получить любую комбинацию горящих и не горящих лампочек. Петя же считает, что любую такую комбинацию можно получить, как ни соединяй лампочки и кнопки – лишь бы по инструкции.
а) При каких n прав Коля?
б) При каких n прав Петя?
Задача 26.
(по мотивам задачи Мартина Гарднера)Число 1210 автобиографичное: его первая цифра показывает, сколько в нём нулей, вторая – сколько единиц, третья – сколько двоек, а четвёртая – сколько троек. Найдите следующее автобиографичное целое число.
Задача 27.
(Александр Перепечко)У барона Мюнхгаузена есть волшебный кубик, в котором две грани – синие, две – красные и две – зелёные.
Если поставить этот кубик на любую грань и запомнить, где какой цвет, то на какую бы другую грань потом ни ставить кубик, не удастся повторить такое же расположение цветов. Может ли так быть?
Задача 28.
(Николай Авилов)Снежинка «соткана» из семи окружностей, на них расположены кружки, по 6 на каждой окружности. В кружках расставлены числа от 1 до 19 (см. рисунок). Переставьте 6 чисел так, чтобы на каждой окружности сумма чисел была одной и той же.
Задача 29.
(Александр Блинков и Антон Акимов)Ноутику и Квантику дали задание: нарисовать какой-нибудь четырёхугольник ABCD, в котором стороны AD и BC параллельны и AN = CM, где M – середина AB, а N – середина CD. Ноутик нарисовал параллелограмм, а Квантик – даже два разных четырёхугольника, но оба не параллелограммы. Могло ли такое быть, если все примеры верные и в каждом AD = 14, AN = CM = 5, а расстояние между AD и BC равно 8?
Задача 30.
(Сергей Костин)В каждой клетке таблицы 7×7 стоит минус. За ход можно в любом квадрате 2×2 поменять все знаки на противоположные. Какое наибольшее количество плюсов можно получить в таблице с помощью таких ходов?
Задача 21.
(Александр Перепечко)Барон Мюнхгаузен огородил свои владения забором в форме шестиугольника. Он утверждает, что каждый внутренний угол этого шестиугольника либо меньше 10°, либо больше 350°. Может ли барон быть прав?
Задача 22.
(Павел Кожевников)Вася написал на листке 10 цифр (среди них могут быть равные) так, чтобы сумма любых трёх написанных цифр не превосходила 14. Какова наибольшая возможная сумма всех 10 цифр? (Приведите пример и докажите, что большую сумму получить нельзя.)
Задача 23.
(Николай Авилов)Ёлочку на рисунке слева разрежьте на четыре части и сложите из них две одинаковые ёлочки, как на рисунке справа.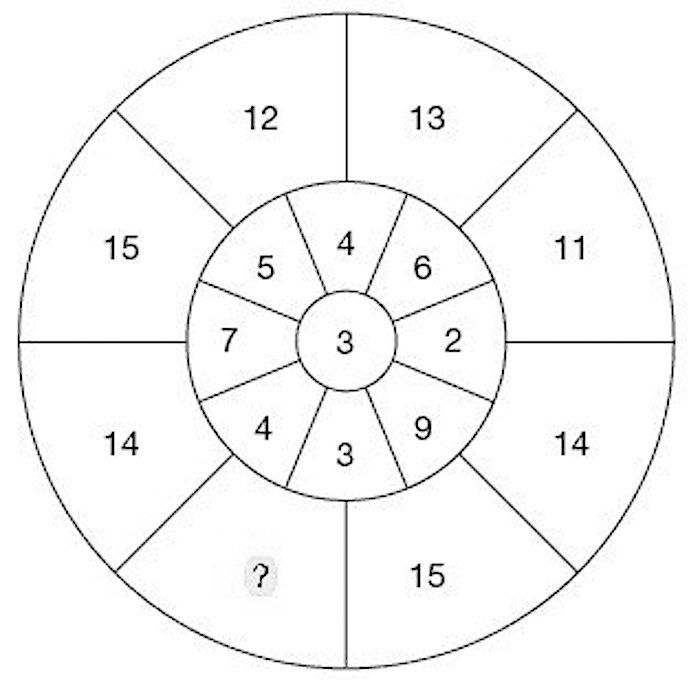
Задача 24.
(Григорий Мерзон)Вычислите сумму
Задача 25.
(Николай Чернятьев)Квантик и Ноутик по очереди закрашивают клетки на доске 8×8, по одной клетке за ход, начинает Квантик. Первый ход можно сделать куда угодно. Каждый следующий ход должен быть таким, что новая клетка граничит по стороне ровно с одной закрашенной клеткой. Кто не может сделать ход, проиграл. Кто может обеспечить себе победу?
Задача 16.
(Александр Хачатурян и Татьяна Казицына)Саша придумал шифр: заменил несколько букв однозначными или двузначными числами, используя только цифры 1 и 2 (разные буквы он заменял разными числами, а одинаковые – одинаковыми). Слово КРОЛИК превратилось в число 1212111212. Слово КРОКОДИЛ тоже превратилось в число. В какое?
Задача 17.
(Михаил Евдокимов)Найдите наименьшее семизначное число, делящееся на 17, в котором все цифры разные.
Задача 18.
Точка K делит основание BC равнобедренного треугольника BAC на отрезки длины x и y, как показано на рисунке. Найдите длину AК, если угол AКC равен 60°.
Задача 19.
Квантик и Ноутик хотят показать такой фокус. Зритель задумывает два натуральных числа, различающихся на 1, и сообщает одно Квантику, а другое – Ноутику. После этого Квантик показывает Ноутику чёрную или белую карточку, и Ноутик сразу угадывает число Квантика. Помогите Квантику и Ноутику договориться о своих действиях, чтобы фокус всегда удавался.
Задача 20.
(Владимир Расторгуев)Разрежьте шестиугольник на рисунке на две равные части.
Задача 11.
(Александр Перепечко)Семь камней весом 1, 2, 3, 4, 5, 6 и 7 тонн можно перевезти в нескольких грузовиках одинаковой грузоподъёмности. Хватит ли для перевозки четырёх таких грузовиков?
Задача 12.
(Борис Френкин)Петя и Вася тренируются на кольцевом велотреке: одновременно стартовали из одной и той же точки и едут с постоянными скоростями.
Петя едет быстрее Васи. Когда Петя прошёл 16 кругов, он встретил в точке старта Васю. А когда Вася прошёл 16 кругов, он встретил в точке старта Петю. Верно ли, что Вася после каждого круга встречал в точке старта Петю?
Задача 13.
(Александр Грибалко)У Саши есть два клетчатых квадрата 7×7. Ему нужно разрезать их по линиям сетки на части так, чтобы частей получилось не более пяти и их можно было уложить в один слой в коробку 10×10. Есть ли способ выполнить это задание?
Задача 14.
(Алексей Воропаев)Квантик и Ноутик загадали по натуральному числу и сказали их Серёже. Серёжа в ответ назвал число 2020 и сказал, что это либо сумма, либо произведение услышанных им чисел. Ноутик подумал и сказал, что не знает, какое число загадал Квантик. Квантик услышал это, но всё равно не смог узнать, какое число загадал Ноутик. Какое число загадал Квантик?
Задача 15.
(ученик 4 класса Петя Ким)На каждой из сторон треугольника ABC выбраны красная и синяя точки так, что красная точка делит сторону в отношении 2 : 1, а синяя – в отношении 1 : 2 (если обходить треугольник по часовой стрелке). Через красные точки провели окружность, и через синие – тоже. Докажите, что отрезок, соединяющий центры этих окружностей, проходит через точку пересечения медиан треугольника ABC.
Задача 6.
(Григорий Гальперин)Каких чисел, все цифры которых различны, больше: девятизначных или десятизначных?
Задача 7.
(Григорий Гальперин)У Квантика есть две квадратные шоколадки, первая – размером 10×10, вторая – размером 11×11. Чтобы разломать первую шоколадку на дольки 1×1, Квантику требуется 1 минута и 39 секунд. Какое время ему потребуется, чтобы разломать на дольки 1×1 вторую шоколадку? На каждый разлом Квантик тратит одно и то же время и за раз ломает какой-то один из имеющихся кусков на две части.
Задача 8.
(Игорь Акулич)Барон Мюнхгаузен рассказывал:
– Я сумел разрезать произвольный треугольник на две части, а потом каждую из них разрезал на 7 равных частей.
Могут ли слова барона быть правдой?
Задача 9.
(Александр Перепечко)Многогранник, изображённый на рисунке, называется октаэдром; у него 6 вершин, 8 треугольных граней и 12 рёбер. В каждой вершине октаэдра поместили лампочку и зажгли одну из них. Далее, за ход можно выбрать любую грань и изменить состояние (потушить, если горит, и зажечь, если не горит) всех лампочек на ней. Можно ли за несколько ходов зажечь все лампочки?
Задача 10.
(Игорь Акулич)Возьмём любое натуральное число, например, 2019. Составим второе число, которое показывает, сколько и каких цифр (в порядке возрастания) содержит исходное число. Получится 10111219, что означает «один нуль, одна единица, одна двойка и одна девятка».
На основе второго числа по тому же принципу образуем третье число 10511219, потом – четвёртое 1041121519, и т. д.
а) Квантик убеждён, что с какого бы числа ни начать, в получившейся последовательности какое-то число непременно встретится дважды. Ноутик считает, что не обязательно – возможна последовательность, в которой все числа различны. Кто прав?
б) Могут ли в такой последовательности встретиться два одинаковых числа подряд?
Задача 1.
(Сергей Дворянинов)Однажды Толик Втулкин должен был найти произведение двух чётных трёхзначных чисел. Он спешил и в записи одного числа пропустил наименьшую цифру, а в записи другого – наибольшую. В итоге он получил 323. Какие числа должен был перемножить Толик?
Задача 2.
(Павел Кожевников)Разрежьте клетчатую доску 12×12 на четыре одинаковых клетчатых многоугольника так, чтобы никакой клетчатый квадрат 2×2 не попал целиком ни в какой многоугольник.
Задача 3.
(Павел Кожевников)Вася хочет выбрать из набора 1, 2, 3, … , 50 как можно больше чисел так, чтобы любые два числа различались хотя бы на 4.
а) Сколько чисел выберет Вася?
б) Сколько способов у Васи сделать это?
Задача 4.
(Михаил Евдокимов)Два квадрата лежат на плоскости так, как показано на рисунке. Докажите, что центр одного квадрата лежит на диагонали другого.
Задача 5.
(Юрий и Сергей Маркеловы)Квантик загадал целое число от 0 до 99, а Ноутик его отгадывает. Число считается отгаданным, если Ноутик его назвал. За ход Ноутик называет четыре целых числа от 0 до 99, обладающих одним из двух свойств: либо первый разряд у всех чисел совпадает, а вторые разряды последовательные, либо второй разряд у всех чисел совпадает, а первые разряды последовательные (у однозначных чисел первый разряд считаем равным 0).
Например, наборы 13, 14, 15, 16 и 3, 13, 23, 33 подходят, а набор 18, 19, 20, 21 – нет. За какое минимальное число ходов Ноутик может гарантированно отгадать число?
Официальный портал Одинцовского Учебно-методического центра «Развитие образования» Одинцовского муниципального района
Сообщение. Пилотный проект. Данная форма не предназначена для приема обращений граждан в порядке Федерального закона от 02.05.2006 № 59-ФЗ «О порядке рассмотрения обращений граждан Российской Федерации» и предоставляет возможность направить электронное сообщение в рамках реализации пилотного проекта по внедрению «Единого окна цифровой обратной связи». Ответ на сообщение будет направлен не позднее 8 рабочих дней после дня его регистрации, а по отдельным тематикам – в укороченные сроки.
Последние новости:
16.03.2023
Художественно-эстетическое развитие дошкольников через приобщение к русской народной культуре
16 марта 2023 года в МБОУ Жаворонковской СОШ дошкольном отделении детском саду №16 состоялся семинар для музыкальных руководителей по теме «Художественно-эстетическое развитие дошкольников через приобщение к русской народной культуре».
Рознова А.С. музыкальный руководитель показала два педагогических мероприятия: «В гостях у сказки» для детей 3-4 лет, «Мы наследники великих традиций» для воспитанников 6-7 лет. На занятиях были представлены различные формы работы с детьми посредством приобщения к русскому народному фольклору.
14.03.2023
Позитивная социализация в процессе игровой деятельности
14 марта 2023 года на базе МБОУ Одинцовского центра «Флагман» дошкольного отделения — детского сада №5 состоялся семинар воспитателей Одинцовского городского округа по теме «Позитивная социализация в процессе игровой деятельности»
01.03.2023
Развитие высших психических функций через конструктивно – модельную деятельность
1 марта 2023 года на базе МБОУ ОЦ «Флагман», дошкольного отделения – детского сада №26 прошел семинар-практикум для воспитателей Одинцовского городского округа на тему: «Развитие высших психических функций через конструктивно – модельную деятельность».
28.02.2023
Плавание как средство профилактики исправления нарушений осанки у детей
28 февраля 2023 года состоялся семинар для инструкторов по физической культуре (плавание) Одинцовского городского округа на базе МБОУ ОЦ «ФЛАГМАН» дошкольного отделения — детского сада № 14 по теме: «Плавание как средство профилактики исправления нарушений осанки у детей». На семинаре решались задачи профилактики и исправление нарушения осанки у детей при обучении плаванию.
15.02.2023
Семинар по реализации программы «Супер Тигры»
15 февраля 2023 года на базе МБОУ Одинцовской СОШ № 12 дошкольного отделения – детского сада № 39 состоялся семинар по реализации программы «Супер Тигры» для педагогов Одинцовского городского округа.
15.02.2023
Творческая мастерская Клуба «Профессионал»
С целью систематизации опыта и совершенствования профессионального мастерства педагогов 15 февраля 2023 года на базе МБОУ Одинцовской СОШ № 12 дошкольного отделения – детского сада № 39 состоялась творческая мастерская Клуба «Профессионал».
09.02.2023
Формирование нравственных ценностей через мир музыкальной сказки
09 февраля 2023 года состоялся семинар для музыкальных руководителей Одинцовского городского округа на тему: «Формирование нравственных ценностей через мир музыкальной сказки» на базе МБОУ «Первая школа имени М.А. Пронина» дошкольного отделения — детского сада № 5.
Элементов нет!
Полезные ресурсы
Шесть кругов | NZ Maths
Последовательность уроков
Занятие 1
Найдите все четыре ответа на задачу шести кругов и убедитесь, что других нет. Попытка показать, что это так. Что вы можете сказать по поводу ответов, которые вы нашли?
Фон
Сначала мы начнем с проблемы, на которой основан весь этот раздел.
Основная задача (задача шести кругов): можно ли разместить числа 1, 2, 3, 4, 5, 6 в кругах так, чтобы суммы трех чисел по обе стороны треугольника были одинаковыми ?
Прежде чем представить задачу классу, стоит немного подумать над ней.
Есть несколько вещей, которые необходимо учитывать.
- Не беспокойтесь слишком сильно о том, чтобы заставить учащихся найти формулу или метод для решения этой задачи. Важная вещь, которую они должны сделать в начале, — это использовать свою интуицию. На самом деле это означает поощрять их пробовать все, что приходит им в голову. Так что поощряйте их угадывать, экспериментировать и не беспокоиться о том, какой метод они используют, даже если он кажется совершенно нематематическим!
- Затем, когда они начнут получать ответы, вам нужно будет заставить их подумать, какие ответы отличаются друг от друга. Дело в том, что, получив один ответ, они могут получить еще пять, просто используя повороты равностороннего треугольника. Поскольку мы можем получить любой из шести из других здесь, мы могли бы также сказать, что они все одинаковы. Итак, мы скажем, что два ответа ниже одинаковы.
- Итак, какие ответы существуют и сколько их? Методом проб и ошибок будет как минимум четыре.
Мы показываем их ниже. Но есть ли еще что-то, что мы еще не показали? - Важно отметить суммы сторон по двум причинам. Во-первых, нам нужно проверить, что сумма на всех трех сторонах одинакова, чтобы убедиться, что у нас есть правильный ответ. Во-вторых, эта сумма окажется фундаментальной в дальнейшем.
Мы показываем их ниже. Но есть ли еще что-то, что мы еще не показали?Что теперь можно сказать об ответах? Есть ли между ними какая-то связь? Есть ли какие-то закономерности, которые мы должны увидеть? Вот список того, что могут найти ваши ученики.
- Угловые круги содержат 1, 2, 3; 4, 5, 6; 1, 3, 5; и 2, 4, 6. Это самые маленькие и самые большие последовательные числа, нечетные числа и четные числа.
- Если вы переместите цифры одного ответа по одному кругу, вы получите другой ответ. Неважно, как вы их двигаете: по часовой или против часовой стрелки. Используя этот ход, A становится D становится A, а B становится C становится B.
- Замена угловых номеров на средние и наоборот меняет один ответ на другой. Это вызывает те же переключатели, что и последний элемент в списке.
- Разница между противоположными угловыми и средними числами одинакова. Посмотрите на А. 4 напротив 1 и 4 – 1 = 3. 5 напротив 2 и 5 – 2 = 3. 6 напротив 3 и 6 – 3 = 3.
- Если вы замените каждое число m на 7 – m, вы получите другой ответ. Таким образом, в B, если вы замените 1 на 6, 2 на 5 и т. д., B превратится в C.
Это вызывает те же переключатели, что и последний элемент в списке.Мы не утверждаем, что это исчерпывающий список. Если ваши ученики найдут какие-то другие свойства четырех ответов, мы будем рады услышать о них и добавить в список.
Последовательность обучения
- Относитесь к этому как к любому из уроков-задач, которые можно найти в другом месте на этом сайте. Представьте проблему и обсудите ее, чтобы убедиться, что все учащиеся понимают, о чем идет речь в вопросе и как его можно решить. Затем в группах от 2 до 4 дайте учащимся возможность решить задачу.
- Когда группы будут придумывать ответы, предложите им найти больше ответов, спросив: «Вы можете найти еще?».
- Когда они решат, что нашли все возможные ответы, предложите им доказать, что ответы, которые они нашли, единственные, которые существуют. («Как вы думаете, почему ответов больше нет?») В рамках этого процесса попросите их подумать, как ответы связаны друг с другом, как мы сделали в списке из пяти пунктов выше. Этот список пригодится позже и является хорошим математическим инструментом — посмотрите на то, что у вас есть, чтобы увидеть, есть ли какой-то способ понять это лучше.
- Обсудите в классе результаты исследования. Попросите разных учащихся написать один ответ на доске, пока они не увидят, когда два ответа совпадают (из-за симметрии треугольника) и что ответов всего четыре. Сделайте предположение о количестве ответов.
- Наконец-то проведите сеанс мозгового центра, чтобы сгенерировать идеи для следующего урока. Как мы можем доказать/обосновать, что ответов всего четыре? Каковы ключевые идеи? Как мы можем ограничить проблему?
Обратите внимание, что вы вполне можете подумать об идеях, которые мы здесь не рассмотрели. Важно, чтобы вы следили за ними, чтобы увидеть, куда они ведут. Если вы получите хорошие результаты, пожалуйста, сообщите нам, чтобы мы могли рассказать другим. Мы обязательно признаем все, что вы размещаете в сети.
Сессия 2
Покажите, что есть только четыре ответа на задачу о шести кругах.
Предыстория
Итак, как и почему на исходный вопрос есть только 4 ответа? И как мы можем установить это вне всяких разумных сомнений? На самом деле есть несколько способов сделать это.
- «Я работаю над этим уже 15 минут и больше не могу найти. Значит, их должно быть только четыре».
Это не доказательство. Мы не можем быть уверены, что не смогли найти другого ответа, уделив проблеме больше времени. Или, может быть, кто-то умнее нас мог бы найти другой ответ. Или, может быть, кто-то в другой стране мог. Здесь слишком много места для сомнений. Это не основание для математического доказательства.
Однако, возможно, это лучшее, что мы можем сделать. Например, на одном этапе мы думали, что планет всего 7. Мы смотрели на небо тысячи лет, а видели только семь.
Если у нас нет инструментов, чтобы что-то урегулировать, нам, возможно, придется полагаться на подход «Я больше не могу найти». Хотя в какой-то момент это может представлять собой наилучшее состояние наших знаний, в математике это в лучшем случае предположение — догадка о том, каков на самом деле ответ. Математика требует доказательства, обоснования, к которому нельзя придраться. Проблема в том, что если вы поработаете еще 10 минут, вы можете просто найти другой ответ.
Но потом появился Джон Адамс и сказал, что если уравнения движения Ньютона верны, то там происходит что-то странное. Было некоторое «колебание» планет, которое навело его на мысль, что есть еще одна планета, которую мы не обнаружили к 1845 году. Он рассчитал, где должна быть планета, а затем кто-то пошел искать и в конце концов нашел ее в сентябре 1846 года.- «Я рассмотрел все варианты, и есть только четыре ответа».
Это достаточно хорошее доказательство, если можно показать, что были рассмотрены все возможные случаи.
Одним из способов сделать это было бы написать компьютерную программу. На первый взгляд, есть 6 способов вставить первое число, 5 — следующее и так далее. Следовательно, существует 6 х 5 х 4 х 3 х 2 х 1 = 720 способов сложить 6 чисел. Это не займет у компьютера много времени. Вы даже можете заставить класс сделать это за разумное время, разделив дела между ними. Ниже мы даем способ сделать это, что означает, что нам не нужно рассматривать все 720 возможностей.
Подумайте, где поставить цифру 1. Из-за симметрии треугольной формы есть только два места, где можно поставить 1: в угловом круге или в круге посередине стороны. Мы показываем эти две ситуации ниже.
На следующем этапе мы хотим поставить двойки во всех возможных местах. Это можно сделать тремя способами для каждого из способов поставить 1.
Теперь в первой из этих трех ситуаций мы можем поставить 3 в четырех местах. Симметрия треугольника нам сейчас совсем не поможет. Если мы поместим 3 в кружок «а», то сумма стороны, которую мы произвели, будет равна 6. Нет другого способа составить 6, поэтому здесь нет возможного ответа.
Если мы поместим 3 в круг «b», то мы получим сумму a + 3 в левой части и a + 3 + c в нижней части. Они никогда не могут быть равны.
Если мы поместим 3 в круг «с», то аналогичное рассуждение показывает, что левая сторона имеет сумму а + 3, а нижняя — сумму а + b + 3. Они тоже никогда не могут быть равны.
Если мы поместим 3 в круг «d», мы должны поставить 4, 5, 6 внизу в некотором порядке. Это дает сумму, которая больше, чем можно получить на двух других сторонах.
Мы оставляем вас и ваш класс на рассмотрение всех остальных дел.
Во всяком случае, вышеизложенное является упражнением в систематичности. Важно делать все осторожно и в определенном порядке, чтобы были учтены все возможности.
Что здесь нужно сделать, так это перечислить все возможные способы размещения чисел от 1 до 6 в 6 кругах, а затем выбрать из этого списка те, которые дают равные суммы по всем трем сторонам.
Поскольку это утомительно, мы сделаем это только для одного случая. Если вы хотите, вы можете заставить свой класс завершить аргумент.
Вы можете разделить вещи так, чтобы разные группы студентов выполняли разные кейсы. Это бы ускорило дело. Возможно, единственное утешение в том, что делать это таким образом, это то, что это намного проще, чем делать 720 разных случаев. Но это некрасиво. Мы надеемся, что есть лучший способ.- Паритет – нечетные и нечетные. «Где я могу поставить четные числа и где я могу поставить нечетные числа?»
Аргумент здесь основан на том факте, что сумма двух четных чисел четна; сумма двух нечетных чисел четна, а сумма четного и нечетного числа нечетна.
Теперь есть только три нечетных числа, и у нас может быть либо нечетное количество нечетных чисел на одной стороне треугольника, либо у нас может быть четное число. При внимательном рассмотрении мы видим, что существует всего четыре возможных расположения шансов и четов.
Теперь мы знаем, куда идут 1, 3, 5. Из-за симметрии равностороннего треугольника числа 1, 3, 5 можно вставить в первую и четвертую указанные выше возможности только одним способом. Оттуда достаточно быстро увидеть, куда должны идти четные числа. Есть три возможных расположения 1, 3, 5 в двух других случаях. Систематическая работа выявит, какие схемы работают, а какие нет. Когда все это будет сделано, мы получим четыре ответа, которые мы нашли ранее.
Мы показываем их ниже. Четные числа указаны в пустых кружках, а нечетные — в кружках, отмеченных буквой «о».- Сократите суммы и произведите суммы.
В этом методе доказательства мы прежде всего показываем, что суммы, которые мы можем получить на каждой стороне треугольника в ответе, довольно ограничены. В конце концов, у вас может быть боковая сумма 24, 18, 13, 12?
Для этого подумайте сначала о 1. В какой наибольшей сумме может быть 1? Самая большая сумма будет с 5 и 6, чтобы дать сумму 12.
Итак, как мы можем получить 9? Делайте это систематически. Если бы мы использовали 6, нам пришлось бы составить 3, используя два числа. Это можно сделать только с 1 и 2. Если бы мы использовали 5, нам пришлось бы составить 4, используя два числа. Это можно сделать только с 1 и 3. (2 и 2 не допускаются.) Если бы мы использовали 4, нам пришлось бы составить 5, используя два числа. Это можно сделать только с 2 и 3. (1 и 4 не допускаются.) Таким образом, есть только три возможности:
6 + 2 + 1; 5 + 3 + 1; 4 + 3 + 2.
У треугольника всего три стороны, поэтому они у нас есть. Вопрос только в том, какие цифры стоят в углах? Но это легко. Это числа, которые встречаются дважды в трех суммах. Так мы быстро получаем четыре ответа, которые получили методом проб и ошибок в первой сессии.
Этот метод доказательства того, что существует ровно четыре ответа, возможно, самый приятный из всех. У него определенно есть хороший аргумент, который показывает, что суммы ограничены от 9 до 12 включительно.
Таким образом, это самая большая сумма, которую мы можем получить. Теперь переверни это. В какой наименьшей сумме может быть 6? Конечно, это с 1 и 2, чтобы получить наименьшую сумму 9. Таким образом, суммы могут лежать только между 9 и 12 включительно.
- Немного алгебры.
Здесь мы пытаемся использовать алгебру, чтобы увидеть, какой прогресс может быть достигнут. Начнем с расстановки букв a, b, c, d, e, f в кружках. Как показано на диаграмме ниже.
Предположим, что сумма по каждой стороне равна s. Тогда у нас есть следующее уравнение:
3s = (a + b + c) + (c + d + e) + (e + f + a)
= (a + b + c + d + e + f) + (a + c + e) Но сумма в первой скобке равна 1 + 2 + 3 + 4 + 5 + 6 в некотором порядке, так что сумма равна 21. Сумма во второй скобке — это просто сумма трех углов. Итак, у нас теперь
3s = 21 + углы.
Но наименьшее значение углов равно 1 + 2 + 3 = 6, а наибольшее значение углов равно 4 + 5 + 6 = 15.
27 = 21 + 6 < 3s < 21 + 15 = 36.
Таким образом, сумма должна лежать между 9 и 12, как мы обнаружили в Методе 4 выше. Но теперь у нас есть бонус, потому что уравнение здесь говорит нам, чему равна сумма углов. Если s = 9, сумма углов равна 6 и, следовательно, 1, 2, 3. Если s = 10, сумма углов равна 9 и, следовательно, 1, 2, 6; 1, 3, 5; или 2, 3, 4. Если s = 11, сумма углов равна 12 и, следовательно, 1, 5, 6; 2, 4, 6; 3, 4, 5. Если s = 12, сумма углов равна 15 и, следовательно, 4, 5, 6.
Для s = 9 и 12 ответы теперь просто выпадают. Для s = 10 и 11 необходимо проделать некоторую работу, но ясно, что, например, если 1, 5 и 6 находятся в углах, невозможно получить сумму 11. Таким образом, работа Это слишком сложно и, возможно, проще, чем найти все способы получить 10. Как бы то ни было, мы все равно получаем четыре ответа, которые продолжаем получать.
Итак, каковы же ставки этого метода на «привлекательность»? Он действительно полагается на знание алгебры, но как только преодолев это препятствие, он довольно быстро дает числа углового круга, а остальные числа встают на свои места.
Итак, у нас есть
Единственная небольшая задержка заключается в том, что мы должны учитывать некоторые угловые числа, которые не работают; но, возможно, это небольшая цена. Конечно, это намного лучше, чем метод 1.Последовательность обучения
- Вспомните задачу и обсудите предположение, сделанное на прошлом уроке. Как мы можем доказать эту гипотезу? Обратите внимание, что было бы хорошо ограничить возможные побочные суммы. «Как мы можем это сделать?» В ходе обсуждения подведите их к некоторым идеям, лежащим в основе различных доказательств.
- В группах по 2 или 4 человека пусть они поработают над придуманными ими идеями. Наш опыт показывает, что с минимальными подмостками учащиеся могут прийти к идее метода 4. Возможно, вам придется помочь им, спросив: «Какова наибольшая сумма, в которую может быть вовлечено 1?», «Какова наименьшая сумма, в которую может быть вовлечено 6». может участвовать?
Любую из более быстрых групп следует поощрять к поиску другого решения. - Когда несколько групп придут к доказательству (возможно, с вашей помощью), проведите отчетную сессию. Пусть один из учащихся скажет, что придумала их группа. Попросите остальную часть класса проверить, что утверждает этот ученик. ‘Есть ли что-то непонятное?’ ‘Есть ли какая-то часть, которой вы не следуете?’ ‘Есть ли какая-то часть, которая неверна?’
- Дайте всему классу возможность написать доказательство своими словами.
- Покажите классу другой способ доказать, что ответов всего четыре. ‘Какое доказательство лучше?’ ‘Какое доказательство ‘лучше’?’
- В качестве введения к следующему уроку попросите их подумать о том, как можно обобщить или расширить проблему. «Какие еще проблемы мы можем сделать из этой?» Именно на этом этапе опыт отдела решения проблем V-sets будет ценным.
Сессия 3
Рассмотрим расширение задачи шести кругов – задачу восьми кругов. Найдите все его ответы и покажите, что других нет.
Фон
Здесь мы рассмотрим задачу, похожую на задачу шести кругов.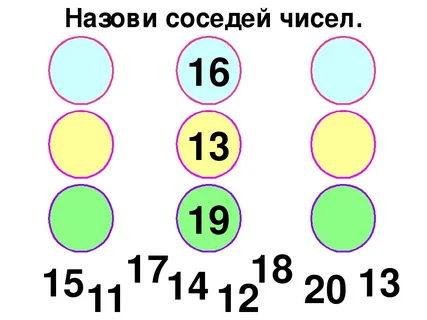
Учитывая опыт, который мы получили с Задачей шести кругов, мы должны быть в состоянии добиться некоторого прогресса в этой новой задаче. Эта задача является расширением задачи шести кругов.
Задача восьми кругов: можно ли расположить числа 1, 2, 3, 4, 5, 6, 7, 8 в кругах так, чтобы суммы трех чисел по обе стороны квадрата были одинаковыми ?
Технику, которую мы использовали с Задачей шести кругов, можно использовать здесь снова. Здесь сработает любой из методов, отмеченных нами при доказательстве гипотезы о четырех ответах (см. Предысторию занятия 2). Однако очевидно, что некоторые из них более эффективны. Например, если у ваших учеников есть достаточные способности к алгебре, мы предлагаем им попробовать метод 5, чтобы получить боковые суммы. Этот метод сокращает количество вариантов более эффективно, чем поиск наибольшей суммы, в которой может быть 1. Таким образом, ваш класс должен обнаружить, что единственными возможными суммами являются 12, 13, 14 и 15.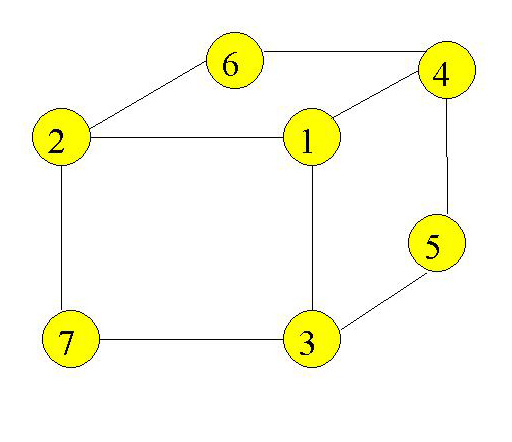
Эта задача требует немного больше усилий, чем задача шести кругов, но в конце, благодаря систематическому подходу к ней, ваши ученики узнают, что нашли все возможные ответы. Из-за дополнительной работы мы предлагаем вашему классу работать в группах не менее 4 человек и распределять работу между ними.
В итоге они должны найти шесть ответов. Мы перечисляем их ниже.
Последовательность обучения
- Предложите учащимся подумать о расширениях или обобщениях задачи шести кругов. Постарайтесь получить от класса несколько идей (некоторые возможности можно найти в этом разделе). Подведите их к задаче о восьми кругах.
- Следуйте шагам Сессии 1, чтобы позволить им решить Задачу Восьми Кругов. Это сложнее, чем задача шести кругов, поэтому может быть полезно, если они разделят определенные части задачи между собой. Соберите их вместе, когда они решат, что у них есть ответы на большинство вопросов. Обсудите, как они могут получить остальные. Обсудите, как они могут доказать, что существует только шесть ответов.
Занятие 4
Обобщите задачу шести кругов, найдя, какие наборы из шести чисел могут заменить 1, 2, 3, 4, 5, 6, и уравновесив суммы по обе стороны треугольника.
Предыстория
Пришло время обобщить.
Задача: Какие другие наборы из 6 чисел можно разместить в шести кругах ниже, чтобы суммы чисел на каждой из сторон были одинаковыми?
Это обобщение исходной задачи шести кругов, поскольку, когда мы находим ответ, он также дает нам ответ на исходную задачу. В этом смысле проблема восьми кругов не является обобщением, потому что ее решение не дает нам немедленно решения проблемы шести кругов.
Еще раз поэкспериментировать. Что вы можете придумать? Вероятно, тот факт, что любые шесть последовательных чисел сработают, не так уж трудно понять. Тогда, возможно, подойдут любые шесть чисел, находящихся на одинаковом расстоянии друг от друга, например 5, 8, 11, 14, 17 и 20. Их можно рассматривать как любую линейную комбинацию 1, 2, 3, 4, 5, 6.
Это потому, что их можно записать в форме {m + in: где i = 1, 2, 3, 4, 5, 6, а m и n — любые целые числа}.
Но разве это единственные возможности? Как насчет {1, 2, 3, 4, 5, 100} или {1, 2, 3, 4, 5, 6, 50} или {1, 2, 3, 4, 5, 7}? Удивительно, но последняя из этих работ дает два ответа. Итак, если бы у нас был набор вроде {a, b, c, d, e, f}, как бы мы узнали, даст он нам ответ или нет? Хитрость здесь заключается в том, чтобы поэкспериментировать и посмотреть, какие предположения вы можете придумать.
И когда вы это сделаете, вы начнете видеть, сколько ответов вы получили для каждого набора. Тогда вы можете задать еще несколько вопросов.
Можете ли вы найти наборы чисел, для которых существует только один способ сделать все суммы равными? Что можно сказать о таких наборах?
Можете ли вы найти наборы чисел, для которых есть ровно два способа сделать все суммы равными? Что можно сказать о таких наборах?
Можете ли вы найти наборы чисел, для которых существует ровно три способа сделать все суммы равными? Что можно сказать о таких наборах?
Можете ли вы найти наборы чисел, для которых существует ровно четыре способа сделать все суммы равными? Что можно сказать о таких наборах?
Но давайте сначала рассмотрим общую проблему.
Мы уже знаем по четырем ответам, которые мы получили в Сессии 1, что
- Разница между противоположными угловыми и средними числами одинакова. Посмотрите на A. 4 напротив 1 и 4 – 1 = 3. 5 напротив 2 и 5 – 2 = 3. 6 напротив 3 и 6 – 3 = 3.
Вы должны обнаружить, что это верно для всех возможных правильных способов заполнить шесть кругов. Разница между противоположными угловыми и средними числами одинакова. Так что возьмите это и немного поработайте с этим, превратив его в гипотезу.
Гипотеза: набор из шести чисел правильно заполнит шесть кругов тогда и только тогда, когда набор состоит из трех различных пар, имеющих общую разность.
Просто чтобы проверить, что это значит, набор из шести чисел должен иметь форму a, a + d; б, б + г; в, в + г.
Но как это доказать? Итак, если мы поместим a, b и c в углы и их пары в противоположный средний круг, мы получим конфигурацию, показанную ниже.
Тогда сумма трех чисел с каждой стороны равна a + b + c + d.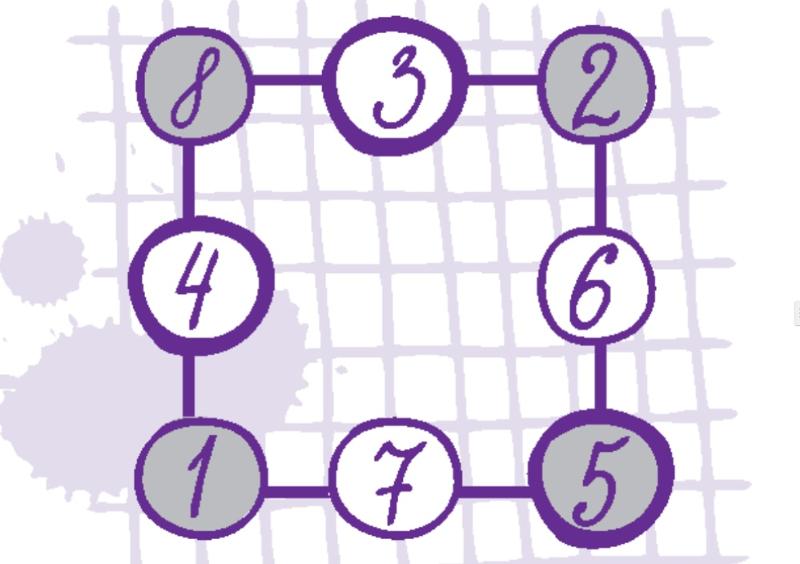
Таким образом, мы получаем законный набор.
Но что, если у нас есть законный набор? Можем ли мы показать, что их можно расположить в три пары с общим различием?
Итак, давайте предположим, что у нас есть ответ, подобный показанному на диаграмме выше, где шесть чисел — это j, k, m, n, p, r. Поскольку у нас есть три равные суммы, то
j + k + m = m + n + p = p + r + j.
Теперь j + k + m = m + n + p подразумевает, что j + k = n + p или что j – n = p – k.
И m + n + p = p + r + j означает, что m + n = r + j или что j – n = m – r.
Это дает j – n = m – r = p – k. Таким образом, набор состоит из трех различных пар, имеющих общую разность.
Итак, теперь, когда мы видим шесть чисел, мы можем сказать, сможем ли мы поместить их в шесть кругов так, чтобы суммы на каждой стороне треугольника были одинаковыми.
Последовательность обучения
- Рассмотрев расширение задачи шести кругов, пора перейти к ее обобщению. В ходе обсуждения предложите им подумать о том, какие наборы из шести чисел могут работать в шести кругах.
- Пусть они разделятся на группы и найдут другие наборы из шести чисел, которые «работают». Предложите им увидеть, что общего у этих наборов.
- Возможно, вам придется снова собрать класс, чтобы подумать о найденных наборах. Нашли ли они какие-либо наборы, кроме линейных комбинаций исходных чисел? Если нет, попросите их попробовать {1, 2, 3, 4, 5, 100} или {1, 2, 3, 4, 5, 6, 50} или {1, 2, 3, 4, 5, 7}. ‘Вы можете придумать что-нибудь еще?’
- Пусть они поработают над этим некоторое время, пока не придут к выводу. Предложите им доказать гипотезу.
- Дайте им возможность обсудить свои доказательства перед всем классом. Пусть пишут доказательство.
В ходе обсуждения предложите им подумать о том, какие наборы из шести чисел могут работать в шести кругах.Сессия 5
Найдите и докажите, что в задаче о шести кругах есть только ноль, два или четыре ответа для любого набора из шести чисел.
Фон
Здесь мы рассмотрим вопросы о том, какие наборы дают 1, 2, 3 или 4 ответа.
Опять же, для начала нужно провести эксперимент, но ключ к проблеме можно найти в списке свойств ответов из Сессии 1. Помните, номер 3 в списке говорит:
Изменение угловых номеров на средние и наоборот меняет один ответ на другой. В результате нетрудно увидеть, что ответы приходят парами. Немного сложнее понять, какие наборы дают четыре ответа, но оказывается, что четыре ответа можно получить, только если набор представляет собой линейную комбинацию чисел 1, 2, 3, 4, 5, 6.
Теорема 1. ответы из набора из шести разных чисел идут парами.
Доказательство. Предположим, что шесть чисел — это a, a + d, b, b + d, c c + d, и они расположены, как мы делали выше, с a, b, c в углах. Тогда нетрудно заметить, что мы можем составить другой ответ с a, b, c в средних кругах и a + d, b + d, c + d соответственно напротив них в углах.
Теорема 2. Набор из шести чисел дает четыре ответа тогда и только тогда, когда набор является линейной комбинацией чисел 1, 2, 3, 4, 5, 6.
Конечно, если у нас есть такая линейная комбинация, мы можно получить четыре ответа, заменив i в исходных четырех ответах на m + in.
Вы можете проверить, что боковые суммы по-прежнему равны. (Обратите внимание, что здесь мы не можем сформировать более четырех ответов, потому что в противном случае замена m + на i даст нам больше ответов на исходную задачу.)
Предположим, что шесть чисел равны a, a + d, b, b + d, c, c + d и что a < b < c. Затем, поскольку у нас есть другой возможный ответ (кроме очевидного), a + e для некоторого, возможно, нового значения e должно равняться одному из пяти других чисел. Посмотрите на возможные 5 случаев.
a + e = c + d: Но поскольку a — наименьшее число, любое другое число в наборе плюс e будет больше, чем c + d. Это невозможно.
a + e = b + d: Очевидно, что d не равно e, иначе a равнялось бы b. Теперь есть три возможности: c + d = c + e; с + д = б + е; и c + d = a + d + e. Единственное, что ведет куда-либо, это c + d = b + e, когда e = 3d, и мы получаем линейную комбинацию a, a + d, a + 2d = b, a + 3d = b + d, a + 4d = c и а + 5d = с + d.
а + е = а + d: Здесь е = d и, следовательно, с + d = с + е; с + д = б + е; и c + d = b + d + e.
Все это приводит к противоречиям или отсутствию прогресса.
а + е = с: Следовательно, с + d = b + е; с + д = б + д + е; и c + d = a + d + e. Все это приводит к противоречиям.
а + е = b: Следовательно, с + d = с + е; с + d = b + d + е; и c + d = a + d + e. Единственное, что ведет куда-либо, это c + d = b + d + e, что дает d = 3e и линейную прогрессию a, a + e = b, a + 2e = c, a + 3e = a + d, a + 4e. = b + d и a + 5e = c + d.
Таким образом, единственная возможность для четырех ответов — это когда у нас есть линейная прогрессия.
Последовательность обучения
В первую очередь стоит отметить, что работы в этом блоке очень много и некоторые вещи можно выкинуть. Мы предполагаем, что доказательство случая с четырьмя ответами может быть единственно возможным, поскольку оно концептуально сложно. Однако они могут дойти хотя бы до предположения, что для любого набора из шести чисел существует не более четырех ответов.
Начните урок с того, что предложите им подумать о том, сколько ответов может дать любой набор.
Это может быть сделано в обстановке всего класса или в их группах. Как обычно, они должны сначала выдвинуть гипотезу, а затем попытаться найти доказательство этой гипотезы.Обсудите их предположения всем классом и поговорите о том, какие методы доказательства можно использовать.
Когда доказательство найдено, попросите учащегося представить его всему классу. Пусть критикуют. Если никто не может найти доказательства, даже с вашей помощью, дайте доказательство сами. Пусть критикуют. (Это может быть полезно, если вы делаете это, чтобы обнаружить странную ошибку, чтобы держать их в напряжении.) Пусть все они напишут доказательство.
Просмотрите и обсудите результаты подразделения в целом. Что им понравилось? Что было тяжело?
Это может быть сделано в обстановке всего класса или в их группах. Как обычно, они должны сначала выдвинуть гипотезу, а затем попытаться найти доказательство этой гипотезы.Натуральные числа, целые числа, рациональные числа, иррациональные числа, вещественные числа и т. д.
Натуральные числа
натуральные числа (или , считая ) числа равны 1, 2, 3, 4, 5 и т.
д.
много натуральных чисел. Набор натуральных чисел {1,2,3,4,5,…},
иногда для краткости пишется N .
целые числа являются натуральными числами вместе с 0.
(Примечание: некоторые учебники не согласны и говорят, что натуральные числа включают 0.)
Сумма любые два натуральных числа также являются натуральным числом (например, 4+2000=2004), а произведение любых двух натуральных чисел — натуральное число (4×2000=8000). Этот однако это неверно для вычитания и деления.
Целые числа
Целые числа представляют собой набор действительных чисел, состоящий из натуральных чисел, их аддитивных инверсий и нуля.
{…,−5,−4,−3,−2,−1,0,1,2,3,4,5,…}
Набор целых чисел иногда пишется J или Z для краткости.
сумма, произведение и разность любых двух целых чисел также являются целыми числами. Но это неверно для деления… просто попробуйте 1÷2.
Рациональные числа
Рациональные числа те числа, которые могут быть выражены как отношение между
два целых числа.
Например, дроби 13 и −11118 равны
рациональное число. Все целые числа входят в число рациональных,
так как любое целое число z может быть записано как отношение z1.
Все десятичные дроби, которые заканчиваются, являются рациональными числами (поскольку 8.27 можно записать как 827100). которые имеют повторяющийся шаблон после некоторого момента, также являются рациональными: например,
0,0833333….=112.
Множество рациональных чисел замкнуто относительно всех четырех основных операций, то есть для любых двух рациональных чисел их сумма, разность, произведение и частное также являются рациональными числами (если мы не делим на 0).
Иррациональные числа
иррациональное число — это число, которое нельзя записать в виде отношения (или дроби). В десятичной форме оно никогда не заканчивается и не повторяется.
древние греки обнаружили, что не все числа рациональны; там
уравнения, которые нельзя решить, используя отношения целых чисел.
Первое такое уравнение для изучения было 2=x2. Что число, умноженное на себя, равно 2?
2 есть около 1,414, потому что 1,4142=1,999396, что близко к 2. Но вы никогда не попадете точно в квадрат дроби (или десятичная дробь). Квадратный корень из 2 является иррациональным числом, т. десятичный эквивалент продолжается вечно, без повторяющегося шаблона:
2=1.41421356237309…
Другие известные иррациональные числа золотое сечение , число с большим значение для биологии:
1+52=1,61803398874989…
π (пи), отношение длины окружности к ее диаметру:
π=3,14159265358979…
и e, самое важное число в исчислении:
e=2,71828182845904…
Иррациональные числа могут быть далее подразделены на алгебраических чисел, которые являются решениями некоторых полиномиальных уравнений (таких как 2 и золотое сечение), и трансцендентных чисел, которые не являются решениями ни одного полиномиального уравнения.
π и e оба трансцендентны.
Вещественные числа
Вещественные числа — это набор чисел, содержащий все рациональные числа и все иррациональные числа. Настоящие числа — это «все числа» на числовой прямой. Существует бесконечно много действительных чисел, так же как бесконечно много чисел в каждом из других наборов чисел. Но можно доказать, что бесконечность действительных чисел равна 9.0381 больше бесконечность.
«Меньший», или исчисляемое бесконечность целых чисел и рациональные числа иногда называют ℵ0 (алеф-ноль), и несчетная бесконечность реалов называется ℵ1 (алеф-один).
Есть еще «большие» бесконечности, но для этого вам нужно пройти курс теории множеств!
Комплексные числа
Комплексные числа множество {a+bi | a и b — действительные числа}, где i — мнимая единица, −1. (нажмите здесь для подробнее о мнимых числах и операциях с комплексными числами).
Комплексные числа включают множество действительных чисел.
Leave A Comment