Модуль вектора равен – Модуль вектора, формула и примеры

Модуль вектора

ВЕКТОРЫ НА ПЛОСКОСТИ

ОСНОВНЫЕ ПОНЯТИЯ И СВОЙСТВА
ОПРЕДЕЛЕНИЕ ВЕКТОРА

Вектором называется направленный отрезок, то есть отрезок, у которого указаны начало (наз. также точкой приложения вектора) и ко­нец.

МОДУЛЬ ВЕКТОРА

Длина направленного отрезка, изо­бражающего вектор, называется длиной, или модулем, вектора. Длина вектора обозначается .
НУЛЬ-ВЕКТОР

Нуль-вектор () — вектор, начало и конец которого совпадают; его модуль равен 0, а направление неопределенное.

КООРДИНАТНОЕ ПРЕДСТАВЛЕНИЕ

Пусть на плоскости задана декартова система координат XOY.

Тогда вектор может быть задан двумя числами:

и

Эти числа и в геометрии называют координатами вектора, а в физике – проекциями вектора на соответствующие оси координат.

При таком определении вектора его модуль , а направление задается углом , который однозначно определяется соотношениями:

и

Нуль-вектор: и

ПРЕДСТАВЛЕНИЕ В СИСТЕМЕ КООРДИНАТ, ЗАДАННОЙ ЕДИНИЧНЫМИ ВЕКТОРАМИ (ОРТАМИ)

Пусть на плоскости задана декартова система координат при помощи единичных векторов и :

Тогда вектор может быть задан следующим образом:

Очевидно, что:

и

При таком определении вектора его модуль , а направление задается углом , который однозначно определяется соотношениями:

и

Нуль-вектор:

КОЛЛИНЕАРНЫЕ ВЕКТОРЫ

Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых.

РАВЕНСТВО ВЕКТОРОВ

Два вектора называются равными

, если они коллинеарны, имеют одинако­вую длину и одинаково направлены.

Все нуль-векторы считаются равными.

СУММА ВЕКТОРОВ

Суммой векторов и называют вектор , идущий из начала вектора в конец век­тора при условии, что начало вектора приложено к концу вектора . Происхождение этого правила связано с правилом параллелограмма сложения векторов, источником которого яв­ляется экспериментальный факт сложе­ния сил (векторных величин) по этому правилу.

Правило треугольника Правило параллелограмма

Координаты коллинеарных векторов удовлетворяют соотношению:

Координаты равных векторов удовлетворяют соотношениям:

и

Координаты вектора суммы двух векторов удовлетворяют соотношениям:

и

Координаты коллинеарных векторов удовлетворяют соотношению:

Координаты равных векторов удовлетворяют соотношениям:

и

Вектор суммы двух векторов:

Построение суммы нескольких векторов ясно из рисунка.

ПРОИЗВЕДЕНИЕ ВЕКТОРА НА ЧИСЛО

Произве­дением вектора на число  называют вектор, коллинеарный вектору , имею­щий длину, равную , и направле­ние, совпадающее с направлением при > 0 и противоположное при ПРОТИВОПОЛОЖНЫЕ ВЕКТОРЫ

Век­тор называется противоположным

вектору и обозначается .

СВОЙСТВА ДЕЙСТВИЙ НАД ВЕКТОРАМИ

Операции сложения векторов и умножения вектора на число обладают след. свойствами:

1) ,

2) ,

3) ,

4),

5) ,

6) ,

7) ,

8).

Координаты вектора суммы нескольких векторов удовлетворяют соотношениям:

Координаты вектора произведения вектора на число удовлетворяют соотношениям:

Координаты противоположных векторов удовлетворяют соотношениям:

Сумма нескольких векторов:

Произведение вектора на число:

Вектор, противоположный :

Скалярное произведение векторов и (обозначается ) — скаляр, определяемый равенством , где — угол между векторами и , приведенными к общему началу:

Скалярное произведение векторов:

Скалярное произведение векторов:

ДОПОЛНЕНИЕ: ТИПЫ ВЕКТОРНЫХ ВЕЛИЧИН В ФИЗИКЕ.

Векторами называются такие геометрические и физические величины, которые однозначно определяются отрезками с заданным положением, направлением и длиной независимо от системы отсчета и подчиняются правилам I – IV (см. далее).
Вектор называется полярным в том случае, когда положение и направление изображающего его отрезка непосредственно дает положение и направление представляемой величины (радиус-вектор, скорость, ускорение, сила, импульс).

Вектор называется осевым (аксиальным) в том случае, если соотношение между представляемой величиной и изображающим ее отрезком устанавливается посредством задания некоторой оси и определенного направления вращения вокруг этой оси. Принято, чтобы направление выбранного на оси отрезка составляло с осью вращения правый винт (угловая скорость, момент сил, вращательные импульсы).

Длина отрезка – модуль вектора в определенном масштабе.
Различают свободные, скользящие и связанные векторы:

Свободные векторы можно произвольно переносить в любое другое параллельное положение, сохраняя при этом их направление и длину (напр., вектор скорости при поступательном движении тела).

Скользящие векторы неотделимы от несущей их прямой, от так называемой линии действия, но вдоль этой прямой они могут перемещаться произвольным образом (напр., угловая скорость; сила, приложенная к твердому телу).

Связанные векторы неотделимы от определенной точки, от так называемой точки приложения вектора (напр., скорость точки тела, движущегося произвольным образом).
Правила выполнения операций над векторами:

I. Два вектора, и равны друг другу, если они имеют одинаковое направление и одинаковую длину; равные скользящие векторы должны иметь, кроме этого, общую линию действия, а равные связанные векторы – общую точку приложения.

II. Вектор получается из вектора следующим образом: из точки приложения вектора откладывается в противоположном направлении отрезок с такой же длиной, как у вектора .

III. Вектор : при m  0 – модуль в m раз больше, при m  0 – по правилу II/

IV. Два вектора, и , имеющие общую точку приложения, складываются по правилу параллелограмма. Разность векторов: .
Правила сложения применимы без ограничения к свободным векторам, к скользящим – только в случае наличия у линий действия векторов общей точки. Во всех остальных случаях действуют другие правила сложения (см., например, условие равновесия твердого тела).
Физическая величина считается векторной, если она подчиняется правилам I – IV. В частности, такому требованию удовлетворяют две скорости, которым одновременно обладает одна и та же материальная точка, или угловые скорости твердого тела, одновременно вращающееся вокруг двух пересекающихся осей.

www.dereksiz.org

4.2. Разложение вектора по ортам. Модуль вектора

1⁰.Разложение вектора по ортам. Из прямоугольного параллелепипеда (рис. 4.1) следует:

.

Но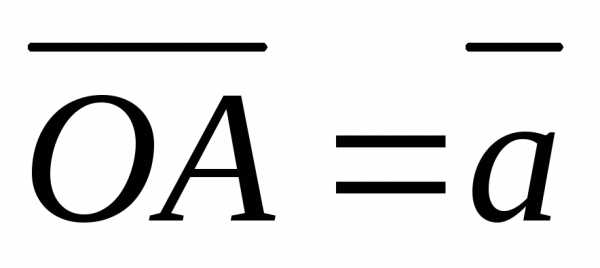

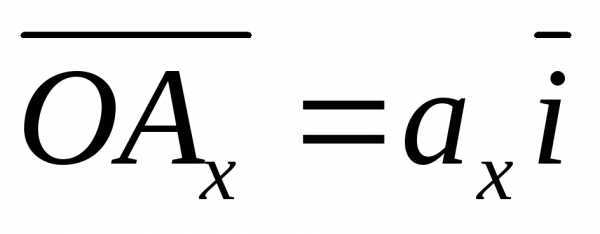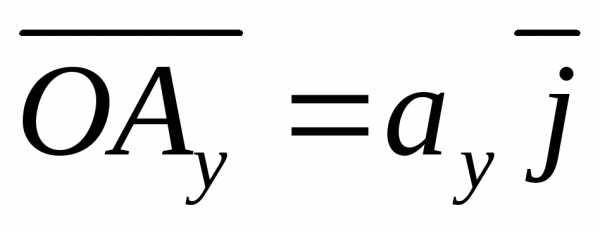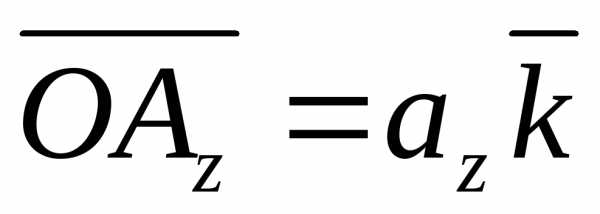,,,, Следовательно,

(4.3)

Равенство (4.3) и есть формула разложения вектора по ортам координатных осей.

Таким образом, координатная запись вектора может быть осуществлена двумя способами:

2⁰.Модуль вектора. Вектор

является диагональю прямоугольного параллелепипеда (рис. 4.1). Квадрат длины диагонали равен сумме квадратов трех его измерений:

,

отсюда следует: , и наконец, получаем искомую формулу:

(4.4)

Модуль вектора равен корню квадратному из суммы квадратов его координат.

4.3. Линейные операции над векторами.

Сформулируем правила действийнад векторами в координатной форме.

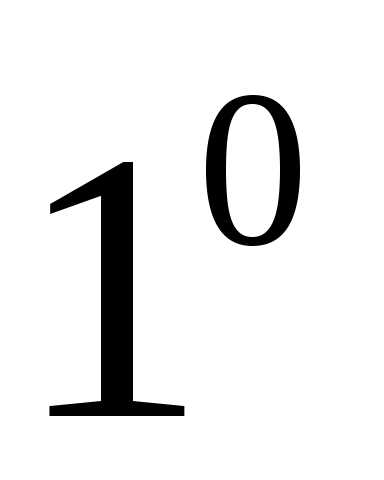.Координаты суммы (разности) векторов равны суммам (разностям) соответствующих координат этих векторов.

Пусть тогда

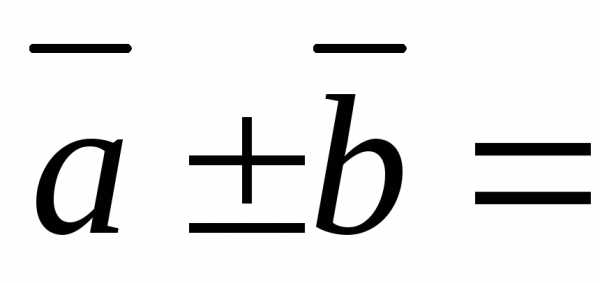
(4.5)

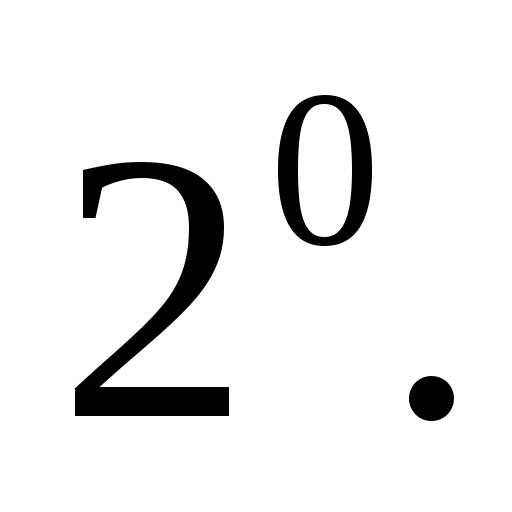При умножении вектора на скаляр его координаты умножаются на этот скаляр.

Если и– скалярная величина, то

(4.6)

Покажем применение рассмотренного в этой главе материала к решению практической задачи.

Задача 4.1. Даны векторы:

Найти: координаты и модуль вектора

Решение.Используем координатную запись векторов и правила линейных операций над ними:

Модуль вектора вычислим по формуле (4.4):

Ответ.

4.4. Направляющие косинусы вектора

Определение 4.2. Направляющими косинусами ненулевого вектора называются косинусы углов, которые этот вектор образуют с осями координат (рис. 4.2).

Выразим координаты вектора через его модуль и углы: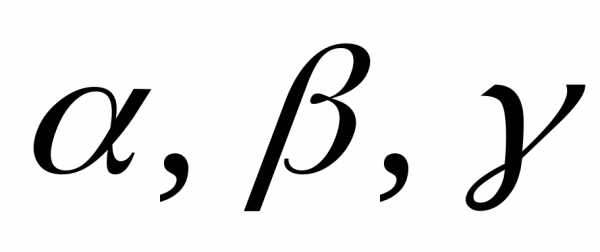

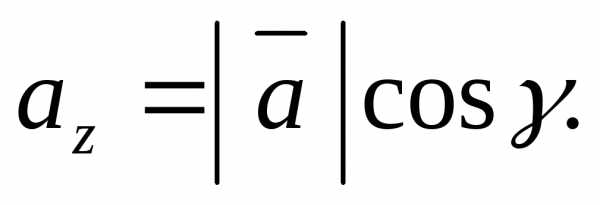
С помощью данных равенств найдем выражения направляющих косинусов через координаты вектора и его модуль:

(4.7)

Вычислим сумму квадратов направляющих косинусов вектора :

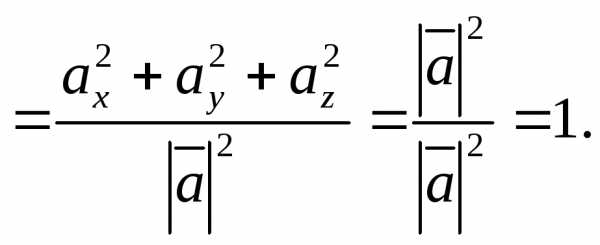
Полученный результат в векторной алгебре сформулирован в виде следующего утверждения:

Сумма квадратов направляющих косинусов ненулевого вектора равна единице:

(4.8)

Задача 4.2.Определить направляющие косинусы вектора а также убедиться в справедливости тождества(4.8).

Решение.1⁰. Определим координаты и модуль вектора:

2⁰. Вычислим направляющие косинусы вектора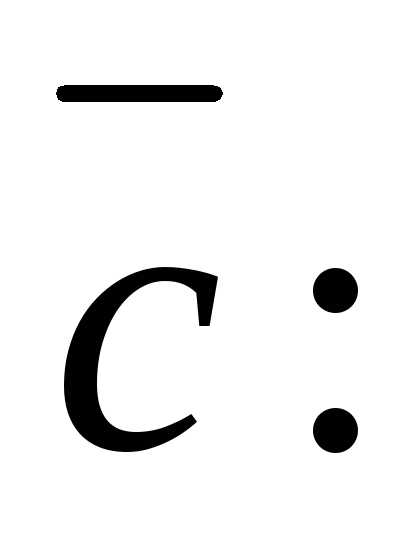

3⁰. Проверим справедливость тождества (4.8):

Ответ.

4.5. Координаты точки в пространстве. Вычисление координат вектора и его модуля по координатам его начала и конца.

Введем понятие координат точки в пространстве через понятие радиус-вектора.

Определение 4.3. Радиус-вектором точки М называется вектор 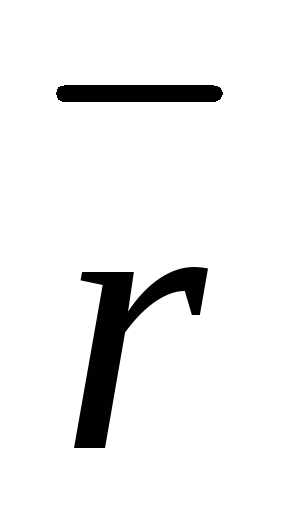с началом в начале координат и концом в точке М, то есть вектор (рис. 4.3).

В качестве координат точки М примем координаты радиус-вектора.

Определение 4.4. Координатами точки в пространстве называются координаты ее радиус-вектора.

Координаты точки М (рис. 4.3) обозначаются символом:, или. Таким образом,

Поставим задачу:найти координаты и модуль вектора 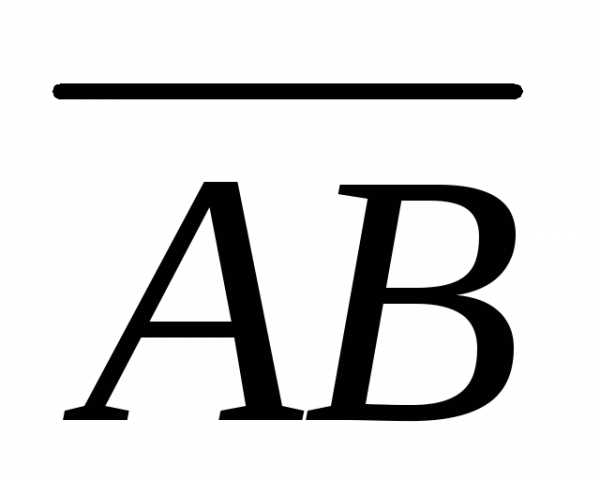, если известны координаты его начала и конца: (рис. 4.4).

Решение.Проведем в точкиАиВ радиус-векторыи, выразим координаты вектора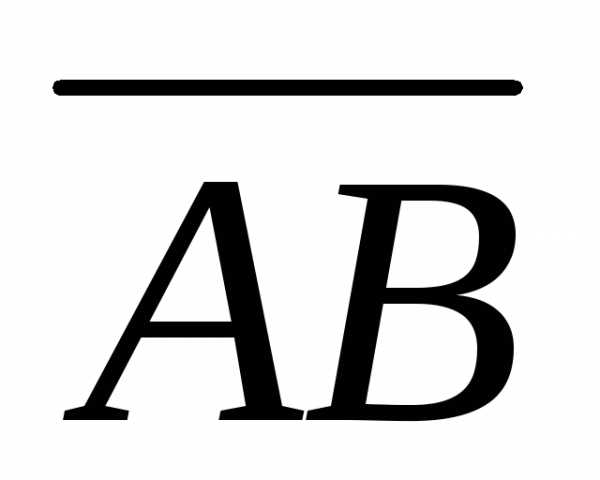через координаты векторови(см. определение 4.4), получим:

(4.9)

Координаты вектора равны соответствующим разностям координат конца и начала этого вектора.

Задача 4.3.Даны две точки: Найти координаты, разложение по ортам координатных осей, модуль и направляющие косинусы вектора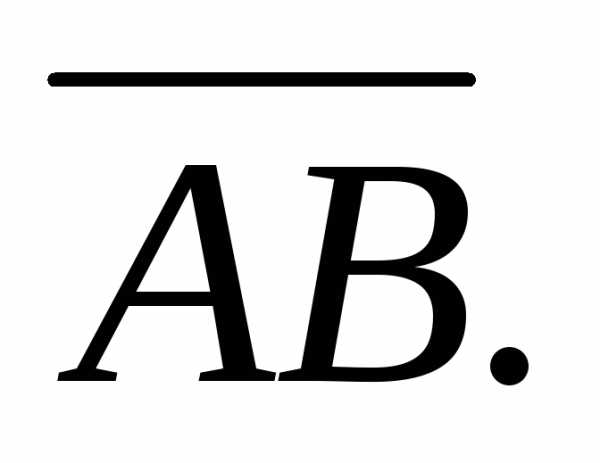

Решение.Для определения координат вектора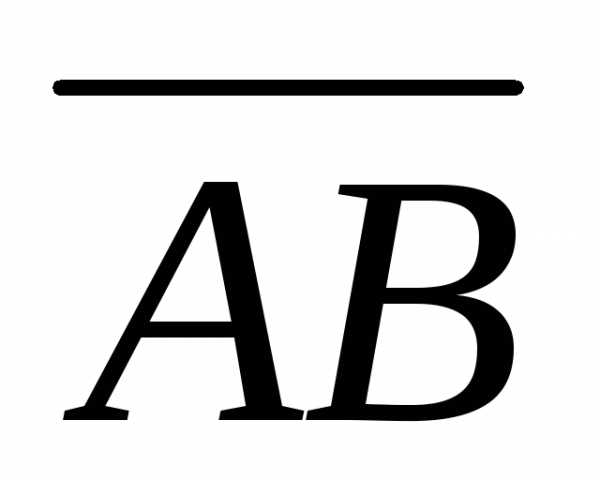воспользуемся формулой (4.9):

По формуле (4.4) вычислим модуль вектора :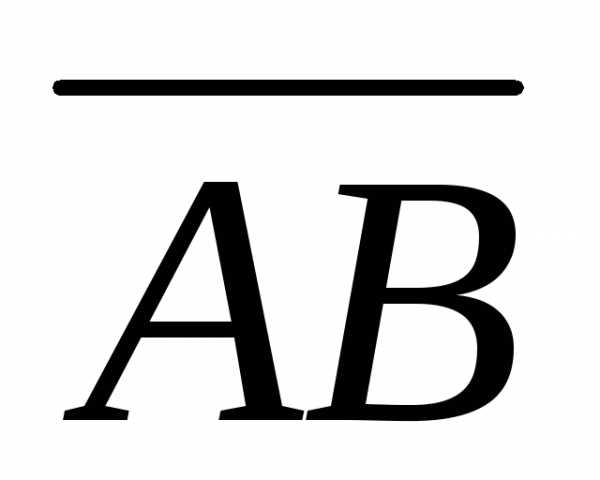

Найдем направляющие косинусы вектора :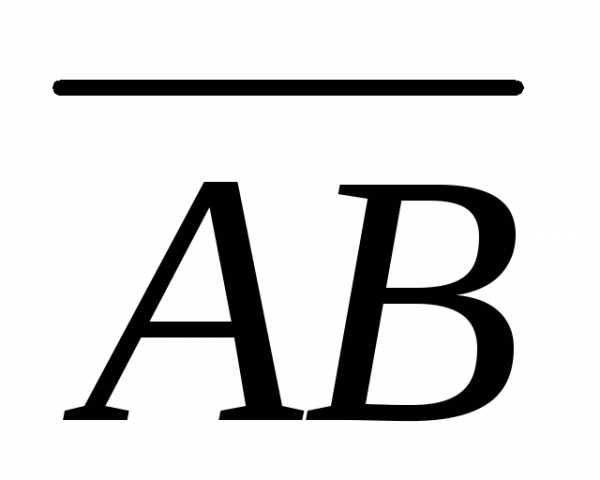

Вычислим сумму квадратов направляющих косинусов:

Ответ.

studfiles.net

Модуль вектора. Длина вектора.

Навигация по странице:

Определение длины вектора

Определение.

Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора AB.

Для обозначения длины вектора используются две вертикальные линии слева и справа |AB|.

Основное соотношение. Длина вектора |a| в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат.

Формулы длины вектора

Формула длины вектора для плоских задач

В случае плоской задачи модуль вектора a = {a_x ; a_y} можно найти воспользовавшись следующей формулой:

Формула длины вектора для пространственных задач

В случае пространственной задачи модуль вектора a = {a_x ; a_y ; a_z} можно найти воспользовавшись следующей формулой:

Формула длины n -мерного вектора

В случае n-мерного пространства модуль вектора a = {a₁ ; a₂; … ; a_n} можно найти воспользовавшись следующей формулой:

|a| = (	n	ai2)1/2
	Σ
	i=1

Примеры задач на вычисление длины вектора

Примеры вычисления длины вектора для плоских задачи

Пример 1. Найти длину вектора a = {2; 4}.

Решение: |a| = √2² + 4² = √4 + 16 = √20 = 2√5.

Пример 2. Найти длину вектора a = {3; -4}.

Решение: |a| = √3² + (-4)² = √9 + 16 = √25 = 5.

Примеры вычисления длины вектора для пространственных задачи

Пример 3. Найти длину вектора a = {2; 4; 4}.

Решение: |a| = √2² + 4² + 4² = √4 + 16 + 16 = √36 = 6.

Пример 4. Найти длину вектора a = {-1; 0; -3}.

Решение: |a| = √(-1)² + 0² + (-3)² = √1 + 0 + 9 = √10.

Примеры вычисления длины вектора для пространств с размерностью большей 3

Пример 5. Найти длину вектора a = {1; -3; 3; -1}.

Решение: |a| = √1² + (-3)² + 3² + (-1)² = √1 + 9 + 9 + 1 = √20 = 2√5

Пример 6. Найти длину вектора a = {2; 4; 4; 6 ; 2}.

Решение: |a| = √2² + 4² + 4² + 6² + 2² = √4 + 16 + 16 + 36 + 4 = √76 = 2√19.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

0oq.ru

Модуль вектора. Длина вектора. — Студопедия.Нет

Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора. Для обозначения модуля вектора используются две вертикальные линии слева и справа |AB|.

Модуль вектора (длина вектора) |a| в прямоугольных декартовых координатах равен квадратному корню из суммы квадратов его координат.

Так в случае плоской задачи модуль вектора можно найти по следующей формуле
|{a}| = sqrt{x_1^2+y_1^2}.

Пример вычисления модуля вектора (длины вектора)
Найти длину вектора {a} = {2;4}.
Решение: |{a}| = sqrt{2^2+4^2}=sqrt{4+16}=sqrt{20}=2sqrt{5}.

 

Так в случае пространственной задачи модуль вектора {a} = {x_1;y_1;z_1} можно найти по следующей формуле |{a}| = sqrt{x_1^2+y_1^2+z_1^2}.

Пример вычисления модуля вектора (длины вектора)
Найти длину вектора {a} = {2; 4; 4}.
Решение: |{a}| = sqrt{2^2+4^2+4^2}=sqrt{4+16+16}=sqrt{36}=6.

 

Ортогональные векторы. Ортонормированный базис.

Определение. Два вектора называются ортогональными, если угол между ними равен прямому углу, т.е. .

Обозначение: – векторы и ортогональны.

Определение. Тройка векторов называется ортогональной, если эти векторы попарно ортогональны друг другу, т.е. , .

Определение. Тройка векторов называется ортонормированной, если она ортогональная и длины всех векторов равны единице: .

Замечание. Из определения следует, что ортогональная и, следовательно, ортонормированная тройка векторов является некомпланарной.

Определение. Упорядоченная некомпланарная тройка векторов , отложенных от одной точки, называется правой (правоориентированной), если при наблюдении с конца третьего вектора на плоскость, в которой лежат первые два вектора и , кратчайший поворот первого вектора ко второму происходит против часовой стрелки. В противном случае тройка векторов называется левой (левоориентированной).

рис.6.

Здесь, на рис.6 изображена правая тройка векторов . На следующем рис.7 изображена левая тройка векторов :

рис.7.

Определение. Базис векторного пространства называется ортонормированным, если ортонормированная тройка векторов.

Обозначение. В дальнейшем мы будем пользоваться правым ортонормированным базисом , см. следующий рисунок:

рис.9.

Любой вектор можно разложить по этому базису:

.

10

Определение скалярного произведения

Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла междуними.

Обозначается ab,а* b(или( а, b)).Итак, по определению,

Формуле (6.1) можно придать иной вид. Так как | a| cosg=пр _ba, (см. рис.14), a |b| cosg = пр _ab, то получаем:

т. е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.

studopedia.net

Модуль вектора — это… Что такое Модуль вектора?



Модуль вектора

Модулем (длиной) вектора называется длина(норма) соответствующего вектора AB и обозначается как .

В евклидовом n-мерном пространстве длина вектора рассчитывается как корень из скалярного произведения этого вектора на себя, в том случае если это произведение задано как (x,y)=x₁ * y₁ + x₂ * y₂,…,x_n * y_n),где (x₁,x₂,…,x_n) (y₁,y₂,…,y_n) координаты векторов x,y в каком-то базисе — то оно: .

Вектор, модуль которого равен 1, называется единичным вектором или ортом.

Wikimedia Foundation. 2010.

• Мусульманские страны
• Ракетный подводный крейсер стратегического назначения

Смотреть что такое «Модуль вектора» в других словарях:

• модуль вектора — величина вектора — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы величина вектора EN absolute value of a vector …   Справочник технического переводчика

• модуль вектора — vektoriaus modulis statusas T sritis fizika atitikmenys: angl. absolute value of vector vok. Vektorbetrag, m rus. длина вектора, f; модуль вектора, m pranc. module d’un vecteur, m …   Fizikos terminų žodynas

• Модуль — (от лат. modulus  «маленькая мера»): В Викисловаре есть статья «модуль» Мо …   Википедия

• Модуль (значения) — Модуль (от лат. modulus  «маленькая мера»)  составная часть, отделимая или хотя бы мысленно выделяемая из общего. Модульной обычно называют вещь, состоящую из чётко выраженных частей, которые нередко можно убирать или добавлять, не разрушая вещь… …   Википедия

• Модуль числа — Абсолютная величина или модуль вещественного или комплексного числа x есть расстояние от x до начала координат. Более точно: Абсолютная величина вещественного числа x есть неотрицательное число, обозначаемое |x| и определяемое следующим образом:… …   Википедия

• модуль волнового вектора — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN magnitude of propagation vector …   Справочник технического переводчика

• модуль конвольвера кодового вектора огибающей — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN shape codevector convolution module …   Справочник технического переводчика

• Модуль комплексного числа — Модулем комплексного числа называется длина вектора, соответствующего этому числу: . Модуль комплексного числа z обычно обозначается | z | или r. Пусть и вещественные числа такие, что комплексное число (обычные обозначения). Тогда Числа …   Википедия

• Модуль (в математике) — Модуль в математике, 1) М. (или абсолютная величина) комплексного числа z = х + iy есть число ═(корень берётся со знаком плюс). При представлении комплексного числа z в тригонометрической форме z = r(cos j + i sin j) действительное число r равно… …   Большая советская энциклопедия

• МОДУЛЬ — абелева группа с кольцом операторов. М. является обобщением (линейного) векторного пространства над полем Кдля случая, когда Кзаменяется нек рым кольцом. Пусть задано кольцо А. Аддитивная абелева группа Мназ. левым А модулем, если определено… …   Математическая энциклопедия

dic.academic.ru

Как вычислить модуль вектора

Под модулем вектора понимают его длину. Если нет возможности измерить ее линейкой, ее можно вычислить. В том случае, когда вектор задан декартовыми координатами применяется специальная формула. Важно уметь вычислить модуль вектора при нахождении суммы или разности двух известных векторов.

Вам понадобится

• координаты вектора;
• сложение и вычитание векторов;
• инженерный калькулятор или ПК.

Инструкция

• Определите координаты вектора в декартовой системе. Для этого параллельным переносом перенесите его так, чтобы начало вектора совпадало с началом координатной плоскости. Координаты конца вектора в этом случае, считайте координатами самого вектора. Другой способ – вычесть от координат конца вектора соответствующие координаты начала. Например, если координаты начала и конца соответственно равны (2;-2) и (-1;2), то координаты вектора будут равны (-1-2;2-(-2))=(-3;4).
• Определите модуль вектора, который численно равен его длине. Для того возведите каждую из его координат в квадрат, найдите их сумму и из полученного числа извлеките квадратный корень d=√(x²+y²). Например, модуль вектора с координатами (-3;4) рассчитайте по формуле d=√(x²+y²)=√((-3)²+4²)=√(25)=5 единичных отрезков.
• Найдите модуль вектора, который является результатом суммирования двух известных векторов. Определите координаты вектора, который является суммой двух данных векторов. Для этого сложите соответствующие координаты известных векторов. Например, если нужно найти сумму векторов (-1;5) и (4;3), то координаты такого вектора будут равны (-1+4;5+3)=(3;8). После этого модуль вектора вычислите по методике, изложенной в предыдущем пункте. Чтобы найти разность векторов, умножьте координаты вычитаемого вектора на -1 и сложите полученные значения.
• Определите модуль вектора, если известны длины векторов d1 и d2, которые складываются и угол α между ними. Постойте параллелограмм на известных векторах и проведите его диагональ, выходящего из угла между векторами. Измерьте длину получившегося отрезка. Это будет модуль вектора, который является суммой двух данных векторов.
• Если нет возможности произвести измерение, рассчитайте модуль. Для этого значение длины каждого из векторов возведите в квадрат. Найдите сумму квадратов, из полученного результата отнимите произведение этих же модулей, умноженное на косинус угла между векторами. Их полученного результата извлеките квадратный корень d=√(d1²+d2²-d1∙d2∙Cos(α)).

completerepair.ru

Как определить модуль вектора

Объектами векторной алгебры являются отрезки прямой, имеющие направление и длину, называемую модулем. Чтобы определить модуль вектора, следует извлечь квадратный корень из величины, представляющей собой сумму квадратов его проекций на координатные оси.

Инструкция

• Векторы характеризуются двумя основными свойствами: длиной и направлением. Длина вектора называется модулем или нормой и представляет собой скалярное значение, расстояние от точки начала до точки конца. Оба свойства применяются для графического изображения различных величин или действий, например, физических сил, движения элементарных частиц и пр.
• Местоположение вектора в двухмерном или трехмерном пространстве не влияет на его свойства. Если перенести его в другое место, то изменятся лишь координаты его концов, однако модуль и направление останутся прежними. Эта независимость позволяет использовать средства векторной алгебры в различных вычислениях, например, определения углов между пространственными прямыми и плоскостями.
• Каждый вектор можно задать координатами его концов. Рассмотрим для начала двухмерное пространство: пусть начало вектора находится в точке А (1, -3), а конец – в точке В (4, -5). Чтобы найти их проекции, опустите перпендикуляры на ось абсцисс и ординат.
• Определите проекции самого вектора, которые можно вычислить по формуле:АВх = (xb — xa) = 3;ABy = (yb — ya) = -2, где:ABx и ABy – проекции вектора на оси Ох и Оу;xa и xb – абсциссы точек А и В;ya и yb – соответствующие ординаты.
• В графическом изображении вы увидите прямоугольный треугольник, образованный катетами с длинами, равными проекциям вектора. Гипотенузой треугольника является величина, которую нужно вычислить, т.е. модуль вектора. Примените теорему Пифагора:|АВ|² = ABx² + ABy² → |AB| = √((xb — xa)² + (yb – ya)²) = √13.
• Очевидно, что для трехмерного пространства формула усложняется путем добавления третьей координаты – аппликат zb и za для концов вектора:|AB| = √((xb — xa)² + (yb – ya)² + (zb — za)²).
• Пусть в рассмотренном примере za = 3, zb = 8, тогда:zb – za = 5;|AB| = √(9 + 4 + 25) = √38.

completerepair.ru