Модуль вектора — это… Что такое Модуль вектора?
- Модуль вектора
Модулем (длиной) вектора
 называется длина(норма) соответствующего вектора AB и обозначается как
называется длина(норма) соответствующего вектора AB и обозначается как  .
.В евклидовом n-мерном пространстве длина вектора рассчитывается как корень из скалярного произведения этого вектора на себя, в том случае если это произведение задано как (x,y)=x1 * y1 + x2 * y2,…,xn * yn),где (x1,x2,…,xn) (y1,y2,…,
 .
.Вектор, модуль которого равен 1, называется единичным вектором или ортом.
Wikimedia Foundation. 2010.
- Мусульманские страны
- Ракетный подводный крейсер стратегического назначения
Смотреть что такое «Модуль вектора» в других словарях:
модуль вектора — величина вектора — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы величина вектора EN absolute value of a vector … Справочник технического переводчика
модуль вектора — vektoriaus modulis statusas T sritis fizika atitikmenys: angl. absolute value of vector vok. Vektorbetrag, m rus. длина вектора, f; модуль вектора, m pranc. module d’un vecteur, m … Fizikos terminų žodynas
Модуль — (от лат. modulus «маленькая мера»): В Викисловаре есть статья «модуль» Мо … Википедия
Модуль (значения) — Модуль (от лат. modulus «маленькая мера») составная часть, отделимая или хотя бы мысленно выделяемая из общего. Модульной обычно называют вещь, состоящую из чётко выраженных частей, которые нередко можно убирать или добавлять, не разрушая вещь… … Википедия
Модуль числа — Абсолютная величина или модуль вещественного или комплексного числа x есть расстояние от x до начала координат. Более точно: Абсолютная величина вещественного числа x есть неотрицательное число, обозначаемое |x| и определяемое следующим образом:… … Википедия
модуль волнового вектора — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN magnitude of propagation vector … Справочник технического переводчика
модуль конвольвера кодового вектора огибающей — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN shape codevector convolution module … Справочник технического переводчика
Модуль комплексного числа — Модулем комплексного числа называется длина вектора, соответствующего этому числу: . Модуль комплексного числа z обычно обозначается | z | или r. Пусть и вещественные числа такие, что комплексное число (обычные обозначения). Тогда Числа … Википедия
Модуль (в математике) — Модуль в математике, 1) М. (или абсолютная величина) комплексного числа z = х + iy есть число ═(корень берётся со знаком плюс). При представлении комплексного числа z в тригонометрической форме z = r(cos j + i sin j) действительное число r равно… … Большая советская энциклопедия
МОДУЛЬ — абелева группа с кольцом операторов. М. является обобщением (линейного) векторного пространства над полем Кдля случая, когда Кзаменяется нек рым кольцом. Пусть задано кольцо А. Аддитивная абелева группа Мназ. левым А модулем, если определено… … Математическая энциклопедия
Модуль вектора онлайн, подробное решение
Модуль вектора — это его длина, которая может быть найдена по формуле:
, где
Из формулы следует, что длина вектора это скаляр всегда больший или равный нулю (если вектор нулевой).
Формула, для вычисления модуля вектора может быть наглядно получена из простых геометрических соображений:
Координаты вектора — это его проекции на оси x и y, следовательно длина вектора представляет собой величину гипотенузы прямоугольного треугольника, которая может быть найдена по теореме Пифагора.
Найти длину вектора поможет наш онлайн калькулятор с бесплатным подробным решением на русском языке.
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
| Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькуляторы (Теория чисел) |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажер сложения |
| Тренажёр вычитания |
| Тренажёр умножения |
| Тренажёр деления |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
| Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
| Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
| Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Модуль вектора. Длина вектора.
Навигация по странице:
Определение длины вектора
Определение.
Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора AB.Для обозначения длины вектора используются две вертикальные линии слева и справа |AB|.
Основное соотношение. Длина вектора |a| в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат.
Формулы длины вектора
Формула длины вектора для плоских задач
В случае плоской задачи модуль вектора a = {ax ; ay} можно найти воспользовавшись следующей формулой:
Формула длины вектора для пространственных задач
В случае пространственной задачи модуль вектора a = {ax ; ay ; az} можно найти воспользовавшись следующей формулой:
Формула длины n -мерного вектора
В случае n-мерного пространства модуль вектора a = {a1 ; a2; … ; an} можно найти воспользовавшись следующей формулой:
| |a| = ( | n | ai2)1/2 |
| Σ | ||
| i=1 |
Примеры задач на вычисление длины вектора
Примеры вычисления длины вектора для плоских задачи
Пример 1. Найти длину вектора a = {2; 4}.Решение: |a| = √22 + 42 = √4 + 16 = √20 = 2√5.
Пример 2. Найти длину вектора a = {3; -4}.Решение: |a| = √32 + (-4)2 = √9 + 16 = √25 = 5.
Примеры вычисления длины вектора для пространственных задачи
Пример 3. Найти длину вектора a = {2; 4; 4}.Решение: |a| = √22 + 42 + 42 = √4 + 16 + 16 = √36 = 6.
Пример 4. Найти длину вектора a = {-1; 0; -3}.Решение: |a| = √(-1)2 + 02 + (-3)2 = √1 + 0 + 9 = √10.
Примеры вычисления длины вектора для пространств с размерностью большей 3
Пример 5. Найти длину вектора a = {1; -3; 3; -1}.Решение: |a| = √12 + (-3)2 + 32 + (-1)2 = √1 + 9 + 9 + 1 = √20 = 2√5
Пример 6. Найти длину вектора a = {2; 4; 4; 6 ; 2}.Решение: |a| = √22 + 42 + 42 + 62 + 22 = √4 + 16 + 16 + 36 + 4 = √76 = 2√19.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Вектор: определение и основные понятия
Определение вектора
Определение. Вектор — это направленный отрезок, то есть отрезок, имеющий длину и определенное направление. Графически вектора изображаются в виде направленных отрезков прямой определенной длины. (рис.1)
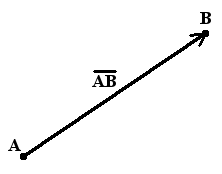 |
| рис. 1 |
Обозначение вектора
Вектор началом которого есть точка А, а концом — точка В, обозначается AB (рис.1). Также вектора обозначают одной маленькой буквой, например a.
Длина вектора
Для обозначения длины вектора используются две вертикальные линии слева и справа |AB|.
Нулевой вектор
Определение. Нулевым вектором называется вектор, у которого начальная и конечная точка совпадают.
Нулевой вектор обычно обозначается как 0.
Длина нулевого вектора равна нулю.
Сонаправленные вектора
Определение. Два коллинеарных вектора a и b называются сонаправленными векторами, если их направления совпадают: a↑↑b (рис. 3).
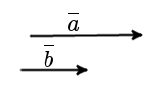 |
| рис. 3 |
Противоположно направленные вектора
Определение. Два коллинеарных вектора a и b называются противоположно направленными векторами, если их направления противоположны: a↑↓b (рис. 4).
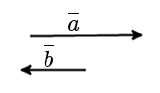 |
| рис. 4 |
Компланарные вектора
Определение. Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами. (рис. 5).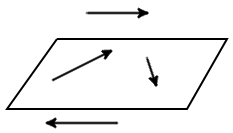 |
| рис. 5 |
Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные.
Равные вектора
Определение. Вектора a и b называются равными, если они лежат на одной или параллельных прямых, их направления совпадают, а длины равны (рис. 6).
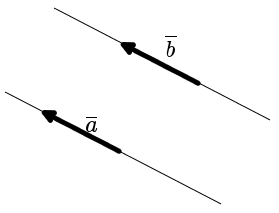 |
| рис. 6 |
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:
a = b, если a↑↑b и |a| = |b|.
Видеоурок 1: Понятие вектора
Видеоурок 2: Равенство векторов
Видеоурок 3: Сложение и вычитание векторов
Видеоурок 4: Умножение вектора на число
Лекция: Вектор, модуль вектора, равенство векторов; сложение векторов и умножение вектора на число
 Вектор
ВекторВектор – это тело, которое изучается в математике, но используется в большом количестве наук. Например, в физике существуют скалярные величины (те, что характеризуются значением – масса, температура и т.д.), а также векторные величины (сила, работа и другие).
Вектор – это величина, которая характеризуется не только значением, но и направлением. Иными словами, это направленный отрезок.

Но кроме его длины, нам также важно, где находится его начало, а где конец.
Если вектор имеет свое начало в некоторой точке А, а заканчивается в точке В, то его обозначают следующим образом:
Кроме двух букв, вектор можно обозначить одной буквой со значком вектора сверху.
Длиной вектора (его модулем) называют расстояние между концом вектора и его началом.
Для определения модуля вектора следует воспользоваться следующей формулой:
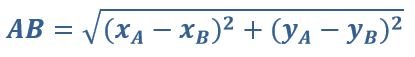
Кроме этого, модуль вектора может обозначаться следующим образом:

Если некоторый вектор имеет начало и конец в одной и той же точке, то такой вектор называют нулевым. Нулевой вектор обозначают, как
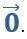
Если длина некоторого вектора равна единичному отрезку, то его называют единичным.
Если некоторые векторы расположены на одной прямой или же параллельны друг другу, то такие векторы называются коллинеарными.
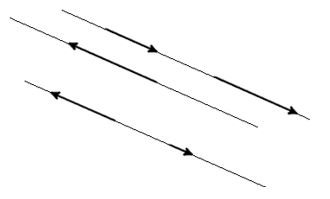
Если некоторые векторы можно назвать коллинеарными, но кроме этого они направлены в одну сторону, то их можно назвать сонаправленными.
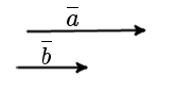
Если же наоборот два коллинеарных вектора смотрят в разные стороны, то их называют противоположно направленными.
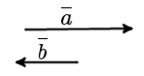
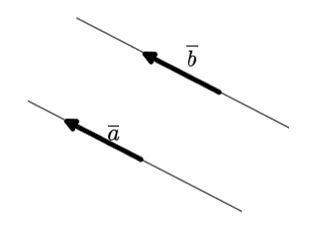
Если же некоторые векторы являются коллинеарными, сонаправленными, а также имеют одинаковую длину (модуль), то их можно назвать равными.
 Координаты вектора
Координаты вектора
Для нахождения координаты вектора следует вычесть соответствующие координаты его конца и начала.
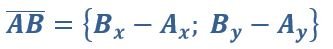
Например, если начало вектора А (3; 6), а конец В (5;9), то этот вектор будет иметь следующие координаты: {2;3}.
 Сложение и вычитание векторов
Сложение и вычитание векторов
Чтобы сложить два вектора для получения нового, необходимо сложить соответствующие координаты.
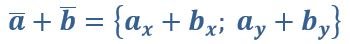
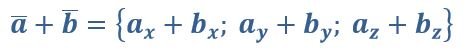
Например, сложим вектор {2;3} с вектором {5;7}. В результате получим новый вектор с координатами {7;10}. С вычитанием все аналогично.
 Умножение вектора на некоторое число
Умножение вектора на некоторое число
Чтобы умножить вектор на некоторое число, следует умножить каждую его координату на данное число.
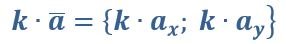
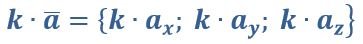
Свойства:
- Первоначальный вектор и вектор умноженный на некоторое число, который равный ему, являются параллельными.
- Если число, на которое умножался вектор, больше нуля, то новый вектор будет сонаправлен первоначальному. Если же число меньше нуля, то векторы будут противоположно направленны.

Формулы векторов
1. Координаты вектора
Если вектор задан координатами своих начала и конца: , то его координаты равны разности соответствующих координат конца и начала:
2. Длина или модуль вектора
Если вектор , то его длина равна корню квадратному из суммы квадратов координат:
3. Сумма векторов
Если векторы и заданы своими координатами, то суммой этих векторов есть вектор, координаты которого равны сумме соответствующих координат векторов-слагаемых:
4. Умножение вектора на число
Чтобы найти произведение вектора на некоторое число , нужно каждую координату заданного вектора умножить на это число:
5. Скалярное произведение векторов
Если векторы и заданы своими координатами, то их скалярное произведение равно сумме произведений соответствующих координат:
6. Векторное произведение векторов
Если векторы и заданы своими координатами в некотором ортонормированном базисе , то их векторное произведение находится по формуле:
7. Смешанное произведение векторов
Если заданы три вектора и , то их смешанное произведение равно определителю, по строкам которого записаны координаты этих векторов:
Замечание. Обычно такой определитель вычисляется методом треугольников.
8. Угол между векторами
Косинус угла между двумя векторами и , заданными своими координатами, равен частному скалярного произведения этих векторов и произведению их модулей:
9. Проекция вектора на вектор
Проекция вектора на направление вектора равна отношение скалярного произведения этих векторов к модулю вектора :
| Понравился сайт? Расскажи друзьям! | |||
Как найти модуль вектора?
Наука
- Анатомия и физиология
- астрономия
- астрофизика
- Биология
- Химия
- наука о планете Земля
- Наука об окружающей среде
- Органическая химия
- физика
математический
- Алгебра
с ++ — Как работает оператор модуля?
Переполнение стека- Товары
- Клиенты
- Случаи использования
- Переполнение стека Публичные вопросы и ответы
- Команды Частные вопросы и ответы для вашей команды
- предприятие Частные вопросы и ответы для вашего предприятия
- работы Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимать технический талант
- реклама Связаться с разработчиками по всему миру
Понимание оператора модуля%
Переполнение стека- Товары
- Клиенты
- Случаи использования
- Переполнение стека Публичные вопросы и ответы
- Команды Частные вопросы и ответы для вашей команды
- предприятие Частные вопросы и ответы для вашего предприятия
- работы Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимать технический талант
- реклама Связаться с разработчиками по всему миру
модуль вектора — это … Что такое модуль вектора?
Модуль непрерывности — В математическом анализе модуль непрерывности — это функция, используемая для количественного измерения однородной непрерывности функций. Таким образом, функция допускает ω как модуль непрерывности тогда и только тогда, когда для всех x и y в области функции f. Так как модули… Википедия
Геометрическая алгебра — В математической физике геометрическая алгебра — это полилинейная алгебра, технически описанная как алгебра Клиффорда над вещественным векторным пространством, снабженным невырожденной квадратичной формой.Неформально, геометрическая алгебра — это алгебра Клиффорда, которая…… Википедия
твердые частицы, механика — ▪ физика Введение в науку, связанную с напряжением (напряжением), деформацией (деформацией и течением) и разрушением твердых материалов и конструкций. Что же тогда является твердым телом? Любой материал, жидкий или твердый, может поддерживать нормальные силы.…… Universalium
Определение уравнения (физика) — Общую номенклатуру базовых величин, используемых в этой статье, см. В разделе Физические величины.Для 4 векторных модификаций, используемых в относительности, см. Четыре вектора. Очень часто определяющие уравнения имеют форму конститутивного уравнения, так как параметры … … Википедия
Комплексное число — Комплексное число может быть визуально представлено в виде пары чисел, образующих вектор на диаграмме, называемой диаграммой Аргана, представляющей комплексную плоскость. Re — действительная ось, Im — мнимая ось, а i — квадратный корень из –1. Комплекс … … Википедия
Дислокация — Синтаксическая операция приведена в разделе Дислокация (синтаксис).Медицинский термин см. Вывих суставов. В материаловедении дислокация — это кристаллографический дефект или нерегулярность внутри кристаллической структуры. Наличие вывихов… Википедия
Алгоритм Шёнхаге-Штрассена — Алгоритм Шёнхаге-Штрассена — это асимптотически быстрый алгоритм умножения для больших целых чисел. Он был разработан Арнольдом Шенхаге и Фолькером Штрассеном в 1971 году. [A. Шенхаге и В. Штрассен, Schnelle Multiplikation großer Zahlen,…… Википедия
Углеродная нанотрубка — Не путать с углеродным волокном.Часть серии статей о наноматериалах Фуллерены… Википедия
Абсолютная ценность — Философский термин см. В разделе Ценность (этика). Для альбома Akrobatik см. Абсолютное значение (альбом). В математике абсолютное значение (или модуль) | a | действительного числа а является числовым значением а без учета его знака. Так, например,… Википедия
Комплексное число с разделением — Часть плоскости комплексного числа с разделением, показывающая подмножества с модулем ноль (красный), один (синий) и минус один (зеленый).В абстрактной алгебре расщепленные комплексные числа (или гиперболические числа) являются двумерной коммутативной алгеброй над вещественной… Wikipedia
Линейная упругость — Механика сплошных сред… Википедия

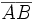 называется длина(норма) соответствующего вектора AB и обозначается как
называется длина(норма) соответствующего вектора AB и обозначается как 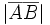 .
.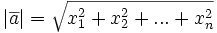 .
.
Leave A Comment