В физике существует несколько видов ускорения, которые используются для описания того или иного типа механического перемещения тел в пространстве. Все эти виды являются векторными величинами. В данной статье не будем рассматривать вопрос, куда направлено ускорение, а сосредоточим свое внимание на формулах модуля ускорения.
Что такое ускорение?
Максимально полное определение этой кинематической характеристики можно привести следующее: ускорение — это величина, показывающая быстроту изменения скорости во времени. Речь идет об изменении как модуля, так и направления. Математически ускорение вычисляют так:
Вам будет интересно:Смоленский государственный институт искусств: факультеты, специальности, сроки обучения, документы для поступления
a = dv/dt.
Оно называется мгновенным, то есть справедливым для конкретного момента времени t. Чтобы найти среднее значение модуля ускорения, формулу такую необходимо использовать:
a = (v2 — v1)/(t2 — t1).
Где v2 и v1 — скорости в моменты времени t2 и t1 соответственно.
Единицами измерения изучаемой физической величины являются метры в квадратную секунду (м/с2). Многих может смутить возведение во вторую степень единиц времени, тем не менее, понять смысл единицы м/с2 несложно, если ее представить в виде [м/с]/с. Последняя запись означает изменение скорости на одну единицу за одну единицу времени.
Движение по прямой и ускорение
Самой простой траекторией для перемещения тел в пространстве является прямая линия. Если скорость при движении по такой траектории не изменяется, то говорить об ускорении не приходится, поскольку оно будет равно нулю.
В технике широко распространено прямолинейное равноускоренное (равнозамедленное) движение. Например, при старте автомобиля или при его торможении мы имеем именно этот вид движения. Для его математического описания пользуются следующими равенствами:
v = v0±a*t;
l = v0*t±a*t2/2.
Здесь v0 — некоторая начальная скорость тела, которая может быть также равна нулю, l — пройденный телом путь к моменту времени t. Знак + говорит об ускорении тела, знак — — о его торможении. Важно запомнить, что время t при использовании записанных формул начинает отсчитываться от момента появления у тела постоянного ускорения a. С учетом записанных равенств, формулы модуля ускорения тела принимают вид:
±a = (v — v0)/t;
±a = 2*(l — v0*t)/t2.
Как правило, если тело ускоряется, то говорят о положительном ускорении, если же оно замедляет свое движение, то говорят об отрицательной величине a. Нетрудно проверить, что обе формулы приводят к одной и той же единице измерения ускорения (м/с2).
Полное ускорение и его компоненты при движении тела по кривой
В случае перемещения тела по криволинейной траектории, величину a удобно представить в виде двух взаимно перпендикулярных составляющих. Они называются тангенциальным at и нормальным an ускорениями. Для такого случая формула модуля ускорения точки принимает вид:
a = √(at2 + an2).
Тангенциальную компоненту следует рассчитывать через производную функции v(t) по времени. Нормальная же компонента определяется не изменением модуля скорости, а самой ее величиной. Для ее расчета пользуются таким выражением:
an = v2/r.
Здесь r — радиус кривизны траектории, который в случае вращения по окружности совпадает с радиусом последней.
Для полноты информации отметим, что криволинейность траектории перемещения тела является достаточным признаком присутствия ненулевой нормальной составляющей ускорения. При этом величина at может быть равна нулю, что является справедливым для равномерного вращения тел.
Угловое ускорение
Как было отмечено во введении, существуют несколько видов ускорения. Одним из них является угловая кинематическая величина. Обозначим ее α. По аналогии с линейным ускорением, формула модуля ускорения углового имеет вид:
α = dω/dt.
Где греческой буквой ω (омега) обозначена скорость угловая, единицами измерения которой являются радианы в секунду. Величина α показывает, как быстро тело увеличивает или замедляет скорость своего вращения.
Ускорение угловое можно связать с линейной величиной. Делается это с помощью такой формулы:
α = at/r.
Важно понимать, что угловое ускорение является удобным способом представления тангенциальной составляющей полного ускорения в случае вращательного движения. Удобство здесь заключается в независимости величины α от расстояния до оси вращения r. В свою очередь, компонента at линейно возрастает при увеличении радиуса кривизны r.
Пример решения задачи
Известно, что тело вращается по окружности, радиус которой составляет 0,2 метра. Вращение является ускоренным, при этом скорость изменяется во времени по следующему закону:
v = 2 + 3*t2 + 2*t3.
Необходимо определить тангенциальное, нормальное, полное и угловое ускорения в момент времени 3 секунды.
Начнем решать эту задачу по порядку. Тангенциальная компонента определяется через производную скорости. Имеем:
at = dv/dt = 6*t + 6*t2 = 6*3 + 6*9 = 76 м/с2.
Отметим, что это очень большое ускорение по сравнению с ускорением свободного падения (9,81 м/с2).
Нормальная компонента вычисляется так:
an = v2/r = 1/r*(2 + 3*t2 + 2*t3)2 = 1/0,2*(2+27+54)2 = 34445 м/c2.
Теперь можно рассчитать полное ускорение. Оно будет равно:
a = √(at2 + an2) = √(76 2 + 34445 2) = 34445,1 м/с2.
То есть, полное ускорение практически полностью образовано нормальной компонентой.
Наконец, ускорение угловое определяется по формуле:
α = at/r = 76/0,2 = 380 рад/с2.
Полученное значение соответствует увеличению скорости угловой приблизительно на 60 оборотов за каждую секунду.
Источник
В физике существует несколько видов ускорения, которые используются для описания того или иного типа механического перемещения тел в пространстве. Все эти виды являются векторными величинами. В данной статье не будем рассматривать вопрос, куда направлено ускорение, а сосредоточим свое внимание на формулах модуля ускорения.
Что такое ускорение?
Максимально полное определение этой кинематической характеристики можно привести следующее: ускорение — это величина, показывающая быстроту изменения скорости во времени. Речь идет об изменении как модуля, так и направления. Математически ускорение вычисляют так:
a = dv/dt.
Оно называется мгновенным, то есть справедливым для конкретного момента времени t. Чтобы найти среднее значение модуля ускорения, формулу такую необходимо использовать:
a = (v2 — v1)/(t2 — t1).
Где v2 и v1 — скорости в моменты времени t2 и t1 соответственно.
Единицами измерения изучаемой физической величины являются метры в квадратную секунду (м/с2). Многих может смутить возведение во вторую степень единиц времени, тем не менее, понять смысл единицы м/с2 несложно, если ее представить в виде [м/с]/с. Последняя запись означает изменение скорости на одну единицу за одну единицу времени.
Движение по прямой и ускорение
Самой простой траекторией для перемещения тел в пространстве является прямая линия. Если скорость при движении по такой траектории не изменяется, то говорить об ускорении не приходится, поскольку оно будет равно нулю.
В технике широко распространено прямолинейное равноускоренное (равнозамедленное) движение. Например, при старте автомобиля или при его торможении мы имеем именно этот вид движения. Для его математического описания пользуются следующими равенствами:
v = v0±a*t;
l = v0*t±a*t2/2.
Здесь v0 — некоторая начальная скорость тела, которая может быть также равна нулю, l — пройденный телом путь к моменту времени t. Знак + говорит об ускорении тела, знак — — о его торможении. Важно запомнить, что время t при использовании записанных формул начинает отсчитываться от момента появления у тела постоянного ускорения a. С учетом записанных равенств, формулы модуля ускорения тела принимают вид:
±a = (v — v0)/t;
±a = 2*(l — v0*t)/t2.
Как правило, если тело ускоряется, то говорят о положительном ускорении, если же оно замедляет свое движение, то говорят об отрицательной величине a. Нетрудно проверить, что обе формулы приводят к одной и той же единице измерения ускорения (м/с
Полное ускорение и его компоненты при движении тела по кривой
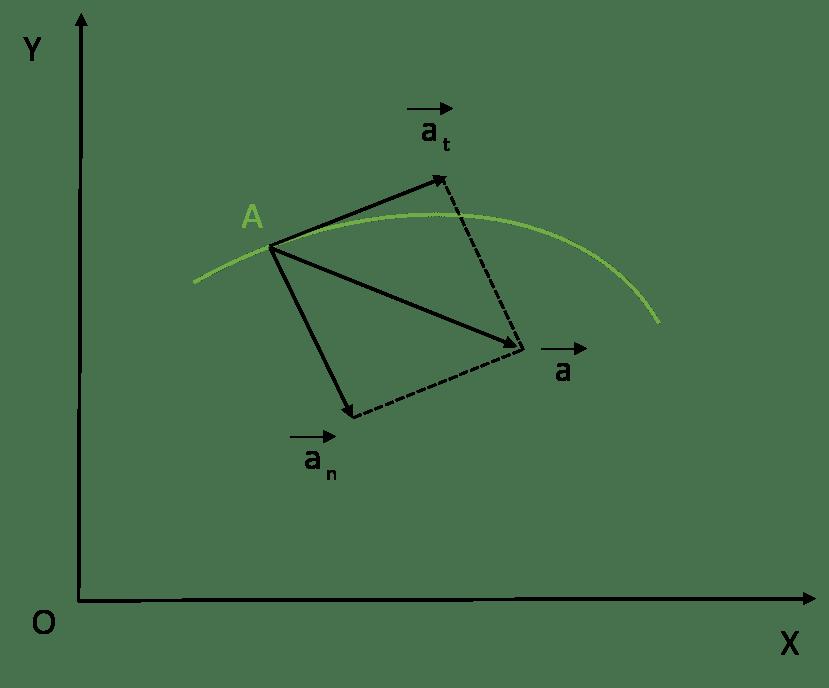
В случае перемещения тела по криволинейной траектории, величину a удобно представить в виде двух взаимно перпендикулярных составляющих. Они называются тангенциальным at и нормальным an ускорениями. Для такого случая формула модуля ускорения точки принимает вид:
a = √(at2 + an2).
Тангенциальную компоненту следует рассчитывать через производную функции v(t) по времени. Нормальная же компонента определяется не изменением модуля скорости, а самой ее величиной. Для ее расчета пользуются таким выражением:
an = v2/r.
Здесь r — радиус кривизны траектории, который в случае вращения по окружности совпадает с радиусом последней.
Для полноты информации отметим, что криволинейность траектории перемещения тела является достаточным признаком присутствия ненулевой нормальной составляющей ускорения. При этом величина at может быть равна нулю, что является справедливым для равномерного вращения тел.
Угловое ускорение
Как было отмечено во введении, существуют несколько видов ускорения. Одним из них является угловая кинематическая величина. Обозначим ее α. По аналогии с линейным ускорением, формула модуля ускорения углового имеет вид:
α = dω/dt.
Где греческой буквой ω (омега) обозначена скорость угловая, единицами измерения которой являются радианы в секунду. Величина α показывает, как быстро тело увеличивает или замедляет скорость своего вращения.
Ускорение угловое можно связать с линейной величиной. Делается это с помощью такой формулы:
α = at/r.
Важно понимать, что угловое ускорение является удобным способом представления тангенциальной составляющей полного ускорения в случае вращательного движения. Удобство здесь заключается в независимости величины α от расстояния до оси вращения r. В свою очередь, компонента at линейно возрастает при увеличении радиуса кривизны r.
Пример решения задачи
Известно, что тело вращается по окружности, радиус которой составляет 0,2 метра. Вращение является ускоренным, при этом скорость изменяется во времени по следующему закону:
v = 2 + 3*t2 + 2*t3.
Необходимо определить тангенциальное, нормальное, полное и угловое ускорения в момент времени 3 секунды.
Начнем решать эту задачу по порядку. Тангенциальная компонента определяется через производную скорости. Имеем:
at = dv/dt = 6*t + 6*t2 = 6*3 + 6*9 = 76 м/с2.
Отметим, что это очень большое ускорение по сравнению с ускорением свободного падения (9,81 м/с2).
Нормальная компонента вычисляется так:
an = v2/r = 1/r*(2 + 3*t2 + 2*t3)2 = 1/0,2*(2+27+54)2 = 34445 м/c2.
Теперь можно рассчитать полное ускорение. Оно будет равно:
a = √(at2 + an2) = √(76 2 + 34445 2) = 34445,1 м/с2.
То есть, полное ускорение практически полностью образовано нормальной компонентой.
Наконец, ускорение угловое определяется по формуле:
α = at/r = 76/0,2 = 380 рад/с2.
Полученное значение соответствует увеличению скорости угловой приблизительно на 60 оборотов за каждую секунду.
Кинематика материальной точки (средняя школа)
Кинематика материальной точки
Равномерным прямолинейным движением называют движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещения. Скорость равномерного движения определяется по формуле:
|
Рис. 1. Перемещение, скорость и ускорение при равномерном прямолинейном движении |
|
Рис. 2. Перемещение, скорость и ускорение при равноускоренном прямолинейном движении |
Равноускоренным прямолинейным движением называется движение, при котором скорость и ускорение направлены вдоль одной прямой и ускорение остается неизменным по модулю. В этом случае модуль ускорения определяется по формуле:
Перемещение, в свою очередь, равно:
где x0 – значение перемещения в момент времени t = 0.
Также используется формула:Примером равноускоренного движения является свободное падение тела с небольшой (по сравнению с радиусом Земли) высоты h в безвоздушном пространстве. Ускорение свободного падения тела не зависит от самого тела и всегда направлено вертикально вниз. Высота тела при этом определяется формулой (при условии, что начальная скорость равна нулю). Время падения с высоты h равно
При равномерном движении со скоростью υ по окружности радиуса R ускорение (центростремительное ускорение) постоянно по модулю:
|
Рис. 3. Равномерное движение по окружности |
Период обращения T – это промежуток времени, в течение которого материальная точка совершает один оборот при равномерном движении по окружности. Модуль скорости движения тела при этом можно записать как:
Частота обращения ν – это число оборотов, совершаемых материальной точкой при равномерном движении по окружности за единицу времени:
Часто используется понятие круговой (или циклической) частоты:
В этом случае центростремительное ускорение записывается в виде:Если модуль скорости движения материальной точки при движении по окружности изменяется, то помимо центростремительного появляется тангенциальное (касательное) ускорение aτ. Оно направлено по касательной к окружности и равно по модулю Полное ускорение в этом случае будет равно:
|
Рис. 4. Нормальное и тангенциальное ускорение |
1.1.4 Ускорение материальной точки
Видеоурок 1: Перемещение, скорость, ускорение
Видеоурок 2: Равноускоренное движение — Физика в опытах и экспериментах
Лекция: Ускорение материальной точки
 Ускорение
УскорениеУскорение — это векторная ФВ, характеризующая быстроту изменения скорости во времени.

Ускорение — это первая производная от скорости, а также вторая — от перемещения.
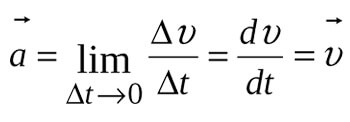
Данная физическая величина показывает, насколько быстро изменяется скорость со временем.
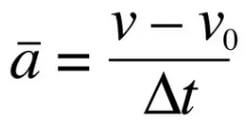 Следует помнить, что ускорением обладает то тело, на которое действует сила.
Следует помнить, что ускорением обладает то тело, на которое действует сила.Основной единицей ускорения является 1м/с2.
В отличие от скорости, направление ускорения не всегда совпадает с направлением движения тела. Если тело ускоряется, то ускорение имеет положительное значение, если же тело замедляется, то ускорение — отрицательно. Иными словами, ускорение имеет то же направление, что и результирующая сила, которая действует на тело.
Если тело двигается по окружности, то ускорение направлено к её центру.

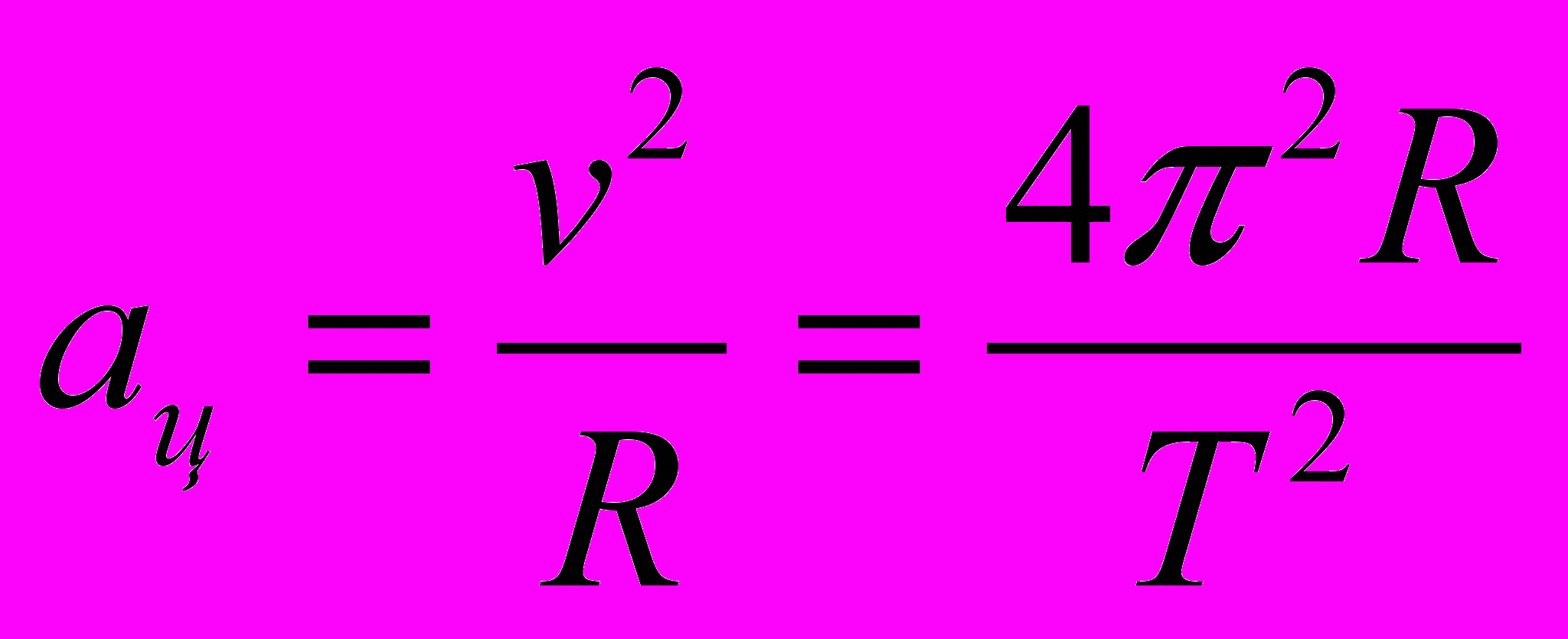
 Геометрический смысл ускорения
Геометрический смысл ускорения
Геометрическим смыслом ускорения является площадь под прямой графика движения в координатах V(t).
Кинематика материальной точки 3
Кинематика материальной точки.
1.Понятие относительности перемещения материальной точки (тела), системы отсчёта.
Движение изменения взаимного расположения тел или матер. Точек.Т.е. мы рассматриваем движение матер точки относительно какого-либо тела или системы тел.
Система отсчёта — это совокупность тела отсчёта, системы координат и часов.
2. Кинематические хар-ки материальной точки.
1)Траектория-линия вдоль которой движется тело.
2)Перемещение-отрезок ,соединяющий начал и конеч положение точки.
3)Скорость-отношение перемещения ко времени для равномер движ.
3.Путь-это расстояние,пройденное материальной точкой по траектории за промежуток времени и равен длине этой траектории.
4 Ра́диус-ве́ктор — вектор, задающий положения точки в пространстве относительно некоторой заранее фиксированной точки, называемой началомкоординат. Для произвольной точки в пространстве, радиус-вектор — это вектор, идущий из начала координат в эту точку.Радиус-вектором точки называется вектор, начало которого совпадает с началом системы координат, а конец — с данной точкой.
5 Вектор скорости-это расстояние,которое тело проходит в определённом направлении за единицу времени.Вектор- скорости указывает и скорость и направление движения.
6Путь — длина отрезка траектории. Траектория — это линия, описываемая материальной точкой при ее движении.
Вычисление пройденного пути
Для равномерного движения
, — весь путь, — весь отрезок времени, — const.Для произвольного движения:
.v1 в течение отрезка Δti приблизительно постоянны, если Δt достаточно мало.
В пределе:
Вектор скорости материальной точки в каждый момент времени определяется производной по времени радиус-вектора
этой точки:Здесь v — модуль скорости,
— направленный вдоль скорости единичный вектор касательной к траектории в точке .8. Кинематическое уравнение r(t) для прямолинейного равномерного движения. Представить в виде проекций на декартовы оси координат.
х=x0+ vx·t.
9. Ускорение материальной точки — векторная физическая величина, характеризующая быстроту изменения скорости и равная приращению скорости за единицу времени. векторускорения равен первой производной от вектора скорости по времени или второй производной от радиуса-вектора по времени
10 Тангенциальное ускорение – быстрота изменения скорости по модулю в данный момент времени; производная от скорости по времени.
Нормальное ускорение – быстрота изменения скорости по направлению в данный момент времени.
Полное ускорение определяется векторной суммой тангенциального нормального ускорений.
15.Враща́тельное движе́ние —движение,при котором все точки тела движутся по окружностям,центры которых лежат на одной и той же прямой,называемой осью вращения
18Первый закон Ньютона..Существуют такие системы отсчёта, относительно которых материальная точка, при отсутствии внешних воздействий, сохраняет состояние покоя или равномерного прямолинейного движения.
Второй закон НьютонаСила, действующая на тело, равна произведению массы тела на создаваемое этой силой ускорение.
Третий закон Ньютона силы равны по модулю и противоположны по направлению .
20. Виды деформации растяжение-сжатие,сдвиг,изгиб,кручение.
21 Абсолютная деформация — величина изменения размеров тел: длины, объема и т.д.Относительная деформация — отношение величины изменения размера тела к его исходному размеру. Часто относительная деформация выражается в процентах.
22. Механическое напряжение — это мера внутренних сил, возникающих в деформируемом теле под влиянием внешних воздействий. Механическое напряжение в точке тела измеряется отношением силы, возникающей в теле при деформации, к площади малого элемента сечения.
24. Модуль Юнга (модуль упругости, англ. Young modulus, modulus of elasticity) — коэффициент, характеризующий сопротивление материала растяжению/сжатию при упругой деформации. В динамических задачах механики модуль Юнга рассматривается в более общем смысле — как функционал среды и процесса.
25 Закон Гука — связь между величиной упругой деформации и силой, действующей на тело. ввести относительное удлинениеε=∆l/L и нормальное напряжение в поперечном сечении σ=F/A. В этих обозначениях закон Гука записывается как
=E .Пусть первоначальная длина нерастянутой проволоки составляла L0. После приложения силы F проволока растянулась и ее длина стала равной L. Величину DL=L-L0 называют абсолютным удлинением проволоки. Величину e=DL/L0 называютотносительным удлинением тела26.Трение скольжения — сила, возникающая при поступательном перемещении одного из контактирующих/взаимодействующих тел относительно другого и действующая на это тело в направлении, противоположном направлению скольжения;
Трение качения — момент сил, возникающий при качении одного из двух контактирующих/взаимодействующих тел относительно другого
.Трение покоя — сила, возникающая между двумя контактирующими телами и препятствующая возникновению относительного движения. Эту силу необходимо преодолеть для того, чтобы привести два контактирующих тела в движение друг относительно друга. Она действует в направлении, противоположном направлению возможного движения.
27.Сила трения скольжения всегда направлена против относительной скорости скольжения соприкасающихся тел.
29. СИЛА ТЯЖЕСТИ Силу, с которой тело притягивается к Земле под действием поля тяготения Земли, называют силой тяжести. По закону всемирного тяготения на поверхности Земли (или вблизи этой поверхности) на тело массой m действует сила тяжести
31. Вес тела — в физике — сила, с которой тело, действует на опору или на подвес.
32. При́нцип относи́тельности — фундаментальный физический принцип, согласно которому все физические процессы в инерциальных системах отсчёта протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения.
33. И́мпульс— векторная физическая величина, характеризующая меру механического движения тела. В классической механике импульс тела равен произведению массы m этой точки на её скорость v,
34. Изолированнаясистема (замкнутая cистема) — термодинамическая система, которая не обменивается с окружающей средой ни веществом, ни энергией
35.Центр масс (центр ине́рции, барице́нтр) в механике — это геометрическая точка, характеризующая движение тела или системы частиц как целого.
36 p=p1+p2=const .Формула выражает закон сохранения импульса в замкнутой системе, который формулируют так: полный импульс замкнутой системы тел остается постоянным при любых взаимодействиях тел этой системы между собой. Dр=Ft. Группу тел, взаимодействующих не только между собой, но и с телами, не входящими в состав этой группы, называют незамкнутой системой
38Работа силы — мера механического действия силы при перемещении точки ее приложения.
Кинети́ческая эне́ргия — энергиямеханической системы, зависящая от скоростей движения её точек.
43.
,т.е. работа силы при деформации тела равна изменению потенциальной энергии этого тела, взятой с обратным знаком.
Величина Еп= тghназывается потенциальной энергией тела, поднятого над Землей
Полной механической энергией системы тел называется сумма кинетической и потенциальной энергий:
Ускорение
Ускорение – это величина, которая характеризует быстроту изменения скорости.
Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).
Среднее ускорение
Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:
где – вектор ускорения.
Направление вектора ускорения совпадает с направлением изменения скорости Δ = — 0 (здесь 0 – это начальная скорость, то есть скорость, с которой тело начало ускоряться).
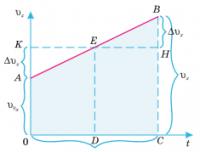
В момент времени t1 (см. рис 1.8) тело имеет скорость 0. В момент времени t2 тело имеет скорость . Согласно правилу вычитания векторов найдём вектор изменения скорости Δ = — 0. Тогда определить ускорение можно так:
Рис. 1.8. Среднее ускорение.
В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть
Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки, при котором за одну секунду скорость этой точки увеличивается на 1 м/с. Иными словами, ускорение определяет, насколько изменяется скорость тела за одну секунду. Например, если ускорение равно 5 м/с2, то это означает, что скорость тела каждую секунду увеличивается на 5 м/с.
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:
Направление ускорения также совпадает с направлением изменения скорости Δ при очень малых значениях промежутка времени, за который происходит изменение скорости. Вектор ускорения может быть задан проекциями на соответствующие оси координат в данной системе отсчёта (проекциями аХ, aY, aZ).
При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть
v2 > v1а направление вектора ускорения совпадает с вектором скорости 2.
Если скорость тела по модулю уменьшается, то есть
v2 1то направление вектора ускорения противоположно направлению вектора скорости 2. Иначе говоря, в данном случае происходит замедление движения, при этом ускорение будет отрицательным (а
Рис. 1.9. Мгновенное ускорение.
При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).
Тангенциальное ускорение
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Рис. 1.10. Тангенциальное ускорение.
Направление вектора тангенциального ускорения τ (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.
Нормальное ускорение
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой n. Вектор нормального ускорения направлен по радиусу кривизны траектории.
Полное ускорение
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
(согласно теореме Пифагора для прямоугольно прямоугольника).
Направление полного ускорения также определяется правилом сложения векторов:
= τ + n
Формула ускорения в физике
Определение и формула ускорения
ОпределениеУскорением (мгновенным ускорением) называют вектор, который определяет быстроту, с которой изменяется скорость перемещающейся материальной точки.
Обычно ускорение обозначают . В теоретической механике встречается обозначение ускорения: . Математическим определением мгновенного ускорения являются выражения:
где – скорость движения материальной точки
или
где – радиус – вектор, который определяет положение материальной точки в пространстве.
Вектор ускорения располагается в плоскости соприкосновения, в которой находится главная нормаль и касательная к траектории, при этом он имеет направление в сторону вогнутости траектории.
Единицы измерения ускорения
Основными единицами измерения ускорения в системе СИ является: [a]=м/с2
в СГС: [a]=см/с2
Виды ускорения
Если построить соприкасающуюся плоскость, в любой точке траектории, то вектор разложим на две взаимно перпендикулярные составляющие:
где — вектор, направленный по главной нормали к центру кривизны траектории материальной точки – это нормальное ускорение; — вектор, направленный по касательной к траектории – это касательное ускорение. При этом выполняются равенства:
где – модуль вектора скорости, R – радиус кривизны траектории, an – проекция вектора на направление единичного вектора главной нормали , aт – проекция вектора на направление единичного вектора касательной . Величина an определяет быстроту изменения направления скорости, а величина aт — быстроту изменения модуля скорости.
Если , то такое движение называют равномерным. Приa_ движение является равнопеременным (при равнозамедленным, при равноускоренным).
Средним ускорением материальной точки на отрезке времени от до называется векторная величина, равная отношению:
При в пределе среднее ускорение совпадает с мгновенным ускорением:
Формула ускорения в разных системах координат
В декартовых координатах проекции ускорения (ax,ay,az) на оси (X,Y,Z)можно представить как:
Соответственно, имеем:
где – единичные орты по осям X,Y.Z. При этом модуль ускорения равен:
В цилиндрической системе координат имеем:
В сферической системе координат модуль ускорения можно найти как:
Примеры решения задач
ПримерЗадание. Материальная точка движется по окружности (рис.1), которая имеет радиус R=2м, уравнение движения: , гдеtв секундах, а S в метрах. Каков модуль ускорения данной точки при t=3 c?
Решение. В качестве основы для решения задачи используем формулу:
Используя заданное уравнение движения, найдем модуль скорости материальной точки:
Продифференцировав уравнение для модуля скорости (1.2) по времени получим тангенциальную составляющую ускорения:
м/с2
Для вычисления нормальной составляющей скорости движения нашей материальной точки следует, используя выражение (1.2) найти:
м/с2
Используя выражение (1.1) вычислим искомое ускорение:
м/с2
Ответ. м/с2
ПримерЗадание. Какова зависимость ускорения материальной точки от времени (a(t)), если частица перемещается по оси Xи ее скорость изменяется в соответствии с уравнением: , где – постоянная большая нуля? В начальный момент времени (при t=0 с) материальная точка находилась в начале координат (x=0 м). Нарисуйте график a(t).
Решение. Из условий задачи можно записать, что:
Используя формулу (2.1) найдем зависимость координаты xот времени (x(t) ):
где постоянную интегрирования найдем из начального условия задачи. Мы знаем, что x(0)=0, значит C=0. Имеем:
Используя формулу для нахождения ускорениядля нашего случая (движение по оси X):
полу
Формула ускорения
Ускорение — это показатель скорости изменения объекта. Итак, ускорение — это изменение скорости, деленное на время. Ускорение имеет величину (значение) и направление. Направление ускорения не должно совпадать с направлением скорости. Единицами ускорения являются квадратные метры в секунду (м / с 2 ).

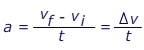
a = ускорение (м / с 2 )
v f = конечная скорость (м / с)
v i = начальная скорость (м / с)
т = время, за которое происходит изменение (с)
Δ v = краткая форма для «изменения» скорости (м / с)
Формула ускорения Вопросы:1) Спортивный автомобиль едет с постоянной скоростью v = 5.00 м / с . Водитель наступает на газ, и машина ускоряется вперед. Через 10,0 секунд водитель прекращает ускорение и поддерживает постоянную скорость v = 25,0 м / с . Каково было ускорение автомобиля?
Ответ: Начальная скорость составляет v i = 5,00 м / с в прямом направлении. Конечная скорость составляет v f = 25,0 м / с в прямом направлении. Время, за которое произошло это изменение, составляет 10,0 с . Ускорение в прямом направлении со значением:
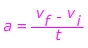
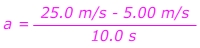
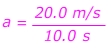
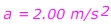
Ускорение автомобиля равно 2.00 м / с 2 , вперед.
2) Ребенок сбрасывает камень со скалы. Камень падает за 15,0 с , прежде чем упасть на землю. Ускорение от силы тяжести составляет г = 9,80 м / с. 2 . Какова была скорость камня за мгновение до того, как он упал на землю?
Ответ: Камень был освобожден от покоя, поэтому начальная скорость равна против и = 0,00 м / с . Время, за которое произошло изменение, составляет 15,0 с .Ускорение составляет 9,80 м / с 2 . Необходимо определить конечную скорость, поэтому измените уравнение:
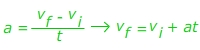
v f = v i + при
v f = 0.00 м / с + (9,80 м / с 2 ) (15,0 с)
v f = 147 м / с
Камень падает, поэтому направление скорости уменьшается.
Формула ускорения— формулы скорости, скорости и ускорения
На общем языке ускорение означает ускорение. Но в физике это имеет очень специфическое значение. Ускорение описывается как скорость изменения скорости объекта, независимо от того, ускоряется он или замедляется. Если оно ускоряется, ускорение считается положительным, а если оно замедляется, ускорение отрицательное. Это вызвано чистой неуравновешенной силой, действующей на объект согласно Второму Закону Ньютона.Ускорение является векторной величиной, поскольку оно описывает скорость изменения скорости во времени, которая является векторной величиной. Ускорение обозначено . Единица измерения СИ: м / с 2 , а размеры: M 0 L 1 T –2 .
Если v 0 , v t и t представляют начальную скорость, конечную скорость и время, необходимое для изменения скорости, то ускорение определяется как:
\ [\ vec a = \ frac {{{{\ vec v} _t} — {{\ vec v} _0}}} {t} \]
В одномерном движении мы можем использовать; \ [a = \ frac {{{v_t} — {v_0}}} {t} \]
Общая формула
: \ [\ vec a = \ frac {{d \ vec v}} {{dt}} = \ frac {{{d ^ 2} \ vec r}} {{d {t ^ 2}}} \ ]
В одномерном движении, где x — смещение, а \ [v = \ frac {{dx}} {{dt}} \] — скорость;
\ [a = \ frac {{dv}} {{dt}} = \ frac {{{d ^ 2} x}} {{d {t ^ 2}}} \]
Тогда; скорость \ [v = \ frac {{dx}} {{dt}} = —2 + 6t \]
Ускорение: \ [a = \ frac {{dv}} {{dt}} = 6 \, \] = 6 м / с 2 .
(Мы видим, что ускорение здесь постоянное. Следовательно, при t = 3 с его значение также составляет 6 м / с. 2 .
Практический вопрос:
Автомобиль разгоняется от покоя с постоянной скоростью $ \ alpha $ в течение некоторого времени, после чего он замедляется с постоянной скоростью $ \ beta $ и останавливается. Если общее время, прошедшее с трассы, составляет т, , то максимальная скорость, полученная автомобилем, составляет(a) $ \ left ( {\ frac {{{\ alpha ^ 2} + {\ beta ^ 2}}} {{\ \ alpha \ beta}}} \ right) \, t $ (b) $ \ left ({\ frac {{{\ alpha ^ 2} — {\ beta ^ 2}}} {{\ alpha \ beta}}} \ right) \, t $ (c) $ \ frac {{(\ alpha + \ beta) \, t}} { {\ alpha \ beta}} $ (d) $ \ frac {{\ alpha \ beta \, t}} {{\ alpha + \ beta}} $
Ответ (d)
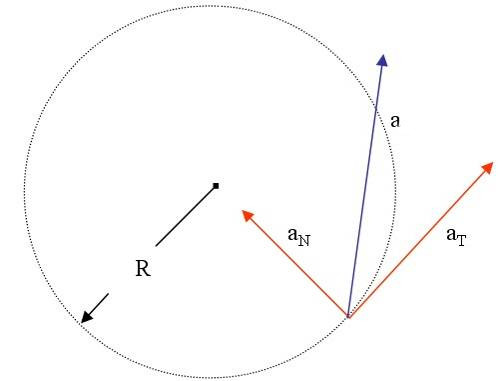
В этом разделе ускорение разбивается на два компонента, называемые тангенциальными и нормальными компонентами. Аналогично тому, как мы разбиваем все векторы на \ (\ hat {\ textbf {i}} \), \ (\ hat {\ textbf {j}} \) и \ (\ hat {\ textbf {k}} \ ) компоненты, мы можем сделать то же самое с ускорением. Добавление этих двух компонентов даст нам общее ускорение.
Введение
Мы привыкли думать об ускорении как о второй производной позиции, и хотя это один из способов взглянуть на общее ускорение, мы можем далее разбить ускорение на две составляющие: тангенциальное и нормальное ускорение.Тангенциальное ускорение, обозначаемое \ (a_T \), позволяет нам узнать, какая часть ускорения действует в направлении движения. Нормальное ускорение \ (a_N \) — это сколько ускорения ортогонально тангенциальному ускорению.
Помните, что векторы имеют величину И направление. Тангенциальное ускорение является мерой скорости изменения величины вектора скорости, то есть скорости, а нормальное ускорение является мерой скорости изменения направления вектора скорости.
Этот подход к ускорению особенно полезен в физических приложениях, потому что нам нужно знать, какая часть полного ускорения действует в любом заданном направлении. Например, проектирование тормозов для автомобиля или двигателя ракеты. Почему может быть полезно разделить ускорение на компоненты?
Теоретическая дискуссия с описательной разработкой
Мы можем найти тангенциальное ускорение, используя Цепное правило, чтобы переписать вектор скорости следующим образом:
\ [\ mathbf {v} = \ dfrac {\ mathrm {d \ textbf {r}}} {\ mathrm {d} t} = \ dfrac {\ mathrm {d \ textbf {r}}} {\ mathrm { d} s} \ dfrac {\ mathrm {d \ textit {s}}} {\ mathrm {d} t} = \ textbf {T} \ dfrac {\ mathrm {d \ mathit {s}}} {\ mathrm { d} t} \]
Теперь, так как ускорение является просто производной скорости, мы находим, что:
\ [\ begin {align} \ mathbf {a} & = \ dfrac {\ mathrm {d \ mathbf {v}}} {\ mathrm {d} t} \\ & = \ dfrac {\ mathrm {d}} {\ mathrm {d} t} (\ mathbf {T} \ dfrac {\ mathrm {d \ mathit {s}}} {\ mathrm {d} t}) \\ & = \ dfrac {\ mathrm {d} ^ 2 \ mathit {s}} {\ mathrm {d} t ^ 2} \ mathbf {T} + \ dfrac {\ mathrm {d} s} {\ mathrm {d} t} \ dfrac {\ mathrm {d} \ mathbf {T}} {\ mathrm {d} t} \\ & = \ dfrac {\ mathrm {d} ^ 2s} {\ mathrm {d} t ^ 2} \ mathbf {T} + \ dfrac {\ mathrm { d} s} {\ mathrm {d} t} \ left (\ dfrac {\ mathrm {d} \ mathbf {T}} {\ mathrm {d} s} \ dfrac {\ mathrm {d} s} {\ mathrm {d} t} \ right) \\ & = \ dfrac {\ mathrm {d} ^ 2s} {\ mathrm {d} t ^ 2} \ mathbf {T} + \ dfrac {\ mathrm {d} s} { \ mathrm {d} t} \ left (\ kappa \ mathbf {N} \ dfrac {\ mathrm {d} s} {\ mathrm {d} t} \ right) \\ & = \ dfrac {\ mathrm {d} ^ 2s} {\ mathrm {d} t ^ 2} \ mathbf {T} + \ kappa \ left (\ dfrac {\ mathrm {d} s} {\ mathrm {d} t} \ right) ^ 2 \ mathbf { N} \ end {align} \]
Примечание
\ [\ dfrac {\ mathrm {d} \ mathbf {T}} {\ mathrm {d} s} = \ kappa \ mathbf {N} \]
Это, в свою очередь, дает нам определение ускорения по компонентам.2} \ label {Normal} \]
Мы можем отнести это обратно к общему физическому принципу равномерного кругового движения. В равномерном циркуляционном движении, когда скорость не изменяется, тангенциальное ускорение отсутствует, только нормальное ускорение указывает на центр круга. Почему вы думаете, что это? Подсказка: посмотрите в разделе введения разницу между двумя компонентами ускорения.
Пример \ (\ PageIndex {1} \)
Не найдя Т, и Н, записывают ускорение движения
\ [\ mathbf {r} (t) = (\ cos t + t \ sin t) \ hat {\ textbf {i}} + (\ sin tt \ cos t) \ hat {\ textbf {j}} \ ] для \ (t> 0 \).2} \\ & = \ sqrt {\ dfrac {20} {9}} \\ & = \ dfrac {2 \ sqrt {5}} {3} \ end {align} \]
\ [\ mathbf {a} (1) = \ dfrac {4} {3} \ mathbf {T} + \ dfrac {2 \ sqrt {5}} {3} \ mathbf {N} \]
,Угловое ускорение обозначается \ [\ alpha \].
Если \ [\ theta \] — угловое смещение, \ [\ omega \] — угловая скорость, а \ [\ alpha \] — угловое ускорение, то;
\ [\ alpha = \ frac {{d \ omega}} {{dt}} = \ frac {{{d ^ 2} \ theta}} {{d {t ^ 2}}} \] (as; \ [\ omega = \ frac {{d \ theta}} {{dt}} \])
Приведенная выше формула дает мгновенное угловое ускорение.
Если \ [\ Delta \ omega \] — это изменение угловой скорости за промежуток времени \ [\ Delta t \], то среднее угловое ускорение определяется как:
\ [\ alpha = \ frac {{\ Delta \ omega }} {{\ Delta t}} \]
В случае равномерного вращения среднее и мгновенное значения совпадают.
Выражается в единицах рад / с 2 или радиан в секунду в квадрате.
Пример 1
Если угловая скорость тела во вращательном движении изменяется от \ [\ frac {\ pi} {2} \] рад / с до \ [\ frac {{3 \ pi}} {4} \] в 0.2} \]
Вопрос: Колесо, вращающееся со скоростью 10 рад / с 2 , с постоянным угловым ускорением 4 рад / с 2 в течение 5 секунд. Число оборотов, выполненных колесом в этом интервале 5 с:
Опции:
(a) \ [\ frac {{20}} {\ pi} \]
(b) \ [\ frac {{40 }} {\ pi} \]
(с) \ [\ frac {{100}} {\ pi} \]
(д) \ [\ frac {{50}} {\ pi} \]
и WER: (д)

Leave A Comment