Путь и перемещение, теория и онлайн калькуляторы
Путь и перемещение, теория и онлайн калькуляторыПри своем движении материальная точка описывает некоторую линию, которую называют ее траекторией движения. Траектория может быть прямой линией, а может представлять собой кривую.
Путь
Определение
Путь — длина участка траектории, который прошла материальная точка за рассматриваемый отрезок времени. Путь — это скалярная величина.
При прямолинейном движении в одном направлении пройденный путь ($\Delta s$) равен модулю изменения координаты тела. Так, если тело двигалось по оси X, то путь можно найти как:
\[\Delta s=\left|x_2-x_1\right|\left(1\right),\]
где $x_1$ — координата начального положения тела; $x_2$ — конечная координата тела.
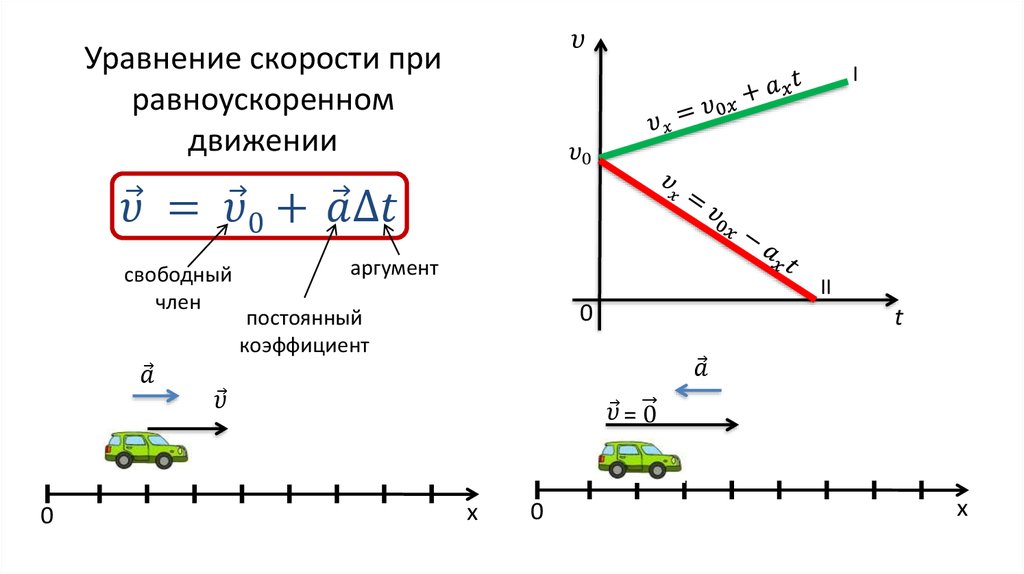
Его можно вычислить, если известен модуль скорости ($v=v_x$):
\[\Delta s=vt\ \left(2\right),\]
где $t$ — время движения тела.
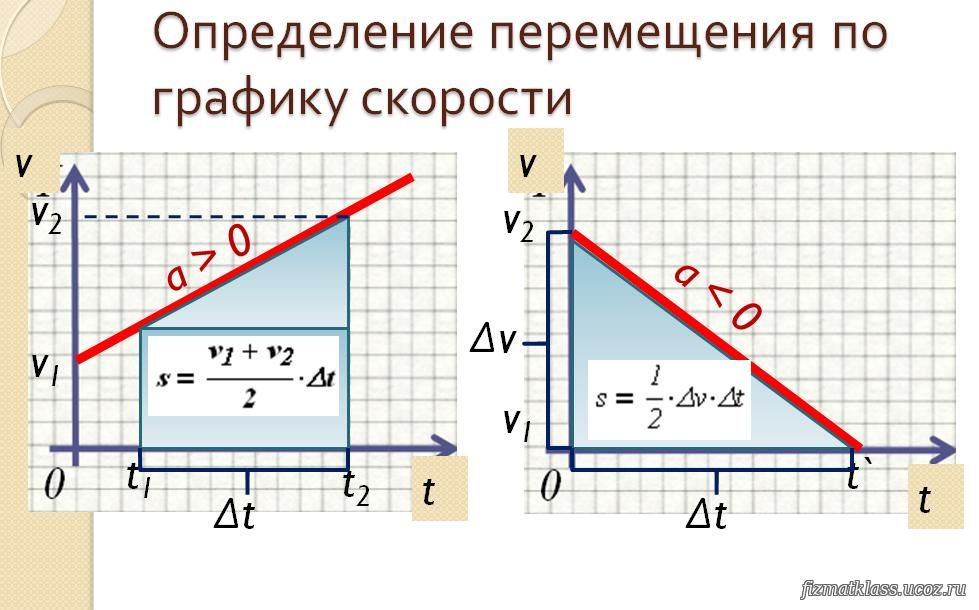
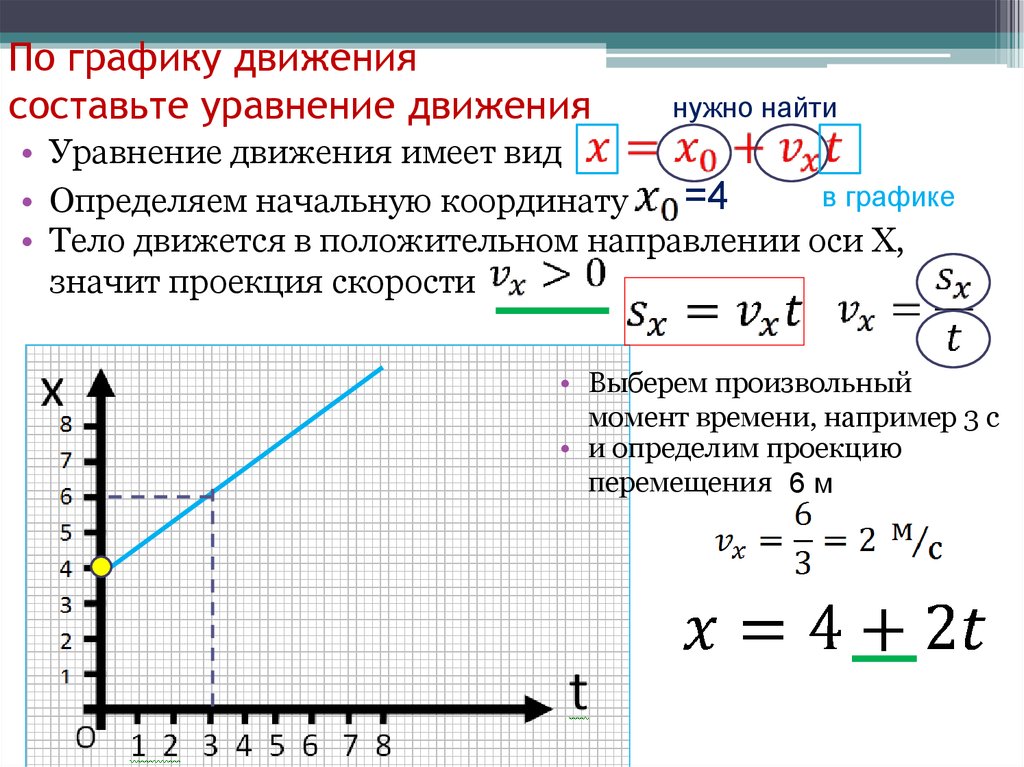
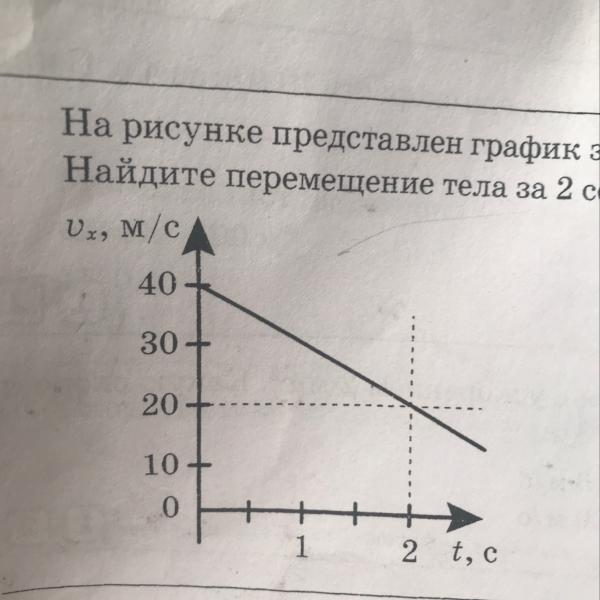
Графиком, который отображает зависимость пути от времени при равномерном прямолинейном движении, является прямая (рис.1). С увеличением величины скорости увеличивается угол наклона прямой относительно оси времени.
Если по графику $\Delta s(t)$ необходимо найти путь, который проделало тело за время $t_1$, то из точки $t_1$ на оси времени проводят перпендикуляр до пересечения с графиком $\Delta s(t)$. Затем из точки пересечения восстанавливают перпендикуляр к оси $\Delta s$. На пересечении оси и перпендикуляра получают точку ${\Delta s}_1$, которая соответствует пройденному пути за время от $t=0\ c$ до $t_1$.
Путь не бывает меньше нуля и не может уменьшаться при движении тела.
Перемещение
Определение
Перемещением называют вектор, который проводят из начального положения движущейся материальной точки в ее конечное положение:
 \]
\]Вектор перемещения численно равен расстоянию между конечной и начальной точками и направлен от начальной точки к конечной.
Приращение радиус-вектора материальной точки — это перемещение ($\Delta \overline{r}$).
В декартовой системе координат радиус-вектор точки представляют в виде:
\[\overline{r\ }\left(t\right)=x\left(t\right)\overline{i}+y\left(t\right)\overline{j}+z\left(t\right)\overline{k}\left(4\right),\]
где $\overline{i}$, $\overline{j}$,$\ \overline{k}$ — единичные орты осей X,Y,Z. Тогда $\Delta \overline{r}$ равен:
\[\Delta \overline{r}=\left[x\left(t+\Delta t\right)-x\left(t\right)\right]\overline{i}+\left[y\left(t+?t\right)-y\left(t\right)\right]\overline{j}+\left[z\left(t+?t\right)-z\left(t\right)\right]\overline{k}\left(5\right).\]
При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и длина вектора перемещения равна пройденному точкой пути:
\[\left|\Delta \overline{r}\right|=\Delta s\ \left(6\right).
Длину вектора перемещения (как и любого вектора) можно обозначать как $\left|\Delta \overline{r}\right|$ или просто $\Delta r$ (без указания стрелки).
Если тело совершает несколько перемещений, то их можно складывать по правилам сложения векторов:
\[\Delta \overline{r}=\Delta {\overline{r}}_1+\Delta {\overline{r}}_2+\dots \left(7\right).\]
Если направление движения тела изменяется, то модуль вектора перемещения не равен пройденному телом пути.
Примеры задач на путь и перемещение
Пример 1
Задание: Мяч бросили вертикально вверх от поверхности Земли. Он долетел до высоты 20 м. и упал на Землю. Чему равен путь, который прошел мяч, каков модуль перемещения?
Решение: Сделаем рисунок.
В нашей задаче мяч движется прямолинейно сначала вверх, затем вниз. Так как путь — длина траектории, то получается, что мяч дважды прошел расстояние h, следовательно:
\[\Delta s=2h. \]
\]
Перемещение — направленный отрезок, соединяющий начальную точку и конечную при движении тела, но тело начало движение из той же точки, в которую вернулось, следовательно, перемещение мяча равно нулю:
Ответ: $\ Путь\ \Delta s=2h$. Перемещение $\Delta r=0$
Пример 2
Задание: В начальный момент времени тело находилось в точке с координатами $(x_0=3;;\ y_0=1)$(см). Через некоторый промежуток времени оно переместилось в точку координаты которой ($x=2;;y=4$) (см). Каковы проекции вектора перемещения на оси X и Y?
Решение: Сделаем рисунок.
Радиус — вектор начальной точки запишем как:
\[{\overline{r\ }}_0\left(t\right)=x_0\left(t\right)\overline{i}+y_0\left(t\right)\overline{j}=3\overline{i}+1\overline{j}\left(2.1\right).\]
Радиус — вектор конечной точки имеет вид:
\[\overline{r}\left(t\right)=x\left(t\right)\overline{i}+y\left(t\right)\overline{j}=2\overline{i}+4\overline{j}\left(2.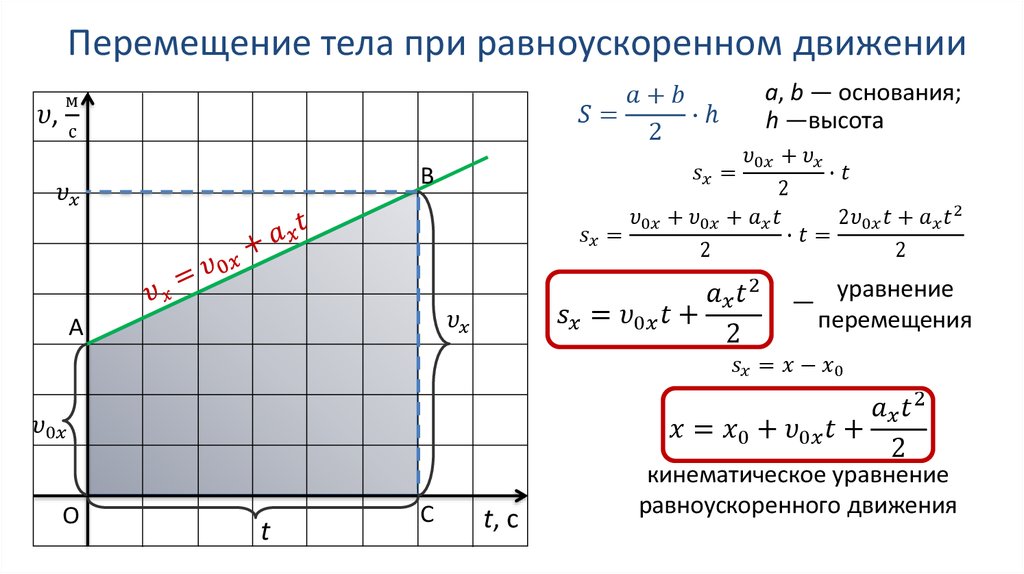 2\right).\]
2\right).\]
Вектор перемещения представим как:
\[\Delta \overline{r}=\left[x\left(t\right)-x_0\left(t\right)\right]\overline{i}+\left[у\left(t\right)-у_0\left(t\right)\right]\overline{j}=\left[2-3\right]+\left[1-4\right]\overline{j}=-1\overline{i}+3\overline{j}(2.3).\]
Из формулы видим, что:
Ответ: $\Delta r_x=-1;;\Delta r_y=3\ $
Читать дальше: равнодействующая всех сил.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Путь и перемещение тела
С понятием пути вы уже неоднократно сталкивались. Познакомимся теперь с новым для вас понятием – перемещением, которое более информативно и полезно в физике, чем понятие пути.
Допустим, из пункта А в пункт В на другом берегу реки нужно переправить груз. Это можно сделать на автомобиле через мост, на катере по реке или на вертолёте. В каждом из этих случаев путь, пройденный грузом, будет разным, но перемещение будет неизменным: из точки А в точку В.
Перемещением называют вектор, проведённый из начального положения тела в его конечное положение. Вектор перемещения показывает расстояние, на которое переместилось тело, и направление перемещения. Обратите внимание, что направление перемещения и направление движения – два разных понятия. Поясним это.
Рассмотрим, например, траекторию движения автомобиля от пункта А до середины моста. Обозначим промежуточные точки – В1, В2, В3 (см. рисунок). Вы видите, что на отрезке АВ1 автомобиль ехал на северо-восток (первая синяя стрелка), на отрезке В1В2 – на юго-восток (вторая синяя стрелка), а на отрезке В2В3 – на север (третья синяя стрелка). Итак, в момент проезда моста (точки В3) направление движения характеризовалось синим вектором В2В3, а направление перемещения – красным вектором АВ3.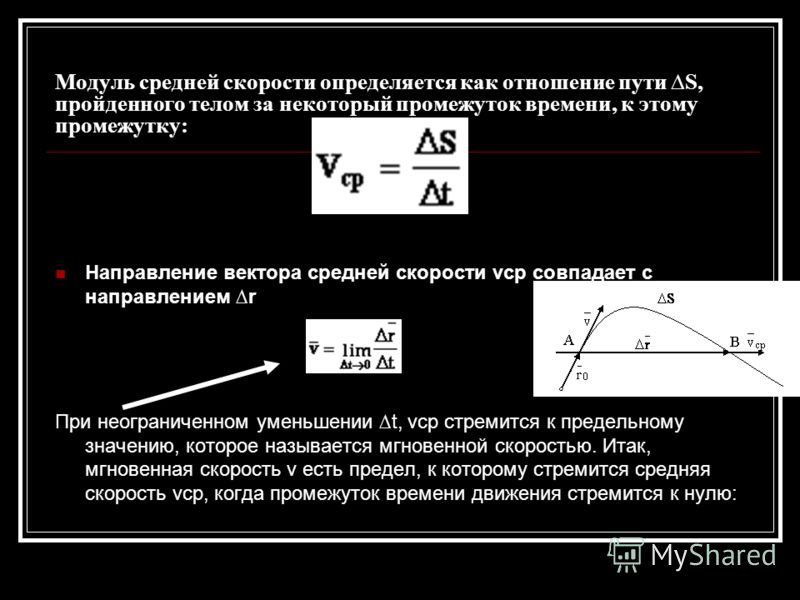
Итак, перемещение тела – векторная величина, то есть имеющая пространственное направление и числовое значение (модуль). В отличие от перемещения, путь – скалярная величина, то есть имеющая только числовое значение (и не имеющая пространственного направления). Путь обозначают символом l, перемещение обозначают символом (важно: со стрелочкой). Символом s без стрелочки обозначают модуль перемещения. Примечание: изображение любого вектора на чертеже (в виде стрелки) или упоминание его в тексте (в виде слова) делает необязательным наличие стрелочки над обозначением.
Почему в физике не ограничились понятием пути, а ввели более сложное (векторное) понятие перемещения? Зная модуль и направление перемещения, всегда можно сказать, где будет находиться тело (по отношению к своему начальному положению). Зная путь, положение тела определить нельзя. Например, зная лишь, что турист прошёл путь 7 км, мы ничего не можем сказать о том, где он сейчас находится.
Задача.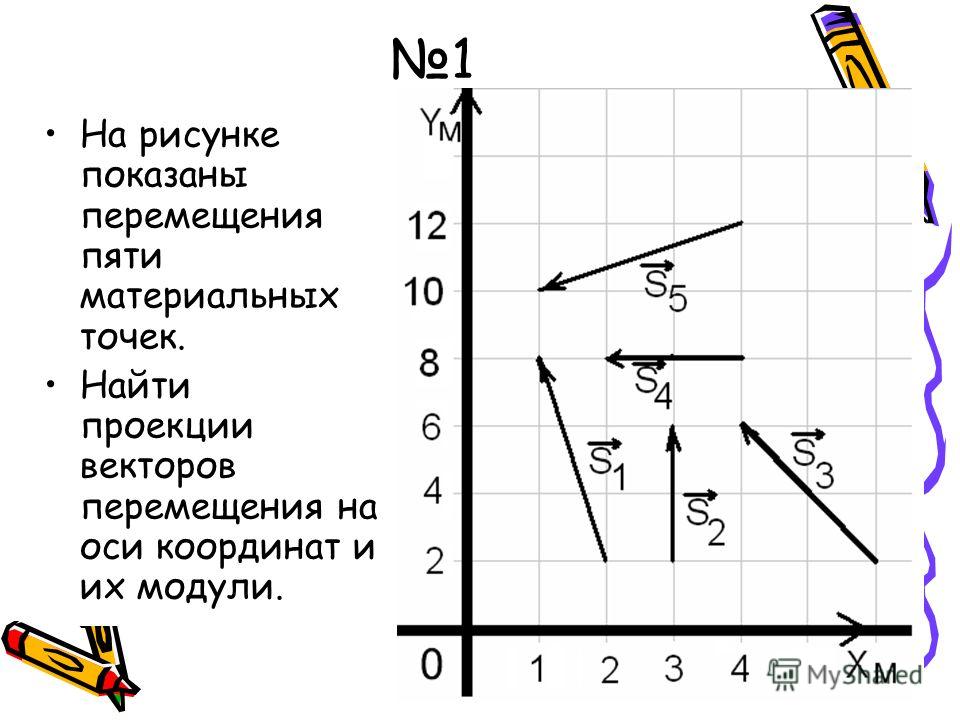 В походе по равнине турист прошёл на север 3 км, затем повернул на восток и прошел ещё 4 км. На каком расстоянии от начальной точки маршрута он оказался? Начертите его перемещение.
В походе по равнине турист прошёл на север 3 км, затем повернул на восток и прошел ещё 4 км. На каком расстоянии от начальной точки маршрута он оказался? Начертите его перемещение.
Решение 1 – с измерениями линейкой и транспортиром.
Перемещение – это вектор, соединяющий начальное и конечное положения тела. Начертим его на клетчатой бумаге в масштабе: 1 км – 1 см (чертёж справа). Измерив линейкой модуль построенного вектора, получим: 5 см. Согласно выбранному нами масштабу, модуль перемещения туриста равен 5 км. Но напомним: знать вектор – значит знать его модуль и направление. Поэтому, применив транспортир, определим: направление перемещения туриста составляет 53° с направлением на север (проверьте сами).
Решение 2 – без использования линейки и транспортира.
Поскольку угол между перемещениями туриста на север и на восток составляет 90°, применим теорему Пифагора и найдём длину гипотенузы, так как она одновременно является и модулем перемещения туриста:
Как видите, это значение совпадает с полученным в первом решении. Теперь определим угол α между перемещением (гипотенузой) и направлением на север (прилежащим катетом треугольника):
Теперь определим угол α между перемещением (гипотенузой) и направлением на север (прилежащим катетом треугольника):
Итак, задача решена двумя способами с совпадающими ответами.
Опубликовано в разделах: 9 класс, Введение в кинематикуПонимание мышц и движения » Метод биомеханики
Понимание мышц и движения
Понимание мышц и движения объясняет в простых для понимания терминах, как все тело движется вместе как интегрированная система мышц, сухожилий, костей, связок и фасция; информация, необходимая для понимания причин проблемных и ограничивающих мышечно-скелетных дисбалансов. Вы также познакомитесь с уникальным подходом метода биомеханики к пониманию того, как гравитация и силы реакции опоры изменяют способ движения тела — знания, необходимые для разработки успешных стратегий корректирующих упражнений.
Посмотреть образец курса
Что содержит курс?
- Онлайн-уроки с цифровыми текстовыми материалами, пошаговыми видеоинструкциями и демонстрационными примерами оценивания
- Формы оценки клиентов*
- Тесты навыков и упражнения для самопроверки*
Что я смогу делать после завершения этого курса? (цели обучения)
- Идентификация важной анатомической информации о мышцах, сухожилиях, костях, связках и фасциях, включая конкретное происхождение, места прикрепления и функции мышц
- Объясните разницу между традиционной и функциональной анатомией и то, как гравитация и силы реакции опоры изменяют способ движения тела
- Распознавать основные группы мышц, которые будут определять стратегии упражнений, используемые для улучшения здоровья опорно-двигательного аппарата и облегчения связанной с ним дисфункции
- Использование результатов анатомии и оценки для разработки и включения корректирующих упражнений в программы обучения клиентов
Что еще мне нужно знать?
Понимание мышц и движения является модулем 2 курса сертификации специалистов по корректирующим упражнениям по методу биомеханики. Его можно приобрести как отдельный курс, чтобы дать учащимся возможность узнать о костно-мышечной системе и о том, как на нее может негативно повлиять дисбаланс, а также предоставить доступный вариант для тех, кто заинтересован в получении сертификата специалиста по корректирующим упражнениям (TBMM-CES).
Его можно приобрести как отдельный курс, чтобы дать учащимся возможность узнать о костно-мышечной системе и о том, как на нее может негативно повлиять дисбаланс, а также предоставить доступный вариант для тех, кто заинтересован в получении сертификата специалиста по корректирующим упражнениям (TBMM-CES).
Остальные компоненты курса TBMM-CES включают:
- Основы структурной оценки
- Основы корректирующих упражнений
- Полная библиотека корректирующих упражнений
- Разработка программы корректирующих упражнений
Метод биомеханики ® Курс корректирующих упражнений представляет собой пошаговую программу обучения. Рекомендуется, чтобы модули курса были завершены, чтобы оптимизировать процесс обучения. Если вы решите пройти все пять компонентов программы, вы получите сертификат, подтверждающий вашу компетентность в качестве специалиста по корректирующим упражнениям по методу биомеханики (TBMM-CES).
Дополнительная информация о курсе
- Право на получение кредита на непрерывное образование в основных организациях здравоохранения и фитнеса (ACE 1.

- Право засчитываться в счет получения полного сертификата TBMM-CES (также необходимо успешно завершить оставшиеся 4 модуля курса, перечисленные выше)
- Цена покупки включает в себя все онлайн-материалы, неограниченное количество пересдач теста при необходимости и доступ к самому курсу.
- Онлайн-курсы не подлежат возврату.
- Цифровые текстовые материалы, включенные в этот курс, не подлежат печати, если они не помечены соответствующим образом. (* указывает на печатные элементы)
- Стоимость курса указана в долларах США.
Анатомические движения Спортивные науки Степень физического воспитания
Q4E Практический пример 20 – Анатомические движения Предлагаемое использование предмета:
При изучении различных суставов тела и анализе их движений полезно охарактеризовать их в соответствии с определенными плоскостями движения и их осями. Плоскость движения может быть определена как воображаемая двумерная поверхность, по которой перемещается конечность или сегмент тела. В человеческом теле есть три плоскости движения (рис. 1), в которых можно классифицировать различные движения суставов. Подобно плоскостям движения, оси вращения можно рассматривать как ряд воображаемых линий, проходящих через тело; есть также три оси вращения (рис. 2), по которым может происходить движение.
|
Цели
- Определить ряд анатомических движений и продемонстрировать эти движения с соответствующими иллюстрациями с помощью программного обеспечения Quintic.
- Определите специфические спортивные навыки, в которых происходят определенные анатомические движения, и определите роль, которую эти движения играют в успешном выполнении спортивного навыка.

Методы
- Видеосъемка с частотой 50 кадров в секунду с использованием камеры Panasonic 3CCD, на которой субъект выполняет анатомические движения. Затем видео были экспортированы в программное обеспечение Quintic Biomechanics 9.03v17.
- Функции смешивания, форм и захвата неподвижных изображений в Quintic использовались для иллюстрации различных анатомических движений из отснятого материала.
- Затем были сняты видеозаписи различных спортивных навыков и открыты в программе Quintic, где они были проанализированы, чтобы определить конкретные движения суставов, из которых состоит навык.
Функции используемого программного обеспечения Quintic:
- Функция одной камеры
- Фотосъемка
- Модуль последовательности фотографий
- Инструменты формы
- Функция смешивания
- Функция скорости воспроизведения
Результаты
Примечание : Все описанные движения предполагают, что тело начинается с анатомического положения, как указано во введении.
1. Сгибание
Сгибание – это сгибательное движение, которое приводит к уменьшению угла в суставе за счет сближения костей. Обычно это происходит в сагиттальной плоскости. В таблице ниже представлены некоторые суставы, в которых может происходить сгибание, и пример этого движения;
Сгибание | |
Соединение | Пример |
Плечо | Поднятие рук вверх и перед собой. |
Колено | Движение предплечья к плечу путем сгибания локтя для уменьшения его угла |
Позвоночник | Перемещение подбородка к груди. |
Бедро | Движение бедренной кости к тазу/приведение колена к груди |
Колено | Перемещение пятки к ягодицам. |
На рисунке 3 ниже показано сгибание лучезапястного сустава. Сгибание лучезапястного сустава является важным движением во многих спортивных навыках, особенно в играх с ракеткой, поскольку оно может обеспечить стабильность и мощность при выступлении. В последующей фазе штрафного броска в баскетболе очевидно сгибание запястья. Цель этого движения, которое технически известно как щелчок запястьем (показано на рис. 4 ниже), состоит в том, чтобы создать усиленное вращение мяча, что, в свою очередь, добавит подъемной силы к траектории (полета мяча), это может увеличить скорость выпуска мяча. мяч и улучшить общую производительность, что делает его важным аспектом выполнения штрафного броска в баскетболе.
2. Разгибание
Это выпрямляющее движение, которое приводит к увеличению угла в суставе за счет дальнейшего разведения костей. Это движение происходит в сагиттальной плоскости и является движением, обратным сгибанию. В таблице ниже представлены суставы тела, в которых может происходить разгибание, и пример;
Удлинитель | |
Соединение | Пример |
Плечо | От сгибания опускание рук вниз и перед собой. |
Колено | После сгибания предплечье отводится от плеча, выпрямляя локоть. |
Позвоночник | Отклонение головы назад, чтобы закончить смотреть прямо вверх. |
Бедро | От сгибания бедра до анатомического положения |
Запястье | Движение руки к тыльной стороне предплечья |
На рис. 5 показано разгибание коленного сустава. Коленный сустав является самым большим суставом в теле и в первую очередь связан с опорой на вес и движением, по этим причинам разгибание колена является частью многочисленных спортивных навыков. Любой вид спорта, требующий прыжков, в значительной степени зависит от разгибания колен для успешного завершения прыжка. Бег является одним из самых основных навыков, когда можно увидеть разгибание колена (на рис. 6 показано разгибание колена). Во время фазы бега ведущая нога вытягивается в коленном суставе, чтобы создать толчок вперед и вверх, который толкает тело, делая разгибание колена основным компонентом бега.
3. Отведение
Отведение
Это боковое движение от средней линии туловища во фронтальной плоскости. В таблице ниже показаны суставы тела, в которых может происходить отведение, а также пример;
Похищение | |
Соединение | Пример |
Плечо | Подъемно-латеральное движение плечевой кости в сторону. |
Бедро | Движение бедренной кости во фронтальной плоскости латерально в сторону от средней линии |
Запястье | Движение кисти со стороны большого пальца в сторону латеральной поверхности предплечья |
Отведение в тазобедренном суставе показано на рисунке 7 ниже. Некоторые игроки в крикет демонстрируют отведение бедра во время быстрой подачи, как показано на рисунке 8 ниже. Чтобы обеспечить высокую скорость выброса мяча, быстрым боулерам требуются высокие крутящие моменты в суставах. Высокие крутящие моменты в суставах могут быть созданы за счет встречного вращения, то есть поворота верхней части туловища в сторону от направления, в котором должен быть брошен мяч. Отведением тазобедренного сустава, а также другими движениями может быть создано противодействие, которое увеличит крутящий момент в суставах и, следовательно, увеличит скорость выпуска мяча. Также из положения, показанного на рисунке 7 ниже, отведение бедра создает большее расстояние для вращения туловища, что позволяет создать больший импульс и мощность.
Некоторые игроки в крикет демонстрируют отведение бедра во время быстрой подачи, как показано на рисунке 8 ниже. Чтобы обеспечить высокую скорость выброса мяча, быстрым боулерам требуются высокие крутящие моменты в суставах. Высокие крутящие моменты в суставах могут быть созданы за счет встречного вращения, то есть поворота верхней части туловища в сторону от направления, в котором должен быть брошен мяч. Отведением тазобедренного сустава, а также другими движениями может быть создано противодействие, которое увеличит крутящий момент в суставах и, следовательно, увеличит скорость выпуска мяча. Также из положения, показанного на рисунке 7 ниже, отведение бедра создает большее расстояние для вращения туловища, что позволяет создать больший импульс и мощность.
4. Приведение
Это движение медиально по направлению к средней линии туловища во фронтальной плоскости. В таблице ниже показаны суставы, в которых можно выполнять приведение, с примерами для каждого сустава;
Приведение | |
Соединение | Пример |
Плечо | От отведения это нисходящее движение плечевой кости во фронтальной плоскости медиально по направлению к телу.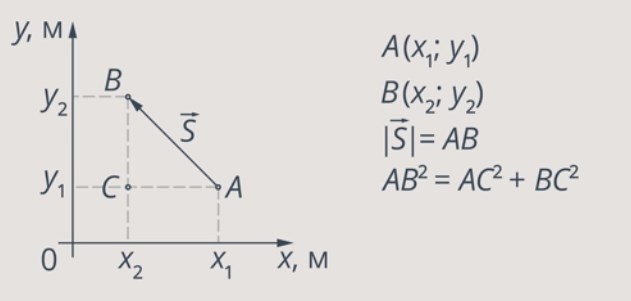 |
Бедро | Из приведения это движение бедренной кости во фронтальной плоскости медиально по направлению к средней линии или перекладывание ноги поперек тела. |
Запястье | Движение стороны мизинца руки к медиальной стороне предплечья. |
Рисунок 9иллюстрирует плечевой сустав, выполняющий приведение. Приведение плеча является ключевым движением при выполнении замаха в гольфе и показано на рисунке 10 ниже. Во время удара в гольфе сегменты тела работают вместе в скоординированной последовательности, чтобы максимизировать скорость головки клюшки при ударе по мячу. Ведущая рука ускоряется до максимального приведения во время обратного замаха, что позволяет игроку в гольф занять подходящее положение для предстоящего замаха и, следовательно, повышает эффективность общего навыка.
5. Внешняя ротация
Внешняя ротация
Это вращательное движение вокруг продольной оси кости от средней линии тела. Это движение происходит в поперечной плоскости и также известно как боковое вращение, наружное вращение и боковое вращение. Суставы, в которых может происходить наружная ротация, показаны в таблице ниже;
Внешнее вращение | |
Соединение | Пример |
Плечо | Смещение плечевой кости латерально в поперечной плоскости вдоль ее длинной оси от срединной линии |
Бедро | Боковое ротационное движение бедренной кости в поперечной плоскости вокруг ее продольной оси и в сторону от средней линии.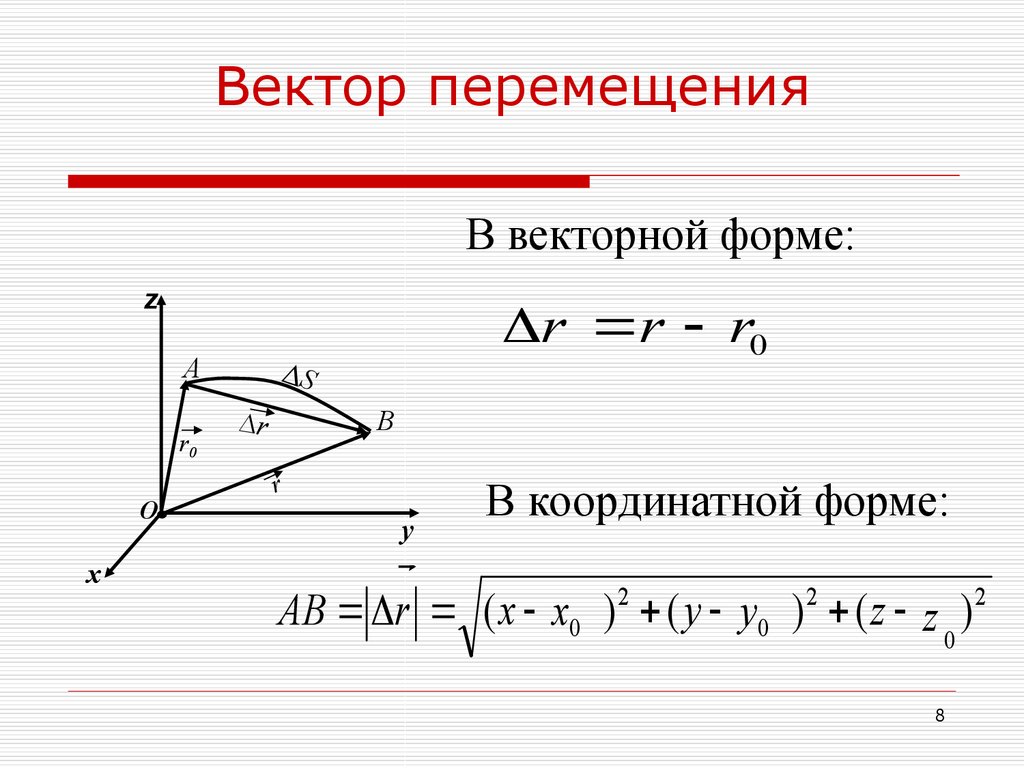 |
Колено | Вращательное движение голени латерально от средней линии. |
На рисунке 11 ниже показана наружная ротация плечевого сустава. Спортивный пример, в котором очевидно внешнее вращение, — это теннисная подача, показанная на Рисунке 12 ниже. Во время завершающей подачи в теннисе плечевой сустав совершает внешнее вращение, чтобы накопить упругую потенциальную энергию, которая может быть передана в поступательное движение подачи, создающее огромное количество силы и импульса. Кроме того, внешнее вращение позволяет ракетке опускаться ниже, это важно, потому что, во-первых, это позволит сформировать больше энергии деформации, а во-вторых, увеличит время ускорения ракетки во время фазы движения вперед, что позволит увеличить время для передачи энергии.
6. Внутренняя ротация
Это вращательное движение вокруг продольной оси кости по направлению к средней линии тела. Это происходит в поперечной плоскости и также известно как вращение медиально и вращение внутрь. Соединения тела, в которых может происходить внутреннее вращение, перечислены в таблице ниже, а также приведены примеры для каждого сустава;
Это происходит в поперечной плоскости и также известно как вращение медиально и вращение внутрь. Соединения тела, в которых может происходить внутреннее вращение, перечислены в таблице ниже, а также приведены примеры для каждого сустава;
Внутреннее вращение | |
Соединение | Пример |
Плечо | Смещение плечевой кости в поперечной плоскости медиально вдоль ее длинной оси к средней линии |
Бедро | Медиальное ротационное движение бедренной кости в поперечной плоскости вокруг ее продольной оси и по направлению к средней линии. |
Колено | Вращательное движение голени медиально по направлению к средней линии.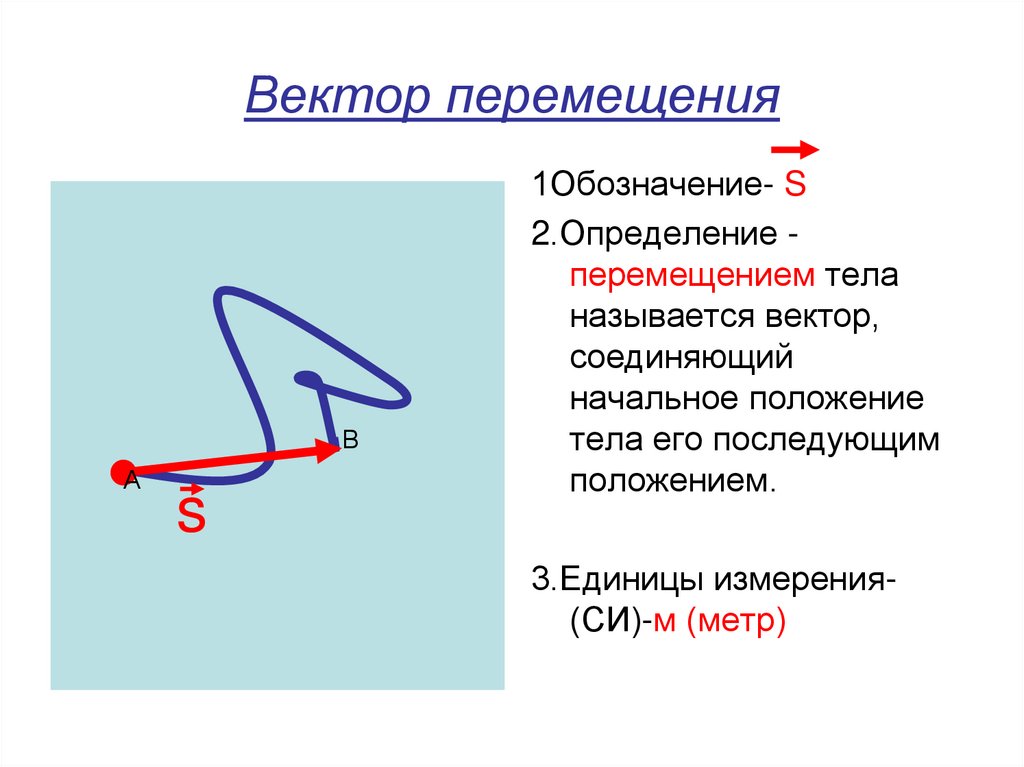 |
Внутреннее вращение — очень распространенное движение в человеческом теле. Когда мы идем или бежим, наши бедра совершают внутреннее вращение с каждым шагом, который мы делаем. Разбег копья демонстрирует внутреннее вращение, как показано на рисунках 13 и 14 ниже. Целью этого движения является создание импульса, который можно передать руке и запястью, чтобы максимизировать скорость выброса копья. Кроме того, последствием внутреннего вращения бедра является сильное вращение туловища, создающее импульс, который можно передать верхней части тела и использовать. По этим причинам внутренняя ротация тазобедренного сустава является важным фактором успешного выполнения метания копья.
Заключение
Хорошее знание анатомических движений необходимо для проведения практического анализа движений человека. Каждое анатомическое движение происходит в определенной плоскости и вокруг определенной оси вращения. Изучая спортивные навыки, вы можете определить отдельные анатомические движения, из которых состоит навык, и, кроме того, оценить влияние отдельных движений на общий успех навыка.

 Совместные действия описываются относительно анатомического положения, которое является универсальным исходным положением для описания движения. Считается, что субъект находится в анатомическом положении, когда он стоит в вертикальном положении, лицом прямо вперед, его ноги сближены и параллельны, а ладони направлены прямо вперед. Это положение показано на рисунке 1 ниже.
Совместные действия описываются относительно анатомического положения, которое является универсальным исходным положением для описания движения. Считается, что субъект находится в анатомическом положении, когда он стоит в вертикальном положении, лицом прямо вперед, его ноги сближены и параллельны, а ладони направлены прямо вперед. Это положение показано на рисунке 1 ниже.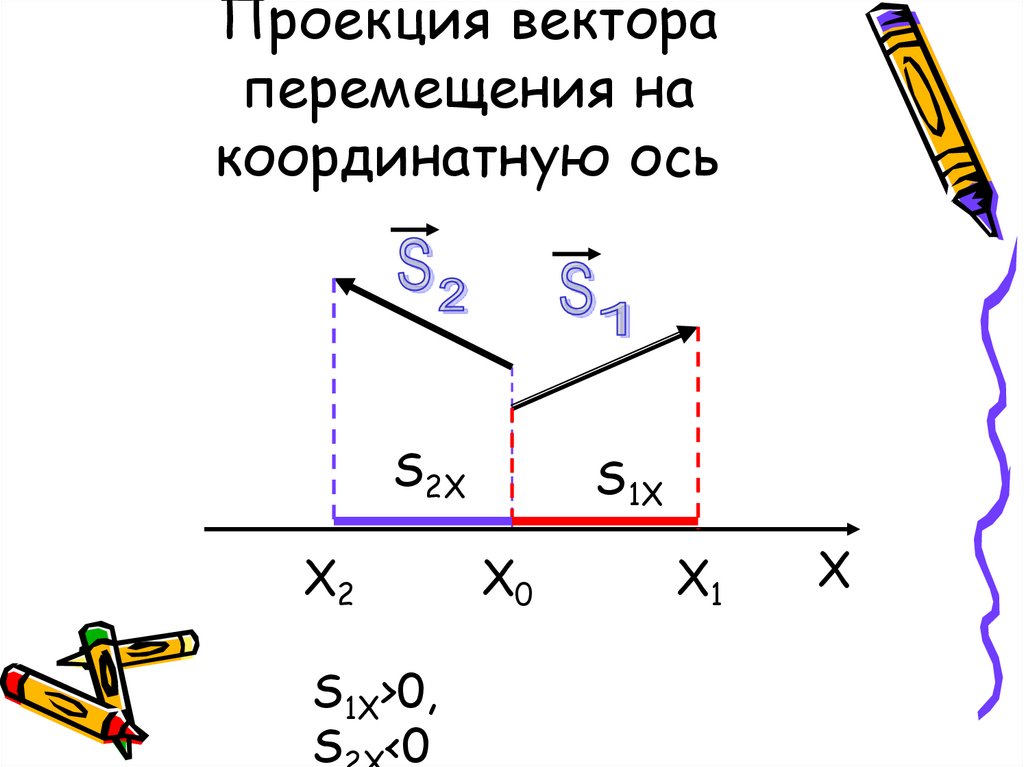 Разделение его на правую и левую симметричные половины. Для движения в сагиттальной плоскости необходимо вращение вокруг горизонтальной оси (поперечной оси).
Разделение его на правую и левую симметричные половины. Для движения в сагиттальной плоскости необходимо вращение вокруг горизонтальной оси (поперечной оси).
Leave A Comment