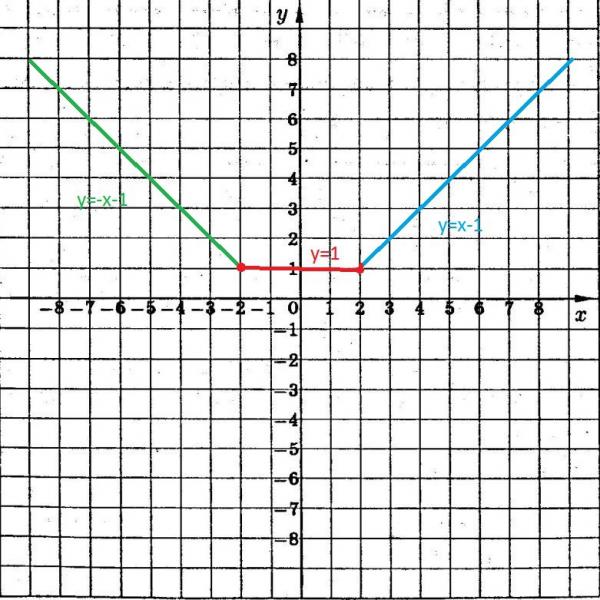
Задача 1. Построить графики функций y=|x| y=|x-1|.
Решение. Сравним его с графиком функции y=|x|.При положительных x имеем |x|=x. Значит, для положительных значений аргумента график y=|x| совпадает с графиком y=x, то есть эта часть графика является лучём, выходящим из начала координат под углом 45 градусов к оси абсцисс. При x< 0 имеем |x|= -x; значит, для отрицательных x график y=|x| совпадает с биссектрисой второго координатного угла.
Впрочем, вторую половину графика (для отрицательных X) легко получить из первой, если заметить, что функция y=|x| — чётная, так как |-a|=|a|. Значит, график функции y=|x| симметричен относительно оси Oy, и вторую половину графика можно приобрести, отразив относительно оси ординат часть, начерченную для положительных x. Получается график:
y=|x|
Для построения берём точки (-2; 2) (-1; 1) (0; 0) (1; 1) (2; 2).
Теперь график y=|x-1|.
Построим графики:
y=|x-1|
Для построения берём точки (-2; 3) (-1; 2) (0; 1) (1; 0) (2; 1).
Это была простенькая задачка. Теперь то, что многих приводит в ужас.
Задача 2. Постройте график функции y=3*|x-4| — x + |x+1|.
Решение. Найдем точки, в которых подмодульные выражения обращаются в нуль, т.е. так называемые «критические» точки функции. Такими точками будут х=-1 и х=4. В этих точках подмодульные выражения могут изменить знак.
Пусть x<-1. Тогда х+1<0, |x+1|=-x-1; x-4<0, |x-4|=-x+4; Следовательно y= 3(-х+4)-х+(-х-1)= -5х+11.
Пусть -1< = x < = 4.
2 — |x| — 3|
Итак, всем спасибо! Теперь мы получили ту базу знаний, необходимую для построения графиков со знаком модуля! А то его так все боятся.
Вот ссылка, которая поможет вам проверить ваши построения:
Постройте график функции и найдите значение k
Постройте график функции y=|x-3|-|x+3| и найдите значение k, при которых прямая y=kx имеет с графиком данной функции ровно одну общую точку.
Решение:
Разберем как строить график с модулем.
y=|x-3|-|x+3|
Найдем точки при переходе которых знак модулей меняется.
Каждое выражения, которое под модулем приравниваем к 0. У нас их два x-3 и x+3.
x-3=0 и x+3=0
x=3 и x=-3
У нас числовая прямая разделится на три интервала (-∞;-3)U(-3;3)U(3;+∞). На каждом интервале нужно определить знак под модульных выражений.
1. Это сделать очень просто, рассмотрим первый интервал (-∞;-3).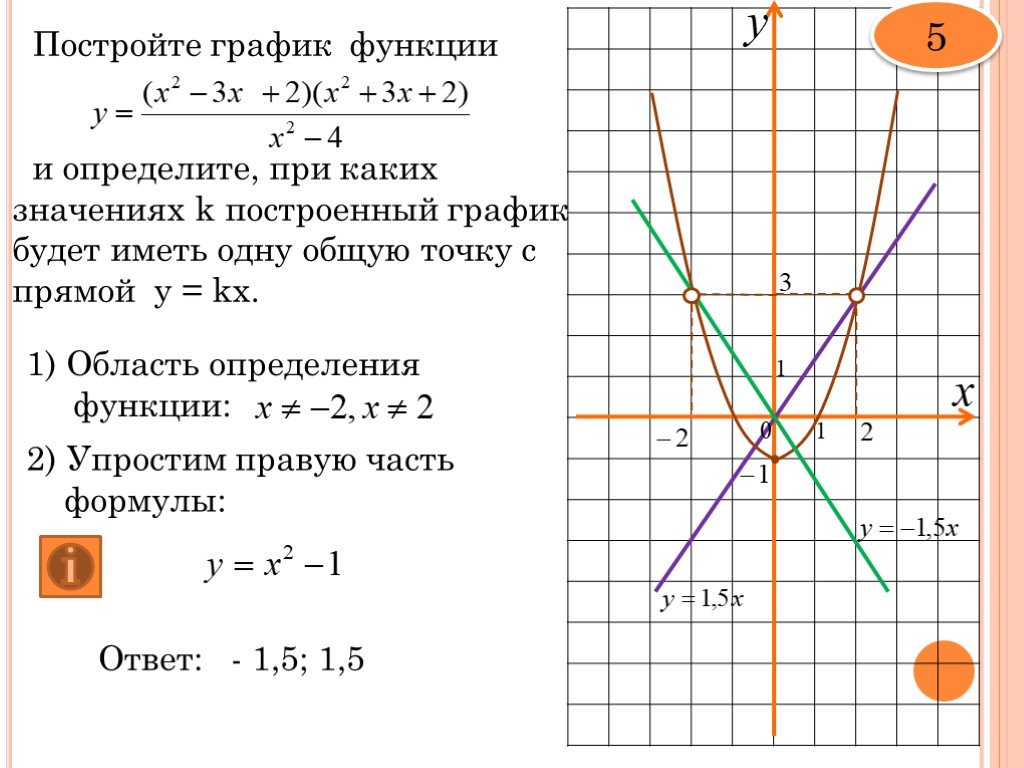
х=-4
x-3=-4-3=-7 и x+3=-4+3=-1
У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞;-3).
y=—(x-3)-(—(x+3))=-х+3+х+3=6
На интервале (-∞;-3) получился график линейной функции (прямой) у=6
2. Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
x-3=0-3=-3 и x+3=0+3=3
У первого выражения x-3 знак отрицательный получился, а у второго выражения x+3 положительный. Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс.
y=—(x-3)-(+(x+3))=-х+3-х-3=-2x
На интервале (-3;3) получился график линейной функции (прямой) у=-2х
3.
Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.
х=5
x-3=5-3=2 и x+3=5+3=8
У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3;+∞).
y=+(x-3)-(+(x+3))=х-3-х-3=-6
На интервале (3;+∞) получился график линейной функции (прямой) у=-6
4. Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
На интервале (-∞;-3) строим график линейной функции (прямой) у=6.
На интервале (-3;3) строим график линейной функции (прямой) у=-2х.
Чтобы построить график у=-2х подберем несколько точек.
x=-3 y=-2*(-3)=6 получилась точка (-3;6)
x=0 y=-2*0=0 получилась точка (0;0)
x=3 y=-2*(3)=-6 получилась точка (3;-6)
На интервале (3;+∞) строим график линейной функции (прямой) у=-6.
5.
Теперь проанализируем результат и ответим на вопрос задания найдем значение k, при которых прямая y=kx имеет с графиком y=|x-3|-|x+3| данной функции ровно одну общую точку.
Прямая y=kx при любом значении k всегда будет проходить через точку (0;0). Поэтому мы можем изменить только наклон данной прямой y=kx, а за наклон у нас отвечает коэффициент k.
Если k будет любое положительное число, то будет одно пересечение прямой y=kx с графиком y=|x-3|-|x+3|. Этот вариант нам подходит.
Если k будет принимать значение (-2;0), то пересечений прямой y=kx с графиком y=|x-3|-|x+3| будет три.Этот вариант нам не подходит.
Если k=-2, решений будет множество [-2;2], потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.
Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.
Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно.
2$ в исходном коде (строка, где $x = 0$) отображается в одну точку цели.
(точка $(0,0)$), а отображение есть открытое погружение на дополнении
этой строки. Поскольку открытые погружения плоские, это говорит о том, что точка $(0,0)$
в цели, где мы должны сосредоточить наше внимание при поиске неплоскости.
(Вот перевод моего замечания об открытых погружениях в алгебраических терминах: если $f$ — любой многочлен от $\mathbb C[x,y]$ с нулевым постоянным членом, то отображение локализаций $\mathbb C[ х, у]_f \к \mathbb C[x,z]_f$ равно — проверьте!)
Существует один идеал, который особенно «чувствителен» к точке $(0,0)$, а именно соответствующий ему максимальный идеал $(x,y) \subset \mathbb C[x,y]$. Итак, давайте попробуем этот идеал.
Нам нужно посмотреть на индуцированное отображение $(x,y)\otimes \mathbb C[x,z]\to \mathbb C[x,z]$. Само уравнение $y = x z$, определяющее отображение $\mathbb C[x,y]
\to \mathbb C[x,z]$ предлагает элемент в ядре, а именно элемент
$y\otimes 1 — x\otimes z$.
Добавлено: Просматривая другие ответы, кажется, что один из пунктов вопрос в том, чтобы действительно проверить, что $y \otimes 1 — x \otimes z$ не равно нулю в $(x,y)\otimes\mathbb C[x,z]$.
Существует стандартный способ вычисления тензорных произведений: по образующим и отношениям. Хотя в конкретных случаях могут быть и другие приемы (см., например, ответ Майкла Джойса), возможно, стоит объяснить этот стандартный подход, поскольку он не требуют любой сообразительности; вы всегда можете просто сделать это.
Начнем с представления идеала $(x,y)$ в виде $\mathbb C[x,y]$-модуля. Это легко: у него есть два образующих, $x$ и $y$, которые
удовлетворяют соотношению $y x — x y = 0$.
Теперь мы тензорируем с помощью $\mathbb C[x,z]$, чтобы получить представление $$ \mathbb C[x,z] \cdot e \to \mathbb C[x,z] \cdot f_1 \oplus \mathbb C[x,z] \cdot f_2 \to (x,y)\otimes \mathbb C[x,z] \to 0,$$ где снова карты даны $e \mapsto (y f_1, -x f_2) = (x z f_1, — x f_2) = x(z f_1,-f_2),$ и $f_1 \mapsto x, f_2 \mapsto y = x z$. (Заметим, что в данном конкретном случае эта точная последовательность также точно слева, но это не является общей чертой этого подхода к вычислению тензорных произведений, поскольку обычно тензорирование является точным справа, но не точно.)
Из этого представления $(x,y)\otimes \mathbb C[x,z]$ мы видим, что
$x\otimes z — y$ (который является образом $(z f_1, -f_2)$) равен ненулевым ,
так как $(z f_1, -f 2)$ не находится на изображении карты из
$\mathbb C[x,z]\cdot e.
$
С другой стороны, это элемент кручения — он уничтожается умножением на $x$ (поскольку $x(z f_1, -f_2)$ — это в образе $\mathbb C[x,z] \cdot e$; действительно это образ $e$). Это отражает тот факт, что если мы локализуем от $x = 0$ (т.е. инвертируем $x$), исходная карта становится плоской, поэтому отображение $(x,y)\otimes\mathbb C[x,z] \to \mathbb C[x,z]$ должно стать инъективным после обращения $x$ ; следовательно, это ядро должно состоять из элементов $x$-кручения.
javascript — каков результат «x по модулю y»?
спросил
Изменено 9 лет, 6 месяцев назад
Просмотрено 3к раз
Ссылка на спецификацию ECMAScript Раздел 5.2:
Запись «x по модулю y» (y должна быть конечной и отличной от нуля) вычисляет значение k того же знака, что и y (или ноль), такое что abs(k) < abs(y) и x−k = q × y для некоторого целого числа q.
поэтому, если y положителен, результат k ‘x по модулю y’ положителен независимо от знака x.
и, если я правильно понимаю, ToInt32(-1) равно ToInt32(1)?
- JavaScript
3
Обозначение x по модулю y используется внутри спецификации для описания результата определенных операций. Так что да, результат k из x по модулю y (по определению) того же знака, что и и . Не утверждается, что оператор % эквивалентен по модулю .
Если вам интересно, актуальную спецификацию для % можно найти в разделе 11.5.3. Интересно, что он не использует по модулю .
9
Скопируйте вставку из моего предыдущего ответа здесь:
Возьмите % b
1. Когда оба +ve, Modulo и Remainder являются одним и тем же 2.Когда a есть -ve, они не совпадают
Когда a есть -ve, они не совпадают
Например;
a = -10, b = 3
Остаток от -10 % 3 = -1
для модуля, прибавьте большее число, кратное 3, к вашему «a» и вычислите остаток.
-10 + 12 = 2
2 % 3 = 2 ваш ответ
Операция по модулю определяется как математическая операция по модулю:
Математические операции, такие как сложение, вычитание, отрицание, умножение, деление и математические функции, определенные позже в этом пункте всегда следует понимать как вычисление точных математические результаты о математических действительных числах, которые не включать бесконечности и не включать отрицательный ноль, т. отличается от положительного нуля.
Ваш вопрос:
ToInt32(-1) равно ToInt32(1)
Ну, нет:
Пусть posInt будет знак(число) * этаж(абс(число)).
posInt = знак(-1) * пол(абс(-1)) = -1;
Пусть int32bit будет posInt по модулю 2 32 ; то есть конечное целое значение k числового типа с положительным знаком и менее 2 32 по величине, например что математическая разница posInt и k математически целое кратное 2 32 .
Leave A Comment