Примеры из ЕГЭ
Пример (ЕГЭ). Найдите значение выражения \(24\sqrt{2}\,cos(-\frac{π}{3})\,sin(-\frac{π}{4})\).
Решение. \(24\sqrt{2}\,cos(-\frac{π}{3})\,sin(-\frac{π}{4})=-24\sqrt{2}\,cos\frac{π}{3}\,sin\frac{π}{4}\).
Из рисунка видно, что и косинус, и синус положителен. Косинус из трех стандартных значений \(\frac{1}{2}\), \(\frac{\sqrt{2}}{2}\), \(\frac{\sqrt{3}}{2}\) принимает наименьшее т.е. \(cos\,\frac{π}{3}=\frac{1}{2}\). Синус из трех стандартных значений будет равен среднему т.е. \(sin\,\frac{π}{4}=\frac{\sqrt{2}}{2}\). Получается:
\(-24\sqrt{2}\,cos\frac{π}{3}\,sin\frac{π}{4}=-24\sqrt{2}\cdot\)\(\frac{1}{2}\)\(\cdot\)\(\frac{\sqrt{2}}{2}\)\(=\)\(\frac{-24\sqrt{2}\cdot\sqrt{2}}{4}\)\(=\)\(\frac{-24\cdot 2}{4}\)\(=-6\cdot2=-12\)
° )=-44\sqrt{3}\cdot(-\sqrt{3})=44\cdot 3=132\).
Ответ: \(132\).
Если вам не понятно, как мы нашли значение тангенса, то читайте статью «Как найти тангенс и котангенс без тригонометрической таблицы?».
Доказательства формул с минусом в аргументе:
Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
1)В воду объемом 1 л ,температура которой 20С°, бросают кусок железа массой 100г, нагретый до 500С°.
2 сколько будет
Решено
Помогите, пожалуйста!!! Очень важно!!! 1)В коробке вперемешку лежат чайные пакетики с черным и зеленым чаем, одинаковые на вид, причем пакетиков с черным чаем в 9 раз больше, чем с зеленым. Найдите
В соляную кислоту сплав серебра с никелем массой 1,5 г,выделился водород объемом 0,224 л(н.у).Массовая доля никеля(в %)
Пользуйтесь нашим приложением
тригонометрических тождеств. Темы по тригонометрии.
Темы | Дом
20
Взаимные тождества
Тождества тангенса и котангенса
Пифагорейские тождества
Формулы суммы и разности
Формулы двойного угла
Формулы половинного угла
Продукты в сумме
Суммы как произведения
ИДЕНТИЧНОСТЬ — ЭТО РАВЕНСТВО, истинное для любого значения переменной.
В алгебре, например, у нас есть такое тождество:
( х + 5)( х — 5) = х 2 — 25.
Значение тождества состоит в том, что в расчетах мы можем заменить один член другим. Мы используем тождество, чтобы придать выражению более удобную форму. В исчислении и всех его приложениях тригонометрические тождества имеют центральное значение.
На этой странице мы представим основные тождества. У студента не будет лучшего способа попрактиковаться в алгебре, чем доказать их. Ссылки на доказательства ниже.
Взаимные тождества
| sin θ | = | 1 csc θ | csc θ | = | 1 sin θ | |
| cos θ | = | 1 с θ | сек θ | = | 1 cos θ | |
| тан θ | = | 1 кроватка θ | детская кроватка θ | = | 1 тан θ | |
Доказательство
Опять же, в расчетах мы можем заменить любой элемент идентичности другим.
Итак, если мы видим «sin θ», то можем, если захотим, заменить его на «»; и, симметрично, если мы видим «», то мы можем заменить его на «sin θ».
Задача 1. Что значит сказать, что csc θ является обратное значение sin θ?
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Это означает, что их произведение равно 1.
sin θ csc θ = 1.
Урок 5 Алгебры.
Задача 2. Оценить
загар 30° csc 30° cot 30°.
| коричневый 30° csc 30° ctg 30° | = | загар 30° cot 30° csc 30° |
| = | 1 · csc 30 ° | |
| = | 2. | |
Тема 4.
Тангенсные и котангенсные тождества
| тангенс θ = | sin θ cos θ | детская кроватка θ = | cos θ sin θ |
Доказательство здесь.
Пример 1. Покажите: tan θ cos θ = sin θ.
Решение: Задача означает, что мы должны написать левую часть, а затем показать с помощью подстановок и алгебры, что мы можем преобразовать ее так, чтобы она выглядела как правая.
Начнем:
| = | при применении касательной идентичности, | ||
| = | об отмене cos θ s. | ||
Мы подошли к правой стороне.
Пифагорейские тождества
| а) | sin 2 θ + cos 2 θ | = | 1. |
| б) | 1 + желто-коричневый 2 θ | = | сек 2 θ |
| в) | 1 + детская кроватка 2 θ | = | csc 2 θ |
| a ‘ ) | sin 2 θ | = | 1 − cos 2 θ. |
| cos 2 θ | = | 1 − sin 2 θ. | |
Они называются тождествами Пифагора, потому что, как мы увидим в их доказательстве, они представляют собой тригонометрическую версию теоремы Пифагора.
Два тождества, помеченные как ‘ ) — «а-простое» — это просто разные версии а). Первый показывает, как мы можем выразить sin θ через cos θ; второй показывает, как мы можем выразить cos θ через sin θ.
Примечание: sin 2 θ — «синус в квадрате тета» — означает (sin θ) 2 .
Задача 3. Треугольник 3-4-5 прямоугольный.
а) Почему?
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Он удовлетворяет теореме Пифагора.
б) Оцените следующее:
| sin 2 θ | = | 16 25 | cos 2 θ | = | 9 25 | sin 2 θ + cos 2 θ | = | 1. |
Пример 2. Показать:
Решение. Снова нужно преобразовать левую часть в правую. Начинаем: | ||
| Взаимные тождества | ||
| при сложении дробей | ||
| Пифагорейские тождества | ||
| Взаимные тождества | ||
Именно это мы и хотели показать.
Формулы суммы и разности
| грех (α + β) | = | sin α cos β + cos α sin β |
| sin (α − β) | = | sin α cos β − cos α sin β |
| соз (α + β) | = | cos α cos β − sin α sin β |
| соз (α − β) | = | cos α cos β + sin α sin β |
Примечание: В формулах синуса + или — слева также + или — справа.
Но в формулах косинуса + слева становится — справа; и наоборот.
Поскольку эти тождества доказываются непосредственно из геометрии, от учащегося обычно не требуется овладевать доказательством. Однако все последующие тождества основаны на этих формулах суммы и разности. Студент обязательно должен их знать.
Вот доказательство формул суммы.
Пример 3. Вычислите sin 15°.
| Раствор. | sin 15° | |||
| Формулы | ||||
| Темы 4 и 5 | ||||
Пример 4.
Докажите:
| Решение. | Идентификация касательной | |||
| Формулы | ||||
| Теперь мы построим tan α, разделив первый член в числителе на cos α cos β. Но тогда мы должны разделить каждый член по cos α cos β: | ||||
Именно это мы и хотели доказать.
Формулы двойного угла
Доказательство
Существует три версии cos 2α. Первый с точки зрения обоих cos α и sin α. Второй только с точки зрения cos α. Третий — только с точки зрения sin α
| Пример 5. Показать: sin 2α |
| Раствор. | грех 2α | = 2 sin α cos α | Формулы | |
| Теперь мы построим tan α путем деления на cos α. Но чтобы сохранить равенство, мы должны также умножить на cos α. | ||||
| Урок 5 Алгебры | ||||
| Взаимные тождества | ||||
| Пифагорейские тождества | ||||
Именно это мы и хотели доказать.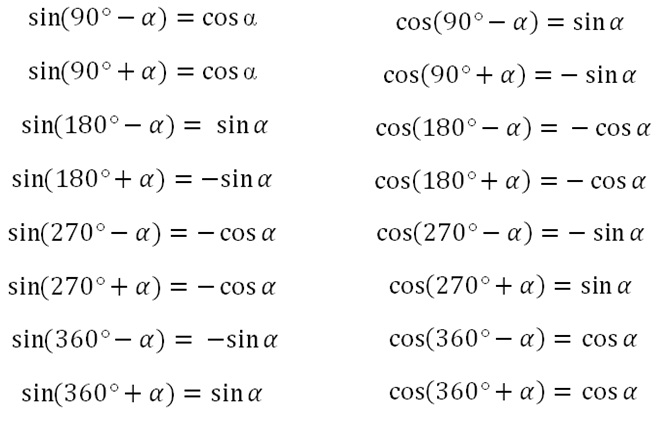
| Пример 6. Показать: |
| Решение. | грех х |
— согласно предыдущему тождеству с α = .
Формулы половинного угла
Следующие формулы половинного угла являются инверсией формул двойного угла, потому что α составляет половину 2α.
Знак плюс или минус зависит от квадранта. Под радикалом косинус имеет знак +; синус, знак -.
Доказательство
| Пример 7. Вычисление cos | № 8 | . |
| Решение . С 90 050 | № 8 | это половина | № 4 | , то по |
| формула половины угла: | ||||
| Тема 4 | |||
| Урок 23 алгебры | |||
| Урок 27 алгебры | |||
Пример 8. Получение идентификатора для загара | α 2 | . |
| Решение . | желтовато-коричневый | α 2 | = | Идентификация касательной | ||
| = | Формулы половинного угла | |||||
| = | ||||||
| = | Урок 19 алгебры | |||||
| = | Пифагорейское тождество ‘ | |||||
| = | ||||||
| = | ||||||
при делении числителя и знаменателя на cos α.
Продукты в сумме
| а) | sin α cos β | = | ½[sin (α + β) + sin (α − β)] | |
| б) | cos α sin β | = | ½[sin (α + β) − sin (α − β)] | |
| в) | cos α cos β | = | ½[cos (α + β) + cos (α − β)] | |
| г) | грех α грех β | = | −½[cos (α + β) − cos (α − β)] | |
Доказательство
Суммы как произведения
| д) | грех А + грех В | = | 2 sin ½ ( A + B ) cos ½ ( A − B ) |
| е) | грех А − грех В | = | 2 sin ½ ( A − B ) cos ½ ( A + B ) |
| г) | cos A + cos B | = | 2 cos ½ ( A + B ) cos ½ ( A − B ) |
| ч) | соз А − соз В | = | −2 sin ½ ( A + B ) sin ½ ( A − B ) |
В доказательствах учащийся увидит, что тождества с е) по з) являются инверсиями а) по d) соответственно, которые доказываются первыми.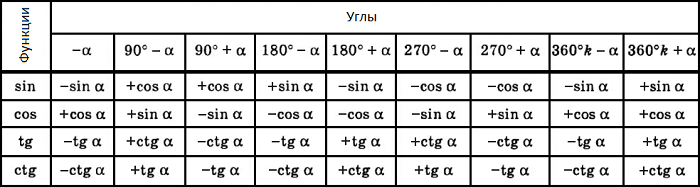
Тождество f) используется для доказательства одной из основных теорем исчисления, а именно производной sin x .
Учащийся не должен пытаться запомнить эти личности. Достаточно попрактиковаться в их доказательствах и увидеть, что они исходят из формул суммы и разности.
Темы | Дом
Copyright © 2022 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: [email protected]
Тригонометрические тождества | Purplemath
Purplemath
В математике «тождество» — это уравнение, которое всегда верно. Они могут быть «тривиально» истинными, например, « x = x », или полезными, такими как теорема Пифагора «9».1284 a 2 + b 2 = c 2 » для прямоугольных треугольников. Существует множество тригонометрических тождеств, но ниже приведены те, которые вы, скорее всего, увидите и используете.
Базовый и пифагорейский, сумма углов и разность, двойной угол, полуугол, сумма, произведение
Содержание продолжается ниже
MathHelp.com
Нужен специальный курс по математике? Основные и пифагорейские тождества
Обратите внимание, что триггерный коэффициент «со-(что-то)» всегда является обратным коэффициенту «не-со». Вы можете использовать этот факт, чтобы понять, что косеканс идет с синусом, а секанс идет с косинусом.
Следующие (в частности, первая из трех ниже) называются «пифагорейскими» тождествами.
SIN 2 ( T ) + COS 2 ( T ) = 1
TAN 2 ( T ) + 1 = SEC 2 ( T ) + 1 = SEC 2 ( T ) + 1 = SEC 2 ( T ) + 1 = Sec 2 ( T ) + 1 = SEC 2 ( T ) + 1 = SEC 2 ( T ).0003
1 + кроватка 2 ( t ) = csc 2 ( t )
Обратите внимание, что три тождества прежде всего включают в себя квадрат и число 1.
Вы можете ясно увидеть пифагорейскую связь, если вы рассмотрим единичный круг, где угол равен t , «противоположная» сторона равна sin( t ) = y , «прилегающая» сторона равна cos( t ) = x , а гипотенуза равно 1.
У нас есть дополнительные тождества, связанные с функциональным состоянием триггерных соотношений:
SIN ( -T ) = — SIN ( T )
COS ( -T ) = COS ( T )
TAN ( –T ) = 9128) =
= ) = 9128) = 9128). t )
Обратите внимание, что синус и тангенс являются нечетными функциями, симметричными относительно начала координат, а косинус является четной функцией, симметричной относительно оси y . Тот факт, что вы можете вынести знак «минус» аргумента за пределы (для синуса и тангенса) или полностью исключить его (для косинуса), может быть полезен при работе со сложными выражениями.
Тождества суммы углов и разностей
sin(α + β) = sin(α) cos(β) + cos(α) sin(β)
sin(α − β) = sin(α ) cos(β) − cos(α) sin(β)
cos(α + β) = cos(α) cos(β) − sin(α) sin(β)
cos(α − β) = cos (α) cos(β) + sin(α) sin(β)
Кстати, в приведенных тождествах углы обозначены греческими буквами.
Буква а-типа «α» называется «альфа», что произносится как «AL-fuh». Буква b-типа, «β», называется «бета», что произносится как «БАЙ-тух».
Двойной угла идентификации
SIN (2 x ) = 2 SIN ( x ) COS ( X )
COS (2 X ) = COS 2 2 (2 X ) = COS 2 (2 X ) = COS 2 (2 X ) = COS 2 (2 X ) = COS ) ) − sin 2 ( x ) = 1 − 2 sin 2 ( x ) = 2 cos 2 ( x ) − 1 Приведенные выше тождества можно переформулировать, возведя каждую сторону в квадрат и удвоив все меры углов. Результаты следующие: sin 2 ( x ) = ½[1 − cos(2 x )] cos 2 ( x ) = ½[1 + cos(2 x )]
Half-Angle Identities
Идентичности суммы
Идентичности произведения
Вы будете использовать все эти тождества или почти все для доказательства других триггерных уравнений и для решения триггерных уравнений.
Leave A Comment