Таблица квадратов натуральных чисел.
Таблица квадратов натуральных чисел.Таблица квадратов натуральных чисел от 1 до 100. Квадрат числа определение: квадратом числа называется результат умножения числа на точно такое число. Говорят, что для того, чтобы возвести число в квадрат, нужно это число умножить само на себя. За математическую точность приведенных определений я ответственности не несу, написал, как понимаю. Для бюрократов от математики советую воспользоваться учебником и выучить определение оттуда. Таблица квадратов натуральных чисел представляет собой натуральные числа от 1 до 100 в степени 2. Все результаты возведения натуральных чисел в квадрат или в степень 2 сведены в таблицу, эту таблицу квадратов натуральных чисел любой желающий может скачать бесплатно.
В таблице квадратов натуральных чисел числа представлены по десяткам, как в таблице умножения. В первом квадратике вы найдете квадраты однозначных чисел до 10 включительно.
Степень 2 для любого числа показывает, что это число умножается само на себя. Любое отрицательное число в степени 2 дает положительный результат потому, что минус на минус при умножении дает плюс. Поэтому приведенная выше таблица является также таблицей квадратов целых чисел. Если вам нужно найти результат возведения отрицательного числа в степень 2, то смело отбрасывайте знак минус перед числом и результат ищите по таблице — он всегда будет положительным. Формулы возведения положительного и отрицательного числа в квадрат или в степень 2 будут выглядеть так:
a² = a · a
(-a)² = (-a) · (-a) = a · a
Рассмотрим несколько примеров. Начинается таблица с единицы. 1 в квадрате или единица во второй степени равняется единице. Минус единица -1 в квадрате так же равняется единице.
1² = 1 · 1 = 1
(-1)² = (-1) · (-1) = 1
2 в квадрате или 2 в степени 2 будет равно четырем. Если двойка отрицательная возводится во 2 степень, -2 в квадрате, это тоже равно четыре. Дважды два равно четыре — эта классика детской математики показывает результат возведения числа 2 в квадрат.
Если двойка отрицательная возводится во 2 степень, -2 в квадрате, это тоже равно четыре. Дважды два равно четыре — эта классика детской математики показывает результат возведения числа 2 в квадрат.
2² = 2 · 2 = 4
(-2)² = (-2) · (-2) = 4
Квадрат числа три или 3 в степени 2 равняется девяти. Трижды три равно девять. Минус три в квадрате равно девять. Не забываем, что минус умножить на минус дает плюс.
3² = 3 · 3 = 9
(-3)² = (-3) · (-3) = 9
Квадрат числа четыре или 4 в степени 2 равняется шестнадцати. Четырежды четыре равно шестнадцать. Минус четыре во второй степени тоже дает шестнадцать.
4² = 4 · 4 = 16
Квадрат числа пять или 5 в степени 2 равняется двадцати пяти. Пять у пять — двадцать пять. Минус пять в степени два дает опять двадцать пять. 2
2
Интегральные функции:
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от
- Chi(x)
- Интегральный гиперболический косинус от x
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.
 3
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- pi
- Число «Пи», которое примерно равно ~3.
 2 = -4 2
2 = -4 2 - -4 В квадрате = -4 × -4 = 16
Квадрат — это двумерная фигура, две стороны которой имеют одинаковую длину. Площадь квадрата определяется произведением двух его измерений. Например, если длина ребра квадрата равна «a» сантиметров, площадь квадрата определяется произведением «a × a», которое равно a 2 . Ребра показанного квадрата равны 4 единицам. Значит, его площадь равна:
a 2 = a × a × a = a 2 = 4 × 4 × 4 = 64 единицы или кубические сантиметры (64 см 2 ) (если мы выберем в качестве единицы измерения площади квадратные сантиметры).
Полный квадрат — это число, которое можно представить как произведение двух равных целых чисел.
Полный квадрат, также называемый квадратным числом, — это число, записанное по формуле S n = n 2 , где n — целое число.
Изображение предоставлено: mathsisfun.com
Обратите внимание, что:
- 0 в квадрате равно 0 (просто сделайте n = 0 в формуле S n = n 2 )
- 1 в квадрате равно 1 (просто сделайте n = 1)
- Отрицательный 0 в квадрате равен 0 (просто сделайте n = 0)
- Отрицательное значение 1 в квадрате равно 1 (просто сделайте n = 1)
Таблица чисел в квадрате или таблица Perfect Square от 0 до 100
2Таблица чисел в квадрате от 0 до 50 2 0 или -0 в квадрате равно 0 2 или -2 в квадрате равно 8 3 или -3 квадрат равен 27 4 или -4 квадрат.  -7 квадрат равен 343
-7 квадрат равен 3438 или -8 квадрат равняется 512 9 или -9 квадрат равняется 729 10 или -10 квадрат. 12 или -12 квадрат равняется 1728 13 или -13 квадрат равняется 2197 14 или -14 квадрат равняется 2744 15 или -15 квалификации. квадрат равен 4096 17 или -17 квадрат равна 4913 18 или -18 квадрат равняется 5832 19 или -19 равенства 6859 20 или -19.0013 21 или -21 квадрат равняется 9261 22 или -22 квадрат равны 10648 23 или -23 квадратные равны 25 квадрат равен 15625 26 или -26 квадрат равняется 17576 27 или -27 квадрат. 30 или -30 квадрат равен 27000 31 или -31 квадрат. -34 квадрат равна 39304 35 или -35 квадрат равен 42875 36 или -36 квадрат равны 46656 37 или -37 Equals 50653 37 или -37 Equals 50653 37 или -37. 
39 или -39 квадрат равен 59319 40 или -40 квадрат равны 64000 41 или -41 квадрат. -43 квадрат равно 79507 44 или -44 квадрат равняется 85184 45 или -45 квадрат.0012 48 или -48 квадрат равен 110592 49 или -49 квадрат равен 117649 50 или -50 квадрат. 100 2 51 или -51 квадрат равняется 132651 52 или -52 квадрат равняется 140608 53 или -53 квадрат.0012 55 или -55 квадрат равняется 166375 56 или -56 квадрат равняется 175616 57 или -57 квадратный равен -59 квадрат равен 205379 60 или -60 квадрат равняется 216000 61 или -61 квадрат.0012 64 or -64 squared equals 262144 65 or -65 squared equals 274625 66 or -66 squared equals 287496 67 or -67 squared equals 300763 68 or -68 квадрат равна 314432 69 или -69 квадрат равна 328509 70 или -70 квадрат.  0012
001273 or -73 squared equals 389017 74 or -74 squared equals 405224 75 or -75 squared equals 421875 76 or -76 squared equals 438976 77 or -77 квадрат равна 456533 78 или -78 квадрат равна 474552 79 или -79 квадрат равен 493039 80 или -80 квадрат.0012 82 или -82 квадрат равняется 551368 83 или -83 квадрат равняется 571787 84 или -84 равенства 592704 или -84 или равенства 592704
11110 или -84 или -84. -86 квадрат равна 63605687 или -87 квадрат равняется 658503 88 или -88 квадрат равны 681472 89 или -89 Сваря.0 квадрат равна 729000 91 или -91 квадрат, равные 753571 92 или -92 квадрат квадрат 778688 93 или -93 Equals 804357 900 93 или -93 Equals 804357 900 93 или -93. 
95 или -95 квадрат равен 857375 96 или -96 квадрат равны 884736 97 или -97 квадрат.0013 99 or -99 squared equals 970299 100 or -100 squared equals 1000000 101 or -101 squared equals 1030301 Sample Squared or Perfect Squares
- 52 squared
- 35 в квадрате
- -74 в квадрате
- 59 в квадрате
- -60 в квадрате
- 9 в квадрате
арифметика — отрицательное число в квадрате?
IMO, это очень помогает понять, как синтаксис языков программирования, а также, в менее простом виде, и математическая нотация, всегда соответствует древовидной структуре данных. Например, $f(g(x), h(y,z))$ на самом деле является кодировкой символьной строки для чего-то вроде $$ \begin{матрица} & & ж & & \\& \nстрелка & & \nстрелка & \\ г & & & & ч \\ \uparrow & & & \narrow & \uparrow \\ х & & у & & г \end{матрица} $$ Термин $-3^2$ или выражение Python
-3**2, означает $$ \begin{матрица} & & -\квадрат\четверка & & \\ & & \стрелка вверх & & \\ & & ** & & \\& \nстрелка & & \nстрелка & \\ 3 & & & & 2 \end{матрица} $$ Это означает , а не . $$
\begin{матрица}
& & ** & &
\\& \nстрелка & & \nстрелка &
\\ -\квадрат & & & & 2
\\ \стрелка вверх\!\!\!\!\! & & & &
\\ 3 \!\!\!\!\! & & & &
\end{матрица}
$$
Почему нет? Ну, это всего лишь соглашения о том, как анализируются выражения: возведение в степень связывает сильнее, чем отрицание (что разумно находится на том же уровне, что и сложение). 92$ в C#, используйте
$$
\begin{матрица}
& & ** & &
\\& \nстрелка & & \nстрелка &
\\ -\квадрат & & & & 2
\\ \стрелка вверх\!\!\!\!\! & & & &
\\ 3 \!\!\!\!\! & & & &
\end{матрица}
$$
Почему нет? Ну, это всего лишь соглашения о том, как анализируются выражения: возведение в степень связывает сильнее, чем отрицание (что разумно находится на том же уровне, что и сложение). 92$ в C#, используйте - Math.pow(3,2).В языках программирования правила синтаксического анализа обычно следующие:
- Скобки группируют поддерево вместе, независимо от того, что происходит вокруг них. Применение функции обычно связано со скобками, так что это также тесно связано.
- Запятая всегда отдельных независимых поддеревьев. Следовательно,
-3вpow(-3,2)не зависит от функции2иpow. Все другие инфиксные операторы, такие как
+и**, имеют некоторую предопределенную фиксированность .

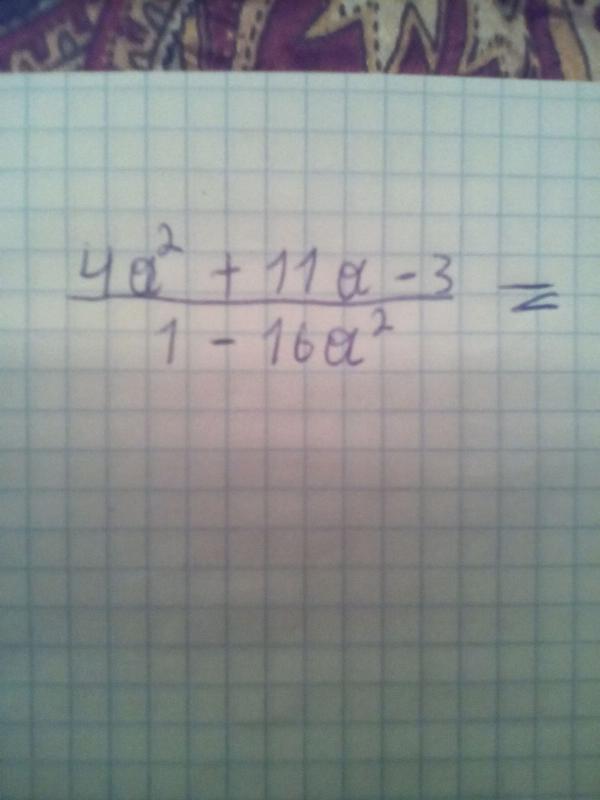 3
3 2 = -4 2
2 = -4 2  -7 квадрат равен 343
-7 квадрат равен 343
 0012
0012
 $$
\begin{матрица}
& & ** & &
\\& \nстрелка & & \nстрелка &
\\ -\квадрат & & & & 2
\\ \стрелка вверх\!\!\!\!\! & & & &
\\ 3 \!\!\!\!\! & & & &
\end{матрица}
$$
Почему нет? Ну, это всего лишь соглашения о том, как анализируются выражения: возведение в степень связывает сильнее, чем отрицание (что разумно находится на том же уровне, что и сложение). 92$ в C#, используйте
$$
\begin{матрица}
& & ** & &
\\& \nстрелка & & \nстрелка &
\\ -\квадрат & & & & 2
\\ \стрелка вверх\!\!\!\!\! & & & &
\\ 3 \!\!\!\!\! & & & &
\end{матрица}
$$
Почему нет? Ну, это всего лишь соглашения о том, как анализируются выражения: возведение в степень связывает сильнее, чем отрицание (что разумно находится на том же уровне, что и сложение). 92$ в C#, используйте 
Leave A Comment