Материальная точка движется из пункта а с координатой ха 35: Материальная точка движется из пункта А в пункт В с координатой Хв = 5 м. Определите координату пункта А, если проекция перемещения точки на ось ОХ равна sx = 9 м.

Кинематика точки и твердого тела. Базовый уровень 10 класс онлайн-подготовка на Ростелеком Лицей

Модели тел и движений

 

Грузовик едет со средней скоростью 70 км/час. Сколько времени он потратит на дорогу из одного города в другой, если расстояние между городами 350 км?

 

Вы решите эту задачу в одно действие, получится 5 часов. Но для водителя может быть важнее ответ на другой вопрос: сколько времени займёт обгон другого такого же грузовика, который движется со скоростью 60 км/ч, а длина каждого грузовика – 7 м? Попробуйте решить задачу самостоятельно, ответ получится около 5 с.

Задачи простые, но вот что интересно: в первой нам было вообще всё равно, совершал ли обгоны грузовик, важно было только общее время движения. Мы рассмотрели его как материальную точку, которая движется с постоянной скоростью. А вторую задачу мы бы не решили, не зная длин грузовиков, здесь модель материальной точки уже неприменима.

У нас есть в запасе различные модели – это инструменты. Которые мы можем с той или иной степенью точности использовать для решения различных практических задач. Если эта точность нас не устраивает, то мы используем другую модель или разрабатываем новую, например, уточняя текущую.

Так, для описания движения в кузове пустого баллона или вибрации двигателя грузовика описанные выше модели не подойдут, понадобятся новые. При этом рассмотренные модели не имеют отношения к грузовику – они могут применяться к автобусу, поезду, бильярдному шару или любому другому объекту. Задачи могут быть самыми разными, но то немногое, что для нас в них является самым важным, может быть описано одной и той же моделью.

Обратите внимание, что в рассмотренных задачах про грузовик нас интересовали только время, скорость и расстояние, которое он проехал. Нам было не важно, как работал двигатель, сколько бензина понадобилось, почему вообще грузовик двигался и тяжелый ли вёз груз.

Решением таких задач занимается кинематика — раздел физики, посвященный моделям движения, которые не учитывают причины движения, а только описывают его. О задачах кинематики и моделях, которые используются для их решения, мы сегодня и будем говорить.

Рассмотрим такую задачу: с горки известной высоты и известного наклона соскальзывает шайба и скатывается шар. На одинаковом ли расстоянии от горки они остановятся?

Рис. 1. Задача на скатывание тел с наклонной поверхности

Может оказаться, что не на одинаковом, даже при одинаковом трении с поверхностью.  Если использовать модель материальной точки и для шайбы, и для шара, то этот результат необъясним.

Рис. 2. В модели материальной точки тела неразличимы

Действительно, потенциальная энергия перешла в кинетическую – можем вычислить скорость тела внизу горки, а по ней рассчитать расстояние, на котором они оба остановятся. Чтобы объяснить разные расстояния, нам придётся учесть вращение шара – тогда потенциальная энергия будет расходоваться не только на увеличение кинетической энергии, но и на увеличение энергии вращения шара. В данном случае для шара мы можем применить модель твёрдого тела, в которой различаются поступательное и вращательное движения.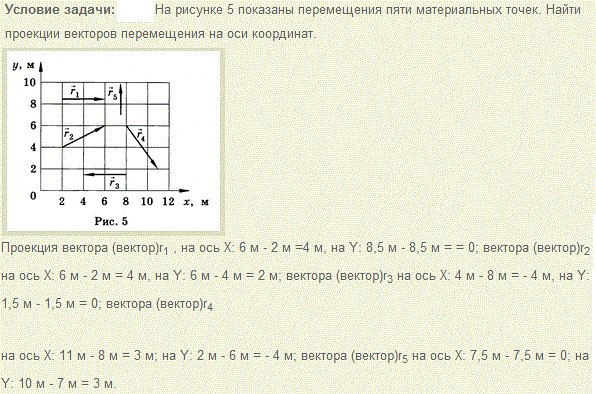

---

 

Поступательное и вращательное движение

Поступательное движение – это такое движение, при котором все точки тела движутся одинаково: с одинаковой скоростью, совершая одинаковое перемещение.

Рис. 3. Поступательное движение

А как еще может быть? Взмахните рукой и проследите: понятно, что ладонь и плечо двигались по-разному. Посмотрите на колесо обозрения: точки вблизи оси почти не движутся, а кабинки движутся с другой скоростью и по другим траекториям.

Рис. 4. Вращательное движение

Посмотрите на прямолинейно движущийся автомобиль: если не учитывать вращение колес и движение частей мотора, все точки автомобиля движутся одинаково, движение автомобиля считаем поступательным. Тогда нет смысла описывать движение каждой точки, можно описать движение одной. Автомобиль считаем материальной точкой. Обратите внимание, что при поступательном движении линия, соединяющая любые две точки тела при движении, остается параллельной сама себе.

Второй вид движения по этой классификации – вращательное движение. При вращательном движении все точки тела движутся по окружности вокруг какой-то одной оси. Эта ось может пересекать тело, как в случае с колесом обозрения, а может не пересекать, как в случае с автомобилем на повороте (рисунок).

Но не любое движение можно отнести к какому-то одному из двух видов. Как описать движение педалей велосипеда относительно земли – это какой-то третий тип? Наша модель удобна тем, что можно рассматривать движение как комбинацию поступательного и вращательного движений: относительно своей оси педали вращаются, а ось вместе со всем велосипедом движется поступательно относительно Земли.

---

Возьмем другой пример: фигуристка вращается на месте, и, когда она прижимает руки к груди, она начинает вращаться значительно быстрее.

Рис. 5. Вращение фигуристки

---

 

Момент инерции

Как узнать, варёное перед нами яйцо или сырое? Можно это определить по вращению. Раскрутить яйцо на столе: варёное будет долго вращаться, а сырое остановится быстрее. Как это объяснить? Для описания вращательного движения ввели понятие момента инерции. Можно провести аналогию с массой.

Масса – это мера инертности при поступательном движении: чтобы разогнать или остановить более тяжелое тело, потребуется бóльшая сила, чем для более легкого тела. Для момента инерции справедливо то же, только описывается вращательное движение и угловая скорость. Кинетическая энергия вращательного движения определяется моментом инерции и угловой скоростью.

Возвращаемся к вращению яйца. У сырого яйца во вращении участвует по сути только скорлупа, её момент инерции меньше, чем момент инерции вареного яйца – сплошного твердого тела. Поэтому и энергия вращения, а значит и время вращения меньше. Мы не учли, что жидкость внутри сырого яйца вязкая и тоже как-то движется, но мы и не делаем точных расчетов, а для сравнения такого предположения достаточно.

Рассмотрим в рамках нашей модели вращение фигуристки.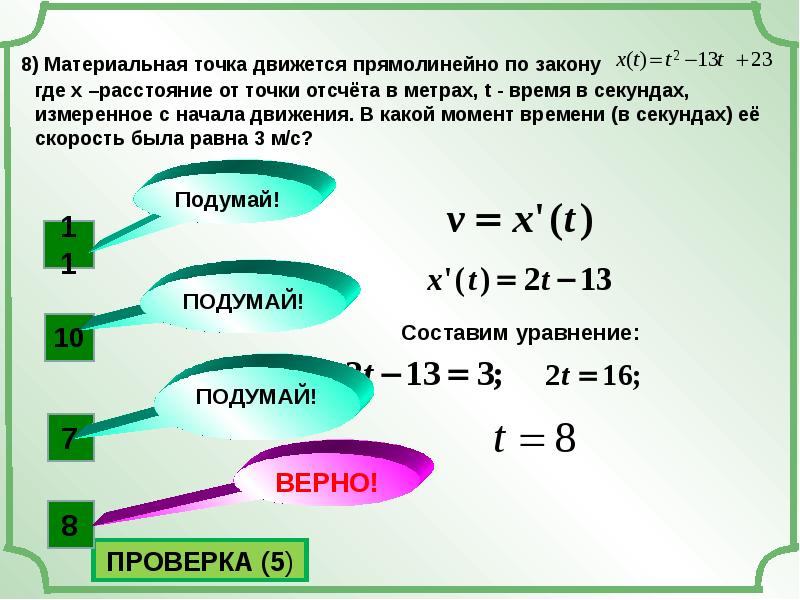 Момент инерции зависит от распределения массы – чем она ближе к оси вращения, тем меньше момент инерции. Прижимая руки к груди, фигуристка меняет распределение массы, и момент инерции уменьшается. И из закона сохранения энергии понятно: если уменьшился момент инерции, увеличилась скорость.

Мы иногда и не замечаем, как используются модели: фигуристка умеет управлять моментом инерции, даже не зная о нём. Задача физики – создать модель, чтобы можно было управлять осознанно. Тогда можно посчитать, как управлять, поставить задачу компьютеру, чтобы он всё рассчитал.

---

В целом ясно, что энергия одного вида движения превращается в энергию другого, и это нельзя описать, считая фигуристку материальной точкой. Как материальная точка она вообще неподвижна.

Как это вращение описать? Удобно использовать то, что уже хорошо разобрали. Обычно, чтобы описать движение тела, достаточно описать движение нескольких его точек, а для описания движения у нас есть готовые инструменты. Например, для катящегося с горки шара можно рассматривать движение одной из точек поверхности относительно центра шара, и движение центра шара относительно горки.

 

Инструменты кинематики

 

 

Итак, несколько моделей в нашем наборе инструментов уже есть: это равномерное и равноускоренное прямолинейное движение материальной точки и равномерное движение по окружности. И некоторые задачи мы уже умеем решать.

 

На уроках математики мы успели овладеть новыми математическими инструментами, такими, как вектор и система координат, с помощью которых мы можем создать более удобные физические модели и решать с их помощью больше задач. Давайте упорядочим информацию о тех инструментах кинематики, которые у нас уже есть, и заодно научимся пользоваться новыми.

Рис. 6. Определение материальной точки

Здесь мы под точкой понимаем то же, что и в геометрии: дать определение точке нельзя, это базовое понятие, но мы можем сформулировать, что мы с её помощью будем описывать – объект, на размеры которого мы при решении данной задачи можем не обращать внимания, но на положение которого мы можем указать. Только в отличие от точки в геометрии, в физике мы ей приписываем еще и массу.

Обратите внимание, что само по себе выражение «материальная точка» — оксюморон (как, например, «живой труп»). Действительно, сама по себе точка не может быть материальной, у неё нет длины, ширины, мы, в принципе, не можем на неё указать. Но в этом и заключается смысл модели – не существовать в реальности, а приближать с достаточной точностью множество реальных ситуаций и помогать их описывать.

Мы говорим о движении, то есть об изменении положения точки со временем. Но изменение положения может быть только относительно других объектов. В жизни, чтобы обозначить положение чего-либо, мы говорим: возле окна, в десяти километрах от города. Можем указать адрес: улица Пушкина, и номер дома и квартиры. Можем указать место в театре: ряд 7, место 15. В зависимости от задачи, которую мы решаем, мы выбираем точку отсчёта и систему координат.

Воспользуемся уже готовым математическим инструментом – декартовой (прямоугольной) системой координат. Но система координат позволяет задать положение точки относительно какого-то объекта, то есть нужно еще задать этот объект – тело отсчета.

Добавим к системе координат и телу отсчета часы, чтобы рассматривать процессы с течением времени, и получим

систему отсчета. Раздел физики, механика, занимается решением следующей задачи, которая так и называется:

Основная задача механики – точно определять положение тела в пространстве в любой момент времени.

В этой стандартной формулировке все слова следует пояснить.

1. Абсолютно точно мы в реальном мире ничего не определяем. Точность всегда конечна: иногда нас устраивает определить положение чего-то с точностью до метра, иногда – до миллиметра, а ведь можно и до десятой, и до тысячной доли миллиметра – на чём-то всё равно остановимся. И, как мы уже много раз говорили, точность определяется конкретной задачей, которую мы сейчас решаем.
2. Для тела можно использовать разные модели, мы договорились изучать модель материальной точки.
3. Нас не интересует любой момент времени, нас интересует конкретный период в рамках решаемой задачи. Если автомобиль едет с постоянной скоростью 70 км/ч, то через 5 часов он будет в 350 километрах от начала пути. В решение мы действительно можем подставить любое время и получить ответ: за 10 часов проедет 700 км, а за месяц обогнёт земной шар. Только эти результаты лишены смысла, автомобиль не будет ехать дальше пункта назначения, и уж тем более плыть во время кругосветного путешествия по океану.

На математическом языке основная задача механики звучит так: определить положение точки в пространстве в данной системе отсчёта, описав изменение её координат x, y, z от времени: то есть, найдя функции x(t), y(t), z(t). Зададим положение точки в пространстве с помощью вектора.

Рассмотрим для простоты точку на плоскости с координатам (x, y) – в пространстве будет то же самое, только на одну координату больше, (x, y, z).

Рис. 7. Трехмерная система координат

Проведем вектор из начала координат (0, 0) в эту точку, и мы получим радиус-вектор, обозначим его , с координатами (x, y).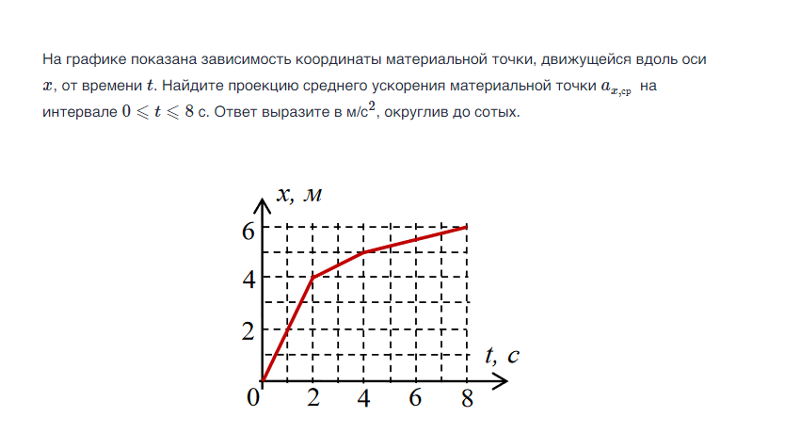

Положение точки в любой момент времени определяется зависимостью радиус-вектора  от времени .

Рис. 8. Радиус-вектор

Зависимость положения материальной точки от времени называют её законом движения.

Рис. 9.   – закон движения

Можно задать положение точки в виде координат, и эти координаты зависят от времени: x(t), y(t) (и, если в пространстве, то еще z(t)). Это будет закон движения в координатной форме. Можно записать закон движения в векторной форме, . Причем проекции вектора на оси координат  и  и будут координатами точки , , и для них мы записали, как они изменяются со временем, x(t), y(t)! Так мы с лёгкостью переходим от одной формы к другой.

Точка движется, меняет положение. Вы помните, что если последовательно соединить все положения материальной точки в процессе её движения, то получим кривую, которую назвали траекторией. Длина участка траектории называется путь, а если соединить отрезком начальную и конечную точки движения, то получим перемещение.

Рис. 10. Путь и перемещение

У нас тогда не было удобной модели, чтобы описать перемещение. Мы говорили о нём как об отрезке, который имеет направление, и это направление мы обозначали знаком плюс или минус – мы рассматривали движение вдоль одной прямой, и этого было достаточно, так как при движении вдоль прямой возможны всего два направления.

Сейчас мы можем строго определить перемещение как вектор, проведённый из начального положения материальной точки в конечное. А в другом обозначении – проведённый из конца радиус-вектора  в конец радиуса-вектора .

Рис. 11. Перемещение как разность радиусов-векторов

Такой вектор – это вектор разности, запишем:

Используя свойства векторов, несложно получить из определения:

Если записать проекции радиус-векторов и перемещения на оси координат, то получим то, что мы записывали для движения вдоль одной оси. Проекции вектора перемещения  равны разностям проекций радиусов-векторов:

Проекция перемещения – это скаляр, равный разности координат точки. А знак скаляра соответствует направлению составляющей вектора перемещения: параллельной оси х или у.

Рис. 12. Проекции перемещения

Модуль перемещения можно найти, как и модуль любого вектора, по его координатам:

Если вектор перемещения параллелен одной из осей, например, х, то составляющая , и:

 

Равномерное и равноускоренное движение

 

 

Мы заново ввели понятие перемещения, используя удобные универсальные инструменты, сделав его тоже более удобным и универсальным. Теперь посмотрим, как в нашу модель вписываются понятия скорости и ускорения, которые мы ввели раньше. Мы различали путевую скорость и скорость по перемещению. Это соответственно путь, пройденный точкой за единицу времени, и перемещение, совершенное точкой за единицу времени.

 

Чаще всего, говоря о скорости, мы подразумеваем скорость по перемещению: это отношение перемещения точки к промежутку времени, за который это перемещение произошло.

Это вектор перемещения, умноженный на скаляр , поэтому по направлению скорость и перемещение совпадают.

Такое определение скорости по сути означает среднюю скорость, с которой тело двигалось на протяжении времени .

Рис. 13. Средняя скорость по перемещению

Мы точно не знаем, как изменялась скорость и каким было перемещение на разных частях этого промежутка. Но разделив всё перемещение на этом промежутке на всё время , мы получаем, что в среднем точка перемещалась каждую секунду на определенное расстояние в определенном направлении. Если в нашей модели скорость меняется, то нужно взять настолько короткий промежуток , чтобы можно было считать, что скорость не успевает измениться.

Рис. 14. Мгновенная скорость

В математике ввели модель:  стремится к нулю, . Среднюю скорость на таком малом промежутке назвали мгновенной (очень короткий промежуток времени часто называют мгновением). Математическая запись всего, что мы указали, выглядит так:

Мы рассматриваем две простейших модели: когда скорость постоянна и когда скорость меняется равномерно. Если скорость постоянна (а скорость – вектор), это значит, что она не меняется ни по направлению, ни по модулю. Значит, в формулу для скорости можно подставлять любой промежуток времени. Будем считать начало наблюдения моментом , а время, прошедшее с этого момента, обозначим просто . За это время перемещение равно:

Тело переместилось из начального положения, соответствующего радиусу-вектору , в некоторое положение, которое нас интересует в момент времени t. Запишем:

Получили закон движения в случае равномерного прямолинейного движения.

Следующая модель – скорость равномерно меняется, то есть, запишем в векторной форме, за равные промежутки времени  изменение скорости одинаково и равно .

Рис. 15. Равноускоренное движение

Чтобы описывать скорость изменения скорости, мы ввели величину ускорение, это для нас не ново. В общем случае скорость может меняться не одинаково в разные промежутки времени, и есть смысл ввести понятие мгновенного ускорения, взять изменение скорости за короткий промежуток времени:

Но если говорить о равноускоренном движении, то ускорение одинаково на любом промежутке времени, и среднее ускорение  за любое время  одинаково. Если считать, что  – это изменение скорости от некоторого нулевого значения  в момент времени  до интересующего нас значения в момент времени  , то можем записать закон изменения скорости:

Уравнение равноускоренного движения мы уже вычисляли для движения вдоль одной оси, и мы получили известную вам формулу:

Главное, что это уравнение справедливо в проекции на каждую ось координат, и в векторной форме оно будет выглядеть похоже:

Уже известный нам закон сложения скоростей тоже можно записать в векторной форме. Напомню, он используется при переходе из одной системы отсчета к другой. Например, у нас есть тело, которое движется в системе отсчета, которая сама движется относительно Земли. Скорость такого тела относительно Земли равна:

Что нам это даёт? Мы теперь не привязаны к одной координатной оси. Если дана точка, которая движется из другой точки с начальной скоростью, а ускорение направлено в произвольном направлении к скорости (рис. 16), то такую задачу мы тоже можем решить.

 

Рис. 16. Криволинейное ускоренное движение

Применяем к точке наши уравнения в векторном виде, записываем их в проекциях на координатные оси, а в проекциях уравнения такие же, как для прямолинейного движения.

Если точка движется прямолинейно, модель тоже работает. Мы можем выбрать систему координат так, чтобы одна из осей координат была параллельна направлению движения. Тогда записанное изначально в векторном виде уравнение в проекции на одну ось даст простой одномерный случай, а в проекции на остальные оси получится уравнение 0=0, на которое можно не обращать внимания.

 

Решение задач. Закон сложения скоростей

 

 

Задача 1. Два автомобиля находятся на расстоянии 625 км и движутся навстречу друг другу. Первый автомобиль движется равномерно со скоростью , а второй начал двигаться со скоростью  и каждый час увеличивал скорость на 10 км/ч. Через какое время и на каком расстоянии от начального положения первого автомобиля они встретятся?

 

Рис. 17. Условие задачи 1

Анализ условия.

В задаче описано равномерное движение одного автомобиля и равноускоренное движение второго. Это как раз те модели, которые охватывает наше уравнение:

Выберем систему координат и будем описывать эти движения математически.

Физическая часть решения задачи.

Выберем систему отсчета: рассмотрим движение автомобилей относительно земли. Так как автомобили движутся друг другу навстречу вдоль одной прямой, удобно направить одну из осей вдоль этой прямой. Начало координат для удобства поместим в начальное положение первого автомобиля, оттуда отсчитывается расстояние до места встречи, как показано на рисунке (рисунок).

Запишем закон движения для каждого автомобиля

В проекции на ось х:

В выбранной системе координат у первого автомобиля начальная координата  равна нулю, проекция ускорения  равна нулю, их можем убрать из уравнения, а проекция начальной скорости равна . Начальная координата второго автомобиля  в этой системе координат равна 625 км, его начальная скорость  равна . Минусом обозначаем, что скорость направлена против оси координат. А ускорение  равно . По условию задачи понятно, что скорость по модулю возрастала, значит ускорение сонаправлено со скоростью, то есть направлено тоже против оси х, поэтому знак проекции ускорения – минус.

В момент встречи  автомобили находятся в одной точке, их координаты равны, запишем это:

Получили систему уравнений, в которую осталось подставить значения и решить. С математической частью решения вы можете ознакомиться в ответвлении.

---

 

Математическая часть решения задачи 1

Запишем систему уравнений сразу с числами:

Значения у нас указаны в одной системе, расстояния в километрах, время в часах, скорость в километрах за час и т.д., поэтому мы позволили себе не переводить их в СИ. Просто получим ответ в той системе, в которой работаем.

Итак, подставим координаты автомобилей в момент встречи в третье уравнение:

Получили квадратное уравнение, решим его:

Разделим обе части уравнения на 5:

Получим два корня уравнения:

Что означает момент времени ? Это момент времени за 25 ч до начала наблюдения, но в момент  движение только началось, поэтому нас этот момент не интересует. Оставляем одно решение: .

Осталось найти расстояние от начального положения первого автомобиля до места встречи, то есть координату места встречи. В момент  оба автомобиля находятся в этой точке, поэтому можно найти координату любого из них. Возьмем уравнение движения первого автомобиля:

Задача решена.

---

Задача 2. Камень бросили вертикально вверх с начальной скоростью 12 м/с. Определите максимальную высоту, на которую поднимется камень. Ускорение свободного падения считайте равным .

Рис. 18. Условие задачи 2

Анализ условия.

В задаче описано движение камня, когда на него не действует ничего, кроме силы тяжести (о трении воздуха ничего не сказано, им пренебрегаем). В таких условиях тело движется с постоянным ускорением – ускорением свободного падения, направленным вниз. Будем применять уравнение равноускоренного движения:

Уравнение для скорости тоже может пригодиться, запишем:

Физическая часть решения задачи.

Выберем систему координат. Давайте направим ось  вертикально вверх, в направлении движения камня, а начало координат поместим в точку броска. Оси x и z будут расположены в горизонтальной плоскости, проекции на них будут равны нулю, поэтому о них можно даже не упоминать. Тогда в проекции на ось  уравнения примут вид:

Начальная координата тела равна нулю, мы ее сразу не записали. Начальная скорость по условию задачи равна 12 м/с и направлена вдоль оси координат. Ускорение свободного падения направлено против оси координат, поэтому его проекция  в данной системе координат равна .

Максимальная высота , на которую поднимется камень – это его координата  в точке, в которой он остановится и начнет падать обратно. Мы не знаем момент времени t, в который камень там окажется, чтобы обойтись первым уравнением, поэтому будем использовать второе. В точке  камень остановится, то есть его скорость  станет равна нулю. Перепишем уравнения и решим систему:

Решение системы вы можете проследить в ответвлении.

---

 

Математическая часть решения задачи 2

Найдем из второго уравнения время t, за которое камень долетит до верхней точки траектории:

Подставим время в первое уравнение:

Получили ответ, осталось подставить численные значения:

Задача решена.

---

 

Границы применимости моделей

 

 

Мы сегодня рассмотрели две модели движения: с постоянной скоростью и постоянным ускорением. И это всё, других моделей быть не может? Нет, это не всё, но это самые простые модели, которые мы можем использовать для приближённого описания реального движения и решения конкретных задач.

 

Мы сегодня говорим о кинематике и не упоминаем причины движения, но вам знаком второй закон Ньютона: ускорение пропорционально силе, действующей на тело (или в нашем случае на материальную точку). Так вот, часто мы можем считать, что силы уравновешены, тогда движение равномерно, или что силу можно считать постоянной, тогда движение равноускорено.

А что если сила равномерно изменяется? Например, когда мы едем на автомобиле и равномерно усиливаем нажатие на педаль газа. Тогда можно дополнить модель: ускорение равномерно увеличивается, можно ввести скорость изменения ускорения  и вывести новые формулы. Получим еще одну модель – всего одну из множества, которые еще можно придумать. Профессиональные гонщики, которым на соревнованиях важны доли секунды, сталкиваются с описанной нами задачей, и конструкторы их автомобилей научились рассчитывать описанную модель разгона. Но мы этого делать не стали, потому что с такими задачами сталкиваемся редко.

Чаще возникают задачи, процессы в которых можно описать как равномерное движение по окружности. Это простая модель: скорость в ней не меняется по модулю, а меняется только по направлению. А окружность можно описать одним параметром: радиусом. Поэтому такое движение достаточно легко описать, вывести для него формулы, решать с их помощью множество задач.

Мы ранее уже подробно разобрали движение материальной точки по окружности, научились вычислять ускорение, которое при равномерном движении по окружности всегда направлено к центру этой окружности и не меняется по модулю.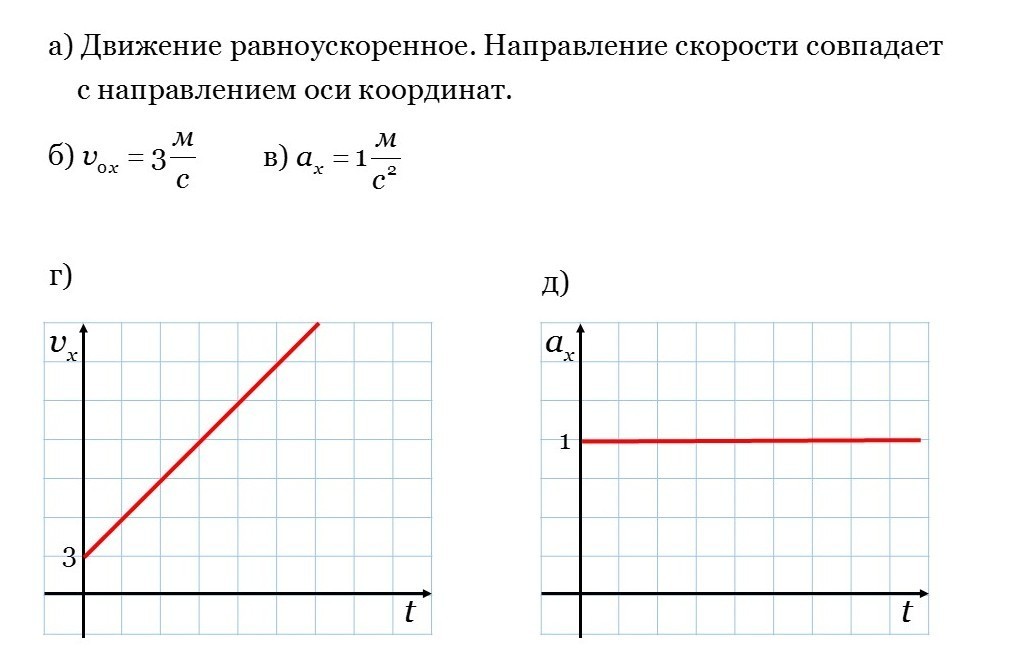

Рис. 19. Движение тела по окружности

Иногда и этого недостаточно: возникают задачи, в которых ускорение всё время меняется и по модулю, и по направлению. Мы пытаемся найти в них закономерности, один из таких примеров – колебательное движение. В случае с гармоническими колебаниями модуль ускорения пропорционален отклонению тела от положения равновесия.

Рис. 20. Колебательное движение

Список моделей может пополняться, по мере возникновения перед человеком тех или иных задач, решение которых в рамках уже разработанных моделей окажется недостаточно точным и будет слишком сильно отличаться от реальности. У любой модели есть границы применимости. Модель – это упрощение, которое справедливо только для описания ограниченного круга задач. К примеру, основная задача механики – описание движения материальной точки в пространстве с течением времени.

А ведь само пространство, для которого справедливы законы геометрии – это идеализированная модель. И время, как мы его в этой модели представили, — тоже идеализация. Оказалось, что при скоростях, близких к скорости света, нельзя считать, что в разных системах отсчета время течет одинаково и пространственные меры не меняются. Эти эффекты стала изучать релятивистская механика, они выходят за границы применимости нашей первой модели, которую назвали классической механикой.

Модель классической механики также неприменима к объектам, размеры которых меньше одного нанометра – это больше размеров атомов, самый большой атом, атом цезия, имеет размер примерно 0,2 нм. В таких масштабах к объектам неприменимы понятия координаты, точного положения и другие. Такие малые объекты изучает квантовая механика. С ней мы познакомимся позже.

 

Список литературы

1. Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. Физика 10. – М.: Просвещение, 2008.
2. Касьянов В.А. Физика 10. – М.: Дрофа, 2000.
3. М.М. Балашов, А.И. Гомонова, А.Б. Долицкий и др. Физика: Механика 10. – М.: Дрофа, 2004.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал Класс!ная физика
2. Интернет-портал Класс!ная физика
3. Интернет-портал Класс!ная физика
4. Интернет-портал Класс!ная физика

Домашнее задание

1. За 2 с прямолинейного равноускоренного движения тело прошло путь 20 м, увеличив свою скорость в 3 раза. Определите конечную скорость тела.
2. Из пункта А в пункт В, расстояние между которыми 30 км, одновременно выехали автомобилист и велосипедист. За час автомобилист проезжает на 55 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 1 час 6 минут позже автомобилиста. Ответ дайте в км/ч.

 

404 Cтраница не найдена

Мы используем файлы cookies для улучшения работы сайта МГТУ и большего удобства его использования. Более подробную информацию об использовании файлов cookies можно найти здесь. Продолжая пользоваться сайтом, вы подтверждаете, что были проинформированы об использовании файлов cookies сайтом ФГБОУ ВО «МГТУ» и согласны с нашими правилами обработки персональных данных.

Размер:

AAA

Изображения Вкл. Выкл.

Обычная версия сайта

К сожалению запрашиваемая страница не найдена.

Но вы можете воспользоваться поиском или картой сайта ниже

Университет Майкопский государственный технологический университет – один из ведущих вузов юга России. История университета Анонсы Объявления Медиа Представителям СМИ Газета «Технолог» О нас пишут Ректорат Структура Филиал Политехнический колледж Медицинский институт Лечебный факультет Педиатрический факультет Фармацевтический факультет Стоматологический факультет Факультет послевузовского профессионального образования Факультеты Кафедры Ученый совет Дополнительное профессиональное образование Бережливый вуз – МГТУ Новости Объявления Лист проблем Лист предложений (Кайдзен) Реализуемые проекты Архив проектов Фабрика процессов Рабочая группа «Бережливый вуз-МГТУ» Вакансии Профсоюз Противодействие терроризму и экстремизму Противодействие коррупции WorldSkills в МГТУ Научная библиотека МГТУ Реквизиты и контакты Автошкола МГТУ Опрос в целях выявления мнения граждан о качестве условий оказания образовательных услуг Управление имущественным комплексом Работа МГТУ в условиях предотвращения COVID-19 Документы, регламентирующие образовательную деятельность Система менеджмента качества университета Региональный центр финансовой грамотности Аккредитационно-симуляционный центр Абитуриентам Подача документов онлайн Абитуриенту 2023 Для поступающих на обучение по программам бакалавриата, специалитета, магистратуры — Прием 2023 Для поступающих на обучение по программам среднего профессионального образования (колледж) Для поступающих на обучение по договорам об оказании платных образовательных услуг Образец договора Образовательный кредит Оплата материнским (семейным) капиталом Банковские реквизиты для оплаты обучения Приказ об установлении стоимости обучения для 1 курса набора 2022-2023 учебного года Для поступающих на обучение по программам ординатуры Для поступающих на обучение по программам аспирантуры Часто задаваемые вопросы (бакалавриат, специалитет, магистратура) Видеоматериалы для постуающих Экран приёма 2022 Иностранным абитуриентам Международная деятельность Общие сведения Кафедры Новости Центр международного образования Академическая мобильность и международное сотрудничество Академическая мобильность и фонды Индивидуальная мобильность студентов и аспирантов Как стать участником программ академической мобильности Дни открытых дверей в МГТУ День открытых дверей online Университетские субботы Дни открытых дверей на факультетах Подготовительные курсы Подготовительное отделение Курсы для выпускников СПО Курсы подготовки к сдаче ОГЭ и ЕГЭ Онлайн-курсы для подготовки к экзаменам Подготовка школьников к участию в олимпиадах Малая технологическая академия Профильный класс Социально-экономический профиль Медико-фармацевтический профиль Инженерно-технологический профиль Эколого-биологический профиль Агротехнологический профиль Индивидуальный проект Кружковое движение юных технологов Олимпиады, конкурсы, фестивали Веб-консультации для абитуриентов и их родителей Веб-консультации для абитуриентов Родительский университет Олимпиады для школьников Отборочный этап Заключительный этап Итоги олимпиад Профориентационная работа Стоимость обучения Студентам Студенческая жизнь Стипендии Организация НИРС в МГТУ Студенческое научное общество Студенческие научные мероприятия Конкурсы Академическая мобильность и международное сотрудничество Образовательные программы Расписание занятий Расписание звонков Онлайн-сервисы Социальная поддержка студентов Общежития Трудоустройство обучающихся и выпускников Вакансии Обеспеченность ПО Инклюзивное образование Условия обучения лиц с ограниченными возможностями Доступная среда Ассоциация выпускников МГТУ Перевод из другого вуза Вакантные места для перевода Студенческое пространство Студенческое пространство Запись на мероприятия Отдел по социально-бытовой и воспитательной работе

Наука и инновации Научная инфраструктура Проректор по научной работе и инновационному развитию Научно-технический совет Управление научной деятельностью Управление послевузовского образования Точка кипения МГТУ О Точке кипения МГТУ Руководитель и сотрудники Документы Контакты Центр коллективного пользования Центр народной дипломатии и межкультурных коммуникаций Студенческое научное общество Научные издания Научный журнал «Новые технологии» Научный журнал «Вестник МГТУ» Научный журнал «Актуальные вопросы науки и образования» Публикационная активность Конкурсы, гранты Научные направления и результаты научно-исследовательской деятельности Основные научные направления университета Отчет о научно-исследовательской деятельности в университете Результативность научных исследований и разработок МГТУ Финансируемые научно-исследовательские работы Объекты интеллектуальной собственности МГТУ Результативность научной деятельности организаций, подведомственных Минобрнауки России (Анкеты по референтным группам) Студенческое научное общество Инновационная инфраструктура Федеральная инновационная площадка Проблемные научно-исследовательские лаборатории Научно-исследовательская лаборатория «Совершенствование системы управления региональной экономикой» Научно-исследовательская лаборатория проблем развития региональной экономики Научно-исследовательская лаборатория организации и технологии защиты информации Научно-исследовательская лаборатория функциональной диагностики (НИЛФД) лечебного факультета медицинского института ФГБОУ ВПО «МГТУ» Научно-исследовательская лаборатория «Инновационных проектов и нанотехнологий» Научно-техническая и опытно-экспериментальная база Центр коллективного пользования Научная библиотека Экспортный контроль Локальный этический комитет Конференции Школа молодого врача Международная научно-практическая конференция «Фундаментальные и прикладные аспекты геологии, геофизики и геоэкологии с использованием современных информационных технологий» Международная научно-практическая конференция «Актуальные вопросы науки и образования» VI Международная научно-практическая онлайн-конференция Наука и университеты Международная деятельность Иностранным студентам Международные партнеры Академические обмены, иностранные преподаватели Академическая мобильность и фонды Индивидуальная мобильность студентов и аспирантов Факультет международного образования Новости факультета Информация о факультете Международная деятельность Кафедры Кафедра русского языка как иностранного Кафедра иностранных языков Центр Международного образования Центр обучения русскому языку иностранных граждан Приказы и распоряжения Курсы русского языка Расписание Академическая мобильность Контактная информация Контактная информация факультета международного образования Сведения об образовательной организации Основные сведения Структура и органы управления образовательной организацией Документы Образование Образовательные стандарты и требования Руководство. Педагогический (научно-педагогический) состав Материально-техническое обеспечение и оснащённость образовательного процесса Стипендии и меры поддержки обучающихся Платные образовательные услуги Финансово-хозяйственная деятельность Вакантные места для приёма (перевода) Международное сотрудничество Доступная среда Организация питания в образовательной организации

СРОЧНЫХ БАЛЛОВ!!!!!! Какова середина CD с координатами C(-4,8) и D(8,-4)? А) 0,0 Б) 2,2

Ответы

Правильные ответы б

---

Связанные вопросы

Если nh = pn + hm = 12 дюймов и ph = 17 дюймов, каково значение hm в дюймах

Ответы

Ph будет равен сумме pn и nh. Таким образом:
ph = pn + nh
17 = pn + 12
pn = 5

nh = pn + hm
12 = 5 + hm
hm = 8 дюймов

Магазин спортивных товаров платит 170 долларов за резиновый плот. Процент наценки 45%. Найдите цену продажи плота.

Ответы

Итак, как говорится в заявлении, магазин спортивных товаров платит 170 долларов, поэтому это означает, что он равен 100%, теперь, поскольку он собирается продавать товар с наценкой 45%, это означает, что он будет добавлен к 100%, поэтому вы’ получу 145% от 170 долларов. После умножьте 170 долларов на 145%, чтобы получить ответ 246,50 долларов. В магазине спортивных товаров резиновый плот продается по цене 246,50 долларов.

Диагонали ромба равны 8 футам и 4 футам соответственно. чему равна площадь этого ромба? а. 12 квадратных футов
б. 16 квадратных футов
в. 24 квадратных фута
д. 36 квадратных футов

Ответы

D — это ответ, умноженный на ширину и длину, чтобы найти площадь четырехугольника, для треугольника используйте основание, умноженное на высоту, деленную на два.

ПРОГОЛОСУЙТЕ, ПОЖАЛУЙСТА, ПОМОГИТЕ НУЖНЫ ОТВЕТЫ КАК МОЖНО СКОРЕЕ Масштаб архитектурного чертежа 2 дюйма = 5 футов: 10 фактически: ______ футов.
А.35 футов
B.20 футов
C.30 футов
D.25 футов

Ответы

Правильный ответ Б.

БУДЕТ ПРОГОЛОСОВАТЬ И ЖЕЛАЕТ ОБЪЯСНЕНИЙ, ПОЖАЛУЙСТА!! В таблице ниже представлена ​​скорость автомобиля как функция времени:

Время
(час)
х Скорость
(миль/час)
г
0 50
1 52
2 54
3 56
Левая сторона — это X, а правая — Y

Часть A: Что представляет собой точка пересечения функции с осью Y и что это говорит вам об автомобиле? (4 балла)

Часть B: Рассчитайте среднюю скорость изменения функции, представленной в таблице, между x = 1 и x = 3 часа, и скажите, что представляет собой средняя скорость. (4 балла)

Часть C: Какой будет область определения функции, если измерять скорость автомобиля до тех пор, пока она не достигнет 60 миль/час, и автомобиль не изменит своего движения? (2 балла)

Ответы

(A): Когда он запрашивает y-перехват, он в основном спрашивает, каково значение y, когда x = 0. В этом случае, когда x=0, y=50. Таким образом, точка пересечения по оси Y равна 50.

(B): Среднее значение. скорость изменения такая же, как и при запросе наклона. Итак, мы хотим использовать формулу наклона -> . Используя значения в вашей таблице -> 

(C) Вы можете сгенерировать линейную функцию с точкой пересечения по оси y и наклоном, используя следующую формулу -> y= (средняя скорость изменения)*x + точка пересечения с y -> Тогда установите y = 60 и найдите x. Ваш домен — [0, решенное значение] с квадратными скобками, так как вы включаете конечные точки.

Надеюсь помог!

Ответ:

(A): Когда он запрашивает y-пересечение, он в основном спрашивает, каково значение y, когда x=0. В этом случае, когда x=0, y=50. Таким образом, точка пересечения по оси Y равна 50.

(B): Среднее значение. скорость изменения такая же, как и при запросе наклона. Итак, мы хотим использовать формулу наклона -> . Используя значения в таблице -> 

(C) Вы можете сгенерировать линейную функцию с точкой пересечения по оси y и наклоном, используя следующую формулу -> y= (средняя скорость изменения)*x + точка пересечения с y -> Тогда установите y = 60 и найдите x. Ваш домен — [0, решенное значение] с квадратными скобками, так как вы включаете конечные точки. 92 + 3g)

Ответы

Правильные ответы — B и C, потому что их можно разложить на множители, чтобы получить противоположности
, пожалуйста, отметь как лучший

Ответ:

b c

Пошаговое объяснение:

Какой набор чисел может представлять длины сторон прямоугольного треугольника? 3, 4, 5

9, 10, 11

8, 12, 16

16, 32, 36

Ответы

Ваш ответ должен быть 3, 4, 5. Надеюсь, это поможет! 92

Какое уравнение больше -7/12? A. -2/3

B. -5/9

C. -13/18

D. -3/4

Ответы

B (-5/9)

Все остальные меньше -7/12, потому что в этом вопросе важен знак минус.

-7/12

Продажи детской спортивной обуви определенной марки выросли с 5 000 000 до 5 800 000 долларов. Найдите процент увеличения продаж. При необходимости округлить до десятых долей процента. Вариантов:
16%

13,8%

86,2%

0,2%

Ответ менее чем за 5 минут!!!

Ответы

Процентное увеличение = (увеличение) x 100 / исходное
Процентное увеличение = (5 800 000 — 5 000 000) x 100 / (5 000 000)
Процентное увеличение = 16%

Увеличение:
5 800 000 долл. США — 5 000 000 долл. США = 800 000 долл. США
Процент увеличения:
800 000  x 100 : 5 000 000 = 16%
Ответ:
А) 16%

Множество всех точек, отстоящих на r единиц от другой точки a. круг
б. квадрат
в. параллельные линии
д. сегмент линии

Ответы

Множество всех точек, которые находятся на расстоянии r единиц от другой точки, A. представляет собой круг.
Окружность — это простая геометрическая фигура, точки привязки которой равноудалены (на одинаковое расстояние) от одной заданной точки.

Каково значение функции при x = 2?

х −4 −2 0 2 4
у 3 4 2 6 7

Ответы

Где функция?

Пусть X=33/65 будет x-координатой точки P(x,y), где конечная сторона угла theta (в стандартном положении) пересекает единичную окружность. Если P находится в квадранте 4, что такое sin theta?

Ответы

Грех ² (тета) = 1 — (33/65)²
sin² (тета) = 1 — 1089/4225
sin² (тета) = 3136/4225
sin² (тета) = — √3136/4225 = — 56/65 (поскольку P находится в квадранте 4)
Ответ: sin (тета ) = — 56/65

Требуемое значение  .

Пусть , будет координатой x точки P(x, y).

Р находится в 4-м квадранте.

По вопросу.

Конечная точка на единичной окружности указывает, что конечная точка на единичной окружности, начинающаяся с (1,0), измеряет угол в градусах или радианах на окружности (двигайтесь против часовой стрелки, если угол положительный, и по часовой стрелке, если угол положительный). отрицательно.)

Координата конечной точки называется конечной точкой.

Общее уравнение единичного круга:

Подставьте в уравнение

 

Теперь ,

P лежит в четвертом квадранте, вы знаете, что синус отрицательный.

Следовательно, требуемое значение  .

Для получения дополнительной информации о Circle нажмите на ссылку ниже.

brainly.com/question/11833983

Пусть f(x) = 3x + 2 и g(x) = 6x — 7. Найдите f(x) — g(x) Варианты ответов
А.) 3x — 9
Б.) -3х — 9
В.) -3x — 5
Д.)2x — 1
очень запутался -_-

Ответы

F(x) — g(x) = 3x + 2 — (6x-7) = 3x + 2 — 6x + 7 = -3x + 9;

Нет правильного ответа!

Зои проектирует шкатулку для драгоценностей в форме прямоугольной призмы. Основание 6 дюймов на 5 дюймов, а высота 4 дюйма. Если Зои хочет обтянуть все грани шкатулки тканью, сколько ей понадобится ткани?

Ответы

Основываясь на информации о призме, необходимая ткань составит 148 дюймов².

Как рассчитать необходимое количество ткани.

Площадь верха и низа будет:

= 2 × 6 × 5 = 60 дюймов²

Площадь сторон = 2 × 5 × 4 = 40 дюймов²

Площадь передней и задней части = 2 × 6 × 4 = 48 дюймов²

Следовательно, необходимая ткань будет:

= 60 + 40 + 48 = 148 дюймов²

Узнайте больше о призме на:

brainly.com/question/23963432

Размер коробки 6 на 5 на 4
Площадь верха и низа = 2* (6*5) = 60 квадратных дюймов
Площадь сторон = 2 * (5 * 4) = 40 квадратных дюймов
Площадь спереди и сзади = 2 * (6 * 4) = 48 квадратных дюймов
60 + 40 + 48 = 148 квадратных дюймов

Напишите уравнение для кубической полиномиальной функции, график которой имеет нули в точках 2, 3 и 5. • Может ли любой из корней иметь кратность?

• Как найти функцию с этими корнями?

Ответы

мы знаем, что

Для полинома, если x=a является нулем функции, то (x−a) является фактором функции. Термин кратность относится к тому, сколько раз связанный с ним множитель появляется в полиноме.

Итак,

В этой задаче

Если кубическая многочленная функция имеет нули в 2, 3 и 5

, то

делители равны

Часть а) Может ли какой-либо из корней иметь кратность?

Ответ: Нет

Если кубическая полиномиальная функция имеет три разных нуля

, то

кратность каждого множителя равна единице

Например, кубическая полиномиальная функция имеет нули

, каждый из которых встречается один раз.

Часть б) Как найти функцию, имеющую эти корни?

Чтобы найти кубическую полиномиальную функцию, умножьте множители и приравняйте к нулю

, следовательно,

, следовательно,

ответ Часть b) равна

функция кубического многочлена равна

Ответ:

Ни один из корней не может иметь кратности, потому что многочлен кубический и дано 3 корня. Запишите каждый корень как линейный множитель, затем умножьте три множителя, чтобы получить выражение для функции.

Пошаговое объяснение: исправить на краю (: надеюсь, что это поможет

В приведенной ниже системе найдите y в первом уравнении. х — 3y = -6
2х — 7у = 10
А. 1/3x+2
Б. -1/3х+6
С.-х+2
D. -1/3x+2

Ответы

Ответ:

Вариант ответа A

Пошаговое объяснение:

имеем

——> первое уравнение

— —> второе уравнение

Найти у в первом уравнении

Это означает——> выделить переменную у в первом уравнении

Разделить на обе части

Правильный ответ должен быть А.

Если бы вы управляли реальной компанией, стоимость материалов была бы важным фактором. Сообразительный деловой человек хотел бы снизить затраты, сводя количество материалов в своих продуктах к минимуму. Как знания о геометрии и объемах различных трехмерных фигур могут помочь в этом процессе принятия решений?

Ответы

Знание того, сколько места занимает объект, поможет свести к минимуму количество материала, потому что они знают, сколько им нужно заказать, и им не нужно будет заказывать ничего лишнего.

Если единицу разделить на число от нуля до единицы, результат А) меньше единицы
Б) меньше нуля
C) больше единицы
D) между нулем и единицей

Ответы

В) Больше единицы.

ПРОГОЛОСУЮ!!:p:p:p<3 Вычислить функцию g(t)=5/2t-3/2 при t=3

A. 6
Б. 9
К. 12
D. 13 1/2

Ответы

Правильный ответ 6

Я ПРОГОЛОСУЮ ВСЕ ОТВЕТЫ Какая упорядоченная пара является решением системы уравнений?

2x−5y=−5
x+2y=11

A. (3, 4)

B. (15, 7)

C. (5, 3)

D. (7, 2)

Ответы

Ответ С. (5,3)

Гибкие методы состоят из 45 подпроцессов, которые организованы в восемь групп процессов. Какое важное изменение произошло после того, как психическое заболевание стало «медицинским»? Часто приходится смотреть на одну и ту же проблему по-разному, чтобы найти ответ. пожалуйста, выберите лучший ответ из предложенных вариантов t f Адекватное потребление витамина D необходимо для обеспечения эффективного усвоения _____. По некоторым оценкам, каждую минуту в США теряется или крадется ____ мобильных телефонов. В каком полушарии находится большая часть Африки? а. северное полушарие б. западное полушарие в. левое полушарие д. восточное полушарие В 1930-е годы, какое влияние оказала Великая депрессия на Латинскую Америку? а. крестьяне добились богатства и статуса. б. экономический кризис вызвал распространение демократии. в. страны Латинской Америки отвергли социалистические идеи. д. люди потеряли веру в идеи либерального правительства В общих чертах, как меняются мозговые волны по мере того, как спящий переходит от стадии 1 сна к стадии 4 сна? Методология, направленная на снижение количества дефектов в бизнес-процессе У людей с Если nh = pn + hm = 12 дюймов и ph = 17 дюймов, каково значение hm в дюймах? Помощь! Мне нужна помощь с этим вопросом. Я не уверен, как это сделать. Был бы признателен за любую помощь, которую вы можете предложить. В заповеднике соотношение бабочек к общему количеству летающих насекомых составляет 36 к 100. Всего летающих насекомых 450. а). Составьте таблицу, сколько бабочек приходится на 1, 50 и 100 летающих насекомых. показать свою работу. б. Сколько бабочек в оранжерее? Показать свою работу. _______ — это процесс проверки данных на достоверность и полноту Идия была маской, созданной какой культурой? 20. Проранжируйте состояния вещества от самой медленной до самой высокой скорости частицы. Сколько затмений обычно происходит каждый год? а. 2. Найдите точные значения x и y, которые максимизируют прибыль монополиста. Определите, является ли каждый набор слов синонимами, антонимами или ни денотативными, ни коннотативными а. синонимы б. антонимы в. ни один Как правильно написать триста тысяч пять тысяч шестьдесят три

Исчисление I — Интерпретация производной

Онлайн-заметки Пола
Главная / Исчисление I / Производные / Толкование производной

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Уведомление для мобильных устройств

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 3.2: Интерпретация производной

Прежде чем перейти к разделу, в котором мы узнаем, как вычислять производные, избегая ограничений, которые мы оценивали в предыдущем разделе, нам нужно бросить беглый взгляд на некоторые интерпретации производных. Все эти интерпретации возникают в результате напоминания о том, как возникло наше определение производной. Определение появилось благодаря тому, что мы заметили, что все задачи, над которыми мы работали в первом разделе главы «Ограничения», требовали от нас оценки одного и того же предела.

Скорость изменения

Первая интерпретация производной – это скорость изменения. 2} — 16t + 35\). Определите каждое из следующих.

1. Объем воды в баке увеличивается или уменьшается в \(t = 1\) минуту?
2. Увеличивается или уменьшается объем воды в баке через \(t = 5\) минут?
3. Объем воды в баке изменяется быстрее через \(t = 1\) или \(t = 5\) минут?
4. Объем воды в баке никогда не меняется? Если да, то когда?

Показать все решения Скрыть все решения

Показать обсуждение

В решении этого примера мы будем использовать оба обозначения для производной просто для того, чтобы вы познакомились с различными обозначениями.

Нам понадобится скорость изменения объема, чтобы ответить на эти вопросы. Это означает, что нам понадобится производная этой функции, так как это даст нам формулу для скорости изменения в любой момент времени \(t\). Теперь обратите внимание, что функция, определяющая объем воды в резервуаре, — это та же самая функция, которую мы видели в примере 1 в последнем разделе, за исключением того, что буквы изменились. Изменение букв между функцией в этом примере и функцией в примере из последнего раздела не повлияет на работу, поэтому мы можем просто использовать ответ из этот пример с соответствующей заменой букв.

Производная.

\[V’\left( t \right) = 4t — 16\hspace{0,5 дюйма}{\rm{OR}}\hspace{0,5 дюйма}\frac{{dV}}{{dt}} = 4t — 16 \]

Вспомним из нашей работы в первом разделе пределов, что мы определили, что если скорость изменения была положительной, то количество увеличивалось, а если скорость изменения была отрицательной, то количество уменьшалось.

Теперь мы можем решить задачу.

а Увеличивается или уменьшается объем воды в баке через \(t = 1\) мин? Показать решение

В этом случае все, что нам нужно, это скорость изменения объема при \(t = 1\)или,

\[V’\влево( 1 \вправо) = — 12\hпробел{0,5 дюйма}{\rm{ИЛИ}}\hпробел{0,5 дюйма}{\влево. {\ frac {{dV}}{{dt}}} \right|_{\,t = 1}} = — 12\]

Итак, при \(t = 1\) скорость изменения отрицательна, поэтому объем в это время должен уменьшаться.

b Увеличивается или уменьшается объем воды в баке через \(t = 5\) минут? Показать решение

Опять же, нам понадобится скорость изменения при \(t = 5\).

\[V’\влево( 5 \вправо) = 4\hпробел{0,5 дюйма}{\rm{ИЛИ}}\hпробел{0,5дюйма}{\влево. {\ frac {{dV}}{{dt}}} \right|_{\,t = 5}} = 4\]

В этом случае скорость изменения положительна, поэтому объем должен увеличиваться при \(t = 5\) .

в Изменяется ли быстрее объем воды в баке через \(t = 1\) или \(t = 5\) минут? Показать решение

Чтобы ответить на этот вопрос, мы обращаем внимание только на величину скорости изменения, и нас не волнует знак скорости изменения. Все, что нам нужно знать, это то, что чем больше число, тем выше скорость изменения. Итак, в данном случае объем изменяется быстрее при \(t = 1\) , чем при \(t = 5\).

d Всегда ли объем воды в баке не меняется? Если да, то когда? Показать решение

Объем не будет изменяться, если его скорость изменения равна нулю. Чтобы иметь скорость изменения, равную нулю, это означает, что производная должна быть равна нулю. Итак, чтобы ответить на этот вопрос, нам нужно будет решить

\[V’\left( t \right) = 0\hspace{0.5in}{\rm{OR}}\hspace{0.5in}\frac{{dV}}{{dt}} = 0\]

Это достаточно легко сделать.

\[4t — 16 = 0\hspace{0,5 дюйма} \Стрелка вправо \hspace{0,5 дюйма}t = 4\]

Итак, при \(t = 4\) громкость не меняется. Обратите внимание, что все это говорит о том, что в течение короткого мгновения громкость не меняется. Это не говорит о том, что в этот момент громкость перестанет меняться постоянно.

Если мы вернемся к нашим ответам из частей (а) и (б), мы сможем получить представление о том, что происходит. При \(t = 1\) объем уменьшается, а при \(t = 5\) объем увеличивается. Итак, в какой-то момент времени громкость должна переключиться с уменьшения на увеличение. Это время равно \(t = 4\).

Это время, в течение которого громкость переходит от уменьшения к увеличению, поэтому в течение самого короткого момента времени громкость перестанет изменяться, поскольку она переходит от уменьшения к увеличению.

Обратите внимание, что одна из наиболее распространенных ошибок, которую учащиеся допускают в подобных задачах, заключается в том, что они пытаются определить возрастание/убывание по значениям функции, а не по производным. В этом случае, если мы возьмем значения функции при \(t = 0\), \(t = 1\) и \(t = 5\), мы получим

\[V\влево( 0 \вправо) = 35\hspace{0,5 дюйма}V\влево( 1 \вправо) = 21\hspace{0,5 дюйма}V\влево( 5 \вправо) = 5\]

Очевидно, что по мере перехода от \(t = 0\) к \(t = 1\) объем уменьшается. Это может привести нас к выводу, что при \(t = 1\) объем уменьшается. Однако мы просто не можем этого сказать. Все, что мы можем сказать, это то, что между \(t = 0\) и \(t = 1\) объем в какой-то момент времени уменьшился. Единственный способ узнать, что происходит прямо в точке \(t = 1\), состоит в том, чтобы вычислить \(V’\left( 1 \right)\) и посмотреть на его знак, чтобы определить увеличение/уменьшение. В этом случае \(V’\left( 1 \right)\) отрицательно, и поэтому объем действительно уменьшается при \(t = 1\).

Теперь, если бы мы использовали функцию, а не производную, мы бы получили правильный ответ для \(t = 1\), хотя наши рассуждения были бы ошибочными. Важно не допустить, чтобы это дало вам представление о том, что так будет всегда. Это просто сработало в случае \(t = 1\).

Чтобы увидеть, что это не всегда работает, давайте теперь посмотрим на \(t = 5\). Если мы подставим \(t = 1\) и \(t = 5\) в объем, мы снова увидим, что по мере перехода от \(t = 1\) к \(t = 5\) объем уменьшился. Опять же, однако все это говорит о том, что объем уменьшился где-то между \(t = 1\) и \(t = 5\). Это НЕ говорит, что объем уменьшается при \(t = 5\). Единственный способ узнать, что происходит прямо в \(t = 5\) заключается в вычислении \(V’\left( 5 \right)\), и в этом случае \(V’\left( 5 \right)\) положительно, и поэтому объем фактически увеличивается при \(t = 5\).

Будьте осторожны. Когда вас попросят определить, возрастает или убывает функция в какой-либо точке, обязательно посмотрите на производную. Это единственный верный способ получить правильный ответ. Мы не пытаемся определить, увеличилась/уменьшилась ли функция к тому времени, когда мы достигли определенной точки. Мы ищем, чтобы определить, увеличивается ли функция в данный момент.

Наклон касательной

Это следующая основная интерпретация производной. Наклон касательной к \(f\left( x \right)\) в точке \(x = a\) равен \(f’\left( a \right)\). Тогда касательная задается как

\[y = f\left( a \right) + f’\left( a \right)\left( {x — a} \right)\]

Пример 2. Найдите касательную к следующей функции в точке \(z = 3\). \[R\влево( z \вправо) = \sqrt {5z — 8} \]

Показать решение

Сначала нам нужна производная функции, и мы нашли ее в примере 3 в последнем разделе. Производная,

\[R’\left( z \right) = \frac{5}{{2\sqrt {5z — 8} }}\]

Теперь все, что нам нужно, это значение функции и производная (для наклона) в точке \(z = 3\).

\[R\left( 3 \right) = \sqrt 7 \hspace{0.5in}m = R’\left( 3 \right) = \frac{5}{{2\sqrt 7 }}\]

Тогда касательная

\[y = \sqrt 7 + \frac{5}{{2\sqrt 7 }}\left( {z — 3} \right)\]

Скорость

Напомним, что это можно рассматривать как частный случай интерпретации скорости изменения. Если положение объекта определяется как \(f\left( t \right)\) через \(t\) единиц времени, то скорость объекта в \(t = a\) определяется как \(f’ \влево( а \вправо)\).

Пример 3. Предположим, что положение объекта через \(t\) часов определяется выражением \[g\left( t \right) = \frac{t}{{t + 1}}\]

Ответьте на два вопроса об этом объекте.

1. Объект движется вправо или влево через \(t = 10\) часов?
2. Объект когда-нибудь перестает двигаться?

Показать все решения Скрыть все решения

92}}}\]

а Движется ли объект вправо или влево через \(t = 10\) часов? Показать решение

Чтобы определить, движется ли объект вправо (скорость положительна) или влево (скорость отрицательна), нам нужна производная при \(t = 10\).

\[g’\влево( {10} \вправо) = \frac{1}{{121}}\]

Итак, скорость в точке \(t = 10\) положительна, поэтому объект движется вправо в точке \(t = 10\).

b Перестает ли когда-нибудь двигаться объект? Показать решение

Объект перестанет двигаться, если его скорость никогда не будет равна нулю. Однако обратите внимание, что рациональное выражение может быть равно нулю только в том случае, если числитель равен нулю. Поскольку числитель производной (и, следовательно, скорости) является константой, он не может быть равен нулю.

Следовательно, объект никогда не перестанет двигаться.

На самом деле здесь можно сказать немного больше. Объект всегда будет двигаться вправо, так как скорость всегда положительна.

Здесь мы рассмотрели три основные интерпретации производной. Вам нужно будет запомнить их, особенно скорость изменений, так как они будут постоянно появляться на протяжении всего курса.

Прежде чем мы покинем этот раздел, давайте поработаем еще с одним примером, который включает в себя некоторые идеи, обсуждаемые здесь, и является просто хорошим примером для работы.

Пример 4 Ниже приведен эскиз функции \(f\left( x \right)\). Нарисуйте график производной этой функции \(f’\left( x \right)\).

Показать решение

На первый взгляд это кажется почти невыполнимой задачей. Однако, если у вас есть базовые знания об интерпретации производной, вы можете получить набросок производной. По большей части это не будет идеальным эскизом, но вы сможете получить большинство основных функций производной в эскизе.

Начнем со следующего наброска функции с парой дополнений.

Обратите внимание, что в точках \(x = — 3\), \(x = — 1\), \(x = 2\) и \(x = 4\) касательная к функции горизонтальна. Это означает, что наклон касательной должен быть равен нулю. Теперь мы знаем, что наклон касательной в определенной точке также является значением производной функции в этой точке. Таким образом, мы теперь знаем, что

\[f’\влево( { — 3} \вправо) = 0\hspace{0.5in}f’\влево( {- 1} \right) = 0\hspace{0.5in}f’\влево( 2 \right) = 0\hspace{0.5in}f’\left( 4 \right) = 0\]

Это хорошая отправная точка для нас. Это дает нам несколько точек на графике производной. Он также разбивает область определения функции на области, в которых функция возрастает и убывает. Из наших обсуждений выше мы знаем, что если функция возрастает в точке, то производная должна быть положительной в этой точке. Точно так же мы знаем, что если функция убывает в какой-то точке, то производная в этой точке должна быть отрицательной.

Теперь мы можем дать следующую информацию о производной.

\[\begin{align*} x & < - 3 & \hspace{0.5in}f'\left( x \right) & < 0\\ - 3 < x & < - 1 & \hspace{0.5in }f'\left( x \right) & > 0\\ — 1 < x & < 2 & \hspace{0.5in}f'\left( x \right) & < 0\\ 2 < x & < 4 & \hspace{0.5in}f'\left( x \right) & < 0\\ x & > 4 & \hspace{0. 5in}f’\left(x \right) & > 0\end{align*}\ ]

Помните, что здесь мы приводим знаки производных, и они зависят исключительно от возрастания или убывания функции. Знак самой функции здесь совершенно безразличен и никак не повлияет на знак производной.

Может показаться, что у нас недостаточно информации для получения эскиза, но мы можем получить немного больше информации о производной из графика функции. Мы знаем, что в диапазоне \(x < - 3\) производная должна быть отрицательной, однако мы также видим, что в этом диапазоне производная должна возрастать. Здесь она отрицательна, пока мы не достигнем \(x = -3\), и в этой точке производная должна быть равна нулю. Единственный способ, чтобы производная была отрицательной слева от \(x = - 3\) и равна нулю в точке \(x = - 3\) означает, что производная будет возрастать по мере увеличения \(x\) до \(x = -3\).

Теперь в диапазоне \( — 3 < x < - 1\) мы знаем, что производная должна быть равна нулю на концах и положительна между двумя концами.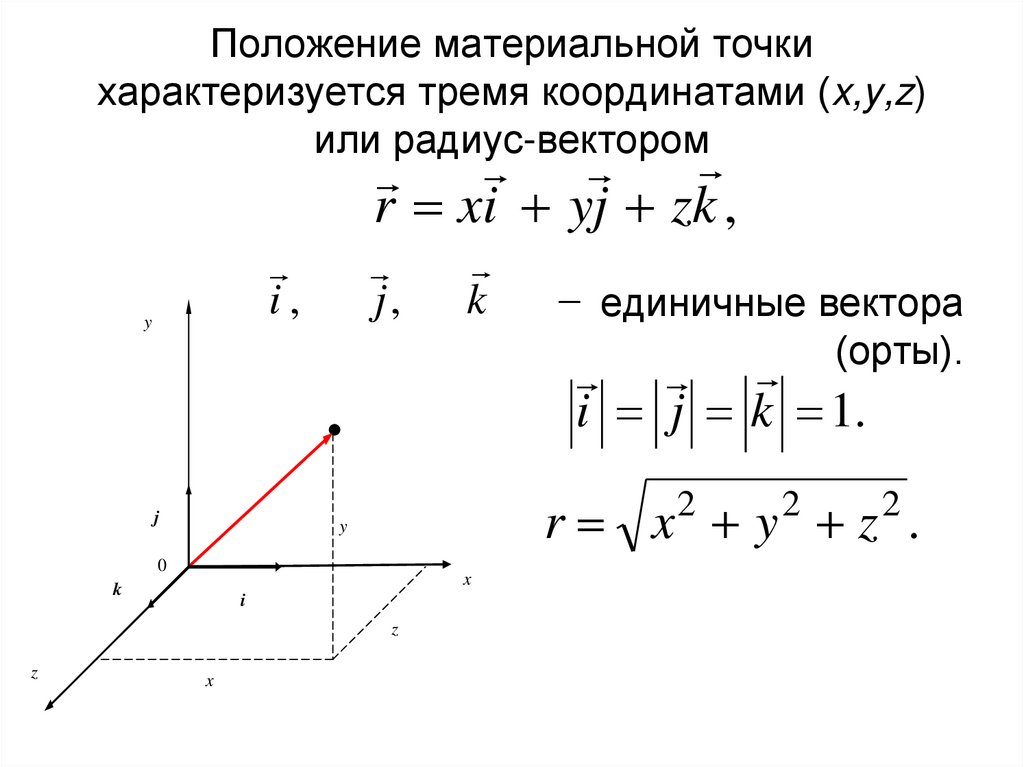 Непосредственно справа от \(x = — 3\) производная также должна возрастать (потому что она начинается с нуля, а затем становится положительной, следовательно, она должна возрастать). Таким образом, производная в этом диапазоне должна начинаться с возрастания и в конечном итоге должна вернуться к нулю при \(x = — 1\). Таким образом, в какой-то момент этого интервала производная должна начать уменьшаться, прежде чем она достигнет \(x = — 1\). Теперь мы должны быть осторожны здесь, потому что это просто общее поведение здесь, на двух конечных точках. Мы не будем знать, где производная переходит от возрастания к убыванию, и она вполне может измениться между увеличением и уменьшением несколько раз, прежде чем мы достигнем \(x = — 1\). Все, что мы можем на самом деле сказать, это то, что непосредственно справа от \(x = — 3\) производная будет возрастать, а непосредственно слева от \(x = — 1\) производная будет уменьшаться.

Далее, для диапазонов \(-1 < x < 2\) и \(2 < x < 4\) мы знаем, что производная будет равна нулю в конечных точках и отрицательной между ними. Кроме того, следуя приведенному выше типу рассуждений, мы можем видеть в каждом из этих диапазонов, что производная будет уменьшаться справа от левой конечной точки и увеличиваться слева от правой конечной точки.

Наконец, в последней области \(x > 4\) мы знаем, что производная равна нулю в точке \(x = 4\) и положительна справа от \(x = 4\). Опять же, следуя приведенным выше рассуждениям, производная также должна возрастать в этом диапазоне.

Соединяя весь этот материал вместе (и всегда используя самые простые варианты увеличения и/или уменьшения информации), мы получаем следующий набросок для производной.

Обратите внимание, что это было сделано с фактической производной и поэтому на самом деле является точным. Любой набросок, который вы сделаете, вероятно, не будет выглядеть точно так же. «Горбы» в каждой из областей могут быть, например, в разных местах и/или на разных высотах. Также обратите внимание, что мы отказались от вертикальной шкалы, потому что, учитывая информацию, которую мы получили на данный момент, не было реального способа узнать эту информацию.

Это не означает, однако, что мы не можем получить некоторое представление о конкретных точках производной, кроме тех, где мы знаем, что производная равна нулю. Чтобы убедиться в этом, давайте посмотрим на следующий график функции (не производной, а функции).

В точках \(x = — 2\) и \(x = 3\) мы нарисовали пару касательных линий. Мы можем использовать базовую концепцию подъема/наклона для оценки значения производной в этих точках.

Начнем с \(x = 3\). У нас есть две точки на линии здесь. Мы можем видеть, что каждый из них находится примерно на четверть пути от линии сетки. Таким образом, принимая это во внимание и тот факт, что мы проходим через одну полную сетку, мы можем видеть, что наклон касательной и, следовательно, производной приблизительно равен -1,5.

При \(x = — 2\) похоже (с некоторой грубой оценкой), что вторая точка находится примерно на 6,5 сетки выше первой точки, и поэтому наклон касательной здесь и, следовательно, производная, составляет приблизительно 6,5 .