Механические колебания — презентация онлайн

Похожие презентации:

Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов

Газовая хроматография

Геофизические исследования скважин

Искусственные алмазы

Трансформаторы тока и напряжения

Транзисторы

Воздушные и кабельные линии электропередач

Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса

Магнитные аномалии

Нанотехнологии

1. Дз Механические колебания 2

1. При гармонических колебаниях
пружинного маятника координата груза
x(t)=Asin(2πt/T+φ0)
изменяется
с
течением времени t, как показано на
рисунке. Период T и амплитуда
колебаний А равны соответственно
A. T = 2 c, А = 6 см
B. T = 3 c, А = √3 см
C. T = 4 c, А = 3 см
D. T = 5 c, А = 6 см
A.
B.
C.
D.
А2. По графику, приведенному на
рисунке, определите амплитуду А и
период Т колебаний.
А = 20 см; Т = 0,9 с
А = 20 см; Т = 0,8 с
А = 10 см; Т = 0,9 с
А = 10 см; Т = 0,8 с
A.
B.
C.
D.
3. Маятник совершает N = 20
колебаний за t =(24,0 ± 0,2) с.
Согласно этим данным, период
колебаний маятника Т равен
(2,40 ±0,02) с
(2,4 ±0,2) с
(1,20 ± 0,01) с
(1,2 ±0,2) с
A.
B.
C.
D.
4. Период колебаний пружинного
маятника 1 с. Каким будет период его
колебаний, если массу груза маятника
увеличить в 2 раза, а жёсткость
пружины вдвое уменьшить?
4с
8с
2с
6с
A.
B.
C.
D.
5.
Пружинный
маятник
совершает
незатухающие колебания с периодом 0,5 с.
В момент времени t = 0 отклонение груза
маятника
от
положения
равновесия
максимально. Сколько раз кинетическая
энергия
маятника
достигнет
своего
максимального значения к моменту времени
2 с?
1) 8
2) 12
3) 1
4) 4
6 Математический маятник с периодом
колебаний Т отклонили на небольшой угол
от положения равновесия и отпустили с
начальной скоростью, равной нулю
(см. рисунок). Через какое время после этого
потенциальная энергия маятника в первый
раз вновь достигнет максимума?
Сопротивлением воздуха пренебречь.
A.
B.
C.
D.
T
1/4 T
1/2 T
1/8 T
1.1. Массивный груз, подвешенный к потолку на
пружине, совершает вертикальные свободные
колебания. Пружина всё время остаётся
растянутой. Как ведёт себя потенциальная энергия
пружины, кинетическая энергия груза, его
потенциальная энергия в поле тяжести, когда груз
движется вниз от положения равновесия?
Потенциальная энергия пружины
характер изменения:
увеличивается
Уменьшается
не изменяется
A.
B.
C.
1.2. Массивный груз, подвешенный к потолку на
пружине, совершает вертикальные свободные
колебания. Пружина всё время остаётся
растянутой. Как ведёт себя потенциальная энергия
пружины, кинетическая энергия груза, его
потенциальная энергия в поле тяжести, когда груз
движется вниз от положения равновесия?
Кинетическая энергия груза
характер изменения:
увеличивается
Уменьшается
не изменяется
A.
B.
C.
1.3. Массивный груз, подвешенный к потолку на
пружине, совершает вертикальные свободные
колебания. Пружина всё время остаётся
растянутой. Как ведёт себя потенциальная энергия
пружины, кинетическая энергия груза, его
потенциальная энергия в поле тяжести, когда груз
движется вниз от положения равновесия?
Потенциальная энергия груза в поле тяжести
характер изменения:
увеличивается
Уменьшается
не изменяется
A.
B.
C.
A.
B.
C.
2.1. Груз изображённого на рисунке
пружинного маятника совершает
гармонические колебания между точками 1
и 3. Как меняется кинетическая энергия
груза маятника, модуль скорости груза и
жёсткость пружины при движении груза
маятника от точки 2 к точке 1?
Кинетическая энергия груза маятника
Увеличивается
Уменьшается
не изменяется
A.
B.
C.
2.2. Груз изображённого на рисунке
пружинного маятника совершает
гармонические колебания между точками 1
и 3.
Как меняется кинетическая энергия
груза маятника, модуль скорости груза и
жёсткость пружины при движении груза
маятника от точки 2 к точке 1?
Модуль скорости груза
Увеличивается
Уменьшается
не изменяется
A.
B.
C.
2.3. Груз изображённого на рисунке
пружинного
маятника
совершает
гармонические колебания между точками 1
и 3. Как меняется кинетическая энергия
груза маятника, модуль скорости груза и
жёсткость пружины при движении груза
маятника от точки 2 к точке 1?
Жёсткость пружины
Увеличивается
Уменьшается
не изменяется
3.1. В первой серии опытов исследовались малые
колебания груза на нити некоторой длины. Затем
этот же груз закрепили на нити большей длины.
Максимальные углы отклонения нити от вертикали в
опытах одинаковы. Как при переходе от первой
серии опытов ко второй изменились период
колебаний, их частота и максимальная кинетическая
энергия груза?
Период колебаний :
A.
увеличилась
уменьшилась
не изменилась
B.
C.
3.2. В первой серии опытов исследовались малые
колебания груза на нити некоторой длины. Затем
этот же груз закрепили на нити большей длины.
Максимальные углы отклонения нити от вертикали в
опытах одинаковы. Как при переходе от первой
серии опытов ко второй изменились период
колебаний, их частота и максимальная кинетическая
энергия груза?
Частота колебаний :
A.
увеличилась
уменьшилась
не изменилась
B.
C.
3.3. В первой серии опытов исследовались малые
колебания груза на нити некоторой длины. Затем
этот же груз закрепили на нити большей длины.
Максимальные углы отклонения нити от вертикали в
опытах одинаковы. Как при переходе от первой
серии опытов ко второй изменились период
колебаний, их частота и максимальная кинетическая
энергия груза?
максимальная кинетическая энергия :
A.
увеличилась
уменьшилась
не изменилась
B.
C.

English     Русский Правила

Подготовка ЕГЭ по физике задание №6

Задание 6. В результате перехода искусственного спутника Земли с одной круговой орбиты на другую его центростремительное ускорение увеличивается. Как изменяются в результате этого перехода скорость движения спутника по орбите и период его обращения вокруг Земли?

Для каждой величины определите соответствующий характер изменения:

1) увеличивается

2) уменьшается

3) не изменяется

Решение.

На спутник действует только сила притяжения земли

,

где M — масса земли; m — масса спутника; R — радиус орбиты. В соответствии со вторым законом Ньютона, можно записать:

,

где a – играет роль центростремительного ускорения. Отсюда видно, что при увеличении ускорения, радиус орбиты будет уменьшаться.

Теперь рассмотрим как изменится скорость движения спутника в зависимости от радиуса орбиты. Подставим вместо ускорения , получим:

.

То есть, при уменьшении R, скорость спутника увеличивается.

Период обращения спутника вокруг Земли – это время, за которое спутник делает один оборот вокруг Земли. Если радиус орбиты уменьшается, а центростремительное ускорение возрастает, то скорость спутника увеличивается. Таким образом, спутник проходит меньшее расстояние с большей скоростью и его период уменьшается.

Ответ: 12.

Задание 6. На шероховатой наклонной плоскости покоится деревянный брусок. Угол наклона плоскости уменьшили. Как изменились при этом сила трения покоя, действующая на брусок, и коэффициент трения бруска о плоскость? Для каждой величины определите соответствующий характер изменения:

1) увеличилась

2) уменьшилась

3) не изменилась

Решение.

Так как брусок покоится на месте, то сила трения покоя уравновешивает силу соскальзывания бруска (тангенциальную силу). При уменьшении угла наклона тангенциальная сила уменьшается, следовательно, в соответствии с третьим законом Ньютона, сила трения покоя также уменьшается.

Коэффициент трения бруска о поверхность зависит только от материала соприкасающихся плоскостей и их площади, то есть он не изменится.

Ответ: 23.

Задание 6. Камень брошен вверх под углом к горизонту. Сопротивление воздуха пренебрежимо мало. Как меняются модуль ускорения камня и его потенциальная энергия в поле тяжести при движении камня вверх?

Для каждой величины определите соответствующий характер изменения:

1) увеличивается

2) уменьшается

3) не изменяется

Решение.

Проекцию движения камня на ось Oy (вертикальную ось) можно записать в виде

.

Из этого выражения видно, что ускорение камня равно g – ускорению свободного падения, то есть не меняется.

Потенциальная энергия камня равна

и возрастает с увеличением высоты, то есть при движении вверх, потенциальная энергия увеличивается.

Ответ: 31.

Задание 6. Массивный груз, подвешенный к потолку на пружине, совершает вертикальные свободные колебания. Пружина всё время остаётся растянутой. Как ведёт себя потенциальная энергия груза в поле тяжести и его скорость, когда груз движется вверх от положения равновесия?

Для каждой величины определите соответствующий характер изменения:

1) увеличивается

2) уменьшается

3) не изменяется

Решение.

Потенциальная энергия груза определяется выражением

,

где m – масса груза; h – высота груза над уровнем земли.

В задаче сказано, что пружина все время растянута и в этом состоянии груз движется вверх. Из формулы видно, что высота груза h увеличивается, следовательно, будет увеличиваться и потенциальная энергия груза. Скорость v тела будет уменьшаться, так как груз движется против силы тяжести и постепенно останавливается.

Ответ: 12.

Задание 6. Груз изображённого на рисунке пружинного маятника совершает свободные гармонические колебания между точками 1 и 3. Как меняется скорость груза и жёсткость пружины при движении груза маятника от точки 1 к точке 2?

Для каждой величины определите соответствующий характер изменения:

1) увеличивается

2) уменьшается

3) не изменяется

Решение.

Так как колебания совершаются между точками 1-3, то в точке 1 груз имеет нулевую скорость, а в точке 2 скорость достигает максимального значения, то есть она увеличивается. Жесткость пружины зависит от физических свойств самой пружины и является константной (неизменной) величиной.

Ответ: 13.

Задание 6. В результате торможения в верхних слоях атмосферы высота полёта искусственного спутника над Землёй уменьшилась с 400 до 300 км. Как изменились в результате этого скорость спутника и его центростремительное ускорение?

Для каждой величины определите соответствующий характер изменения:

1) увеличилась

2) уменьшилась

3) не изменилась

Решение.

Согласно закону всемирного тяготения, спутник будет притягиваться к Земле с силой

,

где m – масса спутника; M – масса Земли; R – радиус орбиты спутника. По второму закону Ньютона можно записать, что

,

где  — центростремительное ускорение спутника. Объединяя эти два выражения, имеем:

.

Из этой формулы видно, что при уменьшении радиуса орбиты R скорость спутника v и его центростремительное ускорение возрастает.

Ответ: 11.

адание 6. В результате перехода спутника Земли с одной круговой орбиты на другую его центростремительное ускорение уменьшается. Как изменяются в результате этого перехода потенциальная энергия спутника в поле силы тяжести Земли и скорость его движения по орбите?

Для каждой величины определите соответствующий характер изменения:

1) увеличивается

2) уменьшается

3) не изменяется

Решение.

Спутник Земли массой m и Земля массой M притягиваются друг к другу на расстоянии R с силой всемирного тяготения

.

В силу второго закона Ньютона данную силу также можно представить в виде

,

где  — центростремительное ускорение спутника. Объединяя уравнения, имеем:

,

откуда радиус орбиты

.

Из последней формулы видно, что при уменьшении центростремительного ускорения радиус орбиты R спутника увеличивается. Найдем как будет меняться потенциальная энергия спутника и скорость его движения по орбите.

Центростремительное ускорение можно записать как , где v – скорость движения спутника, тогда

,

откуда

,

а его потенциальная энергия определяется как гравитационная энергия, обусловленная взаимным притяжением спутника и Земли:

Последние две формулы показывают, что при увеличении R скорость спутника уменьшается, а потенциальная энергия увеличивается (обратите внимание на знак «-» перед формулой потенциальной энергии спутника).

Ответ: 12.

Задание 6. Массивный груз, подвешенный к потолку на пружине, совершает вертикальные свободные колебания. Пружина всё время остаётся растянутой. Как ведёт себя потенциальная энергия пружины и скорость груза, когда груз движется вниз от положения равновесия?

Для каждой величины определите соответствующий характер изменения:

1) увеличивается

2) уменьшается

3) не изменяется

Решение.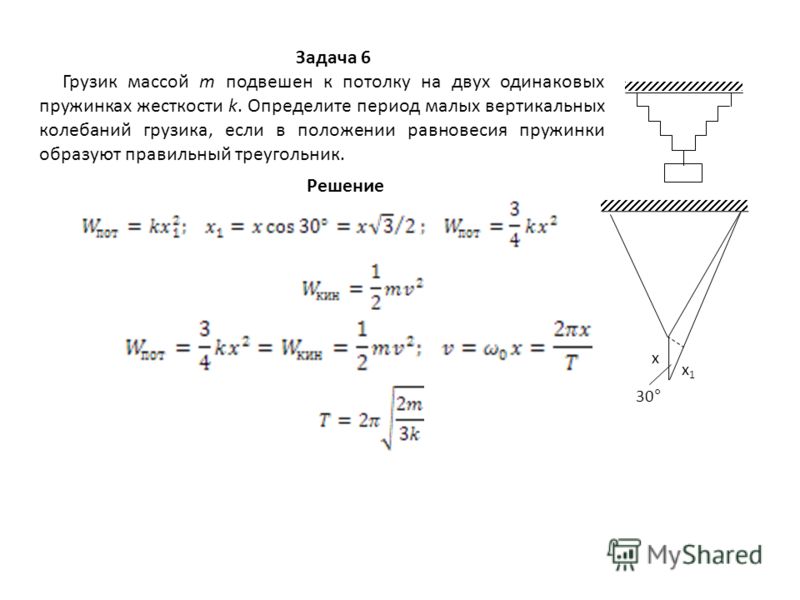

Положение равновесия – это положение с максимальной скоростью при колебательном движении груза. Следовательно, при движении от положения равновесия вниз, скорость груза уменьшается.

Потенциальная энергия пружины пропорциональна деформации пружины и, двигаясь вниз, пружина растягивается и ее потенциальная энергия увеличивается.

Ответ: 12.

Задание 6. На тело массой m, поступательно движущееся в инерциальной системе отсчёта, действует постоянная равнодействующая сила F в течение времени ∆t. Если действующая на тело сила увеличится, то как изменятся модуль импульса силы и модуль изменения импульса тела в течение того же промежутка времени ∆t?

1) увеличится

2) уменьшится

3) не изменится

Решение.

При увеличении силы F=ma ускорение тела  также увеличивается. Увеличение ускорения приводит у увеличению скорости. Следовательно, импульс тела, равный  также будет увеличиваться. Модуль изменения импульса тела  тоже увеличится, так как тело движется с постоянным ускорением , большим чем ранее, а величина  пропорциональна ускорению.

Ответ: 11.

Задание 6. На тело массой m, поступательно движущееся в инерциальной системе отсчёта, действует постоянная равнодействующая сила F в течение времени ∆t. Если действующая на тело сила уменьшится, то как изменятся модуль импульса силы и модуль ускорения тела в течение того же промежутка времени ∆t? Для каждой величины определите соответствующий характер изменения:

1) увеличится

2) уменьшится

3) не изменится

Решение.

При уменьшении силы F=ma, ускорение тела  также уменьшается. Модуль импульса силы, равный изменению импульса тела , при уменьшении ускорения уменьшится, так как конечная скорость v станет меньше.

Ответ: 22.

Задание 6. Шарик, брошенный горизонтально с высоты Н с начальной скоростью v0, за время t пролетел в горизонтальном направлении расстояние L (см. рисунок). Что произойдёт со временем и дальностью полёта, если на этой же установке увеличить начальную скорость шарика в 2 раза? Сопротивлением воздуха пренебречь. Для каждой величины определите соответствующий характер её изменения:

1) увеличится

2) уменьшится

3) не изменится

Решение.

Время полета шарика будет равно времени его падения с высоты H, так как начальная вертикальная скорость равна нулю. Поэтому, меняя начальную горизонтальную скорость шарика в 2 раза, время полета останется прежним.

При увеличении скорости в 2 раза и том же времени полета, длина L=vt увеличится вдвое.

Ответ: 31.

Задание 6. Стальной шарик висит на нитке, привязанной к штативу. Шарик целиком погружён в керосин (рис. 1). Затем стакан с керосином заменили на стакан с водой, и шарик оказался целиком в воде (рис. 2). Как изменились при этом сила натяжения нити и сила Архимеда, действующая на шарик?

 

Для каждой величины определите соответствующий характер её изменения:

1) увеличилась

2) уменьшилась

3) не изменилась

Решение.

Сила натяжения нити по модулю равна результирующей силе, действующей на шарик. На шарик действует сила тяжести mg и выталкивающая сила Архимеда , направленная в противоположную сторону, то есть результирующая сила, а значит, и натяжение нити равны:

,

где V – объем погруженного тела в жидкость;  — плотность жидкости. Так как плотность керосина равна  кг/м3, а плотность воды  кг/м3, то выталкивающая сила Архимеда в случае воды выше, чем при керосине. Следовательно, натяжение нити при замене керосина водой, уменьшится, а сила Архимеда увеличится.

Ответ: 21.

Задание 6. В школьной лаборатории изучают свободные колебания пружинного маятника при различных значениях массы маятника. Как изменятся период его свободных колебаний и период изменения его потенциальной энергии, если увеличить массу маятника, не изменяя жёсткость пружины? Для каждой величины определите соответствующий характер изменения:

1) увеличивается

2) уменьшается

3) не изменяется

Решение.

Период свободных колебаний пружинного маятника массой m и жесткостью пружины k равен . Следовательно, при увеличении массы тела m период колебаний увеличится.

Потенциальная энергия пружинного маятника определяется как , где x – величина деформации пружины. Легко понять, что при увеличении массы маятника растяжение пружины x увеличится, следовательно, увеличится и период изменения потенциальной энергии пружины.

Ответ: 11.

Задание 6. С вершины наклонной плоскости из состояния покоя скользит с ускорением лёгкая коробочка, в которой находится груз массой m (см. рисунок). Как изменятся время движения по наклонной плоскости и модуль работы силы тяжести, если с той же наклонной плоскости будет скользить та же коробочка с грузом массой m/2?

Для каждой величины определите соответствующий характер изменения:

1) увеличится

2) уменьшится

3) не изменится

Решение.

В наклонной плоскости сила тяжести коробочки, создаваемая коробочкой, равна

и противоположна ей сила трения, равная

.

Равнодействующая сил, действующая на коробочку в наклонной плоскости:

,

откуда ускорение коробочки

.

Время, за которое коробочка пройдет по наклонной плоскости, можно найти из формулы

,

откуда

,

где S – длина наклонной плоскости.

Работа силы тяжести есть величина

,

Таким образом, при уменьшении массы груза m время движения коробочки по наклонной плоскости останется прежним, а работа силы тяжести уменьшится.

Ответ: 32.

Задание 6. На поверхности воды плавает сплошной деревянный брусок. Как изменятся глубина погружения бруска и сила Архимеда, действующая на брусок, если его заменить сплошным бруском той же плотности и высоты, но большей массы? Для каждой величины определите соответствующий характер изменения:

1) увеличится

2) уменьшится

3) не изменится

Решение.

Если брусок имеет ту же плотность и высоту, то увеличение массы может осуществляться только за счет увеличения его площади основания, а глубина погружения его в воду останется прежней.

Сила Архимеда определяется как , где V – объем погруженной части тела в воду. Так как этот объем увеличивается (увеличилась площадь бруска), то и сила Архимеда возрастет. Этот же вывод можно сделать на том основании, что сила Архимеда должна компенсировать силу тяжести бруска и так как его масса возрастает, то и сила тяжести mg также возрастет.

Ответ: 31.

Потенциальная энергия (гравитационная и пружинная)

Все физические ресурсы MCAT

8 диагностических тестов 303 практических теста Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 Следующая →

Физическая помощь MCAT » Физика » Ньютоновская механика и движение » Работа, энергия и мощность » Потенциальная энергия (гравитационная и пружинная)

Пружина в автомате для игры в пинбол сжимается из положения равновесия. Его выпускают, и он запускает пинбол со скоростью в игру.

Никакая энергия не теряется на трение, и вся энергия пружины передается пинболу. Какова жесткость пружины?

Возможные ответы:

Правильный ответ:

Объяснение:

Энергия пружины определяется уравнением , где  – постоянная пружины, а   – смещение от положения равновесия. Энергия передается в кинетическую энергию в пинболе.

Кинетическая энергия пинбола находится по уравнению.

Теперь, когда у нас есть кинетическая энергия, мы можем найти равную энергию, которая была запасена весной, чтобы начать.

Сообщить об ошибке

Груз массой 2 кг прикреплен к невесомой пружине с постоянной силой 100 Н/м. Система опирается на горизонтальную поверхность без трения. Какова максимальная скорость груза, если пружину сжать на 5 см, а затем разжать?

Возможные ответы:

25 см/с

35,4 см/с

12,5 см/с

50 см/с

10,2 см /с

Правильный ответ:

35,4 см/с

Пояснение:

Используйте закон сохранения энергии, чтобы сравнить точку максимального сжатия и точку максимальной скорости.

При максимальном сжатии вся энергия является потенциальной энергией пружины, где , а при максимальной скорости вся энергия является кинетической, где . Поскольку энергия должна сохраняться, эти две энергии должны быть равны: .

Подстановка данной информации для E s и решение для v дает следующую серию вычислений:

Сообщить об ошибке

Если к пружине с коэффициентом упругости 20 Н/м и сжатой на 0,1 м прикреплен шарик, какова общая энергия колебаний?

Возможные ответы:

Правильный ответ:

Объяснение:

Полная энергия простой гармонической колебательной системы может быть определена уравнением  . А – амплитуда колебаний, k — жесткость пружины, а E — полная энергия. Подставляя значения, данные уравнением, полная энергия равна 0,1 Дж.

Сообщить об ошибке

Невесомая пружина лежит горизонтально на столе, ее правый конец прикреплен к блоку, а левый конец прикреплен к стене. Затем блок прижимается к пружине, сжимая ее из положения равновесия. После освобождения скорость блока при его движении назад через точку равновесия равна . Какова жесткость этой пружины?

Возможные ответы:

Правильный ответ:

Объяснение:

Используйте закон сохранения энергии, чтобы приравнять начальную потенциальную энергию пружины и конечную кинетическую энергию:

Начальная ситуация определяется, когда пружина и блок сжимаются, а конечная ситуация определяется, когда блок движется обратно через точку равновесия. Для пружины потенциальная энергия максимальна, когда пружина сжата, а кинетическая энергия максимальна, когда масса достигает равновесия. Мы можем составить уравнение, основанное на этих факторах.

Используйте уравнения для потенциальной энергии пружины и для кинетической энергии, чтобы включить в уравнение соответствующие переменные.

Нам даны значения смещения, массы и конечной скорости. Используя эти значения, мы можем выделить постоянную пружины.

Сообщить об ошибке

Брусок массой , прикреплен к пружине с жесткостью . Пружина сжимается на максимальное расстояние и отпускается. Какой максимальной скорости достигнет брусок после отпускания пружины?

Возможные ответы:

Правильный ответ:

Объяснение:

Потенциал пружины задается уравнением, а уравнение для кинетической энергии задается уравнением .

Когда  находится на максимальном расстоянии (амплитуда), скорость равна нулю, а пружина имеет ТОЛЬКО потенциальную энергию. Когда он высвобождается, полная энергия является частично кинетической и частично потенциальной. Когда амплитуда равна нулю (равновесие), скорость максимальна и вся потенциальная энергия преобразуется в кинетическую энергию. Затем мы можем приравнять два уравнения друг к другу, чтобы найти максимальную скорость.

Сообщить об ошибке

Одна плитка шоколада содержит . Как высоко можно поднять штангу, используя энергию, содержащуюся в этом шоколадном батончике?

Возможные ответы:

Правильный ответ:

Пояснение:

Наш первый шаг — перевести килокалории в джоули.

Теперь, когда мы перевели в стандартные единицы, мы можем использовать формулу для гравитационной потенциальной энергии, чтобы найти высоту.

Мы знаем наш предел энергии из шоколадного батончика, массы штанги и гравитационного ускорения.

Решите, чтобы изолировать высоту.

Обратите внимание, что мы получаем километры, потому что в наших расчетах мы использовали килоджоули.

Сообщить об ошибке

Груз массой 2 кг подвешен на веревке, которая наматывается на безфрикционный шкив, прикрепленный к потолку с массой 0,01 кг и радиусом 0,25 м. Другой конец веревки прикреплен к невесомой подвесной платформе, на которую можно поместить груз массой 0,5 кг. В то время как система изначально находится в равновесии, веревка позже перерезается над весом, а платформа впоследствии поднимается, потянув за веревку.

После того, как веревка перерезана и платформа падает, мы хотим поднять платформу на 5 м над землей. Сколько энергии требуется, чтобы поднять платформу?

Возможные ответы:

98J

200J

75J

50J

Правильный ответ: 9 0005

98J

Пояснение:

Во-первых, нам нужно понять, какой тип энергии мы рассматриваем. Поскольку сила сопротивления движению обусловлена ​​гравитацией, мы говорим о гравитационной потенциальной энергии. Нам нужно использовать формулу U = mgh.

Подставляя предоставленные значения, мы можем найти потенциальную энергию (U).

U = (2 кг)(9,8 м/с 2 )(5 м) = 98 Дж

Количество необходимой работы равно изменению потенциальной энергии платформы.

Сообщить об ошибке

Два ученика (ученик X и ученик Y) поднимают валун вертикально из точки A в точку B. Учащийся X поднимает валун непосредственно из точки A в точку B, тогда как учащийся Y использует шкив для подъема валуна . Это позволяет студенту Y применить силу (), которая в три раза меньше, чем сила, приложенная студентом X (). Оба ученика прикладывают усилие вверх и выполняют это задание за одинаковое время.

Расстояние по вертикали между точкой A и точкой B равно .

Ученик Z использует наклонную плоскость, чтобы поднять валун, и прилагает только треть усилия. Какая из следующих величин не равна для студента Z и студента X?

I. Изменение потенциальной энергии

II. Пройденное расстояние

III. Сумма изменения кинетической энергии и изменения потенциальной энергии

Возможные ответы:

Только II

Только I

I и II

I и III

Правильный ответ:

Только II

Пояснение:

Изменение потенциальной энергии определяется как:

Это означает, что потенциальная энергия зависит только от изменения высоты по вертикали, которая одинакова для обоих учеников. Поскольку оба студента проходят одинаковое расстояние, изменение потенциальной энергии одинаково, и утверждение I верно.

Студент X поднимает валун напрямую, тогда как ученик Z использует наклонную плоскость. Учащийся Z скользит по валуну на большее расстояние, чем учащийся X, даже если их общее перемещение становится равным; следовательно, утверждение II неверно.

Напомним, что сумма изменения кинетической энергии и изменения потенциальной энергии равна работе, которая одинакова для обоих студентов (работа не зависит от пути в гравитационном поле). Суммарная работа обоих студентов будет одинаковой, и утверждение III будет верным.

Единственным утверждением, которое не одинаково для обоих студентов, является утверждение II.

Сообщить об ошибке

Свинцовый шар массой 2 кг загружен в пружинную пушку, которая установлена ​​на платформе под углом 45º. Пружина имеет жесткость 100 Н/м, а система шариков и пружин сжимается на 1 м перед пуском. Пока шар находится в полете, сопротивлением воздуха можно пренебречь, и шар заканчивает свой полет, приземляясь на подушку, расположенную на некотором расстоянии от пушки.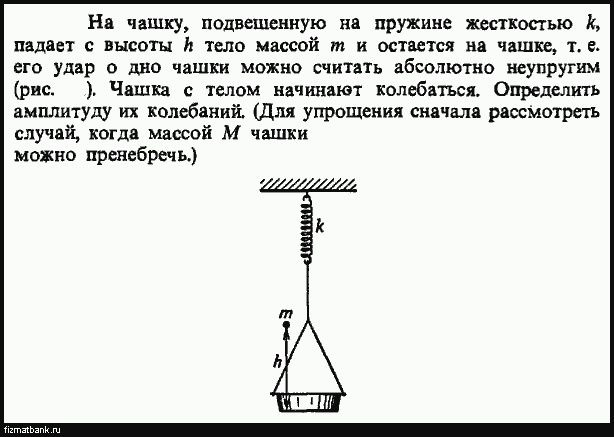

Сколько энергии накапливается в пружине до того, как мяч будет запущен?

Возможные ответы:

50 кДж

50 Дж

20 кДж

20 Дж

Правильный ответ:

50Дж

Объяснение:

Чтобы определить, сколько энергии хранится, нам сначала нужно понять, какой тип энергии мы хотим учитывать. Пружина хранит потенциальную энергию; потенциальная энергия пружины максимальна при максимальном смещении из состояния покоя. Чтобы вычислить накопленную потенциальную энергию, нам нужны как жесткость пружины (100 Н/м), так и смещение из состояния покоя (1 м).

PE s = ½k(Δx) 2 = ½(100 Н/м)(1м) 2 = 50 Дж

Сообщить об ошибке

Двое детей играют с санками на заснеженном холме. Сэм весит 50 кг, а его сани весят 10 кг. Салли весит 40 кг, а ее сани весят 12 кг. Когда они прибывают, они взбираются на холм в ботинках. На полпути к 50-метровому холму Салли поскальзывается и скатывается вниз. Сэм продолжает восхождение, и в конце концов Салли присоединяется к нему наверху.

Затем они решают спуститься с холма на санях, но спорят о том, кто поедет первым.

Сценарий 1:

Сэм спускается с холма первым, утверждая, что он достигнет более высокой скорости. Сэм говорит, что если бы Салли пошла первой, они могли бы столкнуться.

Сценарий 2:

Салли спускается с холма первой, утверждая, что она будет испытывать меньшее трение и, таким образом, достигнет более высокой скорости. Салли говорит, что если бы Сэм пошел первым, они могли бы столкнуться.

Сценарий 3:

Не в силах договориться, Сэм и Салли связывают себя веревкой и вместе спускаются вниз.

Сколько потенциальной энергии у Салли на вершине холма на ее санях?

Возможные ответы:

260 Дж

2,6 кДж

26 000 кДж

260000 Дж

26 кДж

Правильный ответ:

26 кДж

Объяснение:

Это сложный вопрос только потому, что вам нужно держать свои юниты прямо. Формула проста: PE = mgh.

PE = 52 кг * 10 м/с 2 * 50 м = 26 000 Дж = 26 кДж

Сообщить об ошибке

← Назад 1 2 Далее →

Уведомление об авторских правах

Все физические ресурсы MCAT

8 Диагностические тесты 303 практических теста Вопрос дня Карточки Learn by Concept

Наборы задач «Векторы и силы»

Калькулятор, версия 2

Вы просматриваете устаревшую версию Калькулятора. Недавно мы переработали и улучшили Калькулятор. Версия 2 уже доступна!  Мы увеличили количество задач более чем в три раза, разбили каждую часть на несколько небольших однотематических наборов задач и использовали генератор случайных чисел для предоставления числовой информации по каждой задаче. Ответы учащихся оцениваются автоматически, а обратная связь осуществляется мгновенно. И мы сохранили такое же обязательство предоставлять помощь через ссылки на существующие ресурсы. В то время как БЕСПЛАТНАЯ версия делает все вышеперечисленное, учителя с подпиской на Task Tracker могут пойти еще дальше. Они могут модифицировать наши готовые наборы задач, писать свои собственные задачи с помощью нашего простого в использовании Конструктора задач и использовать планшет для разработки собственной программы, выражающей их акцент на использовании математики в физике.

Вернитесь на главную страницу, чтобы перейти к Версии 2. Узнайте больше о Версии 2. Или посетите Магазин, чтобы совершить покупку с помощью средства отслеживания задач.

Векторы и силы в 2D: набор задач

Задача 1:

Для каждого набора перечисленных сил определите векторную сумму или результирующую силу.

Комплект A
58 Н, вправо
42 Н, влево
98 Н, вверх
98 Н, вниз

Набор В
14 Н, влево
16 Н, вверх
16 Н, вниз

Комплект C
12 Н, вверх
8 Н, вниз

  • Решение со звуковым сопровождением
Задача 2:

Гектор выгуливает свою собаку (Фидо) по окрестностям. Прибыв в дом Фиделлы (друга Фидо), Фидо превращается в мула и отказывается продолжать прогулку. Гектор дергает цепь с силой 67,0 Н под углом 30,0° к горизонтали. Определить горизонтальную и вертикальную составляющие силы натяжения.

  • Аудиогид
Задача 3:

Хелен занимается парасейлингом. Она сидит в привязи, которая прикреплена буксировочным тросом к катеру. Канат образует с горизонтом угол 51° и имеет натяжение 350 Н. Определить горизонтальную и вертикальную составляющие силы натяжения.

  • Аудиогид
Задача 4:

В один момент во время обхода квартала на Фидо действуют четыре силы — собака массой 10,0 кг. Силы:

F app = 67,0 Н на 30,0° над горизонтом (вправо и вверх)
F норма = 64,5 Н, вверх
F трение = 27,6 Н, влево
F грав = 98 Н, вниз

Разделите приложенную силу (F , приложение ) на горизонтальную и вертикальную составляющие, затем сложите силы в виде векторов, чтобы определить результирующую силу.

  • Аудиогид
Задача 5:

Джером и Майкл, полузащитники университетской футбольной команды Саута, нанесли сильный удар полузащитнику в игре на прошлых выходных. Нанесение ударов по полузащитнику одновременно с разных направлений со следующими силами:

F Джером = 1230 Н при 53°
F Майкл = 1450 Н при 107°

Определите результирующую силу, приложенную Джеромом и Майклом к ​​полузащитнику. (Направления двух сил указаны как углы поворота против часовой стрелки с востоком.)

  • Решение с аудиогидом
Задача 6:

Стая из трех арктических волков дерется за тушу мертвого белого медведя. Вид сверху на величину и направление трех сил показан на диаграмме справа.

а. Определите равнодействующую или результирующую силу, действующую на каркас.
б. Определить ускорение туши белого медведя массой 750 кг.

  • Аудиогид
Задача 7:

Ли Милон катается на санках со своими друзьями. Раздраженный грубым комментарием, он решает отделиться от группы. На мгновение он прикладывает силу 31 Н к веревке, прикрепленной к его 2,5-килограммовым саням. Веревка образует угол 22° с почти полностью лишенной трения поверхностью. Используйте приведенную ниже структуру, чтобы определить результирующую силу, действующую на сани, и ускорение.

  • Аудиогид
Задача 8:

Рене на весенних каникулах тащит свой 21-килограммовый чемодан через аэропорт с постоянной скоростью 0,47 м/с. Она тянет лямку с силой 120 Н под углом 38° к горизонтали. Определите нормальную силу и общую силу сопротивления (трения и сопротивления воздуха), испытываемую чемоданом.

  • Аудиогид
Задача 9:

Бен Лейборин работает в южном книжном магазине в летние месяцы, помогая подготовиться к осенним распродажам. Книги от одного поставщика доставляются в школу в больших ящиках, снабженных веревочными ручками со всех сторон. Однажды Бен на мгновение потянул с силой 692 Н под углом 36,0° над горизонтом для ускорения ящика с книгами массой 112 кг. Коэффициент трения между ящиками и виниловым полом составляет 0,548. Определить ускорение, которое испытывает ящик. (Предложение: начните со свободной диаграммы тела.)

  • Решение с аудиогидом
Задача 10:

В высотном здании вспыхивает пожар, на место происшествия вызывается спасательный вертолет. Вертолет оснащен спасательной корзиной, прикрепленной прочным тросом к лебедке на вертолете. Спасательная корзина опускается на крышу, и некоторые обитатели верхнего этажа сбегают на крышу и входят в корзину. Когда вертолет взлетает, трос на мгновение образует угол 78,2° с горизонталью, придавая небольшое горизонтальное ускорение 621-килограммовой корзине и пассажирам на крыше. Коэффициент трения между корзиной и крышей равен 0,568, а натяжение троса равно 49.80 Н. Определите ускорение корзины и пассажиров. (Предложение: начните со свободной диаграммы тела.)

  • Решение с аудиогидом
Задача 11:

Смотрители моют пол спортзала между играми на ежегодном празднике баскетбольной классики. Чак воздействует на метлу массой 1,1 кг, когда он идет по полу с постоянной скоростью. Коэффициент трения между полом и метлой равен 0,45, а ручка метлы образует с горизонтом угол 41°. Определите величину силы, с которой Чак толкает вниз (вдоль ручки метлы), чтобы добиться этого движения с постоянной скоростью. (Предложение: начните с диаграммы свободного тела.)

  • Аудиогид
Задача 12:

Лон Мауэр убирает подъездную дорожку после скашивания травы. Он прикладывает внезапную направленную вниз силу 56,8 Н под постоянным углом 54,7° ниже горизонтали, чтобы разогнать свою 1,05-килограммовую метлу из состояния покоя. Коэффициент трения между щетиной метлы и подъездной дорожкой равен 0,567. Определить скорость ускорения метлы. (Предложение: начните со свободной схемы тела.)

  • Решение с аудиогидом
Задача 13:

Юг до сих пор с большой гордостью демонстрирует большую вывеску с изображением женской баскетбольной команды чемпионата штата 1996 года. Знак весом 43,1 кг висит на двух тросах, образующих угол 34,5° с горизонтом. Определить натяжение каждого троса.

  • Аудиогид
Задача 14:

Огромный светильник висит над столом в столовой Джереми. Свет поддерживается четырьмя прочными цепями, которые образуют с горизонтом угол 75,0°. Усилие в каждой цепи 35,8 Н.

а. Определить силу, с которой одна цепь тянет горизонтально и вертикально на свет.
б. Определите массу фонаря.

  • Аудиогид
Задача 15:

Трой Джинометри, владелец местного цветочного магазина, показывает распродажу месяца на витрине своего магазина. Цветочный горшок весом 5,6 кг подвешен на трех цепях к потолку. Цепи составляют угол 25° с вертикалью. Определить натяжение одной из цепей.

  • Аудиогид
Задача 16:

Исторический Центр искусств Стэнли в Ютике, штат Нью-Йорк, является гордым владельцем самой большой в мире светодиодной люстры. Люстра имеет ширину 35 футов, высоту 17 футов и массу 2900 кг. Он напрямую поддерживается четырьмя тросами, образующими с горизонталью угол 63°. Определить натяжение тросов.

  • Аудиогид
Задача 17:

На прошлых выходных Ксавье занимался скалолазанием. Во время одного подъема через узкую вертикальную трубу он поддерживал свой вес, опираясь спиной на одну стенку трубы и отталкиваясь ногами от противоположной стены. Его левая нога составляла угол 26° с горизонтом. Коэффициент трения между его спиной и стенкой дымохода равен 0,508. Определите минимальное усилие, которое потребуется, чтобы выдержать вес его тела массой 86 кг.

а. Определите напряжение в его левой ноге.
б. Определите нормальную силу, при которой стенка дымохода давит на его спину.

  • Аудиогид
Задача 18:

Шарль Блонден известен тем, что пересек Ниагарский водопад по натянутому канату длиной 1100 футов на высоте 160 футов над ущельем. Ноги он совершал несколько раз разными способами – с завязанными глазами, в мешке, неся своего менеджера на плечах, толкая тачку и идя на ходулях. Предположим, что 65-килограммовый Блондин находится в середине натянутой веревки и остановился, чтобы приготовить и съесть омлет. Если канат образует с горизонтом угол 5°, определить натяжение каната.

  • Аудиогид
Задача 19:

Мама и папа привязали веревку к санкам Мэтью и на мгновение тянут его по снегу. Папа тянет с силой A, а мама с силой B.

A: 54 N на 65° к северу от востока
B: 130 N на 22° к югу от востока

a. Определить равнодействующую сил А и В.
b. Определите ускорение, которое эти мгновенные силы создадут для санок массой 39 кг и ребенка (при условии пренебрежимо малого трения).

  • Аудиогид
Проблема 20:

Местный автомобильный дилер решил повесить автомобиль у входа в свой выставочный зал. Автомобиль был модифицирован так, что его масса составляет 645 кг. Вес автомобиля будет поддерживаться мощной цепью, которая будет тянуться вверх и влево. Балка выдвинется наружу, чтобы уравновесить натяжение цепи к стене . Производитель цепи утверждает, что ее прочность на разрыв составляет 17400 ньютонов. Кодекс деревни требует наличия коэффициента безопасности 2,20. То есть фактическое натяжение цепи должно быть не более 1/2,20 разрывного усилия. Каков минимальный угол (между цепью и горизонтальный ) на каком автосалоне можно повесить машину?

  • Аудиогид
Задача 21:

Партнеры лаборатории Анна Литикал и Ноа Формула поместили планер весом 0,500 кг на свою воздушную гусеницу и наклонили гусеницу под углом 15,0° над горизонталью. Определить результирующую силу и ускорение планера на пути без трения. Используйте структуру, предоставленную диаграммой свободного тела, показанной ниже.

  • Решение для аудиогида
Задача 22:

Анна Литикал и Ноа Формула теперь положите кирпич весом 1,38 кг на деревянную доску и наклоните доску под углом 24,0° над горизонталью. Коэффициент трения между кирпичом и доской равен 0,328. Определить результирующую силу и ускорение кирпича. Используйте структуру, предоставленную диаграммой свободного тела, показанной ниже.

  • Аудиогид
Задача 23:

Бен Лаборин прикладывает силу к 86-килограммовому ящику с книгами, толкая его вверх по пандусу погрузочной площадки с постоянной скоростью 24 см/с. Рампа составляет угол 12° с горизонтом. Коэффициент трения между обрешеткой и пандусом равен 0,74. Считая, что Бен давит параллельно наклонной плоскости, определите силу, с которой он давит. (Предложение: начните с диаграммы свободного тела.)

  • Аудиогид
Задача 24:

На печально известной Ломбард-стрит в Сан-Франциско есть аномально крутой квартал, состоящий из нескольких крутых крутых поворотов. В среднем проезжая часть на этом квартале улицы имеет уклон 16°. Определите силу, которая потребуется, чтобы тянуть тележку массой 23 кг с ребенком в гору с постоянной скоростью. Предположим, что сила приложена параллельно дороге и трением можно пренебречь.

  • Решение для аудиогида
Задача 25:

Пытаясь определить коэффициент трения между деревянным бруском и металлической гусеницей, Анна Литикал и Ноа Формула помещают брусок на рельс и медленно поднимают один из его концов, пока брусок, наконец, не сдвинется с места. и скользит вниз по склону. Анна и Ной повторяют несколько попыток и определяют, что блок ускоряется из исходного положения, когда гусеница образует угол 38° над горизонтом. Используйте это значение угла, чтобы определить коэффициент трения. (Предложение: начните с диаграммы свободного тела.)

  • Аудиогид
Задача 26:

Аттракцион Splash Mountain в Волшебном королевстве Уолта Диснея в Орландо, штат Флорида, может похвастаться одним из самых крутых желобов в мире. Лодки погружаются на 52 фута вниз по склону под углом 43 градуса ближе к заключительному этапу поездки. Приняв коэффициент трения 0,12, определить ускорение лодки и всадников.