10 советов по выполнению Task 1 и Task 2
IELTS Writing Task 1 и Task 2 – это описание графика или схемы и написание эссе, соответственно. Как выполнить секцию Writing in IELTS , не допустив самых распространенных ошибок кандидатов? Представляем вашему вниманию десять эффективных советов по выполнению письменной части теста.
Внимательно прочтите задание – лишь потом приступайте к его выполнению.
Ваша задача – ответить на поставленный вопрос. Сосредоточьтесь, а затем внимательно прочтите задание, подчеркните всю информацию, которую собираетесь употребить. Однако в отношении эссе и описания это правило действует по-разному.
В задании к
эссе IELTS
очень часто вся исходная информация уже представлена вместе с вопросом. Убедитесь, что вы отвечаете на конкретный вопрос (например, «Согласны ли вы?»), а не пишете текст «на тему». Если вы скопируете другое свое эссе, написанное на заданную тему — потеряете много баллов.
В первом же задании вся необходимая информация представлена в графике/схеме: прежде чем приступить к описанию, убедитесь, что вы правильно определили основные моменты.
IELTS Writing: инфографика на mbaconsult.ru
Инфографика в полном размере
Не торопитесь! Лучше обдумайте все как следует.
Безусловно, очень важно выполнить оба задания секции Writing, но это не значит, что нужно немедленно приступать к письму. В спешке вы можете написать половину эссе и понять, что не можете его завершить. Начинайте писать только тогда, когда точно знаете, чем закончится ваше повествование.
Для эссе время на обдумывание плана может занять до десяти минут, а в первом задании на это может уйти пять минут. Чем тщательнее вы все обдумаете, тем качественнее и быстрее вы выполните задания.
Не пишите слишком кратко.
Указанные 250 слов во втором задании говорят о том, что необходимо написать по меньшей мере 250 слов, а 150 – минимум 150. Краткость, конечно – сестра таланта. Но не в данном случае!
Краткость, конечно – сестра таланта. Но не в данном случае!
Не пишите слишком много.
Чем больше вы напишете – тем больше у вас шансов допустить ошибки. Больше слов – меньше дела, текст станет менее конкретным и его качество неумолимо снизится. В идеале, вы должны стремиться к написанию эссе, состоящему из 260-280 слов, и описания графика/схемы из 160-180 слов.
Не переписывайте задание дословно.
Если вы целиком перепишете задание – экзаменатор не засчитает эти слова при общем подсчете: так что ваши 260 слов могут превратиться в 230, если вы будете недостаточно внимательны.
Время – ваш враг! Вооружитесь часами и планом действий.
С распределением времени могут возникнуть проблемы. Очень важно следовать плану и ни в коем случае не сбиваться и не останавливаться. Не тратьте на эссе более 40 минут, а на должное выполнение первого задания вам хватит 20 минут.
Эссе и описание графика/схемы – какое задание выполнить первым?
За эссе можно получить вдвое больше баллов, чем за описание графика/схемы.
Проверьте то, что написали.
Крайне важно проверить свои тексты на наличие грамматических ошибок. Перед тем как официально сдавать экзамен, составьте список ваших самых часто встречающихся ошибок.
Расширяйте словарный запас.
В письменной части теста IELTSвам необходимо продемонстрировать богатство лексикона. Поэтому проверьте также свои работы на наличие в них «слов-паразитов» и часто повторяющихся слов. Это не значит, что вы должны использовать длинные многосложные конструкции: наоборот, употребляйте точные слова.
Помните об экзаменаторах – в тексте должны присутствовать абзацы.
Проверка вашего эссе или описания графика/схемы не займет у экзаменатора много времени. Ваши работы должны сразу же вызвать положительную реакцию у экзаменатора и оставить о себе хорошее впечатление. Лучший способ этого достичь – предоставить хорошо структурированный текст с выделенными абзацами. Экзаменатор это оценит по достоинству. Однако если тексты выглядят небрежно, имеют нечеткую структуру – это не будет вам в плюс.Примерное введение и структура эссе:
Ваши работы должны сразу же вызвать положительную реакцию у экзаменатора и оставить о себе хорошее впечатление. Лучший способ этого достичь – предоставить хорошо структурированный текст с выделенными абзацами. Экзаменатор это оценит по достоинству. Однако если тексты выглядят небрежно, имеют нечеткую структуру – это не будет вам в плюс.Примерное введение и структура эссе:
Ещё три простых подсказки, как справиться с IELTS Writing Task 1 – смотрите в этом видео:
У вас всегда есть возможность осуществить подготовку к IELTS онлайн или с репетитором. Пройдите письменную часть теста, применяя этих советы – и вы увидите результат!
По материалам: www.dcielts.com
| ФУКНЦИЯ | |||
|---|---|---|---|
| Описания | Комментарии | ||
| abschange | |||
Абсолютная разница между последним и предыдущим значениями.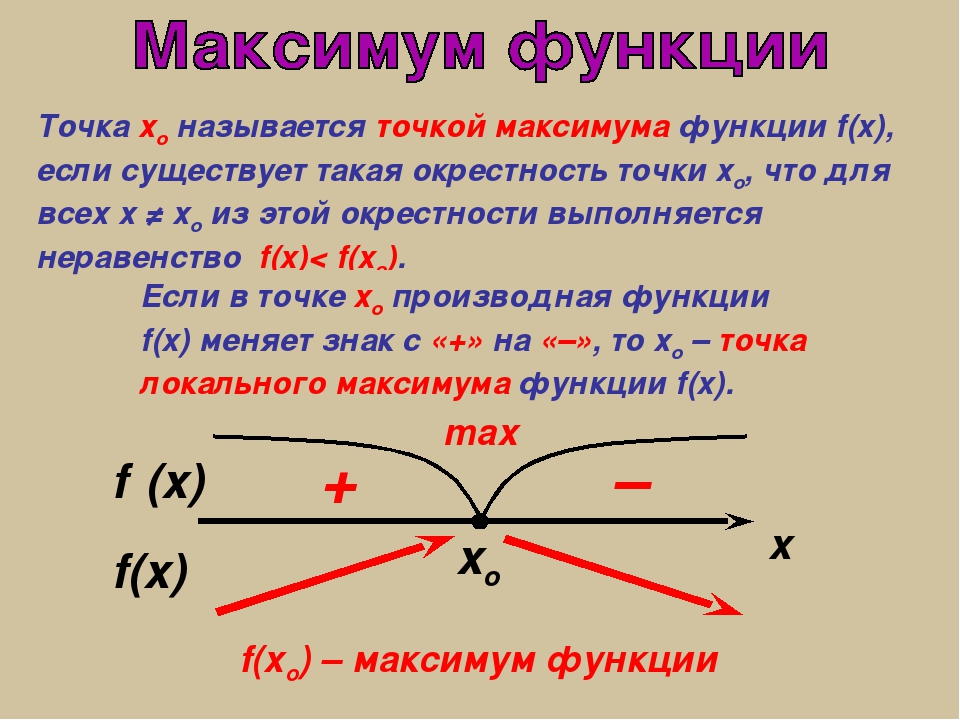 | Поддерживаемые типы значений: float, int, str, text, log Например: Результат для строк: | ||
| avg (сек|#кол-во,<сдвиг_времени>) | |||
| Среднее значение элемента данных за указанный период времени. | сек или кол-во — период вычисления в секундах или в последних собранных значениях (начинается с решетки) сдвиг_времени (опционально) — точка вычисления перемещается на указанное количество секунд назад во времени | Поддерживаемые типы значений: float, int Примеры: Параметр | |
| band (сек|#кол-во,маска,<сдвиг_времени>) | |||
| Значение “побитового И” от значения элемента данных и маски. | сек (игнорируется) или кол-во — N-ое наиболее новое значение маска (обязательна) — 64-битное целое число (0 — 18446744073709551615) сдвиг_времени (опционально) — см. функцию avg() | Обратите внимание, что Хотя сравнение выполняется побитовым образом, все значения должны подставляться и возвращаться в десятичном виде. Например, выполнение проверки 3-го бита, сравнением с 4, не со 100. Примеры: Эта функция поддерживается начиная с Zabbix 2.2.0. | |
| change | |||
| Величина разницы между последним и предыдущим значениями. | Поддерживаемые типы значений: float, int, str, text, log Например: Смотрите также: abschange для сравнения Для строк: | ||
| count (сек|#кол-во,<шаблон>,<оператор>,<сдвиг_времени>) | |||
| Количество собранных значений за указанный период вычисления. | сек или кол-во — период вычисления в секундах или в последних собранных значениях (начинается с решетки) оператор (опционально) Поддерживаемые Обратите внимание: eq (по умолчанию), ne, gt, ge, lt, le, regexp, iregexp поддерживаются числовыми с плавающей точкой элементами данных like (по умолчанию), eq, ne, regexp, iregexp поддерживаются строковыми, текстовыми и журнальными элементами данных сдвиг_времени (опционально) — смотрите avg() | Поддерживаемые типы значений: float, integer, string, text, log Элементы данных с плавающей точкой совпадают с точностью до 0.  000001. 000001.При наличии band третьим параметром, второй параметр При наличии regexp или iregexp третьим параметром, второй параметр Примеры: Параметр | |
| date | |||
| Текущая дата в формате ГГГГММДД. | Поддерживаемые типы значений: любые Пример результата: 20150731 | ||
| dayofmonth | |||
| День месяца в диапазоне от 1 до 31. | Поддерживаемые типы значений: любые Эта функция поддерживается начиная с Zabbix 1.8.5. | ||
| dayofweek | |||
| День недели в диапазоне от 1 до 7 (Пн — 1, Вс — 7). | Поддерживаемые типы значений: любые | ||
| delta (сек|#кол-во,<сдвиг_времени>) | |||
Разницы между максимальным и минимальным значениями за указанный период вычисления (‘max()’ минус ‘min()’). | сек или #кол-во — период вычисления в секундах или в последних собранных значениях (начинается с решетки) сдвиг_времени (опционально) — смотри avg() | Поддерживаемые типы значений: float, int Параметр | |
| diff | |||
| Проверка, различаются ли последнее и предыдущее значения. | Поддерживаемые типы значений: float, int, str, text, log Возвращает: | ||
| forecast (сек|#кол-во,<сдвиг_времени>,время,<аппроксимация>,<режим>) | |||
| Будущее значение, макс, мин, дельта или сред элемента данных. | сек или #кол-во — указывается период вычисления в секундах или в количестве собранных значений (начинается с решетки) сдвиг_времени (опционально) — см.  функцию avg() функцию avg()время — горизон предсказания в секундах аппроксимация (опционально) — используемая функция для аппроксимации данных истории Поддерживаемые Обратите внимание, что: режим (опционально) — запрашиваемый вывод Поддерживаемые Обратите внимание: | Поддерживаемые типы значений: float, int Если возвращаемое значение больше чем 999999999999. Становится не поддерживаемым только, если в выражении имеется злоупотребление (ошибочный тип элемента данных, некорректные параметры), в противном случае возвращает -1 в случае ошибок. Примеры: Эта функция поддерживается начиная с Zabbix 3. | |
| fuzzytime (сек) | |||
| Проверка, на сколько отличается штамп времени значения элемента данных от времени Zabbix сервера. | сек — секунды | Поддерживаемые типы значений: float, int Возвращает: Обычно используется с system.localtime для проверки, что локальное время синхронизировано с локальным временем Zabbix сервера. Пример: | |
| iregexp (шаблон,<сек|#кол-во>) | |||
Функция нечувствительный к регистру аналог функции regexp(). | смотри regexp() | Поддерживаемые типы значений: str, log, text | |
| last (сек|#кол-во,<сдвиг_времени>) | |||
| Самое новое значение. | сек (игнорируется) или #кол-во — N-ое самое новое значение сдвиг_времени (опционально) — смотри avg() | Поддерживаемые типы значений: float, int, str, text, log Обратите внимание, что Zabbix не гарантирует точный порядок значений, если в истории существуют более двух значений менее чем за секунду.. Параметр | |
| logeventid (шаблон) | |||
Проверка, совпадает ли ID события последней записи из журнала указанному регулярному выражению. | шаблон — регулярное выражение описывающее требуемый шаблон, в формате Perl совместимых регулярных выражений (PCRE). | Поддерживаемые типы значений: log Возвращает: Эта функция поддерживается начиная с Zabbix 1.8.5. | |
| logseverity | |||
| Важность события последней записи в журнале. | Поддерживаемые типы значений: log Возвращает: | ||
| logsource (шаблон) | |||
Проверка, соответствует ли регулярному выражению источник последней записи в журнале.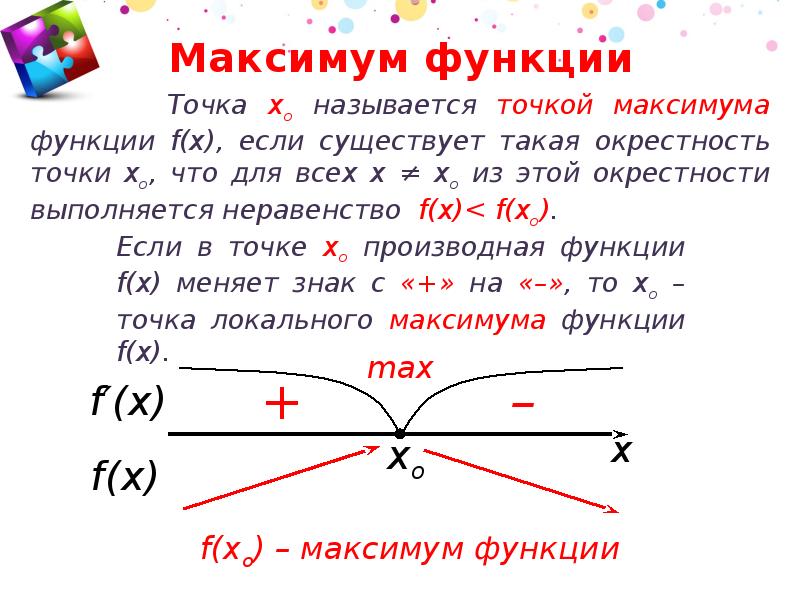 | шаблон — регулярное выражение в виде Perl совместимого регулярного выражения (PCRE), которое описывает необходимый шаблон. | Поддерживаемые типы значений: log Возвращает: | |
| max (сек|#кол-во,<сдвиг_времени>) | |||
| Максимальное значение за указанный период вычисления. | сек или #кол-во — период вычисления в секундах или в последних собранных значениях (начинается с решетки) сдвиг_времени (опционально) — смотри avg() | Поддерживаемые типы значений: float, int Параметр | |
| min (сек|#кол-во,<сдвиг_времени>) | |||
Минимальное значение за указанный период вычисления.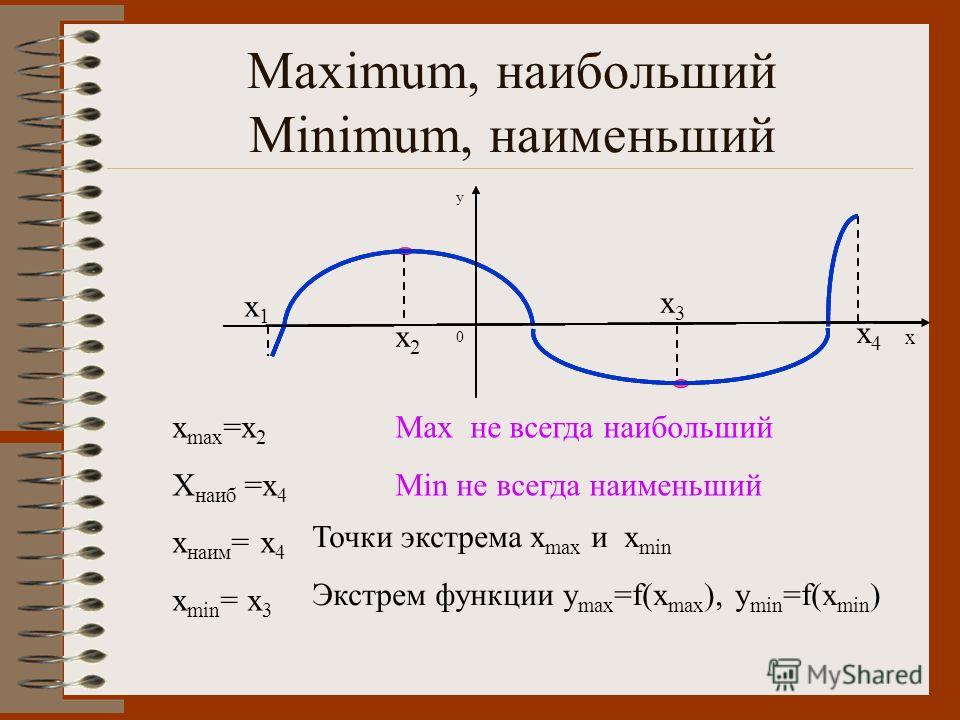 | сек или #кол-во — период вычисления в секундах или в последних собранных значениях (начинается с решетки) сдвиг_времени (опционально) — смотри avg() | Поддерживаемые типы значений: float, int Параметр | |
| nodata (сек) | |||
| Проверка, отсутствия полученных данных. | сек — период вычисления в секундах. Период не должен быть меньше 30 секундам, так как процесс синхронизации истории вычисляет эту функцию каждые 30 секунд. nodata(0) запрещена начиная с Zabbix 3.2.2. | Поддерживаемые типы значений: любые Результат: Обратите внимание, эта функция отобразит ошибку в случае, если за указанный период в первом параметре: | |
| now | |||
| Количество секунд начиная с Epoch (00:00:00 UTC, 1 Января, 1970). | Поддерживаемые типы значений: любые | ||
| percentile (сек|#кол-во,<сдвиг_времени>,процент) | |||
| P-ый процентиль за период, где P (процент) задается третьим параметров. | сек или #кол-во — период вычисления в секундах или в последних собранных значениях (начинается с решетки) time_shift (опционально) — см. функцию avg() процент — число с плавающей точкой между 0 и 100 (включительно) с точностью до 4 цифр после десятичной точки | Поддерживаемые типы значений: float, int Эта функция поддерживается начиная с Zabbix 3. | |
| prev | |||
| Предыдущее значение. | Поддерживаемые типы значений: float, int, str, text, log Результатом является то же самое, что и last(#2). | ||
| regexp (шаблон,<сек|#кол-во>) | |||
| Проверка, совпадает ли последне (самое новое) значение с регулярным выражением. | шаблон — регулярное выражение, в формате Perl совместимых регулярных выражений (PCRE). сек или #кол-во — период вычисления в секундах или в последних собранных значениях (начинается с решетки). В этом случае, может быть обработано более одного значения. | Поддерживаемые типы значений: str, text, log Результат: Если обрабатывается более одного значения, ‘1’ возвращается, если имеется по крайней мере одно совпадающее значение. Эта функция является чувствительной к регистру. | |
| str (шаблон,<сек|#кол-во>) | |||
| Поиск строки в последнем (самом новом) значении. | шаблон — требуемая строка сек или #кол-во — период вычисления в секундах или в последних собранных значениях (начинается с решетки). В этом случае, может быть обработано более одного значения. | Поддерживаемые типы значений: str, text, log Результат: Если обрабатывается более одного значения, ‘1’ возвращается, если имеется по крайней мере одно совпадающее значение. Эта функция является чувствительной к регистру. | |
| strlen (сек|#кол-во,<сдвиг_времени>) | |||
Длина последнего (самого нового) значения в символах (не в байтах). | сек (игнорируется) или #кол-во — N-ое самое новое значение сдвиг_времени (опционально) — смотри avg() | Поддерживаемые типы значений: str, text, log Обратите внимание, что Примеры: Эта функция поддерживается начиная с Zabbix 1.8.4. | |
| sum (сек|#кол-во,<сдвиг_времени>) | |||
| Сумма собранных значений за указанный период вычисления. | сек или #кол-во — период вычисления в секундах или в последних собранных значениях (начинается с решетки) сдвиг_времени (опционально) — смотри avg() | Поддерживаемые типы значений: float, int Параметр | |
| time | |||
| Текущее время в формате ЧЧММСС. | Поддерживаемые типы значений: любые Пример возвращаемого значения: 123055 | ||
| timeleft (сек|#кол-во,<сдвиг_времени>,порог,<аппроксимация>) | |||
| Требуемое время в секундах элементу данных для достижения заданного порога. | сек или #кол-во — период вычисления в секундах или в последних собранных значениях (начинается с решетки) сдвиг_времени (опционально) — см. функцию avg() порог — значение, которое необходимо достичь аппроксимация (опционально) — см. функцию forecast() | Поддерживаемые типы значений: float, int Если возвращаемое значение больше чем 999999999999.9999, возвращаемое значение обрезается до 999999999999. Возвращает 999999999999.9999, если порог нельзя достичь. Становится не поддерживаемым только, если в выражении имеется злоупотребление (ошибочный тип элемента данных, некорректные параметры), в противном случае возвращает -1 в случае ошибок. Примеры: Эта функция поддерживается начиная с Zabbix 3.0.0. | |
| trendavg (период, сдвиг_времени) | |||
| Среднее значение тренда за определенный период времени. | период — период времени (минимум ‘1h’), заданный как <N><единица времени> гдеN — количество единиц времениединица времени — h (час), d (день), w (неделя), M (месяц) или y (год).сдвиг_времени — смещение периода времени: | Примеры: ⇒ trendavg(1h,now/h) → среднее значение за текущий час (например, 12:00-13:00) ⇒ trendavg(1h,now/h-1h) → среднее значение за предыдущий час (11:00-12:00) ⇒ trendavg(1h,now/h-2h) → среднее значение за час два часа назад (10:00-11:00) ⇒ trendavg(1M,now/M-1y) → среднее значение за тот же месяц год назад. Обратите внимание, что временные операции параметра сдвиг_времени вычисляются слева направо без приоритетов. Например, Эта функция поддерживается с Zabbix 5.2.0. | |
| trendcount (период, сдвиг_времени) | |||
| Количество успешно извлеченных значений тренда за определенный период времени. | период — период времени (минимум ‘1h’), заданный как <N><единица времени> гдеN — количество единиц времениединица времени — h (час), d (день), w (неделя), M (месяц) или y (год). сдвиг_времени — смещение периода времени: | Примеры: ⇒ trendcount(1h,now/h) → количество за текущий час (например, 12:00-13:00) ⇒ trendcount(1h,now/h-1h) → количество за предыдущий час (11:00-12:00) ⇒ trendcount(1h,now/h-2h) → количество в период два часа назад (10:00-11:00) ⇒ trendcount(1M,now/M-1y) → количество за тот же месяц один год назад. Обратите внимание, что временные операции параметра сдвиг_времени вычисляются слева направо без приоритетов. Например, Эта функция поддерживается с Zabbix 5.2.0. | |
| trenddelta (период, сдвиг_времени) | |||
| Разница между максимальным и минимальным значениями тренда за определенный период времени. | период — период времени (минимум ‘1h’), заданный как <N><единица времени> гдеN — количество единиц времениединица времени — h (час), d (день), w (неделя), M (месяц) или y (год).сдвиг_времени — смещение периода времени: | Examples: ⇒ trenddelta(1h,now/h) → разница за текущий час (например, 12:00-13:00) ⇒ trenddelta(1h,now/h-1h) → разница за предыдущий час (11:00-12:00) ⇒ trenddelta(1h,now/h-2h) → разница за период два часа назад (10:00-11:00) ⇒ trenddelta(1M,now/M-1y) → разница за тот же месяц один год назад. Обратите внимание, что временные операции параметра сдвиг_времени вычисляются слева направо без приоритетов. Например, Эта функция поддерживается с Zabbix 5.2.0. | |
| trendmax (период, сдвиг_времени) | |||
| Максимальное из значений тренда в определенный период времени. | период — период времени (минимум ‘1h’), заданный как <N><единица времени> гдеN — количество единиц времениединица времени — h (час), d (день), w (неделя), M (месяц) или y (год). сдвиг_времени — смещение периода времени: | Примеры: ⇒ trendmax(1h,now/h) → максимум за текущий час (например, 12:00-13:00) ⇒ trendmax(1h,now/h-1h) → максимум за предыдущий час (11:00-12:00) ⇒ trendmax(1h,now/h-2h) → максимум за период два часа назад (10:00-11:00) ⇒ trendmax(1M,now/M-1y) → максимум за тот же месяц один год назад Обратите внимание, что временные операции параметра сдвиг_времени вычисляются слева направо без приоритетов. Например, Эта функция поддерживается с Zabbix 5.2.0. | |
| trendmin (период, сдвиг_времени) | |||
| Минимальное из значений тренда в определенный период времени. | период — период времени (минимум ‘1h’), заданный как <N><единица времени> гдеN — количество единиц времениединица времени — h (час), d (день), w (неделя), M (месяц) или y (год).сдвиг_времени — смещение периода времени: | Примеры: ⇒ trendmin(1h,now/h) → минимум за текущий час(например, 12:00-13:00) ⇒ trendmin(1h,now/h-1h) → минимум за предыдущий час (11:00-12:00) ⇒ trendmin(1h,now/h-2h) → минимум за период два часа назад (10:00-11:00) ⇒ trendmin(1M,now/M-1y) → минимум за тот же месяц один год назад. Обратите внимание, что временные операции параметра сдвиг_времени вычисляются слева направо без приоритетов. Например, Эта функция поддерживается с Zabbix 5.2.0. | |
| trendsum (период, сдвиг_времени) | |||
| Сумма значений тренда за определенный период времени. | период — период времени (минимум ‘1h’), заданный как <N><единица времени> гдеN — количество единиц времениединица времени — h (час), d (день), w (неделя), M (месяц) или y (год). сдвиг_времени — смещение периода времени: | Примеры: ⇒ trendsum(1h,now/h) → сумма за текущий час (например, 12:00-13:00) ⇒ trendsum(1h,now/h-1h) → сумма за предыдущий час (11:00-12:00) ⇒ trendsum(1h,now/h-2h) → сумма за период два часа назад (10:00-11:00) ⇒ trendsum(1M,now/M-1y) → сумма за тот же месяц один год назад Обратите внимание, что временные операции параметра сдвиг_времени вычисляются слева направо без приоритетов. Например, Эта функция поддерживается с Zabbix 5.2.0. | |
Снюс. Табак бездымный, но не безвредный
Снюс. Табак бездымный, но не безвредный
Снюс – один из видов бездымного табака. Он изготавливается из измельчённых табачных листьев, которые пакуют в пакетики, и при использовании помещают между десной и губой.
Почему этот продукт стал популярен и для чего продвигается табачными компаниями? Для того чтобы человек мог получить очередную дозу никотина там, где курить нельзя (на дискотеках, мероприятиях, в ресторанах и самолётах).
Никотин и другие вещества высвобождаются из снюса в слюну, при этом, никотин и другие химические вещества, содержащиеся в табаке, сразу попадают в кровоток, всасываясь через слизистую полости рта. Распространено заблуждение, что использование бездымного табака менее вредно, по сравнению с курением, поскольку он содержит менее опасные химические вещества. Это не так. Снюс содержит более 30 химических веществ, с потенциальным канцерогенным эффектом. Самые опасные из них- нитрозамины, они образуются ещё при производстве, в процессе ферментации табака.
Самые опасные из них- нитрозамины, они образуются ещё при производстве, в процессе ферментации табака.
Доказано, что люди, которые употребляют снюс, фактически подвергаются воздействию более высоких уровней нитрозаминов и других токсичных веществ, нежели курильщики традиционных сигарет. Причина в том, что снюс остаётся во рту дольше, по сравнению с сигаретным дымом, соответственно, вредные химические вещества дольше воздействуют на организм. Хотя бездымный табак и содержит меньше канцерогенов по сравнению с сигаретами, это не аргумент в его пользу. Даже один единственный канцероген может вызывать мутации, приводящие к раку.
ПОСЛЕДСТВИЯ УПОТРЕБЛЕНИЯ БЕЗДЫМНОГО ТАБАКА
«Безвредность снюса»- опаснейшее заблуждение! Употребление бездымного табака – доказанная причина развития рака полости рта, рака поджелудочной железы, рака пищевода, и рака лёгких.
Длительное использование бездымного табака приводит к пародонтозу, разрушению зубов, появлению зловонного запаха изо рта, тахикардии, гипертонии.
Пользователи бездымного табака получают намного больше никотина по сравнению с курильщиками сигарет. Дело в том, что употребление снюса предполагает, что табак остаётся во рту не менее 30 минут, за это время в организм попадает в десятки раз больше никотина, нежели при выкуривании одной, даже самой крепкой сигареты. Если в самой крепкой сигарете содержится до 1,5 мг никотина, то при употреблении снюса можно получить до 22 мг никотина. Даже если табак находится в полости рта непродолжительное время, порядка 5-10 минут, в кровь все равно поступает большое количество этого никотина.
Высокая концентрация никотина становится причиной более быстрого развития толерантности, и практически молниеносного формирования зависимости. Отказ от использования снюса — процесс более тяжёлый, чем отказ от курения, зачастую невозможный без помощи специалиста и курса реабилитации.
Кроме того, многие потребители бездымного табака затем переходят на курение обычных сигарет.
К сожалению, очень распространено использование снюса в подростковой и молодёжной среде, где он считается не только безопасным, но и модным.
Последствия употребления снюса в подростковом возрасте крайне опасны:
остановка роста;
повышенная агрессивность и возбудимость;
ухудшение когнитивных процессов;
нарушение памяти и концентрации внимания;
высокий риск развития онкологических заболеваний, прежде всего желудка, печени, полости рта;
ослабление устойчивости к инфекционным заболеваниям.
Практически все подростки, впервые использовавшие табак в виде снюса, в течение ближайших четырёх лет становятся курильщиками сигарет.
Снюс не помогает бросить курить, так как этот вид табака содержит тот же самый наркотик, что и сигареты!
Тюменские ученые работают над созданием высокопрочного алюминия
Тюменские ученые намерены дать ответ всему миру — как сделать так, чтобы двигатели в машинах служили если не вечно, то почти. Менее амбициозные планы — создать строительные инструменты, которые тоже не будут ломаться. Секрет — в материале. Причем известном всем, но модернизированном.
Секрет — в материале. Причем известном всем, но модернизированном. На пути к научному прорыву они используют царскую водку. В этом деле она незаменима.
«В нашем понимании это какой-то горячительный напиток, но я вам скажу, что царская водка — это сильно травящее средство. В состав которого входит серная, азотная и соляная кислота», — пояснил главный научный сотрудник Центра перспективных исследований и разработок ТИУ Николай Коленчин.
Ее возможности так велики, что достаточно одной капли, чтобы увидеть внутреннее строение материала. В их случае — алюминия, который стал главным героем научного проекта.
Алюминий в авиастроении с каждым годом становится все востребованнее. В небо поднимаются в том числе самолеты, сделанные в Тюмени. На заводах по производству автомобилей, нефтегазового оборудования, в металлургии, да даже в пиротехнике без алюминия никак. И чем толще, прочнее поверхность металла, тем больше спрос.
Вот экспериментальные образцы. Слой алюминия — меньше миллиметра. Это максимум, который можно нанести на автомобильный поршень двигателя.
Это максимум, который можно нанести на автомобильный поршень двигателя.
«Использование алюминиевых цилиндров породило ряд проблем. Это малая твердость, износоустойчивость рабочей поверхности. Выращивая оксид алюминия мы решаем эту проблему. Его технологические свойства гораздо выше даже иностранных технологий упрочения, которые на данный момент используются», — отметил магистрант ТИУ Денис Денисенко.
Слой высокопрочного алюминия будет два миллиметра, благодаря чему машина прослужит в разы дольше. Такую цель поставили тюменцы. И это громкое заявление для всего мирового сообщества.
Бльшие открытия тюменские ученые вот в таких условиях условиях — есть обычная лаборатория, небольшой склад и идеи творческой команды, которые основательно прижились в металле. Его тюменцы выращивают в прямом смысле слова.
Этим путем еще никто не шел. В фокусе выращивания алюминия на поверхности участвуют ультразвук, вибрации, игольчатый катод и озон. Метод уникальный. Тюменцы уже получили на него патент. Установки тоже разработали по авторским чертежам. И запатентовали. Сейчас работают над инструментами, которые уже привычно сделаны из стали, но алюминий может ее превзойти.
Установки тоже разработали по авторским чертежам. И запатентовали. Сейчас работают над инструментами, которые уже привычно сделаны из стали, но алюминий может ее превзойти.
«Алюминиевый напильник способен при правильных режимах обрабатывать даже закаленную сталь. Без особых ухищрений», — говорит Артем Воронин.
Почему выбрали именно такой материал для опытов? Ответ — в недрах Урала. Запасов много. И уникальных свойств тоже.
К материалу будущего присматриваются компании по сервисному ремонту автомобилей. Ученые говорят, что этот интерес в том числе с опаской. Ведь если делать качественно, как говорят, на века, то работники останутся без дела. Но такой политике бизнеса пора составить конкуренцию. И если что — ученые готовы.
«Это малое инновационное предприятие, на которое мы можем выйти в конечном итоге и показать миру, что мы можем выпускать детали, которые могут работать долго», — заявил Николай Коленчин.
Татьяна Воротилова, Сергей Жернаков, Тюменская служба новостей
Функции min и max в Python
В языке программирования Python есть встроенные функции поиска минимума и максимума. Им можно передавать как один объект, так и непосредственно множество однотипных объектов. Если передается один объект, то им может быть список, любая другая коллекция или итерируемый объект.
Им можно передавать как один объект, так и непосредственно множество однотипных объектов. Если передается один объект, то им может быть список, любая другая коллекция или итерируемый объект.
Если передается один список, то в нем находится минимум или максимум, которые возвращаются функциями min() и max().
>>> a = [11,8,12,0] >>> min(a) 0 >>> max(a) 12
Если передается несколько списков, то целиком возвращается один из переданных списков. При этом сравнение происходит поэлементно: сначала сравниваются первые элементы списков. Если они не равны, то функция min() вернет тот список, первый элемент которого меньше, max() — наоборот. Если первые элементы равны, то будут сравниваться вторые и т. д.
>>> a = [11,8,12,0] >>> b = [11,7,123,9] >>> m = min(a,b) >>> print(m, type(m)) [11, 7, 123, 9] <class 'list'> >>> c = [11,8,12] >>> min(a,c) [11, 8, 12]
Функциям min() и max() можно непосредственно передавать множество чисел:
>>> max(3, 8, -3, 12, 9) 12
Таким образом, если функции получают несколько объектов, то сравниваются сами объекты. И неважно какого они типа: списки, числа или что-то другое.
И неважно какого они типа: списки, числа или что-то другое.
Однако нельзя передать числа и строки или смешанный список. В этом случае функция возвращает ошибку:
>>> s = ['a','d',1] >>> min(s) Traceback (most recent call last): File "<stdin>", line 1, in <module> TypeError: unorderable types: int() < str()
Но:
>>> s = ['a','d','ee'] >>> min(s) 'a'
В функциях min() и max() можно указать необязательный именной параметр key. Ему присваивается одноаргументная функция, которая выполняет какое-то предварительное действие над элементами списка.
>>> a = [8,-11,4,2,-5] >>> max(a) 8 >>> max(a,key=abs) -11
Здесь во втором случае находится максимум среди абсолютных значений чисел. То есть к каждому элементу списка применяется встроенная в Python функция abs(). Однако применить ее к целым спискам нельзя:
>>> max(a,b,key=abs) Traceback (most recent call last): File "<stdin>", line 1, in <module> TypeError: bad operand type for abs(): 'list'
minmax() — CSS | MDN
minmax() это CSS функция, определяющая диапазон размеров, который больше или равен min и меньше или равен max.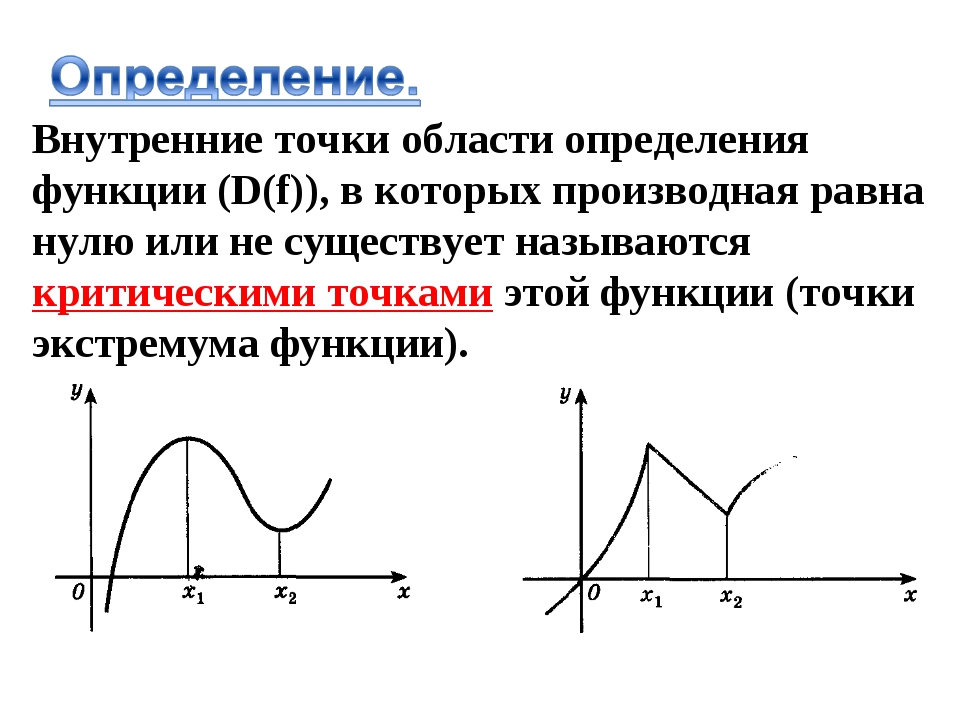 Используется в CSS Grids.
Используется в CSS Grids.
minmax(200px, 1fr)
minmax(400px, 50%)
minmax(30%, 300px)
minmax(100px, max-content)
minmax(min-content, 400px)
minmax(max-content, auto)
minmax(auto, 300px)
minmax(min-content, auto)
minmax(200px, 1fr)
minmax(30%, 300px)
minmax(400px, 50%)
minmax(50%, min-content)
minmax(300px, max-content)
minmax(200px, auto)
minmax(400px, 50%)
minmax(30%, 300px)
minmax(min-content, 200px)
minmax(max-content, 200px)
minmax(auto, 300px)
Функция принимает два параметра, min и max.
Каждый параметр может быть значением <length>, либо <percentage>, либо <flex>, или одним из ключевых слов max-content, min-content, или auto.
Если max < min, то max игнорируется и minmax(min,max) обрабатывается как min. As a maximum, a <flex> value sets the flex factor of a grid track; it is invalid as a minimum.
Значения
<length>- A non-negative length.
<percentage>- A non-negative percentage relative to the inline size of the grid container in column grid tracks, and the block size of the grid container in row grid tracks. If the size of the grid container depends on the size of its tracks, then the
<percentage>must be treated asauto. The user agent may adjust the intrinsic size contributions of the track to the size of the grid container and increase the final size of the track by the minimum amount that would result in honoring the percentage. <flex>- A non-negative dimension with the unit
frspecifying the track’s flex factor. Each<flex>-sized track takes a share of the remaining space in proportion to its flex factor. max-content- Represents the largest max-content contribution of the grid items occupying the grid track.

min-content- Represents the largest min-content contribution of the grid items occupying the grid track.
auto- As a maximum, identical to
max-content. As a minimum it represents the largest minimum size (as specified bymin-width/min-height) of the grid items occupying the grid track.
Формальный синтаксис
CSS
#container {
display: grid;
grid-template-columns: minmax(max-content, 300px) minmax(200px, 1fr) 150px;
grid-gap: 5px;
box-sizing: border-box;
height: 200px;
width: 100%;
background-color: #8cffa0;
padding: 10px;
}
#container > div {
background-color: #8ca0ff;
padding: 5px;
}
HTML
<div>
<div>
Item as wide as the content,<br/>
but at most 300 pixels.
</div>
<div>
Item with flexible width but a minimum of 200 pixels.
</div>
<div>
Inflexible item of 150 pixels width. </div>
</div>
</div>
</div>Результат
BCD tables only load in the browser
Universal App Campaign 2.0 в Google Рекламе — как выжать максимум пользы
Все, кто работает с мобильными приложениями в Google Рекламе, получили такое уведомление:
Что именно произойдет с рекламными кампаниями?
Еще в августе Google анонсировал, что, начиная с 16 октября 2017 года, все новые кампании для приложения будут в формате UAC — Universal App Campaign. Универсальные кампании для приложений работают на основе машинного обучения и позволяют рекламировать приложение одновременно в поисковой и медийной сети, а также в YouTube. Уже с 15 ноября все другие ранее созданные рекламные кампании по продвижению приложений в поисковой и контекстно-медийной сети перестанут работать.
Google обосновывает свое решение тем, что уже сейчас более 50% всех установок из рекламы приходится на универсальные кампании для приложений. Также UAC приводят на 140% конверсий больше за доллар, чем другие типы кампаний. То есть скоро все станет UAC, и тем, кто работает с мобильными приложениями, нужно научиться выжимать максимум эффективности из этого типа рекламных кампаний.
То есть скоро все станет UAC, и тем, кто работает с мобильными приложениями, нужно научиться выжимать максимум эффективности из этого типа рекламных кампаний.
Чем так хороши универсальные кампании?
UAC позволяют быстрее запускать рекламу
Вы не запутаетесь в настройках: создать UAC-кампанию сможет как маркетолог, так и сам разработчик или владелец мобильного приложения. Многим понравится, что больше не нужно собирать ключевые слова для рекламных кампаний, адаптируя привычную семантику под специфику пользовательского поиска на мобильных устройствах. Читайте подробный алгоритм настройки Universal App Campaign.
Рекомендую создавать UAC-кампании именно в новом интерфейсе Google Реклама (Beta), так как в нем доступны новые функции, хотя в целом логика создания рекламных кампаний в старом и новом интерфейсе схожа.
Например, раньше для UAC-кампаний нельзя было выбрать метод показа. В новом интерфейсе эта настройка доступна:
Кампании оптимизируются под любое ценное in-App событие
Так выглядит выбор цели в новом интерфейсе Google Рекламы:
В этом случае для проекта мы используем платную трекинговую систему Adjust и предварительно настроили передачу in-App событий из Adjust в Google Рекламе на вкладке «Отслеживание»:
Конверсии в этом проекте:
В случае использования другой системы аналитики для мобильных приложений следует настроить передачу конверсий в Google Рекламе согласно справочной информации этой системы аналитики. Для связки с Google Рекламой большинству проектов на старте продвижения я могу рекомендовать бесплатное решение — Firebase от Google.
Для связки с Google Рекламой большинству проектов на старте продвижения я могу рекомендовать бесплатное решение — Firebase от Google.
Также можно настроить передачу данных об установках для платформы Android напрямую из Google Play. При этом в случае оптимизации на in-App события важно выставить правильное значение периода учета конверсий для конкретного проекта.
Период учета конверсий — срок после взаимодействия пользователя с рекламным объявлением, в течение которого будет зарегистрирована конверсия. Например, период учета конверсий установлен как 7 дней после клика по объявлению. Значит, если пользователь увидел рекламное объявление и нажал на него, а потом совершил покупку спустя 6 дней, конверсия будет засчитана, а если покупка будет совершена спустя 8 дней, данные останутся без изменений.
Рекламу приложения, которое монетизируется за счет рекламы, можно настроить для получения установок, а другое приложение, в котором присутствуют in-App события, — настроить под покупки. То есть обучение рекламной кампании будет строиться так, чтобы сразу привлекать людей, склонных к совершению покупок.
То есть обучение рекламной кампании будет строиться так, чтобы сразу привлекать людей, склонных к совершению покупок.
Универсальные кампании показывают хорошие результаты
Высокая эффективность этих кампаний достигается благодаря технологии машинного обучения. Раньше я с недоверием относилась к этому: неизвестно, где именно показывается реклама, как она выглядит, а еще иногда такие кампании «воровали» часть показов у брендового поиска, запутывая статистику. Но в UAC машинное обучение работает очень хорошо.
Я протестировала эффективность UAC 2.0 (UAC In-app actions) в новом интерфейсе Google Рекламы. Обратите внимание: желаемая стоимость конверсии в настройках рекламной кампании — по-прежнему стоимость за установку приложения, а не за событие внутри приложения. В тестовом режиме я запустила рекламную кампанию, настроив ее на важное для бизнеса клиента in-App событие. При этом кампания с оптимизацией под установки продолжила работать в том же аккаунте.
Результаты порадовали: по сравнению с другими кампаниями, UAC 2. 0 приносили более дешевые in-App события и установки, которые были вдвое дешевле:
0 приносили более дешевые in-App события и установки, которые были вдвое дешевле:
Затем я тестировала UAC 2.0 с настройкой на событие внутри приложения в других рекламных аккаунтах, и каждый раз эти кампании приносили как in-App события, так и установки по более низкой цене.
Возможность оптимизации под in-App события была реализована и в старом интерфейсе Google Рекламы, но результаты тестов тогда нельзя было назвать удовлетворительными — мы в итоге оставили только UAC-кампании с оптимизацией под установки. По опыту, UAC эффективнее работают для приложений на Android, менее эффективно — для iOS. Все закономерно: система Google Реклама теснее связана с Google Play, алгоритму обучения кампаний доступно больше точных данных о конверсиях и о поведении пользователей именно на Android.
UAC 2.0 легко менять и улучшать
Это фишка нового интерфейса Google Рекламы. Вы можете увидеть эффективность на уровне каждого объявления, перейдя на вкладку «Ресурсы объявления» кампании:
Достаточно просто удалять ресурсы с пометкой «Низкая» и не трогать ресурсы с пометками «Высокая», «Средняя» и «Обучение». Впрочем, я заметила, что не всегда объявления с пометкой «Высокая» приносят конверсии по наименьшей цене. «Группа эффективности» просто говорит о том, как часто тот или иной ресурс выбирается для создания объявлений, не являясь индикатором эффективности с точки зрения получения конверсий по минимальной цене:
Впрочем, я заметила, что не всегда объявления с пометкой «Высокая» приносят конверсии по наименьшей цене. «Группа эффективности» просто говорит о том, как часто тот или иной ресурс выбирается для создания объявлений, не являясь индикатором эффективности с точки зрения получения конверсий по минимальной цене:
Этот отчет стоит анализировать не только по одному столбцу, но на основании показателей, важных для каждого отдельно взятого проекта. К сожалению, на анализе эффективности креативов возможности оптимизировать UAC-кампании заканчиваются.
Как проработать Universal App Campaign 2.0 — фишки и советы
Чтобы рекламная кампания начала приносить хорошие результаты, нужно не менее 100 конверсий. Это минимум данных, благодаря которому алгоритмы могут эффективно прогнозировать: кому, когда и где показывать рекламу вашего приложения. Поэтому для начала не рекомендуется создавать много отдельных кампаний с дроблением по событиям, под которые будут оптимизироваться кампании, или с таргетингом на разные регионы.
Google рекомендует не ограничиваться только текстовыми объявлениями, а добавить еще как минимум 5 баннеров и 1 видео. Затем можно посмотреть результаты по рекламной кампании с разбивкой по сетям и оценить стоимость установок в каждой сети:
Суточный бюджет одной рекламной кампании должен быть не меньше, чем желаемый CPIx50. Например, если вы готовы платить за установку приложения 15грн и установили соответствующую настройку в интерфейсе, то суточный бюджет нужно устанавливать на уровне не менее 750 грн/сутки.
Не рекомендуется вносить резкие изменения в UAC кампании. Если вам нужно уменьшить или увеличить бюджет, то не стоит это делать сразу больше или меньше, чем на 20%. То же самое касается и желаемой стоимости конверсии.
Если кампания настраивается на in-App события, то их количество должно быть не меньше 10 в день. Небольшой лайфхак: если цель вашего бизнеса — редкое in-App событие, можно оптимизировать под микроконверсию, которая предшествует основной конверсии, потому что таких событий будет больше.
В баннерах важно использовать CTA — кнопку призыва к действию. Это может быть надпись «Установить» или «Скачать», или просто кнопка магазина приложений:
Размеры баннеров, которые обеспечат наибольший охват рекламных кампаний: 320×480, 320×50, 300×250, 320×100, 336×280 и 1200×628. Для нативного баннера размером 1200×628 не стоит размещать текст на баннере.
Рекомендуется загрузить изображения высокого качества для маленьких баннеров, чтобы они показывались в высоком разрешении (например, 640×100 для баннера 320×50), так как разрешение экрана на смартфонах современных пользователей становится все больше и баннеры с низким разрешением выглядят непривлекательно.
Видеоролик для UAC 2.0 должен длиться 15-30 секунд. В первые 5 секунд нужно захватить внимание зрителя, а также сразу добавить четкий призыв к действию, чтобы пользователь понял, чего от него хотят. Оптимальный формат: 16:9, 2:3 и 1:1 для всех рекламных мест.
Выводы
Уже с ноября в Google Рекламе для мобильных кампаний останется только один формат — Universal App Campaign. Теперь управлять рекламными кампаниями для приложений в Google Рекламе станет проще, а сами UAC будут гибче в настройках.
Теперь управлять рекламными кампаниями для приложений в Google Рекламе станет проще, а сами UAC будут гибче в настройках.
Чем хороши UAC 2.0:
- Запустить их может даже неспециалист.
- Кампании оптимизируются под любое in-App событие.
- Кампании легко менять и улучшать.
- UAC в новом интерфейсе Google Рекламы показывают очень хорошие результаты.
В UAC 2.0 появились новые фишки: возможность настройки на In-app actions и вкладка «Ресурсы объявления», на основании которой можно анализировать эффективность в разрезе отдельных объявлений.
Netpeak запустил новую услугу «ASO с оплатой за результат» — заказывай через форму:
{«0»:{«lid»:»1531306243545″,»ls»:»10″,»loff»:»»,»li_type»:»nm»,»li_name»:»name»,»li_ph»:»Имя»,»li_req»:»y»,»li_nm»:»name»},»1″:{«lid»:»1573230091466″,»ls»:»20″,»loff»:»»,»li_type»:»ph»,»li_name»:»phone»,»li_req»:»y»,»li_masktype»:»a»,»li_nm»:»phone»},»2″:{«lid»:»1573567927671″,»ls»:»30″,»loff»:»y»,»li_type»:»in»,»li_name»:»surname»,»li_ph»:»Фамилия»,»li_req»:»y»,»li_nm»:»surname»},»3″:{«lid»:»1531306540094″,»ls»:»40″,»loff»:»»,»li_type»:»in»,»li_name»:»domains»,»li_ph»:»Адрес сайта»,»li_rule»:»url»,»li_req»:»y»,»li_nm»:»domains»},»4″:{«lid»:»1573230077755″,»ls»:»50″,»loff»:»»,»li_type»:»em»,»li_name»:»email»,»li_ph»:»Email»,»li_req»:»y»,»li_nm»:»email»},»5″:{«lid»:»1575903646714″,»ls»:»60″,»loff»:»»,»li_type»:»hd»,»li_name»:»comment»,»li_value»:»Автоматический коммент: заявка из блога, без пользовательского комментария»,»li_nm»:»comment»},»6″:{«lid»:»1575903664523″,»ls»:»70″,»loff»:»»,»li_type»:»hd»,»li_name»:»lead_channel_id»,»li_value»:»24″,»li_nm»:»lead_channel_id»},»7″:{«lid»:»1584374224865″,»ls»:»80″,»loff»:»»,»li_type»:»hd»,»li_name»:»ip»,»li_nm»:»ip»},»8″:{«lid»:»1609939359940″,»ls»:»90″,»loff»:»»,»li_type»:»hd»,»li_name»:»post_id»,»li_nm»:»post_id»}}
Поможем обогнать конкурентов
Определение максимума по Merriam-Webster
макс · я · мама | \ ˈMak-s (ə-) məm \ множественные максимумы \ ˈMak- sə- mə \ или максимумы \ ˈMak- s (ə-) məmz \1а : наибольшее количество или ценность, достижимая или достигнутая
б : период наивысшего, наибольшего или предельного развития
2 : верхний предел, разрешенный (в соответствии с законом) или допустимый (в соответствии с обстоятельствами конкретного дела)
3 : наибольшее из набора чисел. конкретно : наибольшее значение, принимаемое действительной непрерывной функцией, определенной на закрытом интервале.
конкретно : наибольшее значение, принимаемое действительной непрерывной функцией, определенной на закрытом интервале.
Исчисление I — минимальное и максимальное значения
Показать мобильное уведомление Показать все заметки Скрыть все заметки Похоже, вы используете устройство с «узкой» шириной экрана ( i. е. вы, вероятно, разговариваете по мобильному телефону). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать их, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, разговариваете по мобильному телефону). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать их, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
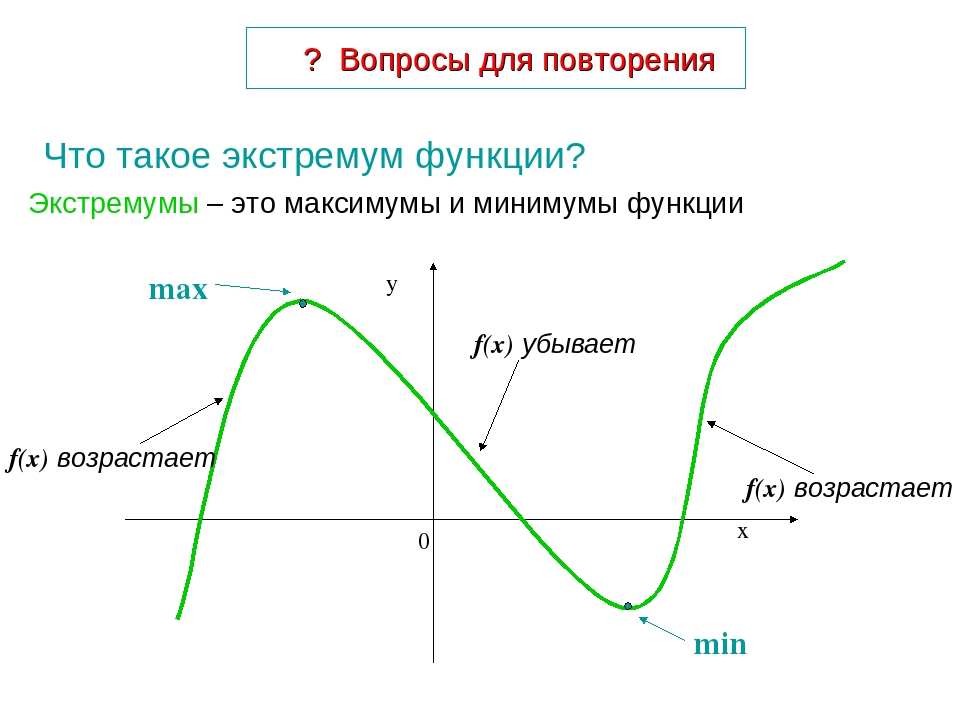
Раздел 4-3: Минимальные и максимальные значения
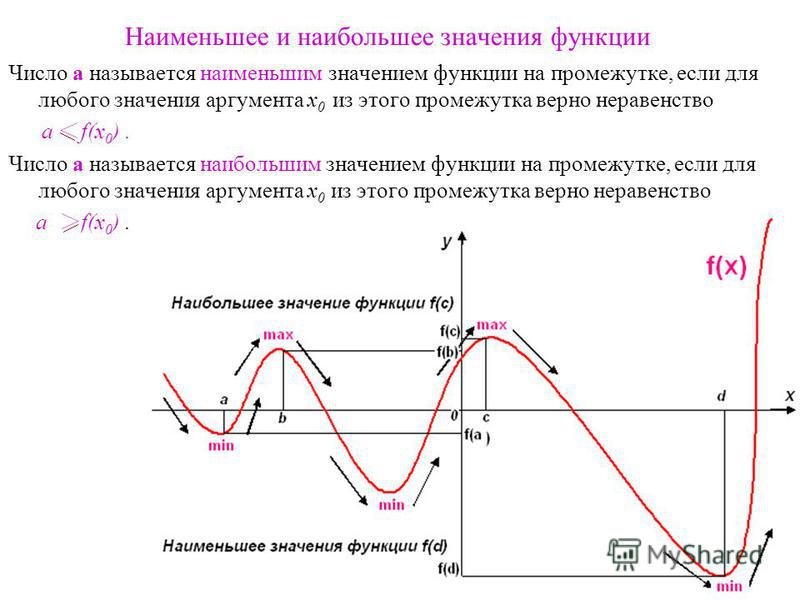
Многие из наших приложений в этой главе будут вращаться вокруг минимального и максимального значений функции.Хотя мы все можем визуализировать минимальные и максимальные значения функции, мы хотим быть более конкретными в нашей работе. В частности, мы хотим различать два типа минимальных и максимальных значений. Следующее определение дает типы минимальных и / или максимальных значений, которые мы будем рассматривать.
Определение
- Мы говорим, что \ (f \ left (x \ right) \) имеет абсолютный (или глобальный) максимум в \ (x = c \), если \ (f \ left (x \ right) \ le f \ left (c \ right) \) для каждого \ (x \) в области, над которой мы работаем.
- Мы говорим, что \ (f \ left (x \ right) \) имеет относительный (или локальный) максимум в \ (x = c \), если \ (f \ left (x \ right) \ le f \ left (c \ right) \) для каждого \ (x \) в некотором открытом интервале вокруг \ (x = c \).
- Мы говорим, что \ (f \ left (x \ right) \) имеет абсолютный (или глобальный) минимум в \ (x = c \), если \ (f \ left (x \ right) \ ge f \ left (c \ right) \) для каждого \ (x \) в области, над которой мы работаем.
- Мы говорим, что \ (f \ left (x \ right) \) имеет относительный (или локальный) минимум в \ (x = c \), если \ (f \ left (x \ right) \ ge f \ left (c \ right) \) для каждого \ (x \) в некотором открытом интервале вокруг \ (x = c \).

Обратите внимание: когда мы говорим «открытый интервал вокруг \ (x = c \)», мы имеем в виду, что мы можем найти некоторый интервал \ (\ left ({a, b} \ right) \), не включая концы, такой, что \ (а <с <Ь \). Или, другими словами, \ (c \) будет содержаться где-то внутри интервала и не будет ни одной из конечных точек.
Кроме того, мы будем совместно называть точки минимума и максимума функции экстремумами функции. Таким образом, относительные экстремумы будут относиться к относительным минимумам и максимумам, тогда как абсолютные экстремумы относятся к абсолютным минимумам и максимумам.
Теперь давайте немного поговорим о тонкой разнице между абсолютным и относительным в приведенном выше определении.
У нас будет абсолютный максимум (или минимум) в \ (x = c \) при условии, что \ (f \ left (c \ right) \) будет наибольшим (или наименьшим) значением, которое функция когда-либо будет принимать в области, которая мы работаем. Кроме того, когда мы говорим «домен, над которым мы работаем», это просто означает диапазон \ (x \), который мы выбрали для работы с данной проблемой.Могут быть и другие значения \ (x \), которые мы действительно можем подключить к функции, но по какой-то причине исключили их.
Кроме того, когда мы говорим «домен, над которым мы работаем», это просто означает диапазон \ (x \), который мы выбрали для работы с данной проблемой.Могут быть и другие значения \ (x \), которые мы действительно можем подключить к функции, но по какой-то причине исключили их.
Относительный максимум или минимум немного отличается. Все, что требуется для точки, чтобы быть относительным максимумом или минимумом, — это чтобы эта точка была максимумом или минимумом в некотором интервале \ (x \) вокруг \ (x = c \). Могут быть большие или меньшие значения функции в другом месте, но относительно \ (x = c \) или локально для \ (x = c \), \ (f \ left (c \ right) \) равно больше или меньше, чем все другие значения функции, которые находятся рядом с ним.
Также обратите внимание, что для того, чтобы точка была относительным экстремумом, мы должны иметь возможность смотреть на значения функций по обе стороны от \ (x = c \), чтобы увидеть, действительно ли это максимум или минимум в этой точке. Это означает, что относительные экстремумы не возникают в конечных точках области. Они могут происходить только внутри домена.
Это означает, что относительные экстремумы не возникают в конечных точках области. Они могут происходить только внутри домена.
На самом деле по предыдущему пункту ведутся споры. Некоторые люди действительно считают, что относительные экстремумы могут возникать в конечных точках области. Однако в этом классе мы будем использовать определение, в котором говорится, что они не могут возникать в конечных точках домена.Это будет обсуждаться более подробно в конце раздела, когда мы рассмотрим соответствующий факт.
Обычно легче понять определения, быстро взглянув на график.
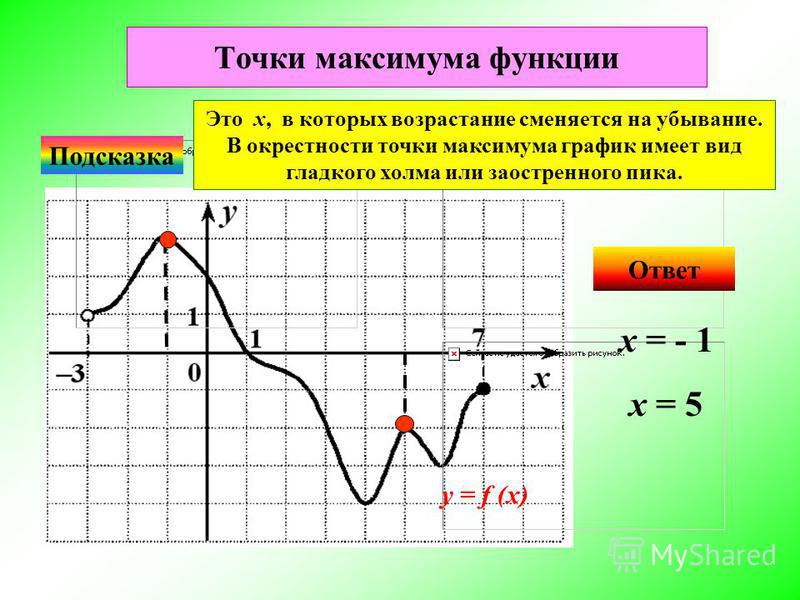
Для функции, показанной на этом графике, мы имеем относительные максимумы в точках \ (x = b \) и \ (x = d \). Обе эти точки являются относительными максимумами, поскольку они находятся внутри показанной области и являются самой большой точкой на графике в некотором интервале вокруг точки.У нас также есть относительный минимум в точке \ (x = c \), поскольку эта точка находится внутри области и является самой низкой точкой на графике в интервале вокруг нее. Крайняя правая конечная точка, \ (x = e \), не будет относительным минимумом, поскольку она является конечной точкой.
Крайняя правая конечная точка, \ (x = e \), не будет относительным минимумом, поскольку она является конечной точкой.
Функция будет иметь абсолютный максимум в точке \ (x = d \) и абсолютный минимум в точке \ (x = a \). Эти две точки являются наибольшим и наименьшим из возможных для функции. Мы также можем заметить, что абсолютные экстремумы для функции будут возникать либо в конечных точках области, либо в относительных экстремумах.2} \ hspace {0,25 дюйма} {\ mbox {on}} \ hspace {0,25 дюйма} \ left [{- 1,2} \ right] \] Показать решение
Так как эту функцию достаточно просто построить график, давайте сделаем это. Однако нам нужен только график на интервале \ (\ left [{- 1,2} \ right] \). Вот график,
Обратите внимание, что мы использовали точки в конце графика, чтобы напомнить нам, что график заканчивается в этих точках.
Теперь мы можем идентифицировать экстремумы на графике. Похоже, у нас есть относительный и абсолютный минимум ноль в точке \ (x = 0 \) и абсолютный максимум четыре в точке \ (x = 2 \). Обратите внимание, что \ (x = — 1 \) не является относительным максимумом, так как он находится в конечной точке интервала.
Похоже, у нас есть относительный и абсолютный минимум ноль в точке \ (x = 0 \) и абсолютный максимум четыре в точке \ (x = 2 \). Обратите внимание, что \ (x = — 1 \) не является относительным максимумом, так как он находится в конечной точке интервала.
Эта функция не имеет относительных максимумов.
Как мы видели в предыдущем примере, функции не обязательно должны иметь относительные экстремумы. Функция вполне может не иметь относительного максимума и / или относительного минимума.2} \ hspace {0,25 дюйма} {\ mbox {on}} \ hspace {0,25 дюйма} \ left [{- 2,2} \ right] \] Показать решение
Вот график этой функции.
В этом случае у нас все еще есть относительный и абсолютный минимум нуля в \ (x = 0 \). У нас также есть абсолютный максимум — четыре. Однако, в отличие от первого примера, это произойдет в двух точках: \ (x = — 2 \) и \ (x = 2 \).
Опять же, функция не имеет относительных максимумов. 2} \]
Показать решение
2} \]
Показать решение
В данном случае мы не указали домен, поэтому предполагаем, что мы возьмем максимально возможный домен. Для этой функции это означает все действительные числа. Вот график.
В этом случае график не перестает расти ни на одном конце, поэтому для этой функции нет никаких максимумов. Независимо от того, какую точку мы выберем на графике, с обеих сторон будут точки как больше, так и меньше, поэтому у нас не может быть никаких максимумов (любых, относительных или абсолютных) на графике.3} \ hspace {0,25 дюйма} {\ mbox {on}} \ hspace {0,25 дюйма} \ left [{- 2,2} \ right] \] Показать решение
Вот график этой функции.
Эта функция имеет абсолютный максимум восемь при \ (x = 2 \) и абсолютный минимум отрицательный восемь при \ (x = — 2 \). У этой функции нет относительных экстремумов.
Итак, функция не обязана иметь относительные экстремумы, как показано в этом примере.
Опять же, на этот раз мы не ограничиваем домен, поэтому вот график.
В этом случае функция не имеет ни относительных, ни абсолютных экстремумов.
Как мы видели в предыдущем примере, функции не обязательно должны иметь какие-либо экстремумы, относительные или абсолютные.
Пример 6 Определите абсолютные и относительные экстремумы для следующей функции.\ [е \ влево (х \ вправо) = \ соз \ влево (х \ вправо) \] Показать решениеМы не ограничивали домен для этой функции. Вот график.
Косинус имеет экстремумы (относительные и абсолютные), которые встречаются во многих точках. Косинус имеет как относительный, так и абсолютный максимум 1 при
. \ [x = \ ldots — 4 \ pi, \, — 2 \ pi, \, \, 0, \, \, 2 \ pi, \, \, 4 \ pi, \ ldots \]Косинус также имеет как относительный, так и абсолютный минимум -1 на
. \ [x = \ ldots — 3 \ pi, \, — \ pi, \, \, \ pi, \, \, 3 \ pi, \ ldots \]
\ [x = \ ldots — 3 \ pi, \, — \ pi, \, \, \ pi, \, \, 3 \ pi, \ ldots \]Как показал этот пример, на самом деле график может иметь экстремумы, возникающие в большом количестве (в данном случае бесконечном) точках.
Мы проработали довольно много примеров, и мы можем использовать эти примеры, чтобы увидеть хороший факт об абсолютных экстремумах. Сначала отметим, что все перечисленные выше функции были непрерывными. Затем обратите внимание, что каждый раз, когда мы ограничивали домен закрытым интервалом (, т.е. интервал содержит его конечные точки), мы получали абсолютные максимумы и абсолютные минимумы. Наконец, только в одном из трех примеров, в которых мы не ограничивали область, мы получили как абсолютный максимум, так и абсолютный минимум.
Эти наблюдения приводят нас к следующей теореме.
Теорема об экстремальном значении
Предположим, что \ (f \ left (x \ right) \) непрерывно на интервале \ (\ left [{a, b} \ right] \), тогда есть два числа \ (a \ le c, d \ le b \), так что \ (f \ left (c \ right) \) является абсолютным максимумом для функции, а \ (f \ left (d \ right) \) является абсолютным минимумом для функции.
Итак, если у нас есть непрерывная функция на интервале \ (\ left [{a, b} \ right] \), то мы гарантированно имеем как абсолютный максимум, так и абсолютный минимум для функции где-то в интервале.Теорема не говорит нам, где они возникнут или будут ли они встречаться более одного раза, но, по крайней мере, она говорит нам, что они где-то существуют. Иногда все, что нам нужно знать, это то, что они действительно существуют.
Эта теорема ничего не говорит об абсолютных экстремумах, если мы не работаем с интервалом. Мы видели примеры функций выше, у которых были как абсолютные экстремумы, так и один абсолютный экстремум, и не было абсолютных экстремумов, когда мы не ограничивались интервалом.
Требование непрерывности функции также необходимо для того, чтобы мы могли использовать теорему.2}}} \ hspace {0,25 дюйма} {\ mbox {on}} \ hspace {0,25 дюйма} [- 1,1] \]
Вот график.
Эта функция не является непрерывной в точке \ (x = 0 \), поскольку мы приближаемся к нулю, функция приближается к бесконечности. 2}}}} \ hspace {0.25 дюймов} {\ mbox {on}} \ hspace {0,25 дюйма} \ left [{\ frac {1} {2}, 1} \ right] \]
2}}}} \ hspace {0.25 дюймов} {\ mbox {on}} \ hspace {0,25 дюйма} \ left [{\ frac {1} {2}, 1} \ right] \]
функция теперь будет иметь оба абсолютных экстремума. Мы можем столкнуться с проблемами только в том случае, если интервал содержит точку разрыва. Если нет, то теорема верна.
Мы также должны отметить, что то, что функция не является непрерывной в точке, не означает, что у нее не будет обоих абсолютных экстремумов в интервале, содержащем эту точку. Ниже приведен график функции, которая не является непрерывной в точке данного интервала, но имеет оба абсолютных экстремума.
Этот график не является непрерывным в точке \ (x = c \), но он имеет как абсолютный максимум (\ (x = b \)), так и абсолютный минимум (\ (x = c \)). Также обратите внимание, что в этом случае один из абсолютных экстремумов произошел в точке разрыва, но это не обязательно. Абсолютный минимум мог просто быть в другой конечной точке или в какой-то другой точке внутри региона. Дело в том, что этот график не является непрерывным и все же имеет оба абсолютных экстремума
Дело в том, что этот график не является непрерывным и все же имеет оба абсолютных экстремума
Смысл всего этого в том, что нам нужно быть осторожными и использовать теорему об экстремальных значениях только при выполнении условий теоремы и не неправильно интерпретировать результаты, если условия не выполняются.
Чтобы использовать теорему об экстремальном значении, у нас должен быть интервал, который включает в себя его конечные точки, часто называемый закрытым интервалом, и функция должна быть непрерывной на этом интервале. Если у нас нет замкнутого интервала и / или функция не является непрерывной на интервале, тогда функция может иметь или не иметь абсолютных экстремумов.
Нам нужно обсудить одну последнюю тему в этом разделе, прежде чем перейти к первому важному применению производной, которое мы собираемся рассмотреть в этой главе.
Теорема Ферма
Если \ (f \ left (x \ right) \) имеет относительные экстремумы в \ (x = c \) и существует \ (f ‘\ left (c \ right) \), то \ (x = c \) является критическая точка \ (f \ left (x \ right) \). 3} \ hпространство {0.2} \]
3} \ hпространство {0.2} \]
Ясно, что \ (x = 0 \) является критической точкой. Однако мы видели в предыдущем примере, что у этой функции нет никаких относительных экстремумов. Итак, критические точки не обязательно должны быть относительными экстремумами.
Также заметьте, что эта теорема ничего не говорит об абсолютных экстремумах. Абсолютные экстремумы могут быть, а могут и не быть критической точкой.
Прежде чем мы покинем этот раздел, нам нужно обсудить пару вопросов.
Во-первых, теорема Ферма работает только для критических точек, в которых \ (f ‘\ left (c \ right) = 0 \).Это, однако, не означает, что относительных экстремумов не будет в критических точках, где не существует производной. Чтобы убедиться в этом, рассмотрим \ (f \ left (x \ right) = \ left | x \ right | \). Эта функция явно имеет относительный минимум в точке \ (x = 0 \), и все же в предыдущем разделе мы показали на примере, что \ (f ‘\ left (0 \ right) \) не существует.
Все это означает, что если мы хотим определить местонахождение относительных экстремумов, все, что нам действительно нужно сделать, это посмотреть на критические точки, поскольку это места, где могут существовать относительные экстремумы.
Наконец, напомним, что в начале раздела мы заявили, что относительных экстремумов не будет в конечных точках рассматриваемого нами интервала. Причина этого в том, что если мы позволим там иметь место относительным экстремумам, это вполне может (и фактически в большинстве случаев) нарушить теорему Ферма. Нет никаких оснований ожидать, что конечные точки интервалов будут критическими точками любого рода. Следовательно, мы не допускаем существования относительных экстремумов на концах интервалов.
Что такое максимум и минимум?
Минимум — это наименьшее значение в наборе данных.Максимум — это наибольшее значение в наборе данных. Узнайте больше о том, почему эта статистика может быть не такой тривиальной.
Фон
Набор количественных данных имеет множество функций. Одна из целей статистики — описать эти функции с помощью значимых значений и предоставить сводку данных без перечисления каждого значения набора данных. Некоторые из этих статистических данных довольно просты и почти кажутся тривиальными. Максимум и минимум являются хорошими примерами того типа описательной статистики, которую легко исключить.Несмотря на то, что эти два числа чрезвычайно легко определить, они появляются при расчетах другой описательной статистики. Как мы видели, определения обеих этих статистических данных очень интуитивно понятны.
Минимум
Начнем с более внимательного изучения статистики, известной как минимум. Это число является значением данных, которое меньше или равно всем другим значениям в нашем наборе данных. Если бы мы упорядочили все наши данные в порядке возрастания, то минимум был бы первым числом в нашем списке.Хотя минимальное значение может повторяться в нашем наборе данных, по определению это уникальное число. Не может быть двух минимумов, потому что одно из этих значений должно быть меньше другого.
Не может быть двух минимумов, потому что одно из этих значений должно быть меньше другого.
Максимум
Теперь переходим к максимуму. Это число является значением данных, которое больше или равно всем другим значениям в нашем наборе данных. Если бы мы упорядочили все наши данные в порядке возрастания, то максимум был бы последним числом в списке. Максимум — это уникальный номер для данного набора данных.Это число может повторяться, но есть только один максимум для набора данных. Не может быть двух максимумов, потому что одно из этих значений было бы больше другого.
Пример
Ниже приводится пример набора данных:
23, 2, 4, 10, 19, 15, 21, 41, 3, 24, 1, 20, 19, 15, 22, 11, 4
Мы упорядочиваем значения в порядке возрастания и видим, что 1 — наименьшее из значений в списке. Это означает, что 1 — это минимум набора данных. Мы также видим, что 41 больше, чем все остальные значения в списке.Это означает, что 41 — это максимум набора данных.
Использование максимума и минимума
Помимо предоставления нам базовой информации о наборе данных, максимальные и минимальные значения отображаются в расчетах для другой сводной статистики.
Оба этих числа используются для вычисления диапазона, который представляет собой просто разницу между максимальным и минимальным значениями.
Максимум и минимум также появляются вместе с первым, вторым и третьим квартилями в составе значений, составляющих сводку из пяти чисел для набора данных.Минимум — это первое число в списке, поскольку оно самое низкое, а максимальное — последнее число в списке, потому что оно самое высокое. Благодаря этой связи с сводкой из пяти чисел, как максимум, так и минимум появляются на диаграмме поля и усов.
Ограничения максимума и минимума
Максимум и минимум очень чувствительны к выбросам. Это происходит по той простой причине, что если к набору данных добавляется какое-либо значение, которое меньше минимального, то минимальное значение изменяется, и это новое значение. Аналогичным образом, если в набор данных включено какое-либо значение, превышающее максимум, то максимальное значение изменится.
Аналогичным образом, если в набор данных включено какое-либо значение, превышающее максимум, то максимальное значение изменится.
Например, предположим, что значение 100 добавлено к набору данных, который мы рассмотрели выше. Это повлияет на максимум, и он изменится с 41 до 100.
Часто максимум или минимум выпадают из нашего набора данных. Чтобы определить, действительно ли они являются выбросами, мы можем использовать правило межквартильного размаха.
Выборслов — «Максимум» против «Максимум»
Короткий ответ: если вы не математик или экономист, разницы нет.Однако существует различие между этими двумя терминами в контексте частично упорядоченных наборов (то есть наборов, в которых не каждая пара элементов должна быть сопоставимой).
Элемент равен максимум , если нет другого элемента больше.
Элемент равен максимум , если он сам больше, чем любой другой элемент.
Если обсуждаемые «элементы» являются числами, определения совпадают, но есть контексты, в которых различие имеет значение.
Например, на выборах можно сказать, что кандидат 1 на строго лучше, чем на кандидат 2, если все потенциальные избиратели предпочитают кандидата 1 кандидату 2.Допустим, три кандидата — Митт, Барри и Адольф — баллотируются на пост президента клуба.
Члены клуба делятся на два равных по размеру контингента. Одна группа единодушно предпочитает Барри Митту и Митта Адольфу, в то время как другая единогласно предпочитает Митта Барри и Барри Адольфу.
Барри и Митт — абсолютно лучшие кандидаты, чем Адольф, поскольку все члены ставят Адольфа на последнее место. Но так как некоторые участники предпочитают Барри Митту, а некоторые предпочитают Митта Барри, ни один из них не лучше другого.Таким образом, ни один из них не может быть максимальным в отношении этого порядка. Однако, поскольку не существует кандидатов, которые были бы строго лучше, чем любой из них, оба кандидата являются максимальными относительно этого порядка.
Математики проводят еще одно различие между терминами при рассмотрении множеств, удовлетворяющих определенному свойству. Например, «клика» — это совокупность людей, которые все знают друг друга. Клика равна максимальным , если добавление кого-либо еще к набору разрушает свойство клики, то есть не существует более крупной клики, которая ее содержит.Клика — это , максимум , если нет более крупной клики. Например, если Алиса, Боб и Кэм знают друг друга, а Деб, Эд, Фрэн и Гей знают друг друга, но
ни один из первых трех не знает ни одного из остальных четырех, тогда Алиса, Боб, Кэм — максимальная клика, но не максимальная клика. Максимальных клик может быть много.
Каждая максимальная клика максимальна, но не наоборот. Другой ответ об обратном отслеживании — это еще один пример этого различия, потому что обратное отслеживание при поиске означает удаление элемента из набора.
Например, «клика» — это совокупность людей, которые все знают друг друга. Клика равна максимальным , если добавление кого-либо еще к набору разрушает свойство клики, то есть не существует более крупной клики, которая ее содержит.Клика — это , максимум , если нет более крупной клики. Например, если Алиса, Боб и Кэм знают друг друга, а Деб, Эд, Фрэн и Гей знают друг друга, но
ни один из первых трех не знает ни одного из остальных четырех, тогда Алиса, Боб, Кэм — максимальная клика, но не максимальная клика. Максимальных клик может быть много.
Каждая максимальная клика максимальна, но не наоборот. Другой ответ об обратном отслеживании — это еще один пример этого различия, потому что обратное отслеживание при поиске означает удаление элемента из набора.
в кембриджском словаре английского языка
大 的, 最高 的, 頂點 的…
Узнать больше最大 の, 最高 の, 最大 限…
Узнать большеазами, en yüksek, en büyük…
Узнать больше максимум, максимум / -продажа, а. е. максимум…
е. максимум…
حَدّ, الحَدّ الأقْصى…
Узнать большеМаксимум, Максимум-, Дет место…
Узнать большеสูงสุด, จำนวน สูงสุด…
Узнать большеtối đa, lượng cực đại…
Узнать большеМаксимум, Максимал, Максималт…
Узнать больше大 的, 最高 的, 顶点 的…
Узнать большеmáximo, máximo / ma [мужской-женский род, единственное число]…
Узнать большеЗамените уродливые IF на MAX или MIN
В этой статье я хочу показать вам, как иногда можно заменить более сложную формулу IF на более элегантную формулу MIN или MAX.
Это очень простой совет, который действительно демонстрирует, как можно использовать формулы Excel для создания умных и компактных решений повседневных проблем.
Для иллюстрации рассмотрим два примера.
Бесплатный обед с MAX
Допустим, у вас есть кредит на 50 долларов в ресторане. Это одноразовый кредит, срок действия которого истекает завтра, поэтому вы пригласите друга на ужин сегодня. Вы разделяете салат, пиццу и пару бокалов пива. Когда придет время применить кредит к счету, вы можете рассчитать баланс следующим образом:
Простая формула.Но что происходит, когда кредит превышает общую сумму?
Если это произойдет, вы увидите отрицательный баланс:
Отрицательный баланс в этом случае не имеет смысла, поэтому вы можете воспользоваться удобной функцией ЕСЛИ:
сальдо = ЕСЛИ (общий-кредит> 0, общий-кредит, 0)
Проблема решена. Функция ЕСЛИ теперь улавливает отрицательные результаты и вместо этого возвращает ноль.
Это работает, но такой подход уродлив и излишен.Функция ЕСЛИ предназначена только для улавливания отрицательных результатов и заставляет вас повторить основную операцию дважды. Должен быть более прямой подход?
Да, действительно, с функцией MAX.
MAX вместо IF
Вы можете не думать о функции MAX в подобной ситуации, потому что она кажется ориентированной на большие наборы данных. Это правда, но MAX одинаково хорошо работает с небольшими, даже крошечными наборами данных.
Предположим, вы хотите, чтобы формула возвращала большее из двух значений: вычисленный баланс или ноль.Это означает, что вы можете написать такую формулу:
Теперь MAX просто возвращает большее из двух вариантов — положительный баланс или ноль. Отрицательные ценности изгоняются и никогда не доходят до конечного результата.
Довольно круто, да?
Ограниченная комиссия с MIN
Таким же образом можно использовать функцию MIN. Например, предположим, что вам нужно рассчитать комиссионный сбор в размере 1,5%, но не более 3000 долларов? Другими словами, используйте 1.5% для расчета комиссии, но не более 3000 долларов.
Например, предположим, что вам нужно рассчитать комиссионный сбор в размере 1,5%, но не более 3000 долларов? Другими словами, используйте 1.5% для расчета комиссии, но не более 3000 долларов.
Вы, конечно, можете использовать IF как это:
= ЕСЛИ (1,5% * сумма> 3000,3000,1,5% * сумма)
Однако с помощью функции MIN вы можете написать компактную формулу, которая полностью соответствует требованию:
Теперь любая комиссия ниже 3000 долларов возвращается в соответствии с расчетом, но общая комиссия никогда не превышает 3000 долларов.
Еще примеры
Вот еще пара примеров использования MAX или MIN для замены IF:
Другие формулы
Как и многие другие вещи в Excel, уловка для изучения большего количества формул заключается в большей открытости.Чтобы помочь вам, мы поддерживаем большую коллекцию примеров формул, которые вы можете просматривать и изучать. Это отличный способ найти конкретные решения многих проблем, с которыми вы, вероятно, столкнетесь в Excel. У нас также есть хорошая библиотека видеокурсов, которые помогут вам быстро учиться в более структурированной среде.
У нас также есть хорошая библиотека видеокурсов, которые помогут вам быстро учиться в более структурированной среде.
Нахождение минимумов и максимумов
Нахождение минимумов и максимумовОтносительный минимум — это точка, которая ниже всех остальных точек. вокруг него. Относительный максимум — это точка, превышающая все остальные указывает вокруг него.Конечно, есть и другие, более точные определения, но это будем работать для того, что мы хотим делать. Общее слово для минимума или максимума: экстремум.
Все калькуляторы
- Решите уравнение относительно Y, если это еще не так.
- Перейти к Y =
- Войдите в функцию
- График посещений
- Измените окно просмотра, если необходимо, чтобы вы могли видеть, где график имеет минимум или максимум. Вам нужно убедиться, что там достаточно слева и справа от экстремума, чтобы выбрать точку.
- Переходите к конкретным шагам для вашего калькулятора.
 Если есть дополнительные
крайности, чтобы найти, вам может потребоваться изменить окно просмотра
и повторить шаги
для каждого экстремума.
Если есть дополнительные
крайности, чтобы найти, вам может потребоваться изменить окно просмотра
и повторить шаги
для каждого экстремума.
TI-82
- Press Calc (2 nd Trace)
- Выберите минимум (# 3) или максимум (# 4)
- Для нижней границы нажмите стрелку слева от экстремума и нажмите клавишу ВВОД.
- Для верхней границы, стрелкой вправо от экстремума и нажмите ввод.
- Для «Угадай» стрелкой к экстремуму и нажмите «Ввод».
- TI-82 вернет значение для x и y. X — это точка экстремума происходит, а y — минимальное или максимальное значение.
TI-83
Для TI-83 вы можете вводить границы слева, справа и угадывать из клавиатуры вместо стрелок и нажатия Enter. Когда он запрашивает значение, просто введите свой номер и нажмите ввод.
- Press Calc (2 nd Trace)
- Выберите минимум (# 3) или максимум (# 4)
- Для левой границы стрелка слева от экстремума.
 и нажмите ввод.
и нажмите ввод. - Для правой границы стрелка вправо от экстремума и нажмите ввод.
- Для «Угадай» стрелкой к экстремуму и нажмите «Ввод».
- ТИ-83 будет вернуть значение для x и y. X — это точка экстремума происходит, а y — минимальное или максимальное значение.
ТИ-85 / ТИ-86
- График давления
- Нажмите «Еще», а затем «Математика» (F1)
- Нажмите нижнюю часть (F1). Стрелка слева от экстремума и нажмите ввод.
- Нажмите верхнее (F2). Стрелка вправо от экстремума и нажмите ввод.
- Нажмите More, а затем FMin (F1) для минимума или FMax (F2) для максимума.
- Стрелка к экстремуму и жмем ввод.
- TI-85 вернет значение для x и y. X — это точка экстремума происходит, а y — минимальное или максимальное значение.
ТИ-89 / ТИ-92
Для TI-89 и TI-92 вы можете ввести нижнюю или верхнюю границы из
клавиатуры вместо стрелок и нажатия Enter. Когда это
спрашивает
для
ценить,
только
введите свой номер и нажмите ввод.
Когда это
спрашивает
для
ценить,
только
введите свой номер и нажмите ввод.
- Пресс-математика (F5)
- Выберите минимум (# 3) или максимум (# 4)
- Для нижней границы нажмите стрелку слева от экстремума и нажмите клавишу ВВОД.
- Для верхней границы, стрелкой вправо от экстремума и нажмите ввод.
- TI-89 вернет значение для x и y. X — это точка экстремума происходит, а y — минимальное или максимальное значение.
Для TI-89 не нужно вводить предположение.Вы должны убедиться, что там только один экстремум в указанном интервале, иначе вы не узнаете, какой это даст вам.
Пример (TI-83 +)
Найдите относительный максимум для y = x 3 — 2x 2 — 4x
Введите функцию в y 1 и затем график. Вам может потребоваться изменить ваше окно просмотра, чтобы было видно максимум. Я использовал десятичный масштаб для этого примера. Я также ввел левую границу, правую границу и угадал с клавиатуры, а не с помощью стрелки и нажатия Enter.
Калькулятор говорит, что решение x = -0,6666651 и y = 1,4814815.
Если вы хотите найти относительный минимум, вам нужно будет изменить смотровое окно. Оставьте немного больше места ниже минимума, чтобы текст поскольку ответ не перезаписывает ваш график.
Для эта проблема, настройки окна: XMin = -1, XMax = 4, YMin = -10 и YMax = 3 работают достаточно хорошо. На изображении ниже показан график с этими настройками окна.
| Окно | График |
|---|---|
Минимум найдешь самостоятельно.Если вы хотите знать, есть ли у вас правильный ответ, это x = 2 и y = -8.
Обратите внимание, что вам не обязательно иметь максимальный показ найти минимум. Это верно для всех функций меню calc. Только интересующая вас часть графика должна быть видна. Другой x-точки пересечения, максимумы, минимумы или точки пересечения не должны отображаться.

 ‘. Также обратите внимание на то, что при разница между большими числами в десятичном (хранится в базе данных) и бинарном (используется Zabbix сервере) представлениях может повлиять на 4 цифру после запятой.
‘. Также обратите внимание на то, что при разница между большими числами в десятичном (хранится в базе данных) и бинарном (используется Zabbix сервере) представлениях может повлиять на 4 цифру после запятой. 6.1.
6.1. 9999 или меньше чем -999999999999.9999,возвращаемое значение обрезается до 999999999999.9999 или -999999999999.9999 соответственно.
9999 или меньше чем -999999999999.9999,возвращаемое значение обрезается до 999999999999.9999 или -999999999999.9999 соответственно. 0.0.
0.0.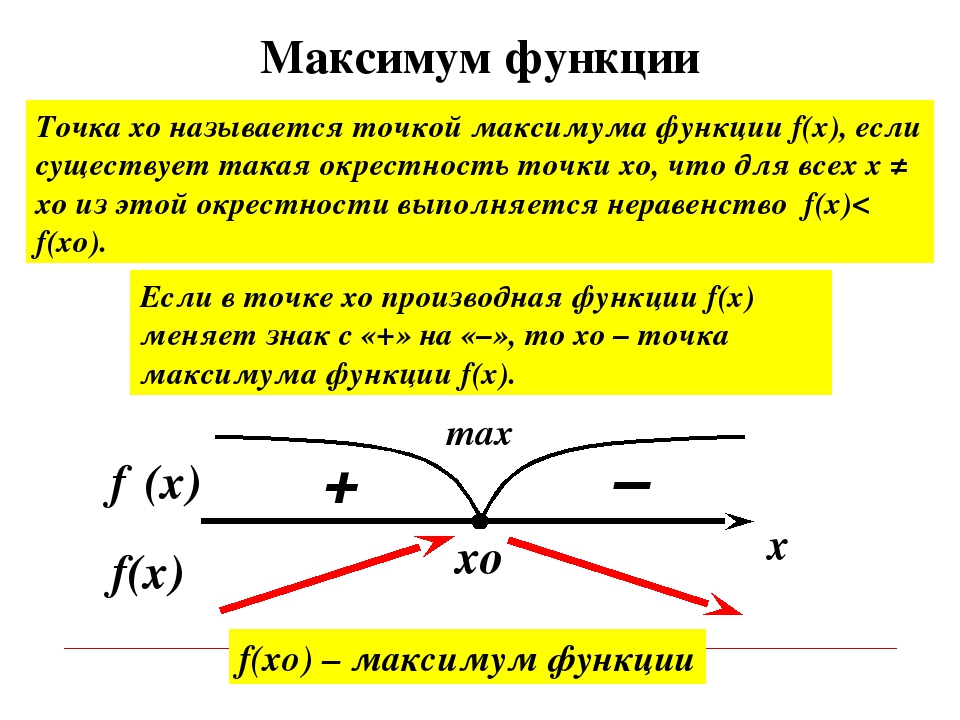
 0.0.
0.0.
 8.2.
8.2. 9999.
9999.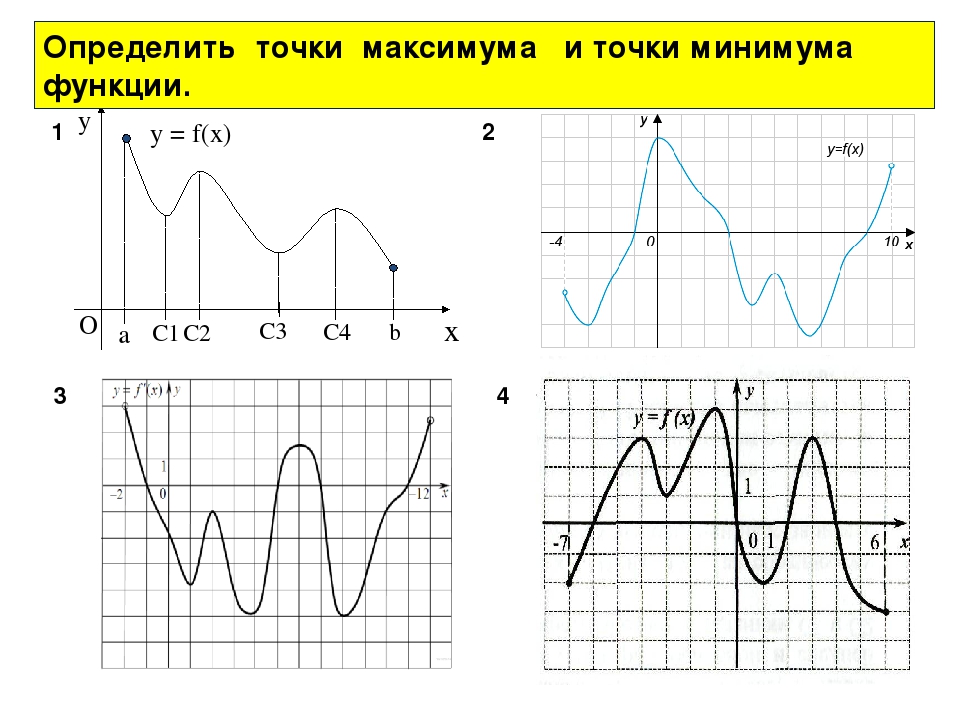 0.6 и 3.2.2.
0.6 и 3.2.2. примеры).
примеры).
 примеры).
примеры).
 примеры).
примеры).

 </div>
</div>
</div>
</div>
 Если есть дополнительные
крайности, чтобы найти, вам может потребоваться изменить окно просмотра
и повторить шаги
для каждого экстремума.
Если есть дополнительные
крайности, чтобы найти, вам может потребоваться изменить окно просмотра
и повторить шаги
для каждого экстремума. и нажмите ввод.
и нажмите ввод.
Leave A Comment