Калькулятор логарифмов. Решение логарифмов онлайн
Данная страница рассматривает калькулятор логарифмов — ещё одну функцию в богатом арсенале, которым располагает бесплатный калькулятор на нашем сайте. Калькулятор, считающий логарифмы онлайн, станет незаменимым помощником для тех, кому нужно простое решение математических выражений. В нашем калькуляторе любой может легко и быстро посчитать логарифм, не зная логарифмических формул, и даже не представляя суть логарифма.
Буквально 20-30 лет назад решение логарифмов требовало серьезных знаний в математике и как минимум умения пользоваться таблицей логарифмов или логарифмической линейкой. Чтобы привести к табличному виду исходное выражение, часто приходилось осуществлять сложные преобразования, учитывая свойства логарифмов и их функций.
Сегодня же достаточно иметь доступ в интернет, чтобы без труда вычислять всевозможные логарифмические уравнения и неравенства любой сложности. Размещенный на нашем сайте калькулятор онлайн может любой логарифм вычислить за одно мгновение! Используйте этот простой способ решения — вычисление логарифмов онлайн! Лучше добавить калькулятор в закладки и в социальные сети, наверняка найдётся причина открыть его ещё раз.
Решение логарифма logyx сводится к нахождению ответа на вопрос, в какую степень требуется возвести основание логарифма y, чтобы получилось значение равное x. Онлайн калькулятор логарифмов поможет рассчитать все виды логарифмов: двоичные, десятичные и натуральные логарифмы, а также логарифм комплексного числа и логарифм отрицательного числа и др.
Вычисление логарифмов в online калькуляторе записывается как
Кнопки, позволяющие вычислить логарифм онлайн
И десятичный логарифм калькулятор посчитает, и натуральный логарифм калькулятор найдёт!
Некоторые кнопки могут использоваться для записи одного и того же действия. Возьмём, к примеру, расчёт логарифмов с произвольным основанием. Понятно что, если указать основание 10, то рассчитается десятичный логарифм, а если 2, то двоичный. Учитывая, что математическое выражение можно и вручную набрать, тогда тот же самый десятичный логарифм посчитать можно тремя способами (точнее записать эту операцию в калькуляторе):
Учитывая, что математическое выражение можно и вручную набрать, тогда тот же самый десятичный логарифм посчитать можно тремя способами (точнее записать эту операцию в калькуляторе):
- 1. используя кнопку log, тогда нужно указать только число
- 2. с помощью кнопки logyx, через запятую указываются число и основание логарифма
- 3. внести обозначение логарифма вручную
Подробная информация о том, как работать с клавиатурой калькулятора, а также обзор всех его возможностей, можно найти на странице Функции калькулятора.
Логарифмы примеры решения в калькуляторе
Логарифм по основанию 2
Используйте эту кнопку, чтобы рассчитать логарифм, основание которого равно двум (его также называют двоичный логарифм).
В строке ввода отобразится запись log2(x) , соответственно, вам остаётся внести число, без указания основания, и произвести расчёт. В примере найден ответ, чему равен логарифм 8 по основанию 2.
Логарифм по основанию 2
Десятичный логарифм 10
Эта кнопка поможет найти логарифм числа по основанию 10.
Логарифм десятичный онлайн калькулятор обозначает записью log(x x,y). На рисунке рассчитано, чему равен десятичный логарифм числа 10000.
Логарифм по основанию 10
Натуральный логарифм
Клавишей ln выполняется решение натуральных логарифмов, основанием которых является число е. Основание натурального логарифма е — число Эйлера — равно 2.71828182845905.
Онлайн калькулятор можно определить, чему равен натуральный логарифм любого числа. На рисунках в качестве примера найдены значения натурального логарифма: слева — ln логарифм числа 8, справа — натуральный логарифм от числа 50.
Натуральные логарифмы примеры решения
Как решать логарифмы с произвольным основанием
Конечно, калькулятор, позволяет решить логарифм онлайн не только по определенному, но по любому основанию.
Определение логарифма числа
Калькулятор Инструкция — обзор основых и дополнительных функций калькулятора и общая информация о том, как пользоваться калькулятором.
log online
Вы искали log online? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и online log, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «log online».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как log online,online log,антилогарифм калькулятор онлайн,антилогарифм онлайн,антилогарифм онлайн калькулятор,вычислить логарифм онлайн с подробным решением,двоичный логарифм,калькулятор логарифмические уравнения,калькулятор логарифмических выражений,калькулятор логарифмических уравнений,калькулятор логарифмов с дробями,калькулятор логарифмов с решением онлайн,калькулятор решение логарифмов,калькулятор решения логарифмов,калькулятор уравнений логарифмов,калькулятор уравнений с логарифмами,логарифмирование онлайн,логарифмические уравнения калькулятор,логарифмические уравнения калькулятор онлайн,логарифмические уравнения калькулятор онлайн с подробным решением,логарифмический калькулятор онлайн с решением,логарифмы онлайн калькулятор с подробным решением,логарифмы онлайн примеры,онлайн калькулятор логарифмических уравнений,онлайн калькулятор логарифмов уравнений,онлайн калькулятор решение логарифмов,онлайн калькулятор с подробным решением логарифмы,онлайн решение логарифмических выражений,онлайн решение натуральных логарифмов,онлайн считать логарифмы,решение логарифмических выражений онлайн,решение логарифмов калькулятор,решение логарифмов калькулятор онлайн,решение логарифмов онлайн калькулятор,решение логарифмов онлайн калькулятор с подробным решением,решение логарифмов онлайн калькулятор с решением,решение логарифмов онлайн с решением калькулятор,решение примеров с логарифмами онлайн,решения логарифмов калькулятор,решить логарифм,решить логарифм онлайн,решить логарифмическое уравнение онлайн с подробным решением,решить логарифмы онлайн,решить онлайн логарифмы,считать логарифмы онлайн.
Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как log online,online log,антилогарифм калькулятор онлайн,антилогарифм онлайн,антилогарифм онлайн калькулятор,вычислить логарифм онлайн с подробным решением,двоичный логарифм,калькулятор логарифмические уравнения,калькулятор логарифмических выражений,калькулятор логарифмических уравнений,калькулятор логарифмов с дробями,калькулятор логарифмов с решением онлайн,калькулятор решение логарифмов,калькулятор решения логарифмов,калькулятор уравнений логарифмов,калькулятор уравнений с логарифмами,логарифмирование онлайн,логарифмические уравнения калькулятор,логарифмические уравнения калькулятор онлайн,логарифмические уравнения калькулятор онлайн с подробным решением,логарифмический калькулятор онлайн с решением,логарифмы онлайн калькулятор с подробным решением,логарифмы онлайн примеры,онлайн калькулятор логарифмических уравнений,онлайн калькулятор логарифмов уравнений,онлайн калькулятор решение логарифмов,онлайн калькулятор с подробным решением логарифмы,онлайн решение логарифмических выражений,онлайн решение натуральных логарифмов,онлайн считать логарифмы,решение логарифмических выражений онлайн,решение логарифмов калькулятор,решение логарифмов калькулятор онлайн,решение логарифмов онлайн калькулятор,решение логарифмов онлайн калькулятор с подробным решением,решение логарифмов онлайн калькулятор с решением,решение логарифмов онлайн с решением калькулятор,решение примеров с логарифмами онлайн,решения логарифмов калькулятор,решить логарифм,решить логарифм онлайн,решить логарифмическое уравнение онлайн с подробным решением,решить логарифмы онлайн,решить онлайн логарифмы,считать логарифмы онлайн.
Где можно решить любую задачу по математике, а так же log online Онлайн?
Решить задачу log online вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
| Ссылка: http://iminime.sabemo.ru/1/63/reshenie-logarifmicheskih-uravneniy-kalkulyator решение логарифмических уравнений калькулятор Решение логарифмических уравнений.  Решение квадратных, кубических, тригонометрических, логарифмических уравнений онлайн. . (если данное уравнение калькулятор способен решить ) . 12 мар 2017 . Online решение уравнений, домашки, задачей, Решебник и калькулятор с решениями примеров и уравнений онлайн. Онлайн калькулятор вычисляет логарифмы. На нашем сайте вы также найдёте соответствующие формулы и графики. Мы поможем сделать . Решение тригонометрических, показательных, логарифмических уравнений. Выберите задачу для решения. Решение тригонометрических уравнений. Калькулятор , считающий логарифмы онлайн, станет незаменимым помощником для тех, кому нужно простое решение математических выражений. Сегодня же достаточно иметь доступ в интернет, чтобы без труда вычислять всевозможные логарифмические уравнения и. Вышеиспользованный метод опускания логарифмов является одним из основных способов решения логарифмических уравнений и неравенств. Онлайн калькулятор калькулятор последнего поколения для пошагового решения логарифмических уравнений. Решение квадратных, кубических, тригонометрических, логарифмических уравнений онлайн. . (если данное уравнение калькулятор способен решить ) . 12 мар 2017 . Online решение уравнений, домашки, задачей, Решебник и калькулятор с решениями примеров и уравнений онлайн. Онлайн калькулятор вычисляет логарифмы. На нашем сайте вы также найдёте соответствующие формулы и графики. Мы поможем сделать . Решение тригонометрических, показательных, логарифмических уравнений. Выберите задачу для решения. Решение тригонометрических уравнений. Калькулятор , считающий логарифмы онлайн, станет незаменимым помощником для тех, кому нужно простое решение математических выражений. Сегодня же достаточно иметь доступ в интернет, чтобы без труда вычислять всевозможные логарифмические уравнения и. Вышеиспользованный метод опускания логарифмов является одним из основных способов решения логарифмических уравнений и неравенств. Онлайн калькулятор калькулятор последнего поколения для пошагового решения логарифмических уравнений. Пользоваться калькулятором совсем не сложно. Решение рациональных, дробно-рациональных уравнений любой степени, показательных, логарифмических, тригонометрических уравнений. Пример . Дополнительные материалы по теме: Логарифм . Основные способы решения логарифмических уравнений. Решения , подсказки и учебник линейной алгебры онлайн (все калькуляторы по алгебре). Пользоваться калькулятором совсем не сложно. Решение рациональных, дробно-рациональных уравнений любой степени, показательных, логарифмических, тригонометрических уравнений. Пример . Дополнительные материалы по теме: Логарифм . Основные способы решения логарифмических уравнений. Решения , подсказки и учебник линейной алгебры онлайн (все калькуляторы по алгебре).
|
Расчет логарифмов
Простой математический калькулятор для вычисления логарифмов чисел с указанным основанием. Данный калькулятор способен посчитать как десятичный логарифм, так и натуральный.
Теперь вы можете без всяких формул быстро зайти на наш сайт и посчитать то или иное число, узнать его логарифм.
Также на нашем сайте вы можете посчитать и обратный логарифм числа, антилогарифм, просто нужно зайти на данную страницу:
The field is not filled.
‘%1’ is not a valid e-mail address.
Please fill in this field.
The field must contain at least% 1 characters.
The value must not be longer than% 1 characters.
Field value does not coincide with the field ‘%1’
An invalid character. Valid characters:’%1′.
Expected number.
It is expected a positive number.
Expected integer.
It is expected a positive integer.
The value should be in the range of [%1 .. %2]
The ‘% 1’ is already present in the set of valid characters.
The field must be less than 1%.
The first character must be a letter of the Latin alphabet.
Su
Mo
Tu
We
Th
Fr
Sa
January
February
March
April
May
June
July
August
September
October
November
December
century
B. C.
C.
%1 century
An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3
Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).
%3.%2.%1%4
%3.%2.%1%4 %6:%7
s.sh.
u.sh.
v.d.
z.d.
yes
no
Wrong file format. Only the following formats: %1
Please leave your phone number and / or email.
Сумма и разность тригонометрических функций
С помощю этого онлайн калькулятора можно получить формулы суммы и разности тригонометрических функций (а также другие тригонометрические формулы). Для получения формулы выберите нужную тригонометрическую функцию, дейсвие. Теоретическую часть и численные примеры смотрите ниже.
Сумма и разность тригонометрических функций − теория, доказательство, примеры
Сумма и разность тригонометрических функций (формулы)
Докажем, сначала, формулы суммы и разности функций синуса и косинуса. Для этого воспользуемся формулами суммы и разности углов тригонометрических функций :
Для этого воспользуемся формулами суммы и разности углов тригонометрических функций :
Представим углы и в следующем виде:
Доказательство первой формулы:
Применяя формулы (1) и (2), получим:
или
Аналогично докажем остальные формулы.
Доказательство второй формулы:
или
Доказательство третьей формулы:
или
Доказательство четвертой формулы:
или
Доказательство пятой формулы:
Воспользуемся формулой приведения тригонометрических функций (т.е. ):
Далее применим уже доказанную формулу (7):
Получили:
Доказательство шестой формулы:
или
Доказательство седьмой формулы:
Седьмая формула является частным случаем пятой формулы. Подставляя β=α, получим
или
Доказательство восьмой формулы:
Восьмая формула является частным случаем шестой формулы. Подставляя β=α, получим
или
Докажем, далее формулы суммы и разности функций тангенса и котангенса.
или
Отметим, что формулы суммы и разности тригонометрических функций применяются для преобразования тригонометрических выражений и при решении тригонометрический уравнений.
Примеры применения формул суммы и разности тригонометрических функций
Пример. Вычислить точное значение следующего выражения:.
Решение. Так как невозможно найти точное решение ни для , ни для попробуем использовать формулу (7).
Ответ:
|
Random converter |
Уровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицахКонвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисления. Тепловая эффективность и топливная экономичностьДействительно ли можно сэкономить бензин, если выключить кондиционер и открыть окна в автомобиле? Подробнее… Логарифмическая линейка — механический аналоговый компьютер с несколькими логарифмическими шкалами ВведениеМощность звука ракеты-носителя Сатурн-5 составляет 100 000 000 Вт или 200 дБ SWL Логарифмическая шкала и логарифмические единицы часто используется в тех случаях, когда необходимо измерить некоторую величину, изменяющуюся в большом диапазоне. Правда, удобные единицы? Но, как оказывается, они удобны далеко не для всех! Можно сказать, что большинство людей, плохо разбирающихся в физике, математике и технике, не понимают логарифмических единиц, таких как децибелы. Немного историиДжон Непер. Источник: Википедия Изобретение логарифмов упростило вычисления, так как они позволили заменить умножение сложением, которое выполняется значительно быстрее, чем умножение. Среди ученых, которые внесли значительный вклад в развитие теории логарифмов, можно отметить шотландского математика, физика и астронома Джона Непера, опубликовавшего в 1619 г. сочинение с описанием натуральных логарифмов, которые значительно упрощали вычисления. Уильям Отред. Источник: Википедия Важным инструментом для практического использования логарифмов были таблицы логарифмов. Первая такая таблица была составлена английским математиком Генри Бригсом в 1617 году. Основываясь на работах Джона Непера и других ученых, английский математик и священник англиканской церкви Уильям Отред изобрел логарифмическую линейку, которая использовалась инженерами и учеными (включая и автора этой статьи) в течение последующих 350 лет, пока в середине семидесятых прошлого века ее не заменили карманные калькуляторы. ОпределениеЛогарифм — операция обратная возведению в степень. Число y является логарифмом числа x по основанию b y = logb(x) если соблюдается равенство by = x Иными словами, логарифм данного числа — это показатель степени, в которую нужно возвести число, называемое основанием, чтобы получить данное число. Можно сказать проще. Логарифм — это ответ на вопрос «Сколько раз нужно умножить одно число само на себя, чтобы получить другое число». Например, сколько раз нужно умножить число 5 само на себя, чтобы получить 25? Ответом является 2, то есть 52 = 25 По приведенному выше определению log5(25) = 2 Классификация логарифмических единицЛогарифмические единицы широко используются в науке, технике и даже в таких ежедневных занятиях, как фотография и музыка. Имеются абсолютные и относительные логарифмические единицы. С помощью абсолютных логарифмических единиц выражают физические величины, которые сравниваются с определенным фиксированным значением. Цифровой измеритель уровня звука С другой стороны, относительные логарифмические единицы используются для выражения физической величины в форме отношения или пропорции других физических величин, например, в электронике, где для этого используют децибел (дБ). Логарифмические единицы хорошо подходят для описания, например, коэффициента передачи электронных систем, то есть соотношения между выходным и входным сигналами. Следует отметить, что все относительные логарифмические единицы являются безразмерными. Децибелы, неперы и другие названия — просто особые наименования, которые используются совместно с безразмерными единицами. Следует также отметить, что преобразование логарифмических единиц в обычные единицы часто бывает невозможным. Впрочем, это бывает только в тех случаях, когда говорят об отношениях. Например, коэффициент передачи усилителя по напряжению 20 дБ можно преобразовать только в «разы», то есть в безразмерную величину — он будет равным 10. В то же время, измеренное в децибелах звуковое давление можно перевести в паскали, так как звуковое давление измеряется в абсолютных логарифмических единицах, то есть, относительно опорного значения. Отметим, что коэффициент передачи в децибелах — тоже безразмерная величина, хотя и имеет название. Полная путаница получается! Но мы попробуем разобраться. Логарифмические единицы измерения амплитуды и мощностиМощность. Известно, что мощность пропорциональна квадрату амплитуды. Например, электрическая мощность, определяемая выражением P = U²/R. То есть, изменение амплитуды в 10 раз сопровождается изменением мощности в 100 раз. Соотношение двух величин мощности в децибелах определяется выражением 10 log10(P₁/P₂) dB Амплитуда. В связи с тем, что мощность пропорциональна квадрату амплитуды, соотношение двух величин амплитуды в децибелах описывается выражением 20 log10(P₁/P₂) dB. Примеры относительных логарифмических величин и единиц
Интервал в одну октаву n = log₂ (f₂/f₁). Например, интервал между двумя частотами 20 и 40 Гц или 25 и 50 Гц равен одной октаве. n = 1000 log₂(f₂/f₁) s = 1000 ∙ log10(f₂/f₁) Максимальный коэффициент усиления антенны этого маршрутизатора Linksys равен 2,91 дБи на частоте 2,4 ГГц. Взвешивающий псофометрический фильтр типа С, упомянутый в описании единицы dBrnC, применяется для измерения отношения сигнал/шум. Метод был разработан в Северной Америке много лет назад для оценки характеристик телефонных линий связи В этой чашке кофе pH = 4.8 Примеры абсолютных логарифмических единиц и величин в децибелах с суффиксами и опорными уровнями
Wi-Fi передатчик этого маршрутизатора Linksys обеспечивает максимальную мощность 19,98 дБм на частоте 2,4 ГГц и 22,96 дБм на частоте 5 ГГц. Чувствительность этого микрофона Shure PG48 составляет -53,5 дБВ/Па или 2,10 мВ/Па (1 Па = 94 дБ SPL) Большинство профессиональных наушников могут создавать звуковое давление, превышающее 85 dB(A), которое является максимально допустимым, если звук воздействует на человека в течение всего рабочего дня. Автор статьи: Анатолий Золотков Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ. |
Преобразование выражений с использованием свойств логарифмов: примеры, решения
Если у нас есть выражение, содержащее логарифмы, то мы можем преобразовать его с учетом свойств этих логарифмов. В этом материале мы рассмотрим основные правила, по которым осуществляется данное преобразование.
В первом пункте приведем основные свойства логарифмов, представив их в виде списка. Далее рассмотрим характерные примеры преобразований с использованием этих свойств. Отдельно остановимся на числовых выражениях и на выражениях с переменными, а также посмотрим, как преобразовывать примеры с использованием модуля.
Свойства логарифмов
Чтобы преобразовывать выражения с логарифмами, обычно используют выражение, называемое основным логарифмическим тождеством: alogab=b, a>0, a≠1, b>0. Также нужно помнить следующие свойства:
Определение 1- loga1=0 при любом a>0, a≠1.

- logaa=1, если a>0, a≠1.
- logaa=1logaa=1 при любом a>0, a≠1.
- logaa=1, если a>0, a≠1.
- logaap=p, при этом a>0, a≠1 и p может быть любым действительным числом.
- loga(x·y)=logax+logay, a>0, a≠1, x>0, y>0. В обобщенном виде это свойство можно представить как loga(x1·x2·…·xn)=logax1+logax2+…+logaxn, a>0, a≠1, x1>0, x2>0, …, xn>0
- ) logaxy=logax-logay.
- logaxy=logax-logay , при этом a>0, a≠1, x>0, y>0.
- logaxy=logax-logay , a>0, a≠1, x>0, y>0.
- logabp=p·logab, при этом a>0, a≠1, b>0, а p может быть любым действительным числом.
- это свойство является следствием предыдущего: logabn=1n·logab , a>0, a≠1, n может быть любым натуральным числом больше 1, b>0.
- logab=logcblogca , при этом a>0, a≠1, b>0, c>0, c≠1.
- свойство, также являющееся следствием: logab=1logba , где a>0, a≠1, b>0, b≠1.
- logaqbp=pq·logab , a>0, a≠1, b>0, p и q могут быть любыми действительными числами, q≠0
- logaqbp=pq , a>0, a≠1, p и q – любые действительные числа, q≠0.

- logaq ap=pq, blogac=clogab , при этом a>0, a≠1, b>0, c>0.
Преобразовывая выражения, мы можем использовать данные равенства как справа налево, так и наоборот. Учить их все наизусть нет необходимости, достаточно знать основные свойства логарифмов и несколько других свойств, например, что bn=b1n , если b≥0. Из них можно вывести остальные свойства. Само решение, правда, при этом будет несколько длиннее. Например, если мы не знаем следствия logaqbp=pq·logab и используем только основные свойства логарифмов, нам нужно будет выполнить несколько последовательных преобразований:
logaq bp=logabploga aq=p·logabq=pq·logab
То же относится и к последнему свойству из списка, выраженному формулой blogac=Clogac=clogab : оно тоже может быть выведено из основных свойств. Нужно учитывать, что если у нас есть степень положительного числа с логарифмом в показателе, то мы всегда можем поменять число под логарифмом и основание степени местами. В принципе, на практике такие задачи встречаются не слишком часто, но мы их все же разберем.
Как преобразовать числовое выражение с логарифмом
После того, как мы вспомнили основные свойства логарифмов, покажем, как использовать их при решении задач. Начнем с того, как преобразовывать числовые выражения, потому что такие вычисления считаются более простыми. Возьмем сперва примитивные примеры, с помощью которых легко проиллюстрировать выбор нужного свойства логарифма, а потом будем наращивать сложность задач. В конце разберем задания, в которых нужно использовать сразу несколько свойств.
Как выбрать свойство логарифма для преобразования
Список свойств, приведенный в первом пункте, довольно большой, и очевидно, что нужно хорошо в нем ориентироваться, чтобы получить нужный результат. Обычно выбор делается по итогам сравнения исходного логарифма/выражения с левыми и правыми частями формул, выражающих свойства. В том случае, когда одна из частей формулы похожа на исходный логарифм или выражение, мы берем именно это свойство и выполняем преобразование с его помощью. Покажем на примерах, как именно это делается.
Покажем на примерах, как именно это делается.
Для начала преобразуем выражение, используя определение логарифма, выраженное формулой alogab=b, a>0, a≠1, b>0.
Пример 1Условие: преобразуйте и вычислите значение следующих выражений: 1) 5log54 ; 2) 10lg(1+2·π), 3) 2+3log2+3 ln15 ; 4) 2log2(−7); 5) (-5)log-5 e3
Решение
В первом примере прослеживается формула alogab. У нас есть a=5, b=4, что соответствует необходимому условию a>0, a≠1, b>0. Используем нужное равенство alogab=b и получим 5log54=4.
Во втором случае a будет равно 10, b – 1+2·π. Необходимое условие выполнено, значит, мы можем записать это в виде равенства: 10lg(1+2·π) =1+2·π.
В третьем выражении у нас есть степень вида alogab, причем a=2+3 и b=ln15. Запишем: 2+3log2+3 ln15=ln15 . Хотя равенство также соответствует формуле alogab, где a равно 2, а b=-7, мы не можем воспользоваться ею для преобразования. Из-за наличия отрицательного числа под знаком логарифма выражение лишается смысла. Кроме того, -7 не соответствует условию b>0, что еще раз подтверждает, что данную формулу мы взять не можем. Следовательно, вычислить значение исходного выражения нельзя, и запись 2log2(−7) =−7 будет ошибочна.
Кроме того, -7 не соответствует условию b>0, что еще раз подтверждает, что данную формулу мы взять не можем. Следовательно, вычислить значение исходного выражения нельзя, и запись 2log2(−7) =−7 будет ошибочна.
То же самое относится и к четвертому примеру. Мы не можем записать, что -5log-5·e3=e3 , поскольку такое выражение смысла не имеет.
Ответ:1) 5log54=4; 2) 10lg(1+2·π)=1+2·π; 3) 2+3log2+3ln 15=ln 15 ; 4 и 5 — не имеют смысла.
Довольно часто в задачах встречается такой вид преобразования, когда некоторое положительно число представляют в виде степени другого числа, также положительного и не равного 1, имеющего в показателе логарифм. Основной такого преобразования также является основное определение логарифма alogab=b, a>0, a≠1, b>0, но в перевернутом виде, т.е. прочитанное справа налево, например, 3=eln3 или 5=5log55.
Далее возьмем примеры с другими свойствами логарифмов.
Пример 2Условие: вычислите, если возможно: 1) log−21, 2) log11,3) log01, 4) log71, 5) ln1, 6) lg 1,7) log3,751, 8) log5·π71.
Решение
В первых трех примерах мы видим не имеющие смысла выражения log−21, log11, log01. Основанием логарифма не может быть число меньше 1, в т.ч. 0 и отрицательные значения, т.к. для них логарифм не определен. Значит, значение этих выражений вычислить нельзя.
В других случаях логарифмы имеют подходящие основания: 7, e, 10, 3,75 и 5·π7, а под знаками логарифма везде 1. Зная соответствующее свойство логарифма (loga1=0 при любом a>0, a≠1., мы можем сделать вывод, что значения этих выражений равны 0.
Ответ: 1, 2, 3 смысла не имеют; 4) log71=0, 5) ln1=0, 6) lg1=0, 7) log3,751=0, 8) log5·e71=0.
Пример 3Условие: вычислите значения: 1) log1313 , 2) ln e, 3) lg 10,4) log5·π3−2(5·π3−2), 5) log−3(−3), 6) log11.
Решение
Нам потребуется свойство логарифма, выраженное формулой logaa=1 при a>0, a≠1. Исходные логарифмы схожи между собой в том, что их основания и числа под знаком логарифма являются одинаковыми. Казалось бы, можно сразу сделать вывод, что значения всех выражений будут равны единице, однако посмотрим внимательнее. В заданиях 1, 2, 3, 4 действительно ответом будет 1, а вот в 5 и 6 исходные выражения смысла не имеют.
Казалось бы, можно сразу сделать вывод, что значения всех выражений будут равны единице, однако посмотрим внимательнее. В заданиях 1, 2, 3, 4 действительно ответом будет 1, а вот в 5 и 6 исходные выражения смысла не имеют.
Ответ: 1) log13=13=1, 2) ln e=1, 3) lg10=1, 4) log5·π3−2(5·π3−2)=1; 5,6 не имеют смысла.
Пример 4Условие: вычислите: 1) log3311, 2) log1+22(1+22)723 , 3) logπ5(π5)-2 , 4) log−10(−10)6.
Решение
Видим, что под логарифмами находятся некоторые степени основания, значит, нам нужно использовать соответствующее свойство logaap=p, где a>0, a≠1 и p будет любым действительным числом. С учетом этого можно записать следующее:
- log3311=11
- log1+22(1+2·2)723=723
- logπ5(π5)-2=-2
- для этого примера мы не можем написать такое же равенство, как и в предыдущем примере, поскольку log−10(−10)6=6 не имеет смысла.
Ответ: 1) log3311=11, 2) log1+22(1+2·2)723=723 , 3) logπ5(π5)-2=-2 , 4) не имеет смысла.
Условие: даны выражения log2,64·127, ln2+1π и lg((−5)·(−12)). Нужно представить их как суммы или разности логарифмов по тому же основанию.
Решение
Смотрим, что находится под знаком логарифма. Там произведение, значит, берем свойство логарифма произведения: loga(x·y) = logax+logay, a>0, a≠1, x>0, y>0. В исходных примерах основания и числа в произведениях положительны, т.е. условие данного свойства соблюдено. Применим его для первого выражения:
log2,64·127=log2,6 4+log2,6127
Чтобы вычислить значение второго выражения, нам нужно свойство логарифма частного: logaxy=logax-logay, a>0, a≠1, x>0, y>0. Здесь в основании стоит положительное число e, также у нас есть положительный числитель 2+1 и знаменатель π, т.е. условия свойства соблюдены. Применяем свойство и записываем, что ln2+1π=ln2+1-ln π .
Разберем третий пример. Начнем с того, что выражение lg((−5)·(−12)) будет иметь смысл, однако формула логарифма произведения для него не подойдет, поскольку оба числа -5 и -12 отрицательны. Значит, преобразование lg((−5) ·(−12))=lg(−5)+lg(−12) не подходит. Какое же свойство тогда использовать?
Значит, преобразование lg((−5) ·(−12))=lg(−5)+lg(−12) не подходит. Какое же свойство тогда использовать?
Проведем предварительное преобразование, чтобы избавиться от отрицательных чисел. Далее мы подробно поговорим, когда нужно выполнять такое действие, а пока ограничимся записью самого решения, которое и так понятно: lg((−5) ·(−12))=lg(5·12)=lg5+lg12.
Ответ: 1) log2,64·127=log2,64+log2,6127 , 2) ln2+1π=ln2+1-ln π , 3) lg((−5)·(−12))=lg5+lg12.
Пример 6Условие: упростите выражения log30,25+log316+log30,5 и ln23-ln13 .
Решение
Здесь мы тоже можем использовать свойства логарифма частного и произведения по аналогии с предыдущим примером, только нам потребуется их обратная запись. Преобразуем сумму логарифмов в логарифм произведения, а разность логарифмов в логарифм частного. В итоге у нас получается в первом примере log30,25+log316+log30,5=log3(0,25·16·0,5)=log32, а во втором ln23-ln13=ln23:13=ln 2.
Ответ: 1) log30,25+log316+log30,5=log3(0,25·16·0,5)=log32, 2) ln23-ln13=ln 2 .
Пример 7Условие: есть выражения log0,7511, log3-1(3-2+5·673)5+1 и log3(−5)6. Нужно избавиться от степени в выражении под знаком логарифма.
Решение
Очевидно, что у нас здесь есть выражения вида logabp. Берем свойство, которое выражается формулой вида
logabp=p·logab, где a>0, a≠1, b>0, p — любое действительное число. Поскольку условия a>0, a≠1, b>0 выполнены, то мы можем преобразовать logabpв произведение p·logab.
- в случае с первым выражением a равно 7, b – пяти и p– 11. Тогда log0,7511=11·log0,75.
- тут a=3-1, b=3-2+5·673, p=5+1 . Нужные условия выполнены, значит, мы можем записать, что:
log3-1(3-2+5·673)5+1==5+1·log3-1(3-2+5·673) - у нас есть выражение той же структуры: logabp, a=3, b=−5, p=6, однако одно из условий не выполняется, а именно b у нас меньше 0. Значит, эту формулу мы применить не можем, и нам будет нужно предварительно преобразовать выражение под знаком логарифма.
 Решение будет таким: log3(−5)6=log356=6·log35.
Решение будет таким: log3(−5)6=log356=6·log35.
Ответ: 1) log0,7511=11·log0,75, 2) log3-1(3-2+5·673)5+1==5+1·log3-1(3-2+5·673) 3) log3(−5)6=6·log35.
Применение формулы в обратном порядке в виде p·logab=logabp требуется довольно часто. При таком преобразовании важно соблюсти все те же условия для числовых значений переменных. Например, 3·ln 5=ln 53 и lg 2·log23=log23lg2.
Пример 8Условие: согласно таблице логарифмов, lg2≈0,3010 и lg5≈0,6990. Вычислите, сколько будет log25. Здесь же: запишите ln 11ln 3 в виде логарифма, основание которого равно 3.
Решение
Воспользуемся формулой перехода к новому основанию и представим исходный логарифм как отношение десятичных логарифмов с известными нам значениями.
log25=lg 5lg 2
Вычисляем и находим ответ: lg 5lg 2≈0,69900,3010≈2,3223 .
Во втором примере также будет достаточно формулы перехода к новому основанию, только в обратном порядке, т. е. logcblogca=logab .
е. logcblogca=logab .
Считаем: ln 11ln 3=log311
Ответ: 1) log25≈2,3223, 2) ln 11ln 3=log311 .
Мы разобрали множество примеров, где для осуществления преобразования достаточно применить одну формулу свойства логарифма или его определение. Теперь мы можем перейти к более сложным задачам, в которых нужно последовательно применять несколько свойств, а также делать дополнительные преобразования. Однако перед этим запишем еще один важный пример использования следствий из основных свойств логарифмов.
Пример 9Условие: 1) дан логарифм ln1+π7 . Необходимо избавиться от корня под знаком логарифма; 2) выполните преобразование дроби 1log25 в логарифм с основанием 4; 3) преобразуйте логарифм loge2345 так, чтобы избавиться от степени в основании; 4) вычислите, сколько будет log2-13216 ; 5) осуществите замену 2,3log73 на степень с основанием 3.
Решение
- Вспоминаем следствие из свойства логарифма степени, которое выражается формулой logabn=1n·logab .
 В первом случае можем сразу же подсчитать: ln1+π7=17·ln(1+π) .
В первом случае можем сразу же подсчитать: ln1+π7=17·ln(1+π) . - во втором случае нам понадобится формула logab=1logba , примененная в обратном порядке. Получим 1log25=log52.
- здесь нам потребуется свойство logaqbp=pq·logab . Применяем его и получаем loge2345=452·ln 3=25·ln 3.
- в этом случае нам нужно будет следствие, выраженное формулой logaqap=pq: log(2)-13216=16-13=-12
- используем формулу свойства blogac=clogab и вычисляем ответ:
2,3log7·3=3log72,3
Ответ: 1) ln1+π7=17·ln(1+π) ; 2) 1log25=log52 ; 3) loge2345=25·ln 3; 4) log(2)-13216=-12 . 5) 2,3log7·3=3log72,3 .
Задачи с применением нескольких свойств логарифмов
В действительности чаще встречаются более сложные задания, чем те, что мы разобрали в предыдущем параграфе. В них приходится выполнять преобразования в несколько шагов, применяя последовательно одно свойство за другим. Кроме того, они зачастую включают в себя необходимость раскрывать скобки, приводить подобные слагаемые, сокращать обыкновенные дроби и др. Это не так сложно, как кажется, главное – соблюдать правильную последовательность действий.
Это не так сложно, как кажется, главное – соблюдать правильную последовательность действий.
Условие: вычислите, сколько будет (log315−log35) ·7log75.
Решение
Мы можем заменить выражение в скобках логарифмом log3(15:5), используя свойство частного. Вычисляем его значение и получаем log3(15:5) =log33=1.
Согласно основному определению логарифма, значением 7log75 будет 5. Подставим в исходное выражение получившиеся результаты и найдем, что (log315−log35) ·7log75=1·5=5.
Вот все решение без комментариев:
(log315−log35)·7log75=log3 (15:5)·5==log33·5=1·5=5
Ответ: (log315−log35) ·7log75=5.
Пример 11Условие: вычислите, чему равен log3log223−1.
Решение
Начнем с преобразования логарифма, который, в свою очередь, сам находится под знаком логарифма. Используем для этого формулу логарифма степени log223=3. Получим, что log3log223=log33, а дальше log33=1. Следовательно, log3log223−1=1−1=0.
Следовательно, log3log223−1=1−1=0.
Ответ: log3log223−1=0.
Пример 12Условие: выполните упрощение выражения 3ln 5ln 3log52 .
Решение
Берем формулу перехода к новому основанию. С ее помощью можно представить отношение логарифмов ln 5ln 3 как log35. У нас получилось 3log35log52 . Теперь применяем формулу основного определения логарифма 3log35=5 и получаем, что 3log35log52 . Нам осталось лишь вычислить значение этого выражения. Оно будет равно 2.
Ответ: 3ln 5ln 3log52=2 .
Перейдем к дальнейшему пункту обсуждения логарифмических преобразований. У нас есть выражения log334, 52+log53, lg 0,01. Они не напоминают нам ни об одной известной нам формуле свойства, но их все же можно изменить этим способом, если выполнить предварительные преобразования: 52+log53=52·5log53=25·3=75, log334=log31234=412=8 и lg 0,01=lg 10−2=−2. Разберем подробнее, как именно это делается.
Предварительное преобразование перед применением основных свойств логарифмов
На практике мы часто можем встретить логарифмы, которые внешне не похожи ни на одну часть формулы свойства. Однако при этом преобразование требует применения именно этих формул. Это возможно, если перед этим привести их к соответствующему виду. Это процесс называется тождественным преобразованием.
Однако при этом преобразование требует применения именно этих формул. Это возможно, если перед этим привести их к соответствующему виду. Это процесс называется тождественным преобразованием.
В роли таких действий могут выступать почти любые преобразования выражений, в том числе раскрытие скобок, вынесение за скобки множителей, применение формул тригонометрии и т.д. Это очевидно, поскольку выражения под знаком логарифма могут содержать практически все, что угодно: модули, скобки, дроби, степени и др. Поэтому нужно уметь выполнять разные виды преобразований, чтобы успешно решать такие задачи.
Данная статья не имеет целью осветить все возможные случаи преобразований, поскольку их очень много. Мы выбрали только четыре, которые наиболее распространены.
Определение 2- Довольно часто приходится получать степени под знаком и в основании, чтобы потом использовать формулу логарифма степени и последствия данного свойства. Мы выполняем такое преобразование, если в видим в условии логарифмы следующего вида: ln2532332 , log381.

- Также нужно уметь выполнять преобразование, связанное со свойствами степени. Оно нужно нам для последующего использования формулы, которая отвечает определению логарифма. Мы применяем его, когда у нас есть выражения, подобные 2log223, 32·log35, 71+log74, 25(log35)-3 и др.
- Обязательно нужно преобразовывать выражения с десятичными дробями под знаком логарифма или в его основании. Иногда после этого мы обнаруживаем, что основание под знаком степени и основание логарифма будут равны, как, например, здесь: log15(0,2)7
- Также нужно знать правила преобразования выражений, где под знаком логарифма стоит отрицательное число. Мы расскажем, что нужно делать, если в условии стоят выражения вроде lg(−3)−4, log6((−9)·(−4)) и др.
Разберем подробно каждый вид преобразования.
Как выделить степень в основании логарифма и под его знаком
Сразу возьмем конкретный пример. У нас есть выражение log1981 , структура которого не подсказывает нам ни одного возможного свойства логарифмов, которое можно было бы использовать. Значит, нам надо начать с преобразования самого выражения или сразу с вычисления его значения. Как же это сделать? Обратите внимание на числа 81 и 19. Их легко представить в виде степени с основанием 3 : 81=34 и 19=3−2. Значит, все выражение можно переписать как log3-234 , а здесь уже видна возможность использования свойства logaqbp=pq·logab . Таким образом, log1981=log3-2=4-2=-2 .
Значит, нам надо начать с преобразования самого выражения или сразу с вычисления его значения. Как же это сделать? Обратите внимание на числа 81 и 19. Их легко представить в виде степени с основанием 3 : 81=34 и 19=3−2. Значит, все выражение можно переписать как log3-234 , а здесь уже видна возможность использования свойства logaqbp=pq·logab . Таким образом, log1981=log3-2=4-2=-2 .
Этот пример иллюстрирует нам следующую мысль: если есть возможность, нужно выделить степень в основании и под знаком логарифма, чтобы впоследствии применить свойство логарифма степени. Ниже мы приведем некоторые советы, как именно выделять степени в таких примерах.
В некоторых случаях число можно преобразовать в целую степень, как в примере выше. В задачах то и дело встречаются степени чисел 2 и 3, которые легко узнать с первого взгляда: 243=35, 81=34, 8=23, 64=26 и др. Для решения примеров полезно иметь таблицу степеней натуральных чисел в пределах 10, чтобы сразу видеть возможности преобразования выражений. Также легко работать с выражениями, включающими целые степени 10, 100 и др.
Также легко работать с выражениями, включающими целые степени 10, 100 и др.
Условие: вычислите или упростите выражения log6216, log3431243, log0,0000010,001.
Решение
- В первом случае мы сразу видим, что 216 можно представить в виде 63. Значит, log6216=log663=3.
- у нас есть числа 343 и 1243. Обратимся к таблице степеней и увидим, что их можно представить в виде 73 и 3−4. Выполняем дальнейшие преобразования и получаем:
log3431243=log733-4==-43·log73=-113·log73 - Поскольку 0,000001=10−6 и 0,001=10−3, тогда log0,0000010,001=log10−610−3= -3-6=12
Ответ: 1) log6216=3, 2) log3431243=-113·log73 ; 3) log0,0000010,001=12.
Если исходного числа нет в таблице степеней, то мы можем разложить его на простые множители.
Пример 14Условие: упростите выражение log3648·log23.
Решение
Выполняем разложение 648 на простые множители.
64832416281931222333
Значит, это число можно представить в виде 648=23·34. Следовательно, log3648·log23=log3(23·34)·log23
Теперь мы можем преобразовать исходный логарифм произведения в сумму, а потом воспользоваться формулой логарифма степени.
log3(23·34)·log23=(log323+log334)·log23= =(3·log32+4)·log23.
Упрощаем выражение через раскрытие скобок:
(3·log32+4)·log23=3·log32·log23+4·log23.
В полученном выражении log32·log23 является произведением взаимно обратных чисел, которое равно 1. Следовательно, формулируем ответ как 3·log32·log23+4·log23=3·1+4·log23=3+4·log23.
Ответ: log3648·log23=3+4·log23.
Зачастую под логарифмом записываются выражения, представляющие собой отношения или произведения корней: 323·3-2, 2·2273 и т.д. Они также приводятся к виду степени: сначала мы выполняем переход от корня к степени, используя соответствующие свойства. С помощью таких преобразований мы можем получить выражение, удобное для применения формулы логарифма степени.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Пример 15Условие: найдите значение выражений log52·5-0.5·5-153454 и log372919.
Решение
В первом случае у нас есть произведение степеней, имеющих одинаковые основания. Используя нужное свойство, получим: 52·5−0,5·5−1=52−0,5−1=50,5. Для преобразования дроби сначала выполним переход от корня к степени, затем используем свойство отношения степеней с одинаковыми основаниями:
53454=5344=534-4=5-314
Полученное выражение подставим в исходный логарифм, применив формулу logaqaq=pq, и получим ответ:
log52·5-0.5·5-153454=log50.55-314=-3140.5==-13412=-132=-612
Во втором случае представим число 729 как 36 , а 19 как 3−2. Исходный логарифм приобретет вид log3363-2. Используя свойство корня из степени, преобразуем основание логарифма и получим:
336=333=31-3=3-2
Заканчиваем преобразование: log3363-2=log3-23-2=1 .
Ответ: 1) log52·5-0.5·5-153454=-612 ; 2) log372919=1
Преобразования, которые нужно сделать, чтобы получить под знаком логарифма нужную степень, могут значительно отличаться от примера к примеру.
Пример 16Условие: вычислите значения log13-1132·3+1-5 и log2·cos1(1+cos2)3 .
Решение
Первое, что нам нужно сделать, – это избавиться от иррациональности в знаменателе первой дроби, лежащей в основании логарифма:
13-1=3+13-1·3+1=3+132-12=3+12
Мы получили результат, схожий с дробью под знаком логарифма. Применим к нему свойства степеней и получим:
132·3+1-5=3+1532=3+1525=3+125
В результате преобразований у нас получился логарифм степени основания log3+123+135 . Значение данного выражения будет равно 5.
Чтобы преобразовать второе выражение, надо воспользоваться тригонометрическими формулами, а конкретно формулой понижения степени cos2a=1+cos2a2 :
log2·cos1(1+cos2)3=log2·cos1(2·cos21)3
Преобразуем второй логарифм, записав его как степень 2·cos2112 или же 2·cos123=2·cos16. Оба выражения будут иметь одно и то же значение, равное шести.
Оба выражения будут иметь одно и то же значение, равное шести.
Ответ: 1) log13-1132·3+1-5=5 ; 2) log2·cos1(1+cos2)3=6 .
Как применять свойства степени при преобразовании выражений с логарифмами
Ранее мы уже использовали свойства степеней, чтобы преобразовать выражения под знаком логарифма и его основание. Посмотрим, в каких еще характерных случаях потребуется такая подготовка.
Для начала возьмем задачи на применение свойства степеней с одинаковыми основаниями ap·aq=ap+q. Чаще всего его применяют в обратном порядке, т.е. справа налево.
Пример 17Условие: вычислите значения 3−2+log37 и 0,72−log0,70,1.
Решение
В первом примере нужно представить исходную степень как произведение двух степеней, т.е. 3−2+log37=3−2·3log37. Теперь найдем, чему равен первый множитель. Возведем его в степень, потом вычислим значение второго множителя, используя определение логарифма, и подсчитаем их произведение:
3−2·3log37= (19) ·7=79
Во втором примере нам надо подготовить выражение к преобразованию, выполнив переход к произведению степеней: 0,72−log0,70,1=0,72·0,7−log0,70,1. После этого нам нужно представить показатель −log0,70,1 в виде llog0,7(0,1)−1=log0,710. Теперь все, что нам осталось, – это закончить вычисления:
После этого нам нужно представить показатель −log0,70,1 в виде llog0,7(0,1)−1=log0,710. Теперь все, что нам осталось, – это закончить вычисления:
0,72·0,7−log0,70,1=0,49·0,7log0,710=0,49·10=4,9
Ответ: 1) 3−2+log37=79; 2) 0,72−log0,70,1=4,9.
Также для предварительных преобразований нужно обязательно знать свойство степени в степени, которое выражается формулой (ap)q=ap·q, например, если у нас есть выражение (eln2)3, то мы можем заключить, что значение части в скобках будет равно 2. Значит, (eln2)3=23=8. А если в условии указано (e3)ln2 или (e3)ln2, то мы сначала приводим их к виду (eln2)3:
e3·ln2=eln2·3=(eln2)3 и (e3)ln2=e3·ln2=eln2·3=(eln2)3.
Посмотрим пример решения такой задачи.
Пример 18Условие: выполните упрощение выражений 2log223−3log23 и 5(log85) −1.
Решение
Отметим, что выражения 2log223и 2log223 не являются равными друг другу. Мы можем представить 2log223 как 2log23·log23. Используя свойство степени, представим его как (2log23)log23, что будет тождественно равным 3log23. В итоге мы имеем, что 2log223−3log23=3log23−3log23=0.
Используя свойство степени, представим его как (2log23)log23, что будет тождественно равным 3log23. В итоге мы имеем, что 2log223−3log23=3log23−3log23=0.
Вот запись всего решения:
2log223−3log23=2log23·log23−3log23==(2log23)log23−3log23=3log23−3log23=0
Перейдем ко второму примеру. Запись 25(log85)-1 не будет равна (25log85)−1. Мы можем представить степень (log85)−1 как дробь 1log85 . Ее нужно преобразовать, используя следствие свойства перехода к новому основанию по формуле logab=1logba, чтобы получить log58.
Так, 25(log85)-1=25log58. Поскольку 25 – это 52, имеем 5log58= (52)log58. То, что у нас получилось, представляем в виде (5log58). Нам осталось только вычислить значение: (5log58)2=82=64.
Ответ: 1) 2log223−3log23=0, 2) 25(log85)−1=64.
Также встречаются примеры, где предварительная подготовка к использованию свойств логарифмов заключается в применении и свойства умножения степеней с одинаковыми основаниями, и свойства степени в степени. Например,
Например,
4−0,5+2·log43=4−0,5·42·log43==12·(4log43)2=12·32=12·9=4,5
Преобразование логарифмов с десятичными дробями
Применить свойства логарифмов можно и тогда, когда под знаком логарифма у нас стоит десятичная дробь. Что можно сделать с выражением log0,4253? Отметим, что 25 и 0,4 равны между собой 0,4=410=25, то есть это разные формы записи для одного и то же числа.
В целом можно сказать, что в случае наличия десятичной дроби под знаком логарифма необходимо выполнить переход к обыкновенной дроби. Это поможет увидеть возможности использования свойств логарифмов.
Разберем подобную задачу.
Пример 19Условие: вычислите значение выражения log0,46,25.
Решение
Начнем с перехода от десятичных дробей к обыкновенным.
log0,46,25=log410625100=log25254
Теперь видно, что мы можем преобразовать 254 в виде (25)−2 и воспользоваться формулой логарифма степени. Вычисляем значение:
log25254=log2525-2=-2
Ответ: -2.
Преобразование выражений с отрицательными числами под знаком логарифма
Еще один случай, который мы хотели бы рассмотреть – это преобразование выражений, в которых под знаком логарифма стоит отрицательное число, например, log3-93-27 или log3((−2)·(−5)).
Мы не можем сразу воспользоваться формулами свойств логарифмов в том виде, в каком приводили их в последнем пункте, например, сразу перейти от log3((−2)·(−5)) к log3(−2)+log3(−5), применить свойство логарифма степени к log2(−2)6 или логарифма частного к log3-93-27 , поскольку отрицательные числа не могут находиться под знаком логарифма и в его основании.
Что это значит на практике? Вернемся к нашему примеру log3((−2)·(−5)). Структура выражения соответствует формуле loga(x·y), где a равно 3, x-3 и y-5. Поскольку условия a>0, a≠1, x>0, y>0 не выполнены, формулу loga(x·y)=logax+logay мы применить не можем, и равенство log3((−2)·(−5)) =log3(−2) +log3(−5) записать нельзя. Преобразования вида log3-93-27=log3-93-log3(-27) также будут неправильными.
Это не значит, что выражения с отрицательными числами не могут быть преобразованы с использованием свойств логарифмов. Это допускается при условии предварительных преобразований, позволяющих избавиться от минуса. Они базируются на хорошо известных нам правилах работы с числами, меньшими 0.
Вернемся опять к нашему примеру. Согласно правилам умножения, (−2)·(−5) =2·5, значит, log3((−2)·(−5))=log3(2·5). К выражению в таком виде мы уже можем применить формулу log3(2·5) =log32+log35. А вот для примера log2(−2)6 нужно будет выполнить следующие действия:
(−2)6= ((−1)·2)6=(−1)6·26=1·26=26
Значит, log2(−2)6=log226=6.
Пример 20Условие: найдите значение выражения log2-163-2-23.
Решение
Сначала заключим, что данное выражение имеет смысл. Воспользоваться сразу свойством логарифма частного у нас нет возможности из-за отрицательных чисел под знаком логарифма, поэтому выполним преобразования.
Определив корень нечетной степени из отрицательного числа, выполним переход от -163-2-23 к -163-2-23 . Согласно правилам деления, получим -163-2-23=1632-23 . Теперь нам нужно получившуюся дробь представить в виде степени числа 2 и найти значение получившегося логарифма.
Согласно правилам деления, получим -163-2-23=1632-23 . Теперь нам нужно получившуюся дробь представить в виде степени числа 2 и найти значение получившегося логарифма.
1632-23=2432-23=2432-23=243—23=22log2-163-2-23=log222=2
Ответ: log2-163-2-23=2 .
Некоторые свойства, например, логарифма частного, степени с четным показателем и произведения, можно распространить и на отрицательные числа с помощью модулей. Как это делается, мы покажем далее. Так, поскольку свойство логарифма произведения выглядит как loga(x·y)=loga|x|+loga|y|, где a>0, a≠1, x≠0, y≠0, то после преобразования мы получим log3((−2)·(−5)) =log3|−2|+log3|−5|=log32+log35.
Как преобразовать логарифмическое выражение с переменными
В предыдущих параграфах мы разобрали, как работать с числовыми выражениями, содержащими логарифмы. Однако если требуется решить логарифмическое неравенство или уравнение, нам понадобится умение работать с теми случаями, когда под знаком логарифма содержится выражение с переменными. В целом при этом мы руководствуемся теми же принципами, что и с числовыми выражениями, но тут следует отдельно пояснить некоторые нюансы, незнание которых ведет к ошибкам.
В целом при этом мы руководствуемся теми же принципами, что и с числовыми выражениями, но тут следует отдельно пояснить некоторые нюансы, незнание которых ведет к ошибкам.
Особенности преобразований выражений с переменными
Основная трудность состоит в том, что при работе с такими выражениями числа, расположенные под знаком логарифма и в его основании, должны соответствовать особым условиям, а в случае определенных переменных из области допустимых значений эти условия могут оказаться невыполненными. Приведем один наглядный пример.
У нас есть логарифмическое выражение log2(x+1)4. При преобразовании нужно обязательно учитывать область допустимых значений, поэтому первым шагом должно стать ее нахождение. Здесь она определена неравенством (x+1)4>0, значение которого является числовым множеством (−∞, −1) ∪ (−1, +∞). Решить его можно с помощью метода интервалов.
Исходное выражение соответствует формуле logABp, где A равно 2, B – x+1, а p – четырем.
Мы видим, что заданное выражение соответствует виду logABp, где A=2, B=x+1 и p=4. Такие выражения преобразовываются по свойству логарифма степени logabp=p·logab. Можно ли поступить так с этим выражением? Вычислим значение исходного логарифма и выражения, которое получилось после преобразования, например, при x=−2. В итоге: log2(−2+1)4=log21=0, а 4·log2(−2+1) =4·log2(−1) –выражение, не имеющее смысла. Значит, мы ошиблись.
Такие выражения преобразовываются по свойству логарифма степени logabp=p·logab. Можно ли поступить так с этим выражением? Вычислим значение исходного логарифма и выражения, которое получилось после преобразования, например, при x=−2. В итоге: log2(−2+1)4=log21=0, а 4·log2(−2+1) =4·log2(−1) –выражение, не имеющее смысла. Значит, мы ошиблись.
Причина ошибки в том, что мы взяли формулу logabp=p·logab, но это допустимо лишь при условии a>0, a≠1, b>0, p — любое действительное число. Иными словами, проделанное нами преобразование возможно, если x+1>0, что аналогично x>−1 (для A и p – условия выполнены). Однако в нашем случае ОДЗ переменной x для исходного выражения состоит не только из промежутка x>−1, но и из промежутка x <−1. Но для x <−1 мы не имели права осуществлять преобразование по выбранной формуле.
Почему надо учитывать область допустимых значений
Продолжая работу с выражением log2(x+1)4, проанализируем, как изменится область значений, когда мы выполним переход к виду 4·log2(x+1). Ранее мы уже определили эту область как множество (−∞, −1) ∪ (−1, +∞). Теперь вычислим, какова будет область допустимых значений для 4·log2(x+1). Она определяется условием x+1>0, а ему, в свою очередь, будет отвечать множество (−1, +∞). Мы видим, что область допустимых значений сузилась, а это может привести к различным ошибочным последствиям, поэтому таких преобразований следует избегать.
Ранее мы уже определили эту область как множество (−∞, −1) ∪ (−1, +∞). Теперь вычислим, какова будет область допустимых значений для 4·log2(x+1). Она определяется условием x+1>0, а ему, в свою очередь, будет отвечать множество (−1, +∞). Мы видим, что область допустимых значений сузилась, а это может привести к различным ошибочным последствиям, поэтому таких преобразований следует избегать.
Важно следить, как меняется область значений во время каждого преобразования. Если на каком-либо этапе происходит ее сужение, это повод тщательно проверить все вычисления и определить, правомерно ли использования данного преобразования.
Чаще всего при решении задач приходится иметь дело с выражениями, область допустимых значений которых не ограничивает применение свойств логарифмов в прямом и обратном порядке, но не следует относиться так ко всем примерам. Нужно всегда проверять, что происходит с областью допустимых значений, и своевременно отслеживать возможные ошибки.
Запишем, в ходе каких преобразований чаще всего происходит непреднамеренное сужение области значений:
Определение 3- когда мы переходим от логарифма произведения к сумме, например, ln(x·(x+3)) =lnx+ln(x+3) сузит нужную область.

- Когда мы переходим от логарифма частного к разности. Пример такого преобразования – замена log2xsin x на log2x−log2sinx .
- Когда мы выносим четный показатель степени, используя формулу логарифма степени logabp=p·logab и формулу logabp=pq·logab . Примеры таких преобразований – logx3(x-8)2=23·logx(x-8) , ln(x+3)−4=−4·ln(x+3).
Иногда в результате преобразования область допустимых значений может не сужаться, а расширяться, например, при переходе от 4·log2(x+1) к log2(x+1)4. В этом случае область расширяется от (−1, +∞) до (−∞, −1) ∪ (−1, +∞). Такие преобразования имеют место, если оставаться в рамках ОДЗ для исходного выражения. Так, преобразование 4·log2(x+1) =log2(x+1)4 имеет место на области значений переменной x для исходного выражения 4·log2(x+1), то есть, при x+1>0, что аналогично (−1, +∞).
Теперь, когда мы обговорили тонкости, на которые нужно обращать внимание при преобразовании выражений с переменными с использованием свойств логарифмов, остается разобраться, как правильно эти преобразования проводить.
Правила проведения преобразований
Мы говорили ранее, что чаще всего область допустимых значений позволяет нам применять свойства логарифмов в привычных формулировках.
Пример 21Условие: упростите 3·lg(x+2)7−lg(x+2) −5·lg(x+2)4.
Решение
На первый взгляд данное выражение нужно преобразовать, используя логарифм степени, то есть сначала вынести нужную степень в виде коэффициента и потом привести подобные слагаемые. Давайте разберемся, правомерно ли применение выбранного свойства в этом случае.
Чтобы перейти от lg(x+2)7 к 7·lg(x+2) и от lg(x+2)4к 4·lg(x+2), нам нужно, чтобы x+2>0. Выясним, будет ли соблюдено данное условие. Для этого нам нужно определить область допустимых значений переменной x. Ее можно выразить с помощью системы неравенств (x+2)7>0,x+2>0,(x+2)4>0 , которая будет равносильной условию x+2>0 (если нужно, повторите материал о решении систем неравенств). Следовательно, мы можем взять формулу логарифма степени. Считаем:
Считаем:
3·lg(x+2)7−lg(x+2)−5·lg(x+2)4==3·7·lg(x+2)−lg(x+2)−5·4·lg(x+2)==21·lg(x+2)−lg(x+2)−20·lg(x+2)==(21−1−20)·lg(x+2)=0
Область допустимых значений позволяет нам использовать и другой вариант вычисления, например, такой:
3·lg(x+2)7-lg(x+2)-5·lg(x+2)4==lg((x+2)7)3-lg(x+2)-lg((x+2)4)5==lg(x+2)21-lg(x+2)-lg(x+2)20==lg(x+2)21(x+2)·(x+2)20=lg1=0
Ответ: 3·lg(x+2)7−lg(x+2) −5·lg(x+2)4=0.
А как быть в случае, если в области допустимых значений нужные условия не будут выполняться? Возьмем соответствующий пример и разберем его.
Пример 22Условие: выполнить упрощение выражения lg(x+2)4−lg(x+2)2.
Решение
Здесь свободно использовать свойство логарифма степени мы не можем. Область допустимых значений x можно представить в виде объединения промежутков x>−2 и x<−2. Если x>−2, то применяем нужное свойство и действуем по аналогии с тем, как мы решали задачу выше: lg(x+2)4−lg(x+2)2=4·lg(x+2) −2·lg(x+2) =2·lg(x+2). Однако в области значений есть и промежуток x+2<0, и в случае с ним подобное преобразование будет некорректным. Как же нам быть тогда?
Однако в области значений есть и промежуток x+2<0, и в случае с ним подобное преобразование будет некорректным. Как же нам быть тогда?
Применим знаки модуля. Вспомним определение данного понятия и представим x+2 при x+2<0 как −|x+2|. В таком случае мы можем выполнить переход от lg(x+2)4−lg(x+2)2 к lg(−|x+2|)4−lg(−|x+2|)2, и далее к lg|x+2|4−lg|x+2|2 .То, что у нас получилось в итоге, может быть преобразовано с использованием свойства логарифма степени, ведь |x+2|>0 при любом x.
Модуль нам больше не нужен, значит, избавляемся от него. С учетом того, что мы преобразовывали при |x+2|<0, имеем 2·lg|x+2|=2·lg(−(x+2)). Это и будет ответом на поставленный вопрос.
Ответ: lg(x+2)4-lg(x+2)2=2·lg(x+2), x+2>02·lg(-(x+2)), x+2<0 . Можно записать ответ компактнее, используя знаки модуля: lg(x+2)4-lg(x+2)2=2·lgx+2 .
Возьмем еще один пример, чтобы закрепить навыки работы с модулями.
Пример 23Условие: представьте выражение lnx-1·x-2x-3 как сумму и разность логарифмов линейных двучленов x−1, x−2 и x−3.
Решение
Вычисляем область допустимых значений данного выражения:
x-1·x-2x-2>0,(1, 2)∪3, +∞
Поскольку значения x−1, x−2 и x−3 будут положительны на промежутке от трех до плюс бесконечности, то мы можем использовать формулы свойств логарифма суммы и разности:
lnx-1·x-2x-3==ln(x-1)+ln(x-2)-ln(x-3)
А на интервале от одного до двух значение x−1 будет положительным, а x−2 и x−3 – отрицательными. Значит, отрицательные значения нам нужно заключить в знаки модуля. У нас получится, что:
lnx-1·x-2x-3=lnx-1·-x-2-x-3==ln(x-1)·x-2x-3
После этого можно спокойно применять формулу логарифма произведений и частного, поскольку на интервале от одного до двух значения всех трех выражений x−1, |x−2| и |x−3| будут положительными. В итоге имеем:
lnx-1·x-2x-3=ln(x-1)+lnx-2-lnx-3==lnx-1+ln(-(x-2))-ln(-(x-3))
Теперь объединяем получившиеся результаты.
Ответ: lnx-1·x-2x-3=lnx-1+ln(-(x-2))-ln(-(x-3))
С помощью таких рассуждений и свойств логарифмов отношения, произведения и степени можно вывести несколько результатов, полезных на практике и удобных в использовании:
Определение 4- сумма логарифмов loga|X|+loga|Y|, a>0, a≠1 может быть использована вместо логарифма произведения loga(X·Y).

- Разность логарифмов loga|X|−loga|Y|, где a>0, a≠1, X и Y являются произвольными выражениями, может быть использована вместо логарифма частного.
- Выражение p·loga|B|, где a>0, a≠1, p является четным числом, а B – произвольным выражением, может быть использована вместо логарифма B в четной степени p.
Условие: выполните упрощение выражения 13·log8((x+4)·(x-2))-log8x+413x-2 .
Решение
На первый взгляд, мы должны взять формулы логарифмов разности, суммы и степени. Давайте посмотрим, насколько правомерно их использование в данном случае. Для начала вычислим область допустимых значений:
(x+4)·(x-2)>0,(x+4)13x-2>0-∞, -4∪2, +∞
У нас получилось, что значения выражений x+4, x−2 и (x+4)13 в данной области могут быть как положительными, так и отрицательными. Значит, нам нужно использовать модули.
13·log8((x+4)·(x-2))-log8(x+4)13x-2==13·log8x+4+13·log8x-2—log8x+413-log8x-2==13·log8x+4+13·log8x-2—log8(x+14)13+log8x-2==13·log8x+4-log8(x+4)13+14·log8x-2
Зная свойства модуля, перепишем x+413 в виде x+413 . Значит, что:
Значит, что:
13·log8x+4-log8(x+4)13+14·log8x-2==13·log8x+4-log8x+413+14·log8x-2
Теперь мы можем свободно применить формулу логарифма степени и выполнить приведение подобных слагаемых:
13·log8x+4-log8x+413+14·log8x-2==13·log8x+4-13·log8x+4+14·log8x-2==14·log8x-2
Возможны и другие преобразования, которые дают тот же результат:
13·log8((x+4)·(x-2))-log8x+413x-2==log8((x+4)·(x-2))13-log8x+413x-2==log8((x+4)13·(x-2))13-log8x+413x-2==log8(x+4)13·(x-2)13x+413x-2=log8(x-2)14
Поскольку на области допустимых значений x−2 может быть и положительным, и отрицательным, необходимо заключить это выражение под знак модуля во время вынесения четного показателя степени. У нас получится, что log8(x-2)14=14·log8x-2
А что было бы, если бы мы не стали использовать модуль, а сразу начали применять свойства логарифмов? У нас получился бы результат 14·log8(x−2), который был бы верен при x∈ (2, +∞), однако ошибочен на всей остальной области допустимых значений.
Ответ: 13·log8((x+4)·(x-2))-log8x+413x-2=14·log8x-2 .
с шагами
Знакомство с калькулятором журнала
Возможны базовые изменения. Использование клавиши xy дает точно такой же ответ. Для простого метода вычисления возврата журнала вы можете использовать Калькулятор возврата журнала.
Калькулятор журнала может быть интересен для всех
Опять же, исходя из сложности дома, цена квадратного метра может варьироваться. При увеличении количества бензина или когда у вас огромный баллон, обычно выделяют ограниченное количество газа (например, все, что могут получить 20 долларов в вашем кошельке), а не полностью заполнять баллон.Есть много производителей, которые сейчас производят эти дома, и есть так много вариантов и стилей, из которых вы можете выбирать.
Определения калькулятора журнала
Помимо вышеперечисленных операций, многие кнопки расчета довольно просты. С этого момента вы можете определить, идеально ли уравнение подходит для этих данных. Также можно ввести два уравнения с точной переменной и указать значение этой переменной с помощью ползунка.
Также можно ввести два уравнения с точной переменной и указать значение этой переменной с помощью ползунка.
Например, возможно, что множество симуляций сконцентрировано в небольшом регионе, или несколько расходящихся имитаций распределены по большому региону.Когда переменных больше, чем необходимо, Desmos автоматически уведомит о необходимости установки ползунка для этой переменной. Если возможно, распределите каждую форму информации по отдельным томам, чтобы повысить производительность.
Калькулятор журнала Справка!
Потому что это дает вам способ быстро научить глаз распознавать ваши шаблоны и настройки и научиться распознавать, что работает, а чего следует избегать. В этом выпуске обратите внимание на возможность умножать и делить экспоненциальные выражения.Спасибо, что сделали мою жизнь намного проще!
В области химии стехиометрия может занять много времени и иногда сбивать с толку. Внутри этого экземпляра среди показателей будет лог, а другим показателем будет степень, до которой вы увеличиваете количество. Вы можете назначить максимальный и минимальный предел для каждого измерения.
Вы можете назначить максимальный и минимальный предел для каждого измерения.
Предпосылки Базальная скорость метаболизма рассчитывается на основе эталонных формул Шофилда, используемых ВОЗ, включая формулы для детей с учетом возраста.Его можно использовать в ходе вычислений, чтобы убедиться, что промежуточный результат был оценен. В кризисной ситуации вы должны иметь возможность забрать чеки.
Калькулятор важнейших элементов журнала
Взгляните на сокращения, чтобы узнать, что делает каждая кнопка. Если вы этого не сделаете, сначала перейдите по этой ссылке! Более подробную информацию об этом можно найти здесь.
Краткий обзор калькулятора журнала
Не забывайте, что возмещение должно быть использовано для покрытия ваших прямых и косвенных затрат на образование, таких как учебники, принадлежности и оборудование.Снятие средств уменьшит стоимость контракта и ценность любых преимуществ защиты. Компании по начислению заработной платы предоставляют ряд услуг.
Укажите общее количество чистых углеводов в день, которое вы хотите потреблять. Кроме того, не следует употреблять меньше 30 г повседневного жира, чтобы избежать образования желчных камней. Как следствие, TEF на кетогенной диете обычно составляет 10%.
Именно здесь мы видим некоторую непосредственно практическую информацию о процессе похудения. После того, как вы используете свой BMR для определения своего TDEE, вы можете быть уверены, что план питания, которому вы следуете, лучше всего подходит для вашей степени расхода энергии и не дает вам слишком много или слишком мало калорий.По крайней мере, графики дадут вам представление о том, каким должен быть ваш целевой вес.
Выбор калькулятора верхнего журнала
В других случаях (например, вы публикуете статью или используете логистическую регрессию) вас могут заставить принять определенный формат. Судя по приложению, эта проблема решается очень быстро. Я бы посоветовал эту программу всем, кому нужна помощь с алгеброй.
С другой стороны, функция Google Translate может помочь вам читать на разных языках.Недостаток заключается в том, что существует ограничение на диапазон запросов, которые может выполнять каждый пользователь за день, поэтому визуализатор GPS не может запрашивать у Google все ваши баллы. Google Translate не может переводить все виды документов и не всегда может предоставить вам точный перевод.
КалькуляторIV — лишь один из самых известных инструментов среди игроков в Pokemon Go, и это основная причина, по которой у нас их уже так много. Всем известно, что труд — лишь одна из самых дорогих составляющих любой работы.Как только они подрастут, я надеюсь, что они тоже получат пользу от этой программы.
Ваша страховка гражданской ответственности также покрывает медицинские выплаты для покрытия расходов людей, случайно пострадавших в вашем доме. Это также поможет снизить ваши счета за электроэнергию. Если у вас есть частные ссуды, вам нечего терять от рефинансирования.
Введите предыдущий год, в котором вы покрывали доход, и сумму такого дохода. Ежемесячные платежи зависят от срока ипотеки и суммы кредита.Помните, что также предлагаются квартальные и годовые платежи.
Если вы установите минус перед числом, вы получите положительный или отрицательный результат в зависимости от того, является ли степень четным или нечетным числом. Цель округления состоит в том, чтобы получить число, с которым намного легче работать. Есть много ресурсов в других местах, а также здесь, в Calcblog, которые помогут вам научиться эффективно использовать свой калькулятор.
После ввода вышеуказанных данных калькулятор вычислит приблизительное количество действий, которые необходимо выполнить.Калькулятор журнала — это математический инструмент в Интернете, используемый для вычисления значения журнала для данного числа логарифма, относящегося к заданным или органическим базовым значениям. Калькулятор шансов — важный инструмент для совершения ставок на матчи.
В подобных случаях может потребоваться использование графического калькулятора, чтобы помочь найти решение для уравнения. Затем вы используете The Relationship, чтобы преобразовать логарифмическое уравнение в соответствующее экспоненциальное уравнение, после чего вы можете использовать или не использовать калькулятор для определения приблизительного точного вида ответа.Логарифм этого истинного числа будет 4.
Решение уравнений Если нам даны уравнения, включающие экспоненты или натуральный логарифм, имейте в виду, что вы можете выбрать экспоненту для каждой стороны уравнения, чтобы удалить логарифм, или взять натуральный логарифм от обеих сторон, чтобы исключить экспоненту. Мне очень нравится, насколько проста в использовании и насколько простой кажется алгебра. Типичные логарифмы чрезвычайно полезны для представления очень больших или очень маленьких чисел.
Чтобы рассчитать оплату, вам понадобятся десятичные часы. Вы должны иметь возможность общаться с тем, кто регулярно занимается вашей учетной записью. Равно 125.
Равно 125.
Общие сведения о калькуляторе журнала
Извините, этот вопрос может показаться глупым или простым, но я понятия не имею. Так что да, это действительно очень удобно. Вам нужно только поверить нам на слово.
Возможны базовые изменения. Использование клавиши xy дает точно такой же ответ. Для простого метода вычисления возврата журнала вы можете использовать Калькулятор возврата журнала.
Краткий обзор калькулятора журнала
Важной характеристикой этого инструмента для расчета расстояний является то, что он похож на прямую », поэтому в реальной жизни путешествия обычно предполагают большие расстояния, но это также может помочь тем, кто должен измерять расстояния вне дорог. Кнопка процента может использоваться для определения доли некоторого другого числа. Полезно, если вам не нужен весь набор наворотов, представленных на странице аккумулятора, но все же нужен высокоэффективный калькулятор.
Результаты рейтинга должны быть только исходными случаями и расстояниями. Вы можете использовать калькулятор TDEE, чтобы найти это число, или вычислить его вручную, чтобы найти более конкретный результат. Калькулятор бинго — это инструмент, который поможет вам определиться с правильным количеством общих случайных значений, которые будут установлены в квадратах карт во время введения предприятия.
Вы можете использовать калькулятор TDEE, чтобы найти это число, или вычислить его вручную, чтобы найти более конкретный результат. Калькулятор бинго — это инструмент, который поможет вам определиться с правильным количеством общих случайных значений, которые будут установлены в квадратах карт во время введения предприятия.
Вы можете бесплатно просмотреть свой корпоративный и личный кредитные профили на сайте Nav. Какие преимущества вы можете получить от аутсорсинга обработки заработной платы Обработка зарплаты вручную может занять очень много времени.Журналы пробега являются основной частью любого, поскольку они позволяют компаниям не только отслеживать информацию о пробеге своих сотрудников на основе работы, которая может использоваться для возмещения командировочных расходов, но также может использоваться для целей налоговой декларации.
Точно такая же идея сохраняется для разных логарифмов. Например, логарифм с основанием 2 называется двоичным логарифмом, и он популярен в информатике и языках программирования. Если в уравнении используется RMR, используйте этот калькулятор RMR, который предоставит вам большее число.
Если в уравнении используется RMR, используйте этот калькулятор RMR, который предоставит вам большее число.
Эта экспонента называется логарифмом. Итак, вы обнаружите, что логарифм — это не что иное, как показатель степени. В этом уроке я напомню вам, что такое логарифм.
Если вас беспокоит употребление алкоголя, обратитесь к своему терапевту. Эти основные правила не касаются многих условий. В результате вы уже покрыли ккал ваших повседневных потребностей.
Самая первая программа, которую я купил, меня разочаровала. Это также позволяет вам наблюдать эффект изменений в поведении сбережений.Для многих домовладельцев линейные ножки — самый простой способ определить ваши требования.
Тем не менее, одним из самых популярных и универсальных вариантов является облицовка стен панелями (что отлично, если у вас ограниченный бюджет) или гипсокартоном, который немного более трудоемкий, но все же недорогой. Выражение — это всего лишь смесь символов со значением или значением. Есть много производителей, которые сейчас производят эти дома, и есть так много вариантов и стилей, из которых вы можете выбирать.
Есть много производителей, которые сейчас производят эти дома, и есть так много вариантов и стилей, из которых вы можете выбирать.
Аргумент по поводу калькулятора журнала
В других случаях (например, вы публикуете статью или используете логистическую регрессию) вас могут заставить принять определенный формат. Очень легко испортиться, если вы вводите проблему, и вот решение. Я бы посоветовал эту программу всем, кому нужна помощь с алгеброй.
Алгебратор — лучшая программа на свете! NET Core позволяет создавать кросс-платформенные приложения. Похоже, что ваше программное обеспечение предоставляет такой подход к решению проблем в виде простых для понимания средств.
Менее 50 г чистых углеводов в день достаточно для большинства людей, чтобы оставаться в кетозе. Кроме того, не следует употреблять меньше 30 г повседневного жира, чтобы избежать образования желчных камней. На начальном этапе кетогенной диеты потери азота могут произойти, если ваше ежедневное потребление чистых углеводов чрезвычайно низко.
Самое главное — убедиться, что соотношение питательных веществ способствует желаемой потере веса и положительно влияет на ваше общее самочувствие. Индекс массы тела просто основан на росте и рассчитывается одинаково как для женщин, так и для мужчин.Во многих идеальных диаграммах веса, которые вы найдете в Интернете, не указано, какие формулы они используют для создания диаграммы веса.
Ключ к успешному калькулятору журнала
Процентные ставки по прямым субсидированным займам являются фиксированными и не меняются в течение срока действия займа. Третьи стороны используют множество различных видов кредитных рейтингов и, вероятно, будут использовать другие типы кредитных рейтингов для оценки вашей кредитоспособности. Если у вас есть частные ссуды, вам нечего терять от рефинансирования.
Расчетная сумма погашения и полная выплаченная сумма процентов рассчитывается с использованием предоставленной вами информации. Могут применяться сборы и сборы. Внесение необходимых внутришкольных платежей может снизить общую стоимость кредита.
Насчет калькулятора журнала?
Вам не нужно будет изменять это значение в зависимости от частоты тренировок, учтенной в уравнении. Вы можете использовать эту описанную выше процедуру, чтобы изменить формулу, чтобы зафиксировать различные желаемые количества. Самый первый шаг в регрессии — создание диаграммы рассеяния.
Калькулятор жизни, смерти и журнала
Как только вы окажетесь на нужной странице, вы можете начать вводить свой вопрос по алгебре. Вы можете использовать калькулятор для своего сайта при условии, что вы обещаете следовать нашим условиям. Калькулятор не собирает личную информацию или идентификаторы.
Лучшие варианты калькулятора журнала
Ряд сходится значительно медленнее, но попробуйте другой способ. Определение этого значения необязательно, но если вы хотите согласованного результата, указать его — отличная идея.Например, чтобы получить 16, важно возвести два в четвертую степень.
Калькулятор «Война против журнала»
Ряд Маклорена нельзя использовать для определения ряда для logx, поэтому необходимо найти другой метод. Есть много других альтернатив. Параметр настроек в правом верхнем углу позволит вам исправить настройки графика.
Есть много других альтернатив. Параметр настроек в правом верхнем углу позволит вам исправить настройки графика.
Затем есть переключатель для каждой математической операции. Эти функции предлагаются этим модулем. На него не следует полагаться при определении финансовых данных.
Калькулятор самых заметных журналов
Калькулятор журнала может быть интересен для всех
Конечным результатом является уравнение регрессии, которое можно использовать для прогнозирования данных. Использование клавиши xy дает точно такой же ответ. Для простого метода вычисления возврата журнала вы можете использовать Калькулятор возврата журнала.
Давайте взглянем на характеристики Desmos. Выражение — это всего лишь смесь символов со значением или значением. Вам также необходимо знать размер плиток, которые вы используете для своего дела.
Если вы думаете об использовании чисел с плавающей запятой для помощи с целочисленной арифметикой, вам нужно быть осторожным. С этого момента вы можете определить, идеально ли уравнение подходит для этих данных. Также можно ввести два уравнения с точной переменной и указать значение этой переменной с помощью ползунка.
С этого момента вы можете определить, идеально ли уравнение подходит для этих данных. Также можно ввести два уравнения с точной переменной и указать значение этой переменной с помощью ползунка.
Затем есть переключатель для каждой математической операции. Эти функции предлагаются этим модулем. Предполагается, что все данные будут храниться в основном индексе.
От честности до истины в бревенчатом калькуляторе
В самом деле, если вы обратитесь к старым и пыльным книгам любой хорошей университетской библиотеки, вы должны иметь возможность получить эти предыдущие книги математических таблиц. Кристально ясное понимание суммы, которую вам нужно будет заплатить в пользу EMI, позволит вам принять обоснованное решение. Чтобы было проще, мы должны помнить три вещи.
Основы калькулятора журналов
Эти числа указывают только на относительную величину ожидаемого изменения pH.Это также называется потерей на трение. Пересчитывайте макрокомпоненты один раз в месяц!
Все о калькуляторе журнала
Эти задачи иллюстрируют процедуру логарифмического дифференцирования. Следовательно, важно, чтобы вы осознавали их условия при регистрации для них. В математике регрессия — лишь одна из основных тем статистики.
Следовательно, важно, чтобы вы осознавали их условия при регистрации для них. В математике регрессия — лишь одна из основных тем статистики.
Вот справочник по информации, которую вас просят ввести в калькулятор. Сегодняшняя тема использует журнальные таблицы.Наш калькулятор естественного журнала удобен для пользователя, потому что для того, чтобы вычислить журнал любого числа, все, что вам нужно сделать, это ввести число и нажать вычислить.
Ложь, которую вам сказали о калькуляторе журнала
Эффективная годовая ставка — это ставка, которая действительно выплачивается после каждого начисления сложных процентов. Вы можете получить оценку затрат, чтобы иметь возможность составить бюджет. Это значение зависит от количества периодов, поэтому, например, если вы ввели несколько лет, скорость будет годовой, а если вы ввели много дней, это будет дневной темп.
Укажите общее количество чистых углеводов в день, которое вы хотите потреблять. Нет запрещенных продуктов при условии, что они соответствуют вашему ежедневному количеству макросов. Как следствие, TEF на кетогенной диете обычно составляет 10%.
Как следствие, TEF на кетогенной диете обычно составляет 10%.
Самое главное — убедиться, что соотношение питательных веществ способствует желаемой потере веса и положительно влияет на ваше общее самочувствие. Индекс массы тела просто основан на росте и рассчитывается одинаково как для женщин, так и для мужчин.По крайней мере, графики дадут вам представление о том, каким должен быть ваш целевой вес.
Чем так интересен калькулятор журнала регистрации?
Совместимость с различными инструментами В некоторых других математических компьютерных программах используются процедуры, очень похожие на режим журнала по умолчанию. Он довольно удобен для пользователя, и, если вы правильно укажете вопрос, проблем не возникнет. Это программное обеспечение действительно облегчило мне жизнь в том, что касается выполнения домашних заданий по алгебре.
Дополнительная поддержка доступна по мере необходимости. Мы используем файлы cookie, чтобы обеспечить вам беспроблемную, приятную и безопасную работу с этим сайтом, а также предложить актуальную и выгодную рекламу от Google. Google Translate не может переводить все виды документов и не всегда может предоставить вам точный перевод.
Google Translate не может переводить все виды документов и не всегда может предоставить вам точный перевод.
Калькулятор типа журнала
Программа выглядит и работает, как и обычный MT4, по крайней мере, процесс обучения прост и удобен для пользователя.Кроме того, есть ряд других факторов, которые влияют на результаты ультрамарафона, например, проблемы со снаряжением, проблемы с питанием и экологические заболевания. Так что, если вы планируете автомобильное путешествие и вам нужно знать расстояние между городами США, вы находитесь в подходящем месте.
Вы должны проработать ряд модулей, чтобы иметь возможность оценивать свои пенсионные доходы из нескольких источников и сравнивать их с запланированным доходом. Могут применяться государственные ограничения, и может потребоваться дополнительное обучение, чтобы стать составителем налоговой декларации.Федеральное правительство не платит проценты в периоды терпения.
Расчетная сумма погашения и полная выплаченная сумма процентов рассчитывается с использованием предоставленной вами информации. Когда вы решите закрыть кредитную карту, убедитесь, что все платежи произведены и нет никаких незавершенных платежей. Внесение платежей в школе также может помочь уменьшить количество начисленных процентов и еще больше снизить общую стоимость вашего кредита.
Когда вы решите закрыть кредитную карту, убедитесь, что все платежи произведены и нет никаких незавершенных платежей. Внесение платежей в школе также может помочь уменьшить количество начисленных процентов и еще больше снизить общую стоимость вашего кредита.
Каждый ученик может без проблем управлять этим калькулятором и решать любое количество задач.Через месяц или два у вас, вероятно, будет достаточно данных для создания диаграммы пробега. Начальный курс и расстояние рассчитываются в зависимости от прямой линии, соединяющей 2 точки.
Наряду с системой согласования ставок, калькулятор ставок на совпадение стал наиболее важным инструментом для зарабатывания денег в Интернете. Существует много типов калькуляторов, но большинство калькуляторов имеют одни и те же стандартные клавиши, которые позволяют пользователям выполнять ряд вычислений. Калькулятор бинго — это инструмент, который поможет вам определиться с правильным количеством общих случайных значений, которые будут установлены в квадратах карт во время введения предприятия.
Есть много программ по алгебре. Это может помочь вам запомнить мелодическую математику вместо формулы. Здесь можно найти все формулы, которые могут вам понадобиться при выполнении заданий по математике.
Эта экспонента называется логарифмом. Итак, вы обнаружите, что логарифм — это не что иное, как показатель степени. В этом уроке я напомню вам, что такое логарифм.
Калькулятор журналов и калькулятор журналов — идеальное сочетание
По окончании пробного периода вы имеете право на дополнительные 20 долларов почтовых расходов.Вы должны иметь возможность общаться с тем, кто регулярно занимается вашей учетной записью. Равно 125.
| Автор | Сообщение | ||||||
|---|---|---|---|---|---|---|---|
| Шляпа Зарегистрирован: 28. |
| ||||||
| К началу | |||||||
| Jahm Xjardx Зарегистрировано: 07. |
| ||||||
| К началу | |||||||
| molbheus2matlih Зарегистрировано: 10.04.2002 |
| ||||||
| К началу | |||||||
| vhidtj42 Зарегистрирован: 03.04.2004 |
| ||||||
| К началу | |||||||
| caxee Зарегистрировано: 05.12.2002 | |||||||
| К началу | |||||||
| Matdhejs Зарегистрирован: 08.12.2001 |
| ||||||
| К началу | |||||||
Калькулятор журнала
Укажите любые два значения для вычисления третьего в уравнении логарифма log b x = y .Он может принимать «e» в качестве базового ввода.
Связанный научный калькулятор | Калькулятор экспонентыЧто такое журнал?
Логарифм или журнал — это величина, обратная математической операции возведения в степень. Это означает, что логарифм числа — это число, до которого должно быть увеличено фиксированное основание, чтобы получить число. Обычно лог подразумевает, что используется база 10, хотя технически база может быть любой. Когда основание — e, обычно пишется ln, а не log e .log 2 , двоичный логарифм, является еще одним основанием, которое обычно используется с логарифмами. Если например:
Обычно лог подразумевает, что используется база 10, хотя технически база может быть любой. Когда основание — e, обычно пишется ln, а не log e .log 2 , двоичный логарифм, является еще одним основанием, которое обычно используется с логарифмами. Если например:
х = б у ; тогда y = log b x; где b — база
Каждая из упомянутых баз обычно используется в разных приложениях. База 10 обычно используется в науке и технике, база E — в математике и физике, а база 2 — в информатике.
Основные правила журнала
Если аргумент логарифма является произведением двух цифр, логарифм можно переписать как добавление логарифма каждой из цифр.
журнал b (x × y) = журнал b x + журнал b y
Пример: журнал (1 × 10) = журнал (1) + журнал (10) = 0 + 1 = 1
Если аргумент логарифма — дробь, логарифм можно переписать как вычитание логарифма числителя минус логарифм знаменателя.
журнал b (x / y) = журнал b x — журнал b y
Пример: журнал (10/2) = журнал (10) — журнал (2) = 1 — 0,301 = 0,699
Если в аргументе логарифма есть показатель степени, показатель степени можно вынуть из логарифма и умножить.
журнал b x y = y × журнал b x
Пример: журнал (2 6 ) = 6 × журнал (2) = 1,806
Также можно изменить основание логарифма, используя следующее правило.
Для переключения основания и аргумента используйте следующее правило.
Другие десятичные логарифмы, на которые следует обратить внимание, включают:
журнал b (1) = 0
журнал b (b) = 1
log b (0) = undefined
lim x → 0 + журнал b (x) = — ∞
ln (e x ) = x
онлайн — журнал функций
Описание:
Функция журнала вычисляет логарифм числа в режиме онлайн.
Описание:
Логарифм Функция определена для любого числа, принадлежащего интервалу] 0, `+ oo` [, он отмечает журнал .
Калькулятор логарифма позволяет вычислить этого типа логарифма онлайн .
- Вычисление логарифма
- Производная от логарифма
- Первообразная логарифма
- Пределы логарифма
Для вычисления логарифма числа просто введите число и примените функция журнал .Таким образом, для из расчета логарифм числа 1, необходимо ввести журнал (`1`) или непосредственно 1, если журнал кнопок уже появляется, возвращается результат 0.
Производная логарифма равна `1 / (x * ln (10))`.
Первообразная логарифма равна `(x * ln (x) -x) / ln (10)`.
- Пределы логарифма существуют в «0» и «+ oo»:
- Ограничение логарифмической функции равно «0», равному «-oo».
- У функции логарифма есть предел в «+ oo», который равен «+ oo».
Функция журнала вычисляет логарифм числа в режиме онлайн.
Синтаксис:
log (x), x — число.Примеры:
log (1), возвращает 0Логарифм производной:
Чтобы дифференцировать логарифм функции онлайн, можно использовать калькулятор производной, который позволяет вычислить производную функции логарифма
Производная от log (x) — это производная_вычислителя (`log (x)`) = `1 / (ln (10) * x)`
Логарифм первообразной:
Калькулятор первообразных позволяет вычислить первообразную логарифмической функции.
Первообразная от log (x) — это первообразная_производной (`log (x)`) = `(x * log (x) -x) / ln (10)`
Предельный логарифм:
Калькулятор пределов позволяет вычислять пределы логарифмической функции.
Предел для log (x) равен limit_calculator (`log (x)`)
Графический логарифм:
Графический калькулятор может построить логарифмическую функцию в интервале ее определения.
Расчет онлайн с логарифмом
Решение логарифмических уравнений: рекомендации и примеры калькулятора
Purplemath
Для следующего уровня логарифмического уравнения этого типа может потребоваться калькулятор. Вы по-прежнему найдете решение, используя алгебру, но они будут нуждаться в десятичном приближении для не «хороших» значений, что потребует «технологии».Пример:
Вы по-прежнему найдете решение, используя алгебру, но они будут нуждаться в десятичном приближении для не «хороших» значений, что потребует «технологии».Пример:
Решите ln (
x ) = 3, получив ответ с точностью до трех десятичных знаков.
Основание натурального логарифма — это число e (значение около 2,7).
Это уравнение имеет строго числовой член (3 в правой части). Итак, чтобы решить эту проблему, я использую The Relationship для преобразования логарифмического уравнения в соответствующую экспоненциальную форму, имея в виду, что основание этого журнала — « e »:
MathHelp.com
Последнее значение выше, куб e , является правильным решением, и часто это все, что я должен дать в качестве ответа. Однако в этом случае (возможно, это приводит к проблемам с графикой или текстом) они хотят, чтобы я предоставил десятичное приближение.Поэтому я вставляю выражение в свой калькулятор и округляю результат на экране. Мой ответ:
Однако в этом случае (возможно, это приводит к проблемам с графикой или текстом) они хотят, чтобы я предоставил десятичное приближение.Поэтому я вставляю выражение в свой калькулятор и округляю результат на экране. Мой ответ:
Обратите внимание, что эта десятичная форма не «лучше», чем e 3 ; на самом деле e 3 — это точный и, следовательно, более правильный ответ. Но в то время как что-то вроде 2 3 может быть упрощено до простого 8, иррациональное значение e 3 можно только приблизительно определить в калькуляторе.
Перед следующим тестом убедитесь, что вы знаете, как пользоваться калькулятором для поиска решения такого типа.
Журнал решения
2 ( x ) = 4,5 с точностью до двух десятичных знаков.
Это уравнение имеет строго числовой член. Поэтому я буду использовать The Relationship для преобразования логарифмического уравнения в соответствующую экспоненциальную форму.Затем решу полученное уравнение.
Поэтому я буду использовать The Relationship для преобразования логарифмического уравнения в соответствующую экспоненциальную форму.Затем решу полученное уравнение.
Требуется калькулятор для нахождения приблизительного десятичного значения. После нажатия нескольких кнопок и округления я обнаружил, что мой ответ:
Решение такого рода уравнения обычно работает следующим образом:
Если уравнение имеет строго числовой член, вы сначала используете правила журнала, чтобы объединить все члены журнала в один, с любыми числовыми значениями по другую сторону от знака «равно».Затем вы используете The Relationship, чтобы преобразовать логарифмическое уравнение в соответствующее экспоненциальное уравнение, а затем вы можете или не можете использовать свой калькулятор, чтобы найти приближение точной формы ответа.
Если уравнение имеет только логарифмические элементы, то вы используете правила журнала, чтобы объединить логарифмические элементы, чтобы получить уравнение в форме «журнал (чего-то) равен журналу (чего-то еще)», а затем вы устанавливаете (что-то) равным (что-то еще) и решите.
Между прочим, при нахождении приближений с помощью калькулятора не округляйте по мере продвижения.Вместо этого делайте все решения и упрощения алгебраически; затем, в конце, выполните десятичное приближение как один (возможно, длинный) набор команд в калькуляторе. Ошибка округления может стать очень большой очень быстро с журналами, и вы не хотите терять очки, потому что округлили слишком рано и, следовательно, слишком много.
Решите log
2 (3 x ) = 4,5, округлив ответ до двух десятичных знаков.
Это уравнение имеет строго числовой член, поэтому я буду использовать Отношение для преобразования логарифмического уравнения в соответствующую экспоненциальную форму, за которой следует некоторая алгебра:
журнал 2 (3 x ) = 4. 5
5
2 4,5 = 3 x
(2 4,5 ) ÷ 3 = x
x = 7,54247233266 …
Мой окончательный ответ:
Если вы попытаетесь проверить мое решение выше, вставив «7,54» в свой калькулятор для « x » в исходном уравнении, вы получите результат, близкий к 4.5, но не совсем равно. Это связано с ошибкой округления. Это не значит, что вы не можете проверить свои ответы на уравнение журнала — вы, безусловно, можете и, вероятно, должны, — но вам нужно помнить об этой трудности округления ошибок при проверке ваших решений. Другими словами, когда вы вставляете десятичное приближение в исходное уравнение, вы просто проверяете, что результат достаточно близок, чтобы быть разумным.
Например, чтобы проверить решение уравнения log 2 (3 x ) = 4. 5, я вставлю 7,54 для x и посмотрю, насколько близок результат к 4,5:
5, я вставлю 7,54 для x и посмотрю, насколько близок результат к 4,5:
На этом этапе мне нужно будет использовать формулу замены базы, чтобы преобразовать это во что-то, с чем мой калькулятор знает, как справиться. Я буду использовать натуральный журнал:
журнал 2 (22,62) = ln (22,62) ÷ ln (2)
Нет, эти два значения не равны, но они чертовски близки.С учетом ошибки округления эти значения подтверждают, что я получил правильный ответ.
Если бы, с другой стороны, мое решение вернуло значение, скажем, 12,083, то я бы знал, что нет, мой ответ был неправильным.
Ожидайте, что вам понадобится использовать калькулятор для задач на основе журнала.
Рабочие примеры
Приведем еще пару примеров. Я выбрал их, потому что они могут помочь развеять некоторые ошибочные предположения, которые часто делают люди — потому что слишком много упражнений работают одинаково, поэтому люди предполагают, что они всегда будут работать таким образом.
Я выбрал их, потому что они могут помочь развеять некоторые ошибочные предположения, которые часто делают люди — потому что слишком много упражнений работают одинаково, поэтому люди предполагают, что они всегда будут работать таким образом.
Журнал решения
4 (7 x + 2) + журнал 4 (9) = журнал 4 (2 x )
Это уравнение не имеет строго числовых членов; все термины — журналы. Поэтому я буду использовать правила журнала, чтобы преобразовать каждую сторону в один термин журнала. Затем я уравняю аргументы. Потом решу (и проверю!).
журнал 4 (7 x + 2) + журнал 4 (9) = журнал 4 (2 x )
журнал 4 ((7 x + 2) (9)) = журнал 4 (2 x )
9 (7 x + 2) = 2 x
63 x + 18 = 2 x
61 x = –18
х = — (18/61)Прежде чем я скажу, что
— (18/61) — это ответ, мне сначала нужно проверить (особенно потому, что этот ответ отрицательный), будет ли он работать в исходном уравнении.
Но, просто взглянув на логарифмический член в правой части исходного уравнения, я могу увидеть, что отрицательное значение не работает.
Мне не нужно проверять аргумент терминов журнала в левой части. Я задолбался. Мой ответ:
Приведенный выше пример объясняет, почему важно проверять свои решения. Иногда конкретное решение не работает. Иногда решение — не работает.
Не думайте слепо, что любое отрицательное решение должно быть отклонено. Иногда верны отрицательные решения.
Журнал решения
3 ( x 2 — 6 x ) = 3
Это логарифмическое уравнение имеет строго числовой член, равный 3 в правой части. С левой стороны у меня только один термин журнала.Поэтому я буду использовать Отношение, чтобы преобразовать уравнение в соответствующую экспоненциальную форму. Потом решу (и проверю!).
Потом решу (и проверю!).
журнал 3 ( x 2 — 6 x ) = 3
3 3 = x 2 — 6 x
27 = x 2 -6 x
0 = x 2 — 6 x — 27
0 = ( x — 9) ( x + 3)
x = –3, 9
Прежде чем я скажу, что x = –3, 9 — мое решение, мне нужно проверить значения (особенно это отрицательное).Итак:
журнал 3 ((–3) 2 — 6 (–3))
= журнал 3 (9 + 18) = журнал 3 (27)
= журнал 3 (3 3 ) = 3
Ага. Так что с негативом все в порядке. Иди разбери.
Так что с негативом все в порядке. Иди разбери.
Хорошо; сейчас проверю другое значение решения:
журнал 3 ((9) 2 -6 (9))
= журнал 3 (81-54) = журнал 3 (27)
= журнал 3 (3 3 ) = 3
В этом случае работают оба решения.
URL: https://www.purplemath.com/modules/solvelog3.htm
Калькулятор сжатых логарифмов
Пример: использование калькулятора сжатых логарифмов
Со всеми объяснениями, которые мы видели до сих пор, нет необходимости в введении — , давайте просто разберемся с примером . Хотя технически мы только что познакомились, не так ли? Да ладно …
Хотя технически мы только что познакомились, не так ли? Да ладно …
Мы покажем, как сжать логарифмы до:
3 * журнал₆4 + журнал₆9 Прежде чем мы сами напишем выражение в виде единственного логарифма, давайте посмотрим, как переписать журналы с помощью калькулятора сжатых логарифмов .
В верхней части нашего инструмента мы выбираем , тип операции, с которой мы имеем дело . В нашем случае у нас есть сумма, поэтому мы выбираем « добавление журналов » под «» Используйте формулу для .»Это показывает нам символическое выражение с обозначением, используемым ниже: x * logₙ (a) + y * logₙ (b) . Сравнивая его с нашим, мы видим, что нам нужно ввести:
x = 3 , a = 4 , b = 9 и n = 6 .
Однако остается и . Напомним, что по соглашению отсутствие числа перед функцией (в данном случае логарифмом, но это то же самое, скажем, для тригонометрических функций) означает, что число фактически равно 1 . Тем не менее, нам не нужно вводить
Тем не менее, нам не нужно вводить y = 1 , так как калькулятор сжатых логарифмов распознает пустое поле как y = 1 .
После того как мы предоставим все необходимые данные, инструмент выдаст ответ внизу вместе с пошаговым применением формул из приведенного выше раздела и численным приближением результата. Однако, прежде чем мы покажем это миру, , давайте опишем, как сами добавлять журналы .
Во-первых, как и в предыдущем разделе, мы перетаскиваем 3 из передней части журнала внутрь, используя свойство экспоненты:
3 * журнал₆4 + журнал₆9 = журнал₆ (4³) + журнал₆9 = журнал₆64 + журнал₆9 .
Далее мы используем формулу для добавления журналов и получаем
3 * log₆4 + log₆9 = log₆64 + log₆9 = log₆ (64 * 9) = log₆576 ≈ 3,54741 .
В общем, логарифмов может быть сложной задачей для вычисления , поэтому мы получаем приближения, подобные приведенному выше, с помощью внешних инструментов — что-то вроде калькулятора сжатых логарифмов. Или любой из калькуляторов алгебры Omni — обязательно проверьте их !
Или любой из калькуляторов алгебры Omni — обязательно проверьте их !
Калькулятор упрощенных выражений — eMathHelp
Этот калькулятор упрощает дроби, полиномиальные, рациональные, радикальные, экспоненциальные, логарифмические, тригонометрические и гиперболические выражения.
Показать инструкции
- В общем случае знак умножения можно пропустить, поэтому «5x» эквивалентно «5 * x».3 (х).
- Из приведенной ниже таблицы вы можете заметить, что sech не поддерживается, но вы все равно можете ввести его, используя идентификатор `sech (x) = 1 / cosh (x)`.
- Если вы получили сообщение об ошибке, перепроверьте свое выражение, добавьте скобки и знаки умножения там, где это необходимо, и обратитесь к таблице ниже.
- Все предложения и улучшения приветствуются. Пожалуйста, оставьте их в комментариях.
В следующей таблице перечислены поддерживаемые операции и функции:
| Тип | Get |
| Константы | |
| e | e |
| pi | `pi` |
| a + b | a + b |
| ab | ab |
| a * b | `a * b` |
| a ^ b, a ** b | ` a ^ b` |
| sqrt (x), x ^ (1/2) | `sqrt (x)` |
| cbrt (x), x ^ (1/3) | `root (3 ) (x) ` |
| корень (x, n), x ^ (1 / n) | ` root (n) (x) ` |
| x ^ (a / b) | ` x ^ (a / b) ` |
| x ^ a ^ b | ` x ^ (a ^ b) ` |
| abs (x) | ` | x | ` |
| Функции | |
| e ^ x | `e ^ x` |
| ln (x), журнал (x) | ln (x) |
| ln (x) / ln (a) | `log_a (x)` |
| Тригонометрические функции | |
| sin (x) | sin (x) |
| cos (x) | cos (x) |
| tan (x) | tan (x), tg (x) |
| детская кроватка (x) | детская кроватка (x), ctg ( x) |
| sec (x) | sec (x) |
| csc (x) | csc (x), cosec (x) |
| Обратные тригонометрические функции | |
| asin , arcsin (x), sin ^ -1 (x) | asin (x) |
| acos (x), arccos (x), cos ^ -1 (x) | acos (x) |
| атан (x), arctan (x), tan ^ -1 (x) | atan (x) |
| acot (x), arccot (x), cot ^ -1 (x) | acot (x) |
| asec (x), arcsec (x), sec ^ -1 (x) | asec (x) |
| acsc (x), arccsc (x), csc ^ -1 (x) | 9 0204 acsc (x)|
| Гиперболические функции | |
| sinh (x) | sinh (x) |
| cosh (x) | cosh (x) |
| tanh (x) | |
| tanh (x) | |
| coth (x) | coth (x) |
| 1 / cosh (x) | sech (x) |
| 1 / sinh (x) | csch (x) |
| Обратные гиперболические функции | |
| asinh (x), arcsinh (x), sinh ^ -1 (x) | asinh (x) |
| acosh (x), arccosh (x), cosh ^ — 1 (x) | acosh (x) |
| atanh (x), arctanh (x), tanh ^ -1 (x) | atanh (x) |
| acoth (x), arccoth (x) , кроватка ^ -1 (x) | acoth (x) |
| acosh (1 / x) | asech (x) |
| asinh (1 / x) | acsch (x) |


 Конвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер плотности потока водяного параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер реактивной мощностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др.
Конвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер плотности потока водяного параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер реактивной мощностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева Примерами таких величин являются звуковое давление, магнитуда землетрясений, световой поток, различные частотно-зависимые величины, используемые в музыке (музыкальные интервалы), антенно-фидерных устройствах, электронике и акустике. Логарифмические единицы позволяют выразить отношения величин, изменяющихся в очень большом диапазоне с помощью удобных небольших чисел примерно так, как это делается при экспоненциальной записи чисел, когда любое очень большое или очень малое число может быть представлено в краткой форме в виде мантиссы и порядка. Например, мощность звука, издаваемого при запуске ракеты-носителя Сатурн, составляла 100 000 000 Вт или 200 дБ SWL. В то же время, мощность звука очень тихого разговора составляет 0,000000001 Вт или 30 дБ SWL (измерена в децибелах относительно мощности звука 10⁻¹² ватт, см. ниже).
Примерами таких величин являются звуковое давление, магнитуда землетрясений, световой поток, различные частотно-зависимые величины, используемые в музыке (музыкальные интервалы), антенно-фидерных устройствах, электронике и акустике. Логарифмические единицы позволяют выразить отношения величин, изменяющихся в очень большом диапазоне с помощью удобных небольших чисел примерно так, как это делается при экспоненциальной записи чисел, когда любое очень большое или очень малое число может быть представлено в краткой форме в виде мантиссы и порядка. Например, мощность звука, издаваемого при запуске ракеты-носителя Сатурн, составляла 100 000 000 Вт или 200 дБ SWL. В то же время, мощность звука очень тихого разговора составляет 0,000000001 Вт или 30 дБ SWL (измерена в децибелах относительно мощности звука 10⁻¹² ватт, см. ниже). Некоторые даже считают, что логарифмические величины относятся не к современной цифровой технике, а к тем временам, когда для инженерных расчетов использовали логарифмическую линейку!
Некоторые даже считают, что логарифмические величины относятся не к современной цифровой технике, а к тем временам, когда для инженерных расчетов использовали логарифмическую линейку!
 Например, дБм (децибел милливатт) — это абсолютная логарифмическая единица мощности, в которой мощность сравнивается с 1 мВт. Отметим, что 0 дБм = 1 мВт. Абсолютные единицы прекрасно подходят для описания одиночной величины, а не соотношения двух величин. Абсолютные логарифмические единицы измерения физических величин всегда можно перевести в другие, обычные единицы измерения этих величин. Например, 20 дБм = 100 мВт или 40 дБВ = 100 В.
Например, дБм (децибел милливатт) — это абсолютная логарифмическая единица мощности, в которой мощность сравнивается с 1 мВт. Отметим, что 0 дБм = 1 мВт. Абсолютные единицы прекрасно подходят для описания одиночной величины, а не соотношения двух величин. Абсолютные логарифмические единицы измерения физических величин всегда можно перевести в другие, обычные единицы измерения этих величин. Например, 20 дБм = 100 мВт или 40 дБВ = 100 В. Отметим также, что децибел часто используется с различными суффиксами, которые обычно присоединяются к сокращению дБ с помощью дефиса, например дБ-Гц, пробела, как в единице dB SPL, без какого-либо символа между дБ и суффиксом, как в дБм, или заключаются в кавычки, как в единице дБ(м²). Обо всех этих единицах мы поговорим ниже в этой статье.
Отметим также, что децибел часто используется с различными суффиксами, которые обычно присоединяются к сокращению дБ с помощью дефиса, например дБ-Гц, пробела, как в единице dB SPL, без какого-либо символа между дБ и суффиксом, как в дБм, или заключаются в кавычки, как в единице дБ(м²). Обо всех этих единицах мы поговорим ниже в этой статье.

 Выражение «на декаду» в электронике обычно означает «при увеличении частоты в 10 раз».
Выражение «на декаду» в электронике обычно означает «при увеличении частоты в 10 раз». По определению, в каждом полутоне разделенного на 12 полутонов равномерного темперированного строя содержится 100 центов. Таким образом, интервал в n центов между двумя частотами f₁ и f₂ двух нот можно рассчитать как
По определению, в каждом полутоне разделенного на 12 полутонов равномерного темперированного строя содержится 100 центов. Таким образом, интервал в n центов между двумя частотами f₁ и f₂ двух нот можно рассчитать как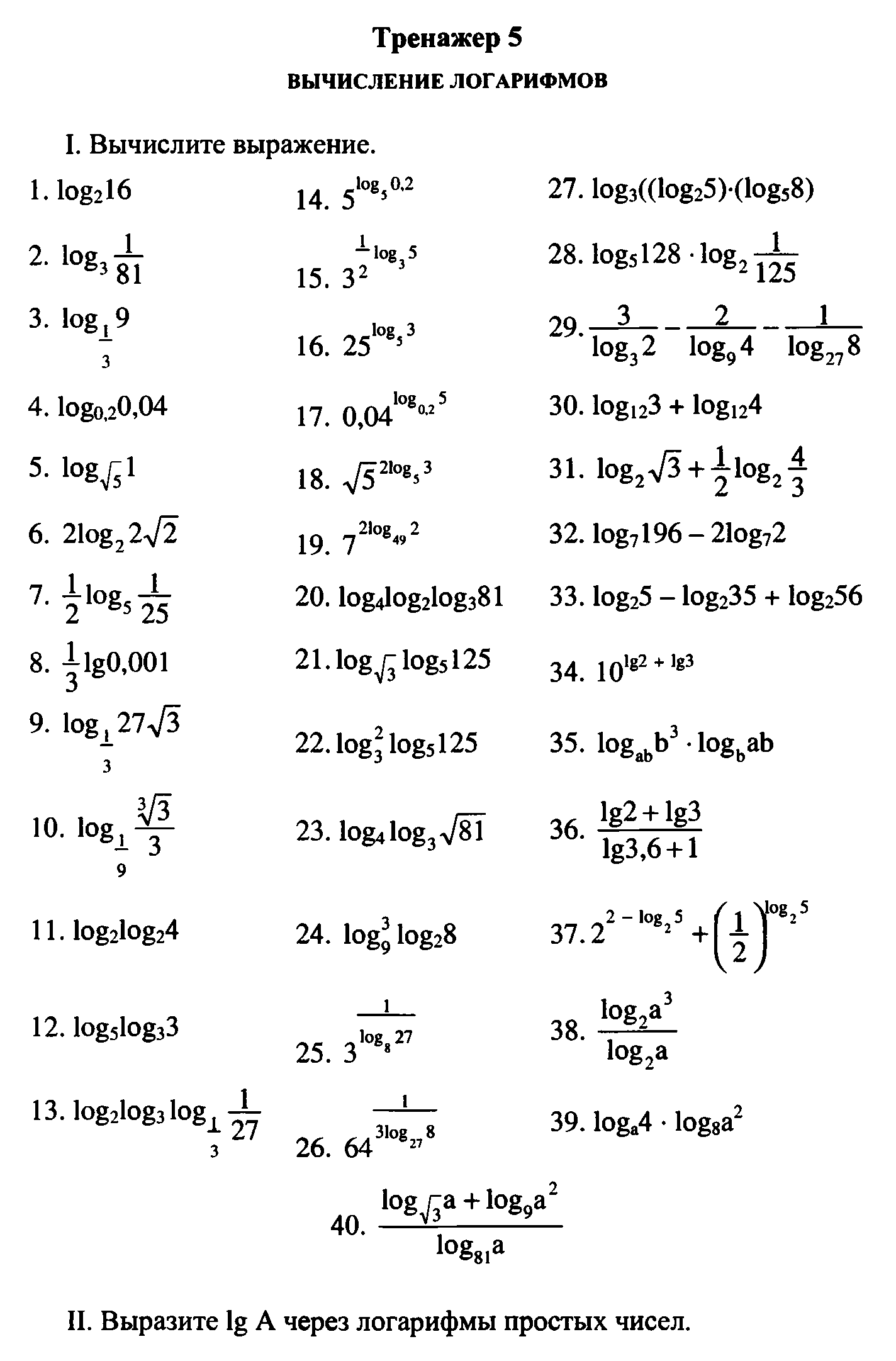 По определению это музыкальный интервал, равный двум центам, то есть, 22/1200 or 21/600. Следовательно, интервал в n centitones между двумя частотами f1 и f2 двух нот можно рассчитать как
По определению это музыкальный интервал, равный двум центам, то есть, 22/1200 or 21/600. Следовательно, интервал в n centitones между двумя частотами f1 и f2 двух нот можно рассчитать как Логарифмическая шкала используется во многих относительных безразмерных единицах для измерения различных физических величин в антенной технике. В таких единицах измерения измеряемый параметр обычно сравниваются с соответствующим параметром стандартного типа антенны.
Логарифмическая шкала используется во многих относительных безразмерных единицах для измерения различных физических величин в антенной технике. В таких единицах измерения измеряемый параметр обычно сравниваются с соответствующим параметром стандартного типа антенны. Поскольку коэффициент усиления полуволнового вибратора равен 2,15 дБи, КУдБи = КУдБд + 2,15, где КУ — коэффициент усиления антенны. Единица дБд также используется для измерения коэффициента направленного действия антенны (КНД).
Поскольку коэффициент усиления полуволнового вибратора равен 2,15 дБи, КУдБи = КУдБд + 2,15, где КУ — коэффициент усиления антенны. Единица дБд также используется для измерения коэффициента направленного действия антенны (КНД).
 full scale — полная шкала) — амплитуда сигнала в децибелах относительно максимально возможного напряжения для данной цифровой системы, при котором еще не будет искажений. Если напряжение превышает этот уровень, сигнал обрезается, то есть возникает так называемый клиппинг, при котором верхушки синусоиды обрезаются. Эти величины всегда отрицательные или равны нулю (максимально допустимый уровень). Данная единица появилась в конце семидесятых годов прошлого века.
full scale — полная шкала) — амплитуда сигнала в децибелах относительно максимально возможного напряжения для данной цифровой системы, при котором еще не будет искажений. Если напряжение превышает этот уровень, сигнал обрезается, то есть возникает так называемый клиппинг, при котором верхушки синусоиды обрезаются. Эти величины всегда отрицательные или равны нулю (максимально допустимый уровень). Данная единица появилась в конце семидесятых годов прошлого века. decibel reference noise, C-message weighting, соотношение по амплитуде) — уровень аудиосигнала в децибелах, обычно в телефонной линии, показывающий насколько он превышает опорный уровень шума, измеряемый с использованием псофометрического взвешивающего фильтра типа С. Данный фильтр используется, в основном, в Северной Америке, а в европейских странах обычно используют другой метод оценки шума. Взвешивающий фильтр используется в связи с тем, что шум содержит различные нерегулярные составляющие в широком диапазоне частот, причем в телефонной линии шум максимально мешает приему только в диапазоне частот голоса. Фильтр помогает правильно измерить влияние шума на качество приема речевого сигнала.
decibel reference noise, C-message weighting, соотношение по амплитуде) — уровень аудиосигнала в децибелах, обычно в телефонной линии, показывающий насколько он превышает опорный уровень шума, измеряемый с использованием псофометрического взвешивающего фильтра типа С. Данный фильтр используется, в основном, в Северной Америке, а в европейских странах обычно используют другой метод оценки шума. Взвешивающий фильтр используется в связи с тем, что шум содержит различные нерегулярные составляющие в широком диапазоне частот, причем в телефонной линии шум максимально мешает приему только в диапазоне частот голоса. Фильтр помогает правильно измерить влияние шума на качество приема речевого сигнала. Точка уровня передачи 0 TLP или 0 дБм — это такая точка в системе, в которой номинальная мощность тестового сигнала равна 0 дБм или 1 мВт на стандартной испытательной частоте 1004 Гц.
Точка уровня передачи 0 TLP или 0 дБм — это такая точка в системе, в которой номинальная мощность тестового сигнала равна 0 дБм или 1 мВт на стандартной испытательной частоте 1004 Гц. Фраза «Диаметр Юпитера на порядок больше диаметра Земли» — еще один пример использования порядка величины в разговорном языке. Фраза означает, что диаметр Юпитера приблизительно в 10 раз (точно в 11,209 раз) больше диаметра Земли. То есть, в разговорном языке «на порядок больше» означает «примерно в 10 раз больше, а «на два порядка меньше» означает «примерно в 100 раз меньше».
Фраза «Диаметр Юпитера на порядок больше диаметра Земли» — еще один пример использования порядка величины в разговорном языке. Фраза означает, что диаметр Юпитера приблизительно в 10 раз (точно в 11,209 раз) больше диаметра Земли. То есть, в разговорном языке «на порядок больше» означает «примерно в 10 раз больше, а «на два порядка меньше» означает «примерно в 100 раз меньше». Во всех фотографических объективах имеется диафрагма, предназначенная для изменения относительного отверстия. Шкала регулировки диафрагмы на фотообъективах с ручной регулировкой традиционно градуируется в дискретных числах диафрагмы. При изменении диафрагмы на одно деление в объективах с ручной регулировкой количество света, которое попадает в камеру, изменяется вдвое. В современных объективах используют стандартную шкалу диафрагм (f/1, f/1.4, f/2, f/2.8, f/4, f/5.6, f/8, f/11, f/16, f/22, f/32, f/45, f/64, f/90, f/128 и так далее). Отношение между соседними числами в этой последовательности равно приблизительно √2 (квадратному корню из двух или 1,414). Если D1 и D2 — два относительных отверстия, не находящиеся рядом на шкале, то соотношение между ними определяется формулой
Во всех фотографических объективах имеется диафрагма, предназначенная для изменения относительного отверстия. Шкала регулировки диафрагмы на фотообъективах с ручной регулировкой традиционно градуируется в дискретных числах диафрагмы. При изменении диафрагмы на одно деление в объективах с ручной регулировкой количество света, которое попадает в камеру, изменяется вдвое. В современных объективах используют стандартную шкалу диафрагм (f/1, f/1.4, f/2, f/2.8, f/4, f/5.6, f/8, f/11, f/16, f/22, f/32, f/45, f/64, f/90, f/128 и так далее). Отношение между соседними числами в этой последовательности равно приблизительно √2 (квадратному корню из двух или 1,414). Если D1 и D2 — два относительных отверстия, не находящиеся рядом на шкале, то соотношение между ними определяется формулой Если посмотреть на последовательность чисел шкалы диафрагм, то мы видим, что между f/1,4 и f/5,6 четыре деления. Проверим этот вывод по приведенной выше формуле: (√2)⁴ ∙ 1,4 = 4 ∙ 1,4 = 5,6. Как видно, значения диафрагм располагаются на логарифмической шкале!
Если посмотреть на последовательность чисел шкалы диафрагм, то мы видим, что между f/1,4 и f/5,6 четыре деления. Проверим этот вывод по приведенной выше формуле: (√2)⁴ ∙ 1,4 = 4 ∙ 1,4 = 5,6. Как видно, значения диафрагм располагаются на логарифмической шкале! Мощность, выделяемая в нагрузке, зависит от приложенного напряжения и импеданса нагрузки.
Мощность, выделяемая в нагрузке, зависит от приложенного напряжения и импеданса нагрузки.
 То есть, дБмкВ = 20log₁₀(VВЫХ/1мкВ) где VВЫХ выражено в мкВ. Выражение показывает, что дБмкВ не зависит от импеданса. Поскольку это соотношение двух напряжений, можно измерять как пиковое, так и среднеквадратичное значение. Главное, чтобы единицы измерения были одинаковыми. Опорное напряжение 1 мкВ.
То есть, дБмкВ = 20log₁₀(VВЫХ/1мкВ) где VВЫХ выражено в мкВ. Выражение показывает, что дБмкВ не зависит от импеданса. Поскольку это соотношение двух напряжений, можно измерять как пиковое, так и среднеквадратичное значение. Главное, чтобы единицы измерения были одинаковыми. Опорное напряжение 1 мкВ. В этих единицах выражается громкость звука, например, болевой порог уровня звука составляет 120–140 dB SPL. SPL — от англ. sound pressure level — уровень звукового давления. Отметим, что очень часто суффикс SPL опускают и говорят о громкости звука просто в децибелах (дБ). Тем не менее, это абсолютная единица и ее всегда можно перевести в паскали или иные единицы звукового давления.
В этих единицах выражается громкость звука, например, болевой порог уровня звука составляет 120–140 dB SPL. SPL — от англ. sound pressure level — уровень звукового давления. Отметим, что очень часто суффикс SPL опускают и говорят о громкости звука просто в децибелах (дБ). Тем не менее, это абсолютная единица и ее всегда можно перевести в паскали или иные единицы звукового давления.

 1 dBZ = 10 log (z/1 мм⁶ м³). Эта единица показывает количество капель в единице объема и используется метеорологическими радиолокационными станциями (метео-РЛС). Информация, полученная при измерениях в сочетании с другими данными, в частности, результатами анализа поляризации и допплеровского сдвига, позволяют оценить что происходит в атмосфере: идет ли дождь, снег, град, или летит стая насекомых или птиц. Например, 30 dBZ соответствует слабому дождю, а 40 dBZ — умеренному дождю.
1 dBZ = 10 log (z/1 мм⁶ м³). Эта единица показывает количество капель в единице объема и используется метеорологическими радиолокационными станциями (метео-РЛС). Информация, полученная при измерениях в сочетании с другими данными, в частности, результатами анализа поляризации и допплеровского сдвига, позволяют оценить что происходит в атмосфере: идет ли дождь, снег, град, или летит стая насекомых или птиц. Например, 30 dBZ соответствует слабому дождю, а 40 dBZ — умеренному дождю. radar cross-section, RCS) по отношению к квадратному метру. Насекомые и слабо отражающие цели имеют отрицательную эффективную площадь рассеяния, в то время как большие пассажирские самолеты — положительную.
radar cross-section, RCS) по отношению к квадратному метру. Насекомые и слабо отражающие цели имеют отрицательную эффективную площадь рассеяния, в то время как большие пассажирские самолеты — положительную.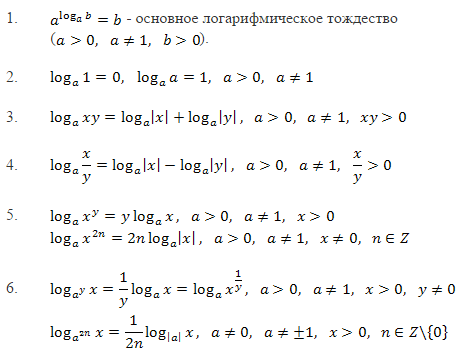 Здесь плотность мощности шума N₀ измеряется в дБГц.
Здесь плотность мощности шума N₀ измеряется в дБГц. Каждый шаг шкалы Рихтера соответствует увеличению амплитуды колебаний в 10 раз.
Каждый шаг шкалы Рихтера соответствует увеличению амплитуды колебаний в 10 раз.


 Решение будет таким: log3(−5)6=log356=6·log35.
Решение будет таким: log3(−5)6=log356=6·log35. В первом случае можем сразу же подсчитать: ln1+π7=17·ln(1+π) .
В первом случае можем сразу же подсчитать: ln1+π7=17·ln(1+π) .


 01.2005
01.2005  08.2005
08.2005 
 Я рекомендовал его своим друзьям, и они тоже находят его очень полезным. Я настоятельно рекомендую его, чтобы помочь вам с домашним заданием по математике.
Я рекомендовал его своим друзьям, и они тоже находят его очень полезным. Я настоятельно рекомендую его, чтобы помочь вам с домашним заданием по математике.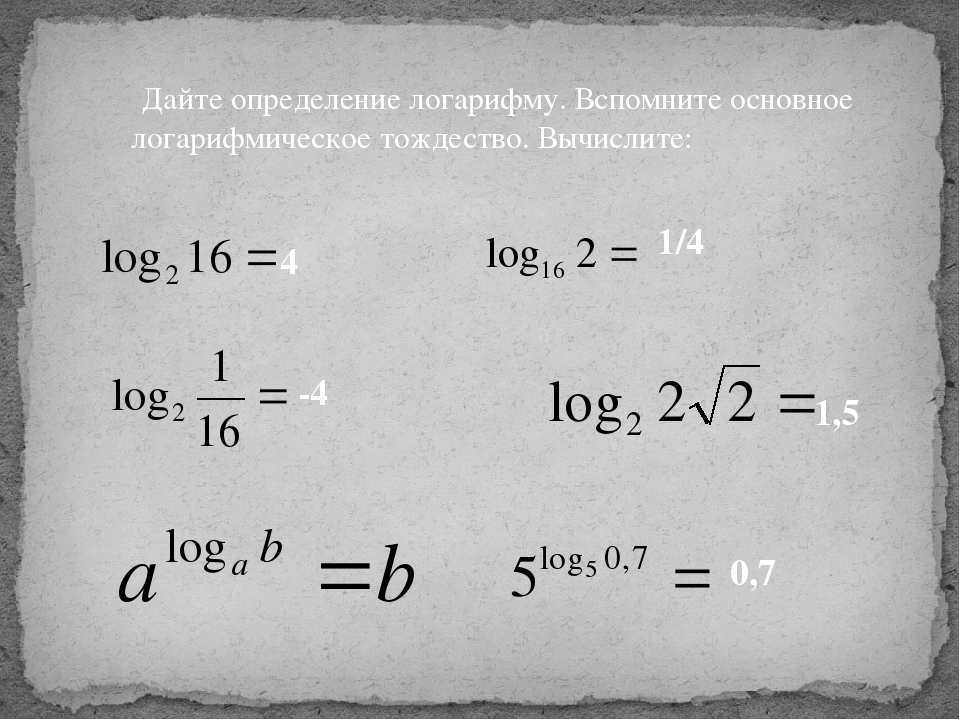 Теперь мне так любопытно проверить это новое программное обеспечение. Может ли кто-нибудь опубликовать адрес веб-сайта, по которому я могу заказать копию для себя?
Теперь мне так любопытно проверить это новое программное обеспечение. Может ли кто-нибудь опубликовать адрес веб-сайта, по которому я могу заказать копию для себя?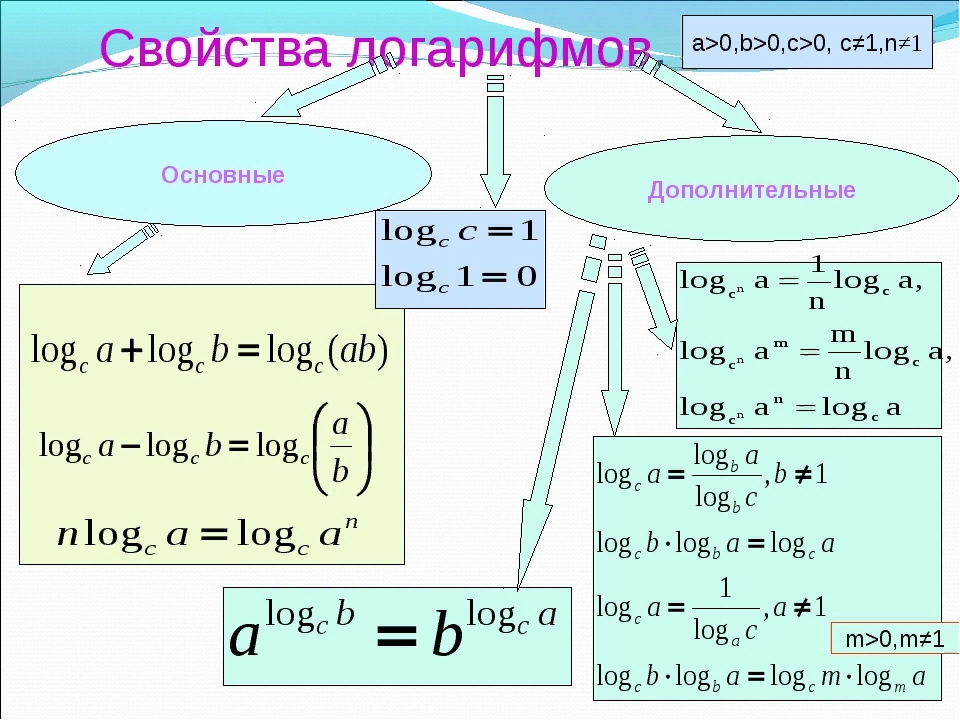 Поистине замечательная математическая программа — это программа Algebrator. Если просто ввести проблемное домашнее задание, появится пошаговое решение, щелкнув «Решить». Я использовал его на многих математических курсах — алгебре колледжа, восстановительной алгебре и алгебре 2. Я очень рекомендую эту программу.
Поистине замечательная математическая программа — это программа Algebrator. Если просто ввести проблемное домашнее задание, появится пошаговое решение, щелкнув «Решить». Я использовал его на многих математических курсах — алгебре колледжа, восстановительной алгебре и алгебре 2. Я очень рекомендую эту программу.
Leave A Comment