Что такое логарифм простыми словами
Многие школьники считают логарифмы сложной темой в курсе математики. Но если разобрать, что такое логарифм подробно, от простого к сложному, то на ЕГЭ вы не станете их опасаться.
Часто у учеников возникает путаница, где аргумент, а где основание логарифма. И что же нужно возвести в степень, чтобы этот логарифм, наконец, посчитать.
В этой статье мы откроем секрет, как легче запомнить принцип решения логарифма.
Итак, давайте разбираться, что такое логарифм.
- Что такое логарифм и как его посчитать
- Зачем логарифмам специальные обозначения
- Основные свойства логарифмов — все формулы в одном месте
- 10 примеров логарифмов с решением
Что такое логарифм и как его посчитать
Логарифм имеет следующий вид:
где a – это основание логарифма,
b – это аргумент логарифма
Чтобы узнать значение логарифма приравняем его к X.и преобразовываем вЗапомните, что именно основание (оно выделено красным) возводится в степень.
Чтобы было легче, можно запоминать так – основание всегда остается внизу (и в первом, и во втором выражении a внизу)!
Приведем пример:
Чтобы вычислить данный логарифм, необходимо приравнять его к X и воспользоваться правилом, описанным выше:А в какую степень нужно возвести 2, чтобы получилось 8? Конечно же в третью степень, таким образом:
Еще раз обращаю ваше внимание, что основание (в нашем случае это – 2) всегда находится внизу и именно оно возводится в степень.
Еще примеры:
Логарифмы со специальным обозначением
Для некоторых логарифмов в математике введены специальные обозначения. Это связано с тем, что такие логарифмы встречаются особенно часто. К таким логарифмам относятся десятичный логарифм и натуральный логарифм. Для этих логарифмов справедливы все правила, что и для обычных логарифмов.
Десятичный логарифм
Десятичный логарифм обозначается lg и имеет основание 10, т.е.
Чтобы вычислить десятичный логарифм, нужно 10 возвести в степень X.
Например, вычислим lg100
Натуральный логарифм
Натуральный логарифм обозначается ln и имеет основание e, то есть
Чтобы вычислить данный логарифм нужно число е возвести в степень x. Некоторые из вас спросят, что это за число такое е? Число е – это иррациональное число, т.е. точное его значение вычислить невозможно. е = 2,718281…
Сейчас не будем подробно разбирать, зачем это число нужно, просто запомним, что
И вычислить его можно таким образом:
Основные свойства логарифмов
Логарифмы можно преобразовывать, но для этого необходимо знать правила, которые называются основными свойствами логарифмов. Данные свойства обязательно нужно знать каждому ученику! Без знания этих свойств невозможно решить ни одну серьезную логарифмическую задачу. Вот эти свойства:
Совет – тренируйтесь применять эти свойства в обе стороны, то есть как слева направо, так и справа налево!
Рассмотрим свойства логарифмов на примерах.
Логарифмический ноль и логарифмическая единица
Это следствия из определения логарифма. И их нужно обязательно запомнить. Эти простейшие свойства нередко вводят учеников в ступор.
Запомните, что логарифм от a по основанию а всегда равен единице:
loga a = 1 – это логарифмическая единица.
Если же в аргументе стоит единица, то такой логарифм всегда равен нулю независимо от основания, так как a0 = 1:
loga 1 = 0 – логарифмический ноль.
Основное логарифмическое тождество
В первой формуле число m становится степенью, которая стоит в аргументе. Данное число может быть любым. Некоторые выражения могут быть решены только с помощью этого тождества.
Вторая формула по сути является просто переформулированным определением логарифма
Разберем применение тождества на примере:
Необходимо найти значение выраженияСначала преобразуем логарифм
Вернемся к исходному выражению и применим правило умножения степеней с одинаковым основанием:Теперь применим основное логарифмическое тождество и получим:
Сумма логарифмов. Разница логарифмов
Логарифмы с одинаковыми основаниями можно складывать:Логарифмы с одинаковыми основаниями можно вычитать:Мы видим, что исходные выражения состояли из логарифмов, которые по отдельности не вычисляются, а при применении свойств логарифмов у нас получились нормальные числа. Поэтому повторим, что основные свойства логарифмов нужно знать обязательно!
Обратите внимание, что формулы суммы и разности логарифмов верны только для логарифмов с одинаковыми основаниями! Если основания разные, то данные свойства применять нельзя!
Вынесение показателя степени из логарифма
Вынесение показателя степени из логарифма:
Переход к новому основанию
Когда мы разбирали формулы суммы и разности логарифмов, то обращали внимание на то, что основания логарифмов должны быть при этом одинаковыми. А что же делать, если основания логарифмов разные? Воспользоваться свойством перехода к новому основанию.
Такие формулы чаще всего нужны при решении логарифмических уравнений и неравенств.
Разберем на примере.
Необходимо найти значение такого выраженияДля начала преобразуем каждый логарифм с помощью свойства вынесения показателя степени из логарифма:
Теперь применим переход к новому основанию для второго логарифма:Подставим полученные результаты в исходное выражение:
10 примеров логарифмов с решением
1. Найти значение выражения2. Найти значение выражения3. Найти значение выражения4. Найти значение выражения5. Найти значение выражения6. Найти значение выраженияСначала найдем значениеДля этого приравняем его к Х:Тогда изначальное выражение принимает вид:
7. Найти значение выраженияПреобразуем наше выражение:Теперь воспользуемся свойством вынесения показателя степени из логарифма и получим: 8. Найти значение выраженияТак как основания логарифмов одинаковые, воспользуемся свойством разности логарифмов:9. Найти значение выраженияТак как основания логарифмов разные, применять свойство суммы логарифмов нельзя. Поэтому решаем каждый логарифм по отдельности:Подставляем полученные значения в исходное выражение:
4 + 3 = 7
10. Найти значение выраженияОбращаем внимание, что данное выражение – это не произведение логарифмов. У логарифма по основанию 4 подлогарифным выражением является log216. Поэтому сначала найдем значение log216, а затем подставим полученный результат в log4:
Надеюсь, теперь вы разобрались, что такое логарифм.
Сегодня мы поговорим о формулах логарифмов и дадим показательные примеры решения. Ранее мы уже познакомились с понятием логарифма. А также рассмотрели основные свойства и примеры решения.
Формулы логарифмов сами по себе подразумевают шаблоны решения согласно основным свойствам логарифмов. Прежде применять формулы логарифмов для решения напомним для вас, сначала все свойства.
Формулы логарифмов. Логарифмы примеры решения






Теперь на основе этих формул(свойств), покажем примеры решения логарифмов.
Примеры решения логарифмов на основании формул
Логарифм положительного числа b по основанию a (обозначается logab) — это показатель степени, в которую надо возвести a, чтобы получить b, при этом b > 0, a > 0, а 1.
Согласно определения logab = x, что равносильно ax = b, поэтому logaax = x.
Логарифмы, примеры:
log28 = 3, т.к. 23 = 8
log749 = 2, т.к. 72 = 49
log51/5 = -1, т.к. 5-1 = 1/5
Десятичный логарифм — это обычный логарифм, в основании которого находится 10. Обозначается как lg.
lg100 = 2
log10100 = 2, т.к. 102 = 100
Натуральный логарифм — также обычный логарифм логарифм, но уже с основанием е (е = 2,71828… — иррациональное число). Обозначается как ln.
Формулы или свойства логарифмов желательно запомнить, потому что они понадобятся нам в дальнейшем при решении логарифмов, логарифмических уравнений и неравенств. Давайте еще раз отработаем каждую формулу на примерах.
Основное логарифмическое тождество
a logab = b
82log83 = (82log83)2 = 32 = 9
Логарифм произведения равен сумме логарифмов loga (bc) = logab + logac
Пример.
log38,1 + log310 = log3 (8,1*10) = log381 = 4
Логарифм частного равен разности логарифмов
loga (b/c) = logab — logac
Пример.
9 log550/9 log52 = 9 log550- log52 = 9 log525 = 9 2 = 81
Свойства степени логарифмируемого числа и основания логарифма
Показатель степени логарифмируемого числа logab m = mlogab
Показатель степени основания логарифма loganb =1/n*logab
loganb m = m/n*logab,
если m = n, получим loganb n = logab
Пример.
log49 = log223 2 = log23
Переход к новому основанию
если c = b, получим logbb = 1
тогда logab = 1/logba
Пример.
log0,83*log31,25 = log0,83*log0,81,25/log0,83 = log0,81,25 = log4/55/4 = -1
Как видите, формулы логарифмов не так сложны как кажутся. Теперь рассмотрев примеры решения логарифмов мы можем переходить к логарифмическим уравнениям.
Источник: https://reshit.ru/formuly-logarifmov-logarifmy-primery-resheniya
Логарифм: что это? Все формулы. Простейшие уравнения и неравенства

Сейчас речь пойдет о трех страшных буквах: l o g.Существовать в нашем бытии они просто так не могут. Обязательно должен быть какой-нибудь индекс — число снизу (основание логарифма) и число после букв (аргумент логарифма).
Прежде, чем мы перейдем к тому, что такое логарифм, решим парочку подводящих примеров.
Чтобы справиться с этим примером, мы проговариваем в голове: какое число нужно дважды (т.к. корень квадратный) умножить само на себя, чтобы получить 81.

А этот пример можно решить по алгоритму (решения показательных уравнений), а можно так же провести разговор с самим собой (главное не вслух, я считаю это нормально, но кого-то вы можете напугать разговором с самим собой): сколько раз нужно число 3 умножить само на себя, чтобы получить 27. Постепенным перемножением мы дойдем до ответа.
Тогда, если дело касается логарифма:
можно сказать так: в какую степень нужно возвести 3 (число снизу — основание логарифма), чтобы получить 27 (число слева — аргумент логарифма). Не напоминает выше стоящий пример?

На самом деле в этом и заключается основная формула (определение логарифма):

Логарифм говорит нам (кому-то кричит): логарифм числа «b» по основанию «a» равняется числу «c». Тогда без логарифма это можно сформулировать так: чтобы получить число «b», требуется число «a» возвести в степень «c». Логарифм — это действие, обратное возведению в степень.
У отца log есть два родных сына: ln и lg. Так же, как сыновья отличаются возрастом (мы говорим о максимальной точности), так и эти логарифмы отличаются основанием (числовым индексом снизу).

Данные логарифмы придумали для упрощения записи. На самом деле в прикладной математики именно логарифмы по такому основанию встречаются чаще всех остальных. А мы все в глубине души народ ленивый, так что почему бы себе жизнь не упростить?
Что нужно запомнить: ln — это обычный логарифм только по основанию e ( e — это число Эйлера, e = 2,7182…, мой номер телефона, кстати, — это последние 11 цифр числа Эйлера, так что буду ждать звонка).
А lg — это обычный логарифм по основанию 10 (10ая система — это система счисления, в которой мы живем, столько пальцев на руках у среднего человека. В общем 10 — это как 9, только на 1 больше).
Как мы не можем существовать без еды, воды, интернета… Так и логарифм не представляет свое существование без ОДЗ.
Всегда, когда существует логарифм, должно быть:
«Почему это так?» — это первый вопрос, который я предоставляю тебе. Советую начать с того, что логарифм — это обратное действие от возведения в степень.
А теперь разберем теорию на практике:
В какую степень нужно возвести два (число в основании), чтобы получить шестнадцать (аргумент логарифма).

Два нужно четыре раза умножить само на себя, чтобы получить 16.
Ответ: 4.
Источник: https://ik-study.ru/ege_math/logharifmy
Логарифмы: правила, основные свойства и формулы :
Логарифмы и правила действий с ними достаточно емкие и простые. Следовательно, разобраться в данной теме вам не составит труда. После того как вы узнаете все правила натуральных логарифмов, любая задача решится самостоятельно.
Первое знакомство с этой темой может показаться скучным и бессмысленным, но именно при помощи логарифмов решились многие проблемы математиков XVI века. «О чем это?» — подумали вы.
Прочтите статью до конца и узнаете, что этот раздел «царицы наук» может быть интересен не только математикам, ученым точных наук, но и простым ученикам средних школ.
Определение логарифма

Начнем с определения логарифма. Как гласят многие учебники: логарифмом числа b по основанию a (logab) является некое число с, для которого выполняется такое равенство: b=ac.
То есть, говоря простыми словами, логарифм — определенная степень, в которую возводим основание, чтобы получить данное число. Но важно помнить, что логарифм вида logab имеет смысл только при: a>0; a — число, отличное от 1; b>0, следовательно, делаем вывод, что логарифм можно найти только у положительных чисел.
Классификация логарифмов по основанию
Логарифмы могут быть с любым положительным числом в основании. Но также существует два вида: натуральный и десятичный логарифмы:
- Натуральный логарифм — логарифм с основанием е (е — число Эйлера, численно приблизительно равняется 2,7, иррациональное число, которое ввели для показательной функции y = ex), обозначается как ln a = logea;
- Десятичный логарифм — логарифм с основанием 10, то есть log10a = lg a.
Основные правила логарифмов
Для начала нужно познакомиться с основным логарифмическим тождеством: alogab=b, далее следуют два таких основных правила:
- loga1 = 0 — так как любое число в нулевой степени равно 1;
- logaa = 1.
Благодаря открытию логарифма для нас не составит труда решить абсолютно любое показательно уравнение, ответ которого нельзя выразить натуральным числом, а только иррациональным. Например: 5х = 9, х = log59 (так как натурального х для данного уравнения не существует).
Действия с логарифмами:

- loga(x · y) = logax+ logay — чтобы найти логарифм произведения, нужно сложить логарифмы сомножителей. Обратите внимание на то, что основания логарифмов одинаковы. Если записать это в обратном порядке, то получим правило сложения логарифмов.
- loga xy = logax — logay — чтобы найти логарифм частного, нужно найти разность логарифмов делимого и делителя. Обратите внимание: основания у логарифмов одинаковы. При записи в обратном порядке получаем правило вычитания логарифмов.
- logakxp = (p/k)*logax — таким образом, если в аргументе и основании логарифма стоят степени, то их можно выносить за знак логарифма.
- logax = logac xc — частный случай предыдущего правила, когда показатели степеней равны, их можно сократить.
- logax = (logbx)(logba) — так называемый модуль перехода, процедура приведения логарифма к другому основанию.
- logax = 1/logxa — частный случай перехода, смена мест основания и данного числа. Все выражение, образно говоря, переворачивается, и логарифм с новым основанием оказывается в знаменателе.
История возникновения логарифмов

В XVI веке возникла необходимость проведения многих приближенных вычислений для решения практических задач, главным образом, в астрономии (например, определение положения судна по Солнцу или звездам).
Эта потребность быстро росла и значительную трудность создавало умножение и деление многозначных чисел. И ученый-математик Непер при тригонометрических расчетах решил заменить трудоемкое умножение на обыкновенное сложение, сопоставив для этого некоторые прогрессии.
Тогда деление, аналогично, заменяется на процедуру попроще и надежнее — вычитание, а дабы извлечь корень n-ой степени, нужно разделить логарифм подкоренного выражения на n. Решение такой нелегкой задачи в математике явно отображало цели Непера в науке.
Вот как он писал об этом в начале своей книги «Рабдология»:
Я всегда старался, насколько позволяли мои силы и способности, освободить людей от трудности и скуки вычислений, докучливость которых обыкновенно отпугивает очень многих от изучения математики.
Название логарифма предложил сам Непер, он был получен путем совмещения греческих слов, которые в сочетании означали “число отношений”.
Основание логарифма ввел Спейдел. Его заимствовал Эйлер из теории о степенях и перенес в теорию логарифмов. Понятие логарифмирования стало известным благодаря Коппе в XIX веке. А использование натуральных и десятичных логарифмов, а также их обозначения появились благодаря Коши.
В 1614 году Джон Непер издал на латыни сочинение «Описание удивительной таблица логарифмов». Там было изложено краткое описание логарифмов, правил и их свойств. Так термин «логарифм» утвердился в точных науках.
Операцию логарифмирования и первое упоминание о ней появилось благодаря Валлису и Иоганну Бернулли, а окончательно установлена она была Эйлером в XVIII веке.

Именно заслуга Эйлера в распространении логарифмической функции вида y = logax на комплексную область. В первой половине XVIII века вышла его книга «Введение в анализ бесконечных», где были современные определения показательной и логарифмической функций.
Логарифмическая функция
Функция вида y = logах (имеет смысл, только если: а > 0, а ≠ 1).
Логарифмическая функция определяется множеством всех положительных чисел, так как запись logах существует только при условии — х > 0;.
Данная функция может принимать абсолютно все значения из множества R (действительных чисел). Так как у всякого действительного числа b есть положительное x, чтобы выполнялось равенство logaх = b, то есть, это уравнение имеет корень — х = аb (следует из того, что logaab= b).
Функция возрастает на промежутке a>0, а убывает на промежутке 01.
Следует помнить, что любые графики логарифмической функции у = logах имеют одну стационарную точку (1;0), так как logа 1 = 0. Это хорошо видно на иллюстрации графика ниже.

Как видим на изображениях, функция не имеет четности или нечетности, не имеет наибольших или наименьших значений, не ограничена сверху или снизу.
Логарифмическая функция y = logаx и показательная функция y = aх, где (а>0, а≠1), взаимно обратные. Это можно видеть на изображении их графиков.
Решение задач с логарифмами
Обычно решение задачи, содержащей логарифмы, основано на преобразовании их в стандартный вид или же направлено на упрощение выражений под знаком логарифма. Или же стоит переводить обычные натуральные числа в логарифмы с нужным основанием, проводить дальнейшие операции по упрощению выражения.
Есть некие тонкости, которые не стоит забывать:
- При решении неравенств, когда обе части стоят под логарифмами по правилу с одним основанием, не спешите «отбрасывать» знак логарифма. Помните о промежутках монотонности логарифмической функции. Так как, если основание больше 1 (случай, когда функция возрастает) — знак неравенства останется без изменений, но когда основание больше 0 и меньше 1 (случай, когда функция убывает) — знак неравенства изменится на противоположный;
- Не забывайте определения логарифма: logах = b, а>0, а≠1 и х>0, чтобы не потерять корней из-за неучтенной области допустимых значений. ОДЗ (область допустимых значений) существует практически для всех сложных функций.
При решении логарифмических уравнений рекомендуется пользоваться равносильными преобразованиями. Также, необходимо быть внимательным и учитывать возможные преобразования, которые способны привести к потере некоторых корней.
Это банальные, но масштабные ошибки, с которыми столкнулись многие на пути поиска верного ответа для задания. Правил решения логарифмов не так уж и много, поэтому эта тема проще, чем другие и последующие, но в ней стоит хорошо разобраться.
Вывод

Данная тема с первого взгляда может показаться сложной и громоздкой, но, исследуя ее глубже и глубже, начинаешь понимать, что тема просто заканчивается, а сложностей так ничего и не вызвало. Мы рассмотрели все свойства, правила и даже ошибки, касающиеся темы логарифмов. Успехов в обучении!
Источник: https://www.syl.ru/article/407401/logarifmyi-pravila-osnovnyie-svoystva-i-formulyi
Свойства логарифмов
Логарифмом положительного числа b по основанию a (a>0, a не равно 1) называют такое число с, что ac = b: log a b=c⇔ a c =b (a>0,a≠1,b>0)
Обратите внимание: логарифм от неположительного числа не определен. Кроме того, в основании логарифма должно быть положительное число, не равное 1. Например, если мы возведем -2 в квадрат, получим число 4, но это не означает, что логарифм по основанию -2 от 4 равен 2.
Основное логарифмическое тождество
a log a b =b (a>0,a≠1) (2)
Важно, что области определения правой и левой частей этой формулы отличаются. Левая часть определена только при b>0, a>0 и a ≠ 1. Правая часть определена при любом b, а от a вообще не зависит. Таким образом, применение основного логарифмического «тождества» при решении уравнений и неравенств может привести к изменению ОДЗ.
Два очевидных следствия определения логарифма
log a a=1 (a>0,a≠1) (3) log a 1=0 (a>0,a≠1) (4)
Действительно, при возведении числа a в первую степень мы получим то же самое число, а при возведении в нулевую степень — единицу.
Логарифм произведения и логарифм частного
log a (bc)= log a b+ log a c (a>0,a≠1,b>0,c>0) (5)
log a b c = log a b− log a c (a>0,a≠1,b>0,c>0) (6)
Хотелось бы предостеречь школьников от бездумного применения данных формул при решении логарифмических уравнений и неравенств. При их использовании «слева направо» происходит сужение ОДЗ, а при переходе от суммы или разности логарифмов к логарифму произведения или частного — расширение ОДЗ.
Действительно, выражение log a (f(x)g(x)) определено в двух случаях: когда обе функции строго положительны либо когда f(x) и g(x) обе меньше нуля.
Преобразуя данное выражение в сумму log a f(x)+ log a g(x) , мы вынуждены ограничиваться только случаем, когда f(x)>0 и g(x)>0. Налицо сужение области допустимых значений, а это категорически недопустимо, т. к. может привести к потере решений. Аналогичная проблема существует и для формулы (6).
Степень можно выносить за знак логарифма
log a b p =p log a b (a>0,a≠1,b>0) (7)
И вновь хотелось бы призвать к аккуратности. Рассмотрим следующий пример:
log a (f (x) 2 =2 log a f(x)
Левая часть равенства определена, очевидно, при всех значениях f(х), кроме нуля. Правая часть — только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени.
Формула перехода к новому основанию
log a b= log c b log c a (a>0,a≠1,b>0,c>0,c≠1) (8)
Тот редкий случай, когда ОДЗ не изменяется при преобразовании. Если вы разумно выбрали основание с (положительное и не равное 1), формула перехода к новому основанию является абсолютно безопасной.
Если в качестве нового основания с выбрать число b, получим важный частный случай формулы (8):
log a b= 1 log b a (a>0,a≠1,b>0,b≠1) (9)
Десятичным логарифмом числа x называется логарифм по основанию 10. Десятичные логарифмы используются довольно часто, поэтому для них введено специальное обозначение: log10x = lg x. Все перечисленные выше формулы сохраняют актуальность для десятичных логарифмов. Например, lg(xy)=lgx+lgy (x>0,y>0) .
Натуральным логарифмом числа x (обозначение lnx) называется логарифм х по основанию e. Число e — иррациональное, приближенно равно 2,71. Например, ln e = 1. Пользуясь формулой (8), можно любой логарифм свести к десятичным или натуральным логарифмам: log a b= lgb lga = lnb lna (a>0,a≠1,b>0)
Несколько простых примеров с логарифмами
Пример 1. Вычислите: lg2 + lg50. Решение. lg2 + lg50 = lg100 = 2. Мы воспользовались формулой суммы логарифмов (5) и определением десятичного логарифма.
Пример 2. Вычислите: lg125/lg5. Решение. lg125/lg5 = log5125 = 3. Мы использовали формулу перехода к новому основанию (8).
| a log a b =b (a>0,a≠1) |
| log a a=1 (a>0,a≠1) |
| log a 1=0 (a>0,a≠1) |
| log a (bc)= log a b+ log a c (a>0,a≠1,b>0,c>0) |
| log a b c = log a b− log a c (a>0,a≠1,b>0,c>0) |
| log a b p =p log a b (a>0,a≠1,b>0) |
| log a b= log c b log c a (a>0,a≠1,b>0,c>0,c≠1) |
| log a b= 1 log b a (a>0,a≠1,b>0,b≠1) |
Источник: http://www.repetitor2000.ru/svoistva_logarifmov_01.html
Факт 1.
\(\bullet\) Логарифм по основанию \(a\) от \(b\) – это число \(t\), которое показывает, в какую степень нужно возвести \(a\), чтобы получить \(b\).
Ограничения: числа \(a\) и \(b\) такие, что \(a>0,\ a\ne 1,\ b>0\).
\[\Large{{\color{blue}{\log_a{b}=t\quad\Leftrightarrow\quad
a^t=b }}}\]
Т.к. мы имеем право возводить в любую степень, то \(t\in
\mathbb{R}\).
Таким образом, верно основное логарифмическое тождество \[{\Large{a^{\log_ab}=b}}\]
\(\bullet\) Справедливы следующие формулы: \[{\large{\begin{array}{|ll|l|}
\hline \qquad \qquad \qquad \qquad {\small{\text{Формулы}}}
&& \qquad \qquad{\small{\text{Ограничения}}}\\
&&\\
\hline \textbf{(1)} \log_a1=0&&a>0, a\ne 1\\
&&\\
\textbf{(2)} \log_aa=1 &&a>0, a\ne 1\\
&&\\
\textbf{(3)} \log_{a}{b^m}=m\log_a|b|&(m —
{\small{\text{четн.}}})&a>0, a\ne 1, b\ne 0\\
&&\\
\textbf{(4)}\log_{a}{b^m}=m\log_ab& (m —
{\small{\text{нечетн.}}})&a>0, a\ne 1, b>0\\
&&\\
\textbf{(5)} \log_{a^n}{b}=\frac 1n\log_{|a|}b&(n —
{\small{\text{четн.}}})&a\ne 0, a\ne 1, b>0\\
&&\\
\textbf{(6)}\log_{a^n}b=\frac1n\log_ab&(n —
{\small{\text{нечетн.}}})&a>0, a\ne 1, b>0\\
&&\\
\textbf{(7)} \log_a{bc}=\log_a|b|+\log_a|c|&&a>0, a\ne 1, bc\ne 0\\
&&\\
\textbf{(8)}
\log_a{\dfrac bc}=\log_a|b|-\log_a|c|&&a>0, a\ne 1,bc\ne 0 \\
&&\\
\textbf{(9)}
a^{\log_ab}=b &&a>0, a\ne 1, b>0\\
&&\\
\textbf{(10)}c^{\log_ab}=b^{\log_ac}&&a>0, a\ne 1, b>0, c>0\\
&&\\
\textbf{(11)} \log_ab\cdot \log_bc=\log_ac && a>0, a\ne 1,b>0, b\ne 1, c>0\\
&&\\
\textbf{(11′}) \log_bc=\dfrac{\log_ac}{\log_ab}&&a>0, a\ne 1,b>0, b\ne 1, c>0\\
&&\\
&&\\
{\small{\text{ЧАСТНЫЕ СЛУЧАИ:}}}&& \\
\textbf{(12)} \log_ab\cdot \log_ba=1 && a>0, a\ne 1, b>0, b\ne 1\\
&&\\
\textbf{(12′}) \log_ab=\dfrac1{\log_ba}&&a>0, a\ne 1, b>0, b\ne 1\\
&&\\ \hline
\end{array}}}\]
Заметим, что при выполнении ограничений данные формулы верны в обе стороны!
Предыдущую статью о показательных уравнениях мы начали с уравнения 2x = 8. Там всё было ясно: x = 3.
А теперь рассмотрим уравнение 2x = 7.
По графику функции y = 2x мы видим, что это уравнение имеет корень, и притом единственный.
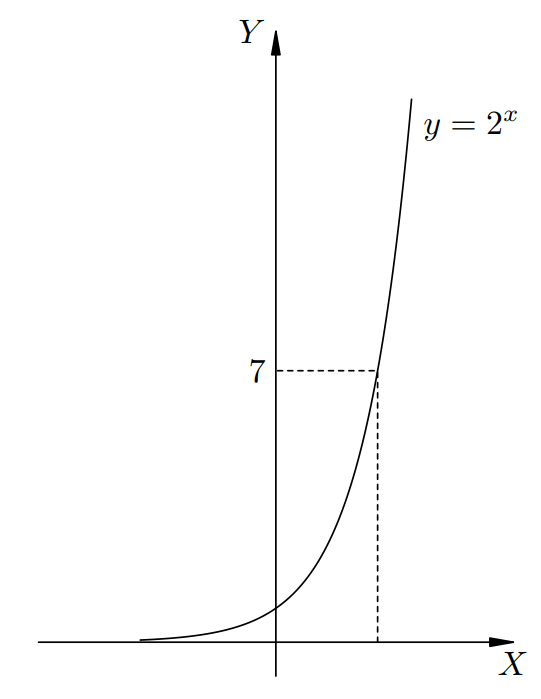
Ясно, что этот корень — не целое число (так как 22 = 4, 23 = 8). Более того, оказывается, что он не является даже рациональным числом, т. е. не представляется в виде обыкновенной дроби. Интуитивно мы чувствуем лишь, что он меньше 3, но не намного.
Этот корень обозначается log27 (читается: «логарифм семи по основанию два». Он является иррациональным числом, т. е. бесконечной непериодической десятичной дробью. Калькулятор даёт: log27 = 2,807354922057604107…
Итак, наше число log27 — это показатель степени, в которую надо возвести 2, чтобы получить 7.
Теперь дадим общее определение логарифма. Пусть a > 0 и a ≠ 1 (условия те же, что и для основания показательной функции).
Определение. Логарифм положительного числа b по основанию a (обозначается logab) — это показатель степени, в которую надо возвести a, чтобы получить b.
Иными словами,

Например:
 так как
так как 
 , так как
, так как 
 так как
так как  ;
;
 , так как
, так как  .
.
Логарифм с основанием 10 называется десятичным и обозначается lg. Например, lg 100 = 2, lg 1000 = 3, lg 0,01 = −2.
Логарифм с основанием e называется натуральным и обозначается ln.
Обратите внимание: логарифм определён только для положительных чисел. Причина заключается в том, что показательная функция может принимать лишь положительные значения. Например, число log2(−4) не существует: в какую бы степень мы ни возводили 2, мы никогда не получим −4.
Не забывайте также про ограничения на основание логарифма: 0 < a < 1 или a > 1.
Основные формулы
По определению, logab — это показатель степени, в которую надо возвести число a, чтобы получить число b:
Формула (1) называется основным логарифмическим тождеством.
Вот еще один вариант записи основного логарифмического тождества:
logaax=x.
Перечислим свойства логарифмов. Они являются простыми следствиями правил действия со степенями. Все логарифмы ниже считаются определёнными.
Логарифм произведения — это сумма логарифмов:
| loga(bc) = logab + logac. | (2) |
Логарифм частного — это разность логарифмов:
| (3) |
Показатель степени логарифмируемого числа «спрыгивает» перед логарифмом:
| (4) |
Показатель степени основания логарифма тоже «спрыгивает», но в виде обратного числа:
| (5) |
Формулы (4) и (5) вместе дают:
 | (6) |
В частности, если m = n, мы получаем формулу:
 | (7) |
Например,  .
.
Наконец, важнейшая формула перехода к новому основанию:
 | (8) |
В частности, если c = b, то logbb = 1, и тогда:
 | (9) |
Приведём несколько примеров из банка заданий.
1.  (применили формулу (2) суммы логарифмов).
(применили формулу (2) суммы логарифмов).
2.  (применили основное логарифмическое тождество(1))
(применили основное логарифмическое тождество(1))
3. (применили формулу (4).
4. (применили формулу (9), перейдя к новому основанию 0,8).
5. (применили формулу (3) разности логарифмов)
Немного истории
Теперь вы поняли, что такое логарифмы и как ими пользоваться. Но для чего они всё-таки нужны? Или это просто такая математическая игрушка с хитрой инструкцией по применению?
Понятие логарифма и логарифмические таблицы появились в 17 веке, и значение их было огромно.
Это в наши дни вычисления не представляют труда — у каждого есть калькулятор. А как считали в «докомпьютерные» времена?
Складывать и вычитать можно было на счётах, а вот умножать и делить приходилось «в столбик» — медленно и трудно.
В 15–17 веках, в эпоху великих географических открытий, стали бурно развиваться торговля, экономика и наука. Требования к математике росли: расчёты становились более сложными, а точность — например, для решения навигационных задач — нужна была всё более высокая.
Необходим был инструмент, позволяющий упростить и ускорить расчёты, и таким инструментом явились логарифмы.
Предположим, что b и c — большие числа, которые надо перемножить. Появление таблиц логарифмов (например, с основанием 10) существенно упростило эту задачу. Теперь вычислителю достаточно было найти по таблицам десятичные логарифмы чисел b и c, сложить их (на счётах) и получить логарифм произведения: lgb + lgc = lg(bc).
А затем по таблице логарифмов найти само произведение чисел b и c.
Недаром французский математик и астроном Лаплас сказал, что изобретение логарифмов удлинило жизнь вычислителей. Логарифмическая линейка (которой инженеры пользовались до 70-х годов двадцатого века) была не менее прогрессивным изобретением, чем современный калькулятор.
Но это еще не всё! Мы не занимались бы логарифмами, если бы они имели лишь историческую, «музейную» ценность. О неожиданных применениях логарифмов мы расскажем в следующей статье, посвящённой логарифмической функции.
ЕГОРОВА ВИКТОРИЯ ВАЛЕРЬЕВНА
Учитель математики
высшей квалификационной категории
ТЕМА: «ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ
ЛОГАРИФМИЧЕСКИХ ВЫРАЖЕНИЙ»
Знания и навыки, которыми должны овладеть учащиеся после изучения данного урока:
знать определение логарифма числа, основное логарифмическое тождество, свойства логарифмов;
уметь выполнять преобразования выражений, содержащих логарифмы, вычислять логарифмы.
Литература:
1. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. и др. Алгебра и начала анализа: учебник для 10-11 классов общеобразовательных учреждений. – М.: Просвещение, 2001.
2. Кочагин В.В., Кочагина М.В., Интенсивный курс подготовки к ЕГЭ. – М.:Эксмо, 2009.
3. Мерзляк А.Г., Полонский В.Б., Якир М.С., Алгебраический тренажер: Пособие для школьников и абитуриентов. – М.:Илекса, 2005.
4. Гусев В.А., Мордкович А.Г. Математика: Справочные материалы: Книга для учащихся. – М.: Просвещение, 2001.
План урока:
Немного истории.
Определение логарифма и основное логарифмическое тождество. Решение примеров.
Натуральный и десятичный логарифмы. Решение примеров.
Формула логарифма произведения двух положительных чисел. Решение примеров.
Формула логарифма частного двух положительных чисел. Решение примеров.
Формула логарифма степени. Решение примеров.
Формула перехода к новому основанию. Решение примеров.
Формула
 . Решение примеров.
. Решение примеров.Решение более сложных примеров.
Подведение итогов.
Контрольное тестирование.
Ход урока:
1) Логарифм – это греческое слово, которое состоит из 2-х слов: “логос”- отношение, “аритмос”- число. Значит, логарифм есть число, измеряющее отношение. В публикации тысяча шестьсот четырнадцатого года сообщалось, что Непер изобрёл логарифмы. Позже им были составлены логарифмические таблицы, которые теперь известны нам как таблицы Брадиса. Менее чем за одно столетие таблицы распространились по всему миру и сделались незаменимым вычислительным средством. В дальнейшем они были, как бы встроены в удобное устройство, чрезвычайно ускоряющее процесс вычисления – логарифмическую линейку, которой пользовались до семидесятых годов двадцатого века.
Приложение 1.
2) Логарифмом положительного числа b по основанию a, причём а больше нуля и не равно единицы, называется показатель степени, в которую нужно возвести число a, чтобы получить число b.
Это равенство, выражающее определение логарифма, называется основным логарифмическим тождеством.
Ц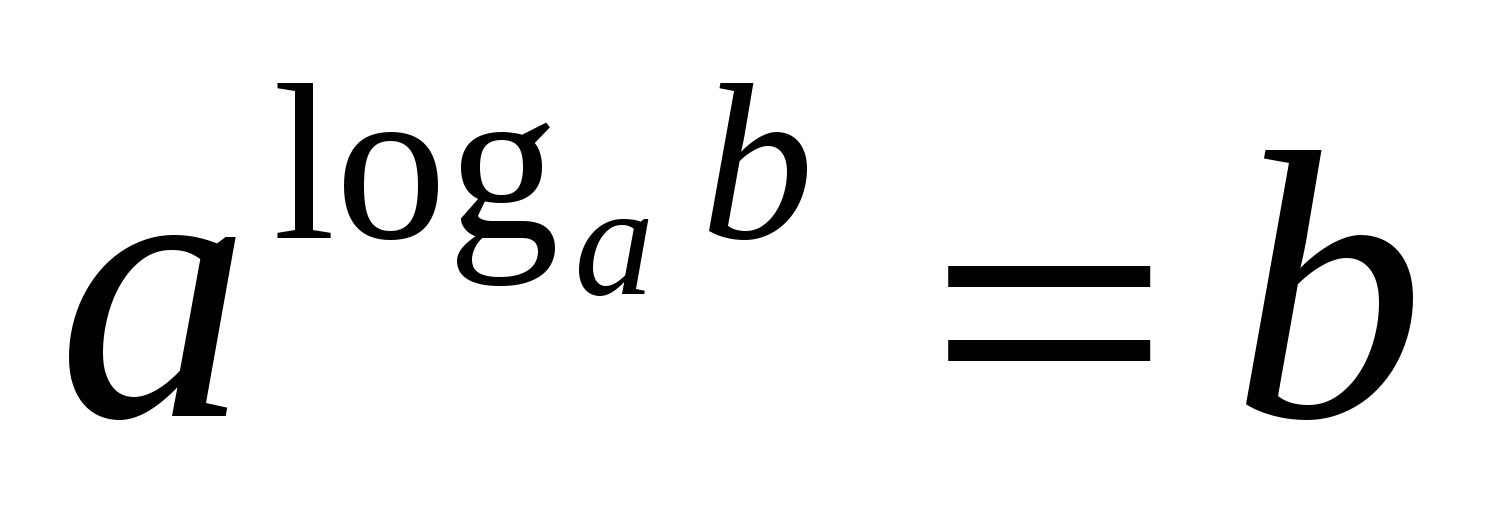
Обратите внимание на основание степени и основание логарифма – они одинаковы.
ОР 1 П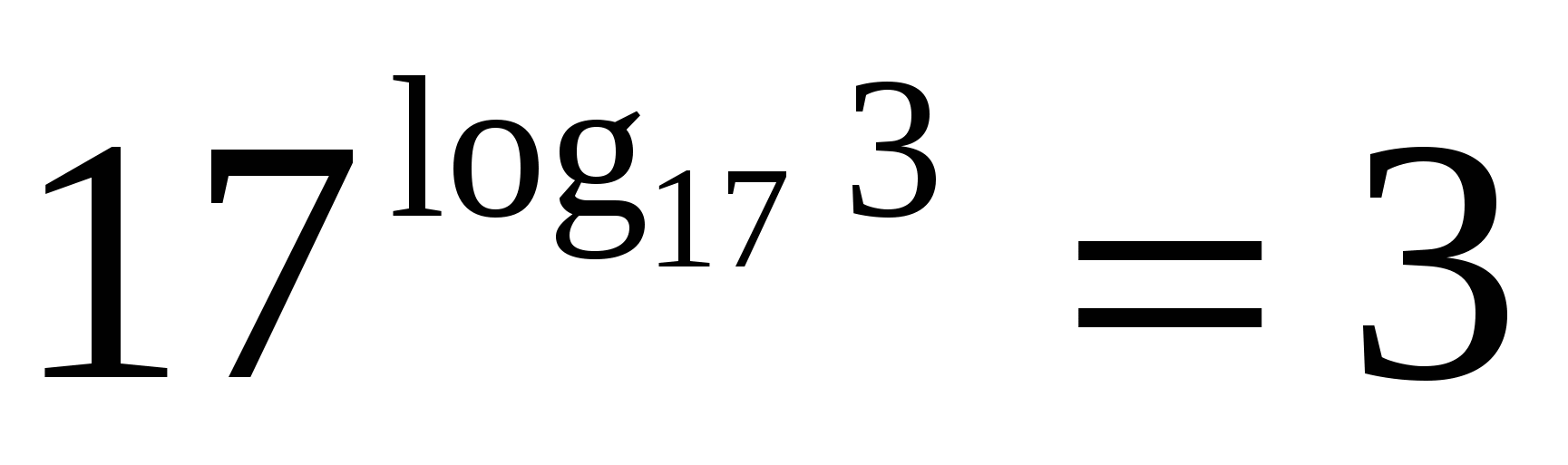
Основание степени и основание логарифма семнадцать, значит по основному логарифмическому тождеству значение выражения равно трём.
оработаем устно: Щ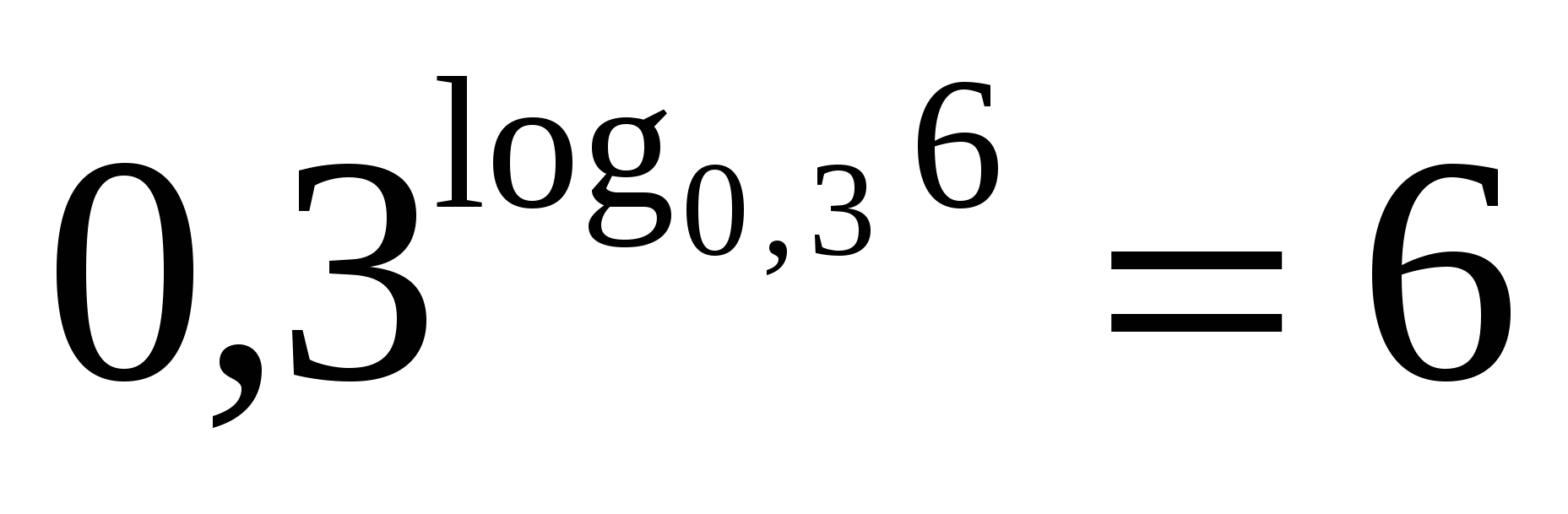 ЕЛЧОК
ЕЛЧОК
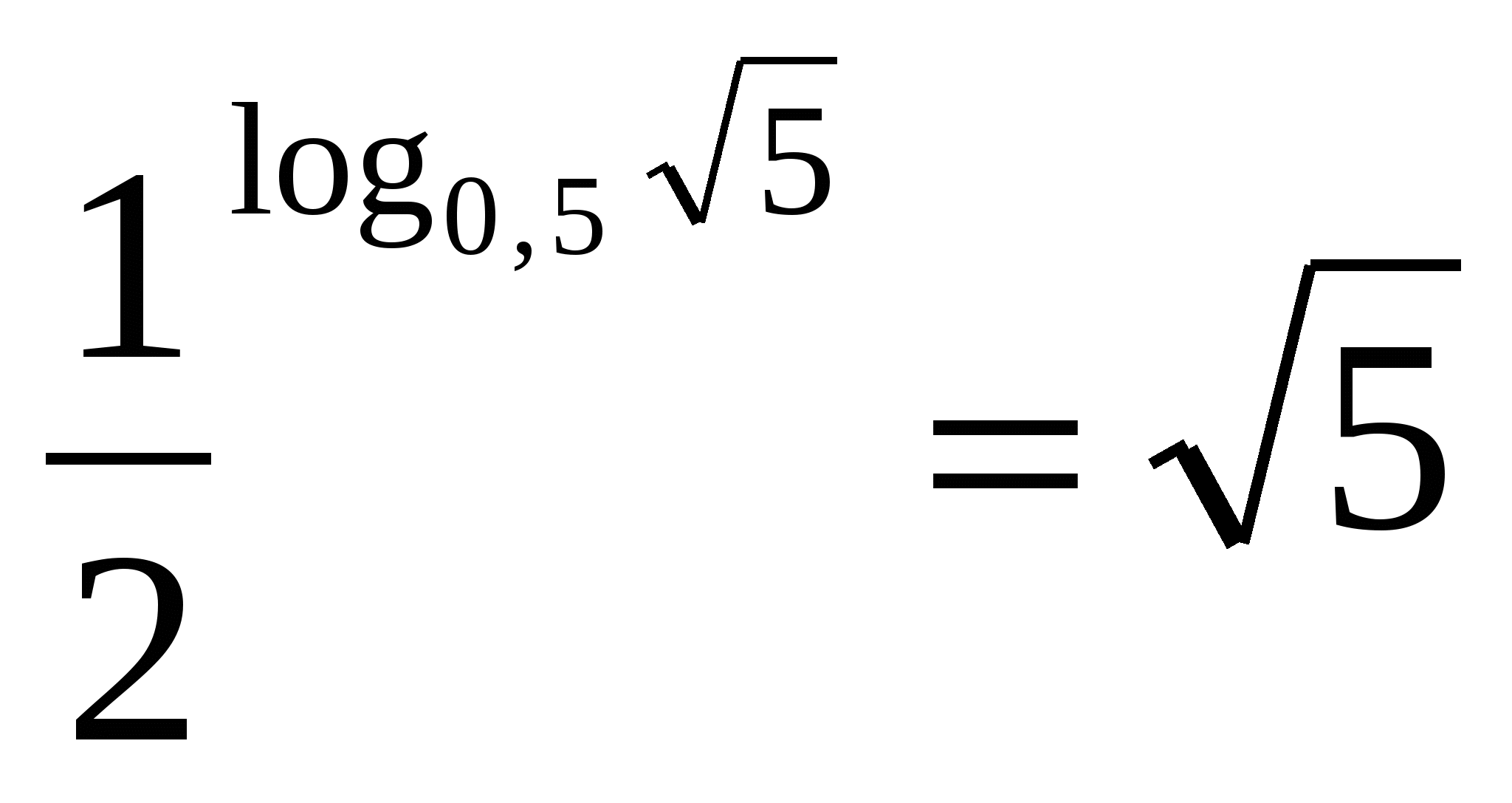
Одна вторая равна нуль целых пяти десятым, значит выражение равно арифметическому квадратному корню из пяти.
П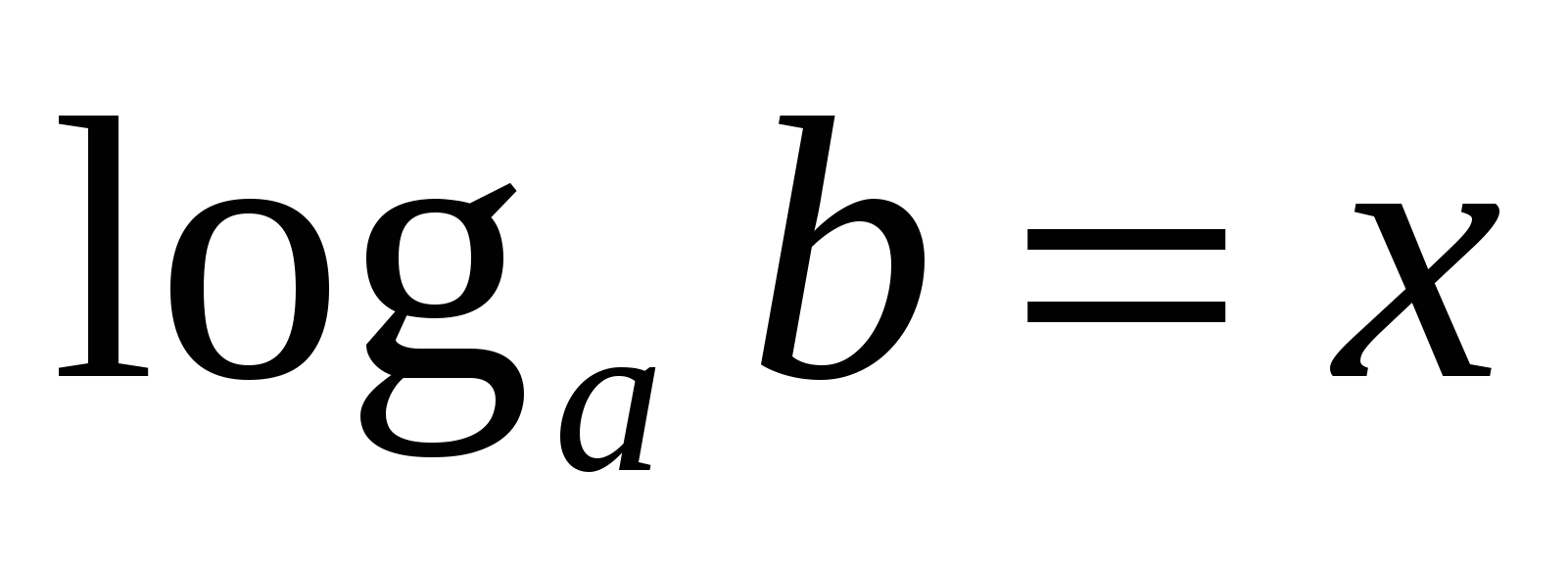
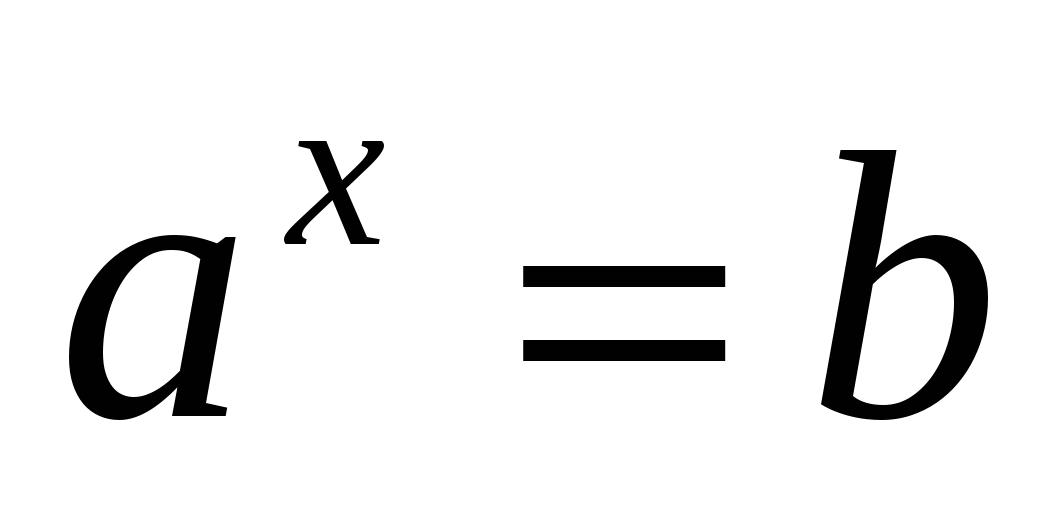 риложение 2.
риложение 2.
Равенство означает, что
Из определения логарифма получаются следующие важные равенства:
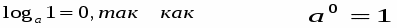

Например:
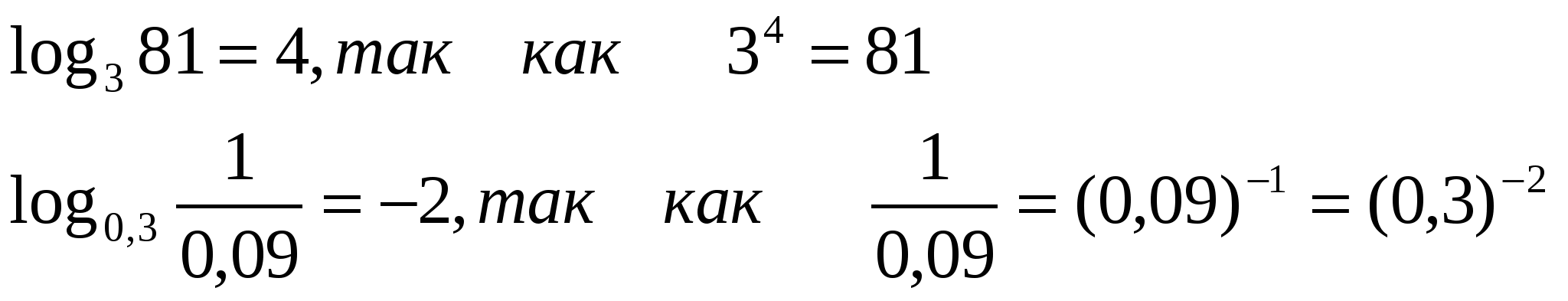
П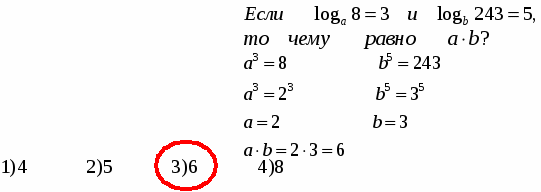 риложение 3.
риложение 3.
Перейдем к заданиям ЕГЭ:
Приложение 4.
3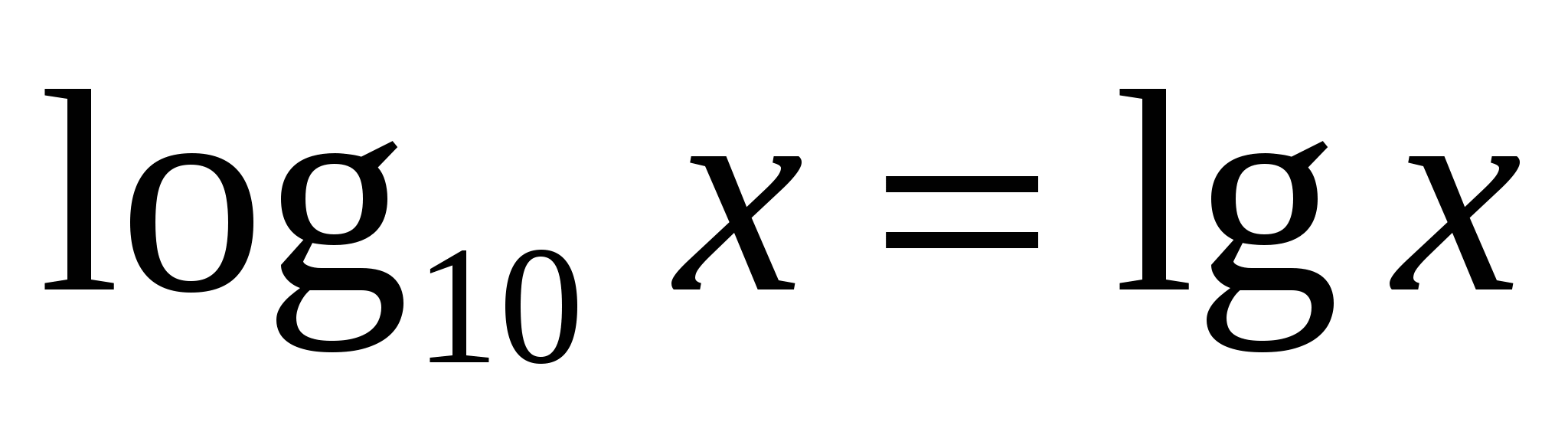 ) Для логарифма по основанию десять существует специальное обозначение и название десятичный логарифм.
) Для логарифма по основанию десять существует специальное обозначение и название десятичный логарифм.
Л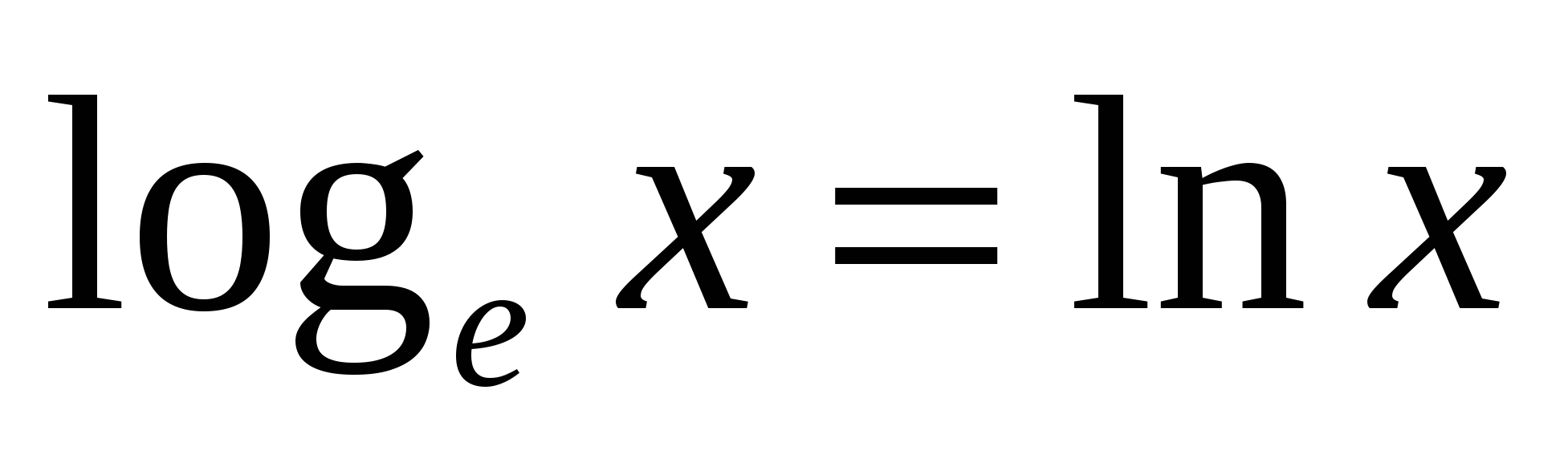 огарифм по основанию е называется натуральным логарифмом.
огарифм по основанию е называется натуральным логарифмом.
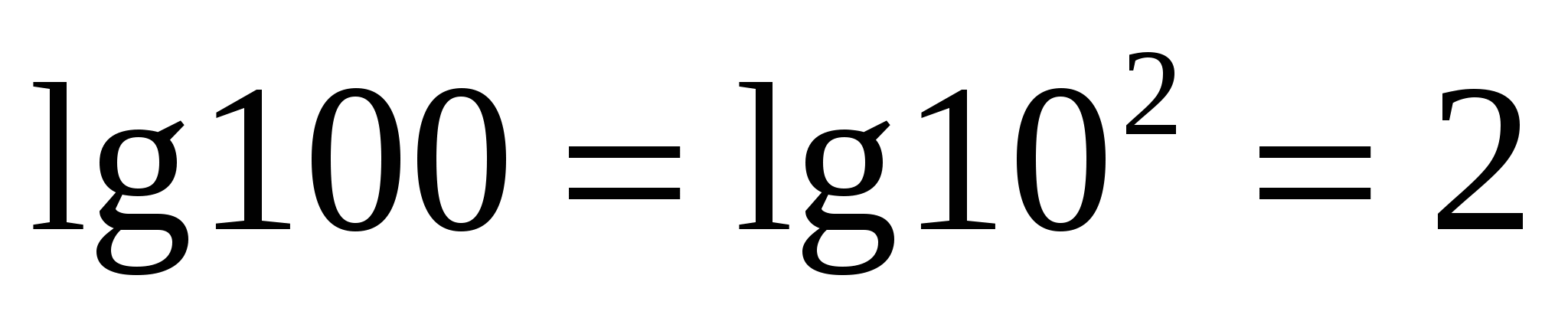
Н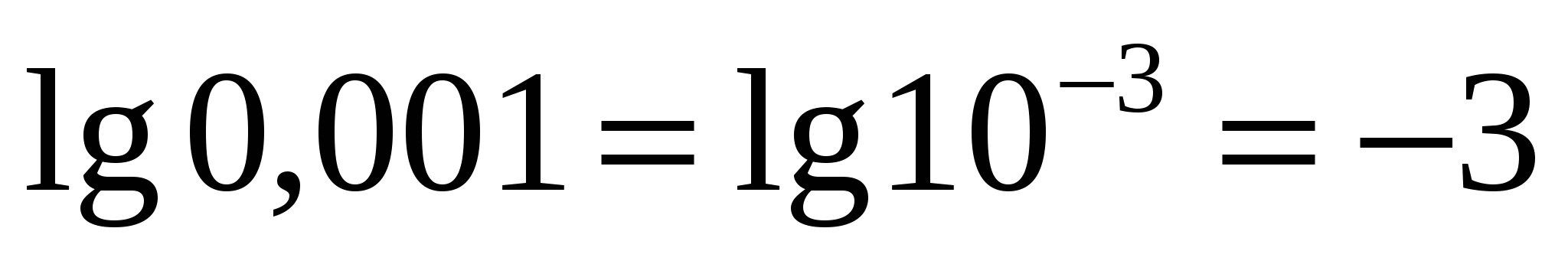 апример,
апример,
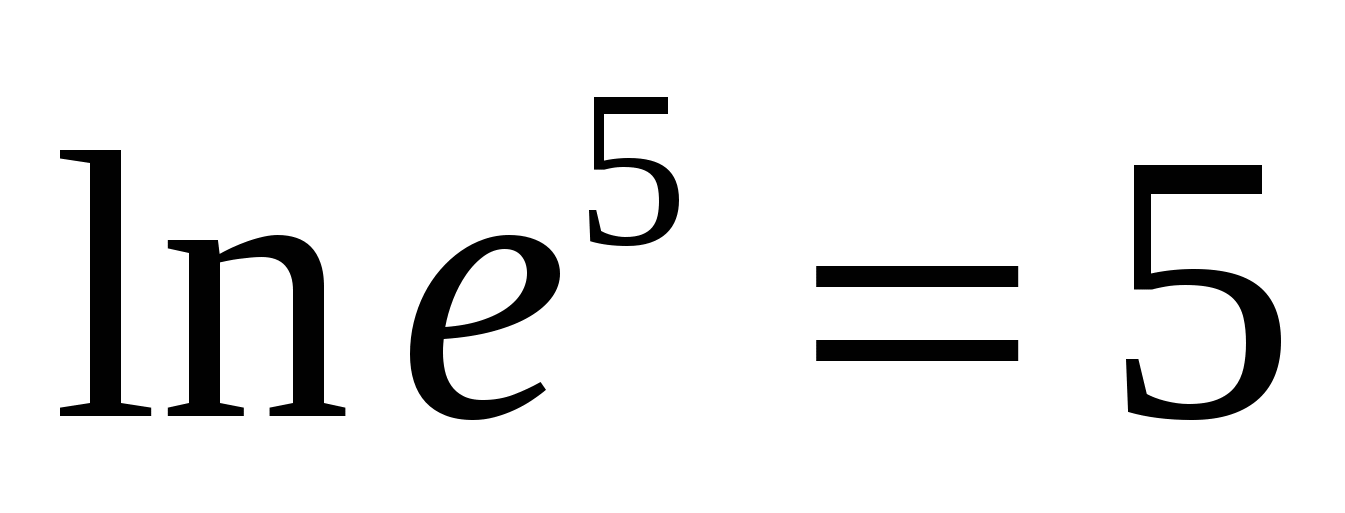
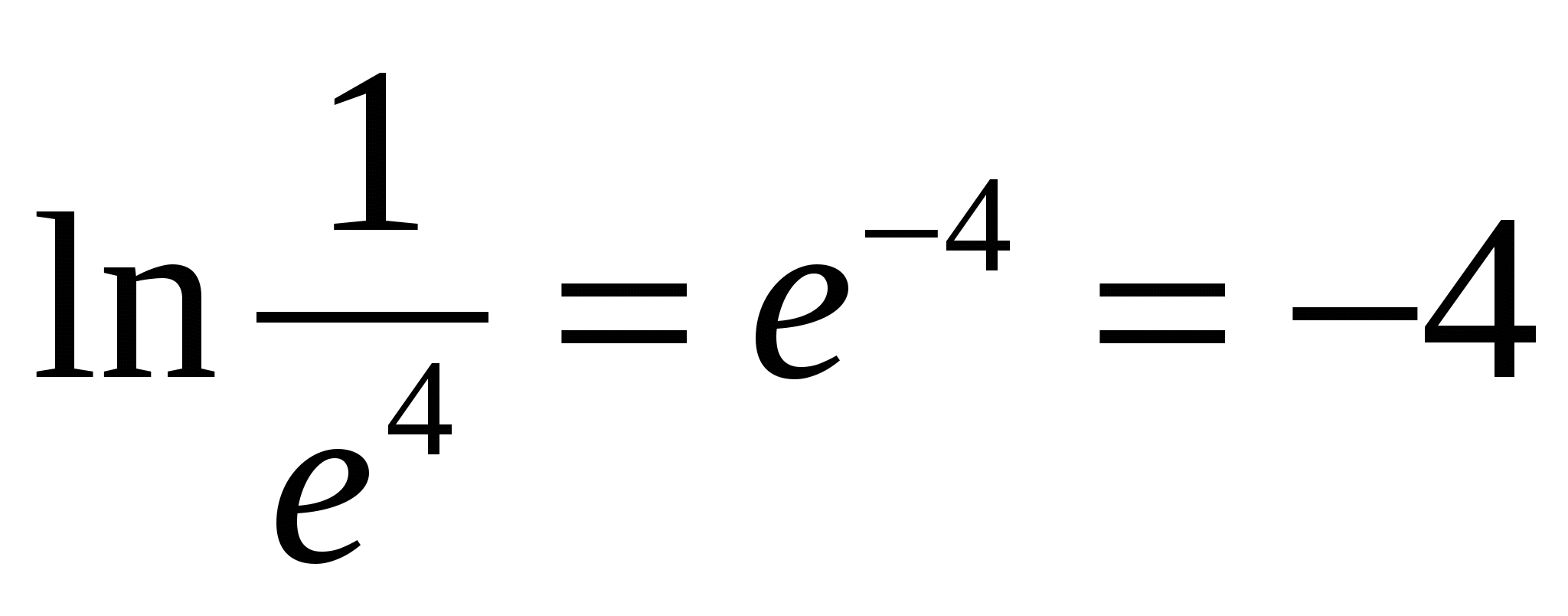
4) Из определения логарифма вытекают следующие его свойства. Все свойства формулируются и доказываются только для положительных значений переменных, содержащихся под знаками логарифмов.
Л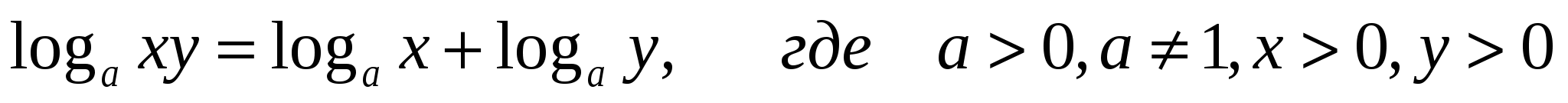 огарифм произведения двух положительных чисел по основанию а равен сумме логарифмов этих чисел с тем же основанием.
огарифм произведения двух положительных чисел по основанию а равен сумме логарифмов этих чисел с тем же основанием.
ЦОР 2
Н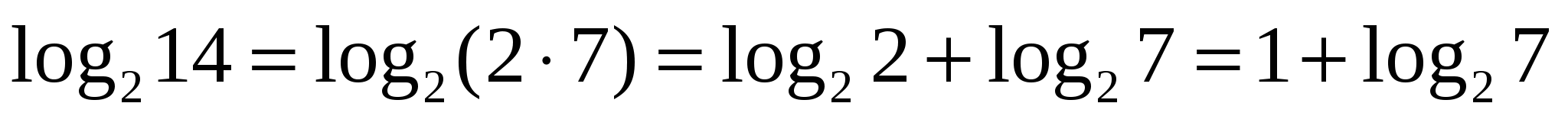 апример,
апример,
З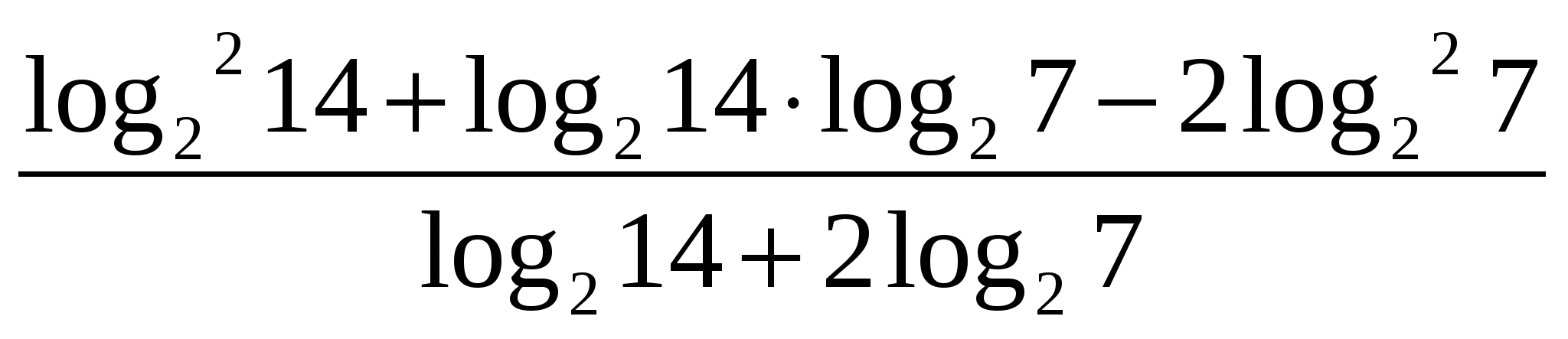 адание 1.
адание 1.
Задание 2. Упростите выражение
В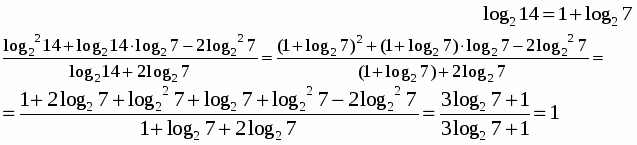 оспользуемся решением предыдущего примера. Заменим
оспользуемся решением предыдущего примера. Заменим
Обратите внимание на то, что логарифм в квадрате, поэтому и сумму необходимо возвести в квадрат. Применяя формулу квадрата суммы, раскроем скобки. Приведём подобные слагаемые.
5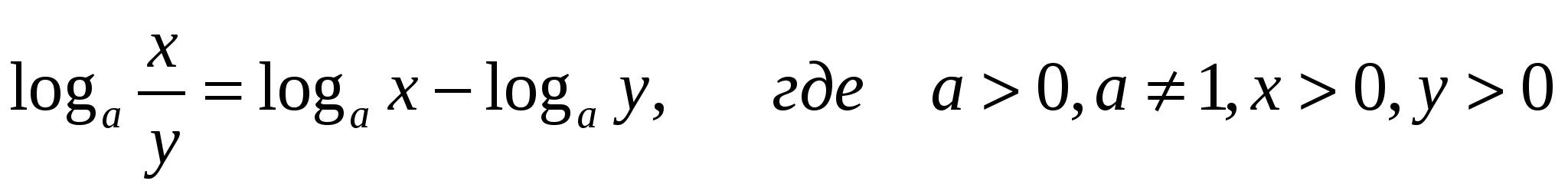 ) Логарифм частного равен разности логарифмов делимого и делителя.
) Логарифм частного равен разности логарифмов делимого и делителя.
Ц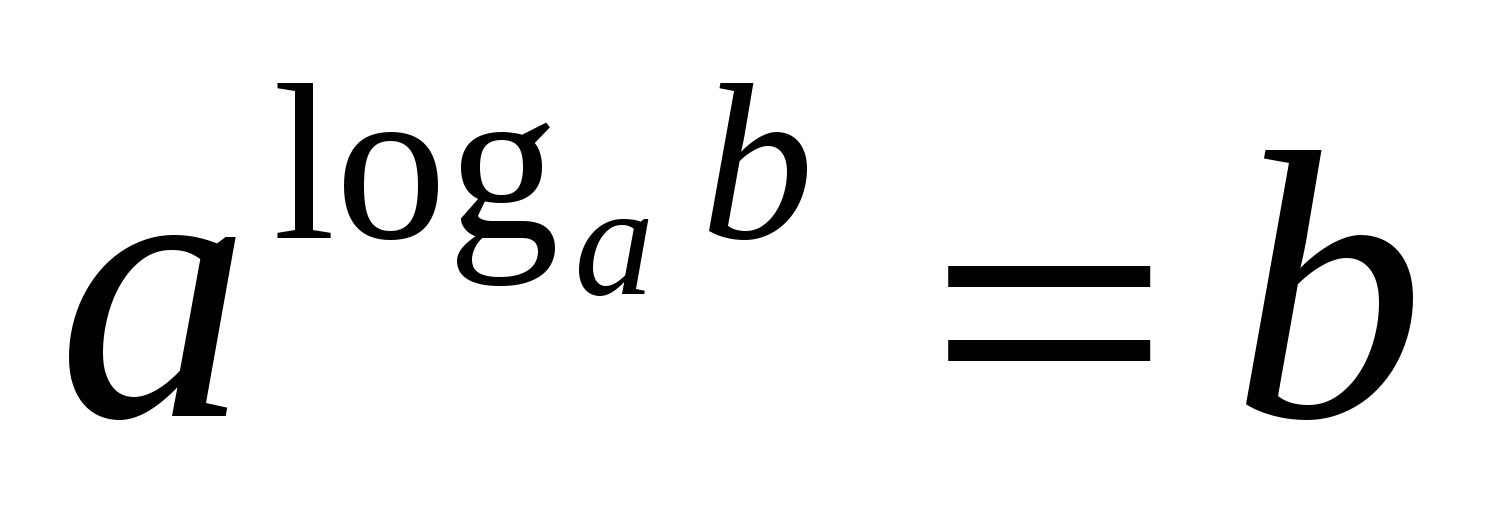
Обратите внимание на основание степени и основание логарифма – они одинаковы.
ОР 3 Р
 ассмотрим применение этой формулы на примере:
ассмотрим применение этой формулы на примере:
З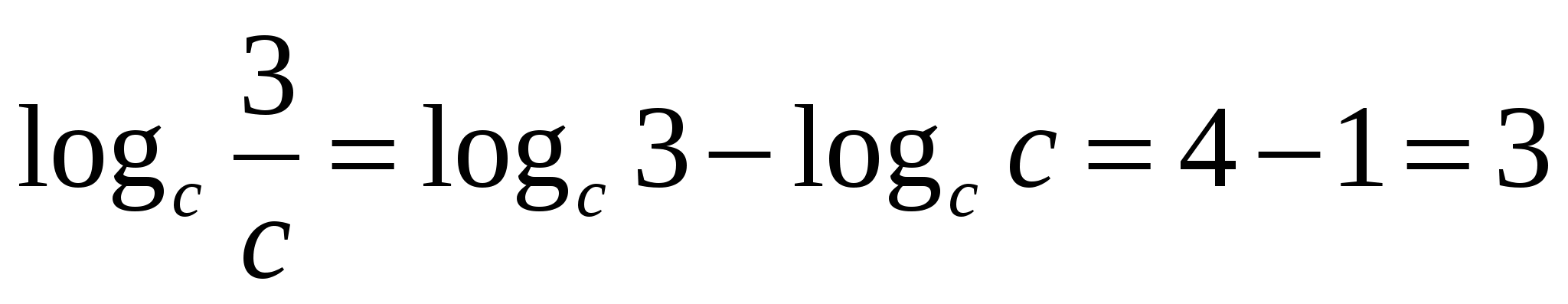 адание 1. Найдите значение выражения , если
адание 1. Найдите значение выражения , если


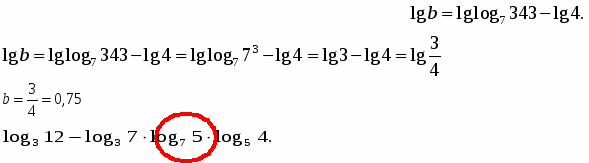
Задание 2. Найдите значение b по его логарифму
6) Логарифм степени по основанию а, равен произведению показателя степени на логарифм по тому же основанию.
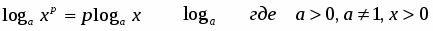
ЦОР 4
Н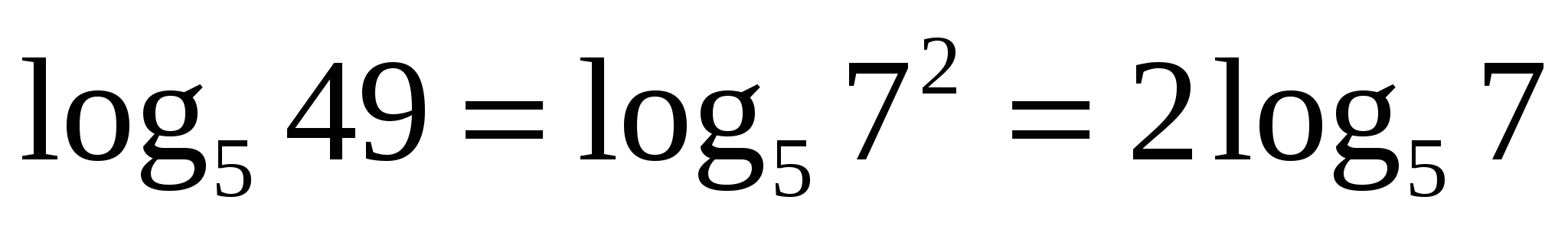 апример,
апример,
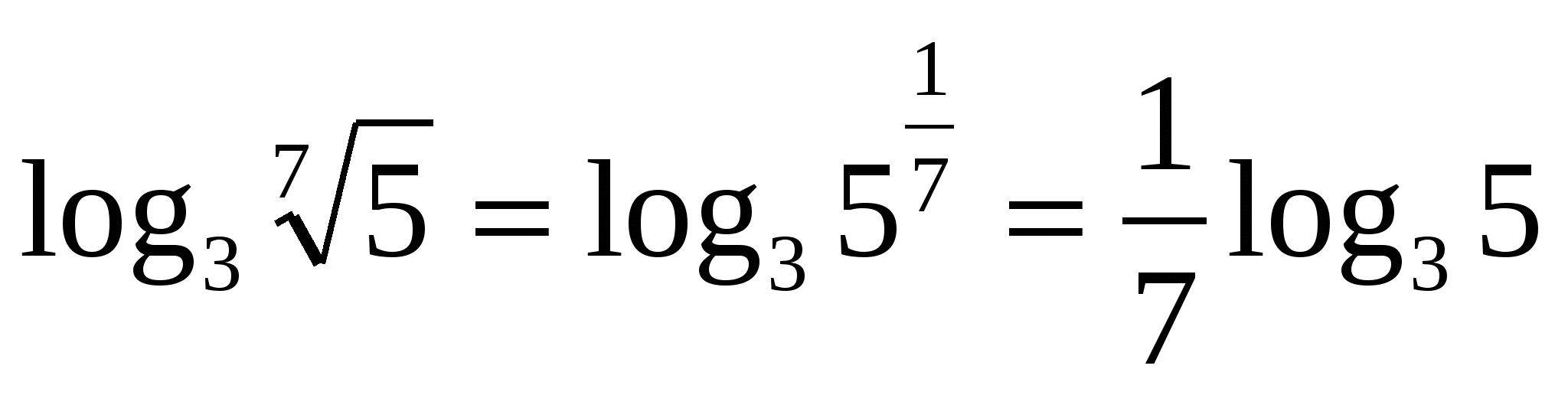
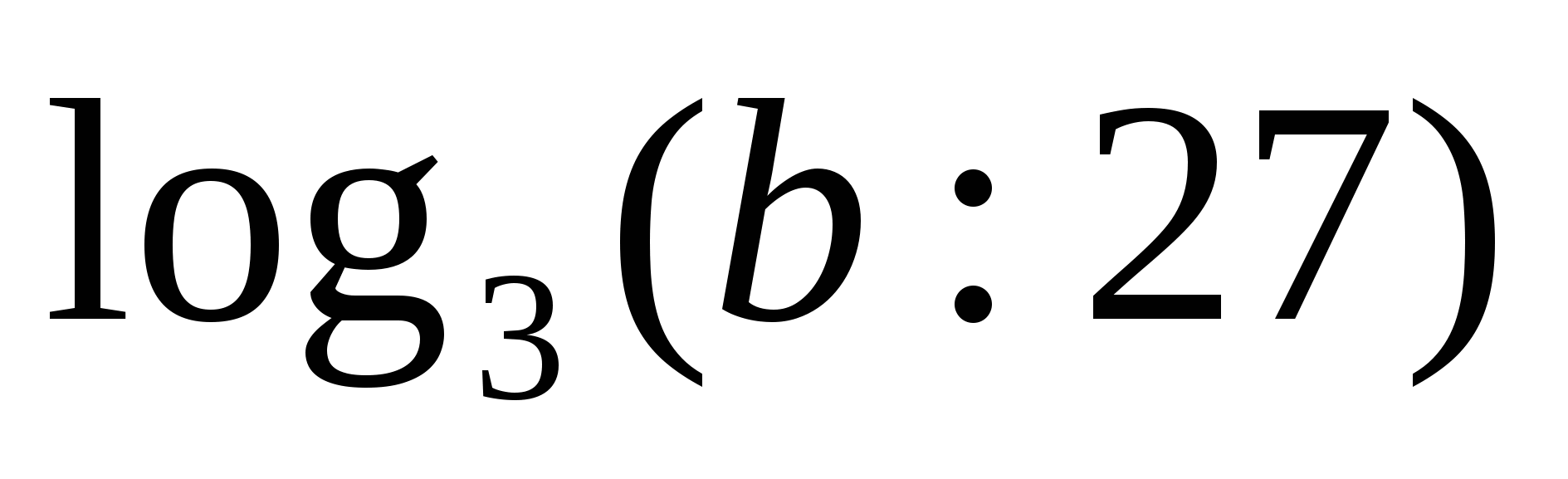
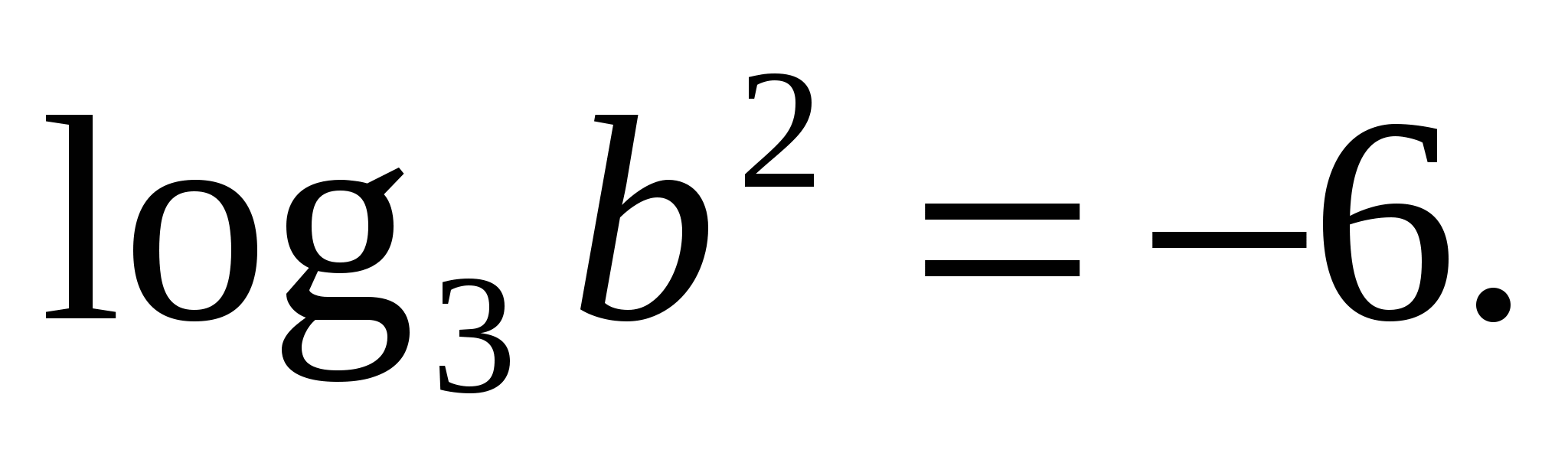
З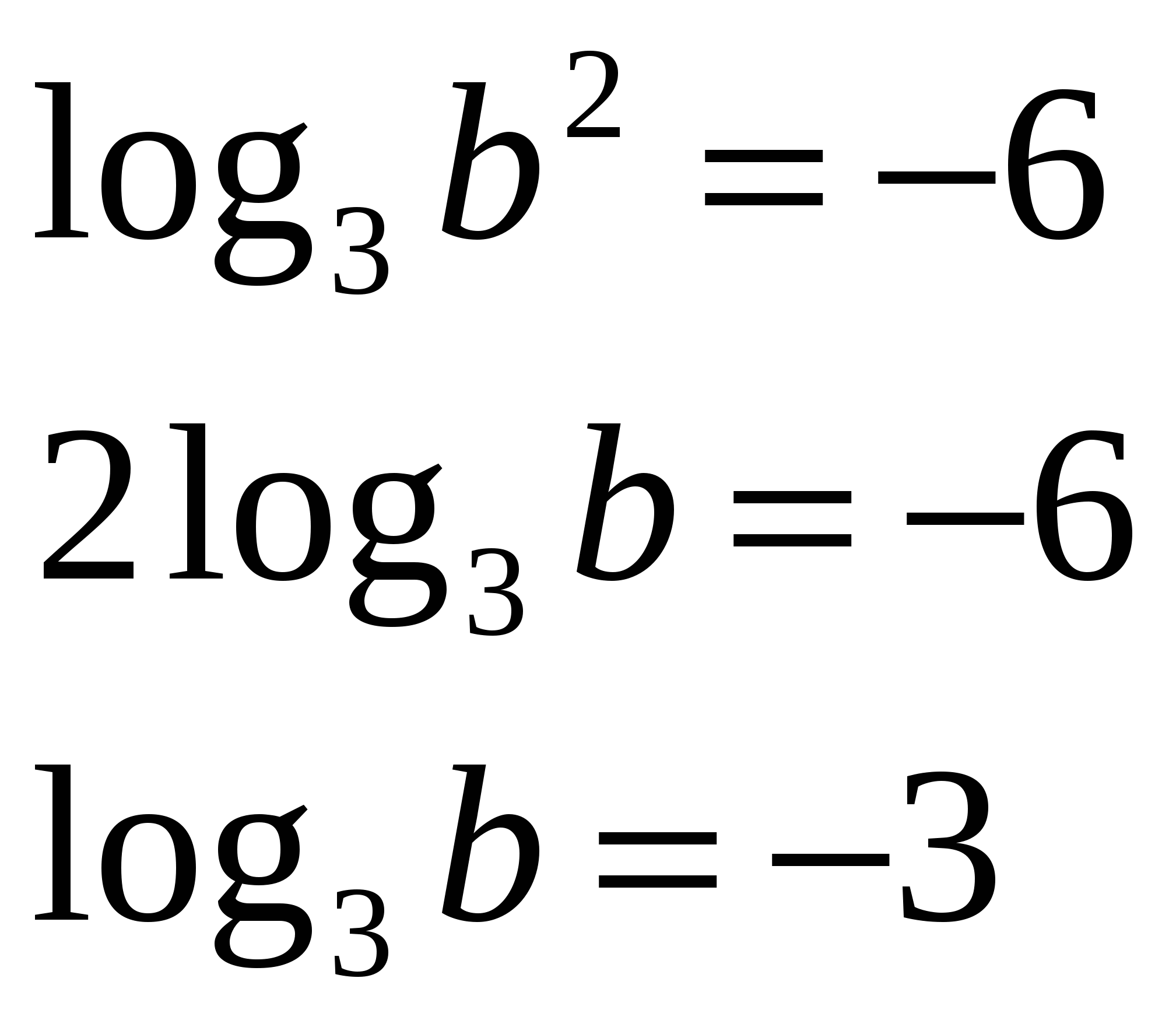 адание 1. Вычислите , если
адание 1. Вычислите , если
Упростим выражение
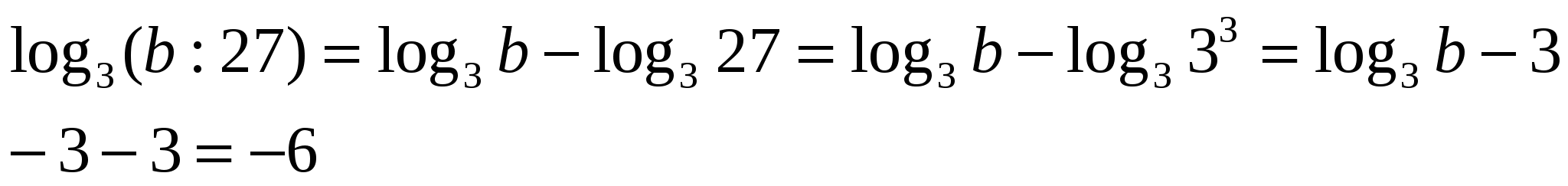


Ф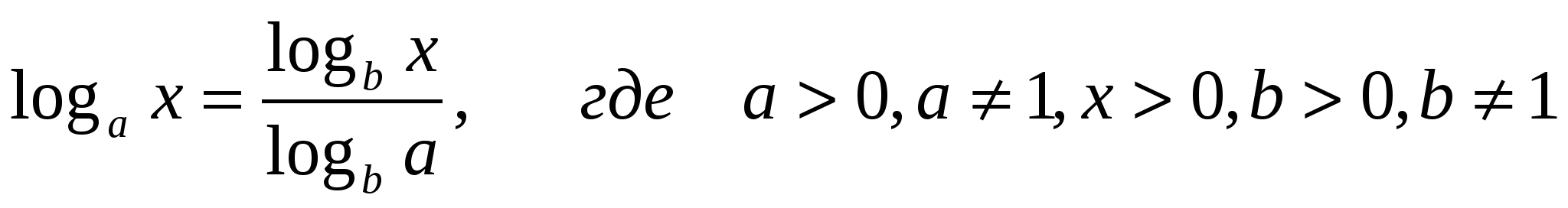 ормула
ормула
называется формулой перехода к новому основанию.
З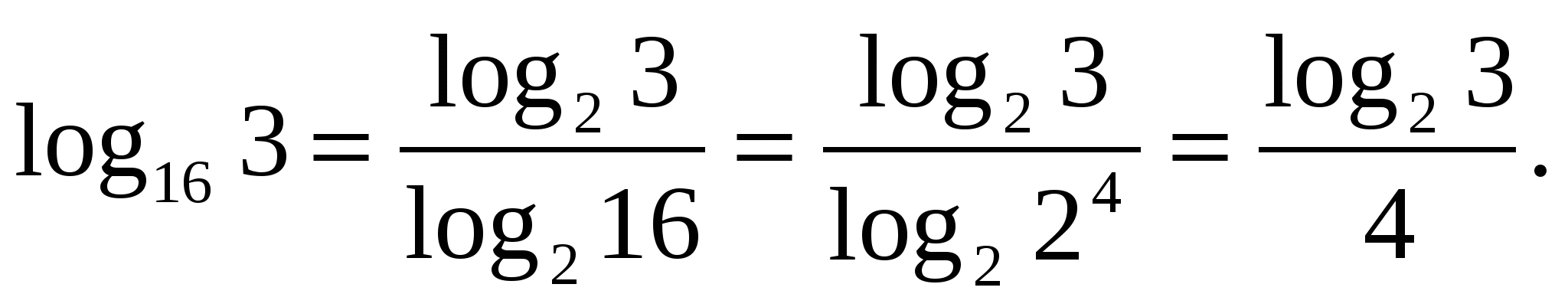
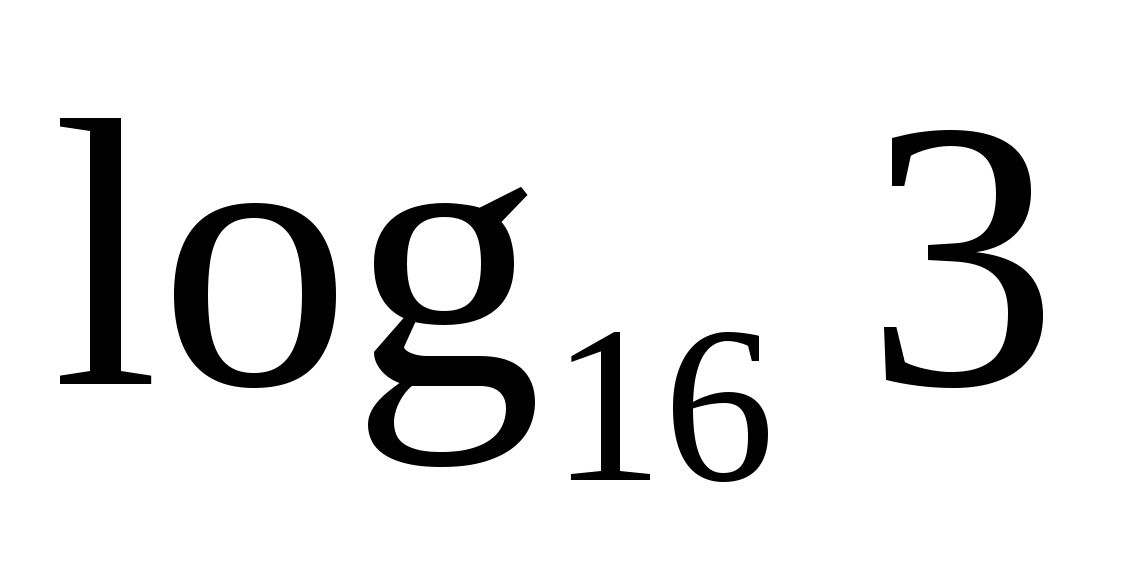 адание 1. Выразить через логарифм с основанием 2.
адание 1. Выразить через логарифм с основанием 2.
З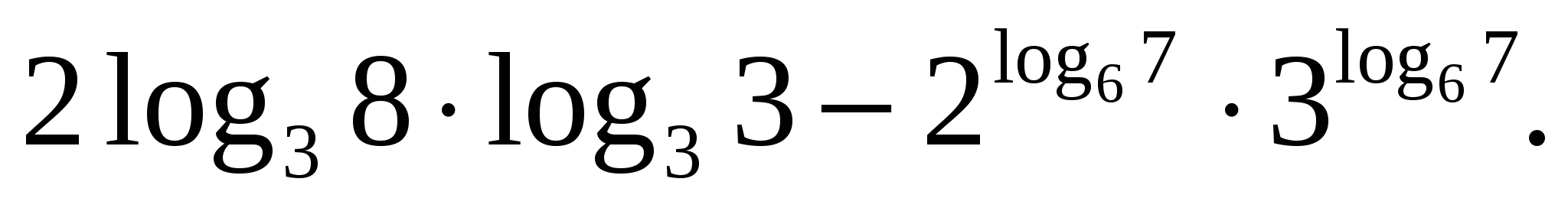
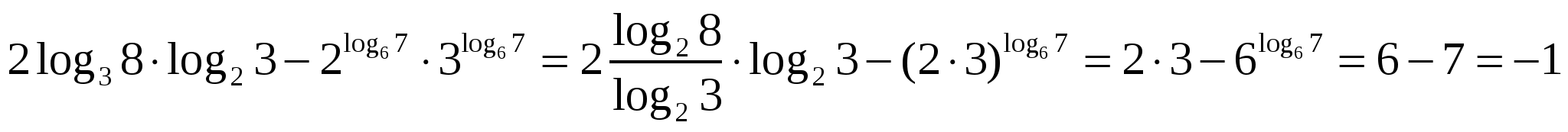 адание 2. Вычислите
адание 2. Вычислите
Ц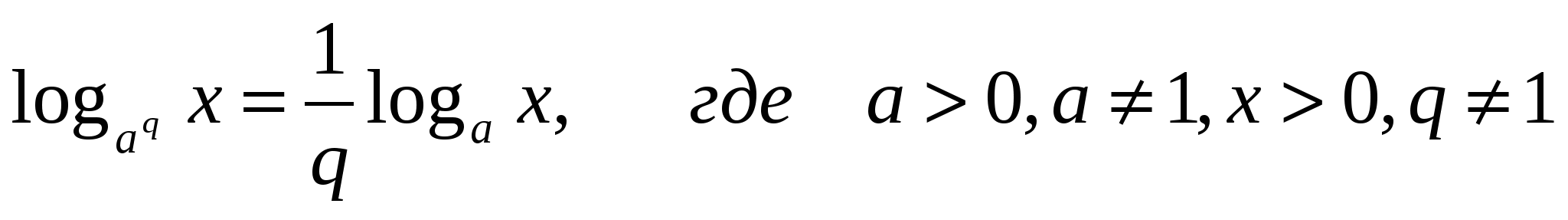 ОР 5
ОР 5
8)
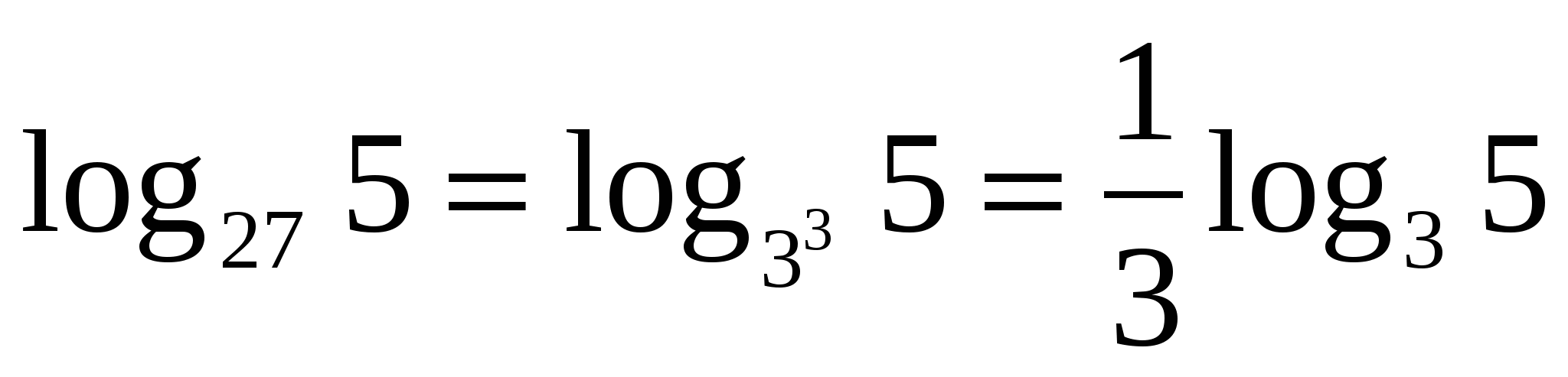 ЦОР 6
ЦОР 6
Например,
З
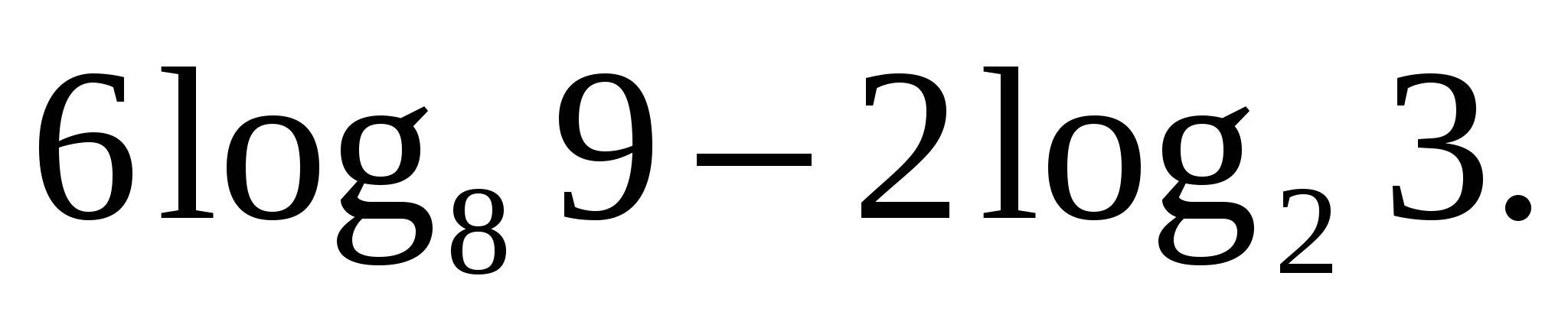
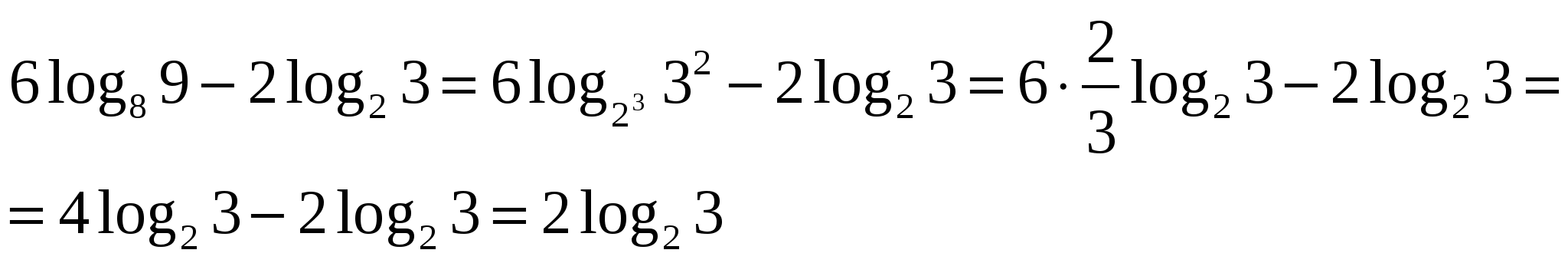

 адание 1. Вычислите
адание 1. Вычислите
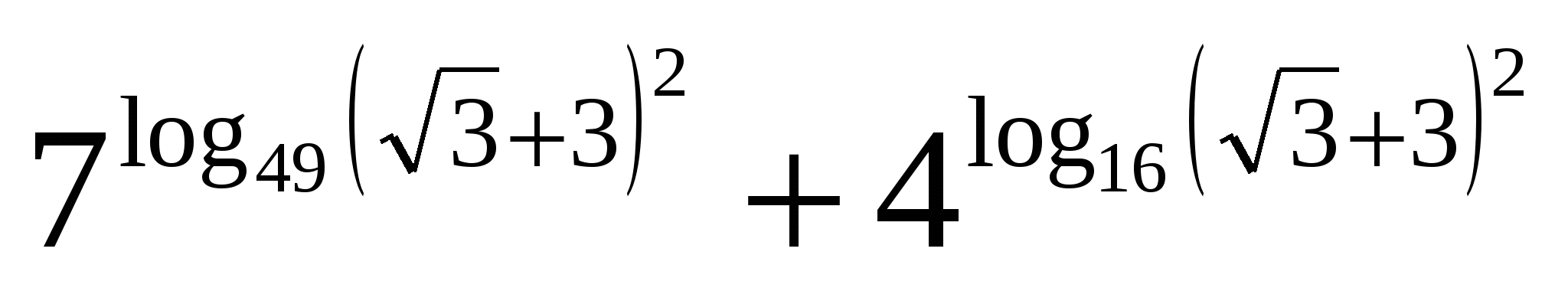
З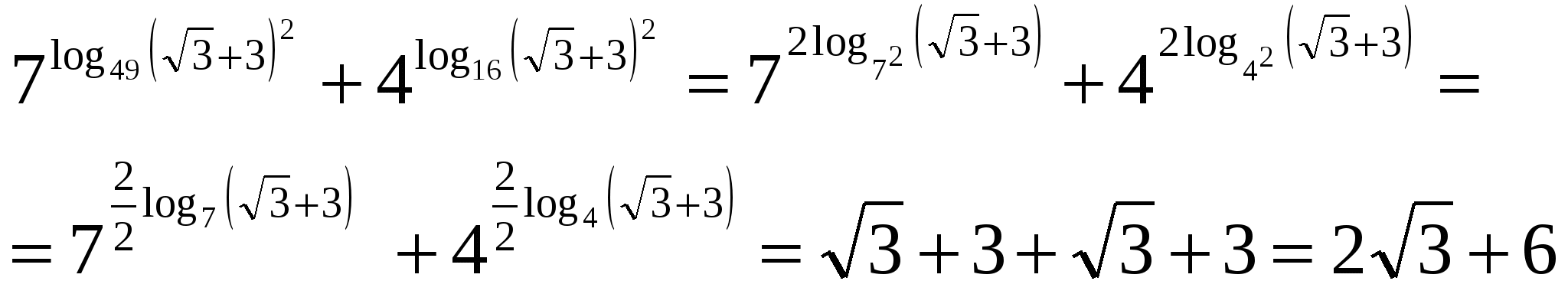 адание 2. Вычислите
адание 2. Вычислите
9) К логарифмическим преобразованиям можно приступать, только в том случаи, если вы запомнили все свойства логарифмов. Повторив их, рассмотрим задания на преобразования логарифмических выражений с другой стороны.
Для преобразования суммы или разности логарифмических выражений иногда достаточно использовать определение логарифма, а чаще всего свойства логарифма произведения или частного.
З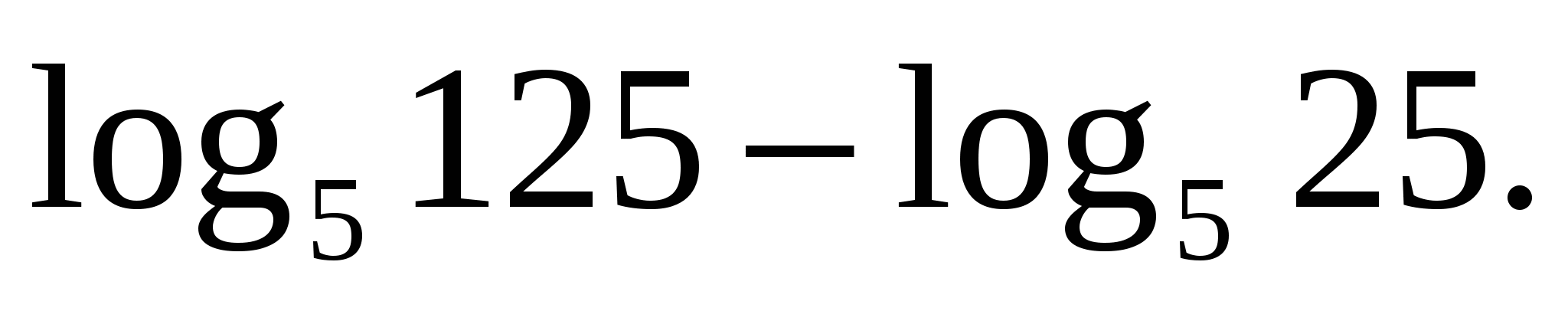 адание 1. Вычислите
адание 1. Вычислите
Решим двумя способами.
1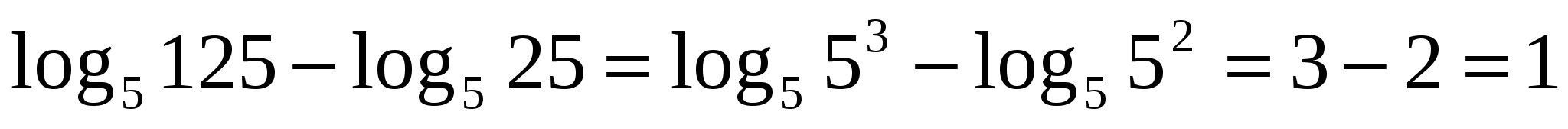 способ, используя определение логарифма:
способ, используя определение логарифма:
2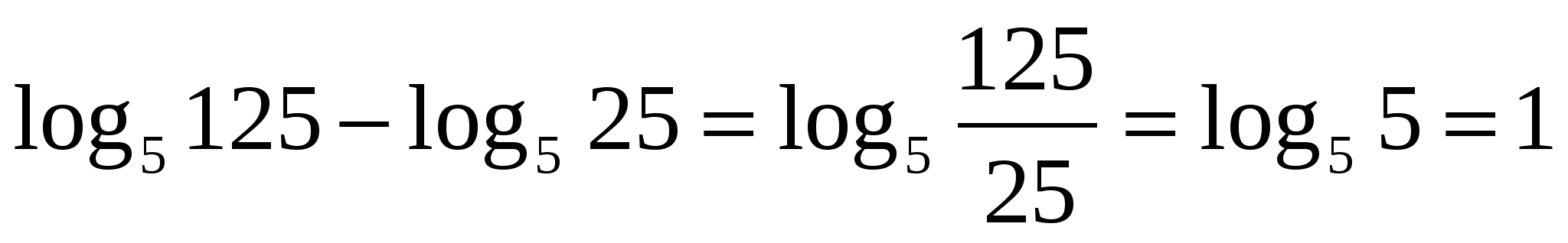 способ, опираясь на свойство логарифма частного:
способ, опираясь на свойство логарифма частного:
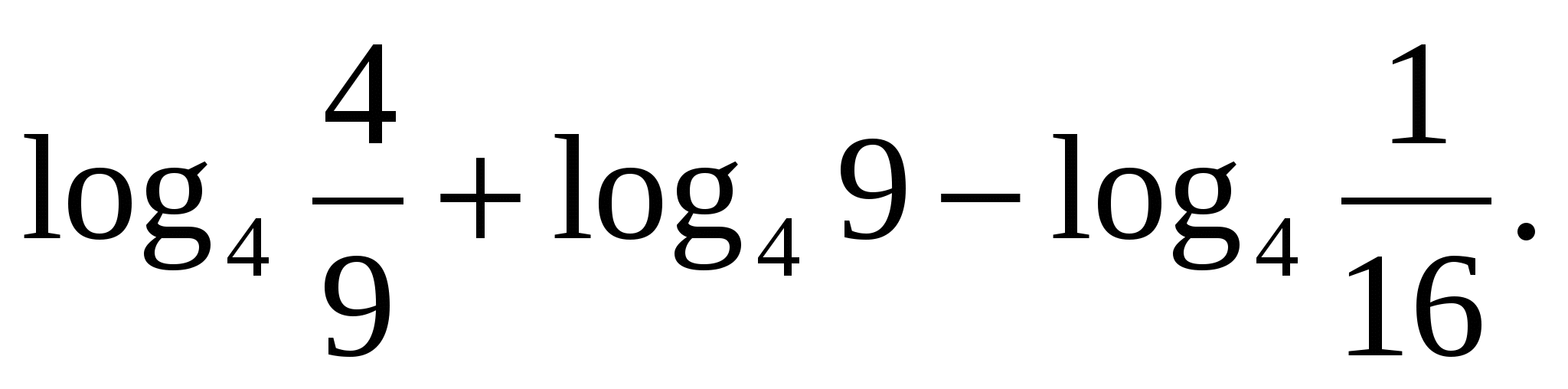
Задание 2. Найдите значение выражения
П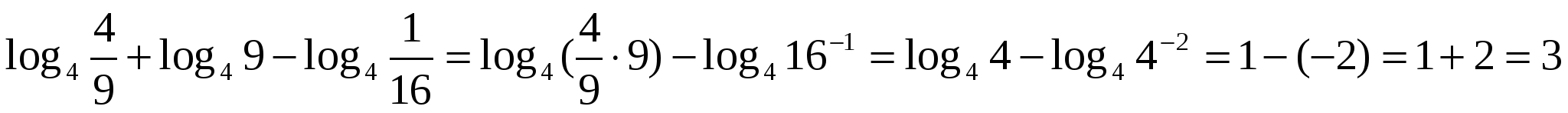 рименим сначала формулу логарифма произведения, затем определение логарифма.
рименим сначала формулу логарифма произведения, затем определение логарифма.
Основное логарифмическое тождество используется при преобразовании выражений, содержащих логарифм в показателе степени. Идея таких операций заключается в получении равных основания степени и основания логарифма.
Иногда необходимо преобразовывать выражение по свойствам логарифма и по свойствам степени, так же можно легко перейти от одного основания к другому, используя формулу перехода. В других случаях следует применять несколько свойств.
З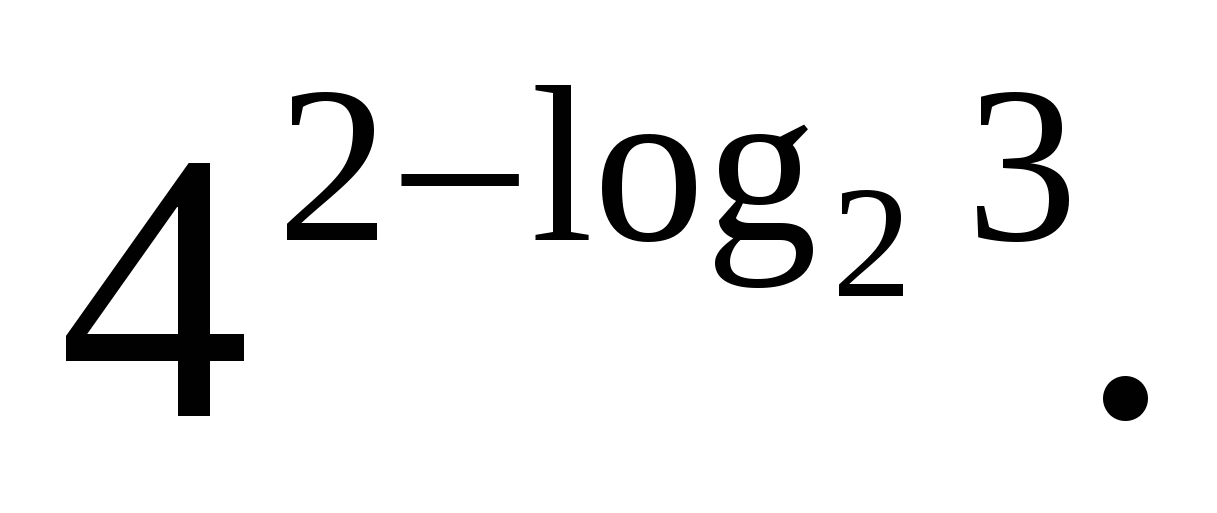 адание 3. Вычислите
адание 3. Вычислите
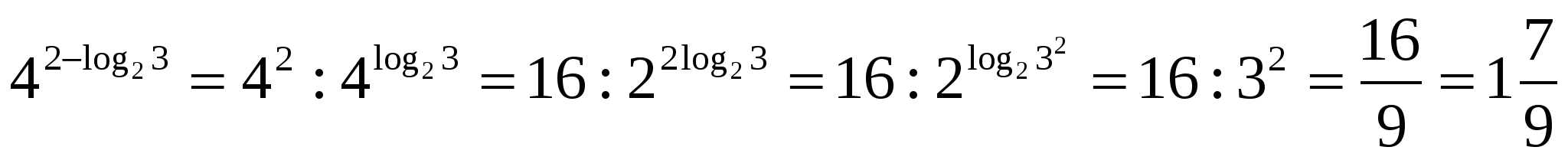
З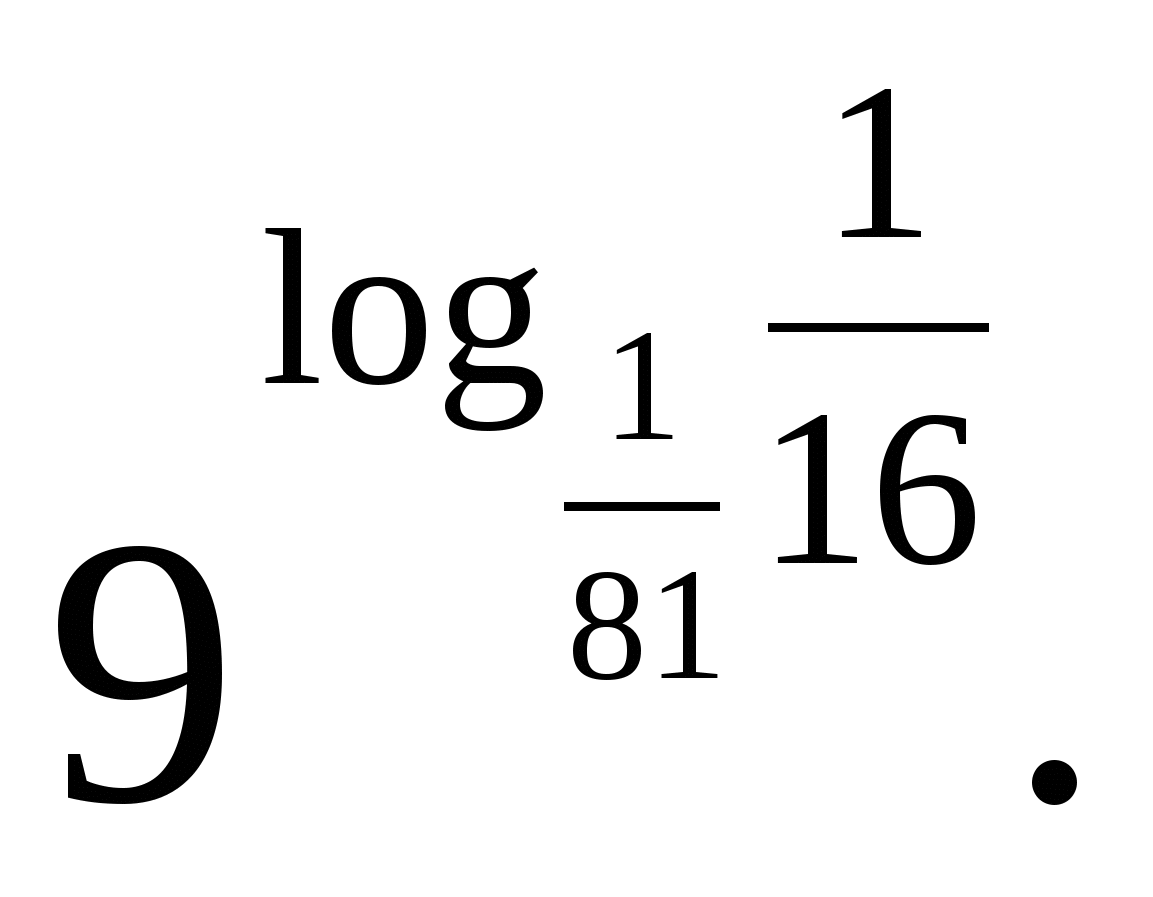 адание 4. Найдите значение выражения
адание 4. Найдите значение выражения
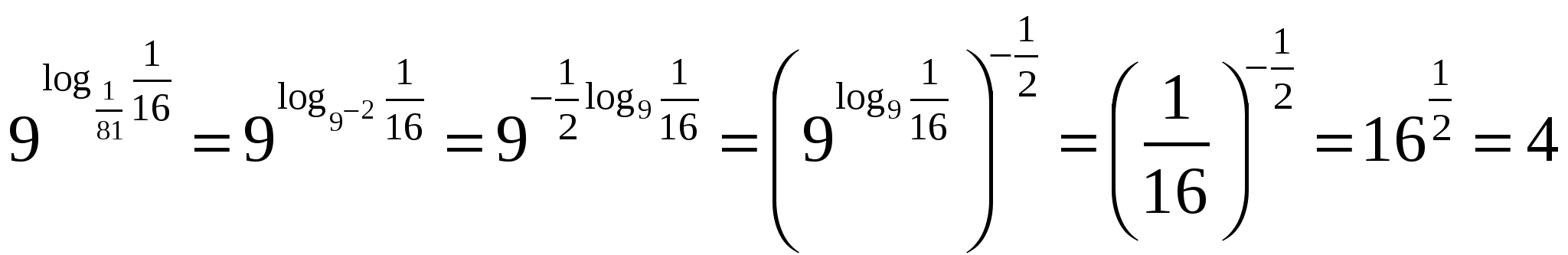
З адание 5. Найдите значение выражения
адание 5. Найдите значение выражения
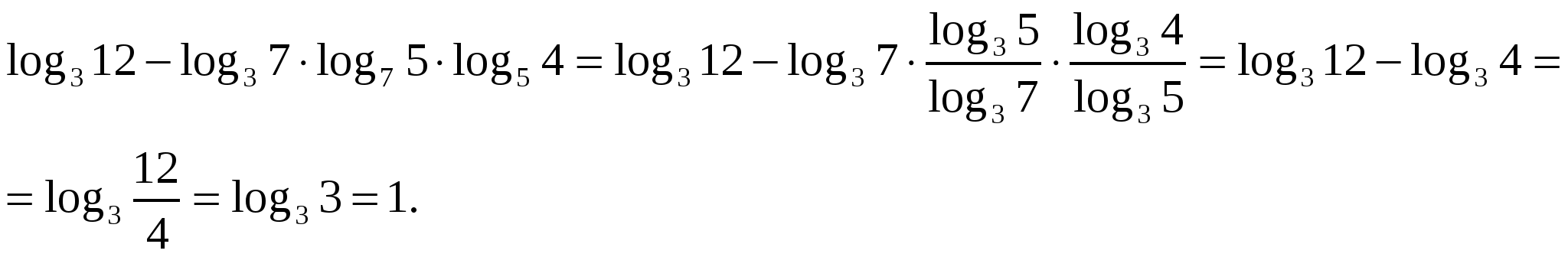
З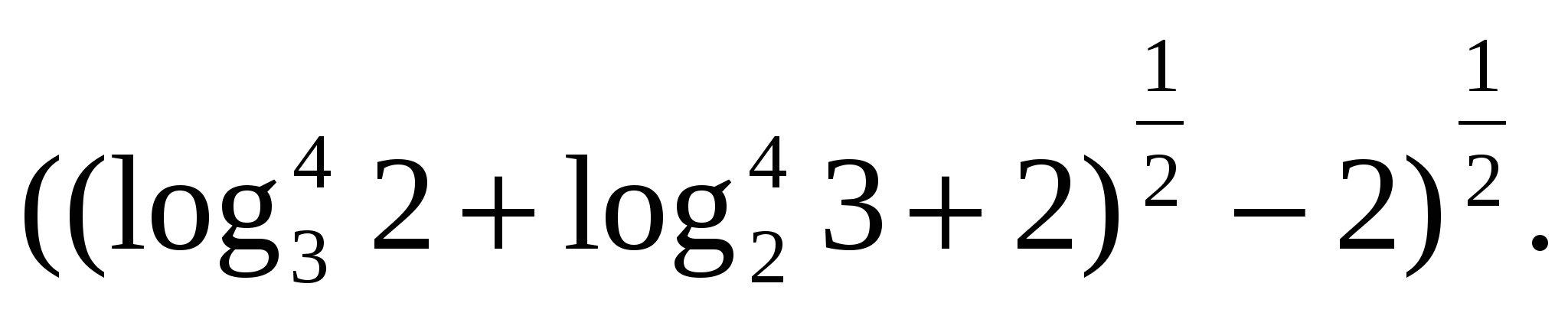 адание 6. Представьте в виде разности логарифмов
адание 6. Представьте в виде разности логарифмов
Н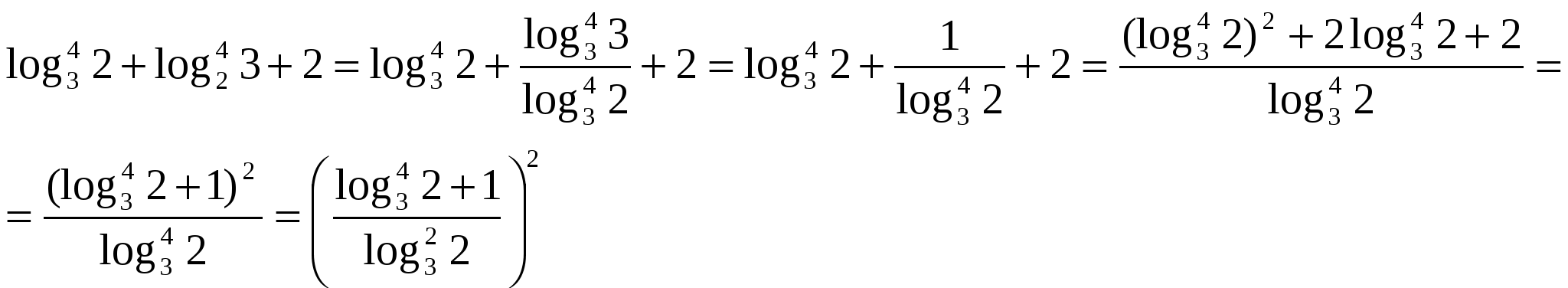 аибольшую трудность представляют преобразования логарифмических выражений, находящихся под радикалом. В процессе преобразований приходится рассматривать модули логарифмических выражений, для раскрытия которых требуется сравнить иррациональные числа или рациональное и иррациональное число. Будем действовать последовательно. Рассмотрим выражение, стоящее под внутренним радикалом.
аибольшую трудность представляют преобразования логарифмических выражений, находящихся под радикалом. В процессе преобразований приходится рассматривать модули логарифмических выражений, для раскрытия которых требуется сравнить иррациональные числа или рациональное и иррациональное число. Будем действовать последовательно. Рассмотрим выражение, стоящее под внутренним радикалом.
Подставим в исходное выражение.
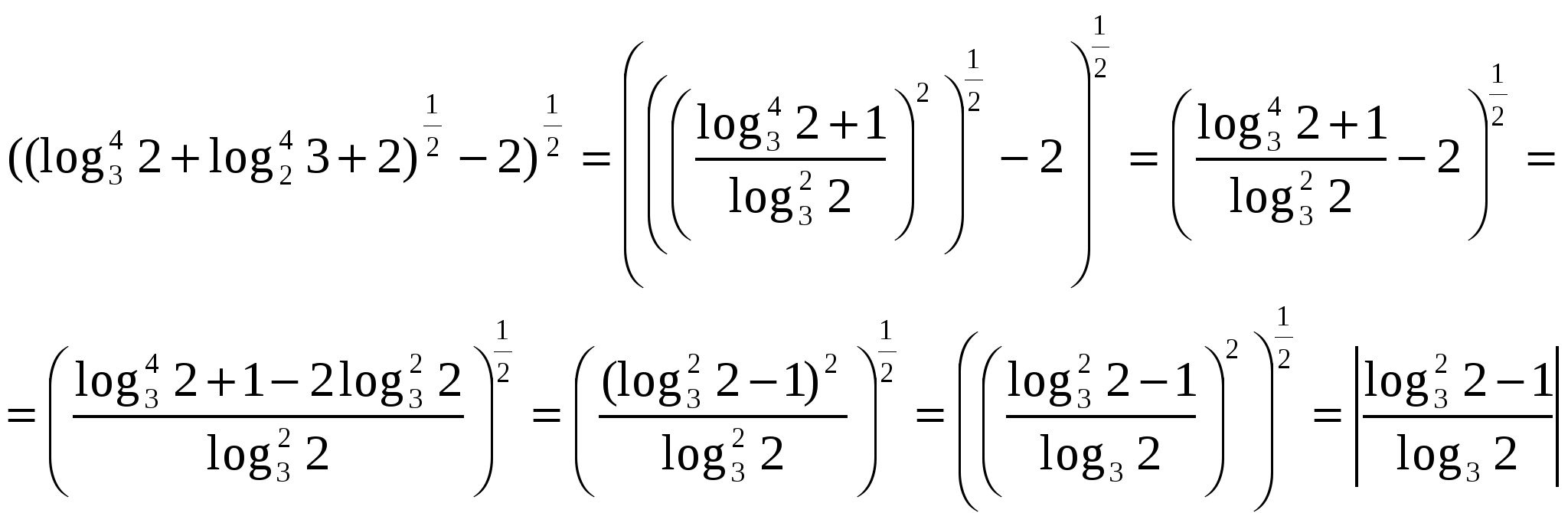
Р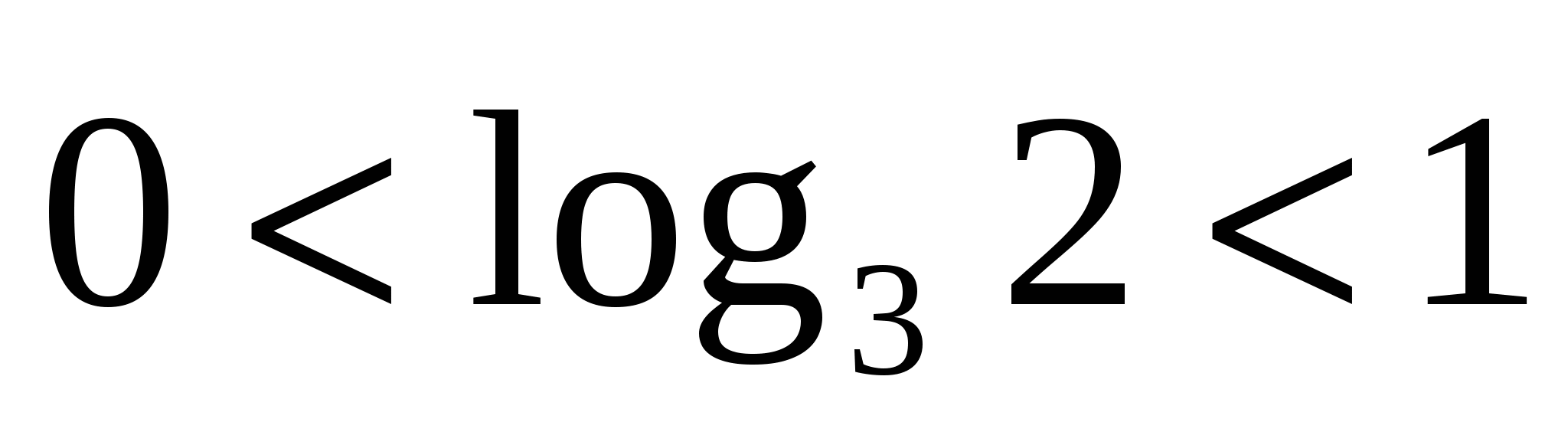
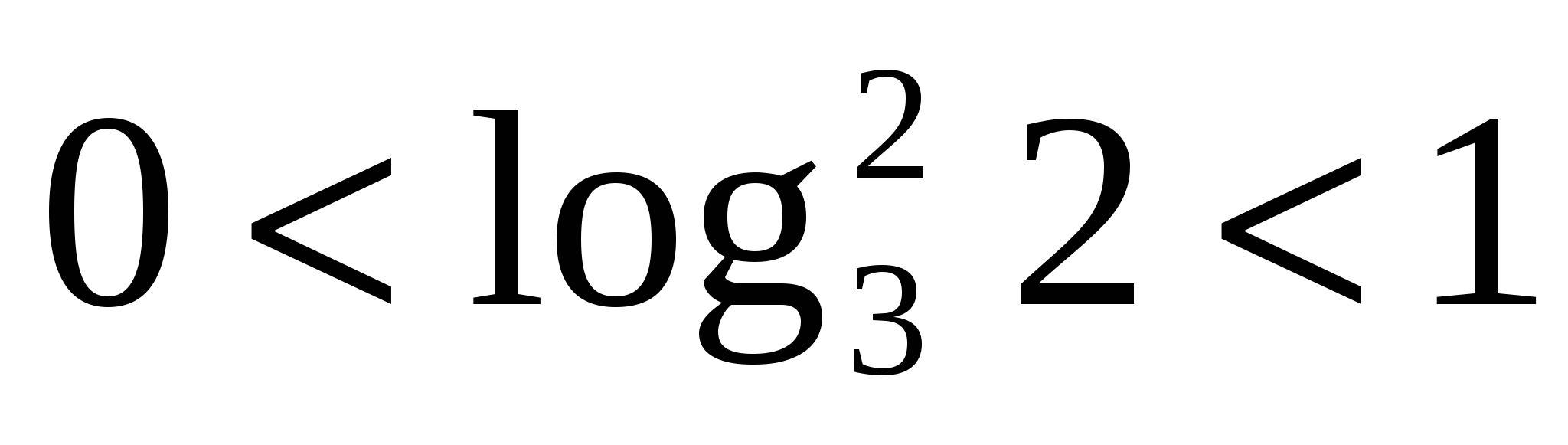 аскроем модуль, учитывая, что знаменатель положителен, а числитель отрицателен.
аскроем модуль, учитывая, что знаменатель положителен, а числитель отрицателен.
М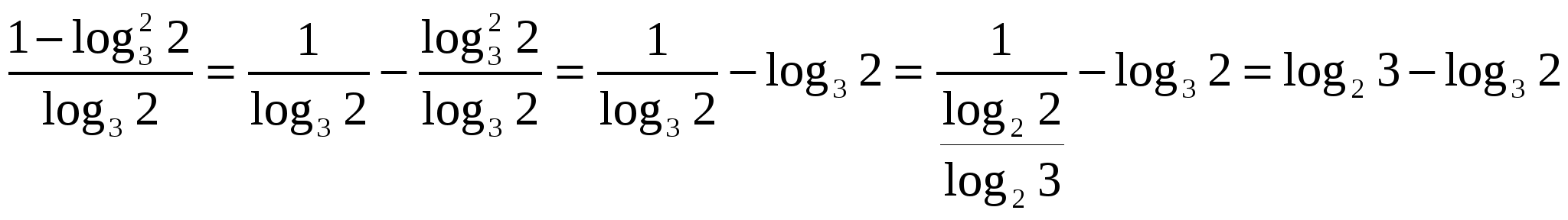 еняем знаки в числителе и упрощаем.
еняем знаки в числителе и упрощаем.
П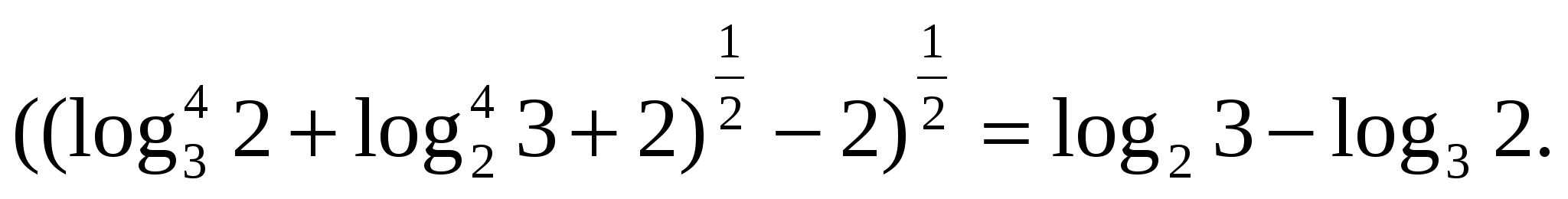 олучим исходное выражение, равное разности логарифмов.
олучим исходное выражение, равное разности логарифмов.
Такие и подобные примеры вам могут встретиться при решении заданий Единого Государственного экзамена.. Следует отметить, что с преобразованием логарифмических выражений можно встретиться и при решении уравнений и неравенств или исследовании функций, поэтому в неявном виде они могут присутствовать и в заданиях групп В и С.
10) Подведение итогов. Вопросы:
Логарифм по основанию 10 называется
2) Какие значения может принимать x в выражении 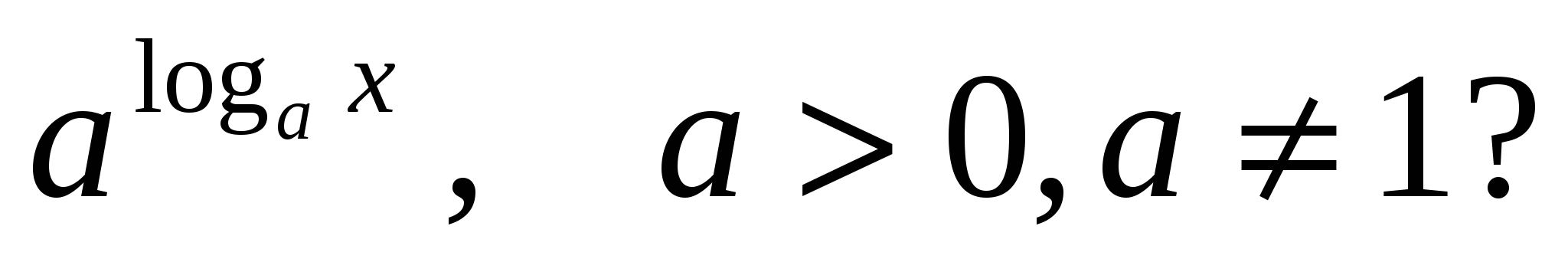
3) Чему равен 
4) Чему равен 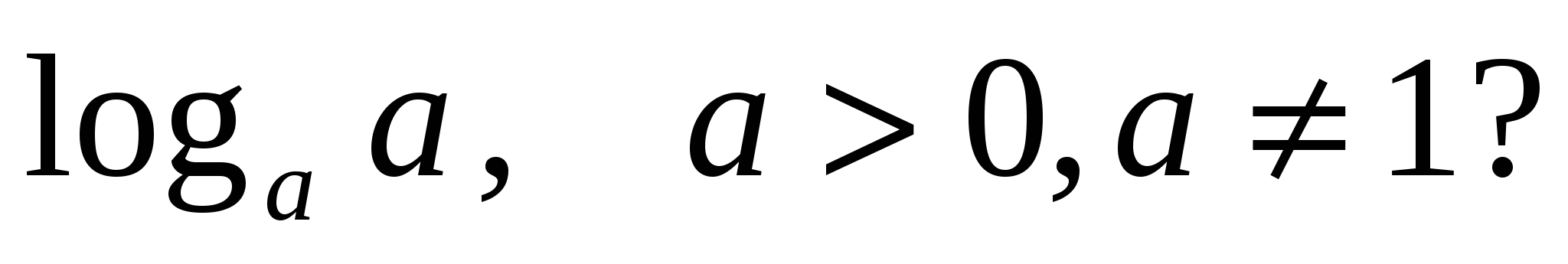
5) Укажите соотношение, которое верно для всех x ≠ 0.
6) Укажите верное соотношение для формулы перехода к новому основанию.
7) Укажите верное равенство при 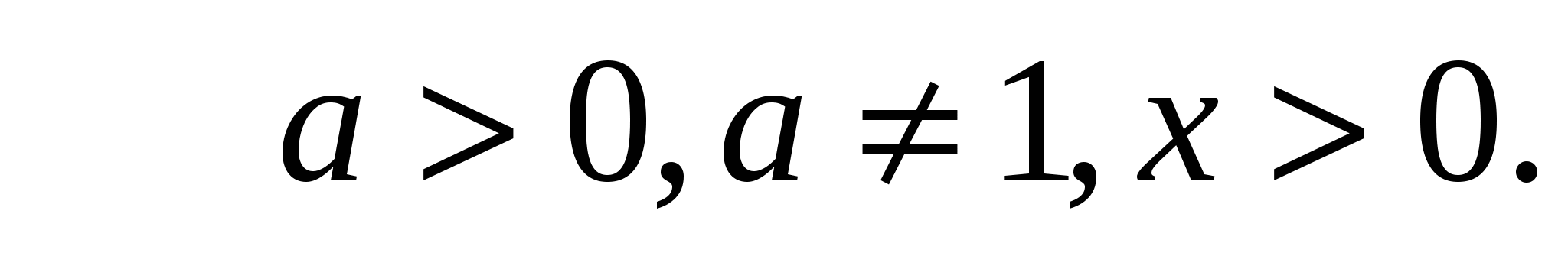
11) Контрольное тестирование.
Преобразование логарифмических выражений
28 Апр 2015
09 Задание (2016)ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
Рассмотрим решение Задания 10 из т/р №111 А. Ларина:
Вычислите: 
Заметим, что в показателе степени у нас стоит логарифм под знаком квадратного корня, поэтому основное логарифмическое тождество мы применить не можем.
Используем прием, который хорошо помогает, если мы имеем дело с произведением или частным логарифмов.
Пусть искомое выражение равно  :
:

Возьмем от обеих частей логарифм по основанию 5. (Могли бы взять логарифм по основанию 2 — в данном случае это не имеет значения)
Получим: 
Преобразуем выражение в правой части равенства. Воспользуемся следующими свойствами логарифмов:



Получим: 




Итак,

Отсюда

Ответ: 1


И.В. Фельдман, репетитор по математике.


Для вас другие записи этой рубрики:

В задаче B7 дается некоторое выражение, которое нужно упростить. В результате должно получиться обычное число, которое можно записать в бланке ответов. Все выражения условно делятся на три типа:
- Логарифмические,
- Показательные,
- Комбинированные.
Показательные и логарифмические выражения в чистом виде практически не встречаются. Однако знать, как они вычисляются, совершенно необходимо.
В целом, задача B7 решается достаточно просто и вполне под силу среднему выпускнику. Отсутствие четких алгоритмов компенсируется в ней стандартностью и однообразностью. Научиться решать такие задачи можно просто за счет большого количества тренировок.
Логарифмические выражения
Подавляющее большинство задач B7 содержат логарифмы в том или ином виде. Эта тема традиционно считается сложной, поскольку ее изучение приходится, как правило, на 11 класс — эпоху массовой подготовки к выпускным экзаменам. В результате многие выпускники имеют весьма смутное представление о логарифмах.
Но в этой задаче никто и не требует глубоких теоретических познаний. Нам будут встречаться лишь самые простые выражения, которые требуют незамысловатых рассуждений и вполне могут быть освоены самостоятельно. Ниже приведены основные формулы, которые надо знать, чтобы справиться с логарифмами:
- loga x + loga y = loga (x · y)
- loga x − loga y = loga (x : y)
- loga xn = n · loga x
-

-

Кроме того, надо уметь заменять корни и дроби на степени с рациональным показателем, иначе в некоторых выражениях выносить из под знака логарифма будет просто нечего. Формулы замены:
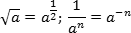
Задача. Найти значения выражений:
log6 270 − log6 7,5
log5 775 − log5 6,2
Первые два выражения преобразуются как разность логарифмов:
log6 270 − log6 7,5 = log6 (270 : 7,5) = log6 36 = 2;
log5 775 − log5 6,2 = log5 (775 : 6,2) = log5 125 = 3.
Для вычисления третьего выражения придется выделять степени — как в основании, так и в аргументе. Для начала найдем внутренний логарифм:
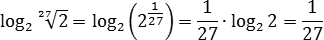
Затем — внешний:
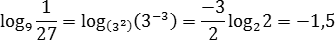
Конструкции вида loga logb x многим кажутся сложными и непонятыми. А между тем, это всего лишь логарифм от логарифма, т.е. loga (logb x). Сначала вычисляется внутренний логарифм (положим logb x = c), а затем внешний: loga c.
Показательные выражения
Будем называть показательным выражением любую конструкцию вида ak, где числа a и k — произвольные постоянные, причем a > 0. Методы работы с такими выражениями достаточно просты и рассматриваются на уроках алгебры 8-го класса.
Ниже приведены основные формулы, которые обязательно надо знать. Применение этих формул на практике, как правило, не вызывает проблем.
- an · am = an + m;
- an / am = an − m;
- (an)m = an · m;
- (a · b)n = an · bn;
- (a : b)n = an : bn.
Если встретилось сложное выражение со степенями, и не понятно, как к нему подступиться, используют универсальный прием — разложение на простые множители. В результате большие числа в основаниях степеней заменяются простыми и понятными элементами. Затем останется лишь применить указанные выше формулы — и задача будет решена.
Задача. Найти значения выражений: 79 · 311 : 218, 247 : 36 : 165, 306 : 65 : 252.
Решение. Разложим все основания степеней на простые множители:
79 · 311 : 218 = 79 · 311 : (7 · 3)8 = 79 · 311 : (78 · 38) = 79 · 311 : 78 : 38 = 7 · 33 = 189.
247 : 36 : 165 = (3 · 23)7 : 36 : (24)5 = 37 · 221 : 36 : 220 = 3 · 2 = 6.
306 : 65 : 252 = (5 · 3 · 2)6 : (3 · 2)5 : (52)2 = 56 · 36 · 26 : 35 : 25 : 54 = 52 · 3 · 2 = 150.
Комбинированные задачи
Если знать формулы, то все показательные и логарифмические выражения решаются буквально в одну строчку. Однако в задаче B7 степени и логарифмы могут объединяться, образуя довольно неслабые комбинации.
Из определения логарифма вытекают две формулы, которые постоянно встречаются в реальных задачах. Эти формулы позволяют заменить знак логарифма нормальными числами:
- loga an = n
-

В чистом виде они, как правило, не встречаются, поэтому общая схема решения комбинированных задач выглядит так:
- Записать там, где это возможно, числа в виде степеней. Например, 25 = 52, 16 = 24, 27 = 33… дальше сами. Корни и дроби тоже надо заменить степенями по уже известным формулам:

- Избавиться от степеней в основаниях логарифмов, если они там есть. Затем все множители, стоящие перед знаком логарифма, нужно внести в аргумент. Например, 5 · log7 2 = log7 25 = log7 32.
- Воспользоваться формулами замены логарифмов, которые приведены выше. Как правило, этого будет достаточно.
На первый взгляд эта схема кажется громоздкой и далеко не оптимальной. Но стоит немного потренироваться — и комбинированные задачи будут решаться за несколько секунд. Особо продвинутые решают их устно.
Задача. Найти значения выражений:

Будем действовать по схеме. Для первого выражения все очевидно:
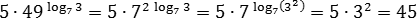
Для второго выражения заметим, что
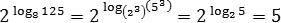
Поэтому имеем:
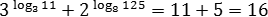
Аналогично поступим с третьим выражением:
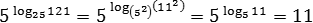
В результате получим:
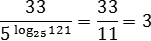
Смотрите также:
- Задача B3 — работа с графиками

- Системы линейных уравнений: основные понятия

- Сравнение дробей

- Пробный ЕГЭ 2012 от 7 декабря. Вариант 2 (без логарифмов)

- Как быстро извлекать квадратные корни

Преобразования журнала Автор (ы) Дэвид М. ЛейнПререквизиты Логарифмы, дополнительные показатели центральной тенденции, формы распределений, двумерные данныеЦели обучения
Преобразование журнала может использоваться для того, чтобы сделать сильно искаженные распределения менее искаженными.Это может быть полезным как для того, чтобы сделать шаблоны в данных более понятными, так и для того, чтобы соответствовать предположениям логической статистики. На рисунке 1 показан пример того, как преобразование журнала может сделать шаблоны более заметными. Оба графика изображают вес мозга животных как функцию веса тела. Необработанные веса показаны на верхней панели; логарифмические веса приведены на нижней панели. Рисунок 1. Диаграммы разброса веса мозга как функции веса тела с точки зрения как необработанных данных (верхняя панель), так и данных, преобразованных в лог (нижняя панель). Трудно различить рисунок на верхней панели, в то время как сильная взаимосвязь четко видна на нижней панели. Сравнение средств лог-преобразованных данных — это фактически сравнение геометрических средства. Это происходит потому, что, как показано ниже, анти-логарифм среднего арифметического логарифмически преобразованных значений является геометрическим средним. В таблице 1 показаны журналы (основание 10) чисел 1, 10 и 100.Среднее арифметическое трех бревен (0 + 1 + 2) / 3 = 1. Антилог этого среднее арифметическое 1 равно 10 1 = 10 , которое является средним геометрическим: (1 x 10 x 100) .3333 = 10. Следовательно, если средние арифметические значения двух наборов логрансформированных данных равны, то геометрические средние значения равны. Пожалуйста, ответьте на вопросы: |
Логарифмическое преобразование — оптимизация
Автор: Хасан Али (ChE 345 Spring 2015)
Управляющий: Дацзюнь Юэ, Фэнци Ю
Логарифмическое преобразование — это метод, используемый для преобразования геометрических программ в их выпуклые формы. Геометрическая программа , или GP , является типом глобальной проблемы оптимизации, которая касается минимизации подчинения ограничительным функциям, чтобы позволить решать уникальные задачи нелинейного программирования. Все геометрические программы содержат функции, называемые посиномами, которые по своей природе невыпуклы.В связи с этим, решение геометрических задач может быть вычислительно интенсивным, и поиск глобального оптимального решения не гарантируется. Однако, создав логарифмическое преобразование для задачи, можно быстрее и проще найти глобально оптимальное решение. Логарифмическое преобразование — не единственное преобразование, которое позволяет. Можно также использовать экспоненциальное преобразование, чтобы получить тот же результат. Логарифмическое преобразование может также использоваться в знаковых программах, которые являются расширением геометрических программ.1,2,3
Фон
Геометрическое программирование
Геометрическое программирование впервые обсуждалось в начале 1960-х годов как класс задач оптимизации, которые можно было решить с помощью геометрических неравенств. Даффин и его коллеги продолжили формулировать основные теории геометрического программирования и его приложений в 1967 году в своем оригинальном учебнике Теория геометрического программирования и приложения .4 Один из их взглядов на геометрическое программирование заметил, что проблемы с сильно нелинейными ограничениями могут быть заявлено эквивалентно с двойной программой .Другими словами, глобальное минимизирующее решение может быть найдено путем решения соответствующей ему задачи двойной максимизации. Это потому, что двойственные ограничения являются линейными. Все, что нужно было бы сделать, — это изменить задачу геометрического программирования из ее стандартной позиномиальной формы в эту «двойную форму» и решить с помощью этих теперь линейных ограничений. 3 Ответ мог быть только локально оптимальным, так как он все еще имел дело с нелинейным программированием (НЛП) методов.
Стандартная проблема GP принимает следующую форму
, где  — это полиномы, а
— это полиномы, а  — это мономы, а все переменные x положительны.
— это мономы, а все переменные x положительны.
Посином
Posynomials являются нелинейными функциями и состоят из набора констант, умноженных на ряд из нескольких переменных, умноженных вместе. Часто эти переменные возводятся в различные степени. Более конкретно, они являются функциями вида:

, где переменные  и коэффициенты
и коэффициенты  являются положительными, действительные числа и все показатели
являются положительными, действительные числа и все показатели  являются действительными числами.4
являются действительными числами.4
Мономы — это особый случай посинома, в котором нет набора терминов, а есть только один член и его константа.Посином — это просто сумма мономов. Пример монома

и пример посинома

Посином, следовательно, не имеет форму

, так как это линейная функция.
Геометрическое программирование Деривация
Проблемы GPне всегда даются и иногда должны быть получены. Возьмем следующий пример стандартной проблемы НЛП
, где переменные x, y и z являются положительными.Стандартная форма GP этой проблемы будет
Затем стандартная задача GP минимизирует посиномиальную функцию, ограничивая ее ограничениями посиномиального неравенства и мономиального равенства. Посиномы являются положительными функциями и содержат лог выпуклости. Это важный аспект, поскольку он позволяет стандартным задачам GP проходить преобразования журнала.1
Логарифмическое Преобразование
«Двухпрограммный» метод Даффина для решения задач ГП все еще используется, но поскольку методы логарифмического и экспоненциального преобразования стали понятными, стало проще просто использовать их для преобразования стандартной задачи ГП в выпуклую задачу ГП и решения с использованием внутренней точки метод. Методы внутренней точки могут решать проблемы GP очень быстро и надежно, поскольку они практически не требуют настройки параметров. Самое главное, что окончательное решение, полученное с помощью этого метода, гарантированно будет глобальным оптимальным решением.Решение стандартной проблемы GP похоже на решение проблемы НЛП. Единственное отличие состоит в том, что проблема GP более ограничена в использовании посиномов и мономов в своей целевой функции и ограничениях. Это делает стандартные задачи GP более эффективными для решения, и они могут быть решены относительно быстро, но, как и проблемы с NLP, нет гарантии, что решение является оптимальным во всем мире. Кроме того, необходимо предоставить первоначальное предположение и тщательно выбрать параметры.
Логарифмические преобразования, таким образом, очень полезны, поскольку они преобразуют стандартную форму GP в ее выпуклую форму, основанную на логарифмическом изменении переменных и логарифмическом преобразовании целевых и ограничительных функций.Таким образом, вместо минимизации цели  логарифм
логарифм  минимизируется. Переменная x заменяется ее логарифмом
минимизируется. Переменная x заменяется ее логарифмом  . Ограничение неравенства теперь
. Ограничение неравенства теперь  вместо
вместо  , а ограничение равенства теперь
, а ограничение равенства теперь  вместо
вместо  .5
.5
Следовательно, выпуклая форма задачи ГП
, где  — это многочлены, а
— это многочлены, а  — это одночлены, а переменные и — все положительные.Эта переформулировка может происходить до тех пор, пока константы в функции положительны.
— это одночлены, а переменные и — все положительные.Эта переформулировка может происходить до тех пор, пока константы в функции положительны.
Методы

 Функция log-sum-exp в
Функция log-sum-exp в  .
.Чтобы увидеть преобразование более понятным, можно показать более подробных шагов . Если целевой функцией является моном формата


где

, которая является аффинной функцией и
Если вышеуказанная целевая функция была вместо этого мономиальным ограничением равенства, таким

, тогда новое ограничение равенства будет равно нулю и будет упрощено до линейного уравнения вида

Любой ГП, имеющий только одночлены, после логарифмического преобразования превращается в линейную программу.Проверка на линейность в мономиальном случае подтвердит правильность преобразования.
Если у GP посином , проблема становится более сложной. Журнал нескольких терминов не может быть упрощен за пределами формы логарифма. Так что, если целевая функция

, где c > 0, тогда новая целевая функция будет

где

, а где  для
для  .Выше может быть написано в более простой форме, как
.Выше может быть написано в более простой форме, как

где A — это матрица размером n на n со строками  , а lse — выпуклая функция log-sum-exp.
, а lse — выпуклая функция log-sum-exp.
Причина логарифмического преобразования, когда экспоненциальное преобразование может быть выполнено за меньшее количество шагов, состоит в том, что экспоненциальная функция может принимать большие значения. Это может создать численные проблемы, а также привести к сложностям в программах оптимизации. Взятие логарифма позволяет восстановить меньшие значения, что дает логарифмическому преобразованию явное преимущество.6
Примеры
В этом разделе представлены несколько целевых функций и ограничений в качестве иллюстративных примеров.
ПРИМЕР 1
После логарифмического преобразования этот GP становится:
ПРИМЕР 2
После логарифмического преобразования этот GP становится:
ПРИМЕР 3
После логарифмического преобразования этот GP становится:
Чтобы доказать, что ответы на приведенные выше примеры действительно выпуклые, можно проверить его выпуклость с помощью теста гессиана на положительную определенность.Переформулировки также могут быть проверены в GAMS.
Технико-экономический анализ
Стандартная проблема GP может быть неосуществимой, т. Е. Ограничения слишком «жесткие» и не позволяют найти решение. Поскольку ограничения из стандартной задачи ГП сохраняются даже при изменении ее выпуклой формы посредством логарифмического преобразования, неосуществимая проблема ГП всегда будет неосуществимой независимо от выпуклости. Вот почему важно проверить невозможность выполнения перед созданием линейного преобразования.Это делается путем прохождения технико-экономического обоснования и настройки ГП следующим образом:
Поскольку s приближается к значению 1, исходная проблема приближается к выполнимости. Конечная цель состоит в том, чтобы найти решение, такое, что s = 1, так что выполнимость проблемы подтверждена.
Приложения
Приложения геометрического программирования включают в себя:
- Электротехника 5
- Контроль мощности
- Размер проволоки
- Маршрутизация
- Оптимальный профиль легирования в полупроводниковом приборостроении
- Размеры затвора для цифровой схемы
- Химическое машиностроение 5
- Оптимальная конструкция реактора
- Оптимизация массопереноса
- Кинетика
- Максимальная надежность реакторов
- Другое
- Транспорт6
- Экономические модели
- Модели инвентаризации
Отличным примером среди этих разнообразных применений является оптимальная конструкция реактора.Химические системы внутри реактора следуют невыпуклым уравнениям кинетики. Если кто-то хотел оптимизировать реактор для данной системы с заданными скоростями реакции, он мог бы легко сделать это с помощью логарифмического преобразования. Возьмите реакцию A + B до C со скоростью реакции  . Логарифмическое преобразование, которое позволило бы получить выпуклое отношение, составляет
. Логарифмическое преобразование, которое позволило бы получить выпуклое отношение, составляет  , где
, где  . С помощью этого нового уравнения вы можете оптимизировать конструкцию своего реактора для данной системы.
. С помощью этого нового уравнения вы можете оптимизировать конструкцию своего реактора для данной системы.
Заключение
Геометрическое программирование — это приложение, которое может решать разную степень сложных задач оптимизации, но из-за их сложности эти проблемы не могут быть легко решены.Решение геометрических задач может потребовать значительных вычислительных ресурсов, а поиск глобального оптимального решения не гарантируется. Это связано с тем, что ВП включают в себя посиномы и мономы, которые по своей природе являются нелинейными. Однако, создав для задачи логарифмическое преобразование , можно быстрее и проще найти глобально оптимальное решение, поскольку ГП изменяется на выпуклую форму. Логарифмические преобразования предлагают преимущество перед другими преобразованиями, поскольку позволяют работать с меньшими значениями, которые менее проблематичны.Логарифмические преобразования могут использоваться везде, где используется геометрическое программирование, которое включает приложения в химической инженерии и экономике.
Рекомендации
- Chiang, M. (2005). Геометрическое программирование для систем связи , Publishers, Inc., ISBN 1-933019-09-3.
- Даффин Р.Дж. (1970). «Линеаризация геометрических программ», SIAM Review 12 (2).
- Biswal, K.K., Ohja, A.K. (2010). «Задачи посиномиального геометрического программирования с несколькими параметрами», Журнал вычислений 2 (1).
- Даффин Р.Дж., Петерсон Э.Л., Зинер К.М. (1967). Теория и применение геометрического программирования , John Wiley & Sons Inc., ISBN 978-0471223702.
- Boyd S., Hassibi A., Kim S.J., Vandenberghe L. (2007). «Учебник по геометрическому программированию», Optim Eng 8 : 67-127.
- Calafiore, G.C., El Ghaoui, L. (2014). Оптимизационные модели и приложения , Издательство Кембриджского университета, ISBN 978-1107050877.
В Экспоненциальной регрессии и регрессии мощности мы рассмотрели четыре типа логарифмического преобразования для моделей регрессии с одной независимой переменной. Теперь мы кратко рассмотрим несколько аналогов регрессии для этих четырех типов преобразований журнала:
Регрессия уровня уровня — это нормальная множественная регрессия, которую мы изучили в Методе наименьших квадратов для анализа множественной регрессии и множественной регрессии.Регрессия логарифмического уровня — это многовариантный аналог экспоненциальной регрессии, рассмотренной в Экспоненциальной регрессии. А именно, взяв экспоненту каждой стороны уравнения, показанного выше, мы получим эквивалентную форму
Аналогично, логарифмическая модель регрессии является многовариантным аналогом модели регрессии мощности, рассмотренной в Power Regression. Мы видим это, взяв экспоненту обеих сторон уравнения, показанного выше, и упрощая, чтобы получить
Так как любая положительная постоянная с может быть выражена как е ln с , мы можем повторно выразить это уравнение через
(где очевидно, что коэффициенты не совпадают, и где мы также включили отрицательные значения).
Теперь мы дадим пример того, где модель регрессии на уровне журнала хорошо подходит для некоторых данных.
Пример 1 : Повторите пример 1 наименьших квадратов для множественной регрессии, используя данные в левой части рисунка 1.
Рисунок 1 — Преобразование логарифмического уровня
Правая часть рисунка показывает логарифмическое преобразование цены: например, ячейка G6 содержит формулу = LN (C6). Затем мы запустим анализ данных регрессии на преобразованных данных журнала.Мы могли бы использовать инструмент Excel Regression , хотя здесь мы используем инструмент анализа данных Real Statistics Linear Regression (как описано в множественном регрессионном анализе) на входе X в диапазоне E5: F16 и вводе Y в диапазоне G5: G16. Результат показан на рисунке 2.
Рисунок 2 — Регрессия на преобразованных данных лог-уровня
Высокое значение для R-квадрата показывает, что преобразованные данные лог-уровня хорошо подходят для модели линейной регрессии.Поскольку ноль не находится в 95% доверительных интервалах для Цвета или Качества, соответствующие коэффициенты значительно отличаются от нуля.
Мы могли бы также использовать формулу массива = LOGEST (C6: C16, A6: B16, TRUE, TRUE), чтобы получить следующий вывод (метки были добавлены вручную):
Рисунок 3 — Использование функции LOGEST
Обратите внимание, что значения наклона / пересечения в строке 7 на рисунке 3 являются экспонентой линейных коэффициентов, рассчитанных на рисунке 2: e.грамм. значение ячейки R7 равно EXP (J23), а значение ячейки T7 равно EXP (J21).
Мы также можем использовать регрессионную модель, чтобы предсказать цену данного алмаза. Например, предположим, что у алмаза есть Color = 4 и Quality = 5 или Color = 7 и Quality = 7, тогда следующие три подхода показывают, как предсказать цену на основе регрессионной модели:
Рисунок 4 — Прогнозирование с использованием модели уровня журнала
Пример 2 : Повторите Пример 1, используя данные в левой части рисунка 5.
Рисунок 5– Преобразование логарифмов
В правой части рисунка показано преобразование цвета, качества и цены. Затем мы запускаем инструмент анализа данных регрессии для преобразованных в журнал данных, то есть с диапазоном E5: F16 в качестве входа X и диапазоном G5: G16 в качестве входа Y. Результат показан на рисунке 6.
Рисунок 6 — Регрессия в лог-преобразованных данных
Как и в предыдущем примере, мы видим из рисунка 6, что модель хорошо подходит для данных.Мы также можем использовать регрессионную модель для прогнозирования. Обратите внимание, что для преобразованных моделей log-log есть функции LOGEST или GROWTH, но у нас все еще есть два следующих подхода к прогнозированию:
Рисунок 7 — Прогнозирование с использованием модели log-log
,
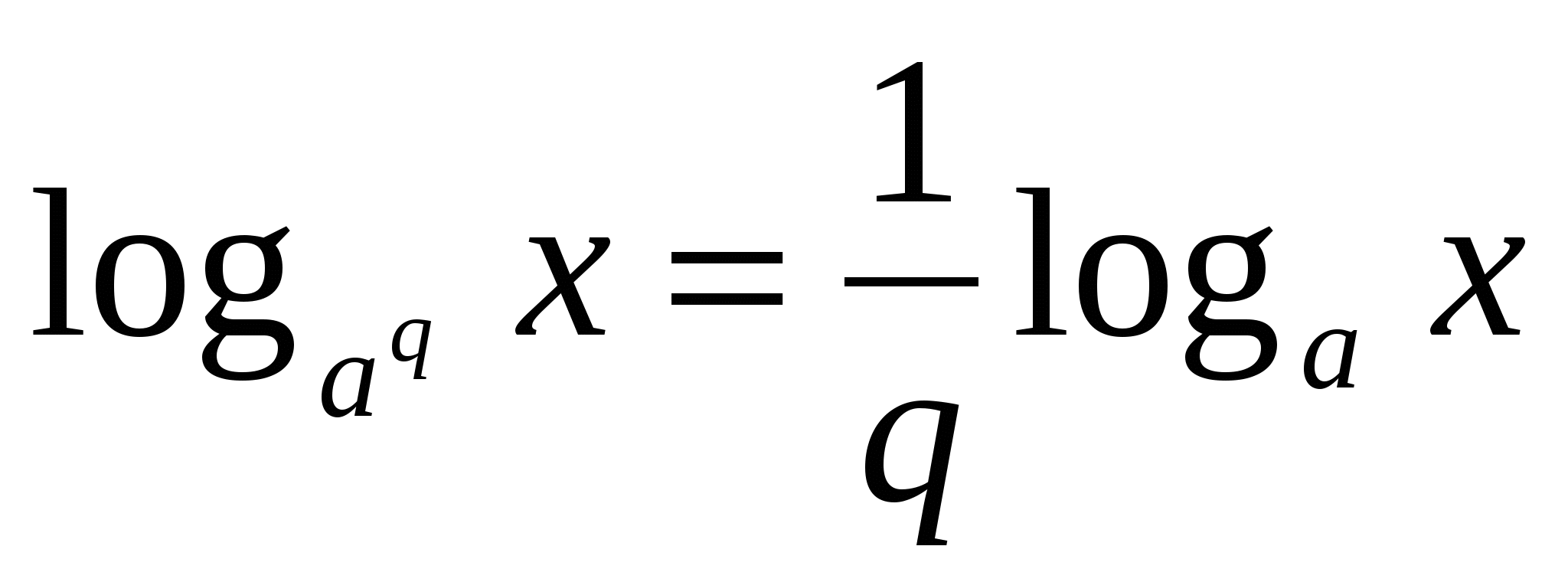 . Решение примеров.
. Решение примеров.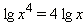
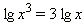
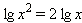
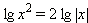
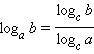
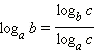
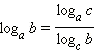
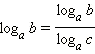
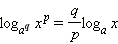
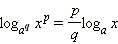
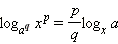
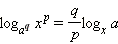
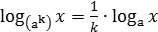
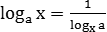
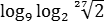
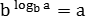
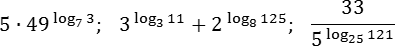


































Leave A Comment