Квадратные уравнения, примеры решений
Теория по квадратным уравнениям
ОПРЕДЕЛЕНИЕ Квадратным уравнением называется уравнение вида , где .Возможны такие случаи:
, тогда имеем квадратное уравнение вида и .
, тогда имеем квадратное уравнение вида , если ; если – корней нет.
, тогда имеем квадратное уравнение вида .
, тогда имеем полное квадратное уравнение , которое решается или с помощью дискриминанта:
Или по теореме Виета:
Примеры
ПРИМЕР 1| Задание | Решить следующие неполные квадратные уравнения
|
| Решение | 1) В уравнении вынесем за скобки . Произведение равно нулю, если один из сомножителей равен нулю, следовательно:
или
2) В уравнении перенесем свободный член вправо и раздели его на коэффициент при :
3) В уравнении перенесем свободный член вправо и раздели его на коэффициент при :
У данного квадратного уравнения нет корней. 4) уравнение равносильно уравнению , которое имеет два совпадающих корня . |
| Ответ |
Корней нет |
| Задание | Решить квадратное уравнение |
| Решение | Подсчитаем для заданного уравнения, чему равен дискриминант:
Так как , то уравнение имеет два совпадающих корня:
|
| Ответ |
| Задание | Решить уравнение |
| Решение | Вычислим дискриминант для исходного уравнения, получим:
Так как , данное уравнение решений не имеет. |
| Ответ | Корней нет. |
| Задание | Решить квадратное уравнение |
| Решение | Дискриминант заданного уравнения, равен
Следовательно, уравнение имеет два различных корня
|
| Ответ |
| Задание | Решить уравнение, используя теорему Виета: |
| Решение | Пусть и – корни квадратного уравнения, по следствию из теоремы Виета
Проанализируем полученные равенства. Произведение корней отрицательно, следовательно, корни имеют разные знаки. Разложим –12 на множители, учитывая, что они должны быть числами разного знака. Возможны такие варианты: –12 и 1; 12 и –1; –6 и 2; 6 и –2; –4 и 3; 4 и –3. Так как сумма корней равна 1, то корнями будут числа и . |
| Ответ |
Решение квадратных уравнений
Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
- Не имеют корней;
- Имеют ровно один корень;
- Имеют два различных корня.
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант.
Дискриминант
Пусть дано квадратное уравнение ax2 + bx + c = 0. Тогда дискриминант — это просто число D = b2 − 4ac.
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
- Если D < 0, корней нет;
- Если D = 0, есть ровно один корень;
- Если D > 0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
- x2 − 8x + 12 = 0;
- 5x2 + 3x + 7 = 0;
- x2 − 6x + 9 = 0.
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8)2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 32 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6)2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D < 0, корней нет — ничего считать не надо.
Задача. Решить квадратные уравнения:
- x2 − 2x − 3 = 0;
- 15 − 2x − x2 = 0;
- x2 + 12x + 36 = 0.
Первое уравнение:
x2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2)2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2x − x2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2)2 − 4 · (−1) · 15 = 64.
D > 0 ⇒ уравнение снова имеет два корня. Найдем их
\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left( -1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left( -1 \right)}=3. \\ \end{align}\]
Наконец, третье уравнение:
x2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 122 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
\[x=\frac{-12+\sqrt{0}}{2\cdot 1}=-6\]
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
- x2 + 9x = 0;
- x2 − 16 = 0.
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax2 + bx + c = 0 называется
неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax2 + c = 0. Немного преобразуем его:
Решение неполного квадратного уравненияПоскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c/a) ≥ 0. Вывод:
- Если в неполном квадратном уравнении вида ax
- Если же (−c/a) < 0, корней нет.
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c/a) ≥ 0. Достаточно выразить величину x2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Теперь разберемся с уравнениями вида ax2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
- x2 − 7x = 0;
- 5x2 + 30 = 0;
- 4x2 − 9 = 0.
x2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x1 = 0; x2 = −(−7)/1 = 7.
5x2 + 30 = 0 ⇒ 5x2 = −30 ⇒ x2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4x2 − 9 = 0 ⇒ 4x2 = 9 ⇒ x2 = 9/4 ⇒ x1 = 3/2 = 1,5; x2 = −1,5.
Смотрите также:
- Теорема Виета
- Следствия из теоремы Виета
- Тест на тему «Значащая часть числа»
- Правила комбинаторики в задаче B6
- Как представить обычную дробь в виде десятичной
- Задача B15: частный случай при работе с квадратичной функцией
www.berdov.com
Решение квадратных уравнений с применением теоремы Виета
Разделы: Математика
Цель: Применение теоремы Виета и ей обратной теоремы при нахождении коэффициентов в квадратных уравнениях, при решении заданий из вариантов ЕГЭ.
Воспитательные задачи: Способствовать формированию умений, применять приемы сравнений, обобщения, выделения главного, переноса знаний в новую ситуацию, развитию творческих способностей. Побуждать учащихся к самоконтролю и взаимоконтролю, самоанализу своей учебной деятельности.
Оборудование: плакаты, компьютер, экран, видеопроектор.
Ход урока
I. Вводная беседа. Устные упражнения (5 мин.)
Сегодня на уроке мы с вами вместе подведем итог, как важно применение теоремы Виета. В каких упражнениях применяется теорема и как важно ее знать и применять. (Учитель показывает презентацию, в которой сформулированы цели, задачи, структура урока). <Приложение 1>
Учащиеся формулируют теорему Виета и ей обратную теорему. У доски два ученика записывают формулы теоремы Виета для приведенного и полного квадратных уравнений:
– формулы для полного квадратного уравнения;
– формулы для приведенного квадратного уравнения;
Трое учащихся решают на дополнительных досках индивидуальные задания.
Решите уравнения и выполните проверку по теореме, обратной теореме Виета:
II. Устные упражнения (5 мин.)
Затем с учащимися решаем устные упражнения:
Найдите корни уравнения:
3. Если в квадратном уравнении сумма коэффициентов a + b + c = 0,
То Используя это свойство, решите уравнения:
4. Теорема Виета применяется при нахождении суммы и произведения корней. Покажите, как это выглядит. Перед вами уравнения:
У какого из данных уравнений:
- Сумма корней равна 6, а произведение – 16?
- Корни равны?
- Один из корней уравнения равен 6?
- Каждый из корней на 2 больше, чем корни уравнения ? Ответ обосновать.
III. Лабораторная работа (3 мин.)
Учащимся предлагается выполнить лабораторную работу.
Составьте квадратные уравнения, которые:
- не имеют корней;
- имеет один из корней, равный 0;
- имеет два корня, равных по модулю, но противоположных по знаку;
- имело бы один корень;
- сумма коэффициентов уравнения равна 0.
Учащиеся выполняют это задание по группам (4–5 учащихся в группе).
Пример лабораторной работы:
IV. Работа с таблицей (3 мин.)
Выполнив лабораторную работу, три группы озвучивают свою лабораторную работу, а остальные группы сдают лабораторные работы на плакатах на проверку (2 мин.).
Один из учащихся (Евсеев А.) заранее готовит презентацию об исследовании знаков в приведенных квадратных уравнениях. <Приложение 2>
Все учащиеся работают с таблицей и отвечают на вопросы о знаках в квадратных уравнениях:
- Когда корни квадратного уравнения имеют одинаковые знаки?
- Когда оба корня положительные, отрицательные?
- Когда корни имеют разные знаки?
- Когда больший по модулю корень отрицателен?
- Когда больший по модулю корень положителен?
Сформулируйте выводы о знаках корней квадратных уравнений.
V. Тренировочные упражнения. Работа у доски (23 мин.)
Следующий этап урока: двое учащихся решают у доски задания о нахождении неизвестных коэффициентов в квадратных уравнениях.
1. В уравнении один из корней равен 7. Найдите другой корень и коэффициент р. Ответ:
2. Один из корней уравнения равен 12,5. Найдите другой корень уравнения и коэффициент с. Ответ:
Такого вида уравнения часто встречаются на экзаменах. Поэтому сейчас Слинько В. предлагает просмотреть презентацию о нахождении коэффициентов в квадратных уравнениях. <Приложение 3>
А после просмотра презентации учащимся предлагается решить 2 уравнения самостоятельно с последующей проверкой.
1. Разность корней квадратного уравнения равна 2. Найдите с.
Ответ: c = 35.
2. Разность корней квадратного уравнения равна 6. Найдите с.
Ответ: c = –8,75.
Использование теоремы Виета дает возможность решать более сложные задания.
Трое учащихся решают задания у доски, комментируя и объясняя ход решения:
1. Один из корней уравнения равен 8. Найдите другой корень и коэффициент в.
Ответ: .
2. Один из корней уравнения равен 5,3. Найдите другой корень и коэффициент с.
Ответ: .
3. В уравнении квадратов корней равна . Найдите с. Ответ: с = 9.
VI. Заключение (6 мин.)
В заключение урока подводим итоги. Учащиеся формулируют применение теоремы Виета.
Теорема Виета применяется:
- при нахождении суммы и произведения корней квадратных уравнений;
- при составлении квадратных уравнений;
- при решении уравнений методом подбора;
- при нахождении коэффициентов в уравнении, свободного члена;
- при сравнении знаков коэффициентов в квадратном уравнении.
Один из учащихся рассказывает стихотворение.
По праву достойна в стихах быть воспета
О свойстве корней теорема Виета.
Что проще скажи постоянства такого?
Умножишь ты корни и дробь уж готова!
В числителе с, в знаменателе а,
А сумма корней тоже дроби равна.
Хоть с минусом дробь эта – что за беда?!
В числителе в, в знаменателе а.
Домашнее задание: № 645, № 667, № 671 из учебника «Алгебра 8», автор Макарычев Ю. Н.
Учитель выставляет оценки за урок, благодарит учащихся за работу на уроке.
Также предлагается посмотреть презентацию о решении квадратных уравнений с параметром, в которой рассматриваются задания повышенной сложности, применяемые на экзаменах и малом ЕГЭ. <Приложение 4>
19.01.2009
xn--i1abbnckbmcl9fb.xn--p1ai
Квадратные уравнения. Их решение по формуле | Учеба-Легко.РФ
Определение квадратного уравнения.
- Квадратным уравнением называется уравнение вида ах²+вх+с=0, где х – переменная, а,в,с – некоторые числа, причем а≠0.
- Числа а, в, с – коэффициенты квадратного уравнения. Число а – первыйкоэффициент, в – второй коэффициент, с – свободный член.
- Если в квадратном уравнении ах²+вх+с=0 хотя бы один из коэффициентов в или с равен нулю, то такое уравнение называется неполным квадратным уравнением.
- Квадратное уравнение, в котором коэффициент а=1 называется приведенным квадратным уравнением.
Примеры квадратных уравнений:
Например:
а) –х²+6х+1,2=0, где а=-1, в=6, с=1,2;
б) 5х²-2=0 – неполное квадратное уравнение, где а=5, в=0, с=-2;
в) -3х²+7х=0 — неполное квадратное уравнение, где а=-3, в=7, с=0;
г) 7х²=0 — неполное квадратное уравнение, где а=7, в=0, с=0;
д) х²+4х-12=0 – приведенное квадратное уравнение, где а=1, в=4, с=-12.
Алгоритм решения квадратного уравнения
Примеры решения квадратных уравнений по формуле
Пример1:
3х²+11х+6=0 а=3; в=11;с=6.
D=11²-4*3*6=121-72=49>0 – уравнение имеет 2 корня
Примеры решения квадратных уравнений по формуле:
Пример2.
9х²-6х+1=0
а=9; в=-11;с=1.
D=(-6)²-4*9*1=36-36=0=0 – уравнение имеет 1 корень.
Х=
Примеры решения квадратных уравнений по формуле:
Пример 3:
-2х²+3х-5=0
а=-2; в=3;с=-5.
D=3²-4*(-2)*5=9-40=-31<0 – уравнение не имеет корней.
1. Алтынов П.А. Тесты. Алгебра.7-9 – Москва, «Дрофа», 2002 год
2. Макарычев Ю.Н. Алгебра, 8 класс – Москва, «Просвещение», 2000 год
3. Ткачева М.В. Домашняя математика, 8 класс- Москва, «Просвещение», 1996 год
4. Худадатова С.С. Математика в ребусах, кроссвордах – Москва, «Школьная Пресса», 2003 год
5. Энциклопедический словарь юного математика –Москва, «Педагогика», 1985 год
6. Энциклопедия «Я познаю мир. Математика» — Москва, АСТ, 1996 год.
uclg.ru
Квадратное уравнение
Квадратное уравнение
— это уравнение вида a x2 + b x + c = 0, где a не равно 0.Геометрический смысл
Графиком квадратичной функции является парабола. Решениями (корнями) квадратного уравнения называют точки пересечения параболы с осью абсцисс. Если парабола, описываемая квадратичной функцией, не пересекается с осью абсцисс, уравнение не имеет вещественных корней. Если парабола пересекается с осью абсцисс в одной точке (вершине параболы), уравнение имеет один вещественный корень (также говорят, что уравнение имеет два совпадающих корня). Если парабола пересекает ось абсцисс в двух точках, уравнение имеет два вещественных корня.
Если коэффициент a положительный, ветви параболы направлены вверх, если отрицательный — ветви параболы направлены вниз. Если коэффициент b положительный, то вершина параболы лежит в левой полуплоскости, если отрицательный — в правой полуплоскости.
Вывод формулы для решения квадратного уравнения
Формулу для решения квадратного уравнения a x2 + b x + c = 0 можно получить так:- перенесем c в правую часть a x2 + b x = — c
- умножим уравнение на 4a (2a x)2 + 4a b x = — 4a c
- добавим b2 к обоим частям (2a x)2 + 4a b x + b2 = b2 — 4a c
- в левой части выделим полный квадрат (2a x + b)2 = b2 — 4a c
- извлечем квадратный корень 2a x + b = ± √b2 — 4a c
- перенесем b в правую часть 2a x = — b ± √b2 — 4a c
- разделим уравнение на 2a
x = -b ± √b2 — 4a c 2 a
Дискриминант квадратного уравнения
Дискриминантом
квадратного уравнения называют число равное D = b2 − 4acКвадратное уравнение с вещественными коэффициентами может иметь от 0 до 2 вещественных корней в зависимости от значения дискриминанта:
- при D > 0 корней два, и они вычисляются по формуле
x1,2 = -b ± √D 2 a - при D = 0 корень один (два равных или совпадающих корня), кратности 2:
- при Dx1,2 = -b ± i√-D 2 a
Теорема Виета
Приведенным квадратным уравнением
называется уравнение, в котором коэффициент при x2 равен единице. Такое уравнение может быть получено делением всего выражения на коэффициент a: x2 + px + q = 0, где p = ba, q = caСумма корней приведённого квадратного уравнения
x2 + px + q = 0 равна коэффициенту p, взятому с обратным знаком, а произведение корней равно свободному члену q:x1 + x2 = -p, x1x2 = q.
Разложение квадратного уравнения на множители
Если известны оба корня квадратного уравнения, его можно разложить по формуле
Примеры решения квадратных уравнений
Например. Найти корни квадратного уравнения: 2x2 + 5x + 3 = 0
D = 52 — 4·3·2 = 25 — 24 = 1
|
|
ru.onlinemschool.com
Материал для подготовки к ЕГЭ (ГИА) по алгебре (9 класс) на тему: Задания на тему «Квадратные уравнения и неравенства» | скачать бесплатно
- Квадратные уравнения:
Вариант 1. Решите уравнение .
Вариант 2. Решите квадратное уравнение .
Вариант 3. Решите уравнение .
Вариант 4. Решите уравнение .
Вариант 5. Решите уравнение .
Вариант 6. Решите квадратное уравнение .
Вариант 7. Решите уравнение .
Вариант 8. Решите уравнение .
Вариант 9. Решите уравнение .
Вариант 10. Решите уравнение .
9-1. Решите уравнение .
9-2. Решите уравнение .
9-3. Решите уравнение .
9-4. Найдите корни уравнения .
9-5. Решите уравнение .
9-6. Решите уравнение .
9-7. Решите уравнение .
9-8. Найдите корни уравнения .
9-9. Найдите корни уравнения .
9-10. Решите уравнение .
9-11. Найдите произведение корней уравнения x2─x+1= -x+10.
9-12. Решите уравнение x2 +2x─3=x─1. В ответ запишите сумму его корней.
9-13. Решите уравнение x(x-1)=3-x. В ответе укажите больший корень уравнения.
9-14. Решите уравнение (x+1)2=1. В ответе укажите только натуральные корни.
9-15. Решите уравнение .
Решите уравнение . В ответе укажите наибольший корень.
2. Решите уравнение
3. Решите уравнение . В ответе укажите наименьший корень.
4. Решите уравнение
5. Решите уравнение . В ответе укажите наибольший корень.
6. Решите уравнение .
7. Решите уравнение . В ответе укажите наименьший корень.
8. Решите уравнение .
9. Решите уравнение . В ответе укажите наибольший корень.
10. Решите уравнение .
2.Квадратные неравенства
2.1. Решите неравенство .
2.2. Решите неравенство .
2.3. Решите неравенство .
2.4. Решите неравенство .
2.5. На рисунке изображен график функции
. Используя график, решите неравенство .
Ответ________________________
2.6. На рисунке изображен график функции
. Используя график, решите неравенство .
Ответ._____________________
2.7. На рисунке изображен график функции
. Используя график, решите неравенство .
Ответ____________________
2.8. На рисунке изображен график функции
. Используя график, решите неравенство .
- Разложение на множители:
Вариант 1. Разложите на множители .
Вариант 2. Разложите на множители .
Вариант 3. Разложите на множители .
Вариант 4. Разложите на множители .
Вариант 5. Разложите на множители .
Вариант 6. Разложите на множители .
Вариант 7. Разложите на множители .
Вариант 8. Разложите на множители .
Вариант 9. Разложите на множители .
Вариант 10. Разложите на множители .
nsportal.ru
Квадратные уравнения (тренажёр) — Документ
Квадратные уравнения (тренажёр).
Вариант 1.
1) Выберите квадратное уравнение, у которого первый коэффициент равен 3, второй коэффициент -5, свободный член 6.
1) 3x2-5x+6=0 3) -5x2+3x+6=0
2) 3x2+5+6=0 4) -3x2-5x+6=0
2) Выберите приведённое квадратное уравнение, у которого второй коэффициент и свободный член равны -2.
1) 2x2-2x-2=0 3) x2+2x-2=0
2) x2-2x-2=0 4) x2-2x+2=0
3) Выберите неполное квадратное уравнение, у которого первый коэффициент равен -5, свободный член равен 7.
1) 7x-5=0 3) -5x2+x+7=0
2) 7x2-5=0 4) -5x2+7=0
4) Выберите неполное квадратное уравнение, у которого первый коэффициент равен 3, второй коэффициент равен 5.
1) 3x2+5x=0 3) 3x+5x2=0
2) 3x2+5=0 4) 3+5x2=0
5) Выберите дискриминант квадратного уравнения 3х-8х-3=0.
1) D=10 3) D=99
2) D=81 4) D=100
6) Не решая уравнение 12х+10х-1, определить, имеет ли данное уравнение корни.
1)да
2)нет
7) При каком условии полное квадратное уравнение имеет единственный корень.
1) D=0 3)D
2) D>0
Решите уравнения:
х-4х+4=0
2 3) 1
3 4) 5
9) 15+х=-49
1) нет решения 3) 7
2) любое 4) 6
10) (х+1)(х-2)=0
1) -1 и 2 3) нет решения
2) -2 и 1 4) -3 и 4
11) (х-2)(х+2)=0
1) 2 и -2 3) 2 и 1
2) 0 и 2 4) 3 и 0
12) (х-1)-1+2х=0
1) 0 и 1 3) 0
2) нет решения 4) 1
13) 2х=800
1) 20 и -20 3) -20
2) 20 4) любое
14) 5х-20=0
1) 2 и -2 3) -2
2) 2 4) 2 и 1
15) 3х=0
1) любое 3) 3
2) 0 4) -3
16) х-х=0
1) 1 и 0 3) 1
2) любое 4) 0
17) х-1=0
1) любое 3) -1
2) 1 4) 1 и -1
18) 2х+х=0
1) 0 и 0,5 3) 0
2) 0 и -0,5 4) 0,5
19) Среди чисел -3; 3; -4; 1 найдите корень уравнения х+5х+6=0.
1) 3 3) -4
2) -3 4) 1
20) Половина периметра прямоугольника равна 10 м, а площадь этого прямоугольника равна 21м. Найдите стороны прямоугольника.
1) 3 и 7 3) -3 и 7
2) 3 и -7 4) 2 и 5
21) Запишите, чему равны сумма и произведение корней квадратного уравнения
х-5х+6=0.
1) х+х=5 3) х+х=5
х*х=6 х*х=-6
2) х+х=-5 4) х+х=-5
х*х=-6 х*х=5
Вариант №2.
1. Выберите квадратное уравнение, у которого первый коэффициент -5, второй коэффициент 3, свободный член -6.
1) 5x+3x-6=0 3) 5x+6x-6=0
2) 5x+3x-6=0 4) -5x+3x-6=0
2. Выберите приведенное уравнение, у которого второй коэффициент и свободный член равны -3.
1) x-3x-3=0 3) -x-3x-3=0
2) x-3x+3=0 4) x+3x-3=0
3. Выберите неполное квадратное уравнение, у которого первый коэффициент равен -3, свободный член равен 5.
1) -3x-5=0 3) -3x+5=0
2) 3x-5=0 4) 3x+5=0
4. Выберите неполное квадратное уравнение, у которого первый коэффициент равен 5, второй коэффициент равен 7.
1) 5x-7x=0 3) -5x+7x=0
2) 5x+7x=0 4) -5x-7x=0
5. Выберите дискриминант квадратного уравнения 2х-3х-2=0.
1) D=16 3) D=7
2) D=25 4) D=36
6. Не решая уравнение 5х+6х-10=0, определить, имеет ли данное уравнение корни.
1) ДА 2) НЕТ
7. При каком условии полное квадратное уравнение не имеет корней
1) D=0 3) D
2) D>0
Решите уравнения:
8. х-6х+9=0
1) 2 3)1
2) 3 4) 4
9. 15-х= -49
1)
3)
2) 4)
10. у(у-5)=0
1) 0;5 2) 0;-5
3) -5 3) 0
11. (х-9)(х+9)= -82
1)
x 2)
2)
3) 9; -9 4) 9
12. -х+3=7х+3
1) 0;-7 2) 0;7
3) 15; 0 4) -15; 0
13. 4х=100
1) 2) 
3) 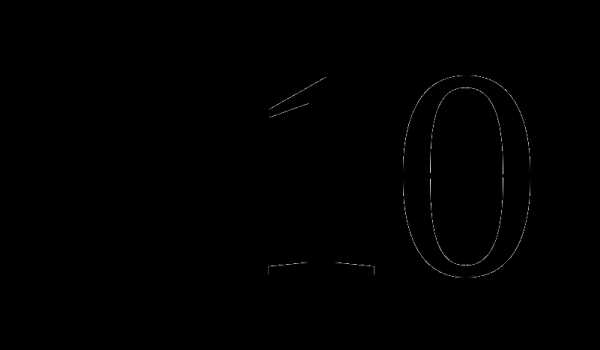 4) 0
4) 0
14. 6х-54=0
1) 3)
2) 4) 3
15. 5х=0
1) 5 2) -5
3) 0 3) нет решения
16. х+х=0
1) 0;-1 2) 0;1
3) -1;0 4) х-любое
17. х-9=0
1)  2)
2)
3) 3) 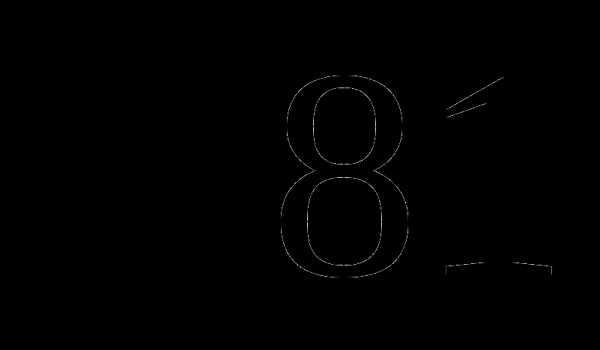
18. 3х-х=0
1) 0; 3 2) 0;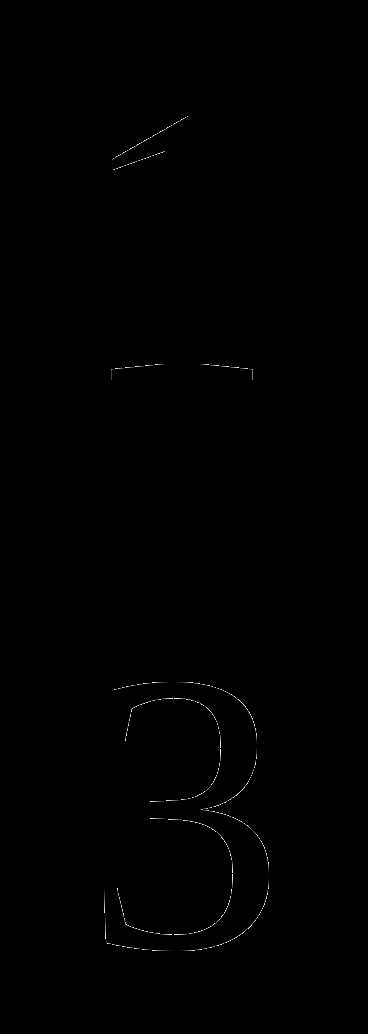 3) -3 4) 0
3) -3 4) 0
19. Среди чисел 2; 3; -3; -4 найдите корень уравнения х- х-12=0
1) -3; 2) 3; 3) 2; 4) -4
20. Найдите длины сторон прямоугольника, если его площадь 20дм, а половина периметра равна 9дм.
1) 3 и 2 2) 4 и 5 3) -4 и 5 4) -3 и 2
21. Запишите, чему равны сумма и произведение корней квадратного уравнения
х-6х+5=0.
1) 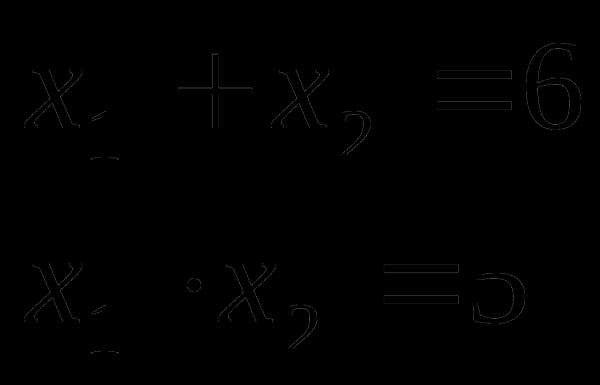 2)
2) 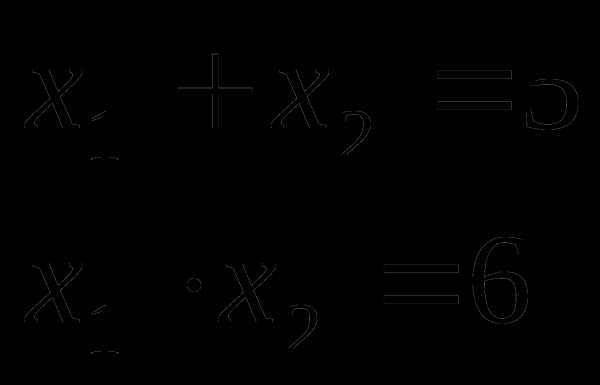 3)
3) 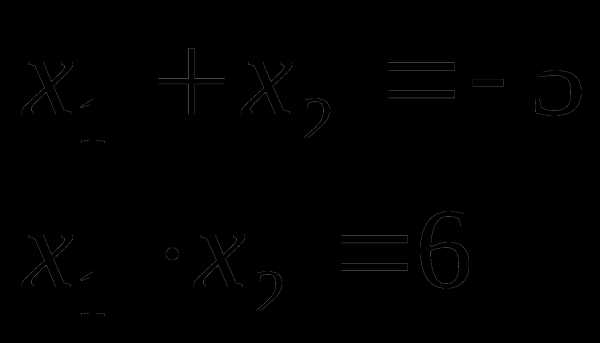 4)
4) 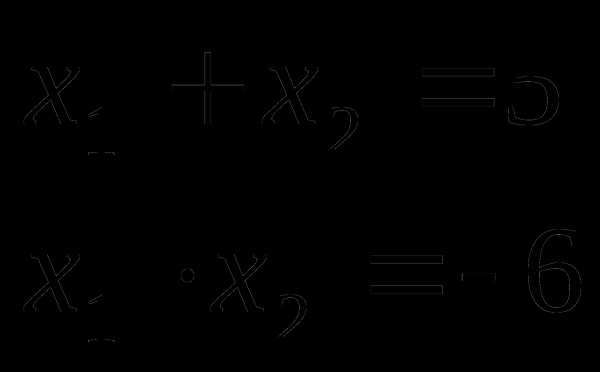
Решение квадратных уравнений
Вариант 1
1.Какое из уравнений не имеет корней:
1) 7х2— 3х – 8 = 0 2) 4х2— 11х + 5 = 0
3) 3х2+ 7х + 2 =0 4) 2х2+ х + 2 =0
2.Найдите разность большего и меньшего корней уравнения: х2-9х+14=0
1) 5
2) 10 3) 3 4) 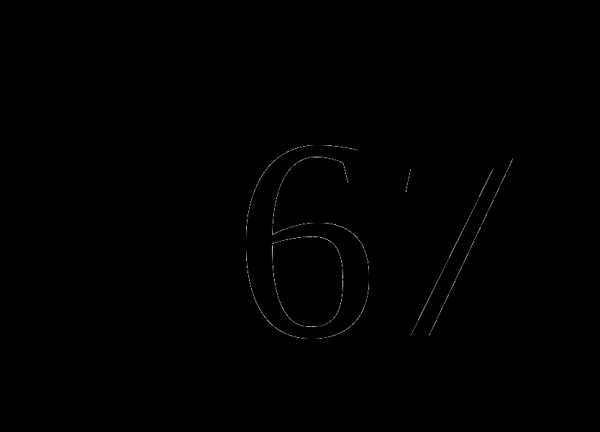
3. Площадь прямоуголника равна 48 см2. Одна его сторона в три раза больше другой. Найдите большую сторону прямоугольника.
1) 12 см 2) 8 см 3) 24 см 4) 16 см
4. Вычислите дискриминант уравнения: 2х2-х+11=0
1) -87 2) 89 3) -21 4) 33
5. Решите
уравнение, 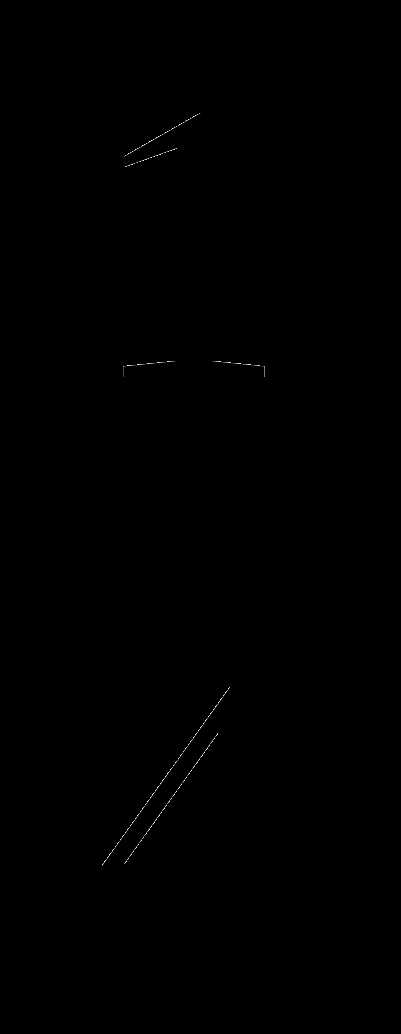 а2=100
а2=100
1) 5 2) 20 3) 5;-5 4) 20; -20
6. Найдите корни уравнения 2х-9 = (х-3)(х+3)
1) -2 2) 2 3) -1; 3 4) 0; 2
7. В
прямоугольном треугольнике один катет
больше другого на 4 см. Гипотенуза равна 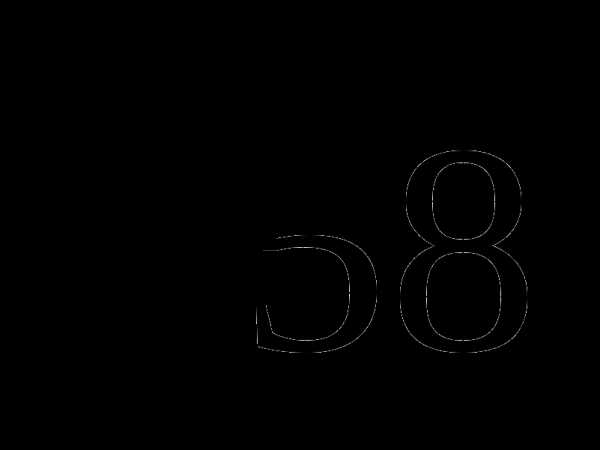 см. Чему равен больший катет?
см. Чему равен больший катет?
1) 3 см 2) 7 см 3) 4 см 4) 8 см
8. Решите уравнение: 3x2-x – 4 =0
1) 2;  .
2) 0; -3. 3) -1; 1.
4) 1; — 1.
.
2) 0; -3. 3) -1; 1.
4) 1; — 1.
9. Решите уравнение: x2+3=10х-6
1) 3; -1 2) 1;9 3) 0; 2 4) -2; 0
10. Одно число меньше другого на 4, а их
Произведение равно 221. Найдите эти числа.
1) 18 и 14 2) 17 и 13 3) 15 и 19 4) 19 и 9.
11. Решите уравнение
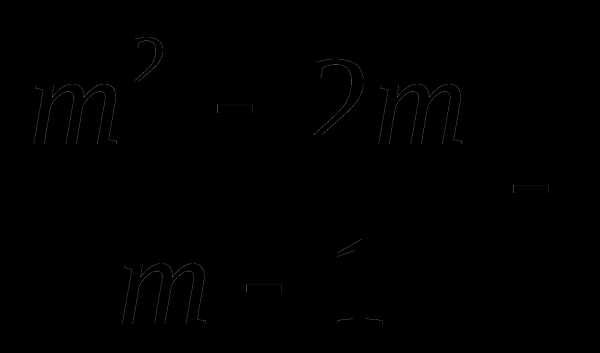
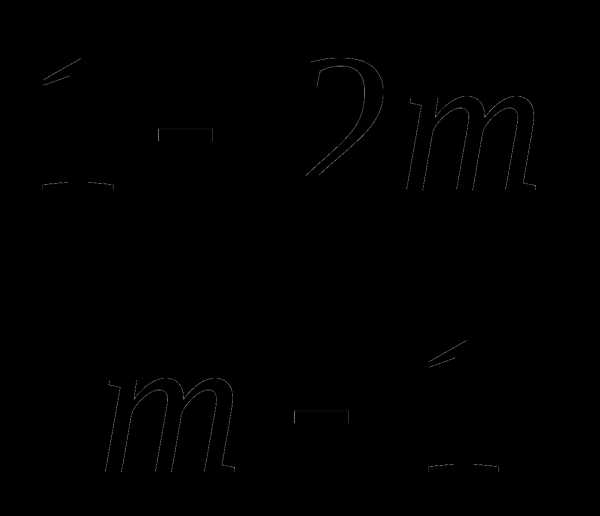 = 0
= 0
1)1;-1; 2)2; 3) ; 4)-1;
12. Если х=3, х=-4 — корни уравнения
х2 + рх + q=0, то
1) р=1; q=-12 3) p=12; q=1;
2) p=-1; q=-12 4) p=-12; q=1;
13. Найдите b в уравнении x2+bx-12=0,если
оно имеет корень 4.
1) 1; 2) -1; 3) 7; 4) -7.
Вариант 2.
1. Какое из уравнений имеет два корня
1)5х2+2х+1=0 3)5х2-2х+1=0
2)5х2+2х-1=0 4)х2+2х+5=0
2. Найдите разность большого и меньшего корней уравнения
х2+5х-24=0
1) 1; 2) 11; 3) 7; 4) 5;
3.Площадь прямоугольника равна 24см2. Одна его сторона в раза больше другой. Найдите меньшую сторону прямоугольника.
1) 4см. 2) 3см. 3) 6см. 4) 8см.
4. Вычислите дискриминант уравнения 7х2+3х-1=0
1) -19; 2) 37; 3) 49; 4) 36;
5. Решите уравнение 0,5у2=8
1) 2;-2; 2) 2; 3) 4;-4; 4) 4;
6. Найдите корни уравнения (3х-1)(3х+1)=9х-1
1)1; 2)-3; 3)0;1; 4)3;0;
7. В прямоугольном треугольнике один катет больше другого на 3см. Площадь треугольника 9см2. Чему равен большой катет?
1)3см. 2)6см. 3)2см. 4)4,5см.
8.Решите уравнение
x+18=10-6x
1) -4;-2. 2)4;-3. 5)2;-4. 4)-2;4
9.Решите уравнение
5 x-11х+2=0
1)-1; ;
2)0;-5 3)2;0,2 4)-2;-0,2
;
2)0;-5 3)2;0,2 4)-2;-0,2
10. Длина прямоугольника больше его ширины на 6 см. Найдите стороны прямоугольника, если площадь равна 112см2.
1)-14 и 8; 2) 17 и 11; 3)8 и 14; 4) 18 и 4;
11.Решите уравнение

1) 0;2 2) 2; 3) 0; 4) 4;
12. Сумма и произведение корней уравнения
x + 7х – 1 = 0 равны
1) х+ х=7; 2)х+ х=1; 3) х+ х=-7; 4) х+ х=-1
хх=1; хх=7; хх=-1; хх=7
13. Найдите с в уравнении 2x+8x+c=0, если оно имеет корень 5.
1) 90; 2) -90; 3) 45; 4) -45.
Решение квадратных уравнений
Вариант 3
1.Какое из уравнений не имеет корней:
1) 2–3х+1=0 3) 3+4х+1=0
2) 2+4х-1=0 4) 3–2х+1=0
2. Найдите разность большего и меньшего корней уравнения 4–8х+3=0
1) -1 3) 2
2) 1 4) -2
3. Периметр прямоугольника равен 10 дм, а площадь 4 дм2. Найти его стороны.
1) 3 дм, 2 дм 3) -1 дм, — 5 дм
2) 1 дм , 4 дм 4) 2 дм, 2 дм
4.Вычислите дискриминант уравнения 10+5х-0,6=0
1) -1 3) 49
2) 1 4) 21,6
5. Решите
уравнение 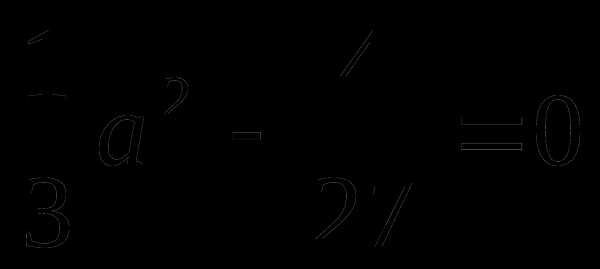
1)  3)
3) 
2) 4)
4) 
6. Найдите корни уравнения +2х-3=2х+6
1) 3 3) 4;1
2) 3 4) -9; -1
7. Найдите катеты прямоугольного треугольника, если их сумма равна 46, а гипотенуза 34.
1) 26;20 3) 6;40
2) 30;16 4) 23;23
8. Решите уравнение 3-4х+1=0
1) 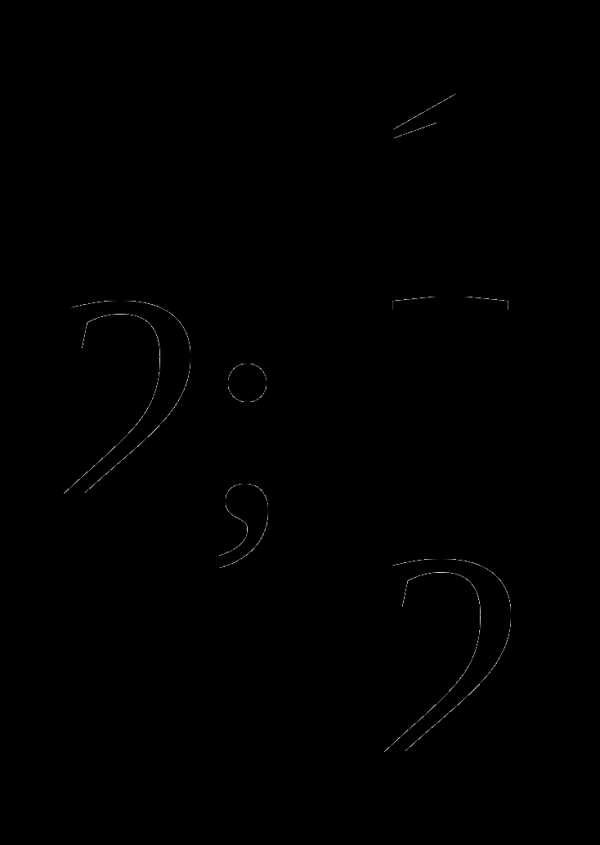 3) -1;
3) -1;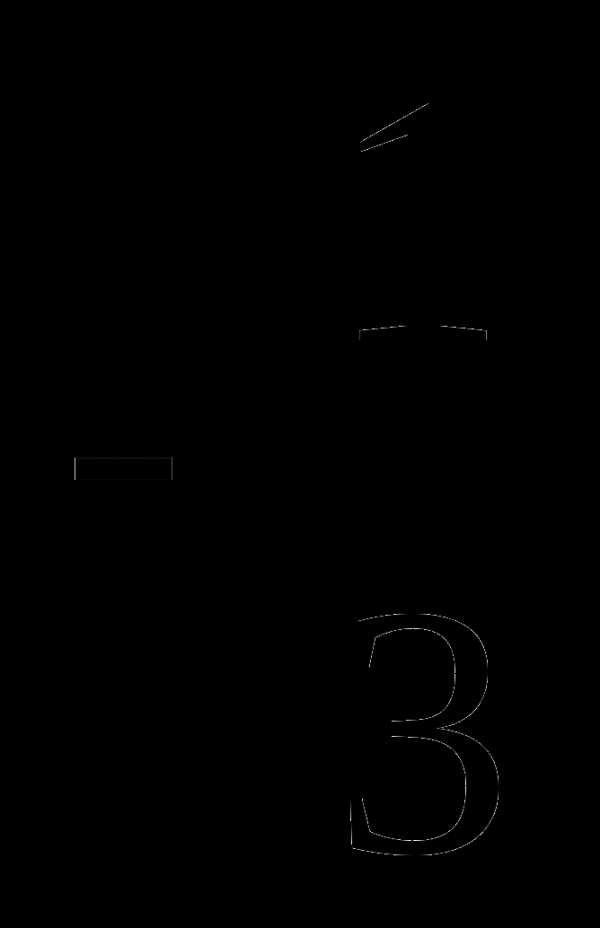
2) 1; 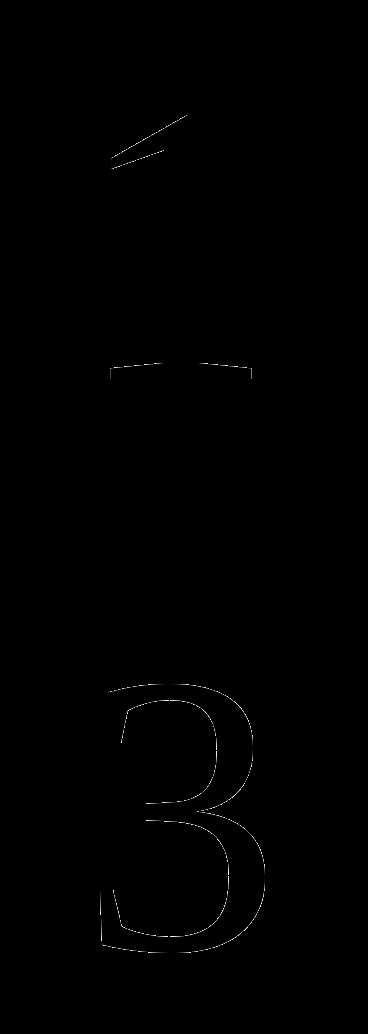 4) -2;
4) -2; 
9. Решите уравнение 5+1=6х
1) 1; 0,2 3) 2; 3
2) -1; -0,2 4) -2; -3
10.
Сократите дробь 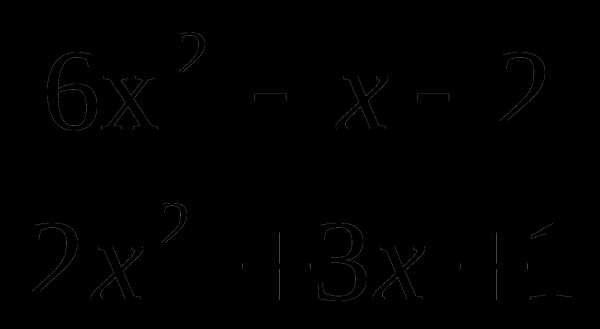
1) 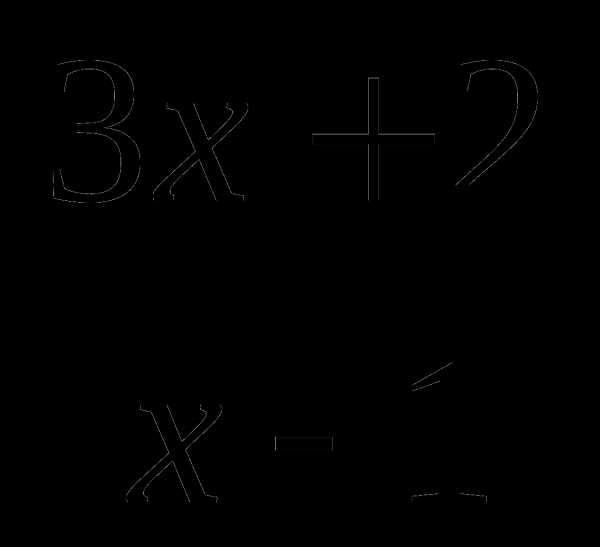 3)
3) 
2)  4)
4) 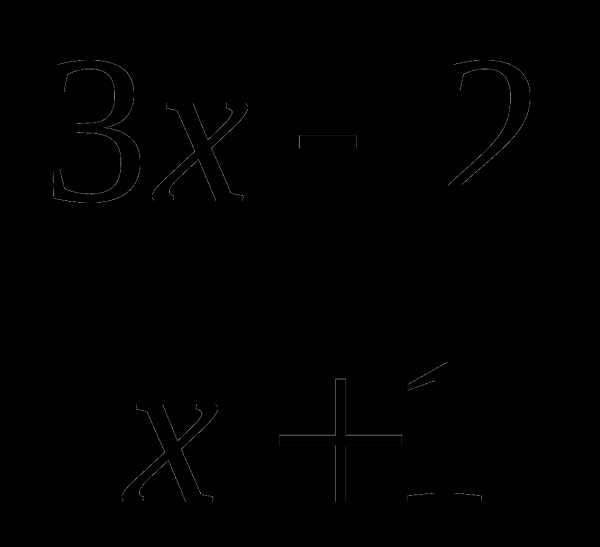
11. Решите уравнение . В ответе укажите их произведение:
9 3) 30
33 4) -30
12. Сумма всех различных корней уравнения является целым числом. Найдите остаток от деления на 3:
1) 1 3) 3
2) 2 4) 0
13. Если 11 — корень уравнения , то значение q равно:
1) 22 3) -264
2) -22 4) 264
Решение квадратных уравнений
Вариант №4
1.Какое из уравнений не имеет корней?
1) 3x2-5x-2=0 3)2x2+4x+5=0
2)3x2-10x+6=0 4)2x2+7x+5=0
2. Найдите разность большего и меньшего корней уравнения: х2+5x-14
1) 5 2) -9 3) 9 4)-5
3. Площадь прямоугольника 480дм2. Найдите его стороны, если периметр прямоугольника равен 94дм.
1) 32;15дм 2) 48;10дм 3) 20;27дм 4) 16;70дм
4. Вычислите дискриминант уравнения 10x2-3x-0,4=0
1)10, 6 2)-7 3)25 4)7, 4
5. Решите
уравнение 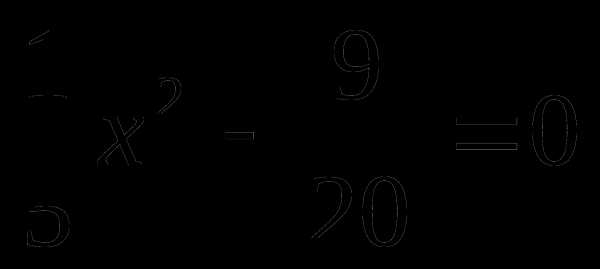
1)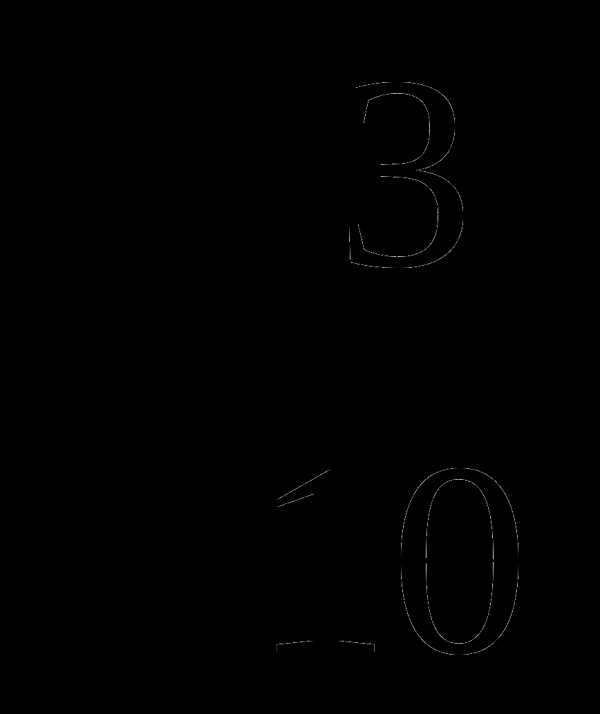 2)
2)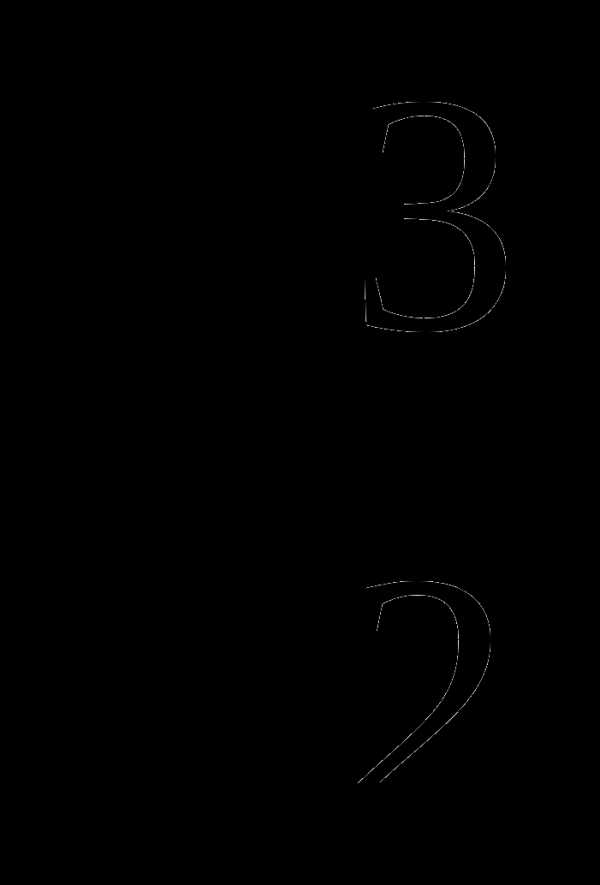 3)
4)
3)
4)
6. Найдите корни уравнения x2-3x-5=11-3x
1) 4 2) 3) 2;-8 4) 8;-2
7. Площадь прямоугольного треугольника 180см2. Найдите катеты треугольника, если их сумма 39
1) 30;9 2) 24;15 3) 15;12 4) 13;26
8. Решите уравнение
1) 6; -1 2) -; 3 3) ; -3 4) -6;1
9. Решите уравнение х(х + 1) = 56
1) 7; -8 2) -7; 8 3) 4; -14 4) -4; 14
10.
Сократите дробь 
а) 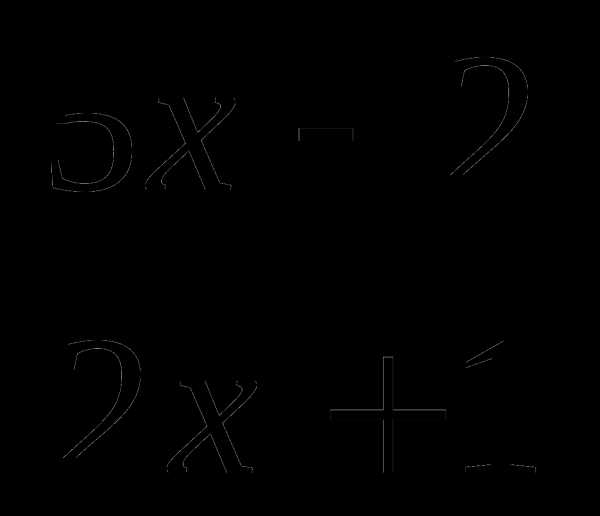 б)
б) 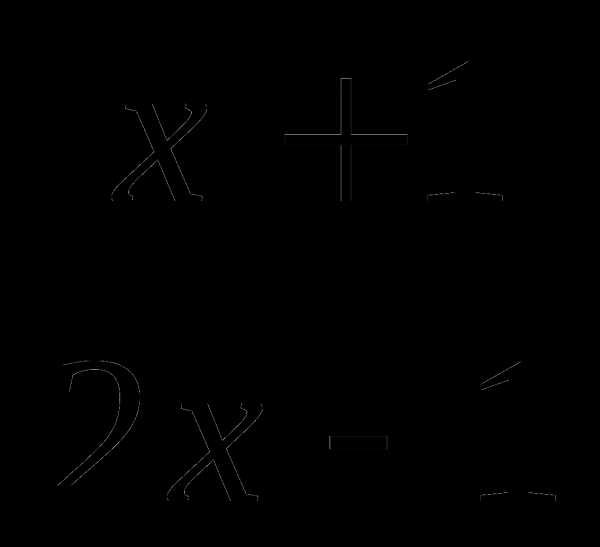 в)
в) 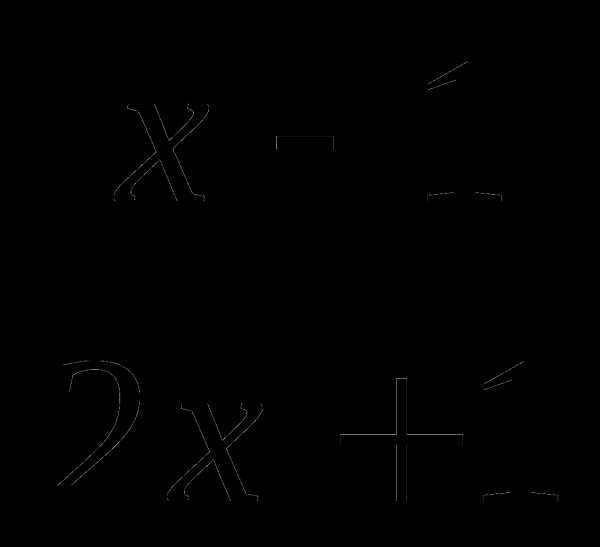 г)
г) 
11.
Решите уравнение 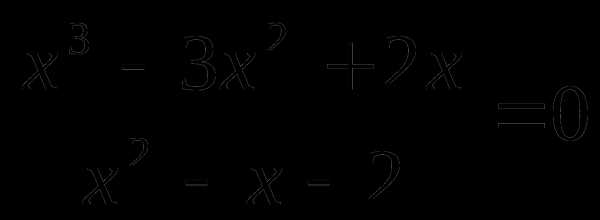 .
В ответе укажите их сумму.
.
В ответе укажите их сумму.
1) 3 2) 1 3)2 4)4
12. Сумма всех различных корней уравнения является целым числом. Найдите остаток от деления этого числа на 5.
1)1 2)3 3) 2 4) 0
13. Если 7 корень уравнения , то значение р равно:
1) -2 2) 2 3) 12 4)-12
gigabaza.ru

Leave A Comment