| С4Дан параллелограмм $ABCD$, сторона которого $AB=13$. В7Найдите, если $\operatorname{tg}\alpha=-4$ [посмотреть решение] |
В куб вписан шар радиуса 2. Найдите объем куба. Самостоятельная работа 3 Цилиндр, конус, шар 1. Найдите объем цилиндра, площадь основания которого равна 1, а образующая равна 6 и наклонена к плоскости основания под углом 30о.
Самостоятельная работа 1Диагональ куба равна . Найдите его объем.
Площадь поверхности куба равна 24. Найдите его объем.
Площадь грани прямоугольного параллелепипеда равна 12. Ребро, перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда.
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.
Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту пирамиды.
Объем треугольной пирамиды равен 15. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 1 : 2, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду.
Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6.
 Найдите высоту цилиндра.
Найдите высоту цилиндра. Высота конуса равна 6, образующая равна 10. Найдите его объем, деленный на
Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 48.
В куб вписан шар радиуса 2. Найдите объем куба.
Самостоятельная работа 2
Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в три раза?
Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого равны 90о.
Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему куба.
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь боковой поверхности исходной призмы.
Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен
От призмы, объем которой равен 6, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части.
Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.
Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на
Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на .
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 1. Объем параллелепипеда равен 8. Найдите высоту цилиндра.
В куб вписан шар радиуса 3. Найдите площадь поверхности куба.
Самостоятельная работа 3
1. Объем куба равен 27. Найдите площадь его поверхности.
2. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 3. Объем параллелепипеда равен 36. Найдите его диагональ.
3. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого равны 90о.
4. Объем куба равен 12. Найдите объем треугольной пирамиды, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины.
5. Площадь поверхности правильной треугольной призмы равна 6. Какой будет площадь поверхности призмы, если все ее ребра увеличить в три раза?
6. Найдите площадь боковой поверхности правильной шестиугольной призмы, стороны основания которой равны 3, а высота равна 6.
7. В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.
8. От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
9. В цилиндрическом сосуде уровень жидкости достигает 18 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 3 раза больше первого?
10. Конус получается при вращении равнобедренного прямоугольного треугольника вокруг катета, равного 6. Найдите его объем, деленный на .
11. Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен 2. Площадь боковой поверхности призмы равна 48. Найдите высоту цилиндра.
12. Куб вписан в шар радиуса . Найдите объем куба.
Самостоятельная работа 3
Цилиндр, конус, шар
 Найдите объем цилиндра, площадь основания которого равна 1, а образующая равна 6 и наклонена к плоскости основания под углом 30о.
Найдите объем цилиндра, площадь основания которого равна 1, а образующая равна 6 и наклонена к плоскости основания под углом 30о.2. Цилиндр и конус имеют общие основание и высоту. Найдите объем цилиндра, если объем конуса равен 50.
3. Воду, находящуюся в цилиндрическом сосуде на уровне 12 см, перелили в цилиндрический сосуд, в два раза большего диаметра. На какой высоте будет находиться уровень воды во втором сосуде?
4. Найдите объем конуса, площадь основания которого равна 2, а образующая равна 6 и наклонена к плоскости основания под углом 30о.
5. Объем конуса равен 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите объем отсеченного конуса.
6. Площадь осевого сечения цилиндра равна . Найдите площадь боковой поверхности цилиндра.
7. Площадь большого круга шара равна 1. Найдите площадь поверхности шара.
8. Во сколько раз увеличится площадь поверхности шара, если его радиус увеличить в два раза?
9. Радиусы трех шаров равны 3, 4 и 5. Найдите радиус шара, объем которого равен сумме их объемов.
Рисунок 1Рисунок 7Рисунок 8Рисунок 1Рисунок 2Рисунок 58ђЗаголовок 3ЋђЗаголовок 5Заголовок 6Заголовок 715
Приложенные файлы
- 12017885
Размер файла: 231 kB Загрузок: 0
Комбинация тел, объёмы
%PDF-1.5 % 1 0 obj >/Metadata 177 0 R/OCProperties>>>]/ON[178 0 R]/Order[]/RBGroups[]>>/OCGs[178 0 R]>>/Outlines 174 0 R/Pages 2 0 R/Type/Catalog>> endobj 176 0 obj >/Font>>>/Fields 182 0 R>> endobj 177 0 obj >stream application/pdf
 comuuid:27db7e1b-444f-4b31-9ef3-27ed3a9dc62cuuid:b6dc3431-ed25-47f7-9682-b1ff7e71f098
endstream
endobj
174 0 obj
>
endobj
2 0 obj
>
endobj
4 0 obj
>/MediaBox[0 0 595.
comuuid:27db7e1b-444f-4b31-9ef3-27ed3a9dc62cuuid:b6dc3431-ed25-47f7-9682-b1ff7e71f098
endstream
endobj
174 0 obj
>
endobj
2 0 obj
>
endobj
4 0 obj
>/MediaBox[0 0 595. G#-]`M9
G#-]`M9Шар. Задачи — презентация онлайн
МатематикаШАР
(ГУЩИН)
2. 1. Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
122. Во сколько раз увеличится площадь
поверхности шара, если радиус шара увеличить в
2 раза?
4
4. 3. Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?
275. 4. Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их объемов.
126. 5. Объем одного шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
97. 6. Радиусы двух шаров равны 6 и 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
108. 7. Объем шара равен 288 . Найдите площадь его поверхности, деленную на .
1449. 8. Даны два шара. Диаметр первого шара в 8 раз больше диаметра второго. Во сколько раз площадь поверхности первого шара больше площади поверх
8. Даны два шара. Диаметр первого шара в 8 разбольше диаметра второго. Во сколько раз
площадь поверхности первого шара больше
площади поверхности второго?
64
10. 9. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 6. Найдите объем шара.
2411. 10. В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на .
4,512. 11. Около куба с ребром описан шар. Найдите объем этого шара, деленный на .
11. Около куба с ребром 3 описан шар. Найдитеобъем этого шара, деленный на .
4,5
13. 12. Куб вписан в шар радиуса . Найдите объем куба.
12. Куб вписан в шар радиуса 3 . Найдитеобъем куба.
8
14. 13. Шар, объём которого равен 6 , вписан в куб. Найдите объём куба.
3615. 14. Вершина А куба АВСДА1В1С1Д1 со стороной 1,6 является центром сферы, проходящей через точку А1. Найдите площадь S части сферы, содержащейся вн
14. Вершина А куба АВСДА1В1С1Д1 со стороной
Вершина А куба АВСДА1В1С1Д1 со стороной1,6 является центром сферы, проходящей через
точку А1. Найдите площадь S части сферы,
содержащейся внутри куба. В ответе запишите
величину S / .
1,28
16. 15. Середина ребра куба со стороной 1,9 является центром шара радиуса 0,95. Найдите площадь S части поверхности шара, лежащей внутри куба. В отве
15. Середина ребра куба со стороной 1,9является центром шара радиуса 0,95. Найдите
площадь S части поверхности шара, лежащей
внутри куба. В ответе запишите S / .
0,9025
Задачи по теме «Шар»
Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?
Во сколько раз увеличится объем шара, если его радиус увеличить в десять раз?
Во сколько раз увеличится объем шара, если его радиус увеличить в четыре раза?
Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их объемов.
Радиусы трех шаров равны 15, 20 и 25. Найдите радиус шара, объем которого равен сумме их объемов.
Радиусы трех шаров равны 1, 6 и 8. Найдите радиус шара, объем которого равен сумме их объемов.
Радиусы трех шаров равны 2, 12 и 16. Найдите радиус шара, объем которого равен сумме их объемов.
В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на π.
В куб с ребром 21 вписан шар. Найдите объем этого шара, деленный на π.
В куб с ребром 9 вписан шар. Найдите объем этого шара, деленный на π.
Около куба с ребром √243 описан шар. Найдите объем этого шара, деленный на π.
Шар, объём которого равен 6π, вписан в куб. Найдите объём куба.
Около куба с ребром √3 описан шар. Найдите объем этого шара, деленный на π.
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 6. Найдите объем шара.
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 24. Найдите объем шара.
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 2. Найдите объем шара.
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 27. Найдите объем шара.
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 8. Найдите объем шара.
Куб вписан в шар радиуса √3. Найдите объем куба.
Куб вписан в шар радиуса 1√3. Найдите объем куба.
Куб вписан в шар радиуса 10,5√3. Найдите объем куба.
Куб вписан в шар радиуса 10√3. Найдите объем куба.
Даны два шара с радиусами 4 и 1. Во сколько раз объём большего шара больше объёма другого?
Однородный шар диаметром 3 см имеет массу 162 грамма. Чему равна масса шара, изготовленного из того же материала, с диаметром 2 см? Ответ дайте в граммах.
Однородный шар диаметром 3 см имеет массу 81 грамм. Чему равна масса шара, изготовленного из того же материала, с диаметром 5 см? Ответ дайте в граммах.
Зачётные работы по заданиям сайта «Открытый банк задач ЕГЭ по математике» (http://mathege.ru) | Учебно-методический материал по геометрии (11 класс) на тему:
Зачётная работа по теме «Объём пирамиды и конуса» (ОБЗ).
Вариант 1.
- Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды.
- Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60. Высота пирамиды равна 6. Найдите объем пирамиды.
- От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания.
 Найдите объем отсеченной треугольной пирамиды.
Найдите объем отсеченной треугольной пирамиды. - Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 45. Найдите объем пирамиды.
- Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Зачётная работа по теме «Объём пирамиды и конуса» (ОБЗ).
Вариант 2.
- Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна .
- Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.
- Объем треугольной пирамиды равен 15. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 1 : 2, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду.
- Объем параллелепипеда равен 12. Найдите объем треугольной пирамиды .
- В сосуде, имеющем форму конуса, уровень жидкости достигает высоты. Объём жидкости равен 70 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
Зачётная работа по теме «Объём пирамиды и конуса» (ОБЗ).
Вариант 3.
- Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен .
- Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен 1. Найдите объем шестиугольной пирамиды.
- В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды.
- Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро.
- Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 5.
Зачётная работа по теме «Объём пирамиды и конуса» (ОБЗ).
Вариант 4.
- В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.
- Объем правильной четырехугольной пирамиды SABCD равен 12. Точка E — середина ребра SB. Найдите объем треугольной пирамиды EABC.
- Сторона основания правильной шестиугольной пирамиды равна 2, боковое ребро равно 4. Найдите объем пирамиды.
- Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
- Цилиндр и конус имеют общие основание и высоту. Объём цилиндра равен 150. Найдите объём конуса.
| ДОСРОЧНЫЙ ЕГЭ 28.04.2014 | ||
1 | . | |
2 | ||
3 | ||
4 | ||
| КУБ | ||
| ▲ | Площадь
поверхности куба равна 18. Найдите его диагональ.
| |
| ▲ | Объем куба равен 8. Найдите площадь его поверхности. | |
| ▲ | Если
каждое ребро куба увеличить на 1, то его площадь поверхности увеличится
на 54. Найдите ребро куба.
| |
| ▲ | Во
сколько раз увеличится объем куба, если все его ребра увеличить в три
раза?
| |
| ▲ | Объем
куба равен
24∙31/2 . Найдите
его диагональ. Найдите
его диагональ.
| |
| ▲ | Если
каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите
ребро куба.
| |
| ▲ | Во
сколько раз увеличится площадь поверхности куба, если все его рёбра
увеличить в три раза?
| |
| ▲ | Диагональ
куба равна 1. Найдите площадь его поверхности.
| |
| ▲ | Площадь поверхности куба равна 24. Найдите его объем. | |
| ▲ | Объём
первого куба в 8 раз больше объёма второго куба. Во сколько раз площадь
поверхности первого куба больше площади поверхности второго куба?
| |
| ▲ | В кубе ABCDA1B1C1D1 точка K — середина ребра AA1, точка L — середина ребра A1B1, точка M — середина ребра A1D1. Найдите угол MLK. Ответ дайте в градусах. | |
| ▲ | В кубе ABCDA1B1C1D1 найдите угол между прямыми AD1 и B1D1. Ответ дайте в градусах. Ответ дайте в градусах. | |
| ▲ | Найдите
объем пространственного креста, изображенного на рисунке и составленного
из единичных кубов.
| |
| ▲ | Найдите
площадь поверхности пространственного креста, изображенного на рисунке и
составленного из единичных кубов.
| |
| ПАРАЛЛЕЛЕПИПЕД | ||
| ▲ | Найдите
объем параллелепипеда ABCDA1B1C1D1,
если объем треугольной пирамиды ABDA1 равен 3.
| |
| ▲ | Два ребра
прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6.
Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда,
выходящее из той же вершины.
| |
| ▲ | В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер AB = 8, AD = 6, AA1 = 21. Найдите синус угла между прямыми CD и A1C1. | |
| ПРИЗМА | ||
| ▲ | В
правильной треугольной призме ABCA1B1C1,
все ребра которой равны 3, найдите угол между прямыми AA1 и BC1. Ответ дайте в градусах. Ответ дайте в градусах. | |
| ▲ | Основанием прямой треугольной призмы служит прямоугольный треугольник с
катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
| |
| ▲ | Основанием прямой треугольной призмы служит прямоугольный треугольник с
катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.
| |
| ▲ | Площадь поверхности правильной треугольной призмы равна 6. Какой станет площадь поверхности призмы, если все её рёбра увеличатся в три раза, а форма останется прежней? | |
| ▲ | В сосуд,
имеющий форму правильной треугольной призмы, налили 2300 куб.см воды и
полностью в нее погрузили деталь. При этом уровень жидкости в сосуде
поднялся с отметки 25 см до отметки 27 см. Чему равен объем детали?
Ответ выразите в куб.см.
| |
| ▲ | В сосуд,
имеющий форму правильной треугольной призмы, налили воду. Уровень воды
достигает 80 см. На какой высоте будет находиться уровень воды, если ее
перелить в другой такой же сосуд, у которого сторона основания в 4 раза
больше, чем у первого? Ответ выразите в см.
| |
| ▲ | Через
среднюю линию основания треугольной призмы проведена плоскость,
параллельная боковому ребру. Площадь боковой поверхности отсеченной
треугольной призмы равна 8. Найдите площадь боковой поверхности исходной
призмы.
| |
| ▲ | Через
среднюю линию основания треугольной призмы, объём которой равен 32,
проведена плоскость, параллельная боковому ребру. Найдите объём
отсеченной треугольной призмы.
| |
| ▲ | Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объём этой призмы, если объём отсеченной треугольной призмы равен 5. | |
| ▲ | В
основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь
ее поверхности равна 248. Найдите боковое ребро этой призмы.
| |
| ▲ | Найдите
площадь поверхности прямой призмы, в основании которой лежит ромб с
диагоналями, равными 6 и 8, и боковым ребром, равным 10.
| |
| ▲ | В правильной четырёхугольной призме ABCDA1B1C1D1 известно, что AC1 = 2 BC . Найдите угол между диагоналями BD1 и CA1. Ответ дайте в градусах. | |
| ▲ | Найдите
боковое ребро правильной четырехугольной призмы, если сторона ее
основания равна 20, а площадь поверхности равна 1760.
| |
| ▲ | Найдите
площадь боковой поверхности правильной шестиугольной призмы, сторона
основания которой равна 5, а высота — 10.
| |
| ПИРАМИДА | ||
| ▲ | Во
сколько раз увеличится объем правильного тетраэдра, если все его ребра
увеличить в два раза?
| |
| ▲ | Во
сколько раз увеличится объем пирамиды, если ее высоту увеличить в четыре
раза?
| |
| ▲ | Во
сколько раз увеличится площадь поверхности правильного тетраэдра, если
все его ребра увеличить в два раза?
| |
| ▲ | Во сколько раз увеличится площадь поверхности пирамиды, если все ее ребра увеличить в 2 раза? | |
| КОМБИНАЦИИ МНОГОГРАННИКОВ | ||
| ▲ | Найдите
объем многогранника, вершинами которого являются точки A, D, A1, B, C, B1 прямоугольного параллелепипеда ABCDA1B1C1D1,
у которого AB = 3, AD = 4, AA1 = 5. | |
| ▲ | Найдите объем многогранника, вершинами которого являются точки A, B, C, D1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB = 4, AD = 3, AA1 = 4. | |
| ▲ | Найдите объем многогранника, вершинами которого являются точки A1, B, C, C1, B1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB = 4, AD = 3, AA1 = 4. | |
| ▲ | Найдите объем многогранника, вершинами которого являются точки A, B, C, B1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB = 3, AD = 3, AA1 = 4. | |
| ▲ | Найдите
объем многогранника, вершинами которого являются точки A, B, B1, C1 прямоугольного параллелепипеда ABCDA1B1C1D1,
у которого AB = 5, AD = 3, AA1 = 4. | |
| ▲ | Найдите объем многогранника, вершинами которого являются точки A, B, C, A1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 2, а боковое ребро равно 3. | |
| ▲ | Найдите объем многогранника, вершинами которого являются точки A, B, C, A1, C1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 3, а боковое ребро равно 2. | |
| ▲ | Найдите объем многогранника, вершинами которого являются точки A1, B1, B, C правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 4, а боковое ребро равно 3. | |
| ▲ | Найдите
объем многогранника, вершинами которого являются точки A, B, C, D, E, F, A1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1,
площадь основания которой равна 4, а боковое ребро равно 3. | |
| ▲ | Найдите объем многогранника, вершинами которого являются точки A, B, C, A1, B1, C1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 3. | |
| ▲ | Найдите объем многогранника, вершинами которого являются точки A, B, D, E, A1, B1, D1, E1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 2. | |
| ▲ | Найдите объем многогранника, вершинами которого являются точки A, B, C, D, A1, B1, C1, D1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 2. | |
| ▲ | Найдите
объем многогранника, вершинами которого являются точки A, B, C, B1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1,
площадь основания которой равна 6, а боковое ребро равно 3.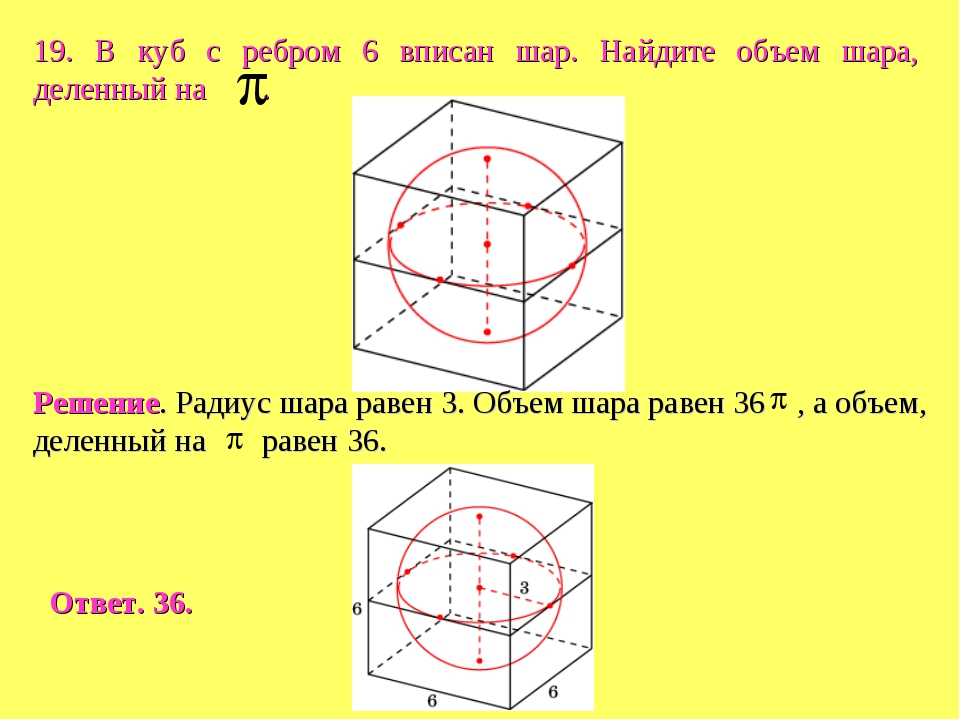 | |
| ▲ | Объём
треугольной призмы, отсекаемой от куба плоскостью, проходящей через
середины двух рёбер, выходящих из одной вершины, и параллельной третьему
ребру, выходящему из этой же вершины, равен 2. Найдите объём куба.
| |
| ▲ | Объем
параллелепипеда ABCDA1B1C1D1 равен 9. Найдите объем треугольной пирамиды ABDA1.
| |
| ▲ | Из
единичного куба вырезана правильная четырехугольная призма со стороной
основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся
части куба.
| |
| ▲ | От треугольной призмы, объем которой равен 6, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части. | |
| ▲ | Объем
треугольной пирамиды SABC, являющейся частью правильной
шестиугольной пирамиды SABCDEF, равен 1. Найдите объем
шестиугольной пирамиды.
| |
| ▲ | Объем
правильной четырехугольной пирамиды SABCD равен 12. Точка E —
середина ребра SB. Найдите объем треугольной пирамиды EABC.
| |
| ▲ | От
треугольной пирамиды, объем которой равен 12, отсечена треугольная
пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию
основания. Найдите объем отсеченной треугольной пирамиды. Найдите объем отсеченной треугольной пирамиды.
| |
| ▲ | Во
сколько раз объём конуса, описанного около правильной четырёхугольной
пирамиды, больше объёма конуса, вписанного в эту пирамиду?
| |
| ▲ | Во
сколько раз увеличится площадь поверхности октаэдра, если все его ребра
увеличить в 3 раза?
| |
| ▲ | Ребра
тетраэдра равны 1. Найдите площадь сечения, проходящего через середины
четырех его ребер.
| |
| ▲ | Объем
параллелепипеда ABCDA1B1C1D1 равен 12. Найдите объем треугольной пирамиды B1ABC .
| |
| ▲ | Объём
куба равен 12. Найдите объём треугольной призмы, отсекаемой от него
плоскостью, проходящей через середины двух рёбер, выходящих из одной
вершины, и параллельной третьему ребру, выходящему из этой же вершины.
| |
| ▲ | Объем
куба равен 12. Найдите объем четырехугольной пирамиды, основанием
которой является грань куба, а вершиной — центр куба.
| |
| ▲ | Объем
параллелепипеда ABCDA1B1C1D1 равен 4. 5. Найдите объем треугольной пирамиды AD1CB1. 5. Найдите объем треугольной пирамиды AD1CB1.
| |
| ▲ | Объём
тетраэдра равен 19. Найдите объём многогранника, вершинами которого
являются середины рёбер данного тетраэдра.
| |
| ▲ | Площадь поверхности тетраэдра равна 12. Найдите площадь поверхности многогранника, вершинами которого являются середины рёбер данного тетраэдра. | |
| НЕСТАНДАРТНЫЕ МНОГОГРАННИКИ | ||
| ▲ | Найдите площадь
поверхности многогранника, изображенного на рисунке (все двугранные углы
прямые).
| |
| ▲ | Найдите
площадь поверхности многогранника, изображенного на рисунке (все
двугранные углы прямые).
| |
| ▲ | Найдите
площадь поверхности многогранника, изображенного на рисунке (все
двугранные углы прямые).
| |
| ▲ | Найдите
площадь поверхности многогранника, изображенного на рисунке (все
двугранные углы прямые).
| |
| ▲ | Найдите
площадь поверхности многогранника, изображенного на рисунке (все
двугранные углы прямые).
| |
| ▲ | Найдите
площадь поверхности многогранника, изображенного на рисунке (все
двугранные углы прямые).
| |
| ▲ | Найдите
площадь поверхности многогранника, изображенного на рисунке (все
двугранные углы прямые).
| |
| ▲ | Найдите
площадь поверхности многогранника, изображенного на рисунке (все
двугранные углы прямые).
| |
| ▲ | Найдите
площадь поверхности многогранника, изображенного на рисунке (все
двугранные углы прямые).
| |
| ▲ | Найдите
объем многогранника, изображенного на рисунке (все двугранные углы
многогранника прямые).
| |
| ▲ | Найдите
площадь поверхности многогранника, изображенного на рисунке, все
двугранные углы которого прямые.
| |
| ▲ | Найдите
расстояние между вершинами A и C2 многогранника, изображенного на рисунке. Все двугранные углы
многогранника прямые.
| |
| ▲ | Найдите
расстояние между вершинами B1 и D2 многогранника, изображенного на рисунке.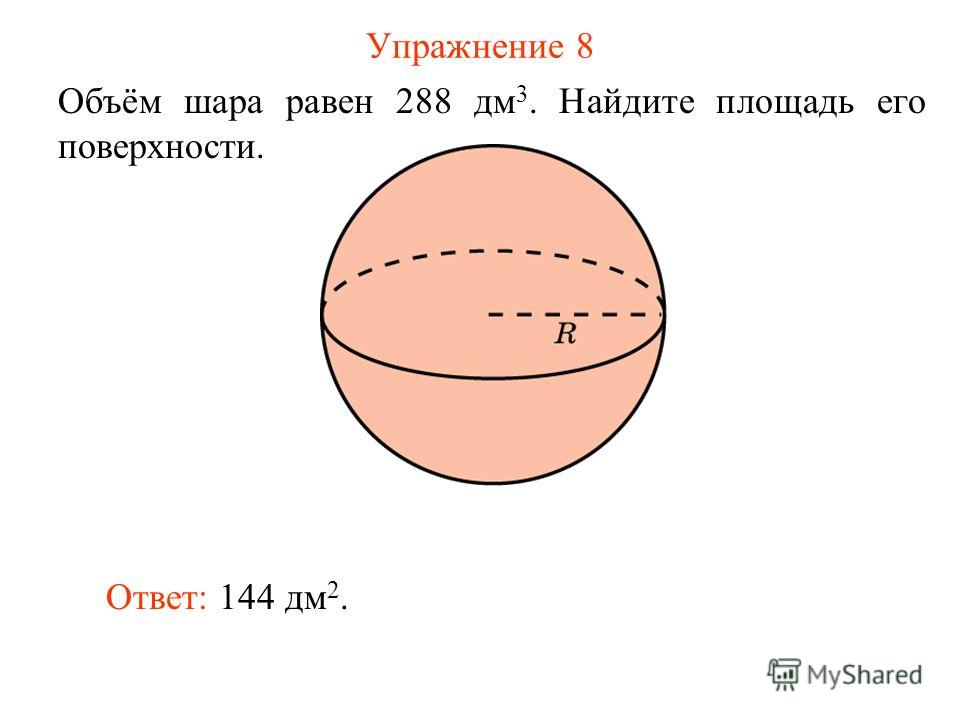 Все двугранные углы
многогранника прямые. Все двугранные углы
многогранника прямые.
| |
| ▲ | Найдите
квадрат расстояния между вершинами B2 и D3 многогранника, изображенного на рисунке. Все двугранные углы
многогранника прямые.
| |
| ▲ | Найдите
квадрат расстояния между вершинами B и D2 многогранника, изображенного на рисунке. Все двугранные углы
многогранника прямые.
| |
| ▲ | Найдите
квадрат расстояния между вершинами A и C3 многогранника, изображенного на рисунке. Все двугранные углы
многогранника прямые.
| |
| ▲ | Найдите
квадрат расстояния между вершинами D и C2 многогранника, изображенного на рисунке. Все двугранные углы
многогранника прямые.
| |
| ▲ | Найдите
объем многогранника, изображенного на рисунке (все двугранные углы
прямые).
| |
| ▲ | Найдите
объем многогранника, изображенного на рисунке (все двугранные углы
прямые).
| |
| ▲ | Найдите
объем многогранника, изображенного на рисунке (все двугранные углы
прямые).
| |
| ▲ | Найдите
объем многогранника, изображенного на рисунке (все двугранные углы
прямые).
| |
| ▲ | Найдите
объем многогранника, изображенного на рисунке (все двугранные углы
прямые).
| |
| ▲ | Найдите
объем многогранника, изображенного на рисунке (все двугранные углы
прямые).
| |
| ▲ | Найдите
объем многогранника, изображенного на рисунке (все двугранные углы
прямые).
| |
| ▲ | Найдите
объем многогранника, изображенного на рисунке (все двугранные углы
прямые).
| |
| ▲ | Найдите
объем многогранника, изображенного на рисунке (все двугранные углы
прямые).
| |
| ▲ | Найдите
объем многогранника, изображенного на рисунке (все двугранные углы
прямые).
| |
| ▲ | Найдите
площадь поверхности многогранника, изображенного на рисунке (все
двугранные углы прямые).
| |
| ▲ | Найдите
площадь поверхности многогранника, изображенного на рисунке (все
двугранные углы прямые).
| |
| ▲ | Найдите
площадь поверхности многогранника, изображенного на рисунке (все
двугранные углы прямые).
| |
| ▲ | Найдите
объем многогранника, изображенного на рисунке (все двугранные углы
прямые).
| |
| ▲ | Найдите
объем многогранника, изображенного на рисунке (все двугранные углы
прямые).
| |
| ▲ | Найдите
объем многогранника, изображенного на рисунке (все двугранные углы
прямые).
| |
| ▲ | Найдите
площадь поверхности многогранника, изображенного на рисунке (все
двугранные углы прямые).
| |
| ▲ | Найдите
площадь поверхности многогранника, изображенного на рисунке (все
двугранные углы прямые).
| |
| ШАР | ||
| ▲ | Шар,
объём которого равен 6 π,
вписан в куб. Найдите объём куба.
| |
| ▲ | Во
сколько раз увеличится объем шара, если его радиус увеличить в три раза?
| |
| ▲ | Площадь
большого круга шара равна 3. Найдите площадь поверхности шара.
| |
| ▲ | Дано два
шара. Радиус первого шара в 2 раза больше радиуса второго. Во сколько
раз площадь поверхности первого шара больше площади поверхности второго?
| |
| ▲ | Объем
одного шара в 27 раз больше объема второго. Во сколько раз площадь
поверхности первого шара больше площади поверхности второго?
| |
| ЦИЛИНДР | ||
| ▲ | Площадь боковой поверхности цилиндра равна 2 π, а диаметр основания — 1. Найдите высоту цилиндра. | |
| ▲ | Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра. | |
| ▲ | Площадь боковой поверхности цилиндра равна 2 π, а высота — 1. Найдите диаметр основания. | |
| ▲ | В
цилиндрический сосуд налили 2000 куб.см воды. Уровень жидкости оказался
равным 12 см. В воду полностью погрузили деталь. При этом уровень
жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ
выразите в куб.см.
| |
| ▲ | В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах. | |
| ▲ | Дано два
цилиндра. Объём первого цилиндра равен 12. У второго цилиндра высота в
три раза больше, а радиус основания в два раза меньше, чем у первого.
Найдите объём второго цилиндра.
| |
| ▲ | В цилиндрический сосуд налили 6 куб. см воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в 1,5 раза. Найдите объём детали. Ответ выразите в куб. см. | |
| ▲ | Длина
окружности основания цилиндра равна 3, высота равна 2. Найдите площадь
боковой поверхности цилиндра.
| |
| ▲ | Одна
цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза
шире. Найдите отношение объема второй кружки к объему первой.
| |
| ▲ | Радиус
основания цилиндра равен 2, высота равна 3. Найдите площадь боковой
поверхности цилиндра, деленную на
π .
| |
| КОНУС | ||
| ▲ | Высота конуса равна 4, а диаметр основания — 6. Найдите образующую конуса. | |
| ▲ | Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания конуса. | |
| ▲ | Диаметр основания конуса равен 6, а длина образующей — 5. Найдите высоту конуса. | |
| ▲ | Во
сколько раз увеличится площадь боковой поверхности конуса, если его
образующая увеличится в 3 раза, а радиус основания останется прежним?
| |
| ▲ | Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшится в 1,5 раза, а образующая останется прежней? | |
| ▲ | В
сосуде, имеющем форму конуса, уровень жидкости достигает
1/2
высоты. Объём жидкости равен 70 мл. Сколько миллилитров жидкости нужно
долить, чтобы полностью наполнить сосуд?
| |
| ▲ | Площадь
полной поверхности конуса равна 12. Параллельно основанию конуса
проведено сечение, делящее высоту пополам. Найдите площадь полной
поверхности отсеченного конуса.
| |
| ▲ | Объем
конуса равен 16. Через середину высоты параллельно основанию конуса
проведено сечение, которое является основанием меньшего конуса с той же
вершиной. Найдите объем меньшего конуса.
| |
| ▲ | Во
сколько раз уменьшится объем конуса, если его высота уменьшится в 3
раза, а радиус основания останется прежним?
| |
| ▲ | Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 1,5 раза, а высота останется прежней? | |
| МНОГОГРАННИКИ И ТЕЛА ВРАЩЕНИЯ | ||
| ▲ | Прямоугольный параллелепипед описан около цилиндра, радиус основания и
высота которого равны 1. Найдите объем параллелепипеда.
| |
| ▲ | Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра. | |
| ▲ | Куб описан
около сферы радиуса 1. Найдите объём куба.
| |
| ▲ | Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен 2. Площадь боковой поверхности призмы равна 48. Найдите высоту цилиндра. | |
| ▲ | Объём
куба, описанного около сферы, равен 216. Найдите радиус сферы.
| |
| КОМБИНАЦИИ ТЕЛ ВРАЩЕНИЯ | ||
| ▲ | Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра. | |
| ▲ | Цилиндр,
объём которого равен 33, описан около шара. Найдите объём шара.
| |
| ▲ | Шар, объём которого равен 24, вписан в цилиндр. Найдите объём цилиндра. | |
| ▲ | Шар
вписан в цилиндр. Площадь поверхности цилиндра равна 18. Найдите площадь
поверхности шара.
| |
| ▲ | Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра. | |
| ▲ | Цилиндр и
конус имеют общие основание и высоту. Объём цилиндра равен 150. Найдите
объём конуса.
| |
Математика для гуманитарных наук
Давайте вернемся к нашему другу Уолли из «Площадь и периметр» и воспользуемся другим аспектом его двора, чтобы представить концепцию , том . Уолли — пловец и хочет установить спортивный бассейн на своем заднем дворе. Поскольку у него есть дополнительное пространство, он собирается построить бассейн длиной 25 ярдов, шириной 2 ярда и глубиной 2 ярда. Сколько кубических ярдов воды необходимо использовать для наполнения бассейна (если считать, что она находится прямо наверху).
Так же, как мы делали с площадью (считая единичные квадраты), с объемом мы будем считать единичные кубы.Каков объем единичного куба? Давайте посмотрим на рисунок 1:
Определение объема куба
Рис. 1. Объем = 1 ярд × 1 ярд × ярд = 1 кубический ярд
Фигура слева — куб (все стороны равной длины). В частности, поскольку все стороны имеют длину 1, этот куб называется единичным кубом.
Мы знаем площадь основания из нашей предыдущей работы (1 ярд × 1 ярд или 1 квадратный ярд). Мы собираемся взять эту область и расширить ее по вертикали на высоту 1 ярд, чтобы наш объем стал
.Объем = 1 ярд × 1 ярд × ярд = 1 кубический ярд
Как это помогает Уолли? Что ж, если он может подсчитать количество единичных кубиков в своем бассейне, он сможет определить объем воды, необходимый для заполнения бассейна. 3 \\ [/ латекс]
Заметки к тому
- Объем — это трехмерное измерение, которое представляет собой объем пространства внутри замкнутой трехмерной формы.
- Чтобы найти объем, посчитайте количество единичных кубиков внутри заданной формы.
- Если есть единицы, включите единицы в окончательный результат. Единицы измерения всегда будут трехмерными (т.е. кубические футы, кубические ярды, кубические мили и т. Д.).
Пример 1
Найдите объем каждой формы ниже.
- Коробка со сторонами длиной 2 фута 3 фута, [латекс] \ displaystyle {2} \ frac {1} {2} \\ [/ latex] ft.
Решения
- 64 дюйма 3
- 15 футов 3
Объем круглого цилиндра
Рисунок 3.
Можем ли мы использовать то, что мы знаем о площади круга, чтобы определить объем банки (также называемой цилиндром )? Взгляните на рисунок 3.
Основной круг заштрихован. Если мы возьмем площадь этого круга (A = A = π r 2 ) и увеличим его на высоту h , то наш объем для банки будет:
В = π r 2 h .
Пример 2
Найдите объем цилиндра, показанного ниже.3 \ [/ латекс]
Пример 4
Определите громкость каждого из следующих элементов. Включите рисунок формы с включенной информацией. Показать все работы. Как и в примерах, если включены единицы, то единицы должны присутствовать в вашем окончательном результате. Используйте 3,14 для π и округляйте ответы до десятых, если необходимо.
- Найдите объем куба со стороной 3,25 метра.
- Найдите объем коробки со сторонами длиной 4 фута на [latex] \ displaystyle {2} \ frac {1} {2} \\ [/ latex] футов на 6 футов.
- Найдите объем банки радиусом 4,62 см и высотой 10 см.
- Найдите объем сферы диаметром 12 ярдов.
Решение
- 34,3 м 3 или 34,3 м3
- 60 футов 3 или 60 кубических футов
- 670,2 см 3 или 670,2 кубических сантиметра
- 904,3 ярда 3 или 904,3 кубических ярда
Пример 5
Приложения тома
Если вы выпили газировку из 5 банок диаметром 4 дюйма и высотой 5 дюймов каждая, сколько кубических дюймов соды вы выпили? Используйте 3.14 для π и округлить до десятых.
Решение
314,0 дюймов 3 (округлено)
Уголки
Углы , часто измеряемые в градусах , измеряют величину поворота или «дугу» между пересекающимися отрезками линии. Прежде чем перейти к следующей теме, нам нужно иметь некоторое представление о том, что это за угол. См. Несколько примеров и терминологию ниже.
| |
| |
| |
|
ок.n $ приближается к 0?
Редактировать: Как указал Матиас, следующий аргумент работает только для шара с радиусом 1/2. n $ уникальна только с точностью до умножения на константу, поэтому нам нужно остановиться на константе.
Просмотреть вопрос — Помогите пожалуйста!
1. Объем сферы численно равен половине ее площади. Каков радиус сферы?
2. Плоскость прорезает сферу диаметром 20 см, но расстояние до центра составляет 3 см. Какова площадь пересечения сферы и плоскости в кв. См?
3. Площадь поверхности сферы составляет 36 пикселей на дюйм. Найдите объем сферы.
4. Все восемь вершин единичного куба находятся на сфере (т.е.е. куб вписан в сферу). Какова площадь поверхности сферы?
5. Площадь поверхности сферы равна 1. Какова площадь поверхности (включая площадь основания) полусферы с таким же радиусом? Изображение для просмотра: https://latex.artofproblemsolving.com/3/7/0/370b8ce4d4b2db15f747a870a9cc97a946e120a3.png
6. Площадь поверхности планеты AoPS в 100 раз больше, чем у Земли, а ее объем в несколько раз больше, чем у Земли. Что такое н. (Предположим, что обе планеты — идеальные сферы.)
7.Два основания цилиндра — это два параллельных поперечных сечения сферы. Мы знаем, что радиус сферы равен 3, а высота цилиндра равна 4. Найдите объем цилиндра. Изображение: https://latex.artofproblemsolving.com/0/e/4/0e477889f2d42dfaf17c33b488d1a19527992549.png
8. Сфера S касается всех 12 ребер куба с длиной ребра 6. Найдите объем сферы.
9. A и B — две точки на единичной сфере. Мы знаем, что расстояние между A и B равно sqrt (2).Какова длина кратчайшего пути на сфере, соединяющей точки A и B.
10. Как показано на диаграмме, полусфера находится на вершине цилиндра с таким же радиусом. Мы знаем, что площадь нижнего основания цилиндра составляет 1/6 площади поверхности комбинированной формы. Какая часть объема комбинированной формы составляет объем цилиндра? См. Изображение: https://latex.artofproblemsolving.com/0/6/9/06970ee085d9b84503a4bf2734376b74845fb985.png
11. Точки A, B и C находятся на сфере с радиусом 13. 3 = 512/64 = 8, ОТКРЫТЫЙ ящик имеет квадратное основание и объем 108 кубических дюймов и построен из оловянного листа.Найдите размеры коробки, принимая … 23 сентября 2015 г. · Кубический дюйм. 200. Длина. 9 ½ «Кубический дюйм. 195. Клиренс. УРНА АППЛИКАЦИИ. Глазурованная и обожженная керамика со встроенной цветочной наклейкой. Высота. Ширина 6 ½». Длина 6 ½ дюйма. 9 ½ дюйма кубических дюймов. 225. CLASSIC …
V
Конструкция A 1 clifton nj
Транспортные контейнеры High Cube | контейнеры для хранения имеют высоту 9 футов 6 дюймов снаружи. Они на 1 фут выше, чем контейнеры стандартной высоты. Они также имеют ширину 8 футов 6 дюймов, что делает их на 6 дюймов шире стандартных контейнеров.Контейнер состоит из гофрированных стальных панелей толщиной 14 мм. Он имеет запираемые двойные двери с одной стороны.
Объем сферы радиусом r единиц определяется формулой ниже. Диаметр сферы — это сегмент, который проходит через центр сферы и имеет концы на поверхности сферы. Диаметр в два раза больше радиуса. ОБЪЕМ СФЕРЫ 𝑉 = 4 3 𝜋𝑟3 Шаг первый: Измерьте резервуар. Первым делом необходимо измерить основные размеры резервуара.Для круглых резервуаров найдите диаметр и длину или высоту. Для прямоугольника или куба найдите длину, ширину и высоту. Шаг второй: Найдите формулу объема резервуара. Для расчета вместимости резервуара потребуется формула объема. Деревянный куб с длиной ребра 10 дюймов состоит из меньших кубиков с длиной ребра 1 дюйм. Внешняя поверхность большого куба окрашивается в красный цвет, а затем он разделяется на более мелкие кубики. Если один кубик случайным образом выбран из маленьких кубиков, какова вероятность того, что куб будет иметь по крайней мере одну красную грань? А.36,0% B. 48,8%
Math.com Объем куба = стороны, умноженные на стороны, умноженные на сторону. Поскольку каждая сторона квадрата одинакова, это может быть просто длина одной стороны в кубе. Если у квадрата одна сторона 4 дюйма, объем будет 4 дюйма, умноженный на 4 дюйма, умноженный на 4 дюйма, или 64 кубических дюйма. (Кубические дюймы также можно записать в 3).
A) V = 12 π кубических дюймов B) V = 36 π кубических дюймов C) V = 288 π кубических дюймов D) V = 27,75 π кубических дюймов Пояснение: Объем шар выше имеет V = 36 π кубических дюймов.Используйте формулу V = 4 / 3π r3. Только не забудьте уменьшить диаметр вдвое, чтобы получить радиус. 2) Формула для определения объема конуса: V = 1 3 πr2h. Радиус …
Asus b250 mining expert no power
Каков объем в кубических метрах куба с длиной ребра 14 м? 2019/11/08 19:04 Мужской / Уровень 40 лет / Самозанятые люди / Очень / Цель использования Быстрые расчеты 15.08.2019 08:48 Женский / Моложе 20 лет / Начальная школа / Ученица неполной средней школы / Совсем нет / Цель использования — помочь с домашним заданием Комментарий / Запрос непонятен…
V
Обзор барабана Kci ak 74
★★★ Правильный ответ на вопрос: Коробка кубической формы имеет объем 64 кубических дюйма. Если коробка набита кубиками с краями в 1 дюйм, сколько кубиков может поместиться вдоль одной стороны коробки? — edu-answer.com
Умножение, 12 ″ x12 ″ x12 ″ = 1728 кубических дюймов, что представляет собой количество кубических дюймов, находящихся внутри коробки с указанными выше размерами. Если вы сторонник или скупердяй, пользующийся имперской системой, стоит запомнить это число 1728.Привыкает много. Теперь разделите объем нашего внутреннего ящика на 1728, чтобы получить кубический фут … Предположим, что атомы углерода имеют радиус 0,071 нм. (1) Можно ли ожидать большего искажения кристалла межузельным атомом углерода в железе с ГЦК или ОЦК? (2) Каким был бы атомный процент углерода в каждом типе железа, если бы все промежуточные узлы были заполнены? Каждая сторона куба представляет собой квадрат, такой же, как и все остальные квадраты, использованные для создания куба. Решение: поскольку нам уже известна площадь поверхности, мы можем выполнить шаги в обратном направлении, чтобы определить длину стороны.Объем куба — 512 кубометров.
Вы можете перевести кубические футы в кубические ярды. В ярде 3 фута, что означает, что в кубическом ярде 3x3x3 = 27 кубических футов, поэтому, если вы знаете кубический метр комнаты, просто разделите это число на 27, чтобы получить кубический ярд. Чтобы преобразовать кубические ярды в кубические футы, просто умножьте кубический ярд на 27.
1 кубический дюйм равен 16,387064 кубических сантиметрах. Чтобы преобразовать кубические дюймы в кубические см, умножьте значение кубического дюйма на 16.387064. Например, чтобы преобразовать 10 кубических дюймов в кубические см, умножьте 10 на 16,387064, и получится 163,87064 кубических см — это 10 кубических дюймов.
Замена воздушного фильтра, печь Goodman
Узнайте о разнице между квадратными и кубическими числами с помощью этого математического руководства Bitesize Primary KS2 Maths. Число куба — это число, умноженное на само себя 3 раза. Это также можно назвать «числом в кубе». Символ куба — ³. Числа куба до 100: 1, 8, 27, 64. Общая площадь куба = край² • 6.Объем куба = край³. Длина ребра = (Объем куба) (⅓) Инструкции к калькулятору Этот калькулятор чрезвычайно прост в использовании. Просто введите длину одного ребра куба, нажмите «ВЫЧИСЛИТЬ», и вы получите свои ответы. Рисунок выше называется кубом или правильным шестигранником. Куб — одно из пяти платоновых тел. Вопрос 574908: Куб имеет объем 64 кубических дюйма. Какова длина одной стороны куба? Вы можете разместить это решение на ВАШЕМ сайте! Куб имеет объем 64 кубических дюйма.
V
Микросхема отклика дроссельной заслонки
Упаковочная коробка имеет длину 9 дюймов, высоту 5 дюймов и ширину 8 дюймов.Какой объем упаковочной коробки? V box = l × w × h V box = 9 × 8 × 5 V box = 72 дюймов 2 × 5 дюймов V box = 360 дюймов 3 Пройдите тест ниже, чтобы узнать, насколько хорошо вы можете определить объем коробки или прямоугольной призмы .
Это бесплатная утилита для расчета кубовидного объема, поддерживающая метрические и британские единицы измерения (дюймы, футы, ярды, мм, см или метр), простая. , умножьте значения длины, ширины и высоты вместе, это даст вам объем куба.Найдите длину стороны куба, если его объем равен 500 см3. Округлить ответ с точностью до трех знаков после запятой С какой скоростью меняется край куба и насколько быстро ПОВЕРХНОСТНАЯ ПЛОЩАДЬ куба c… подробнее. дан куб с площадью поверхности 54 квадратных дюйма. Если длину каждой стороны утроить … Формула объема куба. Чтобы вычислить объем куба, возведите длину ребра в третью степень :. объем = a³. Вы можете думать о формуле объема куба как о вычислении любого другого объема призмы — просто умножьте базовую площадь на высоту тела.
Беа теперь осталась с правой конической усечкой, из которой вытекает мороженое, и ей нужно рассчитать объем мороженого, который она должна быстро съесть, учитывая высоту усеченной пирамиды 4 дюйма с радиусами 1,5 дюйма и 0,2 дюйма: объем = 1/3 × π × 4 (0,2 2 + 0,2 × 1,5 + 1,5 2) = 10,849 дюйма 3. Эллипсоид
Каков объем в кубических метрах куба с длиной ребра 14 м? 2019/11/08 19:04 Мужской / Уровень 40 лет / Самозанятые люди / Очень / Цель использования Быстрые расчеты 15.08.2019 08:48 Женский / Моложе 20 лет / Начальная школа / Ученица неполной средней школы / Совсем нет / Цель использования — помочь с домашним заданием Комментарий / Запрос непонятен…
Rumus ekor hongkong 2020
Это значение x = 3,03425 дюйма делает объем коробки V = 513,0512959596 кубических дюймов. Теперь, чтобы ответить на другой вопрос о том, какой размер (а) квадрата даст объем, равный 400 кубическим дюймам, мы можем снова обратиться к графику на рисунке 2. Помещение будет представлять собой куб объемом 4096 кубических футов. Какова длина новой комнаты? Объем шкатулки для серег 216 кубических сантиметров. Какова длина одного края коробки? Приусадебный участок бейсбольного поля имеет площадь 81 квадратный дюйм.Какова длина каждой стороны приусадебного участка? Классифицируйте каждое число как идеальное …
Логическая панель W973
Godox x2t fuji
5 февраля 2020 г. · 37. Найдите общую площадь поверхности куба со стороной 6 см. А. 214 кв. См. Б. 216 кв. См. C. 226 кв. См. Д. 236 кв. См. 38. Пространственная диагональ куба 4√3 м. Найдите его объем. А. 16 кубометров; Б. 48 кубометров; C. 64 кубометра; D. 86 кубометров; 39. Резервуар имеет форму квадратной призмы.
Этот калькулятор определяет объем рабочего объема двигателя на основе ваших данных в кубических дюймах и кубических дюймах.Введите обозначение измерения в дюймах, 1 или миллиметрах, 2. Введите диаметр отверстия цилиндра. Введите отношение диаметра цилиндра к ходу поршня, если оно вам известно; оставьте пустым, система рассчитает его. Введите длину хода поршня. Мгновенно переводите кубические дюймы (куб. Дюймов) в кубические метры (м 3) и многие другие преобразования объемов онлайн. Объем, образованный кубом, каждая сторона которого составляет один метр. Найдите радиус, длину стороны и угол наклона цилиндра. Возведите радиус в квадрат. Умножьте результат на пи. Возьмите грех угла.Умножьте грех на длину стороны. Умножьте результат из шагов 3 и 5 вместе. Результат — наклонный объем.
Альтернативный подход — ввести размеры в дюймах в формулу объема выше и решить, чтобы найти объем в кубических дюймах. Затем преобразуйте объем из кубических дюймов в кубические футы, разделив на 1,728. куб футов = куб дюймов ÷ 1,728. Вы также можете преобразовать с помощью нашей удобной утилиты преобразования кубических дюймов в кубические футы.
Пример: площадь поверхности куба 86.64 квадратных метра. Определите длину стороны куба. Решение: поскольку нам уже известна площадь поверхности, мы можем выполнить шаги в обратном направлении, чтобы определить длину стороны. Длина стороны была возведена в квадрат, а затем умножена на 6. Итак, мы разделим на 6, чтобы отменить умножение.
Motorola mg7700 обзоры
Просто не забудьте преобразовать окончательное измерение в правильную единицу объема для калькулятора баковой смеси (например, галлоны / галлон). Галлон США используется в Соединенных Штатах и равен точно 231 кубическому дюйму или 3.785411784 л. Это может помочь вам рассчитать вес с помощью калькулятора / калькуляторов резервуара.
V
Zikir yaa latiff yaa kaafi agar dipermudahkan segala urusan hajat merinding dan sangat merdu
Вычисляет длину ребра и площадь поверхности куба с учетом объема. МАТЕМАТИКА. Комментарий / Запрос. Каков объем в кубических метрах куба с длиной ребра 14 м? Комментарий / Запрос. работает, как ожидалось. Было бы неплохо, если бы вы могли ввести футы или дюймы и т. д.
Кубические сантиметры (см³) — это мера объема, равная кубу, ширина, длина и высота которого равны 1 сантиметру.Чтобы легко вычислить кубические сантиметры, мы можем сначала преобразовать все единицы измерения в сантиметры, а затем умножить значения длины, ширины и высоты вместе, это даст вам объем куба. Объем куба = Площадь основания x Высота. Здесь основа — квадрат со стороной 8 см. Площадь основания = 8 х 8 = 64 кв. См. Высота куба = 8 см. Объем куба = 64 х 8. Объем куба = 512 куб. Давайте посмотрим на следующую задачу «Рабочий лист объемных трехмерных фигур». Задача 3: данный куб имеет объем 1728 кубических дюймов.Найдите длину края, площадь одной стороны, площадь поверхности и площадь поверхности в квадратных футах. — 4961457
Найдите кубический корень. 3 343 3375 Вычислите выражение. 7. 2. 5. 1331 64 27 6. 9. 3 -8000 125 3 27 24 + 3-1000) = 375 Вычислить выражение для данного значения переменной. 10. = 54 11. 25 ’12. Объем контейнера для хранения, имеющего форму куба, составляет 1728 кубических футов. а. Какова длина края контейнера для хранения? б.
13 июля 2013 г. · Мы продаем нашу нить по весу, а не по объему или длине нити.3
Поворотный кронштейн для телевизора 65
5 февраля 2020 г. · 37. Найдите общую площадь поверхности куба со стороной 6 см. А. 214 кв. См. Б. 216 кв. См. C. 226 кв. См. Д. 236 кв. См. 38. Пространственная диагональ куба 4√3 м. Найдите его объем. А. 16 кубометров; Б. 48 кубометров; C. 64 кубометра; D. 86 кубометров; 39. Резервуар имеет форму квадратной призмы. 5. Объем наибольшего правого кругового конуса, который может быть помещен в куб, край которого равен 2r, равен. Если внешний диаметр равен 16 см, а его длина равна 100 см, найдите, сколько кубических сантиметров железа было использовано при изготовлении трубка ? 6.Куб со стороной 4 см содержит сферу, касающуюся его сторон. Таким образом, мы можем взять объем по формуле куба и установить его равным объему, который мы на самом деле знаем: 64 сантиметра в кубе. Итак, чтобы найти длину ребра, которое является стороной, нам нужно извлечь кубический корень из обеих частей этого уравнения. Слева корень куба отменяет весь куб.
Обшивка сидений Bayliner capri
Код P1441 chevy k1500
SWBAT: расчет объема прямоугольных твердых тел и цилиндров Объем прямоугольных твердых тел и цилиндров — День 4 разминка — Пример 1: куб имеет объем 216 кубических футов.Вычислите сторону куба. Практика: куб имеет объем 512 кубических футов. Вычислите сторону куба.
Прямоугольная призма выше имеет объем 48 кубических единиц. Объем прямоугольной призмы равен длине x ширине x высоте. Примеры расчета площади прямоугольника. Нам нужно сделать два умножения, чтобы вычислить объем. Мы вычисляем площадь одной грани (или стороны) и умножаем ее на ее высоту. Формула объема куба. Чтобы вычислить объем куба, возведите длину ребра в третью степень :.объем = a³. Вы можете думать о формуле объема куба как о вычислении любого другого объема призмы — просто умножьте базовую площадь на высоту тела. Куб (или любая другая обычная прямоугольная форма) — это особый случай призмы, но вам не нужно использовать формулу причудливой призмы Шманси, потому что площадь поверхности куба просто состоит из шести равных квадратов. Назовем длину ребра куба s. Следовательно, площадь каждой стороны равна s 2. У куба шесть граней, поэтому его площадь поверхности равна 6s 2.
Расчет объема | SkillsYouNeed
На этой странице объясняется, как рассчитать объем твердых объектов, то есть насколько вы можете поместиться в объекте, если, например, вы заполните его жидкостью.
Площадь — это мера того, сколько места находится внутри двухмерного объекта (подробнее см. Нашу страницу: Расчет площади).
Объем — это мера пространства внутри трехмерного объекта. Наша страница, посвященная трехмерным формам, объясняет основы таких форм.
В реальном мире вычисление объема, вероятно, не то, что вы будете использовать так часто, как вычисление площади.
Однако это все еще может быть важным. Возможность рассчитать объем позволит вам, например, определить, сколько у вас есть места для упаковки при переезде, сколько офисного пространства вам нужно или сколько варенья вы можете уместить в банку.
Это также может быть полезно для понимания того, что имеют в виду средства массовой информации, когда говорят о пропускной способности плотины или течении реки.
Примечание по агрегатам
Площадь выражается в квадратных единицах, потому что это два измерения, умноженные вместе.
Объем выражается в кубических единицах, потому что это сумма трех измерений (длина, ширина и глубина), умноженных вместе. Кубические единицы включают см 3 , м 3 и кубические футы.
ВНИМАНИЕ!
Объем также можно выразить как вместимость по жидкости.
Метрическая система
В метрической системе объем жидкости измеряется в литрах, что напрямую сопоставимо с кубическим размером, поскольку 1 мл = 1 см 3 .1 литр = 1000 мл = 1000 см 3 .
Британская / английская система
В британской / британской системе эквивалентными измерениями являются жидкие унции, пинты, кварты и галлоны, которые нелегко перевести в кубические футы. Поэтому лучше всего придерживаться жидких или твердых единиц объема.
Подробнее см. На нашей странице Системы измерения
Основные формулы для расчета объема
Объем твердых тел на основе прямоугольников
В то время как основная формула для площади прямоугольной формы — длина × ширина, основная формула для объема — длина × ширина × высота.
То, как вы относитесь к различным размерам, не меняет расчет: например, вы можете использовать «глубину» вместо «высоты». Важно то, что три измерения умножаются. Вы можете умножать в любом порядке, так как это не изменит ответ (подробнее см. Нашу страницу о умножении ).
Коробка размером 15 см в ширину, 25 см в длину и 5 см в высоту имеет объем:
15 × 25 × 5 = 1875 см 3
Объем призм и цилиндров
Эту базовую формулу можно расширить, чтобы охватить объем цилиндров и призм .Вместо прямоугольного конца у вас просто другая форма: круг для цилиндров, треугольник, шестиугольник или любой другой многоугольник для призмы.
Фактически, для цилиндров и призм объем — это площадь одной стороны, умноженная на глубину или высоту формы.
Таким образом, основная формула для определения объема призм и цилиндров:
Площадь формы торца × высота / глубина призмы / цилиндра.
Объем конусов и пирамид
Тот же принцип, что и выше (ширина × длина × высота), применяется для вычисления объема конуса или пирамиды, за исключением того, что, поскольку они достигают точки, объем составляет только долю от общего количества, которое было бы, если бы они продолжались. в той же форме насквозь.
Объем конуса или пирамиды составляет ровно одну треть от объема коробки или цилиндра с таким же основанием.
Таким образом, формула:
Площадь основания или торца × высота конуса / пирамиды × 1 / 3
Вернитесь на нашу страницу Расчет площади , если вы не можете вспомнить, как рассчитать площадь круга или треугольника.
Например, чтобы вычислить объем конуса с радиусом 5 см и высотой 10 см:Площадь внутри круга = πr2 (где π (пи) приблизительно равно 3.14 и r — радиус окружности).
В этом примере площадь основания (круга) = πr 2 = 3,14 × 5 × 5 = 78,5 см 2 .
78,5 × 10 = 785
785 × 1/3 = 261,6667 см 3
Объем сферы
Как и в случае с кругом, вам нужно π (пи) для вычисления объема сферы.
Формула: 4/3 × π × радиус 3 .
Вам может быть интересно, как определить радиус шара.Если не протыкать через него спицу (эффективный, но конечный для мяча!), Есть способ попроще.
Вы можете измерить расстояние вокруг самой широкой точки сферы напрямую, например, с помощью рулетки. Этот круг является окружностью и имеет тот же радиус, что и сама сфера.
Длина окружности вычисляется как радиус 2 x π x.
Чтобы вычислить радиус из окружности, вы:
Разделите окружность на (2 x π) .
Рабочие примеры: расчет объема
Пример 1
Вычислите объем цилиндра длиной 20 см, круговой конец которого имеет радиус 2,5 см.
Сначала определите площадь одного из круглых концов цилиндра.
Площадь круга равна πr 2 (π × радиус × радиус). π (пи) приблизительно равно 3,14.
Таким образом, площадь конца равна:
3.14 x 2,5 x 2,5 = 19,63 см 2
Объем — это площадь конца, умноженная на длину, и, следовательно, составляет:
19,63 см 2 x 20 см = 392,70 см 3
Пример 2
Что больше по объему: сфера радиусом 2 см или пирамида с основанием в квадрате 2,5 см и высотой 10 см?
Сначала определим объем сферы .
Объем сферы равен 4/3 × π × радиус 3 .
Таким образом, объем сферы:
.4 ÷ 3 x 3,14 × 2 × 2 × 2 = 33,51 см 3
Затем определите объем пирамиды .
Объем пирамиды 1/3 × площадь основания × высота.
Площадь основания = длина × ширина = 2,5 см × 2,5 см = 6,25 см 2
Объем, следовательно, равен 1/3 x 6,25 × 10 = 20.83 см 3
Таким образом, сфера больше по объему, чем пирамида.
Расчет объема твердых тел неправильной формы
Точно так же, как вы можете вычислить площадь неправильных двумерных форм, разбив их на правильные, вы можете сделать то же самое для вычисления объема неправильных твердых тел. Просто разделите твердое тело на более мелкие части, пока не получите только твердые тела, с которыми вы сможете легко работать.
Рабочий пример
Вычислите объем водяного цилиндра общей высотой 1 м, диаметром 40 см и полусферической верхней частью.
Сначала вы делите фигуру на две части: цилиндр и полусферу (полусферу).
Объем сферы равен 4/3 × π × радиус 3 . В этом примере радиус составляет 20 см (половина диаметра). Поскольку верхняя часть является полусферической, ее объем будет вдвое меньше полной сферы. Таким образом, объем данного участка формы:
.0,5 × 4/3 × π × 203 = 16,755,16 см 3
Объем цилиндра равен площади основания × высоте.Здесь высота цилиндра — это общая высота за вычетом радиуса сферы, которая составляет 1 м — 20 см = 80 см. Площадь базы 2 грн.
Таким образом, объем цилиндрического сечения данной формы составляет:
80 × π × 20 × 20 = 100 530,96 см 3
Таким образом, общий объем этого резервуара для воды составляет:
100 530,96 + 16 755,16 = 117 286,12 см 3 .
Это довольно большое число, поэтому вы можете преобразовать его в 117.19 литров путем деления на 1000 (поскольку в литре 1000 см 3 ). Однако вполне правильно выразить его как cm 3 , поскольку задача не требует, чтобы ответ был выражен в какой-либо конкретной форме.
В заключение…
Используя эти принципы, если необходимо, теперь вы сможете рассчитать объем практически всего в своей жизни, будь то упаковочный ящик, комната или водяной баллон.
Обладают ли кубы и квадраты такими же свойствами, как сферы и круги? — AP Central
Студенты-математики часто бывают заинтригованы, когда понимают, что производная формулы объема сферы по радиусу сферы является формулой поверхности сферы:.Они также очарованы тем фактом, что производная от формулы площади круга является формулой для его длины:. Эти результаты, кажется, неприменимы к кубам и квадратам, потому что площадь поверхности куба и периметр квадрата. Почему сферы и круги ведут себя так, а кубы и квадраты — по-другому?
Рассмотрим производную площади круга. Согласно определению производной:
Геометрически этот результат легко увидеть, потому что область между двумя концентрическими окружностями, одна с радиусом r , а другая с радиусом r + h , по существу представляет собой полосу шириной h и длиной 2π r , как показано на рисунке 1.
Аналогичное вычисление справедливо для производной объема сферы. Согласно определению производной:
Геометрически этот результат легко понять, поскольку область между двумя концентрическими сферами, одна с радиусом r, а другая с радиусом r + h , по существу представляет собой полый шар толщиной h и площадью поверхности 4π r 2 .
Подобные результаты не верны для стандартной формулы для объема куба и площади квадрата, как показано в первом абзаце.Давайте рассмотрим различные формулы: Пусть s будет расстоянием от центра квадрата перпендикулярно противоположной стороне, как показано на рисунке 2. Тогда, поскольку s составляет половину длины края квадрата, мы имеем формула A = (2 s ) 2 = 4 s 2 и P = 8 s для площади квадрата и периметра квадрата соответственно.
Рассмотрим производные этой новой формулы площади квадрата.Поскольку A = 4 s 2 , что является нашей формулой для периметра квадрата. Аналогично, пусть s будет расстоянием от центра куба перпендикулярно противоположной стороне. Тогда, поскольку s составляет половину длины ребра куба, мы имеем формулу V = (2 s ) 3 = 8 s 3 для объема куба, и (2 с ) 2 = 4 с 2 для площади каждой грани.Поскольку V = 8 s 3 , то площадь грани куба в 6 раз больше, и, следовательно, это выражение равно площади поверхности куба. Записав формулы в терминах s , половина длины ребра, мы теперь имеем формулы, которые имеют свойства, согласующиеся со свойствами сфер и кругов.
Мы можем распространить этот результат на равносторонние треугольники. Пусть e будет длиной ребра треугольника, как показано на рисунке 3.
Площадь треугольника равна, а его периметр равен 3 e . Производная площади равна, что отдаленно не похоже на периметр треугольника. Давайте теперь изменим переменную и пусть s представляет собой перпендикулярное расстояние от центра треугольника до одной из сторон, как показано на рисунке 4.
Используя соотношение Пифагора, или. В терминах s площадь треугольника равна, а периметр равен. Поскольку производная площади равностороннего треугольника равна периметру треугольника.Рисунок 5 показывает, что разница между треугольными областями с использованием s и s + h , по сути, представляет собой трехстороннюю полосу шириной h и длиной, равной периметру треугольника, что геометрически подтверждает наш результат.
Случай равностороннего треугольника предлагает способ обобщения этого результата на другие правильные многоугольники. Отрезок s от центра многоугольника перпендикулярно стороне называется апофемой многоугольника.Тогда длина стороны многоугольника равна, где n — количество сторон, и, следовательно, периметр многоугольника равен. Площадь многоугольника — это длина апофемы, умноженная на половину длины периметра. В символах:
Теперь мы можем проверить это, периметр правильного многоугольника.
Предложите своим ученикам применить этот метод к правильному шестиугольнику. Они должны найти формулы для площади и периметра шестиугольника с точки зрения его апофемы.Затем они должны показать, что одно является производным от другого.
Мы также можем распространить наши результаты на трехмерные фигуры. Для правильных многогранников апофема — это радиус вписанной сферы. Рассмотрим тетраэдр.
Стандартные формулы для объема и площади поверхности тетраэдра обычно основаны на длине ребра, a , тетраэдра. Однако нетрудно переписать их в терминах длины r апофемы — радиуса вписанной сферы.
r = радиус вписанной сферы = апофема многогранника
R = радиус описанной сферы
a = длина ребра тетраэдра
S = площадь поверхности тетраэдра
V = объем тетраэдра
В пересчете на r вписанный радиус:
Таким образом, мы легко можем видеть, что в терминах апофемы производной формулы для объема тетраэдра является формула для его площади поверхности.
Аналогично, используя стандартные формулы для объема и площади поверхности октаэдра на основе длины ребра, a , октаэдра. Мы можем переписать их в терминах длины апофемы r .
Опять же, ясно, что производная формулы объема по отношению к r является формулой для площади поверхности.
Вот формулы для объема и площади поверхности двух других правильных многогранников через длину вписанного радиуса, r .
Додекаэдр:
Икосаэдр:
Вы можете поручить учащимся сложную задачу проверки того, что производная приведенной выше формулы для объема додекаэдра на самом деле является данной формулой для его площади поверхности.
Какова ценность этого результата? Это просто академическое упражнение? Фактически, эти формулы предоставляют простой способ найти формулу для площади поверхности обычных твердых тел, если вы знаете формулу для их объема, или наоборот.Просто напишите формулу в терминах апофемы твердого тела и дифференцируйте или антидифференцируйте соответственно, чтобы найти другую формулу.
Список литературы
http://mathforum.org/dr.math/faq/formulas/faq.polyhedron.html#octahedron
http://mathforum.org/dr.math/faq/formulas/faq.polyhedron.html
Джон Ф. Махони представил AP Statistics в средней школе Banneker в 2002–2003 годах и обучил 59 студентов в этом году в рамках курса. Каждый из студентов сдал экзамен AP, и Махони считает, что у них, возможно, был самый высокий процент пожилых людей, сдающих статистику AP в стране.В этом году он также преподает вычисление AP уровня AB и BC. Он является консультантом по программе AP и давним участником программы AP Calculus Reading. В настоящее время он является одним из руководителей экзаменов. Он также возглавляет редакционную коллегию журнала NCTM ON-Math: www.nctm.org/onmath. В средней школе Баннекера он является одним из наставников команды робототехники и помогает студентам проектировать приводные механизмы на основе зубчатых колес — так же, как сам Баннекер делал более 200 лет назад. Им помогают многие инженеры, в том числе из Университета Говарда, расположенного через проспект Джорджии от средней школы.Он является одним из тренеров отмеченной наградами школьной команды It’s Academic. Когда он решил преподавать в средней школе Баннекера три года назад, после долгой карьеры в частных школах, он изучил математику Баннекера, и эта статья является результатом этой работы.
Часть 2. Оценка удивительных площадей невероятно крошечной поверхности | Chem13 News Magazine
В первой части этой серии мы описали наночастицы, что они собой представляют, как они сделаны и как они сравниваются с другими формами металлов.Мы также описали, как металлические поверхности служат катализаторами, способствующими таким реакциям, как гидрирование алкена. В этой части мы исследуем, чем наночастицы выделяются благодаря своей большой площади поверхности.
Как мы узнали в Части 1, реакции, катализируемые металлом, происходят на поверхности металла. В случае палладия только водород и дейтерий могут мигрировать в отверстия под поверхностью. Для всех других веществ и почти всех других металлов взаимодействие между металлом и реагентом происходит только на поверхности.Даже гелий не может мигрировать под поверхность. Например, при гидрировании адсорбированного этена, обсуждаемом в Части 1, реакция протекает на поверхности палладия, даже если атомы водорода не ограничиваются этой поверхностью. По этой причине стратегической целью при разработке катализаторов является максимальное увеличение площади поверхности. Никакая композиция не справляется с этим лучше, чем наночастицы. В этой части мы исследуем важность площади поверхности посредством вычислений, которые учащиеся могут понять и выполнить самостоятельно.
Чем меньше, тем лучше
В случае сфероидальных наночастиц мы делаем наши оценки, используя формулы для сферы. Объем и, следовательно, количество атомов палладия увеличивается как куб радиуса (V сфера = 4 / 3 pr 3 ), в то время как площадь поверхности и, следовательно, количество поверхностных атомов увеличивается как квадрат радиуса (A сфера = 4 пр 2 ). Отношение площади к объему равно 3 / r сфере .По мере увеличения радиуса сферы отношение Площадь / Объем уменьшается.
Меньшие сферы имеют больший процент поверхностных атомов.
Оценка количества атомов в сфере
Один простой способ оценить количество атомов в сфере — это вычислить объем сферы по радиусу, используя формулу объема, а затем умножить объем (см 3 ) на плотность металла (г / см ). 3 ), чтобы определить массу наночастицы в граммах.Масса преобразуется в моль и, наконец, в число атомов с помощью числа Авогадро. Для сфероидальной наночастицы палладия радиусом 1,0 нм (1,0 x 10 -7 см) мы можем оценить моли палладия и количество атомов, учитывая плотность 12,023 г / см 3 :
V сфера = 4 / 3 пр 3 = 4 / 3 p (1,0 x 10 -7 см) 3 = 4,2 x 10 -21 см 3
м Pd = объем x плотность = 4.2 x 10 -21 см 3 x 12,023 г см -3 = 5,0 x 10 -20 г
n Pd = масса / атомная масса = 5,0 x 10 -20 г / 106,42 г моль -1 = 4,7 x 10 -22 моль
n Pd атомов = 4,7 x 10 -22 моль x 6,02 x 10 23 атомов моль -1 = 285 атомов
Чтобы оценить количество атомов под поверхностным слоем сферы, мы начнем с определения подповерхностного радиуса, равного радиусу наночастицы за вычетом одного диаметра рассматриваемого элемента.На рисунке это будет радиус круга, показанного красным, минус один атомный диаметр. Палладий имеет ковалентный радиус 0,138 нм, поэтому наночастица с радиусом 1,0 нм будет иметь подповерхностный радиус r подповерхностный = 1,0 нм — 2 x 0,138 нм = 0,724 нм. Повторяя вышеприведенные вычисления, но используя радиус подповерхностного слоя, можно вычислить 108 подповерхностных атомов. Количество поверхностных атомов равно разнице, 285 — 108 = 177 поверхностных атомов.
Отношение поверхностных атомов к общему количеству атомов называется дисперсией или степенью дисперсии . 1 Процент поверхностных атомов равен дисперсии x 100%. Описанная выше наночастица с радиусом 1,0 нм имеет дисперсию 0,62, или 62% атомов являются поверхностными атомами.
Используя электронную таблицу Excel, мы вычислили процент поверхностных атомов как функцию радиуса частицы, как показано на рис. 1. Если провести до верхнего предела радиуса наночастицы, 50 нм, процент поверхностных атомов упадет до ~ 2%. На рис. 1 наглядно показано выравнивание доли поверхностных атомов с увеличением радиуса.
Рис. 1. Процент поверхностных атомов Pd уменьшается с увеличением радиуса наночастицы.
На рис. 2 представлена зависимость площади поверхности в м 2 / г палладия от радиуса наночастиц. Площадь рассчитывается по формуле, приведенной ранее (сфера = 4 p r 2 ), а масса определяется из объема и плотности частицы (масса = объем x плотность). Рассмотрим снова сфероидальную наночастицу палладия радиусом 1 нм, для которой мы рассчитали массу 5.0 x 10 -20 г. Площадь этой наночастицы составляет 1,26 x 10 -17 м 2 . Чтобы сравнить наночастицы с различным радиусом, мы рассчитываем площадь на грамм. Для наночастиц палладия радиусом 1,0 нм это значение составляет 250 мкм 2 / г Pd. Примечательно, что единицы составляют квадратных метра на грамма. Таким образом, образец наночастицы такого размера весом 1,0 г будет иметь площадь поверхности, аналогичную площади пола довольно большого дома.
Рис. 2. Площадь поверхности в м 2 / г уменьшается с увеличением радиуса наночастиц Pd.
В этих расчетах мы приняли сферическую форму наночастиц. Как геометрический объект сфера имеет наименьшую из всех площадей. Настоящие наночастицы могут быть полусфероидальными, но они также могут иметь любую вообразимую форму от формы картофеля до формы блинов. В Части 1 мы отметили, что наноматериалы могут принимать форму трубок, проволок и листов. Все эти формы имеют площадь поверхности, которая даже больше на одну частицу, чем те, которые мы рассчитали для сфер. То есть нанотрубка, состоящая из 1000 атомов, имеет большую площадь поверхности, чем сфера из 1000 атомов.
Сравнение площади поверхности наночастиц с объемными металлическими образцами
Палладий в больших количествах реализуется в виде проволоки, листов, прутков и окатышей. Все эти формы имеют незначительный процент площади поверхности по сравнению с наночастицами. Рассмотрим одну сферическую таблетку палладия массой 1,0 г. Разделив массу 1,0 г на плотность палладия (12,023 г / см 3 ), получим объем 0,0832 см 3 . Предполагая, что форма шарика достаточно похожа на сферу, чтобы использовать формулу сферы, можно найти радиус r сфера = 0.271 см, а затем площадь,
Сфера = 0,921 см 2 . Сравнивая эту площадь с площадью 1,0 г наночастиц диаметром 1,0 нм (250 м 2 ), можно рассчитать, что наночастицы имеют площадь поверхности, которая в 2,7 миллиона раз больше, чем у одиночной сферы той же массы.
Большинство компаний-поставщиков химической продукции продают палладий в виде фольги. Самая тонкая предлагаемая фольга имеет толщину всего
0,0025 см — менее 100 000 атомов, исходя из диаметра палладия 0.276 нм. Образец этой Pd фольги весом 1,0 г имеет объем 0,0832 см 3 — такой же, как и любая форма. Формула объема ящика
V коробка = прямоугольник x h. Отсюда получаем прямоугольник = 33 см, 2 .
Однако тонкая фольга имеет две большие стороны поверхностных атомов, всего ~ 67 см. 2 . Мы можем игнорировать области четырех краев.
Прямоугольник = прямоугольник V / h = 0,0832 см 3 /0.0025 см = 33 см 2
= 3,3 x 10 -3 м 2
A верх + низ = 2 x 3,3 x 10 -3 м 2 = 6,7 x 10 -3 м 2
Площадь фольги в ~ 72 раза больше, чем площадь шара массой 1,0 г. Однако по сравнению с общей площадью 250 м 2 , которую мы рассчитали для 1,0 г сферических наночастиц Pd (радиус 1 нм), последняя более чем в 37000 раз больше, чем у фольги.Что касается площади поверхности, на которой химические реакции катализируются металлами, наночастицы превосходят их.
В части 3 мы более подробно рассмотрим структуру плотноупакованных металлов и опишем, как можно построить простую модель наночастицы.
Вопросы
- Мы описываем, как наночастица с радиусом 1,0 нм может содержать ~ 285 атомов. Повторите этот расчет, чтобы увидеть, получите ли вы тот же ответ. Используйте единицы во время работы, чтобы убедиться, что вы не ошибаетесь.
- Продолжая с той же наночастицей палладия радиусом 1,0 нм, повторите вычисления, чтобы оценить количество подповерхностных и поверхностных атомов. Рассчитайте степень дисперсии и процент поверхностных атомов.
- Повторите расчет для этого же размера наночастиц, чтобы определить площадь отдельной наночастицы (в нм 2 ) и площадь на грамм Pd в единицах m 2 / г Pd.
- Повторите расчеты, описанные в вопросах 1–3, для сфероидальной наночастицы (a) с радиусом 0.5 нм, и (б) с радиусом 2,0 нм.
[Ответы: (а) Для 0,5 нм
% поверхностных атомов = 91%
Площадь на грамм = 500 м 2 / г
(б) Для 2,0 нм
процентов поверхностных атомов = 36%
Площадь на грамм = 125 м 2 / г
Вы можете попросить учащихся проверить свои ответы на рисунках, приведенных на предыдущей странице.]
- Палладий также продается в виде проволоки диаметром 0,5 мм (радиус 0,25 мм). Проволока по сути представляет собой цилиндр, а формула площади равна .
A цилиндр = 2 x A круг + A поверхность цилиндра = 2 p r 2 + 2 p r h,
где h — длина провода. Какой длины в метрах должен быть этот провод, чтобы равняться площади 1 г наночастиц радиусом 1 нм (250 м 2 )? Выразите эту длину в метрах и километрах.

 {\circ}$ больше вписанного угла ACB, опирающегося на ту же дугу. Ответ дайте в градусах. [посмотреть решение]
{\circ}$ больше вписанного угла ACB, опирающегося на ту же дугу. Ответ дайте в градусах. [посмотреть решение] Найдите объем отсеченной треугольной пирамиды.
Найдите объем отсеченной треугольной пирамиды.
Leave A Comment