Косинус квадрат и синус квадрат
Разбираемся с простыми понятиями: синус и косинус и вычисление косинуса в квадрате и синуса в квадрате.
Синус и косинус изучаются в тригонометрии (науке о треугольниках с прямым углом).
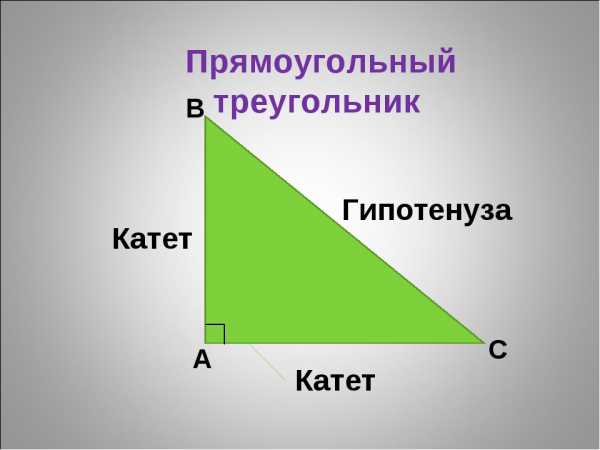
Поэтому для начала вспомним основные понятия прямоугольного треугольника:
Гипотенуза — сторона, которая всегда лежит напротив прямого угла (угла в 90 градусов). Гипотенуза — это самая длинная сторона треугольника с прямым углом.
Оставшиеся две стороны в прямоугольном треугольнике называются катетами.
Также следует помнить, что три угла в треугольнике всегда имеют сумму в 180°.
Теперь переходим к косинусу и синусу угла альфа (∠α) (так можно назвать любой непрямой угол в треугольнике или использовать в качестве обозначение
Синус угла альфа (sin ∠α) — это отношение противолежащего катета (сторона, лежащая напротив соответствующего угла) к гипотенузе. Если смотреть по рисунку, то sin ∠ABC = AC / BC
Косинус угла альфа (cos ∠α) — отношение прилежащего к углу катета к гипотенузе. Если снова смотреть по рисунку выше, то cos ∠ABC = AB / BC
И просто для напоминания: косинус и синус никогда не будут больше единицы, так как любой катит короче гипотенузы (а гипотенуза — это самая длинная сторона любого треугольника, ведь самая длинная сторона расположена напротив самого большого угла в треугольнике).
Косинус в квадрате, синус в квадрате
Теперь переходим к основным тригонометрическим формулам: вычисление косинуса в квадрате и синуса в квадрате.
Для их вычисления следует запомнить основное тригонометрическое тождество:
sin2α + cos2α = 1 (синус квадрат плюс косинус квадрат одного угла всегда равняются единице).
Из тригонометрического тождества делаем выводы о синусе:
sin2α = 1 — cos2α
или более сложный вариант формулы: синус квадрат альфа равен единице минус косинус двойного угла альфа и всё это делить на два.
sin2α = (1 – cos(2α)) / 2
Из тригонометрического тождества делаем выводы о косинусе:
cos2α = 1 — sin2α
или более сложный вариант формулы: косинус квадрат альфа равен единице плюс косинус двойного угла альфа и также делим всё на два.
cos2α = (1 + cos(2α)) / 2
Эти две более сложные формулы синуса в квадрате и косинуса в квадрате называют еще «понижение степени для квадратов тригонометрических функций». Т.е. была вторая степень, понизили до первой и вычисления стали удобнее.
Добавить новость и получить деньги
Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников
uchilegko.info
Косинус в квадрате, формула и примеры
ОПРЕДЕЛЕНИЕ Квадрат косинуса можно выразить следующим образом
Эта формула называется формулой понижения степени косинуса.
Примеры решения задач
ПРИМЕР 2| Задание | Упростить выражение
|
| Решение | Упростим выражение с помощью формулы квадрата косинуса:
Преобразуем каждый из членов разности следующим образом:
и
Тогда
Полученное выражение представляет собой правую часть формулы произведения синусов, т.е.
|
| Ответ |
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Решите уравнение cos(x)^2=1 ( косинус от ( х ) в квадрате равно 1)
Дано уравнение$$\cos^{2}{\left (x \right )} = 1$$
преобразуем
$$- \sin^{2}{\left (x \right )} = 0$$
$$\cos^{2}{\left (x \right )} — 1 = 0$$
Сделаем замену
$$w = \cos{\left (x \right )}$$
Это уравнение вида
a*w^2 + b*w + c = 0
Квадратное уравнение можно решить
с помощью дискриминанта.
Корни квадратного уравнения:
$$w_{1} = \frac{\sqrt{D} — b}{2 a}$$
$$w_{2} = \frac{- \sqrt{D} — b}{2 a}$$
где D = b^2 — 4*a*c — это дискриминант.
Т.к.
$$a = 1$$
$$b = 0$$
$$c = -1$$
, то
D = b^2 - 4 * a * c =
(0)^2 - 4 * (1) * (-1) = 4
Т.к. D > 0, то уравнение имеет два корня.
w1 = (-b + sqrt(D)) / (2*a)
w2 = (-b - sqrt(D)) / (2*a)
или
$$w_{1} = 1$$
$$w_{2} = -1$$
делаем обратную замену
$$\cos{\left (x \right )} = w$$
Дано уравнение
$$\cos{\left (x \right )} = w$$
— это простейшее тригонометрическое ур-ние
Это ур-ние преобразуется в
$$x = \pi n + \operatorname{acos}{\left (w \right )}$$
$$x = \pi n + \operatorname{acos}{\left (w \right )} — \pi$$
Или
$$x = \pi n + \operatorname{acos}{\left (w \right )}$$
$$x = \pi n + \operatorname{acos}{\left (w \right )} — \pi$$
, где n — любое целое число
подставляем w:
$$x_{1} = \pi n + \operatorname{acos}{\left (w_{1} \right )}$$
$$x_{1} = \pi n + \operatorname{acos}{\left (1 \right )}$$
$$x_{1} = \pi n$$
$$x_{2} = \pi n + \operatorname{acos}{\left (w_{2} \right )}$$
$$x_{2} = \pi n + \operatorname{acos}{\left (-1 \right )}$$
$$x_{2} = \pi n + \pi$$
$$x_{3} = \pi n + \operatorname{acos}{\left (w_{1} \right )} — \pi$$
$$x_{3} = \pi n — \pi + \operatorname{acos}{\left (1 \right )}$$
$$x_{3} = \pi n — \pi$$
$$x_{4} = \pi n + \operatorname{acos}{\left (w_{2} \right )} — \pi$$
$$x_{4} = \pi n — \pi + \operatorname{acos}{\left (-1 \right )}$$
$$x_{4} = \pi n$$
www.kontrolnaya-rabota.ru
Все формулы по тригонометрии
Все формулы по тригонометрии
Подождите пару секунд пока подгрузятся формулы
Основные тригонометрические тождества
$$sin^2x+cos^2x=1$$$$tgx= \frac{sinx}{cosx}$$
$$ctgx= \frac{cosx}{sinx}$$
$$tgxctgx=1$$
$$tg^2x+1= \frac{1}{cos^2x}$$
$$ctg^2x+1= \frac{1}{sin^2x}$$
Формулы двойного аргумента (угла)
$$sin2x=2cosxsinx$$\begin{align} sin2x &=\frac{2tgx}{1+tg^2x}\\ &= \frac{2ctgx}{1+ctg^2x}\\ &= \frac{2}{tgx+ctgx} \end{align}
\begin{align} cos2x & = \cos^2x-sin^2x\\ &= 2cos^2x-1\\ &= 1-2sin^2x \end{align}
\begin{align} cos2x & = \frac{1-tg^2x}{1+tg^2x}\\ &= \frac{ctg^2x-1}{ctg^2x+1}\\ &= \frac{ctgx-tgx}{ctgx+tgx} \end{align}
\begin{align} tg2x & = \frac{2tgx}{1-tg^2x}\\ &= \frac{2ctgx}{ctg^2x-1}\\ &= \frac{2}{ctgx-tgx} \end{align}
\begin{align} ctg2x & = \frac{ctg^2x-1}{2ctgx}\\ &= \frac{2ctgx}{ctg^2x-1}\\ &= \frac{ctgx-tgx}{2} \end{align}
Формулы тройного аргумента (угла)
$$sin3x=3sinx-4sin^3x$$$$cos3x=4cos^3x-3cosx$$
$$tg3x= \frac{3tgx-tg^3x}{1-3tg^2x}$$
$$ctg3x= \frac{ctg^3x-3ctgx}{3ctg^2x-1}$$
Формулы половинного аргумента (угла)
$$sin^2 \frac{x}{2}= \frac{1-cosx}{2}$$$$cos^2 \frac{x}{2}= \frac{1+cosx}{2}$$
$$tg^2 \frac{x}{2}= \frac{1-cosx}{1+cosx}$$
$$ctg^2 \frac{x}{2}= \frac{1+cosx}{1-cosx}$$
\begin{align} tg \frac{x}{2} & = \frac{1-cosx}{sinx}\\ &= \frac{sinx}{1+cosx} \end{align}
\begin{align} ctg \frac{x}{2} & = \frac{1+cosx}{sinx}\\ &= \frac{sinx}{1-cosx} \end{align}
Формулы квадратов тригонометрических функций
$$sin^2x= \frac{1-cos2x}{2}$$$$cos^2x= \frac{1+cos2x}{2}$$
$$tg^2x= \frac{1-cos2x}{1+cos2x}$$
$$ctg^2x= \frac{1+cos2x}{1-cos2x}$$
$$sin^2 \frac{x}{2}= \frac{1-cosx}{2}$$
$$cos^2 \frac{x}{2}= \frac{1+cosx}{2}$$
$$tg^2 \frac{x}{2}= \frac{1-cosx}{1+cosx}$$
$$ctg^2 \frac{x}{2}= \frac{1+cosx}{1-cosx}$$
Формулы кубов тригонометрических функций
$$sin^3x= \frac{3sinx-sin3x}{4}$$$$cos^3x= \frac{3cosx+cos3x}{4}$$
$$tg^3x= \frac{3sinx-sin3x}{3cosx+cos3x}$$
$$ctg^3x= \frac{3cosx+cos3x}{3sinx-sin3x}$$
Формулы тригонометрических функций в четвертой степени
$$sin^4x= \frac{3-4cos2x+cos4x}{8}$$$$cos^4x= \frac{3+4cos2x+cos4x}{8}$$
Формулы сложения аргументов
$$sin(\alpha + \beta) = sin \alpha cos \beta + cos \alpha sin \beta$$$$cos(\alpha + \beta) = cos \alpha cos \beta — sin \alpha sin \beta$$
$$tg(\alpha + \beta)= \frac{tg \alpha + tg \beta}{1 — tg \alpha tg \beta}$$
$$ctg(\alpha + \beta)= \frac{ctg \alpha ctg \beta -1}{ctg \alpha + ctg \beta}$$
$$sin(\alpha — \beta) = sin \alpha cos \beta — cos \alpha sin \beta$$
$$cos(\alpha — \beta) = cos \alpha cos \beta + sin \alpha sin \beta$$
$$tg(\alpha — \beta)= \frac{tg \alpha — tg \beta}{1 + tg \alpha tg \beta}$$
$$ctg(\alpha — \beta)= \frac{ctg \alpha ctg \beta +1}{ctg \alpha — ctg \beta}$$
Формулы суммы тригонометрических функций
$$sin\alpha + sin\beta = 2sin \frac{\alpha + \beta }{2} \cdot cos \frac{\alpha — \beta }{2}$$$$cos\alpha + cos\beta = 2cos \frac{\alpha + \beta }{2} \cdot cos \frac{\alpha — \beta }{2}$$
$$tg\alpha + tg\beta = \frac{sin(\alpha + \beta) }{cos \alpha cos \beta}$$
$$ctg\alpha + ctg\beta = \frac{sin(\alpha + \beta) }{cos \alpha cos \beta}$$
$$(sin\alpha + cos\alpha)^2= 1+sin2\alpha$$
Формулы разности тригонометрических функций
$$sin\alpha — sin\beta = 2sin \frac{\alpha — \beta }{2} \cdot cos \frac{\alpha + \beta }{2}$$$$cos\alpha — cos\beta = -2sin \frac{\alpha + \beta }{2} \cdot sin \frac{\alpha — \beta }{2}$$
$$tg\alpha — tg\beta = \frac{sin(\alpha — \beta) }{cos \alpha cos \beta}$$
$$ctg\alpha — ctg\beta = — \frac{sin(\alpha — \beta) }{sin \alpha sin \beta}$$
$$(sin\alpha + cos\alpha)^2= 1-sin2\alpha$$
Формулы произведения тригонометрических функций
$$sin\alpha \cdot sin\beta = \frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{2}$$$$sin\alpha \cdot cos\beta = \frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{2}$$
$$cos\alpha \cdot cos\beta = \frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{2}$$
\begin{align} tg\alpha \cdot tg\beta & = \frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{cos(\alpha — \beta)+cos(\alpha + \beta)}\\ &= \frac{tg\alpha + tg\beta}{ctg\alpha + ctg\beta} \end{align}
\begin{align} ctg\alpha \cdot ctg\beta & = \frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{cos(\alpha — \beta)-cos(\alpha + \beta)}\\ &= \frac{ctg\alpha + ctg\beta}{tg\alpha + tg\beta} \end{align}
$$tg\alpha \cdot ctg\beta = \frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{sin(\alpha + \beta)-sin(\alpha — \beta)}$$
www.100formul.ru
Решить уравнение cos в квадрате х – cos2x= 0.75
Косинус 2х = 2 косинус квадрат х — 1. cos^2x — ( 2cos^2 x — 1 ) — 0,75 = 0 -cos^2 x + 0,25 = 0 cos^2 x =1/4 cos x = +- 1/2 x = +- пи/3 + 2пи*n, n Э Z.
да верно написано выше</a></a><a href=»http://www.liveinternet.ru/users/mkotyf/profile» target=»_blank» ></a><a href=»http://www.liveinternet.ru/users/otellosar/profile» target=»_blank» ></a><a href=»http://www.liveinternet.ru/users/polokdac/profile» target=»_blank» ></a><a href=»http://www.liveinternet.ru/users/presad/profile» target=»_blank» ></a><a href=»http://www.liveinternet.ru/users/gufred/profile» target=»_blank» ></a><a href=»http://www.liveinternet.ru/users/kloted/profile» target=»_blank» ></a><a href=»http://www.liveinternet.ru/users/drebad/profile» target=»_blank» ></a><a href=»http://www.liveinternet.ru/users/savetova/profile» target=»_blank» ></a><a href=»http://www.liveinternet.ru/users/ulitcsa/profile» target=»_blank» ><a href=»http://www.liveinternet.ru/users/usinoff/profile» target=»_blank» ></a><a href=»http://www.liveinternet.ru/users/nlacina/profile» target=»_blank» > 
touch.otvet.mail.ru
Ответы@Mail.Ru: Помогите решить уравнение : 5cos(квадрат) х+6sinx-6=0
Косинус в квадрате заменить на 1-sin^2. Далее заменить синус на t Решить квадратное уравнение относительно t. вернутся к тому, что sinx=t, решить простейшее тригонометрическое уравнение.
косинус в квадрате выразите через синус в квадрате а дальше проще репы пареной!
5*cos²(x)=5-5*sin²(x) Подставляешь это в уравнение — получаешь квадратное уравнение относительно sin(x).
5(1-(sinx)^2)+6sinx-6=0 => 5(sinx)^2-6sinx+1=0. sinx=1 или sinx=1/5.
touch.otvet.mail.ru

Leave A Comment