Косинус квадрат и синус квадрат
Разбираемся с простыми понятиями: синус и косинус и вычисление косинуса в квадрате и синуса в квадрате.
Синус и косинус изучаются в тригонометрии (науке о треугольниках с прямым углом).
Поэтому для начала вспомним основные понятия прямоугольного треугольника:
Гипотенуза — сторона, которая всегда лежит напротив прямого угла (угла в 90 градусов). Гипотенуза — это самая длинная сторона треугольника с прямым углом.
Оставшиеся две стороны в прямоугольном треугольнике называются катетами.
Также следует помнить, что три угла в треугольнике всегда имеют сумму в 180°.
Теперь переходим к косинусу и синусу угла альфа (∠α) (так можно назвать любой непрямой угол в треугольнике или использовать в качестве обозначение икс — «x», что не меняет сути).
Синус угла альфа (sin ∠α)
Косинус угла альфа (cos ∠α) — отношение прилежащего к углу катета к гипотенузе. Если снова смотреть по рисунку выше, то cos ∠ABC = AB / BC
И просто для напоминания: косинус и синус никогда не будут больше единицы, так как любой катит короче гипотенузы (а гипотенуза — это самая длинная сторона любого треугольника, ведь самая длинная сторона расположена напротив самого большого угла в треугольнике).
Косинус в квадрате, синус в квадрате
Теперь переходим к основным тригонометрическим формулам: вычисление косинуса в квадрате и синуса в квадрате.
Для их вычисления следует запомнить основное тригонометрическое тождество:
sin2α + cos2α = 1 (синус квадрат плюс косинус квадрат одного угла всегда равняются единице).
Из тригонометрического тождества делаем выводы о синусе:
sin2α = 1 — cos2α
или более сложный вариант формулы: синус квадрат альфа равен единице минус косинус двойного угла альфа и всё это делить на два.
sin2α = (1 – cos(2α)) / 2
Из тригонометрического тождества делаем выводы о косинусе:
cos2α = 1 — sin2
или более сложный вариант формулы: косинус квадрат альфа равен единице плюс косинус двойного угла альфа и также делим всё на два.
cos2α = (1 + cos(2α)) / 2
Эти две более сложные формулы синуса в квадрате и косинуса в квадрате называют еще «понижение степени для квадратов тригонометрических функций». Т.е. была вторая степень, понизили до первой и вычисления стали удобнее.
Редактировать этот урок и/или добавить задание Добавить свой урок и/или заданиеДобавить интересную новость
Все формулы (уравнения) тригонометрии : sin(x) cos(x) tg(x) ctg(x)
Уравнения разложения тригонометрических функций:квадрат синус альфа, косинус альфа, тангенс альфа, котангенс альфа.




Формулы преобразования функций двойного угла (2α) в выражение через одинарный угол (α)
sin(2α)- через sin и cos:

sin(2α)- через tg и ctg:


cos(2α)- через tg и ctg:

tg(2α) и сtg(2α):

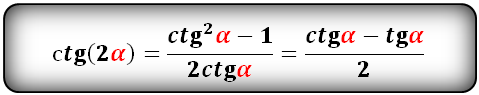
Формулы преобразования функций (синус, косинус, тангенс, котангенс), тройного угла (3α) в выражение через одинарный угол (α):




Тригонометрические формулы преобразования разности аргументов





sin(α)=OA
cos(α)=OC
tg(α)=DE
ctg(α)=MK
R=OB=1
Значения функций для некоторых углов, α

В таблице показаны формулы приведения для тригонометрических функций (sin, cos, tg, ctg).

Косинус в квадрате, формула и примеры
ОПРЕДЕЛЕНИЕ Квадрат косинуса можно выразить следующим образом
Эта формула называется формулой понижения степени косинуса.
Примеры решения задач
ПРИМЕР 2| Задание | Упростить выражение
|
| Решение | Упростим выражение с помощью формулы квадрата косинуса:
Преобразуем каждый из членов разности следующим образом:
и
Тогда
Полученное выражение представляет собой правую часть формулы произведения синусов, т.е.
|
| Ответ |
| Понравился сайт? Расскажи друзьям! | |||
| 01) | Основные тригонометрические тождества | |
| 01.1) | Основное тригонометрическое тождество | формула основного тригонометрического тождества |
| 01.2) | Основное тождество через тангенс и косинус | формула основного тождества через тангенс и косинус |
| 01.3) | Основное тождество через котангенс и синус | формула основного тождества через котангенс и синус |
| 01.4) | Соотношение между тангенсом и котангенсом | формула соотношения между тангенсом и котангенсом |
| 02) | Формулы двойного аргумента (угла) | |
| 02.1) | Синус двойного угла | формула синуса двойного угла |
| 02.2) | формула синуса двойного угла | |
| 02.3) | Косинус двойного угла | формула синуса двойного угла |
| 02.4) | формула синуса двойного угла | |
| 02.5) | Тангенс двойного угла | формула синуса двойного угла |
| 02.6) | Котангенс двойного угла | формула синуса двойного угла |
| 03) | Формулы тройного аргумента (угла) | |
| 03.1) | Синус тройного угла | формула синуса тройного угла |
| 03.2) | Косинус тройного угла | формула косинуса тройного угла |
| 03.3) | Тангенс тройного угла | формула тангенса тройного угла |
| 03.4) | Котангенс тройного угла | формула котангенса тройного угла |
| 04) | Формулы половинного аргумента (угла) | |
| 04.1) | Синус половинного угла | формула синуса половинного угла |
| 04.2) | Косинус половинного угла | формула косинуса половинного угла |
| 04.3) | Тангенс половинного угла | формула тангенса половинного угла |
| 04.4) | Котангенс половинного угла | формула котангенса половинного угла |
| 04.5) | Тангенс половинного угла | формула тангенса половинного угла |
| 04.6) | Котангенс половинного угла | формула котангенса половинного угла |
| 05) | Формулы квадратов тригонометрических функций | |
| 05.1) | Квадрат синуса | формула квадрата синуса |
| 05.2) | Квадрат косинуса | формула квадрата косинуса |
| 05.3) | Квадрат тангенса | формула квадрата тангенса |
| 05.4) | Квадрат котангенса | формула квадрата котангенса |
| 05.5) | Квадрат синуса половинного угла | формула квадрата синуса половинного угла |
| 05.6) | Квадрат косинуса половинного угла | формула квадрата косинуса половинного угла |
| 05.7) | Квадрат тангенса половинного угла | формула квадрата тангенса половинного угла |
| 05.8) | Формулы кубов тригонометрических функций | формула квадрата котангенса половинного угла |
| 06) | Формулы кубов тригонометрических функций | |
| 06.1) | Куб синуса | формула куба синуса |
| 06.2) | Куб косинуса | формула куба косинуса |
| 06.3) | Куб тангенса | формула куба тангенса |
| 06.4) | Куб котангенса | формула куба котангенса |
| 07) | Формулы тригонометрических функций в четвертой степени | |
| 07.1) | Четвертая степень синуса | формула четвертой степени синуса |
| 07.2) | Четвертая степень косинуса | формула четвертой степени косинуса |
| 08) | Формулы сложения и вычитания аргументов | |
| 08.1) | Сложение аргументов синуса | формула сложения аргументов синуса |
| 08.2) | Сложение аргументов косинуса | формула сложения аргументов косинуса |
| 08.3) | Сложение аргументов тангенса | формула сложения аргументов тангенса |
| 08.4) | Сложение аргументов котангенса | формула сложения аргументов котангенса |
| 08.5) | Вычитание аргументов синуса | формула вычитания аргументов синуса |
| 08.6) | Вычитание аргументов косинуса | формула вычитания аргументов косинуса |
| 08.7) | Вычитание аргументов тангенса | формула вычитания аргументов тангенса |
| 08.8) | Вычитание аргументов котангенса | формула вычитания аргументов котангенса |
| 09) | Формулы суммы тригонометрических функций | |
| 09.1) | Сумма синусов | формула суммы синусов |
| 09.2) | Сумма косинусов | формула суммы косинусов |
| 09.3) | Сумма тангенсов | формула суммы тангенсов |
| 09.4) | Сумма котангенсов | формула суммы котангенсов |
| 09.5) | Сумма синуса и косинуса | формула суммы синуса и косинуса |
| 10) | Формулы разности тригонометрических функций | |
| 10.1) | Разность синусов | формула разности суммы синусов |
| 10.2) | Разность косинусов | формула разности суммы косинусов |
| 10.3) | Разность тангенсов | формула разности суммы тангенсов |
| 10.4) | Разность котангенсов | формула разности котангенсов |
| 10.5) | Разность синуса и косинуса | формула разности синуса и косинуса |
| 11) | Формулы произведения тригонометрических функций | |
| 11.1) | Произведение синусов | формула произведения синусов |
| 11.2) | Произведение косинусов | формула произведения косинусов |
| 11.3) | Произведение синуса и косинуса | формула произведения синуса и косинуса |
| 11.4) | Произведение тангенсов | формула произведения тангенсов |
| 11.5) | Произведение котангенсов | формула произведения котангенсов |
| 11.6) | Произведение тангенса и котангенса | формула произведения тангенса и котангенса |
| 12) | Формулы понижения степени | |
| 12.1) | Понижение степени синуса | формула понижения степени синуса |
| 12.2) | Понижение степени косинуса | формула понижение степени косинуса |
| 13) | Формулы суммы и разности разных тригонометрических функций | |
| 13.1) | Сумма синуса и косинуса | формула суммы синуса и косинуса |
| 13.2) | Разность синуса и косинуса | формула разности синуса и косинуса |
| 13.3) | Сумма синуса и косинуса с коэффициентами | формула суммы синуса и косинуса с коэффициентами |
| 13.4) | Разность синуса и косинуса с коэффициентами | формула разности синуса и косинуса с коэффициентами |
| 14) | Формулы общего вида | |
| 14.1) | Формула понижения nй четной степени синуса | формула формулы формулы понижения n четной степени синуса |
| 14.2) | Формула понижения nй четной степени косинуса | формула формулы понижения nй четной степени косинуса |
| 14.3) | Формула понижения nй нечетной степени синуса | формула формулы понижения nй нечетной степени синуса |
| 14.4) | Формула понижения nй нечетной степени косинуса | формула формулы понижения nй нечетной степени косинуса |
Основные формулы — Тригонометрия
Формулы тригонометрических функций суммы углов.




Формулы тригонометрических функций разницы углов.




Формулы тригонометрических функций двойного
sin(2α)- через sin и cos:

sin(2α)- через tg и ctg:

cos(2α)- через sin и cos:

cos(2α)- через tg и ctg:

tg(2α) и сtg(2α):

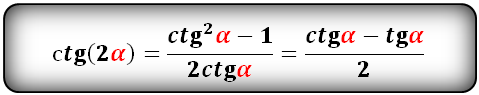
Формулы тригонометрических функций тройного угла




Синус, косинус, тангенс, котангенс половинного угла




Основные формулы тригонометрии | umath.ru
1. Определения синуса, косинуса, тангенса и котангенса угла.
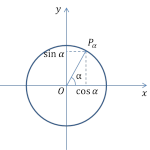 Синус угла
Синус угла  (обозначается
(обозначается 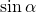 ) – ордината точки
) – ордината точки 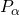 , полученной поворотом точки
, полученной поворотом точки 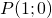 вокруг начала координат на угол
вокруг начала координат на угол 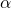 .
.
Косинус угла 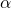 (обозначается
(обозначается 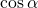 ) – абсцисса точки
) – абсцисса точки 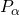 , полученной поворотом точки
, полученной поворотом точки 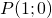 вокруг начала координат на угол
вокруг начала координат на угол 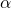 .
.
Тангенс угла 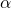 (обозначается
(обозначается 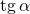 ) – отношение синуса угла
) – отношение синуса угла 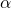 к его косинусу, т.е.
к его косинусу, т.е.
Котангенс угла
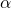 (обозначается
(обозначается 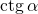 ) – отношение косинуса угла
) – отношение косинуса угла 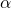 к его синусу, т.е.
к его синусу, т.е. 2. Основное тригонометрическое тождество:
3. Зависимость между синусом, косинусом, тангенсом и котангенсом:
4. Чётность, нечётность и периодичность тригонометрических функций.
Косинус – чётная функция, а синус, тангенс и котангенс – нечётные функции аргумента 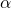 :
:
Синус и косинус – периодические с периодом 2\pi функции, а тангенс и котангенс – периодические с периодом
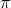 функции:
Число
функции:
Число 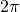 является наименьшим положительным периодом синуса и косинуса, а число
является наименьшим положительным периодом синуса и косинуса, а число 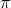 – наименьшим положительным периодом тангенса и котангенса.
– наименьшим положительным периодом тангенса и котангенса.Для любого целого
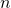 справедливы равенства
справедливы равенства 5. Формулы сложения:
6. Формулы двойного и тройного аргумента:
7. Формулы понижения степени:
8. Формулы приведения:
9. Формулы суммы и разности синусов:
10. Формулы суммы и разности косинусов:
11. Формулы суммы и разности тангенсов:
12. Преобразование произведения синусов и косинусов в сумму (разность):
13. Выражение синуса и косинуса через тангенс половинного аргумента:
Все формулы по тригонометрии
Все формулы по тригонометрии
Подождите пару секунд пока подгрузятся формулы
Основные тригонометрические тождества
$$sin^2x+cos^2x=1$$$$tgx= \frac{sinx}{cosx}$$
$$ctgx= \frac{cosx}{sinx}$$
$$tgxctgx=1$$
$$tg^2x+1= \frac{1}{cos^2x}$$
$$ctg^2x+1= \frac{1}{sin^2x}$$
Формулы двойного аргумента (угла)
$$sin2x=2cosxsinx$$\begin{align} sin2x &=\frac{2tgx}{1+tg^2x}\\ &= \frac{2ctgx}{1+ctg^2x}\\ &= \frac{2}{tgx+ctgx} \end{align}
\begin{align} cos2x & = \cos^2x-sin^2x\\ &= 2cos^2x-1\\ &= 1-2sin^2x \end{align}
\begin{align} cos2x & = \frac{1-tg^2x}{1+tg^2x}\\ &= \frac{ctg^2x-1}{ctg^2x+1}\\ &= \frac{ctgx-tgx}{ctgx+tgx} \end{align}
\begin{align} tg2x & = \frac{2tgx}{1-tg^2x}\\ &= \frac{2ctgx}{ctg^2x-1}\\ &= \frac{2}{ctgx-tgx} \end{align}
\begin{align} ctg2x & = \frac{ctg^2x-1}{2ctgx}\\ &= \frac{2ctgx}{ctg^2x-1}\\ &= \frac{ctgx-tgx}{2} \end{align}
Формулы тройного аргумента (угла)
$$sin3x=3sinx-4sin^3x$$$$cos3x=4cos^3x-3cosx$$
$$tg3x= \frac{3tgx-tg^3x}{1-3tg^2x}$$
$$ctg3x= \frac{ctg^3x-3ctgx}{3ctg^2x-1}$$
Формулы половинного аргумента (угла)
$$sin^2 \frac{x}{2}= \frac{1-cosx}{2}$$$$cos^2 \frac{x}{2}= \frac{1+cosx}{2}$$
$$tg^2 \frac{x}{2}= \frac{1-cosx}{1+cosx}$$
$$ctg^2 \frac{x}{2}= \frac{1+cosx}{1-cosx}$$
\begin{align} tg \frac{x}{2} & = \frac{1-cosx}{sinx}\\ &= \frac{sinx}{1+cosx} \end{align}
\begin{align} ctg \frac{x}{2} & = \frac{1+cosx}{sinx}\\ &= \frac{sinx}{1-cosx} \end{align}
Формулы квадратов тригонометрических функций
$$sin^2x= \frac{1-cos2x}{2}$$$$cos^2x= \frac{1+cos2x}{2}$$
$$tg^2x= \frac{1-cos2x}{1+cos2x}$$
$$ctg^2x= \frac{1+cos2x}{1-cos2x}$$
$$sin^2 \frac{x}{2}= \frac{1-cosx}{2}$$
$$cos^2 \frac{x}{2}= \frac{1+cosx}{2}$$
$$tg^2 \frac{x}{2}= \frac{1-cosx}{1+cosx}$$
$$ctg^2 \frac{x}{2}= \frac{1+cosx}{1-cosx}$$
Формулы кубов тригонометрических функций
$$sin^3x= \frac{3sinx-sin3x}{4}$$$$cos^3x= \frac{3cosx+cos3x}{4}$$
$$tg^3x= \frac{3sinx-sin3x}{3cosx+cos3x}$$
$$ctg^3x= \frac{3cosx+cos3x}{3sinx-sin3x}$$
Формулы тригонометрических функций в четвертой степени
$$sin^4x= \frac{3-4cos2x+cos4x}{8}$$$$cos^4x= \frac{3+4cos2x+cos4x}{8}$$
Формулы сложения аргументов
$$sin(\alpha + \beta) = sin \alpha cos \beta + cos \alpha sin \beta$$$$cos(\alpha + \beta) = cos \alpha cos \beta — sin \alpha sin \beta$$
$$tg(\alpha + \beta)= \frac{tg \alpha + tg \beta}{1 — tg \alpha tg \beta}$$
$$ctg(\alpha + \beta)= \frac{ctg \alpha ctg \beta -1}{ctg \alpha + ctg \beta}$$
$$sin(\alpha — \beta) = sin \alpha cos \beta — cos \alpha sin \beta$$
$$cos(\alpha — \beta) = cos \alpha cos \beta + sin \alpha sin \beta$$
$$tg(\alpha — \beta)= \frac{tg \alpha — tg \beta}{1 + tg \alpha tg \beta}$$
$$ctg(\alpha — \beta)= \frac{ctg \alpha ctg \beta +1}{ctg \alpha — ctg \beta}$$
Формулы суммы тригонометрических функций
$$sin\alpha + sin\beta = 2sin \frac{\alpha + \beta }{2} \cdot cos \frac{\alpha — \beta }{2}$$$$cos\alpha + cos\beta = 2cos \frac{\alpha + \beta }{2} \cdot cos \frac{\alpha — \beta }{2}$$
$$tg\alpha + tg\beta = \frac{sin(\alpha + \beta) }{cos \alpha cos \beta}$$
$$ctg\alpha + ctg\beta = \frac{sin(\alpha + \beta) }{cos \alpha cos \beta}$$
$$(sin\alpha + cos\alpha)^2= 1+sin2\alpha$$
Формулы разности тригонометрических функций
$$sin\alpha — sin\beta = 2sin \frac{\alpha — \beta }{2} \cdot cos \frac{\alpha + \beta }{2}$$$$cos\alpha — cos\beta = -2sin \frac{\alpha + \beta }{2} \cdot sin \frac{\alpha — \beta }{2}$$
$$tg\alpha — tg\beta = \frac{sin(\alpha — \beta) }{cos \alpha cos \beta}$$
$$ctg\alpha — ctg\beta = — \frac{sin(\alpha — \beta) }{sin \alpha sin \beta}$$
$$(sin\alpha + cos\alpha)^2= 1-sin2\alpha$$
Формулы произведения тригонометрических функций
$$sin\alpha \cdot sin\beta = \frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{2}$$$$sin\alpha \cdot cos\beta = \frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{2}$$
$$cos\alpha \cdot cos\beta = \frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{2}$$
\begin{align} tg\alpha \cdot tg\beta & = \frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{cos(\alpha — \beta)+cos(\alpha + \beta)}\\ &= \frac{tg\alpha + tg\beta}{ctg\alpha + ctg\beta} \end{align}
\begin{align} ctg\alpha \cdot ctg\beta & = \frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{cos(\alpha — \beta)-cos(\alpha + \beta)}\\ &= \frac{ctg\alpha + ctg\beta}{tg\alpha + tg\beta} \end{align}
$$tg\alpha \cdot ctg\beta = \frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{sin(\alpha + \beta)-sin(\alpha — \beta)}$$
Функция «Косинус-квадрат» — исчисление
Эта статья посвящена конкретной функции от подмножества действительных чисел до действительных чисел. Информация о функции, включая ее домен, диапазон и ключевые данные, касающиеся построения графиков, дифференциации и интеграции, представлена в статье.
Посмотреть полный список конкретных функций в этой вики
Для функций, включающих углы (тригонометрические функции, обратные тригонометрические функции и т. Д.), Мы следуем соглашению, согласно которому все углы измеряются в радианах.Так, например, уголизмеряется как
.
Определение
Эта функция, обозначенная как 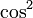 , определяется как сочетание функции квадрата и функции косинуса. Явно это карта:
, определяется как сочетание функции квадрата и функции косинуса. Явно это карта:
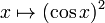
Для краткости запишем 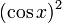 как
как 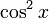 .
.
Основные данные
| Товар | Значение |
|---|---|
| Домен по умолчанию | все числа действительные, т.е. все 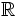 . . |
| диапазон | ![[0,1]](/800/600/https/calculus.subwiki.org/w/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) , т. Е. , т. Е. 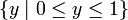 . . |
| период |  , т.е. , т.е.  . . |
| локальные максимальные значения и точки достижения | Все локальные максимальные значения равны 1 и достигаются при целых кратных  . . |
| местные минимальные значения и точки достижения | Все локальные минимальные значения равны 0 и достигаются при нечетных целых числах, кратных 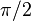 . . |
| точка перегиба (обе координаты) | нечетное число, кратное 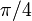 , со значением , со значением 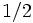 в каждой точке в каждой точке |
| производная | 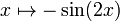 то есть отрицательная функция синусоиды двойного угла. то есть отрицательная функция синусоиды двойного угла. |
| вторая производная | 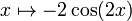 |
| высшие производные | 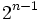 раз выражение, которое равно раз выражение, которое равно 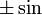 или или  из из  , в зависимости от остатка от , в зависимости от остатка от 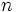 mod 4. mod 4. |
| первообразное |  |
| среднее значение за период | 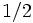 |
| выражение как синусоидальная функция плюс постоянная функция | 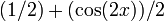 |
| важные симметрии | даже функция В более общем смысле, имеет зеркальную симметрию относительно всех вертикальных линий 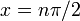 , , 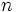 — целое число. — целое число. Также имеет симметрию полуоборота относительно всех точек формы 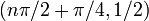 , т.е.е., все точки перегиба. , т.е.е., все точки перегиба. |
| на основе увеличения / уменьшения и вогнутости вверх / вниз | Для каждого целого числа 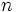 интервал от интервал от 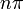 до до 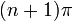 разделен на четыре части: разделен на четыре части: 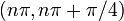 : убывающая и вогнутая вниз : убывающая и вогнутая вниз 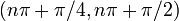 : убывающая и вогнутая вверх : убывающая и вогнутая вверх 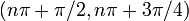 : увеличивающаяся и вогнутая вверх : увеличивающаяся и вогнутая вверх 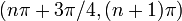 : увеличивающаяся и вогнутая вниз. : увеличивающаяся и вогнутая вниз. |
\ [\ frac {{dy}} {{dx}} = \ mathop {\ lim} \ limits _ {\ Delta x \ to 0} \ frac {{ \ left [{\ cos \ left ({x + \ Delta x} \ right) + \ cos x} \ right] \ left [{\ cos \ left ({x + \ Delta x} \ right) — \ cos x } \ right]}} {{\ Delta x}} \]
По формуле из тригонометрии \ [\ cos A — \ cos B = — 2 \ sin \ left ({\ frac {{A + B}} {2}} \ right) \ sin \ left ({\ frac {{ A — B}} {2}} \ right) \]
\ [\ begin {gather} \ frac {{dy}} {{dx}} = \ mathop {\ lim} \ limits _ {\ Delta x \ to 0 } \ frac {{\ left [{\ cos \ left ({x + \ Delta x} \ right) + \ cos x} \ right] \ left [{- 2 \ sin \ left ({\ frac {{x + \ Delta x + x}} {2}} \ right) \ sin \ left ({\ frac {{x + \ Delta x — x}} {2}} \ right)} \ right]}} {{\ Delta x}} \\ \ Rightarrow \ frac {{dy}} {{dx}} = \ mathop {\ lim} \ limits _ {\ Delta x \ to 0} \ left [{\ cos \ left ({x + \ Delta x} \ right) + \ cos x} \ right] \ times — \ frac {{\ sin \ left ({\ frac {{2x + \ Delta x}} {2}} \ right) \ sin \ left ({ \ frac {{\ Delta x}} {2}} \ right)}} {{\ frac {{\ Delta x}} {2}}} \\ \ Rightarrow \ frac {{dy}} {{dx}} = \ mathop {\ lim} \ limits _ {\ Delta x \ to 0} \ left [{\ cos \ left ({x + \ Delta x} \ right) + \ cos x} \ right] \ times — \ mathop { \ lim} \ limits _ {\ Delta x \ to 0} \ sin \ left ({\ frac {{2x + \ Delta x}} {2}} \ right) \ mathop {\ lim} \ limits _ {\ Delta x \ в 0} \ frac {{\ sin \ left ({\ frac { {\ Delta x}} {2}} \ right)}} {{\ frac {{\ Delta x}} {2}}} \\ \ Rightarrow \ frac {{dy}} {{dx}} = — \ left [{\ cos \ left ({x + 0} \ right) + \ cos x} \ right] \ sin \ left ({\ frac {{2x + 0}} {2}} \ right) \ left (1 \ right) \\ \ Rightarrow \ frac {{dy}} {{dx}} = — 2 \ cos x \ sin x \\ \ end {gather} \]
Пример : Найдите производную от \ [y = f \ left (x \ right) = {\ cos ^ 2} \ left ({{x ^ 2} + 8} \ right) \]
У нас есть заданная функция как
\ [y = {\ cos ^ 2} \ left ({{x ^ 2} + 8} \ right) \]
Дифференцируя по переменной $$ x $$, получаем
\ [\ frac {{dy}} {{dx}} = \ frac {d} {{dx}} {\ cos ^ 2} \ left ({ {x ^ 2} + 8} \ right) \]
Используя правило $$ \ frac {d} {{dx}} {\ cos ^ 2} x = — 2 \ cos x \ sin x $$, получаем
\ [\ begin {gather} \ frac {{dy }} {{dx}} = 2 \ cos \ left ({{x ^ 2} + 8} \ right) \ frac {d} {{dx}} \ cos \ left ({{x ^ 2} + 8} \ right) \\ \ frac {{dy}} {{dx}} = — 2 \ cos \ left ({{x ^ 2} + 8} \ right) \ sin \ left ({{x ^ 2} + 8 } \ right) \ frac {d} {{dx}} \ left ({{x ^ 2} + 8} \ right) \\ \ frac {{dy}} {{dx}} = — 2 \ cos \ left ({{x ^ 2} + 8} \ right) \ sin \ left ({{x ^ 2} + 8} \ right) \ left ({2x + 0} \ right) \\ \ frac {{dy}} {{dx}} = — 4x \ cos \ left ({{x ^ 2} + 8} \ right) \ sin \ left ({{x ^ 2} + 8} \ right) \\ \ end {собрано} \ ]
Функция синус-квадрат — исчисление
Эта статья посвящена конкретной функции от подмножества действительных чисел до действительных чисел. Информация о функции, включая ее домен, диапазон и ключевые данные, касающиеся построения графиков, дифференциации и интеграции, представлена в статье.
Посмотреть полный список конкретных функций в этой вики
Определение
Эта функция, обозначенная как  , определяется как сочетание функции квадрата и функции синуса.Явно это карта:
, определяется как сочетание функции квадрата и функции синуса.Явно это карта:
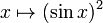
Для краткости запишем 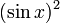 как
как 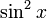 .
.
Ключевые данные
| Товар | Значение |
|---|---|
| Домен по умолчанию | все числа действительные, т.е. все 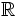 |
| диапазон | ![[0,1]](/800/600/https/calculus.subwiki.org/w/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) , т.е. , т.е. 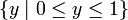 абсолютное максимальное значение: 1, абсолютное минимальное значение: 0 |
| период |  , т.е. , т.е.  |
| локальное максимальное значение и точки достижения | Все локальные максимальные значения равны 1 и достигаются при нечетных целых числах, кратных 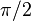 . . |
| местное минимальное значение и точки достижения | Все локальные минимальные значения равны 0 и достигаются при целых кратных  . . |
| точек перегиба (обе координаты) | нечетных кратных 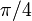 , со значением 1/2 в каждой точке. , со значением 1/2 в каждой точке. |
| производная | 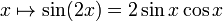 , т. Е. Двухугловая синусоидальная функция. , т. Е. Двухугловая синусоидальная функция. |
| вторая производная | 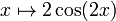 |
 производная производная | 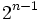 раз выражение, которое равно раз выражение, которое равно 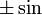 или или  из из  , в зависимости от остатка от , в зависимости от остатка от 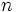 mod mod 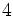 |
| первообразное |  |
| среднее значение за период | 1/2 |
| выражение как синусоидальная функция плюс постоянная функция | 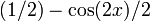 |
| важные симметрии | четная функция (следует из комбинации четной функции с нечетной функцией, четной функцией квадрата и нечетной функцией синуса) в более общем смысле зеркальной симметрией относительно любой вертикальной линии формы 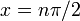 , , 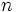 целое число. целое число.Кроме того, симметрия на пол-оборота относительно всех точек формы 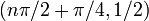 . . |
| на основе увеличения / уменьшения и вогнутости вверх / вниз | Для каждого целого числа 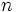 интервал от интервал от 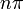 до до 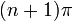 разделен на четыре части: разделен на четыре части: 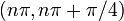 : увеличивающийся и вогнутый вверх : увеличивающийся и вогнутый вверх 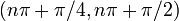 : увеличивающийся и вогнутый вниз : увеличивающийся и вогнутый вниз 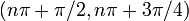 : уменьшающийся и вогнутый вниз, : уменьшающийся и вогнутый вниз,  : уменьшающийся и вогнутый вверх : уменьшающийся и вогнутый вверх |
| степенная серия и серия Тейлора | Степенный ряд около 0 (который, следовательно, также является рядом Тейлора): 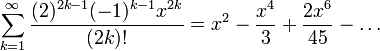 Это глобально сходящийся степенной ряд. |
Личности
У нас есть следующие важные личности, связанные с  :
:
График
Вот график на интервале ![[-2\pi,2\pi]](/800/600/https/calculus.subwiki.org/w/images/math/f/c/d/fcd3f9b324e7bfa715240a4c3fb40b9a.png) в масштабе:
в масштабе:

Вот увеличенный вид графика между 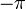 и
и  . Пунктирная горизонтальная линия показывает среднее значение
. Пунктирная горизонтальная линия показывает среднее значение 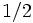 :
:
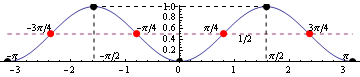
Красные точки указывают точки перегиба, а черные точки указывают локальные экстремальные значения.
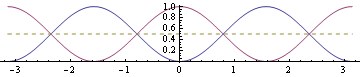
Вот изображение, показывающее функцию (синий) и функцию косинуса-квадрата (фиолетовый) с пунктирной линией 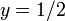 . На рисунке показано, что
. На рисунке показано, что 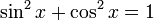 :
:
Дифференциация
Первая производная
ЧТО МЫ ИСПОЛЬЗУЕМ : цепное правило для дифференцирования, правило дифференцирования для степенных функций, функция синуса # Первая производная, формула двойного углового косинуса
У нас есть:
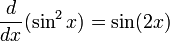
Это можно сделать двумя способами.
Используя цепное правило дифференциации, мы имеем:
![\! \frac{d}{dx}[(\sin x)^2] = 2\sin x \frac{d}{dx} (\sin x) = 2\sin x \cos x](/800/600/https/calculus.subwiki.org/w/images/math/2/b/2/2b2cc43fe01f388596699dd016369c93.png)
По формуле синуса двойного угла это то же самое, что 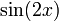 .
.
В качестве альтернативы, используя формулу двойного углового косинуса, мы перепишем:
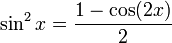
Различая, получаем:
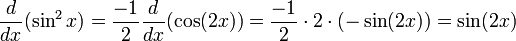
Вторая производная
Снова дифференцируя производную, получаем:
![\frac{d^2}{dx^2}(\sin^2x) = \frac{d}{dx}[\sin(2x)] = \frac{d}{d(2x)}[\sin(2x)]\frac{d(2x)}{dx} = 2\cos(2x)](/800/600/https/calculus.subwiki.org/w/images/math/d/e/e/deec58ad406891f9ceb48cb74697b6ca.png)
График функции с производной
Заполните позже
Точки и интервалы интереса
Критические точки
Рассмотрим 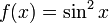 .Как было вычислено ранее, мы имеем:
.Как было вычислено ранее, мы имеем:
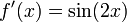
Это равно нулю точно в точках  , где
, где 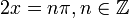 , поэтому
, поэтому 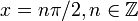 . Другими словами, критические точки возникают при целых кратных
. Другими словами, критические точки возникают при целых кратных 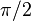 .
.
Интервалы увеличения и уменьшения
Функция 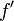 положительна для
положительна для 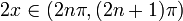 с
с  и отрицательна для
и отрицательна для 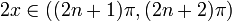 с
с  . Разделив на 2, получаем:
. Разделив на 2, получаем:
Локальные экстремальные значения
Из информации об интервалах увеличения и уменьшения делаем вывод, что:
Интервалы вогнутости вверх и вогнутости вниз
Вторая производная 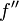 — это функция
— это функция 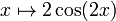 .Это положительный результат для
.Это положительный результат для  и отрицательный для
и отрицательный для 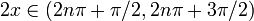 , где
, где  . Таким образом получаем:
. Таким образом получаем:
Точки перегиба
Из определения интервалов, в которых 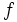 является вогнутым вверх и вогнутым вниз, мы обнаруживаем, что точки перегиба — это точки с координатой
является вогнутым вверх и вогнутым вниз, мы обнаруживаем, что точки перегиба — это точки с координатой  , нечетной кратной
, нечетной кратной 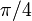 . Значение функции во всех этих точках —
. Значение функции во всех этих точках — 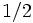 .
.
- В точках с
 функция переходит от вогнутости вверх (слева) к вогнутости вниз (справа).
функция переходит от вогнутости вверх (слева) к вогнутости вниз (справа). - В точках с
 функция переходит от вогнутости вниз (слева) к вогнутости вверх (справа).
функция переходит от вогнутости вниз (слева) к вогнутости вверх (справа).
Интеграция
Первая первообразная
ЧТО МЫ ИСПОЛЬЗУЕМ : формула двойного углового косинуса, рекурсивная версия интегрирования по частям, интегрирование линейного преобразования функции
Использование формулы косинуса двойного угла
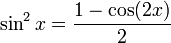
Теперь мы можем выполнить интеграцию:

Чтобы интегрировать 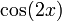 , мы используем метод интегрирования линейного преобразования функции, чтобы получить
, мы используем метод интегрирования линейного преобразования функции, чтобы получить 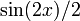 .Подключив это, мы получаем:
.Подключив это, мы получаем:
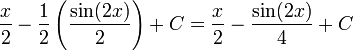
Использование интеграции по частям
Переписываем 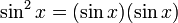 и используем интегрирование по частям в его рекурсивной версии:
и используем интегрирование по частям в его рекурсивной версии:
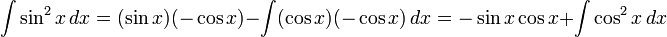
Теперь перепишем  и получим:
и получим:
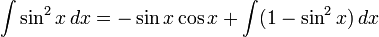
Установив  как выбор первообразной, так что вышеупомянутое выполняется без каких-либо свободно плавающих констант, мы получаем:
как выбор первообразной, так что вышеупомянутое выполняется без каких-либо свободно плавающих констант, мы получаем:

Переставляя, получаем:
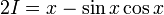
Это дает:
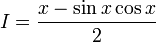
Итак, общая первообразная:
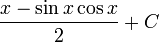
Используя формулу синуса с двойным углом 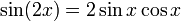 , мы можем убедиться, что это соответствует предыдущему ответу.
, мы можем убедиться, что это соответствует предыдущему ответу.
Для данной непрерывной функции на связном множестве первообразные, полученные разными методами, должны отличаться на константу . В некоторых случаях первообразные могут быть в точности равными, но это , обычно не обязательно .
См. Нулевую производную подразумевает локальную константу
График функции с первообразной
На рисунке ниже мы изображаем  (синий) и функцию
(синий) и функцию 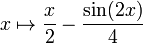 (фиолетовый). Это уникальная первообразная, которая принимает значение 0 на 0.Остальные первообразные можно получить, сдвинув пурпурный график по вертикали:
(фиолетовый). Это уникальная первообразная, которая принимает значение 0 на 0.Остальные первообразные можно получить, сдвинув пурпурный график по вертикали:
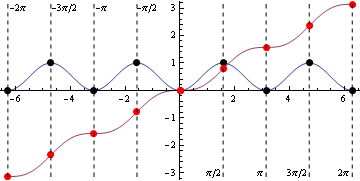
Черные точки соответствуют локальным экстремальным значениям для  , а красные точки соответствуют точкам перегиба первообразной. Каждая черная точка находится на той же вертикальной линии, что и красная точка, как и следовало ожидать, потому что точки перегиба первообразной соответствуют локальным экстремальным значениям исходной функции. Дальше:
, а красные точки соответствуют точкам перегиба первообразной. Каждая черная точка находится на той же вертикальной линии, что и красная точка, как и следовало ожидать, потому что точки перегиба первообразной соответствуют локальным экстремальным значениям исходной функции. Дальше:
Определенные интегралы
Часть 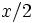 в первообразной означает, что линейная часть первообразной
в первообразной означает, что линейная часть первообразной  имеет наклон
имеет наклон 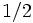 , и это связано с тем фактом, что
, и это связано с тем фактом, что  имеет среднее значение
имеет среднее значение 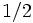 на любом интервале длины, равной периоду.Фактически ясно, что функция является синусоидальной функцией около
на любом интервале длины, равной периоду.Фактически ясно, что функция является синусоидальной функцией около 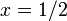 .
.
Таким образом, имеем:
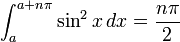
, где 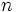 — целое число.
— целое число.
Среднее значение из  на интервале длины, кратной периоду, равно
на интервале длины, кратной периоду, равно 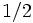 . Таким образом, для очень больших интервалов среднее значение
. Таким образом, для очень больших интервалов среднее значение  очень близко к 1/2, даже если оно не обязательно должно быть точно 1/2. В частности:
очень близко к 1/2, даже если оно не обязательно должно быть точно 1/2. В частности:
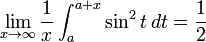
Преобразованные версии
На основе интегрирования  мы также можем интегрировать квадрат любой синусоидальной функции, используя интегрирование линейного преобразования функции:
мы также можем интегрировать квадрат любой синусоидальной функции, используя интегрирование линейного преобразования функции:

Таким образом, мы видим, что среднее значение этой функции также равно 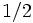 на любом интервале длины, кратной периоду
на любом интервале длины, кратной периоду  .Кроме того, на достаточно большом интервале среднее значение близко к 1/2:
.Кроме того, на достаточно большом интервале среднее значение близко к 1/2:
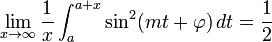
Высшие первообразные
Антидифференцировать  можно более одного раза. Первообразная
можно более одного раза. Первообразная  представляет собой сумму полинома степени
представляет собой сумму полинома степени 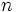 и тригонометрической функции с периодом
и тригонометрической функции с периодом  .
.
Power и серия Тейлора
Вычисление степенного ряда
Мы можем использовать удостоверение личности:
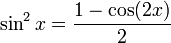
вместе со степенным рядом для функции косинуса, чтобы найти степенной ряд для  .
.
Степенный ряд для функции косинуса везде сходится к функции и равен:

Ряд мощности для 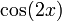 :
:
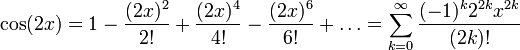
Ряд мощности для 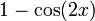 :
:

Разделив на 2, получим степенной ряд для 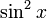 :
:

Вот еще одна формулировка, в которой первые несколько терминов написаны более четко:
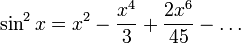
Полиномы Тейлора как приближения
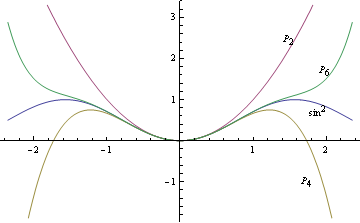
Обратите внимание, что, поскольку  — четная функция, все ее многочлены Тейлора также являются четными многочленами.На рисунке ниже мы рассматриваем графики
— четная функция, все ее многочлены Тейлора также являются четными многочленами.На рисунке ниже мы рассматриваем графики  и его второго, четвертого и шестого тейлоровских приближений.
и его второго, четвертого и шестого тейлоровских приближений.
Предельные вычисления
Порядок нуля
Мы получаем следующий предел из степенного ряда:
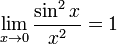
Таким образом, порядок нуля  в нуле равен 2, а остаток равен 1.
в нуле равен 2, а остаток равен 1.
Этот предел можно вычислить разными способами:
Пределы высшего порядка
У нас есть лимит:
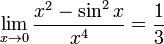
Этот предел можно вычислить разными способами:
,
 измеряется как
измеряется как 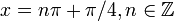 функция переходит от вогнутости вверх (слева) к вогнутости вниз (справа).
функция переходит от вогнутости вверх (слева) к вогнутости вниз (справа).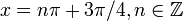 функция переходит от вогнутости вниз (слева) к вогнутости вверх (справа).
функция переходит от вогнутости вниз (слева) к вогнутости вверх (справа).
Leave A Comment