корень 15 2x 3
Вы искали корень 15 2x 3? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и корень из 15 2x 3, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «корень 15 2x 3».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как корень 15 2x 3,корень из 15 2x 3,найдите корень уравнения 15 2x 3.
Где можно решить любую задачу по математике, а так же корень 15 2x 3 Онлайн?
Решить задачу корень 15 2x 3 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
«Коммерсантъ Наука» №15 (3), июнь 2020
анонс номераЭПИДЕМИЯ КОРОНАВИРУСА
SARS-CoV-2.
Продолжение борьбы и прогнозы (3)
Сергей Нетесов
Один из ведущих вирусологов России Сергей Нетесов — о предварительных итогах и первых уроках пандемииДля переболевших стресс — возвращаться в стационар (6)
Насколько плазма крови выздоровевших от COVID-19 на самом деле помогает справиться с коронавирусом, о новых технологиях и оригинальных способах противодействия COVID-19 «Ъ-Науке» рассказал Андрей Буланов, главный внештатный специалист-трансфузиолог Департамента здравоохранения города Москвы, руководитель консультативной трансфузиологической бригады 52-й городской клинической больницы.Хладнокровные вирусные провокации (7)
Елена Васильева
По мере развития знаний о коронавирусе именно многочисленные тромбозы рассматриваются как одна из главных особенностей течения COVID-19. В чем опасность вирусных тромбов, объясняет «Ъ-Науке» Елена Васильева, профессор, заведующая лабораторией атеротромбоза МГМСУ имени А. И. Евдокимова, главный внештатный специалист-кардиолог Департамента здравоохранения города Москвы, член Клинического комитета по COVID-19 города МосквыНелетучая мышь поможет в поиске вакцин от коронавируса (8)
Вирус SARS-CoV-2 приводит к развитию атипичной пневмонии COVID-19 у 20% заразившихся.Болезнь протекает тяжело, а создание лекарств от нее и вакцин против вируса сдерживает отсутствие удобных модельных лабораторных животных, на которых лекарства и вакцины должны пройти доклинические испытания. Такие живые модели — гуманизированные лабораторные мыши — сейчас создаются в Институте биологии гена РАН, и на них начнутся доклинические испытания препаратов и кандидатных вакцин против вируса SARS-CoV-2.
Вспышки проказы связаны с эпохами древних глобализаций (9)
Мария Медникова
Как появлялись и исчезали в далеком прошлом губительные эпидемииТехнологии против кризиса (11)
Елена Туева
В этом году фонд «Сколково» отмечает свое десятилетие. Благодаря его поддержке компании-резиденты создали сотни успешных технологий, которые сегодня помогают бороться с пандемией COVID-19. О работе «Сколково» в период пандемии говорит старший вице-президент по инновациям фонда Кирилл Каем. Мы также продолжаем рассказывать о компаниях, которые вносят важный вклад в преодоление кризиса, связанного с коронавирусом
КАРТИНА МИРА
ОРНИТОЛОГИЯ
Что такое нестбоксинг (12)
Мария Рогова
Пионеры вешали скворечники... Кому-то эти слова вовсе не знакомы, кто-то вспомнит, как советские школьники делали домики для тех птиц, кто не вьет гнезд, а селится в дуплах. Пионеры ушли в небытие. Их заменили более профессиональные защитники птиц: биологи, натуралисты, орнитологи и просто любознательные любители природы. И дело не ограничилось скворечниками.
БИОЛОГИЯ
Как мир стал многоклеточным (14)
Петр Харатьян
Короткая жизнь биолога Алексея Захваткина увенчалась открытием мирового значения
СОБЫТИЯ
ИСТОРИЯ
«К черту вас с вашим Сталиным и его шайкой!» (15)
Кирилл Александров
90 лет назад началась война советской власти против русской деревни — война на уничтожение. Как крестьяне пытались сопротивляться и почему антисталинский протест был задушен — в третьей статье серии, начатой в мартовском номере «Ъ-Науки».АСТРОНОМИЯ
Беглецы от черной дыры (18)
Анатолий Глянцев
Ученые из России выяснили, откуда берутся нейтрино сверхвысоких энергий.Это оставалось загадкой долгие годы. ЭКОНОМИКА
Монетарная политика во время пандемии (19)
Филипп Картаев
Российская экономика столкнулась с кризисом, который вызван двумя событиями: пандемией и резким изменением цен на нефть. Кризис похож на сильный циклический спад, который бывает раз в несколько лет (например, в 2008–2009 годах).АРХЕОЛОГИЯ
Байкальский зуб — американские корни (20)
Мария Роговая
Сибирские археологи из Института археологии и этнографии Сибирского отделения РАН вместе с коллегами из Института эволюционной антропологии Макса Планка исследовали коллекцию с раскопок 1970-х годов. Среди нескольких тысяч артефактов они обнаружили молочный зуб из верхней челюсти Homo sapiens. Владельцем зуба был мальчик 11–13 лет, который жил неподалеку от озера Байкал 14 тыс. лет назад и, как выяснили генетики, имел общие генетические черты с аборигенным (индейским) населением Америки
КАК ЭТО ДЕЛАЕТСЯ
ОКЕАНОЛОГИЯ
Всё ниже, и ниже, и ниже (21)
Владимир Тесленко
Многие передовые страны создают линейку автоматов для освоения океанов.Важная роль принадлежит автономным беспилотным аппаратам с элементами искусственного интеллекта. Самый молодой российский аппарат такого типа — «Витязь-Д» — в мае совершил погружение на дно Марианской впадины МЕДИЦИНА
Коронавирус, ацетилхолин, бунгаротоксин и никотин (24)
Интервью подготовил Алексей Алексеев
В ходе борьбы с пандемией COVID-19 представления о способах борьбы с новым коронавирусом меняются и продолжают меняться. Меняться приходится и тем, кто участвует в этой борьбе, рассказывает директор Института фундаментальной медицины и биологии Казанского федерального университета (КФУ), член-корреспондент Академии наук Республики Татарстан, эксперт РАН Андрей Киясов.ЭНЕРГЕТИКА
Прохлада для турбин (26)
Прохлада для турбин
Генерацию можно сделать эффективнее и дешевле, если охладить
ИССЛЕДОВАНИЯ
ГЕНЕТИКА
Человек генетически пьющий (28)
Человек разумный далеко не единственный вид, который потребляет этанол.Многие млекопитающие, птицы и даже насекомые знакомы с дурманящим эффектом перезрелых фруктов. Но наш вид относится к числу тех, кто довольно хорошо переносит этанол и, более того, имеет мотивацию к его потреблению
ФИЗИКА
Физики научились управлять движением магнитных вихрей (30)
Александр СадовниковМеждународный коллектив ученых исследовал характеристики движения магнитных вихрей в сверхтонких пленках. Сделан важный шаг на пути к полному управлению магнитными вихрями, а умение ими управлять позволит создать устройства для хранения и передачи информации, более эффективные, чем современные жесткие диски.
ОБРАЗОВАНИЕ
МЕТОДОЛОГИЯ
Онлайн все спишет (32)
Екатерина Сивякова
Российские вузы перешли на дистанционное обучение в середине марта — тогда Минобрнауки назвало это решение временным. Но в апреле министерство предположило, что и после пандемии многое останется онлайн, а университеты начали готовить сценарии удаленного образования.Эксперты прогнозируют, что онлайн займет до 80% обучения, а студенты воссоздают здания вузов в Minecraft БУДУЩЕЕ ВРЕМЯ
Здравый смысл и российская школа (34)
Андрей Галиев
Андрей Галиев о здоровье и счастье в современном пониманииREVIEW
«У каждого подростка в жизни много боли» (35)
Записала Алена Прохоренко
Как центр подготовки к ЕГЭ помог школьникам пережить карантинНОВОЕ РУССКОЕ СЛОВО
Язык во владении (36)
Елена Шмелева
ИНТЕРВЬЮ
ФИЗИКА
Самая страшная проблема — жуткая забюрократизированность науки и жизни (37)
Владимир Александров
Академик Михаил Данилов объясняет, почему дошел до Конституционного суда, рассказывает, может ли свет проходить сквозь стену, и делится сомнениями в полноте самой совершенной и элегантной теории материи.
Сайт журнала
Как подписаться
Поликлиника №3 — Новокузнецкий филиал государственного бюджетного учреждения здравоохранения «Кузбасский клинический кардиологический диспансер имени академика Л.
 С. Барбараша»
С. Барбараша»Посмотреть на карте Новокузнецка
Виджет карты использует JavaScript. Включите его в настройках вашего браузера.Адрес: г. Новокузнецк, пр Металлургов, 15
Телефон регистратуры: Единая справочная (3843) 60-00-77
Режим и график работы:
- понедельник–пятница с 8.00-19.00
- суббота и воскресение — выходной
- суббота с 9.00-15.00 работают дежурные врачи по следующим дням:27.01.2018; 17.02.2018; 10.03.2018; 31.03.2018; 21.04.2018; 12.05.2018; 02.06.2018; 23.06.2018;14.07.2018; 04.08.2018; 25.08.2018; 15.09.2018; 20.10.2018; 10.11.2018; 01.12.2018; 22.12.2018
Заведующий поликлиникой Кочергина Татьяна Витальевна 74-37-09
Заведующий терапевтической службой Кинякина Елена Павловна 74-30-67
Старшая мед. сестра Абрамук Светлана Сергеевна 74-55-78
Расписание
Сотрудники подразделения
Виды медицинской помощи
Методы диагностики и лечения
Перечень лекарственных препаратов
Стандарты медицинской помощи
Историческая справка
Поликлиническое отделение по ул. Металлургов, 15 было открыто для приема пациентов в 1957 году. С 01.10.1961года отделение входит в состав МБЛПУ ГКБ №2. Руководство поликлиникой было возложено на компетентных специалистов, высококлассных профессионалов: Животовскую Г.Г., Корень А.Г., Бобылева И.Е., Бобылеву Н.В., Гудкову Т.В. Многие годы терапевтической службой руководили Кондакова Т.А. (1957-1961г.г.), Трапезникова П.М. (1961-1983г.г.), Володина Н.Н., Веремейчук Ф.А., Арвеньтев В.А. С апреля 2004 года заведует поликлиническим отделением №3 Манько Татьяна Анатольевна. В начале 1998 года к поликлинике №3 была присоединена часть поликлиники №1, в связи с расформированием и преобразованием в ЦАК.
Металлургов, 15 было открыто для приема пациентов в 1957 году. С 01.10.1961года отделение входит в состав МБЛПУ ГКБ №2. Руководство поликлиникой было возложено на компетентных специалистов, высококлассных профессионалов: Животовскую Г.Г., Корень А.Г., Бобылева И.Е., Бобылеву Н.В., Гудкову Т.В. Многие годы терапевтической службой руководили Кондакова Т.А. (1957-1961г.г.), Трапезникова П.М. (1961-1983г.г.), Володина Н.Н., Веремейчук Ф.А., Арвеньтев В.А. С апреля 2004 года заведует поликлиническим отделением №3 Манько Татьяна Анатольевна. В начале 1998 года к поликлинике №3 была присоединена часть поликлиники №1, в связи с расформированием и преобразованием в ЦАК.
Годы существования поликлинического отделения отразили этапы становления и преобразования небольшой поликлиники в мощное подразделение , район обслуживания которого включает 18 территориальных участков. Каждый день для пациентов открыты : эндокринологический, неврологический, офтальмологический, кардиологический, отоларингологический кабинеты. В поликлинике функционируют клиническая лаборатория, процедурный кабинет, кабинет доврачебного осмотра, кабинеты статистики и функциональной диагностики.
В поликлинике функционируют клиническая лаборатория, процедурный кабинет, кабинет доврачебного осмотра, кабинеты статистики и функциональной диагностики.
Большой вклад в становление и развитие поликлиники внесли прекрасные специалисты: Борисова Л.А., Тетерина Л.К., Шварцман Е.И., Колтомова В.И., Садурская Н.И., Терентьев П.И., Максименко Е.Л., Бедарева Л.Г., Ганус А.А., Шинкевич М.И. Многие годы средним медицинским персоналом руководила Шертман Хава Абрамовна.
На протяжении многих лет до сегодняшних дней несут медицинскую вахту врачи : Буянова Т.Б., Алмадакова Г.П., Заброда Г.В., Чупина Н.М., Печерская Т.В.,Дружилова Л.З., Мильяшенко С.В.,Демидова О.Д.
Большое спасибо хочется сказать бывшим сотрудникам среднего и младшего медперсонала: Кузнецовой К.И., Лобановой Е.С., Ревиной А.Е., Суховой А.В., Торховой П.Я., Кропотовой А.В., Арсеньевой Л.М., Шеиной Т.А., Лисовенко В.И., Гранатовой З.П., Меркульевой Е.И., Аборкиной М.Д.
Обзор формул — Excel
Если вы еще не Excel в Интернете, скоро вы увидите, что это не просто сетка для ввода чисел в столбцах или строках. Да, с помощью Excel в Интернете можно найти итоги для столбца или строки чисел, но вы также можете вычислять платежи по ипотеке, решать математические или инженерные задачи или находить лучшие сценарии в зависимости от переменных чисел, которые вы подключали.
Да, с помощью Excel в Интернете можно найти итоги для столбца или строки чисел, но вы также можете вычислять платежи по ипотеке, решать математические или инженерные задачи или находить лучшие сценарии в зависимости от переменных чисел, которые вы подключали.
Excel в Интернете делает это с помощью формул в ячейках. Формула выполняет вычисления или другие действия с данными на листе. Формула всегда начинается со знака равенства (=), за которым могут следовать числа, математические операторы (например, знак «плюс» или «минус») и функции, которые значительно расширяют возможности формулы.
Ниже приведен пример формулы, умножающей 2 на 3 и прибавляющей к результату 5, чтобы получить 11.
=2*3+5
Следующая формула использует функцию ПЛТ для вычисления платежа по ипотеке (1 073,64 долларов США) с 5% ставкой (5% разделить на 12 месяцев равняется ежемесячному проценту) на период в 30 лет (360 месяцев) с займом на сумму 200 000 долларов:
=ПЛТ(0,05/12;360;200000)
Ниже приведены примеры формул, которые можно использовать на листах.
-
=A1+A2+A3 Вычисляет сумму значений в ячейках A1, A2 и A3.
-
=КОРЕНЬ(A1) Использует функцию КОРЕНЬ для возврата значения квадратного корня числа в ячейке A1.
-
=СЕГОДНЯ() Возвращает текущую дату.
-
=ПРОПИСН(«привет») Преобразует текст «привет» в «ПРИВЕТ» с помощью функции ПРОПИСН.
-
=ЕСЛИ(A1>0) Анализирует ячейку A1 и проверяет, превышает ли значение в ней нуль.
Элементы формулы
Формула также может содержать один или несколько из таких элементов: функции, ссылки, операторы и константы. («крышка») применяется для возведения числа в степень, а оператор * («звездочка») — для умножения.
(«крышка») применяется для возведения числа в степень, а оператор * («звездочка») — для умножения.
Использование констант в формулах
Константа представляет собой готовое (не вычисляемое) значение, которое всегда остается неизменным. Например, дата 09.10.2008, число 210 и текст «Прибыль за квартал» являются константами. выражение или его значение константами не являются. Если формула в ячейке содержит константы, но не ссылки на другие ячейки (например, имеет вид =30+70+110), значение в такой ячейке изменяется только после изменения формулы.
Использование операторов в формулах
Операторы определяют операции, которые необходимо выполнить над элементами формулы. Вычисления выполняются в стандартном порядке (соответствующем основным правилам арифметики), однако его можно изменить с помощью скобок.
Вычисления выполняются в стандартном порядке (соответствующем основным правилам арифметики), однако его можно изменить с помощью скобок.
Типы операторов
Приложение Microsoft Excel поддерживает четыре типа операторов: арифметические, текстовые, операторы сравнения и операторы ссылок.
Арифметические операторы
Арифметические операторы служат для выполнения базовых арифметических операций, таких как сложение, вычитание, умножение, деление или объединение чисел. Результатом операций являются числа. Арифметические операторы приведены ниже.
Арифметический оператор | Значение | Пример |
|---|---|---|
|
+ (знак «плюс») |
Сложение |
3+3 |
|
– (знак «минус») |
Вычитание |
3–1 |
|
* (звездочка) |
Умножение |
3*3 |
|
/ (косая черта) |
Деление |
3/3 |
|
% (знак процента) |
Доля |
20% |
|
^ (крышка) |
Возведение в степень |
3^2 |
Операторы сравнения
Операторы сравнения используются для сравнения двух значений. Результатом сравнения является логическое значение: ИСТИНА либо ЛОЖЬ.
Результатом сравнения является логическое значение: ИСТИНА либо ЛОЖЬ.
Оператор сравнения | Значение | Пример |
|---|---|---|
|
= (знак равенства) |
Равно |
A1=B1 |
|
> (знак «больше») |
Больше |
A1>B1 |
|
< (знак «меньше») |
Меньше |
A1<B1 |
|
>= (знак «больше или равно») |
Больше или равно |
A1>=B1 |
|
<= (знак «меньше или равно») |
Меньше или равно |
A1<=B1 |
|
<> (знак «не равно») |
Не равно |
A1<>B1 |
Текстовый оператор конкатенации
Амперсанд (&) используется для объединения (соединения) одной или нескольких текстовых строк в одну.
Текстовый оператор | Значение | Пример |
|---|---|---|
|
& (амперсанд) |
Соединение или объединение последовательностей знаков в одну последовательность |
Выражение «Северный»&«ветер» дает результат «Северный ветер». |
Операторы ссылок
Для определения ссылок на диапазоны ячеек можно использовать операторы, указанные ниже.
Оператор ссылки | Значение | Пример |
|---|---|---|
|
: (двоеточие) |
Оператор диапазона, который образует одну ссылку на все ячейки, находящиеся между первой и последней ячейками диапазона, включая эти ячейки. |
B5:B15 |
|
; (точка с запятой) |
Оператор объединения. Объединяет несколько ссылок в одну ссылку. |
СУММ(B5:B15,D5:D15) |
|
(пробел) |
Оператор пересечения множеств, используется для ссылки на общие ячейки двух диапазонов. |
B7:D7 C6:C8 |
Порядок выполнения Excel в Интернете формулах
В некоторых случаях порядок вычисления может повлиять на возвращаемое формулой значение, поэтому для получения нужных результатов важно понимать стандартный порядок вычислений и знать, как можно его изменить.
Порядок вычислений
Формулы вычисляют значения в определенном порядке. Формула всегда начинается со знака равно(=).Excel в Интернете интерпретирует знаки после знака равно как формулу. После знака равно вычисляются элементы (операнды), такие как константы или ссылки на ячейки. Они разделены операторами вычислений. Excel в Интернете вычисляет формулу слева направо в соответствии с определенным порядком для каждого оператора в формуле.
Формула всегда начинается со знака равно(=).Excel в Интернете интерпретирует знаки после знака равно как формулу. После знака равно вычисляются элементы (операнды), такие как константы или ссылки на ячейки. Они разделены операторами вычислений. Excel в Интернете вычисляет формулу слева направо в соответствии с определенным порядком для каждого оператора в формуле.
Приоритет операторов
Если в одной формуле несколько операторов, Excel в Интернете выполняет операции в том порядке, который показан в таблице ниже. Если формула содержит операторы с одинаковым приоритетом, например операторы деления и умножения, Excel в Интернете эти операторы оцениваются слева направо.
Оператор | Описание |
|---|---|
|
: (двоеточие) (один пробел) , (запятая) |
Операторы ссылок |
|
– |
Знак «минус» |
|
% |
Процент |
|
^ |
Возведение в степень |
|
* и / |
Умножение и деление |
|
+ и — |
Сложение и вычитание |
|
& |
Объединение двух текстовых строк в одну |
|
= |
Сравнение |
Использование круглых скобок
Чтобы изменить порядок вычисления формулы, заключите ее часть, которая должна быть выполнена первой, в скобки. Например, следующая формула дает результат 11, так как Excel в Интернете умножение выполняется перед с добавлением. В этой формуле число 2 умножается на 3, а затем к результату прибавляется число 5.
Например, следующая формула дает результат 11, так как Excel в Интернете умножение выполняется перед с добавлением. В этой формуле число 2 умножается на 3, а затем к результату прибавляется число 5.
=5+2*3
Если же изменить синтаксис с помощью скобок, Excel в Интернете сбавляет 5 и 2, а затем умножает результат на 3, чтобы получить 21.
=(5+2)*3
В следующем примере скобки, в которые заключена первая часть формулы, принудительно Excel в Интернете сначала вычислить ячейки B4+25, а затем разделить результат на сумму значений в ячейках D5, E5 и F5.
=(B4+25)/СУММ(D5:F5)
Использование функций и вложенных функций в формулах
Функции — это заранее определенные формулы, которые выполняют вычисления по заданным величинам, называемым аргументами, и в указанном порядке. Эти функции позволяют выполнять как простые, так и сложные вычисления.
Синтаксис функций
Приведенный ниже пример функции ОКРУГЛ, округляющей число в ячейке A10, демонстрирует синтаксис функции.
1. Структура. Структура функции начинается со знака равно (=), за которым следуют имя функции, открывая скобка, аргументы функции, разделенные запятой, и закрывая скобка.
Структура. Структура функции начинается со знака равно (=), за которым следуют имя функции, открывая скобка, аргументы функции, разделенные запятой, и закрывая скобка.
2. Имя функции. Чтобы отобразить список доступных функций, щелкните любую ячейку и нажмите клавиши SHIFT+F3.
3. Аргументы. Существуют различные типы аргументов: числа, текст, логические значения (ИСТИНА и ЛОЖЬ), массивы, значения ошибок (например #Н/Д) или ссылки на ячейки. Используемый аргумент должен возвращать значение, допустимое для данного аргумента. В качестве аргументов также используются константы, формулы и другие функции.
4. Всплывающая подсказка аргумента. При вводе функции появляется всплывающая подсказка с синтаксисом и аргументами. Например, всплывающая подсказка появляется после ввода выражения =ОКРУГЛ(. Всплывающие подсказки отображаются только для встроенных функций.
Всплывающая подсказка аргумента. При вводе функции появляется всплывающая подсказка с синтаксисом и аргументами. Например, всплывающая подсказка появляется после ввода выражения =ОКРУГЛ(. Всплывающие подсказки отображаются только для встроенных функций.
Ввод функций
Диалоговое окно Вставить функцию упрощает ввод функций при создании формул, в которых они содержатся. При вводе функции в формулу в диалоговом окне Вставить функцию отображаются имя функции, все ее аргументы, описание функции и каждого из аргументов, текущий результат функции и всей формулы.
Чтобы упростить создание и редактирование формул и свести к минимуму количество опечаток и синтаксических ошибок, пользуйтесь автозавершением формул. После того как вы введите знак «= » (знак равно) и начинательные буквы или триггер отображения Excel в Интернете под ячейкой будет отображаться динамический список действительных функций, аргументов и имен, которые соответствуют этим буквам или триггеру. После этого элемент из раскрывающегося списка можно вставить в формулу.
После того как вы введите знак «= » (знак равно) и начинательные буквы или триггер отображения Excel в Интернете под ячейкой будет отображаться динамический список действительных функций, аргументов и имен, которые соответствуют этим буквам или триггеру. После этого элемент из раскрывающегося списка можно вставить в формулу.
Вложенные функции
В некоторых случаях может потребоваться использовать функцию в качестве одного из аргументов другой функции. Например, в приведенной ниже формуле для сравнения результата со значением 50 используется вложенная функция СРЗНАЧ.
1. Функции СРЗНАЧ и СУММ вложены в функцию ЕСЛИ.
Функции СРЗНАЧ и СУММ вложены в функцию ЕСЛИ.
Допустимые типы вычисляемых значений Вложенная функция, используемая в качестве аргумента, должна возвращать соответствующий ему тип данных. Например, если аргумент должен быть логическим, т. е. Если эта функция не работает, Excel в Интернете отобразит #VALUE! В противном случае TE102825393 выдаст ошибку «#ЗНАЧ!».
<c0>Предельное количество уровней вложенности функций</c0>. В формулах можно использовать до семи уровней вложенных функций. Если функция Б является аргументом функции А, функция Б находится на втором уровне вложенности. Например, в приведенном выше примере функции СРЗНАЧ и СУММ являются функциями второго уровня, поскольку обе они являются аргументами функции ЕСЛИ. Функция, вложенная в качестве аргумента в функцию СРЗНАЧ, будет функцией третьего уровня, и т. д.
Функция, вложенная в качестве аргумента в функцию СРЗНАЧ, будет функцией третьего уровня, и т. д.
Использование ссылок в формулах
Ссылка указывает на ячейку или диапазон ячеек на сайте и сообщает Excel в Интернете, где искать значения или данные, которые вы хотите использовать в формуле. С помощью ссылок в одной формуле можно использовать данные, которые находятся в разных частях листа, а также значение одной ячейки в нескольких формулах. Вы также можете задавать ссылки на ячейки разных листов одной книги либо на ячейки из других книг. Ссылки на ячейки других книг называются связями или внешними ссылками.
Стиль ссылок A1
Стиль ссылок по умолчанию По умолчанию в Excel в Интернете используется стиль ссылок A1, который ссылается на столбцы буквами (от A до XFD, всего 16 384 столбца) и ссылается на строки с числами (от 1 до 1 048 576). Эти буквы и номера называются заголовками строк и столбцов. Для ссылки на ячейку введите букву столбца, и затем — номер строки. Например, ссылка B2 указывает на ячейку, расположенную на пересечении столбца B и строки 2.
Эти буквы и номера называются заголовками строк и столбцов. Для ссылки на ячейку введите букву столбца, и затем — номер строки. Например, ссылка B2 указывает на ячейку, расположенную на пересечении столбца B и строки 2.
Ячейка или диапазон | Использование |
|---|---|
|
Ячейка на пересечении столбца A и строки 10 |
A10 |
|
Диапазон ячеек: столбец А, строки 10-20. |
A10:A20 |
|
Диапазон ячеек: строка 15, столбцы B-E |
B15:E15 |
|
Все ячейки в строке 5 |
5:5 |
|
Все ячейки в строках с 5 по 10 |
5:10 |
|
Все ячейки в столбце H |
H:H |
|
Все ячейки в столбцах с H по J |
H:J |
|
Диапазон ячеек: столбцы А-E, строки 10-20 |
A10:E20 |
<c0>Ссылка на другой лист</c0>. В приведенном ниже примере функция СРЗНАЧ используется для расчета среднего значения диапазона B1:B10 на листе «Маркетинг» той же книги.
В приведенном ниже примере функция СРЗНАЧ используется для расчета среднего значения диапазона B1:B10 на листе «Маркетинг» той же книги.
1. Ссылка на лист «Маркетинг».
2. Ссылка на диапазон ячеек с B1 по B10 включительно.
3. Ссылка на лист, отделенная от ссылки на диапазон значений.
Различия между абсолютными, относительными и смешанными ссылками
<c0>Относительные ссылки</c0>. Относительная ссылка в формуле, например A1, основана на относительной позиции ячейки, содержащей формулу, и ячейки, на которую указывает ссылка. При изменении позиции ячейки, содержащей формулу, изменяется и ссылка. При копировании или заполнении формулы вдоль строк и вдоль столбцов ссылка автоматически корректируется. По умолчанию в новых формулах используются относительные ссылки. Например, при копировании или заполнении относительной ссылки из ячейки B2 в ячейку B3 она автоматически изменяется с =A1 на =A2.
Относительная ссылка в формуле, например A1, основана на относительной позиции ячейки, содержащей формулу, и ячейки, на которую указывает ссылка. При изменении позиции ячейки, содержащей формулу, изменяется и ссылка. При копировании или заполнении формулы вдоль строк и вдоль столбцов ссылка автоматически корректируется. По умолчанию в новых формулах используются относительные ссылки. Например, при копировании или заполнении относительной ссылки из ячейки B2 в ячейку B3 она автоматически изменяется с =A1 на =A2.
<c0>Абсолютные ссылки</c0>. Абсолютная ссылка на ячейку в формуле, например $A$1, всегда ссылается на ячейку, расположенную в определенном месте. При изменении позиции ячейки, содержащей формулу, абсолютная ссылка не изменяется. При копировании или заполнении формулы по строкам и столбцам абсолютная ссылка не корректируется. По умолчанию в новых формулах используются относительные ссылки, а для использования абсолютных ссылок надо активировать соответствующий параметр. Например, при копировании или заполнении абсолютной ссылки из ячейки B2 в ячейку B3 она остается прежней в обеих ячейках: =$A$1.
По умолчанию в новых формулах используются относительные ссылки, а для использования абсолютных ссылок надо активировать соответствующий параметр. Например, при копировании или заполнении абсолютной ссылки из ячейки B2 в ячейку B3 она остается прежней в обеих ячейках: =$A$1.
Смешанные ссылки Смешанная ссылка имеет абсолютный столбец и относительную строку либо абсолютную строку и относительный столбец. Абсолютная ссылка на столбец принимает форму $A 1, $B 1 и так далее. Абсолютная ссылка на строку имеет форму A$1, B$1 и так далее. При изменении позиции ячейки, содержаной формулу, изменяется относительная ссылка, а абсолютная ссылка не изменяется. При копировании или заполнении формулы по строкам или вниз по столбцам относительная ссылка автоматически корректируется, а абсолютная ссылка не корректируется. Например, при копировании или заполнении смешанной ссылки из ячейки A2 в B3 она будет меняться с =A$1 на =B$1.
Стиль трехмерных ссылок
Удобный способ для ссылки на несколько листов Трехмерные ссылки используются для анализа данных из одной и той же ячейки или диапазона ячеек на нескольких листах одной книги. Трехмерная ссылка содержит ссылку на ячейку или диапазон, перед которой указываются имена листов. Excel в Интернете использует все таблицы, которые хранятся между начальным и конечним именами ссылки. Например, формула =СУММ(Лист2:Лист13!B5) суммирует все значения, содержащиеся в ячейке B5 на всех листах в диапазоне от листа 2 до листа 13 включительно.
-
При помощи трехмерных ссылок можно создавать ссылки на ячейки на других листах, определять имена и создавать формулы с использованием следующих функций: СУММ, СРЗНАЧ, СРЗНАЧА, СЧЁТ, СЧЁТЗ, МАКС, МАКСА, МИН, МИНА, ПРОИЗВЕД, СТАНДОТКЛОН.
 Г, СТАНДОТКЛОН.В, СТАНДОТКЛОНА, СТАНДОТКЛОНПА, ДИСПР, ДИСП.В, ДИСПА и ДИСППА.
Г, СТАНДОТКЛОН.В, СТАНДОТКЛОНА, СТАНДОТКЛОНПА, ДИСПР, ДИСП.В, ДИСПА и ДИСППА. -
Трехмерные ссылки нельзя использовать в формулах массива.
-
Трехмерные ссылки нельзя использовать вместе с оператор пересечения (один пробел), а также в формулах с неявное пересечение.
<c0>Что происходит при перемещении, копировании, вставке или удалении листов</c0>. Нижеследующие примеры поясняют, какие изменения происходят в трехмерных ссылках при перемещении, копировании, вставке и удалении листов, на которые такие ссылки указывают. В примерах используется формула =СУММ(Лист2:Лист6!A2:A5) для суммирования значений в ячейках с A2 по A5 на листах со второго по шестой.
-
Вставка или копирование Если вставить листы между листами 2 и 6, Excel в Интернете будет включать в расчет все значения из ячеек с A2 по A5 на добавленных листах.

-
Удалить Если удалить листы между листами 2 и 6, Excel в Интернете вы вычислите их значения.
-
Переместить Если переместить листы между листами 2 и 6 в место за пределами диапазона, на который имеется ссылка, Excel в Интернете удалит их значения из вычислений.
-
Перемещение конечного листа Если переместить лист 2 или 6 в другое место книги, Excel в Интернете скорректирует сумму с учетом изменения диапазона листов.
-
Удаление конечного листа Если удалить лист 2 или 6, Excel в Интернете скорректирует сумму с учетом изменения диапазона листов между ними.
Стиль ссылок R1C1
Можно использовать такой стиль ссылок, при котором нумеруются и строки, и столбцы. Стиль ссылок R1C1 удобен для вычисления положения столбцов и строк в макросах. В стиле R1C1 Excel в Интернете указывает на расположение ячейки с помощью R, за которым следует номер строки, и C, за которым следует номер столбца.
Стиль ссылок R1C1 удобен для вычисления положения столбцов и строк в макросах. В стиле R1C1 Excel в Интернете указывает на расположение ячейки с помощью R, за которым следует номер строки, и C, за которым следует номер столбца.
Ссылка | Значение |
|---|---|
|
R[-2]C |
относительная ссылка на ячейку, расположенную на две строки выше в том же столбце |
|
R[2]C[2] |
Относительная ссылка на ячейку, расположенную на две строки ниже и на два столбца правее |
|
R2C2 |
Абсолютная ссылка на ячейку, расположенную во второй строке второго столбца |
|
R[-1] |
Относительная ссылка на строку, расположенную выше текущей ячейки |
|
R |
Абсолютная ссылка на текущую строку |
При записи макроса Excel в Интернете некоторые команды с помощью стиля ссылок R1C1. Например, если записать команду (например, нажать кнопку «Автоумма»), чтобы вставить формулу, в которую добавляется диапазон ячеек, Excel в Интернете записи формулы со ссылками с помощью стиля R1C1, а не A1.
Например, если записать команду (например, нажать кнопку «Автоумма»), чтобы вставить формулу, в которую добавляется диапазон ячеек, Excel в Интернете записи формулы со ссылками с помощью стиля R1C1, а не A1.
Использование имен в формулах
Можно создавать определенные имена для представления ячеек, диапазонов ячеек, формул, констант и Excel в Интернете таблиц. Имя — это значимое краткое обозначение, поясняющее предназначение ссылки на ячейку, константы, формулы или таблицы, так как понять их суть с первого взгляда бывает непросто. Ниже приведены примеры имен и показано, как их использование упрощает понимание формул.
Тип примера | Пример использования диапазонов вместо имен | Пример с использованием имен |
|---|---|---|
|
Ссылка |
=СУММ(A16:A20) |
=СУММ(Продажи) |
|
Константа |
=ПРОИЗВЕД(A12,9. |
=ПРОИЗВЕД(Цена,НСП) |
|
Формула |
=ТЕКСТ(ВПР(MAX(A16,A20),A16:B20,2,FALSE),»дд.мм.гггг») |
=ТЕКСТ(ВПР(МАКС(Продажи),ИнформацияОПродажах,2,ЛОЖЬ),»дд.мм.гггг») |
|
Таблица |
A22:B25 |
=ПРОИЗВЕД(Price,Table1[@Tax Rate]) |
Типы имен
Существует несколько типов имен, которые можно создавать и использовать.
Определенное имя Имя, используемое для представления ячейки, диапазона ячеек, формулы или константы. Вы можете создавать собственные определенные имена. Кроме Excel в Интернете иногда задайте определенное имя, например при создании области печати.
Вы можете создавать собственные определенные имена. Кроме Excel в Интернете иногда задайте определенное имя, например при создании области печати.
Имя таблицы Имя таблицы Excel в Интернете, которая является набором данных по определенной теме, которые хранятся в записях (строках) и полях (столбцах). Excel в Интернете создает таблицу Excel в Интернете имя таблицы «Таблица1», «Таблица2» и так далее, каждый раз при вставке таблицы Excel в Интернете, но эти имена можно изменить, чтобы сделать их более осмысленными.
Создание и ввод имен
Имя создается с помощью «Создать имя из выделения». Можно удобно создавать имена из существующих имен строк и столбцов с помощью фрагмента, выделенного на листе.
Примечание: По умолчанию в именах используются абсолютные ссылки на ячейки.
Имя можно ввести указанными ниже способами.
-
Ввод с клавиатуры Введите имя, например, в качестве аргумента формулы.
-
<c0>Автозавершение формул</c0>. Используйте раскрывающийся список автозавершения формул, в котором автоматически выводятся допустимые имена.
Использование формул массива и констант массива
Excel в Интернете не поддерживает создание формул массива. Вы можете просматривать результаты формул массива, созданных в классическом приложении Excel, но не сможете изменить или пересчитать их. Если на вашем компьютере установлено классическое приложение Excel, нажмите кнопку Открыть в Excel, чтобы перейти к работе с массивами.
Вы можете просматривать результаты формул массива, созданных в классическом приложении Excel, но не сможете изменить или пересчитать их. Если на вашем компьютере установлено классическое приложение Excel, нажмите кнопку Открыть в Excel, чтобы перейти к работе с массивами.
В примере формулы массива ниже вычисляется итоговое значение цен на акции; строки ячеек не используются при вычислении и отображении отдельных значений для каждой акции.
При вводе формулы «={СУММ(B2:D2*B3:D3)}» в качестве формулы массива сначала вычисляется значение «Акции» и «Цена» для каждой биржи, а затем — сумма всех результатов.
<c0>Вычисление нескольких значений</c0>. Некоторые функции возвращают массивы значений или требуют массив значений в качестве аргумента. Для вычисления нескольких значений с помощью формулы массива необходимо ввести массив в диапазон ячеек, состоящий из того же числа строк или столбцов, что и аргументы массива.
Некоторые функции возвращают массивы значений или требуют массив значений в качестве аргумента. Для вычисления нескольких значений с помощью формулы массива необходимо ввести массив в диапазон ячеек, состоящий из того же числа строк или столбцов, что и аргументы массива.
Например, по заданному ряду из трех значений продаж (в столбце B) для трех месяцев (в столбце A) функция ТЕНДЕНЦИЯ определяет продолжение линейного ряда объемов продаж. Чтобы можно было отобразить все результаты формулы, она вводится в три ячейки столбца C (C1:C3).
Формула «=ТЕНДЕНЦИЯ(B1:B3;A1:A3)», введенная как формула массива, возвращает три значения (22 196, 17 079 и 11 962), вычисленные по трем объемам продаж за три месяца.
Использование констант массива
В обычную формулу можно ввести ссылку на ячейку со значением или на само значение, также называемое константой. Подобным образом в формулу массива можно ввести ссылку на массив либо массив значений, содержащихся в ячейках (его иногда называют константой массива). Формулы массива принимают константы так же, как и другие формулы, однако константы массива необходимо вводить в определенном формате.
Константы массива могут содержать числа, текст, логические значения, например ИСТИНА или ЛОЖЬ, либо значения ошибок, такие как «#Н/Д». В одной константе массива могут присутствовать значения различных типов, например {1,3,4;ИСТИНА,ЛОЖЬ,ИСТИНА}. Числа в константах массива могут быть целыми, десятичными или иметь экспоненциальный формат. Текст должен быть заключен в двойные кавычки, например «Вторник».
Текст должен быть заключен в двойные кавычки, например «Вторник».
Константы массива не могут содержать ссылки на ячейку, столбцы или строки разной длины, формулы и специальные знаки: $ (знак доллара), круглые скобки или % (знак процента).
При форматировании констант массива убедитесь, что выполняются указанные ниже требования.
-
Константы заключены в фигурные скобки ( { } ).
-
Столбцы разделены запятыми (,). Например, чтобы представить значения 10, 20, 30 и 40, введите {10,20,30,40}.
 Эта константа массива является матрицей размерности 1 на 4 и соответствует ссылке на одну строку и четыре столбца.
Эта константа массива является матрицей размерности 1 на 4 и соответствует ссылке на одну строку и четыре столбца. -
Значения ячеек из разных строк разделены точками с запятой (;). Например, чтобы представить значения 10, 20, 30, 40 и 50, 60, 70, 80, находящиеся в расположенных друг под другом ячейках, можно создать константу массива с размерностью 2 на 4: {10,20,30,40;50,60,70,80}.
15 самых полезных свойств корня имбиря
Имбирь – одно из самых известных лекарственных растений, которое используется и в медицине для лечения различных заболеваний, и в кулинарии для придания блюдам особого, пикантного вкуса. Корень имбиря, употребляемый в пищу – это сырые или переработанные корневища многолетнего растения вида Zingiber officinale, родина которого – страны Южной Азии, хотя сегодня имбирь выращивают в различных тропических регионах: и в Азии, и в Австралии, и даже в Западной Африке.
Лекарственные свойства имбиря известны с незапамятных времен: еще две с половиной тысячи лет назад, в древнем Китае, чай с имбирем готовили для лечения простудных заболеваний, как согревающее средство. Не менее известным было и другое полезное свойство имбиря – а именно, его способность избавлять от тошноты: американские индейцы готовили из корня имбиря отвары, чтобы побороть тошноту. Лекарственные свойства имбиря были хорошо известны в древней Японии, Индии, других странах юго-восточной Азии. А после того, как в Средние века имбирь был впервые завезен в Европу, корень растения быстро стал известен как «чудодейственное» лекарственное средство для предотвращения чумы, страшнейшего бича европейской цивилизации в Средневековье.
Полезные свойства имбиря объясняются достаточно просто: в корневище имбиря содержится очень много полезных витаминов, минералов и аминокислот, в числе которых витамины С, B1, B2, незаменимые аминокислоты, необходимые для нормального функционирования всех систем организма, эфирное масло, минералы (натрий, калий, цинк).
Использование
Корень имбиря обладает множеством полезных свойств и применяется в виде отваров и настоев для лечения и профилактики самых разных заболеваний, от простуды до артрита.
- Одно из основных применений имбиря – использование его для лечения и профилактики простудных заболеваний. Имбирь обладает противовоспалительными свойствами, поэтому чай из имбиря необычайно полезен при лечении заболеваний ротовой полости и горла (например, ангины), простуды, гриппа. В некоторых странах Европы, к примеру, для лечения простуды готовят подогретый имбирный эль и имбирное пиво, которые, как считается, помогают быстрее избавиться от болезни. А в Китае интересным народным средством для лечения кашля считается яичный омлет с имбирным корнем. Кроме того, в том же Китае для лечения кашля из имбирного корня готовят особые леденцы.
- Компрессы из имбиря помогают при некоторых болях – например, при болях в спине или хроническом ревматизме. Кроме того, считается, что имбирь способствует избавлению от головной боли.

- Одно из самых распространенных применений имбиря – борьба с тошнотой. Многочисленные исследования подтвердили, что имбирь способен справиться с любыми причинами и видами тошноты – будь то последствия химиотерапии, токсикоз на ранних стадиях беременности, тошнота, вызванная укачиванием. Благодаря отсутствию побочных эффектов имбирь для избавления от тошноты могут принимать и беременные женщины.
- Еще одно полезное свойство имбиря – это его способность нормализовать работу пищеварительной системы человека. Давно известно, что имбирь улучшает аппетит и работу пищеварительной системы в целом, а также полезен при нарушениях жирового или холестеринового обмена. Именно поэтому еще одно распространенное применение имбиря – это борьба с лишним весом. Имбирь ускоряет обмен веществ, тем самым стимулируя процесс сжигания калорий, необходимый для поддержания нормального веса. Кроме того, имбирь нормализует работу кишечника, облегчая расщепление и усвоение пищи, и регулирует перистальтику – процесс сокращения мускулов кишечника, за счет которого пища продвигается по пищеводу.

Побочные эффекты имбиря
Хотя в целом считается, что имбирь абсолютно безопасен для здоровья человека, он все-таки может вызвать аллергическую реакцию, результатом которой становится появление на коже сыпи. Кроме того, в числе редких побочных эффектов от применения имбиря – вздутие живота, тошнота, отрыжка, изжога (в первую очередь такие побочные эффекты вызывает имбирь в порошковой форме). Свежий имбирь также может вызвать запоры.
Полезные свойства
Спектр лечебных свойств, которыми обладает корень имбиря, весьма широк, он оказывает: противовоспалительное, спазмолитическое, обезболивающее, рассасывающее, возбуждающее, ветрогонное, потогонное, заживляющее и тонизирующее действие. Также имбирь обладает сильным антиоксидантным и успокоительным действием, повышает иммунитет и защищает организм от паразитов.
Употребление имбиря в пищу улучшает секрецию желудка, повышает аппетит, снимает все симптомы «морской» болезни (не только тошноту, но и слабость, головокружение), уменьшает количество холестерина в крови и снижает артериальное давление. Также имбирь полезен как профилактическое средство против развития злокачественных опухолей (рака).
Также имбирь полезен как профилактическое средство против развития злокачественных опухолей (рака).
Синхронный турнир «Балтийский берег» — 2014/15. 3 этап
Дата: 2015-01-01
Редакторы благодарят за тестирование и ценные замечания: Михаила Малкина (Люберцы), Инну Семенову и Андрея Данченко (Винница), Юрия Выменца, Бориса Моносова и Евгения Поникарова (Санкт-Петербург), Артема Корсуна (Львов), Владимира Городецкого (Иерусалим), Дмитрия Слоуща (Гиватаим), Андрея Гатаулина (Караганда), Игоря Тюнькина (Москва), Максима Мерзлякова (Воронеж) и Марину Ножнину (Юрмала).
Показать ответы
Разминка
Вопрос 1: В 1839 году несколько конгрессменов штата Иллинойс от партии вигов выпрыгнули из запертого здания конгресса через окно, чтобы не допустить ЕГО. Назовите ЕГО словом латинского происхождения.
Ответ: Кворум.
У тори было большинство для принятия закона. Чтобы виги не сорвали кворум, тори заперли здание, но Авраам Линкольн и еще двое вигов выскочили в окно. Впрочем, кворум все равно состоялся. Надеемся, все пришли, и можно начинать.
Источник(и): http://en.wikipedia.org/wiki/Joseph_Gillespie
Автор: Юрий Шатц (Рига)
!1 тур
Вопрос 1: Назовите единицу измерения, в полном итальянском названии которой есть слово «ПРИМО».
Ответ: Минута.
Минута полностью называется «minuto primo» [минУто прИмо], от латинского
«первая частица», а секунда — «minuto secondo» [минУто секОндо], от
латинского «вторая частица». Соответствующими латинскими названиями
обозначали шестидесятеричные дроби. Полные названия используются редко,
но в итальянском спортивном репортаже можно прочитать, например, «одна
первая и десять вторых», т. е. минута и десять секунд.
е. минута и десять секунд.
Источник(и):
1. http://it.wikipedia.org/wiki/Minuto
2. http://it.wikipedia.org/wiki/Sistema_sessagesimale
3. http://la.wikipedia.org/wiki/Secundum
Автор: Юрий Шатц (Рига)
!Вопрос 2: Персонаж Шекспира собирается в путь, чтобы завоевать богатую рыжеволосую наследницу. Какой топоним он при этом упоминает?
Ответ: Колхида.
Зачёт: БельмОнт.
БассАно, персонаж «Венецианского купца», едет в город БельмОнт, чтобы жениться на богатой и красивой девушке. По его словам, «солнечные кудри // как золотое светятся руно; // БельмОнт они в Колхиду обращают».
Источник(и): Уильям Шекспир. Венецианский купец. http://lib.ru/SHAKESPEARE/kupec.txt
Автор: Юрий Шатц (Рига)
! Вопрос 3: [Ведущему: дефис не озвучивать, последние слова прочитать как «БЕТУ
ТЕТУ». ]
]
Внимание, в вопросе есть замены.
Согласно одной из интерпретаций, в русском фольклоре БЕТА
символизирует горькую жизнь молодой женщины в доме свёкра, а ТЕТА —
девичью жизнь у родного батюшки. Назовите БЕТУ-ТЕТУ.
Ответ: Калинка-малинка.
Зачёт: «Калина малина» или «калинка малинка» — раздельно, через дефис или через запятую.
Это не просто рифмованное удвоение, а типичное для фольклора противопоставление горькой калины и сладкой малины.
Источник(и): http://www.slovoart.ru/node/820
Автор: Юрий Шатц (Рига)
!Вопрос 4: По информации, бесплатно предоставленной Википедией, еще двое помещались у НЕГО во рту. Назовите ЕГО.
Ответ: Троянский конь.
Тридцать человек в животе и еще двое во рту. Информация есть только в
Википедии и не слишком достоверна, но автор вопроса решил не смотреть в
зубы дареному коню.
Источник(и): http://en.wikipedia.org/wiki/Trojan_Horse
Автор: Юрий Шатц (Рига)
!Вопрос 5:
entanglement
Запутанность — это квантовое явление, при котором координаты, скорости и спины двух объектов оказываются взаимосвязанными. Назовите одним словом то, с чем Джон ПрЕскилл сравнил это явление.
Ответ: Танго.
Согласно расхожему выражению, для танго нужны двое. Слово «entanglement» [энтАнглмент] — «запутанность» по-английски — почти полностью содержит в себе слово «tango».
Источник(и): John Preskill, Spiros Michalakis. Quantum Computers Animated. http://www.youtube.com/watch?v=T2DXrs0OpHU
Автор: Виталий Бреев (Рига — Глазго)
!Вопрос 6: ОНА — это сценарий профессора Эдуарда Френкеля о непредсказуемости жизненных путей мужчины и женщины, об их сближениях и отдалениях. ОНА впервые была поставлена НьЮтоном. Назовите ЕЕ тремя словами.
Ответ: Задача двух тел.
Зачёт: Проблема двух тел.
В классической механике задача двух тел состоит в определении движения двух тел, взаимодействующих между собой. В физике задача двух тел давно решена, а в любви — нет. Профессор Френкель — популяризатор науки, поэтому он и называет пьесы физическими терминами.
Источник(и):
1. http://www.thetwobodyproblem.com/
2. А. Рой. Движение по орбитам. http://stu.alnam.ru/book_mor-47
Автор: Виталий Бреев (Рига — Глазго)
! Вопрос 7:
Перед вами вполне нормальный треугольник. Сумма его углов равна 180 градусам. Напишите величину угла C [Це] с точностью до десятых долей градуса.
Ответ: 36,6.
Зачёт: 36,5.
По странному совпадению, сумма нормальных температур человеческого тела
по Цельсию, Фаренгейту и Реомюру очень близка к 180 градусам. 36,5 по
Цельсию соответствуют 45,6 по Реомюру и 97,7 по Фаренгейту.
z-checkdb: На самом деле 36,5 по Цельсию соответствуют 29,2 по
Реомюру, соответственно сумма равна 163,4.
Источник(и): Наблюдение автора вопроса.
Автор: Юрий Шатц (Рига)
! Вопрос 8: [Ведущему: кавычки не обозначать, «Е» читать как русскую букву.]
ИХ описание приводится в статье о «Формуле Е». Назовите ученого, в
честь которого называется несколько видов ИХ.
Ответ: [НИкола] Тесла.
«Формула Е» в данном случае относится не к математике и не к химии, а к серии гонок на электрических автомобилях. Ведущий производитель электромобилей — это компания «Tesla».
Источник(и): http://ru.wikipedia.org/wiki/Формула_Е
Автор: Виталий Бреев (Рига — Глазго)
!Вопрос 9: Готовясь к битве на североамериканском озере ШамплЕйн, один английский генерал заказал в Европе ТАКИЕ суда. Какое слово, содержащее приставку, корень, суффикс и окончание, мы заменили словом «ТАКИЕ»?
Ответ: Разборные.
Зачёт: Сборные, сборно-разборные, составные.
Детали кораблей перевозились по суше, и корабли собирались на месте. Форма вопроса намекает на грамматический разбор слова.
Источник(и): http://en.wikipedia.org/wiki/Battle_of_Valcour_Island
Автор: Юрий Шатц (Рига)
!Вопрос 10: Серия картин НОрмана РОквелла посвящена важным для американцев понятиям. На картине «Свобода от нужды» художник изобразил американскую семью вокруг НЕЕ. По-португальски ОНА называется «перУ». Назовите ЕЕ.
Ответ: Индейка.
На картине изображена семья за изобильным праздничным столом. После написания картины художник съел свою модель. Португальское название, так же как русское «индейка» и английское «turkey» [тёрки], происходит от названия страны. При этом оно более точное, так как индейка родом из Америки.
Источник(и):
1. http://en.wikipedia.org/wiki/Freedom_from_Want_(painting)
2. http://pt.wiktionary.org/wiki/peru
Автор: Юрий Шатц (Рига)
!Вопрос 11: Один из концертов «Битлз» на юге США был под угрозой отмены, пока организаторы не выполнили требования музыкантов. Рассказывающая об этом статья на сайте beatles.ru [битлз точка ру] озаглавлена «Битлз отказывались выступать посторонним вход запрещен». Какие слова мы заменили в предыдущем предложении?
Ответ: Только для белых.
Статья озаглавлена «Битлз отказывались выступать только для белых». На юге США в 1964 году всё еще были сегрегированные концерты, куда черные либо не допускались совсем, либо допускались только на специальные места. «Битлз» потребовали, чтобы на их концерт пускали всех, и организаторам пришлось согласиться. «Только для белых» — типичная для тех времен табличка в местах, куда черные не допускались.
Источник(и):
1. Р. Гэри Паттерсон. Пол Маккартни: история жертвоприношения.
http://www.wingspan.ru/booksrus/sacr/05.html
2. http://www.beatles.ru/postman/forum_messages.asp?msg_id=20465
3. http://en.wikipedia.org/wiki/Gator_Bowl_Stadium
Автор: Юрий Шатц (Рига)
! Вопрос 12:
Эта фотография озаглавлена так же, как произведение, созданное четверть века назад. Назовите любого из персонажей этого произведения.
Ответ: [Леонид Ильич] Брежнев или [Эрих] Хонеккер.
Автор назвал фотографию «Господи! Помоги мне выжить среди этой смертной любви». Именно так было озаглавлено знаменитое граффити на Берлинской стене, изображающее поцелуй Брежнева и Хонеккера.
Источник(и):
1. https://leprosorium.ru/comments/1810835/#40433941
2. http://ru.wikipedia.org/wiki/Господи!_Помоги_мне_выжить_среди_этой_смертной_любви
Автор: Виталий Бреев (Рига — Глазго)
!2 тур
Вопрос 1:
History of Saudi Arabia
History of Germany
History of Turkey
По мнению Александра Баунова, авторы англоязычных исторических книг не считают свою трактовку истории единственно возможной. Напишите слово, которое мы пропустили в названиях этих книг.
Ответ: A.
Традиционное для английского языка название книг по истории — например, «A History of Germany» [э хистори оф Джёмани], предполагает, что это лишь одна из возможных историй.
Источник(и): http://slon.ru/world/konets_putina_ekonomista-1190302.xhtml
Автор: Юрий Шатц (Рига)
!Вопрос 2: В одной статье говорится, что ОН играет, как сочетание Пифагора и Пеле. Назовите его фамилию, содержащую апострОф.
Ответ: О’Салливан.
Речь идет о легенде снукера Ронни О’Салливане, который забивает много и с геометрической точностью.
Источник(и): http://www.qz.com/307795/
Автор: Виталий Бреев (Рига — Глазго)
!Вопрос 3: Роберт ПрЕктер подсчитал, что при длительности эксперимента, равной ста месяцам, ОНИ покрыли бы всю Италию. Назовите ИХ.
Ответ: Кролики.
Зачёт: Кролики Фибоначчи.
В мысленном эксперименте Фибоначчи каждая пара кроликов раз в месяц производит еще одну пару. Если бы эксперимент состоялся на самом деле, кролики покрыли бы не только друг друга, но и всю Италию. Известный экономист ПрЕктер сильно ошибся, кроликам хватило бы и 70 месяцев. Вероятно, его экономические предсказания так же точны.
Источник(и):
1. http://www.trader-lib.ru/books/498/12.html
2. http://ru.wikipedia.org/wiki/Числа_Фибоначчи
Автор: Юрий Шатц (Рига)
!Вопрос 4: «Книга Оптики» Ибн Аль ХайсАма, написанная в XI веке, более трехсот лет спустя будет переведена на итальянский язык, что повлечет за собой широкое использование ЕЕ. Назовите ЕЕ словом латинского происхождения.
Ответ: Перспектива.
Для правильного изображения перспективы нужны знания оптики и геометрии. Лоренцо ГибЕрти использовал в своих картинах и комментариях эту работу, после чего перспективу стали широко использовать. Написав вопрос в будущем времени, мы попытались намекнуть на перспективу.
Источник(и):
1. http://en.wikipedia.org/wiki/Book_of_Optics
2. http://en.wikipedia.org/wiki/Perspective_(graphical)
Автор: Юрий Шатц (Рига)
! Вопрос 5:
Многогранник, который вы видите на раздаточном материале, иногда называют медузАэдром. Какие пять букв мы заменили в предыдущем предложении?
Ответ: ехидн.
Этот многогранник иногда называют ехиднАэдром, так как он похож на колючее животное, например, на ежа или ехидну. Медуза и Ехидна — не только животные, но и персонажи древнегреческой мифологии.
Источник(и): http://mathworld.wolfram.com/Echidnahedron.html
Автор: Виталий Бреев (Рига — Глазго)
!Вопрос 6: Какую фамилию упоминает один пользователь сайта reddit.com [рЭддит точка ком], комментируя неудачный автопортрет в зеркале, сделанный на iPhone [айфОн]?
Ответ: Магритт.
На селфи, сделанном на iPhone, яблоко закрывает часть лица, как на картине Магритта.
Источник(и): http://www.reddit.com/r/woahdude/comments/2lfj9j/mfw_i_see_mfw_i_see_mfw_i_see_mfw_i_see_mfw_i_see/cluh7ub
Автор: Виталий Бреев (Рига — Глазго)
!Вопрос 7: Исследуя изображения раковых клеток, ученые предложили новый метод их распознавания. Так как больная клетка растет хаотически, она в бОльшей степени является раком, чем здоровая. В одном из слов предыдущего предложения мы пропустили четыре буквы. Напишите это слово в исходном виде.
Ответ: Фракталом.
Зачёт: Фрактал.
Из-за хаотического роста раковой клетки и ее соседей контуры клетки имеют большие и маленькие впадины и зазубрины с элементами самоподобия. Фрактальная размерность — это математическая величина, которую легко вычислить с помощью компьютера и таким образом автоматически распознать раковые клетки.
Источник(и):
1. http://www.lifescience.net/news/177/fractal-geometry-of-cancer-cells/
2. http://habrahabr.ru/post/208368/
3. http://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+%28Diagnostic%29
Автор: Виталий Бреев (Рига — Глазго)
!Вопрос 8:
rhubarb rhubarb
Актеры массовки британского телевидения иногда используют ревень, по-английски — «rhubarb» [рУбарб]. На какую латинскую фразу ссылается статья английского викисловаря, название которой мы вам раздали?
Ответ: Lorem ipsum [лОрем Ипсум].
Зачёт: Lorem ipsum dolor sit amet [лОрем Ипсум дОлор сит Амет] и т.д. в меру знания командами Цицерона.
Чтобы имитировать звуки толпы, статисты повторяют слова «rhubarb rhubarb» [рУбарб рУбарб]. В похожих целях — как заменитель содержательного текста — дизайнеры и журналисты используют отрывок из трактата Цицерона «О пределах добра и зла», начинающийся со слов «lorem ipsum».
Источник(и): http://en.wiktionary.org/wiki/rhubarb_rhubarb
Автор: Виталий Бреев (Рига — Глазго)
!Вопрос 9: Расставшись с любимой, герой романа Фрэнсиса Скотта ФицджЕральда несколько недель горевал. Прийти в себя ему помог вовремя принятый ИКС. Назовите ИКС двумя словами.
Ответ: Сухой закон.
Герой ушел в запой, и только удачно принятый сухой закон привел его в чувство.
Источник(и): Фрэнсис Скотт Фицджеральд. По эту сторону рая. http://fitzgerald.narod.ru/side/rai2-2.html
Автор: Юрий Шатц (Рига)
!Вопрос 10: В математическом журнале упоминается недавно вышедшая книга под названием «Неопубликованные философские эссе». Виталий Бреев иронически замечает, что ее стоило бы прочитать представителям одной профессии. Какой?
Ответ: Цирюльник.
Зачёт: Парикмахер, брадобрей.
Эссе, включенные в книгу, перестали быть неопубликованными. Это вызывает ассоциации с известным парадоксом, в котором цирюльник бреет всех, кто сам не бреется, и не бреет тех, кто бреется сам. В вопросе не случайно упомянута фамилия его автора — Виталия Бреева.
Источник(и): https://www.maa.org/sites/default/files/321927603814.pdf.bannered.pdf
Автор: Виталий Бреев (Рига — Глазго)
!Вопрос 11: После одного из недавних обновлений Windows [вИндоуз] браузер Chrome [хром] стал неправильно показывать календарь: пропала первая среда года. Статья об этом на русскоязычном сайте называется «Хром, СДЕЛАВШИЙ ЭТО». Кто СДЕЛАЛ ЭТО в голливудском фильме?
Ответ: Гринч.
Первая среда 2015 года — это седьмое января. Статья называлась «Хром, укравший Рождество». Ошибка была вызвана изменениями в российских часовых поясах. «Гринч — похититель Рождества» — фильм 2000 года, а сам Гринч — вредный зеленый персонаж, который не любит Рождество.
Источник(и):
1. http://habrahabr.ru/post/239423/
2. http://ru.wikipedia.org/wiki/Гринч_%E2%80%94_похититель_Рождества
Автор: Юрий Шатц (Рига)
!Вопрос 12: Преуспевающий рэпер КЕндрик ЛамАр утверждает, что лучшее место для отдыха — в тени ЭТОГО. Назовите ЭТО двумя словами на одну букву.
Ответ: Денежное дерево.
Ламар метафорически описывает финансовое благополучие. Денежное дерево, или толстянка, — один из символов богатства.
Источник(и): Kendrik Lamar. Money Trees. http://www.genius.com/1142557/Kendrick-lamar-money-trees
Автор: Виталий Бреев (Рига — Глазго)
!3 тур
Вопрос 1: Британская оккупация Нью-Йорка в 1776 году была затруднена из-за ИКСА, который уже в первую ночь пересек даже Бродвей. В каком романе другой подобный ИКС назван неизбежным?
Ответ: «Война и мир».
Когда британские войска вошли в Нью-Йорк, в городе начался пожар, так же как в Москве 1812 года. Бродвей — сравнительно широкая улица, которая могла бы задержать пожар. Так же как и в Москве, обе стороны обвиняли друг друга в поджоге. Лев Толстой отвергал и те, и другие обвинения, считая пожар при таких обстоятельствах неизбежным.
Источник(и):
1. http://en.wikipedia.org/wiki/Great_Fire_of_New_York_(1776)
2. http://ru.wikisource.org/wiki/Война_и_мир_(Толстой)/Том_III/Часть_III/Глава_XXVI
Автор: Юрий Шатц (Рига)
!Вопрос 2: При пожаре Вестминстерского дворца в 1834 году был утерян, в частности, ИКС. По одной из версий, первым ИКСОМ была талия монарха. Какие два слова мы заменили ИКСОМ?
Ответ: Эталон ярда.
Сгорели эталоны ярда и фунта. Обычно считается, что ярд — это длина шага, или длина руки, или окружность талии одного из английских королей.
Источник(и):
1. http://en.wikipedia.org/wiki/Burning_of_Parliament
2. http://en.wikipedia.org/wiki/Yard
Автор: Юрий Шатц (Рига)
! Вопрос 3: [Ведущему: никак не озвучивать кавычки.]
Входя в комнату в своих алых одеждах, персонаж ФицджЕральда монсиньор
ДАрси напоминал ЕГО закат. ЕГО «Пожар» в 1835 году шокировал англичан.
Назовите ЕГО.
Ответ: [Джозеф Мэллорд Уильям] Тёрнер.
Английский художник Джозеф Тёрнер известен, в частности, своими алыми закатами. На его же картине «Пожар Парламента» изображен упомянутый в прошлом вопросе пожар. Картина вызвала неодобрение публики и критиков и была названа, в частности, невыразительной массой пигментов.
Источник(и):
1. Фрэнсис Скотт Фицджеральд. По эту сторону рая.
http://fitzgerald.narod.ru/side/rai2-2.html
2. http://stencils.com.ua/пожар-парламента-скандал-и-тёрнер/
Автор: Юрий Шатц (Рига)
!Вопрос 4: Эдгар По писал, что через Бродвей протекает всё лучшее, что есть в Америке, и сравнивал Бродвей с НЕЙ. Назовите ЕЕ словом, образованным от греческого корня со значением «подвешивать».
Ответ: Аорта.
Как вам уже известно, Бродвей — широкая улица, поэтому логично его сравнить с самой большой артерией. Аристотель произвел слово «аорта» от корня «подвешивать», так как на ней, можно сказать, подвешено сердце.
Источник(и):
1. http://www.vokrugsveta.ru/vs/article/2662/
2. Александр Аникин. Русский этимологический словарь.
https://books.google.lv/books?id=-Z3SAAAAQBAJ&pg=PA238#v=onepage&q&f=false
Автор: Виталий Бреев (Рига — Глазго)
!Вопрос 5: В статье об одной распространенной фобии упоминается закон герцога Мекленбургского об обязательной отсрочке ИХ на три дня. Назовите ИХ.
Ответ: Похороны.
Закон был принят для предотвращения возможного погребения заживо. Боязнь быть похороненным заживо называется тафофобией. Вместе с боязнью похорон и похоронных принадлежностей она считается одной из базовых фобий. Этой фобией страдали, например, Гоголь и Цветаева.
Источник(и): http://ru.wikipedia.org/wiki/Тафофобия
Автор: Юрий Шатц (Рига)
!Вопрос 6:
Ты рвешься ко мне, и я тебя жду терпеливо.
Твои изгибы, твои роскошные формы
Всё ближе. Бежишь, замедляясь.
Кажется, можно коснуться,
Но ты недостижима.
Бегу бесконечно,
мечтая о том,
что вместе
сольемся
и будем
одним.
Перед вами фрагмент перевода одного стихотворения. Назовите ту, от лица которой оно написано.
Ответ: Асимптота.
В очертаниях стихотворения можно увидеть кривую, стремящуюся к асимптоте. Стихотворение, как видно из текста, обращено к кривой, и написано, соответственно, от лица асимптоты.
Источник(и): http://www.reddit.com/r/math/comments/274pxf/my_friends_and_i_play_a_5_minute_poem_game_my/chxk9dw (в переводе автора вопроса)
Автор: Виталий Бреев (Рига — Глазго)
!Вопрос 7: Шекспировский персонаж, по его словам, настолько истощен, что едва ли на нем можно отыскать ИКС. Назовите ИКС двумя словами.
Ответ: Фунт мяса.
Зачёт: Фунт плоти.
Венецианский купец Антонио сильно похудел от свалившихся на него невзгод, и фунта мяса на нем не найдется.
Источник(и): Уильям Шекспир. Венецианский купец. http://lib.ru/SHAKESPEARE/shks_mercant3.txt
Автор: Юрий Шатц (Рига)
!Вопрос 8: В одном из вариантов ИКСА использовались луки и стрелы. Согласно журнальной статье, в таком ИКСЕ ямы и лужи не так страшны, как в традиционном. Какое слово мы заменили ИКСОМ?
Ответ: Гольф.
Гольфисты с луками и стрелами выигрывали у гольфистов с мячом и клюшкой около 20 ударов. При этом выстрелить из ямы или даже из лужи намного легче, чем клюшкой вытолкать оттуда шарик.
Источник(и): «Popular Mechanics», март 1923 г. https://books.google.lv/books?id=XNoDAAAAMBAJ&pg=PA404#v=onepage&q&f=false
Автор: Юрий Шатц (Рига)
!Вопрос 9: Питер Уоттс описывает распадающийся брак: сначала супруги видятся два раза в неделю, затем раз в неделю, затем лишь раз в две недели. Какое составное прилагательное он при этом упоминает?
Ответ: Радиоактивный.
Уоттс сравнивает брак с радиоактивным образцом, который, как известно, распадается по экспоненциальному закону.
Источник(и): Питер Уоттс. Ложная слепота. http://royallib.com/read/uotts_piter/lognaya_slepota.html#40960
Автор: Виталий Бреев (Рига — Глазго)
!Вопрос 10: Ядерный взрыв даже в пределах прямой видимости не должен был выводить пилота из строя полностью. Поэтому американские летчики времен холодной войны использовали ЕЕ, покрытую золотом или свинцом. Кто использует ЕЕ в патриотическом советском фильме 1943 года?
Ответ: Кутузов.
Предполагалось, что ослепший на один глаз пилот снимет повязку и поведет самолет дальше, используя второй глаз. Позже появились шлемы с позолоченными стеклами. В жизни Кутузов не носил повязки на глаз. Впервые она появилась в фильме «Кутузов», возможно, как напоминание, что даже после тяжелого ранения можно остаться в строю.
Источник(и):
1. http://en.wikipedia.org/wiki/Operation_Looking_Glass
2. http://en.wikipedia.org/wiki/Eyepatch
3. http://www.taday.ru/text/1817347.html
Автор: Юрий Шатц (Рига)
!Вопрос 11: ПхулАн ДЕви — это легендарная индийская королева бандитов, которая позже стала политиком. По словам СалмАна РУшди, она могла на расстоянии плавить винтовки и превращать в резину карандаши журналистов с помощью ИХ. Пожалуйста, не называйте никакое из НИХ. Назовите ИХ.
Ответ: Ругательства.
Зачёт: Проклятия.
Пожалуйста, не забудьте оставить свое мнение о пакете в Живом Журнале и «Канделябре».
Источник(и): Салман Рушди. Сатанинские стихи. http://royallib.com/read/rushdi_ahmed/sataninskie_stihi.html#61440
Автор: Юрий Шатц (Рига)
!Вопрос 12: В романе 1960 года Джон Апдайк упоминает ЕЕ, описывая выключающийся телевизор. Для первой ЕЕ стадии характерно покраснение и распухание. Назовите ЕЕ двумя словами.
Ответ: Смерть звезды.
Зачёт: Гибель звезды.
Большинство звезд перед смертью распухают и становятся красными гигантами или супергигантами, а затем, в зависимости от массы, превращаются в белых карликов, в сверхновые, в черные дыры и так далее. В романе Апдайка маленькая звезда, оставленная электричеством, медленно умирает.
Источник(и):
1. John Updike. Rabbit, Run.
http://www.8reads.com/rabbit-run-john-updike?page=0,3
2. http://www.infoplease.com/ipa/A0004429.html
3. http://cse.ssl.berkeley.edu/bmendez/ay10/2000/cycle/cycle.html
Автор: Виталий Бреев (Рига — Глазго)
![TXT] [XML]
Том 15, № 3 (2018)
Исследуется и публикуется неизвестная ранее запись-автограф Ореста Настурела — знаменитого книжного деятеля первой половины XVII в., внесшего существенный вклад в народное просвещение Валахии. Орест Настурел занимал высокую должность второго логофета при дворе валашского господаря Матея Басараба. Несмотря на занятость, значительную часть своего времени он посвящал собирательству древних рукописей, переводам латинских и церковно-славянских книг на румынский язык, а также их изданию. Установление фактов биографии Ореста Настурела основано в историографии на анализе записей, оставленных им на книгах. Научная новизна данного исследования обусловлена тем, что впервые вводится в научный оборот собственноручная владельческая запись Ореста Настурела, обнаруженная в рукописной книге «Поучения огласительные» Феодора Студита в Собрании славяно-русских рукопис ных книг Е.Е. Егорова Российской государственной биб лиотеки (ОР РГБ. Ф. 98. № 949). Согласно этой записи, датированной 1642-м г., Орест Настурел, инспектируя однажды государевы монастыри, нашел в монастыре Снагове (совр. Румыния) древнюю рассыпающуюся от ветхости рукопись. Поскольку спасти ее было невозможно, Орест Настурел совершил длительное путешествие в г. Рыбницу (совр. Приднестровская Молдавская Республика), где известный книжный мастер по имени Николай выполнил для него в 1642 г. копию этой книги, вложенную затем Орестом в Троицкий монастырь Козия (совр. Румыния). В XIX в. книга, по-видимому, была вывезена русскими старообрядцами в Россию, где сначала попала в коллекцию антиквара-букиниста И.Л. Силина, а затем была куплена у него Е.Е. Егоровым. Проведены датировка рукописи по филиграням (40-е гг. XVII в.) и сопоставление почерка записи с известными автографами Ореста Настурела. Отмечается, что прекрасная заставка и инициалы егоровского сборника близки рукописному «Октоиху» середины XVII столетия, хранящемуся в Белграде в Библиотеке Сербской патриархии. Согласно имеющейся в нем приписке, «Октоих» выполнен в одном из славянских монастырей Афона. Установлено, что подобное художест венное оформление было достаточно популярным для южнославянских рукописей в середине XVII в., и, следовательно, оно вряд ли было скопировано писцом Николаем с древнего оригинала. Основными результатами исследования являются обнаружение, идентификация, атрибуция, прочтение и публикация неучтенной ранее записи-автографа, а также географическая и хронологическая локализация списка. Автор подчеркивает ценность егоровского сборника для изучения специалистами в области филологии и лингвистики и ставит перспективную задачу воссоздания содержания, языковых особенностей и датировки утраченного протографа.
квадратный корень из 15 — Как найти квадратный корень из 15?
Квадратный корень из 15 выражается как √15 в радикальной форме и как (15) ½ или (15) 0,5 в экспоненциальной форме. Квадратный корень из 15, округленный до 8 знаков после запятой, составляет 3,872. Это положительное решение уравнения x 2 = 15.
- Квадратный корень из 15: 3.872
6207417 - Квадратный корень из 15 в экспоненциальной форме: (15) ½ или (15) 0.5
- Квадратный корень из 15 в радикальной форме: √15
Что такое квадратный корень из 15?
Мы знаем, что сложение имеет обратную операцию как вычитание, а умножение имеет обратную операцию как деление. Точно так же поиск квадратного корня — это операция, обратная возведению в квадрат. Квадратный корень из 15 — это число, которое умножается на себя, чтобы получить число 15. Итак, мы должны подумать о числе, квадрат которого равен 15. Методом проб и ошибок мы видим, что не существует целого числа, чей квадрат равен 15 Но мы можем найти квадратный корень из 15 с помощью калькулятора и получить √15 приблизительно 3.872983 … Мы можем проверить этот ответ, и нам наверняка понадобится здесь калькулятор, 3,872983 × 3,872983 … примерно 14,9999
289 … Уф! Это довольно близко к 15. Является ли квадратный корень из 15 рациональным или иррациональным?
Квадратный корень из 15 не является рациональным числом. Это иррациональное число. Вот почему. Рациональное число — это число, которое может быть выражено в форме p / q, где p, q ∈ Z и q ≠ 0. Число является иррациональным, если оно не завершается без повторяющихся шаблонов в его десятичной части.Теперь давайте посмотрим на квадратный корень из 15, десятичное представление √15 — 3,872
621 … Как вы думаете, десятичная часть останавливается после 3,872 621 …? Нет, это никогда не кончится. Это непрерывная десятичная дробь с неповторяющимися цифрами. Число 2,15215427125 … нельзя записать в форме p / q, где p и q — целые числа. Итак, квадратный корень из 15 не является рациональным числом. Это иррациональное число. Как найти квадратный корень из 15?
Мы обсудим два метода нахождения квадратного корня из 15.Выразите подкоренное выражение как произведение, состоящее из идеального квадрата (ов) и упростив его
Метод деления в длину для идеальных и несовершенных квадратов. Давайте обсудим первый метод. Упрощение квадратного корня означает его переписывание таким образом, чтобы в подкоренном выражении не осталось полных квадратов. √50 можно упростить до 5√2, но нельзя упростить √15. Давайте узнаем причину. Разложение 15 на простые множители равно 15 = 3 × 5 . Для дальнейшего упрощения √15 нам понадобится одна или несколько пар одинаковых факторов.Таких пар факторов нет. Следовательно, √15 не может быть далее упрощено.Квадратный корень из 15 по длинному делению
Значение квадратного корня из 15 путем деления в столбик определяется с помощью следующих шагов:
- Шаг 1 : Начиная справа, мы объединим цифры в пары, поместив над ними полосу.
- Шаг 2 : Найдите число, умножение которого на само дает, что произведение меньше или равно 15 и близко к 15.Итак, число равно 3. Положив делитель как 3, мы получим частное как 3 (то же, что и делитель), а остаток будет равен 6 .
- Шаг 3: Удвойте делитель и введите его с пробелом справа. Угадайте наибольшую возможную цифру, чтобы заполнить пробел, который станет новой цифрой в частном, так что, когда новый делитель умножается на новое частное, полученное произведение меньше или равно деленному. Разделите и запишите остаток. Повторяйте этот процесс, чтобы получить десятичные знаки, пока не захотите.
Квадратный корень из 15 методом длинного деления = 3,872 (с точностью до трех знаков после запятой)
Аналогично
- Квадратный корень из 20 = 4,472 (с точностью до трех знаков после запятой)
- Квадратный корень из 25 = 5
- Квадратный корень из 16 = 4
- Квадратный корень из 14 = 3,741 (с точностью до трех знаков после запятой)
25 и 16 являются точными квадратами, поскольку их квадратные корни являются целыми числами.
Изучите квадратные корни с помощью иллюстраций и интерактивных примеров
- У Дженни квадратный стол площадью 15 квадратных дюймов.Она накрыла его скатертью площадью 25 квадратных дюймов. На сколько дюймов ткань висит вокруг стола с каждой стороны?
- Квадратный корень — это операция, обратная возведению в квадрат.
- Квадратный корень из 15 может быть выражен как √15 или 15 ½ . Это иррациональное число.
- Мы можем найти квадратный корень из 15, используя метод длинного деления. Квадратный корень из 15 методом длинного деления = 3,872 (с точностью до трех знаков после запятой)
Пример 1 : Mr.Джонсон хочет ограждать свой квадратный сад. Сад имеет площадь 15 квадратных футов. Какова длина каждой стороны сада? Округлите ответ до трех десятичных знаков.
Решение
Мы знаем, что площадь квадрата равна стороне × стороне. Если принять длину сада за x, то x × x = 15
Мы можем легко узнать значение x, используя понятие квадратного корня. Квадратный корень из 15 равен примерно 3,872 √15 (округлено до трех знаков после запятой).
Итак, длина стороны сада примерно 3.872 футов.Пример 2 : У Мэтью есть картон площадью 15 кв. Он измерил, что длина доски каррома составляет 3,872 единицы. Почему это так?
Решение
Мы знаем, что площадь квадрата равна стороне × стороне. Длина квадратной доски каррома составляет 3,872, это означает 3,872 x 3,872 = 14,99 квадратных единиц, а ближайшее целое число равно 15. Найдя квадратный корень из площади 15 квадратных единиц, мы можем найти длину стороны квадрата. доска каррома.
Сторона квадратной доски = √15 = 3,872.
Таким образом, длина стороны каррома составляет 3,872 единицы.Пример: Если площадь квадрата равна 15 из 2 . Найдите длину стороны квадрата.
Решение:
Пусть ‘a’ будет длиной стороны квадрата.
⇒ Площадь квадрата = a 2 = 15 из 2
⇒ a = ± √15 дюймов
Поскольку длина не может быть отрицательной,
⇒ а = √15 = 3.873 из
перейти к слайду перейти к слайду
Разбивайте сложные концепции с помощью простых визуальных элементов.
Математика больше не будет сложным предметом, особенно если вы понимаете концепции посредством визуализации.
Забронируйте бесплатную пробную версию Класс
Часто задаваемые вопросы о квадратном корне из 15
Что такое квадратный корень из 15?
Квадратный корень из 15 равен 3,87298.
Почему квадратный корень из 15 — иррациональное число?
После факторизации на простые множители 15 i.е. 3 1 × 5 1 , 3 в нечетной степени. Следовательно, квадратный корень из 15 иррационален.
Что такое квадратный корень из 5 из 15?
Квадратный корень из 15 равен 3,873. Следовательно, 5 √15 = 5 × 3,873 = 19,365.
Что такое квадрат квадратного корня из 15?
Квадрат квадратного корня из 15 — это само число 15, т.е. (√15) 2 = (15) 2/2 = 15.
Что такое квадратный корень из 15 в простейшей радикальной форме?
Нам нужно выразить 15 как произведение его простых множителей i.е. 15 = 3 × 5. Следовательно, как видно, радикальная форма квадратного корня из 15 не может быть далее упрощена. Следовательно, простейшая радикальная форма квадратного корня из 15 может быть записана как √15
Что такое квадратный корень из -15?
Квадратный корень -15 — мнимое число. Его можно записать как √-15 = √-1 × √15 = i √15 = 3.872i
где i = √-1 и называется мнимой единицей.Калькулятор корня
Калькулятор квадратного корня
Калькулятор кубического корня
Калькулятор общего корня
Калькулятор связанных показателей | Научный калькулятор | Log CalculatorВ математике общий корень или корень n th числа a — это другое число b , которое при умножении на себя n раз равно a .В формате уравнения:
n √a = b
б п = аОценка корня
Некоторые общие корни включают квадратный корень, где n, = 2, и кубический корень, где n, = 3. Вычисление квадратных корней и n -го корня является довольно трудоемким. Это требует оценки, проб и ошибок. Существуют более точные и эффективные способы вычисления квадратных корней, но ниже приведен метод, который не требует значительного понимания более сложных математических концепций.Для расчета √a:
- Оценить число b
- Разделите a на b . Если возвращаемое число c является точным до желаемого десятичного разряда, остановитесь.
- Среднее значение b и c и использовать результат как новое предположение
- Повторите шаг два
EX: Найти √27 до 3 десятичных знаков Предположение: 5.125
27 ÷ 5.125 = 5,268
(5,125 + 5,268) / 2 = 5,197
27 ÷ 5,197 = 5,195
(5,195 + 5,197) / 2 = 5,196
27 ÷ 5,196 = 5,196Оценка n
th КореньВычисление корней n th может быть выполнено с использованием аналогичного метода с изменениями для работы с n . Вычисление квадратного корня полностью вручную утомительно. Оценить более высокие корни n th , даже если использовать калькулятор для промежуточных шагов, значительно утомительнее.Для тех, кто разбирается в рядах, см. Здесь более математический алгоритм для вычисления корней n th . Для более простого, но менее эффективного метода перейдите к следующим шагам и примеру. Для расчета n √a:
- Оценить число b
- Разделите a на b n-1 . Если возвращаемое число c является точным до желаемого десятичного разряда, остановитесь.
- Среднее значение: [b × (n-1) + c] / n
- Повторите шаг два
EX: Найти 8 √15 до 3 знаков после запятой Угадай: 1.432
15 ÷ 1,4327 = 1,405
(1,432 × 7 + 1,405) / 8 = 1,388
15 ÷ 1,388 7 = 1,403
(1,403 × 7 + 1,388) / 8 = 1,402Тогда должно быть ясно, что дальнейшие вычисления приведут к числу, округляемому до 1,403, в результате чего 1,403 будет окончательной оценкой с точностью до 3 знаков после запятой.
Калькулятор квадратного корня. Найдите квадратный корень за один простой шаг.
Наш калькулятор квадратного корня вычисляет квадратный корень любого положительного числа, которое вы хотите.Просто введите выбранный номер и ознакомьтесь с результатами. Все рассчитывается быстро и автоматически ! С помощью этого инструмента вы также можете оценить квадрат желаемого числа (просто введите значение во второе поле), что может оказаться большим подспорьем в поиске точных квадратов по формуле квадратного корня. Вы боретесь с основными арифметическими операциями: сложение квадратных корней, вычитание квадратных корней, умножение квадратных корней или деление квадратных корней? Уже нет! В следующем тексте вы найдете подробное объяснение о различных свойствах квадратного корня, например.g., как упростить квадратные корни, с множеством различных примеров . Из этой статьи вы раз и навсегда узнаете, как находить квадратные корни!
Вы когда-нибудь задумывались, каково происхождение символа квадратного корня √? Уверяем вас, что эта история не так проста, как вы могли подумать вначале. Происхождение символа корня восходит к древним временам, как происхождение знака процента.
Если вы ищете граф квадратного корня или свойства функции квадратного корня, перейдите непосредственно в соответствующий раздел (просто нажмите на ссылки выше!).Здесь мы объясняем, что такое производная квадратного корня, используя определение фундаментального квадратного корня; мы также подробно рассмотрим, как вычислять квадратные корни из экспонент или квадратные корни из дробей. Наконец, если вы будете достаточно настойчивы, вы обнаружите, что квадратный корень из отрицательного числа на самом деле возможен. Таким образом, мы вводим комплексных чисел , которые находят широкое применение в физике и математике.
Символ квадратного корня √
Операция извлечения квадратного корня из числа была известна еще в древности.Самая ранняя глиняная табличка с правильным значением √2 = 1,41421 до 5 знаков после запятой происходит из Вавилонии (1800 г. до н.э. — 1600 г. до н.э.) г. Многие другие документы показывают, что квадратные корни также использовали древние египтяне, индийцы, греки и китайцы. Однако происхождение корневого символа √ все еще остается в значительной степени спекулятивным.
- Многие ученые считают, что квадратные корни происходят от буквы «r» — первой буквы латинского слова Radix, означающего корень,
- другая теория утверждает, что символ квадратного корня был взят из арабской буквы ج , которая была помещена в исходной форме ﺟ в слове جذر — корень (арабский язык пишется справа налево).
Первое использование символа квадратного корня √ не включало горизонтальную «черту» над числами внутри символа квадратного корня (или радикала), √‾. «Бар» на латыни известен как vinculum, что означает облигация . Хотя радикальный символ с винкулумом сейчас используется в повседневной жизни, мы обычно опускаем эту черту во многих текстах, например, в статьях в Интернете. Обозначение высших степеней корня было предложено Альбертом Жираром, который поместил указатель степени в начало знака корня, т.е.г., ³√ или ⁴√.
Последний вопрос: почему операция извлечения квадратного корня называется корнем независимо от ее истинного происхождения? Объяснение станет более очевидным, если мы запишем уравнение x = ⁿ√a в другой форме: xⁿ = a. x называется корнем или радикалом, потому что это скрытое основание a. Таким образом, слово радикальный не означает далеко идущий или крайний , а вместо этого фундаментальный, достигающий первопричины .
Определение квадратного корня
В математике традиционными операциями с числами являются сложение, вычитание, умножение и деление.Тем не менее, мы иногда добавляем в этот список некоторые более сложные операции и манипуляции: квадратных корней , возведение в степень, логарифмические функции и даже тригонометрические функции (например, синус и косинус). В этой статье мы сосредоточимся только на определении квадратного корня.
Квадратный корень из заданного числа
x— это каждое числоy, квадрат которогоy² = y * yдает исходное числоx. Следовательно, формула квадратного корня может быть выражена как:√x = y ⟺ x = y²,, где
⟺— математический символ, который означает тогда и только тогда, когда .Каждое положительное действительное число всегда имеет два квадратных корня — первый положительный, а второй отрицательный. (0.5)В геометрической интерпретации квадратный корень из данной площади квадрата дает длину его стороны. Вот почему в названии
√есть слово , квадрат . Аналогичная ситуация и с кубическим корнем∛. Если вы берете кубический корень из объема куба, вы получаете длину его ребер. В то время как квадратные корни используются при рассмотрении площади поверхности, кубические корни полезны для определения величин, относящихся к объему, например плотности.Как найти квадратный корень?
Может быть, мы не очень скромны, но мы думаем, что лучший ответ на вопрос, как найти квадратный корень, прост: используйте калькулятор квадратного корня! Вы можете использовать его как на компьютере, так и на смартфоне, чтобы быстро вычислить квадратный корень из заданного числа.К сожалению, бывают ситуации, когда можно рассчитывать только на себя, что тогда? Чтобы подготовиться к этому, вы должны запомнить несколько основных идеальных квадратных корней:
- квадратный корень из 1:
√1 = 1, так как1 * 1 = 1; - квадратный корень из 4:
√4 = 2, так как2 * 2 = 4; - квадратный корень из 9:
√9 = 3, так как3 * 3 = 9; - квадратный корень из 16:
√16 = 4, так как4 * 4 = 16; - квадратный корень из 25:
√25 = 5, так как5 * 5 = 25; - квадратный корень из 36:
√36 = 6, так как6 * 6 = 36; - квадратный корень из 49:
√49 = 7, так как7 * 7 = 49; - квадратный корень из 64:
√64 = 8, так как8 * 8 = 64; - квадратный корень из 81:
√81 = 9, так как9 * 9 = 81; - квадратный корень из 100:
√100 = 10, так как10 * 10 = 100; - квадратный корень из 121:
√121 = 11, так как11 * 11 = 121; - квадратный корень из 144:
√144 = 12, так как12 * 12 = 144;
Приведенные выше числа являются простейшими квадратными корнями, потому что каждый раз вы получаете целое число.Попробуй их запомнить! Но что делать, если есть число, у которого нет такого красивого квадратного корня? Есть несколько решений. Прежде всего, можно попробовать спрогнозировать результат методом проб и ошибок . Допустим, вы хотите вычислить квадратный корень из
52:- Вы знаете, что
√49 = 7и√64 = 8, поэтому значение√52должно быть между7и8. Номер -
52ближе к49(фактически ближе к7), поэтому вы можете попробовать угадать, что√52— это7.3. - Затем возводите в квадрат
7,3, получая7,3² = 53,29(как говорит формула квадратного корня), что больше, чем52. Вы должны попробовать с меньшим числом, скажем,7.2. - Квадрат
7,2равен51,84. Теперь у вас меньшее число, но оно намного ближе к52. Если такая точность вас устраивает, можете закончить оценку здесь. В противном случае вы можете повторить процедуру с выбранным числом от7.2и7.3, например,7.22и так далее и так далее.
Другой подход состоит в том, чтобы сначала упростить квадратный корень, а затем использовать приближения квадратных корней из простых чисел (обычно с округлением до двух знаков после запятой):
- квадратный корень из 2:
√2 ≈ 1,41, - квадратный корень из 3:
√3 ≈ 1,73, - квадратный корень из 5:
√5 ≈ 2,24, - квадратный корень из 7:
√7 ≈ 2.65, - квадратный корень из 11:
√11 ≈ 3,32, - квадратный корень из 13:
√13 ≈ 3,61, - квадратный корень из 17:
√17 ≈ 4,12, - квадратный корень из 19:
√19 ≈ 4,34и т. Д.
Давайте попробуем снова найти квадратный корень из
52. Вы можете упростить его до√52 = 2√13(вы узнаете, как упростить квадратный корень в следующем разделе), а затем замените√13 ≈ 3,61. Наконец, произведем умножение√52 ≈ 2 * 3.61 = 7,22. Результат такой же, как и раньше!Вы можете проверить, является ли число простым или нет, с помощью нашего калькулятора простых чисел. Простое число — это натуральное число (больше единицы), которое не может быть получено как произведение двух меньших натуральных чисел. Например, 7 — простое число, потому что вы можете получить его, только умножив
1 * 7или7 * 1. С другой стороны, число 8 не является простым, потому что вы можете сформировать его, умножив2 * 4или4 * 2(помимо произведения 1 и самого 8).Калькулятор квадратного корня
В некоторых ситуациях вам не нужно знать точный результат вычисления квадратного корня. В этом случае наш калькулятор квадратного корня — лучший вариант для оценки значения за каждый квадратный корень, который вы хотите . Например, предположим, вы хотите узнать, больше ли
4√5, чем9. Из калькулятора вы знаете, что√5 ≈ 2,23607, поэтому4√5 ≈ 4 * 2,23607 = 8,. Он очень близок к 9, но не больше его! Калькулятор квадратного корня дает окончательное значение с относительно высокой точностью (до пяти цифр в приведенном выше примере).С помощью калькулятора значащих цифр вы можете вычислить этот результат до любого количества значащих цифр.Помните, что наш калькулятор автоматически пересчитывает числа, введенные в любое из полей. Вы можете найти квадратный корень из определенного числа, заполнив первое окно, или получить квадрат числа, введенного вами во втором окне. Второй вариант удобен в для нахождения идеальных квадратов , которые необходимы во многих аспектах математики и естественных наук.Например, если вы введете
17во второе поле, вы обнаружите, что289— это полный квадрат.В некоторых приложениях извлечения квадратного корня, особенно относящихся к таким наукам, как химия и физика, предпочтение отдается результатам в научных обозначениях. Короче говоря, ответ в научном представлении должен иметь десятичную точку между первыми двумя ненулевыми числами и будет представлен как десятичная дробь, умноженная на 10, возведенная в степень. Например, число
0.00345записывается как3,45 * 10⁻³в экспоненциальном представлении, тогда как145,67записывается как1,4567 * 10²в экспоненциальном представлении. Результаты, полученные с помощью калькулятора квадратного корня, можно преобразовать в экспоненциальную нотацию с помощью калькулятора.Как упростить извлечение квадратного корня?
Во-первых, давайте спросим себя, какие квадратные корни можно упростить. Чтобы ответить на него, вам нужно взять число, стоящее после символа квадратного корня, и найти его множители.Если какой-либо из его множителей является квадратным числом (4, 9, 16, 25, 36, 49, 64 и т. Д.), То вы можете упростить квадратный корень. Почему эти числа квадратные? Они могут быть соответственно выражены как 2², 3², 4², 5², 6², 7² и т. Д. Согласно определению квадратного корня, вы можете назвать их полных квадратов . У нас есть специальный инструмент, называемый калькулятором коэффициентов, который может быть здесь очень кстати. Давайте посмотрим на несколько примеров:
- Можете ли вы упростить √27? С помощью упомянутого выше калькулятора вы получаете множители 27: 1, 3, 9, 27.(1/2) ⟺ √ (x * y) = √x * √y ,
Как вы можете использовать эти знания? Аргумент квадратного корня обычно не является точным квадратом, который можно легко вычислить, но он может содержать идеальный квадрат среди своих множителей. Другими словами, вы можете записать это как умножение двух чисел, где одно из чисел представляет собой полный квадрат, например,
45 = 9 * 5(9 — это полный квадрат). Требование иметь по крайней мере один множитель , который является полным квадратом, необходимо для упрощения квадратного корня.(1/2) = √9 * √5 = 3√5 .Вы успешно упростили свой первый квадратный корень! Конечно, вам не обязательно записывать все эти расчеты. Если вы помните, что квадратный корень эквивалентен степени половины , вы можете сократить их. Попрактикуемся в упрощении квадратных корней на некоторых других примерах:
- Как упростить квадратный корень из 27?
√27 = √ (9 * 3) = √9 * √3 = 3√3; - Как упростить квадратный корень из 8?
√8 = √ (4 * 2) = √4 * √2 = 2√2; - Как упростить квадратный корень из 144?
√144 = √ (4 * 36) = √4 * √36 = 2 * 6 = 12.
В последнем примере вам вообще не нужно было упрощать квадратный корень, потому что 144 — это полный квадрат. Вы можете просто вспомнить, что 12 * 12 = 144. Однако мы хотели показать вам, что с помощью процесса упрощения вы также можете легко вычислить квадратные корни из полных квадратов. Это полезно, когда имеет дело с большими числами .
Наконец, вы можете спросить, как упростить корни более высокого порядка, например, кубические корни. Фактически, этот процесс очень похож на квадратные корни, но в случае кубических корней вы должны найти хотя бы один множитель, который представляет собой идеальный куб , а не идеальный квадрат, т.е.е., 8 = 2³, 27 = 3³, 64 = 4³, 125 = 5³ и так далее. Затем вы делите свое число на две части и кладете под кубический корень. Возьмем следующий пример упрощения ³√192:
∛192 = ∛ (64 * 3) = ∛64 * ∛3 = 4∛3На первый взгляд это может показаться немного сложным, но после некоторой практики вы сможете упростить корни в своей голове . Доверься нам!
Сложение, вычитание, умножение и деление квадратных корней
Сложение квадратных корней и вычитание квадратных корней
К сожалению, сложение или вычитание квадратных корней не так просто, как сложение / вычитание обычных чисел.Например, если 2 + 3 = 5, это не означает, что √2 + √3 равно √5. Это неправильно! Чтобы понять, почему это так, представьте, что у вас есть два разных типа фигур: треугольники 🔺 и круги 🔵. Что произойдет, если вы добавите один треугольник к одному кругу 🔺 + 🔵? Ничего такого! У вас остались один треугольник и один круг 🔺 + 🔵. С другой стороны, что происходит, когда вы пытаетесь добавить три треугольника к пяти треугольникам: 3 🔺 + 5 🔺? У нас получится восемь треугольников 8 🔺.
Сложение квадратного корня очень похоже на это.Результат сложения √2 + √3 по-прежнему равен √2 + √3. Вы не можете упростить это дальше. Однако это другая ситуация, когда оба квадратных корня имеют одинаковое число под символом корня . Затем мы можем складывать их как обычные числа (или треугольники). Например, 3√2 + 5√2 равно 8√2. То же самое и с вычитанием квадратных корней. Давайте посмотрим на другие примеры, иллюстрирующие это свойство квадратного корня:
- Что такое
6√17 + 5√17? Ответ:6√17 + 5√17 = 11√17; - Что такое
4√7 - 7√7? Ответ:4√7 - 7√7 = -3√7; - Что такое
2√2 + 3√8? Ответ:2√2 + 3√8 = 2√2 + 6√2 = 8√2, потому что мы упростили √8 = √ (4 * 2) = √4 * √2 = 2√2; - Что такое
√45 - √20? Ответ:√45 - √20 = 3√5 - 2√5 = √5, потому что мы упростили √45 = √ (9 * 5) = √9 * √5 = 3√5 и √20 = √ (4 * 5) = √4 * √5 = 2√5; - Что такое
7√13 + 2√22? Ответ:7√13 + 2√22, мы не можем упростить это дальше; - Что такое
√3 - √18? Ответ:√3 - √18 = √3 - 3√2, мы не можем упростить это дальше, чем это, но мы, по крайней мере, упростили √18 = √ (9 * 2) = √9 * √2 = 3√ 2.(1/2) ⟺ √x * √y = √ (x * y) .В отличие от сложения, вы можете умножить на каждые два квадратных корня. Помните, что умножение имеет коммутативные свойства , это означает, что порядок, в котором умножаются два числа, не имеет значения. Несколько примеров должны прояснить этот вопрос:
- Что такое
√3 * √2? Ответ:√3 * √2 = √6; - Что такое
2√5 * 5√3? Ответ:2√5 * 5√3 = 2 * 5 * √5 * √3 = 10√15, потому что умножение коммутативно; - Что такое
2√6 * 3√3? Ответ:2√6 * 3√3 = 2 * 3 * √6 * √3 = 6√18 = 18√3, мы упростили √18 = √ (9 * 2) = √9 * √2 = 3√ 2.(1/2) ⟺ √x / √y = √ (x / y) .Все, что вам нужно сделать, это заменить знак умножения на деление. Однако деление не является коммутативным оператором ! Вы должны вычислить числа перед квадратными корнями и числа под квадратными корнями по отдельности. (1/2) .(1/2) ⟺ √x / √y = √ (x / y) ,
, где
x / y— дробная часть. Ниже вы можете найти несколько примеров квадратных корней из дроби:- квадратный корень из 4/9:
√ (4/9) = √4 / √9 = 2/3, - квадратный корень из 1/100:
√ (1/100) = √1 / √100 = 1/10, - квадратный корень из 1/5:
√ (1/5) = √1 / √5 = 1 / √5 = √5 / 5.
Оставлять корни в знаменателе — не очень хорошая привычка. Вот почему мы избавились от него в последнем примере.Мы просто умножили числитель и знаменатель на одно и то же число (мы всегда можем это сделать, так как число, которое мы умножаем на 1), в данном случае на
√5.Функция квадратного корня и график
Функции играют жизненно важную роль не только в математике, но и во многих других областях, таких как физика, статистика или финансы. Функция
f (x)— это не что иное, как формула, которая говорит, как значениеf (x)изменяется с аргументомx. Чтобы увидеть некоторые примеры, ознакомьтесь с нашими финансовыми инструментами, созданными финансовыми специалистами, например, калькулятор сложных процентов или калькулятор будущей стоимости.Там вы найдете несколько функций, которые можно применить в реальной жизни. Они очень полезны, если вы хотите знать, как рассчитать сложные проценты или оценить будущую стоимость аннуитета.Ниже вы можете найти график квадратного корня, составленный из , половина параболы . Проверьте его и попробуйте проверить, например, является ли функция квадратного корня
x = 93, аx = 16равна4(как и должно быть).Давайте вернемся к функции квадратного корня
f (x) = √xи исследуем ее основные свойства .Мы рассматриваем только положительную частьf (x)(как вы можете видеть на графике квадратного корня выше). Итак, функция квадратного корня:- — непрерывно и увеличивается для всех неотрицательных
x, - — это , дифференцируемая для всех положительных
x(дополнительные сведения см. В разделе о производной квадратного корня), - приближается к пределу бесконечности , когда
xприближается к бесконечности (lim √x → ∞, когдаx → ∞), - — это действительное число для всех неотрицательных
xи комплексное число для всех отрицательныхx(подробнее об этом мы пишем в разделе квадратного корня из отрицательного числа).
Вы, наверное, уже заметили, что квадратный корень из площади квадрата дает длину его стороны. Эта функция используется в одном из наших строительных калькуляторов — калькуляторе квадратных метров. Если вы планируете что-либо отремонтировать в будущем, эти инструменты могут вам очень помочь. Не забывайте их использовать!
Производная квадратного корня
Производная функции сообщает нам, насколько быстро эта функция изменяется вместе со своим аргументом. Один из простейших примеров в физике — это положение объекта и его скорость (скорость изменения положения).Допустим, функция
x (t)описывает, как расстояние движущегося автомобиля от определенной точки изменяется со временемt. Вы знаете, что определяет, насколько быстро меняется пройденное вами расстояние? Ответ — скорость машины! Таким образом, производная положенияx (t)— это скоростьv (t)(скорость также может зависеть от времени). Для обозначения производной мы обычно используем апострофv (t) = x '(t)или символ производнойv (t) = dx (t) / dt.(-1/2) = 1 / (2√x) .Так как число в отрицательной степени на единицу больше этого числа, оценка вывода будет включать дроби. У нас есть инструмент, который может оказаться незаменимым при сложении или вычитании дробей с разными знаменателями. Он называется калькулятором НОК и объясняет, как найти наименьшее общее кратное.
Производная квадратного корня необходима для получения коэффициентов в так называемом разложении Тейлора . Мы не хотим слишком углубляться в детали, поэтому, вкратце, серия Тейлора позволяет вам аппроксимировать различные функции с помощью многочленов, которые намного проще вычислить.Например, разложение Тейлора
√ (1 + x)вокруг точкиx = 0дается следующим образом:√ (1 + x) = 1 + 1/2 * x - 1/8 * x² + 1/16 * x³ - 5/128 * x⁴ + ...,, что действительно для
-1 ≤ x ≤ 1. Хотя в приведенном выше выражении содержится бесконечное количество членов, чтобы получить приблизительное значение, вы можете использовать всего несколько первых членов. Давай попробуем! Приx = 0,5и первых пяти членах вы получаете:√ (1,5) = 1 + 1/2 * 0.5 - 1/8 * 0,25 + 1/16 * 0,125 - 5/128 * 0,0625,√ (1,5) ≈ 1,2241,, а действительное значение, предоставленное нашим калькулятором, составляет
√ (1,5) ≈ 1,2247. Достаточно близко!Пока что это было много математики и уравнений. Для тех из вас, кто достаточно настойчив, мы подготовили следующий раздел, в котором объясняется, как вычислить квадратный корень из отрицательного числа.
Корень квадратный из отрицательного числа
В школе вас, вероятно, учили, что квадратного корня из отрицательного числа не существует.Это верно, если рассматривать только действительные числа. Давным-давно для выполнения сложных вычислений математикам приходилось вводить более общий набор чисел — комплексных чисел . Их можно выразить в следующей форме:
х = а + Ь * я,, где
x— комплексное число с действительной частьюaи мнимой частьюb. Что отличает комплексное число от действительного, так это мнимое числоi.Вот несколько примеров комплексных чисел:2 + 3i,5i,1,5 + 4i,2. Вы можете быть удивлены, увидев там2, что является реальным числом. Да, но это также комплексное число сb = 0. Комплексные числа являются обобщением действительных чисел.Пока что воображаемое число
i, наверное, до сих пор для вас загадка. Что это вообще такое? Что ж, хотя это может показаться странным, это определяется следующим уравнением:я = √ (-1),, и это все, что вам нужно для вычисления квадратного корня из каждого числа, независимо от того, положительное оно или нет.Давайте посмотрим на несколько примеров:
- квадратный корень из -9:
√ (-9) = √ (-1 * 9) = √ (-1) √9 = 3i, - квадратный корень из -13:
√ (-13) = √ (-1 * 13) = √ (-1) √13 = i√13, - квадратный корень из -49:
√ (-49) = √ (-1 * 49) = √ (-1) √49 = 7i.
Разве не все просто? Эта проблема не возникает с кубическим корнем, поскольку отрицательное число можно получить, умножив три одинаковых отрицательных числа (чего нельзя сделать с двумя отрицательными числами).Например:
³√ (-64) = ³√ [(- 4) * (- 4) * (- 4)] = -4.Это, вероятно, все, что вам следует знать о квадратных корнях. Мы ценим, что вы остались с нами до этого момента! В качестве награды испеките себе что-нибудь сладкое 🙂 Воспользуйтесь нашим калькулятором идеальных блинов, чтобы узнать, как приготовить идеальный блин, каким бы он вам ни нравился. Вам может понадобиться наш калькулятор граммов в чашки, чтобы помочь вам в этом. Он работает в обоих направлениях, то есть для преобразования граммов в чашки и преобразования чашек в граммы.А если вы спросите себя: «Сколько калорий мне нужно есть в день?», Воспользуйтесь нашим удобным калькулятором калорий!
FAQ
Может ли число иметь более одного квадратного корня?
Да, на самом деле все положительные числа имеют 2 квадратных корня , один положительный, а другой равный первому, но отрицательный. Это потому, что если вы умножите два негатива вместе, негативы аннулируются и результат будет положительным.
Как найти квадратный корень без калькулятора?
- Вычислите квадратного корня.Ближайшее квадратное число приемлемо, если вы в затруднении.
- Разделите число, из которого вы хотите найти квадратный корень, на оценку.
- Добавьте оценку к результату шага 2.
- Разделите результат шага 3 на 2. Это ваша новая оценка .
- Повторите шаги 2–4 с новой оценкой. Чем больше раз это повторяется, тем точнее будет результат.
Как вычислить квадратные корни?
- Найдите ближайшее квадратное число выше и ниже числа, о котором вы думаете.
- Квадратный корень будет между квадратными корнями этих чисел.
- Близость числа к квадратному корню указывает, насколько близок корень. Например, 26 очень близко к 25, поэтому корень будет очень близок к 5.
- Попробуйте несколько раз разобраться в этом .
Является ли квадратный корень из 2 рациональным числом?
Нет, квадратный корень из 2 не является рациональным . Это связано с тем, что, когда 2 записывается как дробь, 2 / 1 , она никогда не может иметь только четные показатели, и поэтому рациональное число не может быть возведено в квадрат для его создания.
Как избавиться от квадратного корня?
В алгебре возведение в квадрат обеих частей уравнения избавит от любых квадратных корней . Результатом этой операции является то, что квадратные корни будут заменены любым числом, из которого они находили квадратный корень.
Являются ли квадратные корни рациональными?
Некоторые квадратные корни являются рациональными , а другие нет. Вы можете определить, является ли квадратный корень рациональным или нет, выяснив, может ли число, которое вы извлекаете квадратным корнем, быть выражено только с помощью четных показателей (например,грамм. 4 = 2 2 /1 2 ). Если может, то его корень рациональный .
Является ли квадратный корень из 5 рациональным числом?
Квадратный корень из 5 — это , не рациональное число . Это связано с тем, что 5 не может быть выражено дробью, если числитель и знаменатель имеют четные показатели. Это означает, что рациональное число нельзя возвести в квадрат, чтобы получить 5.
Является ли квадратный корень из 7 рациональным числом?
Результатом квадратного корня 7 является иррациональное число .7 не может быть записано в виде дроби только с четными показателями, что означает, что число, возведенное в квадрат для достижения 7, не может быть выражено как дробь целых чисел, и поэтому не является рациональным.
Какова производная квадратного корня из x?
Производная квадратного корня x равна x — 1 / 2 / 2 , или 1 / 2SQRT (x) . Это связано с тем, что квадратный корень из x может быть выражен как x 1 / 2 , от которого обычно происходит дифференцирование.
Как найти квадратный корень из десятичной дроби?
- Преобразует десятичную дробь в дробь .
- Найдите любой квадратный корень из дроби или оцените его. Сделайте дробью, равной квадратному корню, который вы нашли в квадрате.
- Отмените квадратный корень и квадрат, оставив вам дробь.
- Перепишите дробь как десятичную в качестве окончательного ответа.
Квадратный корень — Калькулятор капитана
Калькулятор квадратного корня
Обратите внимание: для работы этого калькулятора требуется JavaScript.Определение — Что такое квадратный корень?
Квадратный корень числа — это число, которое при умножении само на себя дает исходное число.
Например, квадратный корень из 9 равен 3, так как 3 x 3 = 9.
Квадратный корень из 25 равен 5, так как 5 x 5 = 25.
Квадратный корень из 49 равен 7, так как 7 x 7 = 49.
Квадратный корень может быть положительным или отрицательным (-3 x -3 равно 9, -5 x -5 = 25 и -7 x -7 = 49). Когда люди говорят «квадратный корень», они обычно имеют в виду положительный квадратный корень.
Противоположность квадратному корню — это вычисление в квадрате (степень двойки).
Для чего используется квадратный корень?
С практической точки зрения, квадратный корень в геометрии может использоваться для определения длины стороны квадрата, когда площадь известна.
Формула— Как вычислить квадратный корень из числа
Не существует быстрой математической формулы для вычисления квадратного корня. Большинство калькуляторов используют метод очень быстрых проб и ошибок.
Метод 1 — Метод проб и ошибок
Метод проб и ошибок подходит для полных квадратов. Это может занять очень много времени для неидеальных квадратов, поскольку в них много десятичных знаков.
Чтобы найти квадратный корень методом проб и ошибок:
- Угадайте число, которое, по вашему мнению, может быть квадратным корнем.
- Умножьте это число само на себя
- Если результат слишком низкий, попробуйте другое большее число. Если результат слишком высокий, попробуйте другое меньшее число.
- Продолжайте, пока не найдете квадратный корень.
Пример. Методом проб и ошибок найти квадратный корень из 64:
- Попробуйте число — 5: 5 умножить на 5 = 25 (слишком мало)
- Попробуйте число, которое больше 6 — 10 — 10 умножить на 10 = 100 (слишком большое
- Попробуйте число от 6 до 10 — 8 — 8 умножить на 8 = 64 (ответ)
Метод 2 — Быстро найти корни из точных квадратных чисел
Этот метод позволяет быстрее найти корень из полного квадратного числа.Однако, если число не является точным корнем, этот метод не сработает.
Метод 3 — Быстрый поиск квадратного корня из любого числа
Этот метод позволяет найти квадратный корень из любого числа (включая неполные квадраты). Это занимает немного больше времени, чем метод 2.
Как ввести квадратный корень?
- Вы можете скопировать символ квадратного корня -> √ <- с этой страницы и вставить его в свой документ.
- На компьютере с Windows откройте карту символов, найдите символ квадратного корня и скопируйте его.Вставьте его там, где хотите символ.
- На компьютере Mac нажмите option + v для символа √.
Таблица чисел квадратного корня — полные квадраты
- √1 = 1, как 1 x 1 = 1
- √4 = 2, как 2 x 2 = 4
- √9 = 3, как 3 x 3 = 9
- √16 = 4, как 4 x 4 = 16
- √25 = 5, поскольку 5 x 5 = 25
- √36 = 6, поскольку 6 x 6 = 36
- √49 = 7, поскольку 7 x 7 = 49
- √64 = 8, как 8 x 8 = 64
- √81 = 9, поскольку 9 x 9 = 81
- √100 = 10, поскольку 10 x 10 = 100
- √121 = 11, поскольку 11 x 11 = 121
- √144 = 12, как 12 x 12 = 144
- √225 = 15, как 15 x 15 = 225
- √289 = 17, как 17 x 17 = 289
- √400 = 20, как 20 x 20 = 400
- √625 = 25, как 25 x 25 = 625
- √900 = 30, как 30 x 30 = 900
- √1089 = 33, так как 33 x 33 = 1,089
- √2025 = 45, так как 45 x 45 = 2,025
- √ 2500 = 50, поскольку 50 x 50 = 2,500
- √3600 = 60, поскольку 60 x 60 = 3,600
- √5625 = 75, поскольку 75 x 75 = 5,625
- √10000 = 100, поскольку 100 x 100 = 10,000
Таблица чисел квадратного корня — несовершенные квадраты
Обратите внимание: для работы этой таблицы требуется JavaScript.Источники и другие ресурсы
Конъюгаты и деление на радикалы
Purplemath
Иногда вам нужно умножать многочленные выражения, содержащие только радикалы.Это ситуация, в которой вертикальное умножение является прекрасным подспорьем.
Упростить
Это упражнение выглядит некрасиво, но оно вполне выполнимо, если я аккуратен и точен в своей работе.
Во-первых, я делаю умножение, используя вертикальный метод, чтобы не усложнять:
MathHelp.com
Затем я устанавливаю исходное выражение, равное последней строке из приведенного выше умножения, и завершаю вычисления, упрощая каждый член:
Упростить:
Сначала делаю умножение:
А потом упрощаю:
Обратите внимание, в последнем примере выше, как я получил все целые числа.(Хорошо, технически они целые числа, но дело в том, что члены , а не , включают в себя какие-либо радикалы.) Я перемножил два радикальных бинома и получил ответ, который не содержал радикалов. Вы также могли заметить, что два «бинома» были одинаковыми, за исключением знака посередине: у одного был «плюс», а у другого — «минус».
Эта пара факторов, где второй фактор отличается только одним знаком посередине, очень важна; на самом деле этот «тот же самый, за исключением знака посередине» второй множитель имеет собственное название:
Учитывая радикальное выражение
, «сопряженный» является выражением.Конъюгат (KAHN-juh-ghitt) имеет те же числа, но с противоположным знаком посередине. Таким образом,
является не только конъюгатом, но и конъюгатом.Кроме того, конъюгаты не обязательно должны быть двухчленными выражениями с радикалами в каждом из терминов. Фактически, любое двухчленное выражение может иметь конъюгат:
1 + sqrt [2] является конъюгатом 1 — sqrt [2] sqrt [7] — 5 sqrt [6] является конъюгатом sqrt [7] + 5 sqrt [6] x + sqrt [y] является конъюгатом x — sqrt [y]Чтобы создать конъюгат, все, что вам нужно сделать, это перевернуть знак посередине.Все остальное остается прежним.
Что такое спряжение 3 + sqrt [5]?
В этом случае я нахожу сопряжение для выражения, в котором только один из терминов имеет радикал. Это хорошо. Независимо от этого, процесс тот же; а именно я переворачиваю знак посередине. Так как они дали мне выражение со знаком «плюс» посередине, спряжение — это те же два члена, но с «минусом» посередине:
Найдите конъюгат –7 sqrt [3] — 2
На этот раз радикал находится в первом из двух членов, и перед первым термином стоит «минус».Это хорошо. Я оставлю первый «минус» в покое, потому что ничего не меняю, кроме среднего знака; Переверну второй «минус» посередине на «плюс»:
Когда мы умножаем конъюгаты, мы делаем нечто похожее на то, что происходит, когда мы умножаем на разность квадратов; а именно:
a 2 — b 2 = ( a + b ) ( a — b )
Когда мы умножаем множители a + b и a — b , средние члены « ab » сокращаются:
То же самое происходит, когда мы умножаем конъюгаты:
Мы вскоре увидим, почему это важно.Чтобы понять это, давайте сначала взглянем на дроби, в знаменателях которых есть радикалы.
Деление на квадратные корниТак же, как мы можем переключаться между умножением радикалов и радикалом, содержащим умножение, мы можем переключаться между делением корней и одним корнем, содержащим деление.
Упростить:
Я могу упростить это, работая внутри, а затем извлекая квадратный корень:
…или иначе, разделив разделение на два радикала, упрощение и исключение:
В любом случае, мой окончательный ответ такой же.
Упростить:
Я вижу, что в знаменателе есть полный квадрат, а в числителе — простое число.Так что упрощение будет легче, если я разделю радикал, содержащий фракцию, на фракцию, содержащую радикалы:
URL: https://www.purplemath.com/modules/radicals4.htm
Калькулятор квадратного корняКалькулятор квадратного корня
О калькуляторе квадратного корня
Калькулятор квадратного корня используется для нахождения квадратного корня из введенного числа.
Квадратный корень
В математике квадратный корень из числа x — это такое число r, что r 2 = x.
Например:
1. Квадратный корень из 25 равен 5, потому что 5 2 = 25.
3. Квадратный корень из 2 приблизительно равен 1,41421356237.
3. Квадратный корень числа пи (π) приблизительно равен 1,77245385102.
Таблица квадратного корня
Ниже приводится таблица квадратного корня от 1 до 1000 с округлением до 5 цифр:
- квадратный корень из 4/9:
- Что такое
- Как упростить квадратный корень из 27?

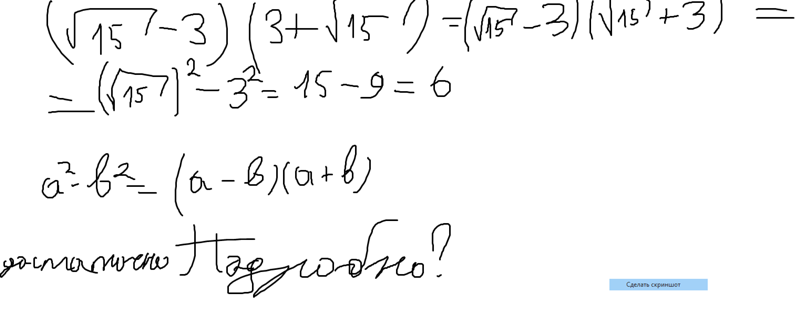 Продолжение борьбы и прогнозы (3)
Продолжение борьбы и прогнозы (3) Болезнь протекает тяжело, а создание лекарств от нее и вакцин против вируса сдерживает отсутствие удобных модельных лабораторных животных, на которых лекарства и вакцины должны пройти доклинические испытания. Такие живые модели — гуманизированные лабораторные мыши — сейчас создаются в Институте биологии гена РАН, и на них начнутся доклинические испытания препаратов и кандидатных вакцин против вируса SARS-CoV-2.
Болезнь протекает тяжело, а создание лекарств от нее и вакцин против вируса сдерживает отсутствие удобных модельных лабораторных животных, на которых лекарства и вакцины должны пройти доклинические испытания. Такие живые модели — гуманизированные лабораторные мыши — сейчас создаются в Институте биологии гена РАН, и на них начнутся доклинические испытания препаратов и кандидатных вакцин против вируса SARS-CoV-2. .. Кому-то эти слова вовсе не знакомы, кто-то вспомнит, как советские школьники делали домики для тех птиц, кто не вьет гнезд, а селится в дуплах. Пионеры ушли в небытие. Их заменили более профессиональные защитники птиц: биологи, натуралисты, орнитологи и просто любознательные любители природы. И дело не ограничилось скворечниками.
.. Кому-то эти слова вовсе не знакомы, кто-то вспомнит, как советские школьники делали домики для тех птиц, кто не вьет гнезд, а селится в дуплах. Пионеры ушли в небытие. Их заменили более профессиональные защитники птиц: биологи, натуралисты, орнитологи и просто любознательные любители природы. И дело не ограничилось скворечниками.

 Многие млекопитающие, птицы и даже насекомые знакомы с дурманящим эффектом перезрелых фруктов. Но наш вид относится к числу тех, кто довольно хорошо переносит этанол и, более того, имеет мотивацию к его потреблению
Многие млекопитающие, птицы и даже насекомые знакомы с дурманящим эффектом перезрелых фруктов. Но наш вид относится к числу тех, кто довольно хорошо переносит этанол и, более того, имеет мотивацию к его потреблению

 Г, СТАНДОТКЛОН.В, СТАНДОТКЛОНА, СТАНДОТКЛОНПА, ДИСПР, ДИСП.В, ДИСПА и ДИСППА.
Г, СТАНДОТКЛОН.В, СТАНДОТКЛОНА, СТАНДОТКЛОНПА, ДИСПР, ДИСП.В, ДИСПА и ДИСППА.
 5%)
5%) Эта константа массива является матрицей размерности 1 на 4 и соответствует ссылке на одну строку и четыре столбца.
Эта константа массива является матрицей размерности 1 на 4 и соответствует ссылке на одну строку и четыре столбца.

Leave A Comment