Проводящий контур в переменном магнитном поле
Пример 11.7.
Магнитный поток через замкнутый проводящий контур сопротивлением R = 10 Ом изменяется со временем t по закону Ф = t2, где = 10 Вб/с2. Определите силу тока I в контуре в момент времени t = 1 мс.
Решение.
Мгновенное значение ЭДС индукции, согласно закону Фарадея, определяется как
.
Тогда ток в контуре по закону Ома равен
мА.
Знак минус в полученном
выражении свидетельствует о том, что
направление индукционного тока
противоположно направлению положительного
обхода контура, которое в свою очередь
согласовано с направлением вектора
нормали к поверхности, натянутой на
контур. Причиной индукционного тока
является вихревое электрическое поле,
порождаемое изменяющимся магнитным
полем, если контур неподвижен, и сила
Лоренца, если он перемещается в
неоднородном постоянном магнитном
поле.
Пример 11.8.
На длинный соленоид, имеющий диаметр сечения d = 5 см и содержащий n = 20 витков на 1 см длины, плотно надет круговой виток из медного провода сечением s = 1 мм2 (удельное сопротивление меди ). Найдите ток в витке, если ток в обмотке соленоида увеличивают с постоянной скоростью100 А/с. Магнитным полем индукционного тока пренебречь.
Решение.
Магнитное поле внутри длинного соленоида однородно и равно
,
где n число витков на единицу длины, а
,
где — площадь поверхности витка.
При увеличении тока в обмотке соленоида магнитный поток через виток возрастает, и возникающий индукционный ток определяется выражением
,
где
,
а знак минус означает, что индукционный
ток течет в направлении, противоположном
направлению положительного обхода
витка, согласованного с направлением
нормали.
Тогда, величина тока через виток в момент времени t равна
мА.
Пример 11.9.
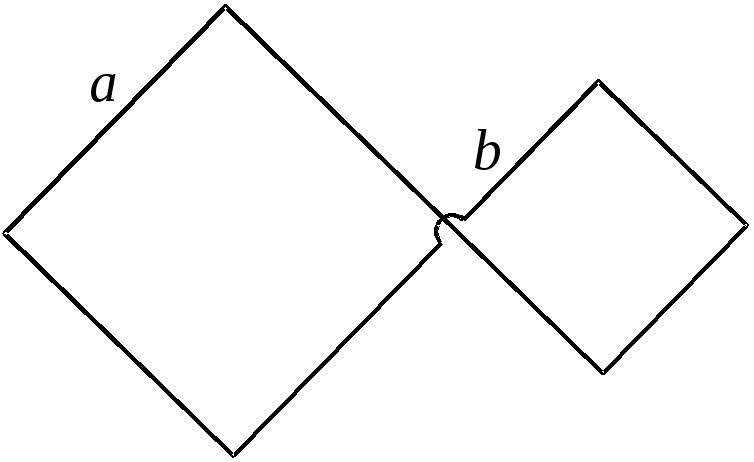
Плоский контур (рис.13), имеющий вид двух квадратов со сторонами a = 20 см и b = 10 см, находится в однородном магнитном поле, перпендикулярном его плоскости. Индукцию поля меняют по закону , гдеB0 = 10 мТл и = 100 с–1. Найдите амплитуду индукционного тока в контуре, если сопротивление единицы его длины . Магнитным полем этого тока пренебречь.
Рис.13
Решение.
Индукционный ток в рамке равен
.
На рис.14 показано
направление магнитного поля, а также
нормалей к поверхности каждого из
квадратов, составляющих контур,
согласованные единым направлением
положительного обхода. С учетом этого
суммарный магнитный поток через контур
равен
С учетом этого
суммарный магнитный поток через контур
равен
.
Рис.14 |
Откуда
.
Учитывая, что сопротивление контура равно , найдем амплитуду индукционного тока
нА
Пример 11.10.
Квадрат, изготовленный из проволоки сопротивлением R = 1 Ом, помещен в однородное магнитное поле, вектор индукции которого перпендикулярен плоскости квадрата. Длина стороны квадратаа = 1 см. Величина индукции магнитного поля сначала равна B=0,1 Тл а затем ее уменьшают до нуля. Найдите величину q заряда, который в результате переместится через поперечное сечение проволоки.
Решение.
Количество электричества, протекающего через любое поперечное сечение контура с сопротивлением R при изменении магнитного потока сквозь контур на величину , равно:
.
Отметим, что величина q не зависит от характера временной зависимости изменения магнитного потока, а определяется только его начальным и конечным значениями. Так как индукция магнитного поля меняется от до нуля, приращение магнитного потока, пронизывающего контур, равно
.
Величина заряда, который протекает по проволоке, определится выражением
Кл.
Глава 23. Закон электромагнитной индукции
Если в магнитном поле находится замкнутый проводящий контур, не содержащий источников тока, то при изменении магнитного поля в контуре возникает электрический ток. Это явление называется электромагнитной индукцией. Появление тока свидетельствует о возникновении в контуре электрического поля, которое может обеспечить замкнутое движение электрических зарядов или, другими словами, о возникновении ЭДС. Электрическое поле, которое возникает при изменении поля магнитного и работа которого при перемещении зарядов по замкнутому контуру не равна нулю, имеет замкнутые силовые линии и называется вихревым.
Для количественного описания электромагнитной индукции вводится понятие магнитного потока (или потока вектора магнитной индукции) через замкнутый контур. Для плоского контура, расположенного в однородном магнитном поле (а только такие ситуации и могут встретиться школьникам на едином государственном экзамене), магнитный поток определяется как
(23.1) |
где — индукция поля, — площадь контура, — угол между вектором индукции и нормалью (перпендикуляром) к плоскости контура (см. рисунок; перпендикуляр к плоскости контура показан пунктиром). Единицей магнитного потока в международной системе единиц измерений СИ является Вебер (Вб), который определяется как магнитный поток через контур площади 1 м
Величина ЭДС индукции , возникающая в контуре при изменении магнитного потока через этот контур, равна скорости изменения магнитного потока
(23. |
Здесь — изменение магнитного потока через контур за малый интервал времени . Важным свойством закона электромагнитной индукции (23.2) является его универсальность по отношению к причинам изменения магнитного потока: магнитный поток через контур может меняться из-за изменения индукции магнитного поля, изменения площади контура или изменения угла между вектором индукции и нормалью, что происходит при вращении контура в поле. Во всех этих случаях по закону (23.2) в контуре будет возникать ЭДС индукции и индукционный ток.
Знак минус в формуле (23.2) «отвечает» за направление тока, возникающего в результате электромагнитной индукции (правило Ленца). Однако понять на языке закона (23.2), к какому направлению индукционного тока приведет этот знак при том или ином изменении магнитного потока через контур, не так-то просто. Но достаточно легко запомнить результат: индукционный ток будет направлен таким образом, что созданное им магнитное поле будет «стремиться» компенсировать то изменение внешнего магнитного поля, которое этот ток и породило.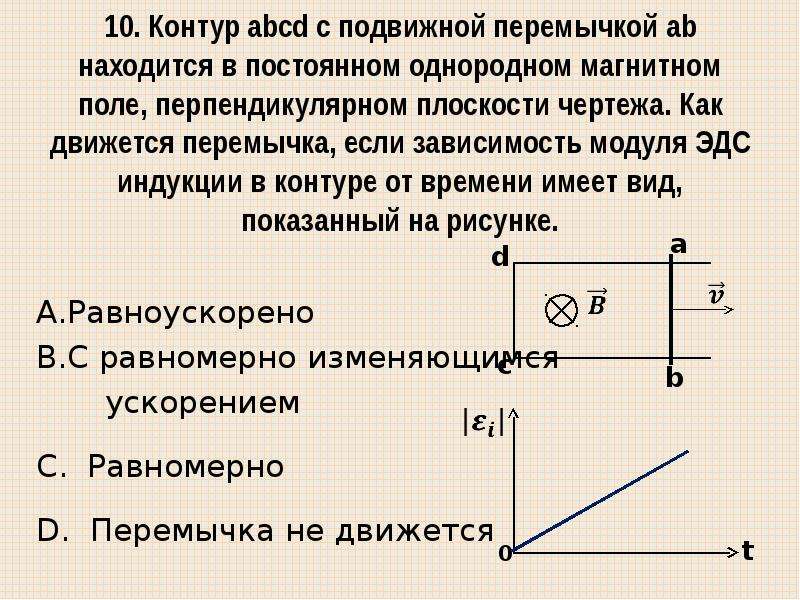
Если в контуре с током ток в силу каких-то причин изменяется, то изменяется и магнитный поток через контур того магнитного поля, которое создано самим этим током. Тогда по закону (23.2) в контуре должна возникать ЭДС индукции. Явление возникновения ЭДС индукции в некоторой электрической цепи в результате изменения тока в самой этой цепи называется самоиндукцией. Для нахождения ЭДС самоиндукции в некоторой электрической цепи необходимо вычислить поток магнитного поля, создаваемого этой цепью через нее саму. Такое вычисление представляет собой сложную проблему из-за неоднородности магнитного поля.
(23.3) |
где — сила тока в цепи, — коэффициент пропорциональности, который характеризует «геометрию» цепи, но не зависит от тока в ней и называется индуктивностью этой цепи. Единицей индуктивности в международной системе единиц СИ является Генри (Гн). 1 Гн определяется как индуктивность такого контура, поток индукции собственного магнитного поля через который равен 1 Вб при силе тока в нем 1 А. С учетом определения индуктивности (23.3) из закона электромагнитной индукции (23.2) получаем для ЭДС самоиндукции
(23.4) |
Благодаря явлению самоиндукции ток в любой электрической цепи обладает определенной «инерционностью» и, следовательно, энергией. Действительно, для создания тока в контуре необходимо совершить работу по преодолению ЭДС самоиндукции. Энергия контура с током и равна этой работе. Необходимо запомнить формулу для энергии контура с током
Действительно, для создания тока в контуре необходимо совершить работу по преодолению ЭДС самоиндукции. Энергия контура с током и равна этой работе. Необходимо запомнить формулу для энергии контура с током
(23.5) |
где — индуктивность контура, — сила тока в нем.
Явление электромагнитной индукции широко применяется в технике. На нем основано создание электрического тока в электрических генераторах и электростанциях. Благодаря закону электромагнитной индукции происходит преобразование механических колебаний в электрические в микрофонах. На основе закона электромагнитной индукции работает, в частности, электрическая цепь, которая называется колебательным контуром (см. следующую главу), и которая является основой любой радиопередающей или радиопринимающей техники.
Рассмотрим теперь задачи.
Из перечисленных в задаче 23.1.1 явлений только одно есть следствие закона электромагнитной индукции — появление тока в кольце при проведении сквозь него постоянного магнита (ответ 3). Все остальное — результат магнитного взаимодействия токов.
Все остальное — результат магнитного взаимодействия токов.
Как указывалось во введении к настоящей главе, явление электромагнитной индукции лежит в основе работы генератора переменного тока (задача 23.1.2), т.е. прибора, создающего переменный ток, заданной частоты (ответ 2).
Индукция магнитного поля, создаваемого постоянным магнитом, уменьшается с увеличением расстояния до него. Поэтому при приближении магнита к кольцу (задача 23.1.3) поток индукции магнитного поля магнита через кольцо изменяется, и в кольце возникает индукционный ток. Очевидно, это будет происходить при приближении магнита к кольцу и северным, и южным полюсом. А вот направление индукционного тока в этих случаях будет различным. Это связано с тем, что при приближении магнита к кольцу разными полюсами, поле в плоскости кольца в одном случае будет направлено противоположно полю в другом. Поэтому для компенсации этих изменений внешнего поля магнитное поле индукционного тока должно быть в этих случаях направлено по-разному. Поэтому и направления индукционных токов в кольце будут противоположными (ответ 4).
Поэтому и направления индукционных токов в кольце будут противоположными (ответ 4).
Для возникновения ЭДС индукции в кольце необходимо, чтобы менялся магнитный поток через кольцо. А поскольку магнитная индукция поля магнита зависит от расстояния до него, то в рассматриваемом в задаче 23.1.4 случае поток через кольцо будет меняться, в кольце возникнет индукционный ток (ответ 1).
При вращении рамки 1 (задача 23.1.5) угол между линиями магнитной индукции (а, значит, и вектором индукции) и плоскостью рамки в любой момент времени равен нулю. Следовательно, магнитный поток через рамку 1 не изменяется (см. формулу (23.1)), и индукционный ток в ней не возникает. В рамке 2 индукционный ток возникнет: в положении показанном на рисунке, магнитный поток через нее равен нулю, когда рамка повернется на четверть оборота — будет равен , где — индукция, — площадь рамки. Еще через четверть оборота поток снова будет равен нулю и т.д. Поэтому поток магнитной индукции через рамку 2 изменяется в процессе ее вращения, следовательно, в ней возникает индукционный ток (ответ 2).
В задаче 23.1.6 индукционный ток возникает только в случае 2 (ответ 2). Действительно, в случае 1 рамка при движении остается на одном и том же расстоянии от проводника, и, следовательно, магнитное поле, созданное этим проводником в плоскости рамки, не изменяется. При удалении рамки от проводника магнитная индукция поля проводника в области рамки изменяется, меняется магнитный поток через рамку, и возникает индукционный ток
В законе электромагнитной индукции утверждается, что индукционный ток в кольце будет течь в такие моменты времени, когда изменяется магнитный поток через это кольцо. Поэтому пока магнит покоится около кольца (задача 23.1.7) индукционный ток в кольце течь не будет. Поэтому правильный ответ в этой задаче — 2.
Согласно закону электромагнитной индукции (23.2) ЭДС индукции в рамке определяется скоростью изменения магнитного потока через нее. А поскольку по условию задачи 23.1.8 индукция магнитного поля в области рамки изменяется равномерно, скорость ее изменения постоянна, величина ЭДС индукции не изменяется в процессе проведения опыта (ответ 3).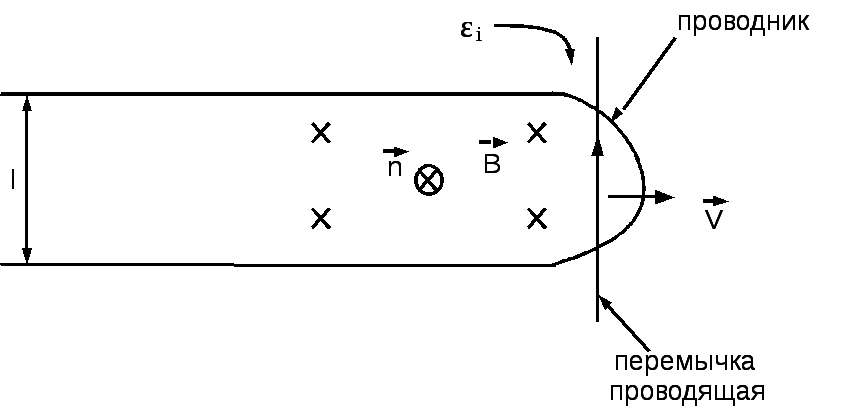
В задаче 23.1.9 ЭДС индукции, возникающая в рамке во втором случае, вчетверо больше ЭДС индукции, возникающей в первом (ответ 4). Это связано с четырехкратным увеличением площади рамки и, соответственно, магнитного потока через нее во втором случае.
В задаче 23.1.10 во втором случае в два раза увеличивается скорость изменения магнитного потока (индукция поля меняется на ту же величину, но за вдвое меньшее время). Поэтому ЭДС электромагнитной индукции, возникающая в рамке во втором случае, в два раза больше, чем в первом (ответ 1).
При увеличении тока в замкнутом проводнике в два раза (задача 23.2.1), величина индукции магнитного поля возрастет в каждой точке пространства в два раза, не изменившись по направлению. Поэтому ровно в два раза изменится магнитный поток через любую малую площадку и, соответственно, и весь проводник (ответ 1). А вот отношение магнитного потока через проводник к току в этом проводнике, которое и представляет собой индуктивность проводника , при этом не изменится (задача 23.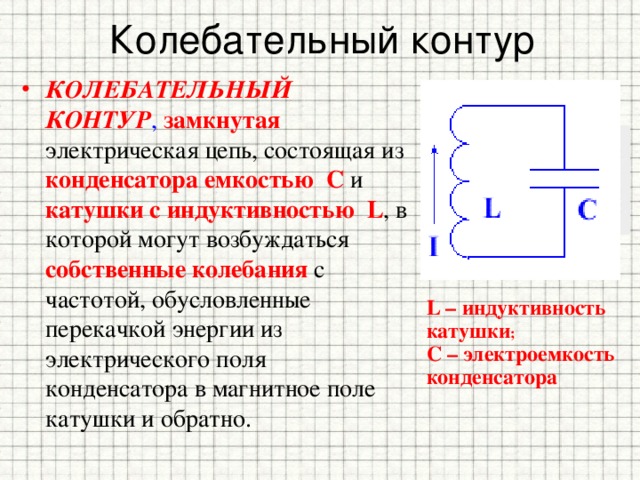 2.2 — ответ 3).
2.2 — ответ 3).
Используя формулу (23.3) находим в задаче 32.2.3 Гн (ответ 4).
Связь между единицами измерений магнитного потока, магнитной индукции и индуктивности (задача 23.2.4) следует из определения индуктивности (23.3): единица магнитного потока (Вб) равна произведению единицы тока (А) на единицу индуктивности (Гн) — ответ 3.
Согласно формуле (23.5) при двукратном увеличении индуктивности катушки и двукратном уменьшении тока в ней (задача 23.2.5) энергия магнитного поля катушки уменьшится в 2 раза (ответ 2).
Когда рамка вращается в однородном магнитном поле, магнитный поток через рамку меняется из-за изменения угла между перпендикуляром к плоскости рамки и вектором индукции магнитного поля. А поскольку и в первом и втором случае в задаче 23.2.6 этот угол меняется по одному и тому же закону (по условию частота вращения рамок одинакова), то ЭДС индукции меняются по одному и тому же закону, и, следовательно, отношение амплитудных значений ЭДС индукции в рамках равно единице (ответ 2).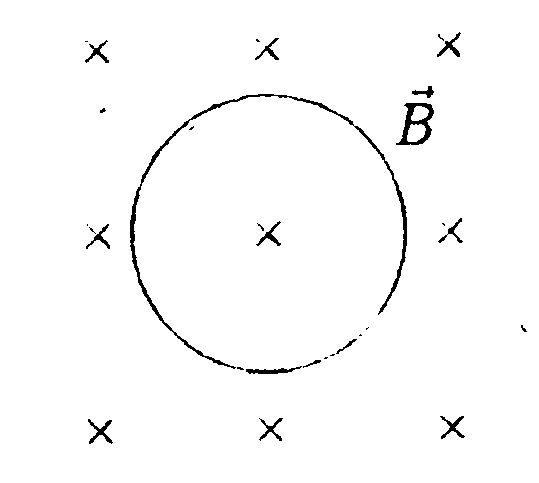
Магнитное поле, создаваемое проводником с током в области рамки (задача 23.2.7), направлено «от нас» (см. решение задач главы 22). Величина индукции поля провода в области рамки при ее удалении от провода будет уменьшаться. Поэтому индукционный ток в рамке должен создать магнитное поле, направленное внутри рамки «от нас». Используя теперь правило буравчика для нахождения направления магнитной индукции, заключаем, что индукционный ток в рамке будет направлен по часовой стрелке (ответ 1).
При увеличении тока в проводе будет возрастать созданное им магнитное поле и в рамке возникнет индукционный ток (задача 23.2.8). В результате возникнет взаимодействие индукционного тока в рамке и тока в проводнике. Чтобы найти направление этого взаимодействия (притяжение или отталкивание) можно найти направление индукционного тока, а затем по формуле Ампера силу взаимодействия рамки с проводом. Но можно поступить и по-другому, используя правило Ленца. Все индукционные явления должны иметь такое направление, чтобы компенсировать вызывающую их причину. А поскольку причина — увеличение тока в рамке, сила взаимодействия индукционного тока и провода должна стремиться уменьшить магнитный поток поля провода через рамку. А поскольку магнитная индукция поля провода убывает с увеличением расстояния до него, то эта сила будет отталкивать рамку от провода (ответ 2). Если бы ток в проводе убывал, то рамка притягивалась бы к проводу.
А поскольку причина — увеличение тока в рамке, сила взаимодействия индукционного тока и провода должна стремиться уменьшить магнитный поток поля провода через рамку. А поскольку магнитная индукция поля провода убывает с увеличением расстояния до него, то эта сила будет отталкивать рамку от провода (ответ 2). Если бы ток в проводе убывал, то рамка притягивалась бы к проводу.
Задача 23.2.9 также связана с направлением индукционных явлений и правилом Ленца. При приближении магнита к проводящему кольцу в нем возникнет индукционный ток, причем направление его будет таким, чтобы компенсировать вызывающую его причину. А поскольку эта причина — приближение магнита, кольцо будет отталкиваться от него (ответ 2). Если магнит отодвигать от кольца, то по тем же причинам возникло бы притяжение кольца к магниту.
Задача 23.2.10 — единственная вычислительная задача в этой главе. Для нахождения ЭДС индукции нужно найти изменение магнитного потока через контур . Это можно сделать так.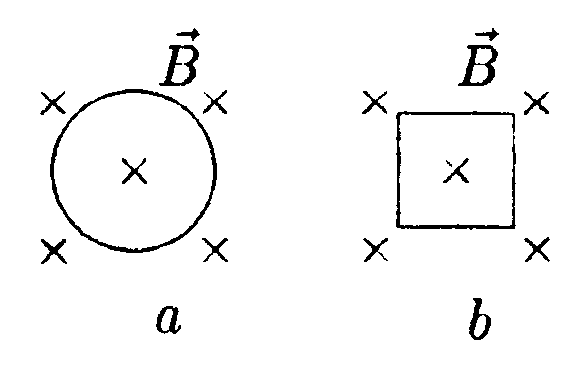 Пусть в некоторый момент времени перемычка находилась в положении, показанном на рисунке, и пусть прошел малый интервал времени . За этот интервал времени перемычка переместится на величину . Это приведет к увеличению площади контура на величину . Поэтому изменение магнитного потока через контур будет равно , а величина ЭДС индукции (ответ 4).
Пусть в некоторый момент времени перемычка находилась в положении, показанном на рисунке, и пусть прошел малый интервал времени . За этот интервал времени перемычка переместится на величину . Это приведет к увеличению площади контура на величину . Поэтому изменение магнитного потока через контур будет равно , а величина ЭДС индукции (ответ 4).
купить все – Официальный магазин Circuit Scribe: обучайте электронике с помощью рисования!
купить все – Официальный магазин Circuit Scribe: обучайте электронике с помощью рисования! перейти к содержаниюПосмотреть все
Мини-комплект20,79 $
Базовый комплект34,99 $
Супер Комплект64,99 $
Продано Распроданный Распроданный Распроданный Распроданный Распроданный Распроданный Распроданный Распроданный Распроданный Распроданный Распроданный Распроданный Распроданный Распроданный Распроданный Распроданный Распроданный Распроданный Распроданный Продано
Ультра Комплект$99,99
Комплект Супер Плюс$99,99
Базовый комплект плюс44,99 $
Посмотреть все
Подписка на пакет модулей9,99 $
Комплект модуля вывода15,99 $
Пакет расширенных модулей$42,99
Посмотреть все
Посмотреть все
Вводный комплект для занятий в классе816,99 $
Базовый комплект для классной комнаты + дополнительный блокнот изобретателя299,99 $
Комплект Super Classroom Kit + Блокнот изобретателя Add’l$599,99
Посмотреть все
Годовая подписка на CS Classroom60,00 $
Подарочные карты Circuit Scribe От
$10.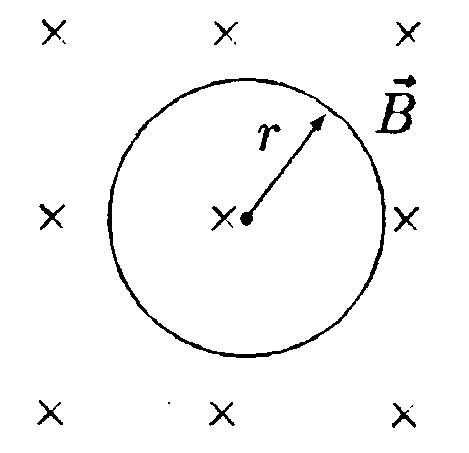 00
00
7,99 $
Ручка с проводящими чернилами Circuit Scribe, 10 шт. в упаковке39,88 $
Посмотреть все
Ручка с токопроводящими чернилами Circuit Scribe7,99 $
Светодиоды (двухсветодиодные)4,99 $
Продано Распроданный Распроданный Распроданный Распроданный Распроданный Распроданный Распроданный Распроданный Распроданный Распроданный Распроданный Распроданный Распроданный Распроданный Распроданный Распроданный Распроданный Распроданный Распроданный Продано
Вентилятор$3,99
бесплатных загрузок — Официальный магазин Circuit Scribe: обучайте электронике с помощью рисования!
Ресурсы Inventor’s Kit Resources
Бесплатная записная книжка изобретателя
Изучение схем дома еще никогда не было таким простым благодаря бесплатной загружаемой версии нашей Записной книжки изобретателя. С его помощью ваш ребенок сможет изучить схемы от простых до сложных и понять, как они работают.
С его помощью ваш ребенок сможет изучить схемы от простых до сложных и понять, как они работают.
Попробуйте использовать Блокнот изобретателя с нашим бесплатным приложением дополненной реальности CS Circuits. Вы должны увидеть это, чтобы поверить в это — доступно на iOS!
Загрузить блокнот Electronic Kits!
Краткое руководство по бесплатному набору Electronics Inventor Kit
Если у вашего ребенка возникли проблемы с погружением в набор Electronics Inventor Kit, следуйте нашему простому пошаговому руководству по созданию своей первой схемы с помощью наших проводящих чернил и модулей. Следуя этому простому руководству, они быстро разберутся со схемой!
Загрузить краткое руководство!
Приложение дополненной реальности CS Circuits
Приложение дополненной реальности CS Circuits научит вашего ребенка рисовать схемы с помощью анимации протекающего тока! Доступно в App Store для iOS и Google Play для Android. Его можно загрузить бесплатно, и он включает в себя следующие функции:
Его можно загрузить бесплатно, и он включает в себя следующие функции:
— Все, что им нужно, — это Блокнот изобретателя (также работает с БЕСПЛАТНЫМИ цифровыми PDF-файлами!)
— Он интерактивен! Ваш ребенок может крутить ручки, нажимать переключатели и смотреть, что происходит.
— Визуализируйте поток и силу тока, когда цепь анимируется в реальном времени!
Ресурсы для набора дронов
Бесплатные чертежи для сборки дронов
Ваш ребенок может научиться собирать и управлять собственным дроном, используя наш набор для сборки дронов и чертежи. Они могут шаг за шагом научиться собирать свой дрон, а затем подняться в небо с помощью приложения CS Pilot!
Скачать чертежи Drone Builder!
Бесплатный учебный курс по дронам
Вы хотите преподавать науку о полетах дронов дома или в классе? Вам повезло! Мы разработали учебные материалы для нашего комплекта Drone Builder Kit, который включает в себя уроки физики, схемотехники и полетов.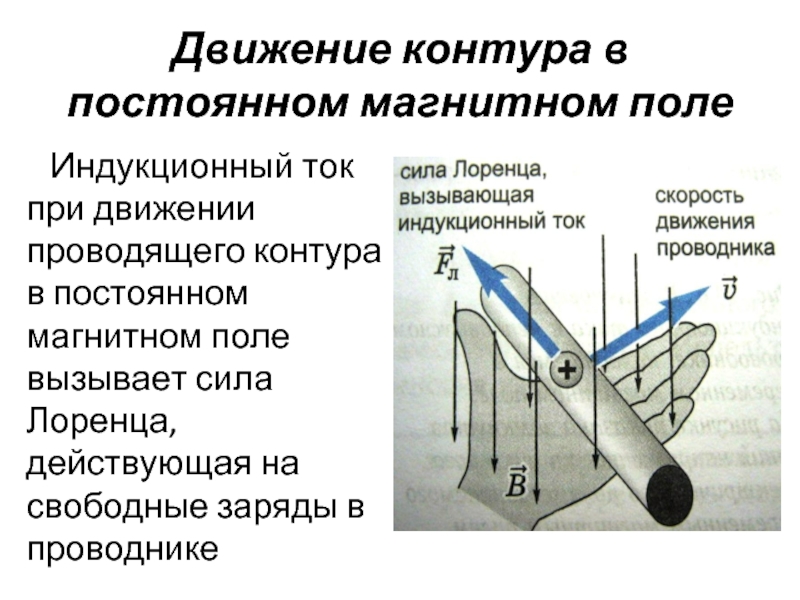


Leave A Comment