Когда положительна производная функции: Производная — Умскул Учебник

В скольких точках производная функции положительна

Не откладывайте! ЗАГОВОРИТЕ на Английском!

ЗАМУЧИЛИ БОЛИ В СПИНЕ?

Александр | 2014-03-24

В этой статье мы рассмотрим несколько задач связанных со свойствами производной функции. Задачи этого типа чрезвычайно просты. Повторять теорию я здесь не буду, она уже подробно изложена на блоге. Рекомендую изучить следующие статьи «Исследование функций. Это нужно знать!» и «Применение производной к исследованию графиков функций», после чего вопросов у вас не останется.

Что хотелось бы отметить особо! При прочтении условия сразу отмечайте какой график дан: график функции или график производной функции. Это важно! Часто именно из-за такой невнимательности выпускники допускают ошибки. Например, график производной принимают за график самой функции и соответственно получают неверный ответ. Рекомендую также изучить статью «Дан график производной функции. Задачи!», в которой схожие задания уже были разобраны. Рассмотрим задачи:

317539. На рисунке изображён график функции у = f(x)  и восемь точек на оси абсцисс: x₁, x₂,  x₃, …,  x₈. В скольких из этих точек производная функции  f(x)  положительна?

Известно, что производная функции положительна на интервалах возрастания. В данном случае таким интервалам принадлежат точки: x₁, x₂, x₅, x₆,  x₇. Всего пять точек.

Ответ: 5

317540. На рисунке изображён график функции у = f(x)  и двенадцать точек на оси абсцисс: x₁, x₂,  x₃, …, x₁₂.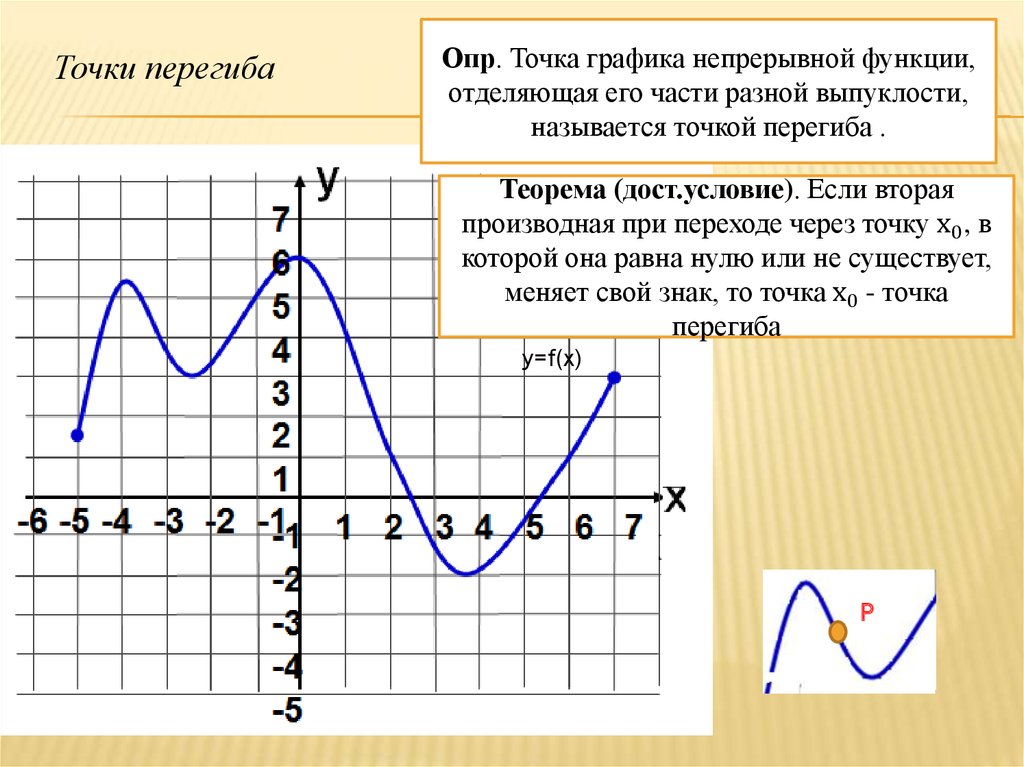 В скольких из этих точек производная функции  f(x)  отрицательна?

 

Известно, что производная отрицательна на интервалах убывания функции. В данном случае таким интервалам принадлежат точки: x₄, x₅, x₆, x₇, x₈, x₁₁, x₁₂. Всего семь точек.

Ответ:  7

317541. На рисунке изображён график у = f’(x)  производной функции  f(x)  и восемь точек на оси абсцисс: x₁, x₂,  x₃, …,    x₈. В скольких из этих точек функция  f(x)  возрастает?

Известно, что на интервалах возрастания функции её производная положительна.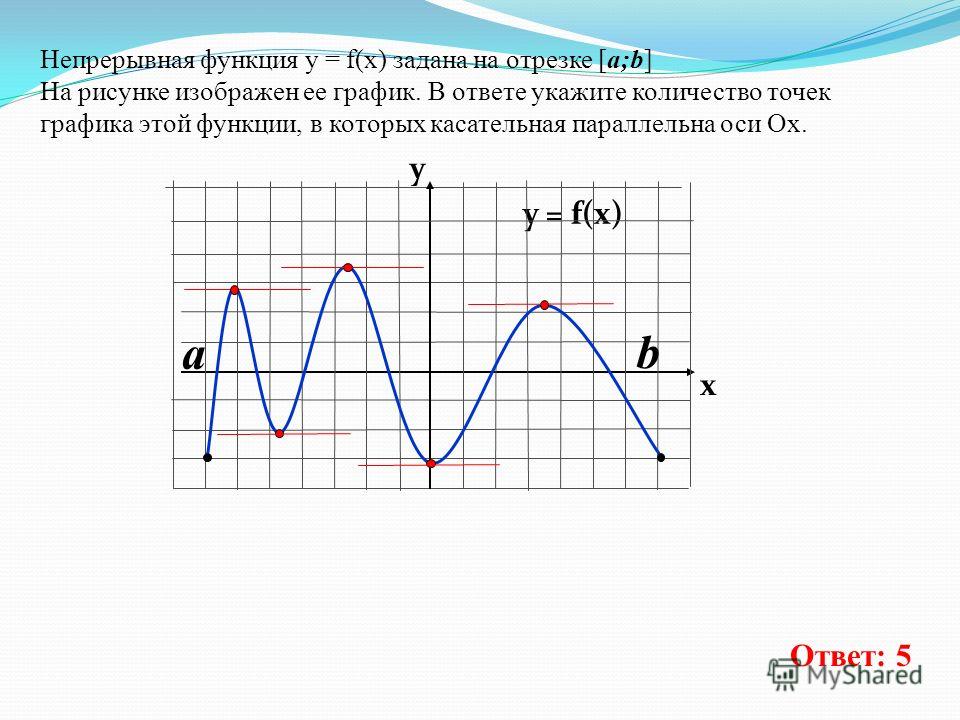 В данном случае производная функции имеет положительное значение в точках x₄, x₅, x₆ (то есть на интервале, где график производной расположен выше оси ох).  Всего три точки.

Ответ: 3

317542. На рисунке изображён график у = f’(x)  производной функции  f(x)  и восемь точек на оси абсцисс: x₁, x₂,  x₃, …,  x₈. В скольких из этих точек функция  f(x) убывает?

Известно, что на интервалах убывания функции её производная отрицательна. В данном случае производная функции имеет отрицательное значение в точках x₁, x₂, x₃, x₄, x₈ (то есть на интервалах, где график производной расположен ниже оси ох).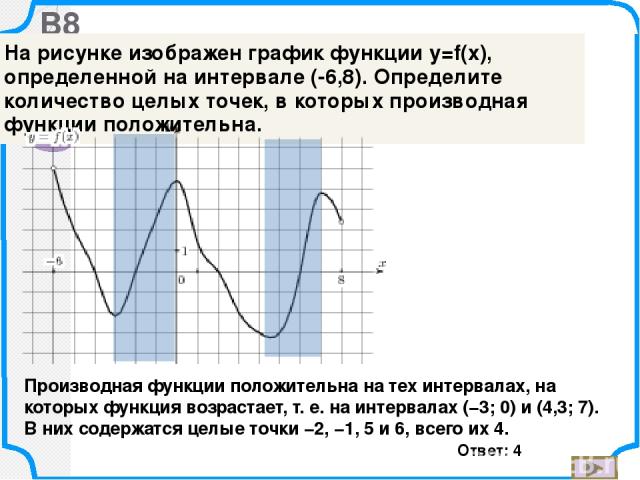 Всего пять точек.

Ответ: 5

500248.  На рисунке изображён график дифференцируемой функции у = f(x). На оси абсцисс отмечены девять точек: x₁, x₂,  x₃, …,    x₉. Среди этих точек найдите все точки, в которых производная функции f(x)  отрицательна. В ответе укажите количество найденных точек. 

Известно, что производная отрицательна на интервалах убывания функции. В данном случае таких интервалов два и им принадлежат точки: x₄, x₅, x₉. Всего три точки.

Ответ: 3

На этом всё. Успеха вам!

С уважением, Александр Крутицких. 

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Категория: Производная Графики Функции MAX MIN | ЕГЭ-№7

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Замучили боль и скованность в мышцах спины?

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

Применение производных

На прошлой лекции мы обсудили, как искать производные. Теперь поговорим о том, как их применять.

17.1Производные и локальное поведение функций

Производная показывает мгновенную скорость возрастания функции. Логично ожидать, что если производная положительна, то функция возрастает, а если отрицательна, то убывает. Мы обсудим различные формализации этого утверждения.

17.1.1Локальная монотонность

Теорема 1. Пусть функция f дифференцируема в точке x0. Если f′(x0)>0, то существует такая окрестность нуля, что для всех Δx из этой окрестности верно следующее: если Δx>0, то f(x0+Δx)>f(x0), а если Δx<0, то f(x0+Δx)<f(x0).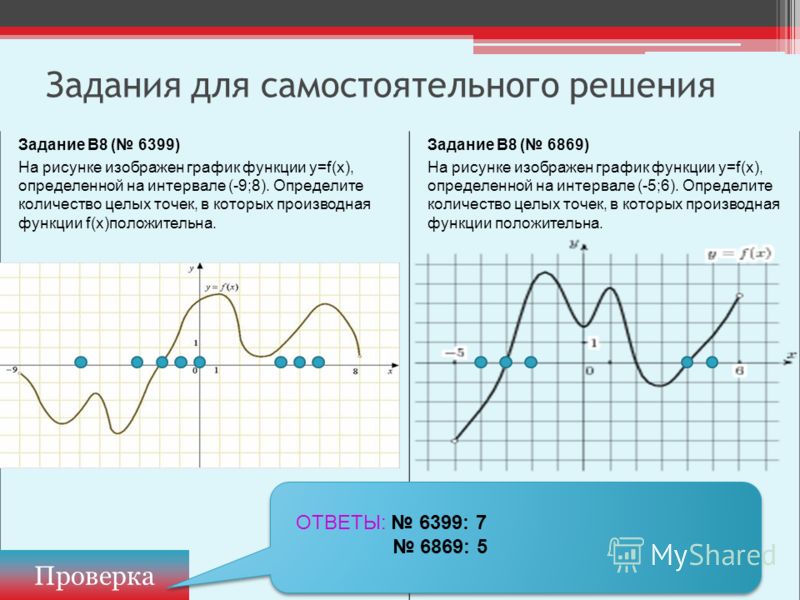

Иными словами, если существует такая окрестность точки x0, что если мы сдвинемся из x0 вправо, оставаясь в этой окрестности, то значение функции увеличится по сравнению с f(x0), а если влево, то уменьшится, см. рис. 17.1

Рис. 17.1: Если мы чуть-чуть сдвинемся из точки x0 вправо, значение функции увеличится по сравнению со значением в x0, а если влево — то уменьшится. Но для точек вне окрестности это может быть неверно: например, f(x1)<f(x0), хотя x1>x0.

Доказательство. Напомним (см. утверждение 1 из лекции 15), что если функция f дифференцируема в x0, то существует такая функция α(Δx), что α(Δx)→0 и

f(x0+Δx)=f(x0)+f′(x0)Δx+α(Δx)⋅Δx.

Вынесем Δx за скобку:

f(x0+Δx)=f(x0)+(f′(x0)+α(Δx))Δx.(17.1)

f(x0+Δx)=f(x0)++(f′(x0)+α(Δx))Δx.(17.1)

Поскольку α(Δx)→0 при Δx→0 и по предположению f′(x0)>0, существует такая окрестность нуля, что для всех Δx из этой окрестности,

|α(Δx)|<f′(x0)2

В этом случае f′(x0)+α(Δx)>f′(x0)/2>0. Значит в выражении (17.1) коэффициент при Δx положительный, и следовательно при положительных Δx правая часть больше, чем f(x0) (мы прибавили к f(x0) положительное число), а при отрицательных — меньше.∎

17.1.2Необходимое условие экстремума

Одно из главных применений производных — поиск экстремумов.

Лемма 1. (Лемма Ферма) Пусть функция f имеет локальный экстремум (минимум или максимум) в точке x0, определена в некоторой окрестности этой точки и дифференцируема в этой точке. Тогда её производная в точке x0 равна нулю, см. рис. 17.3

Рис. 17.3: Иллюстрация лемме Ферма

Доказательство. От противного, пусть в x0 экстремум, но производная не равна нулю. Тогда она либо положительна, либо отрицательна. Пусть для определённости положительна. По теореме 1, значение функции можно увеличить, сдвинувшись из x0 немножко вправо. Это значит, что x0 не является точкой локального максимума. Но по той же теореме значение функции можно уменьшить, сдвинувшись из x0 немножко влево. Значит, x0 и не точка локального минимума. Случай отрицательной производной рассматривается аналогично.

Формально: если точка x0 является точкой локального максимума, у неё существует такая δ1-окрестность, что для всякого x из этой окрестности,

f(x0)≥f(x).

Но по теореме 1 найдётся такая δ2-окрестность точки x0, что для всех x из этой окрестности, если x>x0, то

f(x)>f(x0).

На пересечении этих окрестностей эти неравенства противоречат друг другу.

Аналогичный результат был бы справедлив и если бы в точке x0 был минимум — в этом случае мы бы взяли значения x<x0 и получили неравенство

f(x)<f(x0).

Аналогично рассматривается случай f′(x0)<0.∎

Вопрос 1. Верно ли обратное? Иными словами, правда ли, что если производная функции в некоторой внутренней точке области определения функции равна нулю, то в этой точке обязательно экстремум?

  Верно.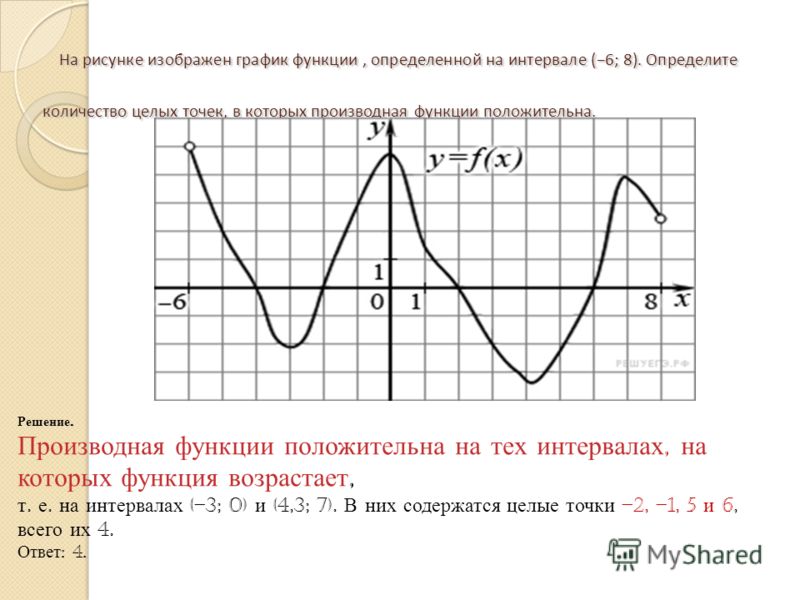

Неверный ответ. Как насчёт функции f(x)=x3?

  Неверно.

Верный ответ. Конечно! Например, у функции f(x)=x3 в нуле производная равна нулю, а экстремума нет.

17.2Производные и поведение функции на отрезке

17.2.1Непрерывная на отрезке функция достигает наибольшего и наименьшего значения

Теорема 2. Пусть функция f непрерывна на отрезке [a,b]. Тогда на этом отрезке существуют точки xmin и xmax, в которых функция принимает минимальное и максимальное значения соответственно (точки глобального минимума и максимума).

Доказательство. Поскольку функция f непрерывна на отрезке, она ограничена на этом отрезке (см. теорему 1 из лекции 14). Значит у множества значений функции есть точная верхняя и точная нижняя грани. Обозначим их через M и m:

M:=sup{f(x)∣x∈[a,b]},m:=inf{f(x)∣x∈[a,b]}.

M:=sup{f(x)∣x∈[a,b]},m:=inf{f(x)∣x∈[a,b]}.

Докажем, что эти верхние грани достигаются, то есть найдутся такие точки xmin и xmax, что f(xmin)=m и f(xmax)=M. Доказательство будет очень похожим на то, как доказывалась теорема об ограниченности непрерывной функции, упомянутая выше.

Поскольку M является точной верхней гранью, для всякого ε>0 найдётся такой x=x(ε)∈[a,b], что f(x)>M−ε. Действительно, если бы это было не так, то существовал бы такой ε>0, что для всех x∈[a,b] выполнялась оценка f(x)<M−ε, то есть число (M−ε) было бы верхней гранью для множества значений функции f, причём меньшей, чем M. Это противоречило бы предположению, что M — точная верхняя грань.

Построим последовательность {xn} следующим образом. Для всех натуральных n положим εn=1/n и пусть

xn=x(εn)=x(1n).

Тогда для всех натуральных n

M≥f(xn)>M−1n.

По теореме о двух милиционерах, f(xn)→M при n→∞.

Все xn∈[a,b] и следовательно последовательность {xn} ограничена. Пользуясь теоремой Больцано — Вейерштрасса, выберем сходящуюся подпоследовательность {xnk}. Пусть xnk→x∞. Поскольку для всех n, a≤xn≤b, по теореме о предельном переходе в неравенствах, a≤x∞≤b. Рассмотрим последовательность {f(xnk)}. Она является подпоследовательностью последовательности {f(xn)} и следовательно имеет тот же предел, то есть сходится к M.

В силу непрерывности функции f в точке x∞, её предел в этой точке существует и равен её значению в этой точке. По определению предела по Гейне,

f(xnk)→limx→x∞f(x)=f(x∞).

Но мы знаем, что f(xnk)→M. Следовательно, f(x∞)=M. Положим xmax:=x∞.

Точка минимума xmin находится аналогично.∎

Пример 1. Как обычно, условие непрерывности в теореме очень важно. Например, рассмотрим такую функцию:

f(x)={x,x∈[0,1)1/2,x=1.

Она не является непрерывной и не достигает своего максимума: для любой точки x на полуинтервале [0,1) всегда есть точка правее (например, (x+1)/2), значение в которой больше, а для точки x=1 есть точка левее (например, x=3/4), значение в которой больше 1/2.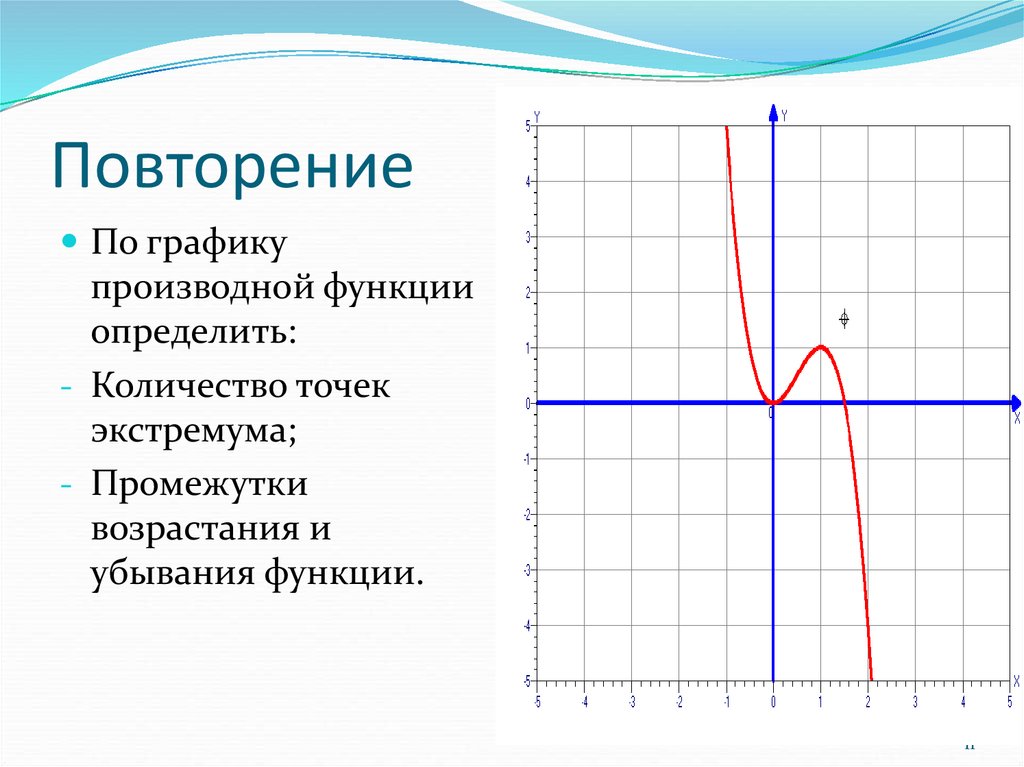

17.2.2Теоремы Ролля и Лагранжа

Теорема 3. (Теорема Ролля) Пусть функция f непрерывна на [a,b] и имеет производную на (a,b). Пусть f(a)=f(b). Тогда существует такая точка c∈(a,b), что f′(c)=0, см. рис. 17.4.

Рис. 17.4: Иллюстрация к теореме Ролля. Точка c с нулевой производной обязательно существует, но не обязательно единственна — на этой картинке есть две подходящие точки.

Доказательство. Поскольку функцию f непрерывна на [a,b], по только что доказанной теореме 2, она достигает своего максимума и минимума в каких-то точках xmax и xmin. Если хотя бы одна из этих точек принадлежит интервалу (a,b), в ней выполняются все условия леммы Ферма и значит производная в ней равна нулю — эту точку мы и возьмём за c. Остаётся разобрать случай когда обе точки xmax и xmin находятся на концах отрезка. Но значения на концах отрезка совпадают, и значит f(xmax)=f(xmin), то есть наибольшее значение функции равно её наименьшему значению. Такое может быть только если функция является константой: для всех x∈[a,b], f(x)=M=m.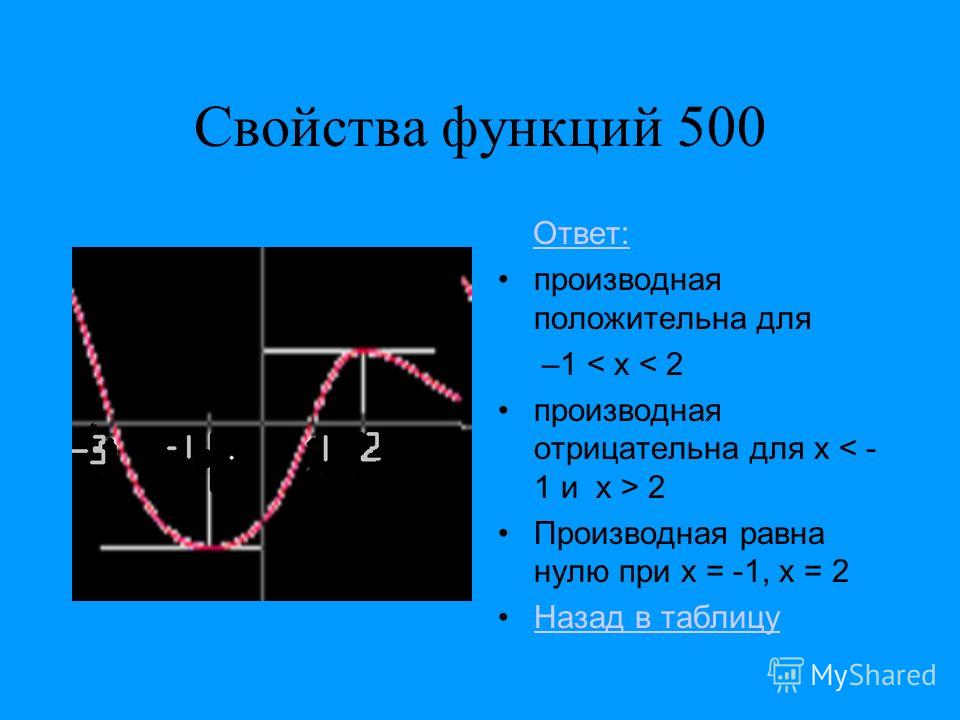

Но константа имеет нулевую производную во всех точках. Значит, возьмём в качестве c любую точку интервала (a,b) — например, его середину c=(a+b)/2.∎

Теорема 4. (Теорема Лагранжа о конечных приращениях) Пусть f непрерывна на отрезке [a,b] и дифференцируема на интервале (a,b). Тогда существует такая точка c∈(a,b), что

f′(c)=f(b)−f(a)b−a.(17.2)

Иными словами, на интервале (a,b) найдётся такая точка, что касательная к графику функции, проведённая в этой точке, параллельна секущей, проходящей через точки (a,f(a)) и (b,f(b)), см. рис. 17.5.

Рис. 17.5: Иллюстрация к теореме Лагранжа

Можно привести такую механическую интерпретацию: пусть мы стартовали в момент времени a и закончили движение в момент b. Правая часть равенства (17.2) — это средняя скорость. Из теоремы Лагранжа следует, что найдётся какой-то момент времени, в который мгновенная скорость будет равна этой средней. Это логично: не может быть такого, чтобы на протяжении всего пути скорость была бы больше средней (какая же она тогда средняя?), равно как и меньше.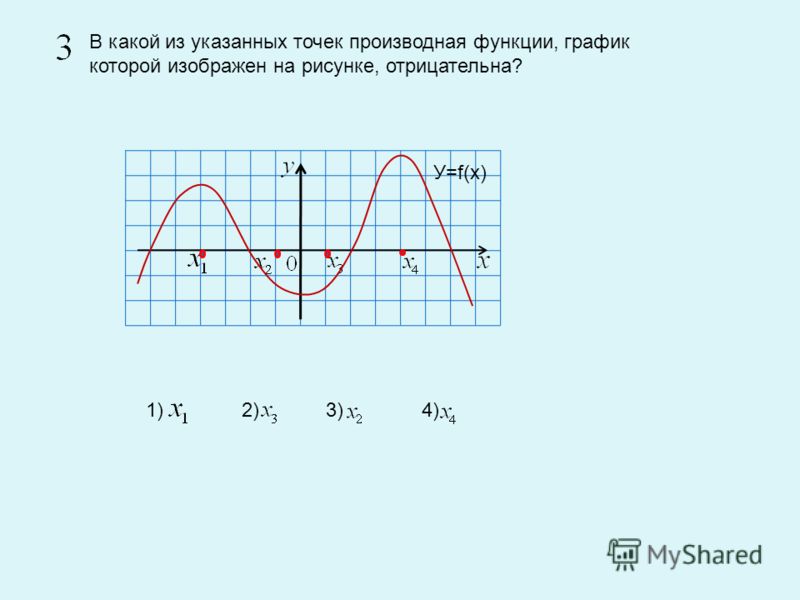

Доказательство. Заметим, что если наклонить рисунок 17.5, так, чтобы секущая стала горизонтальной, касательная тоже станет горизонтальной и получится что-то очень похожее на рисунок 17.4. И это — не совпадение, а ключевая идея доказательства. Правда, буквально наклонить (то есть повернуть) не получится: если график повернуть, он может перестать быть графиком функции. Поэтому мы применим другую операцию — не повернём график, а «скосим» его.

Рассмотрим функцию

h(x)=(x−a)f(b)−f(a)b−a.

Это линейная функция, h(a)=0 и её угловой коэффициент равен угловому коэффициенту секущей. Её график — прямая, проходящая через точку (a,0) параллельно секущей, см. рис. 17.6.

Рис. 17.6: Построение функции g(x)=f(x)−h(x).

Теперь рассмотрим функцию

g(x):=f(x)−h(x)=f(x)−(x−a)f(b)−f(a)b−a.

g(x):=f(x)−h(x)=f(x)−(x−a)f(b)−f(a)b−a.

Эта функция показывает, насколько график y=f(x) проходит выше графика y=h(x).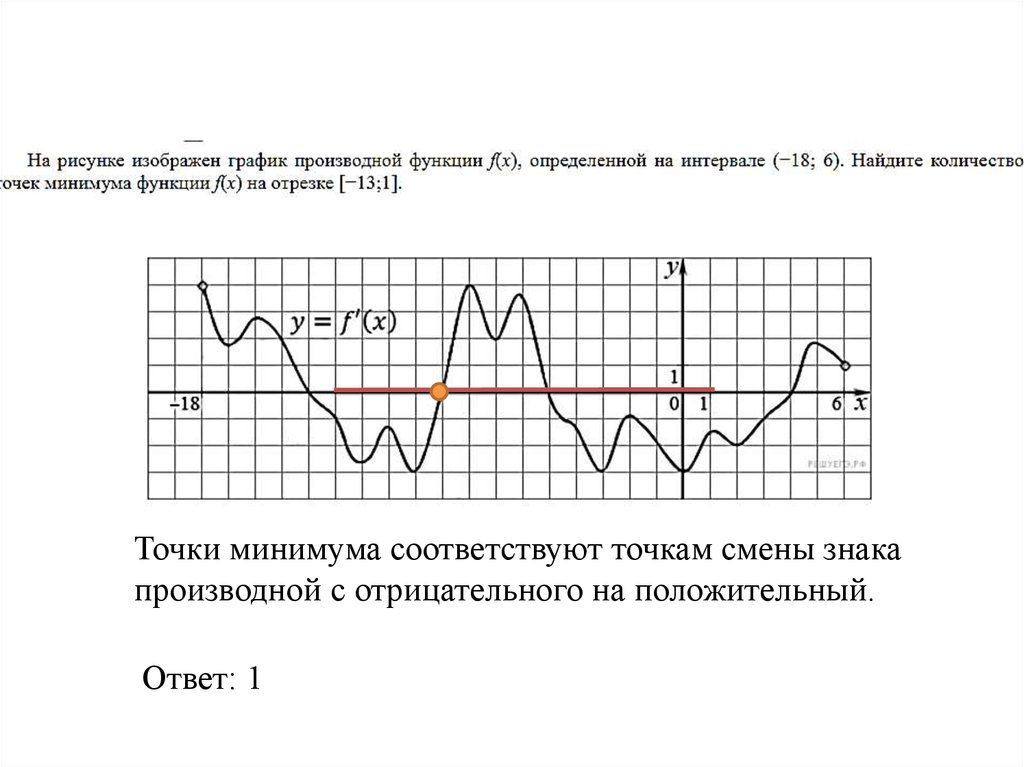 Таким образом, её график выглядит как скошенная версия графика y=f(x).

Заметим, что g(a)=f(a) и g(b)=f(a). Эта функция непрерывна на отрезке [a,b] и дифференцируема на интервале (a,b). Значит, к функции g можно применить теорему Ролля и найдётся такая точка c∈(a,b), что g′(c)=0. Запишем производную:

g′(x)=f′(x)−f(b)−f(a)b−a.

Значит в точке x=c:

0=g′(c)=f′(c)−f(b)−f(a)b−a.

∎

17.2.3Применение теоремы Лагранжа

Теперь мы готовы доказывать утверждения о связи производной и монотонности функций.

Утверждение 1. Пусть функция f непрерывна на отрезке [a,b] и дифференцируема во всех точках интервала (a,b). Пусть также для всех x∈(a,b) выполняется неравенство f′(x)>0. Тогда функция f строго возрастает на отрезке [a,b].

Доказательство. Рассмотрим две произвольные точки x1 и x2 из отрезка [a,b], и пусть x2>x1. Применим теорему Лагранжа к отрезку [x1,x2]. Получим точку c∈[x1,x2], для которой верно равенство (см. (17.3)):

f(x2)=f(x1)+f′(c)(x2−x1).

По условию, f′(c)>0 (потому что c∈(x1,x2)⊂(a,b) и во всех точках интервала (a,b) производная положительна) и по предположению x2−x1>0. Значит, f(x2)>f(x1). Поскольку это утверждение справедливо для всех x1,x2∈[a,b], x2>x1, функция строго возрастает на этом отрезке.∎

Вопрос 2. Верно ли обратное? Правда ли, что если функция строго возрастает на отрезке, то её производная положительна внутри этого отрезка?

  Верно, это следует из теоремы Лагранжа.

Неверный ответ. А как насчёт функции f(x)=x3?

  Неверно, есть контрпример.

Верный ответ. Ага! Например, f(x)=x3, f′(0)=0, хотя функция всюду строго возрастает.

Аналогично с помощью теоремы Лагранжа можно доказывать разные другие утверждение про монотонность функции и производные, вы потренируетесь это делать на семинаре.

17.3Заключение

Значение производной в какой-то точке описывает локальное поведение функции в этой точке. Переход от локальных свойств к глобальным не всегда является простым, и здесь легко ошибиться, как показывает замечание 2. Как правило для доказательства глобальных утвержедний пригождается теорема Лагранжа. Мы вернёмся к ней очень скоро — когда будем обсуждать понятие выпуклости.

---

← Предыдущая глава Следующая глава →

Производные и графики – Неформальное исчисление

35 Производные и графики

Как мы видели, одна из наиболее важных связей между функцией и ее производной заключается в том, что положительная производная означает, что величина возрастает, а отрицательная производная означает количество уменьшается.

Возрастание и убывание

• Наружная температура имеет положительную производную от 3:00 до 15:00 и отрицательную производную от 15:00 до 3:00. Нарисуйте график этого и обозначьте каждую часть графика как «возрастающую» или «убывающую».

  При положительной производной с 3:00 до 15:00 это значение должно повышаться и обозначаться как «возрастающее». С 15:00 до 3:00 график идет вниз и помечен как «убывающий».

На границе между увеличением и уменьшением, в 3 часа дня, температура самая высокая. Это ключ к одному из самых полезных приложений исчисления: оптимизации! Оптимизация — это либо определение того, когда количество максимально или максимально возможно, либо определение того, когда количество минимизировано или минимально возможно. Часто это происходит на границе возрастания и убывания, то есть там, где функция переходит от положительной производной к отрицательной. Следовательно, одна из важнейших максим исчисления: 9Оптимизация 0005 происходит, когда производная равна нулю! Мы вернемся к этому в следующем разделе.

А пока, используя представление о положительной, отрицательной или нулевой производной, мы можем нарисовать грубый набросок производной на основе графика функции.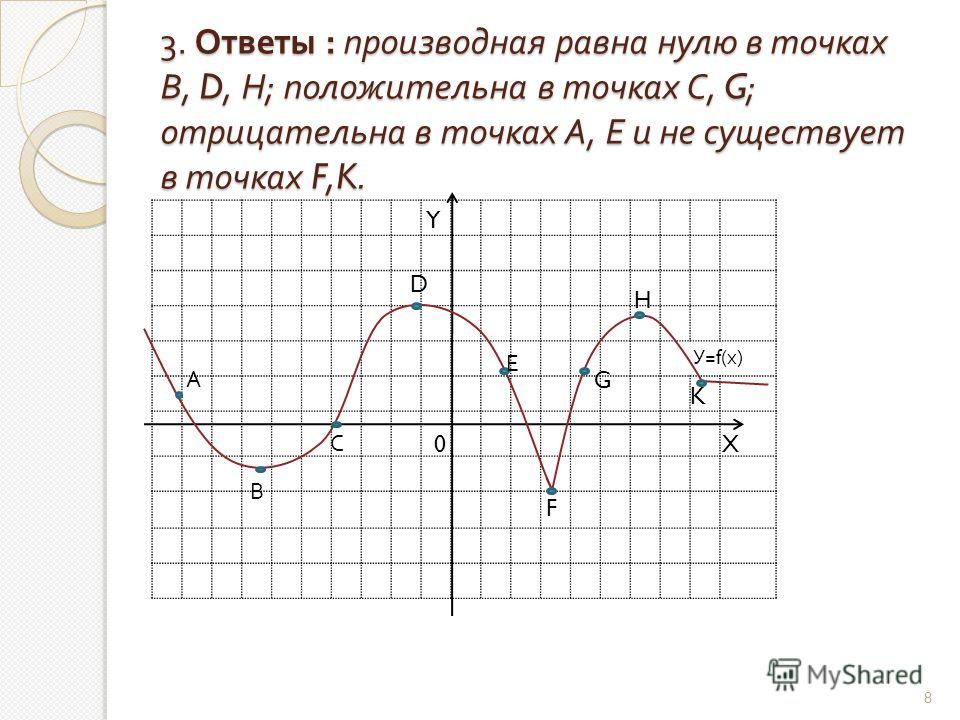 Рассмотрим пример.

Набросок производной

Нарисуйте производную следующей функции.

При наброске производной помните об этой идее: наклонов становятся [латексными]y[/латексными] значениями . Во-первых, давайте отметим, где производная равна нулю:

Это места, которые на графике производной имеют нулевое значение [latex]y[/latex]-значения. Это означает, что это [latex]x[/latex]-перехваты!

Теперь отметим, где производная положительная, а где отрицательная.

Наконец, мы можем использовать это как грубое руководство для скетча, опять же помня, что наклон становится [латекс]y[/латекс]-значениями. Здесь производная выделена черным цветом, а исходная функция — серым.

Давайте посмотрим на другой пример.

Эскиз производной 2

Эскиз производной

В этом случае график всегда идет вниз, поэтому производная всегда отрицательна. На самом деле это мало что говорит вам о том, как выглядит производный граф. Однако здесь есть особая точка, называемая точкой перегиба :

Это не точка, где наклон равен нулю, а место, где наклон ближе всего к нулю. В остальных местах наклон более отрицательный, чем в точке перегиба. Таким образом, на графике производной это становится максимальной или наивысшей точкой, например:

Пока эта точка перегиба является самой высокой точкой (но все еще имеет отрицательное значение [latex]y[/latex] из-за отрицательного наклона исходного графика), это лучшее, что вы можете сделать с этим.

License

Informal Calculus by Tyler Seacrest распространяется под лицензией Creative Commons Attribution 4.0 International License, если не указано иное.

Поделиться этой книгой

Поделиться в Twitter

Понимание того, когда производная функции положительна или отрицательна: обзор и примеры

Понятие производных является одним из наиболее важных понятий в исчислении и может использоваться для определения скорости изменения функции.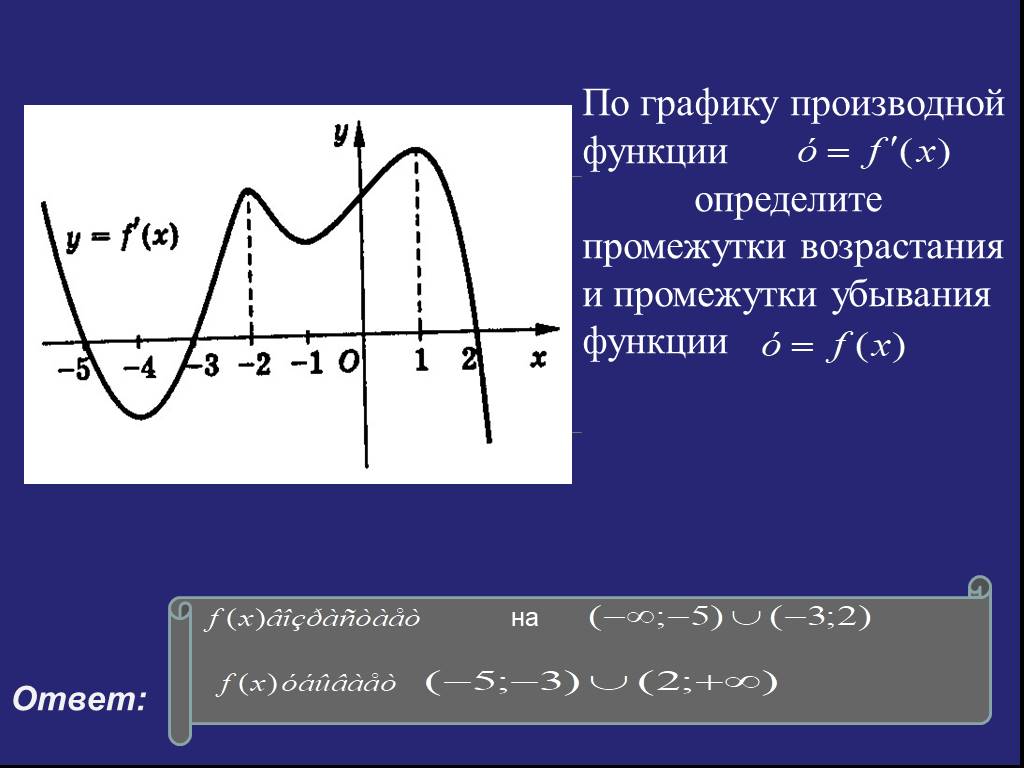 В частности, производная функции говорит нам, когда ее значение увеличивается или уменьшается. Таким образом, понимание того, когда производная функции будет положительной или отрицательной, является ключом к освоению исчисления. В этой статье будет представлен обзор условий, определяющих, является ли производная функции положительной или отрицательной, а также несколько примеров, иллюстрирующих концепцию. Обладая этими знаниями, вы будете лучше подготовлены к решению 9 задач.0075 математических задач с уверенностью.

Если функция имеет отрицательную производную, она всегда является возрастающей. В случае этой функции мы можем найти действительный ответ на графике, который мы создаем. Производная функции с всегда отрицательным значением всегда равна f(x). Чтобы получить формулу для * x f(x), умножьте *x f(x) на *x f(x).

Ранее мы видели, что одной из наиболее важных связей между функцией и ее производной является отношение между количеством элемента и производной.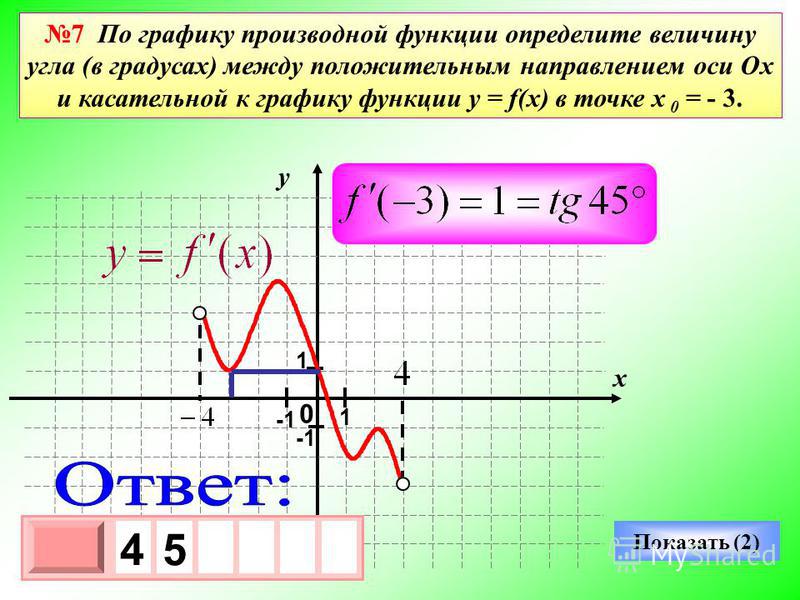

Производная в этой точке говорит вам, является ли кривая вогнутой или вогнутой вверх. Положительная вторая производная указывает на то, что график движется вверх, когда вторая производная присутствует в точке. Поскольку вторая производная отрицательна, график вогнутый.

Производная по направлению — это изменение в этом направлении, которое может быть положительным, отрицательным или нулевым. Другими словами, если функция убывает в этом направлении или возрастает в этом направлении, производная становится отрицательной.

Для какой функции производная всегда положительна?

Источник: google

Производная любой функции всегда положительна, если функция возрастает. Это означает, что функция увеличивается быстрее, чем выходное значение. Когда производная положительна, говорят, что функция вогнута. Примерами функций, имеющих положительную производную, являются экспоненциальные функции, многочлены и тригонометрические функции .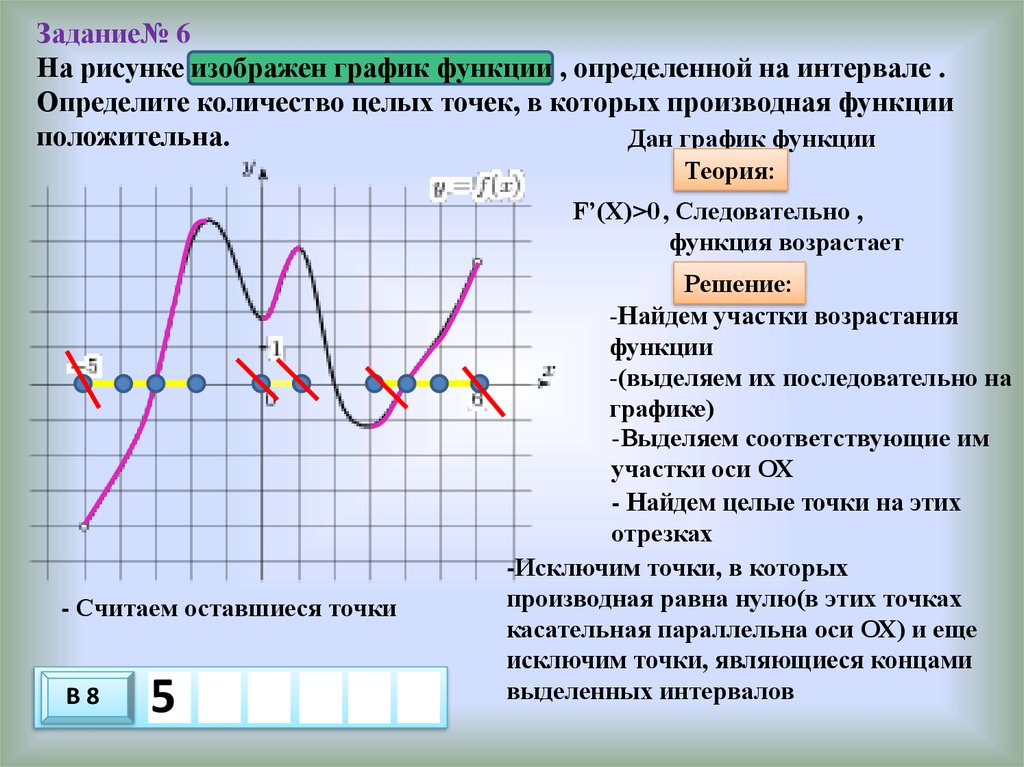 Другими словами, производная любой возрастающей функции всегда положительна.

Какая функция имеет производную, которая всегда отрицательна?

Источник: z-dn

Функция, производная которой всегда отрицательна, называется строго убывающей функцией. Это означает, что выход функции уменьшается по мере увеличения ее входа. Такие функции важны во многих областях математики и естественных наук, включая экономику и инженерию. Например, спрос на продукт уменьшается по мере роста его цены, а это означает, что функция спроса имеет производную, которая всегда отрицательна. Точно так же в технике сила, действующая на мост, уменьшается по мере увеличения его нагрузки, а это означает, что 9Силовая функция 0075 имеет производную, которая всегда отрицательна.

Что означает отрицательная вторая производная? Это означает, что по мере того, как вход функции

увеличивается на , выход уменьшается быстрее, чем раньше. Другими словами, скорость изменения выпуска отрицательна, что говорит о том, что выпуск уменьшается. Это видно на графике функции, где кривая имеет наклон вниз.

Если производная положительна, то функция возрастает

Источник: mathwarehouse

Если производная функции положительна, то функция возрастает. Это означает, что по мере увеличения входной переменной выходная переменная также увеличивается. Другими словами, наклон функции всегда положителен. Это связано с тем, что производная представляет собой скорость изменения функции, и если скорость положительна, то функция возрастает. Таким образом, если производная положительна, то функция возрастает.

Производная функции — важный инструмент для определения того, как ее поведение меняется с каждым интервалом. Когда производная интервала положительна, функция движется вверх, когда производная отрицательна, функция движется вниз, а когда производная равна нулю, она остается постоянной. Производная функции говорит нам, как быстро функция изменяет . Функция возрастает по мере роста ее производной, что указывает на то, что функция растет быстрее при изменении x.