Равнобедренный прямоугольный треугольник – площадь, длина основания, свойства
4.1
Средняя оценка: 4.1
Всего получено оценок: 73.
4.1
Средняя оценка: 4.1
Всего получено оценок: 73.
И равнобедренный, и прямоугольный треугольник достаточно привычны любому, кто знаком с геометрией. Сочетание этих признаков встречается довольно редко и плохо поддается визуальному восприятию. Не всегда можно представить полный набор свойств такого треугольника, поэтому поговорим о нем более подробно.
Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.
Опыт работы учителем математики — более 33 лет.
Определение
Равнобедренный треугольник – это треугольник, боковые стороны которого равны. Прямоугольный треугольник содержит в себе прямой угол. Значит равнобедренный прямоугольный треугольник – это прямоугольный треугольник, катеты которого равны.
Гипотенуза прямоугольного треугольника всегда больше катета. Это следует из теоремы о соотношениях сторон и углов треугольника. Значит, в прямоугольном треугольнике только гипотенуза может быть основанием, а величина гипотенузы будет соответствовать длине основания.
Это следует из теоремы о соотношениях сторон и углов треугольника. Значит, в прямоугольном треугольнике только гипотенуза может быть основанием, а величина гипотенузы будет соответствовать длине основания.
Свойства
Поговорим подробнее о свойствах и формулах. Не совсем ясно, как будут проходить высоты в таком треугольнике, все привыкли пользоваться свойством, которое говорит о том, что в равнобедренном треугольнике высота, проведенная к основанию, совпадает с медианой и биссектрисой.
В равнобедренном прямоугольном треугольнике такая высота всегда будет направлена из прямого угла к гипотенузе. А две другие высоты будут совпадать с катетами.
Рис. 2. Высота прямоугольного равнобедренного треугольникаТеорема Пифагора для равнобедренного треугольника выглядит немного упрощенной:
Квадрат гипотенузы равен удвоенному квадрату катета.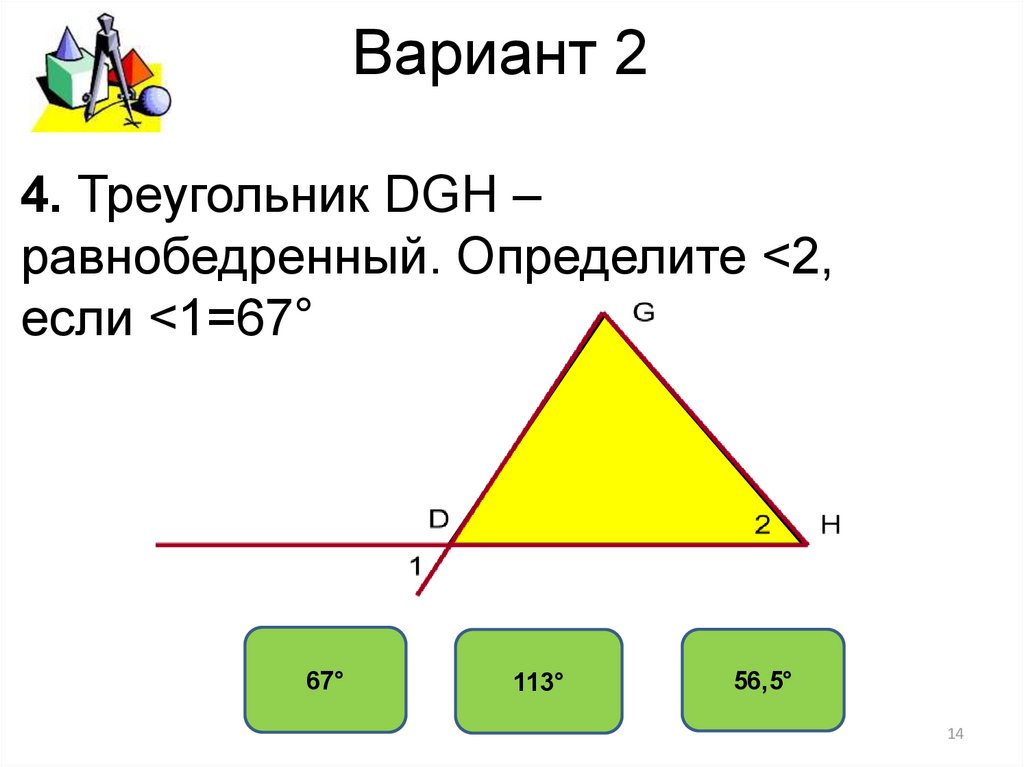 Это значительно упрощает решение.
Это значительно упрощает решение.
Вообще, любые задачи, связанные с прямоугольными равнобедренными треугольниками, решаются очень просто. Любого значения достаточно, чтобы определить все остальное. Значения любого из катетов достаточно, чтобы определить гипотенузу через упрощенную теорему Пифагора, а затем найти периметр и площадь прямоугольного равнобедренного треугольника.
Через гипотенузу можно найти катет и через тригонометрическую функцию, так как все углы прямоугольного равнобедренного треугольника заранее известны: один угол 90 градусов и два по 45.
Рис. 3. Углы прямоугольного равнобедренного треугольникаРазберем подробно, почему известны все углы. В любом прямоугольном треугольнике сумма острых углов равна 90 градусам. Это следует из общей суммы углов в треугольнике, которая всегда равна 180 градусам.
При этом углы при основании равнобедренного треугольника, а в нашем случае это всегда гипотенуза, всегда равны. Значит, чтобы найти каждый из острых углов при гипотенузе, нужно их сумму, т.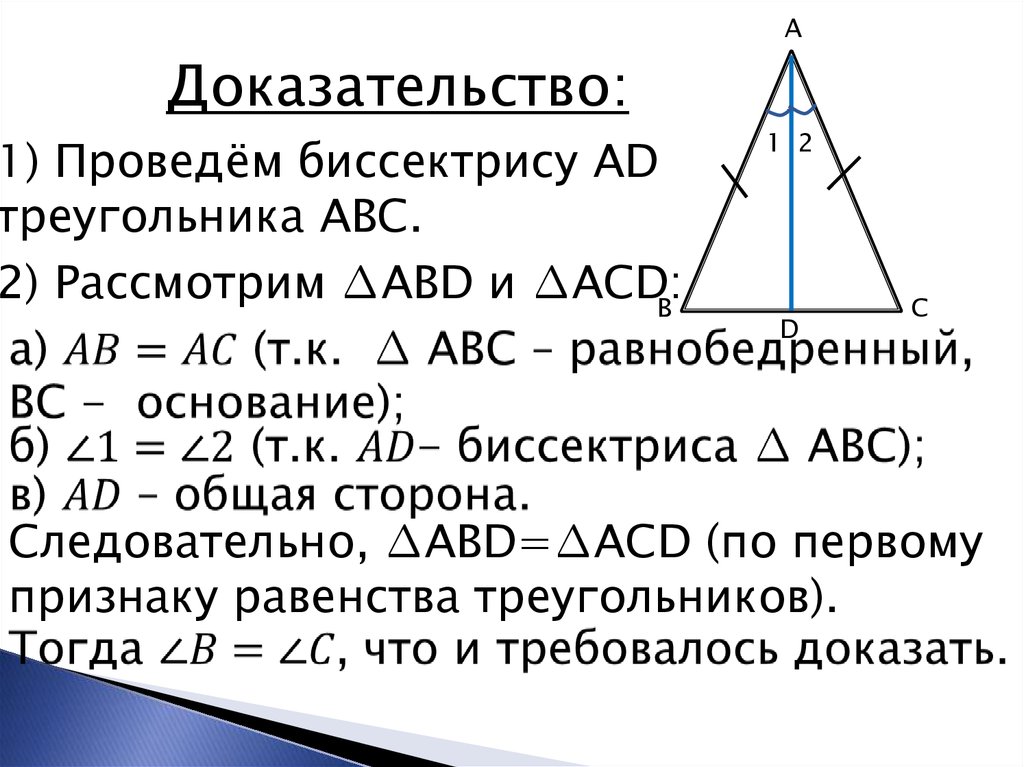
Можно рассмотреть это свойство и с другой стороны: если сумма двух углов треугольника равняется 90 градусам и эти углы равны между собой, то этот треугольник является равнобедренным и прямоугольным.
Из этого же свойства вытекает равенство синусов и косинусов острых углов прямоугольного равнобедренного треугольника между собой, а также равенство их тангенсов и котангенсов.
То есть, синус любого острого угла прямоугольного равнобедренного треугольника равен косинусу любого острого угла данного треугольника и равен $${\sqrt{2}\over2}$$. Тангенс любого острого угла прямоугольного равнобедренного треугольника равен котангенсу любого острого угла данного треугольника и равен 1.
Что мы узнали?
Мы подробно поговорили о всех взаимосвязях свойств прямоугольного и равнобедренного треугольника. А также о том, как эти связи проявляются в равнобедренном прямоугольном треугольнике.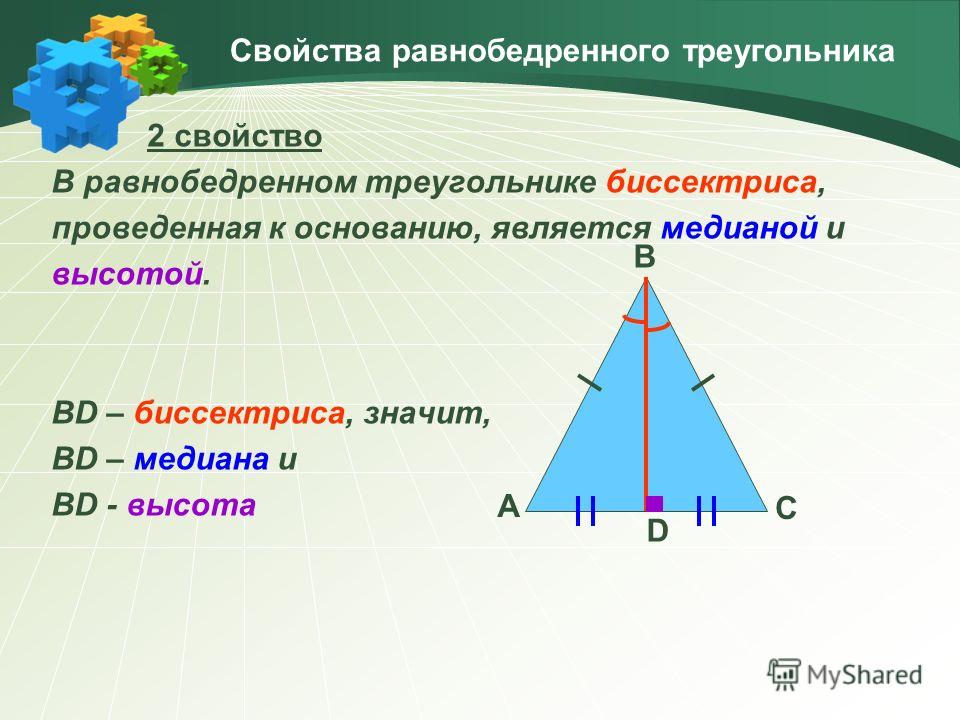 Разобрали в подробностях, почему любые задачи на нахождение параметров прямоугольного равнобедренного треугольника легко решаются и выделили основную и единственную проблему в решениях таких задач: трудность визуального восприятия.
Разобрали в подробностях, почему любые задачи на нахождение параметров прямоугольного равнобедренного треугольника легко решаются и выделили основную и единственную проблему в решениях таких задач: трудность визуального восприятия.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.1
Средняя оценка: 4.1
Всего получено оценок: 73.
А какая ваша оценка?
Гипотенуза равнобедренного прямоугольного треугольника Калькулятор
✖Катетами равнобедренного прямоугольного треугольника являются две равные стороны трех сторон равнобедренного прямоугольного треугольника, которые перпендикулярны друг другу.ⓘ Катеты равнобедренного прямоугольного треугольника [S | створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% |
|
✖Гипотенуза равнобедренного прямоугольного треугольника — это наибольшая сторона равнобедренного прямоугольного треугольника. |
створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр |
⎘ копия |
👎
Формула
сбросить
👍
Гипотенуза равнобедренного прямоугольного треугольника Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Преобразование входов в базовый блок
Катеты равнобедренного прямоугольного треугольника: 8 метр —> 8 метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
11.3137084989848 метр —> Конверсия не требуется
< 5 Гипотенуза равнобедренного прямоугольного треугольника Калькуляторы
Гипотенуза равнобедренного прямоугольного треугольника формула
Гипотенуза равнобедренного прямоугольного треугольника = sqrt(2)*Катеты равнобедренного прямоугольного треугольника
H = sqrt(2)*S
Что такое равнобедренный прямоугольный треугольник?
Равнобедренный прямоугольный треугольник — это прямоугольный треугольник, состоящий из двух ног равной длины. Таким образом, в равнобедренном прямоугольном треугольнике два катета и два острых угла совпадают. Поскольку это прямоугольный треугольник, угол между двумя ножками будет составлять 90 градусов, а ножки, очевидно, будут перпендикулярны друг другу.
Поскольку это прямоугольный треугольник, угол между двумя ножками будет составлять 90 градусов, а ножки, очевидно, будут перпендикулярны друг другу.
Share
Copied!
Равнобедренный треугольник — определение, углы, свойства, примеры
Что такое равнобедренный треугольник?
Треугольник с двумя сторонами равной длины является равнобедренным треугольником.
Примеры равнобедренного треугольника:
Неравнобедренный треугольник:
Примеры равнобедренного треугольника в реальной жизни:
Многие вещи в мире имеют форму равнобедренного треугольника. Некоторые популярные примеры этих треугольников в реальной жизни:
Родственные игры
Части равнобедренного треугольника
Части равнобедренного треугольника
1. Катеты: Две равные стороны равнобедренного треугольника называются катетами. В треугольнике ABC (данном выше) AB и AC являются двумя катетами равнобедренного треугольника.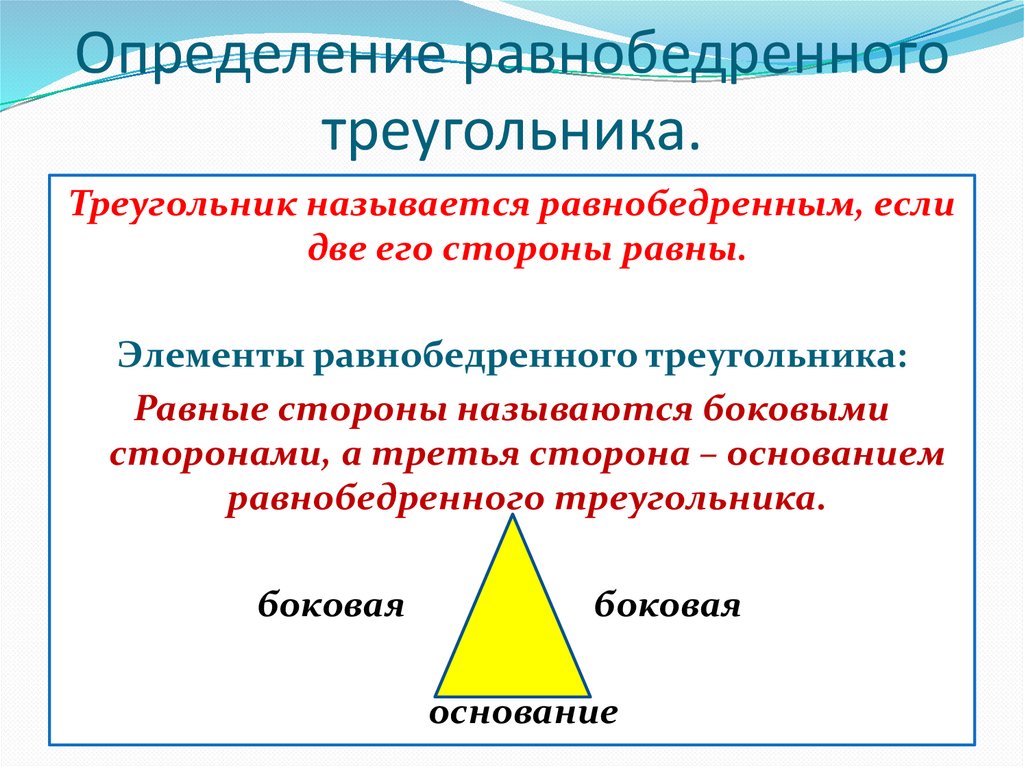
2. Основание: Основанием равнобедренного треугольника является третья и неравная сторона. В треугольнике АВС основание равнобедренного треугольника ВС.
3. Угол при вершине: «Угол при вершине» — это угол, образованный двумя равными сторонами равнобедренного треугольника. ∠BAC — угол при вершине равнобедренного треугольника.
4. Углы при основании: «Углы при основании» — это углы, которые опираются на основание равнобедренного треугольника. ∠ABC и ∠ACB — два угла при основании равнобедренного треугольника.
Похожие рабочие листы
Свойства равнобедренного треугольника
Вот список некоторых свойств равнобедренных треугольников:
- В равнобедренном треугольнике, если две стороны равны, то углы, противоположные двум сторонам, соответствуют друг другу и также всегда равны.
В приведенном выше равнобедренном треугольнике два угла ∠B и ∠C, лежащие напротив равных сторон AB и AC, равны друг другу.
- Равнобедренный треугольник имеет три острых угла, то есть углы меньше 90°.
- Сумма трех углов равнобедренного треугольника всегда равна 180°.
Типы равнобедренных треугольников
Как правило, равнобедренные треугольники подразделяются на три различных типа:
- Равнобедренный остроугольный треугольник: Равнобедренный остроугольный треугольник – это треугольник, в котором все три угла меньше 90°, и по крайней мере два его угла равны по измерению. Одним из примеров углов равнобедренного остроугольного треугольника являются 50 °, 50 ° и 80 °.
- Равнобедренный прямоугольный треугольник: Ниже приведен пример прямоугольного треугольника с двумя катетами (и соответствующими им углами) равной величины.
- Равнобедренный тупоугольный треугольник: Равнобедренный тупоугольный треугольник — это треугольник, в котором один из трех углов тупой (лежит между 90° и 180°), а два других острых угла равны по измерению.
 Один пример углов равнобедренного тупого треугольника составляет 30 °, 30 ° и 120 °.
Один пример углов равнобедренного тупого треугольника составляет 30 °, 30 ° и 120 °.
Площадь и периметр равнобедренного треугольника
- Площадь равнобедренного треугольника находится по следующей формуле:
Площадь (A) = ½ × основание (b) × высота (h)
- Периметр равнобедренного треугольника находится по формуле:
Периметр (P) = 2a + основание (b)
Здесь «a» относится к длине равных сторон равнобедренного треугольника, а «b» относится к длине третьей неравной стороны.
Решенные примеры
Пример 1
Какова высота равнобедренного треугольника с площадью 12 кв.см и основанием 6см?
Решение:
Площадь Isocles Triangle = ½ x основание x Высота
, т.е. 12 = ½ x 6 x Высота
, т.е. равен периметру равнобедренного треугольника, если равные стороны равны a см каждая, а неравная сторона равна b см?
Решение:
Периметр равнобедренного треугольника = сумма его сторон
Периметр равнобедренного треугольника = (a + a + b) см, т. е. (2a + b) см
е. (2a + b) см
Пример 3
Найти периметр равнобедренного треугольника, если основание равно 16 см, а равные стороны по 24 см каждая.
Решение:
Формула периметра равнобедренного треугольника, P = 2a + b
Здесь a (стороны) = 24 см и b (основание) = 16 см
Следовательно, периметр равнобедренного треугольника P = 2(24) + 16 = 64 см.
Следовательно, периметр равен 64 см.
Игры с треугольниками
С SplashLearn есть несколько игр о треугольниках, которые дети могут попробовать. Давайте рассмотрим некоторые из них:
- Определение типов треугольников : В этой игре ваш ребенок будет определять различные типы треугольников. Они будут использовать данные атрибуты, чтобы определить правильный треугольник и изучить характеристики треугольника. Учащиеся выбирают правильный ответ из предложенных.
- Classify Triangles : Игра предлагает вашему ребенку отточить свои навыки, решая ряд задач, связанных с двумерными фигурами, чтобы определить различные типы треугольников.
 Учащиеся будут анализировать стороны треугольника и измерения углов и классифицировать каждую из них в соответствующей категории.
Учащиеся будут анализировать стороны треугольника и измерения углов и классифицировать каждую из них в соответствующей категории.
Другие игры
- Классифицируй треугольники и прямоугольники как замкнутые фигуры : Эта игра поможет детям классифицировать различные типы фигур и поможет их запомнить. Это поможет вашему ребенку быстрее и легче распознавать различные формы.
- Сортировка фигур по имени : Это будет веселая игра, в конце которой ваш ребенок узнает все о различных формах! Игра включает в себя сортировку фигур по их именам, и таким образом ваш юный математик получит больше практики с концепциями 2D-форм. Эта игра подтолкнет вашего ребенка к мастерству, развивая при этом общие математические способности.
Ученикам также может быть сложно запомнить свойства равнобедренных треугольников. Но именно здесь вам потребуется много терпения при обучении вашего ребенка. Позвольте вашему ребенку сиять ярко с SplashLearn .
Позвольте вашему ребенку сиять ярко с SplashLearn .
Практические задачи на равнобедренные треугольники
1
Какова высота равнобедренного треугольника с площадью 10 кв. см и основанием 5 см?
10 см
5 см
2 см
4 см
Правильный ответ: 4 см т. е. высота = 4 см
2
В ΔABC, если ∠A = ∠B, то
AC ≠ BC
AC = BC
AB = AC
AB = BC
Правильный ответ: AC = BC
Стороны, противоположные равным углам, также равны. ∠A = ∠B, BC противоположен ∠A, а AC противоположен углу B. Следовательно, AC = BC в ΔABC.
3
Какова площадь равнобедренного треугольника, указанного ниже?
21 см 2
45 см 2
90 см 2
180 см 2
5
0196 2
Площадь равнобедренного треугольника = ½ x основание x высота = ½ x 15 см x 6 см = 45 см 2
Часто задаваемые вопросы
Как узнать, является ли треугольник равнобедренным?
Треугольник называется равнобедренным, если две его стороны равны.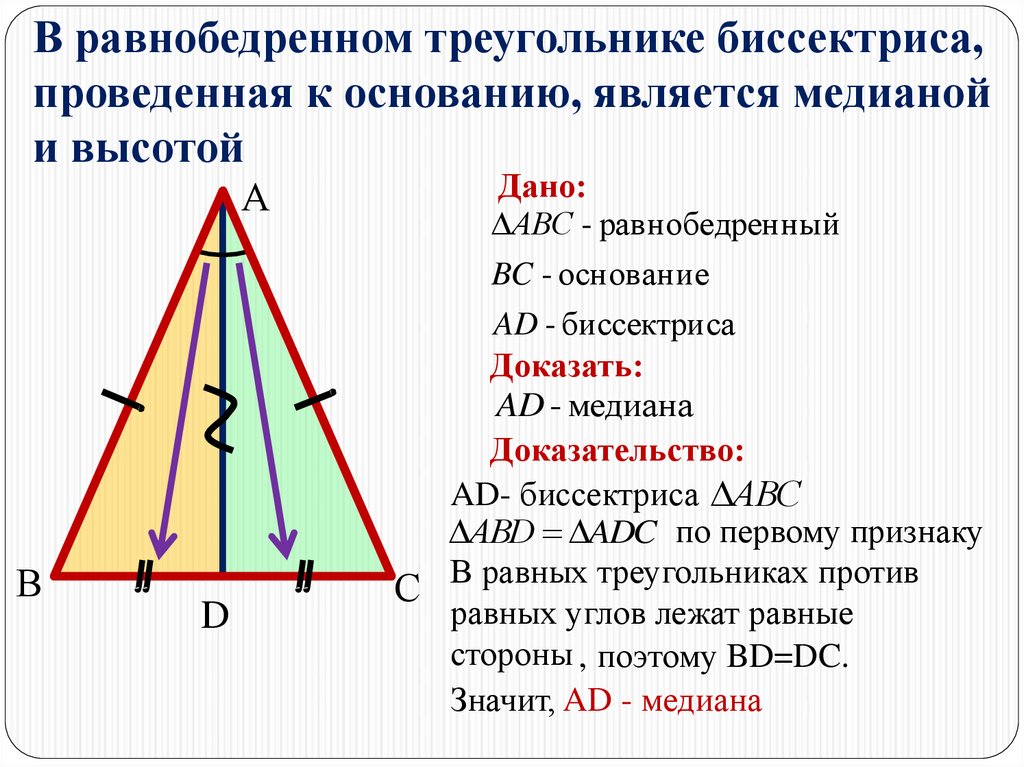 Возьмем треугольник, у которого три стороны АВ, ВС и СА. Если хоть одно из этих утверждений верно — AB = BC, BC = CA или CA = AB, — то треугольник равнобедренный.
Возьмем треугольник, у которого три стороны АВ, ВС и СА. Если хоть одно из этих утверждений верно — AB = BC, BC = CA или CA = AB, — то треугольник равнобедренный.
Может ли прямоугольный треугольник быть равнобедренным?
Да, прямоугольный или прямоугольный треугольник может быть равнобедренным. В равнобедренном прямоугольном треугольнике 1 прямой угол и 2 других угла равны.
Сможете ли вы найти все углы равнобедренного треугольника, если знаете один из равных углов?
Да, если мы знаем два равных угла, то мы можем легко вычесть их сумму из 180°, так как сумма всех углов треугольника равна 180°.
Какими свойствами обладает равнобедренный треугольник?
- Имеет две стороны одинаковой длины.
- Углы, противолежащие равным сторонам, также равны по размеру.
45/45/90 Прямоугольные равнобедренные треугольники — Математика для средней школы
Все ресурсы по математике для средней школы
8 Диагностические тесты 613 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Справка по математике для средней школы » Геометрия » Плоская геометрия » Треугольники » Равнобедренные треугольники » 45/45/90 Прямоугольные равнобедренные треугольники
В равнобедренном прямоугольном треугольнике две стороны равны .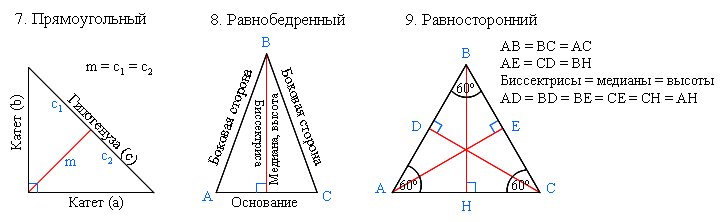 Найдите длину стороны.
Найдите длину стороны.
Возможные ответы:
Правильный ответ:
Пояснение:
Эта задача представляет собой определение длин сторон равнобедренного прямоугольного треугольника. По определению стороны равны , , и . Однако, если вы не помните это определение, то длину стороны также можно найти по теореме Пифагора .
Сообщить об ошибке
ABCD является квадратом, сторона которого равна единицам. Найдите длину диагонали AC.
Возможные ответы:
Ни один из других ответов
Правильный ответ:
Объяснение:
Чтобы найти длину диагонали по двум сторонам квадрата, мы можем составить из квадрата два равных треугольника.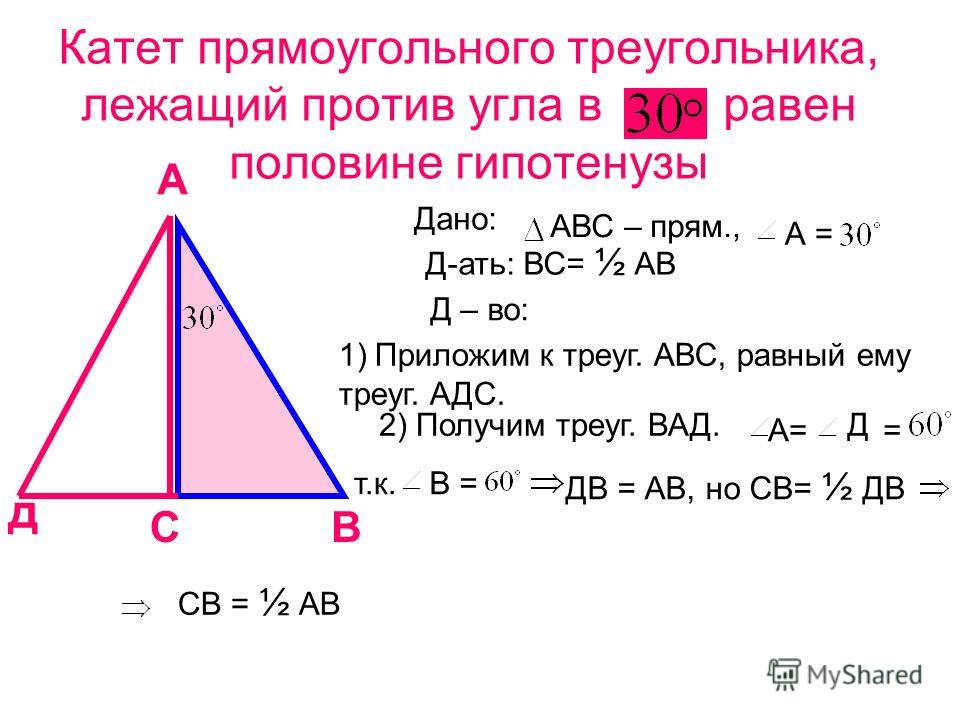 Диагональная линия делит прямые углы квадрата пополам, образуя два треугольника с углами , и градусов. Этот тип треугольника представляет собой особый прямоугольный треугольник, в котором соотношение между стороной, противоположной градусным углам, служит как x, а сторона, противоположная градусному углу, служит как .
Диагональная линия делит прямые углы квадрата пополам, образуя два треугольника с углами , и градусов. Этот тип треугольника представляет собой особый прямоугольный треугольник, в котором соотношение между стороной, противоположной градусным углам, служит как x, а сторона, противоположная градусному углу, служит как .
Применяя это, если мы подставим для , то получим, что сторона, противоположная прямому углу (она же диагональ), равна
Сообщить об ошибке
Площадь квадрата равна . Найдите длину диагонали квадрата.
Возможные ответы:
Правильный ответ:
Объяснение:
Если площадь квадрата равна , мы знаем, что каждая сторона квадрата равна , потому что площадь квадрата равна .
Затем диагональ образует два особых прямоугольных треугольника. Зная, что стороны = , мы можем найти, что гипотенуза (она же диагональ) равна
Сообщить об ошибке
Гипотенуза равнобедренного прямоугольного треугольника равна . Найдите его площадь.
Найдите его площадь.
Возможные ответы:
Недостаточно информации для решения
Правильный ответ:3 908045
Объяснение:
Чтобы вычислить площадь треугольника, нам нужно найти длины его катетов. Равнобедренный треугольник является особым треугольником из-за значений его углов. Эти треугольники называются треугольниками, и длины их сторон соответствуют определенной схеме, которая гласит, что можно рассчитать длину катетов равнобедренного треугольника, разделив длину гипотенузы на квадратный корень из 2.
Теперь мы можем вычислить площадь по формуле
Теперь переведем в футы.
Сообщить об ошибке
Основание прямоугольного равнобедренного треугольника равно 8 дюймам. Гипотенуза не основание. Чему равна площадь треугольника в дюймах?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти площадь треугольника, умножьте основание на высоту, а затем разделите на 2. Поскольку короткие катеты равнобедренного треугольника имеют одинаковую длину, нам нужно знать только один из них, чтобы узнать другой. Поскольку короткая сторона служит основанием треугольника, другая короткая сторона говорит нам о высоте.
Поскольку короткие катеты равнобедренного треугольника имеют одинаковую длину, нам нужно знать только один из них, чтобы узнать другой. Поскольку короткая сторона служит основанием треугольника, другая короткая сторона говорит нам о высоте.
Сообщить об ошибке
Гипотенуза равнобедренного прямоугольного треугольника имеет меру . Найдите его периметр.
Возможные ответы:
Недостаточно информации для решения Пояснение:
Чтобы вычислить периметр треугольника, нам нужно найти длины его катетов. Равнобедренный треугольник является особым треугольником из-за значений его углов. Эти треугольники называются треугольниками, и длины их сторон соответствуют определенному шаблону, который гласит, что можно рассчитать длину катетов равнобедренного треугольника, разделив длину гипотенузы на квадратный корень из 2.
Теперь мы можем вычислить периметр, удвоив и прибавив .
Сообщить об ошибке
Длины сторон равнобедренного прямоугольного треугольника . Найдите его периметр.
Возможные ответы:
Недостаточно информации для решения0182 Пояснение:
Равнобедренный треугольник является особым треугольником из-за значений его углов. Эти треугольники называются треугольниками, а длины их сторон следуют определенной схеме, которая гласит, что вы можете рассчитать длину гипотенузы равнобедренного треугольника, умножив длину одного из катетов на квадратный корень из 2.
Теперь мы можем вычислить периметр, удвоив и добавив .
Сообщить об ошибке
У треугольника два угла равны , а две стороны равны . Чему равен периметр этого треугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
Если треугольник имеет два угла, равных , это должен быть равнобедренный прямоугольный треугольник.
Выкройка сторон а.
Поскольку две стороны равны , этот треугольник будет иметь стороны .
Сложите их все вместе, чтобы получить .
Сообщить об ошибке
Равнобедренный треугольник имеет основание 6 и высоту 4. Чему равен периметр треугольника?
Возможные ответы:
Ни один из этих
Правильный ответ: 100045
Равнобедренный треугольник — это два склеенных прямоугольных треугольника. Равнобедренный треугольник имеет основание, равное 6, а это означает, что длина от середины основания до одного из углов равна 3. Теперь у вас есть прямоугольный треугольник с основанием, равным 3, и высотой, равной 4. Гипотенуза этот прямоугольный треугольник, который является одной из двух конгруэнтных сторон равнобедренного треугольника, имеет длину 5 единиц (согласно теореме Пифагора).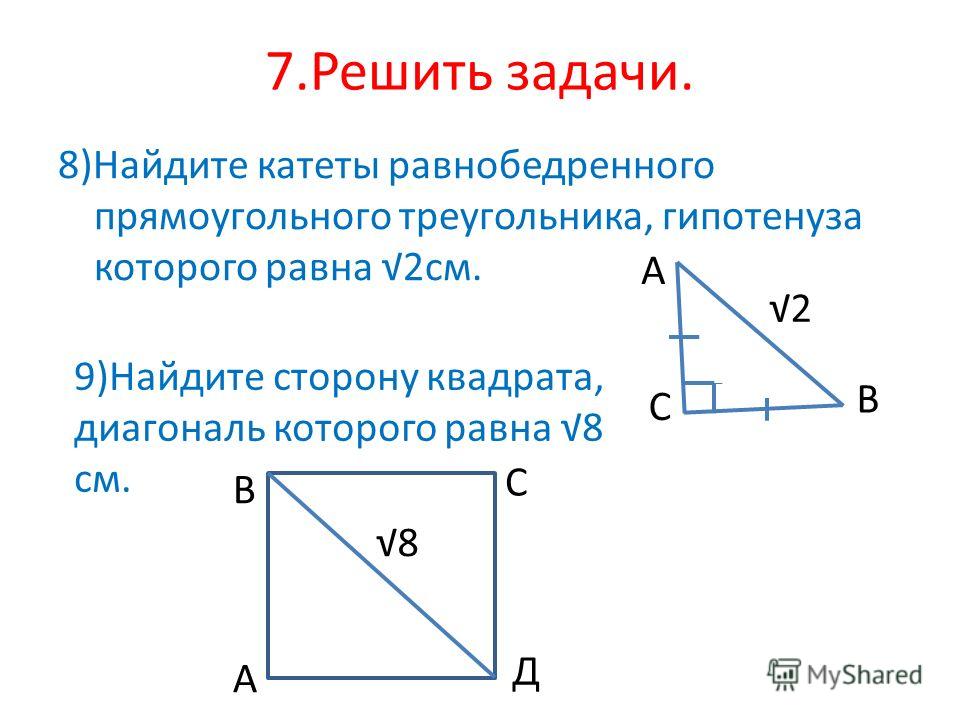

 Один пример углов равнобедренного тупого треугольника составляет 30 °, 30 ° и 120 °.
Один пример углов равнобедренного тупого треугольника составляет 30 °, 30 ° и 120 °. Учащиеся будут анализировать стороны треугольника и измерения углов и классифицировать каждую из них в соответствующей категории.
Учащиеся будут анализировать стороны треугольника и измерения углов и классифицировать каждую из них в соответствующей категории.
Leave A Comment